| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 9 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201117457 | |
| Published online | 26 August 2011 | |
Measuring space-time variation of the fundamental constants with redshifted submillimetre transitions of neutral carbon
1
School of Physics, University of New South Wales,
Sydney
NSW
2052,
Australia
e-mail: sjc@phys.unsw.edu.au
2
Smithsonian Astrophysical Observatory,
60 Garden Street, Cambridge
MA
02138,
USA
Received: 10 June 2011
Accepted: 29 July 2011
We compare the redshifts of neutral carbon and carbon monoxide in the redshifted sources in which the 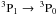 fine structure transition of neutral carbon, [C i], has been detected, in order to measure space-time variation of the fundamental constants. Comparison with the CO rotational lines measures F ≡ α2/μ, where α is the fine structure constant and μ is the electron-proton mass ratio, which is the same combination of constants obtained from the comparison
fine structure transition of neutral carbon, [C i], has been detected, in order to measure space-time variation of the fundamental constants. Comparison with the CO rotational lines measures F ≡ α2/μ, where α is the fine structure constant and μ is the electron-proton mass ratio, which is the same combination of constants obtained from the comparison 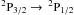 fine structure line of singly ionised carbon, [C ii]. However, neutral carbon has the distinct advantage that it may be spatially coincident with the carbon monoxide, whereas [C ii] could be located in the diffuse medium between molecular clouds, and so any comparison with CO could be dominated by intrinsic velocity differences. Using [C i], we obtain a mean variation of ⟨ ΔF/F ⟩ = (−3.6 ± 8.5) × 10-5, over z = 2.3−4.1, for the eight [C i] systems, which degrades to (−1.5 ± 11) × 10-5, over z = 2.3−6.4 when the two [C ii] systems are included. That is, zero variation over look-back times of 10.8−12.8 Gyr. However, the latest optical results indicate a spatial variation in α, where Δα/α describes a dipole and we see the same direction in ΔF/F. This trend is, however, due to a single source for which the [C i] spectrum is of poor quality. This also applies to one of the two [C ii] spectra previously used to find a zero variation in α2/μ. Quantifying this, we find an anti-correlation between |ΔF/F| and the quality of the carbon detection, as measured by the spectral resolution, indicating that the typical values of ≳50 km s-1, used to obtain a detection, are too coarse to reliably measure changes in the constants. From the fluxes of the known z ≳ 1 CO systems, we predict that current instruments are incapable of the sensitivities required to measure changes in the constants through the comparison of CO and carbon lines. We therefore discuss in detail the use of ALMA for such an undertaking and find that, based upon the current CO detections only, the Full Array configuration is expected to detect ~100 galaxies in [C i] at better than 10 km s-1 spectral resolution, while potentially resolving the individual molecular cloud complexes at redshifts of z ≳ 3. This could provide ≳1000 individual systems with which to obtain accurate measurements of space-time variation of the constants at look-back times in excess of 11 Gyr.
fine structure line of singly ionised carbon, [C ii]. However, neutral carbon has the distinct advantage that it may be spatially coincident with the carbon monoxide, whereas [C ii] could be located in the diffuse medium between molecular clouds, and so any comparison with CO could be dominated by intrinsic velocity differences. Using [C i], we obtain a mean variation of ⟨ ΔF/F ⟩ = (−3.6 ± 8.5) × 10-5, over z = 2.3−4.1, for the eight [C i] systems, which degrades to (−1.5 ± 11) × 10-5, over z = 2.3−6.4 when the two [C ii] systems are included. That is, zero variation over look-back times of 10.8−12.8 Gyr. However, the latest optical results indicate a spatial variation in α, where Δα/α describes a dipole and we see the same direction in ΔF/F. This trend is, however, due to a single source for which the [C i] spectrum is of poor quality. This also applies to one of the two [C ii] spectra previously used to find a zero variation in α2/μ. Quantifying this, we find an anti-correlation between |ΔF/F| and the quality of the carbon detection, as measured by the spectral resolution, indicating that the typical values of ≳50 km s-1, used to obtain a detection, are too coarse to reliably measure changes in the constants. From the fluxes of the known z ≳ 1 CO systems, we predict that current instruments are incapable of the sensitivities required to measure changes in the constants through the comparison of CO and carbon lines. We therefore discuss in detail the use of ALMA for such an undertaking and find that, based upon the current CO detections only, the Full Array configuration is expected to detect ~100 galaxies in [C i] at better than 10 km s-1 spectral resolution, while potentially resolving the individual molecular cloud complexes at redshifts of z ≳ 3. This could provide ≳1000 individual systems with which to obtain accurate measurements of space-time variation of the constants at look-back times in excess of 11 Gyr.
Key words: submillimeter: galaxies / cosmology: observations / cosmology: theory / quasars: emission lines / galaxies: ISM / techniques: spectroscopic
© ESO, 2011
1. Introduction
Atomic carbon is an important tracer of the dense neutral gas within the Galactic and extragalactic interstellar media. With rest frequencies of νrest = 492.160651(55) GHz (Yamamoto & Saito 1991) and νrest = 809.34197(5) GHz (Klein et al. 1998) for the 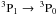 and
and 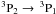 fine structure transitions, respectively, neutral carbon is difficult to observe at low redshift, although submillimetre observations of [C i] in the Galaxy (Ojha et al. 2001), M 82 (White et al. 1994; Stutzki et al. 1997) and other near-by galaxies (Gerin & Phillips 2000; Israel & Baas 2002), show that the [C i] emission is closely associated with that of carbon monoxide. This applies over a wide range of different environments and is most likely due to their similar critical densities (n ~ 103 cm-3). Furthermore, it has been suggested that [C i] can provide a measure of the H2 gas mass independent of CO (Papadopoulos & Greve 2004; Papadopoulos et al. 2004), the standard molecular hydrogen tracer.
fine structure transitions, respectively, neutral carbon is difficult to observe at low redshift, although submillimetre observations of [C i] in the Galaxy (Ojha et al. 2001), M 82 (White et al. 1994; Stutzki et al. 1997) and other near-by galaxies (Gerin & Phillips 2000; Israel & Baas 2002), show that the [C i] emission is closely associated with that of carbon monoxide. This applies over a wide range of different environments and is most likely due to their similar critical densities (n ~ 103 cm-3). Furthermore, it has been suggested that [C i] can provide a measure of the H2 gas mass independent of CO (Papadopoulos & Greve 2004; Papadopoulos et al. 2004), the standard molecular hydrogen tracer.
Although the neutral carbon is generally believed to be located on the surfaces of molecular clouds, it can be found deep inside the cloud (Ikeda et al. 2002), giving the spatial coincidences mentioned above and making the comparison of [C i] and CO redshifts potentially very useful in measuring the values of the fundamental constants at large look-back times. Comparison of the fine structure lines with the CO rotational lines gives ΔF/F, where F = α2/μ, with α being the fine structure constant1 and μ = me/mp the electron-proton mass ratio. Relative shifts in the millimetre-wave band are more than an order of magnitude larger than in the optical (e.g. Murphy et al. 2001), from which the intra-comparison of redshifted ultra-violet electronic transitions, in the absorption spectra of metal-ions in damped Lyman-alpha systems, indicate that α has changed over the history of the Universe (Murphy et al. 2003).
As well as a temporal variation having implications for current grand unified theories, a spatial variation of the constants may address the prominent “fine tuning” issue, where if the fundamental constants (which are dependent upon 27 independent parameters) were even slightly different than the observed values, life could not appear. Such a spatial variation may recently have been detected by Webb et al. (2011), where α has a different values in different regions of the sky, described by a dipole (see also Berengut et al. 2011).
Thus, redshifted [C i] lines are of great interest in measuring the space-time variation of the fundamental constants, especially since the comparison CO line has already been detected in over a hundred cases at z ≳ 1 (see Sect. 3.1), a number which will greatly increase with the advent of the Atacama Large Millimetre Array (ALMA).
Levshakov et al. (2008) have already compared the 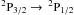 fine structure line of singly ionised carbon2, [C ii], with the rotational transitions of the CO lines, which also gives F = α2/μ, at z = 4.69 and z = 6.423. They find no temporal variation, although the uncertainties are large due to the weak [C ii] spectra, which are very difficult to detect at high redshift (see Curran 2009). Furthermore, unlike the neutral carbon, ionised carbon traces photo-dissociation regions in the diffuse interstellar medium between molecular clouds and is therefore unlikely to be spatially coincident with the CO. In any case, a non-detected temporal variation does not necessarily imply a zero spatial variation, which may possibly account for discrepancies which arise in changes in α when attributed purely to a temporal variation (e.g. Levshakov et al. 2006).
fine structure line of singly ionised carbon2, [C ii], with the rotational transitions of the CO lines, which also gives F = α2/μ, at z = 4.69 and z = 6.423. They find no temporal variation, although the uncertainties are large due to the weak [C ii] spectra, which are very difficult to detect at high redshift (see Curran 2009). Furthermore, unlike the neutral carbon, ionised carbon traces photo-dissociation regions in the diffuse interstellar medium between molecular clouds and is therefore unlikely to be spatially coincident with the CO. In any case, a non-detected temporal variation does not necessarily imply a zero spatial variation, which may possibly account for discrepancies which arise in changes in α when attributed purely to a temporal variation (e.g. Levshakov et al. 2006).
In this paper, we fit the observed [C i] and CO profiles of the known redshifted systems in order to derive the difference in redshifts between the species in each of the sources, thus yielding the values of α2/μ at the redshifts and locations of these quasars.
2. Analysis
2.1. Profile fitting
In Fig. 1 we show the 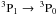 and rotational spectra of the sources in which both [C i] and CO have been detected4.
and rotational spectra of the sources in which both [C i] and CO have been detected4.
 |
Fig. 1 The [C i] |
These have been taken from the references listed in Table 1 and re-sampled in velocity according to the reference frequency of the CO transition. Although the full-width half maxima (FWHMs) are similar between the [C i] and CO, it is seen that in some cases, that there is a noticeable velocity offset between the profiles, which has also been noted by Weiß et al. (2003); Pety et al. (2004)5.
We analyse the spectra in a consistent manner by fitting a Gaussian to each using the gauss_fit.pro routine in idl6. This uses a Lavenburg-Marquadt algorithm (Press et al. 1989), containing up to six terms;
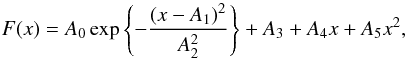 where A1 is the mean of the fit, A2 the standard deviation and A3, A4 and A5 fit the continuum. Since there are no measured uncertainties for the data, gauss_fit.pro uses Poisson statistics to approximate data uncertainties, which is likely to overestimate the errors for the fits.
where A1 is the mean of the fit, A2 the standard deviation and A3, A4 and A5 fit the continuum. Since there are no measured uncertainties for the data, gauss_fit.pro uses Poisson statistics to approximate data uncertainties, which is likely to overestimate the errors for the fits.
Initially, fits were performed using all six terms in order to ensure complete removal of the continuum from the data. Subsequent fits were then performed, adjusting the range of the data being fit, as well as the number of terms used in the fit in order to ensure that the optimum fit was found (quantified by the lowest normalised χ2). Generally, we found that the fits with the smallest errors were those with A3, A4 and A5 set to zero and, when applied, these coefficients had uncertainties larger than their fitted values.
The results of the fits are summarised in Table 1, where the velocity offset (Δv) is defined relative to the reference frequency (νref) for each spectrum, which was then converted to a redshift (zfitted). The values for both the CO and [C i] spectra were then used to derive a fractional offset7.
Summary of the Gaussian fits to the [C i] 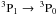 and the CO transitions.
and the CO transitions.
2.2. The comparison of rotational and fine structure transitions
The rotational lines of CO are proportional to μ, while the fine structure lines of neutral or ionised carbon (represented by [C]) are proportional to α2. Comparison of the redshifts of each species measures
![$$ \frac{z_{\rm CO} - z_{\rm [C]}}{z_{\rm CO} +1} = \frac{\Delta F}{F}, ~{\rm where}~F=\frac{\alpha^2}{\mu}\cdot $$](/articles/aa/full_html/2011/09/aa17457-11/aa17457-11-eq112.png) Showing the values for ΔF/F derived from the [C i] lines, along with those from the [C ii] (Levshakov et al. 2008), we find that α2/μ exhibits little evolution with redshift (Fig. 2, left), giving a mean value of ⟨ ΔF/F ⟩ = (−3.6 ± 8.5) × 10-5, for the [C i] systems only, and (−1.5 ± 11) × 10-5, including the [C ii] systems, over z = 2.3−4.1 and z = 2.3−6.4, respectively. Thus, the change in α2/μ is zero, within the observational “noise”.
Showing the values for ΔF/F derived from the [C i] lines, along with those from the [C ii] (Levshakov et al. 2008), we find that α2/μ exhibits little evolution with redshift (Fig. 2, left), giving a mean value of ⟨ ΔF/F ⟩ = (−3.6 ± 8.5) × 10-5, for the [C i] systems only, and (−1.5 ± 11) × 10-5, including the [C ii] systems, over z = 2.3−4.1 and z = 2.3−6.4, respectively. Thus, the change in α2/μ is zero, within the observational “noise”.
Referring to Fig. 2, however, there may a decrease in ΔF/F with distance from the dipole (middle panel) and an increase with r cosθ (right panel) evident, as has been found for Δα/α (Webb et al. 2011).
 |
Fig. 2 ΔF/F derived from the velocity offsets in Table 1 versus the redshift (left), distance from the dipole (middle) and the product of the look-back time with the cosine of the distance from the dipole (right), cf. Webb et al. (2011). The filled black markers show the eight [C i] sources and the unfilled colour markers the two [C ii] sources (see Levshakov et al. 2008). |
The observed range in ΔF/F spans a change of ~40 times that of Δα/α (≲4 × 10-4, cf. ≲1 × 10-5) and interestingly, some theoretical models predict temporal variations of |Δμ/μ| ~ 40 |Δα/α| (Uzan 2003). However, such models are tentatively ruled out by recent observations, which find |Δμ/μ| ≲ 10-6 at z = 0.89 (Henkel et al. 2009; Muller et al. 2011) and ≲3 × 10-6 at z = 2.81 (King et al. 2011).
Removing the dependence of the fine structure constant on the dipole [Δα/α = (1.1 ± 0.2) × 10-6 r cosθ − (1.9 ± 0.8) × 10-6, where r is the look-back time], via, Δμ/μ = 2 Δα/α − ΔF/F, gives the distribution shown in Fig. 3.
 |
Fig. 3 The fractional change in the electron-proton mass ratio versus the product of the look-back time and the cosine of the distance from the dipole, upon the subtraction of 2Δα/α according to the best-fit dipole (Webb et al. 2011). The symbols are as per Fig. 2. |
However, as per those in Fig. 2, any apparent trend is due to the inclusion of APM 08279+5255 (at –10.88 Gyr and ΔF/F = 3.4 × 10-4), which has the weakest [C i] spectrum (Fig. 1), while exhibiting a large offset from the CO redshift (in our fit as well as by Wagg et al. 2006). Indeed, several of the [C i] detection profiles are over very few channels, presumably to increase the signal-to-noise ratio of the spectrum.
In order to quantify the quality of the carbon spectra, in Fig. 4 we show the derived value of ΔF/F versus the spectral resolution, δv, from which we see a distinct correlation.
 |
Fig. 4 The absolute value of ΔF/F versus the spectral resolution of the [C i] and [C ii] detection. The symbols are as per Fig. 2 and the line shows the least-squares fit to all of the points. P(τ) shows the Kendall’s two-sided probability of the distribution occuring by chance and S(τ) the corresponding significance for the [C i] and [C ii]spectra. |
It is surprising that this has a ≤6% probability of occuring by chance, when ideally ΔF/F should exhibit no dependence on δv. This is strong evidence that any large values of ΔF/F in the present data are the result of low quality spectra. In an attempt to compensate for this, if we weight each value of ΔF/F by 1/δv, thus having the lower resolution spectra making a smaller contribution to the mean, we obtain ⟨ ΔF/F ⟩ weighted = (−2.0 ± 8.0) × 10-5 ([C i] only) and (−1.2 ± 9.3) × 10-5 ([C i] and [C ii]), i.e. closer to zero variation.
This interpretation of the measured values of F would explain why the temporal variation of F as indicated by APM 08279+5255 is at odds with other sources at similar redshifts, which all exhibit positive values of ΔF/F (Fig. 2, left panel). As discussed above, such a discrepancy may be expected due to spatial variation of the constants, were the sources in widely separated regions of the sky. However, MM 18423+5938 and PSS 2322+1944 are at 122 and 106 degrees from the dipole, respectively, whereas APM 08279+5255 is at 154 degrees (Fig. 2, middle panel), thus being in the same hemisphere as the other two sources. This supports the suggestion that the derived offset of the [C i] redshift in APM 08279+5255 does not accurately trace ΔF/F.
Apparent offsets may also arise from calibration errors, which have dominated previous measurements of the constants using neutral carbon: the comparison of the ultra-violet neutral carbon resonance lines with the radio-band H i 21-cm hyperfine transition yield ΔX/X, where X ≡ gp α2 μ, with gp being the proton gyromagnetic factor. The three sources in which both species have been detected (all in absorption) have yielded ΔX/X = (7 ± 11) × 10-6 at z = 1.78 (Cowie & Songaila 1995) and (7 ± 7) × 10-6 at z = 1.36−1.56 (Kanekar et al. 2010). The relatively large uncertainties are systematic, arising from the absolute wavelength calibration of the optical spectrum. This is an issue which we avoid through the comparison of redshifted submillimetre transitions, since the frequency calibration of radio and millimetre-wave instruments is phase-locked to an atomic clock frequency standard. Although due to the low spectral resolution of the [C i] detections and the fact that the spectra are emission profiles from entire galaxies, our absolute uncertainties are much larger.
 |
Fig. 5 The velocity integrated intensity of the [C i] |
Lastly, it is entirely possible that the relative velocity shifts between the species are intrinsic, although as noted above, the values of ΔF/F are consistent with observational noise, with most of the error bars in Fig. 2 extending to ΔF/F ≈ 0. Furthermore the FWHMs of the CO and [C i] emission profiles are very similar and the fact that CO is wider than [C i] in only about half of the cases (5 out of 8, although the uncertainties overlap), may indicate that the FWHMs could be the same with apparent differences introduced by the low spectral resolution of the data8. On this issue, it is also possible that systematics may be introduced by unresolved components in the data, again reinforcing the need for higher resolution data. Such data may also be used to ascertain the validity of fitting Gaussians to the profiles, which we believe is a reasonable assumption for the distribution of gas in a galaxy (with the number of Gaussians required depending on the orientation of the galaxy, e.g. Curran 2000). However, the fact that these fits can yield “accuracies” to well within a single channel, gives the relatively small error bars for MM 18423+5938 (at z = 3.9 and ΔF/F = 1.8 × 10-4, Fig. 2). Specifically, ±6 km s-1 from our fit, cf. the ±24 km s-1 (half a channel) quoted by Lestrade et al. (2010). Thus, an artificially small uncertainty could arise since, of all the [C i] spectra, this is the most Gaussian shaped (Fig. 1), when in reality the resolved emission may be too complex to be best fit by a single Gaussian. Again, this is an issue which can only be addressed with higher resolution carbon spectra.
 |
Fig. 6 The flux density (S = I/FWHM) of the CO and [C i] emitters versus redshift. The black stars show the current redshifted CO emitters which also exhibit [C i] emission (designated by coloured stars). The small squares show all of the other published z ≥ 1 CO emitters. The telescope labels show the expected rms noise level per each 50 km s-1 channel after 10 h of observation with the corresponding telescope at 100 GHz (see main text). The look-back time is calculated using H0 = 71 km s-1 Mpc-1, Ωmatter = 0.27 and ΩΛ = 0.73 (Spergel et al. 2003), which we use throughout the paper. |
 |
Fig. 7 As per Fig. 6 but showing the expected flux density of the [C i] emission based upon SCO ≈ 2 × S [C i] (Fig. 5). The dotted, broken and full traces show the rms sensitivity of the full ALMA array per each 1, 10 and 50 km s-1 channel for the conditions used above (10 h on source at a declination of δ = −30° and a vapour column density of 1.262 mm). The lower redshift trace spans the range given by the band-7, 6, 5 and 4 receivers (370−125 GHz) and the higher redshift spans that given by the band-3 and 2 receivers (116−67 GHz). The frequency scale is derived for the redshift of the [C i] |
To surmise, based upon the current eight high redshift [C i] and two [C ii] detections, the data appear to be dominated by scatter. We have shown that this is, at least in part, due to the low spectral resolutions of the carbon detections. Since current instruments are generally capable of much finer resolutions, we suspect that such coarse values have been used in order to tease as strong a detection as possible from the data, leading to the scatter in ΔF/F. Therefore in order to make meaningful measurements of the constants, spectra with much higher signal-to-noise ratios are required.
3. Improving the data
3.1. Prospects with current instruments
Of the known high redshift CO emitters9, most have the 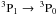 transition of [C i] redshifted into current millimetre bands and are therefore potentially detectable with current instruments, expanding the dataset by an order of magnitude. In order to determine the expected emission strengths of the [C i], from the current detections and those listed in Walter et al. (2011), we find a mean of I [CI] ≈ 0.5 ± 0.2 × ICO (Fig. 5), cf. the ratios of ≈0.1 within the Galaxy (Ojha et al. 2001; Ikeda et al. 2002), ≈0.5 in M 82 (White et al. 1994; Stutzki et al. 1997) and ≈0.2 in other near-by galaxies (Gerin & Phillips 2000). Since the FWHM of the [C i] profile is close to that of the CO in the detected cases (Fig. 1), we can replace the integrated intensities with the line fluxes, in order to estimate the relative telescope sensitivities (Fig. 6).
transition of [C i] redshifted into current millimetre bands and are therefore potentially detectable with current instruments, expanding the dataset by an order of magnitude. In order to determine the expected emission strengths of the [C i], from the current detections and those listed in Walter et al. (2011), we find a mean of I [CI] ≈ 0.5 ± 0.2 × ICO (Fig. 5), cf. the ratios of ≈0.1 within the Galaxy (Ojha et al. 2001; Ikeda et al. 2002), ≈0.5 in M 82 (White et al. 1994; Stutzki et al. 1997) and ≈0.2 in other near-by galaxies (Gerin & Phillips 2000). Since the FWHM of the [C i] profile is close to that of the CO in the detected cases (Fig. 1), we can replace the integrated intensities with the line fluxes, in order to estimate the relative telescope sensitivities (Fig. 6).
In the figure the expected rms noise levels achievable by the telescopes are derived for a spectral resolution of 50 km s-1 (17 MHz at 100 GHz, typical of the current [C i] detections), after 10 h on source. We have used the specified system temperature of Tsys = 250 K for each, which gives an rms of 6 mJy for the Institut de Radioastronomie Millimétrique (IRAM) 30-m, 4 mJy for the Nobeyama Radio Observatory (NRO) 45-m and 1.3 mJy for the Australia Telescope Compact Array (ATCA). These sensitivities do indicate that more detections are to be expected over all redshift ranges with current instruments.
As discussed above, however, in order to measure velocity offsets of high enough quality to measure variation in the constants, the spectral resolution must generally be much finer than for the current [C i] detections, requiring significantly lower rms noise levels than shown in Fig. 6. Furthermore, even with sufficient spectral resolution, current spatial resolutions may be insufficient: The finest of the current carbon detections subtend (unlensed) linear extents in excess of 20 kpc (HPBWs ≈2′′, Downes et al. 1995, 1999; Weiß et al. 2003), although ≳100 kpc is more common. Since, we ideally require a comparison of redshifts from a single complex, namely a giant molecular cloud (GMC), resolutions of ≲100 pc are required, which even the finest spatial resolutions currently available cannot resolve: for example, with a maximum 6-km baseline, the ATCA is capable of a 0.3′′ resolution at 100 GHz, which gives linear extents of between 2.2 kpc (at z = 3.7) and 1.9 kpc (at z = 4.9, the [C i] redshift range observable with the ATCA 3-mm band).
3.2. Prospects with ALMA
On the basis of their sensitivity and spatial resolution, it is clear the current instruments are of limited use in using carbon to measure cosmological variation of the constants. With the ALMA Early Science configuration (16 × 12-m antenna), the maximum 400 metre baseline gives a beam of ≳2′′ at 100 GHz, i.e. a linear extent of ≳1 kpc at z ~ 4 and, after 10 h on source, an rms noise level of 0.19 mJy per each 50 km s-1channel is expected (Fig. 6). For the Full Array configuration (≥50 × 12-m antennas), ≤0.06 mJy per 50 km s-1 channel will be reached after 10 h on source. The finest beam-width will be ≈0.05−0.04′′ over 84−116 GHz (band-3), which corresponds to linear extent of 330 pc at z = 4.9 and 300 pc at z = 3.2. This level of resolution is getting close to the ≲100 pc required to resolve individual GMCs and, in the case where the galaxy is gravitationally lensed by an intervening galaxy, a magnification of only ≳3 is required to achieve sub-100 pc resolution.
With ALMA, we are thus in the realm of Galactic resolution millimetre astronomy at very large look-back times. As such, the spectral resolutions used for the eight [C i] detection experiments (Sect. 2.2) are insufficient in the study of individual GMCs, as well as the application of these in measuring variation in the constants, where, for a ratio of line frequencies of a few parts in ~105, we require spectral resolutions of better than 10 km s-1. Using the ALMA sensitivity calculator10, at the above (50 km s-1) and finer (10 & 1 km s-1) spectral resolutions, we show the rms noise levels expected from the Full Array configuration after 10 h on source (Fig. 7). From this, we see that the currently detected [C i] emitters are likely to be the most luminous of this sample, with the estimated fluxes of those yet to be searched generally lying below the least-squares fit described by these. This suggests that any further detections with current instruments are unlikely to be of higher quality than those in Fig. 1, while the ALMA Full Array will be capable of detecting [C i] in all11 of these at a spectral resolution of 10 km s-1 or better.
As seen from Fig. 7, most of the redshift space is covered, thus making the total number of sources expected to be detected close to the number quoted above. That is, based upon the current CO detections only, the Full Array configuration is expected to detect ~100 galaxies in [C i] at better than 10 km s-1 spectral resolution. With regard to individual complexes, GMC numbers in external galaxies can range from a few (e.g. 6 in M 31, Sheth et al. 2008) to over a hundred (148 in M 33, Engargiola et al. 2003), where observations are of sufficient sensitivity. Therefore, as an order of magnitude estimate, we can expect the detection of ≳1000 [C i] emitters to very large look-back times, a much larger sample with which to measure the constants than available in the optical regime.
4. Conclusions
By fitting the carbon and carbon monoxide emission spectra, we have determined the relative velocity offsets between these species in the eight redshifted sources in which the 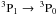 transition of neutral carbon has been detected. Such comparison provides a measure of the fundamental constants, specifically F ≡ α2/μ, where α is the fine structure constant and μ is the electron-proton mass ratio. Being a comparison of fine structure ([C i]) and rotational lines (CO), this gives the same combination of constants as yielded by the comparison of ionised carbon ([C ii]) with CO (Levshakov et al. 2008), although it has the distinct advantage that the neutral carbon may be spatially coincident with the CO, within molecular clouds, whereas the ionised carbon is located between clouds.
transition of neutral carbon has been detected. Such comparison provides a measure of the fundamental constants, specifically F ≡ α2/μ, where α is the fine structure constant and μ is the electron-proton mass ratio. Being a comparison of fine structure ([C i]) and rotational lines (CO), this gives the same combination of constants as yielded by the comparison of ionised carbon ([C ii]) with CO (Levshakov et al. 2008), although it has the distinct advantage that the neutral carbon may be spatially coincident with the CO, within molecular clouds, whereas the ionised carbon is located between clouds.
We find ⟨ ΔF/F ⟩ = (−3.6 ± 8.5) × 10-5 for the eight [C i] systems and ⟨ ΔF/F ⟩ = (−1.5 ± 11) × 10-5, when the two [C ii] systems are included, the former of which we believe to be the most reliable due to the segregation of [C ii] and CO. Both results are consistent with a zero variation over the redshift range z = 2.3−6.4 (look-back times of 10.8−12.8 Gyr), although ΔF/F does appear to vary in the same direction as the spatial dipole defined by the variation in α (Webb et al. 2011). This, however, is dominated by the lowest quality [C i] spectrum, which has a channel spacing of 150 km s-1, giving the largest velocity offset between the [C i] and CO spectra and with the removal of this source no trend is apparent.
Quantifying the quality of the spectra, we find that large values of ΔF/F are favoured by the lower quality carbon spectra, with |ΔF/F| → 0 as δv → 0, where δv is the spectral resolution of the carbon detection. Although the sample is small, this is strong evidence that the non-zero values of ΔF/F are the result of low quality spectra. Conversely, however, the zero variation of constants found from the ionised carbon lines are also unreliable (Levshakov et al. 2008) by this reasoning. Weighting the contribution of each measurement of ΔF/F by 1/δv, gives ⟨ ΔF/F ⟩ weighted = (−2.0 ± 8.0) × 10-5 for [C i] only and (−1.2 ± 9.3) × 10-5 when the two [C ii] systems are included.
Such low spectral resolutions are the result of maximising the signal-to-noise ratio in order to yield the detection. Applying the relation ICO ≈ 2 × I [CI] to the z ≳ 1 sources, indicates that the current [C i] detections would be among the most luminous of the sources already detected in CO. That is, even if current instruments were to detect [C i] emission in the remainder of the CO emitters, the spectra are unlikely to be of sufficient quality to provide meaningful measurements of the constants. Furthermore, from the spatial resolution and spectral profiles of the current detections, it is clear that we are detecting emission over much of the galaxy, when ideally we require comparison of the [C i] and CO lines in a single complex. As such, the best spatial resolution of ≳2 kpc, currently available in the 3-mm band (z [CI] = 3.7−4.9), is incapable of resolving these complexes.
The sensitivity and spectral resolution of ALMA is therefore required in order to fully utilise the use of neutral carbon and carbon monoxide in measuring the constants:
-
After 10 h on source, the Early Scienceconfiguration (16 × 12-m antennas) is expected to reach an rms noise level of ≈0.2 mJy per each 50 km s-1 channel. However:
-
Although sufficient to detect[C i] in all of the currentlyknown z ≳ 1 CO emitters (Fig. 6, cf. Fig. 7), it is clear from this work that spectral resolutions of ≈50 km s-1 are insufficient.
-
Furthermore, the maximum linear resolution of ≳1 kpc, at z ~ 4, is still too coarse to resolve individual GMCs.
-
-
After 10 h on source, the Full Array configuration (≥ 50 × 12-m antennas) is expected to reach a similar rms noise level per each 10 km s-1 channel (Fig. 7).
-
This is sufficient to detect all of the current CO emitters in[C i] which fall into bands-3to 7 (z = 0.33−6.36) at the spectral resolutions required.
-
The maximum angular resolution of ≈0.04′′ at 116 GHz, gives a spatial resolution of ≈300 pc at z = 3.2−4.9, which is still insufficient to resolve a ≲100 pc GMC. However, the majority of distant galaxies in the submillimetre bands may be subject to magnification by gravitational lensing (Blain 1996), as are all of the current [C i] detections (Ofek et al. 2003; Garrett et al. 2005; Ivison et al. 2010 and references therein)12. Lens magnifications of ≳40 may be expected (Blain et al. 1999), although magnifications of only ≳3 are required for ALMA to achieve ≲100 pc resolution at these redshifts.
-
νrest = 1900.5369(1.3) GHz (Cooksy et al. 1986).
From CO and [C ii] in the quasars BR 1202–0725 (Omont et al. 1996; Iono et al. 2006b) and J1148+5251 (Bertoldi et al. 2003; Maiolino et al. 2005).
Lupu et al. (2011) claim a further two detections of the 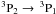 transition at z = 1.786 and 2.308. However, these are so poorly resolved as to be indistinguishable from the CO 7 → 6 line and are thus of little use here.
transition at z = 1.786 and 2.308. However, these are so poorly resolved as to be indistinguishable from the CO 7 → 6 line and are thus of little use here.
There are some differences in the FWHMs, particularly for H 1413+117 and APM 08279+5255, the latter of which has the poorest [C i] spectral resolution (150 km s-1), although the former has the best (17 km s-1). The fact that in some cases the CO spectrum is wider than that of [C i] and vice versa (Table 1), leads us to suspect that the differences may be due to the relatively low quality of the spectra, which may also affect the velocity offsets (see Sect. 2.2).
Although several rotational transitions have been detected in some of the quasars (Barvainis et al. 1997; Downes et al. 1999; Cox et al. 2002; Bertoldi et al. 2003; Walter et al. 2003; Tacconi et al. 2006; Ao et al. 2008; Danielson et al. 2011), in order to minimise differences in the beam filling factors, where available, we use the CO transition (J = 4 → 3) closest in frequency to the [C i] line. Except in the case of H 1413+117 (the Cloverleaf quasar), where the CO 3 → 2 (Weiß et al. 2003) spectrum is of higher quality than the 4 → 3 (Barvainis et al. 1997).
All of our analysis is done using the 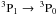 transition and, although the
transition and, although the 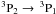 spectrum of [C i] has also been detected in a few of the sources – RX J0911+0551 (Walter et al. 2011), J1148+5251 (Ao et al. 2008), SMM J14011+0252 (Walter et al. 2011), H 1413+117 (Weiß et al. 2003), MM 18423+5938 (Lestrade et al. 2010), SMM J213511–0102 (Danielson et al. 2011), PSS 2322+1944 (Walter et al. 2011), this is often blended with the CO 7 → 6 emission.
spectrum of [C i] has also been detected in a few of the sources – RX J0911+0551 (Walter et al. 2011), J1148+5251 (Ao et al. 2008), SMM J14011+0252 (Walter et al. 2011), H 1413+117 (Weiß et al. 2003), MM 18423+5938 (Lestrade et al. 2010), SMM J213511–0102 (Danielson et al. 2011), PSS 2322+1944 (Walter et al. 2011), this is often blended with the CO 7 → 6 emission.
The mean FWHM of the eight CO spectra is 360 (σ = 150) km s-1, cf. 330 (σ = 110) km s-1 for the [C i] spectra, based upon the values in Table 1.
A total of 103 published thus far (Downes et al. 1995; Ohta et al. 1996; Scoville et al. 1997; Frayer et al. 1998, 1999; Papadopoulos et al. 2000; Cox et al. 2002; De Breuck et al. 2003; Greve et al. 2003; Walter et al. 2003; Weiß et al. 2003; Hainline et al. 2004; De Breuck et al. 2005; Klamer et al. 2005; Kneib et al. 2005; Solomon & Vanden Bout 2005; Iono et al. 2006a; Tacconi et al. 2006; Coppin et al. 2007; Maiolino et al. 2007; Willott et al. 2007; Casey et al. 2011; Daddi et al. 2009; Weiß et al. 2009; Bothwell et al. 2010; Daddi et al. 2010; Lestrade et al. 2010; Riechers et al. 2010; Tacconi et al. 2010; Yan et al. 2010; Danielson et al. 2011; Emonts et al. 2011; Frayer et al. 2011; Lupu et al. 2011; Riechers 2011 and references therein).
No such data yet exists for MM 18423+5938, which has yet to make it onto the NASA/IPAC Extragalactic Database, although the discovery paper (Lestrade et al. 2009) does note multiple components.
Acknowledgments
We would like to thank the referee Paolo Molaro for his prompt and helpful comments as well as Stephen Lo for facilitating the enjoyable seafood lunch overlooking Coogee Bay, during which the ideas for this paper were developed. Also, Nick Tothill who came for coffee afterwards and threw in his two cents worth. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research has also made use of NASA’s Astrophysics Data System Bibliographic Service.
References
- Ao, Y., Weiß, A., Downes, D., et al. 2008, A&A, 491, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barvainis, R., Maloney, P., Antonucci, R., & Alloin, D. 1997, ApJ, 484, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Berengut, J. C., Flambaum, V. V., King, J. A., Curran, S. J., & Webb, J. K. 2011, Phys. Rev. D, 83, 123506 [NASA ADS] [CrossRef] [Google Scholar]
- Bertoldi, F., Cox, P., Neri, R., et al. 2003, A&A, 409, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blain, A. W. 1996, MNRAS, 283, 1340 [NASA ADS] [CrossRef] [Google Scholar]
- Blain, A. W., Möller, O., & Maller, A. H. 1999, MNRAS, 303, 423 [Google Scholar]
- Bothwell, M. S., Chapman, S. C., Tacconi, L., et al. 2010, MNRAS, 405, 219 [NASA ADS] [Google Scholar]
- Casey, C. M., Chapman, S. C., Neri, R., et al. 2011, MNRAS, 415, 2723 [NASA ADS] [CrossRef] [Google Scholar]
- Cooksy, A. L., Blake, G. A., & Saykally, R. J. 1986, ApJ, 305, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Coppin, K. E. K., Swinbank, A. M., Neri, R., et al. 2007, ApJ, 665, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., & Songaila, A. 1995, ApJ, 453, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, P., Omont, A., Djorgovski, S. G., et al. 2002, A&A, 387, 406 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Curran, S. J. 2000, A&AS, 144, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Curran, S. J. 2009, A&A, 497, 351 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daddi, E., Dannerbauer, H., Stern, D., et al. 2009, ApJ, 694, 1517 [Google Scholar]
- Daddi, E., Bournaud, F., Walter, F., et al. 2010, ApJ, 713, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Danielson, A. L. R., Swinbank, A. M., Smail, I., et al. 2011, MNRAS, 410, 1687 [NASA ADS] [Google Scholar]
- De Breuck, C., Neri, R., Morganti, R., et al. 2003, A&A, 401, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Breuck, C., Downes, D., Neri, R., et al. 2005, A&A, 430, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Downes, D., Solomon, P. M., & Radford, S. J. E. 1995, ApJ, 453, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Downes, D., Neri, R., Wiklind, T., Wilner, D. J., & Shaver, P. A. 1999, ApJ, 513, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Emonts, B. H. C., Norris, R. P., Feain, I., et al. 2011, MNRAS, 415, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Engargiola, G., Plambeck, R. L., Rosolowsky, E., & Blitz, L. 2003, ApJS, 149, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Frayer, D. T., Ivison, R. J., Scoville, N. Z., et al. 1998, ApJ, 506, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Frayer, D. T., Ivison, R. J., Scoville, N. Z., et al. 1999, ApJ, 514, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Frayer, D. T., Harris, A. I., Baker, A. J., et al. 2011, ApJ, 726, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Garrett, M. A., Knudsen, K. K., & van der Werf, P. P. 2005, A&A, 431, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genzel, R., Baker, A. J., Tacconi, L. J., et al. 2003, ApJ, 584, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Gerin, M., & Phillips, T. G. 2000, ApJ, 537, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Greve, T. R., Ivison, R. J., & Papadopoulos, P. P. 2003, ApJ, 599, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Hainline, L. J., Scoville, N. Z., Yun, M. S., et al. 2004, ApJ, 609, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Henkel, C., Menten, K. M., Murphy, M. T., et al. 2009, A&A, 500, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ikeda, M., Oka, T., Tatematsu, K., Sekimoto, Y., & Yamamoto, S. 2002, ApJS, 139, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Iono, D., Tamura, Y., Nakanishi, K., et al. 2006a, PASJ, 58, 957 [NASA ADS] [Google Scholar]
- Iono, D., Yun, M. S., Elvis, M., et al. 2006b, ApJ, 645, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, F. P., & Baas, F. 2002, A&A, 383, 82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivison, R. J., Swinbank, A. M., Swinyard, B., et al. 2010, A&A, 518, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kanekar, N., Prochaska, J. X., Ellison, S. L., & Chengalur, J. N. 2010, ApJ, 712, L148 [Google Scholar]
- King, J. A., Murphy, M. T., Ubachs, W., & Webb, J. K. 2011, MNRAS, accepted [arXiv:1106.5786] [Google Scholar]
- Klamer, I. J., Ekers, R. D., Sadler, E. M., et al. 2005, ApJ, 621, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, H., Lewen, F., Schieder, R., Stutzki, J., & Winnewisser, G. 1998, ApJ, 494, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Kneib, J., Neri, R., Smail, I., et al. 2005, A&A, 434, 819 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lestrade, J.-F., Wyatt, M. C., Bertoldi, F., Menten, K. M., & Labaigt, G. 2009, A&A, 506, 1455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lestrade, J.-F., Combes, F., Salomé, P., et al. 2010, A&A, 522, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levshakov, S. A., Centurión, M., Molaro, P., et al. 2006, A&A, 449, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levshakov, S. A., Reimers, D., Kozlov, M. G., Porsev, S. G., & Molaro, P. 2008, A&A, 479, 719 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lupu, R. E., Scott, K. S., Aguirre, J. E., et al. 2011, ApJ, submitted [arXiv:1009.5983] [Google Scholar]
- Maiolino, R., Cox, P., Caselli, P., et al. 2005, A&A, 440, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiolino, R., Neri, R., Beelen, A., et al. 2007, A&A, 472, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muller, S., Beelen, A., Guélin, M., et al. 2011, A&A, submitted [arXiv:1104.3361] [Google Scholar]
- Murphy, M. T., Webb, J. K., Flambaum, V. V., et al. 2001, MNRAS, 327, 1244 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, M. T., Webb, J. K., & Flambaum, V. V. 2003, MNRAS, 345, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Ofek, E. O., Rix, H., & Maoz, D. 2003, MNRAS, 343, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Ohta, K., Yamada, T., Nakanishi, K., et al. 1996, Nat, 382, 426 [Google Scholar]
- Ojha, R., Stark, A. A., Hsieh, H. H., et al. 2001, ApJ, 548, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Omont, A., Petitjean, P., Guilloteau, S., et al. 1996, Nat, 382, 428 [Google Scholar]
- Papadopoulos, P. P., & Greve, T. R. 2004, ApJ, 615, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Papadopoulos, P. P., Röttgering, H. J. A., van der Werf, P. P., et al. 2000, ApJ, 528, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Papadopoulos, P. P., Thi, W.-F., & Viti, S. 2004, MNRAS, 351, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Pety, J., Beelen, A., Cox, P., et al. 2004, A&A, 428, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Flannery, B. P., Teukolsky, S. A., & Vetterling, W. T. 1989, Numerical Recipes: The Art of Scientific Computing (Cambridge: Cambridge University Press) [Google Scholar]
- Riechers, D. A. 2011, ApJ, 730, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Riechers, D. A., Walter, F., Carilli, C. L., & Lewis, G. F. 2009, ApJ, 690, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Riechers, D. A., Capak, P. L., Carilli, C. L., et al. 2010, ApJ, 720, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N. Z., Yun, M. S., Windhorst, R. A., Keel, W. C., & Armus, L. 1997, ApJ, 485, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, K., Vogel, S. N., Wilson, C. D., & Dame, T. M. 2008, ApJ, 675, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., & Van den Bout, P. A. 2005, Ann. Rev. Astr. Ap., 43, 677 [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Stutzki, J., Graf, U. U., Haas, S., et al. 1997, ApJ, 477, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Neri, R., Chapman, S. C., et al. 2006, ApJ, 640, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., Neri, R., et al. 2010, Nature, 463, 781 [Google Scholar]
- Uzan, J. 2003, R. Mod. Phys., 75, 403 [Google Scholar]
- Wagg, J., Wilner, D. J., Neri, R., Downes, D., & Wiklind, T. 2006, ApJ, 46 [Google Scholar]
- Walter, F., Bertoldi, F., Carilli, C., et al. 2003, Nature, 424, 406 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Walter, F., Weiß, A., Downes, D., Decarli, R., & Henkel, C. 2011, ApJ, 730, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Webb, J. K., King, J. A., Murphy, M. T., et al. 2011, PhRvL, submitted [arXiv:1008.3907] [Google Scholar]
- Weiß, A., Henkel, C., Downes, D., & Walter, F. 2003, A&A, 409 [Google Scholar]
- Weiß, A., Downes, D., Henkel, C., & Walter, F. 2005a, A&A, 429, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weiß, A., Downes, D., Walter, F., & Henkel, C. 2005b, A&A, 440, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weiß, A., Ivison, R. J., Downes, D., et al. 2009, ApJ, 705, L45 [Google Scholar]
- White, G. J., Ellison, B., Claude, S., Dent, W. R. F., & Matheson, D. N. 1994, A&A, 284, L23 [NASA ADS] [Google Scholar]
- Willott, C. J., Martínez-Sansigre, A., & Rawlings, S. 2007, AJ, 133, 564 [Google Scholar]
- Yamamoto, S., & Saito, S. 1991, ApJ, 370, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, L., Tacconi, L. J., Fiolet, N., et al. 2010, ApJ, 714, 100 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 The [C i] |
| In the text | |
 |
Fig. 2 ΔF/F derived from the velocity offsets in Table 1 versus the redshift (left), distance from the dipole (middle) and the product of the look-back time with the cosine of the distance from the dipole (right), cf. Webb et al. (2011). The filled black markers show the eight [C i] sources and the unfilled colour markers the two [C ii] sources (see Levshakov et al. 2008). |
| In the text | |
 |
Fig. 3 The fractional change in the electron-proton mass ratio versus the product of the look-back time and the cosine of the distance from the dipole, upon the subtraction of 2Δα/α according to the best-fit dipole (Webb et al. 2011). The symbols are as per Fig. 2. |
| In the text | |
 |
Fig. 4 The absolute value of ΔF/F versus the spectral resolution of the [C i] and [C ii] detection. The symbols are as per Fig. 2 and the line shows the least-squares fit to all of the points. P(τ) shows the Kendall’s two-sided probability of the distribution occuring by chance and S(τ) the corresponding significance for the [C i] and [C ii]spectra. |
| In the text | |
 |
Fig. 5 The velocity integrated intensity of the [C i] |
| In the text | |
 |
Fig. 6 The flux density (S = I/FWHM) of the CO and [C i] emitters versus redshift. The black stars show the current redshifted CO emitters which also exhibit [C i] emission (designated by coloured stars). The small squares show all of the other published z ≥ 1 CO emitters. The telescope labels show the expected rms noise level per each 50 km s-1 channel after 10 h of observation with the corresponding telescope at 100 GHz (see main text). The look-back time is calculated using H0 = 71 km s-1 Mpc-1, Ωmatter = 0.27 and ΩΛ = 0.73 (Spergel et al. 2003), which we use throughout the paper. |
| In the text | |
 |
Fig. 7 As per Fig. 6 but showing the expected flux density of the [C i] emission based upon SCO ≈ 2 × S [C i] (Fig. 5). The dotted, broken and full traces show the rms sensitivity of the full ALMA array per each 1, 10 and 50 km s-1 channel for the conditions used above (10 h on source at a declination of δ = −30° and a vapour column density of 1.262 mm). The lower redshift trace spans the range given by the band-7, 6, 5 and 4 receivers (370−125 GHz) and the higher redshift spans that given by the band-3 and 2 receivers (116−67 GHz). The frequency scale is derived for the redshift of the [C i] |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


