| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201116974 | |
| Published online | 01 September 2011 | |
Decay of a simulated mixed-polarity magnetic field in the solar surface layers
1
Max-Planck-Institut für Sonnensystemforschung,
Katlenburg-Lindau,
Germany
2
Sterrenkundig Instituut, Utrecht University,
Postbus 80000,
3508 TA
Utrecht, The
Netherlands
Received: 29 March 2011
Accepted: 29 July 2011
Magnetic flux is continuously being removed and replenished on the solar surface. To understand the removal process we carried out 3D radiative MHD simulations of the evolution of patches of photospheric magnetic field with equal amounts of positive and negative flux. We find that the flux is removed at a rate corresponding to an effective turbulent diffusivity, ηeff, of 100−340 km2 s-1, depending on the boundary conditions. For average unsigned flux densities above about 70 Gauss, the percentage of surface magnetic energy coming from different field strengths is almost invariant. The overall process is then one where magnetic elements are advected by the horizontal granular motions and occasionally come into contact with opposite-polarity elements. These reconnect above the photosphere on a comparatively short time scale after which the U loops produced rapidly escape through the upper surface while the downward retraction of inverse-U loops is significantly slower, because of the higher inertia and lower plasma beta in the deeper layers.
Key words: magnetic fields / Sun: photosphere / convection
© ESO, 2011
1. Introduction
High-resolution spectropolarimetric observations (e.g. De Pontieu 2002; Martínez González et al. 2007; Centeno et al. 2007; Ishikawa et al. 2010; Kubo et al. 2010; Solanki et al. 2010; Borrero et al. 2010; Danilovic et al. 2010a) show that magnetic flux on the solar surface is continuously removed and replenished. The small scale fields involved are probably a mixture of flux which is left over from the decay of active regions and flux generated in the near-photospheric layers by local-dynamo action (Hagenaar et al. 2003; Vögler & Schüssler 2007; Pietarila Graham et al. 2009, 2010). This field has been described as “salt and pepper”, reflecting small spatial scales on which the polarities are mixed. Reconnection events take place when the surface magnetic fields of opposite polarities, which are continually advected by the granular motions, come into close proximity. If we consider only a layer near the surface, then a field line in the layer can be classified as a U loop if both ends of the field line pass through the upper boundary of the layer, and as a inverse-U loop if both ends pass through the lower boundary. Reconnection of field lines initially passing from the bottom of the layer to the top with field lines going from the top to the bottom produces pairs of U and inverse-U loops. Magnetic tension then causes the loops to retract: inverse-U loops downwards through the photosphere and U loops upwards. Observations indicate that the reconnection occurs above the optical surface, so that the removal of flux from the surface involves the subsequent retraction of U loops (Kubo et al. 2010).
In this paper we study the evolution of a small-scale mixed polarity field using numerical simulations. We concentrate not so much on individual reconnection events but on the statistical properties of the flux removal such as how fast does the removal occur, what are the processes which determine the rate, what are the dynamics of U and inverse-U loops. The observational signature of individual reconnection events has been studied by Danilović (2009).
This paper is organized as follows. In Sect. 2 we briefly sketch the numerical code we have used and the simulation setup. Section 3 presents the simulation results and their dependence on the assumed initial and boundary conditions. Section 4 discusses the results, and Sect. 5 gives our conclusions.
2. Simulations
Our simulations consider the near-surface layers of the Sun extending from about 800 km below the optical surface to 600 km above. The physics is described by the continuity and momentum equations, the induction equation, an energy equation which includes radiative transfer, and an equation of state which allows for the effects of partial ionization. The equations are fully set out in Vögler et al. (2005), where also the details of the MURaM code we have used for this study are described.
The code has been used to investigate numerous aspects of solar-surface magnetic activity, including quiet-Sun magnetism (Keller et al. 2004; Khomenko et al. 2005; Vögler & Schüssler 2007; Pietarila Graham et al. 2009, 2010; Danilovic et al. 2010c,b) pores (Cameron et al. 2007), emerging flux (Cheung et al. 2008; Yelles Chaouche et al. 2009; Cheung et al. 2010), and sunspots (Schüssler & Vögler 2006; Rempel et al. 2009b,a).
For this study we first consider a reference case with a box size of 6 Mm × 6 Mm in the x and y (horizontal) directions and 1.4 Mm in the z (vertical) direction with a grid resolution of 20.8 km in each of the horizontal directions and 14 km in the vertical. The bottom boundary condition allows for in- and outflows as described in Vögler et al. (2005). The magnetic field is vertical at the top boundary, where the vertical component of the velocity vanishes and a free-slip condition (vertical derivatives vanish) is condition is imposed on the horizontal velocity components. The box is periodic in both horizontal directions. The initial condition for our reference case is a height-independent checkerboard (2 × 2) vertical magnetic field, i.e. 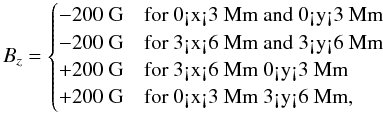 (1)
(1) superposed on a well developed non-magnetic convection simulation. This initial condition is not particularly realistic in that we do not expect purely vertical fields to occur over a region this large in the quiet Sun. The initial condition is instead designed to investigate the manner in which flux in the quiet Sun is dispersed, reconnects and is removed from the surface.
superposed on a well developed non-magnetic convection simulation. This initial condition is not particularly realistic in that we do not expect purely vertical fields to occur over a region this large in the quiet Sun. The initial condition is instead designed to investigate the manner in which flux in the quiet Sun is dispersed, reconnects and is removed from the surface.
We also consider several variations of this setup. We study the effect of the initial condition by starting from a magnetic field configuration consisting of two stripes (2 × 1) of opposite polarity: 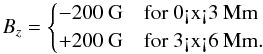 (2)We also investigate the sensitivity to the upper boundary condition by comparing the reference case to ones where the magnetic field was matched to a potential field at the upper boundary, to cases where the top boundary is raised by additional 280 km above the optical surface, and to cases where the top boundary is open to flows. These closed and open upper boundary conditions either completely or partially reflect outgoing waves. The influence of the reflected waves, and of waves otherwise excited in the chromosphere, on the retraction or escape of the loops is not studied beyond using these two different boundary conditions. Finally we consider the effect of varying the magnetic diffusivity, η.
(2)We also investigate the sensitivity to the upper boundary condition by comparing the reference case to ones where the magnetic field was matched to a potential field at the upper boundary, to cases where the top boundary is raised by additional 280 km above the optical surface, and to cases where the top boundary is open to flows. These closed and open upper boundary conditions either completely or partially reflect outgoing waves. The influence of the reflected waves, and of waves otherwise excited in the chromosphere, on the retraction or escape of the loops is not studied beyond using these two different boundary conditions. Finally we consider the effect of varying the magnetic diffusivity, η.
3. Results
3.1. 2 × 2 case
We take as our reference case the simulation starting from the checkerboard (2 × 2) initial condition, with vertical magnetic field boundary condition at the upper boundary, horizontal resolution of 20.8 km, and η = 11 km2 s-1. The magnetic Reynolds number of these simulations is below the critical value required for small-scale dynamo action (Vögler & Schüssler 2007). This means that the simulations are too diffusive to show local dynamo action. Since our boundary conditions do not allow for incoming flux at the lower boundary, the magnetic field must inevitably decay. This can be seen qualitatively in Fig. 1, which shows maps of the vertical magnetic field component on the horizontal surface z = 0, at the average (time and space) height of the optical (τ = 1) surface. The temporal variation of the spatially averaged τ = 1 height for this particular run was calculated for four different times and was found to have rms deviations of 8.5 km. For comparison the spatial rms deviations at any one time are about 4 times larger so that the τ = 1 surface can be regarded as a corrugated suface whose average height only varies slightly.
 |
Fig. 1 Time evolution of Bz on the plane z = 0, corresponding to the average height of the optical surface (left panels) and the bolometric brightness (right panels) for the reference (2 × 2) case at 4 min (top), 80 min (middle), and 200 min (bottom) after introduction of the initial field. The average unsigned magnetic field for these snapshots corresponds to about 200 G, 50 G, and 10 G, respectively. |
To quantitatively analyze the decay we consider the time evolution of the magnetic energy in a horizontal cut at a fixed geometrical height near z = 0, the evolution of the unsigned vertical magnetic flux through the same surface, and the magnetic energy in the whole computational domain. We chose these three quantities because; 1) the vertical flux is the simplest quantity most relevant for comparison with observations; 2) the total magnetic energy because it gives information on the global properties of the simulation, and 3) the magnetic energy at the height of the vertical flux slice gives insight into the connection between previous two. The evolution of these quantities is shown in Fig. 2.
 |
Fig. 2 Decay of total magnetic energy in the entire simulation box, and of unsigned vertical magnetic flux at z = 0 for the reference case. The thin lines are exponential fits. All curves have been normalized such that the fits have a value of unity at t = 0. |
An interesting feature of Fig. 2 is that the unsigned flux, and the magnetic energy density at z = 0 almost evolve in parallel. This runs against the naive expectation that if the magnetic field decays at a rate α, so that B ~ exp(−αt) then B2 ~ exp(−2αt), suggesting that the magnetic energy should decay twice as fast as the unsigned magnetic flux. The reason why this relation does not hold can be seen qualitatively in Fig. 1: a significant amount of the magnetic flux is concentrated in a number of features and it is the number of such features, rather than the field strength in the features, which decreases in time. Therefore both the unsigned flux and the energy are proportional to the number of features and thus decay in parallel. This interpretation is confirmed in Fig. 3, where we see that the percentage of surface magnetic energy corresponding to the different field strengths varies only weakly for the first 2 h. In the third hour we begin to see an increasing contribution from weak field regions, as the number of strong-field elements diminishes. In particular we note that at 200 min there are only two reasonably strong magnetic features, one of each polarity, left (cf. Fig. 1, bottom panels).
 |
Fig. 3 The percentage contribution to the total surface magnetic energy density per 100 Gauss, at different field strengths for different times (2 × 2 reference case). |
Returning to Fig. 2, the total magnetic energy in the entire computational domain decays faster than the surface energy densities and flux. We have estimated the decay rates by fitting an exponential function over the period from t = 30 min to t = 120 min. This period was chosen so that the initial phase, during which flux expulsion acts to increase the energy, is excluded. The e-folding time for the surface flux and magnetic energy, derived from the fits, is 70 min. The e-folding time for the magnetic energy over the entire domain is 52 min. The ratio between the decay rates of surface and volume integrated quantities is thus approximately 0.74, which is intermediate between the naive expectation of 0.5 and the expectation from magnetic elements of 1. This indicates that the magnetic structures become more volume filling (less intermittent) with depth.
To characterize the decay in terms of a turbulent diffusivity, we consider the two-dimensional linear diffusion equation, ∂Bz/∂t = ηeff∇2Bz, where Bz is the vertical component of the field on the plane z = 0. An assumption here is that the vertical flux diffuses as a passive scalar. The slowest decaying eigenmode with the symmetries of the initial condition has a spatial dependence sin(2πx/L)sin(2πy/L) where L = 6000/ km is the wavelength. The e-folding rates determined from the simulation can then be used to evaluate ηeff = 145 km2 s-1, which is about a factor of 13 larger than the explicit diffusivity in the simulation.
km is the wavelength. The e-folding rates determined from the simulation can then be used to evaluate ηeff = 145 km2 s-1, which is about a factor of 13 larger than the explicit diffusivity in the simulation.
The reconnection of the magnetic structures takes place when magnetic structures of opposite polarity come into close proximity.
An example of such a reconnection event is shown in Fig. 4, where two opposite-polarity magnetic features have been brought into contact in an intergranular lane.
The reconnection, which occurs above the surface, has locally heated the plasma. The strong down flows in the upper photosphere are the result of the retraction of inverse-U loops (see Fig. 5) due to magnetic tension. Since the reconnection occurs close to the upper boundary, the corresponding U loops are rapidly removed from the system so that their signature in this reconnection event is very weak.
 |
Fig. 4 Time series of a reconnection event (2 × 2 run, non-grey), approximately 30 min after introduction of magnetic field. The time between snapshots is 30 s. From top to bottom are the vertical component of the magnetic field, the vertical component of the velocity, the temperature and lastly the bolometric intensity. The first three quantities are shown at two heights, near z = 0 km (lower rows) and near z = 300 km (upper rows). The horizontal extent of the maps is 1.75 × 1.75 Mm2. The intensity timeseries corresponds to the continuum intensity at 500 nm. The greyscale for the magnetic field covers the range from –530 G to +530 G at z = 300 km and from –1760 G to 1760 G at z = 0; the velocity range is from –7 km s-1 to 7 km s-1 at z = 300 km and –9 km s-1 to 9 km s-1 at z = 0; the temperature range is from 4000° (blue) to 7500° (red) at z = 300 km and 5000° to 10 000° at z = 0; and the intensity varies between 0.65 and 1.5 of the averge quiet Sun value. |
A detailed description of the process involved and their observational signatures has been given by Danilović (2009). The time scale for the individual reconnection events is of the order of 10 min, which is short compared to the decay rates found here. In what follows we concentrate on the statistical properties of the decay of the field rather than on the detailed reconnection processes. To do so we consider magnetic field lines, which are described by the function X, with ![\begin{equation} \frac{{\rm d} {\vec X}(s,x_0,y_0,z_0)}{{\rm d} s}= \frac{{\vec B}\left[ {\vec X}\left(s\right)\right]} {|{\vec B}\left[ {\vec X}\left(s\right)\right]| + \epsilon} \end{equation}](/articles/aa/full_html/2011/09/aa16974-11/aa16974-11-eq40.png) (3)and
(3)and 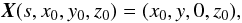 (4)where ϵ = 10-5 prevents problems where B = 0 and s is a coordinate along the field line, and x0,y0,z0 is point in space corresponding to s = 0 and the constant ϵ = 10-5 G prevents problems where B = 0. In regions where B ≫ ϵ, s is the length along the field line.
(4)where ϵ = 10-5 prevents problems where B = 0 and s is a coordinate along the field line, and x0,y0,z0 is point in space corresponding to s = 0 and the constant ϵ = 10-5 G prevents problems where B = 0. In regions where B ≫ ϵ, s is the length along the field line.
For our analysis we consider the set of field lines passing through the centre of each grid cell, i.e., we consider 288 × 288 × 100 values of { x0,y0,z0 } . This mean that near t = 0 each cell will be sampled by 100 field lines, each of which will pass through the centre of at least one cell. As time progresses stronger field regions will become even more oversampled and weak-field regions less sampled. At all times however each cell will be sampled by at least one field line. Through this we are able to capture cells which contain field lines entering and leaving the computational box through different boundaries. For each field line, we integrate Eq. (3) numerically using a fixed step size Δs = 3.5 km until the field line exits the domain through either the upper or lower boundary1. Since the box is periodic in the horizontal directions almost all of the field lines pass through the upper or lower boundary.
 |
Fig. 5 The colored lines are a 3D visualization of field lines at beginning of the reconnection event shown in the 4. The grey-scale corresponds to the vertical component of the field at z = 0. The left panel is a side view, the right panel is a top view. |
The connectivity of the field line is defined by the boundary where it enters and leaves the computational box. A connectivity map is then created by considering the connectivity of all field lines. Since initially the field lines are all purely vertical, they can be classified as passing from the top to the bottom of the box or from the bottom to the top. As reconnection take place, some of these field lines are converted into U and inverse-U loops. Cells can contain field lines with different types of connectivities.
The loops can then retract and leave through the boundaries of the simulation domain. Figure 6 illustrates the connectivity of the field lines at three different heights for a time just after the initial period of flux expulsion and late in the simulation (at 16 and 142 min, respectively). The plane at height z = 420 km is in the upper photosphere, where the density has fallen considerably so that the magnetic tubes fan out and become smooth and space filling. The lowest layer, at z = −420 km, is within the convection zone, where the plasma motions dominate the magnetic field. Hence the magnetic field is more tangled and the connectivity map is more complicated.
 |
Fig. 6 Field line connectivities at 3 heights (from bottom to top: z = −420 km, z = 0 and z = 420 km). As described in the text, field lines were traced from the centre of each of the 288 × 288 × 100 grid cells, so that on average each cell contains many field lines. The left panels correspond to t = 16 min, the right panels to t = 142 min of simulated time. White indicates areas where field lines pass from the bottom of the box to the top. Grey shows areas where field lines run from the top of the box to the bottom. Green indicates cells where all field lines have both legs passing through the bottom of the box (inverse-U loops). Blue indicates U loops with both legs passing through the upper surface. Light (dark) green indicates the presence of both inverse-U loops and field lines running from the bottom of the box to the top (top to bottom), within one grid cell. Light and dark blue regions are similarly defined but for U loops. The orange regions indicate where at least three types of field lines pass through a single grid cell. |
In the connectivity maps 16 min, the initial checkerboard arrangement is still visible at all heights. Inverse-U loops, both ends of which connect through the lower boundary are present mainly near the borders of the opposing polarities, indicating that reconnection has taken place. The U loops, both ends of which leave through the upper boundary mainly occur in the layers above the visible surface. The maps at 142 min are similar, except that the inverse-U loops are present over an even wider region of space and the initial checkerboard pattern is less obvious.
The predominance of inverse-U loops over U loops is a consequence of the fact that the reconnection occurs mainly above the optical surface, where the plasma beta is low and the magnetic field concentrations, expanding to become space filling, first come into contact with each other. The U loops then contain little mass and are quickly pulled upwards by the comparitatively strong tension force. The inverse-U loops, on the other hand, once they are pulled below the τ = 1 level, are loaded with the mass from the subphotosphere and the tension force does not dominate over the other forces in this subsurface region. Magnetic tension is dominant in the current sheets in the low-β region above the surface.
The retraction of the inverse-U loops is thus a much slower process. This explains the time evolution of the amount of flux in the different types of connectivities shown in Fig. 7. Between t = 16 min and t = 142 min, the amount of unsigned flux corresponding to each type of connectivity at all heights has fallen substantially. The slowest decay is seen for the inverse-U loops, where the unsigned flux has fallen by a factor of approximately 3 below the τ = 1 height and by a factor of 3−5 above. The unsigned flux associated with top-to-bottom and bottom-to-top field lines in the same time has fallen by a factor of approximately 7, and the decrease in the flux of the U loops is even more dramatic. This reflects the fact that removal of U loops is a much faster process than the removal of inverse-U loops. Importantly, if the reconnection were mainly occuring in the sub-photospheric region, then the U loops would also be loaded with substantial mass and would only escape much more slowly, so that they would be more abundant.
 |
Fig. 7 Unsigned flux density as a function of height for the four connectivities. The solid lines correspond to the top-bottom and bottom-top connectivities, the dashed lines to inverse-U loops, and the dot-dashed line to U loops. The upper panel is for t = 16 min, soon after the initial transient phase. Already a substantial amount of inverse-U loop flux has been generated. The lower panel is for t = 142 min. The top-bottom and bottom-top connectivities use the same linestyle to reflect the B → (−B) symmetry of the MHD equations. |
3.2. 2 × 1 initial condition.
We now consider the value of ηeff based on the evolution from an initial condition consisting of two stripes (2 × 1) of opposite-polarity magnetic field. Again we quantify the decay rate by considering the decay of the total magnetic energy in the computational domain. This is plotted in Fig. 8. The e-folding time for the decay is found to be 1hr 57 min. The dominant wavelength is 6000 km, so that the estimate for the turbulent diffusivity becomes ηeff = 129 km2 s-1.
 |
Fig. 8 Time evolution of the total magnetic energy starting from the 2 × 1 (striped) initial condition. The curve from the 2 × 2 (reference) case is reproduced for comparison. |
3.3. Upper boundary conditions
We also consider the effect of varying the upper boundary condition on the decay rate. For the magnetic field we assume vertical or matched-to-potential boundary conditions; for the flows we consider either closed or open conditions, following Stein & Nordlund (1998) and Bercik (2002). We also vary the height at which the boundary condition is imposed (z ≈ 600 km above the τ = 1 level to z ≈ 840 km). In each case, we use the 2 × 2 initial condition as in the reference case.
The decay of the total magnetic energy for the different cases can be seen in in Fig. 9. The e-folding time for the magnetic energy and the estimated turbulent diffusivities are listed in Table 1. The values for the turbulent diffusivity resulting from the use of different upper boundary conditions vary by a factor of 3, from 145 km2 s-1 for the vertical field, closed boundary applied at z ≈ 600 km to 341 km2 s-1 for the potential field, open boundary applied at z ≈ 840 km.
Summary of magnetic energy decay rates and ηeff.
 |
Fig. 9 Time evolution of the total magnetic energy for the 2 × 2 case with several different upper boundary conditions located at one of two heights. The “normal, closed, vertical” case refers to our standard 2 × 2 run. The “normal, closed, potential” refers to a case where the magnetic field was matched to a potential field at the top boundary. For the “tall” cases the top boundary was moved upwards by 280 km, and “open” refers to cases where flow, temperature and pressure were smoothly extrapolated through the upper boundary. |
3.4. Explicit magnetic diffusivity parameter, η
We investigated the role of the explicit value of the input parameter η by performing a simulation with twice as many grid points in the horizontal directions and with η = 5.6 km2 s-1. The initial condition was the same as in the reference case, and the time evolution is shown in Fig. 10. The fit to the total energy corresponds to an e-folding time of 1hr 15 min, and hence an effective diffusivity ηeff = 101 km2 s-1. We note that the the fit to the curve in Fig. 10 is sensitive to the time interval over which the fit was made. Fitting over the interval 30−180 min leads to essentially the same estimate for ηeff as was obtained for the 2 × 2 reference case. In this regard it is worth noting that the late-stage evolution in most cases is different from that in the first 2 h or so. This is presumably due to the fact that the random motions move energy from those present in the initial condition modes (e.g. 2 × 2) into other modes (e.g. 1 × 2 or 3 × 2). When these modes dominate the decay, a different decay rate is to be expected.
 |
Fig. 10 Time evolution of the total magnetic energy for a checkerboard (2 × 2) run with η = 5.6 as a function of time. The same curve from the reference case is shown for comparison. |
4. Discussion
The values of ηeff derived from the various runs and listed in Table 1 are within the range deduced from observations over a much larger spatial extent and longer time period (see Schrijver & Zwaan 2000, Table 6.2). To understand the differences between the estimated values of ηeff (i.e. the decay rates) for the different simulation setups, we note that the removal of flux in these simulations is primarily determined by the rate at which opposite polarity patches are brought close enough to one another for the explicit diffusivity to become effective. The differences between the values of ηeff can be understood in terms of how close the magnetic polarities need to come for rapid diffusion to set in. In loose terms this can be rephrased in terms of a “collisional cross section” of the magnetic elements. When we use the potential boundary condition, the magnetic field expands rapidly near the upper boundary, and hence magnetic elements which are still separated near the surface can still come into contact in the upper layers. This is the reason why the reconnection mostly takes place above the surface. It also explains, qualitatively, why the potential boundary condition leads to a higher ηeff then was found in the reference case.
We may compare the values of ηeff with the estimate, ηturb ~ vrmsLcorr/3, for the diffusion of a passive scalar subject to random motions. In this estimate vrms is the rms velocity of the random motions and Lcorr is the correlation length scale of the motions. The first question is then which motions to consider. Since we are mainly concerned with the horizontal motions of the magnetic flux tubes we consider only the horizontal velocity field in a z = 0 slice from the simulations. The rms horizontal velocity is then 2.4 km s-1. However, for the horizontal transport of the flux concentrations in the intergranular lanes, the random horizontal motion of the granules is the relevant quantity. The corresponding rms value, for example as determined by local correlation tracking, is about a factor of two smaller than the above value (Rieutord et al. 2001; Georgobiani et al. 2007; Matloch et al. 2010), i.e. vrms = 1.2 km s-1. For the correlation length of the horizontal velocity, we take Lcorr = 1 Mm, which is about the size of a granule. These values yield ηeff = 400 km2 s-1. This very simple, approximate value is slightly above the actual range of values found in the simulations.
5. Conclusions
We have studied the decay of simple arrangements of magnetic field in the near-surface layers of the Sun. We found that magnetic field is removed from the surface when magnetic elements of opposite polarity, advected by the granular flows, come into close proximity above the surface. Reconnection then produces U loops, which quickly escape through the upper boundary, and inverse-U loops, which retract more slowly into the subphotosphere.
During most of the decay phase, the relative contributions of magnetic energy coming from different field strengths are largely independent of the amount of flux. A weak field tail, however, does appear late in the evolution, when the unsigned flux levels are very low.
The decay of the magnetic field is reasonably well described by turbulent diffusion concept with plausible values of ηeff. The value of ηeff was found to depend on the upper boundary condition. The potential-field, open-boundary condition applied to the tall box is probably the most realistic in this regard. This case has ηeff ≈ 340 km2 s-1. The range of values from the different simulations, from 100 to 340 km2 s-1, gives an indication of the uncertainty due to, for example, the choice of the upper boundary condition.
References
- Bercik, D. J. 2002, Ph.D. Thesis, Michigan State University [Google Scholar]
- Borrero, J. M., Martínez-Pillet, V., Schlichenmaier, R., et al. 2010, ApJ, 723, L144 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, R., Schüssler, M., Vögler, A., & Zakharov, V. 2007, A&A, 474, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Centeno, R., Socas-Navarro, H., Lites, B., et al. 2007, ApJ, 666, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Cheung, M. C. M., Schüssler, M., Tarbell, T. D., & Title, A. M. 2008, ApJ, 687, 1373 [NASA ADS] [CrossRef] [Google Scholar]
- Cheung, M. C. M., Rempel, M., Title, A. M., & Schüssler, M. 2010, ApJ, 720, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Danilović, S. 2009, Ph.D. Thesis, University of Göttingen [Google Scholar]
- Danilovic, S., Beeck, B., Pietarila, A., et al. 2010a, ApJ, 723, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Danilovic, S., Schüssler, M., & Solanki, S. K. 2010b, A&A, 509, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovic, S., Schüssler, M., & Solanki, S. K. 2010c, A&A, 513, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Pontieu, B. 2002, ApJ, 569, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Georgobiani, D., Zhao, J., Kosovichev, A. G., et al. 2007, ApJ, 657, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Hagenaar, H. J., Schrijver, C. J., & Title, A. M. 2003, ApJ, 584, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Ishikawa, R., Tsuneta, S., & Jurčák, J. 2010, ApJ, 713, 1310 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, C. U., Schüssler, M., Vögler, A., & Zakharov, V. 2004, ApJ, 607, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Khomenko, E. V., Shelyag, S., Solanki, S. K., & Vögler, A. 2005, A&A, 442, 1059 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kubo, M., Low, B. C., & Lites, B. W. 2010, ApJ, 712, 1321 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez González, M. J., Collados, M., Ruiz Cobo, B., & Solanki, S. K. 2007, A&A, 469, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matloch, Ł., Cameron, R., Shelyag, S., Schmitt, D., & Schüssler, M. 2010, A&A, 519, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pietari la Graham, J., Danilovic, S., & Schüssler, M. 2009, ApJ, 693, 1728 [Google Scholar]
- Pietari la Graham, J., Cameron, R., & Schüssler, M. 2010, ApJ, 714, 1606 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M., Schüssler, M., Cameron, R. H., & Knölker, M. 2009a, Science, 325, 171 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rempel, M., Schüssler, M., & Knölker, M. 2009b, ApJ, 691, 640 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M., Roudier, T., Ludwig, H., Nordlund, Å., & Stein, R. 2001, A&A, 377, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schrijver, C. J., & Zwaan, C. 2000, Solar and stellar magnetic activity (Cambridge University Press) [Google Scholar]
- Schüssler, M., & Vögler, A. 2006, ApJ, 641, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., Barthol, P., Danilovic, S., et al. 2010, ApJ, 723, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F., & Nordlund, A. 1998, ApJ, 499, 914 [Google Scholar]
- Vögler, A., & Schüssler, M. 2007, A&A, 465, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yelles Chaouche, L., Cheung, M. C. M., Solanki, S. K., Schüssler, M., & Lagg, A. 2009, A&A, 507, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Time evolution of Bz on the plane z = 0, corresponding to the average height of the optical surface (left panels) and the bolometric brightness (right panels) for the reference (2 × 2) case at 4 min (top), 80 min (middle), and 200 min (bottom) after introduction of the initial field. The average unsigned magnetic field for these snapshots corresponds to about 200 G, 50 G, and 10 G, respectively. |
| In the text | |
 |
Fig. 2 Decay of total magnetic energy in the entire simulation box, and of unsigned vertical magnetic flux at z = 0 for the reference case. The thin lines are exponential fits. All curves have been normalized such that the fits have a value of unity at t = 0. |
| In the text | |
 |
Fig. 3 The percentage contribution to the total surface magnetic energy density per 100 Gauss, at different field strengths for different times (2 × 2 reference case). |
| In the text | |
 |
Fig. 4 Time series of a reconnection event (2 × 2 run, non-grey), approximately 30 min after introduction of magnetic field. The time between snapshots is 30 s. From top to bottom are the vertical component of the magnetic field, the vertical component of the velocity, the temperature and lastly the bolometric intensity. The first three quantities are shown at two heights, near z = 0 km (lower rows) and near z = 300 km (upper rows). The horizontal extent of the maps is 1.75 × 1.75 Mm2. The intensity timeseries corresponds to the continuum intensity at 500 nm. The greyscale for the magnetic field covers the range from –530 G to +530 G at z = 300 km and from –1760 G to 1760 G at z = 0; the velocity range is from –7 km s-1 to 7 km s-1 at z = 300 km and –9 km s-1 to 9 km s-1 at z = 0; the temperature range is from 4000° (blue) to 7500° (red) at z = 300 km and 5000° to 10 000° at z = 0; and the intensity varies between 0.65 and 1.5 of the averge quiet Sun value. |
| In the text | |
 |
Fig. 5 The colored lines are a 3D visualization of field lines at beginning of the reconnection event shown in the 4. The grey-scale corresponds to the vertical component of the field at z = 0. The left panel is a side view, the right panel is a top view. |
| In the text | |
 |
Fig. 6 Field line connectivities at 3 heights (from bottom to top: z = −420 km, z = 0 and z = 420 km). As described in the text, field lines were traced from the centre of each of the 288 × 288 × 100 grid cells, so that on average each cell contains many field lines. The left panels correspond to t = 16 min, the right panels to t = 142 min of simulated time. White indicates areas where field lines pass from the bottom of the box to the top. Grey shows areas where field lines run from the top of the box to the bottom. Green indicates cells where all field lines have both legs passing through the bottom of the box (inverse-U loops). Blue indicates U loops with both legs passing through the upper surface. Light (dark) green indicates the presence of both inverse-U loops and field lines running from the bottom of the box to the top (top to bottom), within one grid cell. Light and dark blue regions are similarly defined but for U loops. The orange regions indicate where at least three types of field lines pass through a single grid cell. |
| In the text | |
 |
Fig. 7 Unsigned flux density as a function of height for the four connectivities. The solid lines correspond to the top-bottom and bottom-top connectivities, the dashed lines to inverse-U loops, and the dot-dashed line to U loops. The upper panel is for t = 16 min, soon after the initial transient phase. Already a substantial amount of inverse-U loop flux has been generated. The lower panel is for t = 142 min. The top-bottom and bottom-top connectivities use the same linestyle to reflect the B → (−B) symmetry of the MHD equations. |
| In the text | |
 |
Fig. 8 Time evolution of the total magnetic energy starting from the 2 × 1 (striped) initial condition. The curve from the 2 × 2 (reference) case is reproduced for comparison. |
| In the text | |
 |
Fig. 9 Time evolution of the total magnetic energy for the 2 × 2 case with several different upper boundary conditions located at one of two heights. The “normal, closed, vertical” case refers to our standard 2 × 2 run. The “normal, closed, potential” refers to a case where the magnetic field was matched to a potential field at the top boundary. For the “tall” cases the top boundary was moved upwards by 280 km, and “open” refers to cases where flow, temperature and pressure were smoothly extrapolated through the upper boundary. |
| In the text | |
 |
Fig. 10 Time evolution of the total magnetic energy for a checkerboard (2 × 2) run with η = 5.6 as a function of time. The same curve from the reference case is shown for comparison. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


