| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201116636 | |
| Published online | 18 August 2011 | |
Nebular and global properties of the gravitationally lensed galaxy “the 8 o’clock arc”⋆,⋆⋆
1
Observatoire de Genève, Université de Genève,
51 Ch. des Maillettes,
1290
Sauverny,
Switzerland
e-mail: miroslava.dessauges@unige.ch
2
Excellence Cluster Universe, Technische Universität München, Bolzmanstrasse 2,
85748
Garching,
Germany
3
European Southern Observatory, Karl-Schwarzschildstrasse 2, 85748
Garching,
Germany
4
Laboratoire d’Astrophysique de Toulouse-Tarbes, Université de
Toulouse, CNRS, 14 Avenue E.
Belin, 31400
Toulouse,
France
5
Dark Cosmology Center, Niels Bohr Institute, University of
Copenhagen, Juliane Maries Vej
30, 2100
Copenhagen,
Denmark
6
Centre de Recherche Astrophysique de Lyon, Université Lyon 1,
Observatoire de Lyon, 9 Avenue
Charles André, 69561
Saint Genis Laval Cedex,
France
Received:
2
February
2011
Accepted:
27
May
2011
We present the analysis of new near-infrared, intermediate-resolution spectra of the
gravitationally lensed galaxy “the 8 o’clock arc” at
zsys = 2.7350 obtained with the X-shooter spectrograph on the
Very Large Telescope. These rest-frame optical data, combined with Hubble
and Spitzer Space Telescopes images, provide very valuable
information, which nicely complement our previous detailed rest-frame UV spectral
analysis, and make the 8 o’clock arc one of the better understood “normal” star-forming
galaxies at this early epoch of the history of the Universe. From high-resolution HST
images, we reconstruct the morphology of the arc in the source plane, and identify that
the source is formed of two majors parts, the main galaxy component and a smaller blob
separated by 1.2 kpc in projected distance. The blob, with a twice larger magnification
factor, is resolved in the X-shooter spectra. The multi-Gaussian fitting of detected
nebular emission lines and the spectral energy distribution modeling of the available
multi-wavelength photometry provide the census of gaseous and stellar dust extinctions,
gas-phase metallicities, star-formation rates (SFRs), and stellar, gas, and dynamical
masses for both the main galaxy and the blob. As a result, the 8 o’clock arc shows a
marginal trend for a more attenuated ionized gas than stars, and supports a dependence of
the dust properties on the SFR. With a high specific star-formation rate,
SSFR = 33 ± 19 Gyr-1, this lensed Lyman-break galaxy
deviates from the mass-SFR relation, and is characterized by a young age of
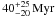 and a
high gas fraction of about 72%. The 8 o’clock arc satisfies the fundamental mass, SFR, and
metallicity relation, and favors that it holds up beyond z ≃ 2.5. We
believe that the blob, with a gas mass
Mgas = (2.2 ± 0.9) × 109 M⊙
(one order of magnitude lower than the mass of the galaxy), a half-light radius
r1/2 = 0.53 ± 0.05 kpc, a star-formation rate
SFRHα = 33 ± 19 M⊙ yr-1,
and in rotation around the main core of the galaxy, is one of these star-forming clumps
commonly observed in z > 1 star-forming galaxies, because it is
characterized by very similar physical properties. The knowledge of detailed physical
properties of these clumps is a very useful input to models that aim to predict the
formation and evolution of these clumps within high-redshift objects.
and a
high gas fraction of about 72%. The 8 o’clock arc satisfies the fundamental mass, SFR, and
metallicity relation, and favors that it holds up beyond z ≃ 2.5. We
believe that the blob, with a gas mass
Mgas = (2.2 ± 0.9) × 109 M⊙
(one order of magnitude lower than the mass of the galaxy), a half-light radius
r1/2 = 0.53 ± 0.05 kpc, a star-formation rate
SFRHα = 33 ± 19 M⊙ yr-1,
and in rotation around the main core of the galaxy, is one of these star-forming clumps
commonly observed in z > 1 star-forming galaxies, because it is
characterized by very similar physical properties. The knowledge of detailed physical
properties of these clumps is a very useful input to models that aim to predict the
formation and evolution of these clumps within high-redshift objects.
Key words: cosmology: observations / galaxies: individual: 8 o’clock arc / galaxies: high-redshift / gravitational lensing: strong
© ESO, 2011
1. Introduction
With the advent of the 8–10 m class optical telescopes on the ground and of the latest generation of space observatories working from X-rays to far-infrared (IR) wavelengths, it has become possible to carry out multi-wavelength spectroscopy and imaging of thousands of galaxies at redshifts between 2 and 4, namely at the peak of the star-formation history of the Universe. In particular, star-forming galaxies, known also as Lyman-break galaxies (LBGs), easily identified by a break in their ultraviolet (UV) continuum that is caused by the Lyman limit from intergalactic and interstellar H i absorption below 912 Å, have been the targets of most studies (Steidel et al. 1996). At z > 2 their absorption from the intergalactic medium (IGM) is more pronounced and the galaxy UV flux is redshifted toward optical wavelengths, where the ground-based telescopes and their instruments have their maximum detection efficiency, and the blocking effect of the atmosphere and the emission from the night sky have its minimum. Color and low-resolution spectral information has been gathered for many of these generally faint galaxies (R ≃ 24.5 at z ~ 3), whereas very long integration times are required, even at the larger telescopes, to acquire intermediate-resolution spectra, which are yet needed to derive their detailed individual physical properties. To gain insights on their average properties, one is thus mostly forced to rely on stacked low-resolution spectra (Shapley et al. 2003; Vanzella et al. 2009).
Instead of waiting for the next-generation telescopes with large collecting areas to obtain good resolution, good signal-to-noise ratio spectra of LBGs, we can take advantage of the light magnification provided by gravitational lensing. In the best cases, the background galaxies can benefit of a boost of their total flux by a factor of 30−50. This implies that intermediate-resolution spectroscopy of individual galaxies, which are intrinsically 3−4 mag fainter than they appear at the telescope, becomes achievable with current instrumentation. As an important byproduct, this approach gives access to a more representative range of the luminosity function of galaxies at z ~ 2−4.
 |
Fig. 1 Left. WFPC2/F450W black/white image of the 8 o’clock arc showing the positions of the four lensed images of the main galaxy component in red and the blob in blue. The two brightest images labeled A2 and A3 were targeted for spectroscopy with X-shooter. The large ellipse corresponds to the external critical line at the redshift of the arc as derived from lens modeling (Sect. 3.2). Right. WFPC2/F450W-F650W-F814W composite-color image showing the reconstructed morphology of the 8 o’clock arc in the source plane, as derived from the best-fit lens model. The source is formed of two major parts, the main galaxy component (on the left) and a smaller blob (on the right) separated by 0.15 arcsec, or equivalently 1.2 kpc in projected distance. The blob has a twice higher magnification factor than the main galaxy component. In both panels, the horizontal scale bar refers to 1 arcsec. |
A handful of studies of these highly magnified star-forming galaxies yielded the physical properties of their stellar population and their interstellar medium (ISM), as well as their dynamical properties. Pettini et al. (2002) pioneered this study approach with the extraordinary bright LBG MS 1512-cB58 (see also Pettini et al. 2000; Teplitz et al. 2000; Savaglio et al. 2002). In the last decade, new search techniques applied to the Sloan Digital Sky Survey (SDSS) and Hubble Space Telescope (HST) images led to the identification of new strongly-lensed, high-redshift galaxies. The brightest galaxies were already targeted for detailed studies at rest-frame UV and/or optical wavelengths (Lemoine-Busserolle et al. 2003; Swinbank et al. 2007, 2009; Stark et al. 2008; Cabanac et al. 2008; Hainline et al. 2009; Quider et al. 2009, 2010; Pettini et al. 2010; Christensen et al. 2010; Jones et al. 2010; Bian et al. 2010; Rigby et al. 2011; Richard et al. 2011). In the era where one of the major objectives of astrophysics is to determine the precise physical properties of high-redshift, star-forming galaxies, the analysis of strongly-lensed LBGs provide very complementary results and informations to the huge efforts done with galaxies selected in blank fields (e.g., Erb et al. 2006a,b,c; Law et al. 2007; Maiolino et al. 2008; Genzel et al. 2008; Mannucci et al. 2009; Förster Schreiber et al. 2006, 2009).
Among the highly magnified objects, a particularly interesting target is the “8 o’clock arc”, discovered by Allam et al. (2007). The lensing by the z = 0.38 luminous red galaxy SDSS J002240.91+143110.4 distorts this Lyman-break galaxy at zsys = 2.7350 into four separate images that correspond to four different images of the same object. Three of them, labeled A1, A2, and A3, form a partial Einstein ring of radius θE = 3.32″ ± 0.16″, extending over 9.6″ in length (see Fig. 1, left-hand panel). Finkelstein et al. (2009) carried out a comprehensive study of the 8 o’clock arc with the help of low-resolution spectra from UV to the K band. In a first paper (Dessauges-Zavadsky et al. 2010, hereafter DZ10) we used intermediate-resolution spectra obtained with the newly installed X-shooter spectrograph (D’Odorico et al. 2006) that cover the observed range from 320 to 1000 nm to further improve the knowledge of properties of this lensed LBG. We derived its stellar and ISM metallicities for the first time and highlighted the main ISM line similarities and differences observed among the few lensed LBGs studied in detail so far. The high quality of the data allowed us also to model the Lyα line profile with 3D radiation transfer codes, and to obtain results fully consistent with the scenario proposed earlier, in which the diversity of Lyα line profiles in LBGs and Lyα emitters, from absorption to emission, can mostly be explained by H i column density and dust content variations (Verhamme et al. 2006, 2008).
In this paper we use new X-shooter observations, which now include the near-infrared spectral range and cover the nebular emission lines of the 8 o’clock arc, and archive HST and Spitzer imaging data to complete our detailed picture of this unique galaxy. The new physical and morphological properties derived make the 8 o’clock arc one of the most deeply studied “normal” star-forming galaxies at this early epoch of the history of the Universe. In Sect. 2 we present the spectroscopic and imaging observations, and the corresponding data reduction procedures. In Sect. 3 we deal with the photometry and the analysis of spectra, in particular we provide the gravitational lens model of the arc and the fits of the nebular emission lines with multi-Gaussian profiles. In Sect. 4 we revisit the properties of the galaxy (dust extinction, metallicity, star-formation rate, age, and stellar, gas, and dynamical masses) as derived from the combination of spectroscopic and imaging data. A final summary of the results and their discussion is presented in Sect. 5. Throughout the paper, we assume a Λ-CDM cosmology with ΩΛ = 0.73, ΩM = 0.27 and h = 0.71. All magnitudes are given in the AB system.
2. Observations and data reduction
2.1. X-shooter spectroscopy
X-shooter is the first of the second-generation instruments on the Very Large Telescope (VLT) at Cerro Paranal, Chile, in operation at the European Southern Observatory (ESO) since October 2009. It consists of three Echelle spectrographs with prism cross-dispersion, mounted on a common structure at the Cassegrain focus of the Unit Telescope 2. The light beam from the telescope is split by two dichroics that direct the light in the spectral ranges of 300−560 nm and 560−1015 nm to the slit of the ultraviolet-blue (UV-B) and visual-red (VIS-R) spectrographs, respectively. The undeviated beam in the spectral range of 1025−2400 nm feeds the near-infrared (NIR) spectrograph. A full description of the instrument is provided by Vernet et al. (2010).
A first set of X-shooter observations of the 8 o’clock arc, made solely with the UV-B and VIS-R spectrograph arms, was obtained during the first commissioning run in November 2008, and allowed a detailed analysis of the rest-frame UV spectrum of this lensed LBG (see DZ10). In November and December 2009, we got additional observations in director’s discretionary time (program ID No. 284.A–5006(A)) to complete the 8 o’clock arc data set with the NIR spectrograph arm and to obtain the rest-frame optical spectrum. The 11″ long entrance slit was rotated to the same position angles on the sky as for the first set of observations, PA = 121° and 13° aligned along the 8 o’clock images A2 and A3 and along the image A2 and the galaxy lens, respectively (see Fig. 1 in DZ10). A total exposure time of 4 × 1200 s per position angle was obtained in good conditions, with clear sky, seeing <1″, and airmass <1.6. Slit widths of 1.3″ in the UV-B, 1.2″ in the VIS-R, and 0.9″ in the NIR were used, corresponding to resolving powers R ≡ λ/Δλ = 4000, 6700, and 5600, respectively. The observations used a nodding along the slit approach, with a typical offset between individual exposures of 5″ for PA = 121° and 3″ for PA = 13°, adapted to avoid any overlapping in the combination of consecutive exposures.
The data were reduced with a preliminary version of the ESO X-shooter pipeline (Goldoni et al. 2006; Modigliani et al. 2010). Bad pixels were found using calibration frames, and cosmic ray hits were detected and cleaned using the L.A. Cosmic routine (van Dokkum 2001). In the NIR arm, the sky background emission was subtracted with the help of adjacent exposures where the two components, either A2−A3 or A2−galaxy lens, were offset along the slit. Then, the data were flat-fielded, and wavelength-calibrated, and the trace of each order detected using calibration frames. The final products from the pipeline are 2D rectified spectra with the individual orders merged in a weighted scheme, using the error spectra derived and propagated in the pipeline.
The respective 1D spectra of the images A2 and A3 of the 8 o’clock arc were extracted from the 2D pipeline-produced spectra, using adapted extraction windows. They were then co-added using their signal-to-noise ratios (S/N) as weights, when several exposures of the same lensed image observed with the same spectrograph arm and at the same position angle were available. Preliminarily the 1D NIR spectra were corrected for telluric absorption by dividing them by the normalized spectra of the B5V star Hip022840 and the B5 star Hip023946, observed with the same instrumental set-up and at approximately the same airmass as the 8 o’clock arc1. Absolute flux calibration applied to the NIR spectra was based on the standard star BD+17 4708 whose spectrum was recorded during the same nights as the 8 o’clock arc. To derive the transmission of X-shooter, we used the fluxes of this star measured with the HST as reference (Bohlin 2007).
2.2. HST imaging
We made use of the high-resolution optical and NIR imaging data taken with the Wide Field Planetary Camera 2 (WFPC2) and Near Infrared Camera and Multi-Object Spectrometer 2 (NICMOS2) instruments on the Hubble Space Telescope, which are available from the HST archive under the program ID No. 11167 (PI: S. S. Allam). The 8 o’clock arc is clearly resolved, and was observed in five bands B, V, I, J, and H, with the respective filters WFPC2/F450W, WFPC2/F606W, WFPC2/F814W, NIC2/F110W, and NIC2/F160W. A total exposure time of 4 × 1100 s per BVI bands, 5120 s in the J band, and 4 × 1280 s in the H band was obtained and consists of independent frames. The WFPC2 BVI frames, with a pixel scale of 0.1″, were arranged in a four-point dither pattern, with random dithered offsets between individual exposures within 1″ in right ascension and declination. The NICMOS2 JH frames, with a pixel scale of 0.075″, were also arranged in a four-point dither pattern, but with offsets between individual exposures of 2.5″.
To combine independent WFPC2 frames into a final frame for each band and reject cosmic ray hits, we used the drizzle routine of Fruchter & Hook (2002), which also corrects for instrument geometric distortions. In the drizzling, we chose the parameters pixfrac = 0.8 and scale = 1.0 to be able to effectively remove noisy pixels from cosmic ray hits, but also extract the morphological information of the lensed structure without introducing artifacts. The chosen parameters resulted in a point-spread function (PSF) FWHM of 0.18−0.2″ for the WFPC2 images. A similar procedure was used for the reduction of NICMOS2 frames, but a number of instrument-specific improvements were included (such as the flagging of hot/cold pixels), following the prescriptions given in Richard et al. (2008). This yielded a PSF FWHM of 0.12″ for the NICMOS2 images. All HST images were then registered onto one another, using bright isolated point sources in the common fields to ensure precise photometry over the same regions of the 8 o’clock arc.
3. Analysis
3.1. Photometry
Because the 8 o’clock arc is fully resolved in the HST images, we could derive the overall photometry in the multiple images of the lensed LBG and, in particular of A2 and A3 chosen for X-shooter spectroscopy. The measurements were performed using the SExtractor software (Berlin & Arnouts 1996) in the “double-image” mode. We used the WFPC2/F450W band as the detection image, and measured the fluxes in 1.0″ diameter apertures across all HST bands. The WFPC2/F450W band was chosen as the detection image because it offers the best contrast to detect the 8 o’clock arc images and to separate their light from the lensing luminous red galaxy. 1.0″ diameter apertures were chosen to match the 0.9″ slit width of the X-shooter NIR spectra, which then allow a direct comparison between HST images and ground based spectra. For NICMOS2 photometry, the WFPC2 images had to be first convolved with a Gaussian filter matching the slightly different FWHM of the NICMOS2 PSF. This ensured accurate color measurements between the WFPC2/F450W and NICMOS2 bands. Then, an estimate of the total flux of A2 and A3 was provided by MAGAUTO measured in the detection image. We checked from the segmentation image that the regions used by SExtractor for the flux measurements correspond well to the entire A2 and A3 counterparts in the image. We estimated an error of 0.1 mag in the absolute flux normalization, but this does not affect the colors used for the SED fitting (see Sect. 4.1). The final photometry of the lensed images A2 and A3, normalized to the absolute flux in the detection image, is given in Table 1.
HST and Spitzer photometry of the 8 o’clock arc images A2 and A3.
The 8 o’clock arc was also observed with the InfraRed Array Camera (IRAC) on the Spitzer Space Telescope in the 3.6, 4.5, 5.8 and 8.0 microns bands. The pre-reduced images are accessible in the Spitzer archive, and the final reduction steps are summarized in Richard et al. (2011). Similarly to what we describe above, we convolved the NICMOS2 images with the PSF of the IRAC frames, and measured the mean NIC2/F160W−IRAC colors over the lensed images A2 + A3, unresolved in the Spitzer images, using larger 3.0″ diameter apertures. Because of the size and distance of the lensing galaxy (located at less than 4″ from the midpoint between A2 and A3), its contamination appeared in the form of an additional background level, nearly constant at the locations where the IRAC colors of A2 + A3 were measured. This was removed when we made the photometric measurements. The comparison of the IRAC-PSF-convolved NIC2/F160W photometry with or without the central galaxy modeled and subtracted, however, leads to a contamination of less than 5% in the overall photometry. The derived IR colors are listed in Table 1.
 |
Fig. 2 Selection of nebular emission lines, free from strong atmospheric absorption, detected in the lensed image A2 (left-hand panels) and in the lensed image A3 (right-hand panels) of the 8 o’clock arc. In all panels, the black histogram represents the flux-calibrated data with 1σ errors as a function of vacuum-heliocentric-corrected wavelengths. The red continuous line is the best-fitted profile, and the red dotted line shows the fit of the two best individual Gaussian components with the respective parameters given in Table 3. The cyan shaded area represents 68% of the Monte Carlo runs, generated from the perturbation of the observed spectrum with a random realization of the error spectrum. The respective atmospheric transmission is plotted below each panel. The flux is set to zero (with large error bars) whenever the atmospheric transmission falls below 10%. |
3.2. Gravitational lens modeling
In order to derive accurate magnification factors and reconstruct the morphology of the
8 o’clock arc in the source plane, we had to correct for distortions produced by the
galaxy lens. To do so, we constructed the gravitational lens model of the system, using
the public software LENSTOOL (Kneib et al. 1993;
Jullo et al. 2007). The high resolution of WFPC2
and NICMOS2 HST images allowed us to pin down precisely the bright centroid in each of the
four detected counterpart images A1 to A4 of the lensed LBG. We used these multiple images
as independent constraints on the mass distribution, assuming it follows a
pseudo-isothermal elliptical profile (see Limousin et al.
2007 and Richard et al. 2010 for a precise
description of this profile). We fixed the center of the mass distribution on the bright
central galaxy of the system, but kept the ellipticity, e, position
angle, θ, velocity dispersion, σ, and core radius,
rc, as free parameters. The best-fit parameters of the mass
distribution are obtained with e = 0.44 ± 0.16,
θ = 14° ± 2° (east from the north),
σ = 348 ± 77 km s-1, and
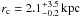 ; the
associated error bars are estimated from the range of models sampled by the Markov Chain
Monte Carlo (MCMC) sampler (Jullo et al. 2007). The
external critical line at the redshift of the 8 o’clock arc is overplotted in Fig. 1 (left-hand panel). The best lens model yields an
integrated mass within the Einstein radius (<3.32″) of
1.96 × 1012 M⊙, under the assumed cosmology.
This is very close to the earlier lens modeling of the 8 o’clock arc made by Allam et al. (2007), who found an integrated mass of
1.93 × 1012 M⊙ within the same Einstein radius.
Similarly, the authors found a comparable central velocity dispersion
σ = 390 ± 10 km s-1, but with an error certainly
underestimated because of the specific model (single isothermal elliptical) they assumed.
; the
associated error bars are estimated from the range of models sampled by the Markov Chain
Monte Carlo (MCMC) sampler (Jullo et al. 2007). The
external critical line at the redshift of the 8 o’clock arc is overplotted in Fig. 1 (left-hand panel). The best lens model yields an
integrated mass within the Einstein radius (<3.32″) of
1.96 × 1012 M⊙, under the assumed cosmology.
This is very close to the earlier lens modeling of the 8 o’clock arc made by Allam et al. (2007), who found an integrated mass of
1.93 × 1012 M⊙ within the same Einstein radius.
Similarly, the authors found a comparable central velocity dispersion
σ = 390 ± 10 km s-1, but with an error certainly
underestimated because of the specific model (single isothermal elliptical) they assumed.
The best-fit model allowed us to estimate the overall magnification factors, μ, for each image A2 and A3 targeted with the X-shooter spectrograph. These values are given in Table 4. More importantly, the best-fit model could then be used to derive the geometrical transformation necessary for mapping the image plane coordinates into the source plane, and hence reconstruct the morphology of the 8 o’clock arc seen in the HST images in the source plane at z = 2.7350. A reconstructed WFPC2/F450W-F650W-F814W composite-color image is shown in Fig. 1 (right-hand panel). We clearly see that the source is formed of two major parts, the main galaxy component and a smaller blob separated by 0.15 arcsec, or equivalently 1.2 kpc in projected distance. The corresponding lensed images of both the main component and the blob are indicated in Fig. 1 (left-hand panel). It is certainly the higher magnification factor of the blob (twice the one of the main galaxy component) that enables us to resolve it in the source plane. The respective sizes (half-light radii) of the main galaxy component and the blob are 1.8 ± 0.2 kpc and 0.53 ± 0.05 kpc. Their errors were estimated by running SExtractor in a sample of source plane realizations, sampling the MCMC parameters of the lens model.
Nebular emission lines identified in the 8 o’clock arc images A2 and A3 with their fluxes.
Parameters of the Gaussian two-component fits for the 8 o’clock arc images A2 and A3 as constrained from the Hγ profile.
3.3. Nebular emission lines
Our X-shooter spectra cover two of the four lensed images of the 8 o’clock arc, a star-forming galaxy at the systemic redshift zsys = 2.7350 ± 0.0003 (DZ10). They exhibit a rich rest-frame UV spectrum studied in detail by DZ10, and a rich rest-frame optical spectrum with a number of nebular emission lines superposed on a weak continuum, which we describe below. The achieved S/N in the NIR allows us to analyze the spectra of the images A2 and A3 independently. Emission lines blueward of Hγ were previously not reported by Finkelstein et al. (2009), because they are not covered by their spectra. In Table 2 we list the detected nebular emission lines in A2 and A3. A selection of them, free from atmospheric absorption lines, is reproduced in Fig. 2.
As seen in Fig. 2, the nebular lines of the 8 o’clock arc show asymmetric profiles, suggesting they consist of more than one component, and more surprisingly, they show different profiles between the lensed images A2 and A3. Inspection of the 2D spectra (see Fig. 3 showing the 2D Hγ profile) confirms the presence of mainly two components and a difference in the emission distribution between A2 and A3. In the image A2 the two components are clearly distinguishable, being separated by ~130 km s-1 in the spectral direction and spatially shifted by ~1″, while in the image A3 we observe two components with a very similar separation in the spectral direction, but with the bluer component that is significantly weaker and without spatial separation. We are tempted to interpret the redder, spatially shifted component of A2 as the spectral signature of the star-forming blob identified in the reconstructed source plane (Sect. 3.2). Indeed, with a magnification factor more than twice higher than that of the main galaxy, we may expect that its emission is sufficiently boosted by gravitational lensing to be spectroscopically detected. The blob should also have a counterpart image toward A3 with a similar magnification factor μ = 11.9 (Fig. 1, left-hand panel). The redder component of A3 might correspond to the emission from the blob, because it is almost at an identical velocity to that of the redder component in A2 (see Table 3). To explain the lack of its spatial shift and its significantly larger strength relative to the bluer component, while the redder and bluer components are roughly the same strength in A2, we can possibly blame the slit orientation, which did not optimally cover the lensed image A3, resulting in a partial loss of the spectral information, either on the blob’s or main galaxy’s spatial and velocity structure. As an alternative explanation, we can advocate a local magnification of the image A2 owing to the presence of substructure in the lens plane, which makes it looks a bit more extended/brighter compared to the other lensed image A3. Follow-up observations are necessary to distinguish between these two possibilities and to understand the complex velocity structure of images A2 and A3 in the rest-frame optical spectra.
The nebular emission lines were analyzed with a multi-Gaussian fitting procedure based on the non-linear χ2 minimization and the Levenberg-Marquardt algorithm. Windows of the NIR spectrum with atmospheric transmissions falling below 10% were excluded from the multi-Gaussian fitting. Varying the number of possible Gaussian components in the fits, a combination of two Gaussian profiles yielded the best-fit solution for all observed line profiles. Hγ, the most reliable line, which is free from telluric absorption and sky residuals, was used to constrain the best-fit values of redshifts (Gaussian centroids), zem, and velocity dispersions2 (Gaussian widths), σ, of the two Gaussian functions. We also used it for the fitting of all other nebular lines; only amplitudes were allowed to vary. Hβ, [O iii] λ4960 and the [O ii] doublet, all heavily affected by atmospheric absorption lines, were even fitted by fixing the amplitude ratio of the two Gaussian profiles to that of the Hγ profile. Errors on the values of zem, σ and fluxes were estimated using a Monte Carlo approach, whereby the observed spectrum was perturbed with a random realization of the error spectrum and refitted. The process was repeated 1000 times and the error in each quantity was taken to be the standard deviation of the values generated by the 1000 Monte Carlo runs.
 |
Fig. 3 Zoom on the wavelength-calibrated rectified sky-subtracted 2D spectrum around the nebular emission line Hγ plotted between 1618 and 1625 nm. The wavelength scale grows from left to right, and the pixel scale perpendicular to the dispersion direction is equal to 0.2″/pixel. Residuals of two sky lines are observed on both sides of the Hγ emission. The lower trace corresponds to the Hγ emission from A2 and the upper trace to the Hγ emission from A3. In the lensed image A2, two emission components are clearly distinguishable in the 2D Hγ profile, separated in the spectral direction by ~130 km s-1 and in the spatial direction by ~1″. In the lensed image A3, one can also perceive two emission components, separated in the spectral direction only and with the bluest one being significantly weaker. |
We obtained a satisfactory fit for all nebular lines, which demonstrates the robustness of the procedure and the reliability of the Hγ profile as calibrator. The corresponding best-fitted Gaussian profiles with their errors are shown in Fig. 2 with red continuous lines and cyan-shaded areas that delimit 68% of the generated Monte Carlo runs. Moreover, the best fit obtained in this way for the blend of the light that comes from the main galaxy and the blob in A2 agrees within 1σ with the results we obtained when we separately and manually extracted the two corresponding signals from the 2D Hγ profile. Given the limited S/N of our observations, we believe that a single extraction from the 2D spectrum and a multi-Gaussian treatment of the blended components leads to the most reliable results.
In Table 3 we list the best values of redshifts and velocity dispersions as constrained from the Hγ profile for the two Gaussian functions that were used to fit all observed nebular lines of the 8 o’clock arc images A2 and A3. Averaging the four redshifts of the two Gaussian functions of A2 and A3 yields a mean redshift of the ionized gas of ⟨ zem ⟩ = 2.7348 ± 0.0005, which excellently agrees with zsys = 2.7350 ± 0.0003 determined for the 8 o’clock arc by DZ10 from photospheric absorption lines and emission lines detected in the rest-frame UV spectrum. Our wavelength calibration solution was, in addition, cross-checked over the entire NIR spectral range by fitting Gaussian functions to the more than 400 sky lines listed in Rousselot et al. (2000). We obtained a median accuracy of the wavelength solution of 0.2 Å, i.e., half a pixel, or ~10 km s-1. This definitely confirms an offset of about 225 km s-1 between the systemic redshift as determined from X-shooter spectra and by Finkelstein et al. (2009, zsys = 2.7322 ± 0.0012. The superiority of our data because of a 10 × higher spectral resolution clearly makes our redshift determination more reliable.
The measured nebular line fluxes are listed in Table 2. We provide the respective individual fluxes of the two Gaussian profiles plus the total fluxes (sum of the two profiles) for the image A2 and the total fluxes only for the image A3. Our total line fluxes derived for Hα and Hγ agree very well with the measurements obtained by Finkelstein et al. (2009) for both the images A2 and A3. For Hβ, [O iii] λ4960, as well as [N ii] λ6585, the discrepancy is large, on the other hand. The Hβ and [O iii] lines are heavily affected by atmospheric absorption lines in the J and H bands and the [N ii] line is relatively weak, which makes their respective flux measurement particularly difficult. Benefiting from higher quality NIR spectra than those of Finkelstein et al., our flux measurements are expected to be more accurate.
Physical properties derived for the 8 o’clock arc images A2 and A3.
4. Physical properties
Thanks to the magnification provided by gravitational lensing, we detected a larger number of nebular emission lines in the 8 o’clock arc and this with a higher S/N than what is typically seen in unlensed high-redshift objects. These emission line fluxes which are collected in Table 2 and their ratios allow us to probe several physical properties that characterize the ionized gas of the lensed LBG and the galaxy itself. The multi-wavelength photometry (Table 1) also provides complementary valuable physical quantities on the galaxy via the spectral energy distribution (SED) modeling. In the following, we make the assumption that the gas in the 8 o’clock arc is ionized by OB stars, with negligible contributions from an active galactic nucleus (AGN), given the low [N ii]/Hα line ratio of ~0.15. Table 4 lists all the physical properties derived as described in the sections below. For the lensed image A2, we separately report the physical quantities corresponding to the total A2 line profile (Col. 2) and to the decomposition of the A2 line profile into the main galaxy component (Col. 3) and the smaller blob (Col. 4), as identified in the reconstructed source plane (Sect. 3.2). For the lensed image A3, we report only the physical quantities corresponding to the total A3 line profile (Col. 5).
4.1. SED modeling
To estimate the physical properties of the stellar population of the 8 o’clock arc, we fitted the observed broad-band SED with our fitting tool described in Schaerer & de Barros (2009, 2010). To estimate uncertainties on the fit parameters, we used Monte Carlo simulations with typically 1000 realizations of the data. The images A2 and A3 were fitted separately, using the photometry given in Table 1 after correcting for magnification by factors μA2 = 5.0 and μA3 = 3.9, respectively. Because A2 and A3 are different images of the same galaxy and because their (lensing-corrected) photometry is quite consistent, we determined the physical properties of this object from the total probability distribution function of the two lensed images. The indicated uncertainties are derived from the 68% confidence interval.
In practice, the SED fits are carried out with the following assumptions and templates, and varying the following parameters. We adopted the Bruzual & Charlot (2003) spectral templates with solar metallicity, assuming a Salpeter (1955) initial mass function (IMF) from 0.1 to 100 M⊙. We allowed for 10 exponentially declining star-formation histories with e-folding times between 30 Myr and 3 Gyr and for a constant star-formation rate. Nebular emission (lines and continuum) was optionally included, following the Schaerer & de Barros (2009, 2010) prescriptions. The Lyα emission line flux was set to zero, as observed and understood from radiation transfer models (see DZ10). Extinction, described by the Calzetti et al. (2000) attenuation law, was varied from A(V) = 0 to 2 mag, in steps of 0.05 mag. A Galactic foreground extinction E(B − V)Gal = 0.056 was taken into account (Schlegel et al. 1998). The redshift is fixed by the spectroscopic observations.
 |
Fig. 4 Observed SED of the 8 o’clock arc with the photometry of the lensed image A2 not corrected for gravitational lensing (blue points with error bars). Best-fit SED models obtained with templates with nebular emission (black line and red crosses showing the synthetic fluxes in the broad-band filters) and without nebular emission (magenta line). The dotted magenta lines show the contributions of a two-population fit, assuming a maximally old stellar population (~2.3 Gyr for an instantaneous burst), plus a younger stellar population with a variable age and star-formation history. The sum of the two (green dashed line) also provides a reasonable fit. Its stellar mass, however, significantly exceeds the dynamical mass. |
The derived fitting parameters are the visual extinction, A(V), the age of the stellar population (defined as the age since the onset of star formation), the stellar mass, Mstars, and the current star-formation rate, SFRSED. When nebular emission is included, we also predict the Hα rest-frame equivalent width, W0(Hα)SED, which can be compared to values obtained from our observations. The 1D confidence level for each physical parameter is derived by marginalization over all other parameters.
Good fits are obtained with and without nebular emission, as shown in Fig. 4, and the respective overall physical properties are
quite similar. The resulting ages and star-formation timescales are comparable, implying
that the derived parameters are similar to values obtained if we assume a constant SFR.
Typically, we find, within 68% confidence level,
A(V) ~ 0.55−1 mag, ages of
~20−65 Myr, stellar masses of
Mstars ~ (6−11) × 109 M⊙,
and star-formation rates of
SFRSED ~ 55−340 M⊙ yr-1
from models with and without nebular emission3. The
main differences between SED models with and without nebular emission are observed in ages
and dust extinctions; they remain compatible within 68% confidence level, however. For
example, we find 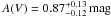 for
standard templates and
A(V)stars = 0.65 ± 0.10 mag with nebular
emission. The latter fits may indicate a somewhat lower extinction than derived from the
Balmer decrement (see Sect. 4.2), but the difference
is not significant, as discussed in Sect. 5.1. The
predicted Hα rest-frame equivalent width of the model with nebular
emission, W0(Hα) = 255 ± 95 Å, is slightly
too large compared to the observations (see Sect. 4.5).
for
standard templates and
A(V)stars = 0.65 ± 0.10 mag with nebular
emission. The latter fits may indicate a somewhat lower extinction than derived from the
Balmer decrement (see Sect. 4.2), but the difference
is not significant, as discussed in Sect. 5.1. The
predicted Hα rest-frame equivalent width of the model with nebular
emission, W0(Hα) = 255 ± 95 Å, is slightly
too large compared to the observations (see Sect. 4.5).
Comparing our results to the SED fits obtained by Finkelstein et al. (2009), we note that our stellar mass estimate is significantly lower than theirs, Mstars ~ 4.2 × 1011 M⊙ determined with a Salpeter IMF, by more than one order of magnitude. Their photometry comes from the SDSS, plus H and K′ images from the Near InfraRed Imager and Spectrometer (NIRI) on the Gemini North telescope, whereas we used the more reliable HST and Spitzer photometry up to 8.0 microns. Assuming that the SEDs shown in their Fig. 7 correspond to observed, lensing-corrected fluxes, it appears that the NIR fluxes (for instance in the H band) agree quite well for the image A2, but for the image A3 their H-band flux is nearly twice as high as ours (assuming a magnification factor μA3 = 3.9). Moreover, they incorrectly determine the galaxy stellar mass by summing the contributions from images A2 and A3, whereas A2 and A3 represent two lensed images of the same object. The main difference probably comes from their preference for a two-burst stellar population model with a maximally old component, which yields stellar masses of Mstars ~ (1−3) × 1011 M⊙ for images A2 and A3. We have investigated to which extent an old stellar population (~2.3 Gyr for an instantaneous burst) may be present. The IRAC fluxes from 3.6 to 8.0 μm are, indeed, compatible with such a population, which accounts for up to ~50% of the IRAC fluxes, as shown in Fig. 4. In this case, we obtain a stellar mass as large as Mstars ~ 1.8 × 1011 M⊙ for the old population, similarly to Finkelstein et al. (2009), plus a 7−8 × lower mass for the younger population. There is not much more room for a larger contribution of the old population because otherwise the NIR SED (≲ 2 μm) is underpredicted by the young population. Nevertheless, such a large stellar mass is not compatible with our dynamical mass estimate (see Sect. 4.6.2), because it should not exceed the dynamical mass. In summary, we exclude the presence of a dominating old stellar population. With a stellar mass of Mstars ~ (1−2) × 1010 M⊙ (with the Salpeter IMF), derived from our SED fits based on recent WFPC2, NICMOS2 and IRAC observations onboard HST and Spitzer and using our well-tested fitting tools, the 8 o’clock galaxy falls close to the median of the Mstars distribution of z ~ 2 star-forming galaxies (Erb et al. 2006b).
4.2. Dust extinction
The dust extinction is best derived from the Balmer decrement because the Balmer lines
have well constrained flux ratios from statistical equilibrium calculations. Any deviation
from the theoretical values are attributed to the gas-phase (nebular) dust reddening. In
the 8 o’clock arc, the Hα/Hγ ratio leads to the most
reliable dust extinction estimate because these two lines are the least affected by
telluric absorptions and sky residuals. As is common practice in the analysis of H ii
regions, we assumed Case B recombination, an electron temperature
Te = 104 K, and electron densities in the range
ne = 102−104 cm-3 for
the intrinsic Balmer line ratios (Osterbrock 1989).
The corresponding intrinsic Hα/Hγ ratio is equal to
6.159. Considering the Calzetti et al. (2000)
starburst reddening curve, the observed Hα/Hγ ratios
imply gas-phase color excesses 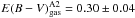 for
the image A2 and
for
the image A2 and 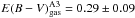 for the image A3. We
stress that the correction of the Galactic extinction,
E(B − V)Gal = 0.056, at
the position of the LBG (Schlegel et al. 1998), is
negligible at the observed NIR wavelengths of Balmer lines.
for the image A3. We
stress that the correction of the Galactic extinction,
E(B − V)Gal = 0.056, at
the position of the LBG (Schlegel et al. 1998), is
negligible at the observed NIR wavelengths of Balmer lines.
The respective gas-phase color excesses of images A2 and A3 agree very well, as do their respective V − I colors (see Table 1). Indeed, the UV slopes, β, measured from the observed (V − I) colors, following the prescriptions of Bouwens et al. (2009), are β = −1.20 ± 0.43 (−1.50 ± 0.43) for A2 (A3). This translates to E(B − V)β = 0.23 ± 0.10 (0.16 ± 0.10) for A2 (A3). As a result, the respective gas-phase and stellar dust extinctions of the two images A2 and A3 are very similar. This is what is expected because in the context of the gravitational lens modeling, the lensed images A2 and A3 represent physically the same regions. Our derived E(B − V)gas excellently agrees with the color excess of A2 determined by Finkelstein et al. (2009) from the same Hα/Hγ ratio. However, they find a significant dust extinction difference between images A2 and A3, both on the basis of the Hα/Hγ ratio and broadband photometry (see their Table 3 and Fig. 7), which we here confirm, based on better data (X-shooter spectra and HST images), should not be the case.
The Gaussian decomposition of the A2 line profile into a first component associated with
the main galaxy and a second one with the star-forming blob yields
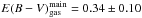 and
and
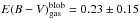 , respectively. These values
show a trend toward a smaller color excess in the blob, however, the trend is only
marginal because all measurements are within 1σ errors.
, respectively. These values
show a trend toward a smaller color excess in the blob, however, the trend is only
marginal because all measurements are within 1σ errors.
One important application of the determined dust extinction is for inferring fluxes of Balmer lines, when those are only partially or not detected. This is particularly interesting in the case of the 8 o’clock arc for the Hβ line, whose profile is only partially detected because the atmospheric transmission falls locally below 10%. The Hβ flux can then be determined from the observed Hγ flux and our estimate of E(B − V)gas. The Hβ fluxes so derived are listed in Table 2. They are within 1 σ from the measured values, a nice agreement that provides another demonstration of the robustness of our Gaussian fitting procedure.
4.3. Metallicity
Nebular emission lines are commonly used to estimate the metallicity in extragalactic
H ii regions. There are several empirical metallicity calibrations, leading to
oxygen abundance estimates, from various emission line ratios. Because we detected
[N ii] and [Ne iii] in the 8 o’clock arc, we use the N2 index from
Pettini & Pagel (2004): ![\begin{equation} \label{eq:N2} 12+\log({\rm O/H}) = 8.90+0.57\times \log [F([\ion{N}{ii}]\,\lambda6585)/F({\rm H}\alpha)]\,, \end{equation}](/articles/aa/full_html/2011/09/aa16636-11/aa16636-11-eq324.png) (1)and the Ne3O2
index from Nagao et al. (2006):
(1)and the Ne3O2
index from Nagao et al. (2006): ![\begin{eqnarray} \label{eq:NeIIIOII} \log [F([\ion{Ne}{iii}]\,\lambda3869)/(F([\ion{O}{ii}]\,\lambda3727)+F([\ion{O}{ii}]\,\lambda3729))] \nonumber \\ = -82.202 + 32.014x - 4.0706x^2 + 0.16784x^3, \end{eqnarray}](/articles/aa/full_html/2011/09/aa16636-11/aa16636-11-eq325.png) (2)where
x = 12 + log (O/H). The two indices have the advantage of having a
single-valued dependence on the oxygen abundance and are relatively robust with respect to
flux calibration and dust extinction (because one uses ratios of lines that are close in
wavelength). Given the uncertain flux measurements of both the [O ii] and
[O iii] doublets, the popular R23 index (Pagel et al. 1979) is hardly applicable for the
8 o’clock arc.
(2)where
x = 12 + log (O/H). The two indices have the advantage of having a
single-valued dependence on the oxygen abundance and are relatively robust with respect to
flux calibration and dust extinction (because one uses ratios of lines that are close in
wavelength). Given the uncertain flux measurements of both the [O ii] and
[O iii] doublets, the popular R23 index (Pagel et al. 1979) is hardly applicable for the
8 o’clock arc.
We find from the N2 index 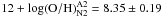 for the image A2 and
for the image A2 and
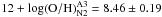 for the image A3. The two
measurements agree very well within 1σ errors, and also agree with the
metallicity derived by Finkelstein et al. (2009),
12 + log (O/H)N2 = 8.58 ± 0.18. From our data, we determine an average
gas-phase metallicity
for the image A3. The two
measurements agree very well within 1σ errors, and also agree with the
metallicity derived by Finkelstein et al. (2009),
12 + log (O/H)N2 = 8.58 ± 0.18. From our data, we determine an average
gas-phase metallicity 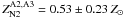 for the 8 o’clock
arc, when adopting a solar value of 12 + log (O/H)⊙ = 8.69 (Asplund et al. 2009). The oxygen abundances deduced from
the Ne3O2 index,
for the 8 o’clock
arc, when adopting a solar value of 12 + log (O/H)⊙ = 8.69 (Asplund et al. 2009). The oxygen abundances deduced from
the Ne3O2 index, 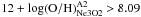 (
(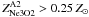 ) for the image A2
and
) for the image A2
and 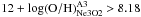 (
(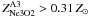 ) for the image A3,
are consistent with the N2 index results. They are considered as lower limits, because of
the likely underestimation of the flux of the [O ii] lines, heavily affected by
atmospheric absorptions.
) for the image A3,
are consistent with the N2 index results. They are considered as lower limits, because of
the likely underestimation of the flux of the [O ii] lines, heavily affected by
atmospheric absorptions.
In comparison with the stellar metallicity, Zstars = 0.82 Z⊙, and the metallicity of the interstellar medium, ZISM = 0.65 Z⊙, of the 8 o’clock arc determined in DZ10, our gas-phase metallicity estimate agrees well, keeping in mind that (i) the [N ii] λ6585 line we use is detected at only 2−3σ, being located at a wavelength where the detector noise significantly increases; and (ii) the H ii region metallicity calibrations (1) and (2) have a systematic 1σ uncertainty of ± 0.2 dex. Adopting Zmean = 0.67 ± 0.23 Z⊙, the mean of all the metallicity indicators available for the 8 o’clock arc, as the metallicity of this high-redshift LBG, seems to be a reasonable estimate.
Considering separately the contributions from the main galaxy and the star-forming blob
in the lensed image A2, we derive from the N2 index
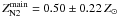 for the main
component, while the blob shows a trend toward a lower metallicity with
for the main
component, while the blob shows a trend toward a lower metallicity with
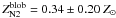 . This remains a
speculative result, given the weak S/N over the [N ii] λ6585
line profile.
. This remains a
speculative result, given the weak S/N over the [N ii] λ6585
line profile.
4.4. Star-formation rate
We can obtain an estimate of the star-formation rate (SFR) from the luminosity in the
Hα emission line, through the calibration by Kennicutt (1998): 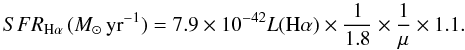 (3)The three correction
factors (last three terms in (3)) added to
the Kennicutt (1998) law are (from left to right):
(1) the flattening of the stellar IMF for masses below 1 M⊙ (Chabrier 2003) compared to the single power law of the
Salpeter (1955) IMF assumed by Kennicutt (1998); (2) the gravitational lensing
magnification factor, μ, deduced for the lensed images A2 and A3 and for
the star-forming blob from the gravitational lens modeling (Sect. 3.2); and (3) the light loss through the spectrograph slit, which we
estimate, from the convolution of the seeing profile and the slit width, assuming an
average seeing of 0.7″ during our NIR observations and a slit width of 0.9″, to be a
factor of 1.1. The Hα luminosity (in erg s-1) can be
directly derived from the Hα line flux, knowing the redshift of the
galaxy. The intrinsic Hα fluxes of the 8 o’clock arc, corrected for dust
extinction E(B − V)gas
determined from the Hα/Hγ Balmer decrement as described
in Sect. 4.2, are listed in Table 2.
(3)The three correction
factors (last three terms in (3)) added to
the Kennicutt (1998) law are (from left to right):
(1) the flattening of the stellar IMF for masses below 1 M⊙ (Chabrier 2003) compared to the single power law of the
Salpeter (1955) IMF assumed by Kennicutt (1998); (2) the gravitational lensing
magnification factor, μ, deduced for the lensed images A2 and A3 and for
the star-forming blob from the gravitational lens modeling (Sect. 3.2); and (3) the light loss through the spectrograph slit, which we
estimate, from the convolution of the seeing profile and the slit width, assuming an
average seeing of 0.7″ during our NIR observations and a slit width of 0.9″, to be a
factor of 1.1. The Hα luminosity (in erg s-1) can be
directly derived from the Hα line flux, knowing the redshift of the
galaxy. The intrinsic Hα fluxes of the 8 o’clock arc, corrected for dust
extinction E(B − V)gas
determined from the Hα/Hγ Balmer decrement as described
in Sect. 4.2, are listed in Table 2.
We obtain as an extinction/lensing-corrected star-formation rate
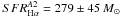 yr-1 for
the image A2 and
yr-1 for
the image A2 and 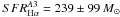 yr-1 for
the image A3, again consistent within 1σ errors. These results also agree
well with the previous estimates of the SFR in the 8 o’clock arc derived by Allam et al. (2007) and Finkelstein et al. (2009). This confirms that this LBG has a high SFR, which
falls toward the upper end of the
SFRHα distribution of
z ~ 2 LBGs (e.g., Erb et al.
2006b).
yr-1 for
the image A3, again consistent within 1σ errors. These results also agree
well with the previous estimates of the SFR in the 8 o’clock arc derived by Allam et al. (2007) and Finkelstein et al. (2009). This confirms that this LBG has a high SFR, which
falls toward the upper end of the
SFRHα distribution of
z ~ 2 LBGs (e.g., Erb et al.
2006b).
Regarding the line-profile decomposition of the image A2, the
extinction/lensing-corrected SFR of the star-forming blob,
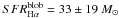 yr-1,
appears to be significantly lower relative to the SFR of the main galaxy,
yr-1,
appears to be significantly lower relative to the SFR of the main galaxy,
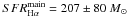 yr-1. The
SFR hence provides the first clear evidence of possibly different physical conditions
characterizing the blob compared to those of the main galaxy.
yr-1. The
SFR hence provides the first clear evidence of possibly different physical conditions
characterizing the blob compared to those of the main galaxy.
An independent measure of the star-formation rate is provided by the UV continuum from OB
stars. From the V-band photometry (Table 1) we have the rest-frame UV continuum flux,
fν(1600), near 1600 Å derived from the
definition of AB magnitudes. The corresponding luminosity,
Lν(1600) in
erg s-1 Hz-1, in turn implies
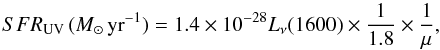 (4)with the Kennicutt (1998) scaling between
LUV and SFR (valid over the wavelength range 1500−2800 Å),
and applying the same corrections as above for the Chabrier (2003) IMF and magnification factors. The SFR so derived has then to be
corrected for dust extinction.
(4)with the Kennicutt (1998) scaling between
LUV and SFR (valid over the wavelength range 1500−2800 Å),
and applying the same corrections as above for the Chabrier (2003) IMF and magnification factors. The SFR so derived has then to be
corrected for dust extinction.
Using the stellar dust extinction
E(B − V)stars determined
from the SED modeling (Sect. 4.1) because the UV
continuum is dominated by the stellar light from OB stars, and the Calzetti et al. (2000) reddening curve, we obtain as an
extinction/lensing-corrected star-formation rate from the rest-frame UV continuum
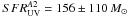 yr-1 for
the image A2 and
yr-1 for
the image A2 and 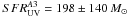 yr-1 for
the image A3. These dust-corrected rest-frame UV SFRs agree very well with
yr-1 for
the image A3. These dust-corrected rest-frame UV SFRs agree very well with
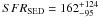 derived from the full SED fit (see Sect. 4.1), while
they are lower than the
SFRHα measurements
reported above and corrected for the gas-phase (nebular) color excess
E(B − V)gas. This
difference essentially comes from the different dust extinction corrections applied,
E(B − V)stars versus
E(B − V)gas. Indeed, the
attenuation of the stellar UV light and the nebular emission may differ in general (Calzetti et al. 2000; Calzetti 2001), and also appears to differ, although marginally, for this
object, as discussed in Sect. 5.1.
derived from the full SED fit (see Sect. 4.1), while
they are lower than the
SFRHα measurements
reported above and corrected for the gas-phase (nebular) color excess
E(B − V)gas. This
difference essentially comes from the different dust extinction corrections applied,
E(B − V)stars versus
E(B − V)gas. Indeed, the
attenuation of the stellar UV light and the nebular emission may differ in general (Calzetti et al. 2000; Calzetti 2001), and also appears to differ, although marginally, for this
object, as discussed in Sect. 5.1.
4.5. Hα and Hβ equivalent widths
The Hβ and Hα equivalent widths, W(Hβ) and W(Hα), provide an additional tool to investigate the star-formation history. As the ratio of the Hβ(Hα) luminosity to the underlying stellar continuum, W(Hβ)(W(Hα)) is a measure of the current to past average star formation. With a reliable stellar continuum detection in the vicinity of the Hβ line and a more tentative one around the Hα line because of the larger noise in the X-shooter spectra at these wavelengths, we nevertheless obtain a direct measure of the Hβ and Hα rest-frame equivalent widths: W0(Hβ)A2 = 30 ± 2 Å and W0(Hα)A2 = 134 ± 67 Å for the image A2, and W0(Hβ)A3 = 29 ± 3 Å and W0(Hα)A3 = 139 ± 72 Å for the image A3. The measurements show an excellent agreement between A2 and A3. No slit loss and dust extinction corrections are applied in this case, which indirectly assumes that the nebular emission lines and the stellar continuum suffer the same attenuation. In Table 4 we also provide the Hβ and Hα equivalent widths corrected for the different dust attenuations, nebular emission versus stellar continuum. We used these equivalent widths as an additional cross-check of the SED fits, which include the treatment of both the nebular emission continuum and lines (see Sect. 4.1).
4.6. Mass
4.6.1. Gas mass
Because of the lack of CO measurements, one usually relies on the Schmidt-Kennicutt
relation between star-formation rate and gas-mass surface density to determine the gas
masses of high-redshift galaxies (e.g., Erb et al.
2006b; Förster Schreiber et al. 2009).
This relation has been established for local star-forming galaxies (e.g., Kennicutt 1998), and its validity has recently been
tested at high redshifts from direct measurements of CO molecular lines in bright
sub-millimeter galaxies (Bouché et al. 2007; Tacconi et al. 2006, 2008) and in several rest-UV/optically selected star-forming galaxies (BzK and
BX objects) at z ~ 1−2.5 (Daddi et al. 2008, 2010; Genzel et al. 2010; Tacconi et al. 2010). All show that both local and high-redshift star-forming
galaxies lie approximately along the universal Schmidt-Kennicutt relation. To estimate
the gas mass in the 8 o’clock arc, we use the Bouché
et al. (2007) calibration valid for both local and high-redshift galaxies:
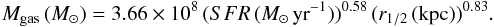 (5)The half-light
radius, r1/2, is directly measured from the reconstructed
source plane image, obtained from the gravitational lens modeling (Sect. 3.2). By using this half-light radius to estimate the
gas mass, we indirectly assume that r1/2, as measured from
the rest-frame UV light, also applies to the molecular gas. In applying (5), we take half of the inferred
star-formation rate for the area enclosed within r1/2, and
multiply by two to get the total gas mass. Genzel et al.
(2010) have recently proposed a revised calibration of the Schmidt-Kennicutt
relation, which they compare with previous calibrations, and discuss in detail the
various possible origins of differences (see their Sect. 4.4). The authors conclude that
the total systematic uncertainty of slope determinations probably is ±0.2 to ±0.25.
(5)The half-light
radius, r1/2, is directly measured from the reconstructed
source plane image, obtained from the gravitational lens modeling (Sect. 3.2). By using this half-light radius to estimate the
gas mass, we indirectly assume that r1/2, as measured from
the rest-frame UV light, also applies to the molecular gas. In applying (5), we take half of the inferred
star-formation rate for the area enclosed within r1/2, and
multiply by two to get the total gas mass. Genzel et al.
(2010) have recently proposed a revised calibration of the Schmidt-Kennicutt
relation, which they compare with previous calibrations, and discuss in detail the
various possible origins of differences (see their Sect. 4.4). The authors conclude that
the total systematic uncertainty of slope determinations probably is ±0.2 to ±0.25.
Using the star-formation rates as derived from the Hα luminosity and
corrected for gas-phase dust extinction and lensing, we derive a gas mass
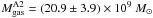 for the image A2
and
for the image A2
and 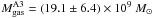 for the image A3.
These measurements obtained for the two lensed images of the 8 o’clock arc agree very
well. They are reliable within a factor of up to ~1.4, depending on the
star-formation rates we are referring to,
SFRHα versus
SFRUV. The overall order of magnitude of
the inferred gas masses agrees with the gas-mass estimate of the 8 o’clock arc obtained
by Finkelstein et al. (2009).
for the image A3.
These measurements obtained for the two lensed images of the 8 o’clock arc agree very
well. They are reliable within a factor of up to ~1.4, depending on the
star-formation rates we are referring to,
SFRHα versus
SFRUV. The overall order of magnitude of
the inferred gas masses agrees with the gas-mass estimate of the 8 o’clock arc obtained
by Finkelstein et al. (2009).
Considering the separate contributions from the main galaxy and the star-forming blob
identified in the image A2, we derive a significantly smaller gas mass for the blob,
 , than for the
main galaxy,
, than for the
main galaxy, 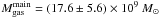 . This results from
the one order of magnitude lower
SFRHα and the three
times smaller half-light radius of the blob. The link between the blob and the main
galaxy is discussed in Sect. 5.4.
. This results from
the one order of magnitude lower
SFRHα and the three
times smaller half-light radius of the blob. The link between the blob and the main
galaxy is discussed in Sect. 5.4.
4.6.2. Dynamical mass
Dynamical masses can be calculated from the line widths via the relation (Erb et al. 2006b):
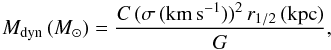 (6)where
(6)where
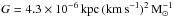 is the gravitational constant, and the factor C depends on the galaxy’s
mass density profile, the velocity anisotropy, the relative contributions
to σ from random motions or rotation, and the assumption of a
spherical or disk-like system. Under the assumption that a disk rotation is appropriate,
we begin with
is the gravitational constant, and the factor C depends on the galaxy’s
mass density profile, the velocity anisotropy, the relative contributions
to σ from random motions or rotation, and the assumption of a
spherical or disk-like system. Under the assumption that a disk rotation is appropriate,
we begin with 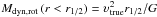 . We incorporate an average
inclination correction
⟨ υtrue ⟩ = υFWHM/ ⟨ sin(i) ⟩ ,
where ⟨ sin(i) ⟩ = π/4 and the observed half-width
velocity
υFWHM = FWHM/2 = 2.355σ/2.
Hence, for rotation-dominated objects the enclosed dynamical mass within the half-light
radius, r1/2, is
Mdyn,rot (r < r1/2) = (2.25σ2r1/2)/G.
We then multiply this resulting mass by two to obtain the total dynamical mass. For
dispersion-dominated objects, we apply the isotropic virial estimator with
Mdyn,disp = (6.7σ2r1/2)/G,
appropriate for a variety of galactic mass distributions (Binney & Tremaine 2008). In this case,
Mdyn,disp represents the total dynamical mass.
. We incorporate an average
inclination correction
⟨ υtrue ⟩ = υFWHM/ ⟨ sin(i) ⟩ ,
where ⟨ sin(i) ⟩ = π/4 and the observed half-width
velocity
υFWHM = FWHM/2 = 2.355σ/2.
Hence, for rotation-dominated objects the enclosed dynamical mass within the half-light
radius, r1/2, is
Mdyn,rot (r < r1/2) = (2.25σ2r1/2)/G.
We then multiply this resulting mass by two to obtain the total dynamical mass. For
dispersion-dominated objects, we apply the isotropic virial estimator with
Mdyn,disp = (6.7σ2r1/2)/G,
appropriate for a variety of galactic mass distributions (Binney & Tremaine 2008). In this case,
Mdyn,disp represents the total dynamical mass.
The Gaussian two-component decomposition of the line profiles within the image A2,
proposed to be associated with the main galaxy and the star-forming blob, respectively,
as observed in the reconstructed source plane image (see Fig. 1), yields a dynamical mass 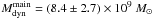 ((12.6 ± 4.0) × 109 M⊙) for the main
component of the galaxy and
((12.6 ± 4.0) × 109 M⊙) for the main
component of the galaxy and 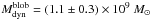 ((1.7 ± 0.5) × 109 M⊙) for the blob, under
the assumption of rotation(dispersion)-dominated kinematics. This confirms the one order
of magnitude smaller mass of the blob with respect to the main component of the galaxy.
((1.7 ± 0.5) × 109 M⊙) for the blob, under
the assumption of rotation(dispersion)-dominated kinematics. This confirms the one order
of magnitude smaller mass of the blob with respect to the main component of the galaxy.
With the dynamical masses in hand, we may try to infer whether the star-forming blob is
in rotation around the main core of the galaxy. Knowing the distance,
d = 1.2 ± 0.1 kpc, between the blob and the galaxy from the source
reconstruction (Sect. 3.2), we can calculate the
expected velocity of the blob in rotation around the galaxy from
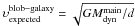 ,
and check whether it agrees with the observed velocity of the blob relative to the
galaxy,
,
and check whether it agrees with the observed velocity of the blob relative to the
galaxy, 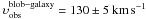 ,
as measured from the Gaussian two-component best-fit of the line profiles (velocity
difference between the Gaussian centroids of the blob and the galaxy; Table 3). With the derived dynamical mass of the main core
of the galaxy (rotation-dominated value), we obtain with an average inclination
correction
,
as measured from the Gaussian two-component best-fit of the line profiles (velocity
difference between the Gaussian centroids of the blob and the galaxy; Table 3). With the derived dynamical mass of the main core
of the galaxy (rotation-dominated value), we obtain with an average inclination
correction 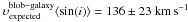 ,
which excellently agrees with the observed velocity of the blob relative to the galaxy.
This strongly suggests that the blob is in rotation around the main core of the galaxy.
Considering the dynamical mass of the main core of the galaxy as derived assuming a
dispersion-dominated kinematics, we still observe an agreement with
,
which excellently agrees with the observed velocity of the blob relative to the galaxy.
This strongly suggests that the blob is in rotation around the main core of the galaxy.
Considering the dynamical mass of the main core of the galaxy as derived assuming a
dispersion-dominated kinematics, we still observe an agreement with
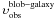 within 1.5σ error.
within 1.5σ error.
Assuming the blob and the main component are embedded in the same system, with the blob
in rotation around the main core of the galaxy, then the size of the combined
main + blob system should be used for the system size estimate and the best-fit Gaussian
two-component velocity dispersions, given in Table 3, summed up in quadrature, should be used for the system half-width velocity
estimate. As a result, we find a total dynamical mass
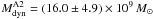 for the image A2
and
for the image A2
and 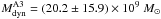 for the image A3.
Again the two measurements obtained for the two lensed images A2 and A3 of the 8 o’clock
arc give consistent values within 1 σ errors, as expected. On the
other hand, if the blob and the main component of the galaxy are merging, then the
dynamical masses of each should be combined for a total dynamical mass. This yields a
total dynamical mass
Mdyn = (14.3 ± 4.5) × 109 M⊙.
for the image A3.
Again the two measurements obtained for the two lensed images A2 and A3 of the 8 o’clock
arc give consistent values within 1 σ errors, as expected. On the
other hand, if the blob and the main component of the galaxy are merging, then the
dynamical masses of each should be combined for a total dynamical mass. This yields a
total dynamical mass
Mdyn = (14.3 ± 4.5) × 109 M⊙.
5. Summary of the results and discussion
5.1. Extinction correction and star formation
Thanks to the gravitational lensing, the 8 o’clock arc offers a rare opportunity to
compare the dust extinction corrections as derived from the Balmer decrement and from the
SED modeling of multi-band photometric data in an LBG at z = 2.7350.
Studies of local starburst galaxies show that the ionized gas is more attenuated than
stars (Calzetti et al. 2000; Calzetti 2001), a difference that is usually interpreted as indicating
that young hot ionizing stars are associated with dustier regions than the bulk of the
(cooler) stellar population across the galaxies. Calzetti
(2001) gives the following relation between the color excess observed for gas and
stars:
E(B − V)stars = 0.44 × E(B − V)gas.
In the 8 o’clock arc, we find for gas 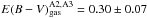 and for stars
E(B − V)stars = 0.19 ± 0.04.
Taking these results at face value, we observe a trend in the 8 o’clock arc toward a
larger dust attenuation in the ionized gas than in stars, in line with the Calzetti (2001) relation, although this may appear
marginal because the two color excesses are comparable within 2–3σ when
considering the measurement and SED modeling uncertainties. The UV slope,
β, measured from the observed (V − I)
colors is βA2,A3 = −1.35 ± 0.43, typical of
z ~ 2.5 LBGs at the same UV luminosities
(MUV = −22.3 after correction for lensing). This
translates to
and for stars
E(B − V)stars = 0.19 ± 0.04.
Taking these results at face value, we observe a trend in the 8 o’clock arc toward a
larger dust attenuation in the ionized gas than in stars, in line with the Calzetti (2001) relation, although this may appear
marginal because the two color excesses are comparable within 2–3σ when
considering the measurement and SED modeling uncertainties. The UV slope,
β, measured from the observed (V − I)
colors is βA2,A3 = −1.35 ± 0.43, typical of
z ~ 2.5 LBGs at the same UV luminosities
(MUV = −22.3 after correction for lensing). This
translates to 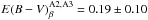 , which excellently agrees with
the stellar dust extinction
E(B − V)stars derived from
the SED fits. The larger uncertainty on
E(B − V)β,
nevertheless, reduces the confidence level on the observed difference between gaseous and
stellar dust attenuations.
, which excellently agrees with
the stellar dust extinction
E(B − V)stars derived from
the SED fits. The larger uncertainty on
E(B − V)β,
nevertheless, reduces the confidence level on the observed difference between gaseous and
stellar dust attenuations.
Differences between gaseous and stellar extinction corrections have recently been investigated by Yoshikawa et al. (2010) at z ~ 2 in K-band selected star-forming galaxies. The authors’ comparison of the Hα, UV, and Spitzer/MIPS 24 μm fluxes shows that the SFRs of lower SFR galaxies (≲100 M⊙ yr-1) agree well for the equal-extinction case E(B − V)stars = E(B − V)gas, while those of higher SFR galaxies agree better for the Calzetti (2001) relation, although SFRHα are systematically higher than SFRUV by 0.3 dex (see also Hayashi et al. 2009). This suggests that the relation between dust properties of stellar continuum and nebular lines is different depending on the intrinsic SFR. The 8 o’clock arc with SFRHα,UV > 100 M⊙ yr-1, as well as another lensed LBG the Cosmic Horseshoe at z = 2.38 (Hainline et al. 2009), tend to support this trend. However, whether these differences are true or caused by other effect(s) needs to be established more firmly.
The stellar masses derived from the SED modeling are often compared with the SFRs to search for correlation. While some authors report a significant correlation, others find that a fraction of galaxies deviates from the bulk of the distribution, showing a general trend of increasing SFRs with stellar masses (Erb et al. 2006c; Daddi et al. 2007, 2008, 2010; Hayashi et al. 2009; Magdis et al. 2010; Yoshikawa et al. 2010). Erb et al. (2006b) found that these outliers are galaxies with Mdyn/Mstars > 10, young ages <100 Myr, high Hα rest-frame equivalent widths W0(Hα) > 200 Å, and high gas fractions μgas > 60%. Yoshikawa et al. (2010) further confirmed that whatever dust extinction correction is applied (Calzetti (2001)-type or equal-type), these outliers remain outliers, and are characterized by particularly high specific star-formation rates, SSFR = SFR/Mstars > 10 Gyr-1. They thus also support young ages for these galaxies, with the majority of their stellar mass being formed in a recent starburst.
 |
Fig. 5 Comparison of the derived extinction-corrected SFRs and stellar mass of the 8 o’clock arc (large black circles, showing the results with/without nebular emission and with SFRHα/SFRSED) with those from other samples of LBGs at z ~ 2−3. The black triangles and small circles show the z ~ 2 objects from Erb et al. (2006b,c) with dust-corrected SFRs determined from Hα and from SED fitting, respectively. The red circles show the objects from Yoshikawa et al. (2010) with SFRHα corrected for dust extinction by assuming a different nebular and stellar attenuation. The yellow crosses are the z ~ 3 IRAC detected LBGs from Magdis et al. (2010). The green and blue crosses correspond to the U-dropout (z ~ 3) sample from the GOODS South field, analyzed by de Barros et al. (in prep.), with different assumptions in the SED fits (green crosses: constant SFR only, no nebular emission; blue crosses: variable star-formation histories, including nebular emission). All results were rescaled to the Chabrier (2003) IMF, if necessary. The dotted and dashed lines show the mass-SFR relations suggested by Sawicki et al. (2007) and Daddi et al. (2007) for z ~ 2 galaxies. The thin solid lines show the locii of constant specific star-formation rates, SSFR = 100, 10, and 1 Gyr-1, respectively. |
In Fig. 5 we plot the extinction-corrected star-formation rates and stellar masses of the 8 o’clock arc and other comparison samples of star-forming galaxies at z ~ 2−3 (LBGs, K-band selected star-forming galaxies, and IRAC-detected LBGs from Erb et al. 2006b,c, Yoshikawa et al. 2010, Magdis et al. 2010, and de Barros et al., in prep.). The results were scaled to the Chabrier (2003) IMF, if necessary. All plotted stellar masses were obtained from SED fits, but the detailed models that were used differ somehow, which may introduce some scatter between the different studies. The 8 o’clock arc shows a relatively high SFR for its stellar mass, corresponding to a specific SFR on the order of SSFRA2,A3 = 33 ± 19 Gyr-1. Compared to the two samples with SFRHα measurements, we see that this is clearly higher than the typical values derived by Erb et al. (2006c), although not exceptionally higher, and when compared to the sample of Yoshikawa et al. (2010). We do not know if there is a physical reason for this high SSFR, but we note that the 8 o’clock arc also shows a relatively high gas fraction (see below) and a young age, features pointed out by Erb et al. (2006c) for their objects that have the largest specific star-formation rates.
5.2. Gas fraction
As an important result, we assess at the same time the stellar mass, the gas mass, and
the dynamical mass of the 8 o’clock arc. Those masses were obtained from independent
quantities, the multi-wavelength photometry, the Hα luminosity, and the
nebular emission line width, respectively. The sum of the stellar mass and gas mass
determines the baryonic mass
Mbar = Mstars + Mgas,
and the fraction
μgas = Mgas/(Mstars + Mgas)
determines the gas fraction. We derive for the 8 o’clock arc the baryonic mass
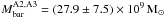 , which can be
compared to the dynamical mass
, which can be
compared to the dynamical mass 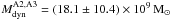 ((14.3 ± 4.5) × 109 M⊙) as derived under the
rotation(dispersion)-dominated kinematics assumption (see Table 4 and Sect. 4.6.2). The two
measurements agree within a factor of 1.5−2, which is very good given the significant
uncertainties carried by the respective masses (observational plus systematic), and is in
line with the Mbar versus Mdyn
dispersion observed for z ~ 2 LBGs (Erb et al. 2006b). We find that the 8 o’clock arc has a high gas
fraction with μgas ≃ 72%, contrary to the Finkelstein et al. (2009) result, where the authors
inferred a μgas of only ~12% because of their large
stellar mass estimate. A high gas fraction is yet the overall trend of
z ~ 2 LBGs that show a mean gas fraction of 50%. Moreover, the
derived physical properties in our lensed LBG support the observed correlations of
decreasing μgas with increasing stellar mass and age (Erb et al. 2006b; Reddy
et al. 2006). The 8 o’clock arc consequently appears as a young starburst with a
still significant gas fraction and a low fraction of baryonic mass that already turned out
into stellar mass.
((14.3 ± 4.5) × 109 M⊙) as derived under the
rotation(dispersion)-dominated kinematics assumption (see Table 4 and Sect. 4.6.2). The two
measurements agree within a factor of 1.5−2, which is very good given the significant
uncertainties carried by the respective masses (observational plus systematic), and is in
line with the Mbar versus Mdyn
dispersion observed for z ~ 2 LBGs (Erb et al. 2006b). We find that the 8 o’clock arc has a high gas
fraction with μgas ≃ 72%, contrary to the Finkelstein et al. (2009) result, where the authors
inferred a μgas of only ~12% because of their large
stellar mass estimate. A high gas fraction is yet the overall trend of
z ~ 2 LBGs that show a mean gas fraction of 50%. Moreover, the
derived physical properties in our lensed LBG support the observed correlations of
decreasing μgas with increasing stellar mass and age (Erb et al. 2006b; Reddy
et al. 2006). The 8 o’clock arc consequently appears as a young starburst with a
still significant gas fraction and a low fraction of baryonic mass that already turned out
into stellar mass.
5.3. A fundamental mass, SFR, and metallicity relation beyond z ≃ 2.5?
Recently, Mannucci et al. (2010) studied the dependence of gas-phase metallicity, 12 + log (O/H), on stellar mass, Mstars, and star-formation rate, SFRHα, and found a fundamental mass, SFR, and metallicity relation satisfied by local SDSS galaxies’ metallicities down to a dispersion of about 0.05 dex. The well-known mass-metallicity relation is in fact one particular projection of this fundamental relation into one plane, and the observed evolution of the mass-metallicity relation (Savaglio et al. 2005; Erb et al. 2006a; Maiolino et al. 2008; Mannucci et al. 2009) is caused by the increase of the average SFR with redshift, which results in sampling different parts of the fundamental relation at different redshifts. This fundamental relation seems to hold up to z ≃ 2.5 without any evolution, which means that the same physical processes are in place in the local Universe and at high redshifts. Beyond this redshift, the few available measurements (Maiolino et al. 2008; Mannucci et al. 2009) show hints of evolution.
The 8 o’clock arc at z = 2.7350 provides a nice opportunity to test the
fundamental relation in the high-redshift regime thanks to the available accurate
measurements of metallicity, stellar mass, and SFR. Considering the parameterization of
the metallicity as a linear combination of
SFRHα and
Mstars (relation (5) in Mannucci et al. (2010)), we expect for the 8 o’clock arc a metallicity
12 + log (O/H) ≃ 8.49, which agrees very well with the measured metallicity,
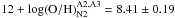 , derived from the N2 index
(see Table 4). This suggests that the fundamental
relation may hold up beyond z = 2.5, as also supported by two other
lensed LBGs at 2.5 < z < 3.5 studied by Richard et al. (2011). Larger statistics is clearly
needed to determine the trend in the fundamental relation at higher redshifts.
, derived from the N2 index
(see Table 4). This suggests that the fundamental
relation may hold up beyond z = 2.5, as also supported by two other
lensed LBGs at 2.5 < z < 3.5 studied by Richard et al. (2011). Larger statistics is clearly
needed to determine the trend in the fundamental relation at higher redshifts.
5.4. The blob and its interpretation
Spatially-resolved kinematics of massive z = 1.5−2.5 star-forming galaxies from the SINS survey (Genzel et al. 2006, 2008; Förster Schreiber et al. 2009) provide some of the most convincing evidence for the existence of large, turbulent, gas-rich rotating disks and for secular processes in non-major merging systems playing a significant role in growing galaxies at z ~ 2. Key properties of these early disks are high intrinsic velocity dispersions of σ ~ 30−80 km s-1, and high gas fractions μgas > 30%. In several of these disks, kpc-sized star-forming clumps are observed in Hα emission. Clump stellar and gas masses are 108−109.5 M⊙, and akin to the ubiquitous rest-frame UV clumps in HST optical imaging of z > 1 star-forming galaxies (e.g., Elmegreen et al. 2009). Clumpy galaxies are, indeed, not rare. These giant massive clumps could be the telltale signature of disk fragmentation through Jeans instabilities, and could migrate inward to the disk center and coalesce into a slowly rotating bulge (Bournaud et al. 2007; Elmegreen et al. 2008). However, this bulge formation scenario is still a matter of current debate because it hinges on the survival of clumps in the presence of stellar feedback (outflows driven by stellar winds, supernovae and radiation pressure). State-of-art theory and simulations (Krumholz & Dekel 2010; Murray et al. 2010; Genel et al. 2010) lead to contradictory predictions on clump stability, and urgently call for empirical constraints.
With a flux accounting for about 14% of the integrated Hα flux of the entire galaxy (lensing-corrected), a mass one order of magnitude lower than the main core of the galaxy, a half-light radius smaller than that of all z ~ 1−2 galaxies studied so far (e.g., Law et al. 2007, 2009; Förster Schreiber et al. 2009), and a small spatial offset from the main core of the galaxy d = 1.2 ± 0.1 kpc, we believe that the resolved star-forming blob in the 8 o’clock arc galaxy is one of these clumps commonly observed in high-redshift objects. The physical properties of the blob, such as its gas and dynamical masses Mgas,dyn = (1.1−2.2) × 109 M⊙, star-formation rate SFRHα = 33 ± 19 M⊙ yr-1, and size r1/2 = 0.53 ± 0.05 kpc (see Table 4), indeed much resemble the properties of the clumps studied by Swinbank et al. (2009), Jones et al. (2010), and Genzel et al. (2011). In particular, the blob perfectly satisfies the mass-size and size-SFR relations observed for high-redshift clumps. It hence additionally supports the conjecture that these high-redshift H ii regions are comparable in size and mass to the largest local star-forming complexes, and are consistent with the mass-size relation observed locally, but have a ~100 × higher SFR than in local spiral galaxies. The blob in the 8 o’clock arc even nicely extrapolates the size-SFR relation toward a domain with higher SFRs and sizes. Moreover, similarly to the modest clump-to-clump and inside-out disk variations observed in the oxygen abundances by Genzel et al. (2011), we do also see some changes between the metallicity of the main galaxy and the blob, with the blob showing a trend toward a lower metallicity by about 0.17 dex. According to a simple model (Sect. 4.6.2), the blob appears to be in rotation around the main core of the galaxy, which suggests that the 8 o’clock arc LBG may be one of these turbulent, gas-rich rotating disk. Additional knowledge of detailed physical properties of these clumps is a very useful input to models trying to predict their formation and evolution within high-redshift star-forming galaxies.
The stellar masses and star-formation rates were corrected by the factor of 1.8 to account for the flattening of the Chabrier (2003) IMF compared to the Salpeter (1955) IMF, and have consistent results with those of Sects. 4.4 and 4.6.
Acknowledgments
We are very grateful to Frédéric Courbin and Roser Pelló for helpful discussions, and we thank the anonymous referee for her/his very careful and constructive report. We thank the Paranal ESO Observatory for the high-quality data acquired in service mode for this programme. M.D.-Z. and D.S. acknowledge support from the Swiss National Science Foundation, and J.R. from an EU Marie-Curie Fellowship.
References
- Allam, S. S., Tucker, D. L., Lin, H., et al. 2007, ApJ, 662, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bian, F., Fan, X., Bechtold, J., et al. 2010, ApJ, 725, 1877 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics, 2nd edn (Princeton, NJ USA: Princeton University Press) [Google Scholar]
- Bohlin, R. C. 2007, ASPC, 364, 315 [Google Scholar]
- Bouché, N., Cresci, G., Davies, R., et al. 2007, ApJ, 671, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., Elmegreen, B. G., & Elmegreen, D. M. 2007, ApJ, 670, 237 [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Franx, M., et al. 2009, ApJ, 705, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Cabanac, R. A., Valls-Gabaud, D., & Lidman, C. 2008, MNRAS, 386, 2065 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D. 2001, PASP, 113, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen, L., D’Odorico, S., Pettini, M., et al. 2010, MNRAS, 406, 2616 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Dannerbauer, H., Elbaz, D., et al. 2008, ApJ, 673, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Bournaud, F., Walter, F., et al. 2010, ApJ, 713, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Dessauges-Zavadsky, M., D’Odorico, S., Schaerer, D., et al. 2010, A&A, 510, 26 [DZ10] [Google Scholar]
- D’Odorico, S.,Dekker, H.,Mazzoleni, R. et al. 2006, SPIE, 6269, 98 [Google Scholar]
- Elmegreen, B. G., Bournaud, F., & Elmegreen, D. M. 2008, ApJ, 688, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Elmegreen, D. M., Fernandez, M. X., & Lemonias, J. J. 2009, ApJ, 692, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Erb, D. K., Shapley, A. E., Pettini, M., et al. 2006a, ApJ, 644, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Erb, D. K., Steidel, C. C., Shapley, A. E., et al. 2006b, ApJ, 646, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Erb, D. K., Steidel, C. C., Shapley, A. E., et al. 2006c, ApJ, 647, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Finkelstein, S. L., Papovich, C., Rudnick, G., et al. 2009, ApJ, 700, 376 [NASA ADS] [CrossRef] [Google Scholar]
- FörsterSchreiber, N. M., Genzel, R., Bouché, N., et al. 2009, ApJ, 706, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- FörsterSchreiber, N. M., Genzel, R., Lehnert, M. D., et al. 2006, ApJ, 645, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Fruchter, A. S., & Hook, R. N. 2002, PASP, 114, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Genel, S., Naab, T., Genzel, R., et al. 2010, ApJL, submitted [arXiv:1011.0433] [Google Scholar]
- Genzel, R., Tacconi, L. J., Eisenhauer, F., et al. 2006, Nature, 442, 786 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Genzel, R., Burkert, A., Bouché, N., et al. 2008, ApJ, 687, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Tacconi, L. J., Gracia-Carpio, J., et al. 2010, MNRAS, 407, 2091 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Newman, S., Jones, T., et al. 2011, ApJ, 733, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Goldoni, P., Royer, F., François, P., et al. 2006, SPIE, 6269, 80 [Google Scholar]
- Hainline, K. N., Shapley, A. E., Kornei, K. A., et al. 2009, ApJ, 701, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, M., Motohara, K., Shimasaku, K., et al. 2009, ApJ, 691, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, T. A., Swinbank, A. M., Ellis, R. S., Richard, J., & Stark, D. P. 2010, MNRAS, 404, 1247 [NASA ADS] [Google Scholar]
- Jullo, Kneib, J.-P., Limousin, M., Elíasdóttir, A., Marshall, P. J., & Verdugo, T. 2007, New J. Phys., 9, 447 [Google Scholar]
- Kennicutt, R. C., Jr. 1998, ARA&A, 36, 189 [Google Scholar]
- Kneib, J.-P., Mellier, Y., Fort, B., & Mathez, G. 1993, A&A, 273, 367 [NASA ADS] [Google Scholar]
- Krumholz, M. R., & Dekel, A. 2010, MNRAS, 406, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Law, D. R., Steidel, C. C., Erb, D. K., et al. 2007, ApJ, 669, 929 [NASA ADS] [CrossRef] [Google Scholar]
- Law, D. R., Steidel, C. C., Erb, D. K., et al. 2009, ApJ, 697, 2057 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Leão, J. R. S., Heckman, T. M., et al. 2001, ApJ, 550, 724 [NASA ADS] [CrossRef] [Google Scholar]
- Lemoine-Busserolle, M., Contini, T., Pelló, R., et al. 2003, A&A, 397, 839 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Limousin, M., Kneib, J.-P., Bardeau, S., et al. 2007, A&A, 461, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magdis, G. E., Rigopoulou, D., Huang, J.-S., & Fazio, G. G. 2010, MNRAS, 401, 1521 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., et al. 2009, MNRAS, 398, 1915 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Modigliani, A., Goldoni, P., Royer, F., et al. 2010, SPIE, 7737, 56 [Google Scholar]
- Murray, N., Quataert, E., & Thompson, T. A. 2010, ApJ, 709, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Nagao, T., Maiolino, R., & Marconi, A. 2006, A&A, 459, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osterbrock, D. E. 1989, Astrophysics of gaseous nebulae and active galactic nuclei (Mill Valley, CA USA: University Science Books) [Google Scholar]
- Pagel, B. E. J., Edmunds, M. G., Blackwell, D. E., Chun, M. S., & Smith, G. 1979, MNRAS, 189, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, 59 [Google Scholar]
- Pettini, M., Steidel, C. C., Adelberger, K. L., Dickinson, M., & Giavalisco, M. 2000, ApJ, 528, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., Rix, S. A., Steidel, C. C., et al. 2002, ApJ, 569, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M.,Christensen, L., D’Odorico, S., et al. 2010, MNRAS, 402, 2335 [NASA ADS] [CrossRef] [Google Scholar]
- Quider, A. M., Pettini, M., Shapley, A. E., & Steidel, C. C. 2009, MNRAS, 398, 1263 [NASA ADS] [CrossRef] [Google Scholar]
- Quider, A. M., Shapley, A. E., Pettini, M., Steidel, C. C., & Stark, D. P. 2010, MNRAS, 402, 1467 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Steidel, C. C., Fadda, D., et al. 2006, ApJ, 644, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, J., Stark, D. P., Ellis, R. S., et al. 2008, ApJ, 685, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, J., Smith, G. P., Kneib, J.-P., et al. 2010, MNRAS, 404, 325 [NASA ADS] [Google Scholar]
- Richard, J., Jones, T., Ellis, R., et al. 2011, MNRAS, 413, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Rigby, J. R., Wuyts, E., Gladders, M. D., Sharon, K., & Becker, G. D. 2011, ApJ, 732, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Rousselot, P., Lidman, C., Cuby, J.-G., Moreels, G., & Monnet, G. 2000, A&A, 354, 1134 [NASA ADS] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Savaglio, S., Panagia, N., & Padovani, P. 2002, ApJ, 567, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Savaglio, S.,Glazebrook, K., Le Borgne, D., et al. 2005, ApJ, 635, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Sawicki, M., Iwata, I., Ohta, K., et al. 2007, in Deepest Astronomical Surveys, ed. J. Afonso, H. C. Ferguson, B. Mobasher, & R. Norris, ASP Conf. Ser., 380, 433 [Google Scholar]
- Schaerer, D., & de Barros, S. 2009, A&A, 502, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D., & de Barros, S. 2010, A&A, 515, 73 [Google Scholar]
- Shapley, A. E., Steidel, C. C., Pettini, M., & Adelberger, K. L. 2003, ApJ, 588, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Swinbank, A. M., Ellis, R. S., et al. 2008, Nature, 455, 775 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Steidel, C. C., Giavalisco, M., Pettini, M., Dickinson, M., & Adelberger, K. L. 1996, ApJ, 462, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Swinbank, A. M., Bower, R. G., Smith, G. P., et al. 2007, MNRAS, 376, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Swinbank, A. M., Webb, T. M., Richard, J., et al. 2009, MNRAS, 400, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Neri, R., Chapman, S. C., et al. 2006, ApJ, 640, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., Smail, I., et al. 2008, ApJ, 680, 246 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tacconi, L. J., Genzel, R., Neri, R., et al. 2010, Nature, 463, 781 [Google Scholar]
- Teplitz, H. I., McLean, I. S., Becklin, E. E., et al. 2000, ApJ, 533, L65 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van Dokkum, P. G. 2001, PASP, 113, 1420 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Giavalisco, M., Dickinson, M., et al. 2009, ApJ, 695, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Verhamme, A., Schaerer, D., & Maselli, A. 2006, A&A, 460, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verhamme, A., Schaerer, D., Atek, H., & Tapken, C. 2008, A&A, 491, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vernet, J.,Dekker, H., D’Odorico, S., et al. 2010, SPIE, 7735, 50 [NASA ADS] [Google Scholar]
- Yoshikawa, T., Akiyama, M., Kajisawa, M., et al. 2010, ApJ, 718, 112 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Nebular emission lines identified in the 8 o’clock arc images A2 and A3 with their fluxes.
Parameters of the Gaussian two-component fits for the 8 o’clock arc images A2 and A3 as constrained from the Hγ profile.
All Figures
 |
Fig. 1 Left. WFPC2/F450W black/white image of the 8 o’clock arc showing the positions of the four lensed images of the main galaxy component in red and the blob in blue. The two brightest images labeled A2 and A3 were targeted for spectroscopy with X-shooter. The large ellipse corresponds to the external critical line at the redshift of the arc as derived from lens modeling (Sect. 3.2). Right. WFPC2/F450W-F650W-F814W composite-color image showing the reconstructed morphology of the 8 o’clock arc in the source plane, as derived from the best-fit lens model. The source is formed of two major parts, the main galaxy component (on the left) and a smaller blob (on the right) separated by 0.15 arcsec, or equivalently 1.2 kpc in projected distance. The blob has a twice higher magnification factor than the main galaxy component. In both panels, the horizontal scale bar refers to 1 arcsec. |
| In the text | |
 |
Fig. 2 Selection of nebular emission lines, free from strong atmospheric absorption, detected in the lensed image A2 (left-hand panels) and in the lensed image A3 (right-hand panels) of the 8 o’clock arc. In all panels, the black histogram represents the flux-calibrated data with 1σ errors as a function of vacuum-heliocentric-corrected wavelengths. The red continuous line is the best-fitted profile, and the red dotted line shows the fit of the two best individual Gaussian components with the respective parameters given in Table 3. The cyan shaded area represents 68% of the Monte Carlo runs, generated from the perturbation of the observed spectrum with a random realization of the error spectrum. The respective atmospheric transmission is plotted below each panel. The flux is set to zero (with large error bars) whenever the atmospheric transmission falls below 10%. |
| In the text | |
 |
Fig. 3 Zoom on the wavelength-calibrated rectified sky-subtracted 2D spectrum around the nebular emission line Hγ plotted between 1618 and 1625 nm. The wavelength scale grows from left to right, and the pixel scale perpendicular to the dispersion direction is equal to 0.2″/pixel. Residuals of two sky lines are observed on both sides of the Hγ emission. The lower trace corresponds to the Hγ emission from A2 and the upper trace to the Hγ emission from A3. In the lensed image A2, two emission components are clearly distinguishable in the 2D Hγ profile, separated in the spectral direction by ~130 km s-1 and in the spatial direction by ~1″. In the lensed image A3, one can also perceive two emission components, separated in the spectral direction only and with the bluest one being significantly weaker. |
| In the text | |
 |
Fig. 4 Observed SED of the 8 o’clock arc with the photometry of the lensed image A2 not corrected for gravitational lensing (blue points with error bars). Best-fit SED models obtained with templates with nebular emission (black line and red crosses showing the synthetic fluxes in the broad-band filters) and without nebular emission (magenta line). The dotted magenta lines show the contributions of a two-population fit, assuming a maximally old stellar population (~2.3 Gyr for an instantaneous burst), plus a younger stellar population with a variable age and star-formation history. The sum of the two (green dashed line) also provides a reasonable fit. Its stellar mass, however, significantly exceeds the dynamical mass. |
| In the text | |
 |
Fig. 5 Comparison of the derived extinction-corrected SFRs and stellar mass of the 8 o’clock arc (large black circles, showing the results with/without nebular emission and with SFRHα/SFRSED) with those from other samples of LBGs at z ~ 2−3. The black triangles and small circles show the z ~ 2 objects from Erb et al. (2006b,c) with dust-corrected SFRs determined from Hα and from SED fitting, respectively. The red circles show the objects from Yoshikawa et al. (2010) with SFRHα corrected for dust extinction by assuming a different nebular and stellar attenuation. The yellow crosses are the z ~ 3 IRAC detected LBGs from Magdis et al. (2010). The green and blue crosses correspond to the U-dropout (z ~ 3) sample from the GOODS South field, analyzed by de Barros et al. (in prep.), with different assumptions in the SED fits (green crosses: constant SFR only, no nebular emission; blue crosses: variable star-formation histories, including nebular emission). All results were rescaled to the Chabrier (2003) IMF, if necessary. The dotted and dashed lines show the mass-SFR relations suggested by Sawicki et al. (2007) and Daddi et al. (2007) for z ~ 2 galaxies. The thin solid lines show the locii of constant specific star-formation rates, SSFR = 100, 10, and 1 Gyr-1, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


