| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201016424 | |
| Published online | 26 July 2011 | |
The EFIGI catalogue of 4458 nearby galaxies with morphology
II. Statistical properties along the Hubble sequence
1
Université Pierre et Marie Curie-Paris 6, Institut d’Astrophysique de Paris, 98 bis Boulevard Arago, 75014 Paris, France
e-mail: lapparen@iap.fr
2
CNRS, UMR 7095, Institut d’Astrophysique de Paris, 98 bis Boulevard Arago, 75014 Paris, France
Received: 31 December 2010
Accepted: 22 March 2011
Aims. The EFIGI catalogue of 4458 galaxies extracted from the PGC and SDSS DR4 was designed to provide a multiwavelength reference database of the morphological properties of nearby galaxies. The sample is limited in apparent diameter and densely samples all RC3 Hubble types.
Methods. We examine the statistics of the 16 EFIGI shape attributes, describing the various dynamical components, the texture, and the contamination by the environment of each galaxy. Using the redshifts from SDSS, HyperLeda, or NED for 99.53% of EFIGI galaxies, we derive estimates of absolute major isophotal diameters and the corresponding mean surface brightness in the SDSS g-band.
Results. We study the variations of the EFIGI morphological attributes with Hubble type and confirm that the visual Hubble sequence is a decreasing sequence of bulge-to-total ratio and an increasing sequence of disk contribution to the total galaxy flux. There is, nevertheless, a total spread of approximately five types for a given bulge-to-total ratio, because the Hubble sequence is primarily based on the strength and pitch angle of the spiral arms, independently from the bulge-to-total ratio. A steep decrease in the presence of dust from Sb to Sbc-Sc types appears to produce the grand spiral design of the Sc galaxies. In contrast, the scattered and giant HII regions show different strength variation patterns, with peaks for types Scd and Sm; hence, they do not appear to directly participate in the establishment of the visual Hubble sequence. The distortions from a symmetric profile also incidentally increase along the sequence. Bars and inner rings are frequent and occur in 41% and 25% of the disk galaxies respectively. Outer rings are half as frequent than inner rings, and outer pseudo-rings occur in 11% of barred galaxies. Finally, we find a smooth decrease in mean surface brightness and intrinsic size along the Hubble sequence. The largest galaxies are cD, ellipticals and Sab-Sbc intermediate spirals (20–50 kpc in D25), whereas Sd and later spirals are nearly half as big. S0 are intermediate in size (15–35 kpc in D25), and irregulars, compact and dwarf ellipticals are confirmed as small objects (5–15 kpc in D25). Dwarf spiral galaxies of type Sa to Scd are rare in the EFIGI catalogue, we only find two such objects.
Conclusions. The EFIGI sample provides us for the first time with a quantitative description of the visual Hubble sequence in terms of the specific morphological features of the various galaxy types.
Key words: astronomical databases: miscellaneous / galaxies: fundamental parameters / galaxies: structure / galaxies: elliptical and lenticular, cD / galaxies: spiral / galaxies: dwarf
© ESO, 2011
1. Introduction
The large variety of galaxy morphological types, their evolution with redshift, their relationship with galaxy masses and star formation rate, and their different spatial distribution with galaxy density indicate that galaxy morphometry – measuring the shape parameters of galaxies – is important for understanding galaxy formation and evolution.
With the availability of deep and extensive digital surveys with well-resolved galaxy images such as the Sloan Digital Sky Survey (SDSS), the CFHTLS (Canada-France-Hawaii Telescope Legacy Survey), and the coming LSST (Large Synoptic Survey Telescope) and DES (Dark Energy Survey), as well as state-of-the-art automatic software such as the last version of SExtractor (Bertin & Arnouts 1996; Bertin 2010), astronomers are becoming able to perform automatic morphometry analyses for large statistical samples out to redshift ~ 1.
Understanding evolution in galaxy morphology requires a detailed knowledge of the present-day Universe. This so far relies on large compilations from various galaxy catalogues made from photographic plates, in which only the Hubble morphological type and some estimate of size and isophote orientation are known for each object (see for example the Principal Galaxy Catalogue, hereafter PGC, Paturel et al. 1995). Detailed studies of specific morphological features do exist, but they are limited to some specific features within limited statistical samples or limited regions of the sky (Kormendy 1979; Buta 1995; Naim et al. 1997; Buta et al. 2006, 2007).
Definition of the EFIGI morphological attributes grouped by attribute type.
To obtain a reference sample for morphological studies, we have designed the EFIGI (“Extraction de Formes Idéalisées de Galaxies en Imagerie”) catalogue, a multiwavelength database of 4458 galaxies with resolved digital images and detailed morphological information. The sample is described in Baillard (2008) and in the companion article (Baillard et al. 2011,Paper I hereafter). The objects were selected from the PGC for their reliable RC3 morphological types (de Vaucouleurs et al. 1991, 1995) and for their inclusion within the SDSS1 DR4 photometric survey (photometric and spectroscopic data were obtained from the SDSS DR5 catalogue however). The resulting EFIGI database provides a large diversity of types and galaxy characteristics over the full 6670 deg2 of the SDSS DR4. The EFIGI catalogue is publicly available and may be queried from a web browser at http://www.efigi.org, and from the “Centre de Données Astronomiques de Strasbourg” (CDS) using the ViZiER Catalogue Service.
EFIGI morphological types.
The EFIGI morphological description includes an updated RC3-based Hubble type, and 16 shape attributes determined visually by 10 astronomers, which were subsequently homogenised. The attributes measure the significance of the different components of a galaxy (bulge, spiral arms and other dynamical features, texture) as well as its appearance on the sky (inclination or elongation) and its environment (contamination and multiplicity). Paper I describes the various statistical tests that demonstrate the reliability of this morphological description, and reports on the properties of the catalogue in terms of sky coverage, clustering, galaxy counts, magnitude completeness, and morphological fractions. The variety of the EFIGI database provides a unique description of the local Universe and allows one to perform quantitative statistical analyses over a large variety of morphological properties at z ≲ 0.05.
In Sect. 2 we briefly describe the EFIGI attributes, the redshifts and magnitudes used in the present analysis, and the catalogue diameter and magnitude limits. We then examine in Sect. 3 the statistics of the various EFIGI attributes as a function of morphological type. We show that they provide a detailed and quantitative description of the Hubble sequence. Finally, we examine in Sect. 4 the variations in apparent diameter and mean surface brightness of the EFIGI galaxies as a function of morphological type.
2. The EFIGI catalogue
2.1. Morphological attributes and types
The EFIGI Hubble type and 16 morphological attributes were measured by visual examination of the composite “gri” colour image of each galaxy, derived from the SDSS FITS images using the AstrOmatic software2. Table 1 lists the definition of the 16 attributes. Each attribute can take five possible values and has a lower and upper confidence limit. Note that we here convert the original decimal values ranging from 0 to 1 in Paper I into integer values ranging from 0 to 4. We also use the inverse square of the confidence interval to weight the attributes. This interval is defined as the difference between the upper and lower limit plus 1, and thus takes values between 1 and 5. Throughout the article, we refer to attribute values 1, 2, 3, and 4 by “weak”, “moderate”, “strong”, and “very strong” respectively, except for bars, which we describe as “short”, “intermediate”, “long”, and “ very long”.
The EFIGI morphological sequence is based on the RC3 “Revised Hubble Sequence” (RHS hereafter), and we call it the “EFIGI Morphological Sequence” (EMS hereafter). The major difference between the two sequences is that in the RHS non-magellanic irregulars (I0 type) are not considered as a separate type in the EMS, but as galaxies of some type of the EMS which undergo distortions in their profile measured by the Perturbation attribute. Moreover, the EMS contains one additional type, gathering the dwarf elliptical, dwarf lenticular, and dwarf spheroidal galaxies, whereas they are classified as ellipticals in the RHS. Finally, the different ellongation stages of elliptical galaxies in the RHS are not distinguished in the EMS, because this is measured by the EFIGI Inclination-Elongation attribute. The various EFIGI morphological types (hereafter “EM-types”) of the EMS are listed in Table 2.
2.2. Redshifts
We completed the EFIGI catalogue with the different measures of redshifts extracted from the PGC (Paturel et al. 1995), HyperLeda (Paturel et al. 2003), NED, and SDSS. The vast majority of EFIGI galaxies (4415) have a HyperLeda redshift measurement. Many also have a NED redshift (4404). The advantage of the HyperLeda database is that it provides redshifts corrected for Virgocentric infall, which is particularly important for nearby galaxies such as in the EFIGI catalogue. When the HyperLeda and NED heliocentric redshifts differ by more than 0.0001 (which is about a 3-sigma difference in both types of redshift, as well as the typical uncertainty of SDSS redshifts), we adopted the NED heliocentric redshift, which shows the individual redshift values and allows one to trace the sources of discrepancies.
As a result, we use the HyperLeda heliocentric redshift for 4079 of EFIGI galaxies, the NED redshift for 349 galaxies, and the SDSS redshift for 9 galaxies (there is no need to use the PGC redshifts). The SDSS and PGC redshifts are very useful however to check the consistency with the HyperLeda and NED redshifts, and to distinguish among both values when they differ; this also allowed us to discard some rare erroneous HyperLeda and NED redshifts.
In total, 4437 EFIGI galaxies among 4458 have an heliocentric redshift, corresponding to a redshift completeness of 99.53%. When a catalogue other than HyperLeda is used to assign an heliocentric redshift to an object, we adopted the HyperLeda correction for virgocentric infall if the adopted redshift differs from the HyperLeda value by less than 0.0005. This yields 4411 galaxies with a redshift corrected for Virgocentric infall.
Twelve galaxies have a negative HyperLeda redshift, even after correction for virgocentric infall. Because these galaxies are very nearby (velocities between –8 km s-1 and –350 km s-1), their redshifts cannot be used as an estimate of distance, and we discarded them.
Figure 1 shows the resulting redshift distribution after the separation of EFIGI galaxies into groups of two or three morphological types. The strong excess at z ~ 0.005 is caused by the Virgo cluster. There are only 72 EFIGI galaxies beyond z = 0.05, because the RC3 catalogue mainly contains galaxies with recession velocities lower than the corresponding value of 15 000 km s-1, that is, below a luminosity distance of ~220 Mpc. Throughout the article, we convert redshifts into distances using a Hubble constant H0 = 70 km s-1/Mpc (Freedman et al. 2001), and the currently standard cosmological parameters Ωm = 0.3 and ΩΛ = 0.7 (Dunkley et al. 2009).
Figure 1 shows that the various morphological types of giant galaxies – cD, E, S0 and spirals earlier than Sd (see Sect. 4.1) – are detected at all redshifts in the EFIGI catalogue (although cD galaxies are too few to be sampled in the whole redshift range). The intrinsically smaller and fainter objects – Sdm, Sm, Im, cE, dE – are detected preferentially at lower redshifts, owing to the apparent diameter limit of the RC3. This is discussed in more detail in Sect. 2.4 below.
 |
Fig. 1 Redshift distribution of all EFIGI galaxies separated by EFIGI morphological type, grouped as follows: cE-dE (light grey); E-cD (grey); S0−-S0-S0+ (orange); S0a-Sa-Sab (yellow); Sb-Sbc (pink); Sc-Scd-Sd (green); Sdm-Sm-Im (blue). |
 |
Fig. 2 Absolute magnitude distribution in the g-band for all EFIGI galaxies separated by EFIGI morphological type, grouped as follows: cE-dE (light grey); E-cD (grey); S0−–S0-S0+ (orange); S0a-Sa-Sab (yellow); Sb-Sbc (pink); Sc-Scd-Sd (green); Sdm-Sm-Im (blue). |
2.3. Photometry
Because the SDSS photometric pipeline was designed for galaxies smaller than 2 arcmin in diameter, whereas the SDSS contains many larger galaxies (up to several degrees in isophotal diameter; see Fig. 3), the pipeline fails for large galaxies, which are truncated into several units. We showed in Fig. 24 of Paper I that there can be as much as an 8-mag difference for some objects, mostly late-type galaxies.
de Lapparent & Bertin (2011a, in prep.) have thus recalculated the magnitudes of all EFIGI galaxies from the SDSS ugriz images using the new version of SExtractor (Bertin & Arnouts 1996; Bertin 2010), with the option to fit a bulge+disk PSF-convolved profile. The resulting apparent magnitudes in the SDSS ugriz bands (see Fig. 1 of de Lapparent & Bertin 2011a, in prep.) confirm the disappearance of the spurious tail at faint apparent magnitude, which is seen when using the SDSS photometry (in Fig. 23 of Paper I). The analysis of de Lapparent & Bertin (2011a, in prep.) also shows that the SDSS DR5 fluxes undergo losses of 0.5 to 2 mag for bright galaxies (9 ≤ g ≤ 16), owing to an overestimate of the sky background around large objects; an improved sky background procedure has been implemented in the SDSS DR8, Blanton et al. (2011).
The apparent magnitudes and luminosity distances are used to derive absolute magnitudes for all EFIGI galaxies. In this calculation, we use the k-corrections provided by the VAGC DR4 “low-z” catalogue (Blanton et al. 2005; Blanton & Roweis 2007) for 1725 EFIGI galaxies to derive linear estimates of the k-corrections as a function of redshift and in each filter for the remaining objects; the whole process is described in detail in de Lapparent & Bertin (2011a, in prep.).
The resulting distributions of absolute magnitudes in the SDSS g-band (the most sensitive SDSS band) are shown in Fig. 2 after separating EFIGI galaxies into groups of two or three morphological types. These curves result from the combination of the apparent magnitude distributions, the luminosity functions of the different galaxy types (de Lapparent et al. 2003), and the selection function of the EFIGI catalogue (see Sect. 2.4). The graph shows that the EFIGI catalogue densely samples the various types over a wide absolute magnitude interval, including both the bright ends of the lenticular and spiral galaxy distributions, and the faint ends of the late spirals and irregulars.
2.4. A diameter-limited catalogue
 |
Fig. 3 Distribution of apparent major isophotal diameter D25 converted into arcminutes as a function of g-magnitudes measured by de Lapparent & Bertin (2011a, in prep.) for the 4204 EFIGI galaxies for which these parameters are defined. Different symbols and colours are used for different EM-types. The histogram of D25 in intervals of 0.1 arcmin, overplotted vertically on a log scale and with corresponding labels on the top axis of the graph, demonstrates the strong incompleteness in the catalogue for D25 < 1′ and BT > 15.5, materialised by the horizontal and vertical dashed lines. The diagonal dashed line corresponds to a surface brightness limit of 25 mag/arcsec2. The EFIGI catalogue is most complete between these diameter and surface brightness limits, and the crossing of these two lines causes the disappearance of data points fainter than g ~ 16.5. |
Because the EFIGI sample was restricted to PGC galaxies having a reliable RC3 measurement of Hubble type, the sample undergoes the selection effects of the RC3 (de Vaucouleurs et al. 1991). This latter catalogue was aimed at being reasonably complete for galaxies having an apparent diameter D253 larger than 1 arcmin, a total BT magnitude brighter than about 15.5, and a recession velocity not in excess of 15 000 km s-1. Half of the RC3 objects however are galaxies that satisfy only the diameter or magnitude condition, and in addition may have velocities higher than 15 000 km s-1.
The resulting selection effects are shown in Fig. 3, where we plot the distribution of D25 apparent diameters converted into arcminutes, as a function of the g-band magnitudes measured by de Lapparent & Bertin (2011a, in prep.) The overplotted vertical histogram of D25 shows strong incompleteness for D25 < 1 arcmin, below the horizontal dashed line, where there are 1204 galaxies, which is more than one quarter of the full EFIGI catalogue. This allows the inclusion in the sample of galaxies with smaller diameter than the rest of the objects, like cE galaxies, some of which reach D25 ≃ 0.2 arcmin (and at g > 15.5). Following the RC3 selection, almost all of the galaxies with D25 < 1 arcmin are brighter than g ~ 15.5, as indicated by the vertical dashed line. Moreover, we find that for each Hubble type (including cD and dE), the galaxies with D25 < 1 arcmin (hence g < 15.5) represent a comparable fraction of 1/3 to 1/4 of the objects.
 |
Fig. 4 Distribution of apparent major isophotal diameter D25 converted into kpc as a function of g magnitudes, for the 4104 EFIGI galaxies for which these parameters are defined. Different symbols and colours are used for different EM-types (beware of the different spiral grouping from that in Fig. 3). The D25 < 1′ limit is plotted as a dashed line. Galaxies below this diameter limit extend the minimum detectable diameter for a given distance to a lower value. |
Finally, a diagonal dashed line shows the 25 mag/arcsec2 limit in surface brightness, below which lie most EFIGI galaxies, except a few Sd-Sm and Im types (this is best seen in Fig. 19, Sect. 4.2). This surface brightness limit corresponds to the level below which it is difficult to visually detect isophotes or entire objects from a paper copy of the Palomar Observatory Sky Survey plates (Abell 1959). We therefore expect a high completeness rate for the EFIGI sample above this surface brightness limit, that is, for D25 below the diagonal line in Fig. 3.
The diameter limit of the RC3 results in a distance-dependent limit in the physical size of EFIGI galaxies. We estimated the intrinsic diameter of galaxies by multiplying the apparent diameter D25 by the angular-diameter distance. This is applicable to a subsample of 4152 EFIGI galaxies: among the total number of 4458 EFIGI galaxies, 257 have no measure of D25 in the RC3, and 49 additional galaxies have no measure of redshift. We show in Fig. 4 the resulting variations in the intrinsic absolute major diameter as a function of luminosity distance for the EFIGI catalogue. The incompleteness at D25 < 1 arcmin in Fig. 3 results in a minimal detectable diameter for each distance, materialised as a diagonal line in Fig. 4. The 1204 EFIGI galaxies located below this diameter limit make up a sample of intrinsically smaller galaxies of all Hubble types: for example cE galaxies, which can be detected up to large distances in the EFIGI catalogue (~200 Mpc). We notice that the various types are located at different positions along the D25 = 1 arcmin line, according to their range of absolute magnitude.
Another selection effect that adds on the RC3 apparent diameter limit is the following: over the area of sky covered by the SDSS photometric DR4 survey, the EFIGI sample contains all PGC galaxies having an RC3 morphological classification based on several measurements to guarantee a reliable RC3 type (see Paper I). This effect implies that fewer high inclination spiral galaxies are selected, because of the poorer visibility of their morphological features (see Sect. 3.1). This selection effect can only be evaluated by comparison to a complete census of galaxies brighter than g ~ 17 and with reliable photometry; this is not provided by the SDSS because the various releases contain a large number of spurious sources and the photometry pipeline fails for large objects (Paper I). As a result, the galaxy groups, clusters and large-scale structures contained in the EFIGI catalogue might not be sampled in proportion to their true spatial density. The more than ≈ 80% completeness of the EFIGI catalogue for galaxies with 10 < g < 14 (Paper I) limits the amplitude of this “density bias” at bright magnitudes, however.
Statistics of the EFIGI “Environment” attributes given as a percentage of galaxies with given attribute values.
Interestingly, because of the various selection effects at play in the EFIGI sample, the number of EFIGI galaxies per morphological type undergoes a limited spread after excluding the intrinsically rare types (cE, cD, dE). The median number of galaxies per type is ~257, corresponding to Sa galaxies, the lowest value is 152 for S0+, and the four highest values are 518 for Sb, 472 for Sbc, 445 for Scd, and 355 for Sdm; all remaining types have numbers of galaxies that deviate from the median by less than 50% of its value. This constitutes a major difference between the EFIGI catalogue and the other recent morphological follow-up studies (Nair & Abraham 2010; Lintott et al. 2008), which are based on apparent magnitude-limited subsamples of the SDSS. As shown in Paper I, the EFIGI catalogue largely oversamples late spirals (Sd-Sdm-Sm) and irregulars compared to magnitude-limited surveys. Part of these excess late-type galaxies in the EFIGI catalogue are located in the small diameter extension of Fig. 3, at D25 < 1 arcmin and g ≤ 15.5.
3. Morphological characteristics along the Hubble sequence
3.1. Environment and appearance
Before examining the EFIGI morphological attributes per se, that is, those which contribute to the description of the morphological type, we examine the “environment” and “appearance” EFIGI attributes, which are independent of the internal galaxy properties for Inclination-Elongation and Contamination, and only indirectly related for Multiplicity (via the morphology-density relation, e.g. Blanton & Moustakas 2009). We also examine here the Arm Rotation attribute, which can also be considered an “appearance” attribute, because the direction of winding of the spiral arms depends on the orientation of the galaxy with respect to the line-of-sight.
Table 3 shows the fraction of galaxies with no, weak, moderate, strong, or very strong Contamination and Multiplicity; attribute values with less than ~10% galaxies have been grouped together (1 and 2 for Multiplicity, and 3 and 4 for Contamination and Multiplicity). The listed fractions show no dependence of Contamination on EM-type for types S0− and later. Compared to the other types, there is a ~10% deficiency in cD and cE-E galaxies with Contamination = 0, and a corresponding excess of objects with Contamination = 2. This is probably because of the large envelopes of E, and even more so cD galaxies, which increases the probability of contamination by any type of real objects (stars or galaxies), or by artefacts.
In all tables of attribute statistics listed in the article, the quoted error bars are the Poisson uncertainties in the considered fractions of objects. For the large part of lower and upper confidence limits equal to the attribute value plus and minus one level, that is a confidence interval of 3, these uncertainty estimates are adequate. For the attribute values that are equal to one or both of their lower or upper confidence limit, that is, a confidence interval of 1 or 2, we choose to be conservative by ignoring the reduction in uncertainty from the Poisson estimates. Listed fractions and uncertainties are rounded to the closest percent, and uncertainties in the interval 0.1 to 0.5% are rounded to 1%.
The statistics for the Multiplicity attribute also show that spirals, Im and dE galaxies have similar Multiplicity distributions values (82–93% with attribute value 0, and 7–14% with values 1–2), whereas E, cE and S0 galaxies undergo a higher rate of weak Multiplicity (74–82% with attribute value 0, and 26–17% with values 1–2), owing to their large envelopes. The combination of the richer environment of clusters of galaxies and their higher density in cD, E, S0, Im and dE galaxies also increases the probability of overlapping by another galaxy, hence the higher percentages of objects with Multiplicity = 1–2 for these types. The very extended envelopes of cD galaxies explain why there is an even more drastic increase in their fractions of objects with weak and strong Multiplicity (15 ± 6% for attribute values 3–4, 39 ± 11% for 1–2 attribute values), and nearly a factor of 2 decrease in the fraction of galaxies with null attribute value: cD galaxies are located in the potential wells of rich galaxy clusters, where the galaxy density is the highest, hence the presence of neighbouring galaxies is high.
Table 4 shows the distribution of the Inclination- Elongation attribute (Incl-Elong hereafter) grouped by types with similar values of the attribute. As expected, none of the pure-bulge galaxies (cE, E, and cD) have an Incl-Elong attribute value of 4, because this high value can only occur for highly inclined disks; and only a few cD galaxies have an attribute value of 3. Note however the apparent systematically higher elongation of cD galaxies compared to cE and E in the EFIGI catalogue. This may be a true physical effect, caused by the dissipationless collapse of aspherical mass concentrations and its impact on first-ranked galaxies in clusters (Rhee & Roos 1990).
The other statistics in Table 4 show the wide variety of disk inclinations for the selected EFIGI lenticular and spiral galaxies, whose mean statistics are indicated in the last line labelled “All disks”. We emphasize that the fewer disk galaxies selected at high Incl-Elong values (3–4) in no way reflect any preferential orientation of galaxies on the sky, but are probably due to the less reliable RC3 types for these objects, hence their under-representation in the EFIGI sample. There is also a diversity of elongations for Im and dE galaxies, with a noticeable deficiency in round objects compared to spirals (for Incl-Elong = 0).
Statistics of the EFIGI “Appearance” attributes given as a percentage of galaxies with given attribute values.
Finally, Table 4 shows the distribution of the Arm Rotation attribute, measuring the winding direction of the spiral arms: an approximately symmetric distribution about the no-rotation value of 2 is measured for all types, within the dispersion caused by the number of galaxies in each EM class. As expected, only very few (and weak) spiral arms are visible in S0−, S0, Im and dE galaxies, hence the small fractions with attribute values different from 2. When averaging over all disk galaxies, the fractions of galaxies with the arm winding clockwise (Arm Rotation = 0 or 1) and counterclockwise (Arm Rotation= 3 or 4) agree to within ~1.5σ, showing no systematic effect in the EFIGI sample.
Below, we examine in detail the remaining 12 EFIGI attributes, which each characterise a specific morphological feature of galaxies, and hence contribute to the determination of the Hubble sequence.
3.2. Bulge-to-total ratio
 |
Fig. 5 Distribution of B/T attribute versus the EFIGI morphological type for the 4458 galaxies in the EFIGI catalogue (see Table 2 for the correspondence with types). In order to see the relative density of data points, they are spread in the horizontal and vertical direction, hence the apparent rectangles. The weighted mean and weighted rms dispersion in B/T are also plotted for each type along with the corresponding number of galaxies. This graph shows the strong correlation of morphological type with B/T. |
The attribute measuring the ratio of light from the bulge over the total light of a galaxy, denoted B/T, is tightly correlated with the morphological type, as shown in Fig. 5 (the correspondence between the EM-types and their ID number is listed in Table 2). There is a large dispersion of EM-type for each value of B/T, however. This is best seen in Fig. 6, where we plot the histograms of EM-type for each of the five values of B/T: the open circles and horizontal error bars show the weighted mean and ± 1σ dispersion within each B/T class, with σ = 1.4, 1.8, 2.0, 1.9, and 1.3 for B/T = 0, 1, 2, 3, and 4 respectively. These dispersion values cannot be caused only by the EFIGI uncertainties in the morphological type, because one third of EFIGI galaxies have a half confidence interval of 0.5, another third of 1, and 80% of the last third of 1.5.
In Fig. 5 we overplot the weighted mean value and ± 1σ dispersion in the B/T attribute for each of the 18 EM-types. The dispersion has the lowest values for types E (0.41) and Im (0.28), and the highest value for types S0− (1.26) and dE (1.41). For the latter, the large dispersion is because nearly half of the dE galaxies are nucleated (Binggeli & Cameron 1991), hence an attribute value of 1 or 2 has been given to these objects (the B/T attribute value of 3 corresponds to PGC0009283, which has a central hot spot with an attribute value of 2). For the S0, S0+ and spiral galaxies, the ± 1σ dispersion in the B/T attrbute lies in the tight interval between 0.84 for Scd and 1.10 for Sc, with a median value of 1.04. These values are nearly unchanged when using only the 3106 galaxies with Incl-Elong ≤ 2, or the 1400 galaxies without contamination (Contamination = 0).
 |
Fig. 6 Histograms of EFIGI morphological type for the five values of B/T (decreasing from left to right). The weighted mean and rms dispersion in the morphological type are plotted above each histogram along with the corresponding number of galaxies. This graph shows the large dispersion in morphological type for a given B/T. |
The dispersion in EMT-type per B/T attribute value seen in Fig. 6 could simply be a binning effect becasue there are 18 EM-types and 5 B/T attribute values, so that a spread of 18/5 ~ 3.6 is expected for each B/T value. Moreover, the half confidence interval in the B/T attribute is 0.5 for 1504 galaxies, 1 for 2923 galaxies, and 1.5 for 98 EFIGI galaxies. To evaluate whether there is some intrinsic dispersion in morphological type for a given B/T beyond the uncertainties in the visual eye estimates of EMT and B/T, we performed a simple test. We assumed a linear relation between EM-type and B/T with the two boundary conditions indicated in Fig. 5: B/T = 4 for EM-type = –5 (E), and B/T = 0 for EM-type = 10 (Im). The resulting relation is B/T = −4/15 EM − type + 8/34. For each value of EM-type in the catalogue, we then introduced a dispersion in B/T by adding white noise in EM-type with a maximum spread N, which projects onto a maximum spread of 4N/15 in B/T. We then rounded the values of B/T to the integer values 0 to 4, and calculated the dispersion among these integer values for each EM-type. This procedure has the advantage that it includes the effect of discretisation of B/T. The ± 1σ dispersion in the measured B/T reaches values as high as 1.0 for most spiral types when N = 5; for N = 6, the dispersion reaches values of 1.2 for several spiral types, which is too high. Note that N = 5 is higher than the confidence intervals in the EM-types of 1, 2, and 3 for every third of the EFIGI galaxies, and therefore cannot be the result solely of these uncertainties in the estimated types.
In conclusion, a total spread of the EFIGI morphological types over five types for a given B/T is necessary to reproduce the observed dispersion in the discretised B/T for the various types. This is because the Hubble sequence is primarily based on the properties of the spiral arms such as their strength and curvature, independently of the B/T ratio (see Sect. 3.6).
3.3. Characteristics of the spiral arms
 |
Fig. 7 Distribution of the Arm Strength (top) and Arm Curvature attributes (bottom) for the 3881 and 2127 EFIGI galaxies for which these attributes are defined (same presentation as in Fig. 5). The top panel shows the tight relation between the relative flux in the spiral arms and the morphological type, with an increase of the Arm Strength from types Sa to Sc, then a decrease from types Sd to Im. The bottom panel shows a decrease of the Arm Curvature for increasing spiral types. |
Two EFIGI attributes characterise the spiral arms: Arm Strength, which measures the fraction of the total flux included in the spiral arms, and Arm Curvature, which measures the average curvature of the spiral arms.
 |
Fig. 8 Distribution of the Bar Length attribute as a function of EFIGI morphological type for the 3878 EFIGI galaxies for which this attribute is defined (same presentation as in Fig. 7). This graph shows that bars are frequent among all galaxy types except for the cE, E, cD, and dE galaxies, and the strongest bars lie in early-type spirals. |
The top panel of Fig. 7 shows a strong correlation between Arm Strength and EM-type. The graph is restricted to the 3881 galaxies for which the Arm Strength attribute is defined. These galaxies also all have a confidence interval of 3 for this attribute. As expected, Arm Strength is null for ellipticals, all lenticular types, cE and cD galaxies. Then the fraction of flux in the spiral arm steeply increases from types S0a up to Sc, and subsequently decreases from types Sd to Im. The Arm Strength attribute measures the fraction of the total light of the galaxy that is neither included in the bulge nor in the disk, bar, or rings. Because the B/T ratio decreases with increasing EM-type, the increase of Arm Strength from types Sa to Sc indicates that the fraction of light included in the spiral structure increases at the expense of the bulge along these types. In contrast, the simultaneous decrease in the relative fraction of light in the bulge and in the spiral arms from types Sd to Im indicates an increasing fraction of light in the disk along these types.
The diffuse spiral arms detected in the few S0 and S0+ galaxies with Arm Strength above 0 resemble the distorted “plumes” or “loops” of matter seen in merging galaxies. Also, the few Sdm galaxies with Arm Strength = 3 or 4 have almost no disk emission, hence although the spiral arms are very diffuse for those types, they contain a major fraction of the galaxy flux in these particular objects.
In the bottom panel of Fig. 7 one can observe a decrease of Arm Curvature from spiral types S0a to Sm, where the Sa galaxies have the most tightly wound arms and the Sm the most loosely wound arms of all spirals. Note, however, that the winding of the spiral arms shows a “plateau” from Sb to Sc galaxies. Indeed, the Hubble type separation of these four types is based on an increasing continuity of the spiral arm design, which is also based on a decrease in the patchiness of the dust, despite an increase in the arm flocculence (see Sect. 3.5).
3.4. Dynamical components and features: bars, rings, pseudo-rings and perturbation
Dynamical features of galaxies such as spiral arms, bars, and rings are the major drivers of secular evolution via the flow of gas from the disk to the central regions of galaxies (see the review by Knapen 2010). Mergers and interactions, which cause distorted profiles, also contribute to this evolution. Bars allow a transfer of angular momentum to the disk and the halo, and rings trace resonances in the disk.
3.4.1. Bars
Statistics of the EFIGI Bar Length attribute for Incl-Elong ≤ 2, given as a percentage of galaxies with given attribute values.
The EFIGI Bar Length attribute measures the bar’s length relative to the galaxy D25 isophotal diameter (see Sect. 2.4). Figure 8 shows the distribution of Bar Length for all EFIGI galaxies, except for the 580 galaxies for which this attribute is undefined, which are essentially galaxies with Incl-Elong = 3 or 4. Because the identification of bars is less reliable in highly inclined disks, we restrict the analysis to the 3106 galaxies with Incl-Elong ≤ 2. We also separate as “unsure” the 348 and 10 galaxies with Bar Length = 1 and 2 respectively, which have a lower confidence limit set to 0, because the probability that no bar exists at all in these galaxies was considered as non-negligible. To this end, special attention was brought to setting the confidence limits for Bar Length = 1. In the following, we also use “unsure” bars as providers of more realistic error estimates.
Figure 9 shows the fractions of galaxies with Incl-Elong ≤ 2 as a function of morphological type for the various values of the Bar Length attribute. The EFIGI cE, E, and cD galaxies have no detectable bars, whereas bars of all lengths are visible in all other galaxy types, from lenticulars to dE. The galaxy fractions are given in Table 5 for each Bar Length attribute value and for “unsure” bars; statistics for groups of two or three types are also listed, as well as for “all disks”, “all spirals”, and “all types”.
Excluding galaxies with “unsure” bars, 183 (6 ± 1%) have a short bar, 462 (15 ± 1%) an intermediate bar, 310 (10 ± 1%) a strong bar, and 123 (4 ± 1%) a very strong bar; no bar was detected in 1660 galaxies (54 ± 2%). Bars are therefore frequent in EFIGI galaxies, because they are present down to small sizes in ~35 ± 1% of galaxies. The “unsure” bars were extracted from Bar Length = 1 (see above), and a comparison of both columns of Table 5 shows that they correspond to more than half the total number of objects with an attribute value of 1. The separation of the galaxies with “unsure” bars from those with Bar Length = 0 is also unclear, because 3/4 of the latter have an upper confidence limit for a Bar Length of 1, hence a “short” bar is not excluded at the 70% level. The total 12 ± 1% of “unsure” bars therefore illustrate that the uncertainties in the frequency of galaxies with Bar Length = 0 (54 ± 2%) or with Bar Length = 1 (6 ± 1%) may be significantly larger.
 |
Fig. 9 Fraction of galaxies with different values of the Bar Length attribute as a function of EFIGI morphological type for the 3106 EFIGI galaxies with Inclination-Elongation ≤ 2. This graph shows that bars are frequent among all galaxy types except E and dE, and the strongest bars lie in early-type spirals. For clarity, the Poisson error bars in the fractions with Bar Length = 2 are not plotted; these are listed in Table 5 and are comparable to those for the other plotted attribute values. |
An examination of Fig. 9 and Table 5 shows that the long and very long bars (Bar Length = 3 and 4) are preferentially present in S0 + , S0a, and early spiral types Sa to Sbc, with a peak for Sab galaxies, which show a probability of 27 ± 5% to have a long bar, and 16 ± 3% a very long bar. In contrast, Sm is the spiral galaxy type with the lowest fraction of bars altogether, which is also the case for long and very long bars, whereas S0, Sc, Scd, and Sd types show the highest fraction of short bars (12–13%). The Im and dE galaxies have a small but similar fraction of bars (7–9%; bars reside in the dS0 galaxies, which are included in the dE class). No very long bars are detected in EFIGI Sm and Im types.
A comparison of the EFIGI bar frequencies yields results in rough agreement with those stated by Laurikainen et al. (2009) for their selected sample of ~130 S0 and ~200 spiral galaxies, using the RC3 classes (see their Table 1). In particular, Table 5 confirms that S0 galaxies have fewer and shorter bars than S0a and than all spirals together. Here, we add the detail that galaxies with the intermediate type S0− have only short bars, which are much less frequent than in S0 (at least a factor 2, if one takes into account the “unsure” bars). In contrast, the rates of short, intermediate, and long bars in S0+ galaxies are closer to those of S0a galaxies than in S0 galaxies.
 |
Fig. 10 Distribution of the Inner Ring (left) and Outer Ring (right) attributes as a function of EFIGI morphological type for the 3698 and 3549 EFIGI galaxies for which these attributes are defined (same presentation as in Fig. 5). Strong inner rings dominate among S0a, Sa, and Sab galaxies, whereas outer rings show a marked peak in strength for S0a galaxies only. |
For a more detailed comparison with Table 1 of Laurikainen et al. (2009), we added in Table 5 the fractions for the following groups of galaxy types: S0−-S0-S0+, Sa-Sab, Sb-Sbc, Sc-Scd, Sdm-Sm. In Laurikainen et al. (2009), the fraction of bars of all lengths for the former four groups of types are 53 ± 6%, 65 ± 7%, 69 ± 6%, and 64 ± 7% respectively. Only the EFIGI fraction for Sa-Sab (61 ± 6%) agrees within 1σ. For the other groups of types, the EFIGI fractions are systematically lower, probably because of a poorer sensitivity, which has more impact for types with large fractions of short bars (S0 and late spirals). However, if one consider the EFIGI 8% to 12% of “unsure” bars as an estimate of the uncertainty, the differences between the type fractions are reduced to 2σ.
Although the four levels (“no bar”, “short”, “medium”, and “long”) on which Laurikainen et al. (2009) grade bars complicate the comparison with the five levels of the EFIGI Bar Length attribute, one can notice other differences between both samples. Laurikainen et al. (2009) quote S0a as the type with the highest fraction of bars (93 ± 5% compared to 42 ± 6% in the EFIGI catalogue), which is mostly owing to a higher fraction of strong bars than in the other types, whereas in our sample the highest fraction of strong and very strong bars (Bar Length = 3 or 4) occurs in Sab. Moreover, the three largest fractions of bars in the EFIGI catalogue occur in Sab, Sb, and Sd, which show a probability of 71 ± 9%, 52 ± 5%, and 57 ± 8% respectively to have a bar. This is because of 27 ± 5% and 16 ± 3% of galaxies with Bar Length = 3 and 4 respectively in Sab, and 22 ± 3% and 9 ± 2% respectively in Sb, whereas the high frequency of bars in Sd is due to 13 ± 3% and 29 ± 5% of galaxies with Bar Length = 1 and 2 respectively, and only 12 ± 3% and 3 ± 2% with Bar Length = 3 and 4 respectively. These differences in bar fractions may be caused by the lack of spirals later than Scd and the reduced statistics in the ~ 330 galaxy sample of Laurikainen et al. (2009) compared to the EFIGI catalogue; differences between the EFIGI Bar Length attribute definition and the RC3 bar classification may also be at play (see discussion in Nair & Abraham 2010).
Statistics of the EFIGI Inner Ringand Outer Ring attributes for Incl-Elong ≤ 2, given as a percentage of galaxies with given attribute values.
The EFIGI statistics of the Bar Length attribute differ from the minimum in bar fraction at stage Sc and the very high bar fraction at stage Sm found in Buta et al. (2007,see their Fig. 1.14) for a subsample in isophotal diameter and isophotal elongation. The EFIGI results also do not confirm the increasing fraction of bars in disk-dominated, hence late-type spirals, obtained by Barazza et al. (2008), using ellipse-fitting of bars in SDSS r-band images of ~3700 disk galaxies: the last two columns of Table 5 show that the EFIGI fraction of bars of all lengths peaks for Sab galaxies, and regularly decreases for later types. These authors however find a ~50% overall percentage of bars in disk galaxies, which agrees well with the 50–60% value obtained by Knapen et al. (2000) using the RC3 bar classification. Yet the 12% of EFIGI “unsure” bars for “All types” reduces the EFIGI 35% overall rate of bars to a 1σ difference compared with those measured by Barazza et al. (2008), Laurikainen et al. (2009), and Knapen et al. (2000). Nair & Abraham (2010) find an even smaller fraction of 25% of bars in ~14 000 SDSS galaxies, despite a consistent scale of the bar “strength” with EFIGI (Paper I). This illustrates the impact of the different selection criteria (threshold, intensity scale etc.), even when using the same image material.
3.4.2. Rings
The strength of the three EFIGI ring attributes (Inner Ring, Outer Ring, and Pseudo-Ring) is a monotonically increasing function of the fraction of the galaxy flux (dominated by the g-band), which is held in each feature relative to that of the whole galaxy; each strength scale also depends on the most extreme cases found in the EFIGI catalogue.
Figure 10 shows the distribution of the Inner Ring and Outer Ring attributes for all EFIGI galaxies: both graphs show systematic variations in ring strength, with peaks for early-type spirals. For further examination, we list in Table 6 and plot in Fig. 11 the various statistics of the Inner Ring and Outer Ring attributes.
 |
Fig. 11 Fraction of galaxies with different values of the Inner Ring (left) and Outer Ring (right) attributes as a function of EFIGI morphological type for the 3119 galaxies with Inclination-Elongation ≤ 2. For clarity, only the Poisson error bars in the fractions with Bar Length = 3–4 are plotted. This graph shows that the frequency for inner rings peaks for S0a to Sab types, whereas the outer rings are most frequent in S0a and Sa galaxies. |
We again restricted the analysis to the 3106 galaxies with Incl-Elong ≤ 2, because ring attributes are difficult to determine for highly inclined disks. Indeed, Inner Ring and Outer Ring are defined for only 6% to 4% galaxies with Incl-Elong = 4. Although these proportions increase to 80–63% for Incl-Elong = 3, the fractions of galaxies for a given attribute value of Inner Ring and Outer Ring show a poor correlation with the fractions for Incl-Elong ≤ 2. For Inner Ring, we also separated as “unsure” rings the 360 and 4 galaxies with Inner Ring = 1 and 2 respectively, which have a lower confidence limit set to 0; we were not able to perform this distinction during the homogenisation process of the Outer Ring and Pseudo-Ring attributes, owing to the very low contrast of both types of feature.
The left panel of Fig. 11 shows that inner rings are most frequent in S0a, Sa, and Sab types, occurring in 55 ± 7%, 57 ± 7% and 65 ± 8% of these objects (see Table 6). Together with S0+, these EM-types also have the highest fractions of strong and/or very strong inner rings. Interestingly, weak and moderate inner rings also show a peak in frequency for Sa and Sab respectively. Altogether, inner rings are present in 23 ± 1% of disks (types S0− to Sd), and in 21 ± 1% of galaxies of all types. For all attribute values, the frequency of objects decreases for types earlier than S0a, and for types later than Sab. Finally, S0−, Scd, Sd, Sm, and dE galaxies have Inner Ring fractions between 2 and 5%, whereas E, cE, cD, Sm, and Im have no internal rings at all.
Outer rings are less frequent than inner rings by nearly a factor of 2 and occur in only 11 ± 1% of disk galaxies, and 9 ± 1% of all EFIGI galaxies, as shown in Table 6. Moreover, the distribution of outer rings is shifted towards earlier types, with a peak for S0a galaxies (right panel of Fig. 11), as expected from the definition of this EM-type. Earlier S0-S0+ types on the one hand, as well as later Sa-Sab types have frequencies of outer rings between 15 ± 3% to 43 ± 3%. Outer rings occur in less than 5% of S0−, Sbc to Sm, and dE types, and are completely absent from E, cE, cD, and Im galaxies.
Figure 12 shows the frequency distribution of the small population of galaxies (less than 100) that have outer pseudo-rings including the 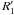 “eight-shape” pattern, and the
“eight-shape” pattern, and the 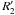 and intermediate
and intermediate 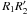 patterns, as defined by Buta & Combes (1996,see Paper I for details of this attribute strength and for colour images of pseudo-rings; see also Buta 1995. These features occur essentially in S0+, S0a, Sa, Sab, and Sb galaxies, with a marked peak for Sab (13 ± 3%), and frequencies of 3 to 8% for the other types. Figure 12 also shows that although Pseudo-Ring = 1 and 2 peak for Sab, the frequency of galaxies with Pseudo-Ring = 3 and 4 regularly decreases from S0a to Sbc. The lower fraction of outer rings compared to inner rings and the even lower fraction of outer pseudo-rings was also found in the RC3 catalogue by Buta & Combes (1996). All these objects are a sub-population of galaxies with a bar, as shown below.
patterns, as defined by Buta & Combes (1996,see Paper I for details of this attribute strength and for colour images of pseudo-rings; see also Buta 1995. These features occur essentially in S0+, S0a, Sa, Sab, and Sb galaxies, with a marked peak for Sab (13 ± 3%), and frequencies of 3 to 8% for the other types. Figure 12 also shows that although Pseudo-Ring = 1 and 2 peak for Sab, the frequency of galaxies with Pseudo-Ring = 3 and 4 regularly decreases from S0a to Sbc. The lower fraction of outer rings compared to inner rings and the even lower fraction of outer pseudo-rings was also found in the RC3 catalogue by Buta & Combes (1996). All these objects are a sub-population of galaxies with a bar, as shown below.
Statistics of the EFIGI Pseudo-Ring attribute for Incl-Elong ≤ 2 given as a percentage of galaxies with given attribute values
 |
Fig. 12 Fraction of galaxies with different values of the Pseudo-Ring attribute as a function of EFIGI morphological type for the 3105 galaxies with Inclination-Elongation ≤ 2. For clarity, no errorbars are plotted, as these are large due to the small number of objects (see Table 7). The outer pseudo-ring pattern is essentially present in S0+, S0a, Sa, Sab and Sb galaxies. |
We list in Table 8 the fractions of galaxies with Bar Length, Inner Ring, Outer Ring, and Pseudo-Ring attributes equal to 0 or in the 1–4 interval (listed in the Table header), which have one of the other attribute in the 1–4 interval (“unsure” galaxies with Bar Length = 1–2 or Inner Ring = 1–2 are discarded). First, this Table shows that the percentage of barred galaxies is similar among galaxies with inner or outer rings (66 ± 4% and 54 ± 5% respectively). However, inner rings are twice as frequent in barred galaxies (39 ± 2%) than in non-barred galaxies (11 ± 1%), and outer rings are 3.5 times more frequent (10 ± 1% and 6 ± 1% of barred and non-barred galaxies respectively). Moreover, outer rings are two to four times less frequent than inner rings in non-barred and barred galaxies.
Both types of rings also appear to be tightly correlated: inner rings are four times more frequent in galaxies with an outer ring (64 ± 6%) than without (16 ± 1%); outer rings are nine times more frequent in galaxies with an inner ring (27 ± 2%) than without (3 ± 1%). These statistics also indicate that an outer ring implies the presence of an inner ring with a 64 ± 6% probability, whereas an inner ring implies an outer ring with a 27 ± 2% probability.
Table 8 confirms quantitatively that the vast majority of pseudo-rings also contain a bar (95 ± 15%) and an inner ring (84 ± 14%), these structural properties being most likely dynamically related. In comparison, only 33 ± 1% of galaxies with no pseudo-ring host a bar and 19 ± 1% an inner ring. Pseudo-rings are indeed nearly 50 times more frequent in barred (11 ± 1%) than in non-barred galaxies (0.2 ± 0.2%), and about 10 times more frequent in galaxies with an inner ring (12 ± 2%) than without (0.9 ± 0.4%). Note also that 58 ± 11% of galaxies with a pseudo-ring are classified as having an outer ring: this occurs when the pseudo-ring is sufficiently round to mimic a single ring; as a result, pseudo-rings are six times more frequent in galaxies with an outer ring (19 ± 3%) than without (3 ± 1%).
Correlations of the EFIGI Bar Length, Inner Ring, Outer Ring, and Pseudo-Ring attributes for Incl-Elong ≤ 2, measured as the percentage of galaxies among the intervals of attributes listed in the header that have another attribute in the interval listed in the left column.
3.4.3. Perturbation
 |
Fig. 13 Distribution of the Perturbation attribute for all 4458 EFIGI galaxies (same presentation as in Fig. 5). This graph shows the increasing Perturbation for types Sd, Sdm, Sm, and Im. |
Statistics of the EFIGI Perturbation attribute given as a percentage of galaxies with given attribute values.
The deviations from smooth and/or symmetric profiles have been quantified by Conselice (2006). These features are also of a dynamical origin, because numerical simulations show that morphological perturbation is the sign of interactions between galaxies (Teyssier et al. 2010).
Figure 13 shows that the EFIGI Perturbation attribute increases for the latest spiral types Sd, Sdm, and Sm; for Im types, the attribute is as high as for Sm galaxies. Table 9 shows that between 1/3 to 2/3 of types from S0+ to Sdm have perturbed profiles, and the percentage increases to 79 ± 7% for Sm and 71 ± 7% for Im galaxies. Altogether, 53 ± 2% of the spiral galaxies exhibit some distortion in their profile. In contrast, only 22 ± 4% of S0, 9 ± 2% of E and 5 ± 2% of S0− are perturbed.
Table 9 also shows that Sm and Im types are more frequently strongly perturbed (Perturbation = 3) than earlier spiral types: this attribute value occurs in 20 to 21 ± 3% of Sm-Im galaxies and in less than 7 ± 1% of earlier spiral types and S0. One possible origin for the higher rate of detectable perturbed profiles in Sm and Im galaxies could be their lower luminosity (de Lapparent & Bertin 2011b, in prep.), hence mass, which might make them more sensitive to tidal effects by neighbouring galaxies. That Im galaxies are more numerous in the dense environments of clusters of galaxies might contribute to increasing their frequency of tidal distortions.
3.5. Texture: dust, flocculence, hot spots
 |
Fig. 14 Distribution of the Visible Dust (left) and Dust Dispersion (right) attributes for the 4458 and 1905 EFIGI galaxies for which these attributes are defined (same presentation as in Fig. 5). The left panel shows the large amounts of dust for early and intermediate spiral types (Sa to Scd), with a peak for Sb galaxies, and the lower values for late spiral (Sd to Sm) and Im types. The right panel shows the increasing Dust Dispersion for spiral galaxies of later type. |
We now examine another four attributes that further define the properties of the spiral structure in spiral galaxies and play a role in the visual definition of the morphological sequence: the presence of dust (Visible Dust), the patchiness of its distribution (Dust Dispersion), the significance of the scattered and giant HII regions (Flocculence and Hot Spots respectively).
3.5.1. Dust
In Fig. 14 we show the distribution of the Visible Dust and Dust Dispersion attributes as a function of EFIGI type; note that Dust Dispersion is defined only for the 1905 galaxies with Visible Dust ≥ 2. In Table 10 we list the fractions of galaxy types for each value of the Visible Dust attribute and for all values of Incl-Elong. Contrary to the bar and ring attributes, dust is also visible in highly inclined or edge-on galaxies and is even easier to detect owing to a higher contrast; this is measured by the systematically higher fractions of galaxies with Visible Dust = 3–4 for Incl-Elong = 3–4 compared to Incl-Elong = 1–2.
Dust appears to be frequent in galaxies: altogether, 90 ± 2% of EFIGI spirals and 71 ± 2% of all types show visually detectable dust. The variations in Visible Dust with type bear some ressemblance with those in Arm Strength, which peaks for Sc, but there are some significant differences. Figure 14 shows a sharply increasing amount of dust for the intermediate lenticular types S0+ and S0a (58 ± 8% and 76 ± 8% host dust) up to the early and intermediate type spirals (Sa to Scd), with a peak for Sb types: more than 90% of Sa to Scd types host dust, with 15 to 32% at a strong level; and Sb types have 13 ± 2% of galaxies with Visible Dust = 4. There is a much smaller relative amount of dust in late spirals (Sd to Sm) however, with a decreasing fraction of 79 ± 7% to 70 ± 7% galaxies altogether, less than 5 ± 1% of these types at the strong level, and 25 ± 3% to 16 ± 3% at the moderate level. The overall frequency of Visible Dust decreases to only 26 ± 4% in Im galaxies. The low values of the Visible Dust attribute for late spiral and irregular types is a combination of the lesser dust content of lower luminosity galaxies (van den Bergh & Pierce 1990), and the lower luminosity of late spirals and irregulars (de Lapparent & Bertin 2011a, in prep.).
The right panel of Fig. 14 shows that the Dust Dispersion is low for Sa galaxies, reaches a peak for Sb types followed by a decrease and a “plateau” for intermediate types (Sbc to Scd), then increases again for later spiral types. Strongly patchy dust is essentially observed in types Sab to Sm.
Statistics of the EFIGI Visible Dust attribute given as a percentage of galaxies with given attribute values.
 |
Fig. 15 Same as Fig. 7 for the Flocculence (left) and Hot Spots (right) attributes. The left panel shows the nearly constant level of Flocculence for all spiral types Sb and later and the lower values for Sa and Im galaxies. The right panel shows a nearly constant level of Hot Spots for all spiral types from Sb to Sdm and an increased Hot Spots attribute for Sm and Im types. |
Statistics of the EFIGI Flocculence and Hot Spots “Texture” attributes given as a percentage of galaxies with given attribute values.
3.5.2. Flocculence and hot spots
Finally, the Flocculence and Hot Spots attributes are useful for quantifying the fraction of light in the scattered and giant HII regions of galaxies. These are rare in elliptical, cD, and lenticular galaxies and increase at types S0+ and later. Figure 15 then shows a roughly constant level of Flocculence and Hot Spots for all spiral types from Sb to Sm, and Sb to Sdm. Then the Flocculence decreases for Im and dE galaxies, whereas the Hot Spots attribute shows a marked increase for types Sm and Im, and again decreases for dE.
Table 11 shows that some level of flocculence is detected in more than 95% of spiral galaxies with types Sab to Sm, whereas hot spots occur in nearly one third of Sb, Sbc, Sc, and Scd types, in half of Sd and Sdm types, in 84 ± 8% of Sm types, and in 75 ± 7% of Im types. For Sa and Sab, hot spots occur in less than 2−10% of galaxies, and in ~5−6% of S0+ and S0a types. cE have a high fraction of 21 ± 12% of objects with evidence for hot spots, which are superimposed on the dense central parts of the objects. The high rate of dE with Hot Spots ≥ 1 (29 ± 7%) is due to the nucleated dS0 contained in this class. About half of these nuclei seem associated with recent star formation as evidenced by the marked blue colours in their vicinity (see also Paudel et al. 2010, who recently showed that the stellar populations of these nuclei in Virgo galaxies are young and metal-enhanced).
Altogether, 97 ± 2% of spiral galaxies show evidence for flocculence, and 37 ± 1% for hot spots. The increase of the Flocculence and Hot Spots attributes along the Hubble sequence is tightly related to the gas content of the galaxies and the resulting star formation, which both increase along the Hubble sequence. Because dust is produced by star formation, the distribution of visible dust is somewhat related to the flocculence, this comparison is complicated however by the fact that dust-enshrouded star formation is not detectable in the optical. The similar trends in the distributions (left panels of Figs. 14 and 15) and statistics of the Visible Dust and Flocculence attributes may result from this relation.
3.6. Specifying the Hubble sequence
We showed in the above sub-sections that all EFIGI morphological attributes vary systematically with morphological type, thus providing us with a quantitative description of the Hubble sequence in terms of each specific morphological features. We summarise these relations here:
-
the B/T ratio decreases regularly along the Hubblesequence, but there is a large 2σ spread of nearly five types for a given B/T value;
-
the regular increase in the Arm Strength attribute results in an increase in the disk contribution along the Hubble sequence, with the latest spirals being disk-dominated, whereas the early-type spirals are clearly bulge-dominated. It is only in intermediate type spirals (Sb and Sbc) that most of the disk light emission lies in the spiral arms;
-
the mean curvature of the spiral pattern regularly decreases (and the pitch angle increases) for later spiral types.
-
Bars are frequent among all galaxy types except E and dE, and are detected in 28 and 7% of S0 and Im galaxies and in 22 to 56% of spirals; the strongest bars lie in early spirals, with a peak frequency of strong and very strong bars in Sab;
-
inner rings occur in 55% or more of S0a, Sa, Sab galaxies, whereas outer rings decrease from 51% to 15% in these types; inner rings are also strongest for these three types and decrease in strength for earlier (S0) and later (spiral) types; outer rings are strongest in S0a types and occur essentially in early-type disks (S0, S0+, S0a, Sa and Sab);
-
the outer pseudo-ring pattern occurs in approximately 10% of barred S0a, Sa, Sab and Sb galaxies;
-
non-disk galaxies and S0− show rare evidence for distortions in their symmetry. Nearly half of the types S0 to Sdm have perturbed symmetry at a low and moderate level, whereas the latest galaxy types, Sm and Im, show evidence for frequent and significant perturbations (79 and 71%);
-
Visible Dust is present in significant amounts in types S0 and later, with a peak for Sb galaxies, and in decreasing amounts for spirals types approaching Sb; however, the Dust Dispersion regularly increases for types later than Scd;
-
there is an increase of the strength of the Flocculence and Hot Spots attributes from Sa to Sb, then both attributes remain constant between Sb and Sdm types. Although the flocculence is stable for Sm and decreases for Im, the strength of the hot spots increases for both types.
These relations confirm the increasing pitch angle of the spiral arms as the primary criterion for defining the progression along spiral types in the Hubble sequence (van den Bergh 1998). Moreover, the increasing strength in the spiral arms along the spiral sequence results from the decreasing disk contribution across the full sequence from ellipticals through lenticulars and down to spirals.
We also propose to interpret the original distinction between Sb to Sc types, based on the increasing continuity of the spiral arm design (van den Bergh 1998), as resulting from the simultaneous steep increase in the relative flux in the spiral arms and the decrease in the amount of dust from types Sb to Sbc-Sc. In contrast, the increase in the fraction of light in the scattered and giant HII regions does not appear to directly participate in the establishment of the Hubble sequence.
We emphasize that although the Hubble morphological types constitute a decreasing sequence of B/T ratio and an increasing sequence of disk contribution to the total galaxy flux, the large 2σ spread of approximately five types per value of B/T results from the prevalence of the spiral arm properties over the B/T ratio for defining the spiral sequence.
4. Size and surface brightness along the Hubble sequence
4.1. D25 distribution
Figure 16 shows the distribution of intrinsic isophotal diameters calculated in Sect. 2.4 as a function of EM-type. The statistics for each value are overplotted: mean and dispersion, both using 3-sigma clipping to exclude galaxies with possible erroneous redshifts and/or intrinsic D25 estimate. As expected, the large cD envelopes and the small cE and dE objects are at the high and low ends of the size distribution, respectively. For all galaxy types, the rms dispersion is in the range of 30–50% of the mean value. The galaxies with high values of intrinsic D25 compared the bulk of the objects for a given EM-type (for exemple the Sm galaxy with D25 ≃ 52 kpc or the dE galaxies with D25 ≥ 15 kpc) might have their D25 overestimated because of a faint extension of the isophotes at large radii; indeed, the fitted disk scale lengths of these objects are within the range of values for the other galaxies of same EM-type (de Lapparent & Bertin 2011a, in prep.).
 |
Fig. 16 Distribution of intrinsic isophotal diameter in kpc for 4196 EFIGI galaxies as a function of EFIGI morphological type. For each type, the weighted mean and rms dispersion (with 3-sigma clipping) are plotted as a circle and vertical error-bar. The largest galaxies are the cD, Sbc and E, the smallest the cE, Im and dE. To guide the eye, a horizontal dotted line is drawn at 10 kpc. |
Moreover, the S0− have statistics comparable to E types, whereas S0 and S0+ galaxies have a lower mean intrinsic D25, of ~24 kpc. This provides interesting support to the suggestion by van den Bergh (1990) that some of the S0 and S0+ (those with small diameters) may not be intermediate between E and Sa. The Sa galaxies also have a mean D25 ≳ 30 kpc, but with fewer galaxies at the small diameter end compared to E types, which could be evidence that the E galaxies are contaminated by small face-on lenticulars. In contrast, S0a types do appear to be intermediate in size between S0+ and Sa. The systematically smaller mean diameter for Sb galaxies compared to Sab and Sbc must be checked by comparing the measured disk scale lengths of the EFIGI spiral galaxies using the bulge+disk modelling (this is reported in de Lapparent & Bertin 2011a, in prep.).
Overall, Fig. 16 shows a clear trend of steadily increasing mean diameter with EM-type for spiral galaxies from S0a up to Sab-Sbc galaxies. Then, a gradual decrease occurs from Sc types to Im, with dE galaxies having a similar size distribution as Im types. The ellipticals, lenticulars, and spirals earlier than Sd have mean diameters of 24 to 39 kpc, whereas galaxies from Sd to dE have mean diameters of 7 to 21 kpc.
Moreover, small galaxies are few among Sa to Scd types: less than 5% of these EM-types have D25 < 10 kpc (horizontal dotted line). S0− galaxy types have slightly higher fractions of 7% of galaxies with D25 < 10 kpc, and S0 and S0+ even higher fractions of 10% and 15% respectively. Despite their even smaller mean diameters of 21 kpc, Sd galaxies also have a low fraction of 7% of such galaxies. In contrast, small spirals become frequent among Sdm and Sm types, with fractions of 17% and 68% of galaxies with D25 < 10 kpc. Of course, cE, Im and dE galaxies have the bulk of their objects below the D25 = 10 kpc, whereas cD galaxies are all above this limit.
We have searched the EFIGI catalogue for dwarf spiral galaxies among types Sa to Scd. These are expected to be rare (Schombert et al. 1995; Sandage & Binggeli 1984). We found two such objects using the criteria Arm Strength ≥ 2, and g absolute magnitude fainter than –17: PGC0039483 and PGC0040705, with magnitudes − 16.9 and − 14.8, and intrinsic D25 values of 5.7 kpc and 1.9 kpc. Both galaxies are located in the direction of the Virgo cluster, with J2000 RA and Dec coordinates (184.499°,6.654°) and (186.635°,12.610°), but with significantly smaller recession velocities of 791 km s-1 and 193 km s-1 (corrected for virgocentric infall). Other names for PGC0039483 are NGC 4241 and IC 3115, whereas PGC0040705 is also named NGC 4413 (NED also provides NGC 4407, but it is not recognised in HyperLeda).
Figure 17 shows irg colour images of both galaxies, obtained using the STIFF software5. Both galaxies have a short bar (Bar Length = 2) and weak flocculence (Flocculence = 1). PGC0039483 has open arms (Arm Curvature = 3), whereas those of PGC0040705 have an intermediate curvature (Arm Curvature = 2). The well designed spiral arms and small B/T ratio of PGC0039483 result in its assigned Scd type in both the RC3 and the EFIGI catalogue. In contrast, PGC0040705 was classified as Sab in the RC3, probably because of its tightly wound spiral arms, whereas in the EFIGI classification, it was assigned an Sc type that reflects its low B/T ratio and flocculence.
By its small size, very faint absolute magnitude, and central nucleus, PGC0040705 recalls the spiral structure seen in some of the EFIGI dE galaxies, which also have a nucleus and a bar. Barazza et al. (2002) and Lisker et al. (2006) showed that these objects are frequent among bright dE galaxies in the Virgo cluster, in contrast with the faint magnitude of PGC0040705. Because the EFIGI catalogue is restricted to galaxies with several measurements of RC3 Hubble types, and is only ~80% complete at bright magnitudes (Paper I), some other nearby dwarf spirals might be missing. A systematic search for dwarf spirals over the whole SDSS survey is necessary to evaluate their true spatial frequency.
 |
Fig. 17 “True colour” irg images of the two dwarf spiral galaxies found in the EFIGI catalogue. These galaxies have redshifts 0.0026385 and 0.0006414, absolute g magnitudes of − 16.9 and − 14.8, and intrinsic D25 values of 5.7 kpc and 1.9 kpc. |
4.2. Mean surface brightness
One may wonder whether the small intrinsic diameters for the late EM-type galaxies in Fig. 16 is caused by some selection effect at low surface brightness that characterises late spiral, irregular and dE galaxies. We examined this effect by estimating the mean surface brightness (SB hereafter) for the EFIGI galaxies, using again the apparent major isophotal diameter in the D25 system. This estimate is much fainter than the central SB or that calculated at the effective radius, but it still allows one to perform an internal comparison among the various EM-types. We only use the 2348 galaxies with small inclination (Incl-Elong ≤ 2), and with no or negligible contamination (Contamination ≤ 1): high contamination evidently biases the SB towards bright values, whereas the SB of highly inclined galaxies is biased towards faint values due to systematically higher dust extinction of both the bulge and the disk than for face-on galaxies (Driver et al. 2007).
Figure 18 shows, the distribution of mean SB using the g-band magnitudes measured from the SDSS images by de Lapparent & Bertin (2011a, in prep.) as a function of EM-type. This graph confirms the compactness of the cE galaxies, which show the highest mean SB. If we exclude the cD galaxies, we observe a dimming in mean SB along the whole Hubble sequence, starting with E types. Combined with the decrease in diameter for later spiral types shown in Fig. 16, this results in the progressive decrease in absolute luminosity of spiral galaxies along the Hubble sequence, as shown by Sandage et al. (1985) using the luminosity functions per morphological type in the Virgo Cluster (see de Lapparent 2003, for a review, and de Lapparent & Bertin (2011b, in prep.) for luminosity functions in the EFIGI catalogue). The systematically brighter SB of Sb and Sm types compared to the monotonically increasing curve relating SB to EM-type is examined by de Lapparent & Bertin (2011a, in prep.) using SB estimates obtained from the bulge+disk modelling of each galaxy profile after convolution by the PSF.
A comparison of the mean SB of EFIGI galaxies with their intrinsic major diameters, as shown in Fig. 19, allows one to evaluate how these two galaxy characteristics could be biased by selection effects. First, the SB limit at 25 mag/arcsec2 mentioned in Sect. 2.4 seems to potentially affect mostly late spirals and irregulars, because types earlier than Sd appear to be intrinsically limited in SB at ~24 mag/arcsec2 or brighter.
 |
Fig. 18 Distribution of mean surface brightness in the g-band within the D25 diameter for the 2278 EFIGI galaxies with Inclination-Elongation ≤ 2 and Contamination ≤ 1 as a function of EFIGI morphological type. For each type, the weighted mean and rms dispersion (with 3-sigma clipping) are also plotted as a circle and vertical error-bar. The mean surface brightness is decreasing along the Hubble sequence from cE to Im types. |
 |
Fig. 19 Distribution of apparent major isophotal diameter D25 converted into kpc as a function of mean surface brightness in the g-band within the D25 diameter for the 2278 EFIGI galaxies for which these parameters are defined and with Inclination-Elongation ≤ 2 and Contamination ≤ 1. Different symbols are used for different EM-types. This graph shows that galaxies with a surface brightness of dE but a more extended diameter could be detected in the EFIGI catalogue. |
Moreover, the large galaxies (those with an intrinsic major diameter larger than 1 kpc) have an SB fainter than a limit determined by the sum of the brightest absolute magnitude and 5lnD25, where D25 is the intrinsic major diameter in kpc. This yields the diagonal boundary in the lower right part of Fig. 19. There is also an apparent boundary in the upper right part of the graph, indicating that the EFIGI catalogue is deficient in large galaxies with very low SB (Malin 1 type objects). It is not clear whether these objects are frequent in the nearby universe and whether this boundary in Fig. 19 is an intrinsic or a selection effect; there is at present no complete census of the galaxy distribution at very low SB (see McGaugh et al. 1995; Dalcanton et al. 1997).
At the small intrinsic diameter limit, one can see that the cE, dE, and Im galaxies span the whole range of mean SB from bright to faint values. The Im galaxies have a fainter SB tail than the dE galaxies (see also Fig. 16). The scarcity of galaxies with a mean SB brighter than 22 is due to the combination of the upper limit in galaxy absolute luminosities (de Lapparent & Bertin 2011b, in prep.) and the D25 > 1 arcmin limit on the angular size (see Fig. 3).
Moreover, Fig. 19 shows that galaxies larger than dE but with the same mean SB could be detected in the EFIGI catalogue: these galaxies would lie in the central part of the data cloud, which is mostly populated by the brightest of the Sd to Sm types, the smallest of the Sbc to Sbc types, and a fair number of S0 to S0a and Sa to Sb galaxies. This suggests that the small intrinsic diameter of dE galaxies in Fig. 16 is likely not due to a selection bias, but to an intrinsic upper limit for this galaxy type. Similarly, Fig. 19 indicates that larger galaxies of types Sd to Im could also be detected in the EFIGI sample. The small diameter of these galaxies therefore appears to be an intrinsic feature of these objects.
5. Conclusions
In addition to the surface brightness limit inherent to all galaxy catalogues, the EFIGI sample is limited in apparent diameter: following the RC3 selection, the majority of the EFIGI galaxies have a major isophotal diameter larger than 1 arcmin in the RC2 D25 system (de Vaucouleurs et al. 1976). This yields a dense sampling of all Hubble types that differs from volume or magnitude limited surveys by oversampling late spirals and irregulars, and therefore does not reflect the real galaxy mix. A strong advantage in this sampling is that it provides us with large numbers of galaxies for each Hubble type (except for the rare cE, cD and dE types), whose full diversity of morphological characteristics can in turn be described using the EFIGI attributes. The various galaxy types are also widely distributed over the redshift and absolute magnitude intervals of the survey.
The high completeness rate of the EFIGI catalogue between the surface brightness and apparent diameter limits does legitimate a statistical analysis of the EFIGI attributes as a function of Hubble type. We thus examined the statistics of the 16 morphological attributes which were measured visually for each of the 4458 EFIGI galaxies, in order to describe their various components, their dynamical features, texture, contamination, and environment. We estimated the frequency of each attribute and its variations among the different Hubble types.
The analysis of EFIGI attributes confirms that the Hubble sequence is an increasing sequence of bulge-to-total ratio and of disk contribution to the total galaxy flux. Nevertheless, there is a large 2σ spread of nearly five types for a given bulge-to-total ratio, resulting from the prevalence of the spiral design in the progression along the spiral sequence. The sequence is indeed characterized by a decreasing mean curvature of the spiral arms. We also propose that the decrease in visible dust from Sb to Sbc-Sc types combined with a steep increase in the strength of the spiral arms between these types contributes to the emergence of the grand spiral design of Sc galaxies. The strength of the scattered and giant HII regions does not vary monotonically along the Hubble sequence, but along sub-portions of the sequence, with peaks and “plateaux” for specific types (the Flocculence and Hot Spots attributes peak for Scd and Sm respectively); hence these attributes do not seem to directly participate in the establishment of the visual Hubble sequence. We also find that the deviation from a symmetric profile regularly increases along the Hubble sequence, but this is an incidental feature in the definition of the sequence.
Dynamical features such as bars and inner rings are present in all types of disk galaxies, and occur in ~40% and ~25% of them, with stronger bar/ring components in early-type spirals and weaker components in late-type spirals. Outer rings are nearly half as rare as inner rings, and both types of rings are tightly correlated. Outer pseudo-rings occur in only ~10% of barred galaxies.
Owing to its ~80% photometric completeness with respect to the SDSS (Paper I), with a preferential choice of galaxies with a reliable RC3 type, the spatial sampling of galaxy concentrations may suffer some bias, however. Systematic effects within each morphological type might exist, for example caused by the combination of the variations from type to type in the Inclination-Elongation attribute and the fact that the RC3 Hubble types were easier to define for weakly inclined galaxies. The numerical values of the frequencies of the various EFIGI attributes as a function of type should therefore be used with caution. The detected systematic tendencies in the various attributes along the Hubble sequence are nevertheless likely to reflect intrinsic galaxy properties.
By cross-matching with the HyperLeda, NED, and SDSS catalogues we obtained redshifts for 99.53% of EFIGI galaxies (z ≲ 0.05), which, combined with the D25 measures, yield estimates of absolute major diameter and mean surface brightness in the SDSS g-band. We derive that the largest galaxies are cD, E, Sab, and Sbc galaxies (20–50 kpc in D25), and find a smooth decrease in size along the Hubble sequence. Late spirals are nearly twice smaller than Sab-Sbc spirals, and Im, dE and cE types are indeed dwarf galaxies (5–15 kpc in D25). The lenticular galaxies are intermediate in size (15–35 kpc in D25). The surface brightness also smoothly decreases along the Hubble sequence, but its selection limits within the EFIGI sample do not exclude the detection of large late-type galaxies.
In addition, we find that there are very few dwarf galaxies of types Sa to Scd, in agreement with the observations of Sandage & Binggeli (1984) in the Virgo cluster: we find only two dwarf spirals in the EFIGI catalogue with well designed spiral arms. We also notice an extension of Sb types to small D25 diameter, which must be examined in greater detail using a more reliable estimate of size (de Lapparent & Bertin 2011a, in prep.). Profile fitting could also allow one to distinguish E galaxies from face-on S0, because these types might be confused in visual morphological classifications (van den Bergh 1990).
If the present analysis of the EFIGI catalogue provides us with a description of the Hubble sequence in terms of each specific morphological feature, one step further is made by applying supervised learning tasks using “Support Vector Machines”. In this context, Baillard (2008) showed that one can determine the Hubble type from a reduced number of EFIGI morphological attributes, which are, in decreasing order of significance: the bulge-to-total luminosity ratio, the strength of spiral arms, and the curvature of spiral arms. In that analysis, the amounts of visible dust and flocculence play a less significant role in determining the Hubble type. These various results agree with the present analysis.
Two forthcoming articles provide examples of the type of advanced morphological studies that can be performed using the EFIGI database. A multi-component profile adjustment of each EFIGI galaxy is carried out using the last version of SExtractor (Bertin & Arnouts 1996; Bertin 2010), and the visual EFIGI attributes are used to calibrate and optimize the automatic profile fitting. These analyses report on a bi-modality in the bulge and disk colours derived from the fitted light profiles to EFIGI galaxies (de Lapparent & Bertin 2011a, in prep.), and present the luminosity functions for the EFIGI sample as a function of morphological type and galaxy component (de Lapparent & Bertin 2011b, in prep.)
Defined in the RC2 system (de Vaucouleurs et al. 1976) as the apparent major isophotal diameter measured at or reduced to a surface brightness level of 25.0 B/mag2, in units of 0.1 arcmin.
Acknowledgments
We are grateful to the referee, Ron Buta, for his very useful comments. This work has been supported by grant 04-5500 (“ACI masse de données”) from the French Ministry of Research.
This research made use of the HyperLeda database (http://leda.univ-lyon1.fr), the VizieR catalogue access tool (Ochsenbein et al. 2000) and the Sesame service at CDS (Strasbourg, France), and the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
This publication also made use of the Sloan Digital Sky Survey images and catalogues. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the U.S. Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced
Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.
References
- Abell, G. O. 1959, Leaflet ASP, 8, 121 [Google Scholar]
- Baillard, A. 2008, Détermination automatique des paramètres morphologiques des galaxies (École Nationale Supérieure de Télécommunications) [Google Scholar]
- Baillard, B., Bertin, E., de Lapparent, V., et al. 2011, A&A, 532, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barazza, F. D., Binggeli, B., & Jerjen, H. 2002, A&A, 391, 823 [Google Scholar]
- Barazza, F. D., Jogee, S., & Marinova, I. 2008, in ASP Conf. Ser., 396 ed. J. G. Funes, & E. M. Corsini, 351 [Google Scholar]
- Bertin, E. 2010, in Astronomical Data Analysis Software and Systems XX [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binggeli, B., & Cameron, L. M. 1991, A&A, 252, 27 [NASA ADS] [Google Scholar]
- Blanton, M. R., & Roweis, S. 2007, AJ, 133, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., & Moustakas, J. 2009, ARA&A, 47, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Kazin, E., Muna, D., et al. 2011, AJ, 142, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Schlegel, D. J., Strauss, M. A., et al. 2005, AJ, 129, 2562 [NASA ADS] [CrossRef] [Google Scholar]
- Buta, R. 1995, ApJS, 96, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Buta, R., & Combes, F. 1996, Fund. Cosmic Phys., 17, 95 [Google Scholar]
- Buta, R., Laurikainen, E., Salo, H., Block, D. L., & Knapen, J. H. 2006, AJ, 132, 1859 [NASA ADS] [CrossRef] [Google Scholar]
- Buta, R. J., Corwin, H. G., & Odewahn, S. C. 2007, The de Vaucouleurs Altlas of Galaxies, ed. Buta, R. J., Corwin, H. G., & Odewahn, S. C. (Cambridge University Press) [Google Scholar]
- Conselice, C. J. 2006, MNRAS, 373, 1389 [NASA ADS] [CrossRef] [Google Scholar]
- Dalcanton, J. J., Spergel, D. N., Gunn, J. E., Schmidt, M., & Schneider, D. P. 1997, AJ, 114, 635 [NASA ADS] [CrossRef] [Google Scholar]
- de Lapparent, V. 2003, A&A, 408, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Lapparent, V., Galaz, G., Bardelli, S., & Arnouts, S. 2003, A&A, 404, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., & Corwin, J. R. 1976, in Second reference catalogue of bright galaxies (Austin: University of Texas Press.), 0 [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, Jr., H. G., et al. 1991, Third Reference Catalogue of Bright Galaxies Vol. 1–3, XII, 2069, 7 figs. (Berlin, Heidelberg, New York: Springer-Verlag) [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G., et al. 1995, VizieR Online Data Catalog, 7155, [Google Scholar]
- Driver, S. P., Popescu, C. C., Tuffs, R. J., et al. 2007, MNRAS, 379, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Dunkley, J., Komatsu, E., Nolta, M. R., et al. 2009, ApJS, 180, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Knapen, J. H. 2010, in Galaxies and their Masks, ed. L. Block David, C. Freeman Kenneth, P., & Ivânio (Springer Science & Business Medi LLC), 201 [Google Scholar]
- Knapen, J. H., Shlosman, I., & Peletier, R. F. 2000, ApJ, 529, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J. 1979, ApJ, 227, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Laurikainen, E., Salo, H., Buta, R., & Knapen, J. H. 2009, ApJ, 692, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Lintott, C. J., Schawinski, K., Slosar, A., et al. 2008, MNRAS, 389, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Lisker, T., Grebel, E. K., & Binggeli, B. 2006, AJ, 132, 497 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S., Bothun, G. D., & Schombert, J. M. 1995, AJ, 110, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Naim, A., Ratnatunga, K. U., & Griffiths, R. E. 1997, ApJ, 476, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Nair, P. B., & Abraham, R. G. 2010, ApJS, 186, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Ochsenbein, F., Bauer, P., & Marcout, J. 2000, A&AS, 143, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paturel, G., Fouque, P., Bottinelli, L., & Gouguenheim, L. 1995, VizieR Online Data Catalog, 7119, [Google Scholar]
- Paturel, G., Petit, C., Prugniel, P., et al. 2003, A&A, 412, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paudel, S., Lisker, T., & Kuntschner, H. 2011, MNRAS, 413, 1764 [NASA ADS] [CrossRef] [Google Scholar]
- Rhee, G., & Roos, N. 1990, MNRAS, 243, 629 [NASA ADS] [Google Scholar]
- Sandage, A., & Binggeli, B. 1984, AJ, 89, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., Binggeli, B., & Tammann, G. A. 1985, AJ, 90, 1759 [NASA ADS] [CrossRef] [Google Scholar]
- Schombert, J. M., Pildis, R. A., Eder, J. A., & Oemler, Jr., A. 1995, AJ, 110, 2067 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R., Chapon, D., & Bournaud, F. 2010, ApJ, 720, L149 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bergh, S. 1990, ApJ, 348, 57 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bergh, S. 1998, Galaxy Morphology and Classification, ed. S. van den Bergh [Google Scholar]
- van den Bergh, S., & Pierce, M. J. 1990, ApJ, 364, 444 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Statistics of the EFIGI “Environment” attributes given as a percentage of galaxies with given attribute values.
Statistics of the EFIGI “Appearance” attributes given as a percentage of galaxies with given attribute values.
Statistics of the EFIGI Bar Length attribute for Incl-Elong ≤ 2, given as a percentage of galaxies with given attribute values.
Statistics of the EFIGI Inner Ringand Outer Ring attributes for Incl-Elong ≤ 2, given as a percentage of galaxies with given attribute values.
Statistics of the EFIGI Pseudo-Ring attribute for Incl-Elong ≤ 2 given as a percentage of galaxies with given attribute values
Correlations of the EFIGI Bar Length, Inner Ring, Outer Ring, and Pseudo-Ring attributes for Incl-Elong ≤ 2, measured as the percentage of galaxies among the intervals of attributes listed in the header that have another attribute in the interval listed in the left column.
Statistics of the EFIGI Perturbation attribute given as a percentage of galaxies with given attribute values.
Statistics of the EFIGI Visible Dust attribute given as a percentage of galaxies with given attribute values.
Statistics of the EFIGI Flocculence and Hot Spots “Texture” attributes given as a percentage of galaxies with given attribute values.
All Figures
 |
Fig. 1 Redshift distribution of all EFIGI galaxies separated by EFIGI morphological type, grouped as follows: cE-dE (light grey); E-cD (grey); S0−-S0-S0+ (orange); S0a-Sa-Sab (yellow); Sb-Sbc (pink); Sc-Scd-Sd (green); Sdm-Sm-Im (blue). |
| In the text | |
 |
Fig. 2 Absolute magnitude distribution in the g-band for all EFIGI galaxies separated by EFIGI morphological type, grouped as follows: cE-dE (light grey); E-cD (grey); S0−–S0-S0+ (orange); S0a-Sa-Sab (yellow); Sb-Sbc (pink); Sc-Scd-Sd (green); Sdm-Sm-Im (blue). |
| In the text | |
 |
Fig. 3 Distribution of apparent major isophotal diameter D25 converted into arcminutes as a function of g-magnitudes measured by de Lapparent & Bertin (2011a, in prep.) for the 4204 EFIGI galaxies for which these parameters are defined. Different symbols and colours are used for different EM-types. The histogram of D25 in intervals of 0.1 arcmin, overplotted vertically on a log scale and with corresponding labels on the top axis of the graph, demonstrates the strong incompleteness in the catalogue for D25 < 1′ and BT > 15.5, materialised by the horizontal and vertical dashed lines. The diagonal dashed line corresponds to a surface brightness limit of 25 mag/arcsec2. The EFIGI catalogue is most complete between these diameter and surface brightness limits, and the crossing of these two lines causes the disappearance of data points fainter than g ~ 16.5. |
| In the text | |
 |
Fig. 4 Distribution of apparent major isophotal diameter D25 converted into kpc as a function of g magnitudes, for the 4104 EFIGI galaxies for which these parameters are defined. Different symbols and colours are used for different EM-types (beware of the different spiral grouping from that in Fig. 3). The D25 < 1′ limit is plotted as a dashed line. Galaxies below this diameter limit extend the minimum detectable diameter for a given distance to a lower value. |
| In the text | |
 |
Fig. 5 Distribution of B/T attribute versus the EFIGI morphological type for the 4458 galaxies in the EFIGI catalogue (see Table 2 for the correspondence with types). In order to see the relative density of data points, they are spread in the horizontal and vertical direction, hence the apparent rectangles. The weighted mean and weighted rms dispersion in B/T are also plotted for each type along with the corresponding number of galaxies. This graph shows the strong correlation of morphological type with B/T. |
| In the text | |
 |
Fig. 6 Histograms of EFIGI morphological type for the five values of B/T (decreasing from left to right). The weighted mean and rms dispersion in the morphological type are plotted above each histogram along with the corresponding number of galaxies. This graph shows the large dispersion in morphological type for a given B/T. |
| In the text | |
 |
Fig. 7 Distribution of the Arm Strength (top) and Arm Curvature attributes (bottom) for the 3881 and 2127 EFIGI galaxies for which these attributes are defined (same presentation as in Fig. 5). The top panel shows the tight relation between the relative flux in the spiral arms and the morphological type, with an increase of the Arm Strength from types Sa to Sc, then a decrease from types Sd to Im. The bottom panel shows a decrease of the Arm Curvature for increasing spiral types. |
| In the text | |
 |
Fig. 8 Distribution of the Bar Length attribute as a function of EFIGI morphological type for the 3878 EFIGI galaxies for which this attribute is defined (same presentation as in Fig. 7). This graph shows that bars are frequent among all galaxy types except for the cE, E, cD, and dE galaxies, and the strongest bars lie in early-type spirals. |
| In the text | |
 |
Fig. 9 Fraction of galaxies with different values of the Bar Length attribute as a function of EFIGI morphological type for the 3106 EFIGI galaxies with Inclination-Elongation ≤ 2. This graph shows that bars are frequent among all galaxy types except E and dE, and the strongest bars lie in early-type spirals. For clarity, the Poisson error bars in the fractions with Bar Length = 2 are not plotted; these are listed in Table 5 and are comparable to those for the other plotted attribute values. |
| In the text | |
 |
Fig. 10 Distribution of the Inner Ring (left) and Outer Ring (right) attributes as a function of EFIGI morphological type for the 3698 and 3549 EFIGI galaxies for which these attributes are defined (same presentation as in Fig. 5). Strong inner rings dominate among S0a, Sa, and Sab galaxies, whereas outer rings show a marked peak in strength for S0a galaxies only. |
| In the text | |
 |
Fig. 11 Fraction of galaxies with different values of the Inner Ring (left) and Outer Ring (right) attributes as a function of EFIGI morphological type for the 3119 galaxies with Inclination-Elongation ≤ 2. For clarity, only the Poisson error bars in the fractions with Bar Length = 3–4 are plotted. This graph shows that the frequency for inner rings peaks for S0a to Sab types, whereas the outer rings are most frequent in S0a and Sa galaxies. |
| In the text | |
 |
Fig. 12 Fraction of galaxies with different values of the Pseudo-Ring attribute as a function of EFIGI morphological type for the 3105 galaxies with Inclination-Elongation ≤ 2. For clarity, no errorbars are plotted, as these are large due to the small number of objects (see Table 7). The outer pseudo-ring pattern is essentially present in S0+, S0a, Sa, Sab and Sb galaxies. |
| In the text | |
 |
Fig. 13 Distribution of the Perturbation attribute for all 4458 EFIGI galaxies (same presentation as in Fig. 5). This graph shows the increasing Perturbation for types Sd, Sdm, Sm, and Im. |
| In the text | |
 |
Fig. 14 Distribution of the Visible Dust (left) and Dust Dispersion (right) attributes for the 4458 and 1905 EFIGI galaxies for which these attributes are defined (same presentation as in Fig. 5). The left panel shows the large amounts of dust for early and intermediate spiral types (Sa to Scd), with a peak for Sb galaxies, and the lower values for late spiral (Sd to Sm) and Im types. The right panel shows the increasing Dust Dispersion for spiral galaxies of later type. |
| In the text | |
 |
Fig. 15 Same as Fig. 7 for the Flocculence (left) and Hot Spots (right) attributes. The left panel shows the nearly constant level of Flocculence for all spiral types Sb and later and the lower values for Sa and Im galaxies. The right panel shows a nearly constant level of Hot Spots for all spiral types from Sb to Sdm and an increased Hot Spots attribute for Sm and Im types. |
| In the text | |
 |
Fig. 16 Distribution of intrinsic isophotal diameter in kpc for 4196 EFIGI galaxies as a function of EFIGI morphological type. For each type, the weighted mean and rms dispersion (with 3-sigma clipping) are plotted as a circle and vertical error-bar. The largest galaxies are the cD, Sbc and E, the smallest the cE, Im and dE. To guide the eye, a horizontal dotted line is drawn at 10 kpc. |
| In the text | |
 |
Fig. 17 “True colour” irg images of the two dwarf spiral galaxies found in the EFIGI catalogue. These galaxies have redshifts 0.0026385 and 0.0006414, absolute g magnitudes of − 16.9 and − 14.8, and intrinsic D25 values of 5.7 kpc and 1.9 kpc. |
| In the text | |
 |
Fig. 18 Distribution of mean surface brightness in the g-band within the D25 diameter for the 2278 EFIGI galaxies with Inclination-Elongation ≤ 2 and Contamination ≤ 1 as a function of EFIGI morphological type. For each type, the weighted mean and rms dispersion (with 3-sigma clipping) are also plotted as a circle and vertical error-bar. The mean surface brightness is decreasing along the Hubble sequence from cE to Im types. |
| In the text | |
 |
Fig. 19 Distribution of apparent major isophotal diameter D25 converted into kpc as a function of mean surface brightness in the g-band within the D25 diameter for the 2278 EFIGI galaxies for which these parameters are defined and with Inclination-Elongation ≤ 2 and Contamination ≤ 1. Different symbols are used for different EM-types. This graph shows that galaxies with a surface brightness of dE but a more extended diameter could be detected in the EFIGI catalogue. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


