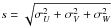| Issue |
A&A
Volume 530, June 2011
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 21 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201016276 | |
| Published online | 26 May 2011 | |
New constraints on the chemical evolution of the solar neighbourhood and Galactic disc(s)
Improved astrophysical parameters for the Geneva-Copenhagen Survey⋆
1
Max Planck Institute for Astrophysics, Postfach 1317, 85741 Garching, Germany
e-mail: luca@MPA-Garching.MPG.DE
2
INAF-Osservatorio Astronomico di Collurania, via Maggini, 64100 Teramo, Italy
3
The Observatories of the Carnegie Institution for Science, 813 Santa Barbara Street, Pasadena, CA 91101, USA
4
Departamento de Astronomia do IAG/USP, Universidade de São Paulo, Rua do Matão 1226, São Paulo, 05508-900, SP, Brasil
5
European Southern Observatory, Alonso de Cordova 3107, Vitacura, Casilla 19001, Santiago 19, Chile
6
Lund Observatory, Box 43, 22100 Lund, Sweden
Received: 7 December 2010
Accepted: 23 March 2011
We present a re-analysis of the Geneva-Copenhagen survey, which benefits from the infrared flux method to improve the accuracy of the derived stellar effective temperatures and uses the latter to build a consistent and improved metallicity scale. Metallicities are calibrated on high-resolution spectroscopy and checked against four open clusters and a moving group, showing excellent consistency. The new temperature and metallicity scales provide a better match to theoretical isochrones, which are used for a Bayesian analysis of stellar ages. With respect to previous analyses, our stars are on average 100 K hotter and 0.1 dex more metal rich, which shift the peak of the metallicity distribution function around the solar value. From Strömgren photometry we are able to derive for the first time a proxy for [α/Fe] abundances, which enables us to perform a tentative dissection of the chemical thin and thick disc. We find evidence for the latter being composed of an old, mildly but systematically alpha-enhanced population that extends to super solar metallicities, in agreement with spectroscopic studies. Our revision offers the largest existing kinematically unbiased sample of the solar neighbourhood that contains full information on kinematics, metallicities, and ages and thus provides better constraints on the physical processes relevant in the build-up of the Milky Way disc, enabling a better understanding of the Sun in a Galactic context.
Key words: stars: abundances / stars: fundamental parameters / Hertzsprung-Russell and C-M diagrams / stars: kinematics and dynamics / Galaxy: disk / solar neighborhood
Catalogue (Table 2) is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/530/A138
© ESO, 2011
1. Introduction
Late-type dwarf stars are long-lived objects and can be regarded as snapshots of the stellar populations that are formed at different times and places over the history of our Galaxy. Not only their kinematics carry residual information on their dynamical histories, but their atmospheres retain a fossil record of the composition of elements in the interstellar medium at the time and place of their formation. Therefore, F, G, and – to a lesser extent – K dwarfs have been traditionally used to study various aspects of the chemical evolution of the Milky Way.
The region in the Milky Way for which this task can be most easily achieved is the solar neighbourhood; starting from pioneering works using spectra or ultraviolet and colour excess to estimate the metal abundance of stars in a Galactic context (e.g., Wallerstein 1962; van den Bergh 1962; Eggen et al. 1962; Schmidt 1963), this endeavour has continued over the years with steadily improving spectroscopic and photometric studies. The latter (e.g., Twarog 1980; Olsen 1983; Strömgren 1987; Nordström et al. 2004; Haywood 2008) comprise large catalogues, but have to pay for this by being only able to derive one single parameter for metallicity, and no detailed elemental abundances. On the other hand, spectroscopic studies are still limited to small samples of a few hundred or about a thousand stars at most. While some studies (e.g., Edvardsson et al. 1993; Favata et al. 1997; Fuhrmann 2008) rely on kinematically unbiased samples, many investigations (e.g., Feltzing & Gustafsson 1998; Bensby et al. 2003; Reddy et al. 2006; Bensby et al. 2007; Ramírez et al. 2007; Soubiran et al. 2008) make use of sophisticated kinematic selections to achieve significant numbers of members belonging to different subpopulations in their sample. Even though the abundance trends in these studies are better traced thanks to this strategy, a quantitative interpretation can be more difficult.
Galactic chemo-dynamic studies are now entering a new realm with current (e.g., RAVE Steinmetz et al. 2006; SDSS Ivezić et al. 2008) and forthcoming (e.g., SkyMapper, APOGEE, HERMES, LSST, Gaia) large photometric, spectroscopic and astrometric surveys targeting different and fainter components of the Galaxy. These tremendous observational efforts, however, must be supported by equal investments to minimize the errors that plague the determination of stellar parameters. The most important parameter is the effective temperature (Teff): its determination has implications for the derived abundances, for surface gravities and for the inferred ages, masses, and distances via isochrone fitting. If we aim to deconstruct the formation and evolution of the Milky Way in a star-by-star fashion, it is fundamental to have full control over all potential sources of errors.
The preferred stellar Teff scale has been a long debated issue, with various scales differing systematically by 100 K or more. Though this is still true in many areas of the HR diagram, recent data on solar twins (Meléndez et al. 2009; Ramírez et al. 2009), new data and analyses of interferometric angular diameters (Boyajian et al. 2010; Chiavassa et al. 2010) and improved HST absolute spectrophotometry (Bohlin 2007) have allowed to pin down the source of these discrepancies via the infrared flux method (IRFM). This gives a good base for the zeropoint of the temperature scale of dwarfs and subgiants, which has now an uncertainty of the order of only 20 K (Casagrande et al. 2010). For solar-type stars, the new IRFM scale supports effective temperatures approximately 100 K hotter than those of Alonso et al. (1996), which has been the de facto choice in many studies until now. Such a shift on the zeropoint has an immediate consequence on the abundances and ages derived for nearby, solar-like stars (see also Meléndez et al. 2010b) and therefore for interpreting the most basic constraints on Galactic chemical evolution models, namely the metallicity distribution function and the age–metallicity relation. The HR diagram constructed using our newly derived Teff scale matches very well that predicted by stellar models for evolved F and G dwarfs (VandenBerg et al. 2010; Brasseur et al. 2010), thus avoiding the introduction of any ad hoc shifts to the Teff scale as was the case in some previous studies (e.g., Nordström et al. 2004).
The purpose of the present work is to carry out a revision of the astrophysical parameters in the Geneva-Copenhagen Survey (Nordström et al. 2004; Holmberg et al. 2007, 2009) with the new effective temperature scale presented in Casagrande et al. (2010) as a starting point to derive new metallicities and ages. We improve not only on the accuracy, i.e. reduce zeropoint systematics, but also the precision by reducing internal errors stemming from photometric transformations, resulting in highly homogeneous astrophysical parameters. These improvements turn out to be crucial to provide more stringent observational constraints on Galactic chemical evolution theories and hence on the history of the Milky Way. In fact, a knowledge of the metallicity distribution together with Galactic abundance gradients can improve our understanding of the impact and shape of the stellar migration process in the Galactic disc (Schönrich & Binney 2009a,b). Because models including radial migration relax the classical tight correlation between age and metallicity, this relation becomes effectively an additional constraint independent from the metallicity distribution.
As we will demonstrate, an estimate of [α/Fe] for most of the stars is also obtained here for the first time from Strömgren indices. Having an indication of [α/Fe] allows for a tentative dissection of the chemical thin and thick disc. These estimates are far less accurate than those obtained by high-resolution spectroscopy, yet this sample exceeds the largest spectroscopic studies available so far by more than an order of magnitude and it is not biased by any kinematic selection.
The paper is organized as follows. We present the sample and the determination of new effective temperatures and metallicities in Sect. 2. Correspondingly, new ages and masses for the stars are derived in Sect. 3. In Sect. 4 we use this information for studying the metallicity distribution function in the solar neighbourhood and briefly discuss a possible signature of the Galactic bar. The age–dispersion relation is discussed in Sect. 5, while Sect. 6 is devoted to a better understanding of the disc and its metallicity gradient. We finally present our conclusions in Sect. 7.
2. Determination of astrophysical parameters
The Geneva-Copenhagen Survey (GCS) is the most comprehensive catalogue of late-type solar neighbourhood stars, providing kinematics and Galactic orbits for a magnitude-limited and kinematically unbiased sample of 16682 of FG(K) dwarfs brighter than V ~ 8.3. Some 63000 radial velocity measurements were used to assemble the catalogue, which, complemented with Tycho2 proper motions and Hipparcos parallaxes, also provides binarity indication and distances. Because the selection of stars into the final catalogue was purely based on colour and magnitude cuts, the survey provides (apart from effects by the photometric selection) a kinematically unbiased census of the solar neighbourhood. While we do not have access to the original sample selection performed in assembling the catalogue, we refer to Nordström et al. (2004) for a comprehensive discussion on the adopted selection criteria and relative completeness. Homogeneous Strömgren photometry was used to derive Teff and [Fe/H] for nearly all stars in the survey. The original catalogue (Nordström et al. 2004, GCSI) has undergone a number of revisions to improve the temperature and metallicity calibrations (Holmberg et al. 2007, GCSII) and to account for the new reduction of the Hipparcos parallaxes (Holmberg et al. 2009, GCSIII).
However, recent work has shown that the temperature scale adopted in GCSI-III is too cold (Casagrande et al. 2010; Meléndez et al. 2010b). This has far-reaching implications: hotter temperatures imply higher spectroscopic metallicities and –when relying on stellar isochrones – lower age estimates.
Because we use photometry to derive astrophysical parameters, it is crucial to clean the sample from binaries, variable stars and/or less certain measurements. A description of our selection leading to stars with the best photometry (irfm sample) with respect to the remaining ones (clbr sample) is given in Sect. 2.1, where we also briefly present our implementation of the IRFM and the new effective temperatures derived for the entire GCS catalogue. Notice that the distinction between the two samples is based exclusively on the photometric criteria applied and therefore does not introduce any apparent kinematic bias (Fig. 1). The corresponding new metallicity scale and ages are then discussed in Sects. 2.2 and 3, respectively.
2.1. A new effective temperature scale
The effective temperatures in the GCSI were derived using the Strömgren calibration of Alonso et al. (1996), which however lacked a sufficient number of stars bluer (i.e. hotter) than (b − y) ~ 0.3 (Teff ~ 6500 K). In GCSII this problem was tackled by deriving a new (b − y) vs. Teff calibration, where effective temperatures for all stars were first obtained using the (V − K) calibration of di Benedetto (1998) and then Teff were re-derived by applying this new (b − y) calibration to the full catalogue. However, the calibration of di Benedetto (1998) is defined in Johnson K, enforcing a colour transformation from the 2MASS KS used in GCSII. Because the standards of the Johnson system are all saturated in 2MASS, this renders the transformation between the two systems less precise (Carpenter 2001). In addition, the metallicity effect is largely reduced but not zero even in (V − K), and the calibration of di Benedetto (1998) does not account for this effect. The zeropoint of the di Benedetto (1998) temperature scale is roughly intermediate between that of the Alonso et al. (1996) scale and our own, which is some 50 K hotter (see below and the comparison in Casagrande et al. 2006).
2.1.1. Reddening
 |
Fig. 1 Distributions in the velocity planes of the two subsamples defined in this work. |
When deriving Teff from photometry it is crucial to correct for reddening, if present. Fortunately, given the solar neighbourhood nature of the sample used here, most of the stars are unaffected by this problem. Reddening estimates derived from Strömgren photometry are known to be generally reliable (in this case with a stated precision σE(b − y) = 0.009 mag, Holmberg et al. 2007; but see also Karataş & Schuster 2010, for a recent revision), and we adopted a procedure similar to GCS for all stars1 i.e. a reddening correction is applied for stars with E(b − y) greater than 0.01 mag and farther away than 40 pc, otherwise a value of zero is assumed.
Thus, only about one quarter of the stars in the GCS catalogue need to be corrected for reddening, the median E(b − y) being 0.02 mag, as one would expect given the nearby nature of the sample (see also Holmberg et al. 2007, for a plot of the colour excess in different distance intervals). Note that the effect of colour excess on Teff derived via IRFM amounts to ~50 K for every 0.01 mag (see Casagrande et al. 2010, for further details) whereas in the case of colour-temperature calibrations its effect can be directly estimated.
Although the temperature and metallicity scales are unchanged between GCSII and III, we noticed important differences between the two catalogues. These differences show a correlation with the adopted E(b − y), reaching several hundred K in Teff and almost 1 dex in [Fe/H] for stars with the highest colour excesses. This suggests that stars in GCSIII have not been corrected for reddening and because of this we will only use the kinematic data from GCSIII and the stellar parameters from GCSII when making comparisons.
2.1.2. irfm sample
The IRFM implementation described in Casagrande et al. (2010) not only improves the accuracy of the zeropoint of the derived stellar parameters, but also their precision by employing Tycho2 BTVT and 2MASS JHKS photometry to simultaneously recover the bolometric flux – ℱBol(Earth) – and the effective temperature of each star. It is well suited to be applied to the Geneva-Copenhagen catalogue directly, avoiding the use of colour calibrations as well as transformations among different photometric systems.
 |
Fig. 2 Panels a) and b) ΔTeff (ours minus GCSII) as a function of our Teff (upper) and [Fe/H] (lower) for stars in the irfm sample. Panels c) and d) same as before, but for all remaining GCS stars in the clbr sample (see discussion in Sect. 2.1). Contour levels are computed on abscissa intervals of 25 K and 0.025 dex, respectively, to equally represent regions with fewer stars. Dashed and dotted lines indicate the mean difference and standard deviation of the entire sample; because they are symmetric and are dominated by regions with the highest overdensity of stars, the dashed and dotted lines are in some cases offset from the local 1σ contour levels. |
Given its nature, it is crucial to have good photometry in all bands for the stars we apply the IRFM to. From the GCSII we exclude stars flagged as variable or having multiple components. We retrieve Tycho2 BTVT magnitudes for all targets (Høg et al. 2000) and additionally cross-check and discard those classified as variable or non-single in Hipparcos. The faintest stars might have uncertain photometry in Tycho2, whereas the brightest can be saturated in 2MASS: when applying the IRFM we consider only stars with photometric errors σBT + σVT < 0.10 and “j_” + “h_” + “k_msigcom” < 0.10 all having quality flag “A” in 2MASS2. Stars having Teff < 5000 K emit considerable amount of flux in the red. The computation of the bolometric flux (and thus Teff) is inaccurate if one uses only Tycho2 and 2MASS photometry (Casagrande et al. 2010) and therefore we exclude stars cooler than this limit. This cut concerns only a minor part (326 stars out of 16682) of the sample in the GCS.
In our implementation of the IRFM an iterative procedure is adopted to cope with the mildly model-dependent nature of the bolometric correction: given an initial estimate of Teff, we interpolate over a grid of synthetic stellar fluxes at the appropriate [Fe/H] (as determined in Sect. 2.2) and log g of each star, until convergence in Teff is reached within 1 K.
For all stars, log g is determined from the fundamental relation  (1)where L is the bolometric luminosity3 and ℳ is the mass of the star, obtained by interpolating over isochrones. Notice that in Eq. (1) mass plays only a secondary role: varying it by 10% changes log g by 0.04 dex. We used the masses reported in GCSII as a starting value and the BASTI mass expectation values (cf. Appendix) for a second iteration. Even variations as large as ± 0.5 dex in surface gravity change the Teff obtained via IRFM by only a few tens of a K (Casagrande et al. 2006, 2010), thus having negligible impact. The bolometric luminosity L is computed from ℱBol(Earth) using the new Hipparcos parallaxes (van Leeuwen 2007), and an iterative procedure was adopted to converge in log g using at each step the corresponding effective temperature and luminosity obtained from the IRFM. Although in the GCSI a photometric selection was made to cut out giant stars, there is a handful of them left. We exclude those labelled as suspected giants in the GCS and restrict the irfm sample to log g ≥ 3.0. Altogether, we are left with a sample of 6670 stars that satisfy all of the above criteria on photometric quality, non-binarity, and surface gravity. To these we can apply the IRFM. A MonteCarlo simulation using the measured observational errors (σBT,σVT, “j_”, “h_”, “k_msigcom” and σ [Fe/H] ) was used to estimate the random error in the resulting Teff and ℱBol(Earth) of each star, to which the systematic uncertainty arising from the adopted absolute calibration was added (see Casagrande et al. 2006, 2010).
(1)where L is the bolometric luminosity3 and ℳ is the mass of the star, obtained by interpolating over isochrones. Notice that in Eq. (1) mass plays only a secondary role: varying it by 10% changes log g by 0.04 dex. We used the masses reported in GCSII as a starting value and the BASTI mass expectation values (cf. Appendix) for a second iteration. Even variations as large as ± 0.5 dex in surface gravity change the Teff obtained via IRFM by only a few tens of a K (Casagrande et al. 2006, 2010), thus having negligible impact. The bolometric luminosity L is computed from ℱBol(Earth) using the new Hipparcos parallaxes (van Leeuwen 2007), and an iterative procedure was adopted to converge in log g using at each step the corresponding effective temperature and luminosity obtained from the IRFM. Although in the GCSI a photometric selection was made to cut out giant stars, there is a handful of them left. We exclude those labelled as suspected giants in the GCS and restrict the irfm sample to log g ≥ 3.0. Altogether, we are left with a sample of 6670 stars that satisfy all of the above criteria on photometric quality, non-binarity, and surface gravity. To these we can apply the IRFM. A MonteCarlo simulation using the measured observational errors (σBT,σVT, “j_”, “h_”, “k_msigcom” and σ [Fe/H] ) was used to estimate the random error in the resulting Teff and ℱBol(Earth) of each star, to which the systematic uncertainty arising from the adopted absolute calibration was added (see Casagrande et al. 2006, 2010).
2.1.3. clbr sample
For all remaining stars in the GCSII effective temperatures and bolometric fluxes were computed using the colour calibrations in (b − y), (BT − VT), (VT − J), (VT − H) and (VT − KS) from Casagrande et al. (2010), which extend also below 5000 K. We only took into consideration photometry with σBT < 0.05, σVT < 0.05, “j_msigcom” < 0.04, “h_msigcom” < 0.04, “k_msigcom” < 0.04 (which in the colour–temperature relations imply formal uncertainties similar to those of the stars analysed using the IRFM). We computed the average Teff and ℱBol(Earth) if more than one index was used and applied a 3σ clipping if more than two indices were present. In the latter case, the standard deviation was used to estimate the error in the derived Teff. Notice that these calibrations (as any available in literature) do not include an explicit log g dependence. However, because surface gravities of dwarfs and subgiants decrease when moving to hotter Teff, an intrinsic dependence on such a term is likely to be built into them (see also the discussion in Casagrande et al. 2010). Our colour–temperature calibrations indeed perform extremely well along most of the CMD morphology defined by F and G dwarfs and subgiants (VandenBerg et al. 2010).
Figure 2 shows the comparison between Teff derived in Sects. 2.1.2 and 2.1.3 and those in GCSII. A mean difference of about 100 K appears, and there are trends at the highest and lowest Teff, as well as at the lowest metallicities. The latter trend could arise from the absence of an explicit metallicity dependence in di Benedetto (1998) or from the limitation of the standard functional form used in literature when fitting effective temperatures and metallicities as function of (b − y) (see Casagrande et al. 2010). We note that the IRFM depends only marginally on the assumed metallicity, and we verified for the GCS stars that changing [Fe/H] by ± 0.2 dex affects Teff by about 20 K at most. The impact can indeed be larger when one uses colour–Teff relations that involve optical bands.
2.2. A new Strömgren metallicity scale
The uvby photometric4 system (Strömgren 1963) is well suited for the determination of basic stellar atmospheric parameters through the colour indices (b − y), m1 = (v − b) − (b − y) and c1 = (u − v) − (v − b). The m1 index is designed to measure the depression owing to metal lines around 4100 Å (v band), and hence is suitable to infer the metallicity in a variety of stars (e.g., Bessell 2005, and references therein). The c1 index is designed to evaluate the Balmer discontinuity, which is a temperature indicator for B- and A-type stars and a surface gravity indicator for late-type stars, though for stars comparable to or cooler than the Sun it also carries metallicity information (e.g., Twarog et al. 2002; Önehag et al. 2009; Meléndez et al. 2010b). Several calibrations exist in the literature that link Strömgren colours to astrophysical parameters, following either theoretical (i.e. based on model atmospheres) or empirical approaches (see Önehag et al. 2009; and Árnadóttir et al. 2010; respectively, for recent reviews).
Throughout the paper, we talk of metallicity both in terms of iron abundance [Fe/H] and overall metal content [M/H] , if a clear distinction is not needed. Notice though that Eqs. (2) and (3) given later in this section are calibrated against spectroscopic measurements of [Fe/H] and thus are strictly referring to iron abundance. The overall metal content – always indicated by [M/H] in this work – was obtained using the same functional forms, but accounting for [α/Fe] in the calibration sample. Later in this section we develop a new estimator for the α-element content in most of the GCS stars.
 |
Fig. 3 ΔTeff (ours minus spectroscopic values) for the 1498 stars in our calibration sample as function of Teff (panel a)) and [Fe/H] (panel b)). Contour levels and lines as in Fig. 2. |
The metallicity calibration adopted in GCSII patches the red (b − y ≥ 0.46) and blue (b − y ≤ 0.30) calibrations derived in the GCSI with a new calibration containing all possible combinations of (b − y), m1 and c1 to third order for 0.30 < (b − y) < 0.46. Those three calibrations are built by linking Strömgren indices to spectroscopic metallicities gathered from a large number of studies, affecting the homogeneity of the results. In addition, the calibration in the 0.30 < (b − y) < 0.46 range is based on spectroscopic studies with a Teff scale broadly consistent with that adopted in the GCSII, i.e. cooler than the one used in this study, implying an offset in the zeropoint of the metallicity scale. The adopted Teff scale is in fact the main driver in setting the zeropoint of the metallicity scale.
Over the past few years an increasing number of high-resolution and high signal-to-noise spectroscopic investigations have targeted hundreds of stars in the solar neighbourhood. This allows us to build a large and homogeneous spectroscopic catalogue, which we use to derive a new metallicity calibration. To this purpose we have taken only three large surveys, namely Valenti & Fischer (2005, V05), Sousa et al. (2008, S08) and Bensby et al. (2011, in prep., B11; which includes over 600 stars in addition to 102 from Bensby et al. 2003; and Bensby et al. 2005). Apart from spectroscopically determined Teff and [Fe/H] , all these surveys provide α abundances: Si and Ti in the case of Valenti & Fischer (2005), and Mg, Si, Ca, Ti for the other two studies (for the Sousa et al. 2008, sample the abundances are given in the companion paper of Neves et al. 2009, N09). They are all very consistent, with mean differences (all in the sense B11-V05 and B11-S08 for 142 and 85 stars in common, respectively) of Δ [Fe/H] = 0.034 ± 0.004 (σ = 0.050 dex) and 0.047 ± 0.005 (σ = 0.046 dex) and Δ [α/Fe] = 0.06 ± 0.01 (σ = 0.16 dex) and 0.01 ± 0.02 (σ = 0.20 dex). These differences are small and consistent with the scatter; we also made an attempt to homogenise all stars on a common scale (B11) by fitting the differences with respect to B11 as linear or parabolic function of [Fe/H] , log g and Teff but this approach only had a minor effect on the overall metallicity calibration. A comparison with the homogenised spectroscopic catalogue of Árnadóttir et al. (2010) confirms this conclusion (see below).
Our final sample contains 1522 stars, all having Strömgren colours, [Fe/H] and [α/Fe] . If a star was found in more than one study, we chose the [Fe/H] and [α/Fe] from the one that had Teff closest to our estimate. The mean difference between photometric and spectroscopic Teff is 13 ± 95 K. We also applied a 3σ clipping to remove the major outliers, and obtained a final calibration sample of 1498 stars (ΔTeff = 14 ± 83 K), half of which are in the irfm sample. Figure 3 compares our effective temperatures with those of the three spectroscopic studies. The systematic offset between older photometric and spectroscopic Teff (e.g., Ramírez & Meléndez 2004) is now clearly removed thanks to our new IRFM implementation. There are no significant trends as function of effective temperature, except for the very few stars below ~5000 K where spectroscopic estimates have the tendency to return hotter Teff than photometric ones (see also the discussion in Sousa et al. 2008). When plotting ΔTeff as function of [Fe/H] , the metal-poor stars are on average well reproduced despite an increasing scatter. There is a minor trend in the range −0.5 < [Fe/H] < 0.5 dex, with 1σ contour going from + 50 K to − 50 K: this could potentially introduce a mild systematic bias (as well as affect the width of the metallicity distribution function) of the order of ∓ 0.05 dex throughout this range, though for a single star this is below the accuracy of our calibration (see below) and spectroscopic measurements are themselves not immune from deficiencies. On average there is no significant zeropoint offset or trend.
 |
Fig. 4 Left panel: [Fe/H] versus m1 for our 1498 calibrating stars in different (b − y) ranges represented by different symbols (median values as indicated in the labels). The size of the symbols increases with higher values of c1. Dotted and continuous lines represent Eq. (2) at these median values for the 10th and 90th percentiles of the c1 distribution. Central panel: same as left panel, but for Eq. (3), which applies only to cool stars. Right panel: theoretical [Fe/H] versus m1 relation when using synthetic colours from the “MARCS-standard” library and log g instead of c1 (see text for discussion). |
In the literature various approaches have been used to calibrate Strömgren photometry to derive metallicities, either based on how much the colour indices m1 and c1 differ from a given standard relation (usually derived for the Hyades, e.g., Olsen 1984; Haywood 2002; van Leeuwen 2009) or using direct combinations of the Strömgren indices m1,c1 and (b − y). This is the choice made in most of the recent works (e.g., Schuster & Nissen 1989; Haywood 2002; Nordström et al. 2004; Ramírez & Meléndez 2005; Holmberg et al. 2007; Twarog et al. 2007). We adopt the latter approach, but we are aware that even though our calibrating sample includes a large number of stars, some regions of the [Fe/H] , Teff and log g space are less well sampled than others (see also Fig. 4). To limit possible biases, we checked our findings against synthetic colours. Despite the inaccuracies that might still plague synthetic Strömgren colours (e.g., Meléndez et al. 2010b), in many cases they can be used at least to provide guidance on general trends (Önehag et al. 2009). For this work, synthetic indices were computed for the full grid of “MARCS-standard”5 model spectra (Gustafsson et al. 2008) using the zeropoints and filter transmission curves described in Meléndez et al. (2010b). Note that the purpose of using synthetic colours is for verification only, and they do not enter into our calibrations, which remain fully empirical.
Figure 4 shows the sensitivity of m1 to [Fe/H] for our 1498 calibrating stars, in different (b − y) (basically Teff) ranges. The asymptotic behaviour towards the most metal-poor stars reflects the decreasing sensitivity of m1 in this regime and it can be well represented by a logarithmic term (Schuster & Nissen 1989). Therefore, rather than including all possible combination of indices in some high-order polynomial, we started with a simple form of the kind 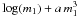 and introduced mixed terms to allow for a change of slope with (b − y) and c1, where the ratio between the logarithmic and cubic terms, a, was optimized by treating it as a free parameter in the fitting process. This accounts for the first six terms in the following equation
and introduced mixed terms to allow for a change of slope with (b − y) and c1, where the ratio between the logarithmic and cubic terms, a, was optimized by treating it as a free parameter in the fitting process. This accounts for the first six terms in the following equation 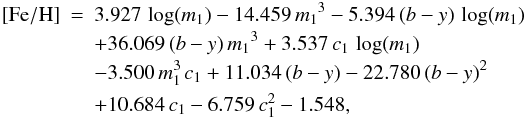 (2)where the additional terms that have a linear and quadratic dependence on (b − y) and c1 were introduced after verifying that they improved the residuals. We also checked that the inclusion of terms of higher order did not lead to any further gain. Equation (2) applies to stars in the following ranges: 0.23 ≤ (b − y) ≤ 0.63, 0.05 ≤ m1 ≤ 0.68 and 0.13 ≤ c1 ≤ 0.60 with a standard deviation of 0.10 dex. We remark that for stars with [Fe/H] ≲ − 2 Strömgren indices effectively lose sensitivity to metallicity. We verified this using an additional sample of 26 metal-poor dwarfs taken from Casagrande et al. (2010) and Meléndez et al. (2010a). Those stars, all in the range −3.3 < [Fe/H] < −2.0, did not show any significant dependence on metallicity6 and were therefore not used in the fitting process, which was limited to the 1498 stars shown in Fig. 4.
(2)where the additional terms that have a linear and quadratic dependence on (b − y) and c1 were introduced after verifying that they improved the residuals. We also checked that the inclusion of terms of higher order did not lead to any further gain. Equation (2) applies to stars in the following ranges: 0.23 ≤ (b − y) ≤ 0.63, 0.05 ≤ m1 ≤ 0.68 and 0.13 ≤ c1 ≤ 0.60 with a standard deviation of 0.10 dex. We remark that for stars with [Fe/H] ≲ − 2 Strömgren indices effectively lose sensitivity to metallicity. We verified this using an additional sample of 26 metal-poor dwarfs taken from Casagrande et al. (2010) and Meléndez et al. (2010a). Those stars, all in the range −3.3 < [Fe/H] < −2.0, did not show any significant dependence on metallicity6 and were therefore not used in the fitting process, which was limited to the 1498 stars shown in Fig. 4.
While the hottest stars in Fig. 4 display a remarkably tight correlation with [Fe/H] , for decreasing Teff also c1 correlates well with metallicity (Twarog et al. 2002; Meléndez et al. 2010b). In fact, different metallicity calibrations are often given for F and GK dwarfs separately (e.g Schuster & Nissen 1989; Nordström et al. 2004). While Eq. (2) applies also to cool stars ((b − y) > 0.43, i.e. Teff ≲ 5600 K), for those we found an additional function of the kind 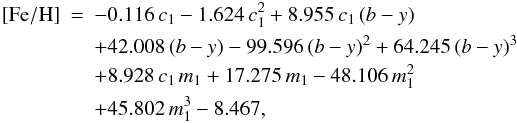 (3)which applies to stars with 0.43 ≤ (b − y) ≤ 0.63, 0.07 ≤ m1 ≤ 0.68 and 0.16 ≤ c1 ≤ 0.49 with a standard deviation of 0.12 dex (the same σ is obtained considering instead Eq. (2) for equally red stars, but averaging with this latter form helps to reduce the zeropoint offset for cool stars). With respect to the functional form used in Schuster & Nissen (1989), ours has the same standard deviation, but performs significantly better for [Fe/H] ≲ −1.0.
(3)which applies to stars with 0.43 ≤ (b − y) ≤ 0.63, 0.07 ≤ m1 ≤ 0.68 and 0.16 ≤ c1 ≤ 0.49 with a standard deviation of 0.12 dex (the same σ is obtained considering instead Eq. (2) for equally red stars, but averaging with this latter form helps to reduce the zeropoint offset for cool stars). With respect to the functional form used in Schuster & Nissen (1989), ours has the same standard deviation, but performs significantly better for [Fe/H] ≲ −1.0.
The right hand panel of Fig. 4 shows predictions using “MARCS-standard” synthetic colours: models capture the main trends, especially at higher Teff and different surface gravities, where the choice of various log g in the synthetic spectra is approximated by the 10 and 90 percentiles of the c1 distribution in the data (assuming lower values of c1 to trace higher log g, which does not hold exactly towards the coolest Teff, because of contamination between dwarfs and subgiants). The main point from Fig. 4 is that our adopted functional form is a good representation of the data, even in poorly sampled regions of the plot and the trend at super-solar metallicities, where we do have calibration stars, is real.
 |
Fig. 5 Panel a) spectroscopic versus photometric metallicities obtained using the calibration presented in Sect. 2.2 for 1498 stars. Filled circles are for stars having (b − y) < 0.43, open circles for redder (i.e. cooler) stars. Panel b) same as above, but showing residuals (ours minus spectroscopic). Dotted lines are 1σ scatter and boxes the median values in non overlapping intervals of 0.2 dex. Panel c) same as in the previous one, but as a function of Teff, with boxes computed in non overlapping intervals of 100 K. The overall zeropoint offset is μ = −0.003 dex and σ = 0.097 dex. Panel d) distribution of the residuals of our calibration against spectroscopy with a Gaussian of width σ and centred at μ overplotted. Panel e) standard deviation associated to each square computed in panel b) with error bars being the standard deviation of the mean. |
We applied Eq. (2) to all stars in the GCS, but for stars redder than (b − y) ≥ 0.43 we also used Eq. (3) and then took the average of both estimates as our final value. The comparison between the input spectroscopic metallicities and our photometrically derived values is shown in Fig. 5. Both equations provide a good representation of spectroscopic measurements and, within their accuracy, we do not introduce any obvious discontinuity. Our procedure gives a more homogeneous sample, avoiding the presence of breaks in different colour ranges, as was the case in the previous GCSII (see Fig. 6). Uncertainties in the observed Strömgren colours also bear on derived metallicities. On average, the effect amounts to 0.04−0.05 dex in [M/H] and [Fe/H] , estimated running a MonteCarlo simulation with observational errors in (b − y), m1 and c1 as given in Olsen (1983). Errors in the derived metallicities tend to increase towards the blue- and red-most indices.
A comparison with the homogenized spectroscopic sample of Árnadóttir et al. (2010) confirms the quality of our calibration with a median (mean) difference (ours minus Arnadottir) of 0.002 (0.007) dex and a scatter σ = 0.13 dex. Note that as discussed throughout the text, the overall scatter of our calibration with respect to the spectroscopic sample is slightly below 0.1 dex, though this comparison folds the uncertainties that affect spectroscopic estimates. The test on open clusters (see Sect. 2.2.1) suggests that the intrinsic scatter in the metal-rich regime is actually somewhat lower. Using the recently determined uvby solar colours of Meléndez et al. (2010b), we obtain [Fe/H] ⊙ = −0.006 dex, which agrees well with the zeropoint of our metallicity calibration.
 |
Fig. 6 Δ [Fe/H] (in the sense ours minus GCSII) as function of Teff (panel a)) and [Fe/H] (panel b)) for stars in the irfm sample satisfying the applicability range of our metallicity calibration. Notice the two breaks at 5500 K and 6500 K which correspond to the discontinuities introduced by the three calibrations used in GCSII for different (b − y). Contour levels and lines as in Fig. 2. |
2.2.1. Further test of the [Fe/H] scale
We already checked our metallicity scale against the homogenized stellar sample of Árnadóttir et al. (2010) and the solar colours of Meléndez et al. (2010b). Here we further test it by using open clusters and a moving group; finally we comment upon the limit of our calibration for intrinsically bright stars.
Hyades and Coma are two nearby, virtually reddening-free clusters often used to check the metallicity scale (e.g Haywood 2006), though Holmberg et al. (2007) claim that GCS uvby photometry of stars belonging to the Hyades cluster is not on the same scale as the rest of the catalogue, possibly because they were observed at higher air masses from Chile. In the case of Hyades, its controversial c1 colour anomaly is also of concern (i.e. the systematic difference in the c1 vs. (b − y) diagram between the sequence of unevolved stars in Hyades and the corresponding sequence for unevolved Coma and field stars with similar δm1; see e.g., Crawford 1975; Strömgren et al. 1982, for more details).
We took Strömgren photometry for the Hyades cluster from Crawford & Perry (1966)7 and compared the result of our metallicity calibration with the detailed spectroscopic study of Hyades stars of Paulson et al. (2003) (who adopt a Teff scale rather close to our IRFM scale). There are 10 single stars in common and we find a mean [Fe/H] = 0.09 ± 0.02 dex (σ = 0.06 dex). This value is slightly lower than the mean obtained using the same stars in Paulson et al. (2003), which amounts to [Fe/H] = 0.14 ± 0.01 dex (σ = 0.04 dex) and nearly coincides with the mean value derived by Paulson et al. (2003) using a larger sample of cluster members. We note that for this cluster a typical metallicity around 0.1 dex is commonly cited in the literature (e.g., Taylor & Joner 2004; Schuler et al. 2006).
The Hyades open cluster is known to be underabundant in helium for its metallicity (ΔY ~ 0.02 see e.g., VandenBerg et al. 2010, and references therein), a feature which would be tempting to associate to the c1 colour anomaly (Strömgren et al. 1982). However, synthetic colours show that variations of helium of this order affect c1 to a negligible extent (Meléndez et al. 2010b). Another possibility is that the anomaly is caused by variations in other elements. In fact the Hyades anomaly could simply be the [Fe/H] difference between stars of similar δm1 as the following comparison with the Coma cluster suggests. For 17 stars in the Coma cluster we took the photometry of Crawford & Barnes (1969) and derived [Fe/H] = −0.08 ± 0.02 (σ = 0.07 dex) using our calibration, which implies a metallicity difference with respect to Hyades that excellently agrees with that spectroscopically measured by Boesgaard & Friel (1990) and Friel & Boesgaard (1992).
Another open cluster originally observed by Crawford & Barnes (1970) is NGC 752. This cluster also has relatively low reddening E(b − y) = 0.027 (Anthony-Twarog & Twarog 2006). Using all dwarfs in Crawford & Barnes (1970) (within the colour range of our calibration) gives [Fe/H] = −0.07 ± 0.02 dex (σ = 0.11 dex), and a similar value (− 0.05 ± 0.04 dex, σ = 0.09 dex) when restricting the same photometric measurements to the smaller – yet with cleaner membership – sample of Anthony-Twarog & Twarog (2006).
Finally, using observations of F-type stars in the Pleiades (which are less affected by activity stemming from the young age of this open cluster) from Crawford & Perry (1976) and adopting E(B − V) = 0.04 (e.g., van Leeuwen 2009), we derive [Fe/H] = 0.00 ± 0.02 dex (σ = 0.10). The difference with respect to the Hyades again excellently agrees with that obtained from the spectroscopic comparison of Boesgaard & Friel (1990), after correcting the Pleiades for known non-members (An et al. 2007). Our [Fe/H] also agrees well with recent spectroscopic estimates based on a Teff scale consistent with our own (Soderblom et al. 2009). For the last two clusters, we also checked that a typical uncertainty of E(b − y) = 0.01 affects [Fe/H] by ~ 0.01 dex.
An additional check on the precision of our metallicity calibrations comes from the HR1614 moving group (Eggen 1978; Feltzing & Holmberg 2000). Chemical tagging via high-resolution spectroscopy of kinematically selected members allows us to clearly identify interlopers amongst the group members (De Silva et al. 2007). Figure 7 shows the differential Fe abundance Δ [Fe/H] for a number of candidate members in common between De Silva et al. (2007) and GCS, using our metallicity calibration. The plot is relative to the mean metallicity of the sample, and thus largely independent on the underlying Teff scale adopted. The comparison agrees remarkably well with Fig. 2 in De Silva et al. (2007), clearly allowing us to identify spurious members of the moving group. We determine the group to have a mean [Fe/H] = 0.28 ± 0.02 dex (σ = 0.07 dex), in good agreement with the spectroscopic value of 0.25 dex in De Silva et al. (2007).
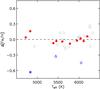 |
Fig. 7 Differential Fe abundances of kinematically selected members of HR1614. Filled circles are metal-rich members, while asterisk (HIP13513), triangle (HIP6762) and diamond (HIP25840) are spurious members according to the chemical tagging performed by De Silva et al. (2007). Open circles are the analogous comparison with the group members from Feltzing & Holmberg (2000). |
Finally, we comment on the accuracy of our photometric metallicities for intrinsically bright stars. The spectroscopic sample upon which our calibration is built extends to magnitudes only slightly brighter than MVT ~ 2, which are typical for F dwarfs; however, the GCS contains some hundreds of stars more luminous than this (also compare with Fig. 12). These stars are close to the instability strip and are therefore possibly contaminated by δ Scuti pulsators and/or chemically peculiar A/F stars (the latter often being overabundant in Fe and possibly with peculiar colours, e.g., Gebran et al. 2008; Netopil et al. 2008). Our calibrations include a dependence on the c1 index (a good surface gravity indicator for hot stars), so in principle, we can expect them to work for decreasing log g. Figure 8 shows a clear trend for the brightest stars in the GCS, which tend to be more metal-rich than the remaining part of the sample (left panel). Because they are preferentially metal-rich, an age determination based on isochrones also biases them to even younger values. These bright stars also stand out in the study of the metallicity distribution function (Sect. 4) and in kinematic (Fig. 17). Some uptrend in this figure (starting around MVT ~ 3) is expected from colour/spectral-type cuts in the original GCS sample selection, because at a given colour metal-poor dwarfs are fainter (cf. also Fig. 14). However, at the bright end (in particular from MVT ~ 2) the calibration seems to deviate too strongly. Interestingly, those stars are preferentially the most distant ones and thus have increasing reddening uncertainties as well as the largest parallax errors, which could misleadingly place intrinsically bright stars at fainter absolute magnitudes. Also notice that by sampling larger distances, where the GCS is not complete anymore, intrinsically luminous stars are preferentially found around the peak of the metallicity distribution function, which could partly account for their rather high [Fe/H] . In addition, preferentially higher metallicities could also stem from these objects originating from the inner disc (cf. Sect. 6), a feature of which we do not find any significant indication, though. Even if not conclusive, this seems to suggest that removing stars with an absolute magnitude MVT brighter than 2 would be a safe choice when using GCS stars for deriving local constraint on Galactic chemical evolution.
 |
Fig. 8 Panel a) [Fe/H] distribution when slicing in absolute magnitude (MVT) 5976 stars (grey circles) that belong to the irfm sample and are within the metallicity calibration range. Contour levels are computed on abscissa intervals of 0.1 mag to equally represent regions with fewer stars. Panel b) and c) [Fe/H] distribution of the same stars, but plotted as a function of distance and parallax error. In all panels, stars with MVT < 2 are overplotted as black squares (271 in total). |
2.3. The mild sensitivity of Strömgren photometry to the α-elements
For all 1498 calibrating stars presented in Sect. 2.2 we have [Fe/H] and [α/Fe] from high-resolution spectroscopy. From this the overall metal-to-hydrogen ratio [M/H] can be computed (e.g., Yi et al. 2001). Interestingly, when fitting functional forms of the kind of Eqs. (2) and (3) to [M/H] , the scatter of the resulting calibrations decreases to 0.07 and 0.10 dex respectively, thus suggesting (cf. e.g., Yong et al. 2008) that Strömgren indices carry information on the overall metal content (apart from a few of the most metal-poor stars in the sample, which indicates diminishing sensitivity to [M/H] because of the intrinsically fewer lines).
 |
Fig. 9 [α/Fe] versus (v − y) − (b − u) for our 1498 calibrating stars. Bluer (redder) colours indicate hotter (cooler) stars, according to their (b − y), as shown in the top right box. Squares are synthetic colours computed from MARCS model fluxes at fixed [α/Fe] (as available from MARCS library) for selected values of (b − y) = 0.4,0.5,0.6 (from left to right) and [Fe/H] = 0.00 dex with [α/Fe] = 0:0.4 dex (continuous line) [Fe/H] = −0.25 dex with [α/Fe] = 0:0.1:0.4 dex (dotted lines), [Fe/H] = −0.50 dex with [α/Fe] = 0:0.2:0.4 dex (dashed lines), [Fe/H] = −0.75 dex with [α/Fe] = 0:0.3:0.4 dex (dot-dashed lines), [Fe/H] = −1.00 dex with [α/Fe] = 0:0.4 dex (triple-dot-dashed lines). Stars within 0.01 mag of the selected (b − y) interval are shown with open circles to highlight the trend. Grey dotted lines are fiducials built for those stars. Lower left panel is a zoom of the (b − y) = 0.4 data set for 2.2 ≤ (v − y) − (b − u) ≤ 2.8. |
It would be possible to apply our calibrations as a function of [Fe/H] and [M/H] and from those derive an estimate of [α/Fe] . In practice though, there is some degree of correlation in the results since the same functional form and indices are used over 2 dex in metallicity to estimate typical alpha-enhancements within ~ 0.5 dex. We experimented with different combinations of Strömgren colours and found a1 = (v − y) − (b − u) to be sensitive8 to [α/Fe] at a given Teff. Figure 9 shows [α/Fe] versus our index a1 as well as the comparison with synthetic colours at a few (b − y) values for the sets of alpha-enhanced and -poor models available through the MARCS library.
In Fig. 9 a dependence on [Fe/H] is certainly built in given that stars with lower [Fe/H] have preferentially higher levels of alpha-enhancements. Nevertheless, the comparison with synthetic colours shows that the trend is real at fixed metallicities. As we already pointed out, Strömgren synthetic colours are not immune to deficiencies, and combinations of the adopted filters are – by construction – also sensitive to metallicity and surface gravity. Changing the latter parameter shifts synthetic colours to the right or left with respect to the position shown in Fig. 9, which refers to log g = 4.5. However, we checked that the shape of the slopes remains unaffected by the exact value of log g. Limitations in synthetic colours as well as surface gravity dependence could explain why the bulk of calibrating stars is fitted by models having [Fe/H] = −0.5 rather than a higher metallicity, which is more representative of the sample (cf. also with Fig. 4). According to the models, in Fig. 9 the sensitivity to [α/Fe] is more pronounced (i.e. it has a shallower slope) at cooler effective temperatures, which are therefore likely to be better recovered. Determining [α/Fe] becomes increasingly difficult for the hottest and most metal-poor stars, as expected because both atomic and molecular lines get weaker in this regime (e.g. Coelho et al. 2005). Yet, even at the bluest colours the data seem to show a clearer trend with [α/Fe] than models. Aware of these warnings, the mild correlation of the a1 index with alpha-enhancement seems to work for drawing meaningful conclusions when one has a statistically large sample of stars (see also Fig. 11).
For each (b − y) in Fig. 9 we constructed a fiducial using stars of similar Teff and derived a value of [α/Fe] according to their (v − y) − (b − u) with respect to that of the corresponding fiducial. Despite models show a spread with metallicity in Fig. 9, we did not include any dependence on [Fe/H] in building the fiducial to avoid any risk of introducing a spurious trend of increasing alpha with decreasing [Fe/H] . The comparison between the spectroscopic measurements and our photometric estimates is shown in Fig. 10. The overall agreement is indeed good (formally σ = 0.09 dex), though there are a few caveats: [α/Fe] for stars with [Fe/H] ≲ − 1 is not well recovered (the calibration saturates, filled squares), as expected from our previous discussion on metal-poor stars. Also, for thin-disc stars [α/Fe] tends to be slightly underestimated/overestimated at higher/lower metallicities. This reflects the shape of the fiducials used to derive [α/Fe] from Fig. 9. In fact, Fig. 11 shows that our [α/Fe] calibration does not allow us to recover any gap between thin and thick disc stars. The shape of the overall narrow trend is thus driven from the fiducial, yet within this trend a distinction between alpha-rich and -poor stars is possible, though in a statistical sense only. This is shown by selecting calibration stars on the right (left) of the dotted (dashed) line in Fig. 11, with the same distinction right vs. left still being preserved when we use our [Fe/H] and [α/Fe] calibrations, which are represented by upward vs. downward triangles. Notice that using our [α/Fe] the dispersion of the photometric [M/H] with respect to the spectroscopic measurements is 0.08 dex, compared to 0.10 dex (previous section) when using [Fe/H] only.
In conclusion, the sensitivity of our approach to the alpha elements is real, but mild and works only for [Fe/H] > − 1 or slightly higher values. Also, a statistical distinction between alpha-rich and -poor stars is possible, but only within the functional form of our calibration so that other finer structures could still be missing. Thus, the values of alpha-enhancements we derive are not exact measurements of [α/Fe] , but rather a proxy of them for stars of similar [Fe/H] . For this reason we will refer to our estimate as αFe instead of [α/Fe] throughout the paper. Nevertheless, as we show below, when one deals with several thousands of stars, as is the case in the GCS, our αFe can give important insight into the formation and evolution of the Galactic disc(s).
 |
Fig. 10 Upper panel: spectroscopic versus Strömgren [α/Fe] estimates for our 1498 calibrating stars. Crosses (circles) are stars having probability > 90 percent of being thin (thick) disc based on their kinematic (using U,V,W velocities from the GCS). Downward triangles are stars with lower probability or for which kinematic information was not available. Filled squares are stars having [Fe/H] ≤ − 1 (independently of their kinematic thin/thick membership, if available). Lower panel: same symbols as above, showing the difference spectroscopic minus ours. |
3. New age and mass determinations
Revising metallicities and effective temperatures also affects age and mass estimates for the stars. Figure 12 shows comparisons between isochrones and stars with metallicities close to those of the plotted isochrones. Compared to previous studies, our improved effective temperatures are hotter, and the large systematic discrepancies between theoretical isochrones and observed data that plagued e.g., Pont & Eyer (2004) almost entirely disappear. As can be seen, only at the lowest metallicities and luminosities the theoretical main sequence has the tendency to fall beneath the stars, i.e., the isochrones are too hot. However, the discrepancy is considerably reduced from earlier GCS analyses where shifts in the effective temperature of the isochrones have to be introduced below solar (Nordström et al. 2004) or even at all (Holmberg et al. 2007) metallicities9. Our new temperature and metallicity scales prove to agree very well with those of theoretical isochrones, at least for metallicities higher than about [M/H] > −0.5, which includes the vast majority of stars in our sample (cf. Fig. 15). Indeed, for the sake of Fig. 12 a metallicity bias stemming from the wings of the metallicity distribution function will also play a role, as we discuss in greater detail in Appendix, as well as the monotonic decrease (increase) of stars with metallicity in the metal-rich (-poor) tail of the metallicity distribution function by which the average metallicity in a given interval can be lower (higher) than the middle value of the interval. This can be clearly seen in the net bias of hotter and more metal-poor (cooler and more metal-rich) stars in the top left (bottom right) panel of Fig. 12, where stars are selected in symmetric intervals around the metallicity of the isochrones10.
 |
Fig. 11 [Fe/H] versus [α/Fe] for the 1498 stars in the spectroscopic sample (filled circles). Dotted and dashed lines are arbitrarily used to select stars on the right and left locus of the plot (only for [Fe/H] > − 1). Downward (upward) triangles represent stars selected according to this criterion, but using our [Fe/H] and [α/Fe] Strömgren calibrations. |
As pointed out by Pont & Eyer (2004), naïve fits to isochrones lead to severe biases, e.g. what they name a terminal age bias. This happens because some places on isochrones are more densely populated than others because of the mapping from mass to colours/luminosity owing to the initial mass function and to the time scales involved in stellar evolution. Just looking for the closest match ignores these facts and might erroneously place too many stars into sparsely populated regions. Biases of this kind can be accounted for by taking a Bayesian approach as in Pont & Eyer (2004) and Jørgensen & Lindegren (2005), who did a Bayesian age determination on the old GCSI-II. A detailed discussion can also be found in Burnett & Binney (2010). In our sample the errors vary significantly between stars, but they depend only weakly on the derived stellar parameters, so that we can neglect this influence on the age distribution. We only used log (Teff), absolute Johnson V magnitude and metallicity information to estimate the ages and masses of stars. In principle more information could be in the colours, but essentially this is already exploited by the colour-dependent calibrations. Moreover, a direct use of colour information would imply relying directly on synthetic colours (with the uvby bands being more troublesome than others, see e.g., Önehag et al. 2009; Árnadóttir et al. 2010; Meléndez et al. 2010b), which we wanted to avoid. Further, especially Strömgren colours depend on [M/H] , thus requiring an even denser grid of metallicities than the one we use.
 |
Fig. 12 BASTI isochrones for different ages at a given metallicity (continuous lines) compared to stars of similar [M/H] , where the difference ± 0.1 or ± 0.2 dex is coded by colours. Larger symbols are for stars with higher parallax accuracy as labelled in the top left panel. Only stars in the irfm sample are shown. |
The isochrones provide us with a natural grid for calculating the probability distribution function for the parameters of a given star. Every isochrone point has to be weighed by the volume of parameter space it has to cover and by the a priori assumptions. To avoid any factor that could contribute to the particular age distribution that we find in the sample, we assume a flat age prior for 0 − 14 Gyr, i.e. a constant density 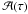 of stars over age,
of stars over age, 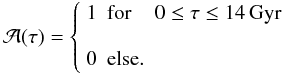 As different positions of stars in the Hertzsprung-Russell diagram imply different underlying selection functions that bias the intrinsic age distribution at this place, this approach also avoids making further assumptions that could potentially weaken the interpretation of the results. The mass prior is a Salpeter IMF (Salpeter 1955) and we do not set any dependence on age. In the mass interval of interest here (cf. Fig. 14), a Salpeter IMF is indeed still appropriate, whereas considerably larger uncertainties exist regarding the lower and higher mass range (e.g., Bastian et al. 2010). We further tested the extreme case of a flat IMF, and even this unrealistic assumption has negligible impact on our results (see Appendix, where we provide details on the Bayesian scheme adopted for dealing with the observational errors in Teff, metallicities and absolute magnitudes).
As different positions of stars in the Hertzsprung-Russell diagram imply different underlying selection functions that bias the intrinsic age distribution at this place, this approach also avoids making further assumptions that could potentially weaken the interpretation of the results. The mass prior is a Salpeter IMF (Salpeter 1955) and we do not set any dependence on age. In the mass interval of interest here (cf. Fig. 14), a Salpeter IMF is indeed still appropriate, whereas considerably larger uncertainties exist regarding the lower and higher mass range (e.g., Bastian et al. 2010). We further tested the extreme case of a flat IMF, and even this unrealistic assumption has negligible impact on our results (see Appendix, where we provide details on the Bayesian scheme adopted for dealing with the observational errors in Teff, metallicities and absolute magnitudes).
In order to study differences between different isochrones, we used grids of the BASTI11 (Pietrinferni et al. 2004, 2006, 2009) and Padova12 isochrones (Bertelli et al. 2008, 2009). The Padova grid has a logarithmic age spacing of 0.01 dex, i.e. it rises from 23 Myr at τ = 1 Gyr to 230 Myr at τ = 10 Gyr. We queried a total of 56 metallicities from the database, which are created by interpolating among the nine available metallicities, ranging from Z = 0.0001 to Z = 0.07. The solar isochrone has Y⊙ = 0.26 and Z⊙ = 0.017 (Grevesse & Sauval 1998). The helium-to-metallicity enrichment ratio was chosen to be ΔY/ΔZ = 2.1, which is consistent with the value inferred from the study of metal-rich local K dwarfs (Casagrande et al. 2007). At the lowest metallicities this falls somewhat short of Y = 0.23 (the lower helium abundance in the database, lower than the current preferred estimate from WMAP + BBN, see e.g., Steigman 2010), and for those objects we kept this value of Y. For the BASTI isochrones (Y⊙ = 0.2734 and Z⊙ = 0.0198 from Grevesse & Noels 1993) we used a denser grid than the published one. This grid was specially calculated for this purpose to include 20 metallicities at ΔY/ΔZ = 1.45 (leading to a primordial helium abundance in agreement with the cosmological estimate) in the range Z = 0.0001 to 0.04, with a time spacing of 100 Myr maximum, making this grid denser (sparser) at high (lower) ages compared to the logarithmic age spacing in the Padova isochrones. Both sets of isochrones assume solar-scaled abundances (i.e. constant ratio of the single metals with respect to the Sun), which are appropriate because it has been shown that for the range of metallicities covered by the present study, isochrones for enhanced α abundances can be reproduced remarkably well by those for solar scaled mixtures if Z is the same (e.g., Chieffi et al. 1991; Chaboyer et al. 1992; Salaris & Weiss 1998; VandenBerg et al. 2000). We also checked the difference when using [Fe/H] rather than [M/H] in determining ages: the overall difference is fairly small, with a scatter of about 0.5 Gyr.
 |
Fig. 13 Normalized age probability distribution for all stars in the sample having both BASTI (continuous thick) and Padova (continuous thin) ages and only for stars in the irfm sample (dotted thick and thin lines) having good ages and MVT ≥ 2. |
 |
Fig. 14 Ages versus masses for stars belonging to the irfm sample. Colours are for stars with well determined ages, going from metal-poor (blue) to -rich (red), while grey dots are for the remaining stars. Squares are stars brighter than MVT = 2. Inner panel: same as outer panel, but with a metallicity colour coding also for stars with less reliable ages. |
Figure 13 shows the age probability distributions for all stars in the GCS with ages determined from both BASTI and Padova isochrones and also for all stars with good ages. Throughout the paper, ages are defined to be good if σ < 1 Gyr or the relative uncertainty is better than 25 percent (see also Appendix). While these criteria are arbitrary, they balance a reasonable determination of absolute ages for young objects with a reasonable relative determination for older ones. The distribution strongly peaks around 2 Gyr, which is caused by the selection effects on the sample (see also Nordström et al. 2004).
The GCS is in fact limited near the plane of the disc, while older stars usually have a considerably more extended vertical distribution, which brings their orbits high above the plane and thereby lowers their presence in this survey. In addition, the magnitude limits of the catalogue give a larger volume to bright, young stars, and the exclusion of giant and very blue stars from the sample leads again to a net bias against very young and especially against old objects. An estimate of the age of the disc can thus not be done directly using the age of the stars in the present sample, but requires modelling the star-formation history of the solar neighbourhood, returning a considerably older disc (> 10.5 Gyr, see e.g., Aumer & Binney 2009; Schönrich & Binney 2009a). Also notice that because of the young ages, our sample is fairly immune to atomic diffusion, possibly apart for a few of the oldest stars.
Figure 14 clearly summarizes all main issues in dating stars. Ages are most readily determined for stars in the upper envelope of Fig. 14, which roughly maps the turn-off region. At low masses, apart from the most metal-poor subdwarfs, reliable ages are difficult to derive (grey dots) because the majority of these stars are still on the main sequence due to their long lifetimes. In addition, somewhat below 1 M⊙ the GCS starts losing completeness, being mostly limited to FG dwarfs. The youngest stars cover a short mass range (cf. blue points in the middle panel of Fig. 16): more massive young stars are in fact brighter and hotter than sample selection limits, apart from a handful of bright objects (squares). The reliability of our metallicity calibration for those stars was already discussed in Sect. 2.2.1. The depletion of stars longward of the kink at ~1.5 M⊙ precisely suggests that at masses higher than this value the sample is partly incomplete (which roughly corresponds to MVT ~ 2, using the mass-luminosity relation of e.g. Henry & McCarthy 1993; Fang & Yan-Ning 2010). On the contrary, no obvious biases seems to be present in the range 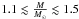 .
.
 |
Fig. 15 MDF of the solar neighbourhood in terms of [Fe/H] (upper panel) and [M/H] (lower panel). Continuous line refers to stars belonging to the irfm sample (5976 stars within the colour ranges of the metallicity calibration), dashed line when considering only stars fainter than MVT = 2, dotted line to all clbr stars (8470 within the colour ranges of the metallicity calibration) and dot-dashed when applying the same luminosity cut as above. Poisson error bars are shown for a representative case in both panels. |
4. The metallicity distribution function
Metallicity distribution function.
Given its complete nature (see Sect. 2), the GCS is well suited for the study of the metallicity distribution function (MDF) in the solar neighbourhood (Nordström et al. 2004; Holmberg et al. 2007). However, this does not mean that the MDF shown here can be directly compared to theoretical expectations. For the same reasons presented above when discussing the age distribution, sample selection effects enter the results. For a quantitative comparison those selection effects have to be taken into account in theoretical models (cf. Schönrich & Binney 2009a).
We already argued in Sect. 2 that dividing the original sample into two groups does not introduce any bias. Stars with the best photometry show lower dispersion, but the average properties are robust and are the same for both the irfm and clbr samples. This is shown in Fig. 15 for [Fe/H] and [M/H] , with the relevant statistical parameters given in Table 1. A Kolmogorov-Smirnov test between the irfm and clbr samples for [Fe/H] and [M/H] tells that the probability of both samples being drawn from the same distribution is below 1 percent, i.e. not significant. The reason for this lies in the broader wings of the clbr sample, partly because the lower quality of the latter sample could be responsible for less reliably determined metallicities that over-populate the wings, and/or older ages (see below). When restricting the selection to − 0.5 ≤ [Fe/H] ≤ 0.5, the irfm and clbr samples are in fact drawn from the same distribution to a level better than 5 percent, under the null hypothesis that the two distribution are drawn from the same parent population. Identical conclusions to the Kolmogorov-Smirnov statistic are reached using instead the Wilcoxon Rank-Sum test for comparison. We find that the MDF for young and old stars look considerably different (see below). We note that because the clbr sample contains a few more cooler stars than the irfm sample (see Sect. 2.1.2), the cooler stars being preferentially older and thus with a broader MDF (see below), this could also be partly responsible for the different broadening of the wings.
Slicing the MDF into different age intervals shows an interesting feature: young stars have a considerably narrower distribution than old stars, though the peak always remains around the solar value (Fig. 16). Notice that because of the selection effects on the sample age, an uneven slicing – denser at young ages – is more appropriate (cf. Fig. 13). While the MDF has been historically used to constrain the gas infall rate (e.g. Lynden-Bell 1975; Tinsley 1980; Matteucci & Francois 1989; Chiappini et al. 1997), the increasing broadening with age suggests that old stars are also a relevant ingredient in describing the wings of the MDF. A natural explanation is provided by the radial migration of stars (Sellwood & Binney 2002). In this picture the solar neighbourhood is not only assembled from local stars, following a local age metallicity relation, but also from stars originating from the inner (more metal-rich) and outer (more metal-poor) Galactic disc that have migrated to the present position on different timescales (Roškar et al. 2008; Schönrich & Binney 2009a). Because of the higher density of stars in the inner disc, migration would favour metal-rich stars, which could compensate the metal-poor tail typical of local chemical evolution, which would explain the rather symmetric shape of the MDF we derived. A more quantitative explanation, however, requires modelling of the chemical evolution.
The presence of a metal-rich tail in Fig. 16 could be a signature of the Galactic bar (e.g., Grenon 1999): such a detection is however very difficult to claim even with the current sample. Indeed, we only detect a conspicuous young metal-rich population at the brightest magnitudes, where the accuracy of the metallicity calibration could be lower (see the discussion in Sect. 2.2). The presence of a bar would rather imply the existence of an old metal-rich population, which we do not detect (but see Minchev & Famaey 2010; Minchev et al. 2011, for a recent discussion on the effect of the bar). Although we do not have access to the sample selection performed in the original assembly of the GCS, we regard the presence of a bias against old metal-rich stars as unlikely, and we refer to Nordström et al. (2004) for more details on the completeness of the sample. We also investigated whether the metal-rich stars display any conspicuous feature in the UV velocity plane and did not find any. Notice though that the fraction of these young metal-rich stars in the total sample is fairly small and they do not bear considerably on the overall MDF of Fig. 15.
Apart from the aforementioned bright stars, the metal-rich wing of the MDF is not an artefact caused by the sample selection on colours (contrary, e.g., to Kotoneva et al. 2002), because high-metallicity stars are present throughout the entire mass range (middle panel in Fig. 16). Also, on the metal-poor side there is a clear contribution of (nearly) unevolved subdwarfs – for which a determination of ages is more uncertain – with a trend in mass mirroring that already observed in luminosity (cf. Figs. 8 and 14).
The peak of the MDF is only slightly subsolar (median [Fe/H] ~ − 0.05, [M/H] ~ − 0.01), in agreement with e.g., Haywood (2001), Taylor & Croxall (2005), Luck & Heiter (2006) and Fuhrmann (2008), but in contrast with other studies, which rather favour a peak in the range − 0.2 to − 0.1 dex (e.g., Wyse & Gilmore 1995; Rocha-Pinto & Maciel 1996; Allende Prieto et al. 2004; Nordström et al. 2004; Holmberg et al. 2007). In most cases the reason for this difference stems from the Teff scale we use, which supports spectroscopic studies that adopt similar effective temperatures and results in higher metallicities. As a side remark, we note that the MDF determined from M dwarfs (Bonfils et al. 2005; Casagrande et al. 2008; Casagrande 2008) is likely to peak around solar metallicity if the recent spectroscopic findings of Johnson & Apps (2009) are confirmed and photometric determinations for those stars are recalibrated accordingly.
The peak at nearly solar metallicity of the local MDF at all ages also has implications for understanding secular processes associated with disc evolution, by investigating whither and whence the Sun is moving (e.g., Wielen et al. 1996; Bland-Hawthorn et al. 2010), and it is also an important test of the overall solar metallicity (Asplund et al. 2009).
 |
Fig. 16 Top panel: MDF for stars belonging to the irfm sample divided into different age intervals. Stars having age < 1 Gyr are shown with a continuous line, 1 ≤ age < 5 Gyr with a dashed line and age ≥ 5 Gyr with a dot-dashed line. Shaded areas identify the subgroup of stars in the same age intervals as above, but with absolute magnitudes (< 2); no such bright stars are present in the old sample. Only stars with well determined ages (see Sect. 3) are used. Bars indicate Poisson errors. Middle panel: [Fe/H] versus stellar mass. Colours have the same meaning as in the top panel, with grey dots now referring to the remaining stars having more uncertain ages. Filled squares identify stars with bright absolute magnitudes (< 2). Lower panel: same symbols and colours as in the middle panel, but showing the age–metallicity relation. Shown for comparison (asterisks) are the ages and metallicities of the halo Globular Clusters studied in VandenBerg et al. (2010) (in the latter case, a different zeropoint on the age scale is possible, also depending on the input physics adopted in the stellar models employed). |
5. The age–dispersion relation
 |
Fig. 17 Velocity dispersion |
Figure 17 shows the velocity dispersion s for stars in the irfm sample as a function of stellar age. Ages are determined using the BASTI isochrones, apart from one case where the result of using Padova isochrones is shown for comparison. The difference between requiring well determined ages (according to the definition of Sect. 3, black line) or not (cyan line) suggests that the signature of a continuous rise becomes even more prominent, confirming earlier studies of the GCS (Nordström et al. 2004; Holmberg et al. 2007). This has to be expected; because of the pronounced overdensity of stars around ages of 2 Gyr (cf. Fig. 13), excluding unreliable ages gives less contamination to the rarer very young and especially to the older stars. However, because velocity dispersion roughly increases with age to the power 1/3 (Spitzer & Schwarzschild 1953), and because of the ~Gyr uncertainty in ages, it is actually difficult to distinguish between a plateau and a real increase.
When no metallicity nor kinematic cut is applied, a strong rise appears at the oldest ages (blue line). This feature is likely caused by contamination of moderately metal-poor stars that might belong to the Galactic halo. This disappears when using a very conservative cut at [Fe/H] > −0.5 dex or a milder one at [Fe/H] > −0.8 dex but only considering stars with V > −150 km s-1. These cuts exclude some tens of stars, consistent with expectations from local disc-to-halo normalization which, despite large uncertainties, is in the range of a few hundreds-to-one (e.g. Morrison 1993; Gould et al. 1998; Jurić et al. 2008) Because the isochrones might fail to exactly match metal-poor stars (Sect. 3), the derived age distribution of low metallicity stars can be biased to older ages. Difficulties in understanding selection criteria are likely to be responsible for the different findings of Quillen & Garnett (2000) who – essentially using the sample of 189 stars studied in Edvardsson et al. (1993) – claimed the presence of a plateau in the dispersion over all intermediate ages followed by a quick rise at about ~10 Gyr.
6. Disc
6.1. Metallicity gradient
 |
Fig. 18 Panel a) and b) metallicity as function of orbital and guiding centre radius, respectively. The probability of a star to belong to the thin disc is represented by colour. Stars with halo membership higher than 50% are plotted in black. Filled diamonds and squares identify stars having VLSR < −40 km s-1 and >20 km s-1, respectively (cf. with Fig. 20). Panel c) cumulative metallicity gradient ([Fe/H] and [M/H] ) when including stars of increasingly older ages. Error bars are shown in one representative case. The gradient is computed using the mean orbital radius of stars as baseline. A kinematic cut to exclude halo stars (as described in the text) is also adopted for comparison. Panel d) same panel c), but using the guiding centre radius as baseline. Panel e) metallicity gradient centred at different ages, weighting all other stars with a Gaussian of width 1.5 Gyr and using the mean orbital radius as baseline. Panel f) same as panel e), but using the guiding centre radius. Only stars with well determined ages (Sect. 3) are used in all instances. |
Abundance gradients across the Galactic stellar disc provide fundamental constraints on the chemical evolution of this component of the Milky Way, and on the physical assumptions adopted in chemical evolution models (e.g., Portinari & Chiosi 1999; Chiappini et al. 2001). Despite its local nature, the large number of stars in the GCS would suggest that it is possible to use it for estimating the radial metallicity gradient in the Galaxy (cf. e.g., Nordström et al. 2004).
While Galactic radial positions (RGal) are snapshots of stars at the present time, covering a very limited range in distances (at most 0.3 − 0.4 kpc for the GCS), their mean orbital radii Rm (left panels in Fig. 18) allow us to probe larger distances (up to a few kpc) and thus are better suited for deriving the metallicity gradient (e.g. Nordström et al. 2004; Holmberg et al. 2007). Orbital radii depend on the adopted Galactic potential; RGal and V velocities offer an alternative and model-independent approach via the guiding centre radius 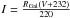 under the assumption of a constant circular rotation speed of 220 km s-1 (right panels in Fig. 18).
under the assumption of a constant circular rotation speed of 220 km s-1 (right panels in Fig. 18).
Using only stars that belong to the irfm sample and are within the calibration range, the exact value of the gradient still depends on whether or not a cut at the lowest metallicities is imposed to exclude contamination from halo stars. In Fig. 18 we show the case of applying neither kinematic nor metallicity cuts, as well as a kinematic selection to retain only stars with probability higher than 90 percent of belonging to the thin or thick disc (see e.g. Ramírez et al. 2007, for more details on this kind of selection procedure). Cutting the sample to exclude metallicities lower than about − 0.8 dex has a similar effect as the kinematic selection. Metal poor (halo) stars having small orbital (and guiding centre) radii are in fact responsible for the strong positive rise in the metallicity gradient.
It appears obvious that taking all stars at their face values does not provide a meaningful measure of the gradient in the disc. Indeed its value depends on the adopted kinematic or metallicity cuts, the age interval considered, and also whether orbital or guiding centre radii are used for the computation (Fig. 18). Difficulties in estimating e.g. the interdependence between age and kinematic cuts (as stars with increasing asymmetric drift are preferentially older) as well as the increasing scatter in the age–metallicity relation and in the age–dispersion relation further complicate the picture.
Figure 18 (middle panels) suggests the presence of a moderate negative radial gradient, consistent with studies using other indicators at various Galactocentric distances such as Cepheids, HII regions, B stars, open clusters and planetary nebulae (see e.g., Maciel & Costa 2010, and references therein). When restricting the analysis to different age intervals (lower panels) there is an indication of a flattening and even a reversal of the gradient with increasing age, but we stress once more that the adopted kinematic or metallicity cuts affect the results. Such a signature comes from older thick (as well as halo) stars (Spagna et al. 2010), while the GCS is mostly limited to the younger objects that are situated in the thin rather than the thick disc.
As already mentioned in Sect. 4, the different behaviour for younger and older stars can be understood in terms of radial migration, where the increasing age that is responsible for a broadening of the MDF could also soften the gradient, but more data and extended analyses are needed to explore this scenario.
6.2. Thin, thick or stirred?
Observations of external edge-on galaxies show the presence of both a thin and thick disc component (Burstein 1979; Dalcanton & Bernstein 2002; Yoachim & Dalcanton 2006). The Milky Way seems to have a two-component disc as well, which was first proposed to fit the vertical density profile derived from star counts (Yoshii 1982; Gilmore & Reid 1983). Disentangling the nature and origin of these components is therefore highly relevant for understanding galaxy formation. While models in which thick and thin discs form sequentially via a rapid or dissipative collapse of protogalactic clouds became disfavoured during the past years (e.g., Majewski 1993), it is not yet clear how the stellar disc can form a thick component with time, if this is caused by to internal (scattering, dynamical interaction or radial mixing, e.g., Schönrich & Binney 2009b; Loebman et al. 2011) or external (satellite accretion, mergers of gas-rich systems, minor mergers, e.g., Abadi et al. 2003; Brook et al. 2007; Villalobos & Helmi 2008; Scannapieco et al. 2009) mechanisms.
Though limited to the solar neighbourhood, the GCS can provide important insights into this puzzle, because it is essentially free from kinematic selections. Our metallicities and αFe (Sect. 2.3) provide for the first time a way to investigate this with a more complete sample.
Figure 19 shows all stars with a reliably determined [Fe/H] and αFe and for which the U,V,W velocities are known, so that the same kinematic probabilistic selection scheme to the thin or thick disc adopted in the previous section can be applied (Ramírez et al. 2007). The small scatter and overall shape of the plot simply reflects the fiducial used to derive αFe, which squeezes up most of the metal-poor stars and also prevents us from seeing any gap between the thin and the thick discs (see discussion in Sect. 2.3). Despite these limitations, a qualitative picture can be drawn. Stars kinematically attributed to the thick disc populate the upper envelope of Fig. 19 for subsolar metallicities, while merging into the thin disc around solar [Fe/H] , in agreement with similar findings obtained by studies based on high-resolution spectroscopy (e.g., Reddy et al. 2006; Bensby et al. 2007).
 |
Fig. 19 [Fe/H] vs. αFe for stars in the irfm sample within the metallicity calibration ranges and with kinematic information to assign statistical membership to the thin or thick disc. Only stars with a membership probability higher than 90 percent are shown (4655 stars in total). A Gaussian noise of 0.005 dex was added on both axes for better displaying all stars. |
Similarly, Fig. 20 shows the αFe vs. [Fe/H] plane for stars belonging to the irfm sample. Stars are separated by their rotation velocities (V) as depicted in the middle panel showing V vs. [Fe/H] . Clearly, this is only a rough criterion for the division and this selection is not stringent in targeting single disc “components”, yet a striking difference appears. At each metallicity, the stars with high negative V velocities (open circles) have higher average αFe; the difference is indeed small in terms of αFe, but statistical significant. This can be expected because stars with such a large asymmetric drift should be significantly older than the remaining population (because of the asymmetric drift–dispersion and the age–dispersion relations), which is confirmed by their age distribution in the lower right panel, which is indeed far older. Our analysis thus clearly confirms a similar result drawn by Haywood (2008) from a smaller spectroscopic sample. Comparison with Fig. 18 also shows the correspondence between our identification based on rotational velocities and the orbital radii of stars. It is interesting to notice that Edvardsson et al. (1993) found a hint that stars with high/low orbital radii lie on the lower/upper envelope of the [α/Fe] vs. [Fe/H] plot, consistent with what we see here.
Because of the tight age–metallicity relation in chemical evolution models without radial migration (e.g., Chiappini et al. 1997), older and alpha-richer stars are expected to be more metal-poor. Yet Fig. 20 rather tells the opposite, with the old and alpha-rich stars also being on average more metal-rich than the population with high rotation velocities (filled diamonds). The emergence of a metal-rich, old thick disc was already present in spectroscopic sample of Feltzing & Bensby (2008). This apparently surprising behaviour is however readily explained if there is no strong age–metallicity dependence, as is the case in radial migration models, and if the lagging metal-rich population comprises – to some extent at least – objects from the inner disc, which are more metal-rich thanks to the Galactic metallicity gradient (Schönrich & Binney 2009a).
 |
Fig. 20 Panel a) αFe for stars in the irfm sample having VLSR = V + V⊙ > 20 km s-1 (filled diamonds) or < −40 km s-1 (open circles). Only [Fe/H] > −0.73 dex were selected to avoid a metal-poor tail in stars with negative velocities (the cut in [Fe/H] was selected to be the same as the lower-most value encountered in stars having VLSR > 20 km s-1, but its exact choice is anyway irrelevant for the discussion). A few stars with clear halo kinematics were also excluded. Lower/upper continuous line connects the mean αFe in different [Fe/H] intervals for filled diamonds/open circles. Error bars (slightly offset in abscissa for clearer comparison) are the standard deviation of the mean in each [Fe/H] bin. Panel b) VLSR as function of metallicity for all stars in sample irfm with kinematic information. Filled diamonds and open circles as in the previous panel. Panels c) and d) normalized metallicity and age distributions for the two previous group of stars having VLSR > 20 km s-1 (continuous line) or < − 40 km s-1 (dashed line). The value V⊙ = 12.24km s-1 was adopted (Schönrich et al. 2010). |
7. Conclusions
Low mass, long lived stars are crucial witnesses of the chemical and dynamical evolution of the Milky Way, but to properly harvest this information, we must ensure that we have determined their astrophysical parameters to the highest accuracy possible, given the observational limitations. The Geneva-Copenhagen Survey provides the ideal database to achieve this goal: it is kinematically unbiased, all its stars have highly homogeneous Strömgren photometry, from which stellar abundance information can be readily derived and merging this catalogue with Tycho2 and 2MASS provides the multi-band optical and infrared photometry needed to derive Teff via the infrared flux method.
We have carried out a revision of the GCS not only benefiting from the latest developments in setting the zeropoint of the effective temperature scale, but also improving upon the homogeneity of the stellar parameters for all stars in the sample. In comparison to previous GCS calibrations, our effective temperatures are hotter; at the same time the improved methodology often reduces the intrinsic uncertainty per star to below 100 K. This leads to a much better agreement between stars and isochrones in the HR diagram, which allows us to directly derive ages via a Bayesian approach. Because we did not make use of metallicity–dependent temperature shifts to reconcile isochrones with data, the risk of introducing an artificial age–metallicity relationship is reduced. Since the adopted effective temperature scale has immediate consequences on abundances, we recalibrated Strömgren indices versus stellar metallicities using a sample of nearly 1500 stars with high-resolution spectroscopic abundances derived adopting Teff consistent with ours. We thus warn that when comparing our results with other studies, it should always be kept in mind that differences in metallicities could simply reflect the different Teff scales adopted. As a consequence, the mean metallicity of previous GCS analyses is increased by ~0.1 dex, now peaking at [M/H] ~ −0.01 dex and thus making the Sun a completely average star given its metallicity (see also Asplund et al. 2009). It is intriguing to note that in the past the higher metallicity of the Sun compared to local dwarfs was used in support of radial migration (e.g. Wielen et al. 1996); our analysis suggests that the Sun is not atypical, at least in metallicity. Instead, we derive other atypical properties for disc stars, to explain which, radial migration could be a relevant ingredient.
For the first time we are able to derive [α/Fe] estimates from Strömgren photometry (named αFe for the sake of clarity). The method becomes more unreliable for increasingly hotter objects and also for metal-poor stars (roughly below − 1 dex), but focusing on disc stars gives a reasonable guidance on the relative alpha enhancements for the whole sample. The ability to reach this tentative distinction enabled us to bring the metallicity calibration to significantly better accuracy by reducing the uncertainty in [α/Fe] enhancement. The new metallicity scale was then checked against open clusters and a moving group, showing indeed a high degree of internal consistency with a suggested intrinsic scatter below 0.10 dex in [Fe/H] . The recently measured uvby solar colours finally corroborate the agreement between the temperature and metallicity scales.
Having this at hand, we revised and complemented the largest existing sample of F and G dwarf stars in the solar neighbourhood that is kinematically unbiased and gives information on ages, the abundance plane, and kinematics. A preliminary analysis of this dataset supports a scenario with a strong interplay among those three characters: the metallicity distribution function shows increasing broadening at older ages, suggesting that its wings could mostly comprise stars born at various Galactocentric radii and migrated at the current position over different timescales. This scenario could also account for the radial gradient getting flatter for older ages, though this detection is yet uncertain partly because of the short distance baseline covered by the GCS, and partly because of the difficulties in disentangling metallicities, ages, and kinematic selection in the sample.
A more robust and striking feature comes instead from the division of stars in the rotation velocity plane, which are shown to have different patterns in the abundance plane and in ages, a feature which is unexpected in classical chemical evolution models, but seen in spectroscopic studies and naturally explained if stellar radial migrations is taken into account. Despite that our data show clear support for the radial migration scenario, many different processes enter the picture of galaxy formation and evolution; future larger surveys will thus be invaluable to further constrain the interplay of various scenarios. The results presented here are thus an example of the importance of having at the same time kinematic, metallicity, and age information to uncover the past of our Galaxy.
In the irfm sample the colour excess has been scaled according to intrinsic colour of the star (see Casagrande et al. 2010) from which the following mean reddening relations were computed and used for the clbr sample: E(BT − VT) = 1.32 E(b − y), E(VT − J) = 3.18 E(b − y), E(VT − H) = 3.66 E(b − y), E(VT − KS) = 3.93 E(b − y) and RBT = 4.23, RVT = 3.24, RJ = 0.86, RH = 0.50, RKS = 0.30, where 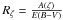 , A(ζ) is the extinction in a given ζ band. For the Strömgren indices E(m1) = −0.30 E(b − y) and E(c1) = 0.20 E(b − y) were adopted from Crawford & Barnes (1970).
, A(ζ) is the extinction in a given ζ band. For the Strömgren indices E(m1) = −0.30 E(b − y) and E(c1) = 0.20 E(b − y) were adopted from Crawford & Barnes (1970).
I.e. with best photometric detection http://www.ipac.caltech.edu/2mass/releases/allsky/doc/sec1_6b.html#phqual
In this work we take L⊙ = 3.842 × 1033 erg s-1 (Bahcall et al. 2006).
http://marcs.astro.uu.se where standard refers to the chemical composition, i.e. [α/Fe] = 0.0 for [Fe/H] ≥ 0.0, a linear increase of [α/Fe] from 0.1 at [Fe/H] = −0.25 to [α/Fe] = 0.4 at [Fe/H] = −1.0 and [α/Fe] = 0.4 for [Fe/H] ≤ − 1.0.
This appears not to be the case for very metal-poor giants above the horizontal branch where in fact m1 follows [Fe/H] tightly (e.g. Adén et al. 2011, Adén et al. to be submitted).
The extension of the original uvby system to cool and metal-poor stars is based on two main sets of standard stars, those of Bond (1980) and Olsen (1993), respectively. The main discrepancy between the two concerns the c1 index, stemming from differences in u band (see discussion in Olsen 1995). Our metallicity calibration uses GCS photometry, which is built on the Olsen standards (see Nordström et al. 2004, and references therein). For testing in the metal-rich regime, as we do here, these differences are of no concern since the original set of observations defining the uvby system (and therefore adopted also by Olsen) is used.
Note that in GCSII also the solar isochrone, which is constructed to fit the Sun, has to be cooled by 0.005 dex in log Teff, corresponding to approximately 70 K, in agreement with the offset in Fig. 2.
At the same time, a stronger disagreement for metal-poor low main sequence stars – for which their position on the HR diagram is substantially age independent – was noticed by Casagrande et al. (2007) and it could have potential implications for studies of multiple stellar populations (Portinari et al. 2010). The same Teff scale adopted here compares well with isochrones for nearby, evolved subdwarfs, suggesting that this disagreement seems now reduced at least for log Teff > 3.7 (compare with Fig. 10 in VandenBerg et al. 2010), though further investigations are encouraged.
Acknowledgments
It is a pleasure to acknowledge an anonymous referee for his/her insightful comments and excellent review, which has considerably strengthened the paper. We thank Chris Flynn and Laura Portinari for a careful reading of the manuscript and useful discussions. We are indebted to Birgitta Nordström, Johannes Andersen and Johan Holmberg for useful discussions on this revision, providing Strömgren colours in advance of publication and for previous versions of the Geneva-Copenhagen Survey, without which our work would have not been possible in the first place. This work was performed in part (IR) under contract with the California Institute of Technology (Caltech) funded by NASA through the Sagan Fellowship Program. S.F.’s research is partly supported by the grant 624-2008-4095 from the Swedish Research Council. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
References
- Abadi, M. G., Navarro, J. F., Steinmetz, M., & Eke, V. R. 2003, ApJ, 597, 21 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Adén, D., Eriksson, K., Feltzing, S., et al. 2011, A&A, 525, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen de Prieto, C., Barklem, P. S., Lambert, D. L., & Cunha, K. 2004, A&A, 420, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1996, A&A, 313, 873 [NASA ADS] [Google Scholar]
- An, D., Terndrup, D. M., Pinsonneault, M. H., et al. 2007, ApJ, 655, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Anthony-Twarog, B. J., & Twarog, B. A. 2006, PASP, 118, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Árnadóttir, A. S., Feltzing, S., & Lundström, I. 2010, A&A, 521, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Aumer, M., & Binney, J. J. 2009, MNRAS, 397, 1286 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., Serenelli, A. M., & Basu, S. 2006, ApJS, 165, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., Covey, K. R., & Meyer, M. R. 2010, ARA&A, 48, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., & Lundström, I. 2003, A&A, 410, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., Lundström, I., & Ilyin, I. 2005, A&A, 433, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Zenn, A. R., Oey, M. S., & Feltzing, S. 2007, ApJ, 663, L13 [CrossRef] [Google Scholar]
- Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertelli, G., Nasi, E., Girardi, L., & Marigo, P. 2009, A&A, 508, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bessell, M. S. 2005, ARA&A, 43, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Bland-Hawthorn, J., Krumholz, M. R., & Freeman, K. 2010, MNRAS, 713, 166 [Google Scholar]
- Boesgaard, A. M., & Friel, E. D. 1990, ApJ, 351, 467 [Google Scholar]
- Bohlin, R. C. 2007, in The Future of Photometric, Spectrophotometric and Polarimetric Standardization, ed. C. Sterken, ASP Conf. Ser., 364, 315 [Google Scholar]
- Bond, H. E. 1980, ApJS, 44, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2005, A&A, 442, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boyajian, T. S., von Braun, K., van Belle, G., et al. 2010 [arXiv:1012.0542] [Google Scholar]
- Brasseur, C. M., Stetson, P. B., VandenBerg, D. A., et al. 2010, AJ, 140, 1672 [NASA ADS] [CrossRef] [Google Scholar]
- Brook, C., Richard, S., Kawata, D., Martel, H., & Gibson, B. K. 2007, ApJ, 658, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Burnett, B., & Binney, J. 2010, MNRAS, 407, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Burstein, D. 1979, ApJ, 234, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M. 2001, AJ, 121, 2851 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L. 2008, Phys. Scripta T, 133, 014020 [Google Scholar]
- Casagrande, L., Portinari, L., & Flynn, C. 2006, MNRAS, 373, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Flynn, C., Portinari, L., Girardi, L., & Jimenez, R. 2007, MNRAS, 382, 1516 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Flynn, C., & Bessell, M. 2008, MNRAS, 389, 585 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaboyer, B., Sarajedini, A., & Demarque, P. 1992, ApJ, 394, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Matteucci, F., & Gratton, R. 1997, ApJ, 477, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Chiavassa, A., Collet, R., Casagrande, L., & Asplund, M. 2010, A&A, 524, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chieffi, A., Straniero, O., & Salaris, M. 1991, in The Formation and Evolution of Star Clusters, ed. K. Janes, ASP Conf. Ser., 13, 219 [Google Scholar]
- Coelho, P., Barbuy, B., Meléndez, J., Schiavon, R. P., & Castilho, B. V. 2005, A&A, 443, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crawford, D. L. 1975, AJ, 80, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L., & Barnes, J. V. 1969, AJ, 74, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L., & Barnes, J. V. 1970, AJ, 75, 946 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L., & Perry, C. L. 1966, AJ, 71, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L., & Perry, C. L. 1976, AJ, 81, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Dalcanton, J. J., & Bernstein, R. A. 2002, AJ, 124, 1328 [NASA ADS] [CrossRef] [Google Scholar]
- De Silva, G. M., Freeman, K. C., Bland-Hawthorn, J., Asplund, M., & Bessell, M. S. 2007, AJ, 133, 694 [NASA ADS] [CrossRef] [Google Scholar]
- di Benedetto, G. P. 1998, A&A, 339, 858 [NASA ADS] [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
- Eggen, O. J. 1978, ApJ, 222, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Eggen, O. J., Lynden-Bell, D., & Sandage, A. R. 1962, ApJ, 136, 748 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, X., & Yan-Ning, F. 2010, Chin. Astron. Astrophys., 34, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Favata, F., Micela, G., & Sciortino, S. 1997, A&A, 323, 809 [NASA ADS] [Google Scholar]
- Feltzing, S., & Bensby, T. 2008, Physica Scripta Vol. T, 133, 014031 [Google Scholar]
- Feltzing, S., & Gustafsson, B. 1998, A&AS, 129, 237 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feltzing, S., & Holmberg, J. 2000, A&A, 357, 153 [NASA ADS] [Google Scholar]
- Friel, E. D., & Boesgaard, A. M. 1992, ApJ, 387, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmann, K. 2008, MNRAS, 384, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Gebran, M., Monier, R., & Richard, O. 2008, A&A, 479, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilmore, G., & Reid, N. 1983, MNRAS, 202, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A., Flynn, C., & Bahcall, J. N. 1998, ApJ, 503, 798 [Google Scholar]
- Grenon, M. 1999, Ap&SS, 265, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, ed. N. Prantzos, E. Vangioni-Flam, & M. Casse, 15 [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M. 2001, MNRAS, 325, 1365 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M. 2002, MNRAS, 337, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M. 2006, MNRAS, 371, 1760 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M. 2008, MNRAS, 388, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, T. J., & McCarthy, Jr., D. W. 1993, AJ, 106, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2009, A&A, 501, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivezić, Ž., Sesar, B., Jurić, M., et al. 2008, ApJ, 684, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., & Apps, K. 2009, ApJ, 699, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, B. R., & Lindegren, L. 2005, A&A, 436, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jurić, M., Ivezić, Ž., Brooks, A., et al. 2008, ApJ, 673, 864 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Karataş, Y., & Schuster, W. J. 2010, New Astron., 15, 444 [NASA ADS] [CrossRef] [Google Scholar]
- Kotoneva, E., Flynn, C., Chiappini, C., & Matteucci, F. 2002, MNRAS, 336, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Loebman, S. R., Roskar, R., Debattista, V. P., et al. 2011, Bull. American Astron. Soc., 43 [arXiv:1009.5997] [Google Scholar]
- Luck, R. E., & Heiter, U. 2006, AJ, 131, 3069 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D. 1975, Vistas Astron., 19, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Maciel, W. J., & Costa, R. D. D. 2010, in IAU Symp., ed. K. Cunha, M. Spite, & B. Barbuy, 265, 317 [Google Scholar]
- Majewski, S. R. 1993, ARA&A, 31, 575 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Matteucci, F., & Francois, P. 1989, MNRAS, 239, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., Asplund, M., Gustafsson, B., & Yong, D. 2009, ApJ, 704, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., Casagrande, L., Ramírez, I., Asplund, M., & Schuster, W. J. 2010a, A&A, 515, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meléndez, J., Schuster, W. J., Silva, J. S., et al. 2010b, A&A, 522, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., & Famaey, B. 2010, ApJ, 722, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Famaey, B., Combes, F., et al. 2011, A&A, 527, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morrison, H. L. 1993, AJ, 106, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Netopil, M., Paunzen, E., Maitzen, H. M., North, P., & Hubrig, S. 2008, A&A, 491, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neves, V., Santos, N. C., Sousa, S. G., Correia, A. C. M., & Israelian, G. 2009, A&A, 497, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olsen, E. H. 1983, A&AS, 54, 55 [Google Scholar]
- Olsen, E. H. 1984, A&AS, 57, 443 [Google Scholar]
- Olsen, E. H. 1993, A&AS, 102, 89 [Google Scholar]
- Olsen, E. H. 1995, A&A, 295, 710 [NASA ADS] [Google Scholar]
- Önehag, A., Gustafsson, B., Eriksson, K., & Edvardsson, B. 2009, A&A, 498, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paulson, D. B., Sneden, C., & Cochran, W. D. 2003, AJ, 125, 3185 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., Percival, S., & Ferguson, J. W. 2009, ApJ, 697, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., & Eyer, L. 2004, ApJ, 351, 487 [Google Scholar]
- Portinari, L., & Chiosi, C. 1999, A&A, 350, 827 [NASA ADS] [Google Scholar]
- Portinari, L., Casagrande, L., & Flynn, C. 2010, MNRAS, 406, 1570 [NASA ADS] [Google Scholar]
- Quillen, A. C., & Garnett, D. R. 2000, [arXiv:astro-ph/0004210] [Google Scholar]
- Ramírez, I., & Meléndez, J. 2004, ApJ, 609, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., & Meléndez, J. 2005, ApJ, 626, 446 [Google Scholar]
- Ramírez, I., Allen de Prieto, C., & Lambert, D. L. 2007, A&A, 465, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Meléndez, J., & Asplund, M. 2009, A&A, 508, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reddy, B. E., Lambert, D. L., & Allen de Prieto, C. 2006, MNRAS, 367, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Rocha-Pinto, H. J., & Maciel, W. J. 1996, MNRAS, 279, 447 [NASA ADS] [Google Scholar]
- Roškar, R., Debattista, V. P., Quinn, T. R., Stinson, G. S., & Wadsley, J. 2008, ApJ, 684, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., & Weiss, A. 1998, A&A, 335, 943 [NASA ADS] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Scannapieco, C., White, S. D. M., Springel, V., & Tissera, P. B. 2009, MNRAS, 396, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1963, ApJ, 137, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., & Binney, J. 2009a, MNRAS, 396, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., & Binney, J. 2009b, MNRAS, 399, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., Binney, J., & Dehnen, W. 2010, MNRAS, 403, 1829 [NASA ADS] [CrossRef] [Google Scholar]
- Schuler, S. C., Hatzes, A. P., King, J. R., Kürster, M., & The, L. 2006, AJ, 131, 1057 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Schuster, W. J., & Nissen, P. E. 1989, A&A, 221, 65 [NASA ADS] [Google Scholar]
- Sellwood, J. A., & Binney, J. J. 2002, MNRAS, 336, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Soderblom, D. R., Laskar, T., Valenti, J. A., Stauffer, J. R., & Rebull, L. M. 2009, AJ, 138, 1292 [NASA ADS] [CrossRef] [Google Scholar]
- Soubiran, C., Bienaymé, O., Mishenina, T. V., & Kovtyukh, V. V. 2008, A&A, 480, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Spagna, A., Lattanzi, M. G., Re Fiorentin, P., & Smart, R. L. 2010, A&A, 510, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitzer, Jr., L., & Schwarzschild, M. 1953, ApJ, 118, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Steigman, G. 2010, J. Cosmology Astropart. Phys., 4, 29 [Google Scholar]
- Steinmetz, M., Zwitter, T., Siebert, A., et al. 2006, AJ, 132, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Strömgren, B. 1963, QJRAS, 4, 8 [NASA ADS] [Google Scholar]
- Strömgren, B. 1987, in NATO ASIC Proc., 207, The Galaxy, ed. G. Gilmore, & B. Carswell, 229 [Google Scholar]
- Strömgren, B., Gustafsson, B., & Olsen, E. H. 1982, PASP, 94, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, B. J., & Joner, M. D. 2004, in BAAS, 36, 787 [Google Scholar]
- Taylor, B. J., & Croxall, K. 2005, MNRAS, 357, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Tinsley, B. M. 1980, Fund. Cosmic Phys., 5, 287 [Google Scholar]
- Twarog, B. A. 1980, ApJ, 242, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Twarog, B. A., Anthony-Twarog, B. J., & Tanner, D. 2002, AJ, 123, 2715 [NASA ADS] [CrossRef] [Google Scholar]
- Twarog, B. A., Vargas, L. C., & Anthony-Twarog, B. J. 2007, AJ, 134, 1777 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- van den Bergh, S. 1962, AJ, 67, 486 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2009, A&A, 497, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- VandenBerg, D. A., Casagrande, L., & Stetson, P. B. 2010, AJ, 140, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- VandenBerg, D. A., Swenson, F. J., Rogers, F. J., Iglesias, C. A., & Alexander, D. R. 2000, ApJ, 532, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Villalobos, Á., & Helmi, A. 2008, MNRAS, 391, 1806 [NASA ADS] [CrossRef] [Google Scholar]
- Wallerstein, G. 1962, ApJS, 6, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Wielen, R., Fuchs, B., & Dettbarn, C. 1996, A&A, 314, 438 [NASA ADS] [Google Scholar]
- Wyse, R. F. G., & Gilmore, G. 1995, AJ, 110, 2771 [NASA ADS] [CrossRef] [Google Scholar]
- Yi, S., Demarque, P., Kim, Y., et al. 2001, ApJS, 136, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Yoachim, P., & Dalcanton, J. J. 2006, AJ, 131, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Yong, D., Grundahl, F., Johnson, J. A., & Asplund, M. 2008, ApJ, 684, 1159 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshii, Y. 1982, PASJ, 34, 365 [NASA ADS] [Google Scholar]
Appendix A: Bayesian age determination
For the effective temperatures we assume a Gaussian error, which is derived for each star as described in Sect. 2.1.2 or 2.1.3 for the irfm and clbr sample, respectively. Things get slightly more complicated for the magnitude errors. The magnitude is estimated from the photometric measurements and the parallax of these stars, while the latter measurement completely dominates the error. So, assuming a Gaussian distribution in the parallax, we can write 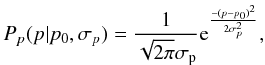 (A.1)where p0 is the best estimate for the parallax, σ0 the adopted parallax error. Converting to magnitude space we thus have
(A.1)where p0 is the best estimate for the parallax, σ0 the adopted parallax error. Converting to magnitude space we thus have 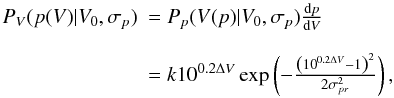 (A.2)where ΔV = V − V0 is the difference between the magnitude V and the best parallax-based estimate for the magnitude V0, σpr = σp/p0 is the relative parallax error and k is some normalization constant. For small relative parallax errors this treatment does not imply any significant changes, because the error distribution approaches a Gaussian. However, for σpr ≳ 0.1, the V magnitude distribution becomes increasingly skewed, because the lower parallaxes produce an extended tail towards brighter magnitudes (see also Casagrande et al. 2007, for an analytic estimate of the bias in case of low parallax errors).
(A.2)where ΔV = V − V0 is the difference between the magnitude V and the best parallax-based estimate for the magnitude V0, σpr = σp/p0 is the relative parallax error and k is some normalization constant. For small relative parallax errors this treatment does not imply any significant changes, because the error distribution approaches a Gaussian. However, for σpr ≳ 0.1, the V magnitude distribution becomes increasingly skewed, because the lower parallaxes produce an extended tail towards brighter magnitudes (see also Casagrande et al. 2007, for an analytic estimate of the bias in case of low parallax errors).
 |
Fig. A.1 Comparison between ages derived assuming the Salpeter vs. flat IMF. Red dots are stars belonging to the irfm sample. |
It is crucial to correct the estimated metallicities for systematic biases. In the wings of the MDF more stars are scattered out from the more densely populated central regions, so that there is a net bias to be expected in the metallicities in the wings of the distribution, e.g. stars on the high-metallicity wing have on average overestimated metallicities, while stars on the left wing of the MDF are expected to have an increased fraction of metallicity underestimates. Because of these shifts, a naïve use of the measured metallicities would introduce an age underestimate on the high-metallicity side and an age overestimate on the low-metallicity wing, which would give rise to an artificial age–metallicity correlation. This bias can be reduced and in the best case removed by an appropriate metallicity prior that reflects the underlying “real” metallicity distribution. It might be tempting to use the metallicity distribution itself as metallicity prior in an iterative process. However, this is intrinsically unstable, because stars would assemble in peaks, growing by attraction of more objects. So we took an analytical function that approximates the sample distribution:  with
with  On the right hand side we simply choose a Gaussian term as prior. On the left hand side this is considerably flattened by adding the “correction” term. This function has to be multiplied with the Gaussian error term in metallicity. Mainly its relative slope decides about shifts in the adopted probability distribution in metallicity. So with the correction term that flattens the distribution at low metallicities we can hope to reproduce the actual data sufficiently well.
On the right hand side we simply choose a Gaussian term as prior. On the left hand side this is considerably flattened by adding the “correction” term. This function has to be multiplied with the Gaussian error term in metallicity. Mainly its relative slope decides about shifts in the adopted probability distribution in metallicity. So with the correction term that flattens the distribution at low metallicities we can hope to reproduce the actual data sufficiently well.
 |
Fig. A.2 Comparison between our revised ages on those in GCSII for the full catalogue. ΔAge is in the sense ours minus GCSII. Contour levels in the lower panel same as in Fig. 2. |
Altogether the probability distributions in each parameter of a star are gained by running over the isochrone points. The probability distribution in one parameter xi is gained by  where the sum runs over all isochrone points is. G((y − y0),σy) is a Gaussian function with y − y0 in the counter of the exponent and with dispersion σy, min,is is the initial mass of the star on an isochrone point,
where the sum runs over all isochrone points is. G((y − y0),σy) is a Gaussian function with y − y0 in the counter of the exponent and with dispersion σy, min,is is the initial mass of the star on an isochrone point, 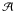 is the age prior, dm, dτ and d [M/H] denote the effective volume covered by an isochrone point, i.e. half the distances to its neighbours in initial mass, age and [M/H] , and subscript is denotes the values of the isochrone point. From the probability distribution the maximum likelihood, median, expectation and 5, 16, 84, 95 percent values of the age are derived. The error σ for any given age is defined as half difference of the 84 minus 16 percent value and the relative uncertainty as the ratio of σ over expectation age. Throughout the paper, BASTI expectation ages and masses are used in the analysis if not otherwise specified. In all instances a Salpeter IMF was used, and the effect of this choice on P(xi) is minimal. Figure A.1 shows the difference in BASTI expectation ages when a flat IMF is used instead.
is the age prior, dm, dτ and d [M/H] denote the effective volume covered by an isochrone point, i.e. half the distances to its neighbours in initial mass, age and [M/H] , and subscript is denotes the values of the isochrone point. From the probability distribution the maximum likelihood, median, expectation and 5, 16, 84, 95 percent values of the age are derived. The error σ for any given age is defined as half difference of the 84 minus 16 percent value and the relative uncertainty as the ratio of σ over expectation age. Throughout the paper, BASTI expectation ages and masses are used in the analysis if not otherwise specified. In all instances a Salpeter IMF was used, and the effect of this choice on P(xi) is minimal. Figure A.1 shows the difference in BASTI expectation ages when a flat IMF is used instead.
A comparison between our BASTI expectation ages and those derived in GCSII is shown in Fig. A.2. Age determinations are subject to many subtleties: because we do not have access to some technicalities used in GCSII, it is difficult to explain all trends that arise in the comparison. Some of the breaks (e.g. the depletion of stars around 5 Gyr) could arise because isochrones in GCSII were shifted to agree with the data. Similarly, we notice that stars in GCSII with undetermined lower confidence limits are preferentially assigned young ages, which are responsible for some of the horizontal stripes seen in the upper panel of Fig. A.2.
All Tables
All Figures
 |
Fig. 1 Distributions in the velocity planes of the two subsamples defined in this work. |
| In the text | |
 |
Fig. 2 Panels a) and b) ΔTeff (ours minus GCSII) as a function of our Teff (upper) and [Fe/H] (lower) for stars in the irfm sample. Panels c) and d) same as before, but for all remaining GCS stars in the clbr sample (see discussion in Sect. 2.1). Contour levels are computed on abscissa intervals of 25 K and 0.025 dex, respectively, to equally represent regions with fewer stars. Dashed and dotted lines indicate the mean difference and standard deviation of the entire sample; because they are symmetric and are dominated by regions with the highest overdensity of stars, the dashed and dotted lines are in some cases offset from the local 1σ contour levels. |
| In the text | |
 |
Fig. 3 ΔTeff (ours minus spectroscopic values) for the 1498 stars in our calibration sample as function of Teff (panel a)) and [Fe/H] (panel b)). Contour levels and lines as in Fig. 2. |
| In the text | |
 |
Fig. 4 Left panel: [Fe/H] versus m1 for our 1498 calibrating stars in different (b − y) ranges represented by different symbols (median values as indicated in the labels). The size of the symbols increases with higher values of c1. Dotted and continuous lines represent Eq. (2) at these median values for the 10th and 90th percentiles of the c1 distribution. Central panel: same as left panel, but for Eq. (3), which applies only to cool stars. Right panel: theoretical [Fe/H] versus m1 relation when using synthetic colours from the “MARCS-standard” library and log g instead of c1 (see text for discussion). |
| In the text | |
 |
Fig. 5 Panel a) spectroscopic versus photometric metallicities obtained using the calibration presented in Sect. 2.2 for 1498 stars. Filled circles are for stars having (b − y) < 0.43, open circles for redder (i.e. cooler) stars. Panel b) same as above, but showing residuals (ours minus spectroscopic). Dotted lines are 1σ scatter and boxes the median values in non overlapping intervals of 0.2 dex. Panel c) same as in the previous one, but as a function of Teff, with boxes computed in non overlapping intervals of 100 K. The overall zeropoint offset is μ = −0.003 dex and σ = 0.097 dex. Panel d) distribution of the residuals of our calibration against spectroscopy with a Gaussian of width σ and centred at μ overplotted. Panel e) standard deviation associated to each square computed in panel b) with error bars being the standard deviation of the mean. |
| In the text | |
 |
Fig. 6 Δ [Fe/H] (in the sense ours minus GCSII) as function of Teff (panel a)) and [Fe/H] (panel b)) for stars in the irfm sample satisfying the applicability range of our metallicity calibration. Notice the two breaks at 5500 K and 6500 K which correspond to the discontinuities introduced by the three calibrations used in GCSII for different (b − y). Contour levels and lines as in Fig. 2. |
| In the text | |
 |
Fig. 7 Differential Fe abundances of kinematically selected members of HR1614. Filled circles are metal-rich members, while asterisk (HIP13513), triangle (HIP6762) and diamond (HIP25840) are spurious members according to the chemical tagging performed by De Silva et al. (2007). Open circles are the analogous comparison with the group members from Feltzing & Holmberg (2000). |
| In the text | |
 |
Fig. 8 Panel a) [Fe/H] distribution when slicing in absolute magnitude (MVT) 5976 stars (grey circles) that belong to the irfm sample and are within the metallicity calibration range. Contour levels are computed on abscissa intervals of 0.1 mag to equally represent regions with fewer stars. Panel b) and c) [Fe/H] distribution of the same stars, but plotted as a function of distance and parallax error. In all panels, stars with MVT < 2 are overplotted as black squares (271 in total). |
| In the text | |
 |
Fig. 9 [α/Fe] versus (v − y) − (b − u) for our 1498 calibrating stars. Bluer (redder) colours indicate hotter (cooler) stars, according to their (b − y), as shown in the top right box. Squares are synthetic colours computed from MARCS model fluxes at fixed [α/Fe] (as available from MARCS library) for selected values of (b − y) = 0.4,0.5,0.6 (from left to right) and [Fe/H] = 0.00 dex with [α/Fe] = 0:0.4 dex (continuous line) [Fe/H] = −0.25 dex with [α/Fe] = 0:0.1:0.4 dex (dotted lines), [Fe/H] = −0.50 dex with [α/Fe] = 0:0.2:0.4 dex (dashed lines), [Fe/H] = −0.75 dex with [α/Fe] = 0:0.3:0.4 dex (dot-dashed lines), [Fe/H] = −1.00 dex with [α/Fe] = 0:0.4 dex (triple-dot-dashed lines). Stars within 0.01 mag of the selected (b − y) interval are shown with open circles to highlight the trend. Grey dotted lines are fiducials built for those stars. Lower left panel is a zoom of the (b − y) = 0.4 data set for 2.2 ≤ (v − y) − (b − u) ≤ 2.8. |
| In the text | |
 |
Fig. 10 Upper panel: spectroscopic versus Strömgren [α/Fe] estimates for our 1498 calibrating stars. Crosses (circles) are stars having probability > 90 percent of being thin (thick) disc based on their kinematic (using U,V,W velocities from the GCS). Downward triangles are stars with lower probability or for which kinematic information was not available. Filled squares are stars having [Fe/H] ≤ − 1 (independently of their kinematic thin/thick membership, if available). Lower panel: same symbols as above, showing the difference spectroscopic minus ours. |
| In the text | |
 |
Fig. 11 [Fe/H] versus [α/Fe] for the 1498 stars in the spectroscopic sample (filled circles). Dotted and dashed lines are arbitrarily used to select stars on the right and left locus of the plot (only for [Fe/H] > − 1). Downward (upward) triangles represent stars selected according to this criterion, but using our [Fe/H] and [α/Fe] Strömgren calibrations. |
| In the text | |
 |
Fig. 12 BASTI isochrones for different ages at a given metallicity (continuous lines) compared to stars of similar [M/H] , where the difference ± 0.1 or ± 0.2 dex is coded by colours. Larger symbols are for stars with higher parallax accuracy as labelled in the top left panel. Only stars in the irfm sample are shown. |
| In the text | |
 |
Fig. 13 Normalized age probability distribution for all stars in the sample having both BASTI (continuous thick) and Padova (continuous thin) ages and only for stars in the irfm sample (dotted thick and thin lines) having good ages and MVT ≥ 2. |
| In the text | |
 |
Fig. 14 Ages versus masses for stars belonging to the irfm sample. Colours are for stars with well determined ages, going from metal-poor (blue) to -rich (red), while grey dots are for the remaining stars. Squares are stars brighter than MVT = 2. Inner panel: same as outer panel, but with a metallicity colour coding also for stars with less reliable ages. |
| In the text | |
 |
Fig. 15 MDF of the solar neighbourhood in terms of [Fe/H] (upper panel) and [M/H] (lower panel). Continuous line refers to stars belonging to the irfm sample (5976 stars within the colour ranges of the metallicity calibration), dashed line when considering only stars fainter than MVT = 2, dotted line to all clbr stars (8470 within the colour ranges of the metallicity calibration) and dot-dashed when applying the same luminosity cut as above. Poisson error bars are shown for a representative case in both panels. |
| In the text | |
 |
Fig. 16 Top panel: MDF for stars belonging to the irfm sample divided into different age intervals. Stars having age < 1 Gyr are shown with a continuous line, 1 ≤ age < 5 Gyr with a dashed line and age ≥ 5 Gyr with a dot-dashed line. Shaded areas identify the subgroup of stars in the same age intervals as above, but with absolute magnitudes (< 2); no such bright stars are present in the old sample. Only stars with well determined ages (see Sect. 3) are used. Bars indicate Poisson errors. Middle panel: [Fe/H] versus stellar mass. Colours have the same meaning as in the top panel, with grey dots now referring to the remaining stars having more uncertain ages. Filled squares identify stars with bright absolute magnitudes (< 2). Lower panel: same symbols and colours as in the middle panel, but showing the age–metallicity relation. Shown for comparison (asterisks) are the ages and metallicities of the halo Globular Clusters studied in VandenBerg et al. (2010) (in the latter case, a different zeropoint on the age scale is possible, also depending on the input physics adopted in the stellar models employed). |
| In the text | |
 |
Fig. 17 Velocity dispersion |
| In the text | |
 |
Fig. 18 Panel a) and b) metallicity as function of orbital and guiding centre radius, respectively. The probability of a star to belong to the thin disc is represented by colour. Stars with halo membership higher than 50% are plotted in black. Filled diamonds and squares identify stars having VLSR < −40 km s-1 and >20 km s-1, respectively (cf. with Fig. 20). Panel c) cumulative metallicity gradient ([Fe/H] and [M/H] ) when including stars of increasingly older ages. Error bars are shown in one representative case. The gradient is computed using the mean orbital radius of stars as baseline. A kinematic cut to exclude halo stars (as described in the text) is also adopted for comparison. Panel d) same panel c), but using the guiding centre radius as baseline. Panel e) metallicity gradient centred at different ages, weighting all other stars with a Gaussian of width 1.5 Gyr and using the mean orbital radius as baseline. Panel f) same as panel e), but using the guiding centre radius. Only stars with well determined ages (Sect. 3) are used in all instances. |
| In the text | |
 |
Fig. 19 [Fe/H] vs. αFe for stars in the irfm sample within the metallicity calibration ranges and with kinematic information to assign statistical membership to the thin or thick disc. Only stars with a membership probability higher than 90 percent are shown (4655 stars in total). A Gaussian noise of 0.005 dex was added on both axes for better displaying all stars. |
| In the text | |
 |
Fig. 20 Panel a) αFe for stars in the irfm sample having VLSR = V + V⊙ > 20 km s-1 (filled diamonds) or < −40 km s-1 (open circles). Only [Fe/H] > −0.73 dex were selected to avoid a metal-poor tail in stars with negative velocities (the cut in [Fe/H] was selected to be the same as the lower-most value encountered in stars having VLSR > 20 km s-1, but its exact choice is anyway irrelevant for the discussion). A few stars with clear halo kinematics were also excluded. Lower/upper continuous line connects the mean αFe in different [Fe/H] intervals for filled diamonds/open circles. Error bars (slightly offset in abscissa for clearer comparison) are the standard deviation of the mean in each [Fe/H] bin. Panel b) VLSR as function of metallicity for all stars in sample irfm with kinematic information. Filled diamonds and open circles as in the previous panel. Panels c) and d) normalized metallicity and age distributions for the two previous group of stars having VLSR > 20 km s-1 (continuous line) or < − 40 km s-1 (dashed line). The value V⊙ = 12.24km s-1 was adopted (Schönrich et al. 2010). |
| In the text | |
 |
Fig. A.1 Comparison between ages derived assuming the Salpeter vs. flat IMF. Red dots are stars belonging to the irfm sample. |
| In the text | |
 |
Fig. A.2 Comparison between our revised ages on those in GCSII for the full catalogue. ΔAge is in the sense ours minus GCSII. Contour levels in the lower panel same as in Fig. 2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.