EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 530 (June 2011) A&A, 530 (2011) A96 Full HTML
Free Access
Issue
A&A
Volume 530, June 2011
Article Number A96
Number of page(s) 8
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201016051
Published online 18 May 2011

© ESO, 2011

1. Introduction

The spectra of several protostellar objects exhibit a strong absorption feature at 4.62 microns (2165 cm-1), called the XCN band, which is commonly attributed to the solid-phase cyanate ion OCN− (Grim & Greenberg 1987; Lowenthal et al. 2000; Novozamsky et al. 2001; van Broekhuizen et al. 2005). A systematic study of this feature with the VLT-ISAAC spectrometer shows large source-to-source abundance variations (van Broekhuizen et al. 2005). However, this feature seems absent from the limited sample of starless dark molecular clouds investigated by Knez et al. (2005). Thus, the OCN− band is often seen as a manifestation of thermal or non-thermal energetic processes of the protostellar environment.

The formation of the solid-state cyanate ion OCN− can be explained by different processes: proton bombardment (Moore et al. 1983), electron bombardment (Bennett et al. 2010), vacuum ultraviolet photolysis of NH3:CO:H2O ices where the photochemical formation of isocyanic acid HNCO is followed by a proton transfer to ammonia NH3 (d’Hendecourt et al. 1986; Grim et al. 1989), or directly from a acid-base reaction of HNCO with solid NH3 or H2O (Demyk et al. 1998; Raunier et al. 2003b; van Broekhuizen et al. 2004). A good review of all the experiments carried out on OCN− and of the processes that lead to its formation is given in Table 1 of van Broekhuizen et al. (2005) and a quantitative comparison of these different processes is given in van Broekhuizen et al. (2004). Based on UV fluence and NH3 abundance arguments, the authors conclude that the UV photoprocessing of NH3:CO:H2O ices may not account for the observed OCN− abundances, and that OCN− is most likely formed thermally from HNCO. The VLT studies of low-mass young stellar objects (YSOs) (van Broekhuizen et al. 2005) show that if OCN− abundances allow quantitatively for a photochemical mechanism, the large variations in abundances are more difficult to explain by photochemistry; thus the thermal formation, with either NH3 or H2O, should be seriously considered. However, the validity of these mechanisms to reproduce or not the observed abundances of OCN− depends on their respective kinetics, and no kinetical studies have been available so far.

Experimental and theoretical low-temperature studies on the acid-base reaction of HNCO with solid NH3 have confirmed the spontaneous character and the effectiveness of its formation from HNCO (Raunier et al. 2003a,b, 2004; van Broekhuizen et al. 2004). Moreover, the thermal deprotonation of HNCO by H2O is observed (Raunier et al. 2003b), though it is less effective than the deprotonation of HNCO by NH3, which indicates a higher activation energy. However, whatever their activation energies are, these reactions are limited by the diffusion and the abundances of available reactants. If we consider an average temperature of 30 − 40 K for YSOs ices, the mobility of H2O, NH3 or HNCO is negligible, therefore the most likely reaction to occur is statistically set by the most abundant reactants species, i.e. H2O, because the NH3 abundance with respect to H2O is typically less than 5% (van Broekhuizen et al. 2005). Thus one can think that the dominant reaction may be the thermal reaction of H2O with HNCO, and that the OCN− abundance is mostly set by the kinetics of the H2O + HNCO reaction, assuming the presence of the solid-state HNCO reactant within interstellar ices.

However, HNCO has never been observed in the solid phase of the ISM. Yet, gas phase isocyanic acid HNCO was one of the first interstellar molecules identified in the interstellar medium (ISM) (Snyder & Buhl 1972). HNCO is also the simplest species containing all four most abundant elements, H, N, C and O, and four isomers have this elemental composition: isocyanic acid HNCO, cyanic acid HOCN, fulminic acid HCNO and isofulminic acid HONC. HNCO is the most stable isomer, and ab initio calculations give the energies of their ground electronic singlet states relative to HNCO to be 24.7, 70.7 and 84.1 kcal mol-1, respectively (Mladenović & Lewerenz 2008). However, it is only recently that fulminic acid HCNO has been detected and the HNCO/HCNO abundance ratio is observed to change by one order of magnitude depending on the object (Marcelino et al. 2009). Cyanic acid HOCN has also been tentatively identified in SgrB2 (Brünken et al. 2009) and the HOCN/HNCO abundance ratio estimated at 0.5%. What can be deduced from this ratio is strongly dependent on the chemical pathways that lead to the formation of the two isomers and on the isomerization pathways from one isomer to another. The chemistry related to HNCO and its isomers is not known and there has been much speculation about HNCO formation. For some authors, HNCO is formed only in the gas phase (Turner et al. 1999; Iglesias 1977), for other authors, HNCO is formed on grain surfaces and then desorbed (Hasegawa et al. 1992; Garrod et al. 2008; Tideswell et al. 2010). For the latter authors, HNCO is a transient species that is rapidly processed to OCN− on grain surface during the collapse phase, and then, during the hot core stage, these species are desorbed and subsequently destroyed in the gas-phase returning to HNCO (Tideswell et al. 2010). HNCO is also proposed to be formed in the gas-phase in post-shock gas because HNCO abundance is enhanced in the presence of shocks and correlates well the SiO abundances (Zinchenko et al. 2000).

In this paper we address the solid-state chemistry of the HNCO/OCN−/HOCN/H2O system on the basis of laboratory experiments using Fourier-transform infrared (FTIR) spectroscopy on interstellar ice analogs. Without speculating on HNCO formation mechanisms in the interstellar medium, we study the kinetics of the conversion of HNCO into OCN− and then into HOCN in a pure H2O environment. The H2O + HNCO reaction gives the salt H3O+OCN− with an activation energy E1 = 26  ±  2 kJ mol-1 (3127 K) (1 kJ mol-1 = 120.272 K). Then, the proton is transferred from H3O+ to OCN− to give the isocyanic acid HOCN, with an activation energy E2 = 36  ±  1 kJ mol-1 (4330 K). We show that OCN− follows a kinetic law that can be written as dx(OCN−)/dt = k1 × x(HNCO)2 − k2  ×  x(OCN−)2. We also study the desorption kinetics of HNCO and OCN− to derive their desorption energies, Edes(HNCO) = 37  ±  3 kJ mol-1 (4450 K) and Edes(OCN−) = 40  ±  3 kJ mol-1 (4811 K). This laboratory work on the isolated system HNCO:H2O provides the reference input data to a gas-grain chemistry model that we will use to investigate the observed solid-state OCN− abundances in a complete interstellar ice.

2. Experimental

The HNCO monomer is synthetized from the thermal decomposition of the cyanuric acid polymer (Aldrich Chemical Co., 98%) at 6500C under a primary vacuum (Raunier et al. 2003b). HNCO and H2O are inserted and outgassed in two separated vacuum lines using standard manometric techniques, and then they are co-deposited. The two gases are sprayed onto a highly polished copper surface maintained at 10 K using closed-cycle helium cryostats (ARS Cryo, model DE-204 SB) in a vacuum chamber at 10-8 mbar. The temperature is controlled between 10 K and 300 K using a heating resistance and a Lakeshore Model 336 temperature controller. The IR spectra are recorded at different temperatures in the reflection mode using a Vertex 70 spectrometer with a MCT detector. A typical spectrum has a 1 cm-1 resolution and is averaged over one hundred interferograms.

The concentration ratio of the different mixtures is first set at room temperature before deposition using leak valves to adjust fluxes and then derived at 10 K after deposition from the IR spectra by integrating the bands to estimate the column density of HNCO, according to their band strengths. For H2O, we use the values of 3.1  ×  10-17 cm molecule-1 for the band strength of the libration mode at 760 cm-1 and 2.0  ×  10-16 cm molecule-1 for the band strength of the OH stretching mode at 3280 cm-1 (d’Hendecourt & Allamandola 1986). For HNCO, we adopt the value 7.2  ×  10-17 cm molecule-1 for the band strength of the νasNCO mode at 2251 cm-1, which is the value given for a H2O-rich ice (van Broekhuizen et al. 2004). For OCN− we use the value 1.3  ×  10-16 cm molecule-1 for the band strength of the νasNCO mode (van Broekhuizen et al. 2004). We also use these bands to monitor the evolution of the HNCO, OCN− abundances because they are consumed or produced during the reactions to estimate the different kinetical parameters. However, the calculated concentration ratio depends on the band strengths provided by the literature. These values depend on the nature, composition, and temperature of the ice in which they are found, and this dependence is a major source of uncertainties when evaluating the column densities of frozen molecules. A 20% uncertainty on the band strengths and consequently on calculated column densities is probably sufficiently conservative. Moreover, some bands are overlapping in the HNCO:H2O mixture, especially the H2O libration mode and the δHNC mode of HNCO, which adds uncertainty to the column density determination.

In a typical kinetic experiment, the temperature is set to a fixed value using the temperature controller and measured using a DTGS 670 silicon diode with a 0.1 K uncertainty. Infrared spectra are recorded at this fixed temperature at fixed intervals of time.

The activation energy of desorption and the order of desorption for HNCO, OCN− and HOCN can be obtained from temperature program desorption (TPD) experiments followed either by mass spectrometry of the desorbed gas phase species or infrared spectroscopy of the remaining solid-state species on their respective characteristic bands. The latter technique has the advantage to distinguish between the desorption of HNCO, OCN− and HOCN, whereas their fragmentation is identical in a quadrupole mass spectrometer. The IR solid-phase signal from the remaining material correlates with the desorbing gas phase material measured with a quadrupole mass spectrometer within the measurement uncertainty (Bossa et al. 2009). Thus we will follow the TPD experiments using IR spectroscopy of the solid-state species. The TPD linear variation of the temperature with time (temperature ramp, T = T0 + β  ×  t) is performed using the temperature controller.

3. Results

3.1. Formation of H3O+OCN− and HOCN from a HNCO:H2O ice mixture

We start with a HNCO:H2O ice mixture where H2O is in excess with respect to HNCO. Figure 2 shows the thermal evolution of a HNCO:H2O ice mixture in a 1:5 ratio deposited between 10 and 14 K. A typical ice sample has a thickness of few 100 monolayers. At 10 K the spectrum is dominated by the strong water absorption bands at 3280, 1628, and 760 cm-1, assigned to the OH stretching mode, OH bending mode, and libration mode, respectively. Isocyanic acid HNCO is characterized by strong bands located at 3373, 3233, 2251, and 858 cm-1, but only the 2251 cm-1 band, assigned to the NCO antisymmetric stretch vibration, is not blended by the water bands, which is why it will be used to monitor the HNCO evolution. The 2251 cm-1 band has actually two components: one component at 2260 cm-1 corresponding to HNCO in a H2O environment (Raunier et al. 2003b), and a component 2234 cm-1 corresponding to HNCO in a HNCO environment. The proportion of the two components in the 2251 cm-1 band depends on the ice sample deposition, and accordingly the position of the band may be shifted from one deposition to another by few wavenumbers. The position and shape of this band are also slightly changing while HNCO is reorganizing around 120 K. Figure 1 shows a typical HNCO:H2O mixture spectrum just after the temperature is brought to 120 K. Although the HNCO + H2O reaction is not possible in the gas phase at room temperature, during the deposition step when the gases are thermalizing from 300 K to 14 K on the cold surface, a little amount of OCN− is formed, as can be seen from its band at 2170 cm-1 as seen in Fig. 1. The amount of initially formed OCN− varies from one deposition to another.

thumbnail Fig. 1

Infrared spectrum of a HNCO:H2O mixture in a 1:5 concentration ratio at T = 120 K. A small amount of OCN− is formed during the deposition.

All the observed bands are listed in Table 1 along with their corresponding assignments and band strengths.

Table 1

Positions and integrated band strengths of a HNCO:H2O ice mixture at 10 K.

thumbnail Fig. 2

Infrared spectrum a) and difference spectrum (spectrum at time t minus spectrum at t = 0) b) of a HNCO:H2O mixture at T = 120 K at t = 0 s, 3300 s, 21   300 s and 53 700 s. OCN− has a band at 2170 cm-1 and HOCN at 2295 cm-1. The HNCO band has two components: one component at 2260 cm-1 corresponding to HNCO in a H2O environment and one component at 2234 cm-1 corresponding to HNCO in a HNCO environment. The variation of the second component is the result of a rearrangement that can give a positive band a 2251 cm-1 in some spectra. The bands at 2349 cm-1 correspond to fluctuations of the gas phase CO2.

When the temperature is set to a fixed value between 100 K and 130 K, the OCN− band at 2170 cm-1 is progressively growing while the bands corresponding to HNCO and H2O decrease as can be seen in Fig. 2. The OCN− feature keeps growing until it reaches a stationary state corresponding to this temperature. This indicates that the H3O+OCN− species is formed thermally by the reaction involving HNCO and H2O. Owing to their low band strengths it is impossible to see the H3O+ features at 1205, 1750 and 2900 cm-1 (Falk & Guiguere 1957), but because H2O is the only other species, the counter ion of OCN− is necessarily H3O+, and the H3O+OCN− species is formed from a thermally induced proton transfer from HNCO to H2O. It is important to know whether the reaction HNCO + H2O that gives OCN−+ H3O+ is a total reaction (HNCO + H2O  →  OCN−+ H3O+) or an equilibrium (HNCO + H2O  ⇆  OCN−+ H3O+). In the former case all HNCO is consumed to give OCN− after a certain time; in the latter case the reverse reaction occurs where OCN− gives HNCO, and an equilibrium depending on the temperature and Gibbs energies is reached. In the former case the HNCO/OCN− ratio is only defined by the kinetics, in the latter case the HNCO/OCN− ratio is defined by the thermodynamics.

We can see from Fig. 2 that the reaction is not total, and thus, the system should be in an equilibrium. If this is true, we should be able to derive an equilibrium constant from the final abundances of the reactants and products, the equilibrium constant being dependent on the temperature. To test this latter assumption, after waiting for a sufficiently long time for a stationary state to be achieved at a fixed temperature of 125 K, the temperature is lowered by 5 K to displace the equilibrium constant. The system does not respond to the temperature variation, the abundance of each species remains the same as at 125 K, and no displacement of the equilibrium constant is observed. Thus, we conclude that the system is not in equilibrium either. At that point we see that we cannot push the analogy between liquid solutions and solid solutions further. Some molecules are in configurations that enable the total reaction, some molecules are not, like in clusters of pure HNCO for example. Only a limited set of HNCO molecules are in a favorable configuration, one HNCO molecule making a hydrogen bond with the electron lone pair of one H2O molecule and being activated enough (Raunier et al. 2003b). We conclude that for the population of molecules that are statistically in a favorable configuration, the reaction is total, because the reverse reaction is not observed.

Figure 2 shows that in addition to the the OCN− band at 2170 cm-1, a new band appears at 2295 cm-1. We assign this band to the νasNCO mode of cyanic acid HOCN (Raunier et al. 2003b), since this transition has been observed at 2280 cm-1 in a rare gas matrix environment at 13 K (Teles et al. 1989). The +15 cm-1 difference observed for HOCN is consistent with the +8 cm-1 frequency difference observed for the νasNCO band between an Argon matrix at 10 K, 2259 cm-1, and a solid HNCO:H2O ice mixture at 120 K, 2251 cm-1. Not all experiments show a HOCN band. This can be explained because the yield of conversion of HNCO into OCN− is a few percents of the total amount of HNCO, the speed of conversion of this low amount of OCN− into HOCN must be very slow and HOCN should not be observed. The amount of HOCN formed during the experiment must therefore come from the initial amount of OCN−, formed at t = 0 during the deposition when the gas is thermalizing on the surface from 300 K to 10 K. Not all experiments have enough OCN− formed initially at the deposition to form an observable amount of HOCN during the experiment.

In the first reaction a proton is transferred at a rate k1 from the HNCO nitrogen atom to the H2O oxygen atom to form the H3O+OCN− species. In the second reaction, a proton is transferred at rate k2 from the H3O+ oxygen atom to the OCN− oxygen atom (via an assisted proton transfer through a chain of H2O molecules) to form HOCN as expressed in system of Eqs. (1): 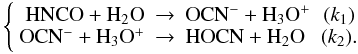(1)Indeed, to derive the rates of formation (k1) and destruction (k2) of OCN−, we need to include the desorption of each species in the total reaction network, as expressed in the system of Eqs. (2): 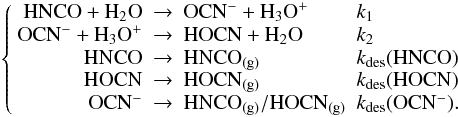(2)To extract the reaction rates k1 and k2 from our experimental kinetic data we need to derive the kdes(HNCO), kdes(OCN−) and kdes(HOCN) desorption rates. As for the desorption of OCN−, we do not know whether the proton is attaching to the nitrogen or the oxygen before desorbing, and it desorbs either as HNCO or HOCN.

3.2. HNCO and OCN− desorption

Figure 4 shows the decrease of the solid phase material along with the temperature ramp during a TPD experiment.

The desorption curves obtained from the IR signal are fitted to the expression Bossa et al. (2009) 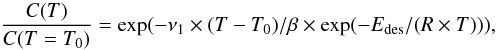(3)where C(T) is the column density of the solid-phase molecules at temperature T. T0 and β are the initial temperature and the heating rate respectively, ν1 the first-order pre-exponential term, Edes the desorption energy and R the ideal gas constant.

The desorption curves depend on the HNCO:H2O concentration ratio. If the HNCO:H2O concentration ratio is high, as seen in Fig. 4, the desorption curves shows two inflexion points corresponding to two desorption events. The first one corresponds to the desorption of pure HNCO, and the second one corresponds to HNCO embedded in water ice, desorbing along with the H2O mantle. Indeed, the second inflexion point gives the desorption energies of H2O, Edes(H2O)  ≈  44 kJ mol-1. If the HNCO:H2O concentration ratio is low, the desorption curves gives the desorption energies of H2O.

Averaging the desorption energies obtained from different temperature programed experiments, at different temperature ramp rate and HNCO:H2O concentration ratios, considering pure desorption and not desorption along with water, we obtain the following desorption energies: Edes(HNCO) = 37    ±  3 kJ mol-1, and Edes(OCN − ) = 40    ±  3 kJ mol-1. HOCN is produced in an insufficient amount and mainly desorbs along with H2O, so that it has not been possible to measure its desorption energy. We were unable to derive the pre-exponential parameter of the desorption kinetics, but it is possible to use a value of ν0 = 2.9  ×  1012 s-1 using the expression for the characteristic desorption frequency given in Hasegawa et al. (1992). These TPD experiments also tell us about the residence time of the species. If the temperature is higher than 130 K, the residence time will be shorter than any chemical reaction timescale.

3.3. Kinetics studies on the HNCO:OCN−:HOCN:H2O system

We see that in two consecutive steps process isocyanic acid HNCO is isomerized into cyanic acid HOCN: a proton is first dragged from the nitrogen atom to a water molecule, and second a proton from another water molecule is attached to the oxygen atom of OCN−. This reaction is purely thermal, and does not necessitate an earlier photochemical formation of radicals. To derive a kinetic law for the formation of OCN− from HNCO and the subsequent formation of HOCN from OCN−, we need to carry out experiments at a temperature high enough that the formation can be measured in a realistic time scale of a few hours. This corresponds to a temperature above 100 K. However, as can be seen in Fig. 4, for a temperature above 130 K, the desorption of HNCO, OCN−, and HOCN needs to be taken into account to solve system 2, because they are desorbing at a timescale close to the chemical reactions involved in this system. Measuring kinetics below 130 K allows us to conveniently simplify system 2 into system 1. However, measures at 130 K are very convenient because the kinetics are fast and the HOCN band is clearly visible. In this case the desorption equations need to be taken into account. Above 130 K the desorption process is dominant.

3.3.1. The temperature dependence of the reaction rates

To simplify the system of Eqs. (2) into the system of Eqs. (1) we will first only consider the chemical reactions while neglecting the desorption of the species as long as the temperature is lower than, or equal to, approximately 120 K. The general form of the kinetic law for the first reaction can be written as 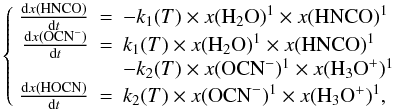(4)where x(H2O), x(HNCO), x(OCN−) and x(HOCN) are H2O, HNCO, OCN− and HOCN molar fractions, respectively. For example we have x(HNCO) = . When H2O is much more abundant than any other species, H2O is a solvent in a solid solution and molar fractions tend to concentrations.

thumbnail Fig. 3

Time evolution of the HNCO (circles), OCN− (crosses) and HOCN (squares) normalized abundances recorded by FTIR spectroscopy at 120 K for a HNCO:H2O mixture in a 1:3 concentration ratio. Fitting the experimental data to the analytical expressions of evolution for each species (dashed lines) gives the reaction rates at T = 120 K.

To determine the temperature dependance of k1(T) and k2(T) we record the time evolution of the HNCO:OCN−:HOCN:H2O system at a fixed temperature and for different HNCO:H2O concentration ratios. Figure 3 shows the evolution of the HNCO, OCN−, and HOCN integrated abundances at T = 120 K for a 1:3 concentration ratio, which is equivalent to (HNCO) = 0.25. To monitor the time evolution of HNCO, we record the integrated absorbance of the 2260 cm-1 band on a difference spectrum, i.e. spectrum at time t minus spectrum at t = 0. This band corresponds to HNCO in a H2O environment at 120 K that is consumed during the reaction. The OCN− evolution is monitored using the 2170 cm-1 band and HOCN the 2295 cm-1 band. Moreover, because of the two components in the HNCO band, the changes in the HNCO band at 2260 cm-1 are difficult to monitor, which is why integrating the OCN − 2170 cm-1 band gives more accurate results on the k1 rate and is thus preferable.

thumbnail Fig. 4

Desorption rate curves from the integrated absorbtion bands of pure HNCO (full squares) and HNCO for a HNCO:H2O mixture where H2O is in excess (crosses) and where H2O is not in excess (full circles). The dotted lines are the results from the fits using a first-order desorption rate (Eq. (3)). Inset: OCN− (triangles) desorption curve in a HNCO:H2O mixture where H2O is not in a 1:5 concentration ratio. Only the first part of the desorption curve is fitted, corresponding to the desorption of OCN− alone.

We separate the H2O molecules population into two kinds. The first kind, x(H2Oreaction), are H2O molecules that are making a favorable hydrogen bond with the HNCO nitrogen atom, in a configuration that the reaction is possible (Raunier et al. 2003b). The second kind, x(H2Ocatalysis), are H2O molecules either far from HNCO or close to HNCO, but they do not form a hydrogen bond with the HNCO nitrogen atom. Thus the x(H2Ocatalysis) molecules cannot react with HNCO, but they have a catalytic effect by decreasing the activation barrier of the proton transfer by long-range interactions (Raunier et al. 2003b). This population does not enter into the kinetic laws, but is indirectly taken into account in the value of the activation barrier. This ice catalytic effect is shown by the fact that the HNCO + H2O reaction does not occur at room temperature in the gas phase if we mix the two reactants in the same volume at a few mbars pressure. Thus we can write x(H2O)reaction = x(HNCO), since one HNCO molecule can react with only one H2Oreaction. This is equivalent to write . In the same way, because one molecule of OCN− reacts one at one with one molecule of H3O+, which is making a favorable hydrogen bond with its oxygen atom, we can write x(OCN−) = x(H3O+) and give an order 2 to this reaction.

Assuming such an order two for the two reactions, we can rewrite system 4 as (5)We can then derive the analytical expressions for each species. Because HOCN originates in the OCN− formed at t = 0, k1 is not taken into account in the kinetics of x(HOCN), which is only determined by the k2 rate. The initial amount of OCN−(t = 0) does need to be considered for the expressions of HNCO(t) and OCN −(t) because we are working on a difference spectrum, where the initial amount OCN−(t = 0) does not appear. Moreover k2 does not need to be taken into account in the kinetics of x(OCN−). The contribution of the second term in the expression of the kinetics of x(OCN−) is a small correction that can be neglected, because x(OCN−)2  ≪  x(HNCO)2. Indeed, experimentally, the OCN− band keeps growing along with time showing no influence of k2 as an intermediate species should, and its evolution is perfectly fitted taking only k1 into account. With these approximations we can write the analytical expressions of the species as (6)Fitting the experimental data against these analytical expressions at a fixed temperature, as shown in Fig. 3, allows us to extract k1 and k2 for this temperature. We record the kinetics of the reaction between 110 K and 130 K as seen in Table 2. The rate at T = 130 K is obtained adding a desorption term to system 4, since the molecules at the surface are desorbing while the molecules in the mantle are reacting. The accuracy on each reaction rate is estimated by reproducing individual identical experiments at both 120 K and 130 K. That our analytical expressions correctly fit the experimental data supports our assumptions on the partial orders.

Table 2

Experimental reaction rates k1 (HNCO + H2O  →  OCN−+ H3O+ reaction) and k2 (OCN−+ H3O+  →  HOCN + H2O reaction) as a function of temperature.

We can now determine the temperature dependence of k1(T) by fitting the reaction rates at different temperatures against an Arrhenius law k1(T) = ν1  ×  , as shown in Fig. 5.

thumbnail Fig. 5

ln(k1) (crosses) and ln(k2) (circles) as a function of the inverse of the temperature, k1 and k2 being the rates for the HNCO + H2O  →  OCN−+H3O+ and the OCN−+H3O+  →  HOCN + H2O reactions respectively. The uncertainty on a point is given by the dispersion of the measurements for the same temperature around the averaged value. The dashed lines represent the fit of the experimental points against an Arrhenius law.

We find an activation energy E1 = 26  ±  2 kJ mol-1 and a pre-exponential factor ν1 = 3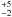  ×  108 s-1. This latter value is on the same order of magnitude than typical pre-exponential factors for second-order reactions in liquid solutions. However, the uncertainty on the derived pre-exponential factor is high. The value we derive for the activation energy is lower than the 42 kJ mol-1 calculated in Raunier et al. (2003b). This can be explained because this value has been derived for a HNCO molecule adsorbed on a H2O surface. The experimentally derived value corresponds to bulk H2O ice, which corresponds to double the solvatation effect and thus lowers the barrier height even more. Given the uncertainties on the reaction rates, it is impossible to determine a possible temperature dependence of the pre-exponential factor as in a modified Arrhenius law. Consequently we can write the reaction rate for the HNCO + H2O  →  OCN−+ H3O+ reaction as  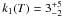 ×  108  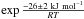×   s-1.

As for the OCN−+ H3O+  →  HOCN + H2O reaction, we find an activation energy E2 = 36  ±  1 kJ mol-1, and a pre-exponential factor of ν2 = 4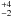  ×  1013 s-1. Accordingly we can write the reaction rate for the OCN−+ H3O+  ⇄  HOCN + H2O reaction as k2(T) = 4  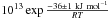×   s-1.

4. Discussion

We showed that the HNCO+H2O acid-base reaction converts HNCO into the H3O+OCN− species. This salt then transforms into HOCN and H2O, the overall process being the isomerization of the isocyanic acid HNCO into cyanic acid HOCN within ice. We derive the expressions for the kinetic laws and reaction rates of formation and destruction of OCN− from the HNCO + H2O and OCN− + H3O+ reactions respectively. Whether or not this purely thermal mechanism is relevant to OCN− formation in the interstellar environment is a question, first, of the kinetics of this reaction at a particular temperature and other competitive reactions such as photodissociations or hydrogenations, and second, of the physical environment the ice is located in. Indeed, in a protostellar environment, the grains are subjected to different temperatures, photon fluxes and density conditions depending on their location in the YSO, and OCN− can be formed, desorbed, or destroyed accordingly. We will now look at the observed OCN− abundances in different objects and then discuss the production of OCN− from the HNCO+H2O reaction, first in a dense molecular cloud and then in a YSO.

4.1. Observed OCN− abundances in the IR spectra of young stellar objects

Table 3 shows OCN− abundances observed for several background stars and low-mass YSOs. We can see first that the OCN− band is absent in the three background stars Elias 13, Elias 16, and EC 118 spectra (Knez et al. 2005). These objects give the column densities of solid-state material in dense molecular clouds before the star formation process begins. Thus, when the star starts collapsing, there is no OCN−. On the other hand, all low-mass YSOs exhibit a OCN− feature, with varying column densities and abundances with respect to H2O, from one object to another. These differences in OCN− abundances could be explained by (i) a difference of elapsed time, i.e. the older a YSO is, the more OCN− is formed; (ii) a difference in environmental conditions (temperature, radiation flux, density). To test the first hypothesis, we can compare the OCN− abundances of Class I objects with Class II or Class III objects. Within Class I objects, we can compare abundances for objects of a decreasing spectral index α, which is defined as the derivative of the spectral energy distribution (SED) between 2 and 14 μm. We do not observe any obvious trend between the OCN− abundances and the class of an YSO or its spectral index. This might rule out the first hypothesis, and the variations of OCN− abundances could be explained by a difference in environmental conditions: differences of masses, luminosities, of portion of the ice warmed. However, there are so few data that it is impossible to draw a reliable conclusion at that point.

Table 3

Column densities of OCN− and H2O, and abundance of OCN− in background stars (top of the table) and low-mass YSO (bottom of the table).

4.2. Modeling OCN− abundances in a dense molecular cloud

HNCO, H2O, OCN− and HOCN can be produced and destroyed in the gas and in the solid phase by different types of reactions, or go from one phase to the other by accretion and desorption. To take into account all these competitive reactions in a dense molecular cloud, we use a rate equations gas-grain model Hasegawa et al. (1992) along with the usual physical parameters used in this reference, hydrogen density N(H) = n(H) + n(H2) = 2  ×  10-4 cm-3, dust to gas mass ratio 1%, density 3 g cm-3, surface sites of adsorption 106, a high visual extinction Av = 500, and the initial gas-phase conditions with all hydrogen into its molecular form at the initial time. We use the most recent reactions database for the gas phase (OSU database) and the solid phase (Garrod et al. 2008). The HNCO+H2O and H3O++OCN− reactions we measured in this work are added to this reaction network with their measured kinetic parameters, along with the desorption energies of each species. The latter reaction is the only one in the reactions network that can produce OCN− and for which kinetics parameters are known. Solid HNCO can be produced in the gas phase from various reactions and then be accreted on the grains, or it can be formed from surface reactions, essentially from the reaction NH + CO, which has no activation energy barrier according to Garrod et al. (2008) reaction network. Because we calculate a very low quantity of the HNCO parent molecule in the solid-state, 1  ×  10-14 cm-3 after 105 years, and because the OCN− that can be converted from this quantity is even lower, we cannot expect OCN− to be produced. Indeed, using the derived expression for the temperature dependence of the k1 reaction rate, 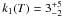  × 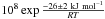  s-1, we can calculate that 1  ×  10-144 s-1  ≤  k1(10 K)  ≤  3  ×  10-133 s-1, which makes this reaction impossible to occur at such a low temperature, which is typical of a molecular cloud. No OCN− is produced in a dense molecular cloud, which fits with the observations of background stars.

We now investigate which reactions and which parameters govern the OCN− production in a homogeneous object such as a molecular cloud. Figure 6 shows that the abundance of solid HNCO is decreasing after 100 years, which could prevent any OCN− formation from HNCO at higher temperature. This decrease cannot be explained by evaporation, which is almost zero at 10 K, or by photodissociation reactions caused by the high visual extinction and as shown by the absence of any photoproduct. To investigate why no OCN− is formed from the HNCO+H2O reaction the and why the amount of HNCO decreases, at 3  ×  105 years, we arbitrarily impose the solid HNCO density to be 5% of the solid H2O density, which is on the order of the amount necessary to produce observed quantities of OCN− (van Broekhuizen et al. 2004), and monitor which products this injected quantity is directed to. As seen in Fig. 6, where the arrow shows the arbitrary input of HNCO in the model, none of this quantity is directed into OCN−. However, all abundances of the products from the reactions of HNCO with H atom or NH, NH2, OH, CH3, CH3O, CH2OH or HCO radicals, are correlated to the sudden addition of solid HNCO. The two hydrogenation reactions HNCO + H  →  HNCHO and HNCO + H  →  NH2CO are especially important, with rates on the order of 1012 s-1 (Garrod et al. 2008). Indeed, their two products HNCHO and NH2CO are closely correlated with HNCO.

thumbnail Fig. 6

Time evolution of the abundances with respect to solid-state water of HNCO (solid line), HNCHO (dotted line) and NH2CHO (dashed line) in a dense molecular cloud where solid HNCO density is arbitrarily fixed to be 5% of solid H2O density at 3  ×  105 years (arrow). No OCN− is produced from the HNCO + H2O thermal reaction at 10 K and OCN− density is zero all the time. Almost all HNCO is consumed in hydrogenation reactions toward HNCHO and NH2CHO, whose increases in density are directly correlated to HNCO decrease. In addition to add 5% of HNCO compared to the solid H2O density, H and H2 are reduced by 6 orders of magnitude (dot-dashed line): the HNCO abundance is only slightly decreasing. Inset: zoom of the evolution of the different abundances after t = 3  ×  105 years.

To confirm the predominance of the hydrogenation reactions, at 3  ×  105 years, in addition to impose the solid HNCO density to be 5% of the solid H2O density, we arbitrarily decrease the quantity of H and H2 by 6 orders of magnitude. When we do this, solid HNCO is almost stable, slightly decreasing, and this slight decrease is nevertheless directed into reactions with hydrogen, as shown in Fig. 6. We can therefore conclude that the hydrogenation reactions are dominating the disappearance of HNCO, and that the reactions of formation of OCN− must counterbalance them to explain the observed quantities of OCN−.

The HNCO+H2O reaction has an activation energy that is too high to compete with the hydrogenation reactions. However, the HNCO + NH3 reaction can also produce OCN− and is known to have a very low activation energy (Raunier et al. 2003a). There are currently no experimental data on the kinetics of the HNCO:NH3:H2O system, so we will arbitrarily appoint a low activation energy to this reaction, between 0 and 5 kJ mol-1. With 0 kJ mol-1 it is possible to produce OCN− at 10 K from the reaction with NH3, although with a very low abundance, as is shown by the correlated formation of NH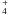. It is impossible to produce OCN− with a 5 kJ mol-1 activation energy at 10 K, but it is possible at 40 K. This shows the importance of measuring the value of the HNCO + NH3 reaction activation energy and to experimentally investigate the HNCO hydrogenation reactions.

4.3. Modeling OCN− abundances in a young stellar object

We then investigated if there is in an YSO a particular region or time where OCN− can be formed from the reaction HNCO+H2O. Using the measured expression for k1(T) at T = 80 K, which is close to the limit temperature to encounter water ice and HNCO on grains, we have 5  ×  10-11  ≤  k1(80 K)  ≤  2  ×  10-7 s-1, with an average reaction rate of k1(80 K)  ≈  0.1 yr-1, which may be enough to counterbalance hydrogenation reactions. Indeed, if the surface temperature is warmer, the residence time of H on grains is shorter and hydrogenation reactions may not be dominant anymore. For this investigation, we choose to use a very simple disk model (Aikawa & Herbst 1999). This model corresponds to a class I/II object and is stationary. We define a grid along the R radial direction and Z transverse direction of the disk. For each point of the grid, the code is run for 106 years, which is the extreme limit of validity of this model. The initial conditions for all molecules except solid HNCO are fixed by running the model from the diffuse medium to the dense molecular cloud medium for 3  ×  105 years. At the initial time there is no OCN− as discussed in the previous paragraph. The abundance of solid HNCO is fixed to be 5% of the abundance of H2O, which is the quantity necessary to reproduce observed OCN− abundances (van Broekhuizen et al. 2005) using thermal reactions. After 106 years, OCN− cannot be formed from the HNCO + H2O reaction alone. Once again HNCO is directed into its hydrogenation products. This disagrees with existing solid OCN− observations. This means that alternative reactions with very low activation energies, such as the HNCO + NH3 reaction, can counterbalance the hydrogenation reactions and produce OCN− from HNCO, or that OCN− is produced from another route than from HNCO. Additional experimental work is needed on both the HNCO + NH3 reaction and the HNCO hydrogenation reactions to be able to discuss quantitatively the different ways of OCN− formation.

5. Conclusion

We studied the kinetics of the conversion of isocyanic acid HNCO into OCN− and then of OCN− into cyanic acid HOCN

in a H2O environment. The H2O + HNCO reaction gives the H3O+OCN− species with a kinetic rate k1(T) = ν1  ×  exp(− Ea/RT), ν1 = 3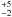  ×  108 s-1, E1 = 26  ±  2 kJ mol-1 (3127 K). The H3O+ to OCN− reaction has a kinetic rate k2(T) = ν2  ×  exp(− E2/RT), ν2 = 4 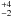 ×  10-13 s-1, E2 = 36  ±  1 kJ mol-1 (4330 K). We show that OCN− follows a kinetic law that can be written as dx(OCN−)/dt = k1  ×  x(HNCO)2 − k2  ×  x(OCN−)2. The desorption energies of HNCO and OCN− are measured to be Edes(HNCO) = 37  ±  3 kJ mol-1 (4450 K) and Edes(OCN−) = 40  ±  3 kJ mol-1 (4811 K), respectively. An attempt to incorporate the derived kinetics laws into an existing gas-grain model was unsuccessful in explaining the observed abundances of OCN− in YSO ices. The model shows that hydrogenation reactions present in reactions databases are dominating the chemistry of HNCO, preventing the formation of OCN− from the HNCO + H2O reaction only. Experimental data on the hydrogenation of HNCO are therefore needed. Moreover, other reactions may be responsible of the OCN− formation, such as the HNCO + NH3 reaction. We need similar kinetics measurements on these reactions to compare them with hydrogenation reactions.

Acknowledgments

This work has been founded by the French national program Physique Chimie du Milieu Interstellaire (PCMI) and the Centre National d’Études Spatiales (CNES). P. Theulé particularly thanks the Academia Sinica Institute for Astonomy and Astrophysics for hosting him during several stays.

References

  1. Aikawa, Y., & Herbst, E. 1999, A&A, 351, 233 [NASA ADS] [Google Scholar]
  2. Bennett, C. J., Jones, B., Knox, E., et al. 2010, ApJ, 723, 641 [NASA ADS] [CrossRef] [Google Scholar]
  3. Boogert, A. C. A., Pontoppidan, K. M., Knez, C., et al. 2008, ApJ, 678, 985 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bossa, J. B., Theule, P., Duvernay, F., & Chiavassa, T. 2009, ApJ, 707, 1524 [NASA ADS] [CrossRef] [Google Scholar]
  5. Brünken, S., Gottlieb, C. A., McCarthy, M. C., & Thaddeus, P. 2009, ApJ, 697, 880 [NASA ADS] [CrossRef] [Google Scholar]
  6. Demyk, K., Dartois, E., d’Hendecourt, L. B., et al. 1998, A&A, 339, 353 [Google Scholar]
  7. d’Hendecourt, L. B., & Allamandola, L. J. 1986, A&AS, 64, 453 [NASA ADS] [Google Scholar]
  8. d’Hendecourt, L. B., Allamandola, L. J., Grim, R. J. A., & Greenberg, J. M. 1986, A&A, 158, 119 [NASA ADS] [Google Scholar]
  9. Falk, M., & Guigere, P. A. 1957, Can. J. Chem, 35, 1195 [Google Scholar]
  10. Garrod, R. T., Weaver, S. L. W., & Herbst, E. 2008, ApJ, 682, 283 [NASA ADS] [CrossRef] [Google Scholar]
  11. Grim, R. J. A., & Greenberg, J. M. 1987, ApJ, 321, L91 [NASA ADS] [CrossRef] [Google Scholar]
  12. Grim, R. J. A., Greenberg, J. M., de Groot, M. S., et al. 1989, A&AS, 78, 161 [NASA ADS] [Google Scholar]
  13. Hasegawa, T., Herbst, E., & Leung, C. M. 1992, A&AS, 82, 167 [Google Scholar]
  14. Iglesias, E. 1977, ApJ, 218, 697 [NASA ADS] [CrossRef] [Google Scholar]
  15. Knez, C., Boogert, A. C. A., Pontoppidan, K. M., et al. 2005, ApJ, 635, L145 [NASA ADS] [CrossRef] [Google Scholar]
  16. Lowenthal, M. S., Khanna, R. K., & Moore, M. H. 2000, BAAS, 32, 1108 [NASA ADS] [Google Scholar]
  17. Marcelino, N., Cernicharo, J., Tercero, B., & Roueff, E. 2009, ApJ, 690, L27 [NASA ADS] [CrossRef] [Google Scholar]
  18. Mladenović, M., & Lewerenz, M. 2008, Chem. Phys., 343, 129 [NASA ADS] [CrossRef] [Google Scholar]
  19. Moore, M. H., Donn, B., Khanna, R., & A’Hearn, M. F. 1983, Icarus, 54, 388 [NASA ADS] [CrossRef] [Google Scholar]
  20. Novozamsky, J. H., Schutte, W. A., & Keane, J. V. 2001, A&A, 379, 588 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. OSU astrochemistry database, network 2009 [Google Scholar]
  22. Raunier, S., Chiavassa, T., Marinelli, F., Allouche, A., & Aycard, J.-P. 2003a, Chem. Phys. Lett., 368, 594 [NASA ADS] [CrossRef] [Google Scholar]
  23. Raunier, S. S., Chiavassa, T., Allouche, A., Marinelli, F., & Aycard, J.-P. 2003b, Chem. Phys., 288, 197 [NASA ADS] [CrossRef] [Google Scholar]
  24. Raunier, S., Chiavassa, T., Marinelli, F., & Aycard, J.-P. 2004, Chem. Phys., 302, 259 [NASA ADS] [CrossRef] [Google Scholar]
  25. Snyder, L. E., & Buhl, D. 1972, ApJ, 177, 619 [NASA ADS] [CrossRef] [Google Scholar]
  26. Teles, J. H., Maier, G., Hess, B. A., et al. 1989, Chemische Berichte, 122, 753 [CrossRef] [Google Scholar]
  27. Tideswell, D. M., Fuller, G. A., Millar, T. J., & Markwick, A. J. 2010, A&A, 510, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Turner, B. E., Terzieva, R., & Herbst, E. 1999, ApJ, 518, 699 [NASA ADS] [CrossRef] [Google Scholar]
  29. van Broekhuizen, F. A., Keane, J. V., & Schutte, W. A. 2004, A&A, 415, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. van Broekhuizen, F. A., Pontoppidan, K. M., Fraser, H. J., & van Dishoeck, E. F. 2005, A&A, 441, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Zinchenko, I., Henkel, C., & Mao, R. Q. 2000, A&A, 361, 1079 [NASA ADS] [Google Scholar]

All Tables

Table 1

Positions and integrated band strengths of a HNCO:H2O ice mixture at 10 K.

In the text
Table 2

Experimental reaction rates k1 (HNCO + H2O  →  OCN−+ H3O+ reaction) and k2 (OCN−+ H3O+  →  HOCN + H2O reaction) as a function of temperature.

In the text
Table 3

Column densities of OCN− and H2O, and abundance of OCN− in background stars (top of the table) and low-mass YSO (bottom of the table).

In the text

All Figures

thumbnail Fig. 1

Infrared spectrum of a HNCO:H2O mixture in a 1:5 concentration ratio at T = 120 K. A small amount of OCN− is formed during the deposition.
In the text
thumbnail Fig. 2

Infrared spectrum a) and difference spectrum (spectrum at time t minus spectrum at t = 0) b) of a HNCO:H2O mixture at T = 120 K at t = 0 s, 3300 s, 21   300 s and 53 700 s. OCN− has a band at 2170 cm-1 and HOCN at 2295 cm-1. The HNCO band has two components: one component at 2260 cm-1 corresponding to HNCO in a H2O environment and one component at 2234 cm-1 corresponding to HNCO in a HNCO environment. The variation of the second component is the result of a rearrangement that can give a positive band a 2251 cm-1 in some spectra. The bands at 2349 cm-1 correspond to fluctuations of the gas phase CO2.
In the text
thumbnail Fig. 3

Time evolution of the HNCO (circles), OCN− (crosses) and HOCN (squares) normalized abundances recorded by FTIR spectroscopy at 120 K for a HNCO:H2O mixture in a 1:3 concentration ratio. Fitting the experimental data to the analytical expressions of evolution for each species (dashed lines) gives the reaction rates at T = 120 K.
In the text
thumbnail Fig. 4

Desorption rate curves from the integrated absorbtion bands of pure HNCO (full squares) and HNCO for a HNCO:H2O mixture where H2O is in excess (crosses) and where H2O is not in excess (full circles). The dotted lines are the results from the fits using a first-order desorption rate (Eq. (3)). Inset: OCN− (triangles) desorption curve in a HNCO:H2O mixture where H2O is not in a 1:5 concentration ratio. Only the first part of the desorption curve is fitted, corresponding to the desorption of OCN− alone.
In the text
thumbnail Fig. 5

ln(k1) (crosses) and ln(k2) (circles) as a function of the inverse of the temperature, k1 and k2 being the rates for the HNCO + H2O  →  OCN−+H3O+ and the OCN−+H3O+  →  HOCN + H2O reactions respectively. The uncertainty on a point is given by the dispersion of the measurements for the same temperature around the averaged value. The dashed lines represent the fit of the experimental points against an Arrhenius law.
In the text
thumbnail Fig. 6

Time evolution of the abundances with respect to solid-state water of HNCO (solid line), HNCHO (dotted line) and NH2CHO (dashed line) in a dense molecular cloud where solid HNCO density is arbitrarily fixed to be 5% of solid H2O density at 3  ×  105 years (arrow). No OCN− is produced from the HNCO + H2O thermal reaction at 10 K and OCN− density is zero all the time. Almost all HNCO is consumed in hydrogenation reactions toward HNCHO and NH2CHO, whose increases in density are directly correlated to HNCO decrease. In addition to add 5% of HNCO compared to the solid H2O density, H and H2 are reduced by 6 orders of magnitude (dot-dashed line): the HNCO abundance is only slightly decreasing. Inset: zoom of the evolution of the different abundances after t = 3  ×  105 years.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.