| Issue |
A&A
Volume 529, May 2011
|
|
|---|---|---|
| Article Number | A136 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201016356 | |
| Published online | 20 April 2011 | |
Mass-loss rates for transiting exoplanets⋆
1
Institut de planétologie et d’astrophysique de Grenoble (IPAG), Université
Joseph Fourier-Grenoble 1, CNRS (UMR 5274), BP 53, 38041
Grenoble Cedex 9,
France
e-mail: david.ehrenreich@obs.ujf-grenoble.fr
2
Harvard-Smithsonian Center for Astrophysics,
60 Garden street, Cambridge, Massachusetts
02138,
USA
e-mail: jdesert@cfa.harvard.edu
Received:
17
December
2010
Accepted:
23
February
2011
Exoplanets at small orbital distances from their host stars are submitted to intense levels of energetic radiations, X-rays, and extreme ultraviolet (EUV). Depending on the masses and densities of the planets and on the atmospheric heating efficiencies, the stellar energetic inputs can lead to atmospheric mass loss. These evaporation processes are observable in the ultraviolet during planetary transits. The aim of the present work is to quantify the mass-loss rates (ṁ), heating efficiencies (η), and lifetimes for the whole sample of transiting exoplanets, now including hot Jupiters, hot Neptunes, and hot super-Earths. The mass-loss rates and lifetimes are estimated from an “energy diagram” for exoplanets, which compares the planet gravitational potential energy to the stellar X/EUV energy deposited in the atmosphere. We estimate the mass-loss rates of all detected transiting planets to be within 106 to 1013 g s-1 for various conservative assumptions. High heating efficiencies would imply that hot exoplanets such the gas giants WASP-12b and WASP-17b could be completely evaporated within 1 Gyr. We also show that the heating efficiency can be constrained when ṁ is inferred from observations and the stellar X/EUV luminosity is known. This leads us to suggest that η ≈ 100% in the atmosphere of the hot Jupiter HD 209458b, while it could be lower for HD 189733b. Simultaneous observations of transits in the ultraviolet and X-rays are necessary to further constrain the exospheric properties of exoplanets.
Key words: planets and satellites: general / planets and satellites: atmospheres / ultraviolet: planetary systems / ultraviolet: stars / X-rays: stars
Table 1 is available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
More than 500 extrasolar planets have been detected so far. A high percentage (~30%) of them lie at close distances to their host stars, below 0.1 AU. Early on, that most detected planets were so close to their stars and massive enough to be most certainly gaseous, challenged theoreticians about their origins and their fates. “Hot Jupiters” cannot form at their observed locations, but have to migrate inward (Lin et al. 1996). Meanwhile, why these planets stopped migrating at such distances is still an open question. In contrast, one could wonder what happened to those giant planets that migrated further in. Of particular interest, is the question of the atmospheric stability at extreme levels of irradiation. How fast can giant planets be despoiled of their atmospheres? Could lighter, Neptune- or Earth-mass planets form or migrate as well into environments, which would challenge their atmospheric stability? Can such “evaporation” of exoplanets explain the apparent desert of planets below ~0.01 AU? In fact, the closest planets should also be the easiest to detect because the transit frequency and probability increase inversely to the semi-major axis.
Observations of exoplanet transits hold the keys to these questions. For the >100 known transiting planets, it is possible to measure the planet-to-star radius ratio and, for the few planets observed in the ultraviolet, constrain the size and mass-loss rate of their evaporating upper atmospheres. Transit observations of hot Jupiters in the stellar Lyman-α emission of neutral hydrogen (H i Lyα at 1 215.67 Å) yield typical estimations of the mass-loss rates of ṁ ~ 1010 to 1011 g s-1 for the planets HD 209458b (Vidal-Madjar et al. 2003, 2004, 2008; Ehrenreich et al. 2008; Linsky et al. 2010), HD 189733b (Lecavelier des Etangs et al. 2010) and WASP-12b (Fossati et al. 2010). Such values are predicted by numerous theoretical works and imply that the evolution of known hot Jupiters is not significantly affected by atmospheric evaporation (Lammer et al. 2003; Lecavelier des Etangs et al. 2004; Baraffe et al. 2004, 2005, 2006; Yelle 2004, 2006; Jaritz et al. 2005; Tian et al. 2005; García-Muñoz 2007; Holmström et al. 2008; Stone & Proga 2009; Murray-Clay et al. 2009).
Lecavelier des Etangs (2007) compares the stellar energy received by the upper atmospheres to the gravitational energies of the planets in a so-called “energy diagram”. This diagram allows estimations of the mass-loss rates and lifetimes for the population of close-in planets. This author uses the sample of exoplanets known as of June 2006, including ten transiting planets. Recently, Davis & Wheatley (2009) have provided an updated energy diagram containing 36 transiting hot Jupiters, while Lammer et al. (2009) have determined the mass loss limit for 57 transiting planets. These studies point out that an evaporation-forbidden region should exist into which a lost population of planets have been significantly eroded by this process, possibly leaving evaporation remnants, coined “chthonian planets” (Lecavelier des Etangs et al. 2004).
In this article, we aim at providing comparative estimations of the mass-loss rates and lifetimes of the whole sample of transiting planets currently known (in October 2010, 105 planets). As the sample of transiting planets steadily increases in time, the explored ranges of mass and density expand to new kinds of exoplanets: hot Neptunes and hot super-Earths. The existence of such close-in low-mass and high-density planets is a test for atmospheric evaporation theories. Moreover, predictions from the energy diagram enable the observable transit signature of evaporating planets to estimated (e.g., Ehrenreich et al. 2011).
The method of deriving the energy diagram is explained in Sect. 2. Aforementioned theoretical studies point out the role of X and extreme ultraviolet (EUV) stellar radiations as the main source of exospheric heating leading to mass loss. Because recent X/EUV surveys were dedicated to exoplanet host stars (Kashyap et al. 2008; Sanz-Forcada et al. 2010; Poppenhaeger et al. 2010), we examine the impact of the constraints brought by these studies on the energy diagram (Sect. 3). In a few cases, measurements of the stellar X flux and estimations of the mass-loss rate from observations of ultraviolet transits make it possible to constrain the mechanisms of atmospheric evaporation in terms of heating efficiency. This is discussed in Sect. 4. Finally, the estimation of the atmospheric mass-loss rates raises questions about the atmospheric stability and the lifetime of evaporating planets, which is discussed in Sect. 5.
2. Updated energy diagram
The energy diagram for extrasolar planets measures the gravitational potential energy per mass unit of a planet, as a function of the X and EUV irradiations received by it. Next, we recall the main steps of the calculations explained in detail in Lecavelier des Etangs (2007). All the properties of the planets and host stars used for these calculations are extracted from the Extrasolar Planets Encyclopædia (Schneider 2010) and are given in Table 3.
The framework is that of an energy-limited escape; i.e., an atmospheric mass unit can
escape when the gravitational potential (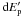 ) is filled by the stellar X/EUV energetic
input (dEX/EUV) into the planet upper atmosphere,
) is filled by the stellar X/EUV energetic
input (dEX/EUV) into the planet upper atmosphere, 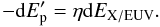 (1)The key factor η is the
heating efficiency in the exoplanet thermosphere that encapsulates most of the physics of
the problem. This factor value is high when most of the incoming stellar energy is
effectively used to escape the atmosphere. It depends mainly on how many energetic photons
are absorbed by atmospheric atoms, how deep in the atmosphere the absorption takes place,
and how thick the absorbing region is.
(1)The key factor η is the
heating efficiency in the exoplanet thermosphere that encapsulates most of the physics of
the problem. This factor value is high when most of the incoming stellar energy is
effectively used to escape the atmosphere. It depends mainly on how many energetic photons
are absorbed by atmospheric atoms, how deep in the atmosphere the absorption takes place,
and how thick the absorbing region is.
Lecavelier des Etangs (2007) consider the extreme case η = 1, where all the stellar flux is used to escape the atmosphere. Considering (without quantifying) energetic losses by thermal emission by atmospheric hydrogen, Tian et al. (2005) model the atmospheric escape process of the hot Jupiter HD 209458b using η = 0.15. This value was initially chosen by Watson et al. (1981) in their pioneering work about Earth’s atmospheric escape. A similar value (η = 0.1) was also employed by Valencia et al. (2010), who estimate the atmospheric loss for Corot-7b. In fact, the value of η for the strongly irradiated atmospheres of extrasolar planets remains largely unconstrained (though see Cecchi-Pestellini et al. 2009, and Sect. 4). In the following, we treat η as a free parameter with a possible value between 0.01 and 1, until we show in Sect. 4 how it is possible to obtain observing constraints on this parameter.
We present the updated energy diagram in Fig. 1 with
98 transiting planets. The vertical axis of the energy diagram measures the potential energy
required to escape the planetary atmosphere. The potential energy per atmospheric mass unit
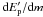 of a planet of radius
Rp and mass Mp includes the
contribution of tidal forces and is calculated according to Eq. (8) in Lecavelier des Etangs
(2007).
of a planet of radius
Rp and mass Mp includes the
contribution of tidal forces and is calculated according to Eq. (8) in Lecavelier des Etangs
(2007).
The horizontal axis of the energy diagram measures the amount of stellar energy available
on top of the planetary atmosphere. Cecchi-Pestellini et al. (2009) have studied how EUV photons (30–912 Å) and X-rays (1–30 Å) can
heat the upper and lower atmospheric layers, respectively. This heating makes the atoms and
ions of the upper atmosphere escaping the gravitational well of the planet. Lecavelier des
Etangs (2007) estimates the amount of X/EUV energy
received per unit of time as 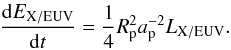 (2)The X/EUV luminosity
LX/EUV (1–912 Å) is generally not known for host stars of
transiting planets (but see Sect. 3). Lecavelier des
Etangs (2007) uses the Wood et al. (1994) correlation between the stellar rotation velocity
vrot and the EUV flux FEUV
measured in the S2 bandpass of the Rosat satellite (110−195 Å) as a proxy
to estimate the EUV flux of the 11 transited stars known in 2007,
(2)The X/EUV luminosity
LX/EUV (1–912 Å) is generally not known for host stars of
transiting planets (but see Sect. 3). Lecavelier des
Etangs (2007) uses the Wood et al. (1994) correlation between the stellar rotation velocity
vrot and the EUV flux FEUV
measured in the S2 bandpass of the Rosat satellite (110−195 Å) as a proxy
to estimate the EUV flux of the 11 transited stars known in 2007,  (3)The luminosity and flux at 1 AU are related
through
LEUV = 4π(1 AU)2FEUV(1 AU).
We caution here that such an activity-rotation relation is only valid for stars with a
convective zone. We therefore consider this estimation to be doubtful for stars earlier than
~F5 (about 11% of transited stars). In particular, the position of WASP-33b (A5 star)
in Fig. 1 should be regarded with caution.
(3)The luminosity and flux at 1 AU are related
through
LEUV = 4π(1 AU)2FEUV(1 AU).
We caution here that such an activity-rotation relation is only valid for stars with a
convective zone. We therefore consider this estimation to be doubtful for stars earlier than
~F5 (about 11% of transited stars). In particular, the position of WASP-33b (A5 star)
in Fig. 1 should be regarded with caution.
 |
Fig. 1 The energy diagram for 98 transiting planets: the energy needed to escape a unit of mass of the planet atmosphere versus the X/EUV flux reaching the top of the atmosphere per unit of time. The dotted lines indicate constant mass loss rates of ṁ = 1015 to 105 g s-1 (from left to right). Data points are calculated with η = 15%. Variations of η between 1% and 100% are represented with horizontal grey error bars. Coloured points and labels indicate transiting planets of particular interest, which are discussed in the text. |
 |
Fig. 2 Mass-loss rate (η = 0.15) as a function of the planet mass for 98 transiting planets. The vertical error bars represent a variation of η from 0.01 (lower values) to 1 (higher values). Planets of interest are coloured accordingly to Fig. 1. |
The measured vrotsini⋆ have been retrieved from the literature for 98 stars in Table 3. We also assume that the sine of the stellar inclination i⋆ is ~1 for transiting systems. The data points in Fig. 1 are calculated by assuming η = 0.15. The value of this factor dominates the uncertainties on such calculations. Therefore, the positions of planets in the diagram are shown with conservative error bars representing possible η values in the range [0.01,1] . Curves of constant mass-loss rates ṁ are overplotted in Fig. 1. All transiting planets in the diagram have ṁ values between 106 g s-1 and 1013 g s-1, assuming all possible values of η.
Two “outliers”, WASP-33b and HD 80606b, appear in the diagram with the highest and lowest mass-loss rates, respectively. Meanwhile, the mass-loss rate of WASP-33b is probably overestimated for the reason detailed above. The mass-loss rate of the extremely eccentric (e = 0.93) planet HD 80606b is likely underestimated, at least when the planet is at periastron, since the mass-loss rates are calculated with the semi-major axis of transiting planets instead of the periastron distances.
The iso-mass-loss rates are represented by linear curves in Fig. 1. The mass-loss rate is also plotted as a function of the planet’s mass
in Fig. 2. Both Figs. 1 and 2 show that maximum mass loss rates
(10.5 ≲ log ṁ ≲ 12) are reached with η = 0.15 for
planets with masses between ~0.4 and ~4
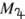 . In Fig. 2, there is a dearth of low-mass planets with high ṁ, which is
expected if low-mass planets are despoiled of their atmospheres at high ṁ.
The remaining cores (or chthonian planets) would be more difficult to detect in transit.
Assuming a different value for η would simply scale the resulting mass-loss
rates up or down, if one assumes a similar value of η for all planets. See
Sect. 4 for a discussion of this aspect.
. In Fig. 2, there is a dearth of low-mass planets with high ṁ, which is
expected if low-mass planets are despoiled of their atmospheres at high ṁ.
The remaining cores (or chthonian planets) would be more difficult to detect in transit.
Assuming a different value for η would simply scale the resulting mass-loss
rates up or down, if one assumes a similar value of η for all planets. See
Sect. 4 for a discussion of this aspect.
3. Measurements of X/EUV fluxes
To take the highest-energy photons able to heat the upper atmospheres of the transiting planets into account, it is necessary to estimate the X/EUV fluxes of planet-hosting stars. Observational and archival surveys have been started for this purpose. Kashyap et al. (2008) carried out a survey of X-ray emission combining archival and targeted data from Asca, Exosat, Einstein, Rosat, XMM-Newton, and Chandra missions. These authors present X-ray flux values or upper limits for 235 planet-hosting stars. These values cover a pass band of 0.1–4.5 keV (3–124 Å). There are 35 transiting systems among their sample, among which only five have a detected X-ray emission (GJ 436, HD 209458, HD 189733, OGLE-TR-10, and SWEEPS-11).
Sanz-Forcada et al. (2010) study a sample of 65 planetary systems with XMM-Newton and Chandra archival data. The data sets are the same as in Kashyap et al. (2008), but some estimations of stellar X luminosities are revised. According to Sanz-Forcada et al. (2010), these differences appear in some cases (noticeably for HD 209458) where the stellar proper motion is not taken into account, leading to suspicious source identification. Concerning transiting systems, Sanz-Forcada et al. (2010) report lower values than Kashyap et al. (2008) for HD 189733 (by 0.2 dex) and GJ 436 (by 1 dex). They give an upper limit for HD 209458, significantly lower (by 0.7 dex) than the values reported elsewhere. A recent reassessment of HD 209458’s X-ray flux yielded an upper limit (log LX < 26.40) twice as large as the former value (Sanz-Forcada, priv. comm.; Sanz-Forcada et al. 2011).
Poppenhaeger et al. (2010) present a similar work to these studies. They add new XMM-Newton data points for stars previously devoided of X-ray measurements. Unfortunately, their new data set does not encompass additional transiting systems. They report similar X-ray luminosity values for HD 189733 and GJ 436, although their calculated uncertainties are larger than those estimated in Kashyap et al. (2008).
For some active stars, the X-ray luminosity may vary outside the range allowed by the uncertainties reported in these works. In fact, a detailed analysis of archival XMM-Newton observations of the active star HD 189733 at two different epochs show that these uncertainties probably underestimate the intrinsic source variability (Pillitteri et al. 2010). Pillitteri et al. (2010) indeed find that the X-ray flux of this star has varied by 45% between 2007 and 2009.
Multiple X-ray detection reports in the literature for stars hosting transiting planets.
 |
Fig. 3 The energy diagram for 35 transiting planets with X-ray emission detections or upper limits (arrows) reported in the literature. Caption is the same as for Fig. 1. Data points are calculated with η = 15%. Planets of interest are outlined with different colours. |
The values of LX/EUV found in the literature have been injected in Eq. (2) to obtain the energy diagram shown in Fig. 3. Among the five transiting systems with measured X-ray emissions (Kashyap et al. 2008), HD 189733b and GJ 436b stay at about the same location as in Fig. 1 for η = 0.15, with ṁ between 1010 and 1011 g s-1 for HD 189733b and ~109 g s-1 for GJ 436b. In contrast, the mass loss rate of HD 209458b is about 1.5 order-of-magnitudes lower than with the previous estimation. Noticeably, the ṁ value for OGLE-TR-10b dramatically increases by ~2 orders of magnitude. Finally, the case of SWEEPS-11 is troublesome. There is no reported value for the rotational velocity of this star in the literature, so we were not able to include this object in Fig. 1. The X/EUV flux reported by Kashyap et al. (2008) for this star is more than 10 times higher than for HD 189733. SWEEPS-11 is a 20th-magnitude star belonging to a crowded region in the Galactic bulge1. The possibility that the detected emission does not come from this star is therefore not negligible.
Overall, there are multiple reports of the X-ray emissions of only three transiting systems in the literature. These are HD 189733, HD 209458, and GJ 436. The different values reported for these three systems are summarized in Table 2.
4. Constraints on the heating efficiency
For the majority of transiting planets, the two largest uncertainties in the calculation of ṁ are the heating efficiency η and the X/EUV luminosity. Cecchi-Pestellini et al. (2009) have studied the relative role of X/EUV radiation in the heating of the hydrogen-rich atmosphere of HD 209458b. In their model, the flux of stellar X/EUV photons incident upon the planetary atmosphere of solar-like composition photoionizes the gas producing a flux of high-energy photo-electrons, which deposit their energy into the gas. They calculated heating efficiencies as a function of photon energy, electron fraction in the gas, and vertical column density of the atmosphere. The results strongly depend on the coupled ionization and density structures as shown by Yelle (2004), García-Muñoz (2007), and Murray-Clay et al. (2009). For a fractional electron concentration of 10%, Cecchi-Pestellini et al. (2009) find heating efficiencies of ~0.9, 0.75, and 0.7 for column densities ≳1019, 1021, and 1022 cm-2, respectively, and for photon energies of 50 eV (λ = 248 Å), 300 eV (41 Å), and 1 000 eV (12 Å), respectively. These efficiencies decrease to 0.18, 0.04, and 0.02 when the electron fraction is 10-6.
The work of Cecchi-Pestellini et al. (2009) shows
that depending on the atmospheric properties, the heating efficiency can take nearly all
possible values. In contrast, measuring the heating efficiency η could
provide some constraints on these atmospheric properties. In the few cases where transits
have been observed in the UV, it is possible to constrain ṁ. This can be
done (i) numerically using a particle simulation with ṁ set as a free
parameter to reproduce the absorption during transit caused by the cloud of escaping
hydrogen atoms (Lecavelier des Etangs et al. 2010);
or (ii) analytically by assuming a density profile – usually a power law – for the
hydrodynamically escaping atmosphere (Linsky et al. 2010). If the X/EUV luminosity is known, UV transits can thus bring constraints on
η. In fact, starting from Eq. (1), the heating efficiency can be expressed as the ratio of the two powers
LX/EUV and Lṁ
depending on the star and planet properties, respectively, 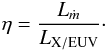 (4)If tidal forces are neglected, the “mass loss
power” Lṁ has a simple expression,
(4)If tidal forces are neglected, the “mass loss
power” Lṁ has a simple expression,
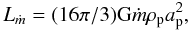 (5)where
(5)where 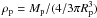 is the mean density of the planet.
is the mean density of the planet.
In the following, all the calculations are performed taking tidal forces into account. To constrain the value of η, we introduce in Fig. 4 a “power diagram” for extrasolar planets. There are observational constraints on both ṁ and LX/EUV for only two transiting planets: HD 209458b and HD 189733b. For HD 209458b, we considered the value of 1010 g s-1 for the mass-loss rate given by Vidal-Madjar et al. (2003) as a lower limit. This value results from the (15 ± 4)% absorption detected over ~1/3 of the H i Lyman α line. It is a lower limit because there is no way to measure the absorption over the central part of the line hidden by the interstellar medium absorption. Higher ṁ values, (8–40) × 1010 g s-1, have recently been reported by Linsky et al. (2010). As discussed below, these authors have inferred hydrogen mass-loss rates from a (8 ± 1)% absorption in the emission line of singly ionized carbon (C ii) during the transit of the planet.
 |
Fig. 4 The power diagram for evaporating extrasolar planets. The “mass-loss power” Lṁ (Eq. (5)) is plotted as a function of the X/EUV luminosity. Constant η values are represented by the dotted lines. The hatched regions show the position of HD 189733b (orange) and HD 209458b (crimson). For HD 209458b, the right-pointing arrow shows the upper limit on the X/EUV luminosity reported by Sanz-Forcada et al. (2011). |
Lecavelier des Etangs et al. (2010) have estimated the mass-loss rate of HD 189733b from a H i Lyα transit light curve for different values of the X/EUV flux. For a best-fit value FX/EUV of 20 times the solar value, they report a 1-σ range of 3.2 × 109 < ṁ < 1.4 × 1011 g s-1.
The X-ray luminosities are taken from Kashyap et al. (2008) for HD 209458 and Pillitteri et al. (2010) for HD 189733. A weakly efficient evaporation, with η ~ 1%, seems to be excluded from the observations of HD 189733. In contrast, only values of η > 1 are compatible with the observations of HD 209458b, which is not physically plausible. In fact, it is not clear what possible energy source could significantly cumulate with the stellar radiation to drive such a “super-efficient” mass loss. The situation is even more troublesome for HD 209458b if one considers the upper limits on LX/EUV given by Sanz-Forcada et al. (2011).
The uncertainties on the measured values of LX/EUV and ṁ are a first possible explanation of the apparent “super-efficiency” of HD 209458b’s mass loss. In fact, a large part of the EUV spectrum (roughly from 200 to 912 Å) does not contribute to the “X/EUV” flux measured with Rosat or XMM-Newton. If HD 209458 is as luminous between 200 and 912 Å as it is below 200 Å, then the position of the planet in the power diagram (Fig. 4) would become compatible with a very efficient (η ~ 100%) mass loss. However, in the case of the lower luminosity estimations of Sanz-Forcada et al. (2011), the star would have to be at least an order of magnitude more luminous in the EUV above 200 Å than below.
Another possible explanation for the super-efficiency of HD 209458b’s mass loss may be found in the way the mass-loss rate was estimated by Linsky et al. (2010), which strongly depends on the assumed density profile of the exosphere, up to the Roche lobe (Lecavelier des Etangs, priv. com.).
It is also possible that LX/EUV was larger during the observations of Linsky et al. (2010) than in 2003. An increase by ~1 or ~1.5 order(s) of magnitude, from the value of Kashyap et al. (2008) or Sanz-Forcada et al. (2011), respectively, is needed to have η values below 1, within the error bars. Such a large X luminosity variation might not be expected for a solar-type star like HD 209458. Meanwhile, the only way to solve this question is to obtain simultaneous measurements of the X-ray flux and the escape rate. This should be possible with current space instrumentation.
Assuming the X/EUV luminosity from Kashyap et al. (2008) and the escape rate ṁ between 1010 and 4 × 1011 g s-1, it is possible to infer exospheric properties out of the power diagram. In fact, while the ṁ estimation of Vidal-Madjar et al. (2003), which is marginally compatible with η = 1, is based on the observation of an absorption in the H i stellar emission, the higher estimation of Linsky et al. (2010) is derived from the observation of an absorption in the singly ionized carbon (C ii) stellar emission. For this line, these authors measured an (8 ± 1)% absorption, yielding ṁ(C ii) = 2.1 × 107 g s-1. To go from this value to a total (hydrogen) mass-loss rate ṁ ≈ 8 × 1010 g s-1, they rely on the assumptions that (i) all the carbon is ionized (i.e., [C ii/C] = 1) and (ii) that the carbon abundance is solar ([C/H] ⊙ = 2.7 × 10-4; Asplund et al. 2009) in the upper atmosphere of HD 209458b. The total (hydrogen) mass-loss rate is then ṁ ≡ ṁ(H i) = ṁ(C ii)/ [C/H] .
Therefore, an apparent superefficient evaporation process with η > 1, as shown in Fig. 4 could mean that [C/H] is underestimated. The [C/H] ratio would have to be increased by at least an order of magnitude with respect to [C/H] ⊙ to give an ṁ value compatible with η = 1, assuming LX/EUV values from Kashyap et al. (2008). On the other hand, if log LX/EUV < 26.40 (Sanz-Forcada et al. 2011), then the upper atmosphere should be extremely carbon-rich with [C/H]/[C/H] ⊙ > 100. An underestimated [C/H] could also imply that the carbon ionization fraction is unity, as predicted by models of HD 209458b’s atmosphere (García-Muñoz 2007).
Nevertheless, we caution that the measurements of ṁ and LX/EUV for transiting planets may not be accurate enough at the present time to allow firm conclusions to be drawn out of the power diagram. Meanwhile, this shows how it could be possible to constrain the exospheric composition when precise measurements are available.
5. Stability of evaporating atmospheres
The lifetime of evaporating gaseous planets can be estimated as the time needed to exhaust
the available reservoir of gas for a given mass-loss rate. An approximation of this life
time can be obtained in an “integrated” version of the energy diagram shown in Fig. 1. We use the total potential energy
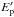 of a planet including tidal forces, defined
by Eq. (10) in Lecavelier des Etangs (2007).
of a planet including tidal forces, defined
by Eq. (10) in Lecavelier des Etangs (2007).
The mean energy received ⟨ dEX/EUV/dt ⟩ is
calculated by integrating Eq. (2) over a
given time interval. When doing so, one should account for the evolution of
LX/EUV(t) in time. In fact, the high-energy
radiation output from a star is stronger when the star is younger and varies with time as a
power-law
LX/EUV(t > τsat) ∝ t−α
(e.g., Penz et al. 2008), with α close to 1. Stars younger than
τsat are in the “saturation regime” where the evolution of
LX/EUV(t) is almost flat. As discussed by
Davis & Wheatley (2009), the duration
τsat of the saturation period depends on the spectral type
(see, e.g., Reiners et al. 2009 for M dwarfs). Here,
we consider the equations used by Sanz-Forcada et al. (2010) 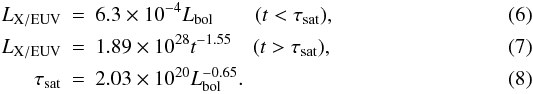 We use this set of equations to estimate
⟨ LX/EUV ⟩ , the mean amount of X/EUV irradiation received
during the lifetime of our sample stars per billion year,
We use this set of equations to estimate
⟨ LX/EUV ⟩ , the mean amount of X/EUV irradiation received
during the lifetime of our sample stars per billion year, 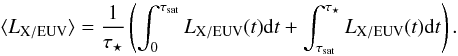 (9)After injecting Eqs. (6) to (8) into Eq. (9), we obtain
(9)After injecting Eqs. (6) to (8) into Eq. (9), we obtain
![\begin{eqnarray*} \langle L_\xeuv \rangle &&= \frac{1}{\tau_\star} \left[ 1.28\times10^{17}\Lbol^{0.35} + 2.33\times10^{17}\Lbol^{0.3575} \right. \\ &&\quad- \left. 3.44\times10^{28}\tau_\star^{-0.55} \right], \end{eqnarray*}](/articles/aa/full_html/2011/05/aa16356-10/aa16356-10-eq110.png) where Lbol and
τ⋆ are the present-day bolometric luminosity in
erg s-1 and age of the star in Gyr, respectively. We calculate
Lbol for our sample stars with Stefan-Boltzmann’s law,
where Lbol and
τ⋆ are the present-day bolometric luminosity in
erg s-1 and age of the star in Gyr, respectively. We calculate
Lbol for our sample stars with Stefan-Boltzmann’s law,
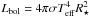 , where the effective temperatures and
stellar radii are taken from the literature and listed in Table 3. For M, K, G, F, and A stars, we assumed typical stellar ages of 10, 7,
5, 3, and 1 Gyr, respectively.
, where the effective temperatures and
stellar radii are taken from the literature and listed in Table 3. For M, K, G, F, and A stars, we assumed typical stellar ages of 10, 7,
5, 3, and 1 Gyr, respectively.
We want to know by how much the X/EUV irradiation is underestimated when the time evolution
of LX/EUV is ignored. For this purpose, we introduce the factor
γ (see also Lecavelier des Etangs 2007), 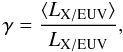 (10)where LX/EUV at the
denominator is calculated using Eq. (7) with
t = τ⋆. The values of γ are
listed in Table 3. We found a mean value of
γ = 38 ± 9 (1σ). We apply this γ
correction to the values of ⟨ dEX/EUV/dt ⟩
calculated by integrating Eq. (2).
(10)where LX/EUV at the
denominator is calculated using Eq. (7) with
t = τ⋆. The values of γ are
listed in Table 3. We found a mean value of
γ = 38 ± 9 (1σ). We apply this γ
correction to the values of ⟨ dEX/EUV/dt ⟩
calculated by integrating Eq. (2).
This parameterization neglects that the heating efficiency might be notably lower at early
times when the stellar luminosity is higher. Under high X/EUV illumination, Murray-Clay
et al. (2009) indeed suggest that the mass-loss
regime should depart from an energy-limited escape (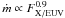 ) and instead become
“radiation/recombination”-limited (
) and instead become
“radiation/recombination”-limited (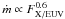 ). This effect would increase the lifetimes
calculated here, where we assume that the heating efficiency remains constant over time.
). This effect would increase the lifetimes
calculated here, where we assume that the heating efficiency remains constant over time.
These integrated energies are calculated for our sample of transiting planets, and the
result is shown in Fig. 5 for different values of
η. The ratio between 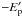 (in erg) and
⟨ dEX/EUV/dt ⟩ (in erg Gyr-1) is
equivalent to a lifetime. As can be seen in Fig. 5,
only a few planets have lifetimes below 10 Gyr. Meanwhile, this figure also highlights that
any firm conclusions have to rely on an assumed value of η. For instance,
if η is close to 1 for WASP-17b, WASP-33b, or WASP-12b, then the
atmospheres of these planets should be lost in less than 1 Gyr. Noteworthy is that WASP-12b
may well fill its Roche lobe fully enough to lose mass faster than the process considered
here would predict (Li et al. 2010).
(in erg) and
⟨ dEX/EUV/dt ⟩ (in erg Gyr-1) is
equivalent to a lifetime. As can be seen in Fig. 5,
only a few planets have lifetimes below 10 Gyr. Meanwhile, this figure also highlights that
any firm conclusions have to rely on an assumed value of η. For instance,
if η is close to 1 for WASP-17b, WASP-33b, or WASP-12b, then the
atmospheres of these planets should be lost in less than 1 Gyr. Noteworthy is that WASP-12b
may well fill its Roche lobe fully enough to lose mass faster than the process considered
here would predict (Li et al. 2010).
An interesting case is that of Corot-7b. If this planet were made of gas, its whole mass
would be evaporated within ≲5 Gyr for η ≳ 0.15. Considering that Corot-7b
is probably made of rock (Léger et al. 2009, 2011; Queloz et al. 2009), this means that the atmosphere of this planet could have been completely
evaporated. This would make Corot-7b the first evaporation remnant detected. Possible
origins of Corot-7b are discussed by Jackson et al. (2010). These authors conclude that this planet could have indeed started with a
gas envelope, whose total mass should have been <2/3 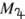 .
.
 |
Fig. 5 The “integrated” energy diagram for 98 transiting planets: the energy needed to escape the whole planet mass versus the X/EUV energy received per billion year. The dotted lines represent constant lifetimes of 1, 5, and 10 Gyr (from bottom to top). Data points are calculated with η = 0.15. Variations of η between 0.01 and 1 are represented as horizontal grey error bars. |
6. Conclusion
We have calculated mass-loss rates for transiting exoplanets using an energy diagram. This approach assumes that mass loss occurs as a consequence of a massive stellar irradiation. Mass-loss rates for the complete sample of transiting planets are found between 106 and 1013 g s-1. This (wide) range encompasses all possible values of the atmospheric heating efficiency.
We showed that measurements of the heating efficiency can be constrained in a power diagram when the mass-loss rate, derived from observations of evaporating atmospheres, and the X/EUV flux are both estimated. At the present time, it is only possible to spot two planets in this diagram. While the precision on heating efficiency is limited by the estimation of the mass-loss rate, we showed how it could be possible to infer exospheric properties, such as relative abundances, out of more precise measurements. In particular, simultaneous transit observations in UV and X-rays, feasible with current space instrumentation, will bring stronger constraints on the atmospheric heating efficiencies.
The mass-loss rates are used to determine the lifetimes of evaporating planets. We have found that few planets have lifetimes below 1 Gyr but this requires a highly efficient heating with η ~ 1.
Online material
Properties of known transiting planets and their host stars.
Acknowledgments
We thank the anonymous referee of this work. We are grateful to Alain Lecavelier des Etangs for all the discussions and advice about this work. We also thank Alfred Vidal-Madjar and Peter Wheatley for inspiration, and Jorge Sanz-Forcada for kindly providing us with updated X-ray flux measurements. D.E. is supported by the Centre National d’Études Spatiales (CNES).
References
- Anderson, D. R., Gillon, M., Hellier, C., et al. 2008, MNRAS, 387, L4 [NASA ADS] [Google Scholar]
- Anderson, D. R., Hellier, C., Gillon, M., et al. 2010, ApJ, 709, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Pat, S. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Noyes, R. W., Kovács, G., et al. 2007a, ApJ, 656, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Kovács, G., Torres, G., et al. 2007b, ApJ, 670, 826 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Shporer, A., Pál, A., et al. 2007c, ApJ, 671, 173 [Google Scholar]
- Bakos, G. Á., Pál, A., Torres, G., et al. 2009a, ApJ, 696, 1950 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Howard, A. W., Noyes, R. W., et al. 2009b, ApJ, 707, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Torres, G., Pál, A., et al. 2010a, ApJ, 710, 1724 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Hartman, J., Torres, G., et al. 2010b, ApJ, submitted [arXiv:1008.3388] [Google Scholar]
- Baraffe, I., Selsis, F., Chabrier, G., et al. 2004, A&A, 419, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., et al. 2005, A&A, 436, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Alibert, Y., Chabrier, G., & Benz, W. 2006, A&A, 450, 1221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barros, S. C. C., Faedi, F., Collier Cameron, A., et al. 2011, A&A, 525, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barge, P., Baglin, A., Auvergne, M., et al. 2008, A&A, 482, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Batalha, N. M., Borucki, W. J., Bryson, S. T., et al. 2011, ApJ, 729, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Bonomo, A., Santerne, A., Alonson, R., et al. 2010, A&A, 520, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bordé, P., Bouchy, F., Deleuil, M., et al. 2010, A&A, 520, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D. G., Brown, T. M., et al. 2010, ApJ, 713, L126 [NASA ADS] [CrossRef] [Google Scholar]
- Bouchy, F., Pont, F., Santos, N. C., et al. 2004, A&A, 421, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Udry, S., Mayor, M., et al. 2005, A&A, 444, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Queloz, D., Deleuil, M., et al. 2008, A&A, 482, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Hebb, L., Skillen, I., et al. 2010, A&A, 519, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, T. M., Charbonneau, D., Gilliland, R. L., Noyes, R. W., & Burrows, A. 2001, ApJ, 552, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Buchhave, L. A., Bakos, G. Á., Hartman, J. D., et al. 2010, ApJ, 720, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Burke, C. J., McCullough, P. R., Valenti, J. A., et al. 2007, ApJ, 671, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, R. P., Vogt, S. S., Marcy, G. W., et al. 2004, ApJ, 617, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrera, J., Bruntt, H., Ollivier, M., et al. 2010, A&A, 522, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cecchi-Pestellini, C., Ciaravella, A., Micela, G., et al. 2009, A&A, 496, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonneau, D., Berta, Z. K., Irwin, J., et al. 2009, Nature, 462, 891 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Christian, D. J., Gibson, N. P., Simpson, E. K., et al. 2009, MNRAS, 392, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Christiansen, J. L., Ballard, S., Charbonneau, D., et al. 2011, ApJ, 726, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Collier Cameron, A., Bouchy, F., Hébrard, G., et al. 2007, MNRAS, 375, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Collier-Cameron, A., Guenther, E., Smalley, B., et al. 2010, MNRAS, 407, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, T. A., & Wheatley, P. J. 2009, MNRAS, 396, 1012 [NASA ADS] [CrossRef] [Google Scholar]
- Deeg, H. J., Moutou, C., Erikson, A., et al. 2010, Nature, 464, 384 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Deleuil, M., Deeg, H. J., Alonso, R., et al. 2008, A&A, 491, 889 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dunham, E. W., Borucki, W. J., Koch, D. G., et al. 2010, ApJ, 713, L136 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenreich, D., Lecavelier des Etangs, A., Vidal-Madjar, A., et al. 2008, A&A, 483, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ehrenreich, D., Lecavelier des Etangs, A., & Delfosse, X. 2011, A&A, 529, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Enoch, B., Collier Cameron, A., Anderson, D. R., et al. 2011, MNRAS, 410, 1631 [NASA ADS] [Google Scholar]
- Fossati, L., Haswell, C. A., Froning, C. S., et al. 2010, ApJ, 714, L222 [NASA ADS] [CrossRef] [Google Scholar]
- Fridlund, M., Hébrard, G., Alonso, R., et al. 2010, A&A, 512, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gandolfi, D., Hébrard, G., Alonso, R., et al. 2010, A&A, 524, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Muñoz 2007, Planet. Space Sci., 55, 1426 [NASA ADS] [CrossRef] [Google Scholar]
- Gillon, M., Anderson, D. R., Triaud, A. H. M. J., et al. 2009, A&A, 501, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Hatzes, A., Csizmadia, Sz., et al. 2010, A&A, 520, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Torres, G., et al. 2009, ApJ, 706, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Sato, B., et al. 2011a, ApJ, 726, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Kipping, D., et al. 2011b, ApJ, 728, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Hebb, L., Collier Cameron, A., Lœillet, B., et al. 2009, ApJ, 693, 1920 [NASA ADS] [CrossRef] [Google Scholar]
- Hebb, L., Collier Cameron, A., Triaud, A. H. M. J., et al. 2010, ApJ, 708, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Hébrard, G., Bouchy, F., Pont, F., et al. 2008, A&A, 488, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hellier, C., Anderson, D. R., Collier Cameron, A., et al. 2009a, Nature, 460, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C., Anderson, D. R., Gillon, M., et al. 2009b, ApJ, 690, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C., Anderson, D. R., Collier Cameron, A., et al. 2010, ApJ, 723, L60 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, M. J., Fabrycky, D. C., Daniel, C., et al. 2010, Science, 330, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Holmström, M., Ekenbäck, A., Selsis, F., et al. 2008, Nature, 451, 970 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Howard, A. W., Bakos, G. Á., Hartman, J., et al. 2010, ApJ, submitted [arXiv:1008.3898] [Google Scholar]
- Jackson, B., Miller, N., Barnes, R., et al. 2010, MNRAS, 407, 910 [NASA ADS] [CrossRef] [Google Scholar]
- Jaritz, G. F., Endler, S., Langmayr, D., et al. 2005, A&A, 439, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jenkins, J. M., Borucki, W. J., Koch, D. G., et al. 2010, ApJ, 724, 1108 [NASA ADS] [CrossRef] [Google Scholar]
- Johns-Krull, C. M., McCullough, P. R., Burke, C. J., et al. 2008, ApJ, 677, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Joshi, Y. C., Pollacco, D., Collier Cameron, A., et al. 2008, MNRAS, 392, 1532 [Google Scholar]
- Kashyap, V. L., Drake, J. J., & Saar, S. H. 2008, ApJ, 687, 1339 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M., Bakos, G. Á., Hartman, J. D., et al. 2010, ApJ, 725, 2017 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, D. G., Borucki, W. J., Rowe, J. F., et al. 2010, ApJ, 713, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Kovács, G., Bakos, G. Á., Hartman, J. D., et al. 2010, ApJ, 724, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Lammer, H., Selsis, F., Ribas, I., et al. 2003, ApJ, 598, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Lammer, H., Odert, P., Leitzinger, M., et al. 2009, A&A, 506, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Latham, D. W., Bakos, G. Á., Torres, G., et al. 2009, ApJ, 704, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Latham, D. W., Borucki, W. J., Koch, D. G., et al. 2010, ApJ, 713, L140 [NASA ADS] [CrossRef] [Google Scholar]
- Laughlin, G., Wolf, A., Vanmunster, T., et al. 2005, ApJ, 621, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Lecavelier des Etangs, A. 2007, A&A, 461, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lecavelier des Etangs, A., Vidal-Madjar, A., McConnell, J. C., & Hébrard, G. 2004, A&A, 418, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lecavelier des Etangs, A., Ehrenreich, D., Vidal-Madjar, A., et al. 2010, A&A, 514, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Léger, A., Rouan, D., Schneider, J., et al. 2009, A&A, 506, 287 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Léger, A., Grasset, O., Fegley, B., et al. 2011, Icarus, accepted [arXiv:1102.1629] [Google Scholar]
- Li, S., Miller, N., Lin, D. N. C., & Fortney, J. J. 2010, Nature, 463, 1054 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lin, D. N. C., Bodenheimer, P., & Richardson, D. C. 1996, Nature, 380, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Linsky, J. L., Yang, H., France, K., et al. 2010, ApJ, 717, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, T. A., Anderson, D. R., Gillon, M., et al. 2009, ApJ, 703, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L., Anderson, D. R., Gillon, M., et al. 2010, AJ, 140, 2007 [NASA ADS] [CrossRef] [Google Scholar]
- McCullough, P. R., Stys, J. E., Valenti, J. A., et al. 2006, ApJ, 648, 1228 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- McCullough, P. R., Burke, C. J., Valenti, J. A., et al. 2008, ApJ, submitted [arXiv:0805.2921] [Google Scholar]
- Moutou, C., Bruntt, H., Guillot, T., et al. 2008, A&A, 488, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moutou, C., Hébrard, G., Bouchy, F., et al. 2009, A&A, 498, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murray-Clay, R. A., Chiang, E. I., & Murray, N. 2009, 693, 23 [Google Scholar]
- Noyes, R. W., Bakos, G. Á., Torres, G., et al. 2008, ApJ, 673, 79 [Google Scholar]
- Pál, A., Bakos, G. Á., Torres, G., et al. 2008, ApJ, 680, 1450 [NASA ADS] [CrossRef] [Google Scholar]
- Pál, A., Bakos, G. Á., Fernandez, J., et al. 2009, ApJ, 700, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Pillitteri, I., Wolk, S. J., Cohen, O., et al. 2010, ApJ, 722, 1216 [NASA ADS] [CrossRef] [Google Scholar]
- Poppenhaeger, K., Robrade, J., Schmitt, J. H. M. M., et al. 2010, A&A, 515, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pont, F., Bouchy, F., Queloz, D., et al. 2004, A&A, 426, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Queloz, D., Eggenberger, A., Mayor, M., et al. 2000, A&A, 359, L13 [NASA ADS] [Google Scholar]
- Queloz, D., Bouchy, F., Moutou, C., et al. 2009, A&A, 506, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Queloz, D., Anderson, D. R., Collier Cameron, A., et al. 2010, A&A, 517, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quinn, S. N., Bakos, G. Á., Hartman, J., et al. 2010, ApJ, submitted [arXiv:1008.3565] [Google Scholar]
- Rauer, H., Queloz, D., Csizmadia, Sz., et al. 2009, A&A, 506, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reiners, A., Basri, G., & Browning, M. 2009, ApJ, 692, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Sanz-Forcada, J., Ribas, I., Micela, G., et al. 2010, A&A, 511, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanz-Forcada, J., et al. 2011, A&A, submitted [Google Scholar]
- Sato, B., Fischer, D. A., Henry, G. W., et al. 2005, ApJ, 633, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Saumon, D., Chabrier, G., & Van Horn, H. M. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, J. 2010, The extrasolar planets encyclopædia, http://exoplanet.eu [Google Scholar]
- Schporer, A., Bakos, G. Á., Bouchy, F., et al. 2009, ApJ, 690, 1393 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, E. K., Faedi, F., Barros, S. C. C., et al. 2011, AJ, 141, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Skillen, I., Pollacco, D., Collier Cameron, A., et al. 2009, A&A, 502, 391 [Google Scholar]
- Smalley, B., Anderson, D. R., Collier Cameron, A., et al. 2011, A&A, 526, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snellen, I. A. G., Koppenhoefer, J., & van der Burg, R. F. J. 2009, A&A, 497, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stone, J. M., & Proga, D. 2009, ApJ, 694, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Street, R. A., Simpson, E., Barros, S. C. C., et al. 2010, ApJ, 720, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Sozzetti, A., Torres, G., Charbonneau, D., et al. 2009, ApJ, 691, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, F., Toon, O. B., Pavlov, A. A., et al. 2005, ApJ, 621, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G. 2007, ApJ, 671, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Bakos, G. Á., Kovács, G., et al. 2007, ApJ, 666, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Bakos, G. Á., Hartman, J., et al. 2010, ApJ, 715, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Fressin, F., Batalha, N. M., et al. 2011, ApJ, 727, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Valencia, D., Ikoma, M., Guillot, T., & Nettelmann, N. 2010, A&A, 516, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vidal-Madjar, A., Lecavelier des Etangs, A., Désert, J.-M., et al. 2003, Nature, 422, 143 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Vidal-Madjar, A., Désert, J.-M., Lecavelier des Etangs, A., et al. 2004, ApJ, 604, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal-Madjar, A., Lecavelier, A., Désert, J.-M., et al. 2008, ApJ, 676, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, A. J., Donahue, T. M., & Walker, J. C. G. 1981, Icarus, 48, 150 [NASA ADS] [CrossRef] [Google Scholar]
- West, R. G., Collier Cameron, A., Hebb, L., et al. 2009, A&A, 502, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, D. M., Gillon, M., Hellier, C., et al. 2008, ApJ, 675, 113 [Google Scholar]
- Winn, J. N., Holman, M. J., Henry, G. W., et al. 2007, AJ, 133, 1828 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Holman, M. J., Henry, G. W., et al. 2009, ApJ, 693, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, B. E., Brown, A., Linsky, J. L., et al. 1994, ApJS, 93, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Yelle, R. 2004, Icarus, 170, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Yelle, R. 2006, Icarus, 183, 508 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Multiple X-ray detection reports in the literature for stars hosting transiting planets.
All Figures
 |
Fig. 1 The energy diagram for 98 transiting planets: the energy needed to escape a unit of mass of the planet atmosphere versus the X/EUV flux reaching the top of the atmosphere per unit of time. The dotted lines indicate constant mass loss rates of ṁ = 1015 to 105 g s-1 (from left to right). Data points are calculated with η = 15%. Variations of η between 1% and 100% are represented with horizontal grey error bars. Coloured points and labels indicate transiting planets of particular interest, which are discussed in the text. |
| In the text | |
 |
Fig. 2 Mass-loss rate (η = 0.15) as a function of the planet mass for 98 transiting planets. The vertical error bars represent a variation of η from 0.01 (lower values) to 1 (higher values). Planets of interest are coloured accordingly to Fig. 1. |
| In the text | |
 |
Fig. 3 The energy diagram for 35 transiting planets with X-ray emission detections or upper limits (arrows) reported in the literature. Caption is the same as for Fig. 1. Data points are calculated with η = 15%. Planets of interest are outlined with different colours. |
| In the text | |
 |
Fig. 4 The power diagram for evaporating extrasolar planets. The “mass-loss power” Lṁ (Eq. (5)) is plotted as a function of the X/EUV luminosity. Constant η values are represented by the dotted lines. The hatched regions show the position of HD 189733b (orange) and HD 209458b (crimson). For HD 209458b, the right-pointing arrow shows the upper limit on the X/EUV luminosity reported by Sanz-Forcada et al. (2011). |
| In the text | |
 |
Fig. 5 The “integrated” energy diagram for 98 transiting planets: the energy needed to escape the whole planet mass versus the X/EUV energy received per billion year. The dotted lines represent constant lifetimes of 1, 5, and 10 Gyr (from bottom to top). Data points are calculated with η = 0.15. Variations of η between 0.01 and 1 are represented as horizontal grey error bars. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


