| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 25 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201016317 | |
| Published online | 14 March 2011 | |
Spectral optical monitoring of 3C 390.3 in 1995–2007
II. Variability of the spectral line parameters⋆
1 Astronomical Observatory, Volgina 7, 11160 Belgrade 74, Serbia
e-mail: lpopovic@aob.rs
2 Isaac Newton Institute of Chile, Yugoslavia Branch
3
Special Astrophysical Observatory of the Russian AS, Nizhnij Arkhyz, 369167 Karachaevo-Cherkesia, Russia
4
Department of Astronomy, Faculty of Mathematics, University of Belgrade, Studentski trg 16, 11000 Belgrade, Serbia
5
Institut für Astrophysik, Friedrich-Hund-Platz 1, Göttingen, Germany
6
Instituto Nacional de Astrofísica, Óptica y Electrónica, Apartado Postal 51, CP 72000, Puebla, Pue, Mexico
7
Sternberg Astronomical Institute, Moscow, Russia
8
Aalto University Metsähovi Radio Observatory, Metsähovintie 114, 02540 Kylmälä, Finland
Received: 14 December 2010
Accepted: 24 January 2011
Context. We present a study of the variability of the broad emission-line parameters of 3C390.3, an active galaxy with the double-peaked emission-line profiles. We give a detailed analysis of the variation in the broad Hα and Hβ emission-line profiles, the ratios, and the Balmer decrement of different line segments.
Aims. We explore the disk structure with an investigation of the variability of the broad-line profiles. This is assumed to emit the broad double-peaked Hβ and Hα emission lines in the spectrum of 3C390.3.
Methods. We divided the observed spectra into two periods (before and after the outburst in 2002) and separately analyzed the variation in these two periods. First we analyzed the spectral emission-line profiles of the Hα and Hβ lines and measured the peak positions. Then, we divided the lines into several segments and measured the line-segment fluxes. The Balmer decrement variation for the entire Hα and Hβ fluxes and for the line segments was investigated and discussed. Additionally, we modeled the variations in the line parameters with an accretion disk model and compared our modeled line parameter variations with observed ones.
Results. We compared the variability in the observed line parameters with the disk model predictions and found that the variation in line profiles and in the line segments corresponds to the emission of a disk-like broad-line region (BLR). But there is probably another additional emission component that contributes to the Hα and Hβ line center. We found that the variation in the line profiles is caused by the variation in the parameters of the disk-like BLR, first of all in the inner (outer) radius, which can well explain the line parameters variations in Period I. The Balmer decrement across the line profile has a bell-like shape and is affected not only by physical processes in the disk, but also by different emitting disk dimension of the Hα and Hβ line.
Conclusions. The geometry of the BLR of 3C390.3 seems to be very complex, and inflows/outflows may be present, but evidently the broad-line region with its disk-like geometry is the dominant emitter.
Key words: galaxies: active / quasars: individual: 3C 390.3 / line: profiles
Tables 3–5, Figs. 2, 3, 8, 11, and complement of Fig. 17 are only available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
The broad emission lines (BELs) are often observed in optical and ultraviolet spectra of active galactic nuclei (AGN). The study of the profiles and intensities of BELs can give us relevant information about the geometry and physics of the broad-line region (BLR). The physics and geometry of the BLR are uncertain, and an investigation of the BEL shape variability in a long period is very useful for determining the BLR nature. The profiles of the BELs in AGN can indicate the geometry of emitting plasma in the BLR (see Sulentic et al. 2000; Popović et al. 2004; Gaskell 2009; Zamfir et al. 2010, etc.).
Particularly interesting objects are AGNs with unusual broad emission-line profiles, where broad Balmer lines show double peaks or double “shoulders”, so called double-peaked emitters. The double-peaked line profiles may be caused by an accretion disk emission. On the other hand, the presence of an accretion-disk emission in the BLR is expected, and double-peaked line profiles of some AGN indicate this (Perez et al. 1988; Eracleous & Halpern 1994, 2004; Eracleous et al. 2009). One of the well known AGN with broad double-peaked emission lines in its spectrum is the radio-loud active galaxy 3C 390.3. Although the double-peaked line profiles can be explained by different hypotheses (see e.g. Veilleux & Zheng 1991) such as e.g. super-massive binary black holes (Gaskell 1996) or outflowing bi-conical gas streams (Zheng 1996), it seems that in this case there is a disk emission from the BLR (Shapovalova et al. 2010, hereafter Paper I). There is a possibility that a jet emission can affect the optical emission in 3C 390.3 (Arshakian et al. 2010), and there could be some perturbations in disk (Jovanović et al. 2010), which can affect the double-peaked line profiles as well.
Long-term variability in the line/continuum flux and in the line profiles is observed in objects with broad double-peaked lines (see e.g. Dietrich et al. 1988; Shapovalova et al. 2001; Sergeev et al. 2002, 2010; Shapovalova et al. 2010; Lewis et al. 2010). Long-term variability of broad-line profiles is intriguing because it is usually unrelated to more rapid changes in the continuum flux, but is probably related to physical changes in the accretion disk, such as e.g. brightness of some part of the disk, or changes in the disk size and distance to the central black hole. The double-peaked broad-line profile-variability can be exploited to test various models for the accretion disk (as e.g. circular or elliptical). Moreover, the double-peaked broad-line studies can provide important information about the accretion disk, such as e.g. inclination, dimension, and emissivity of the disk as well as probes of dynamical phenomena that may occur in the disk (for more detail see Eracleous et al. 2009, and references therein).
In Paper I we presented the results of the long-term (1995–2007) spectral monitoring of 3C 390.3. We analyzed the light curves of the broad Hα and Hβ line fluxes and the continuum flux in the 13-year period. We also found that quasi-periodical oscillations (QPO) may be present in the continuum and Hβ light curves. We studied averaged profile of the Hα and Hβ line in two periods (Period I from 1995 to 2002, and Period II from 2003 to 2007) and their characteristics ( such as e.g. peaks separation and their intensity ratio, or FWHM). From the cross-correlations (ICCF and ZCCF) between the continuum flux and Hβ and Hα lines we found a lag of ~95 days for Hβ and ~120 days for Hα (see Paper I for details). We concluded that the broad emission region has a disk-like structure, but there could probably also be an additional component, non-disk or also disk-like, with different parameters that contributes to the line emission. We found differences in the Hα and Hβ line profiles before and after the beginning of the activity phase in 2002, consequently we divided our spectra into two periods (before March 05, 2002 – Period I and after that – Period II, see Paper I).
In this paper we study in more detail the Hα and Hβ line profiles and ratios, taking into account the changes during the monitoring period. The aim of this paper is to investigate the changes in the the BLR structure of 3C 390.3 that cause the line profile variations. To perform this investigation we analyzed the peak separation variations, variations in line segments and variations in the Balmer decrement. With a relatively simple disk model, we try to qualitatively explain the changes in disk structure that can cause the variations in the line parameters.
The paper is organized as follow: in Sect. 2 we describe of our observations; in Sect. 3 we present the analysis of the Hα and Hβ line profiles variability, the peak-velocity variability and the Balmer decrement; in Sect. 4 we study the line-segment variations; in Sect. 5 the Balmer decrement variation is analyzed; in Sect. 6 we discuss the obtained results, and finally in Sect. 7 we outline our conclusions.
2. Observations
In 1995–2007 spectra of 3C 390.3 were taken with the 6 m and 1 m telescopes of the SAO RAS and with INAOE’s 2.1 m telescope of the Guillermo Haro Observatory (GHO) at Cananea, Sonora, México. They were acquired using long-slit spectrographs, equipped with CCD detector arrays. The typical wavelength interval covered was from 4000 Å to 7500 Å, the spectral resolution varied between (4.5–15) Å. The spectra were scaled using the [O iii] λλ4959+5007 (for blue spectra) and the [OI]6300A (for red spectra) integrated line flux under the assumption that fluxes of these lines did not change during the time interval of our observations (1995–2007). The narrow components of Hα and Hβ were removed by applying the modified method of Van Groningen & Wanders (1992) (see also Shapovalova et al. 2004) using the spectral template for narrow components as reference spectrum. More details about the observations can be found in Paper I.
3. Analysis of the broad-line profiles
In Paper I we explained the continuum- and narrow-line subtraction that we performed to obtain only the broad Hα and Hβ line profiles, and here we will not repeat this explanation. With the broad-line component only we now analyze the line parameters: month- and year-averaged line profiles (see Figs. 1–3), the position (and separation) of prominent peaks, the fluxes of the line segments and the Hα/Hβ ratios (or Balmer decrement – BD). In this section we first analyze the observed broad-line parameters and then the corresponding modeled line parameters, which we obtained with an accretion-disk model to learn about changes in the disk structure that may cause the line-parameter variability.
 |
Fig. 1 Month-averaged profiles of the Hα and Hβ broad emission lines in the period 1995–2007. The abscissa (OX) shows radial velocities with respect to the narrow component of the Hα or Hβ line. The ordinate (OY) shows the line flux in units of 10-16 erg cm-2 s-1 Å-1. |
 |
Fig. 4 Hα vs. Hβ peak velocity for the central (top), blue (middle) and red (down) peak. The dashed line represents the expected function for an equal peak position in both lines, while solid line represents the best fit of the measured data. |
 |
Fig. 5 Annual averaged radial velocities of the blue peak. The different symbols represent: stars – the Hβ data from Gaskell (1996), open squares – the Hβ measurements given in Veilleux & Zheng (1991), year-averaged to match other data, full circles – the Hα data from Eracleous et al. (1997), open and full triangles – our data for Hβ and Hα, respectively. |
As reported in Paper I, there is a differences in the Hα and Hβ line profiles before and after the beginning of the activity phase in 2002. Therefore, we separately consider the line profiles obtained in the period before March 05, 2002 (Period I, JD 2 452 339.01, when was the minimum in Hβ) and after that date (Period II, see Paper I). We also found that the observations in 2001 and 2002 sometimes have similar characteristics to the data in Period II, therefore we marked these observations separately in some plots as 2001–2002.
3.1. The averaged profiles of the Hα and Hβ broad emission lines
We also reported in Paper I that the line profiles of Hα and Hβ were changing during the monitored period. In Fig. 1 we show the month- and in Figs. 2 and 3 the year-averaged profiles of the Hα and Hβ. As can be seen in Fig. 1, the line profiles of Hα (left) and Hβ (right) vary, showing clearly two and sometimes three peaks. Similar variations are visible in the year-averaged profiles (see Fig. 2 for Hα and Fig. 3 for Hβ). In both periods the blue peak is higher, which is expected for a relativistic accretion disk. The most interesting is the central peak at the zero velocity (clearly visible in 1995 and 1996), which may indicate perturbation in the disk or an additional emitting region. We found that this central peak (sometimes weaker) exists almost always during both periods, therefore we measured the position of the blue, the central, and the red peak. Our measurements are given in Table 1. Sometimes the red peak could not be properly measured (because it was too weak or even absent), thus in that case the measurements are not given in Table 1. The measurements show that the position of the peaks are changing, and as can be seen in Fig. 4, these changes are more prominent in the Hβ than in Hα line. The position of the blue peak varies around several hundred km s-1 (e.g. in Hα it is −3550 ± 250 km s-1, in Hβ −3500 ± 400 km s-1), while the position of the red peak has a higher variation (for Hα ~ + 5000 ± 1000 km s-1, and for Hβ ~ 5250 ± 1700 km s-1). This may indicate that the emission is coming relatively close to the central black hole.
There is a difference between the Hα and Hβ red- and blue-peak velocities (see Fig. 4), which can be expected owing to the stratification of the disk, i.e. the different dimensions of the disk region that emits Hα or Hβ. It is interesting that the central peak seems to stay at similar position in both lines, as we show in Fig. 4 (panel top), where the points nicely follow the linear bijection function (represented as dashed line). This could indicate that the central peak is connected with some kind of perturbation in a disk or an additional region that in the same way affects the Hβ and Hα line profiles. The so-called central peak was slightly shifted to the blue side (or close to the zero shift) in 1996–1997 (see Fig. 1), but after that this peak has been redshifted (between 1500 and 2500 km s-1).
Measurements of the peak position velocities (blue, central, red) from month-averaged Hα and Hβ profiles.
In order to compare the variability of the blue peak position during a longer period, we present in Fig. 5 our measurements for the blue peak position and measurements obtained by Veilleux & Zheng (1991), Gaskell (1996) and Eracleous et al. (1997). The estimates of the blue-peak position in the Hα line is more uncertain than in Hβ, owing to the substraction of the atmosphere B-band (Paper I), while Hβ is more uncertain in the red part due to subtraction of the [OIII] lines (see Sect. 4.1). As can be seen in Fig. 5, the measurements follow the previous observations well, and there is an increase of the blue-peak position velocity from 1970 to 1990 (1995), while after 1995, the the blue-peak position velocity is slightly decreasing.
 |
Fig. 6 Modeled line profiles for the Hα (top) and Hβ (bottom) lines for different disk parameters (noted in the plots). |
 |
Fig. 7 Difference between the blue- and red-peak velocities vs. the blue-peak velocity for the Hα (top) and Hβ line (bottom). The model parameters are marked with full squares, while observations are denoted with full circles. |
3.2. Simulation of the variations in the line parameters
One can fit the broad double-peaked line profiles to extract some disk parameters (see Eracleous & Halpern 1994, 2004; Flohic & Eracleous 2008; Lewis et al. 2010; Jovanović et al. 2010, etc.), but because here we have a huge set of observational data, we will use a simple model to simulate variations in different disk parameters and give some qualitative conclusions.
To qualitatively explain the changes in the disk structure that can cause the variations in the line parameters, we simulated the disk emission with a disk model introduced by Chen et al. (1989) and Chen & Halpern (1989). The model assumes a relativistic, geometrically thin and circular disk (see for more details Chen et al. 1989; Chen & Halpern 1989). In this model the relativistic effects are partly included and the limit of the inner radius is Rinn > 100 Rg (Rg = GM/c2 – gravitational radius), but the estimated inner radius for 3C 390.3 is significantly larger (see Flohic & Eracleous 2008). Consequently, the model of Chen et al. (1989) and Chen & Halpern (1989) can be properly used, i.e. it is not necessary to include a full relativistic calculation (as e.g. in Jovanović et al. 2010).
To obtain the double-peaked line profiles we generated a set of different disk-like line profiles. For the starting parameters of the Hα line we used the results of Flohic & Eracleous (2008). They obtained the following disk parameters from fitting the observed Hα line of 3C 390.3: the inner radius Rinn = 450 Rg, the outer radius Rout = 1400 Rg, the disk inclination i = 27deg, the random velocity in the disk σ = 1300 km s-1, with the emissivity r − q, where q = 3 is assumed. To model the parameters for the Hβ line, we took into account the results from Paper I: the dimension of the Hα emitting region is ~120 light days, and of Hβ is ~95 light days. Consequently we proportionally (95/120) rescaled the Hβ disk parameters for the outer radius (i.e. Rout = 1200 Rg), keeping other parameters as for the Hα disk. We assumed that the inner radius for both Hα and Hβ is the same. It is an approximation, but one may expect that the plasma conditions (temperature and density) are probably changing fast in the inner part of disk. At some distance from the black hole therefore, the plasma should be in a condition to emit Balmer lines (i.e. recombination stays effective). On the other hand, at larger distances from the black hole, the conditions in the plasma will be slowly changing (as a function of radius) and from some distance there may be significant emission in the Hα line and very weak (or absent) Hβ emission because of the different transition probabilities.
We also tested what the consequence would be when we change the disk emissivity in the models. We found that this has little influence on the double peaked line profiles (see also Bon et al. 2009).
To probe a different type of variability, we first considered that in a different time, a different part of the disk can contribute to the emission of the broad Hα and Hβ lines, i.e. we keep the relative size of the disk regions responsible for the emission of Hα and Hβ lines constant, but we changed the locations of these regions with respect to the central black hole. Then the emitting region can be closer, i.e. inner and outer radius are closer to the black hole. To obtain these models, we shifted the emitting region closer to the black hole for a step of ΔR = 50 Rg. This was performed by varying the inner and outer radius, keeping all other parameters constant (except for the random velocity, which was changed accordingly, but this has also little influence on the line profiles). In Fig. 6 we present the simulated line profiles. The range of the inner radius was Rinn = 250 − 600 Rg, where the broadest line in Fig. 6 corresponds to the Rinn = 250 Rg. Consequently, the outer radius was in the range of Rout = 1200 − 1550 Rg for Hα and Rout = 1000 − 1350 Rg for Hβ (see Fig. 6).
 |
Fig. 9 Line segment vs. line segment response. The observations in Period I are denoted with full circles and in Period II with open squares. The line-segment flux is in units 10-14 erg m-2 s-1. The Pearson correlation coefficient r and the null hypothesis value P0 are given in each plot for both periods. |
Beginning and ending radial velocities, Vbeg and Vend, for different segments in the line profiles of Hα and Hβ.
From the models we measured the velocities of the blue and red peak (Vblue and Vred). We could not obtain the central peak because as was mentioned above, it probably has a different origin. Either it originates outside of the disk, or it is caused by some disk perturbations.
To compare the modeled and observed values, we plot in Fig. 7 the difference between the blue- and read-peak velocities Vred − Vblue as a function of the blue-peak velocity for Hα (top) and Hβ line (bottom). The modeled values are presented as full squares. Figure 7 shows that the modeled values generally agree with the observed ones, which show a considerable scattering around the modeled trend however. It seems that the emission of the different parts of the disk in different epochs can explain the peak position variations. In this scenario, the line profile variability can be explained as follows: when the inner radius is closer to the central black hole, the separation between peaks stays larger and the blue peak is more blue-shifted, but when the inner radius is farther from the central black hole, the distance between peaks is smaller and the blue peak is shifted to the center of the line. Shapovalova et al. (2001) found the anticorrelation between the continuum flux and Vred − Vblue in the period 1995–1999.
 |
Fig. 10 Far blue (left) and far red (right) wings flux against the continuum-flux variation for Hβ (top) and Hα (down). The notation is the same as in Fig. 9. The Pearson correlation coefficient r and the null hypothesis value P0 are given in each plot for both periods. |
4. The Hα and Hβ line-segments variation
To see if there are any changes in the structure of the disk or disk like-region, we investigated the light curves for the different segments of the Hα and Hβ broad emission lines. First, we divided the line profiles along the velocity scale into nine segments. The size of the intervals is defined as 2000 km s-1 for segments from 0 to ± 3 and 3000 km s-1 for segment ± 4 (the segments and corresponding intervals are given in Table 2).
The observational uncertainties were determined for each segment of the Hα and Hβ light curves. In evaluating the uncertainties, we account for errors owing to the effect of the subtraction of the template spectrum (or the narrow components and continuum). We compared the fluxes of pairs of spectra obtained in the time interval from 0 to 2 days. In Table 3 we present the year-averaged uncertainties (in percent) for each segment of Hα and Hβ and the corresponding mean year-flux. We adopted the years for each line where the frequency and number of observations were sufficient to estimate error-bars. The mean values of uncertainties for all segments are also given. As one can see from Table 3, for the far wings (segments ± 4) the errorbars are greater (~30–50%) in Hβ than in Hα (~20%). But when comparing the errorbars in the far red and blue wings of each lines, we find that the errorbars are similar. Larger errorbars are also visible in the central part of the Hα owing to the narrow line subtraction.
Our measurements of line-segment fluxes for Hα and Hβ are given in Tables 4 and 5. The light curves for each segment of the Hα and Hβ lines are presented in Fig. 8, where we show blue part (crosses), red part (pluses), core (full circles), and continuum (solid line) in arbitrary units for comparison. As can be seen in Fig. 8, the fluxes from the 0 to ± 4 segments of both lines show a similar behavior during the monitored period. As a rule, the blue segments are brighter or equal to the red ones. Only in ± 4 in the period of 1997–1999 are the red segments brighter than the blue ones. The red and blue wings of Hβ in 1995–1997 show only little difference in brightness, while in 2006 the blue peak was about 30% brighter than the red one.
The variation in line segments of the Hα and Hβ are similar, and there are more observations of Hβ than of Hα. Below we will consider only the segment variation of the Hβ line, except for segments ± 4, where we consider both Hα and Hβ.
4.1. Line segment vs. line segment and continuum variations
We studied the response of symmetrical line segments (–4 vs. 4, etc.), and Fig. 9 shows that there is only a weak response from the far blue to the far red segment in Period I. We plotted the best linear fits for Period I and Period II and found that the correlation between the far wings (segment –4 vs. segment +4) has a negative tendency with low significance (the Pearson correlation coefficient r = −0.29, the null hypothesis value P0 = 0.13E-01), but in the Period II there is a linear response of the blue to the red wing with significant correlation (r = 0.84, P0 = 0.35E-15). In other segments, obviously the change in the blue wing in Period I was smaller than in the red one (Fig. 9). In Period I the flux of the far blue wing (–4) stays nearly constant, while the flux of the red part (+4) is increasing. Even if we consider Period I without the period 2001–2002, the correlation is weak and insignificant (r = 0.03, P0 = 0.84) and in favor of the previous statement.
To see whether there is a similar response of the line segments to the continuum flux, we constructed the plots in Figs. 10 and 11, where the flux of all segments against the continuum flux are presented. These figures show that there is a relatively good response of the line segments to the continuum flux (see plots for the values of the Pearson correlation coefficient r and the null hypothesis P0 for both periods). However, the line segments (± 4) (especially for the Hβ line (Fig. 10, top)) in Period I have a weak response (or even absent response, for segment +4) to the continuum flux. For example, the flux in the far red segment (Hβ +4) increases about 4–5 times without an increase of the continuum flux.
In the Hβ segment +4 one can expect higher errors owing to the subtraction of the bright [OIII] lines. As a consistency check, we plot in Fig. 10 (bottom) Hα (± 4) segment fluxes vs. continuum flux. Evidently the trend is similar to Hβ, and also in Period I the Hα segment (± 4) fluxes do not respond to the continuum flux. This may indicate that there are periods when some processes in the disk are not connected with the central continuum source.
 |
Fig. 12 Response of the line segments to the central segment 0 (from − 1000 to 1000 km s-1). The observations in Period I are denoted with full circles and in Period II with open squares. The line-segment flux is in units 10-14 erg m-2 s-1. The Pearson correlation coefficient r and the null hypothesis value P0 are given in each plot for both periods. |
 |
Fig. 13 Ratio between the blue-wing flux (two blue segments, −4 and −3) and the central segment as a function of the ratio of the red-wing (two red segments, +4 and +3) and the central segment. Observations in Period I are denoted with full circles, in Period II with open squares, while observations from 2001–2002 are denoted with open triangles. |
As mentioned above, there is a central peak that is probably coming from an additional emission region or is created by some perturbation in the disk. Therefore we plot in Fig. 12 the line-segment fluxes vs. the flux of the central line-segment 0 (measured between − 1000 and +1000 km s-1). Obviously there is a good correlation between the central line-segment flux and fluxes of other segments, but one can conclude that the responses were better in Period II. Thus, it seems that in this period both the disk-line and additional component effectively respond to the continuum variation. One can also see that the flux of the red part (segment +4) in Period I has a weak response to the central line-segment 0 (r = 0.58, P0 = 0.76E-07), which is similar to the segment and continuum flux correlation (Fig. 10). This may have the same physical reason, namely that some kind of perturbation in disk was present in Period I.
4.2. Modeling of the line-segment variation of the Hβ line
We used the same models as described in Sect. 3.2, but now measured the line-segments fluxes for the modeled lines, which are defined in the same way as for the observed lines. We plot in Fig. 13 the sum of the − 4 and − 3 segment fluxes as a function of the sum of the +4 and +3 segment fluxes normalized on the central 0 segment, i.e. Fblue wing = [F(− 4) + F(−3)] /F(0) vs. Fred wing = [F(+ 4) + F(+ 3)] /F(0).
Observations in Period I are denoted with full circles and in Period II with open squares (see Fig. 13). We also see that observations in 2001 and 2002 are closer to the Period II, so we denoted these with open triangles. It is interesting that in the first period a good correlation between Fblue wing and Fred wing is present. The modeled Fblue wing vs. Fred wing relation, marked with full triangles, appears to follow the trend of the observed points in Period I, but is shifted below the observed correlation pattern. To find the causes for this disagreement, we measured the shift of the Hβ averaged profiles for two periods (given in Paper I) with respect to the averaged profile constructed from the modeled profiles (for different positions of the Hβ emitting disk). We measured the shift at the center of the width of the Hβ line at half maximum and at 20% of the maximum. We found that the shift of the modeled average profile is +900 km s-1 at 20% of the maximum and +600 km s-1 at half maximum, while the measurements for Period I are ~+700 km s-1 at 20% of the maximum and ~+110 km s-1 at half maximum. In Period II the observed averaged Hβ line was more blue-shifted with respect to the modeled one. We found ~+310 km s-1 at 20% of the maximum and ~ −330 km s-1 at half maximum. Therefore we simulated the segment variation (Fig. 13) taking into account that the whole disk line is blue-shifted by 300 km s-1 (open circles in Fig. 13), and 850 km s-1 (diamonds in Fig. 13). Figure 13 shows the modeled values, which well fit the observations from Period I (line blue-shifted for 300 km s-1) and Period II (line blue-shifted for 800 km s-1). In Period I there are changes in the location of disk regions responsible for the lines emission (from Rinn = 250 Rg to Rinn = 550 Rg), while in Period II, the inner disk radius appears to have been changed by a smaller amount (from 350 Rg to 450 Rg). This indicates that in the first period (excluding 2001–2002) the variability can be well explained by variation of the disk position with respect to the black hole, while in Period II and 2001–2002 (when outburst is starting), the disk position probably does not change so much. Apparently here the part of the disk emitting the broad lines has only become brighter.
4.3. 2D CCF of the Hβ line profiles
We now investigate in detail the cross-correlation function (CCF) of the line-profile variations of Hβ. We proceed in the same way as for the line-profile variations in Mrk 110 (Kollatschny & Bischoff 2002; Kollatschny 2003).
 |
Fig. 14 Maximum response of the correlation functions of the Hβ line segment light curves with the continuum light curve. |
 |
Fig. 15 Time delay of the individual line segments of Hβ for the first half of the observing period from 1995–2002 (filled squares) and for the second half from 2003–2007 (filled triangles) with respect to the continuum light curve in velocity space. |
Figure 14 shows the maximum response of the correlation functions of the Hβ line segment light curves with the continuum light curve, and Fig. 15 shows the delays of the individual Hβ line segments in velocity space. Figure 15 gives the delays of the individual line segments of Hβ separately for the two observing periods: from 1995–2002 (filled squares) and from 2003–2007 (filled triangles).
The outer blue- and red-line wings show the shortest delay, clearly indicating that the line emitting region is connected with an accretion disk (e.g. Welsh & Horne 1991; Horne et al. 2004). A careful inspection of the delays of the individual line segments in Fig. 15 indicates that a second trend is superimposed. An earlier response of the red-line wing compared with the blue-line wing is seen in Fig. 15 for the second half of the observing period. This behavior is consistent with the prediction from disk-wind models (Königl & Kartje 1994).
It is intriguing that the very broad-line AGN 3C 390.3 shows the same pattern in the velocity-delay maps as the narrow-line AGN Mrk 110 (see Kollatschny & Bischoff 2002; Kollatschny 2003). The outer red and blue wings respond much faster to continuum variations than the central regions.
 |
Fig. 16 Variations in the continuum flux at 5100 Å (first panel), in the Hα and Hβ line fluxes (second and third panel, respectively), and in the integral Balmer decrement BD = F(Hα)/F(Hβ) (fourth panel) of the month-averaged profiles. The abscissa (OX) gives the modified Julian date (bottom) and the corresponding year (top). The continuum flux is in units 10-15 erg m-2 s-1 Å-1 and line flux is in 10-13 erg m-2 s-1. The bottom panel gives the BD as a function of the continuum flux, where full circles denote the observations in Period I and open squares in Period II (see text). |
5. Balmer decrement (BD) variation
The ratio of Hα and Hβ depends on the physical processes in the BLR, and variations in the Balmer decrement (BD) during the monitored time can indicate changes in physical properties of the BLR. Using the month-averaged profiles of the broad Hα and Hβ lines, we determined their integrated fluxes in the range between − 10 000 and +10 000 km s-1 in radial velocity, i.e. the integrated flux ratio F(Hα)/F(Hβ) or integrated BD. In Fig. 16 we plot the time variation of the continuum flux, Hα and Hβ line fluxes and the BD. The BD reached its maximum in 2002 when the fluxes of lines and continuum were at the minimum. Figure 16 shows that there is no correlation between BD and line/continuum variation. But, as evident from the very bottom panel in Fig. 16, which shows separate BDs for two periods (full circles represent Period I, and open squares Period II), there is some tendency that the BD is higher for weaker continuum flux. When the BD is plotted versus the continuum flux (Fig. 16 bottom panel), a negative trend seems to be present below 1.75 × 10-15 erg cm-2 s-1 Å-1. For higher values of the flux the BD stays roughly constant. A similar BD behavior was observed by Sergeev et al. (2010).
 |
Fig. 17 Variations in the Balmer decrement (BD = Hα/Hβ) as a function of the radial velocity for month-averaged spectra of 3C 390.3. Upper panel represents BD from the period of 1995–1998, and bottom panel from 2007. These two panels are chosen because they represent the characteristic behavior of BD vs. velocity. The abscissa (OX) indicates the radial velocities with respect to the narrow components. The position of the blue, central and red peaks are marked with blue, black and pink line, for Hα (solid line) and Hβ (dashed line). The rest of the panels are available electronically only. |
5.1. The BD as function of the velocity along line profile
Furthermore, we investigated BDs for each line segment (as described in Sect. 4), and plots of the BD against velocity are presented in Fig. 17 (a part of this figure is available electronically only). Figure 17 shows some common features in the trends of the BD of the different line segments plotted vs. velocity over an extended period of time, from 1995 to 2007. For example, for almost all observations there is a minimum in the far blue and red wings (around ±9000 km s-1) and two maxima in the red and blue part (around ± 6000 km s-1). There is also a central minimum (around 0 km s-1) that in 2001 and 2002 is moving to +2000 km s-1, while in 2005 and 2006 it moved to −2000 km s-1. From 2007 to the end of the monitoring period only a peak in the blue part (between −6000 to −4000 km s-1) is dominant, while the BD from −2000 to +6000 km s-1 tends to be constant with values between 3.5 and 4.5.
5.2. Modeling of the Balmer decrement
It is known that the BD depends on physical processes. But the BD as a function of the velocities along the line profile may also depend on the geometry of the Hα- and Hβ-emitting region. If the line emission region of Hα and Hβ are not the same, one may expect that the Hα and Hβ flux ratio will be a function of the gas velocity. Therefore, we modeled the shape of the BD vs. velocity.
In order to test the influence of the geometry to the BD vs. velocity along the line, we used modeled disk profiles (see Sect. 3.2), but now we consider two cases: a) the disk regions emitting Hα and Hβ have different sizes but the same inner radii that vary accordingly (as discussed in Sect. 3.2); b) the inner radius of the Hα-emitting region differ from the fixed radius of the Hβ region by ± 50 Rg, ±100 Rg.
 |
Fig. 18 Balmer decrement versus velocity. First two panels – the inner radius is the same, but different positions of the Hα and Hβ disk with respect to the black hole are assumed. The bottom panel shows the cases where the one of the two emitting regions is closer to the central black hole. The inner and outer radii assumed in models are labeled in each panel. The BD points are normalized to the one at − 4000 km s-1. |
Our simulations of the BD vs. velocity are given in Fig. 18, which shows that the disk model (assuming different dimensions of the emission disk that emits Hα and Hβ) can reproduce very similar BD profiles along the velocity field, especially as they are observed in Period I. There is a difference in shape that is probably caused by the physical conditions in the disk and is caused by the central component emission. We found bell-like profiles of the BD, which also have two peaks (in the red and blue part) and a small minimum in the center. The shape of the BD vs. velocity observed in Period II, where a peak in the blue part is prominent (see Fig. 17) and in some cases has a deeper red minimum than the blue one, cannot be obtained by modeling the BD vs. velocity. This may be because of the influence of the central component, but also because of the outburst in Period II, or possibly due to different physical processes in the disk.
As can be seen from Fig. 18 (bottom panel, open squares), a big difference between the modeled BD vs. velocity and observed one appears where the Hα emitting region is closer to the black hole by 100 Rg. This indicates that the disk part that emits Hα cannot be significantly closer to the central black hole than the one that emits the Hβ line.
6. Discussion
We performed a detailed study of the variations in the line parameters (peak separation, variation of the line segments, Balmer decrement) during a 13-year long period. As we noted above, the line profiles of the 3C 390.3 in the monitoring period have a disk-like shape, i.e. there are mainly two peaks, of which the blue one is more enhanced. In some periods, there is a central peak, which probably originates in an additional emission region or extra emission caused by some perturbation in the disk (see e.g. Jovanović et al. 2010). In order to confirm the disk emission hypothesis we modeled the peak position variation with a semi-relativistic model, and found that peak position variations can be explained with the disk model.
We also investigated line-segment flux variation and found that the ratios of the line segments are well fitted by a disk model. The response of the line-segment flux to line-segment flux is better in Period II than in Period I. The same is true for the response of the segment fluxes to the continuum flux. It seems that in Period I, the variability in the line profile was not caused only by an outburst in the ionizing continuum, but also by some perturbations in the accretion disk (see e.g. Jovanović et al. 2010). In Period II though, it could be that the disk structure remains essentially the same and that the variability in the line parameters is primarily caused by the outburst in the continuum.
The Balmer decrement as a function of the continuum has a decreasing trend in Period I (with the increase of the continuum) and is constant in Period II. Moreover, there is a different shape of the BD vs. velocity in different periods. The characteristic shape of the BD vs. velocity has two peaks (blue and red) that do not correspond to the line peaks (they are in the far wings, see Fig. 17), there are minima in the far blue and red wing, as well as a minimum in the center. The shape of the BD vs. velocity is similar to what we expect from an accretion disk, where the dimensions of the disk for Hα and Hβ are different. In the period (Period II) of the highest brighteners in the continuum and in lines, the BD vs. velocity shapes show a blue peak and a more or less flat red part, which is probably caused by some other emission in addition to that of the disk, and also by different physical conditions in these two sub-regions. Our modeled shapes of the BD vs. velocity show that a disk emission with different dimensions of the Hα- and Hβ-emitting disks, can explain bell-like shapes of the BD vs. velocity. We did not consider physical processes in the emitting disk that can affect the shape of the BD vs. velocity. Comparing the dimensions of the disk, we arrived at the same conclusion as we did from the CCF (see Paper I): the Hα-emitting disk is larger than the Hβ one, but the inner radius of both disks seems to be similar.
6.1. Variability and the BLR structure of 3C 390.3
Before we discuss the BLR structure, let us recall some results that we obtained in Paper I and in this paper: i) the CCF analysis shows that the dimension of the BLR that emits Hβ is smaller than one that emits Hα; ii) there is a possibility that there are quasi-periodic oscillations, which may be connected with the instability in the disk or disk-like emitting region; iii) concerning the line profile variations, the variability observed in 13-year period can be divided into two periods, before and after the outburst in 2002; iv) there are three peaks, two of which are expected in the disk emission, and one central one, that probably originates in disk perturbations or in an additional emitting region; v) the shapes of Hβ and Hα observed in the same period are similar, especially in Period I (in Period II there are differences in the center and red wings); vi) our simulation of the variability, taking into account only different disk position with respect to the central black hole, can qualitatively explain the observed broad-line parameters variations; vii) comparing the shifts of the modeled and the observed Hβ line, we found that there is a blue-shift in the observed Hβ compared with the modeled one, which is also different in two periods: around 300 km s-1 in Period I and around 850 km s-1 in Period II; viii) the inspection of the delays of the individual line segments (see Sect. 4.3) indicates a disk and also a wind, i.e. the disk-wind model may be applicable to the BLR of 3C 390.3.
Additionally, the disk-like structure of the 3C 390.3 BLR is favored in several recent papers (see e.g. Flohic & Eracleous 2008; Jovanović et al. 2010) assuming an elliptical disk (Flohic & Eracleous 2008) or perturbations in the disk (Jovanović et al. 2010).
Taking into account the above, one can speculate about the BLR structure and the nature of these variations. Let us consider that, in principle, there is an accreting material that is optically thick, and the light from a central source is able to photoionize only a small thin region above (below) the accreting material (or thick disk, see Fig. 19), let us call this region a “disk-like broad-line region” (disk-like BLR1). Emitting gas in this region has a disk-like motion, because it is located in the disk periphery and follows the disk kinematics. The brightness of the broad lines, which are coming from this region, will be caused by the central ionizing continuum source, but the line parameters will depend on the dimensions of the region as well as the location of the BLR1 with respect to the central black hole. Of course, other parameters such as emissivity or local velocity dispersion can slightly affect the line profiles, but it seems that the change in the inner/outer radius is the most important.
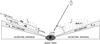 |
Fig. 19 Model of the BLR that is composed of the disk-like BLR1, and an outflowing/inflowing BLR2. |
The shape of the broad lines confirms the disk-like geometry, and the correlation between the broad-line and continuum fluxes confirms the influence of the central source on the line intensity (see Paper I). The optical continuum and the Hβ flux variations are probably related to changes in the X-ray emission that are modulated by variable accretion rate, i.e. the change of the surface temperature of the disk as a result of the variable X-ray irradiation (Ulrich 2000). But the question is, what can cause the changes in the dimension (as well in position) of the broad-line emitting region? Obviously it is not the continuum flux, because the variation in the continuum does not correlate with the line parameters variations.
The variation in the line parameters may be related to the perturbations in the accreting material that is feeding the disk-like BLR with scattered gas. The density and optical depth of this gas from the accreting material may cause in different epochs that the disk-like BLR has different dimensions and positions with respect to the central black holes. If scattered material (gas) of the accreting material is absent in some parts, it will affect the line parameters in a similar way as the change in the dimensions (position) of the disk-like BLR.
On the other hand, the observed broad double-peaked lines have a blue-shift with respect to the modeled one. This may indicate that there is some kind of wind in the disk, probably caused by the radiation of the central source. Recently Tombesi et al. (2010) performed a uniform and systematic search for the blueshifted Fe Kα absorption lines in the X-ray spectra of 3C 390.3 observed with Suzaku and detected absorption lines at energies higher than 7 keV. This implies that the origin of the Fe Kα is in the highly ionized outflowing gas with mildly relativistic velocities (in the velocity range from 0.04 to 0.15 light speed). Taking into account that the optical line emission is probably originating farther away than the X-ray, one can expect significantly lower outflow velocities in the optical lines.
One can expect that perturbations in the thick disk (or accreting material) will affect the emitting disk-like region. This may cause some perturbation or spiral shocks in the disk-like BLR (see e.g. Chakrabarti & Wiita 1994; Jovanović et al. 2010). Chakrabarti & Wiita (1994) found that the observed variability of the double-peaked broad emission lines (observed in some active galactic nuclei) can be caused by two-armed spiral shocks in the accretion disk. With this model they successfully fitted the observations of 3C 390.3 made at different epochs with self-similar spiral shock models that incorporate relativistic corrections.
Alternatively, Jovanović et al. (2010) fitted the observations of 3C 390.3 from different epochs with a model that includes moving perturbation across the disk. The perturbations/shocks in the disk model can explain different line profiles, and also the central peak (see e.g. Jovanović et al. 2010). But the central peak may be emitted from a broad-line region that does not follow the disk geometry, it may be very similar to the two-component model, i.e. we have composite emission from the disk and an additional region (see e.g. Popović et al. 2004; Ilić et al. 2006; Bon et al. 2009). Also, Arshakian et al. (2010) considered that the BLR of 3C390.3 has a complex structure composed of two components: 1) BLR1 – the traditional BLR (accretion disk), 2) BLR2 – a sub-region (outflow) that surrounds the compact radio jet. In this paper we suggest that there is a jet-excited outflowing BLR, which may question the general assumption of a virialized BLR.
The central component is present during the whole monitoring period, and that in 1995–1996 it was located at the center and later shifted to the red part of line. This redshift is not expected if there is an outflow in the BLR. But let us recall the results obtained in the study of dynamics of the line-driven disk-wind, where the kinematics of the gas show that both infall and outflow can occur in different regions of the wind at the same time (see Proga et al. 1998, 2000), which depends on radiation force. Also, recently Gaskell (2009) reported the possibility that an inflow is present in the BLR of AGN.
Finally, one can consider a model as proposed in Fig. 19: the disk-like BLR1 follows the kinematics of the accreting material, and from time to time perturbations can appear in this region (similar as in the fully accreting disk). The emitting gas in the BLR1 originates in (is ejected from) the accreting material and is ionized by the central source. The radiation pressure may contribute in a way that we have a wind (an outflow) in this region. There may also be a region above the disk-like BLR1 (a BLR2 in Fig. 19) where the ionized gas may be in motion with respect to the central black hole, and depending on the radiation pressure, the velocities are different in different periods.
6.2. Different nature of variation in broad lines of 3C 390.3
It is interesting to discuss the difference between the variation in Period I and Period II. It is obvious that the disk-parameters variation can explain the observed variations in the line parameters (as e.g. in the peak separation and line-segment fluxes variations). There were several quasi-periodical low-intensity outbursts in Period I (see Paper I), and it seems that the line, and consequently the disk-like geometrical parameters, is changed. It may be that in this period the outbursts are caused by some perturbations in the disk (in the inner part, which emits the X-ray radiation and in the outer part, which emits the broad lines). These perturbations affect the line profiles and probably partly the line fluxes (especially in the far wings). As modeled variations show, the inner/outer radius is significantly changed.
In Period II there is a strong outburst, which caused the increase of the brightness in the continuum and lines. The lines stay brighter, but the structure (inner/outer radius) of the disk-like region is not changing much. There is a different response of the continuum to the line segments in Period I and Period II, i.e. in Period II there is a higher correlation between the continuum and line-segment fluxes.
On the other hand, the BD in Period I has a decreasing trend with the increase of the continuum flux, while it stays almost constant in Period II. This may indicate the different nature of the variability. It seems that in Period I, beside the ionizing continuum influence on the line intensities (especially in the far wings), there was an additional effect that influenced the line profiles and intensities. It was probably caused by some perturbations or shocks in the disk-like BLR (Chakrabarti & Wiita 1994; Jovanović et al. 2010) that produced changes in the structure of the disk-like BLR.
7. Conclusions
We presented line profile variations of 3C 390.3 in a long period. Owing to the change of line profiles, we divided the observations into two periods (before and after the minimum in 2002: Period I and II, respectively) and found difference in the line segments and Balmer decrement variations in these two periods. From our investigation, the main conclusions are:
-
i)
The line profiles during the monitoring period are changing, always showing the disk-like profile with the more pronounced blue peak. There is also the central peak that may come from the emission region additional to the disk, but as it was mentioned in Jovanović et al. (2010), it may also be caused by the perturbation in the disk.
-
ii)
The far-wings flux variation in the first period, where the far-red wing flux does not respond well to the continuum flux, is probably caused by some physical processes in the innermost part of the disk. The observed changes in Hα and Hβ may be interpreted in the framework of a disk model with changes in the location and size of the disk line emitting regions. In Period II, the good correlation between the continuum and line-segment flux suggests that the brightness of the disk is connected with the ionizing continuum, and that the structure of the disk does not significantly change.
-
iii)
The Balmer decrement is also different for these two periods. In the first period the BD decreases with the continuum flux, while in the second period the BD stays more-less constant (around 4.5). The segment BD shows two maxima (around ± 6000 km s-1), which do not correspond to the red and blue peak, but instead are farther in the blue and red wing (than peaks velocities). One minimum around zero velocity is also present. This minimum changed position between ± 2000 km s-1 around zero velocity. This central minimum (as well as shifted maxima) may be caused by the additional emission that perhaps is present in the 3C 390.3 broad lines. These results suggest that in addition to the physical conditions across disk, the size of the Hα and Hβ emitting regions of the disk plays an important role. We modeled bell-like BD vs. velocity profiles in the case when the Hα disk is larger than Hβ one.
-
iv)
The variation observed in the line parameters can be well modeled if one assumes changes in position of the emitting disk with respect to the central black hole. The emission of the disk-like region is dominant, but there is the indication of the additional emission. Therefore, to explain the complex line-profile variability one should consider a complex model that may have a disk geometry together with outflows/inflows (see Fig. 19).
Online material
 |
Fig. 2 Year-averaged profiles (solid line) and their rms (dashed line) of the Hα broad emission line in 1995–2007. The abscissa (OX) shows the radial velocities with respect to the narrow component of the Hα line. The ordinate (OY) shows the flux in units of 10-16 erg cm-2 s-1 Å-1. |
 |
Fig. 8 Light curves for different segments of the Hα (top) and Hβ (bottom) broad emission lines. The line-segment fluxes are given in 10-14 and 10-15 erg cm-2 s-1 for Hα and Hβ, respectively, while the date is given in the modified Julian Date as MJD = JD-2400000.5. The mean velocity for the segment number is: (± 4) corresponds to (± 8500) km s-1; (± 3) corresponds to (± 6000) km s-1; (± 2) corresponds to (± 4000) km s-1; (± 1) corresponds to (± 2000) km s-1; 0 corresponds to (1000) km s-1. The blue part is denoted with crosses, the red part with pluses, and the line core with full circles. The solid line represents the continuum flux in arbitrary units for comparison. |
 |
Fig. 17 continued. |
 |
Fig. 17 continued. |
 |
Fig. 17 continued. |
The errors of measurements (e ± σ) for line segments of Hα and Hβ are given in percent.
The line-segment fluxes for Hα line in units 10-14 erg cm-2 s-1 Å-1.
The line-segment fluxes for Hβ line in units 10-14 erg cm-2 s-1 Å-1.
Acknowledgments
This work was supported by INTAS (grant N96-0328), RFBR (grants N97-02-17625 N00-02-16272, N03-02-17123, 06-02-16843, and N09-02-01136), State program “Astronomy” (Russia), CONACYT research grant 39560-F and 54480 (México) and the Ministry of Science and Technological Development of Republic of Serbia through the project Astrophysical Spectroscopy of Extragalactic Objects. L.Č.P., W.K. and D.I. are grateful to the Alexander von Humboldt fondation for support in the frame of program “Research Group Linkage”. We thank the anonymous referee for useful suggestions that improved the clarity of this manuscript.
References
- Arshakian, T. G., Len-Tavares, J., Lobanov, A. P., et al. 2010, MNRAS, 401, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Bon, E., Popović, L. Č., Gavrilović, N., La Mura, G., & Mediavilla, E. 2009, MNRAS, 400, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Chakrabarti, S. K., & Wiita, P. J. 1994, ApJ, 434, 518 ch94 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, K., & Halpern, J. P. 1989, ApJ, 344, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, K., Halpern, J. P., & Filippenko, A. V. 1989, ApJ, 339, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Dietrich, M., Peterson, B. M., Albrecht, P., et al. 1988, ApJS, 115, 185 [Google Scholar]
- Eracleous, M., & Halpern, J. P. 1994, ApJS, 90, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Eracleous, M., & Halpern, J. P. 2004, ApJS, 150, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Eracleous, M., Halpern, J. P., Gilbert, A. M., et al. 1997, ApJ, 490, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Eracleous, M., Lewis, K. T., & Flohic, H. M. L. G. 2009, NewAR, 53, 133 [Google Scholar]
- Flohic, H. M. L. G., & Eracleous, M. 2008, ApJ, 686, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Horne, K., Peterson, B. M., Collier, S. J., & Netzer, H. 2004, PASP, 116, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, C. M. 1996, ApJ, 464, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, C. M. 2009, NewAR, 53, 140 [Google Scholar]
- Ilić, D., Popović, L. Č., Bon, E., Mediavilla, E. G., & Chavushyan, V. H. 2006, MNRAS, 371, 1610 [NASA ADS] [CrossRef] [Google Scholar]
- Jovanović, P., Popović, L. Č., Stalevski, M., & Shapovalova, A. I. 2010, ApJ, 718, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Kollatschny, W. 2003, A&A, 407, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kollatschny, W., & Bischoff, K. 2002, A&A, 386, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Königl, A., & Kartje, J. F. 1994, ApJ, 434, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, K. T., Eracleous, M., & Storchi-Bergmann, T. 2010, ApJS, 187, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Perez, E., Mediavilla, E., Penston, M. V., Tadhunter, C., & Moles, M. 1988, MNRAS, 230, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Popović, L. Č., Mediavilla, E., Bon, E., & Ilić, D. 2004, A&A, 423, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Proga, D., Stone, J. M., & Drew, J. E. 1998, MNRAS, 295, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Proga, D., Stone, J. M., & Kallman, T. R. 2000, ApJ, 543, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Sergeev, S. G., Pronik, V. I., Peterson, B. M., Sergeeva, E. A., & Zheng, W. 2002, ApJ, 576, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Sergeev, S. G., Klimanov, S. A., Doroshenko, V. T., et al. 2010, MNRAS, submitted [Google Scholar]
- Shapovalova, A. I., Burenkov, A. N., Carrasco, L., et al. 2001, A&A, 376, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shapovalova, A. I., Doroshenko, V. T., Bochkarev, N. G., et al. 2004, A&A, 422, 925 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shapovalova, A. I., Popović, L. Č., Burenkov, A. N., et al. 2010, A&A, 517, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sulentic, J. W., Marziani, P., & Dultzin-Hacyan, D. 2000, ARA&A, 38, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Tombesi, F., Sambruna, R. M., Reeves, J. N., et al. 2010, ApJ, 719, 700 [NASA ADS] [CrossRef] [Google Scholar]
- Ulrich, M.-H. 2000, A&ARv, 10, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Van Groningen, E., & Wanders, I. 1992, PASP, 104, 700 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., & Zheng, W. 1991, ApJ, 377, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Welsh, W. F., & Horne, K. 1991, ApJ, 379, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Zamfir, S., Sulentic, J. W., Marziani, P., & Dultzin, D. 2010, MNRAS, 403, 1759 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, W. 1996, AJ, 111, 1498 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Measurements of the peak position velocities (blue, central, red) from month-averaged Hα and Hβ profiles.
Beginning and ending radial velocities, Vbeg and Vend, for different segments in the line profiles of Hα and Hβ.
The errors of measurements (e ± σ) for line segments of Hα and Hβ are given in percent.
All Figures
 |
Fig. 1 Month-averaged profiles of the Hα and Hβ broad emission lines in the period 1995–2007. The abscissa (OX) shows radial velocities with respect to the narrow component of the Hα or Hβ line. The ordinate (OY) shows the line flux in units of 10-16 erg cm-2 s-1 Å-1. |
| In the text | |
 |
Fig. 4 Hα vs. Hβ peak velocity for the central (top), blue (middle) and red (down) peak. The dashed line represents the expected function for an equal peak position in both lines, while solid line represents the best fit of the measured data. |
| In the text | |
 |
Fig. 5 Annual averaged radial velocities of the blue peak. The different symbols represent: stars – the Hβ data from Gaskell (1996), open squares – the Hβ measurements given in Veilleux & Zheng (1991), year-averaged to match other data, full circles – the Hα data from Eracleous et al. (1997), open and full triangles – our data for Hβ and Hα, respectively. |
| In the text | |
 |
Fig. 6 Modeled line profiles for the Hα (top) and Hβ (bottom) lines for different disk parameters (noted in the plots). |
| In the text | |
 |
Fig. 7 Difference between the blue- and red-peak velocities vs. the blue-peak velocity for the Hα (top) and Hβ line (bottom). The model parameters are marked with full squares, while observations are denoted with full circles. |
| In the text | |
 |
Fig. 9 Line segment vs. line segment response. The observations in Period I are denoted with full circles and in Period II with open squares. The line-segment flux is in units 10-14 erg m-2 s-1. The Pearson correlation coefficient r and the null hypothesis value P0 are given in each plot for both periods. |
| In the text | |
 |
Fig. 10 Far blue (left) and far red (right) wings flux against the continuum-flux variation for Hβ (top) and Hα (down). The notation is the same as in Fig. 9. The Pearson correlation coefficient r and the null hypothesis value P0 are given in each plot for both periods. |
| In the text | |
 |
Fig. 12 Response of the line segments to the central segment 0 (from − 1000 to 1000 km s-1). The observations in Period I are denoted with full circles and in Period II with open squares. The line-segment flux is in units 10-14 erg m-2 s-1. The Pearson correlation coefficient r and the null hypothesis value P0 are given in each plot for both periods. |
| In the text | |
 |
Fig. 13 Ratio between the blue-wing flux (two blue segments, −4 and −3) and the central segment as a function of the ratio of the red-wing (two red segments, +4 and +3) and the central segment. Observations in Period I are denoted with full circles, in Period II with open squares, while observations from 2001–2002 are denoted with open triangles. |
| In the text | |
 |
Fig. 14 Maximum response of the correlation functions of the Hβ line segment light curves with the continuum light curve. |
| In the text | |
 |
Fig. 15 Time delay of the individual line segments of Hβ for the first half of the observing period from 1995–2002 (filled squares) and for the second half from 2003–2007 (filled triangles) with respect to the continuum light curve in velocity space. |
| In the text | |
 |
Fig. 16 Variations in the continuum flux at 5100 Å (first panel), in the Hα and Hβ line fluxes (second and third panel, respectively), and in the integral Balmer decrement BD = F(Hα)/F(Hβ) (fourth panel) of the month-averaged profiles. The abscissa (OX) gives the modified Julian date (bottom) and the corresponding year (top). The continuum flux is in units 10-15 erg m-2 s-1 Å-1 and line flux is in 10-13 erg m-2 s-1. The bottom panel gives the BD as a function of the continuum flux, where full circles denote the observations in Period I and open squares in Period II (see text). |
| In the text | |
 |
Fig. 17 Variations in the Balmer decrement (BD = Hα/Hβ) as a function of the radial velocity for month-averaged spectra of 3C 390.3. Upper panel represents BD from the period of 1995–1998, and bottom panel from 2007. These two panels are chosen because they represent the characteristic behavior of BD vs. velocity. The abscissa (OX) indicates the radial velocities with respect to the narrow components. The position of the blue, central and red peaks are marked with blue, black and pink line, for Hα (solid line) and Hβ (dashed line). The rest of the panels are available electronically only. |
| In the text | |
 |
Fig. 18 Balmer decrement versus velocity. First two panels – the inner radius is the same, but different positions of the Hα and Hβ disk with respect to the black hole are assumed. The bottom panel shows the cases where the one of the two emitting regions is closer to the central black hole. The inner and outer radii assumed in models are labeled in each panel. The BD points are normalized to the one at − 4000 km s-1. |
| In the text | |
 |
Fig. 19 Model of the BLR that is composed of the disk-like BLR1, and an outflowing/inflowing BLR2. |
| In the text | |
 |
Fig. 2 Year-averaged profiles (solid line) and their rms (dashed line) of the Hα broad emission line in 1995–2007. The abscissa (OX) shows the radial velocities with respect to the narrow component of the Hα line. The ordinate (OY) shows the flux in units of 10-16 erg cm-2 s-1 Å-1. |
| In the text | |
 |
Fig. 3 The same as in Fig. 2, but for Hβ broad emission line. |
| In the text | |
 |
Fig. 8 Light curves for different segments of the Hα (top) and Hβ (bottom) broad emission lines. The line-segment fluxes are given in 10-14 and 10-15 erg cm-2 s-1 for Hα and Hβ, respectively, while the date is given in the modified Julian Date as MJD = JD-2400000.5. The mean velocity for the segment number is: (± 4) corresponds to (± 8500) km s-1; (± 3) corresponds to (± 6000) km s-1; (± 2) corresponds to (± 4000) km s-1; (± 1) corresponds to (± 2000) km s-1; 0 corresponds to (1000) km s-1. The blue part is denoted with crosses, the red part with pluses, and the line core with full circles. The solid line represents the continuum flux in arbitrary units for comparison. |
| In the text | |
 |
Fig. 11 The same as in Fig. 10, but for the rest of line-segments: −3, −2, −1, 0, 1, 2, 3. |
| In the text | |
 |
Fig. 17 continued. |
| In the text | |
 |
Fig. 17 continued. |
| In the text | |
 |
Fig. 17 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


