| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201016168 | |
| Published online | 04 March 2011 | |
The solar magnetic field since 1700
II. Physical reconstruction of total, polar and open flux
Max-Planck-Institut für Sonnensystemforschung, 37191 Katlenburg-Lindau, Germany
e-mail: cameron@mps.mpg.de
Received: 18 November 2010
Accepted: 31 January 2011
We have used semi-synthetic records of emerging sunspot groups based on sunspot number data as input for a surface flux transport model to reconstruct the evolution of the large-scale solar magnetic field and the open heliospheric flux from the year 1700 onward. The statistical properties of the semi-synthetic sunspot group records reflect those of the observed Royal Greenwich Observatory photoheliographic results. These include correlations between the sunspot numbers and sunspot group latitudes, longitudes, areas and tilt angles. The reconstruction results for the total surface flux, the polar field, and the heliospheric open flux (determined by a current sheet source surface extrapolation) agree well with the available observational or empirically derived data and reconstructions. We confirm a significant positive correlation between the polar field during activity minimum periods and the strength of the subsequent sunspot cycle, which has implications for flux transport dynamo models for the solar cycle. Just prior to the Dalton minimum, at the end of the 18th century, a long cycle was followed by a weak cycle. We find that introducing a possibly “lost” cycle between 1793 and 1800 leads to a shift of the minimum of the open flux by 15 years which is inconsistent with the cosmogenic isotope record.
Key words: Sun: heliosphere / Sun: surface magnetism / Sun: dynamo
© ESO, 2011
1. Introduction
Information about the global properties of the solar magnetic field during past centuries provides important constraints for models of the Sun’s global dynamo and is also relevant for studies of the past terrestrial climate (Usoskin 2008). However, regular synoptic direct observations of the large-scale solar surface field and space-based measurements of the interplanetary magnetic field cover only a few decades. The aim of our work is to reconstruct the Sun’s large-scale magnetic field and its heliospheric open flux from 1700 onwards on the basis of sunspot number records. The tool used for this reconstruction is a surface flux transport model (SFTM, Baumann et al. 2004; Jiang et al. 2010a). In contrast to previous attempts at such reconstructions (e.g., Wang et al. 2005; Schrijver et al. 2002), the source input for our SFTM model consists of semi-synthetic records of sunspot groups whose properties (such as the distributions of emergence latitudes, areas, and tilt angles) obey the empirical statistical relationships with the activity cycle strength studied in Jiang et al. (2011, henceforth referred to as Paper I). The heliospheric open flux is extrapolated from the distribution of surface flux using the current sheet source surface (CSSS) model (Zhao & Hoeksema 1995a,b). The obtained open flux can be compared with reconstructions based upon the geomagnetic aa index (Russell 1975; Lockwood et al. 1999; Svalgaard & Cliver 2005; Rouillard et al. 2007) or upon cosmogenic radionuclide data such as the concentration of 10Be in ice cores (Bard et al. 1997; Caballero-Lopez et al. 2004; McCracken 2007; Steinhilber et al. 2010).
This paper is organized as follows. The SFTM, the treatment of its sources, and the CSSS extrapolation are described in Sect. 2. Observations and results from Cameron et al. (2010, hereafter referred to as CJSS10) are used to validate the model in Sect. 3. The results including the polar field, the total and the open magnetic flux from 1700 onwards are presented in Sect. 4 and possible errors are assessed in Sect. 5. Our conclusions are given in Sect. 6.
2. Model description
2.1. Solar surface flux transport model
The evolution of the large scale magnetic field on the solar surface can be studied using two-dimensional flux transport models (Devore et al. 1984; Wang et al. 1989; Mackay et al. 2000; Schrijver et al. 2002; Baumann et al. 2004), which describe the passive transport of the radial component of the magnetic field, B, under the effect of differential rotation, Ω, meridional flow, v (Babcock 1961), and turbulent surface diffusivity, ηH (Leighton 1964). A slow decay due to the fact that diffusion occurs in three dimensions (Schrijver et al. 2002) is modeled here in the manner described in Baumann et al. (2006), introducing the parameter ηr.
The governing equation of the surface flux transport model (SFTM) is ![\begin{eqnarray} \label{eqn:SFT} \nonumber\frac{\partial B}{\partial t}=& & -\Omega(\lambda,t) \frac{\partial B}{\partial \phi} - \frac{1}{\rsun \cos\lambda} \frac{\partial}{\partial \lambda}[v(\lambda,t) B \cos \lambda] \\ \noalign{\vskip 2mm} & & +\eta_{\rm H} \left[\frac{1}{\rsun^2 \cos{\lambda}} \frac{\partial}{\partial \lambda}\left(\cos\lambda \frac{\partial B}{\partial \lambda}\right) + \frac{1}{\rsun^2 \cos^2{\lambda}}\frac{\partial^2 B}{\partial \phi^2}\right]\\ \noalign{\vskip 2mm} \nonumber & & + S(\lambda,\phi,t) +D(\eta_r), \end{eqnarray}](/articles/aa/full_html/2011/04/aa16168-10/aa16168-10-eq8.png) (1)where S(λ,φ,t) is the source term of the magnetic flux, which describes the emergence of bipolar magnetic regions as a function of latitude λ, longitude φ and time t. D(ηr) is a linear operator describing the decay due to radial diffusion. The value of ηr is discussed in Sect. 3. Concerning the horizontal diffusivity, ηH, we use the reference value in CJSS10 as ηH = 250 km2 s-1. The profiles of both differential rotation, Ω (Snodgrass 1983) and meridional flow, v (van Ballegooijen et al. 1998) are the same as in CJSS10: Ω = 13.38−2.30sin2λ − 1.62sin4λ (in degrees per day) and
(1)where S(λ,φ,t) is the source term of the magnetic flux, which describes the emergence of bipolar magnetic regions as a function of latitude λ, longitude φ and time t. D(ηr) is a linear operator describing the decay due to radial diffusion. The value of ηr is discussed in Sect. 3. Concerning the horizontal diffusivity, ηH, we use the reference value in CJSS10 as ηH = 250 km2 s-1. The profiles of both differential rotation, Ω (Snodgrass 1983) and meridional flow, v (van Ballegooijen et al. 1998) are the same as in CJSS10: Ω = 13.38−2.30sin2λ − 1.62sin4λ (in degrees per day) and 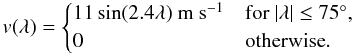 (2)While we take the meridional flow velocity to be time-independent, latitudinal inflows towards the active regions are taken into account via a reduction of the tilt angle as described in the next subsection (see also CJSS10; Jiang et al. 2010b; Cameron & Schüssler 2010). For the initial field distribution, we follow van Ballegooijen et al. (1998) and CJSS10. The strength of the initial field is determined by the parameter B0 corresponding to the field strength at the poles. The values used are discussed in Sect. 4.
(2)While we take the meridional flow velocity to be time-independent, latitudinal inflows towards the active regions are taken into account via a reduction of the tilt angle as described in the next subsection (see also CJSS10; Jiang et al. 2010b; Cameron & Schüssler 2010). For the initial field distribution, we follow van Ballegooijen et al. (1998) and CJSS10. The strength of the initial field is determined by the parameter B0 corresponding to the field strength at the poles. The values used are discussed in Sect. 4.
The solution of the linear Eq. (1) may be expressed in terms of spherical harmonics 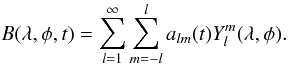 (3)The axial dipole (l = 1,m = 0) and equatorial dipole components (l = 1,m = ± 1) are considered in the presentation of our results. We use the same definitions as Wang et al. (2005) to calculate the solar surface axial (Dax) and equatorial (Deq) dipole strengths. The polar field is defined as the average over a polar cap of 15° latitude extension. The total surface flux is obtained by integrating the unsigned magnetic field over the whole surface.
(3)The axial dipole (l = 1,m = 0) and equatorial dipole components (l = 1,m = ± 1) are considered in the presentation of our results. We use the same definitions as Wang et al. (2005) to calculate the solar surface axial (Dax) and equatorial (Deq) dipole strengths. The polar field is defined as the average over a polar cap of 15° latitude extension. The total surface flux is obtained by integrating the unsigned magnetic field over the whole surface.
2.2. Sources of magnetic flux
Here we describe how we model the magnetic flux source term, S(λ,φ,t), in Eq. (1). We use the semi-synthetic sunspot group records determined in Paper I on the basis of either the group sunspot number, RG (Hoyt & Schatten 1998) or the Wolf sunspot number, RZ, the 12-month running averages of which are shown in Fig. 1 from 1700 onwards. Each sunspot group in the semi-synthetic record is taken to represent a bipolar magnetic region (BMR). The area of a BMR, being the sum of the umbral, penumbral and facular areas, is calculated from the area of the corresponding sunspot group using the empirical relation found by Chapman et al. (1997). The tilt angle of the BMR, α, is assumed to be 70% of that of the sunspot group. This factor (70%) was empirically determined in CJSS10 and reflects the effect of the localized inflows into active regions.
 |
Fig. 1 12-month running average of monthly Wolf (RZ, blue) and group (RG, red) sunspot numbers during 1700–2010. RG in cycle 23 uses the values of RZ. |
In Paper I, the tendency of sunspots to appear in activity nests was measured by considering which combination of uniformly distributed random emergence longitudes and completely ordered longitudes match the degree of non-randomness in the sunspot record of the Royal Greenwich Observatory since 1874. Here we follow the same approach and use both the semi-synthetic datasets with ordered and random emergence longitudes. How the resulting fields are combined is discussed in Sect. 3.
The magnetic field distribution of each new BMR is given by B(λ,φ) = B + (λ,φ) − B − (λ,φ) with ![\begin{eqnarray} B^{\pm}(\lambda,\phi)=B_{\mathrm{max}} \left(\frac{0.4 \Delta\beta}{\delta}\right)^2 \mathrm{\exp} \left\{-\frac{2[1-\cos\beta_{\pm}(\lambda,\phi)]}{\delta^2}\right\}, \end{eqnarray}](/articles/aa/full_html/2011/04/aa16168-10/aa16168-10-eq30.png) (4)where β ± (λ,φ) are the heliocentric angles between the location of the sunspot group,(λ,φ), and the centers of each polarity, (λ ± ,φ ± ). Δβ is the separation between the two polarities. We take
(4)where β ± (λ,φ) are the heliocentric angles between the location of the sunspot group,(λ,φ), and the centers of each polarity, (λ ± ,φ ± ). Δβ is the separation between the two polarities. We take 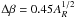 , where AR is the total area of the sunspot groups, and δ = 4° (van Ballegooijen et al. 1998; Baumann et al. 2004). Bmax is the peak field strength of a BMR. Following CJSS10, we take Bmax = 374 G.
, where AR is the total area of the sunspot groups, and δ = 4° (van Ballegooijen et al. 1998; Baumann et al. 2004). Bmax is the peak field strength of a BMR. Following CJSS10, we take Bmax = 374 G.
Δβ and the tilt angle, α, determine the latitudinal separation, Δβsinα, of the two polarities of a BMR. This quantity is important for the axial dipole moment of the global magnetic field and affects the polar field and the open flux during activity minima. The longitudinal separation, given by Δβcosα(cosλ)-1, dominates the equatorial dipole moment and the open flux during activity maximum phases.
Associated with the nth BMR in the semi-synthetic sunspot record is the time tn when the BMR appears. The contribution to the source term S(λ,φ,t) from the nth BMR is taken to be δ(t − tn)(B + (λ,φ) − B − (λ,φ)), where δ is the Dirac delta function. This corresponds to modeling the sunspot group emergence process as being instantaneous.
2.3. Extrapolation into the heliosphere
The SFTM describes the evolution of the magnetic field on the Sun’s surface. To obtain the heliospheric open flux we have to extrapolate the surface field outward. Since the often used potential field source surface model does not well represent the Ulysses spacecraft data (Schüssler & Baumann 2006), we use the better suited current sheet source surface (CSSS) extrapolation (Zhao & Hoeksema 1995a,b).
There are three parameters in the CSSS extrapolation, namely, one associated with the thickness of the current sheet, a, the radius of the cusp surface, Rcs, and the radius of the source surface, Rss. The values for the three parameters are taken from the reference case in CJSS10, i.e., a = 0.2 R⊙, Rcs = 1.55 R⊙, Rss = 10.0 R⊙. The location of the cusp surface determines the amount of the open flux, which is calculated by the integration of unsigned magnetic field over the whole cusp surface.
3. Comparison of the model for the time period from 1913 to 1986
In CJSS10, we used the SFTM with a source term based on the actually observed sunspot longitudes, latitudes, areas and cycle-averaged tilt angles to reconstruct the surface field and open flux for the period 1913–1986. The time evolution of the open flux derived from geomagnetic indices (Lockwood 2003; Lockwood et al. 2009), and the reversal times of polar fields (Makarov et al. 2003) were well reproduced. We therefore begin by comparing the results obtained using the current model based on sunspot numbers with those in CJSS10.
To do so we have to consider the tendency for sunspots to occur in activity nests at specific longitudes, because this affects equatorial dipole moment and the open flux around activity maxima. We performed simulations with BMRs emerging at randomly distributed longitudes and simulations where all BMRs appear at longitudes 90° in the northern hemisphere and 270° in the southern hemisphere. Since both the SFTM and the CSSS extrapolation are linear, we can combine the fields from the two kinds of simulations using 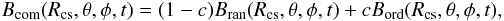 (5)where c is a measure of the strength of the activity nesting. In Paper I we found that the value c = 0.15 is appropriate for a determination of the open flux. This is confirmed here. Figure 2 shows the evolution of the open flux from CJSS10 compared with cases with c = 0 (purely random) and c = 0.15. The case with random longitudes generates too low open flux at solar maxima. The rms difference between the results from CJSS10 is 1.19 × 1014 Wb when c = 0 (the purely random case) compared to 1.09 × 1014 Wb when c = 0.15. When we consider only the cycle maximum values of the open flux for each cycle, the difference is greater, with the rms deviation falling from 1.93 × 1014 Wb for c = 0 to 1.00 × 1014 Wb for c = 0.15.
(5)where c is a measure of the strength of the activity nesting. In Paper I we found that the value c = 0.15 is appropriate for a determination of the open flux. This is confirmed here. Figure 2 shows the evolution of the open flux from CJSS10 compared with cases with c = 0 (purely random) and c = 0.15. The case with random longitudes generates too low open flux at solar maxima. The rms difference between the results from CJSS10 is 1.19 × 1014 Wb when c = 0 (the purely random case) compared to 1.09 × 1014 Wb when c = 0.15. When we consider only the cycle maximum values of the open flux for each cycle, the difference is greater, with the rms deviation falling from 1.93 × 1014 Wb for c = 0 to 1.00 × 1014 Wb for c = 0.15.
 |
Fig. 2 Open flux from CJSS10 (solid black curve), from the semi-synthetic sunspot group record with random longitudes (dotted blue curve), and from a combination of semi-synthetic models with random and ordered longitudes Bcom = (1 − c)Bran + cBord with c = 0.15 (red curve). The asterisks show the maximum value for each cylce. Results using the semi-synthetic data are averages over 20 realizations. |
Next we compare our simulations during 1913–1986 (cycles 12–21) based on RG and RZ with the results from CJSS10 and with the observed data. Note that all results shown are based on averages over 20 sets of random realizations of the semi-synthetic sunspot records. We first set the radial diffusivity to ηr = 0. Figure 3a compares the time evolution of total flux from CJSS10 with the models based on RG and RZ, respectively. The three curves almost overlap. For the period from the early 1970s onwards, the direct magnetic measurements from the Mount Wilson and Wilcox observatories are also shown. Figure 3c shows the evolution of the polar field for both hemispheres. Since the input of the BMRs emergences is randomly distributed on the two hemispheres, our reconstructed north and south polar fields are similar. The reversal times (indicated by cyan vertical lines) are similar to those given by Makarov et al. (2003). The largest differences between the models occur in cycle 19. Figure 3d shows the evolution of the modeled open flux in comparison with that inferred from the geomagnetic aa index (Lockwood et al. 2009). For the whole time period, the rms difference between the inferred values from the aa index and CJSS10, RZ and RG are 0.99, 0.92, 0.96 × 1014 Wb, respectively, corresponding to about 14% of the average value of 6.92 × 1014 Wb of the Lockwood et al. (2009) data.
 |
Fig. 3 Comparison of the model results based on RZ (blue curves) and RG (red curves) with the reconstruction of CJSS10 (black curves) for the period 1913–1986. Panels a)–d) show the case without radial diffusion. a) Total surface flux. Square and plus symbols during the last 2 cycles denote the observations from the Wilcox and Mount Wilson solar observatories, respectively. b) Time-latitude diagram of the longitudinally averaged signed surface magnetic field from the model based on RZ. c) Polar field. Dashed and solid curves are for the southern and northern hemispheres, respectively. The cyan vertical lines indicate the inferred times of polar field reversals from Makarov et al. (2003). d) Open heliospheric flux. The dash-dotted curve represents the result inferred from the geomagnetic aa index (Lockwood et al. 2009). e), f): results with radial diffusivity ηr = 25 km2s-1. e) Polar field. f) Open heliospheric flux. |
The time-latitude plot of the longitudinal averaged signed photospheric field (magnetic butterfly diagram) during this time period is shown in Fig. 3b for the reconstruction based on RZ. As found in previous studies, the latitude separation of the two polarities leads to a net flux when azimuthally averaged. The advection of this flux to the poles reverses the polar fields each cycle. The regular polar field reversals and the anti-phase between the polar field and the low latitude field are well reproduced.
These results show that our SFTM with sources based on the sunspot numbers RZ or RG is consistent with the reconstruction of CJSS10, which used the recorded properties of the actually sunspot groups, and also compares well with the observed photospheric and the heliospheric magnetic field.
 |
Fig. 4 Reconstruction based on RG during 1700–2010. a) Total surface flux. b) Polar field. Solid and dashed curves are for the northern and southern hemisphere, respectively. c) Open heliospheric flux. The red curve gives the reconstruction, the grey curve is the 11-yr running average. The open flux as inferred from the geomagnetic aa index (Lockwood et al. 2009) is represented by the black curve. d) Axial (solid curve) and equatorial (dashed curve) dipole field strength. |
Because the sunspot number data are less reliable before 1849 (Vaquero 2007; Svalgaard & Cliver 2010) we have chosen to use a non-vanishing value for the radial diffusivity ηr. This was found to be necessary because when ηr = 0 is used, the e-folding decay time due to ηH alone is approximately 4000 years. This timescale was obtained numerically, and is considerably longer than the simple estimate 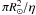 because the meridional flow tends to keep the magnetic field at the two poles separated. The long e-folding time means that the field at any given time is affected by errors in the sunspot numbers at all previous times. This is very undesirable because noisy data at the beginning of the dataset then contribute for the entire period covered by the simulations without significant damping. Introducing a weak radial diffusivity ηr = 25 km2 s-1 (which leads to a decay time about 20 yr, as found by Baumann et al.2006) is aimed at keeping ηr small while still being able to sensibly use the early data. Figure 3e shows the polar field evolution with the weak radial diffusion included. Compared to Fig. 3c, the largest differences are on the order of 20%. The time evolution of the corresponding open fluxes is shown in Fig. 3f. During the minimum phases of some cycles, the model is now closer to the data inferred from the aa index (e.g. RG model around 1955 and RZ model around 1976), while other deviate more strongly (e.g., RZ model around 1924 and 1936). For the whole time period, the rms deviations for the models based on RZ and RG are 0.93 and 0.96 in 1014 Wb, respectively.
because the meridional flow tends to keep the magnetic field at the two poles separated. The long e-folding time means that the field at any given time is affected by errors in the sunspot numbers at all previous times. This is very undesirable because noisy data at the beginning of the dataset then contribute for the entire period covered by the simulations without significant damping. Introducing a weak radial diffusivity ηr = 25 km2 s-1 (which leads to a decay time about 20 yr, as found by Baumann et al.2006) is aimed at keeping ηr small while still being able to sensibly use the early data. Figure 3e shows the polar field evolution with the weak radial diffusion included. Compared to Fig. 3c, the largest differences are on the order of 20%. The time evolution of the corresponding open fluxes is shown in Fig. 3f. During the minimum phases of some cycles, the model is now closer to the data inferred from the aa index (e.g. RG model around 1955 and RZ model around 1976), while other deviate more strongly (e.g., RZ model around 1924 and 1936). For the whole time period, the rms deviations for the models based on RZ and RG are 0.93 and 0.96 in 1014 Wb, respectively.
CJSS10 found a strong correlation between the polar field of cycle n and the strength of the subsequent cycle n + 1. Without radial diffusion, the correlation coefficients are 0.80 and 0.52 for the RZ and RG, cases respectively. In our case with a sample size of 7, a significance level of p = 0.05 corresponds to r = 0.74. For all cases, there is no correlation between the polar field around the activity minimum of cycle n and the strength of the same cycle. The introduction of radial diffusivity and the corresponding decay of the polar field decreases the correlation between the polar field and its subsequent cycle strength and somewhat increases the correlation between the polar field of cycle n and the strength of the same cycle. All these correlation coefficients do not exceed the level required for significance at the p = 0.05 level.
We conclude that the SFTM with input data based on sunspot numbers effectively describes the solar magnetic field since 1913. Although the introduction of a non-vanishing radial diffusivity leads to some possibly undesired decay of the polar field, it decreases the error caused by the noisy early sunspot numbers. The photospheric and the heliospheric field are reasonably well reproduced. In the next section, we present the results back to 1700.
4. Results
4.1. Time evolution of the reconstructed field
Figures 4 and 5 show time series of various properties of the reconstructed solar magnetic field, based on RG and RZ, respectively. Yearly values for the reconstructed open fluxes are given in Tables 1 and 2. All results shown correspond to averages over 20 sets of random realizations of the semi-synthetic sunspot records. The evolution of the total unsigned flux (panels a), polar field (panels b), open flux (panels c), axial and equatorial dipole field strength (panels d) are shown. The first ~ 20 yrs of these series are still affected by the choice of the amplitude of the initial field, B0. Since cycle − 4 (1700–1712) is very weak in the RG data, we set B0 = 0 in this case. For RZ we used B0 = 3 G.
The polar field displays regular reversals, except for the RG case during the Dalton minimum, when a reversal appears to fail. The flux transported to the poles during the weak cycle 5 just cancels the strong polar field generated by the strong and long cycle 4. On the other hand, a clear reversal occurs in the case based on RZ (cf. Fig. 5). Owing to the uncertainties in the sunspot number record, it cannot be determined with any confidence whether the polar field actually reversed or not. The grey curves in Panels (c) of Figs. 4 and 5 are the 11-yr running average of the open flux. The long-term trend is compared with other independent reconstructions in Sect. 4.3.
Panels (d) of Figs. 4 and 5 show the time evolution of the axial dipole field, Dax, and the equatorial dipole field, Deq. Deq is approximately in phase with the evolution of the sunspot number and the total flux. Since we define the polar field as the average over latitudes poleward of ± 75°, Dax varies in phase with the polar field. Due to the persistent emergence of sunspot groups in different locations, the evolution of Deq is noisier than that of Dax. This is partly mitigated by the fact that we show the average over 20 semi-synthetic sunspot group record realizations.
Reconstructed open flux based on RG.
Reconstructed open flux based on RZ.
4.2. Correlations with sunspot numbers
The relation between the maximum polar field at the end of a cycle and the cycle strength (highest sunspot number during the cycle) is shown in the left panel of Fig. 6. The middle panel gives the relation between the cycle strength and the sum of the maximum polar field of the preceding and the same cycle. This represents the change in the polar field from one cycle to the next. The correlation is expected to be stronger in this case, because the tilted BMRs first reverse the polar field of the old cycle and then built up that of the new cycle. The right panel of Fig. 6 shows the relation between the maximum polar field at the end of a cycle and the strength of the next cycle. All correlations are significant at the p ≤ 0.05 level. From the results described in Sect. 3, we expect that for ηR = 0 the correlation between polar field and strength of the next cycle would be even stronger. Such a correlation is potentially relevant in connection with flux transport dynamo models (e.g., Chatterjee et al. 2004; Dikpati et al. 2004).
 |
Fig. 6 Left: relation between the maximum sunspot numbers of cycle n and the maximum of the polar field at the end of cycle n for the RZ case (blue symbols) and the RG case (red symbols). Middle: relation between maximum sunspot numbers of cycle n and the sum of the maximum polar fields of cycles n − 1 and n. Right: relation between the maximum polar field of cycle n and the maximum sunspot number of cycle n + 1. Correlation coefficients, r, and significance levels, p are indicated. |
Figure 7 shows the relationship between the total unsigned flux and the sunspot number. During activity maxima, many BMRs emerge and the polar fields are weak. Hence there is a strong correlation between the sunspot number and the total unsigned flux. During the minima fewer sunspots emerge, and the total surface flux has a stronger contribution from the polar region. This leads to a weaker correlation between the total surface field and the sunspot numbers during solar minima. On longer timescales, the total flux is roughly proportional to the sunspot number.
 |
Fig. 7 Relation between sunspot number and total surface flux during cycle maxima (upper panel) and during cycle minima (lower panel). Red symbols refer to the RG case and blue symbols to the RZ case. |
 |
Fig. 8 Top: relation between maximum sunspot number and the maximum open flux during a cycle. Bottom: relation between minimum sunspot number and the minimum open flux during a cycle. |
 |
Fig. 9 Comparison of the reconstructed open flux with other reconstructions. Loc09: see Lockwood (2003) and Lockwood et al. (2009). WLS05: Wang et al. (2005); solid and dashed green are their models S1 and S2, respectively. SC10: Svalgaard & Cliver (2010). A factor 0.4 used to convert their data into open flux. VS10: Vieira & Solanki (2010). SABM10: Steinhilber et al. (2010, PCA composite). McC07: McCracken (2007). All data are 11-yr running averages, except SABM10 which is a 25-yr running average. |
Since the contribution to the field strength of the multipole of order l falls off with radius as r − (l + 2), the lowest-order multipoles dominate the amplitude of the open heliospheric flux (Wang & Sheeley 2002). The emergence of any given BMR may increase or decrease the open flux, depending on whether its dipole moment vector is oriented so as to reinforce or reduce that of the pre-existing field (Wang et al. 2000). The left panel of Fig. 8 shows that the maximum value of open flux during a cycle and the maximum sunspot number are strongly correlated. This results from the large number of BMRs emerging during the solar maximum period together with activity nesting, which generate a strong equatorial dipole field. On the other hand, the correlation is much weaker between the minimum value of open flux over a cycle and the minimum sunspot number. This is because the open flux during minimum phases is dominated by the axial dipole field corresponding to the polar field that has accumulated over the cycle. Note that the maxima of the open flux usually occur 1–2 yrs after sunspot maximum (cf. Wang & Sheeley 2002) while the minima of the open flux are almost in phase with the sunspot numbers.
4.3. Comparison of open flux with other reconstructions
Figure 9 shows the comparison of our 11-yr running average of the reconstructed open flux since 1700 with results based on geomagnetic aa index by Lockwood et al. (2009, Loc09) and Svalgaard & Cliver (2010, SC10), from the cosmogenic isotope 10Be data by McCracken (2007, McC07) and Steinhilber et al. (2010, SABM10), and from other models based on sunspot numbers by Vieira & Solanki (2010, VS10) and Wang et al. (2005, WLS05). Our reconstructed open flux refers to the unsigned radial component of the magnetic field at the orbit of Earth. Since the values given in SC10 correspond to the heliospheric vector magnetic field amplitude, a factor 0.4 has been applied. This factor is close to the value used by Svalgaard & Cliver (2006) to convert the magnitude of the vector field to the radial component.
All reconstructions show a similar behavior in the second half of the time period covered. The values given by SABM10 are systematically higher than the others by approximately 10%. The minimum open flux over the period studied is about 1–2 × 1014 Wb and the maximum value is about 8 × 1014 Wb.
Before ~1800, there is a distinct difference between the results based on 10Be data (McC07, SABM10) and the other methods. The values inferred from 10Be are particularly high from 1720 to 1750, when the RG data indicate rather low solar activity. Although the RZ values are somewhat higher than RG during this time period, our reconstructed open flux is still about 30% weaker than that of McC07 and SABM10.
4.4. A “lost cycle”?
Since the years 1790–1794 are poorly covered by sunspot observations, it has been suggested that the unusually long cycle number 4 (1784.7–1798.3) may actually consist of two shorter cycles, so that a weak “lost” cycle could be missing in the existing sunspot number records (Usoskin et al. 2001). There is an ongoing discussion on this topic (Krivova et al. 2002; Arlt 2008; Usoskin et al. 2009), so that it seems reasonable to investigate how adding a “lost” cycle 4′ would affect our reconstructions.
Using RG data, we followed Usoskin et al. (2001) and changed the cycle minimum times to 1784.3 (cycle 4), 1793.1 (cycle 4′, the possible lost cycle) and 1799.8 (cycle 5). All other cycle minima times were left unchanged (for values, see Table 1 of Paper I). We then generated new semi-synthetic sunspot group records according to the method of Paper I. In accordance with Hale’s polarity laws, the magnetic polarity orientation of the sunspot groups in cycle 4′ was taken to be the same as that of the original cycle 4 and the orientations for all cycles before cycle 4′ were reversed.
Figure 10 shows the comparison of the time evolution of the polar field between the cases with and without cycle 4′. The polar field generated during cycle 4 is only slightly diminished by the short and weak cycle 4′ and no reversal takes place. The following cycle 5 has the same polarities as cycle 4 and thus strengthens the polar field even further. Thus the addition of the extra cycle leads to a strong polar field being maintained throughout the whole period between about 1790 and 1810. This is followed by a period of weak polar field between 1820 and 1830. In contrast to these results, the standard case without extra cycle predicts weak polar field between 1805 and 1820.
 |
Fig. 10 Time evolution of the reconstructed (southern) polar field during 1760–1880 after adding the “lost” cycle indicated by the two vertical lines between 1793.1 and 1799.8 (red curve) and without the additional cycle (standard case, black curve). Both reconstructions are based on RG. |
Comparing the reconstructed open heliospheric flux with the measured 10Be concentration in ice cores should, at least in qualitative terms, give an indication which model is to be preferred. Figure 11 shows the evolution of 11-yr running average of the reconstructed open flux in both cases together with the 10Be data of Beer et al. (1990). The introduction of the extra cycle shifts the minimum of the open flux from about 1810 to about 1825, which is clearly inconsistent with the 10Be data showing maxima (corresponding to low open flux) around 1810 and 1817. The same inconsistency arises also when comparing with the other reconstructions of the open flux shown in Fig. 9.
 |
Fig. 11 Time evolution of the reconstructed open heliospheric flux (11-yrs running average) during 1780–1840 with the “lost” cycle (red curve) and without (black curve), in comparison to the measured 10Be concentration in ice cores (Beer et al. 1990). Note the inverted scale for the 10Be data. |
The strong unreversed polar field and the delay of the open flux minimum at the beginning of the 19th century by ~ 15 years, which result from the introduction of extra cycle 4′, appear to be highly anomalous and seem to be ruled out by comparison with the 10Be record. Our reconstructions therefore argue against the existence of a “lost” cycle 4′.
5. Possible sources of error in the reconstruction
Our reconstructions are based on the datasets of the sunspot numbers RZ and RG. Both of these have errors, partly due to sparse observations during the early period (Vaquero 2007) and partly due to subjective definitions of what to include by the different observers over the centuries (Svalgaard & Cliver 2010). Errors in sunspot numbers obviously affect our reconstruction of the magnetic field. In the following, we analyze the effect of possible errors in the sunspot numbers on the reconstructed magnetic field by considering a weak cycle (cycle 6, 1810.6–1823.3) and a strong cycle (cycle 19, 1954.3–1964.9) as extreme examples. We restrict this analysis to the reconstruction based on RZ, noting that the results for the RG case are very similar.
The effects of a change of the sunspot number data on the polar field and the open flux in cycle 6 (left panels) and cycle 19 (right panels) are displayed in Fig. 12. The upper panels illustrate a reduction of the sunspot number by 30% (dotted curves) and an increase by 30% (dashed curves), respectively, of the original values. The solid curves represent the unchanged data. The previous 5 yr before the cycle starts and the subsequent 45 yr after the cycle ends are shown as well.
 |
Fig. 12 Effect of varying the sunspot number (upper panels) by an increase of 30% (dashed curves) and by a decrease of 30% (dotted curves) on the evolution of the polar field (middle panels, average absolute value of the northern and southern poles) and the open flux (lower panels). The weak cycle 6 (1810.6–1823.3, left panels) and the strong cycle 19 (1954.3–1964.9, right panels) of the RZ case are considered. The Roman numbers denote 5 time intervals which are affected by the variation of the sunspot numbers in different ways (see text). |
To simplify the discussion, we denote cycle 6 and cycle 19 as cycle n, cycles 7 and 20 as n + 1, and so on. The effect of the variation of sunspot number of cycle n on the following cycles has a periodicity of two cycles and an amplitude which decays with an e-folding time of ~20 years. To reveal the effects in more detail, we have broken the time period into 5 intervals. Part I corresponds to the rising phase of cycle n (from the start to the maximum). The polar field (shown in middle panels of Fig. 12) is only weakly affected during this interval, during which the emerging BMRs reverse the polar field of the previous cycle. Hence higher sunspot numbers cause the polar field to become weaker and to reverse earlier. The variation of the open flux (lower panels of Fig. 12) during this time period is dominated by the variation of equatorial dipole field which is directly connected to the sunspot number. Due to the competing effects of the axial dipole field (polar field), the relative variation of the open flux is less than that of the sunspot number.
Period II corresponds to the decaying phases of cycle n (from the maximum to the end of cycle). Part III is the rising phase of cycle n + 1. During these two periods, the polar field and the open flux are strongly affected. More sunspots produce a stronger polar field and vice versa. The relative variation of the open flux is similar to the relative change of the sunspot number during period II, but the effect is weaker for part III since during the rise to the next maximum the equatorial dipole moment of cycle n + 1, which is unchanged, begins to dominate.
Period IV mainly includes the decaying phases of cycle n + 1 and rising phases of cycle n + 2. The polar field is still significantly affected but less so than during the periods II and III, owing to the effect of radial diffusion. More sunspots in cycle n produce a stronger polar field during this time. In period V, the effect of a variation of the sunspot number in cycle n becomes less and less important owing to the decay caused by the radial diffusion.
In addition, the derivation of the sources for the SFTM depends on the spatial and temporal properties of BMR emergences. Because we derive the source in terms of correlations, the model has random components. Figure 13 shows the mean values and standard deviations arising from this randomness, derived using 20 independent realizations of the semi-synthetic sunspot group records. Again the results for a weak cycle (cycle 6) and a strong cycle (cycle 19) are shown. The standard deviations are small for the polar field, but more significant for the open flux during the maximum periods and reach up to 13% of the open flux. The average standard deviations of the polar field and the open flux over the whole simulation time series are about 10% of the corresponding mean values.
 |
Fig. 13 The effect of the random component in generating the sources for the SFTM. The reconstructed polar field (upper panels) and open flux (lower panels) are shown for cycle 6 (left) and cycle 19 (right). The red vertical bars indicate the standard deviations corresponding to a set of twenty synthetic sunspot group records with different random numbers. |
6. Conclusion
We have provided a physical reconstruction of the large-scale solar magnetic field and the open heliospheric flux since 1700 with a surface flux transport model with sources based on sunspot number data and on the statistical properties of the sunspot groups in the RGO photoheliographic results. The model has been validated through comparison with reconstructions based on the actual sunspot group record and with directly measured or observationally inferred quantities.
Our source term, S, is based on the semi-synthetic sunspot group record of Paper I. It in turn is based upon correlations between the cycle amplitudes and cycle phase, and sunspot group areas, emergence latitudes and tilt angles. Hence while the surface evolution described by the SFTM model is linear, our model of the source term introduces nonlinearities into the reconstruction. These nonlinearities partly explain why the reconstruction for the period from 1874 to 1976 has polar field reversals each cycle without the need to invoke variations in the meridional flow (Wang & Sheeley 2002) or extra terms which cause the field to decay (Schrijver et al. 2002). This was also found in CJSS10. The sunspot numbers are less reliable prior to 1874, and we needed to introduce a slow decay of the field to produce polar fields which reverse each cycle.
The reconstructions considerably extend the basis for correlations studies, such as the relation between the polar field amplitude during activity minima and the strengths of the preceding and subsequent cycles, with implications for dynamo models. Introducing a possibly “lost” cycle at the end of the 18th century leads to a shift of the open flux minimum during the Dalton minimum which is incompatible with the 10Be record.
Acknowledgments
We are grateful to Y.-M. Wang, L. E. A. Vieira, M. Lockwood, and F. Steinhilber for kindly providing their reconstructed open flux data.
References
- Arlt, R. 2008, Sol. Phys., 247, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Babcock, H. W. 1961, ApJ, 133, 572 [Google Scholar]
- Bard, E., Raisbeck, G. M., Yiou, F., & Jouzel, J. 1997, Earth Planetary Sci. Lett., 150, 453 [Google Scholar]
- Baumann, I., Schmitt, D., Schüssler, M., & Solanki, S. K. 2004, A&A, 426, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baumann, I., Schmitt, D., & Schüssler, M. 2006, A&A, 446, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beer, J., Blinov, A., Bonani, G., Hofmann, H. J., & Finkel, R. C. 1990, Nature, 347, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Caballero-Lopez, R. A., Moraal, H., McCracken, K. G., & McDonald, F. B. 2004, J. Geophys. Res., 109, 12102 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, R. H., & Schüssler, M. 2010, ApJ, 720, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, R. H., Jiang, J., Schmitt, D., & Schüssler, M. 2010, ApJ, 719, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, G. A., Cookson, A. M., & Dobias, J. J. 1997, ApJ, 482, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, P., Nandy, D., & Choudhuri, A. R. 2004, A&A, 427, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Devore, C. R., Boris, J. P., & Sheeley, Jr., N. R. 1984, Sol. Phys., 92, 1 [Google Scholar]
- Dikpati, M., de Toma, G., Gilman, P. A., Arge, C. N., & White, O. R. 2004, ApJ, 601, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyt, D. V., & Schatten, K. H. 1998, Sol. Phys., 179, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, J., Cameron, R. H., Schmitt, D., & Schüssler, M. 2010a, ApJ, 709, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, J., Işik, E., Cameron, R. H., Schmitt, D., & Schüssler, M. 2010b, ApJ, 717, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, J., Cameron, R. H., Schmitt, D., & Schüssler, M. 2011, A&A, 528, A82 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivova, N. A., Solanki, S. K., & Beer, J. 2002, A&A, 396, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leighton, R. B. 1964, ApJ, 140, 1547 [Google Scholar]
- Lockwood, M. 2003, J. Geophys. Res., 108, 1128 [Google Scholar]
- Lockwood, M., Stamper, R., & Wild, M. N. 1999, Nature, 399, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, M., Owens, M., & Rouillard, A. P. 2009, J. Geophys. Res., 114, 11104 [Google Scholar]
- Mackay, D. H., Gaizauskas, V., & van Ballegooijen, A. A. 2000, ApJ, 544, 1122 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, V. I., Tlatov, A. G., & Sivaraman, K. R. 2003, Sol. Phys., 214, 41 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, K. G. 2007, J. Geophys. Res., 112, 9106 [Google Scholar]
- Rouillard, A. P., Lockwood, M., & Finch, I. 2007, J. Geophys. Res., 112, 5103 [NASA ADS] [Google Scholar]
- Russell, C. T. 1975, Sol. Phys., 42, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., De Rosa, M. L., & Title, A. M. 2002, ApJ, 577, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Schüssler, M., & Baumann, I. 2006, A&A, 459, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snodgrass, H. B. 1983, ApJ, 270, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Steinhilber, F., Abreu, J. A., Beer, J., & McCracken, K. G. 2010, J. Geophys. Res., 115, 1104 [NASA ADS] [CrossRef] [Google Scholar]
- Svalgaard, L., & Cliver, E. W. 2005, J. Geophys. Res., 110, 12103 [NASA ADS] [CrossRef] [Google Scholar]
- Svalgaard, L., & Cliver, E. W. 2006, J. Geophys Res., 111, 9110 [CrossRef] [Google Scholar]
- Svalgaard, L., & Cliver, E. W. 2010, J. Geophys. Res., 115, 9111 [Google Scholar]
- Usoskin, I. G. 2008, Liv. Rev. Sol. Phys., 5, 3 [Google Scholar]
- Usoskin, I. G., Mursula, K., & Kovaltsov, G. A. 2001, A&A, 370, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Usoskin, I. G., Mursula, K., Arlt, R., & Kovaltsov, G. A. 2009, ApJ, 700, L154 [Google Scholar]
- van Ballegooijen, A. A., Cartledge, N. P., & Priest, E. R. 1998, ApJ, 501, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Vaquero, J. M. 2007, Adv. Space Res., 40, 929 [Google Scholar]
- Vieira, L. E. A., & Solanki, S. K. 2010, A&A, 509, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, Y., & Sheeley, N. R. 2002, J. Geophys. Res., 107, 1302 [Google Scholar]
- Wang, Y.-M., Nash, A. G., & Sheeley, N. R. 1989, Science, 245, 712 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wang, Y., Sheeley, N. R., & Lean, J. 2000, Geophys. Res. Lett., 27, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y., Lean, J. L., & Sheeley, Jr., N. R. 2005, ApJ, 625, 522 [Google Scholar]
- Zhao, X., & Hoeksema, J. T. 1995a, Adv. Space Res., 16, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, X., & Hoeksema, J. T. 1995b, J. Geophys. Res., 100, 19 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 12-month running average of monthly Wolf (RZ, blue) and group (RG, red) sunspot numbers during 1700–2010. RG in cycle 23 uses the values of RZ. |
| In the text | |
 |
Fig. 2 Open flux from CJSS10 (solid black curve), from the semi-synthetic sunspot group record with random longitudes (dotted blue curve), and from a combination of semi-synthetic models with random and ordered longitudes Bcom = (1 − c)Bran + cBord with c = 0.15 (red curve). The asterisks show the maximum value for each cylce. Results using the semi-synthetic data are averages over 20 realizations. |
| In the text | |
 |
Fig. 3 Comparison of the model results based on RZ (blue curves) and RG (red curves) with the reconstruction of CJSS10 (black curves) for the period 1913–1986. Panels a)–d) show the case without radial diffusion. a) Total surface flux. Square and plus symbols during the last 2 cycles denote the observations from the Wilcox and Mount Wilson solar observatories, respectively. b) Time-latitude diagram of the longitudinally averaged signed surface magnetic field from the model based on RZ. c) Polar field. Dashed and solid curves are for the southern and northern hemispheres, respectively. The cyan vertical lines indicate the inferred times of polar field reversals from Makarov et al. (2003). d) Open heliospheric flux. The dash-dotted curve represents the result inferred from the geomagnetic aa index (Lockwood et al. 2009). e), f): results with radial diffusivity ηr = 25 km2s-1. e) Polar field. f) Open heliospheric flux. |
| In the text | |
 |
Fig. 4 Reconstruction based on RG during 1700–2010. a) Total surface flux. b) Polar field. Solid and dashed curves are for the northern and southern hemisphere, respectively. c) Open heliospheric flux. The red curve gives the reconstruction, the grey curve is the 11-yr running average. The open flux as inferred from the geomagnetic aa index (Lockwood et al. 2009) is represented by the black curve. d) Axial (solid curve) and equatorial (dashed curve) dipole field strength. |
| In the text | |
 |
Fig. 5 Same as Fig. 4, but for the reconstruction based on RZ. |
| In the text | |
 |
Fig. 6 Left: relation between the maximum sunspot numbers of cycle n and the maximum of the polar field at the end of cycle n for the RZ case (blue symbols) and the RG case (red symbols). Middle: relation between maximum sunspot numbers of cycle n and the sum of the maximum polar fields of cycles n − 1 and n. Right: relation between the maximum polar field of cycle n and the maximum sunspot number of cycle n + 1. Correlation coefficients, r, and significance levels, p are indicated. |
| In the text | |
 |
Fig. 7 Relation between sunspot number and total surface flux during cycle maxima (upper panel) and during cycle minima (lower panel). Red symbols refer to the RG case and blue symbols to the RZ case. |
| In the text | |
 |
Fig. 8 Top: relation between maximum sunspot number and the maximum open flux during a cycle. Bottom: relation between minimum sunspot number and the minimum open flux during a cycle. |
| In the text | |
 |
Fig. 9 Comparison of the reconstructed open flux with other reconstructions. Loc09: see Lockwood (2003) and Lockwood et al. (2009). WLS05: Wang et al. (2005); solid and dashed green are their models S1 and S2, respectively. SC10: Svalgaard & Cliver (2010). A factor 0.4 used to convert their data into open flux. VS10: Vieira & Solanki (2010). SABM10: Steinhilber et al. (2010, PCA composite). McC07: McCracken (2007). All data are 11-yr running averages, except SABM10 which is a 25-yr running average. |
| In the text | |
 |
Fig. 10 Time evolution of the reconstructed (southern) polar field during 1760–1880 after adding the “lost” cycle indicated by the two vertical lines between 1793.1 and 1799.8 (red curve) and without the additional cycle (standard case, black curve). Both reconstructions are based on RG. |
| In the text | |
 |
Fig. 11 Time evolution of the reconstructed open heliospheric flux (11-yrs running average) during 1780–1840 with the “lost” cycle (red curve) and without (black curve), in comparison to the measured 10Be concentration in ice cores (Beer et al. 1990). Note the inverted scale for the 10Be data. |
| In the text | |
 |
Fig. 12 Effect of varying the sunspot number (upper panels) by an increase of 30% (dashed curves) and by a decrease of 30% (dotted curves) on the evolution of the polar field (middle panels, average absolute value of the northern and southern poles) and the open flux (lower panels). The weak cycle 6 (1810.6–1823.3, left panels) and the strong cycle 19 (1954.3–1964.9, right panels) of the RZ case are considered. The Roman numbers denote 5 time intervals which are affected by the variation of the sunspot numbers in different ways (see text). |
| In the text | |
 |
Fig. 13 The effect of the random component in generating the sources for the SFTM. The reconstructed polar field (upper panels) and open flux (lower panels) are shown for cycle 6 (left) and cycle 19 (right). The red vertical bars indicate the standard deviations corresponding to a set of twenty synthetic sunspot group records with different random numbers. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


