| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 18 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201015945 | |
| Published online | 09 March 2011 | |
General relativistic magnetohydrodynamics in axisymmetric dynamical spacetimes: the X-ECHO code
1
NORDITA, AlbaNova University Center, Roslagstullsbacken 23, 10691
Stockholm,
Sweden
e-mail: niccolo@nordita.org
2
Dipartimento di Fisica e Astronomia, Università di
Firenze, Largo E. Fermi
2, 50125
Firenze,
Italy
e-mail: luca.delzanna@unifi.it
Received:
18
October
2010
Accepted:
13
January
2011
We present a new numerical code, X-ECHO, for general relativistic magnetohydrodynamics (GRMHD) in dynamical spacetimes. This aims at studying astrophysical situations where strong gravity and magnetic fields are both supposed to play an important role, such as in the evolution of magnetized neutron stars or in the gravitational collapse of the magnetized rotating cores of massive stars, which is the astrophysical scenario believed to eventually lead to (long) GRB events. The code extends the Eulerian conservative high-order (ECHO) scheme (Del Zanna et al. 2007, A&A, 473, 11) for GRMHD, here coupled to a novel solver of the Einstein equations in the extended conformally flat condition (XCFC). We solve the equations in the 3 + 1 formalism, assuming axisymmetry and adopting spherical coordinates for the conformal background metric. The GRMHD conservation laws are solved by means of shock-capturing methods within a finite-difference discretization, whereas, on the same numerical grid, the Einstein elliptic equations are treated by resorting to spherical harmonics decomposition and are solved, for each harmonic, by inverting band diagonal matrices. As a side product, we built and make available to the community a code to produce GRMHD axisymmetric equilibria for polytropic relativistic stars in the presence of differential rotation and a purely toroidal magnetic field. This uses the same XCFC metric solver of the main code and has been named XNS. Both XNS and the full X-ECHO codes are validated through several tests of astrophysical interest.
Key words: gravitation / relativistic processes / magnetohydrodynamics (MHD) / gamma-ray burst: general / methods: numerical
© ESO, 2011
1. Introduction
The most spectacular phenomena in high-energy astrophysics, such as those associated to active galactic nuclei (AGNs), galactic X-ray binary systems, or gamma-ray bursts (GRBs), typically involve rotating compact objects and magnetic fields. In some cases, such as the merging of binary systems (formed by either neutron stars, NSs, or black holes, BHs) or the collapse of rotating cores of massive stars towards an NS or BH, the interplay between matter, electromagnetic fields, and gravity is so strong that the MHD equations governing the fluid motions must be solved self-consistently with the Einstein equations for the spacetime metric. Even for less violent phenomena,such as the oscillations of neutron stars (Font et al. 2002), a self consistent solution of the fluid equations, together with the spacetime evolution, is essential to properly estimate the frequencies of the eigenmodes. In the case of a binary NS merger, which is a possible mechanism to account for short GRBs, a strong magnetic field could be produced by the induced shear (Price & Rosswog 2006). Long GRBs are instead associated to supernova events and to the core collapse of massive stars (Woosley & Bloom 2006), leading to the subsequent formation of a rotating and strongly magnetized compact object. The mainstream collapsar model (Woosley 1993) implies the rapid formation of a maximally rotating Kerr BH at the center, accreting material from a torus and likely to lose energy through the Blandford-Znajeck mechanism (Barkov & Komissarov 2008). However, a promising alternative for the GRB central engine involves a millisecond magnetar with B ≳ 1015 G (Usov 1992). The origin of such enormous fields for magnetars is probably the efficient dynamo action during the neutrino cooling phase in the hot, deleptonizing proto-NS (Duncan & Thompson 1992). On the observational side, magnetars are the accepted explanation for anomalous X-ray pulsars and soft gamma-ray repeaters (Kouveliotou et al. 1998).
On the computational side, the past decade has witnessed a very rapid evolution in the construction of shock-capturing codes for general relativistic MHD (GRMHD) in both static and dynamical spacetimes, with a wealth of astrophysical applications to the situations outlined above (Font 2008). In the present paper we describe a novel code for GRMHD in dynamical spacetimes, named X-ECHO, aimed at studying the evolution of magnetized relativistic stars and the gravitational collapse of the magnetized rotating cores of massive stars. X-ECHO is built on top of the Eulerian conservative high-order code (Del Zanna et al. 2007) for GRMHD in a given and stationary background metric (Cowling approximation), which in turn has upgraded the previous version for a Minkowskian spacetime (Del Zanna & Bucciantini 2002; Del Zanna et al. 2003). ECHO relies on robust shock-capturing methods within a finite-difference discretization scheme (two-wave Riemann solvers and limited high-order reconstruction routines), with a staggered constrained-transport method used to preserve the divergence-free condition for the magnetic field (to machine accuracy for second order of spatial accuracy), as proposed by Londrillo & Del Zanna (2000, 2004). The ECHO code has already been successfully applied to a variety of astrophysical situations involving magnetized plasmas around compact objects, like the dynamics and non-thermal emission of pulsar wind nebulae (Bucciantini et al. 2003; Del Zanna et al. 2004; Bucciantini et al. 2004, 2005a,b; Del Zanna et al. 2006; Volpi et al. 2008), emission of relativistic MHD winds from rotating NSs (Bucciantini et al. 2006), magnetar winds producing long GRB jets escaping the stellar progenitor (Bucciantini et al. 2008, 2009), and post-merger accreting disks around Kerr BHs (Zanotti et al. 2010). Although the code is fully 3D, because of the nature of the sources, invariably a plasma surrounding a central compact object, all the above applications were performed in 2D axisymmetric spacetimes using spherical-type coordinates (either in Minkowski, Schwarzschild, or Kerr metric). The X-ECHO version presented and tested here shares the same philosophy, and, in view of the future applications mentioned above, only the axisymmetric case is considered.
The Einstein and GRMHD equations in X-ECHO are written by fully exploiting the so-called 3 + 1 formalism (like in ECHO), in which the original equations are split into their temporal and spatial components. The 3 + 1 formalism is nowadays adopted in basically all numerical schemes for general relativity (Alcubierre 2008; Baumgarte & Shapiro 2010), where the system of Einstein equations is treated like a Cauchy problem with some initial data to be evolved in time through hyperbolic equations. However, as for the solenoidal condition for the magnetic field, non-evolutionary constraints must be preserved in the numerical evolution, and computational methods for modern codes are divided into two main classes: 1) free-evolution schemes, mainly based on hyperbolic equations alone, where this problem is alleviated by appropriate reformulations of the equations (BSSN: Shibata & Nakamura 1995; Baumgarte & Shapiro 1999), eventually with the addition of propagating modes and damping terms (Z4: Bona et al. 2003; Bernuzzi & Hilditch 2010); 2) fully constrained schemes, where the constraints are enforced at each timestep through the solution of elliptic equations (Bonazzola et al. 2004), a more robust but computationally demanding option, since elliptic solvers are notoriously difficult to parallelize. Most of the state-of-the-art 3D codes for GRMHD in dynamical spacetimes are based on free-evolution schemes in Cartesian coordinates (Duez et al. 2005; Shibata & Sekiguchi 2005; Anderson et al. 2006; Giacomazzo & Rezzolla 2007; Montero et al. 2008; Farris et al. 2008), and have been used for gravitational collapse in the presence of magnetized plasmas (Duez et al. 2006a; Shibata et al. 2006a,b; Stephens et al. 2007, 2008), evolution of NSs (Duez et al. 2006b; Kiuchi et al. 2008; Liebling et al. 2010), binary NS mergers (Anderson et al. 2008; Liu et al. 2008; Giacomazzo et al. 2009, 2011), and accreting tori around Kerr BHs (Montero et al. 2010).
Provided the emission of gravitational waves is not of primary interest, a good option in the class of the fully constrained schemes is represented by the conformally flat condition (CFC) schemes (e.g. Wilson & Mathews 2003; Isenberg 2008), an approximation often employed for studying gravitational collapse or NS stability and evolution (Dimmelmeier et al. 2002; Saijo 2004; Dimmelmeier et al. 2006; Cerdá-Durán et al. 2008; Abdikamalov et al. 2009). CFC is typically associated to axisymmetric configurations and spherical coordinates, and it is exact in the spherically symmetric case. Deviations from full GR solutions in the axisymmetric case for this kind of application have already been shown to be negligible (Shibata & Sekiguchi 2004; Ott et al. 2007), though the nonlinear equations may show serious uniqueness problems for highly compact NSs or nascent BHs (see Cordero-Carrión et al. 2009, and references therein). Moreover, CFC requires the solution of all the elliptic equations for the metric terms at the same time, usually by means of iteration of Poisson solvers, together with the inversion of conservative to primitive fluid/MHD variables, another iterative numerical process. All these difficulties have been resolved recently by the extended conformally flat condition (XCFC) formulation (Cordero-Carrión et al. 2009): all the elliptic equations (now eight rather than five) are hierarchically decoupled and local uniqueness is ensured (see also Saijo 2004), thus this it is our choice for X-ECHO.
In the present work we propose and test a new numerical solver based on XCFC for an axisymmetric spacetime in conformally flat spherical-like coordinates. We employed the same numerical grid as was used for the evolution of the fluid and magnetic quantities through the ECHO scheme, and the Poisson-like equations are solved through a hybrid method based on spherical harmonics decomposition and direct inversion of band diagonal matrices, resulting from a second-order finite-difference discretization of the radial equations, for each harmonic. As a side product, we built and make available to the community a numerical code based on XCFC to produce self-consistent GRMHD axisymmetric equilibria for polytropic relativistic stars in the presence of differential rotation and toroidal magnetic fields, here named XNS. Both XNS and the full X-ECHO codes are validated through several tests of astrophysical interest, including accuracy checks in the initial data for various NS equilibrium configurations, accuracy in finding the frequencies of their normal modes of oscillations, an evolutionary test of migration of NS unstable equilibria to stable branches, a test of the stability of a differentially rotating, magnetized NS with a toroidal field, 1D and 2D collapse of an unstable NS toward a BH, and a toy collapse of a differentially rotating NS with poloidal fields, as a first step towards more realistic magneto-rotational core collapse simulations.
The paper is structured as follows. In Sect. 2 we
introduce and review the Einstein equations in the 3 + 1 formalism, first in their general
form and then specialized in the CFC approximation, and we review the GRMHD equations. In
Sect. 3 we discuss the new numerical XCFC solver
assuming axisymmetry and spherical coordinates for the conformal flat 3-metric, whereas the
description of our novel XNS code for NS initial data can be found in Sect. 4. Numerical validation and testing of various cases of NS
equilibria, oscillations and collapse are presented in Sect. 5, while Sect. 6 is devoted to the
conclusions. In the following we assume a signature {−, +, +, +} for the spacetime
metric and use Greek letters μ,ν,λ,... (running from 0 to
3) for 4D spacetime tensor components, while Latin letters
i,j,k,... (running from 1 to 3) are employed for 3D
spatial tensor components. Moreover, we set
c = G = M⊙ = 1, and we
absorb the 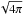 factors in the definition of the electromagnetic quantities.
factors in the definition of the electromagnetic quantities.
2. Basic equations in the 3 + 1 formalism
In the present section we present the 3 + 1 formalism for Einstein equations. Further details can be found in recent books and reviews of 3 + 1 numerical relativity (Gourgoulhon 2007; Alcubierre 2008; Baumgarte & Shapiro 2010). We briefly discuss the constrained evolution schemes, focusing on the elliptic CFC and XCFC solvers. Finally, in Sect. 2.3 we review the GRMHD equations in 3 + 1 conservative form, as implemented in the original ECHO scheme (Del Zanna et al. 2007).
2.1. The Einstein equations for conformal flatness
The field equations of general relativity expressed in the 4D fully covariant form
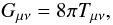 (1)where
Gμν is the Einstein tensor containing the
derivatives of the metric tensor gμν, and
Tμν is the matter and/or electromagnetic
energy-momentum tensor, are not appropriate for numerical computations since time and
space are treated on an equal footing, whereas one would like to cast them in the form of
an initial value (or Cauchy) problem and evolve them in time. The most widely used
approach to this goal is based on the so-called 3 + 1 formalism, in which the generic
spacetime (ℳ,gμν) is split into space-like
hyper-surfaces Σt. If
nμ indicates the time-like unit normal
to Σt (also known as the velocity of the Eulerian
observer,
nμnμ = −1),
the induced threemetric on each hypersurface and the related extrinsic curvature
can be defined respectively as
(1)where
Gμν is the Einstein tensor containing the
derivatives of the metric tensor gμν, and
Tμν is the matter and/or electromagnetic
energy-momentum tensor, are not appropriate for numerical computations since time and
space are treated on an equal footing, whereas one would like to cast them in the form of
an initial value (or Cauchy) problem and evolve them in time. The most widely used
approach to this goal is based on the so-called 3 + 1 formalism, in which the generic
spacetime (ℳ,gμν) is split into space-like
hyper-surfaces Σt. If
nμ indicates the time-like unit normal
to Σt (also known as the velocity of the Eulerian
observer,
nμnμ = −1),
the induced threemetric on each hypersurface and the related extrinsic curvature
can be defined respectively as
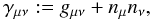 (2)
(2)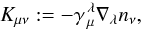 (3)where
∇μ is the covariant derivative with respect to
gμν (so that
∇λgμν = 0). In
general, any fourvector or tensor can be decomposed into normal and spatial components by
contracting with −nμ or with the
projector
(3)where
∇μ is the covariant derivative with respect to
gμν (so that
∇λgμν = 0). In
general, any fourvector or tensor can be decomposed into normal and spatial components by
contracting with −nμ or with the
projector 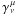 ,
respectively. In particular, both γμν and
Kμν are purely spatial (and symmetric)
tensors.
,
respectively. In particular, both γμν and
Kμν are purely spatial (and symmetric)
tensors.
If
xμ: = (t,xi)
are the spacetime coordinates adapted to the foliation of ℳ introduced above, the line
element is usually written in the so-called ADM form
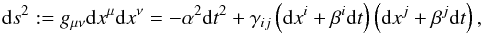 (4)where the lapse
function α and the shift vector
βi (a purely spatial vector) are
free gauge functions. In this adapted coordinate system, the unit normal
vector has components
nμ = (1/α, − βi/α)
and
nμ = (−α,0i).
In the 3 + 1 formalism, the Einstein equations of Eq. (1) are split into a set of evolutionary equations for
γij and the extrinsic curvature
Kij
(4)where the lapse
function α and the shift vector
βi (a purely spatial vector) are
free gauge functions. In this adapted coordinate system, the unit normal
vector has components
nμ = (1/α, − βi/α)
and
nμ = (−α,0i).
In the 3 + 1 formalism, the Einstein equations of Eq. (1) are split into a set of evolutionary equations for
γij and the extrinsic curvature
Kij![\begin{eqnarray} \label{eq:evol_gamma} \partial_t \gamma_{ij} &=& -2\alpha K_{ij} + \dev_i\beta_j + \dev_j\beta_i, \\ \partial_t K_{ij} &=& \beta^k\dev_k K_{ij} + K_{ik}\dev_j\beta^k + K_{jk}\dev_i\beta^k -\dev_i\dev_j\alpha \nonumber\\ \label{eq:evol_K}&&+\, \alpha \left[R_{ij}\!+\!KK_{ij}\!-\!2K_{ik}K_j^k\right] \!+\!4\pi\alpha \left[\gamma_{ij}(S-E)\!-\!2S_{ij}\right], \end{eqnarray}](/articles/aa/full_html/2011/04/aa15945-10/aa15945-10-eq33.png) plus
a set of constraints that must be satisfied at all times
plus
a set of constraints that must be satisfied at all times  named
Hamiltonian and momentum constraints, respectively. Here
named
Hamiltonian and momentum constraints, respectively. Here
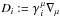 is the covariant
derivative with respect to the 3-metric γij
(so that
Dkγij = 0),
Rij is the Ricci tensor, again with respect
to γij,
is the covariant
derivative with respect to the 3-metric γij
(so that
Dkγij = 0),
Rij is the Ricci tensor, again with respect
to γij,
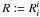 the corresponding
Ricci scalar,
the corresponding
Ricci scalar, 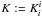 is the trace of the
extrinsic curvature. As far as the fluid sources are concerned
E: = nμnνTμν,
is the trace of the
extrinsic curvature. As far as the fluid sources are concerned
E: = nμnνTμν,
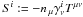 , and
, and
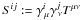 (of trace
(of trace
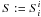 ) are, respectively,
the energy density, momentum density, and the stress-energy tensor as measured by the
Eulerian observers.
) are, respectively,
the energy density, momentum density, and the stress-energy tensor as measured by the
Eulerian observers.
The constraints introduced above are notoriously difficult to maintain in the numerical evolution of Eqs. (5) and (6), and two possible approaches can be followed. The most widely used one relies on hyperbolic formulations of the initial value problem, the constraints are imposed only for the initial data, and numerical errors are just monitored or damped during time evolution (free evolution schemes). On the other hand, the constraints can be enforced at each timestep during the numerical simulation, leading to the so-called constrained evolution schemes, where the main idea is to maximize the number of elliptic equations, usually more stable than hyperbolic equations. Moreover, in the steady state case, the set of equations should easily reduce to those used for stationary spacetimes and for the construction of initial data. An example is the so-called fully constrained formalism (FCF) for asymptotically flat spacetimes in full GR (Bonazzola et al. 2004), which contains the widely used set of CFC elliptic equations as an approximation. In the following we describe the general assumptions of conformal flatness and review the set of CFC equations.
We start by applying a Lichnerowicz conformal decomposition 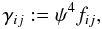 (9)assuming a flat
background metric fij
(time independent and not necessarily in Cartesian
coordinates), where the conformal factor satisfies
ψ = (γ/f)1/12, with
f: = detfij. A second
assumption is the condition of maximum slicing of foliations
(9)assuming a flat
background metric fij
(time independent and not necessarily in Cartesian
coordinates), where the conformal factor satisfies
ψ = (γ/f)1/12, with
f: = detfij. A second
assumption is the condition of maximum slicing of foliations
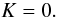 (10)Under these
assumptions, to be preserved during time evolution, the trace of Eq. (5) and its traceless part become, respectively,
(10)Under these
assumptions, to be preserved during time evolution, the trace of Eq. (5) and its traceless part become, respectively,
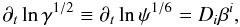 (11)
(11)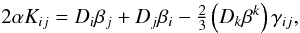 (12)where
∂tγ = 0 if, and only if,
Diβi = 0
and the extrinsic curvature can be expressed in terms of derivatives of the shift vector
alone. The next step is to use covariant derivatives associated to the flat 3-metric
fij, which will be indicated here by the
usual nabla operator ∇i (and
∇kfij = 0).
When Eq. (9) holds, it is possible to
demonstrate that the Ricci scalar for γij
(that for fij is zero) is
(12)where
∂tγ = 0 if, and only if,
Diβi = 0
and the extrinsic curvature can be expressed in terms of derivatives of the shift vector
alone. The next step is to use covariant derivatives associated to the flat 3-metric
fij, which will be indicated here by the
usual nabla operator ∇i (and
∇kfij = 0).
When Eq. (9) holds, it is possible to
demonstrate that the Ricci scalar for γij
(that for fij is zero) is
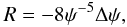 (13)in which
Δ: = ∇i∇i is the usual
Laplacian of flat space. The above relation combined first with the Hamiltonian constraint
in Eq. (7) and then with the trace of
Eq. (6) provides the following two scalar
Poisson-like equations for the conformal factor ψ and the lapse function
α
(13)in which
Δ: = ∇i∇i is the usual
Laplacian of flat space. The above relation combined first with the Hamiltonian constraint
in Eq. (7) and then with the trace of
Eq. (6) provides the following two scalar
Poisson-like equations for the conformal factor ψ and the lapse function
α![\begin{eqnarray} \Delta \psi &=& - \left[2\pi E+\textstyle{\frac{1}{8}} K_{ij}K^{ij} \right] \,\psi^5, \\ \Delta (\alpha\psi) &=& \left[2\pi (E+2S) + \textstyle{\frac{7}{8}} K_{ij}K^{ij} \right] \,\alpha\psi^5, \end{eqnarray}](/articles/aa/full_html/2011/04/aa15945-10/aa15945-10-eq58.png) where
we still need to write Kij in terms of flat
space derivatives of the shift vector.
where
we still need to write Kij in terms of flat
space derivatives of the shift vector.
To the traceless extrinsic curvature 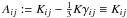 is then applied a
conformal time-evolution rescaling
is then applied a
conformal time-evolution rescaling 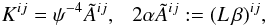 (16)where the
conformal Killing operator associated to the flat metric and applied to
the vector βi is defined as
(16)where the
conformal Killing operator associated to the flat metric and applied to
the vector βi is defined as
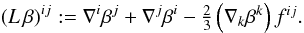 (17)This scaling is
also employed in the so-called conformal thin sandwich (CTS) approach to
initial data. This scaling is quite natural, because of Eq. (12), and since, within a conformally flat decomposition of the metric,
we have
(17)This scaling is
also employed in the so-called conformal thin sandwich (CTS) approach to
initial data. This scaling is quite natural, because of Eq. (12), and since, within a conformally flat decomposition of the metric,
we have 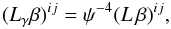 (18)where
Lγ indicates the conformal Killing operator
associated to γij. On the other hand, in
conformal flatness we also have
(18)where
Lγ indicates the conformal Killing operator
associated to γij. On the other hand, in
conformal flatness we also have 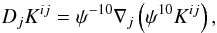 (19)to be used with the
above rescaling in the momentum constraint to find an equation for
βi.
(19)to be used with the
above rescaling in the momentum constraint to find an equation for
βi.
Thanks to all the relations derived so far, the final set of CFC elliptic equations may
be written in terms of the sources and of 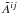 (containing
α and first derivatives of
βi) as
(containing
α and first derivatives of
βi) as ![\begin{eqnarray} \label{eq:cfc_psi}\Delta \psi &=& - \left[2\pi E+ \textstyle{\frac{1}{8}}f_{ik}f_{jl}\Atil^{ij}\Atil^{kl} \right] \,\psi^5 , \\ \label{eq:cfc_alpha}\Delta (\alpha\psi) &=& \left[2\pi (E+2S) + \textstyle{\frac{7}{8}} f_{ik}f_{jl}\Atil^{ij}\Atil^{kl} \right] \,\alpha\psi^5, \\ \label{eq:cfc_beta}\Delta_L \,\beta^i &=& 16\pi \alpha \psi^4 S^i + 2\psi^6 \Atil^{ij}\der_j \left(\alpha\psi^{-6}\right), \end{eqnarray}](/articles/aa/full_html/2011/04/aa15945-10/aa15945-10-eq66.png) where
where
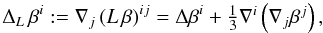 (23)is the so-called
conformal vector Laplacian operator, associated to the flat 3-metric
fij and applied to
βi.
(23)is the so-called
conformal vector Laplacian operator, associated to the flat 3-metric
fij and applied to
βi.
2.2. From CFC to XCFC
A slightly different approach to the Einstein equations for asymptotically flat spacetimes has been presented recently (Cordero-Carrión et al. 2009). This involves a rewriting of the elliptical part of the FCF system for full GR through a different decomposition of the extrinsic curvature. Here we just describe its conformal flatness approximation, leading to the so-called extended conformal flatness condition (XCFC) system of elliptic equations, improving on the CFC ones described in the previous section. The set of XCFC equations is our choice for the metric evolution in X-ECHO.
The new approach still relies on the usual conformal decomposition in Eq. (9) and on the maximum slicing condition of
Eq. (10), but the choice for the
decomposition of the (traceless) extrinsic curvature is different. We use here the
momentum-constraint rescaling and the so-called York conformal
transverse traceless (CTT) decomposition, first introduced for initial data,
that is 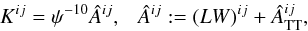 (24)where the
conformal Killing operator associated to the unknown vector
Wi gives the longitudinal
part of
(24)where the
conformal Killing operator associated to the unknown vector
Wi gives the longitudinal
part of 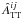 , whereas
, whereas
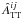 is a
transverse (
is a
transverse (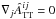 ), traceless
(
), traceless
(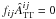 ) tensor. Consistency between the
CTS and CTT decompositions (notice that
) tensor. Consistency between the
CTS and CTT decompositions (notice that 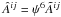 ) should require a
non-vanishing
) should require a
non-vanishing 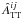 . However, it
has been demonstrated that this quantity is even smaller than the non-conformal part of
the spatial metric within the CFC approach, so can be safely neglected on the level of the
CFC approximation. Thus, as an additional hypothesis,we set
. However, it
has been demonstrated that this quantity is even smaller than the non-conformal part of
the spatial metric within the CFC approach, so can be safely neglected on the level of the
CFC approximation. Thus, as an additional hypothesis,we set
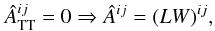 (25)so that
Âij is defined in terms of the auxiliary
vector Wi alone. The latter is derived from
the momentum constraint using Eq. (19),
which is simply
(25)so that
Âij is defined in terms of the auxiliary
vector Wi alone. The latter is derived from
the momentum constraint using Eq. (19),
which is simply 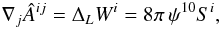 (26)to be added to the other
CFC equations.
(26)to be added to the other
CFC equations.
The final augmented set of CFC elliptic equations, also known as XCFC
equations, is then the following ![\begin{eqnarray} \Delta_L W^i &=& 8\pi f^{ij}\Sbar_j, \\ \label{eq:xcfc_psi}\Delta \psi &=& - 2\pi\Ebar\, \psi^{-1} - \textstyle{\frac{1}{8}}f_{ik}f_{jl}\Ahat^{kl}\Ahat^{ij}\, \psi^{-7} , \\ \label{eq:xcfc_alpha}\Delta (\alpha\psi) &=& \left[2\pi \left(\Ebar+2\Sbar\right)\, \psi^{-2} + \textstyle{\frac{7}{8}} f_{ik}f_{jl}\Ahat^{kl}\Ahat^{ij} \, \psi^{-8} \right] \, \alpha\psi, \\ \label{eq:xcxf_beta}\Delta_L \,\beta^i &=& 16\pi \,\alpha\psi^{-6} f^{ij}\Sbar_j + 2\Ahat^{ij}\der_j \left(\alpha\psi^{-6}\right), \end{eqnarray}](/articles/aa/full_html/2011/04/aa15945-10/aa15945-10-eq77.png) where
for convenience we have introduced rescaled fluid source terms of the form
where
for convenience we have introduced rescaled fluid source terms of the form
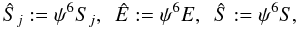 (31)and we recall that
(31)and we recall that
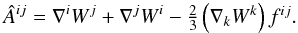 (32)Some comments and
comparisons between the CFC and XCFC sets of equations are now due.
(32)Some comments and
comparisons between the CFC and XCFC sets of equations are now due.
-
There are now 8 rather than 5 (Wi, ψ, α, βi) unknown functions, and this is reflected by the augmented number of elliptic equations. There is a new vector Poisson equation for the auxiliary variable Wi.
-
While all the equations were strongly coupled in CFC, here the equations can be solved hierarchically one by one, in the given order, since each right-hand side just contains known functions or the variable itself (in the two scalar Poisson-like equations for ψ and αψ).
-
As we will see in the next subsection, schemes for general relativistic hydrodynamics or MHD (like ECHO), given a metric in 3 + 1 form, actually evolve the conservative variables γ1/2Sj and γ1/2E in time, rather than Si and E. Since ψ6 = γ1/2/f1/2 and f1/2 is known and time-independent, the sources Ŝj and Ê are basically known after each computational timestep without the need of an updated value of ψ. This will only be needed to work out Ŝ = ψ6γijSij, after the new value of ψ has been provided by Eq. (28) and the inversion of conservative to primitive variables has been achieved. Primitive variables are then updated self-consistently together with the new values for the metric, whereas this was not possible in CFC. In that case, one could either use Eq. (11) to derive a guess of the updated ψ (a method easily prone to both convergence problems and discretization errors), or one is forced to iterate simultaneously over the metric solver (the whole CFC set) and the inversion routine for the primitive variables (typically itself a numerical iterative Raphson-Newton method).
-
The last, and certainly not least, issue is related to the mathematical nature of the scalar Poisson-like equations. In both cases we have a structure of the form
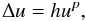 (33)where
u is the generic variable (ψ or
αψ), h is the generic source term, and
p provides the exponent of the non-linearity
(p = 0 for a canonical Poisson equation). It can be demonstrated
that the condition ph ≥ 0 implies that the solution
u is locally unique. While this is always true
in XCFC, since we have two contributions with p = −1 and
p = −7, both with h ≤ 0, in Eq. (28), and one contribution with
p = + 1 and h ≥ 0 in Eq. (29), local uniqueness cannot be
guaranteed for the CFC system, since Eq. (21) contains a term that certainly violates the requirement (the second
one, due to the presence of a factor α-1 in
(33)where
u is the generic variable (ψ or
αψ), h is the generic source term, and
p provides the exponent of the non-linearity
(p = 0 for a canonical Poisson equation). It can be demonstrated
that the condition ph ≥ 0 implies that the solution
u is locally unique. While this is always true
in XCFC, since we have two contributions with p = −1 and
p = −7, both with h ≤ 0, in Eq. (28), and one contribution with
p = + 1 and h ≥ 0 in Eq. (29), local uniqueness cannot be
guaranteed for the CFC system, since Eq. (21) contains a term that certainly violates the requirement (the second
one, due to the presence of a factor α-1 in
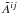 ).
).
2.3. The GRMHD equations and the ECHO scheme
The equations for an ideal, magnetized, perfectly conducting plasma are
 the
continuity equation, the conservation law for momentum-energy, and the sourceless Maxwell
equation, respectively. Here ρ is the mass density as measured in the
frame comoving with the fluid fourvelocity
uμ, and the total momentum-energy tensor
is
the
continuity equation, the conservation law for momentum-energy, and the sourceless Maxwell
equation, respectively. Here ρ is the mass density as measured in the
frame comoving with the fluid fourvelocity
uμ, and the total momentum-energy tensor
is 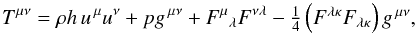 (37)with
h = 1 + ε + p/ρ
the specific enthalpy, ϵ the specific internal energy,
p = p(ρ,ε) the thermal pressure
(provided by some form of equation of state, EoS). Moreover,
Fμν is the Faraday (antisymmetric)
electromagnetic tensor, with the associated dual
(37)with
h = 1 + ε + p/ρ
the specific enthalpy, ϵ the specific internal energy,
p = p(ρ,ε) the thermal pressure
(provided by some form of equation of state, EoS). Moreover,
Fμν is the Faraday (antisymmetric)
electromagnetic tensor, with the associated dual 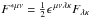 , where
ϵ μνλκ = (−g)−1/2 [μνλκ]
is the spacetime Levi-Civita pseudo-tensor
(ϵμνλκ = − (−g)1/2 [μνλκ]),
with g = detgμν, and
[μνλκ] is the alternating Levi-Civita symbol. The system is closed
by Ohm’s law for a perfectly conducting plasma, which becomes a constraint for a vanishing
electric field in the frame comoving with the fluid
, where
ϵ μνλκ = (−g)−1/2 [μνλκ]
is the spacetime Levi-Civita pseudo-tensor
(ϵμνλκ = − (−g)1/2 [μνλκ]),
with g = detgμν, and
[μνλκ] is the alternating Levi-Civita symbol. The system is closed
by Ohm’s law for a perfectly conducting plasma, which becomes a constraint for a vanishing
electric field in the frame comoving with the fluid 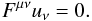 (38)This basically
replaces the Maxwell equation
∇μFμν = −Jν,
where the fourcurrent Jν is a derived
quantity as in classical MHD.
(38)This basically
replaces the Maxwell equation
∇μFμν = −Jν,
where the fourcurrent Jν is a derived
quantity as in classical MHD.
To derive the GRMHD equations in 3 + 1 form, as employed in ECHO, we must decompose all
fourvectors and tensors into their spatial and temporal components on each slice
Σt of the time evolution. This can be easily achieved by
using the unit normal vector nμ introduced
in the previous section 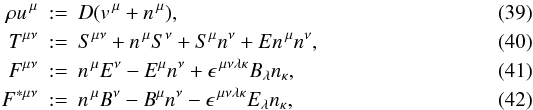 where
every new quantity is now purely spatial, as measured by the Eulerian observer. In
particular, D: = ρΓ is the rest mass density,
vi is the fluid velocity,
Γ: = (1 − vivi)−1/2
is the usual Lorentz factor, whose definition follows from the condition
uμuμ = −1.
The stress-energy 3-tensor Sij, its trace
S, the momentum density
Si, and the energy density E
are the same quantities appearing in the 3 + 1 Einstein equations (notations have been
slightly modified with respect to the original ECHO paper), and are respectively given by
where
every new quantity is now purely spatial, as measured by the Eulerian observer. In
particular, D: = ρΓ is the rest mass density,
vi is the fluid velocity,
Γ: = (1 − vivi)−1/2
is the usual Lorentz factor, whose definition follows from the condition
uμuμ = −1.
The stress-energy 3-tensor Sij, its trace
S, the momentum density
Si, and the energy density E
are the same quantities appearing in the 3 + 1 Einstein equations (notations have been
slightly modified with respect to the original ECHO paper), and are respectively given by
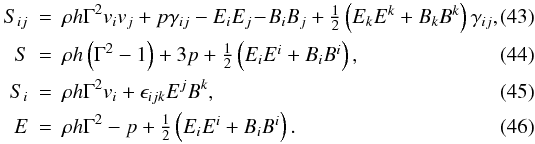 The
electric and magnetic fields as measured by the Eulerian observer are defined as
The
electric and magnetic fields as measured by the Eulerian observer are defined as
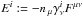 and
and
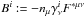 .
Because of condition in Eq. (38), the
electric field is a derived quantity precisely as in classical MHD
.
Because of condition in Eq. (38), the
electric field is a derived quantity precisely as in classical MHD
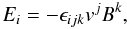 (47)where
ϵijk = γ1/2 [ijk]
(ϵijk = γ−1/2 [ijk])
is the Levi-Civita pseudo-tensor for the 3-metric
γij, and [ijk] is
the alternating symbol taking values + 1, −1, or 0.
(47)where
ϵijk = γ1/2 [ijk]
(ϵijk = γ−1/2 [ijk])
is the Levi-Civita pseudo-tensor for the 3-metric
γij, and [ijk] is
the alternating symbol taking values + 1, −1, or 0.
Thanks to the above decompositions, the GRMHD equations can be entirely rewritten in
terms of purely spatial vectors, while retaining the original conservation form. We end up
with a subset of fluid-like balance laws in divergence form 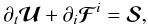 (48)plus a magnetic subset
with the induction equation in curl form and the associated divergence-free condition, to
be preserved at all times during evolution
(48)plus a magnetic subset
with the induction equation in curl form and the associated divergence-free condition, to
be preserved at all times during evolution ![\begin{equation} \partial_t \mathcal{B}^i + [ijk] \partial_j \mathcal{E}_k = 0,~~~\partial_i \mathcal{B}^i=0. \label{eq:dbdt} \end{equation}](/articles/aa/full_html/2011/04/aa15945-10/aa15945-10-eq136.png) (49)The set of
conservative fluid variables and the set of associated fluxes are,
respectively
(49)The set of
conservative fluid variables and the set of associated fluxes are,
respectively ![\begin{equation} \vec{\mathcal{U}} := \gamma^{1/2}\!\left[\begin{array}{c} \!D\! \\ \!S_j\! \\ \!E\! \end{array}\right],~~~ \vec{\mathcal{F}}^i := \gamma^{1/2}\!\left[\begin{array}{c} \! (\alpha v^i - \beta^i) D \! \\ \!\alpha S^i_j-\beta^i S_j\! \\ \!\alpha S^i-\beta^i E\! \end{array}\right], \end{equation}](/articles/aa/full_html/2011/04/aa15945-10/aa15945-10-eq137.png) (50)whereas the set of source
terms contain the derivative of the metric and thus the curvature effects
(50)whereas the set of source
terms contain the derivative of the metric and thus the curvature effects
![\begin{equation} \vec{\mathcal{S}} := \gamma^{1/2}\!\left[\begin{array}{c} 0 \\ \frac{1}{2}\alpha S^{ik}\partial_j\gamma_{ik}+ S_i\partial_j\beta^i-E\partial_j\alpha \\ \alpha K_{ij}S^{ij}-S^j\partial_j\alpha\! \end{array}\right]\!. \end{equation}](/articles/aa/full_html/2011/04/aa15945-10/aa15945-10-eq138.png) (51)Here
Kij is the extrinsic curvature introduced
in the previous section, whose evolution is directly provided by the Einstein equations in
the 3 + 1 formalism, together with γij, or
may be given in terms of the derivatives of the metric terms. For a dynamical spacetime
under the maximal slicing condition, from Eq. (12) we can write
(51)Here
Kij is the extrinsic curvature introduced
in the previous section, whose evolution is directly provided by the Einstein equations in
the 3 + 1 formalism, together with γij, or
may be given in terms of the derivatives of the metric terms. For a dynamical spacetime
under the maximal slicing condition, from Eq. (12) we can write ![\begin{equation} \alpha K_{ij}S^{ij}=\textstyle{\frac{1}{2}}\beta^jS^{ik}\partial_j\gamma_{ik} + S_i^j\partial_j\beta^i - \textstyle{\frac{1}{3}} [\gamma^{-1/2}\partial_i(\gamma^{1/2}\beta^i)] S, \end{equation}](/articles/aa/full_html/2011/04/aa15945-10/aa15945-10-eq139.png) (52)and the same
expression without the last term may be used for any stationary spacetime (Cowling
approximation). As far as the induction equation is concerned, we have defined
(52)and the same
expression without the last term may be used for any stationary spacetime (Cowling
approximation). As far as the induction equation is concerned, we have defined
![\begin{eqnarray} \mathcal{B}^i \! &:=& \! \gamma^{1/2}B^i, \\ \mathcal{E}_i \! &:=& \! \alpha E_i + \epsilon_{ijk}\beta^jB^k \! = \! - \gamma^{1/2}[ijk]\left(\alpha v^j-\beta^j\right)B^k, \end{eqnarray}](/articles/aa/full_html/2011/04/aa15945-10/aa15945-10-eq140.png) where
the vector
αvi−βi
is sometimes called transport velocity. The induction equation may also be written in the
equivalent divergence form as
where
the vector
αvi−βi
is sometimes called transport velocity. The induction equation may also be written in the
equivalent divergence form as ![\begin{equation} \partial_t \mathcal{B}^j + \partial_i \{ \gamma^{1/2} [(\alpha v^i - \beta^i)B^j - B^i(\alpha v^j - \beta^j)] \}=0, \end{equation}](/articles/aa/full_html/2011/04/aa15945-10/aa15945-10-eq142.png) (55)and the antisymmetric
nature of the magnetic fluxes reflects that of the original electromagnetic tensor.
Regardless of the adopted choice for the form of the induction equation, we have a final
set of eight hyperbolic equations. Usually the corresponding variables are named
primitive variables, for example the set
(55)and the antisymmetric
nature of the magnetic fluxes reflects that of the original electromagnetic tensor.
Regardless of the adopted choice for the form of the induction equation, we have a final
set of eight hyperbolic equations. Usually the corresponding variables are named
primitive variables, for example the set
![\begin{equation} \vec{\mathcal{P}}:=\left[\rho,v^i,p,B^i\right]^{\rm T}, \end{equation}](/articles/aa/full_html/2011/04/aa15945-10/aa15945-10-eq143.png) (56)for which
(56)for which
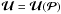 ,
,
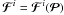 ,
and
,
and 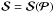 ,
where for simplicity we consider here the augmented system with
ℬj in
,
where for simplicity we consider here the augmented system with
ℬj in 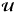 .
.
As discussed in the previous section, the inversion of the non-linear system
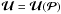 to recover the set of primitive variables is achieved through a numerical iterative scheme
and requires knowledge of the volume element γ1/2, for
consistency updated at the same time level as
to recover the set of primitive variables is achieved through a numerical iterative scheme
and requires knowledge of the volume element γ1/2, for
consistency updated at the same time level as 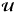 .
Moreover, as discussed in Del Zanna et al. (2007),
the conservative to primitive variables inversion is the most delicate part of a
relativistic MHD code, as high Lorentz factor flows or strong magnetic fields (i.e. in an
NS magnetosphere) may easily lead to errors in the values of the conservative variables.
The whole procedure can be reduced to the solution of two coupled nonlinear equations, for
any given EoS. In X-ECHO we leave complete freedom in the choice
p = p(ρ,ε), however in the present
paper, given the nature of the numerical tests proposed, we limit this choice to either an
ideal γ-law EoS
.
Moreover, as discussed in Del Zanna et al. (2007),
the conservative to primitive variables inversion is the most delicate part of a
relativistic MHD code, as high Lorentz factor flows or strong magnetic fields (i.e. in an
NS magnetosphere) may easily lead to errors in the values of the conservative variables.
The whole procedure can be reduced to the solution of two coupled nonlinear equations, for
any given EoS. In X-ECHO we leave complete freedom in the choice
p = p(ρ,ε), however in the present
paper, given the nature of the numerical tests proposed, we limit this choice to either an
ideal γ-law EoS 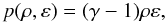 (57)or to a
polytropic law EoS
(57)or to a
polytropic law EoS 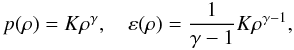 (58)where
γ and K are given constants. When the first option is
used, the root-finding procedure solves for the variable
x = vivi,
according to the third method described in the ECHO paper, where the nested second
equation (a cubic) for y = ρhΓ2 can be solved
either analytically or iteratively with an inner loop (and we typically adopt this latter
choice). When
SiBi = 0,
or in general for a purely fluid simulation, the equation for y is linear
and can be solved readily. On the other hand, for a polytropic law, the energy equation
becomes redundant, since all thermodynamical quantities are now functions of the density
alone, and the overall inversion procedure simply reduces to a root-finding iterative
solver for x.
(58)where
γ and K are given constants. When the first option is
used, the root-finding procedure solves for the variable
x = vivi,
according to the third method described in the ECHO paper, where the nested second
equation (a cubic) for y = ρhΓ2 can be solved
either analytically or iteratively with an inner loop (and we typically adopt this latter
choice). When
SiBi = 0,
or in general for a purely fluid simulation, the equation for y is linear
and can be solved readily. On the other hand, for a polytropic law, the energy equation
becomes redundant, since all thermodynamical quantities are now functions of the density
alone, and the overall inversion procedure simply reduces to a root-finding iterative
solver for x.
3. The XCFC solver for axisymmetric spacetimes
The X-ECHO code for GRMHD in dynamical spacetimes is built upon the ECHO scheme, coupled to a novel solver for the XCFC equations described in Sect. 2.2. All the necessary definitions and equations have been provided in the previous section, and we reduce here the equations to the particular implementation of X-ECHO we are mostly interested in, which assumes axisymmetric GRMHD configurations, adopting spherical-like coordinates xi = (r,θ,φ) for the conformal flat metric.
Thus, as a first step we assume in Eq. (9)
the usual spherical coordinates 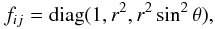 (59)so that
(59)so that ![\begin{eqnarray} {\rm d}s^2&=&-\alpha^2 {\rm d}t^2+\psi^4\left[\left({\rm d}r+\beta^r{\rm d}t\right)^2+ r^2\left({\rm d}\theta+\beta^\theta {\rm d}t\right)^2 \right. \nonumber\\ \label{eq:cfc_sph}&&\left.+r^2\sin^2\theta\left({\rm d}\phi+\beta^\phi {\rm d}t\right)^2\right], \end{eqnarray}](/articles/aa/full_html/2011/04/aa15945-10/aa15945-10-eq161.png) (60)with
f1/2 = r2sinθ
and
γ1/2 = ψ6 r2sinθ.
Moreover, we are going to consider the axisymmetric case, thus the condition
(60)with
f1/2 = r2sinθ
and
γ1/2 = ψ6 r2sinθ.
Moreover, we are going to consider the axisymmetric case, thus the condition
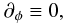 (61)is assumed
throughout the paper. Within the flat metric
fij, it is convenient to introduce the
orthonormal basis
(61)is assumed
throughout the paper. Within the flat metric
fij, it is convenient to introduce the
orthonormal basis 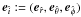 ,
with
,
with 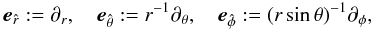 (62)for which
fîĵ = diag(1,1,1), where a
similar notation as in Bonazzola et al. (2004) has
been assumed. Any generic vector X can be expressed then in
the usual form as
(62)for which
fîĵ = diag(1,1,1), where a
similar notation as in Bonazzola et al. (2004) has
been assumed. Any generic vector X can be expressed then in
the usual form as 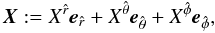 (63)where the orthonormal
(with respect to fij) components
Xî are, respectively
(63)where the orthonormal
(with respect to fij) components
Xî are, respectively
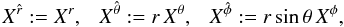 (64)while the relation to
covariant components still involves the function ψ, since
Xi = ψ4fijXj.
As far as covariant derivatives are concerned, the change of basis allows one to use the
∇î operator of spherical coordinates. In particular, the
Laplacian of a generic scalar function u(r,θ) is
(64)while the relation to
covariant components still involves the function ψ, since
Xi = ψ4fijXj.
As far as covariant derivatives are concerned, the change of basis allows one to use the
∇î operator of spherical coordinates. In particular, the
Laplacian of a generic scalar function u(r,θ) is
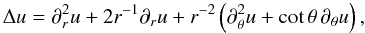 (65)whereas the orthonormal
components of the conformal vector Laplacian are, respectively
(65)whereas the orthonormal
components of the conformal vector Laplacian are, respectively 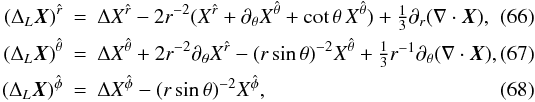 where
the divergence of X is
where
the divergence of X is 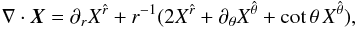 (69)precisely the formulae
of vector calculus in spherical coordinates.
(69)precisely the formulae
of vector calculus in spherical coordinates.
The Poisson-like elliptic equations used in XCFC to compute the eight metric terms consist
of two scalar equations in the form of Eq. (33), for the variables u = ψ and
u = αψ, and two vector equations for the generic unknown
vector
Xi = Wi
and
Xi = βi.
Due to non-linearity, the scalar equations are better solved iteratively for the quantity
qn: = un − 1,
which in both cases gives the deviation from asymptotic flatness ψ → 1 and
α → 1, where the new value at step n is computed using
the previous value at step n − 1 in the source term, until convergence is
reached within some prescribed tolerance. Summarizing, the metric equations are expressed in
one of the two generic forms 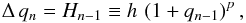 (70)and, using the
orthonormal basis introduced above,
(70)and, using the
orthonormal basis introduced above, 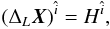 (71)where
h and H are generic scalar and vector
source terms, to be provided by the XCFC equations, so that both the right-hand sides above
are known functions of (r,θ).
(71)where
h and H are generic scalar and vector
source terms, to be provided by the XCFC equations, so that both the right-hand sides above
are known functions of (r,θ).
Numerical methods available for solving these elliptic partial differential equations (PDEs) can be divided into three main categories (see, for methods and discussions Grandclément et al. 2001; Dimmelmeier et al. 2005; Grandclément & Novak 2009): direct inversion, full relaxation, spectral decomposition. Direct inversion codes are able to solve the complete system of CFC (or XCFC) at once using Newton-Raphson solver (or any other inversion technique) on the entire computational grid over which the metric solution is desired. They have very good convergence to machine accuracy within a few steps, but they suffer serious limitations: the initial guess must be close enough to the solution to avoid convergence on local minima (instead of global minima). The memory requirement for matrix allocation is typically very large (usually a sparse matrix is needed in the whole 2D domain); in general, direct inversion schemes solve the metric on smaller grids than the one over which the fluid variables are evolved and require interpolation between the two, with problems that may arise at the boundaries. Full relaxation codes use SOR, multigrid, or other relaxation techniques. The schemes are fast and require little memory allocation, but usually suffer from poor convergence properties: the convergence is in general slow (compared to direct or spectral schemes) and might fail on the axis or at the center due to the singular nature of some metric elements. Spectral schemes decompose the set of CFC (or XCFC) equations using a combination of spherical harmonics (based on Legendre polynomials) in the angular directions and Chebyshev polynomials in the radial direction. This ensures a correct behavior on the axis and at the center even with a limited number of eigenfunctions, but they require specific grids and sometimes complex compactifications or multi-domain decomposition techniques with appropriate boundary conditions for each multipole and each domain. The metric solver in X-ECHO uses a mixed technique. In the angular direction we use a decompition in spherical harmonics, to preserve the correct asymptotic form on the axis. However, the set of ordinary differential equations (ODEs) obtained for each harmonic is then solved using direct inversion over the same radial grid as in the GRMHD code, with no need for interpolation or compactification. At second-order accuracy in a finite difference discretization, the scalar equations reduce to the simple inversion of tridiagonal matrices (band diagonal matrices for the poloidal components of the vector Poisson equations), where appropriate solvers are fast, require little memory allocation, and typically converge with high accuracy.
For the scalar Poisson-like Eq. (70) we
then decompose, for each level n of iteration (here omitted), the unknown
q as ![\begin{equation} q(r,\theta):=\sum_{l=0}^\infty \left[A_l(r) Y_l(\theta) \right], \end{equation}](/articles/aa/full_html/2011/04/aa15945-10/aa15945-10-eq192.png) (72)where
(72)where
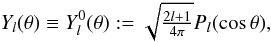 (73)with
Pl the Legendre polynomial of degree
l and the axisymmetry condition has been imposed
(m = 0). The PDE, where the Laplacian is provided in Eq. (65), may then be split into the series of radial
ODEs for each harmonic
l
(73)with
Pl the Legendre polynomial of degree
l and the axisymmetry condition has been imposed
(m = 0). The PDE, where the Laplacian is provided in Eq. (65), may then be split into the series of radial
ODEs for each harmonic
l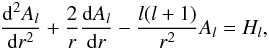 (74)where the new source
term is
(74)where the new source
term is 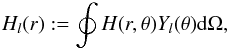 (75)with
dΩ = 2πsinθdθ and the integral running
from θ = 0 to θ = π due to axisymmetry.
(75)with
dΩ = 2πsinθdθ and the integral running
from θ = 0 to θ = π due to axisymmetry.
As far as the vector Poisson equation in Eq. (71) is concerned, the unknown vector X is first
decomposed into vector spherical harmonics, that is, in the axisymmetric case
![\begin{equation} \vec{X}(r,\theta):= \sum_{l=0}^\infty \left[A_l(r) Y_l(\theta)\vec{e}_{\hat r} + B_l(r) Y^\prime_l(\theta)\vec{e}_{\hat\theta} + C_l(r) Y^\prime_l(\theta)\vec{e}_{\hat\phi} \right], \end{equation}](/articles/aa/full_html/2011/04/aa15945-10/aa15945-10-eq202.png) (76)where
(76)where
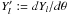 . As is apparent from the operators
in Eqs. (66)–(69), the set of equations split into a series of ODEs with, for each
harmonic l, a coupled poloidal part for the radial functions
Al(r) and
Bl(r)
. As is apparent from the operators
in Eqs. (66)–(69), the set of equations split into a series of ODEs with, for each
harmonic l, a coupled poloidal part for the radial functions
Al(r) and
Bl(r)
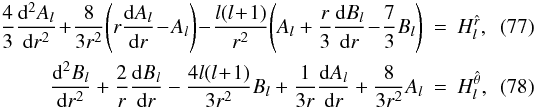 and
a toroidal part
and
a toroidal part 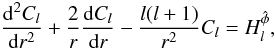 (79)for
Cl(r) alone. The new source
terms are given by
(79)for
Cl(r) alone. The new source
terms are given by 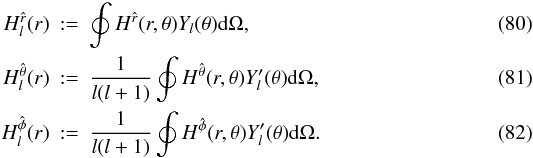 These
integrals, as well as that in Eq. (75), are
computed in X-ECHO by using Gaussian quadrature points, so the original source terms must
first be interpolated on the required locations.
These
integrals, as well as that in Eq. (75), are
computed in X-ECHO by using Gaussian quadrature points, so the original source terms must
first be interpolated on the required locations.
As anticipated, we use finite differences and a second-order approximation for first and second spatial derivatives, so that, for each harmonic l, the two coupled poloidal equations are reduced to the inversion of a sparse matrix of bandwidth 7, whereas the toroidal equation leads to a tridiagonal matrix (standard open source routines are employed in their solution). Boundary conditions at r = 0 and r = rmax are given by the parity and asymptotic properties of the multipole corresponding to the harmonic l. In particular, we assume that at the center Al(r) has parity (−1)l, whereas Bl(r) and Cl(r) have parity (−1)l + 1, and the multipoles are forced to decay as r − l(l + 1) at large distances from the central sources.
4. Axisymmetric GRMHD equilibria: the XNS code
One of the most common applications of the fully constrained formalism is the search for
self-consistent (axisymmetric) equilibrium configurations (i.e. fluid quantities and metric)
for compact relativistic stars (we simply refer to these objects with the term NS), a
typical case of initial data problem in GR (Cook
2000; Stergioulas 2003; Gourgoulhon 2010). Several codes have been presented in the years to
address this issue (Komatsu et al. 1989a,b; Cook et al.
1994; Stergioulas & Friedman 1995;
Nozawa et al. 1998; Bonazzola et al. 1998; Kiuchi & Yoshida
2008), and, despite the different approaches and upgrades (e.g. differential
rotation, toroidal magnetic field), all of them adopt the so-called quasi-isotropic
coordinates. Under the conditions
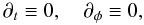 (83)we write here the
corresponding line element in the form
(83)we write here the
corresponding line element in the form 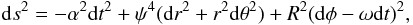 (84)which resembles
that of the CFC metric for axisymmetric spacetimes of Eq. (60) in spherical coordinates and reduces to it when
(84)which resembles
that of the CFC metric for axisymmetric spacetimes of Eq. (60) in spherical coordinates and reduces to it when 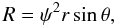 (85)where only in this case
the function ψ in Eq. (84)
recovers the meaning of conformal factor. In general, we can think the metric function
(85)where only in this case
the function ψ in Eq. (84)
recovers the meaning of conformal factor. In general, we can think the metric function
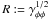 is
a sort of generalized cylindrical radius, whereas
ω: = −βφ is the intrinsic
angular velocity about the symmetry axis of the zero angular momentum observers
(ZAMOs: Bardeen et al. 1972), which are the
normal (Eulerian) observers for an axisymmetric spacetime. When ω = 0, the
spacetime is spherically symmetric and the two metrics both reduce to the one in isotropic
Schwarzschild coordinates. In the following we briefly re-derive the GRMHD equilibrium
condition (a Bernoulli-like integral) for purely toroidal flows and magnetic fields in
quasi-isotropic coordinates. More general derivations can be found in (Kiuchi & Yoshida 2008) or (Komissarov 2006). This latter work applies to magnetized tori around rotating BHs
(see also the final numerical test in Del Zanna et al.
2007).
is
a sort of generalized cylindrical radius, whereas
ω: = −βφ is the intrinsic
angular velocity about the symmetry axis of the zero angular momentum observers
(ZAMOs: Bardeen et al. 1972), which are the
normal (Eulerian) observers for an axisymmetric spacetime. When ω = 0, the
spacetime is spherically symmetric and the two metrics both reduce to the one in isotropic
Schwarzschild coordinates. In the following we briefly re-derive the GRMHD equilibrium
condition (a Bernoulli-like integral) for purely toroidal flows and magnetic fields in
quasi-isotropic coordinates. More general derivations can be found in (Kiuchi & Yoshida 2008) or (Komissarov 2006). This latter work applies to magnetized tori around rotating BHs
(see also the final numerical test in Del Zanna et al.
2007).
The only non vanishing components of the spatial (Eulerian) 3-vectors
vi and
Bi are the azimuthal ones, and the
corresponding moduli are 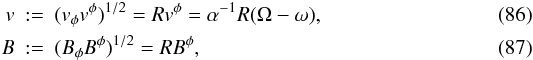 where
we have used the 3 + 1 relations
uφ = Γ(vφ + ω/α),
ut = Γ/α, and we defined
Ω: = uφ/ut = dφ/dt,
the angular velocity of the fluid seen by an observer at rest at infinity (a function of
r and θ for a differentially rotating NS). The
equilibrium condition we are looking for can be derived directly from the 3 + 1 conservative
form of the GRMHD equations, in which the only non vanishing contribution comes from the two
poloidal components of the momentum conservation in Eq. (48)
where
we have used the 3 + 1 relations
uφ = Γ(vφ + ω/α),
ut = Γ/α, and we defined
Ω: = uφ/ut = dφ/dt,
the angular velocity of the fluid seen by an observer at rest at infinity (a function of
r and θ for a differentially rotating NS). The
equilibrium condition we are looking for can be derived directly from the 3 + 1 conservative
form of the GRMHD equations, in which the only non vanishing contribution comes from the two
poloidal components of the momentum conservation in Eq. (48) ![\begin{eqnarray} \gamma^{-1/2} \partial_j \left[\gamma^{1/2}\alpha \left(p +\textstyle{\frac{1}{2}} B^2\right)\right] - \alpha (p +\textstyle{\frac{1}{2}} B^2)\textstyle{\frac{1}{2}}\gamma^{ii}\partial_j\gamma_{ii}\nonumber \\ \quad\quad - \alpha \left(\rho h \Gamma^2 v^2 - B^2\right) \textstyle{\frac{1}{2}} R^{-2}\partial_j R^2 + \rho h \Gamma^2 Rv \,\partial_j\omega \nonumber\\ \quad\quad\quad\quad+ \left(\rho h \Gamma^2 - p + \textstyle{\frac{1}{2}}B^2\right)\partial_j\alpha=0, \end{eqnarray}](/articles/aa/full_html/2011/04/aa15945-10/aa15945-10-eq228.png) (88)where
j is either r or θ, and we recall that
the electric field vanishes. Recalling that
(88)where
j is either r or θ, and we recall that
the electric field vanishes. Recalling that 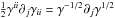 and
differentiating the definition of v, after a few algebraic steps the
following condition can be found:
and
differentiating the definition of v, after a few algebraic steps the
following condition can be found: 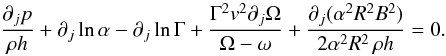 (89)Integrability of this
equation demands the following conditions:
(89)Integrability of this
equation demands the following conditions:
-
a barotropic EoS, p = p(ρh). The simplest choice and the most common assumption is a polytropic law
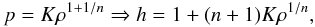 (90)where
n is the polytropic index (the corresponding adiabatic index is
γ = 1 + 1/n);
(90)where
n is the polytropic index (the corresponding adiabatic index is
γ = 1 + 1/n); -
the quantity F: = uφut ≡ Γ2v2/(Ω − ω), related to the specific angular momentum ℓ: = −uφ/ut, is a function of the angular velocity Ω alone. A commonly adopted differential rotation law (e.g. Stergioulas 2003) is
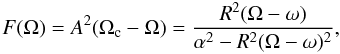 (91)where Ωc
is the central angular velocity and A is a measure of the
differential rotation rate. For uniform rotators Ω ≡ Ωc (and
A → ∞), and this contribution can be excluded from the Bernoulli
integral;
(91)where Ωc
is the central angular velocity and A is a measure of the
differential rotation rate. For uniform rotators Ω ≡ Ωc (and
A → ∞), and this contribution can be excluded from the Bernoulli
integral; -
a sort of magnetic barotropic law, where αRB is a function of α2R2ρh. The simplest choice is a magnetic polytropic law
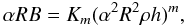 (92)where
m is the magnetic polytropic index, with m ≥ 1
(Kiuchi & Yoshida 2008).
(92)where
m is the magnetic polytropic index, with m ≥ 1
(Kiuchi & Yoshida 2008).
Using the above prescriptions we can easily derive the final GRMHD Bernoulli integral
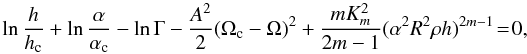 (93)where again we indicate
values at the center with the subscript c.
(93)where again we indicate
values at the center with the subscript c.
The above derivation is exact for quasi-isotropic coordinates and obviously also applies to the CFC subcase. In the non-magnetized case, it has been demonstrated that, even for rapid rotators close to the mass shedding limit (see Sect. 5.3), solutions obtained with the RNS numerical code (Stergioulas & Friedman 1995) show very little deviations from a CFC metric, so one should expect the CFC limit to provide a reasonably good approximation of the correct solution for compact relativistic stars. Given the above-mentioned computational advantages in the solution of the XCFC system of equations with respect to the original set of coupled PDE of fully constrained schemes, our choice has been to build a novel numerical code (written in Fortran90), which we name XNS and which can be freely downloaded at http://sites.google.com/site/niccolobucciantini/xns This takes advantage of the same XCFC metric solvers as were developed for the X-ECHO scheme described in this section. A comparison between equilibria found with XNS and RNS is presented in Sect. 5.3, together with a discussion of the results.
XNS employs a self-consistent method in the search for the axisymmetric equilibrium solutions of relativistic compact stars, in the presence of differential rotation and a purely toroidal magnetic field, thus metric terms and fluid-like quantities are derived at the same time. Given the values of the six free parameters K,n,A,Ωc,Km,m, plus a guess for the central density ρc, the following steps are taken
-
A starting guess for the CFC metric terms(α,ψ,ω) is provided from the previous step, with R given by Eq. (85). The first time, the spherically symmetric Tolman-Oppenheimer-Volkoff (TOV) solution in isotropic coordinates (Tolman 1934), for the metric of a non-rotating and non-magnetized NS with a central density value ρc, is computed through a shooting method for ODEs.
-
On top of these metric terms and for each grid point, Ω is derived by inverting Eq. (91), then v (and Γ) can be determined from Eq. (86). Finally, hc is a known function of ρc and the Bernoulli integral in Eq. (93) is solved via a Newton method to find the local values of h and ρ, allowing us to also determine the magnetic field strength from Eq. (92).
-
The new conserved quantities Ê,Ŝj are derived by combining the updated fluid quantities with the old metric.
-
The set of XCFC equations is solved for this set of conserved variables, and a new metric computed. Here only the azimuthal components for the vector Poisson equations are treated, in order to find Wφ and then βφ. We recall here that the conservative to primitive variables inversion must be enforced between the solutions to the two scalar Poisson-like equations, namely after the new value of ψ is found and before that of α.
These steps are repeated until convergence to a desired tolerance is achieved. However, a
word of caution is in order here. Since XNS is based on the XCFC metric solver, which works
on the conservative variables densitized with ψ6, convergence is
actually enforced on the central value of the quantity
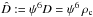 .
Therefore, given that the final conformal factor ψ for the self-consistent
2D equilibrium may be quite different from the one derived from the radial TOV solution at
the first step, the final value of ρ at the center is expected to differ
from the parameter ρc in the Bernoulli integral. If one wants to
find an equilibrium converging exactly to a central density ρc,
an additional overall iterative loop is needed.
.
Therefore, given that the final conformal factor ψ for the self-consistent
2D equilibrium may be quite different from the one derived from the radial TOV solution at
the first step, the final value of ρ at the center is expected to differ
from the parameter ρc in the Bernoulli integral. If one wants to
find an equilibrium converging exactly to a central density ρc,
an additional overall iterative loop is needed.
Before concluding this section, some remarks are in order. One might question the choice of a purely toroidal field versus a more realistic configuration including a poloidal component. However, equilibrium with poloidal fields is only possible for uniform rotators, with magnetic field fully confined within the star. It is well known (Goldreich & Julian 1969) that any poloidal magnetic field extending outside a rotating NS will eventually lead to a spin-down of the same, even for a dipole aligned with the rotation axis, unless the star is surrounded by a true vacuum. A low charge density of about 1020 cm-3 pairs is enough to break this assumption, even in the case of millisecond rotators with B ~ 1017 G, and the timescale to replenish an evacuated magnetosphere is close to the rotation period. For such strong magnetic fields, affecting the overall equilibrium of the NS and providing a non negligible contribution to the global stress-energy tensor in the Einstein equations (lower fields have small dynamical effects and can be easily treated as perturbations), the problem becomes particularly severe because the typical spin-down time for millisecond rotators can be as short as 50 ms. Weaker magnetic field can lead to much longer spin-down times, and those configurations might be considered quasi-equilibrium cases, at least for the time of a typical numerical run (a few thousands M). However they are of little interest, as stated above.
One might also question whether purely toroidal configurations are stable, and, if not, what is the growth rate of instabilities. A recent study of the stability properties of neutron star with strong toroidal field has been presented by Kiuchi et al. (2008). Their results show that non-rotating neutron stars with a magnetic polytropic law with m ≥ 2 are always unstable and that (uniformly) rotating systems are stable only if their kinetic energy exceed the magnetic energy by at least a factor 5. However, even if their conclusions about stability are supported by numerical simulations, it must be pointed out that their criterion is derived analytically only in the Newtonian regime, where magnetic field and spacetime metric are not coupled. Moreover, their full GR results do not consider intermediate cases with 1 < m < 2, thus further investigation is certainly needed.
5. Numerical results
We present here a set of numerical tests of the X-ECHO scheme. Standard HD/MHD tests in a static background metric (Cowling approximation) have already been presented elsewhere both for a flat metric (Del Zanna & Bucciantini 2002; Del Zanna et al. 2003) and for a given stationary curved spacetime (Del Zanna et al. 2007). As discussed in the introduction, the performances of the ECHO code in astrophysical scenarios involving a variety of different conditions such as strong shocks, relativistic outflows, strong gravity, and highly magnetized systems, have also already been assessed in numerous papers. For these reasons, the results presented here focus mostly on evaluating the quality of our novel metric solver and on the performances of the HD/MHD ECHO algorithms when coupled with a dynamical spacetime. Moreover, the original ECHO scheme was designed for high-order accuracy, whereas the metric solver implemented in X-ECHO is formally only second order in space. Given that the performances of high-order reconstruction techniques have already been tested (Del Zanna et al. 2007), for simplicity, we have decided to limit our set-up to second order accuracy, both in space and time, which is always a good compromise between efficiency, accuracy, and robustness.
As discussed in the introduction, only in recent years have stable numerical schemes for GRMHD in dynamical spacetimes started to appear. This, together with the intrinsic degrees of freedom in the choice of gauge and coordinate systems typical of GR, have resulted in a lack of well-defined, agreed-upon, standard numerical tests (in the spirit as that of shock-tube problems in flat spacetime or accretion/outflows solutions for a stationary curved metric). While in 1D a few problems have emerged as standard benchmarks, this cannot be said about multidimensional cases yet, also because of a lack of analytical solutions for fully multidimensional dynamical problems. Some of the tests that we selected here, have already been published in the literature, using different numerical schemes, both fully constrained (Dimmelmeier et al. 2002; Stergioulas et al. 2004; Dimmelmeier et al. 2006; Cordero-Carrión et al. 2009) and hyperbolic (Font et al. 2002; Bernuzzi & Hilditch 2010), so that we can validate our code against existing results. Some other have been done in the perturbative regime and compared with the results of linear theory, and when possible also with previous numerical simulations. However, in an attempt to evaluate the performances under different conditions, we also present some novel cases.
Unless otherwise stated, in all our numerical tests we use a Courant number of 0.4, an ideal gas EoS with γ = 2 (corresponding to a polytropic index n = 1 for the initial data in XNS), and we solve the full GRMHD system, including the equation for the total energy density E, often neglected in isentropic tests for a given polytropic law. For the approximate Riemann solver, we use the HLLC solver by Mignone & Bodo (2006) here for the first time, which was never applied before to GRMHD studies in curved, evolving spacetimes, to our knowledge. This choice is imposed by the sharp transition between the rotating NS and the external atmosphere, since the two-wave solver HLL is found to be too diffusive on the contact discontinuity.
In almost all of our tests we have included an extended atmosphere in the domain, which is left free to evolve and respond to the evolution of the NS. This choice was dictated by the astrophysical problems we are mostly interested in, and toward which the X-ECHO scheme has been developed. Problems which involve the ability to simultaneously handle the high-density NS and any low-density outflow/atmosphere/magnetosphere that might surround it. We are aware that a common practice in the literature is to reset floor values outside the NS, but we believe that this procedure may in principle lead to violations of conservation properties of the scheme at the NS surface. For the same reasons, as stated above, simulations have been performed using an ideal gas EoS, which allows us to handle systems where matter in different thermal conditions (a cold NS versus a hot atmosphere) is present.
Reconstruction at cell boundaries is achieved for simplicity through a monotonized-central (MC) algorithm, though the other choices described in the appendix of Del Zanna et al. (2007) are also possible. The XCFC metric solver is invoked every 10 steps of the HD/MHD Runge-Kutta evolution scheme. In 2D runs we use 50 Gaussian quadrature points and 20 spherical harmonics. With these settings, we have managed to make the computational time taken by the metric solver, usually slower, comparable to the time taken by a single Runge-Kutta cycle of the fluid solver. Thus, solving XCFC at every fluid step will only double the overall times, but no significant improvement has been noticed in the results. Finally, grid spacing will be constant both along the radial direction r and the polar angle θ, so the number of points are enough to specify the grid in each direction.
5.1. Stability of a TOV stable radial solution
Our first test consists in the evolution of a stable 1D radial NS configuration. We adopt, as initial condition, a solution of the TOV equations in isotropic coordinates, corresponding to a polytropic gas with K = 100,n = 1, and central density ρc = 1.280 × 10-3, a model also known as A0 (AU0) or B0 (BU0) in the literature (Font et al. 2000; Stergioulas et al. 2004; Dimmelmeier et al. 2006). This corresponds to an NS extending to a radius r = 8.13. It is possible to show that this star lies on the stable part of the mass-radius curve, so we expect the code to be able to maintain this configuration for longer times than their typical sound crossing time (~0.5 ms). Outside the star we assume, at the beginning of the run, a low density and hot (ρ ≃ 10-7, p/ρ ≃ 0.2) atmosphere in hydrostatic equilibrium (αh = const.), in pressure balance at the surface of the NS. Contrary to previous treatments, where the atmosphere was reset at every time step to keep it stationary, we leave it free to evolve (collapse or expand) in response to the NS oscillations. Given its low density, the atmosphere has negligible feedback on the star. The simulation is performed using 625 grid points in the radial domain r = [0,20] , corresponding to a star resolved over 250 points. The evolution is followed for a time tmax = 1500 corresponding in physical units to ≃7.5 ms.
 |
Fig. 1 Evolution of a stable TOV solution in spherical symmetry and isotropic coordinates. The upper panel shows a comparison between density in the initial solution (solid line) and the result at tmax = 1500 (diamonds). For clarity the result a tmax is shown every 5 points. The insert shows the residuals. The spike at r ≈ 8 comes from to diffusive relaxation at the NS boundary. The middle panel shows the relative variations in time of the central density. The lower panel shows the Fourier transform of the central density. The solid line and diamonds indicate the power of the Fourier series in arbitrary units. The vertical markers indicate the frequency of known eigenmodes. The frequency resolution of our time series is ~150 Hz. |
Figure 1 shows a comparison between the initial density profile and that at tmax, together with a plot of the central density ρc as a function of time. Relative variations in density in the NS interior are on order of 10-4, with major deviations only at the contact discontinuity of the NS surface, due to diffusion over the much lower density atmosphere. This triggers the natural vibration modes of the NS, which are the observed fluctuations, which are the natural outcome of this physical system. The central density, plotted in the insert of Fig. 1, shows fluctuations on order of 10-3 at most, but no sign of any secular trend. This is due to the large number of points over which the star is resolved. The slow damping of the oscillations, from 10-3 to a few 10-4, comes from the thermal dissipation associated to the use of an ideal gas EoS and to the numerical viscosity of the scheme, whereas it is not present if a polytropic EoS is used (see next Sect. 5.2 for a comparison between the two EoS). At the beginning of the simulation we observe a relaxation of the central density to a value that is ~2 × 10-4 lower than the initial condition, probably because of discretization errors. However the average value seems to remain constant at later times. This shows the ability of the code to maintain a stable equilibrium, even for several (~10) sound crossing times. It also shows that the presence of a dynamical atmosphere causes no problem for the stability of the TOV solution. In contrast, the atmosphere itself seems to be quite stable, as shown by the fact that its density changes by a factor smaller than 1%.
In the bottom panel of Fig. 1 we plot a Fourier transform of the central density in time. Markers indicate the positions of the known eigenmodes. This is a test of the performance of the code in handling a dynamical spacetime, at least in the linear regime, for small perturbations. The values of the eigenmodes, the fundamental in particular, are quite different in the Cowling approximation where the metric is kept fixed in time (Font et al. 2002). It is also interesting to note that no initial perturbation has been introduced and that the oscillations of the star are only due to the relaxation of the initial conditions and possible round off-errors. Indeed, the large power present in the higher frequency modes suggests that the initial excitation is confined to small scales, most likely at the surface of the star. The presence of a freely evolving atmosphere does not seem to affect the frequency of the modes, at least within the accuracy of our temporal series.
5.2. Migration of an unstable TOV radial solution
A genuinely non-trivial situation in the fully non-linear regime, involving large variations in the metric and fluid structure, is the migration of an unstable 1D TOV solution. Following Font et al. (2002), Cordero-Carrión et al. (2009), and Bernuzzi & Hilditch (2010), we select a solution of the TOV equations in isotropic coordinates, corresponding to a polytropic gas again with K = 100,n = 1, and central density ρc = 7.993 × 10-3. This corresponds to a star extending to a radius r = 4.26, on the unstable part of the mass-radius curve. The external atmosphere is set as in the previous test. Due to truncation errors and the initial relaxation of the NS/atmosphere transition, this configuration migrates to the stable branch. This evolution causes large amplitude pulsations and the formation of a shock between the outer mantle and inner core of the star, where part of the kinetic energy is dissipated into heat. During the evolution the star expands to quite large radii. The run is done using 900 grid points in the radial domain r = [0,30] . A small fraction of the stellar mass (less than ~10-3) is lost at the outer radius during the first bounce. The evolution is followed for a time tmax = 1500 corresponding in physical units to ≃7.5 ms.
 |
Fig. 2 Evolution of the central density for the migrating unstable TOV solution in spherical symmetry and isotropic coordinates. The solid line is the evolution for an ideal gas EoS, the dotted line is the evolution for a polytropic EoS. The horizontal dashed line indicates the density of the stable TOV solution corresponding to the same mass ρc = 1.650 × 10-3. |
Figure 2 shows the evolution of the central density in time. Results agree with what has been presented previously, including the amplitude of the fluctuations, the value of the density at the first minimum and at the first and second maxima, the frequency of the oscillations, their non-sinusoidal shape, and the asymptotic value of the central density with respect to the expected value for a stable configuration with the same mass. As already noted in Font et al. (2002), the lower average central density at later times (with respect to that of a stable model with the same mass) is due to shock heating during the bounce phase, which changes the thermal content of the star. We repeated the same simulation using a polytropic EoS for the NS (while the ideal gas EoS is still used for the free atmosphere). Results are shown in Fig. 2. It is evident that the oscillations are not damped for a polytropic EoS, and the system appears to converge to the correct asymptotic value of the central density. Comparison with previous results (Font et al. 2002; Cordero-Carrión et al. 2009) agrees both in the amplitude of the oscillations and in their phase shift with respect to the case with an ideal gas EoS.
5.3. Accuracy of uniformly rotating 2D equilibria
Following Sect. 4, we built a series of 2D equilibrium models for rigidly rotating neutron star in the XCFC approximation for the metric. The computational grid covers the domain r = [0,20] and θ = [0,π] , with 650 zones in radius and 100 zones in angle. In this section we compare them with equivalent models built using the publicly available code RNS (Stergioulas & Friedman 1995; Nozawa et al. 1998; Stergioulas 2003), which for us constitutes a reference benchmark. RNS is an accurate solver for non-magnetized, uniformly rotating NS configurations in quasi-isotropic coordinates, for which we recall that in 2D R2 ≠ ψ4r2sin2θ in Eq. (84). This is both a test of the quality of the XCFC approximation, for genuinely non-spherically symmetric systems and an evaluation of the performances of our metric solver. We have selected the BU series of models from the literature (Stergioulas et al. 2004; Dimmelmeier et al. 2006), with a fixed central density ρc = 1.280 × 10-3, the usual polytropic law with K = 100,n = 1, but different values of the uniform rotation rates. Table 1 presents the models and compares some global properties derived using RNS with those derived using our implementation of the XCFC solver in XNS. Results agree within the accuracy of the models themselves (Δr = 0.03). The model BU9 represents an equilibrium at the mass-shedding limit, and it is particularly sensitive to accuracy and round-off errors. Indeed, when solving the Bernoulli condition Eq. (93) to derive the matter distribution, in the case of model BU9, we had to impose the further condition ρ = 0 for r > 11.6, to avoid unbounded solutions.
Comparison between RNS and XNS for rigidly rotating compact stars.
 |
Fig. 3 Comparison between RNS and XNS solutions for model BU8. The upper panel shows the fluid quantities. The solid (dotted) line represents the density at the equator (polar axis) derived using RNS, both normalized against ρc. The dashed line is the profile of the rotational velocity module v, normalized to its maximum (0.37462). Diamonds, crosses and pluses represent values of the same quantities as derived using XNS, where we report one symbol every 5 radial points for clarity. The lower panel shows the residual of various metric terms at the equator. The green solid line is the relative error between the lapse α computed with XNS and RNS. Dashed magenta and dotted blue lines represent the relative error between the conformal factor ψ of the CFC metric with respect to the one in quasi-isotropic coordinates and the quantity [R/(rsinθ)] 1/2. The dot-dashed red line represents the difference between ψ and [R/(rsinθ)] 1/2 both computed in quasi-isotropic coordinates, and can be considered a measure of the non conformal flatness of the RNS solution. |
In Fig. 3 we show the comparison between the model BU8 (we already pointed out the problems for model BU9) derived using our solver for the CFC metric and the solution of RNS. It is clear that the CFC approximation provides a good description of the matter and fluid properties of the equilibrium configuration, throughout the entire star. The densities along the polar axis and at the equator, together with the velocity profile v: = (vφvφ)−1/2, are all well reproduced. In terms of the metric coefficient, we see that the discrepancy is of order 10-3, and is comparable with the level of approximation of the conformally flat condition, defined as the difference between ψ and [R/(rsinθ)] 1/2 in Eq. (84). Somewhat larger deviations, of a few 10-3 in the NS interior, are characteristic of the shift βφ, increasing at larger radii where the value of the shift approaches zero, analogously to what was observed by Dimmelmeier et al. (2002).
5.4. Stability of uniformly rotating 2D equilibria
In the same spirit as for the numerical test presented in Sect. 5.1, we show here the result of a time evolution of two equilibrium configurations, BU2 and BU8. They correspond to a mildly rotating star and to a case of rapid rotation, respectively. The initial conditions are derived according to the recipe given in Sect. 4 in conformally flat metric, and their accuracy has already been discussed in the previous section. The domain, r = [0,16] and θ = [0,π] , is spanned by 200 zones in the radial direction and 100 zones in angle. The star is resolved on average over about 100 radial zones. The evolution is followed for a time tmax = 1500, corresponding in physical units to ≃7.5 ms. As in the previous tests, we initialize a hot and low density atmosphere outside the star, initially in equilibrium, and then allowed to freely evolve in time. As already noted in the previous 1D cases, the presence of this freely evolving atmosphere has negligible dynamical effects on the star, even in 2D, due to its low density, and there is no need to enforce a reset to the initial values.
 |
Fig. 4 Evolution of a stable BU2 solution. The upper panel shows a comparison between the initial values (solid lines) of equatorial (green) and axial (blue) densities and of equatorial rotational velocity v (magenta), against the value of the same quantities at at tmax = 1500 (dashed lines). The densities are normalized to the central initial value ρc, the velocity to its maximum initial value (0.1619). The insert shows the relative difference between the equatorial densities as a function of radius. The spike at r ≈ 8 is due to diffusion at the NS surface, also partly visible in the velocity profile. The middle panel shows the variation in time of the central density. The bottom panel shows the Fourier transform of the the density (green solid line), vr (red dotted line), vφ (magenta dashed line), and vθ (blue dot-dashed line), at the point r = 3.0, θ = 45° of model BU2. The vertical markers indicate the frequency of known eigenmodes. The frequency resolution of our time series is ~150 Hz. |
For the model BU2, Fig. 4 compares the equatorial
and axial densities, together with the module of the rotational velocity
v, at time t = 0 and
t = tmax. The evolution of the central
density is also shown. The oscillations on order or 10-3 are due to the
excitation of the stellar eigenmodes by initial round-off errors and relaxation at the
boundary between the star and the atmosphere. No initial perturbation was introduced into
the model. Changes in the value of the equatorial density at the end of the run with
respect to the initial values are close to the amplitude of the oscillations that are
excited by the initial relaxation. A small secular drift of
~5 × 10-4 in the average value of the central density is visible
by the end of the run. It stems from the lower number of points in the radial direction
over which the star is resolved (~100), compared to the 1D case
(~250) where no drift was observed. In the bottom panel of Fig. 4, we plot a Fourier transform of various fluid
quantities in time. The quantities are all measured at a selected location inside the
star: r = 3.0 and θ = π/4. Normal
mode analysis is beyond the scope of this paper, so here we just present a simple
single-point analysis. Selecting other points in the star does not change the location of
the peaks in the power series (though it affects their relative amplitude). Given that no
perturbation is introduced in the initial data, modes are excited differently, depending
on the initial relaxation (certain modes cannot in principle even be excited). Markers
indicate the positions of the known l = 0, l = 2, and
l = 4 eigenmodes (Dimmelmeier et al.
2006). This is a test of the performance of the code in handling an axisymmetric
dynamical spacetime, at least in the linear regime for small perturbations. The
fundamental F and first overtone H1 of the
l = 0 mode are correctly recovered, together with the
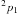 for the
dipolar l = 2 mode, and the
for the
dipolar l = 2 mode, and the 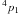 for the
quadrupolar l = 4 mode. The
for the
quadrupolar l = 4 mode. The 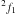 dipolar mode
is only visible in the spectrum of vθ. The
vθ spectrum also shows a peak at 2.45 kHz,
which does not correspond to any of the known low frequency modes. It is possible that its
origin might be due to some form of non-linear coupling, or perhaps an effect of the free
atmosphere. However, as already noted in the 1D radial case, the presence of a freely
evolving atmosphere does not seem to affect the frequency of the modes, at least within
the accuracy of our temporal series. It is interesting to recall that inertial modes can
also be excited with a continuum spectrum extending in a frequency range between 0 and 2Ω
(Font et al. 2002). The peak at 500 Hz,
corresponds in fact to the rotation frequency of the star.
dipolar mode
is only visible in the spectrum of vθ. The
vθ spectrum also shows a peak at 2.45 kHz,
which does not correspond to any of the known low frequency modes. It is possible that its
origin might be due to some form of non-linear coupling, or perhaps an effect of the free
atmosphere. However, as already noted in the 1D radial case, the presence of a freely
evolving atmosphere does not seem to affect the frequency of the modes, at least within
the accuracy of our temporal series. It is interesting to recall that inertial modes can
also be excited with a continuum spectrum extending in a frequency range between 0 and 2Ω
(Font et al. 2002). The peak at 500 Hz,
corresponds in fact to the rotation frequency of the star.
 |
Fig. 5 Evolution of a stable BU8 solution. The upper panel shows a comparison between the initial values (solid lines) of equatorial (green) and axial (blue) densities, and equatorial rotational velocity v (magenta), against the value of the same quantities at tmax = 1500 (dashed lines). The densities are normalized to the central initial value ρc, the velocity to its maximum initial value (0.3499). The insert shows the relative difference between the equatorial densities as a function of radius. The spike at r ≈ 10 is due to diffusion at the NS surface, also partly visible in the velocity profile. The middle panel shows the variation in time of the central density. The bottom panel shows the Fourier transform of the the density (green solid line), vr (red dotted line), vφ (magenta dashed line), and vθ (blue dot-dashed line), at the point r = 3.0, θ = 45° of model BU8. The vertical markers indicate the frequency of known eigenmodes. The frequency resolution of our time series is ~150 Hz. |
We repeated the same analysis for the model BU8, with the same simulation setup. This
represents a rapidly rotating case, close to the mass shedding limit, and it is a more
demanding test than the mildly rotating case, BU2. Results are shown in Fig. 5. Many of the same considerations as for the previous
BU2 case still apply and are not repeated. Typical deviations in the value of the density
are larger (about a factor 2) than in the previous case. There is also evidence for a
secular drift (increase) of the central density, whose average value at the end of the run
is a factor 10-3 higher than at the beginning. Again this drift seems to be
twice what is observed in the BU2 case, suggesting a drop in accuracy at higher rotation
rates. We also show a Fourier transform of various fluid quantities in time. These are all
monitored at the same selected location: r = 3.0 and
θ = π/4. It is clear that in this case the first
l = 0 mode F is by far the most strongly excited.
However, power in the first l = 0 overtone
H1, at the quadrupole l = 4 mode
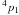 , and
l = 2 overtone
, and
l = 2 overtone 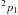 , is also
present. Little power seems to be present at the l = 2
, is also
present. Little power seems to be present at the l = 2
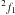 mode. The
time evolution of the vθ component is quite
noisy: there is no evidence of power at the H mode frequency, the peak at
1.7 kHz might be a poorly resolved
mode. The
time evolution of the vθ component is quite
noisy: there is no evidence of power at the H mode frequency, the peak at
1.7 kHz might be a poorly resolved 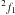 mode, or a
contaminated inertial mode close to 2Ω frequency. The power that is visible around
700–800 Hz is likely due to inertial modes, and, analogously to the BU2 case, its
frequency corresponds to the rotation frequency of the star.
mode, or a
contaminated inertial mode close to 2Ω frequency. The power that is visible around
700–800 Hz is likely due to inertial modes, and, analogously to the BU2 case, its
frequency corresponds to the rotation frequency of the star.
5.5. Stability of differentially rotating magnetized equilibria
We present here the evolution of an equilibrium configuration, which is both differentially rotating and contains a strong toroidal magnetic field. The conditions for such equilibrium and how to build it have been described in Sect. 4. There are no similar tests presented in the literature, and, as a consequence, no reference against which to compare our results. However, this setup allows us to investigate a strongly magnetized case, where we expect the magnetic field to have significant dynamical effects. Tests in the literature have, at most, focused on the case of weak poloidal fields (Cerdá-Durán et al. 2008), for the reasons discussed in Sect. 4. However, we are interested here in evaluating a case with a magnetic field that is not simply a small perturbation, but that has enough energy to modify the underlying equilibrium. Given that the algorithm described in Sect. 4 consider only toroidal fields, we limit our analysis to such a case, and we hope that the proposed test can become a standard, once our XNS solver is available for open use.
The equilibrium model has the same central density as the non-magnetized cases ρc = 1.280 × 10-3, and the usual polytropic law K = 100,n = 1. We adopt a differential rotation profile with Ωc = 0.02575, A2 = 70, and a magnetic field characterized by a magnetic polytropic index m = 1 and coefficient Km = 3, corresponding to a maximum magnetic field inside the star of ≃5 × 1017 G, and to a ratio of magnetic energy to total internal energy ≃0.1. We name this new model BM. With respect to an equilibrium with a very similar rotational structure but no magnetic field (model B2: Stergioulas et al. 2004; Dimmelmeier et al. 2006), the star is a factor ~1.5 larger in equatorial radius. The domain, r = [0,16] and θ = [0,π] , is covered with 200 zones in the radial direction and 100 zones in angle. The star is resolved on average over about 120 radial zones. The evolution is followed until a final time tmax = 1500 corresponding in physical units to ≃7.5 ms.
 |
Fig. 6 Evolution of a stable magnetized solution. The upper panel shows a comparison between the initial profiles (solid lines) of the equatorial (green) and axial (blue) densities, the equatorial rotational velocity v (magenta) and toroidal magnetic field B (red), and the value of the same quantities at at t = 1500 (dashed lines). Densities are normalized to the initial central value, velocity to its maximum (0.09810) initial value, and magnetic field to its maximum initial value too. The insert shows the relative difference between the equatorial densities as a function of radius. The spike at r ≈ 12 is due to diffusive relaxation at the boundary between the high density star and low density atmosphere. The lower panel shown the variation in time of the central density, at θ = π/2. |
Figure 6 compares the equatorial and axial profiles of the density, together with the rotational velocity v = (vφvφ)1/2, and the magnetic field B = (BφBφ)1/2, at time t = 0 and t = tmax. There is evidence of a secular drift (increase) of the central density, whose average value at the end of the run is a factor 1.5 × 10-3 higher than at the beginning, together with typical oscillation of similar amplitude. Larger deviations on the order of 10-2 characterize the outer layer of the star for r > 10, where the ratio of magnetic pressure to gas pressure is higher. This is also visible in the broader shear layer that form at the boundary with the atmosphere, compared to non-magnetized cases (Figs. 4, 5). There is also some evidence of a drop in the rotation rate of the core. The reason is not clear. It could either stem from some angular momentum redistribution from the core to the outer layer of the star or to some convection taking place in the core, possibly excited by initial relaxation. It is likely that, due to round-off errors and to the initial relaxation, some free energy might be injected into the star to power convective motions in regions of marginal convective stability as the core. We have, however, verified that the typical poloidal velocities in the core are ~10-4, which implies that it will be necessary to follow the system for a much longer time in order to see whether these convective motions are stabilized. This also agrees with the results presented by Kiuchi et al. (2008), which suggest, even for the case of strong instabilities, typical convective timescales of a few thousand M.
A detailed analysis of the stability of strongly magnetized configurations is beyond the scope of this paper. This test, however, demonstrates that stable configurations are preserved for many sound-crossing times, in cases involving strong magnetic fields, too. We have not carried out a full mode investigation, as in the previous cases, because there are no known values to compare our results to. There is also no reference solution, as in the case of RNS for non-magnetized rigid rotators. However, already from the plot of the central density, it is possible to see an oscillatory behavior, with a typical frequency 900 Hz. The amplitude of the oscillations, 10-3, is about one order of magnitude smaller than the result of Kiuchi et al. (2008). This frequency can be compared with the fundamental mode of a non-magnetized configuration, with a similar velocity profile (Ωc = 0.02575, and A2 = 70), which is located at 1.37 kHz (Dimmelmeier et al. 2006). There are also some hints that the first l = 0 overtone might have a similarly smaller frequency, even if there is little power in it and its identification in the spectrum is not certain. A lower frequency for l = 0 modes can easily be understood, if one recall that it is well known (e.g. Bucciantini et al. 2003) that toroidal magnetic fields behave as gas with adiabatic index 4/3, for l = 0 perturbations. Compared with the gas, which has adiabatic index 2, the presence of strong toroidal magnetic field leads to a softening of the generalized EoS of the perturbations, corresponding to a lower sound speed and longer vibrational periods. The larger radial extent of the star also contributes, given that the period or radial compressive modes scales as the sound crossing time.
5.6. Radial and axisymmetric collapse to a black hole
The migration test performed in Sect. 5.2 already shows the ability of the XCFC algorithm to handle the dynamical evolution of very compact configurations. Although that test is failed by the original CFC (Dimmelmeier et al. 2002), Marek et al. (2006) have shown that it can still be succesfully simulated by using a modified version. The superiority of XCFC formulation fully manifests itself in cases where the evolution leads to the formation of black holes and appparent horizons (AHs) (York 1989; Baumgarte & Shapiro 2003; Thornburg 2007). To properly evaluate the strength of our XCFC solver, we present the results of two simulations of the collapse of unstable neutron stars to black holes in this section: a 1D collapse of a spherically symmetric NS and a 2D collapse of a rapidly rotating one (Bernuzzi & Hilditch 2010; Cordero-Carrión et al. 2009; Baiotti et al. 2005). In the 1D case, the AH is found using a zero-finding algorithm, while for the 2D collapse we use a simple minimization algorithm, with the AH parametrized as a surface in terms of spherical harmonics (for details on the algorithms see Sect. 8 of Thornburg 2007; Sect. 6.7 of Alcubierre 2008; and Shibata 1997).
For the 1D case we consider the same unstable configuration of the migration test,
Sect. 5.2, and following Bernuzzi & Hilditch (2010) we add a perturbation of the form
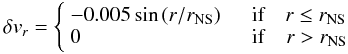 (94)where
rNS is the initial radius of the neutron star. The
computational domain r = [0,10] is covered by 300 equally spaced
radial zones. A hot low-density atmosphere is set outside the NS and allowed to evolve
freely. An ideal gas EoS is used, but given that the evolution of the collapse does not
lead to shocks and dissipative heating, results are equivalent to the case of a polytropic
EoS. Despite our resolution being 300 times worse than the central resolution used by
Cordero-Carrión et al. (2009), we are able to
follow the evolution of the system past the formation of an apparent horizon.
(94)where
rNS is the initial radius of the neutron star. The
computational domain r = [0,10] is covered by 300 equally spaced
radial zones. A hot low-density atmosphere is set outside the NS and allowed to evolve
freely. An ideal gas EoS is used, but given that the evolution of the collapse does not
lead to shocks and dissipative heating, results are equivalent to the case of a polytropic
EoS. Despite our resolution being 300 times worse than the central resolution used by
Cordero-Carrión et al. (2009), we are able to
follow the evolution of the system past the formation of an apparent horizon.
 |
Fig. 7 Collapse to BH. Upper panel: the monotonically rising red curves represent the evolution of the central density with respect to the intial value ρc/ρc(t = 0) (as explained in the text the curves are truncated at the formation of the apparent horizon), while the monotonically decreasing blue curves represent the value of the lapse α at the origin. Solid lines indicate the spherically symmetric collapse and dashed lines the collapse of the rotating NS model D4. Bottom panel: the rising red curves represent the radius of the apparent horizon, while the decreasing blue curves are the ratio of the rest mass outside the apparent horizon with respect to the total rest mass. Again, solid lines indicate the spherically symmetric collapse and dashed lines the collapse of the rotating NS model D4. The vertical dotted line indicates the time tAH when the apperent horizon forms. |
 |
Fig. 8 Evolution of the collapse of the rotating unstable equilibrium model D4 (density in Log10 units): upper panel, density at t = tAH − 6; middle panel density at t = tAH; lower panel, density at t = tAH + 6. The dashed countour in the middle and lower panel indicates the position of the apparent horizon. |
In Fig. 7 we show the evolution of a few quantities. The apparent horizon forms at a time tAH ≃ 47 to be compared to tAH ≃ 48 in Bernuzzi & Hilditch (2010). When the AH forms, its location is r = 0.61, the rest mass outside it is 0.28 of the initial rest mass, and the value of the lapse at the center is αc = 0.028. Our results agree with what is shown in Fig. 3 of Cordero-Carrión et al. (2009) and Fig. 8 of Bernuzzi & Hilditch (2010). In Fig. 7 we also show the value of the central density. However, a cautionary remark is in order here about this quantity. As the collapse proceeds, the metric becomes progressively more curved in the origin and the density correspondingly steeper, to the point where interpolation and round-off errors become more and more relevant. In Cordero-Carrión et al. (2009), despite their much higher resolution, already at t ~ tAH − 10 noise is present in the plot of the central density, which is no longer monotonically increasing. In our case we find that, as the system approaches the formation of the AH, the confidence and accuracy with which we can derive the central density at r = 0, by extrapolating the values on the numerical grid, rapidly decreases. At the time the AH forms we have evaluated that the extrapolation accuracy is such that the possible error on the density is ~10%, and it increases rapidly afterward. For this reason, we truncate the central density plot at the formation of the AH. It should be reminded that the standard practice to handle systems after the formation of an AH is to excise the region inside the AH itself, excluding it from the computational domain (Baiotti et al. 2005; Hawke et al. 2005). The precise value of the cental density is obviously not an important quantity, as far as the global evolution of the system is concerned. Indeed, quantities that depend on global properties of the system like the AH radius, rAH, the rest mass left outside it, the value of the lapse at the center (which depends on the global distribution of matter in the domain), all agree very well with what has been previously found in the literature.
 |
Fig. 9 Evolution of the toy collapse model. Panels show the rest mass density and the mangetic field lines (represented by arrows) at three different instants of the evolution. Left panel: t = 50, initial aspherical collapse. Note that the star is collapsing along the axis but expanding at the equator. Middle panel: t = 100, bounce. Right panel: t = 200, later expansion. |
For the 2D case we consider the model D4 of Baiotti et al. (2005) and Cordero-Carrión et al. (2009). This corresponds to a uniformly rotating neutron star with a central density ρc = 3.116 × 10-3, a rotation rate Ω = 0.0395, a gravitational mass M = 1.86, an equatorial radius re = 7.6, and an ellipticity rp/re = 0.65. Following Cordero-Carrión et al. (2009), the collapse is triggered by reducing the pressure 2% with respect to the equilibrium value. The computational domain r = [0,10] , θ = [0,π] is covered by 200 equally spaced radial zones and 100 equally spaced angular zones. As usual, a hot low-density atmosphere is set outside the NS, and allowed to evolve freely and an ideal gas EoS is used. Again, despite our radial resolution being 50 times worse than the central resolution used by Cordero-Carrión et al. (2009), we are able to follow the evolution of the system past the formation of an AH.
In Fig. 7 we show the evolution of a few quantities. The AH forms at a time tAH ≃ 126, to be compared to tAH ≃ 130 in Cordero-Carrión et al. (2009), its location at that moment is r = 0.75, the rest mass outside is 23% of the initial rest mass, and the value of the lapse at the center is αc = 0.025. Our results agree with what is shown in Fig. 3 of Cordero-Carrión et al. (2009). The same considerations stated above for the central density still apply. Interestingly, we are able to follow the evolution of the model D4 for a much longer time after the formation of the AH with respect to Cordero-Carrión et al. (2009). Figure 8 shows the evolution of the NS as the AH forms and grows. The middle panel represents the system at the moment of the formation of the AH, as in their Fig. 4 (warning: km units were used on the axes). The lower panel shows the density at t = tAH + 6. Clearly a disk has formed as in Baiotti et al. (2005): the NS has been completely accreted inside the AH in the polar region up to a latitude of around 30°, while matter is still present in the equatorial region up to r ~ 3.
5.7. Toy collapse
Core-collapse simulations are often presented as a test of code performances. However, they often aim at simulating realistic systems and involve complex physics: to the complexity of exact MHD solutions in a dynamical metric (Bocquet et al. 1995), they usually add sophisticated initial conditions from stellar evolution, tabulated EoS, and neutrino transport. While all these elements are undoubtedly important in the study of the physics of core collapse, there might be questions whether they are truly necessary to evaluate the performances of the metric solver. Moreover, the diversity in setup, EoS, and transport algorithms makes a direct comparison among different codes quite difficult. Such simulations are also hard to reproduce, if, for example, initial conditions or tabulated EoS are not easily and freely available, or require specific code implementations. Moreover, results themselves often show the growth of turbulence (convection) and MRI (Cerdá-Durán et al. 2008), for which comparison should be done in phase space and not on selected snapshots at arbitrary times. In an attempt to construct a simple run with fully defined initial conditions, a simple EoS, and no complex physics, we have designed a novel test run of what we call a toy collapse. However, this incorporates some of the important elements of a fully 2D non-linear evolution typical of a more realistic collapse scenario, and it also includes a poloidal magnetic field.
The chosen initial conditions are the following ![\begin{eqnarray} &&\left\{ \begin{array}{ll} \rho=10^{-4} & \quad \\ p=\mathrm{max}\left[\pi/3\, \left(10^2-r^2\right)\rho^2 , 10^{-9}\right] & \quad {\rm if}\quad r \le 10\\ v^\phi=\alpha^{-1}\left(0.025+\beta^\phi\right) & \quad \end{array} \right. \\ &&\left\{ \begin{array}{ll} \rho=10^{-7} & \quad \\ p=10^{-9} & \quad {\rm if} \quad r > 10\\ v^\phi=0.0 & \quad \end{array} \right. \end{eqnarray}](/articles/aa/full_html/2011/04/aa15945-10/aa15945-10-eq387.png) corresponding
to a rigidly rotating uniform sphere. The kinetic pressure is halfof the hydrostatic value
for the same matter distribution, in Newtonian gravity and with no rotation. To this
configuration a poloidal magnetic field is added using a generator potential
corresponding
to a rigidly rotating uniform sphere. The kinetic pressure is halfof the hydrostatic value
for the same matter distribution, in Newtonian gravity and with no rotation. To this
configuration a poloidal magnetic field is added using a generator potential
![\begin{equation} A_\phi = \mathrm{max}\left[3-\sqrt{\left[8(r-6)^2+36(\theta-\pi/2)^2\right]},0.\right], \end{equation}](/articles/aa/full_html/2011/04/aa15945-10/aa15945-10-eq388.png) (97)yielding the
components
(97)yielding the
components  where
we recall that
γ1/2 = ψ6r2sinθ.
where
we recall that
γ1/2 = ψ6r2sinθ.
The initial conditions are found by solving the XCFC equations, together with the above conditions for the fluid and magnetic variables. This provides us with a self-consistent set of conserved variables and metric coefficients, corresponding to our choice of primitive variables. Our definition of velocity implicitly involves the metric. The evolution of this configuration incorporates various elements of strongly dynamical and aspherical collapse. The original uniform sphere collapses primarily along the polar axis, where there is no centrifugal support, while it tends to expand at the equator, where rotation is stronger, forming a strongly oblate disk. Due to the stiff EoS, the system bounces when the central density has increased of about 50%, then the structure re-inflates, driving a shock into the lower density of the surrounding atmosphere. During the collapse the poloidal field is stretched, compressed, and twisted by rotation, but remains confined inside the star. In Fig. 9 we show three snapshots of the evolution, which we describe as follows: the quasi-spherical initial collapse, the bounce, and the final structure. The numerical domain, r = [0,35] and θ = [0,π] , is made up of 500 zones in the radial direction and by 150 zones in angle. The initial high-density sphere is resolved over about 150 radial zones. The evolution is followed for a time tmax = 200 corresponding in physical units to ≃1 ms. At t = 100 the star has turned into a disk with aspect ratio ~1/10. At t = 200, in the later expansion, the density is about 15% of the initial value. A density bump is formed distorting the magnetic field.
6. Conclusions
In this paper we have upgraded the Eulerian conservative high-order code for GRMHD (ECHO: Del Zanna et al. 2007) to dynamical spacetimes. We chose a fully constrained method and conformal flatness for the Einstein equations, and in particular we have built a numerical solver based on the extended conformally flat condition scheme (XCFC: Cordero-Carrión et al. 2009) for the elliptic equations providing the metric terms. This is known to improve on the previous CFC formulation (e.g. Wilson & Mathews 2003), because of the hierarchical nature of the equations to solve (the elliptic equations are fully decoupled), and because local uniqueness of the solution is ensured even for highly dynamical non-linear cases. Our novel scheme is here named X-ECHO, and we also presented a code for producing self-consistent initial data (metric terms and GRMHD quantities) for polytropic, differentially rotating, relativistic (neutron) stars with a toroidal magnetic field named XNS. This code is publicly available at http://sites.google.com/site/niccolobucciantini/xns, and we hope it will provide a useful benchmark and initial data for the evolution of NSs or for core collapse in the magnetized case.
Both X-ECHO and XNS work in spherical coordinates of the conformally flat metric, and axisymmetry is assumed. The 2D metric solver for the elliptic equations (Poisson-like scalar PDEs and vector Poisson PDEs) use a mixed technique: spectral decomposition in spherical harmonics (or vector spherical harmonics) in the angular direction and finite-differences leading to the inversion of band-diagonal matrices in the radial direction. This is achieved on the same numerical grid as is used for evolving the fluid/MHD quantities, thus avoiding the need for interpolation over different meshes. We fully test the codes against known problems involving fluid configurations in dynamical spacetimes, basically 1D and 2D evolution and vibration modes for NS configurations, migration to stable branches, 1D and 2D collapse of an unstable NS towards a BH, including the formation of an apparent horizon, and we propose a couple of novel GRMHD test problems, the evolution of a differentially rotating magnetized NS and a toy collapse simulation in the presence of poloidal magnetic fields. The metric solver is fast, and in the cases we have tested, the CPU time required to solve the XCFC system is comparable to the time taken to update the MHD fluid quantities, despite the use of a fast Riemann solver (HLL/HLLC). For higher than second-order reconstruction techniques, the computational time is always dominated by the HD/MHD module. The code was validated against previous results obtained with both free-evolution and fully costrained schemes and with the linear theory for perturbations. Performances in the presence of strong magnetic fields, violently dynamical configurations, large deviation from sphericity, and even apparent horizons, show that the method and its implementation with the HD/MHD module are stable in the situations of interest. Moreover we have shown that, in the case of NSs surrounded by a low-density atmosphere, there is no need to apply any reset procedure to the atmosphere itself, which can be allowed to evolve freely, without altering the stability or the results of the simulations.
For the immediate future we plan to investigate the stability and to find the characteristic vibrational modes of a set of magnetized NS configurations, with and without differential rotation, for both stable and unstable magnetic profiles. We also plan to investigate the growth of magnetic field due to MRI in differentially rotating NS, which might be of some interest to explain the late flaring activity that is observed in long duration GRBs, and that, within the millisecond-magnetar model, is commonly attributed to bursty magnetic activity in the cooled and convectively stable NS. However, the final goal is to include a more realistic treatment of the microphysics, going beyond the simple ideal gas law implemented here for reproducibility of the numerical tests, especially as far as neutrino heating is concerned, and possibly to couple our code with a transport algorithm for neutrinos as required for collapse calculations. This will allow us to study the magnetized core-collapse scenario in details, and to investigate the role of a strong magnetic field in shaping and regulating the collapse. In particular, we also plan to derive a more realistic setup from magnetized collapse simulations for the (long) GRB model recently proposed by Bucciantini et al. (2009), where a newly born millisecond proto-magnetar drives a GRMHD wind, that, due to confinement of the external stellar envelopes, collimates relativistic jets escaping the progenitor along the poles.
Acknowledgments
We sincerely thank Sebastiano Bernuzzi for having introduced us to the world of the Einstein equations and for suggesting some useful tests and benchmarks, and Luca Franci for practical help with the use of the RNS code for initial data. We also thank the anonymous referee for her/his helpful suggestions. The work of N.B. has been supported by a NORDITA fellowship grant.
References
- Abdikamalov, E. B., Dimmelmeier, H., Rezzolla, L., & Miller, J. C. 2009, MNRAS, 392, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Alcubierre, M. 2008, Introduction to 3+1 Numerical Relativity (Oxford University Press) [Google Scholar]
- Anderson, M., Hirschmann, E. W., Liebling, S. L., & Neilsen, D. 2006, Classical and Quantum Gravity, 23, 6503 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, M., Hirschmann, E. W., Lehner, L., et al. 2008, Phys. Rev. Lett., 100, 191101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Baiotti, L., Hawke, I., Montero, P. J., et al. 2005, Phys. Rev. D, 71, 024035 [NASA ADS] [CrossRef] [Google Scholar]
- Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Barkov, M. V., & Komissarov, S. S. 2008, MNRAS, 385, L28 [NASA ADS] [Google Scholar]
- Baumgarte, T. W., & Shapiro, S. L. 1999, Phys. Rev. D, 59, 024007 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Baumgarte, T. W., & Shapiro, S. L. 2003, ApJ, 585, 921 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgarte, T. W., & Shapiro, S. L. 2010, Numerical Relativity. Solving Einstein’s Equations on the Computer, ed. C. U. Press (Oxford University Press) [Google Scholar]
- Bernuzzi, S., & Hilditch, D. 2010, Phys. Rev. D, 81, 084003 [NASA ADS] [CrossRef] [Google Scholar]
- Bocquet, M., Bonazzola, S., Gourgoulhon, E., & Novak, J. 1995, A&A, 301, 757 [NASA ADS] [Google Scholar]
- Bona, C., Ledvinka, T., Palenzuela, C., & Žáček, M. 2003, Phys. Rev. D, 67, 104005 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bonazzola, S., Gourgoulhon, E., & Marck, J. 1998, Phys. Rev. D, 58, 104020 [NASA ADS] [CrossRef] [Google Scholar]
- Bonazzola, S., Gourgoulhon, E., Grandclément, P., & Novak, J. 2004, Phys. Rev. D, 70, 104007 [NASA ADS] [CrossRef] [Google Scholar]
- Bucciantini, N., Blondin, J. M., Del Zanna, L., & Amato, E. 2003, A&A, 405, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bucciantini, N., Bandiera, R., Blondin, J. M., Amato, E., & Del Zanna, L. 2004, A&A, 422, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bucciantini, N., Amato, E., & Del Zanna, L. 2005a, A&A, 434, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bucciantini, N., del Zanna, L., Amato, E., & Volpi, D. 2005b, A&A, 443, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bucciantini, N., Thompson, T. A., Arons, J., Quataert, E., & Del Zanna, L. 2006, MNRAS, 368, 1717 [NASA ADS] [CrossRef] [Google Scholar]
- Bucciantini, N., Quataert, E., Arons, J., Metzger, B. D., & Thompson, T. A. 2008, MNRAS, 383, L25 [NASA ADS] [Google Scholar]
- Bucciantini, N., Quataert, E., Metzger, B. D., et al. 2009, MNRAS, 396, 2038 [NASA ADS] [CrossRef] [Google Scholar]
- Cerdá-Durán, P., Font, J. A., Antón, L., & Müller, E. 2008, A&A, 492, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cook, G. 2000, Liv. Rev. Rel., 3 [Google Scholar]
- Cook, G. B., Shapiro, S. L., & Teukolsky, S. A. 1994, ApJ, 424, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Cordero-Carrión, I., Cerdá-Durán, P., Dimmelmeier, H., et al. 2009, Phys. Rev. D, 79, 024017 [NASA ADS] [CrossRef] [Google Scholar]
- Del Zanna, L., & Bucciantini, N. 2002, A&A, 390, 1177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, L., Bucciantini, N., & Londrillo, P. 2003, A&A, 400, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, L., Amato, E., & Bucciantini, N. 2004, A&A, 421, 1063 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, L., Volpi, D., Amato, E., & Bucciantini, N. 2006, A&A, 453, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, L., Zanotti, O., Bucciantini, N., & Londrillo, P. 2007, A&A, 473, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dimmelmeier, H., Font, J. A., & Müller, E. 2002, A&A, 388, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dimmelmeier, H., Novak, J., Font, J. A., Ibáñez, J. M., & Müller, E. 2005, Phys. Rev. D, 71, 064023 [NASA ADS] [CrossRef] [Google Scholar]
- Dimmelmeier, H., Stergioulas, N., & Font, J. A. 2006, MNRAS, 368, 1609 [NASA ADS] [CrossRef] [Google Scholar]
- Duez, M. D., Liu, Y. T., Shapiro, S. L., & Stephens, B. C. 2005, Phys. Rev. D, 72, 024028 [NASA ADS] [CrossRef] [Google Scholar]
- Duez, M. D., Liu, Y. T., Shapiro, S. L., Shibata, M., & Stephens, B. C. 2006a, Phys. Rev. Lett., 96, 031101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Duez, M. D., Liu, Y. T., Shapiro, S. L., Shibata, M., & Stephens, B. C. 2006b, Phys. Rev. D, 73, 104015 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, R. C., & Thompson, C. 1992, ApJ, 392, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Farris, B. D., Li, T. K., Liu, Y. T., & Shapiro, S. L. 2008, Phys. Rev. D, 78, 024023 [NASA ADS] [CrossRef] [Google Scholar]
- Font, J. A. 2008, Liv. Rev. Rel., 11, 7 [Google Scholar]
- Font, J. A., Goodale, T., Iyer, S., et al. 2002, Phys. Rev. D, 65, 084024 [NASA ADS] [CrossRef] [Google Scholar]
- Font, J. A., Stergioulas, N., & Kokkotas, K. D. 2000, MNRAS, 313, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Giacomazzo, B., & Rezzolla, L. 2007, Classical and Quantum Gravity, 24, 235 [Google Scholar]
- Giacomazzo, B., Rezzolla, L., & Baiotti, L. 2009, MNRAS, 399, L164 [NASA ADS] [Google Scholar]
- Giacomazzo, B., Rezzolla, L., & Baiotti, L. 2011, Phys. Rev. D, 83, 044014 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Julian, W. H. 1969, ApJ, 157, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Gourgoulhon, E. 2007, unpublished [arXiv:gr-qc/0703035] [Google Scholar]
- Gourgoulhon, E. 2010, unpublished [arXiv:1003.5015] [Google Scholar]
- Grandclément, P., & Novak, J. 2009, Liv. Rev. Rel., 12, 1 [Google Scholar]
- Grandclément, P., Bonazzola, S., Gourgoulhon, E., & Marck, J. 2001, J. Comput. Phys., 170, 231 [Google Scholar]
- Hawke, I., Löffler, F., & Nerozzi, A. 2005, Phys. Rev. D, 71, 104006 [NASA ADS] [CrossRef] [Google Scholar]
- Isenberg, J. A. 2008, Int. J. Mod. Phys. D, 17, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Kiuchi, K., & Yoshida, S. 2008, Phys. Rev. D, 78, 044045 [NASA ADS] [CrossRef] [Google Scholar]
- Kiuchi, K., Shibata, M., & Yoshida, S. 2008, Phys. Rev. D, 78, 024029 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, H., Eriguchi, Y., & Hachisu, I. 1989a, MNRAS, 237, 355 [NASA ADS] [Google Scholar]
- Komatsu, H., Eriguchi, Y., & Hachisu, I. 1989b, MNRAS, 239, 153 [NASA ADS] [Google Scholar]
- Komissarov, S. S. 2006, MNRAS, 368, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Kouveliotou, C., Dieters, S., Strohmayer, T., et al. 1998, Nature, 393, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Liebling, S. L., Lehner, L., Neilsen, D., & Palenzuela, C. 2010, Phys. Rev. D, 81, 124023 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y. T., Shapiro, S. L., Etienne, Z. B., & Taniguchi, K. 2008, Phys. Rev. D, 78, 024012 [NASA ADS] [CrossRef] [Google Scholar]
- Londrillo, P., & Del Zanna, L. 2000, ApJ, 530, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Londrillo, P., & Del Zanna, L. 2004, J. Comput. Phys., 195, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Marek, A., Dimmelmeier, H., Janka, H., Müller, E., & Buras, R. 2006, A&A, 445, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignone, A., & Bodo, G. 2006, MNRAS, 368, 1040 [NASA ADS] [CrossRef] [Google Scholar]
- Montero, P. J., Font, J. A., & Shibata, M. 2008, Phys. Rev. D, 78, 064037 [NASA ADS] [CrossRef] [Google Scholar]
- Montero, P. J., Font, J. A., & Shibata, M. 2010, Phys. Rev. Lett., 104, 191101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nozawa, T., Stergioulas, N., Gourgoulhon, E., & Eriguchi, Y. 1998, A&AS, 132, 431 [Google Scholar]
- Ott, C. D., Dimmelmeier, H., Marek, A., et al. 2007, Classical and Quantum Gravity, 24, 139 [Google Scholar]
- Price, D. J., & Rosswog, S. 2006, Science, 312, 719 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Saijo, M. 2004, ApJ, 615, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, M. 1997, Phys. Rev. D, 55, 2002 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, M., & Nakamura, T. 1995, Phys. Rev. D, 52, 5428 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Shibata, M., & Sekiguchi, Y. 2004, Phys. Rev. D, 69, 084024 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, M., & Sekiguchi, Y.-I. 2005, Phys. Rev. D, 72, 044014 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, M., Duez, M. D., Liu, Y. T., Shapiro, S. L., & Stephens, B. C. 2006a, Phys. Rev. Lett., 96, 031102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Shibata, M., Liu, Y. T., Shapiro, S. L., & Stephens, B. C. 2006b, Phys. Rev. D, 74, 104026 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, B. C., Duez, M. D., Liu, Y. T., Shapiro, S. L., & Shibata, M. 2007, Classical and Quantum Gravity, 24, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, B. C., Shapiro, S. L., & Liu, Y. T. 2008, Phys. Rev. D, 77, 044001 [NASA ADS] [CrossRef] [Google Scholar]
- Stergioulas, N. 2003, Liv. Rev. Rel., 6, 3 [Google Scholar]
- Stergioulas, N., & Friedman, J. L. 1995, ApJ, 444, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Stergioulas, N., Apostolatos, T. A., & Font, J. A. 2004, MNRAS, 352, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Thornburg, J. 2007, Liv. Rev. Rel., 10, 3 [Google Scholar]
- Tolman, R. C. 1934, Relativity, Thermodynamics, and Cosmology (Oxford: Clarendon Press) [Google Scholar]
- Usov, V. V. 1992, Nature, 357, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Volpi, D., Del Zanna, L., Amato, E., & Bucciantini, N. 2008, A&A, 485, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, J. R., & Mathews, G. J. 2003, Relativistic Numerical Hydrodynamics (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Woosley, S. E. 1993, ApJ, 405, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Bloom, J. S. 2006, ARA&A, 44, 507 [NASA ADS] [CrossRef] [Google Scholar]
- York, Jr., J. W. 1989, Initial Data for Collisions of Black Holes and Other Gravitational Miscellany, ed. C. R. Evans, L. S. Finn, & D. W. Hobill, 89 [Google Scholar]
- Zanotti, O., Rezzolla, L., Del Zanna, L., & Palenzuela, C. 2010, A&A, 523, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Evolution of a stable TOV solution in spherical symmetry and isotropic coordinates. The upper panel shows a comparison between density in the initial solution (solid line) and the result at tmax = 1500 (diamonds). For clarity the result a tmax is shown every 5 points. The insert shows the residuals. The spike at r ≈ 8 comes from to diffusive relaxation at the NS boundary. The middle panel shows the relative variations in time of the central density. The lower panel shows the Fourier transform of the central density. The solid line and diamonds indicate the power of the Fourier series in arbitrary units. The vertical markers indicate the frequency of known eigenmodes. The frequency resolution of our time series is ~150 Hz. |
| In the text | |
 |
Fig. 2 Evolution of the central density for the migrating unstable TOV solution in spherical symmetry and isotropic coordinates. The solid line is the evolution for an ideal gas EoS, the dotted line is the evolution for a polytropic EoS. The horizontal dashed line indicates the density of the stable TOV solution corresponding to the same mass ρc = 1.650 × 10-3. |
| In the text | |
 |
Fig. 3 Comparison between RNS and XNS solutions for model BU8. The upper panel shows the fluid quantities. The solid (dotted) line represents the density at the equator (polar axis) derived using RNS, both normalized against ρc. The dashed line is the profile of the rotational velocity module v, normalized to its maximum (0.37462). Diamonds, crosses and pluses represent values of the same quantities as derived using XNS, where we report one symbol every 5 radial points for clarity. The lower panel shows the residual of various metric terms at the equator. The green solid line is the relative error between the lapse α computed with XNS and RNS. Dashed magenta and dotted blue lines represent the relative error between the conformal factor ψ of the CFC metric with respect to the one in quasi-isotropic coordinates and the quantity [R/(rsinθ)] 1/2. The dot-dashed red line represents the difference between ψ and [R/(rsinθ)] 1/2 both computed in quasi-isotropic coordinates, and can be considered a measure of the non conformal flatness of the RNS solution. |
| In the text | |
 |
Fig. 4 Evolution of a stable BU2 solution. The upper panel shows a comparison between the initial values (solid lines) of equatorial (green) and axial (blue) densities and of equatorial rotational velocity v (magenta), against the value of the same quantities at at tmax = 1500 (dashed lines). The densities are normalized to the central initial value ρc, the velocity to its maximum initial value (0.1619). The insert shows the relative difference between the equatorial densities as a function of radius. The spike at r ≈ 8 is due to diffusion at the NS surface, also partly visible in the velocity profile. The middle panel shows the variation in time of the central density. The bottom panel shows the Fourier transform of the the density (green solid line), vr (red dotted line), vφ (magenta dashed line), and vθ (blue dot-dashed line), at the point r = 3.0, θ = 45° of model BU2. The vertical markers indicate the frequency of known eigenmodes. The frequency resolution of our time series is ~150 Hz. |
| In the text | |
 |
Fig. 5 Evolution of a stable BU8 solution. The upper panel shows a comparison between the initial values (solid lines) of equatorial (green) and axial (blue) densities, and equatorial rotational velocity v (magenta), against the value of the same quantities at tmax = 1500 (dashed lines). The densities are normalized to the central initial value ρc, the velocity to its maximum initial value (0.3499). The insert shows the relative difference between the equatorial densities as a function of radius. The spike at r ≈ 10 is due to diffusion at the NS surface, also partly visible in the velocity profile. The middle panel shows the variation in time of the central density. The bottom panel shows the Fourier transform of the the density (green solid line), vr (red dotted line), vφ (magenta dashed line), and vθ (blue dot-dashed line), at the point r = 3.0, θ = 45° of model BU8. The vertical markers indicate the frequency of known eigenmodes. The frequency resolution of our time series is ~150 Hz. |
| In the text | |
 |
Fig. 6 Evolution of a stable magnetized solution. The upper panel shows a comparison between the initial profiles (solid lines) of the equatorial (green) and axial (blue) densities, the equatorial rotational velocity v (magenta) and toroidal magnetic field B (red), and the value of the same quantities at at t = 1500 (dashed lines). Densities are normalized to the initial central value, velocity to its maximum (0.09810) initial value, and magnetic field to its maximum initial value too. The insert shows the relative difference between the equatorial densities as a function of radius. The spike at r ≈ 12 is due to diffusive relaxation at the boundary between the high density star and low density atmosphere. The lower panel shown the variation in time of the central density, at θ = π/2. |
| In the text | |
 |
Fig. 7 Collapse to BH. Upper panel: the monotonically rising red curves represent the evolution of the central density with respect to the intial value ρc/ρc(t = 0) (as explained in the text the curves are truncated at the formation of the apparent horizon), while the monotonically decreasing blue curves represent the value of the lapse α at the origin. Solid lines indicate the spherically symmetric collapse and dashed lines the collapse of the rotating NS model D4. Bottom panel: the rising red curves represent the radius of the apparent horizon, while the decreasing blue curves are the ratio of the rest mass outside the apparent horizon with respect to the total rest mass. Again, solid lines indicate the spherically symmetric collapse and dashed lines the collapse of the rotating NS model D4. The vertical dotted line indicates the time tAH when the apperent horizon forms. |
| In the text | |
 |
Fig. 8 Evolution of the collapse of the rotating unstable equilibrium model D4 (density in Log10 units): upper panel, density at t = tAH − 6; middle panel density at t = tAH; lower panel, density at t = tAH + 6. The dashed countour in the middle and lower panel indicates the position of the apparent horizon. |
| In the text | |
 |
Fig. 9 Evolution of the toy collapse model. Panels show the rest mass density and the mangetic field lines (represented by arrows) at three different instants of the evolution. Left panel: t = 50, initial aspherical collapse. Note that the star is collapsing along the axis but expanding at the equator. Middle panel: t = 100, bounce. Right panel: t = 200, later expansion. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


