EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 528 (April 2011) A&A, 528 (2011) A97 Full HTML
Free Access
Issue
A&A
Volume 528, April 2011
Article Number A97
Number of page(s) 7
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201015480
Published online 08 March 2011

© ESO, 2011

1. Introduction

Transiting exoplanets offer greater opportunities for the study and understanding of exoplanetary systems than those discovered by radial velocity measurements. Analysis of transit light curves yields planetary radii and enables tests for rings (Barnes & Fortney 2004), moons (Sartoretti & Schneider 1999) and other planets through transit timing variations (Maciejewski et al. 2010), while high-precision observations of primary and secondary transits can reveal some details of planetary atmospheres (which is not currently possible for nontransiting planets) and albedos (e.g., Deming & Seager 2009), which is easier for transiting exoplanets but still possible for others.

The potential of transiting exoplanets has inspired considerable effort towards their discovery, both from the ground and from space. While ground-based searches have discovered the majority of known transiting exoplanets to this point, space-based missions offer greater potential for discovery. Observing from space allows nearly continuous sampling and much better photometric precision, which is adversely affected by the atmosphere. This makes it possible to detect long-period transiting exoplanets, whose transits can easily be longer than a typical night, and smaller exoplanets, whose transits are too shallow to be detected from ground.

The CoRoT (COnvection ROtation and planetary Transits space mission was the first space mission dedicated primarily to searching for transits (Baglin et al. 2009). The mission has successfully demonstrated the advantages to space. Given its orbit and the lack of atmosphere, it can observe the same field continuously for up to five months with remarkably high relative precision. This enabled the discovery of both the first transiting “Super-Earth” (Léger et al. 2009; Queloz et al. 2009, CoRoT-7b:) and the first temperate transiting gas giant (Deeg et al. 2010, CoRoT-9b).

In this paper, we announce the discovery of the 14th transiting planet discovered by CoRoT; an unusually massive exoplanet orbiting an F9V star with metallicity consistent with Solar. In Sect. 2, we detail the CoRoT photometry. In Sect. 3, we describe the ground-based follow-up observations that we used to confirm the planetary nature of CoRoT-14b. In Sect. 4, we discuss our analysis of the light curves to extract the transit parameters and present the inferred planetary parameters. In Sect. 5, we analyze the parent star. Finally, we conclude our paper in Sect. 6, where we discuss how the properties CoRoT-14b compare to the ensemble of known transiting planets.

thumbnail Fig. 1

The processed and normalized transit light curve of CoRoT-14. The final processed photometry, corrected for jitter and other effects, but not hot pixels, is plotted on top. The middle plot depicts the same data, corrected for hot pixels. The bottom plot contains the same hot-pixel data binned, with a best-fit sinusoid overplotted. See text for more details.

Table 1

IDs, coordinates and magnitudes.

2. CoRoT observations

CoRoT monitored the field which contains CoRoT-14b during its second long-run anti-center pointing (LRa02). This run lasted from 16 Nov. 2008 to 11 Mar. 2009 and imaged a 3.5 square degree field in the constellation Monoceros. The details of the observations that comprise this run will appear in a forthcoming paper. Table 1 lists various IDs, coordinates, and magnitudes for CoRoT-14b.

CoRoT-14b was first identified as an object of interest on 9 Dec 2008 by the “alarm mode” pipeline (Surace et al. 2008) and the time sampling was subsequently switched from the standard value of 512 s to the 32 s sampling reserved for interesting targets. Figure 1 shows several different versions of the final monochromatic light curve, containing 220 188 photometric samples covering over 114 days. This light curve is the output of the standard CoRoT pipeline (see Auvergne et al. 2009, version 2.1) in conjunction with further processing to remove outliers and correct for systematics, as described in, e.g. Barge et al. (2008) and Alonso et al. (2008). It exhibits many discontinuities due to cosmic ray hits on the detector, which is a common occurrence in CoRoT light curves, as the satellite’s orbit crosses through the energetic-particle-rich South-Atlantic Anomaly. These can be corrected for, however, yielding a fairly good cleaned light curve with a σrms of only around 2 mmag, which indicates that the star is not particularly active. While the final correctly light curve appears to exhibit a weak sinusoidal variation, this is in fact not the case: removing the best-fit sinusoid, which has an amplitude of about 1.6 mmag and a period about 46 days (corresponding to neither the rotation period of the star, the period of the transit, nor any known instrument effect), reduces the σrms by only 10% and is therefore not likely to be significant.

The periodic transit signals are easily detected in the cleaned light curve. It contains some 89 transits, 74 of them after the sampling rate increased, yielding a final duty cycle of 82.7%. The initial trapezoid fitting, using the method outlined in Alonso et al. (2008), yielded a period (P) of 1.15214 ± 0.00013 d and a primary transit epoch (T0) of 2   454   787.6694 ± 0.00053 and a depth of about 5 mmag. This information was passed on to the photometric and spectroscopic follow-up groups, to help schedule the ground-based follow-up observations necessary for confirmation or rejection.

3. Ground-based observations

The detection of a transit-like event in a light curve is only the beginning of the process: we find 10 to 20 candidates with CoRoT for each planet. To exclude as many candidates as possible without resorting to precious HARPS/HIRES observing time, we performed a carefully considered sequence of ground-based follow-up observations.

3.1. Imaging-contamination

The first step is to image the field around the start for possible sources of photometric contamination that may combine with light from the target star to masquerade as a transit-like event and to estimate how much, if any, nearby stars dilute the transit (Deeg et al. 2009). This is necessary for CoRoT, in particular, because the light passes through a bi-prism to disperse the light over many pixels. While this allows much longer exposures (much like an ordinary defocusing would have) and some color information, it comes at the expense of an increase in contamination from nearby (and occasionally not so nearby) stars.

The photometric follow-up group obtained 20 images of the candidate during mid-transit on 27 Feb. 2009 and 20 images out-of-transit on 14 Apr. 2009 with the IAC80 telescope on Tenerife, which has an aperture of 80 cm and a 10.6 × 10.6 arcmin field of view. Analysis revealed no strong signals in nearby stars that could be capable of producing a false positive or any bright very close neighbors, but was not sensitive enough to detect the transit with any confidence. These images, when stacked, have similar quality and depth to those in large surveys such as 2MASS, so we are confident that no unknown, readily identifiable stars have eluded us. Contamination analysis (Deeg et al. 2009) reveals that 93 ± 0.5% of total light in the CoRoT mask came from the target, with most of the rest (~6%) coming from a star about 3 mag fainter and 2.5 arcsec to the south. This factor was included in the final transit analysis in Sect. 4.

Table 2

Radial velocity measures, errors, and bisectors.

3.2. Radial velocities – spectroscopy/orbital fit

We planned radial velocity (RV) observations only after the photometric imaging with the IAC80 showed that this candidate only had a slight risk of being a false positive. Radial velocity (RV) observations of CoRoT-14 were performed with the HARPS spectrograph (Mayor et al. 2003), based on the 3.6 m ESO telescope (Chile) and the HIRES spectrograph (Vogt et al. 1994) installed on the 10 m Keck telescope in Hawaii.

HARPS was used with the observing mode obj_AB, without simultaneous thorium in order to monitor the Moon background light on the second fiber. The intrinsic stability of this spectrograph frees us from the need to capture a simultaneous thorium spectrum, as the instrumental drift during an exposure is always smaller than the stellar RV photon noise uncertainties in this case. We took a series of eight spectra with one hour exposures between 22 Nov. 2009 and 20 Feb. 2010 (ESO program 184.C-0639). We analyzed the HARPS data with the pipeline based on the cross-correlation techniques (Baranne et al. 1996; Pepe et al. 2002). The signal-to-noise per pixel at 550 nm of individual spectrum is in the range 3.7 to 7.1 for this faint target, one of the faintest followed up by HARPS. Radial velocities were obtained by weighted cross-correlation with a numerical G2 mask.

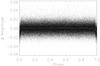thumbnail Fig. 2

The full phase-folded light curve of CoRoT-14. The light curve shown has been corrected for jitter, hot pixels, and other effects, then folded with the known period for CoRoT-14b, with the center of transit at 0. These observations were also binned into 100 evenly-spaced bins, represented by a gray line. No out-of-transit variations are apparent.

thumbnail Fig. 3

RV orbital fit. This figure shows the orbital fit to the HIRES and HARPS observations, using the period found by the CoRoT photometry, along with the residuals, assuming a circular orbit. A fit was made without this assumption, but returned a value for the eccentricity that was consistent with zero.

We used HIRES in combination with its iodine (I2) cell to measure precise RVs. All observations were taken with a 7 arcsec long slit of 0.861 arcsec width, which yields a spectral resolving power of R ≈ 50   000. We obtained one spectrum of CoRoT-14 on 5 Dec. 2009 without the I2-cell to serve as stellar template for the RV computation, which is required for calibration, and to determine stellar parameters. We took a single 1200 s exposure, which had a signal-to-noise ratio (per pixel) of only 10 at 550 nm, as seeing conditions on this particular night were less than optimal. We also took one exposure with the I2-cell, to get an RV measurement that night. We collected five additional spectra of CoRoT-14 during January 2010 with the I2-cell over the course of three nights. The signal-to-noise ratios of these data range from 15 to 19 (at 550 nm). We used our Austral Doppler code (Endl et al. 2000) to compute precise differential RVs. The results are given in Table 2. Since the template spectrum had such a poor S/N, we used a HIRES template of a similar, but much brighter, star (HD 12800) for the RV computation.

The results of the bisector analysis accompany the corresponding radial velocity measurements in Table 2. The bisector analysis was only possible with the HARPS spectra, as the HIRES spectra do not have sufficient resolution to yield meaningful results in this case. The bisectors anti-correlate weakly with the differential RVs (linear correlation coefficient R = −0.198), which in turn yields a probability of 0.637 that the bisectors and RVs are physically unrelated. We therefore conclude that the bisector analysis is consistent, albeit weakly, with no correlation.

We computed a Keplerian orbital solution for the HARPS and HIRES RV data using the Gaussfit generalized least-squares software of Jefferys et al. (1988). We kept the values of the orbital period and primary transit epoch fixed to the parameters determined by the CoRoT photometry. The individual velocity zero points of the HARPS and HIRES data were included as free parameters in the fitting process. We first fit a circular orbit to the data (see Fig. 3). The 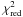χred2\hbox{$\chi^{2}_{\rm red}$} of this solution is 1.50, and the values of the residual rms scatter around the fit are 118 m s-1 (HARPS) and 78 m s-1 (HIRES). The orbital fit yields an RV semi-amplitude K of 1230 ± 34 m s-1. Adopting a stellar mass of 1.13 ± 0.09 M⊙ for CoRoT-14 (see next section), we obtain a mass of 7.6 ± 0.6 MJup for the planet. From this, we can conclude that CoRoT-14b is a very massive gas giant for its relatively short 1.5 day orbit and orbits only 0.027 AU from its parent star. The orbital parameters are summarized in Table 4.

We also explored the possibility of an eccentric orbit. Allowing the eccentricity and periastron argument to be free parameters, we derive an eccentricity of e = 0.019 ± 0.046, with a 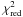χred2\hbox{$\chi^{2}_{\rm red}$} of 1.63. We therefore conclude that the current RV data for CoRoT-14 are consistent with a completely circularized orbit.

4. Analysis of the transit

We used the methodology described in Alonso et al. (2008) to extract the transit parameters from the CoRoT photometry. To summarize, we used trapezoid fitting to obtain the period and transit epoch, then a χ2 analysis described by Giménez (2006) on the phase-folded transit to determine transit and stellar parameters (the transit center Tc, the orbital phase at first contact θ1, the ratio of radii k, the orbital inclination i and u+ and u− coefficients, which are related to the quadratic limb darkening coefficients). We performed the transit fitting using a bootstrap analysis to constrain parameter space, based on the prescription outlined in Barge et al. (2008) and Alonso et al. (2008). Due to the faintness of the target, we chose not to fit the limb darkening coefficients: instead, we took the values from Sing (2010), with (conservative) error bars for these based on the uncertainties in the stellar parameters (ua = 0.43 ± 0.03 and ub = 0.24 ± 0.1). For each of the 500 bootstrap curves, we fixed the limb darkening coefficients, but instead of always using the same values, we extracted them from an random normal distribution with the appropriate width. Thus, for each bootstrap curve, we changed the contamination factor, the limb darkening coefficients, and the residuals, which we shifted circularly, with the initial parameters for the amoeba minimization algorithm perturbed randomly. The results of this analysis can be found in Table 4, and the transit and best fit can be seen in Fig. 4.

5. Analysis of the parent star

We co-added the HARPS spectra to perform the analysis of the parent star, which yielded R    ~  110   000 and S/N ≃ 45 at 5500 Å. From this, we were able to determine the vsini (=9 ± 0.5 km s-1). We obtained a first estimation of the effective temperature of  ~5900 K by fitting the Hα line. We used these values as a starting point for detailed analysis of the HARPS spectra with the VWA package (Bruntt et al. 2010). This analysis returned the following atmospheric parameters: Teff = 6035 ± 100 K, log    g = 4.35 ± 0.15 cgs, [M/H]  = 0.05 ± 0.15 dex, plus individual abundances for several elements, which are listed in Table 3 and shown in Fig. 5.

thumbnail Fig. 4

Phase-folded transit and residuals. This figure shows the phase-folded transit from the CoRoT photometry with the best-fit model transit (top) along with the O–C residuals (bottom).

thumbnail Fig. 5

Mean abundances for 14 elements in CoRoT-14 HARPS spectrum. White circles correspond to neutral lines, red boxes to singly ionized lines, and the yellow area represents the mean metallicity within one sigma error bar.

Table 3

Abundances of some chemical elements for the fitted lines in the HARPS spectrum, with listed abundances relative to the solar value.

Table 4

Planet and star parameters.

The large error bars, especially on the surface gravity and the metallicity, come from the low signal-to-noise ratio of the spectra due to the faintness of the star. Using the density from the transit fit and the effective temperature and the metallicity from the spectroscopic analysis, we derived a mass of 1.13 ± 0.09   M⊙, and a radius of 1.21 ± 0.08   R⊙ for the star using the dedicated STAREVOL evolutionary tracks (Palacios, priv. comm.; Siess 2006). As a final check, we ascertained that the inferred surface gravity agreed with the spectroscopic value, log    gevol = 4.33 ± 0.14 cgs.

As the RV spectra are slightly less than ideal, an examination of the activity of the parent star is warranted. While the star is photometrically variable on the level of only a few millimags, other methods can be used to corroborate this, in particular the Ca II H and K lines. These are shown in Fig. 6 and show no evidence of emission in the cores of these lines. This is consistent with a star of low magnetic activity, which corresponds to what we observe. It is not zero, however, so we decided to attempt to estimate the stellar rotation period from the CoRoT light curve using an auto-correlation analysis. The results of this analysis can be seen in Fig. 7. We discover local peaks in the auto-correlation that are separated by 5.66 days, which we infer to be the rotation period of the star. This compares fairly well with the rotational period that can be inferred from vsini and the radius of the star: 6.8 ± 0.8 days, assuming the stellar rotation axis is perpendicular to the line of sight. This result is confirmed by a discrete Fourier transform of the photometric time series, although the results are somewhat less convincing (see Fig. 8). Also apparent in this figure are a number short, sharp periodic features, caused by the auto-correlation of the period transits.

thumbnail Fig. 6

Calcium II H and K lines. This plot shows the calcium II H and K lines obtained from the HIRES spectra, with Ca II K on the left (centered at about 3929 Å) and Ca II H on the right (centered at about 3978 Å. No evidence of emission in the cores of these lines can be seen, which is consistent with a star of low magnetic activity.

thumbnail Fig. 7

Rotational period from auto-correlation of the CoRoT-14 photometry. This diagram is created by correlating the light curve with a temporally-shifted version of itself (the lag listed on the X-axis). The broad local maxima at multiples of 5.66 days (marked by the vertical black lines) correspond to the rotation of the star, visible through the photometric footprints of activity-induced variations on the stellar photosphere.

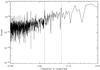thumbnail Fig. 8

Rotational period using the discrete Fourier transform power series of the CoRoT-14 photometry. The vertical dotted lines represent the period of the transit (left) and the rotation period of the star found using the autocorrelation technique (right).

thumbnail Fig. 9

Planetary period vs. eccentricity and mass. This figure shows period plotted against eccentricity for all transiting exoplanets with periods less than 10 days, with circle size indicative of planetary mass. Two-thirds of the 12 planets with M > 2MJ have non-zero eccentricities; those with zero eccentricity include the lowest mass planet in the sample (Kepler-5b) and the most massive (CoRoT-3b). All planetary parameters from the Exoplanet Encyclopedia (http://exoplanet.eu), except for CoRoT-14b.

thumbnail Fig. 10

Circularization timescale vs. eccentricity and planetary mass. This figure shows the tidal circularization timescales of the known transiting exoplanets plotted again eccentricity assuming that the tidal quality factor Q = 106, with circle size indicative of the planetary mass. The circles along the bottom of the plot indicate the different planet mass ranges for each symbol size. CoRoT-14b is shaded gray and is otherwise readily identifiable by its high mass, zero eccentricity, and short circularization timescale. Planetary parameters from the Exoplanet Encyclopedia (http://exoplanet.eu), except for CoRoT-14b.

We estimated the distance of the star to be 1340 ± 110 pc by comparing the Teff to the tables in Allen’s Astrophysical Quantities (Cox 2000) to obtain the absolute V magnitude and corresponding (J − K) color to constrain the extinction. This was then combined with the observed V magnitude to get the distance.

6. Discussion

The most interesting quality of CoRoT-14b is its mass relative to its period. Figure 9 demonstrates this, plotting period vs. eccentricity for the know exoplanets with periods less than 10 days. From this plot, we can see that only WASP-18b is both more massive and dense, while being closer to its parent star – and moreover it has a small but significantly non-zero eccentricity (Triaud et al. 2010). When examining this plot, another characteristic of massive planets becomes apparent: a strong tendency towards elliptical orbits. Only 3 of the 12 (~25%) transiting exoplanets that have masses greater than 2 MJ and periods less than 10 days have e = 0, not including those planets with unknown eccentricity, while 3 more of these orbit stars too faint to allow the orbital eccentricity to be measured readily. In contrast, transiting planets with masses below 2 MJ and periods less than 10 days have only a  ~21% chance (13/63) of having a non-zero eccentricity. While it is impossible to draw any definitive conclusions with such a small sample size, these numbers suggest that more massive planets may in truth have longer periods and higher eccentricities than less massive planets, although it is possible that some of these non-zero eccentricities are artifacts arising from the small number of RV measurements (Shen & Turner 2008).

An examination of the theory for tidal circularization and orbital decay, arising from tides induced by the parent star on the exoplanet, shows that this is expected (see Fig. 10). Both of these phenomena have timescales that proportional to 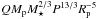QMpM⋆2/3P13/3Rp-5\hbox{$Q M_{\rm p}M_\star^{2/3}P^{13/3}R_{\rm p}^{-5}$} (see e.g., Dobb-Dixon et al. 2004; Ferraz-Mello et al. 2008).

The tidal quality factor Q is a critical and technically unknown value – short-period transiting exoplanets offer perhaps the best laboratory for increasing our understanding of this value. If we nevertheless assume that it is approximately equal for all gas giants, we would expect that high-mass planets with small radii will maintain their eccentricity (and semi-major axis) longer – a tendency further accentuated by the fact that more massive planets have higher surface gravity, allowing them to resist inflation caused in part by incident radiation from the parent star, therefore having smaller radii.

However, this does not explain the circular orbit of the high mass planet/brown dwarf CoRoT-3b (Bouchy et al. 2008), because its circularization timescale is significantly longer than the age of the universe. It is possible that CoRoT-3b might be eccentric, since the RV observations used to measure this parameter are scattered over a year, making it difficult to rule out small, non-zero eccentricities. If both the adopted zero eccentricity and Q factor are correct, the properties of CoRoT-3b would indicate in situ formation rather than migration, the generally accepted process by which short-period planets end up where they are. In contrast, CoRoT-14b is less massive and closer to its host star, leading to a much shorter circularization timescale. The observations of CoRoT-14b are currently consistent with a circular orbit, so it would therefore come as no surprise if this turns out to be the case in the end.

Acknowledgments

The team at the IAC acknowledges support by grant ESP2007-65480-C02-02 of the Spanish Ministerio de Ciencia e Inovación. Some of the data published here were acquired with the IAC80 telescope operated by the Instituto de Astrofísica de Tenerife at the Observatorio del Teide and we thank its observing staff. M. Gillon acknowledges support from the Belgian Science Policy Office in the form of a Return Grant. Data presented herein were obtained at the W. M. Keck Observatory from telescope time allocated to the National Aeronautics and Space Administration through the agency’s scientific partnership with the California Institute of Technology and the University of California. The Observatory was made possible by the generous financial support of the W. M. Keck Foundation. The HIRES observations we obtained fell under the auspices of NASA’s key science program to support the CoRoT mission. The authors wish to recognize and acknowledge the very significant cultural role and reverence that the summit of Mauna Kea has always had within the indigenous Hawaiian community. We are most fortunate to have the opportunity to conduct observations from this mountain.

References

  1. Alonso, R., Auvergne, M., Baglin, A., et al. 2008, A&A, 482, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Baglin, A., Auvergne, M., Barge, P., et al. 2009, Transiting Planets, Proc. IAU Symp., 253, 71 [NASA ADS] [CrossRef] [Google Scholar]
  4. Baranne, A., Queloz, D., Mayor, M., et al. 1994, A&AS, 119, 373 [Google Scholar]
  5. Barge, P., Baglin, A., Auvergne, M., et al. 2008, A&A, 482, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Barnes, J. W., & Fortney, J. J. 2004, ApJ, 616, 1193 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bouchy, F., Queloz, D., Deleuil, M., et al. 2008, A&A, 482, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bruntt, H., et al. 2010, MNRAS, in press [Google Scholar]
  9. Cox, A. N. 2000, Allen’s Astrophysical Quantities (New York: Springer) [Google Scholar]
  10. Deming, D., & Seager, S. 2009, Nature, 462, 302 [Google Scholar]
  11. Deeg, H. J., Gillon, M., Shporer, A., et al. 2009, A&A, 506, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Deeg, H. J., Moutou, C., Eriksson, A., et al. 2010, Nature, 464, 384 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  13. Deleuil, M., Deeg, H. J., Alonso, R., et al. 2008, A&A, 491, 889 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Dobb-Dixon, I., Lin, D. N. C., & Mardling, R. A. 2004, ApJ, 610, 464 [NASA ADS] [CrossRef] [Google Scholar]
  15. Endl, M., Kürster, M., & Els, S. 2000, A&A, 362, 585 [Google Scholar]
  16. Ferraz-Mello, S., Rodriguez, A., & Hussmann, H. 2008, Cel. Mech. Dyn. Astron., 101, 171 [NASA ADS] [CrossRef] [Google Scholar]
  17. Giménez, A. 2006, A&A, 450, 1231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Jefferys, W. H., Fitzpatrick, M. J., & McArthur, B. E. 1988, Celest. Mech., 41, 3 [Google Scholar]
  19. Léger, A., Rouan, D., Schneider, J., et al. 2009, A&A, 506, 287 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  20. Maciejewski, G., Dimitrov, D., Neuhaeuser, A., et al. 2010, MNRAS, accepted [Google Scholar]
  21. Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
  22. Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Queloz, D., Bouchy, F., Moutou, C., et al. 2009, A&A, 506, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Sartoretti, P., & Schneider, J. 1999, A&AS, 134, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Seager, S., & Mallén-Ornelas, G. 2003, ApJ, 585, 1038 [NASA ADS] [CrossRef] [Google Scholar]
  26. Shen, Y., & Turner, E. L. 2008, ApJ, 685, 553 [NASA ADS] [CrossRef] [Google Scholar]
  27. Siess, L. 2006, A&A, 448, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Sing, D. K. 2010, A&A, 510, 21 [Google Scholar]
  29. Sozzetti, A., Torres, G., Charbonneau, D., et al. 2007, ApJ, 664, 1190 [NASA ADS] [CrossRef] [Google Scholar]
  30. Surace, C., Alonso, R., Barge, P., et al. 2008, Proc. SPIE, 7019 [Google Scholar]
  31. Triaud, A. H. M. J., et al. 2010, A&A, submitted [Google Scholar]
  32. Vogt, S. S., Allen, S. L., Bigelow, B. C., et al. 1994, SPIE, 2198, 362 [Google Scholar]

All Tables

Table 1

IDs, coordinates and magnitudes.

In the text
Table 2

Radial velocity measures, errors, and bisectors.

In the text
Table 3

Abundances of some chemical elements for the fitted lines in the HARPS spectrum, with listed abundances relative to the solar value.

In the text
Table 4

Planet and star parameters.

In the text

All Figures

thumbnail Fig. 1

The processed and normalized transit light curve of CoRoT-14. The final processed photometry, corrected for jitter and other effects, but not hot pixels, is plotted on top. The middle plot depicts the same data, corrected for hot pixels. The bottom plot contains the same hot-pixel data binned, with a best-fit sinusoid overplotted. See text for more details.
In the text
thumbnail Fig. 2

The full phase-folded light curve of CoRoT-14. The light curve shown has been corrected for jitter, hot pixels, and other effects, then folded with the known period for CoRoT-14b, with the center of transit at 0. These observations were also binned into 100 evenly-spaced bins, represented by a gray line. No out-of-transit variations are apparent.

In the text
thumbnail Fig. 3

RV orbital fit. This figure shows the orbital fit to the HIRES and HARPS observations, using the period found by the CoRoT photometry, along with the residuals, assuming a circular orbit. A fit was made without this assumption, but returned a value for the eccentricity that was consistent with zero.
In the text
thumbnail Fig. 4

Phase-folded transit and residuals. This figure shows the phase-folded transit from the CoRoT photometry with the best-fit model transit (top) along with the O–C residuals (bottom).
In the text
thumbnail Fig. 5

Mean abundances for 14 elements in CoRoT-14 HARPS spectrum. White circles correspond to neutral lines, red boxes to singly ionized lines, and the yellow area represents the mean metallicity within one sigma error bar.
In the text
thumbnail Fig. 6

Calcium II H and K lines. This plot shows the calcium II H and K lines obtained from the HIRES spectra, with Ca II K on the left (centered at about 3929 Å) and Ca II H on the right (centered at about 3978 Å. No evidence of emission in the cores of these lines can be seen, which is consistent with a star of low magnetic activity.
In the text
thumbnail Fig. 7

Rotational period from auto-correlation of the CoRoT-14 photometry. This diagram is created by correlating the light curve with a temporally-shifted version of itself (the lag listed on the X-axis). The broad local maxima at multiples of 5.66 days (marked by the vertical black lines) correspond to the rotation of the star, visible through the photometric footprints of activity-induced variations on the stellar photosphere.
In the text
thumbnail Fig. 8

Rotational period using the discrete Fourier transform power series of the CoRoT-14 photometry. The vertical dotted lines represent the period of the transit (left) and the rotation period of the star found using the autocorrelation technique (right).
In the text
thumbnail Fig. 9

Planetary period vs. eccentricity and mass. This figure shows period plotted against eccentricity for all transiting exoplanets with periods less than 10 days, with circle size indicative of planetary mass. Two-thirds of the 12 planets with M > 2MJ have non-zero eccentricities; those with zero eccentricity include the lowest mass planet in the sample (Kepler-5b) and the most massive (CoRoT-3b). All planetary parameters from the Exoplanet Encyclopedia (http://exoplanet.eu), except for CoRoT-14b.
In the text
thumbnail Fig. 10

Circularization timescale vs. eccentricity and planetary mass. This figure shows the tidal circularization timescales of the known transiting exoplanets plotted again eccentricity assuming that the tidal quality factor Q = 106, with circle size indicative of the planetary mass. The circles along the bottom of the plot indicate the different planet mass ranges for each symbol size. CoRoT-14b is shaded gray and is otherwise readily identifiable by its high mass, zero eccentricity, and short circularization timescale. Planetary parameters from the Exoplanet Encyclopedia (http://exoplanet.eu), except for CoRoT-14b.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.