| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A110 | |
| Number of page(s) | 32 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201015379 | |
| Published online | 10 March 2011 | |
The B3-VLA CSS sample⋆
VIII. New optical identifications from the Sloan Digital Sky Survey The ultraviolet-optical spectral energy distribution of the young radio sources
1
Istituto di Radioastronomia – INAF, via Gobetti 101,
40129
Bologna,
Italy
e-mail: a.zanichelli@ira.inaf.it
2
Dipartimento di Astronomia, Università di Bologna,
via Ranzani 1, 40127
Bologna,
Italy
Received:
12
July
2010
Accepted:
22
December
2010
Context. Compact steep-spectrum radio sources and giga-hertz peaked spectrum radio sources (CSS/GPS) are generally considered to be mostly young radio sources. In recent years we studied at many wavelengths a sample of these objects selected from the B3-VLA catalog: the B3-VLA CSS sample. Only ≈60% of the sources were optically identified.
Aims. We aim to increase the number of optical identifications and study the properties of the host galaxies of young radio sources.
Methods. We cross-correlated the CSS B3-VLA sample with the Sloan Digital Sky Survey (SDSS), DR7, and complemented the SDSS photometry with available GALEX (DR 4/5 and 6) and near-IR data from UKIRT and 2MASS.
Results. We obtained new identifications and photometric redshifts for eight faint galaxies and for one quasar and two quasar candidates. Overall we have 27 galaxies with SDSS photometry in five bands, for which we derived the ultraviolet-optical spectral energy distribution (UV-O-SED). We extended our investigation to additional CSS/GPS selected from the literature. Most of the galaxies show an excess of ultra-violet (UV) radiation compared with the UV-O-SED of local radio-quiet ellipticals. We found a strong dependence of the UV excess on redshift and analyzed it assuming that it is generated either from the nucleus (hidden quasar) or from a young stellar population (YSP).
We also compare the UV-O-SEDs of our CSS/GPS sources with those of a selection of large size (LSO) powerful radio sources from the literature.
Conclusions. If the major process of the UV excess is caused by a YSP, our conclusion is that it is the result of the merger process that also triggered the onset of the radio source with some time delay. We do not see evidence for a major contribution from a YSP triggered by the radio sources itself.
Key words: galaxies: active / galaxies: starburst / galaxies: evolution / galaxies: photometry / galaxies: interactions / ultraviolet: galaxies
© ESO, 2011
1. Introduction
Giga-hertz peaked spectrum (GPS) and compact steep-spectrum (CSS) radio sources (of subgalactic radio size) with a double-lobed structure, which are referred to as CSOs and MSOs (compact and medium-size symmetric objects), have been suggested for several years to be the young precursors of the large size powerful radio galaxies (Fanti et al. 1995; Readhead et al. 1996; O’Dea & Baum 1997). Since then a considerable amount of data have been produced to shed light on their properties and to develop theoretical models about their radio evolution (e.g. Kaiser 2009, and references therein).
Much interest was given as well to the optical hosts of these radio sources. de Vries et al. (1998, 2000) showed that the hosts are old giant ellipticals. Interactions of the radio source with the galaxy interstellar medium are clear from the study of the emission lines (see, e.g., Labiano et al. 2005; Holt et al. 2009). The presence of young stellar populations in these objects has been revealed several times (Holt 2009; Labiano et al. 2008; deVries et al. 2007; Tadhunter et al. 2002). Their origin is attributed to the shocks generated by the young radio source expanding into the interstellar medium (Rees 1989; Mellema et al. 2002; Bicknell et al. 2000), and/or as the result of a galaxy merger process which, at some later epoch, also triggered the onset of the radio source (Raimann et al. 2005; Holt 2009).
In this paper we present UV-Optical data for a composite sample of CSOs/MSOs sources, which allows us to obtain the UV-O-SED of this class of radio sources and to test the presence of young stellar populations.
The paper is organized as follows.
In Sects. 2 and 3 we describe the B3-VLA CSS sample (Fanti et al. 2001) and its cross-correlation with the SDSS. From this we obtainedphotometry in five bands for 35 radio sources, 12 of which are new identifications. We discuss some properties of the sample.
In Sect. 4 we derive the UV-O-SEDs of the B3-VLA CSS sources and of those CSOs/MSOs, taken from the literature, for which SDSS data exist. The SDSS data were supplemented with UV data from the GALEX surveys (Martin et al. 2005) and with near-IR data (J, H, K bands) from the 2MASS survey (Skrutskie et al. 2006) and from UKIRT literature data. We show that the hosts of these radio galaxies exhibit an excess of UV radiation (UV-excess) compared with the standard UV-O-SED of old elliptical galaxies.
In Sect. 5 we discuss some properties of the UV-excess and its possible origin. In Sects. 6 and 7 we repeat the analysis for a sample of large size radio galaxies (LSO) and compare their UV properties with those of the small size sources. Section 9 gives our conclusions.
Appendices contain supporting data tables, notes, and figures showing the UV-O-SEDs for both compact and extended radio galaxies.
2. The B3-VLA CSS sample
The B3-VLA CSS sample (Fanti et al. 2001, Paper I) is a complete subset of the B3-VLA catalog (Vigotti et al. 1989). It counts 87 radio sources with angular size less than a few arcsecs, corresponding to a linear size ≲20 kpc (for H0 = 100 km s-1, q0 = 0.5, values used in Paper I), divided into two different flux density bins: 0.8–1.6 Jy and ≥1.6 Jy at 408 MHz.
The sample was observed at several radio frequencies with the VLA (4.9 and 8.4 GHz, Paper I; 15 GHz Rossetti et al. 2006). Several subsets were also observed with the Merlin and VLBI arrays at 1.6 GHz (Dallacasa et al. 2002a,b) and at 5.0 GHz (Orienti et al. 2004). Polarization studies have been presented in Fanti et al. (2004) and in Rossetti et al. (2008). The high-resolution radio imaging showed that about 90% of the sources have a double structure and are therefore classified CSOs (≈30%) or MSO. The remaining sources are either core-jets or have a complex morphology.
Initially (Vigotti et al. 1989) systematic optical information was obtained only down to the limiting magnitude of the Palomar Observatory Sky Survey (POSS), i.e.:
-
a)
all quasar candidates were observed spectroscopically andtheir redshifts measured ( Vigotti et al. 1997 ) ;
-
b)
for galaxies visible on the POSS (mR ≲ 20.5), photometric redshifts (up to ≈0.5) were determined from the apparent red magnitude as described in Vigotti et al. (1989);
-
c)
≈75% of the sources (referred to as “empty fields” or “E” sources) had no optical identification.
Information for a few additional objects was also available from the literature (see the notes in Sect. A.1). Later on, deeper optical identifications in the R and K bands were carried out at random for sources without an optical counterpart on the POSS (Mc Carthy et al. 1991; Phare & Djorgovski 1995; Thompson et al. 1994; Maxfield et al. 1995). In this way a number of new identifications were obtained, mostly galaxies with redshifts either spectroscopic (zsp) or photometric (zK) from the redshift-magnitude relation in the K-band.
At the time of writing Paper I the percentage of the optically unidentified radio sources was still ≈40% and it has not decreased much since then.
3. Search for new optical identifications with the SDSS
3.1. The search criteria
Fifty-seven radio sources of the B3-VLA CSS sample are located in the sky area covered by SDSS, DR7 (Abazajian et al. 2009). Optical counterparts have been searched for in the five wavelength bands u (λ = 3551 Å), g (4686 Å), r (6165 Å), i (7481 Å), z (8931 Å) with the procedures available on the SDSS site (CAS Database). The completeness magnitude limits of the SDSS are: ≈22.0 (u); ≈22.2 (g); ≈22.2 (r); ≈21.3 (i); ≈20.5 (z), although objects fainter than these limits can also be found.
The primary search area around each radio source position was a circle of 1.2 arcsec in radius, adequate for the accuracy of the optical and radio positions and for the uncertainties in the registration of the radio and optical reference frames. The search was then repeated in a more extended area, 2.4 arcsec in radius, which generally encompassed the total size of the radio source, in order to check for cases of displacement of the radio centroid from the optical position and to evaluate the number of spurious coincidences. No additional object was found. We found 35 optical objects within the 1.2 arcsec search radius including 23 already known and hence confirmed objects. Furthermore the source 1016+443 is now definitely identified with another galaxy fainter than the one reported earlier. Finally the previous identification for 1350+432 is rejected because of a positional disagreement between the radio source and the optical object originally assumed as counterpart, and this source is now classified as “E”.
A number of the 35 objects are rather faint, with magnitudes below the completeness limits in some photometric bands, four of them are below the limit in all bands. Because there may be some doubts about the reliability of these faint objects, we made a blind search at about one hundred random positions, always with a search area of 1.2 arcsec radius, and found no object at all at any magnitude. Therefore we are confident that we have no misidentifications with either real or spurious objects.Nevertheless some of the objects have a signal-to-noise ratio ≲3σ (magnitude error ≈0.4), i.e. are undetected, in one or more bands. Specifically the detection rate is ≈50% in the u band, ≈90% in the g and r bands and 100% in the i and z bands. As a consequence ≈49% of sources are detected in all SDSS bands. Another ≈34% are detected in four bands, ≈14% in three bands and only one object in two bands.
On the other hand, 10 galaxies that are known from the earlier optical identification projects were not found in the SDSS. This is not surprising, because seven of them have red magnitudes (from earlier works) much fainter than the SDSS limit and the remaining three, with unknown red magnitudes, have high redshifts (two spectroscopic >2.0 and one, photometric, z ≈ 1.2) and are likely fainter than the SDSS magnitude limits.
3.2. The new identifications
The SDSS classification of either quasar or galaxy is based on the extent of the optical object (star-like objects are quasar candidates). Additional support for the classification is based on the location in the Hubble diagrams (Sect. 3.4) and on the UV-O-SEDs (Sect. 4).
 |
Fig. 1 Comparison between the SDSS r magnitudes and those taken from Paper I. |
Eight new galaxies (including the change of identification for 1016+443) and one new quasar with spectroscopic redshift were found. Finally there are two other identifications with star-like objects, possible quasar candidates. The quasar classification of one of them (1055+404A) is supported by its core-jet radio structure.
At present the fraction of optically identified B3–VLA CSS sources in this sub-sample matching the SDSS area has risen from ≈60% to ≈80%. Table A.1 gives the available optical data of the sample.
The present identification status of the 57 SDSS radio sources is then the following:
-
a)
Thirty-seven galaxies (G), all but three with redshift, either spectroscopic (zsp) or photometric (zph2, Sect. 3.3). Twenty-seven have SDSS photometry.
-
b)
Six quasars (Q), five with zsp and one with z photometric, and two quasar candidates (no redshift);
-
c)
twelve still unidentified sources (E), listed in Table A.2. Actually, at the radio position of three of them very faint, unclassifiable objects have been detected by other authors (see notes in Sect. A.1).
Figure 1 shows the comparison between the old and the new red magnitudes. The old magnitudes (that we indicate with mR) are fairly heterogeneous (see notes in Sect. A.1) and errors are not quoted. In the comparison we did not apply galactic extinction corrections because of a lack of information on the filters used for several objects. However, because the typical reddening is low (E(B − V) ≈ 0.018), the extinction is expected to be similar in any red band used and therefore there should be no effects in the magnitude comparison. For galaxies the two sets of data have a relative dispersion of ≈0.5 mag with null offset. We suppose that the scatter is largely caused by the (not quoted) errors of the mR magnitudes, because the errors on rSDSS are generally smaller. For the four quasars though there is a significant offset of ~0.4 mag (SDSS being fainter) with small dispersion. For them we found in the literature other measures, which were well consistent with those from Paper I. We found no explanation for this apparent offset.
 |
Fig. 2 Distribution of the r magnitudes for the optically identified galaxies (left) and quasars (right). Hatched bins indicate the new identifications (Q? included). |
In Fig. 2 we show the r-magnitude distribution of the identified objects.
3.3. SDSS photometric redshifts
The eight newly identified galaxies are too faint to have been observed spectroscopically in the Sloan Survey. We derived their photometric redshifts (zph, 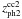 and
and 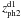 ) from the multi-band SDSS photometry, using the SDSS available routines. The zph is based on galaxy templates, while the zph2 is based on neural nets acting in a five-color space (cc2) or in a magnitude space (d1), and also employs concentration indices (see description in “Help – algorithms – Photoz”, in the SDSS site). The zph2 is recommended by the SDSS group for faint objects, as in our case.
) from the multi-band SDSS photometry, using the SDSS available routines. The zph is based on galaxy templates, while the zph2 is based on neural nets acting in a five-color space (cc2) or in a magnitude space (d1), and also employs concentration indices (see description in “Help – algorithms – Photoz”, in the SDSS site). The zph2 is recommended by the SDSS group for faint objects, as in our case.
For six out of the eight galaxies the SDSS routines gave consistent values of 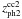 and
and 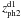 . The zph are instead underestimated compared with the zph2. For the two remaining new galaxies (0814+441 and 1441+409) the fitting routines failed in giving zph2, while the zph have very low (≈0.15), implausible values for objects with r ≳ 23.0.
. The zph are instead underestimated compared with the zph2. For the two remaining new galaxies (0814+441 and 1441+409) the fitting routines failed in giving zph2, while the zph have very low (≈0.15), implausible values for objects with r ≳ 23.0.
In order to evaluate the reliability of these six photometric redshifts we determined zph and zph2 for the 18 galaxies with known zsp as well. Only for one source (1159+395) no zph2 fits were obtained, and zph = 0.62 ± 0.2 strongly disagrees with zsp = 2.37. For the other 17 sources the 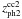 and
and 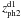 again generally agree well, while the zph are underestimated with respect to zph2 for z ≳ 0.5.
again generally agree well, while the zph are underestimated with respect to zph2 for z ≳ 0.5.
In Fig. 3 we show the comparison between zsp and 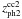 . Clearly there is a good correlation up to z ≈ 1, with a systematic difference of ≈23% (zph2 being lower than zsp) and a scatter of ≈20%. Additionally
. Clearly there is a good correlation up to z ≈ 1, with a systematic difference of ≈23% (zph2 being lower than zsp) and a scatter of ≈20%. Additionally 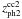 is totally wrong for the two high-redshift (zsp ≳ 1.5) objects (0744+464 and 1314+453A). The case of 1159+395, mentioned just above, is a similar one. A similar result is obtained, with a ≈29% offset, using
is totally wrong for the two high-redshift (zsp ≳ 1.5) objects (0744+464 and 1314+453A). The case of 1159+395, mentioned just above, is a similar one. A similar result is obtained, with a ≈29% offset, using 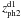 . Hence for the newly identified galaxies we give the average of the two zph2, each one corrected for its own offset.
. Hence for the newly identified galaxies we give the average of the two zph2, each one corrected for its own offset.
The reason for this systematic discrepancy between zph2 and zsp and for the wrong photometric values at high redshifts will be discussed in Sect. 4.2 and is illustrated in Fig. 8.
3.4. Hubble diagrams
We built the Hubble diagrams in the five SDSS bands for both radio galaxies and quasars (Fig. 4). Only the magnitudes corresponding to significant (≥3σ) detection were used. We applied corrections for galactic extinction according to Schlegel et al. (1998). In the diagrams we also plotted the newly identified galaxies with photometric redshifts (zph2 corrected for the systematic difference with respect to zsp discussed in Sect. 3.3). Because we do not have specific information on emission lines, we cannot make corrections for them. Nevertheless we made a statistical estimate of their effect, considering the relations between radio power and emission line luminosities (see Labiano 2008, and references therein), typical of [O ii]3727, [O iii]4959/5007 and Hα. The expected effect is generally a contribution of some percent, with a maximum effect for lines well centered in a given band of up to ≈20% in flux for the highest radio power sources. Accordingly no major problems are expected to occur.
In the r band Hubble diagram, central panel in Fig. 4, we also plot the faint galaxies (squares) that are undetected in the SDSS, using mR, i.e. the old red magnitudes (Col. 3 of Table A.1). We also plot two lines from a recent plot of radio galaxies with z ≤ 1 (Labiano et al. 2007), which includes more than 90% of those plotted objects. We also show the best-fit line for GPS galaxies by Snellen et al. (2002).
In our plot the large majority of galaxies are distributed within the two limiting lines by Labiano et al. (2007) and are slightly brighter than a typical GPS. We note two galaxies out of those boundaries. One is the highest spectroscopic redshift source (0744+464), which appears very luminous and well out of the extrapolation of the radio galaxies band up to its redshift, but it is too weak for a morphological classification. It shows strong broad lines (Mc Carthy et al. 1991), which may significantly contribute to the SDSS magnitudes, and is classified as broad line radio galaxy (and not as a quasar) on the basis of details of the Lyα, He ii and C iv lines. The other one, 1143+456 (z = 0.762), which is not detected in the SDSS, is at least two magnitudes fainter than other objects with a similar redshift.
The objects with corrected zph2 (Sect. 3.3) fit the distribution well (crosses in the figure). Had we not introduced the correction factor, they would have been systematically fainter than the galaxies with zsp in the same range.
Four out of the six quasars with redshift are located below the galaxies region (are brighter), as expected, and another (1242+410) is at the borderline of the two classes of objects. The last one (0800+472) is mixed, instead, with the galaxies (see notes in Sect. A.1).
 |
Fig. 3 Comparison between photometric |
 |
Fig. 4 Hubble diagrams in the five SDSS bands for quasars (+), galaxies with zsp (∗ ) and with zph2 (× ) only. The squares are the faint galaxies undetected in the SDSS. The horizontal lines represent the declared magnitude limits of SDSS. In the central panel the two parallel lines are from Labiano et al. (2007) and the curve is the best-fit line for GPSs from Snellen et al. (2002). |
The g, i, and z band Hubble diagrams reproduce the main features of the r diagram. The dispersion of the points is somewhat reduced in the i and z bands. In these diagrams six of the galaxies with corrected zph2 fit very well. The remaining one (1016+443) is about 1.5 mag too faint in the i and z diagrams and, according to its magnitudes, could have a redshift up to 1.2.
We used the r, i, z Hubble diagrams best fit lines to make an estimate of the redshifts for the two galaxies with multi-band photometry for which the SDSS routines failed to give a zph2. For 0814+441 we estimate z ≈ 1.2. For 1441+409, whose magnitudes are out of the ranges covered by our objects, the extrapolation would give z ≈ 2.0.
The u band Hubble diagram is less populated because only ≈50% of the identified objects are detected in this band. The magnitudes show a smaller dependence on redshift compared with the other Hubble diagrams.
3.5. Completeness of the identifications
The Hubble diagrams show that the identified galaxies with redshift (either spectroscopic or photometric) appear to end at z ≈ 1, and this effect seems essentially due to the SDSS magnitude limits. This led us to assume that the identifications are reasonably complete up to that redshift. In order to reinforce this conclusion, we show in Fig. 5 the redshift distribution for the detected (bottom) and undetected galaxies (top) by the SDSS. Only one of the SDSS non detections (1143+456, already mentioned in Sect. 3.4), is at z < 1.
It is likely that the remaining E sources have the same redshift distribution of the set of galaxies above zsp ≥ 1.2.
4. UV-optical spectral energy distributions of CSOs/MSOs
We supplemented the B3-VLA CSS sample with a set of CSOs/MSOs with SDSS photometry, both quasars and galaxies (11 and 12 respectively), taken from the 3C and PW catalogs (Fanti et al. 1995), from Labiano et al. (2007) and 9C catalog (Inskip et al. 2006b). All these sources are reported in Table D.1. The samples are separated by horizontal lines and are, in the order from top to bottom: B3-VLA, 3C, PW, Labiano et al. (2007) and 9C.
We transformed the SDSS magnitudes into flux densities following the prescriptions given in the SDSS site. The SDSS photometry is given in terms of asinh magnitudes (Lupton et al. 1999), defined as
![$$ m = - (2.5/\ln 10)~ \Big [{\rm asinh}~ \left((f/f_{0})/2 b\right) + \ln(b)\Big] , $$](/articles/aa/full_html/2011/04/aa15379-10/aa15379-10-eq54.png) where f is the flux density of the object and f0 = 3631 Jy is the zero point of the AB scale, to which the SDSS photometry is calibrated. The asinh magnitudes are more appropriate for faint objects and become identical to the traditional magnitudes at high signal-to-noise ratios. The parameter b, determining the flux level over which the asinh magnitudes are similar to the traditional magnitudes is tabulated, e.g., in Abazajian et al. (2009). The flux densities in the various SDSS bands were derived from the magnitudes by inverting the above formula.
where f is the flux density of the object and f0 = 3631 Jy is the zero point of the AB scale, to which the SDSS photometry is calibrated. The asinh magnitudes are more appropriate for faint objects and become identical to the traditional magnitudes at high signal-to-noise ratios. The parameter b, determining the flux level over which the asinh magnitudes are similar to the traditional magnitudes is tabulated, e.g., in Abazajian et al. (2009). The flux densities in the various SDSS bands were derived from the magnitudes by inverting the above formula.
In order to extend the spectral coverage at wavelengths shorter and longer than those of the SDSS we made a systematic search in the GALEX survey catalogs (DR 4/5 and 6; FUV band λeff ≈ 1539 Å, NUV band λeff ≈ 2316 Å) and in the near-IR (J, H, K bands) 2MASS (point sources survey for quasars, extended sources survey for galaxies) and UKIRT literature data. The search was made within a circle of 4 arcsec in radius around each radio position, which is adequate for the positional accuracy of the UV and near-IR objects. The positions of the objects found were checked with those of the SDSS and were found to be consistent with them.
All magnitudes were converted into flux densities with the appropriate conversion formulæ.
Briefly we comment that
-
a)
the coverage of the GALEX surveys is incomplete and is dependent on the sky region. For our objects the best coverage, ≈80%, is obtained with the All Sky Survey (AIS), which is the less deep of the GALEX surveys we searched for. Deepest surveys, as MIS, NGS, GI have a lower sky coverage. The majority of the detections are from those deep surveys. All observed quasars were detected in one or both bands, while the detection fraction for galaxies is ≈42%, and the incompleteness is more pronounced for redshifts ≳ 0.6. Instead all but one of the objects undetected in the SDSS are also undetected by GALEX. We derived luminosity upper limits for the undetected objects, but they were too high to be useful.
-
b)
the 2MASS extended objects survey gives total magnitudes. The UKIRT magnitudes are at fixed apertures, and we always took those with the largest ones, but we suspect that in a few cases they may not have been wide enough. When both types of magnitudes exist for the same galaxy we chose the 2MASS. In total we have near-IR data for ≈30% of our objects. Dividing these into quasars and galaxies, the percentages become ≈60% and 25%. None of the SDSS undetected objects was found.
The GALEX and near-IR data that we found are reported in Table B.1.
 |
Fig. 5 Distribution of redshifts for galaxies found in (below) and missed by (top) the SDSS. The hatched bins represent the (corrected) photometric redshifts. |
After correction for galactic extinction (Schlegel et al. 1998), luminosities at the “source-frame” (sf) wavelength, λsf = λobs/(1 + z), were computed according to the Concordance Cosmology parameters (H0 = 73 km s-1 Mpc-1, Ωm = 0.27, ΩΛ = 0.73), after correction for the (1 + z) factor of the k-correction, and are expressed in units of 107 L⊙ Å-1.
4.1. Quasars
Overall we have six quasars from the B3-VLA sample and 11 from the literature samples.
The UV-O-SEDs (not shown) are generally rising at shorter wavelengths and can be well fitted in a minority of cases by a single power law, L(λ) ∝ λ−αλ, or, more commonly, by two power laws matching at ≈3000–3500 Å, the one at the shorter wavelengths being the flatter1. It is also worth noting that the four quasars with data points at λ ≲ 1000 Å (B3 0701+392, B3 0805+406, 3C 186 and 1442+101) show a sharp drop in luminosity below that wavelength. The UV-O-SEDs of the two quasar candidates without redshift (1055+404A and 1340+439) have an indeterminate shape.
Table C.1 gives the parameters of the individual UV-O-SEDs.
 |
Fig. 6 Composite plot of the UV-O-SED of quasars in the source-framearbitrarily normalized to each other at λ ≈ 3000 Å. The curved line is the best fit of the data in the range 1500–5000 Å. The straight line is from Vanden Berk et al. (2001) (see text). |
The αλ coefficients above ≈3000 Å have a mean value 1.44 ± 0.14, in agreement with the composite quasar spectrum by Vanden Berk et al. (2001) (αλ = 1.56 in the range ≈1500–6000 Å), obtained from a homogeneous data set of over 2200 spectra from the SDSS, and derived from two emission-line free widely spaced spectral regions. On the contrary, at λs ≲ 3000 Å, ≈40% of our quasars have a significantly flatter spectrum. These findings are emphasized by the composite plot of the 17 UV-O-SEDs (Fig. 6). The power law fit of the composite quasar spectrum by Vanden Berk et al. (2001) is with a few exceptions a good representation of our data for λ ≳ 2600 Å. At shorter wavelengths there are many more significant discrepancies because of the individual UV-O-SEDs curvature.
Besides effects caused by contamination from emission lines, we mention among the possible explanations for the above discrepancies:
-
i)
at λ ≲ 2600 Å: internal dust reddening has been suggested by Baker & Hunstead (1995) from an analysis of the optical spectra of CSS quasars from the Molonglo Quasar Sample. They quote a spectral index αν = 1.5 (f(ν) ∝ ν−αν), steeper than in other quasar classes, which is well consistent with the αλ values we obtained in the short wavelengths range. Their suggestion of internal reddening is also supported by the relatively prominent Balmer decrement (AV ≈ 4) they find in these objects. Nevertheless, they also mention some contradictions with such a high extinction. We tried to check the consistency of the curved shape of our composite spectrum with the hypothesis of dust reddening, using the extinction models by Cardelli et al. (1989). We find an acceptable consistency for 0.05 ≲ AV ≲ 0.15 and 1.0 ≲ RV ≲ 2.0. To our knowledge, however, these RV values seem too low. An alternative possibility is that the curvature of the spectrum is intrinsic. At λs ≲ 1000 Å the Lyman α forest is responsible for the fast drop, as is well shown, e.g., by the SDSS spectrum of 1442+101 available from the SDSS site;
-
ii)
at λ ≳ 4000 Å: the luminosity contribution of the host galaxy, in case of an under-luminous nuclear emission. B3 0800+472, B3 1242+410 (see Sect. 3.4 and notes in Sect. A.1) and 1153+32 are possible cases.
The median logarithmic luminosity at 3000 Å is 3.3 × 108 L⊙ Å-1, or ≈8 × 1045 erg s-1 integrated in the optical-UV band, with a dispersion of a factor ≈6.
4.2. Galaxies
Overall we have 25 galaxies from the B3-VLA sample with redshift (zsp or zph2) and another 12 from the literature samples.
The individual UV-O-SEDs in the source-frame are shown in Figs. E.1, E.2 (B3-VLA galaxies with spectroscopic and photometric redshift respectively) and Fig. E.3 (literature samples). They also include data from GALEX NUV and FUV bands (14 objects) and from 2MASS and UKIRT (9 objects). To facilitate the comparison, we overimposed to each UV-O-SED an elliptical galaxy model of 13 Gyr by Bruzual & Charlot (2003), hereafter B&C, normalized at the longest SDSS wavelengths. This model describes the UV-O-SED of the present epoch elliptical galaxies2.
Depending on the galaxy redshift, the five SDSS bands cover different rest-frame wavelength ranges; three galaxies at z ≳ 1.5 (B3 0744+464, B3 1159+395, and B3 1314+453A) have their entire UV-O-SED at λ ≤ 4000 Å, and in these cases the normalization is rather arbitrary.
The majority of the sources shows a decrease in luminosity at λ ≲ 4000 Å, as in the elliptical galaxy model. But this decrease is definitely less pronounced than in the model, and in some cases it is followed by a turn-up at shorter wavelengths (see e.g.: B3 0809+404, B3 1049+384, B3 1241+411, 3C 237, 3C 241). The UV-O-SED of 1314+453A is rising monotonically and can be fitted by a power law as for quasars, with αλ = 1.2. Nevertheless, because the optical object is clearly extended (see notes in Sect. A.1), we keep the “galaxy” classification.
In order to better emphasize the above findings, we show in Fig. 7 a rest-frame composite plot of the UV-O-SEDs of galaxies with zsp, each one scaled in luminosity, at wavelengths λ ≥ 4500 Å, to the 13 Gyr age, 1012 M⊙ stellar mass, elliptical galaxy model by B&C.
Clearly in the large majority of cases there is an excess in luminosity at λ ≲ 4000 Å, (referred to as UV-excess), which becomes more prominent when the GALEX data are added. Therefore, in addition to the old stellar component, another source of light (whose luminosity we indicate by LUV) is required, which is responsible for most of the radiation at wavelengths shorter than 4000 Å. It is likely that LUV does also contribute to some extent to the UV-O-SED at λ ≥ 4000 Å.
In order to properly visualize the UV-excess, we remark that one should have normalized the UV-O-SEDS, in Fig. 7 as well as in Figs. E.1, E.2 and E.3 at wavelengths much longer than 4500 Å, where the contribution of the new component would be small or negligible. Our normalization instead necessarily leads to some underestimate of the UV-excess. Near-IR data (e.g. J, H, K band), which are more representative of the UV-O-SED of an elliptical galaxy, would be very useful. However, as already mentioned, only nine galaxies of this combined sample have some near-IR data. For them our normalization produces an underestimate of the UV-excess from a few % up to ≳ 60% compared with that based on the near-IR data.
 |
Fig. 7 Composite plot of the SEDs in the source-frame for the radio galaxies with spectroscopic redshift. The thick line is the B&C model of an elliptical galaxy of 13 Gyr and 1012 M⊙ (see footnote on page ). The individual UV-O-SEDs are normalized to this model. The broken lines indicate the sources 0744+464, 1159+395, 1314+453A, and 3C 237, which do not have data-points at λ > 4000 Å and whose UV-O-SED normalization is therefore quite arbitrary. |
Anyhow, in spite of the normalization uncertainties, the UV-excess appears quite clear: almost all the UV-O-SEDs lie above the B&C model at λ ≲ 4000 Å.
It is worth commenting on which information GALEX adds to the SDSS. Eight objects with GALEX data show a rise of the UV-O-SED in the NUV or FUV band, which indicates a second peak at λ ≲ 1500 Å, with a luminosity comparable to that at λs ≳ 4000 Å. The other six instead show a decreasing or constant luminosity in the GALEX bands, which is still compatible with a peak in the far-UV, but of much lower luminosity.
4.2.1. The UV-excess
 |
Fig. 8 Fit of the B&C old stellar population galaxy model to the sources 1049+384 (left) and 1136+420 (right), for different redshifts. Two of the lines are marked with zsp and zph; the two intermediate lines represent the two zph2. In 1049+384 the dash-dotted line (marked with zemp, for empirical) gives the best χ2 of all and corresponds to z = 0.05. In 1136+420 a blind fit would provide z ~ 0.45 i.e. identical to zph and it is not plotted. |
We quantify the UV-excess by means of the source-frame luminosity, L0.30, at 3000 Å (0.30 μm), where the excess over the elliptical galaxy model is mostly evident, compared with the luminosity, L0.45, at 4500 Å (0.45 μm), and their ratio, 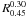 .For a standard elliptical galaxy 13 Gyr old at the present time (z = 0) that has experienced passive evolution (Sect. 5),
.For a standard elliptical galaxy 13 Gyr old at the present time (z = 0) that has experienced passive evolution (Sect. 5), 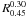 is ≈0.16 and increases slowly up to ≈0.23 at z = 1.5 (Eq. (1), page ).
is ≈0.16 and increases slowly up to ≈0.23 at z = 1.5 (Eq. (1), page ).
The choice of these two wavelengths is a necessary compromise because of the source-frame wavelength range available to us. L0.30 is known for all the sources at z ≲ 1.0, including those with photometric redshifts only, while luminosities at λs < 3000 Å are available only for a fraction of the objects owing to the GALEX detection incompleteness. For instance L0.20, at 2000 Å, is known for ≈70% of the sample, with higher incompleteness at higher redshifts. On the other side, without near-IR data, for a few sources with z > 1.0 we do not have L0.45 and 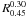 , because their SDSS wavelengths are all ≤ 4500 Å in the source-frame.
, because their SDSS wavelengths are all ≤ 4500 Å in the source-frame.
L0.30, L0.45 and their ratios are reported in Table D.1.
The UV-excess allows us to understand the systematic differences between photometric and spectroscopic redshifts.
In Fig. 8 we show two sample galaxies in which the SDSS data points are compared with a B&C elliptical galaxy model shifted to the observed wavelength by using zsp, 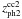 ,
, 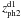 and zph.The galaxy stellar mass is the best-fit free parameter. Each curve is the one which gives the best χ2 for the corresponding redshift. The fit agreement improves as we move from zsp to zph. In addition we show in the plot of 1049+384 the curve (dash-dotted) obtained by blindly fitting the data with the B&C model. It provides the absolutely best χ2 and would correspond to a redshift of z = 0.05. We note that the photometric redshifts, independent of the method used to derive them, give a better description of the UV-O-SEDs in terms of a standard elliptical galaxy and therefore, in order to account for at least a part of the UV-excess, the fits require a redshift lower than the true one.
and zph.The galaxy stellar mass is the best-fit free parameter. Each curve is the one which gives the best χ2 for the corresponding redshift. The fit agreement improves as we move from zsp to zph. In addition we show in the plot of 1049+384 the curve (dash-dotted) obtained by blindly fitting the data with the B&C model. It provides the absolutely best χ2 and would correspond to a redshift of z = 0.05. We note that the photometric redshifts, independent of the method used to derive them, give a better description of the UV-O-SEDs in terms of a standard elliptical galaxy and therefore, in order to account for at least a part of the UV-excess, the fits require a redshift lower than the true one.
4.2.2. Dependencies of the UV-excess on source parameters
Before examining the behavior of L0.30, L0.45 and 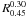 , against (1 + z), P1.4 and LS, the parameters to which the UV-excess could be more likely related, we mention some caveats about our composite sample.
, against (1 + z), P1.4 and LS, the parameters to which the UV-excess could be more likely related, we mention some caveats about our composite sample.
-
i)
Correlations of any quantity with redshift and radio power may suffer for the degeneracy problem caused by the observationally induced correlation between redshift and radio power. This is particularly severe for flux-limited samples.
-
ii)
More generally, our composite sample (B3-VLA plus literature objects) does not uniformly cover the 3D-space radio power – size – redshift, so that, in addition to the degeneracy problem, some apparent effects could be artifacts caused by the inadequate coverage.
-
iii)
The statistics in our sample is limited.
Concerning the first caveat, we point out that our composite sample does not have one single flux density limit, but it is built with three sets of sources (two sub-sets of the B3-VLA catalog, Sect. 2, and 3CR+PW and Labiano lists) that have different flux density limits (≈0.33. 0.66 and 2.1 Jy respectively when extrapolated at 1.4 GHz). Their combination allows us to remove the degeneracy in some ranges of radio power and redshift. Indeed we can see in Fig. 9 that in the P1.4–(1 + z) plane there is an area (Box 1) where 15 objects with approximately the same values of P1.4 (7 × 1026 ≤ P1.4(W Hz-1) ≤ 4 × 1027) cover the redshift range from ≈0.3 to ≈1.
 |
Fig. 9 Distribution of Log(radio power) vs. Log(1 + z) for the galaxies of the composite sample. Empty circles represent 3CR&PW sources; crosses and plus signs are the two B3-VLA sub-samples. The lines correspond to flux densities S1.4 = 2.1 Jy, 0.66 Jy and 0.33 Jy, representing the flux density limits of the three samples extrapolated at 1.4 GHz. |
 |
Fig. 10 Correlations between Log(L0.30), Log(L0.45) and Log( |
A second area (Box 2, 0.11 ≤ log (1 + z) ≤ 0.2 and P1.4 ≥ 1026 W Hz-1) contains 14 objects with roughly the same range of (1 + z), which cover a radio power range of a factor ≈30. In these two boxes we may break the degeneracy between the two parameters.
Revenons à nos moutons 3
We plot in Figs. 10–12L0.30, L0.45, 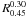 vs. (1 + z), P1.4 and LS.
vs. (1 + z), P1.4 and LS.
 |
Fig. 11 Top panels: enlargement of left hand panels of Fig. 10 for the sources in Box 1. Bottom panels: enlargement of right hand panels of Fig. 10 for the sources in Box 2 (to the right of the vertical line), and for the sources with z ≤ 0.3 (to the left of the vertical line). The lines through the plotted data are the best-fits. |
We recall that some data-points are missing, at high (1 + z), in the plots of L0.45 and of 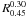 , because the rest-frame UV-O-SEDs at z > 1.5 are shifted to such short wavelengths that without IR observations it is impossible to determine L0.45. In the plots vs. (1 + z) (Fig. 10, left) the data-points are grouped into three classes of radio power (in W Hz-1 at 1.4 GHz): P1.4 ≤ 7 × 1026 (11 sources), 7 × 1026 < P1.4 < 4 × 1027 (15 sources) and P1.4 > 4 × 1027 (6 sources) and are plotted with different symbols; in the plots against P1.4 and LS (Fig. 10, right and Fig. 12) they are instead grouped into two classes of redshift, z < 0.6 and z > 0.6 and are again plotted with different symbols.
, because the rest-frame UV-O-SEDs at z > 1.5 are shifted to such short wavelengths that without IR observations it is impossible to determine L0.45. In the plots vs. (1 + z) (Fig. 10, left) the data-points are grouped into three classes of radio power (in W Hz-1 at 1.4 GHz): P1.4 ≤ 7 × 1026 (11 sources), 7 × 1026 < P1.4 < 4 × 1027 (15 sources) and P1.4 > 4 × 1027 (6 sources) and are plotted with different symbols; in the plots against P1.4 and LS (Fig. 10, right and Fig. 12) they are instead grouped into two classes of redshift, z < 0.6 and z > 0.6 and are again plotted with different symbols.
In spite of the data point dispersion some trends are visible in Fig. 10:
-
a)
both L0.30 and L0.45 significantly increase with redshift, the L0.30 vs. (1 + z) dependence being the steeper. As a consequence also
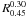 increases with (1 + z), but less steeply. The scatter of the data around the median is somewhat large, ≈ 0.3 in Log, for L0.30 and L0.45, but definitely smaller for
increases with (1 + z), but less steeply. The scatter of the data around the median is somewhat large, ≈ 0.3 in Log, for L0.30 and L0.45, but definitely smaller for 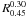 , indicating that the scatter of L0.30 and L0.45 is intrinsic and not caused only by errors.
, indicating that the scatter of L0.30 and L0.45 is intrinsic and not caused only by errors. -
b)
Correlations are found also with P 1.4 .
-
c)
Sub-kpc sources have smaller L 0.30 , L 0.45 and
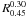 ,
compared with the larger ones (Fig.
12
).
,
compared with the larger ones (Fig.
12
).
The findings at points a) and b) are not independent because of the P1.4–(1 + z) degeneracy. However, if we consider in Fig. 10 the objects of Box 1 (7 × 1026 < P1.4(W Hz-1) < 4 × 1027, filled symbols, amplified in Fig. 11, top), we see that the dependencies of L0.30, L0.45 and also 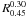 (not shown) on (1 + z), for 0.3 ≤ z ≤ 1, are clearly visible. They cannot be induced by a P1.4 dependence, as P1.4 does not vary appreciably in the explored redshift interval. The galaxies with photometric redshift only, not plotted, also very nicely fit the redshift dependence.
(not shown) on (1 + z), for 0.3 ≤ z ≤ 1, are clearly visible. They cannot be induced by a P1.4 dependence, as P1.4 does not vary appreciably in the explored redshift interval. The galaxies with photometric redshift only, not plotted, also very nicely fit the redshift dependence.
Conversely, looking at the objects of Box 2 (0.3 ≤ z ≤ 0.6,P1.4 ≥ 1026 W Hz-1), we do not find (Fig. 11, bottom) any significant dependence of either L0.30 and L0.45 on P1.4.The same constancy of L0.30 and L0.45 with P1.4 extends also to sources with z ≤ 0.3 and P1.4 ≤ 1026 W Hz-1, as shown in Fig. 11 (left of the vertical line).
So the only clear dependence seen in the data is with (1 + z). This dependence appears to change across the explored redshift interval. For objects in the intermediate radio power and redshift range (Box 1) it is stronger than the average dependence over the whole redshift range (L0.30 ∝ (1 + z)5.8±1.2 and L0.45 ∝ (1 + z)3.6±1.1 against L0.30 ∝ (1 + z)4.5±0.4 and L0.45 ∝ (1 + z)2.4± 0.5). At low redshifts (z ≲ 0.3) there might be no dependence at all on (1 + z) for both luminosities, which is consistent with Labiano et al. (2008).
 |
Fig. 12 Same as in Fig. 10, but vs. Log(LS). The horizontal lines approximately separate objects with z < 0.6 and z > 0.6. |
In order to give a simple physical interpretation of these behaviors, we assume that L0.30(z) and L0.45(z) are the combination of a term, LUV(λ,1 + z), responsible for the UV-excess (whose nature we ignore at this point, but we shall discuss it in Sect. 5) and a second one from the underlying old elliptical galaxy. We assume the simplest possible model, i.e. a power law for LUV(λ,1 + z) and an elliptical galaxy model of 13 Gyr age at the present epoch (B&C) undergoing passive evolution (Sect. 5). A galaxy stellar mass of 4 × 1011 M⊙ is taken (Sect. 5.2) and its contribution to the luminosity, kλ, at the two considered wavelengths, can be approximated from the B&C models 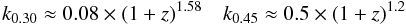 (1)(kλ in units of 107 L⊙ Å-1). Therefore
(1)(kλ in units of 107 L⊙ Å-1). Therefore ![\begin{equation} L_{\lambda}= L_{\rm UV}[\lambda,{(1+z)}] + k_{\lambda} = B_{\lambda}\times \left(\frac{{1+z}}{1.6}\right)^{a_{\lambda}} + k_{\lambda}, \label{L_lam} \end{equation}](/articles/aa/full_html/2011/04/aa15379-10/aa15379-10-eq150.png) (2)where the power law LUV has been normalized at z = 0.6, which is the median value of the redshift for the sample. Lλ and Bλ are in units of 107 L⊙ Å-1.
(2)where the power law LUV has been normalized at z = 0.6, which is the median value of the redshift for the sample. Lλ and Bλ are in units of 107 L⊙ Å-1.
We fitted this law to the L0.30(z) and L0.45(z) data, with aλ, Bλ as free parameters. We limited the fit at z ≤ 1.5, in order to have the same objects at both wavelengths. We obtained  The fits of this model to the data are shown in Fig. 10 (left panels).
The fits of this model to the data are shown in Fig. 10 (left panels).
The values of the parameters a0.30 and a0.45 are not significantly different from each other, and their average value would allow a fair fit for both L0.30 and L0.45. However, the same value for a0.30 and a0.45 implies an almost null dependence of 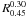 on (1 + z), contrary to the observations. Therefore the difference between the aλ coefficients must be kept.
on (1 + z), contrary to the observations. Therefore the difference between the aλ coefficients must be kept.
Finally, the apparent effect of smaller L0.30, L0.45 and 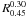 for sub-kpc sources, compared with the larger ones (point c), visible in Fig. 12, arises because in our composite sample there are basically no sub-kpc objects at z ≥ 0.6. If the analysis is restricted to objects with z ≤ 0.6, namely comparing sub-kpc and larger size objects in the same redshift range, the effect disappears.
for sub-kpc sources, compared with the larger ones (point c), visible in Fig. 12, arises because in our composite sample there are basically no sub-kpc objects at z ≥ 0.6. If the analysis is restricted to objects with z ≤ 0.6, namely comparing sub-kpc and larger size objects in the same redshift range, the effect disappears.
In spite of the data incompleteness, we also checked the subset of luminosities at 2000 Å, L0.20, and found results fully consistent with those for L0.30.
Our conclusion is therefore that all trends we observe are largely accounted for by a dependence on redshift of the LUV component. Nevertheless, because of the limited statistics and the non uniform coverage of the redshift – radio power – size space we cannot exclude second order relations with the other parameters.
5. The origin of the UV-excess in CSOs/MSOs galaxies
There are different physical processes that can be responsible for the UV-excess (Best et al. 1998; Tadhunter et al. 2002; Labiano et al. 2008):
-
1)
AGN radiation either from an unobscured nucleus or scattered by the medium surrounding an obscured nucleus;
-
2)
radiation from young stellar populations (YSP);
-
3)
nebular continuum.
As discussed by Tadhunter et al. (2002), the nebular continuum can be derived from the Hβ flux. However, because we do not have this spectroscopic information we cannot make any assessment about this process.
 |
Fig. 13 Example of different models yielding similar fits: left hand and center panels fits with two YSP models of ages 0.1 and 0.06 Gyr respectively; right hand panel fit with the power law model. The dotted lines represent an OSP model (at the longer wavelengths) and either a power law (right-hand panels) or two different YSP models (left hand and middle panels). The line through the data points is the sum of the two sub-components. |
Hence we considered only AGN light contribution either direct or scattered, and a contribution from young stellar population(s). Accordingly each UV-O-SED was fitted twice with a combination of an old stellar population (OSP) elliptical galaxy model plus a power law (Sect. 5.1) or a YSP model (Sect. 5.2). Of course we cannot exclude partial contributions in the UV region from both processes in the same object.
For the UV-O-SEDs of the OSP and YSP we used the stellar synthesis models by B&C, computed for an instantaneous star-burst, with the initial mass function (IMF) by Chabrier (2003) and with solar metallicity. For the OSP we assume an age of 13 Gyr at z = 0 (corresponding to a galaxy formation redshift ≥10) and progressively shorter ages, according to the galaxy redshift, down to ~4.3 Gyr at z = 1.5. Galaxies are assumed to experience passive evolution as they age.
In this range of redshifts/ages the luminosity of an elliptical galaxy was higher in the past (with a small dependence of this trend on λ), approximately ∝ (1 + z) for λs ≳ 4500 Å (to be compared with Eq. (1) for shorter λs). Therefore the UV-O-SEDs maintain approximately the same shape, apart from a scaling factor. The other scaling factor between model and data represents the OSP stellar mass, which is a free parameter of the fit. The other free parameters are either the power law parameters or the YSP stellar masses and ages.
For each source we used all the available data in the fit. GALEX data are very important to constrain both the AGN model and the YSP model. However, because these data exist for only a redshift-biased minority (≈42%) of objects, we also made fits without GALEX in order to derive statistical results for a redshift-unbiased set of objects. We then examine the systematic differences between the two sets of fits with and without GALEX data.
The best fits are obtained by minimizing the χ2 considering only the formal photometric errors. The χ2 vary from reasonably good to quite bad. Excluding the trivial explanation of a totally wrong model, there are several reasons that may justify a bad χ2:
-
i)
the formal errors on magnitudes might be underestimated (for instance assuming a minimum error of 0.05 mag. most of the bad χ2 improve significantly);
-
ii)
effects caused by emission lines, which we could not remove. In some cases a data point at λsf ≈ 6500 Å is too high for any possible model probably because of a strong contribution from Hα. In such cases we ignored that data point in the fit. Moreover, for the two stellar population models:
-
iii)
we used a grid of YSP models at discrete values of age (Sect. 5.2);
-
iv)
because in many cases we have only five data points we use only a two-population model, but we know that more than one YSP may be present (e.g. Holt et al. 2007);
-
v)
there may be uncertainties in the shape details of the population models themselves, related to special parameter choices such as IMF, metallicity, reddening, etc.
For all these reasons we paid more attention to a general visual agreement of the model shape with the data than to the actual values of χ2. We also anticipate that in a number of cases the fit quality of the YSP models is more or less similar to that of the power law models, and it is often difficult to distinguish between these two possibilities. (see, e.g., Fig. 13).
The results of the fits without GALEX are reported in Table D.1. End-of-table notes refer to model changes required by GALEX data. For 1159+395 no fit was possible, as all data are at λrest shorter than 3000 Å (Fig. E.1). For 1014+392 the SDSS data are contradictory with the near-IR and GALEX data (Fig. E.1) and we derived a model using only the last two sets.
5.1. AGN contribution?
Because we do not have spatial resolution (like, e.g., in Labiano et al. 2008), we cannot state whether the UV-excess comes from either an extended volume or from a nuclear point source. We cannot exclude nuclear scattered light, because not only we have no information on spatial distribution and orientation, but we also have no optical polarization information.
We remark also that with the possible exceptions of 0744+464 and 1314+435A, the possibility that some galaxy is a misclassified quasar can be excluded, because quasars are a factor ≈50 brighter in the UV than our galaxies. On the other hand, we cannot exclude the presence of low/moderate luminosity AGNs in some galaxies.
For the AGN model, we used the power law 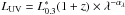 with αλ consistent with the average quasar UV-O-SED (Sect. 4.1). We find that often this agrees fairly well with the data, although there are cases in which the agreement is definitively bad.
with αλ consistent with the average quasar UV-O-SED (Sect. 4.1). We find that often this agrees fairly well with the data, although there are cases in which the agreement is definitively bad.
In three cases out of 14 the GALEX data allow us to reject the power law model. In the remaining cases GALEX does not provide significant differences: bad fits remain bad and good ones remain good.
The results of the fit are given in Cols. 14–16 of Table D.1.
At 3000 Å the power law contribution dominates over that of the underlying galaxy. The opposite is true at λs ≳ 4500 Å. 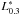 turns out to be increasing with redshift as (1 + z)3.5±0.9. The OSP stellar masses are in the range of (2−20) × 1011 M⊙ and are ∝ (1 + z)1.5±0.6. This strong dependence (increase) of the OSP stellar mass with redshift is hard to explain in the light of models of galaxy evolution, so we are led to conclude that a model with AGN contribution only is not acceptable.
turns out to be increasing with redshift as (1 + z)3.5±0.9. The OSP stellar masses are in the range of (2−20) × 1011 M⊙ and are ∝ (1 + z)1.5±0.6. This strong dependence (increase) of the OSP stellar mass with redshift is hard to explain in the light of models of galaxy evolution, so we are led to conclude that a model with AGN contribution only is not acceptable.
5.2. Young stellar population(s)?
The presence of young stellar populations (YSP) in young radio galaxies has been pointed out by several authors (see, e.g., Holt 2009; Labiano et al. 2008). Two major processes are invoked for their origin: jet induced star formation and galaxy merger. In the first case one would expect the YSP to have an age approximately equal to that of the radio source, typically in the range ~103 to ~3 × 105 yrs for our sources (see, e.g., Murgia 2003). In the second one, instead, the YSP could be much older because a long time delay (0.1–1 Gyr) is expected between the star burst triggered by the merger and the onset of the radio source.
 |
Fig. 14 Examples of model-fitting. The thin lines represent an OSP model (at the longer wavelengths) and either a power law (right-hand panels) or two different YSP models (left hand and middle panels) which give similar fits to the data. The line through the data points is the sum of the two sub-components. GALEX data, not used in the fits, are overplotted as empty circles. Top row: the GALEX point does not discriminate among the three models based on SDSS data. Center row: the GALEX point is in better agreement with the second, SDSS based, YSP model, which can be slightly improved by minor changes. Bottom row: the left hand and right hand panels show the best fits with the SDSS data only. The center panel shows a slight modification of the 0.3 Gyr YSP model which, although unsatisfactory at the shortest wavelengths, represents the best model when the GALEX data are added. |
For the YSPs we considered a wide discrete range of ages (1, 0.6, 0.3, 0.1, 0.06, 0.03, 0.01 Gyr and 6, 3, 1, 0.6 Myr). Note that for a fixed stellar mass, the younger the YSP is, the shorter is the wavelength at which LUV dominates the UV-O-SED, hence the importance of short wavelengths to reveal very young stellar populations.
We present the results in Cols. 8–13 of Table D.1.
We stress that for each UV-O-SED there are often two or three more or less equivalent models (Fig. 13), differing from each other in age and stellar mass of the YSP and somewhat less in the UV-OSP stellar mass. Since the wavelengths are sampled in a limited range, the UV-O-SEDs of YSPs differing in age by a factor ≈3 are similar in shape, therefore, by properly choosing the stellar mass, they can reproduce more or less the same light contribution in the SDSS bands. The fitting model is more constrained when a broader range of wavelengths (e.g., GALEX and near-IR) is available. In addition, for some objects at high redshift (z > 0.7) and without near-IR data, the OSP stellar mass is little constrained. In these cases we report the maximum stellar mass allowed by the data. For the high-redshift sources 0744+464 and 1314+453A the UV-O-SEDs could be fitted by an YSP alone. In general the YSP contribution is dominant at ≲3000 Å, but at high redshifts it becomes important also at 4500 Å and may overwhelm the OSP contribution.
It is interesting to compare the stellar populations parameters derived with and without the GALEX for the objects with GALEX data. We find that for ≈40% of objects the model is unchanged or marginally changed, and that for the remaining ones a YSP model a factor ≈2 older, and hence with masses ≈a factor two larger, is preferred. The fits tend to be worse in the cases where the luminosity increases again in the GALEX NUV band and shows, or suggests, a peak at λ ≲ 1500 Å. Actually this observed peak appears narrower than or somewhat displaced from the peak present in the YSP models.
In Fig. 14 we show examples of objects with GALEX data to demonstrate their effect in the fits.
The YSP luminosities at 3000 Å and at 4500 Å are ∝ (1 + z)4.4±1.0 and ∝ (1 + z)3.7±0.9 respectively, which is consistent with the LUV dependences on (1 + z) at the two wavelengths that we found in Sect. 4.2.2.
The YSP ages derived without GALEX data are generally in the range 0.06–0.8 Gyr, with a median value ≈0.2 Gyr. The average YSP stellar mass is ≈1010 M⊙, with a dispersion of a factor ≈4. We find that the YSP mass is correlated with (1 + z) and with L0.3, while the YSP age is independent of (1 + z).
If instead we also use GALEX data when available, the YSP ages of most objects with z ≲ 0.5 are shifted to the range 0.2−1.2 Gyr, and the median value is ≈0.4 Gyr. While the majority of the higher redshift objects are not detected by GALEX, for three out of four with these data, the models have marginal non-systematic changes, while the fourth one (3C 237) requires the YSP age to be ≈4 times shorter. The correlation between YSP mass and (1 + z) may disappear, but because of the large incompleteness at higher redshift we leave this as an open question.
The OSP stellar masses are fairly independent of GALEX data. After correction for passive evolution, they are in the range of (1−10) 1011 M⊙, with an average value of 4 × 1011 M⊙, independent of (1 + z), radio power and radio size.
The above findings are consistent with an OSP undergoing a passive evolution (as in B&C) plus a YSP of a small stellar mass (a few % of the OSP stellar mass), which makes a major contribution to the UV luminosity, and a minor one at longer wavelengths, except for the high redshift, where the contribution can be substantial.
With our data we have no evidence for a YSP with an age comparable to that of the radio source, namely <106 yr. If present, it would be a minor contributor to the UV-excess. Therefore we prefer the scenario in which the YSP responsible for the UV-excess is caused by a merger event, which at a later stage triggered the onset of the radio source.
6. A comparison sample of large size radio galaxies
It has been well known for a long time, even earlier than for CSOs/MSOs, that there is an UV-excess in the hosts of powerful large size radio galaxies (several hundred kpc; LSOs). This UV emission is generally aligned with the radio structure and the phenomenon is referred to as the alignment effect (see, e.g., Chambers et al. 1987; McCarthy et al. 1987). A set of 3CR and 6C sources at redshift ≈1 has been investigated with great detail in the nineties (Best et al. 1997, 1998, 1999) to understand this effect (see also Inskip et al. 2006a, and references therein). More recently the UV-excess has been found in local samples of radio galaxies as well (Aretxaga et al. 2001; Raimann et al. 2005).
In order to compare the UV-O-SEDs of the objects of our composite sample of young radio sources with the hosts of radio sources with large linear size (LS ≳ 30 kpc) and with a redshift distribution similar to ours, we selected the 3CR FRII LSOs that fall in the area covered by the SDSS. This sample, containing 37 radio galaxies (the set of 3C sources at z ≈ 1 studied by Best et al. (1997) is included), was supplemented by the six 6C sources with z ≈ 1, from Best et al. (1999), with SDSS data. This second small sub-sample, with radio power lower by a factor ≈7 compared with 3CR sources at the same redshift, allows us to manage the degeneration between radio power and redshift, which cannot be avoided by dealing with the 3CR sample alone.
Overall we have a sample of 43 large-size radio galaxies with SDSS data (see Table F.1). For these, we have almost complete data in the near-IR (mostly UKIRT data). In addition, ≈75% have been observed by GALEX (mostly AIS), two thirds of which were detected in NUV and eventually FUV band with slightly larger incompleteness at highest redshifts.
We produced the UV-O-SEDs following the same procedure as for the CSOs/MSOs. They are presented in Fig. G.1. Visually we see the UV excess in the majority of cases. The most impressive result is the bright peak around 1000–1500 Å in the high-redshift galaxies (see, e.g. 3C 265, 6C1011+36). This peak was also noted in a fraction of CSOs/MSOs, but here it is sometimes very bright compared with the λ > 4000 Å peak/plateau. Hints for these peaks can be seen in the SDSS u band alone as well, but they become very clear when adding GALEX data.
For these sources we repeated the analysis described in Sects. 4.2.2 and 5.
6.1. Correlations
The same caveats as discussed in Sect. 4.2.2 hold also for the analysis of the LSO sample.But the use of the small set of 6C sources in addition to the 3CR sample allows us, as for the MSOs/CSOs, to select two subsamples:
-
i)
Subsample 1: thirteen sources in a narrow redshift range (0.9 ≲ z ≲ 1.2) and in a broad radio power range (7 × 1026 ≲ P1.4(W Hz-1) ≲ 3 × 1028);
-
ii)
Subsample 2: twelve sources in a narrow radio power range (7 × 1026 ≤ P1.4(W Hz-1) ≤ 4 × 1027) and in a broad redshift range (0.2 ≲ z ≲ 1.2).
These two subsamples allow us to examine the relations with radio power at ≈constant redshift and vice versa.
In Fig. 15 we present plots of L0.30, L0.45 and 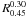 vs. (1 + z) only to save space.
vs. (1 + z) only to save space.
 |
Fig. 15 Plots of Log(L0.30), Log(L0.45) and Log( |
 |
Fig. 16 Examples of fits with three stellar population models: one OSP, one YSP of intermediate age (0.01–1 Gyr) and a very young population with the age of the radio source (< 10-2 Gyr, for an assumed expansion speed of 0.1c). |
We repeated the analysis described for the small sources in Sect. 5.2. From the plots in Fig. 15 the following trends are apparent:
-
i)
for the sources of subsample 2 (filled symbols in Fig. 15) there is a clear dependence of L0.30 and
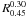 on (1 + z), and a much smaller one, if any, for L0.45. These dependences extend reasonably well also to the lower power sources with z ≲ 0.20. Therefore, for the sources with P1.4 ≤ 4 × 1027 W Hz-1, L0.30, L0.45 and
on (1 + z), and a much smaller one, if any, for L0.45. These dependences extend reasonably well also to the lower power sources with z ≲ 0.20. Therefore, for the sources with P1.4 ≤ 4 × 1027 W Hz-1, L0.30, L0.45 and 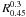 can be described with a dependence on (1 + z) only, independent of radio power. The curves plotted in Fig. 15 are derived by fitting the same model used for the CSOs/MSOs (Eq. (2)), with the appropriate parameters;
can be described with a dependence on (1 + z) only, independent of radio power. The curves plotted in Fig. 15 are derived by fitting the same model used for the CSOs/MSOs (Eq. (2)), with the appropriate parameters; -
ii)
the more powerful radio galaxies, P1.4(W Hz-1) ≥ 4 × 1027 (squares), describe a separate sequence compared with the less powerful objects at the same redshift, on average a factor ≈2 brighter in both L0.30 and L0.45.If we isolate among them those of subsample 1 (0.9 ≤ z ≤ 1.2), we can derive for these high-power sources the dependence of L0.30 and L0.45 on P1.4.
We attempted to describe quantitatively the above findings with a modification of Eq. (2). In order to take into account the radio power dependence, we added a new term, dependent on radio power only. This new term introduces the possibility of an additional and independent mechanism for the production of the UV-excess: ![\begin{equation} L_{\lambda}= \left[B'_{\lambda}\times \left( \frac{\rm{1+z}}{1.6}\right) ^{a'_{\lambda}} + k_{\lambda}\right] + v_{\lambda}\times\left( \frac{P_{1.4}}{10^{27}}\right) ^{w_{\lambda}} \label{L_lam-P} \end{equation}](/articles/aa/full_html/2011/04/aa15379-10/aa15379-10-eq204.png) (3)(kλ from Eq. (1), Sect. 4.2.2). Units are 107 Å-1 for Lλ and W Hz-1 for P1.4.
(3)(kλ from Eq. (1), Sect. 4.2.2). Units are 107 Å-1 for Lλ and W Hz-1 for P1.4.
For this model we find 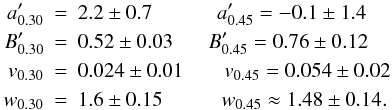 After the dependences on (1 + z) and P1.4 are taken off the data, no significant residual dependence is found on LS.
After the dependences on (1 + z) and P1.4 are taken off the data, no significant residual dependence is found on LS.
As for CSOs/MSOs, in spite of the incompleteness, we also examined the luminosities, L0.20, at 2000 Å and found results well consistent with those for L0.30.
6.2. YSP models
We applied the two stellar population galaxy models, as in Sect. 5.2, and derived OSP and YSP stellar masses and ages4.
The ages of the YSP derived without GALEX data span a range of values from 0.04 to 0.8 Gyr, with a mean value of ≈0.16 Gyr, similar to what was found for CSOs/MSOs, but the addition of the GALEX data tends to indicate younger YSP models, especially for the high-redshift galaxies. This effect is often caused by the rapid increase of luminosity in the NUV (and FUV, when detected) band, namely by the bright peak mentioned earlier. On average the effect is of rejuvenating the YSPs by a factor ≳ 3 and consequently of decreasing their masses by about the same factor. Nevertheless, in general the models fail in properly reproducing the fast rising of the peak with decreasing wavelength.
We attempted to see if the bright peak can be caused by an additional contribution of UV radiation and modeled the UV-O-SEDs of a few sources with the best-quality data with three stellar populations: one OSP, one YSP of intermediate age (0.01–1 Gyr) and a very young population with the age of the radio source (≲10-2 Gyr), derived from the source linear size and an assumed expansion speed of 0.1c. We display two examples in Fig. 16. The results suggest that a second very young YSP may be possible, although these fits are insignificantly better than those with a single YSP only.
The OSP stellar masses are fairly independent of the GALEX data and are similar to those of the CSOs/MSOs sample. The average mass is 4 ± 0.5 × 1011 M⊙. There are no significant relations of the OSP stellar mass with redshift, radio power or radio linear size5.
6.3. AGN contribution?
As for CSOs/MSOs, we attempted to fit the UV-O-SEDs of these large sources with an old elliptical galaxy template plus a power law spectrum (AGN) as well. Differently from what was found for CSOs/MSOs, in these sources the great majority of which has near-IR and GALEX data, there are a number of cases where these fits are worse than those of the YSP model, and none with better fits. We stress the difference with our sample of small size sources, for which we have near-IR and GALEX data only in a minority of cases, and often we could not distinguish between AGN and YSP models. With data in a broader wavelength range, it is easier to discriminate between the two models.
Anyhow the ranges of values for 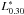 , αλ and MOSP are the same as those we derived for CSOs/MSOs. Also
, αλ and MOSP are the same as those we derived for CSOs/MSOs. Also 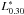 and MOSP show the same dependence with (1 + z) of CSOs/MSOs. As for CSOs/MSOs, we consider the dependence of MOSP on (1 + z) unrealistic.
and MOSP show the same dependence with (1 + z) of CSOs/MSOs. As for CSOs/MSOs, we consider the dependence of MOSP on (1 + z) unrealistic.
 |
Fig. 17 Distribution of the CSOs/MSOs (black points) and LSOs (empty circles) in the radio power – linear size plane. The two lines represent an evolutionary model where P1.4 ∝ LS-0.5 (see text). |
7. Young versus old radio galaxies
In the previous sections we analyzed the UV-O-SEDs and the UV-excess of small (CSOs/MSOs) and large size (LSOs) radio galaxies. The two samples, very different in source radio size, have a similar redshift distribution and span the same range in radio luminosity, although with a difference of a factor ≈2.5 in their median values (see Fig. 17).
Within the evolutionary scenario, in which the CSOs/MSOs are the young and the LSOs the aged phases of the extragalactic radio source population, any comparison between properties of the two classes should be made between samples selected in radio power and size according to the evolution scenario. Typically radio sources are expected to dim while growing in size. As an example, in Fig. 17 we overplotted two evolutionary lines of a model in which P1.4 ∝ LS-0.5 (see Baldwin 1982; Fanti et al. 1995). According to this model CSOs/MSOs (black points) within those lines would evolve into the LSOs (open circles) enclosed within the same lines. Other models with different dependences between P1.4 and LS were also considered. The previous analysis on CSOs/MSOs (Sects. 4.2.2 and 5) and on LSOs (Sect. 6) was made considering the two samples separately and without taking any evolutionary model into account. Therefore we repeated the analysis, selecting from each set of sources the objects within the evolutionary band. We found negligible changes and, therefore we use below the results reported in Sects. 4.2.2, 5, and 6.
The main points in comparing the results obtained for the two classes of sources are:
-
i)
the luminosities L0.30 and L0.45 and their ratio have similar ranges of values in small (≲30 kpc) and in large (≫30) kpc radio galaxies.
-
ii)
L0.30 and L0.45 show a dependence on (1 + z), both in CSOs/MSOs and LSOs. However, these dependences are different at ≳2σ level, the LSOs showing a weaker dependence.
-
iii)
In LSOs a dependence of L0.30 and L0.45 on P1.4, not found for CSOs/MSOs, shows up for P1.4 ≳ 4 × 1027 W Hz-1. In the fitting procedure we described the dependence on P1.4 with an additional term (see the parameters of Eqs. (2) and (3)). Note, however, that among the small sources we have only a few objects in that radio power range and we cannot exclude that we missed a P1.4 dependence.
-
iv)
At λ < 2000 Å the high-redshift (high-radio power) LSOs very often show pronounced peaks in their UV-O-SEDs, which are also seen, although not as bright, in the CSOs/MSOs.
-
v)
The YSP ages associated with high-redshift high-radio power LSOs appear shorter by a factor ≳ 3 with respect to the CSOs/MSOs.
-
vi)
The OSP have similar stellar masses in the two sets of radio sources.
Under the assumption that the UV-excess is predominantly caused by the presence of a YSP population, we discuss the similarities and the differences in the framework of a composite scenario that combines the two different processes which may generate YSP populations.
The first process is the galaxy merger, which generates a burst (or several bursts) of star formation (the YSPmerger). With a time delay ≲1 Gyr some residuals of the stellar mass reach the super-massive black hole of the more massive galaxy or the two black holes of the merging galaxies coalesce, thus triggering the formation of the radio source. The second process is the generation of shocks in the outer medium, caused by the expansion of the radio source, which, at the end, produces another burst of star formation (YSPrs). This new population is expected to be more or less distributed along the source axis, explaining the alignment effect, and would have an age comparable with that of the radio source, namely ≲0.01 Gyr for an expansion speed ≈0.1c (Arshakian & Longair 2000). Looking at the UV-O-SED of the host galaxy of a radio source one would observe at the same time the YSPmerger, with an age of ≲1 Gyr, the YSPrs with an age of ≲107 yrs and the old elliptical galaxy, with an age of several Gyr. Owing to its longer time scale the YSPmerger should appear similar in small (CSOs/MSOs) and in large size (LSOs) radio sources. Furthermore the (YSPrs) would be expected to show properties related to radio source parameters, like radio power (amount of shocks generated) and linear size (time required to build up the very young YSPrs and its later decay).
The dependence of a fraction of LUV (see Eq. (3)) on radio power in the powerful LSOs could be a marker of the YSPrs. This fraction would be responsible for the alignment effect seen in these objects (Best et al. 1998). On the contrary, the lack of dependence of LUV on radio power in small radio sources would indicate that the YSPrs is still in the stage of being formed and the YSPmerger dominates. The UV-O-SEDs that we obtain using GALEX data for the most powerful LSOs leave open the possibility for an additional YSP with an age comparable with that of the radio source (see Fig. 16).
The major problem with the composite scenario is that in the LSOs the redshift-dependent LUV component has a dependence on (1 + z) significantly different from that of CSOs/MSOs. If, as we assume, this component is caused by the YSPmerger, which has a time scale much longer than the radio source life-time, it should display the same properties in both classes of sources and, in particular, it should exhibit the same (1 + z) dependence. We attempted to force the same redshift dependence on both small and large sources, but we only achieved a very poor agreement.
We might wonder whether a YSPrs may be produced not only by the very high-radio power sources (P > 1027 W Hz-1), but also by the less powerful ones, without a dependence on radio power, weak or null dependence on (1 + z) and be dominant in LUV, in a way to wash out the redshift behavior of the LUV of the YSPmerger. But then we would expect the LSOs to be systematically brighter than the CSOs/MSOs, which seems not to be the case.
Alternatively we could imagine that the LSO life-times are longer than assumed and comparable with those of the YSPmerger, so that when the YSPrs is fully developed, the other is already fading out.
If instead the origin of the UV-excess is the merger process only, we should conclude that more powerful radio sources are produced when major mergers that involve an amount of fuel (stellar mass) above a certain threshold occur. Furthermore, in order to explain the alignment effect, we should assume that mergers occur anisotropically and that the radio jet, when born, is oriented along the direction of falling material (see West 1994, as cited by Inskip et al. 2006a, for a model of this kind). However, the different redshift dependences of the UV-excess remain an open problem.
From the above our data do not allow us to reach an unquestionable conclusion although there are some hints in favor of the composite scenario.
Perhaps our approach and our data are not sufficient to deal with this subject, and a more refined analysis, additional data (e.g. spectroscopic, as in Holt et al. 2007), and a more complex scenario is required that also includes other processes such as AGN contribution, emission lines, and nebular continuum effects.
8. Conclusions
The main results from this work can be summarized as follows.
-
1)
The Sloan Digital Sky Survey (SDSS) data allowed us to obtain new optical identifications for radio sources in a sub-set of 57 objects from the B3-VLA CSS sample laying in the area covered by the SDSS. Eight of the new identifications are with galaxies and three with quasars or quasar candidates. In this sample the fraction of identified sources has increased from ≈60% to ≈80%.
-
2)
In total, including also earlier identifications, we have photometry in the five SDSS bands for 27 galaxies and 8 quasars or quasar candidates.
-
3)
Photometric redshifts (zph2) for 17 of the identified galaxies with zsp were obtained using the SDSS routines. A comparison between the two types of redshifts showed that the zph2 are underestimated on average by ≈26%. A correction of this amount was applied to the zph2 of the newly identified galaxies. With these corrected redshifts the new identification are well located in the Hubble diagrams, mixed with the galaxies with spectroscopic redshifts.
-
4)
Including also galaxies with photometric redshifts only, the optical identifications are considered complete up to z ≈ 1.0.
-
5)
After extending the B3-VLA CSS sample with CSOs/MSOs from the literature, we derived the source-frame optical spectral energy distribution (UV-O-SED) for galaxies and quasars with the SDSS 5-band photometry. We added to the SDSS data those in the far UV from the GALEX surveys and in the near-IR from the 2MASS survey, and from literature the UKIRT observations. Although they are incomplete, these data give very valuable information. In quasars the UV-O-SEDs are described to a good approximation by a single power law, or, more commonly, by two power laws matching at ≈3000–3500 Å, the one at the shorter wavelengths being the flatter. The UV-O-SEDs of galaxies show in the large majority of cases a luminosity excess in the UV (λ < 4000 Å), when compared with the UV-O-SED of an old elliptical galaxy.
-
6)
We analyzed this excess in terms of the source-frame luminosities at 3000 Å and 4500 Å and of their ratio as a function of redshift, radio luminosity, and radio linear size. We found that the main dependence is on the redshift, while there are no significant dependences with the other parameters. We described the UV-excess as caused by a source of radiation overimposed on the UV-O-SED of an old elliptical galaxy undergoing passive evolution. The UV component becomes more and more important as the redshift increases: ∝ (1 + z)a with a ≈ 5.0 and 4.0 at 3000 Å and 4500 Å respectively. For the fraction of objects with GALEX observations we also examined the behavior of L0.20, which agrees with the results of L0.30.
-
7)
We attempted to describe this UV component with two models: an AGN component with a quasar-like power law spectrum, and a Young Stellar Population (YSP) component, described by the models developed by B&C. For CSOs/MSOs both models are equally plausible for the majority of sources, and we cannot make a clear choice between them. Yet there is a different implication between the two: the AGN model requires an evolution for the OSP stellar mass with time, with stellar masses larger in the past than at present epoch, while in the YSP model the OSP stellar mass is roughly constant.
-
8)
We performed an analysis of the UV-O-SEDs for a composite sample of large size (≫30 kpc) sources with radio power and redshifts similar to CSO/MSO’s, taken from the literature, using the SDSS photometry plus UV GALEX data and near-IR data often available from the literature, in order to explore the relations with our smaller size radio sources, which are considered to be the young precursors of those with larger size. The two sets of sources show a number of common properties as well as some clear differences, so that it is difficult to draw firm conclusions. The popular scenario where the UV-excess is caused by a first generation YSP from a galaxy merger, which later triggered the radio source, and a second generation YSP produced by shock of the expanding radio source, has some hints of support and some contradictions as well.
Online material
Appendix A: The B3-VLA-SDSS sample and notes
The B3_VLA – SDSS sample.
A.1. Notes to Table A.1 and Table A.2
0701+392: spectroscopic redshift from Lahulla et al. (1991). The old red magnitude is a visual estimate from the Palomar Sky Survey Prints (Vigotti et al. 1989).
0703+468: Stanghellini et al. (1993) report a possible identification with a 23 mag. object.
0744+464: redshift by Mc Carthy et al. (1991) from Lyα, [C iv]1549 and He ii1640. McCarthy classified the optical object as Broad Line Radio Galaxy (see Sect. 3.4).
0754+396: redshift from Vigotti (priv. comm.).
0800+472: classified as quasar in the SDSS, from the optical spectrum and point-like appearance; in the Hubble diagram (Fig. 4) it is located in the galaxy area.
0805+406: photometric redshift by Richards et al. (2004). A range of values 1.5–1.95 is quoted, with 0.935 probability.
0809+404: the spectra in Vigotti et al. (1997) and in the SDSS show strong [O iii]5007 and [O ii]3727 lines. Vigotti et al. (1997) say that the object is point-like, but in the SDSS it isclearly extended. Also the UV-O-SED in Fig. E.1 clearly supports the galaxy classification. In the magnitude-redshift diagram (Fig. 4) it is located at the separation between quasars and galaxies.
Unidentified radio sources in the SDSS B3-VLA CSS sample.
0810+460B: identification and redshift from Cruz et al. (2006). Strong [O ii]3727, [Ne iii]3869, Hγ, [O iii] 4959,5007 lines are present. The [O ii/[O iii] ratio (2.8) shows a low level of excitation consistent with a shock heating mechanism.
0822+394: a photometric redshift z = 1.18 (1.0–1.4) is reported by Lilly (1989); (in a note z ≈ 1.2 is given). Later authors (e.g. Law-Green (1995) and Roche et al. (1998)) report z = 1.21, without specifying that it is a photometric redshift.
0856+406: redshift by Phare & Djorgovski (1995) from Hα line. It is erroneously reported as a QSO in NED. Old red magnitude from Vigotti (priv. comm.).
0930+389: redshift by Eales & Rawlings (1996) from Hα line.
0935+428A: redshift and r magnitude by Thompson et al. (1994). Emission lines of C ii]2326 and Mg ii2798.
0951+422: redshift by Falco et al. (1998), from Si iv, C iv, [C iii] and Mg ii lines.
1014+392: the reported optical identification and the redshift are from Gandhi et al. (2006), who classify this object as a strongly obscured type 2 quasar with an intrinsic 2–10 keV luminosity 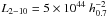 erg s-1. [O ii]3727 and [O iii]5007 lines, with ratio ≈2, are present. Near-IR magnitudes are given in Gandhi et al. (2004).
erg s-1. [O ii]3727 and [O iii]5007 lines, with ratio ≈2, are present. Near-IR magnitudes are given in Gandhi et al. (2004).
1016+443: the identification reported in Paper I (mR = 19.7, z = 0.33) is rejected because of radio-optical positional disagreement. The new identification reported here is from the SDSS.
1025+390B: r magnitude and redshift from Allington Smith et al. (1988). [Ne iii]3869 and [O iii]4959,5007 are seen.
1044+454: photometric redshift from K-mag from Vigotti (priv. comm.).
1049+384: redshift and r magnitude from Allington Smith et al. (1988). High excitation narrow lines system (large [O iii]/[O ii] ratio) and broad Mg ii2799 emission.
1055+404A: point-like in the SDSS and therefore quasar candidate.
1128+455: redshift from Vigotti et al. (1997). [O ii]3727 and [O iii]5007 present.
1136+420: redshift and red magnitude from Vigotti (priv. comm.).
1141+466: redshift from SDSS4. Strong [O ii]3727 and Hα, very weak [O iii]5007.
1143+456: r magnitude and redshift, from [O ii]3727 line, by Thompson et al. (1994).
1157+460: r magnitude and redshift, from [O ii]3727 line, by Maxfield et al. (1995).
1159+395: redshift by Vigotti (priv. comm.); r magnitude from Maxfield et al. (1995).
1201+394: the SDSS spectrum shows [O ii]3727 and [O iii]5007 lines, with low excitation status.
1204+401: redshift and r magnitude by Thompson et al. (1994); Lyα, C iv, [C iii] and C ii] lines are seen.
1212+380: K-mag. photometric redshift from Vigotti (priv. comm.).
1216+402: r magnitude and Redshift, from [O ii]3727 and [Ne iii]3869, by Thompson et al. (1994).
1217+427: Maxfield et al. (1995) report a possible identification with g,r ≥ 23.0 and i ≥ 22.5.
1225+442: redshift from Wegner et al. (2003); the optical object is classified as Seyfert 2. Red magnitude from Vigotti (priv. comm.).
1241+411: Vigotti et al. (1997) classify the optical object as Seyfert. In the SDSS it has an extended image and, according to strong broad lines in the spectrum, it is classified as QSO. In the m-z diagram (Fig. 4) it is located at the separation between quasars and galaxies. [O ii]3727 and [O iii]5007 present.
1242+410: redshift by Xu et al. (1994) and Vigotti et al. (1997). [C iii]1909, Mg ii2798, Hβ, [O ii]3727, [O iii]4959,5007 are seen.
1314+453A: redshift, red magnitude and optical classification from Vigotti (priv. comm.). The UV-O-SED is consistent with a quasar classification (Sect. 4.2). However the object is clearly extended in the SDSS image.
1340+439: point-like in the SDSS and therefore quasar candidate; reported as G in NED, perhaps from Maxfield et al. (1995) who report an object of 23.4, 22.8, and 22.1 in the g,r and i bands.
1343+386: redshift and red magnitude from Vigotti et al. (1997). The SDSS spectrum shows strong and broad [Si iv], C iv, [C iii] and Mg ii.
1350+432: the identification in Paper I is now rejected because of radio-optical positional disagreement.
1432+428B: Maxfield et al. (1995) report a possible identification with g,r ≥ 23.0 and i ≥ 22.5.
1441+409: Maxfield et al. (1995) report a possible identification with g,r,i = 23.0, 22.6 and 22.1. However the positional agreement is obscure.
1445+410: redshift from SDSS4. Hα, [O ii]3727 and weak [O iii]5007 lines.
1458+433: redshift and red magnitude from Vigotti (priv. comm.).
Appendix B: UV-GALEX and near-IR data
GALEX and near-IR data.
Appendix C: The combined CSOs/MSOs Quasar sample
The combined quasar sample.
Appendix D: The CSO/MSO composite SDSS galaxy sample
The CSO/MSO SDSS galaxy sample.
Appendix E: UV-O-SEDs of B3_CSS VLA and other compact sources
 |
Fig. E.1 Individual SEDs for galaxies with spectroscopic redshift. Empty circles are GALEX data. The dotted line represents a B&C model normalized to the long-wavelength SDSS data only (see notes to 1014+392). |
 |
Fig. E.1 continued. |
 |
Fig. E.2 Individual SEDs for galaxies with photometric redshift. The dotted line represents a B&C model normalized to the long-wavelength SDSS data only. |
 |
Fig. E.3 Individual SEDs for the NON B3 galaxies with spectroscopic redshift. Empty circles are the GALEX data. The dotted line represents a B&C model normalized to the long-wavelength SDSS data only. |
Appendix F: The 3C/6C LSO sample
Extended radio sources.
Appendix G: UV-O-SEDs of 3CR & 6C LSOs
 |
Fig. G.1 Individual 3CR and 6C LSO from Table F.1. The empty circles are GALEX data. The dotted line represents a B&C model normalized to the long-wavelength SDSS data only. |
 |
Fig. G.1 continued. |
 |
Fig. G.1 continued. |
 |
Fig. G.1 continued. |
For the 3CR sources of Best et al. (1997) we used in the fits their HST data as well (5400 ≤ λobs. fr ≤ 8600).
The low-redshift radio galaxies 3C 236, 3C 285, and 3C 321 have been studied spectroscopically by Holt et al. (2007), with the aim of determining the properties of the YSPs. These authors also use in their fits in addition to the UV-O-SEDs stellar absorption lines, power law contributions, and various reddening recipes. The comparison of their results with ours shows that our age estimates differ within a factor ≈3 from theirs. The luminosities of their and our YSPs are also different by the amount expected from the differences in age. We attempted to fit our SDSS data using their ages, but the corresponding fits are worse than ours. We think that the differences in the results are not surprising because the data and parameters that we are using are different from those in Holt et al. (2007).
Acknowledgments
We thank an anonymous referee for pointing us to the use of the UV GALEX data and for several useful comments, which helped to improve the presentation of the paper.
This search is based on the use of the SDSS Archive, funding for the creation and distribution of which was provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS was managed by the Astrophysical Research Consortium for the Participating Institutions.
The authors also made use of the data from the NASA Galaxy Evolution Explorer database, from the Two Micron All Sky Survey and from the NASA/IPAC Extragalactic Database (NED). GALEX is operated for NASA by the California Institute of Technology under NASA contract NAS5-98034. The Two Micron All Sky Survey is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. The NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agueros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Allington-Smith, J. R., Spinrad, H., Djorgovski, S., & Liebert, J. 1988, MNRAS, 234, 109 [Google Scholar]
- Aretxaga, I., Terlevich, E., Terlevich, R., et al. 2001, MNRAS, 325, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Arshakian, T. G., & Longair, M. S. 2000, MNRAS, 311, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Baker, J. C., & Hunstead, R. W. 1995, ApJ, 452, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. E. 1982, in Extragalactic Radio Sources, ed. D. S. Heeschen, & C. M. Wade (Reidel), Proc. IAU Symp., 97, 21 [Google Scholar]
- Best, P. N., Longair, M. S., & Rottgering, H. J. 1997, MNRAS, 292, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N., Longair, M. S., & Roettgering, H. J. A. 1998, MNRAS, 295, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N., Eales, S. A., & Longair, M. S. 1999, MNRAS, 303, 616 [NASA ADS] [CrossRef] [Google Scholar]
- Bicknell, G. V., Sutherland, R. S., van Breugel, W. J. M., et al. 2000, ApJ, 540, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 (B&C) [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, K. C., Miley, G. K., & van Breugel, W. J. M. 1987, Nature, 329, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Cruz, M. J., Jarvis, M. J., Blundell, K. M., et al. 2006, MNRAS, 373, 1531 [NASA ADS] [CrossRef] [Google Scholar]
- Dallacasa, D., Fanti, C., Giacintucci, S., et al. 2002b, A&A, 389, 126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dallacasa, D., Tinti, S., Fanti, C., et al. 2002a, A&A, 389, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Vries, N., Snellen, I. A. G., Schilizzi, R. T., et al. 2007, A&A, 464, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Vries, W. H., O’Dea, C. P., Baum, S. A., et al. 1998, ApJ, 503, 156 [NASA ADS] [CrossRef] [Google Scholar]
- de Vries, W. H., O’Dea, C. P., Barthel, P. D., et al. 2000, AJ, 120, 2300 [NASA ADS] [CrossRef] [Google Scholar]
- Eales, S. A., & Rawlings, S. 1996, ApJ, 460, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Falco, E. E., Kochanek, C. S., & Munoz, J. A. 1998, ApJ, 494, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Fanti, C., Fanti, R., Dallacasa, D., et al. 1995, A&A, 302, 317 [NASA ADS] [Google Scholar]
- Fanti, C., Pozzi, F., Dallacasa, D., et al. 2001, A&A, 369, 380 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fanti, C., Branchesi, M., Cotton, W. D., et al. 2004, A&A, 427, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gandhi, P., Fabian, A. C., & Crawford, C. S. 2006, MNRAS, 369, 1566 [NASA ADS] [CrossRef] [Google Scholar]
- Gandhi, P., Crawford, C. S., Fabian, A. C., & Johnstone, R. M. 2004, MNRAS, 348, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Holt, J. 2009, Astron. Nachr., 330, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Holt, J., Tadhunter, C. N., Gonzales Delgado, R. M., et al. 2007, MNRAS, 381, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Holt, J., Tadhunter, C. N., & Morganti, R. 2009, MNRAS, 400, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Inskip, K. I., Best, P. N., & Longair, M. S. 2006a, MNRAS, 367, 693I [NASA ADS] [CrossRef] [Google Scholar]
- Inskip, K. I., Lee, D., & Cotter, G. 2006b, MNRAS, 370, 1585I [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, C. R. 2009, Astron. Nachr., 330, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Labiano, A. 2008, A&A, 488, L59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Labiano, A., O’Dea, C. P., Gelderman, R., et al. 2005, A&A, 436, 493 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Labiano, A., Barthel, P. D., O’Dea, C. P., et al. 2007, A&A, 463, L97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Labiano, A., O’Dea, C. P., Barthel, P. D., et al. 2008, A&A, 477, L491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lahulla, J. F., Merighi, R., Vettolani, G., & Vigotti, M. 1991, A&AS, 88, 525 [NASA ADS] [Google Scholar]
- Law-Green, J. D. B., Leahy, J. P., Alexander, J. R., et al. 1995, MNRAS, 274, 939 [NASA ADS] [Google Scholar]
- Lupton, R. H., Gunn, J. E., & Szalay, A. S. 1999, AJ, 118, 1406 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J. 1989, ApJ, 340, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
- Maxfield, L., Thompson, D., Djorgovski, S., Vigotti, M., & Grueff, G. 1995, PASP, 107, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Mellema, G., Kurk, j.d., & Rottgering, H. J. A. 2002, A&A, 395, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCarthy, P. J. 1991, AJ, 102, 518 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, P. J., van Breugel, W. J. M., Spinrad, H., & Djorgovski, S. 1987, ApJ, 321, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Murgia, M. 2003, PASA, 20, 19 [NASA ADS] [CrossRef] [Google Scholar]
- O’Dea, C. P., & Baum, S. A. 1997, AJ, 113, 1480 [Google Scholar]
- Orienti, M., Dallacasa, D., Fanti, C., et al. 2004, A&A, 426, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pahre, M. A., & Djorgovski, S. G. 1995, AJ, 449, L1 [Google Scholar]
- Raimann, D., Storchi-Bergmann, T., Quintana, H., et al. 2005, MNRAS, 364, 1239 [NASA ADS] [CrossRef] [Google Scholar]
- Readhead, A. C. S., Taylor, G. B., Pearson, T. J., et al. 1996, ApJ, 460, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J. 1989, MNRAS, 239, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Nichol, R. C., Gray, A. G., et al. 2004, ApJS, 155, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Roche, N., Eales, S., & Rawlings, S. 1998, MNRAS, 297, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Rossetti, A., Fanti, C., Fanti, R., et al. 2006, A&A, 449, 49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rossetti, A., Dallacasa, D., Fanti, C., Fanti, R., & Mack, K.-H. 2008, A&A, 487, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A. G., Lehnert, M. D., Bremer, M. N., et al. 2002, MNRAS, 337, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Stanghellini, C., O’Dea, C. P., Baum, S. A., et al. 1993, ApJS, 88, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Tadhunter, C., Dickson, R., Morganti, R., et al. 2002, MNRAS, 330, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, D., Djorgovski, S., Vigotti, M., & Grueff, G. 1994, AJ, 108, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Vanden Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Vigotti, M., Grueff, G., Perley, R., Clark, B. G., & Bridle, A. H. 1989, AJ, 98, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Vigotti, M., Vettolani, G., Merighi, R., Lahulla, J. F., & Pedani, M. 1990, A&AS, 123, 219 [Google Scholar]
- Wegner, G., Salzer, J., Jangren, A., Gronwall, C., & Melbourne, J. 2003, AJ, 125, 237 [Google Scholar]
- West, M. J. 1994, MNRAS, 268, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, W., Lawrence, C. R., Readhead, A. C. S., & Pearson, T. J. 1994, AJ, 108, 395 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Comparison between the SDSS r magnitudes and those taken from Paper I. |
| In the text | |
 |
Fig. 2 Distribution of the r magnitudes for the optically identified galaxies (left) and quasars (right). Hatched bins indicate the new identifications (Q? included). |
| In the text | |
 |
Fig. 3 Comparison between photometric |
| In the text | |
 |
Fig. 4 Hubble diagrams in the five SDSS bands for quasars (+), galaxies with zsp (∗ ) and with zph2 (× ) only. The squares are the faint galaxies undetected in the SDSS. The horizontal lines represent the declared magnitude limits of SDSS. In the central panel the two parallel lines are from Labiano et al. (2007) and the curve is the best-fit line for GPSs from Snellen et al. (2002). |
| In the text | |
 |
Fig. 5 Distribution of redshifts for galaxies found in (below) and missed by (top) the SDSS. The hatched bins represent the (corrected) photometric redshifts. |
| In the text | |
 |
Fig. 6 Composite plot of the UV-O-SED of quasars in the source-framearbitrarily normalized to each other at λ ≈ 3000 Å. The curved line is the best fit of the data in the range 1500–5000 Å. The straight line is from Vanden Berk et al. (2001) (see text). |
| In the text | |
 |
Fig. 7 Composite plot of the SEDs in the source-frame for the radio galaxies with spectroscopic redshift. The thick line is the B&C model of an elliptical galaxy of 13 Gyr and 1012 M⊙ (see footnote on page ). The individual UV-O-SEDs are normalized to this model. The broken lines indicate the sources 0744+464, 1159+395, 1314+453A, and 3C 237, which do not have data-points at λ > 4000 Å and whose UV-O-SED normalization is therefore quite arbitrary. |
| In the text | |
 |
Fig. 8 Fit of the B&C old stellar population galaxy model to the sources 1049+384 (left) and 1136+420 (right), for different redshifts. Two of the lines are marked with zsp and zph; the two intermediate lines represent the two zph2. In 1049+384 the dash-dotted line (marked with zemp, for empirical) gives the best χ2 of all and corresponds to z = 0.05. In 1136+420 a blind fit would provide z ~ 0.45 i.e. identical to zph and it is not plotted. |
| In the text | |
 |
Fig. 9 Distribution of Log(radio power) vs. Log(1 + z) for the galaxies of the composite sample. Empty circles represent 3CR&PW sources; crosses and plus signs are the two B3-VLA sub-samples. The lines correspond to flux densities S1.4 = 2.1 Jy, 0.66 Jy and 0.33 Jy, representing the flux density limits of the three samples extrapolated at 1.4 GHz. |
| In the text | |
 |
Fig. 10 Correlations between Log(L0.30), Log(L0.45) and Log( |
| In the text | |
 |
Fig. 11 Top panels: enlargement of left hand panels of Fig. 10 for the sources in Box 1. Bottom panels: enlargement of right hand panels of Fig. 10 for the sources in Box 2 (to the right of the vertical line), and for the sources with z ≤ 0.3 (to the left of the vertical line). The lines through the plotted data are the best-fits. |
| In the text | |
 |
Fig. 12 Same as in Fig. 10, but vs. Log(LS). The horizontal lines approximately separate objects with z < 0.6 and z > 0.6. |
| In the text | |
 |
Fig. 13 Example of different models yielding similar fits: left hand and center panels fits with two YSP models of ages 0.1 and 0.06 Gyr respectively; right hand panel fit with the power law model. The dotted lines represent an OSP model (at the longer wavelengths) and either a power law (right-hand panels) or two different YSP models (left hand and middle panels). The line through the data points is the sum of the two sub-components. |
| In the text | |
 |
Fig. 14 Examples of model-fitting. The thin lines represent an OSP model (at the longer wavelengths) and either a power law (right-hand panels) or two different YSP models (left hand and middle panels) which give similar fits to the data. The line through the data points is the sum of the two sub-components. GALEX data, not used in the fits, are overplotted as empty circles. Top row: the GALEX point does not discriminate among the three models based on SDSS data. Center row: the GALEX point is in better agreement with the second, SDSS based, YSP model, which can be slightly improved by minor changes. Bottom row: the left hand and right hand panels show the best fits with the SDSS data only. The center panel shows a slight modification of the 0.3 Gyr YSP model which, although unsatisfactory at the shortest wavelengths, represents the best model when the GALEX data are added. |
| In the text | |
 |
Fig. 15 Plots of Log(L0.30), Log(L0.45) and Log( |
| In the text | |
 |
Fig. 16 Examples of fits with three stellar population models: one OSP, one YSP of intermediate age (0.01–1 Gyr) and a very young population with the age of the radio source (< 10-2 Gyr, for an assumed expansion speed of 0.1c). |
| In the text | |
 |
Fig. 17 Distribution of the CSOs/MSOs (black points) and LSOs (empty circles) in the radio power – linear size plane. The two lines represent an evolutionary model where P1.4 ∝ LS-0.5 (see text). |
| In the text | |
 |
Fig. E.1 Individual SEDs for galaxies with spectroscopic redshift. Empty circles are GALEX data. The dotted line represents a B&C model normalized to the long-wavelength SDSS data only (see notes to 1014+392). |
| In the text | |
 |
Fig. E.1 continued. |
| In the text | |
 |
Fig. E.2 Individual SEDs for galaxies with photometric redshift. The dotted line represents a B&C model normalized to the long-wavelength SDSS data only. |
| In the text | |
 |
Fig. E.3 Individual SEDs for the NON B3 galaxies with spectroscopic redshift. Empty circles are the GALEX data. The dotted line represents a B&C model normalized to the long-wavelength SDSS data only. |
| In the text | |
 |
Fig. G.1 Individual 3CR and 6C LSO from Table F.1. The empty circles are GALEX data. The dotted line represents a B&C model normalized to the long-wavelength SDSS data only. |
| In the text | |
 |
Fig. G.1 continued. |
| In the text | |
 |
Fig. G.1 continued. |
| In the text | |
 |
Fig. G.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


