| Issue |
A&A
Volume 527, March 2011
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 18 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201015676 | |
| Published online | 03 February 2011 | |
VLTI/AMBER spectro-interferometry of the Herbig Be star MWC 297 with spectral resolution 12 000⋆
1
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
e-mail: weigelt@mpifr.de
2
Pulkovo Observatory of RAS, Pulkovskoe shosse 65, St. Petersburg
196140,
Russia
3
V.V. Sobolev Astronomical Institute, St. Petersburg University, St. Petersburg,
Russia
4
Department of Astronomy, University of Michigan,
500 Church Street, Ann Arbor, MI
48109,
USA
5
University of North Carolina at Greensboro, PO Box 26170,
Greensboro, NC
27402,
USA
6
INAF-Osservatorio Astrofisico di Arcetri, Istituto Nazionale di
Astrofisica, Largo E. Fermi 5, 50125
Firenze,
Italy
7
Deutsches Zentrum für Luft- und Raumfahrt e.V., Königswinterer
Str. 522-524, 53227
Bonn,
Germany
8
Laboratoire H. Fizeau, University of Nice Sophia Antipolis, CNRS, OCA, Parc Valrose,
06108
Nice,
France
9
Laboratoire d’Astrophysique de Grenoble, UMR 5571 Université
Joseph Fourier/CNRS, BP
53, 38041
Grenoble Cedex 9,
France
Received: 2 September 2010
Accepted: 27 November 2010
Context. Circumstellar disks and outflows play a fundamental role in star formation. Infrared spectro-interferometry allows the inner accretion-ejection region to be resolved.
Aims. We study the disk and Brγ-emitting region of MWC 297 with high spatial and spectral resolution and compare our observations with disk-wind models.
Methods. We measured interferometric visibilities, wavelength-differential phases, and closure phases of MWC 297 with a spectral resolution of 12 000. To interpret our MWC 297 observations, we employed disk-wind models.
Results. The measured continuum visibilities confirm previous results that the continuum-emitting region of MWC 297 is remarkably compact. We derive a continuum ring-fit radius of ~2.2 mas (~0.56 AU at a distance of 250 pc), which is ~5.4 times smaller than the 3 AU dust sublimation radius expected for silicate grains (in the absence of radiation-shielding material). The strongly wavelength-dependent and asymmetric Brγ-emitting region is more extended (~2.7 times) than the continuum-emitting region. At the center of the Brγ line, we derive a Gaussian fit radius of ~6.3 mas HWHM (~1.6 AU). To interpret the observations, we employ a magneto-centrifugally driven disk-wind model consisting of an accretion disk, which emits the observed continuum radiation, and a disk wind, which emits the Brγ line. The calculated wavelength-dependent model intensity distributions and Brγ line profiles are compared with the observations (i.e., K-band spectrum, visibilities, differential phases, and closure phases). The closest fitting model predicts a continuum-emitting disk with an inner radius of ~0.3 AU and a disk wind ejection region with an inner radius of ~ 0.5 AU (~17.5 stellar radii). We obtain a disk-wind half-opening angle (the angle between the rotation axis and the innermost streamline of the disk wind) of ~80°, which is larger than in T Tau models, and a disk inclination angle of ~20° (i.e., almost pole-on).
Conclusions. Our observations with a spectral resolution of 12 000 allow us to study the AU-scale environment of MWC 297 in ~10 different spectral channels across the Brγ emission line. We show that the K-band flux, visibilities, and remarkably strong phases can be explained by the employed magneto-centrifugally driven disk wind model.
Key words: stars: individual: MWC 297 / stars: pre-main sequence / stars: winds, outflows / circumstellar matter / techniques: interferometric / techniques: spectroscopic
© ESO, 2011
1. Introduction
Circumstellar disks and outflows play a fundamental role in star formation. Testing theoretical accretion-ejection models is very challenging since important processes occur on AU and sub-AU scales, which cannot be resolved by conventional imaging. However, infrared spectro-interferometric observations with milli-arcsecond spatial resolution and high spectral resolution allow unprecedented studies of the inner accretion region, which hosts fascinating astrophysical objects such as inner gaseous accretion disks, dust disks, disk winds, jets, etc. Interferometry in the near- and mid-infrared is able to probe the gas and dust distribution on these scales and constrain their physical properties. These observations allow us to study the nature of the accretion process and the launching of jets and winds.
Log of the VLTI/AMBER/FINITO observations of MWC 297.
With a spectral type of B1.5V, a mass of ~0 M⊙, and a distance of 250 ± 50 pc (Drew et al. 1997), MWC 297 is one of the nearest massive young stars. The geometry of the disk of MWC 297 has been investigated by various techniques at near-infrared (Millan-Gabet et al. 2001; Eisner et al. 2004; Monnier et al. 2006; Malbet et al. 2007; Acke et al. 2008; Kraus et al. 2008a), mid-infrared (Acke et al. 2008), and radio wavelengths (Mannings & Sargent 1997; Drew et al. 1997). Interestingly, several interferometric observations of MWC 297 (Eisner et al. 2004; Monnier et al. 2005; Malbet et al. 2007; Acke et al. 2008; Kraus et al. 2008a) have shown that the compact characteristic size of the near-infrared continuum-emitting region is several times smaller than the theoretically expected ~3 AU radius of the dust sublimation rim (the expected radius if there is no shielding of the stellar radiation; Monnier et al. 2005).
The estimates of the inclination angle of MWC 297’s circumstellar disk have been highly controversial. Drew et al. (1997) argued for an almost edge-on disk orientation. Moderate inclination angles of the circumstellar disk of MWC 297 were found with infrared interferometric observations. For instance, Malbet et al. (2007) obtained VLTI/AMBER observations with a medium spectral resolution of 1500 and measured the wavelength dependence of the visibility across the Brγ line. Malbet et al. (2007) interpreted their spectro-interferometric measurements of MWC 297 with an anisotropic stellar-wind model (Stee & de Araujo 1994; Stee et al. 1995) and found an inclination of ~20°. Acke et al. (2008) obtained both near-infrared AMBER H- and K-band observations and mid-infrared MIDI observations and concluded that the inclination is smaller than 40°.
In this paper, we present the first spectro-interferometric measurements of the inner circumstellar environment of MWC 297 with AMBER’s high spectral resolution mode (R = 12 000). This high spectral resolution allows us to spectrally resolve the Brγ emission line and measure the interferometric observables (spectrum, visibilities, wavelength-differential phases, and closure phases) in ~10 different spectral channels across the line. In Sect. 2, we present the AMBER observations. In Sect. 3, we derive characteristic continuum and Brγ line sizes of the circumstellar environment using simple geometric models. In Sect. 4, we present radiative transfer modeling of the disk and disk wind and compare the K-band flux, visibilities, and phases with the model predictions in the continuum and several spectral channels across the Brγ emission line. In the Appendix, we discuss the disk-wind modeling, spectroscopy of MWC 297, wavelength calibration, and the use of AMBER’s Beam Commutation Device.
2. Interferometric VLTI/AMBER/FINITO observations with spectral resolution of 12 000
We observed MWC 297 on 6 April 2008 with ESO’s Very Large Telescope Interferometer (VLTI) and its AMBER beam combiner instrument in the course of the AMBER-GTO program 081.D-0230(A). AMBER (Petrov et al. 2007) allows interferometric three-telescope observations with low, medium, or high spectral resolution. The observations are described in Table 1. For these observations, the E0-G0-H0 array of the 1.8 m auxiliary telescopes (ATs) and AMBER’s high resolution mode (HR mode; R = 12 000) were employed. To obtain interferograms with a high signal-to-noise ratio (SNR), we used the fringe tracker FINITO and a detector integration time of 8.0 s per interferogram. With excellent atmospheric conditions (seeing 0.4–0.6″), the FINITO instrument in the co-phasing mode allowed us to stabilize the atmospheric and mechanically induced fringe motion. FINITO records temporally modulated H-band interferograms with a high frequency, from which the atmospheric phase shift is determined and then compensated for using the VLTI delay lines.
For data reduction, we used AMBER’s amdlib data reduction software (release 2.2), which employs the P2VM algorithm (Tatulli et al. 2007) to derive wavelength-dependent visibilities, wavelength-differential phases, and closure phases. In addition, the spectrum can be extracted as an additional observable.
Along with the science observation of MWC 297, we observed the interferometric calibrator star HD 175 583, which allowed us to calibrate the atmospheric transfer function. We recorded 100 target interferograms (plus 40 calibrator interferograms) without AMBER’s beam commutation device (BCD OUT data) and 100 target interferograms plus 40 calibrator interferograms with the BCD (BCD IN data). The BCD allows the study of systematic instrumental effects (see Appendix C). A fraction of the interferograms were of lower quality because of the lower FINITO performance. Therefore, we selected the 50% of the BCD OUT data and 50% of the BCD IN data with the highest fringe SNR among both the target and the calibrator interferograms to improve the visibility calibration (Tatulli et al. 2007). From this data, we derived the spectrum, visibilities, wavelength-differential phases, and closure phases, observed along the position angle (PA) of 68.0° on the sky (see Fig. 1). The differential phases and closure phases derived from both independent data sets (BCD OUT and BCD IN) are shown in Fig. C.1 of Appendix C. Subtraction of the closure phases obtained with and without BCD cancels potential instrumental phase drifts. Figure C.2 presents the derived closure phase and a fit of a constant to the continuum closure phases. The obtained averaged continuum (2.147–2.194 μm) closure phase is −1.28 ± 0.42°.
 |
Fig. 1 AMBER observations of MWC 297 with spectral resolution of 12 000: (from top to bottom) wavelength dependence of flux, visibilities, wavelength-differential phases (for better visibility, the differential phases of the shortest and longest baselines are shifted by +40 and − 40°, respectively), and closure phase observed at projected baselines of 14.0, 28.0, and 42.1 m along the position angle (PA) of 68.0° on the sky. The wavelength scale at the bottom is the directly observed one, i.e. without heliocentric or LSR correction (see text). However, the radial velocity scale at the top, gives spectrum, visibilities, and phases as a function of the Brγ Doppler shift in the Local Standard of Rest (LSR) frame. The dashed vertical line indicates the centroid Brγ vacuum wavelength (2.1661 μm) in the LSR frame. |
With the high spectral resolution of R = 12 000, it is possible to spectrally resolve the Brγ line and measure the visibilities and phases in ~10 different spectral channels across the Doppler-broadened Brγ line. The visibilities show a strong wavelength dependence of the size of the line-emitting region. The wavelength-differential phases and the closure phase indicate remarkably strong photocenter shifts and asymmetries, respectively, of the circumstellar environment in many spectral channels across the Brγ line. We show in Sect. 4 that this strong wavelength dependence and the large values of the phases can be explained by disk-wind models.
The wavelength calibration of the AMBER data in Fig. 1 was accomplished using the many telluric lines present in the region 2.15–2.19 μm, as described in Appendix B. We estimate an uncertainty in the wavelength calibration of ~3 km s-1. The spectrum in Fig. 1 (top) was normalized to the nearby continuum. The wavelength scale at the bottom is shown without heliocentric or Local Standard of Rest (LSR) correction. However, the radial velocity scale at the top of Fig. 1 is calibrated to give spectrum, visibilities, and phases as a function of the Brγ Doppler shift in the Local Standard of Rest (LSR) frame (16.5 km s-1 has to be subtracted to convert the LSR values to the heliocentric frame).
The obtained Brγ line profile has an equivalent width of −17.2 Å. Using AMBER’s HR mode, we were able to resolve the Brγ line and determined a FWHM of ~60 km s-1. By performing a Gaussian fitting of the line profile, a centroid LSR velocity of 13.8 ± 3 km s-1 was obtained. No P-Cygni absorption or double-peaked emission is seen. The FWHM of the Brγ line is compatible with the value of 53 km s-1 found by Drew et al. (1997) for Brα. On the other hand, the centroid velocity of Brγ is more similar to the one measured for Hα and Hβ (16 and 19 km s-1, respectively, Drew et al. 1997) than to that of Brα (3 km s-1, Drew et al. 1997).
Geometric model fit diameters of MWC 297 in the continuum and the center of the Brγ emission line.
 |
Fig. 2 Left: fit of a two-component Gaussian plus a point source with a 10% flux contribution to the wavelength-averaged (2.147–2.194 μm) K-band continuum visibilities near Brγ. Right: fit of a compact ring plus Gaussian halo plus a point source with a 10% flux contribution to the K-band continuum visibilities. |
 |
Fig. 3 Left: Gaussian FWHM fit diameters of the Brγ line-emitting region for several individual spectral channels (in the center and the line wings) across the Brγ emission line (red bullets). The diameters are derived from continuum-compensated visibilities. Therefore, they are the diameters of the Brγ line-emitting region and not of the emission region of both line plus continuum. The AMBER spectrum of MWC 297 is shown for comparison (green curve). Right: Gaussian fit to the continuum-compensated AMBER visibilities at the peak intensity of the Brγ emission line. |
3. Comparison of the observations with geometric models
3.1. Characteristic size of the continuum-emitting region
To measure the characteristic size of the circumstellar environment in the K-band continuum, we fitted geometric models to the visibilities obtained along the PA of 68.0° on the sky (see Table 2). As pointed out by Acke et al. (2008), who observed MWC 297 with the same VLTI E0-G0-H0 array, one-component uniform-disk, ring, and Gaussian disk models are unable to fit the shape of the continuum visibility. Therefore, we fitted a two-component Gaussian plus a point source with a 10% flux contribution (derived from the SED, as in Acke et al. 2008) to the wavelength-averaged continuum visibilities. Our observations are averages over the continuum wavelengths between 2.147 and 2.194 μm (except the line region) because of the narrower wavelength range of AMBER’s HR mode.
Figure 2 (left) shows that the fitted two-component Gaussian consists of a dominant compact Gaussian with a FWHM diameter of 4.63 ± 0.21 mas (corresponding to 1.16 ± 0.05 AU at a distance of 250 pc) in addition to an extended Gaussian halo with a FWHM diameter of ~22 mas (see Table 2). Owing to the lack of data at low spatial frequencies, the size and shape of the extended halo component is not well constrained. The flux ratio of the dominant compact component to the extended halo component is 4.6. Our FWHM diameter of ~4.6 mas obtained for the dominant compact Gaussian component is in good agreement with the diameter of ~4.3 mas reported by Acke et al. (2008).
To verify MWC 297’s location in the size-luminosity relation (where ring fits are used; Monnier et al. 2005; Kraus et al. 2008a), we determined its ring-fit radius for a ring thickness of 20% of the radius. Figure 2 (right) shows the fit obtained of a compact ring, an extended Gaussian halo, and a 10% point source to the wavelength-averaged (2.147–2.194 μm) continuum visibilities. The fitted FWHM diameter (inner ring diameter) of the dominant compact model ring is 4.47 ± 0.20 mas (corresponding to 1.12 ± 0.05 AU for a distance of 250 pc; see Table 2).
The measured continuum ring radius of 0.56 AU is ~5.4 times smaller than the ~3 AU dust sublimation radius of MWC 297 predicted by the size-luminosity relation, if there is no shielding of the stellar radiation (Monnier et al. 2005; Kraus et al. 2008a). This surprisingly compact size was already discussed by several other authors (Eisner et al. 2004; Monnier et al. 2005, 2006; Malbet et al. 2007; Kraus et al. 2008a; Acke et al. 2008). The correct interpretation of the compact continuum-emitted region of MWC 297 and several other Herbig Be stars remains disputed. Possible explanations include the absorption of the stellar light by an inner gas disk allowing dust to survive closer to the star (e.g., Millan-Gabet et al. 2001; Monnier et al. 2005; Malbet et al. 2007), emission from an optically thick inner gas disk (e.g., Monnier et al. 2005; Kraus et al. 2008b), and emission from special types of dust grains that can survive at higher temperatures (e.g., Benisty et al. 2010).
3.2. The characteristic size of the Brγ-emitting region
The high spectral resolution of the AMBER data allows us to measure the characteristic size of the Brγ line-emitting region for several individual spectral channels across the Brγ emission line (see Fig. 3 left). These diameters were determined by fitting Gaussians to the continuum-compensated Brγ visibilities (which are the visibilities free from contributions from the underlying continuum within the line region). The right panel of Fig. 3 shows such a Gaussian fit for the central wavelength of the Brγ emission line.
The continuum-compensated visibilities required for the size determination of the line-emitting region discussed above were calculated in the following way. Within the wavelength region of Brγ, the measured visibility has two constituents, a pure line-emitting component and a continuum-emitting one, the second of which includes emission of both the circumstellar environment and the unresolved star. The emission line visibility VBrγ can be written as (Weigelt et al. 2007)  (1)where Vtot (Ftot) denotes the measured total visibility (flux) in the Brγ line, Vc (Fc) is the measured visibility (flux) in the continuum, and Φ describes the measured wavelength-differential phase within the Brγ line. From the AMBER spectrum (see Fig. 1), we find Ftot = 4.5 and FBrγ = 3.5 × Fc at the emission line center.
(1)where Vtot (Ftot) denotes the measured total visibility (flux) in the Brγ line, Vc (Fc) is the measured visibility (flux) in the continuum, and Φ describes the measured wavelength-differential phase within the Brγ line. From the AMBER spectrum (see Fig. 1), we find Ftot = 4.5 and FBrγ = 3.5 × Fc at the emission line center.
We derived a large continuum-compensated radius (HWHM) of 6.3 ± 0.4 mas (1.6 ± 0.1 AU) for the line-emitting region at the peak wavelength of the emission line, which is ~3 times larger than the 0.56 AU HWHM radius of the compact continuum-emitting Gaussian component. The smaller line-continuum size ratio obtained by Kraus et al. (2008a) can be explained by the lower spectral resolution of R = 1500, which leads to an averaging over different diameters corresponding to different wavelengths. Figure 3 also shows that the size of the line-emitting region is smaller in the wings of the Brγ emission line than at the line center. This wavelength dependence is one of several observational results that have to be explained by models, such as the disk-wind model presented in the next section.
4. Comparison of the observations with a model of a magneto-centrifugally driven disk wind
 |
Fig. 4 Sketch of the MWC 297 disk-wind model adopted in this paper. |
We now present a disk-wind model and compare the observed spectrum, visibilities, and phases of MWC 297 with the model predictions. In this disk-wind model, mass ejection is driven by magneto-centrifugal forces. The theory of these winds was originally proposed by Blandford & Payne (1982) and has been elaborated by many authors, mainly for T Tauri stars (see Königl & Pudritz 2000; Pudritz & Banerjee 2005; Ferreira 2007, and references therein). An important property of the launching mechanism in magneto-centrifugally driven disk winds is the topology of the magnetic field in the disk: magnetic field lines in the wind-launching region are inclined with respect to the disk plane by less than 60° (Blandford & Payne 1982). The radiation pressure of hot stars probably changes the trajectories of the gas streams, leading to a flatter disk wind (de Kool & Begelman 1995; Drew et al. 1998; Everett et al. 2001). Figure 4 shows a sketch of the disk-wind model that we consider. It assumes that both an accretion disk and a disk wind contribute to the observed emission.
4.1. Geometry and kinematics of the disk wind
To model the extended disk wind, we follow an approach used by Shlosman & Vitello (1993) in their studies of disk winds in cataclysmic variables. This approach provides a simple parametrization of a disk wind, which has geometrical and kinematical properties similar to those used by Kurosawa et al. (2006) for T Tauri stars (see Fig. A.1 in the Appendix). Here, we use a similar description of the kinematical parameters of the wind where according to the conservation of angular momentum, the tangential velocity u decreases along a streamline from the Keplerian velocity at the base of streamline. The radial velocity v increases along the streamline from the initial value v0 to v∞ (see Eqs. (A.1) and (A.2) and Fig. A.2 in Appendix A), where v0 and v∞ are the model parameters.
The local mass-loss rate per unit area of the disk, ṁw, is a function of the cylindric radius ω. To describe ṁw, we use a simple power-law 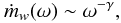 (2)where γ is a free parameter. The other model parameter is the total mass-loss rate
(2)where γ is a free parameter. The other model parameter is the total mass-loss rate 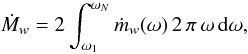 (3)where ω1 and ωN are the inner and outer boundaries of the disk-wind ejection region, and the factor two accounts for the mass loss from both sides of the disk surface.
(3)where ω1 and ωN are the inner and outer boundaries of the disk-wind ejection region, and the factor two accounts for the mass loss from both sides of the disk surface.
4.2. The parameters of the accretion disk
In classical accretion-disk models, the surface density increases toward the star as 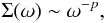 (4)where p = 1–1.5 (see, e.g., Calvet et al. 2000). At a mass accretion rate of Ṁacc ≥ 10-7 M⊙ yr-1, this disk is optically thick (due to the gas opacity) between the dust evaporation radius and either the stellar magnetosphere (Muzerolle et al. 2004) or the stellar surface. For MWC 297, the value of Ṁacc is fairly uncertain (see Malbet et al. 2007). If the surface density in the accretion disk of MWC 297 changes as ω-1, then this disk will be optically thick up to the stellar surface. However, if the accretion disk extended to the innermost vicinity of the star, the disk luminosity at near-infrared wavelengths would exceed the observed one. This is the main reason why an inner disk gap is required.
(4)where p = 1–1.5 (see, e.g., Calvet et al. 2000). At a mass accretion rate of Ṁacc ≥ 10-7 M⊙ yr-1, this disk is optically thick (due to the gas opacity) between the dust evaporation radius and either the stellar magnetosphere (Muzerolle et al. 2004) or the stellar surface. For MWC 297, the value of Ṁacc is fairly uncertain (see Malbet et al. 2007). If the surface density in the accretion disk of MWC 297 changes as ω-1, then this disk will be optically thick up to the stellar surface. However, if the accretion disk extended to the innermost vicinity of the star, the disk luminosity at near-infrared wavelengths would exceed the observed one. This is the main reason why an inner disk gap is required.
As in Acke et al. (2008), we used a blackbody approximation with a power-law distribution of the disk temperature Td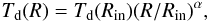 (5)where Rin is the inner radius of the disk, and α is a parameter. The parameter α is equal to − 3/4 in the two important special cases when a flat disk is just heated by the stellar radiation (passive disk; Adams & Shu 1986) or radiates due to the viscous dissipation (Lynden-Bell & Pringle 1974). However, this disk (as well as other simple power-law disk models) fails to reproduce the shape of the observed continuum visibilities (Acke et al. 2008). More sophisticated models can be obtained with two-component temperature-gradient models with slightly different temperature gradients (see below).
(5)where Rin is the inner radius of the disk, and α is a parameter. The parameter α is equal to − 3/4 in the two important special cases when a flat disk is just heated by the stellar radiation (passive disk; Adams & Shu 1986) or radiates due to the viscous dissipation (Lynden-Bell & Pringle 1974). However, this disk (as well as other simple power-law disk models) fails to reproduce the shape of the observed continuum visibilities (Acke et al. 2008). More sophisticated models can be obtained with two-component temperature-gradient models with slightly different temperature gradients (see below).
4.3. Model calculations
For simplicity, it is assumed that the disk wind contains only hydrogen atoms. For the calculations of the ionization state and the number densities of the atomic levels, we adopted the numerical codes developed by Grinin & Mitskevich (1990) and Tambovtseva et al. (2001) for moving media. These codes are based on the Sobolev (1960) approximation in combination with the exact integration of the line intensities (see Appendix A). This method takes into account the radiative coupling in the local environment of each point caused by multiple scattering.
The stellar radiation of MWC 297 is described by a model atmosphere (Kurucz 1979) with an effective temperature Teff = 25 000 K, log g = 4, and the stellar radius R∗ = 6.1 R⊙ as in Drew et al. (1997). The calculations were performed for an isothermal wind. We adopted electron temperature Te values in the range 8000–10 000 K, which are typical of the disk winds of young stars (see, e.g., Kurosawa et al. 2006). In our models, we adopted the fixed parameters stellar mass M∗ = 10 M⊙ and a distance of 250 pc (Drew et al. 1997).
 |
Fig. 5 Intensity distributions of our best-fit disk-wind model 5 (i.e., intensity distribution of the continuum disk plus the disk wind; the central star is not shown; see Tables 3 and A.1) at the center of the Brγ line (v = 0 km s-1) and at 14 other velocities (the labels give the velocity in km s-1). For the calculation of the model images in this figure, a clockwise motion of the disk wind was assumed. Therefore, in the blue-shifted images (left panels), mainly the disk regions on the right hand side of the star are bright. The radius of the inner edge of the disk wind ejection region (i.e., radius of the inner hole) is ω1 = 17.5 R∗ (~0.3 AU). The inclination angle (angle between the polar axis and the viewing direction) of the model is i = 20° (i.e., almost pole-on). The colors represent the intensity in erg ster-1 s-1 Å-1 cm-2. In these images, AMBER’s spectral resolution of 12 000 was modeled, as described in Sect. A.3. |
Figure 5 presents examples of the intensity distributions (projected on the plane of the sky) of our best-fit continuum-disk and disk-wind model number 5 (see Tables A.1 and 3). The inclination angle of the model (i.e., angle between the polar axis and the viewing direction) is i = 20°, i.e., almost pole-on. Model images at 15 different wavelengths (Doppler shifts) across the Brγ line profile are shown. The images are highly asymmetric and wavelength-dependent. Their wavelength-dependent photocenter shift (with respect to the continuum image) and asymmetric shape change across the line, resulting in wavelength-dependent visibilities, differential phases, and closure phases. This asymmetry of the model images is the result of the Doppler shift of the radiation due to the gas motion in the emitting region. The main part of the Brγ line emission is formed near the base of the disk wind where the dominant motion is Keplerian rotation. For the calculation of the model images shown in Fig. 5, a clockwise motion of the disk wind was assumed. When comparing with the observations, we calculated the model images for both clockwise and anti-clockwise motion.
 |
Fig. 6 Normalized Brγ line profiles of the disk-wind model 5 from Table A.1 at the inclination angles i = 10° (dotted line), 20° (solid), 40° (dashed), and 60° (dashed-dotted; high spectral resolution, not degraded to the spectral resolution of AMBER). |
Examples of theoretical Brγ line profiles of model 5 for different inclination angles i between the polar disk axis and the viewing direction (10, 20, 40, and 60°) are shown in Fig. 6. They suggest that a small inclination of the circumstellar disk (20 ± 10°) is needed to explain the observed line profiles (Fig. 1).
In our model calculations, we calculated more than 100 different models to examine the parameter space described in Table 3. Five examples of these models are listed in Table A.1. Closest agreement is obtained for a two-component disk model (with two temperature-gradient regimes) consisting of two zones from Rin = 0.3 AU to RS = 0.9 AU and from RS = 0.9 AU to Rout = 3 AU separated at Rs = 0.9 AU with inner and outer radii Rin = 0.3 AU and Rout = 3 AU, respectively, and a power-law temperature distribution in each zone given by
If we choose, for example, a stronger temperature gradient, then the effective average disk size becomes smaller leading to model visibilities that are higher than those observed. The calculations show that a similar agreement between model and observations can also be obtained if the disk parameters vary within the ranges given by Rin = 0.4 ± 0.1 AU, Td(Rin) = 1700 ± 100 K, and α1 = 0.5 ± 0.05 up to R = 0.9 AU and α2 = 0.4 ± 0.05 for R ≥ 1 AU.
Range of parameter variations for our continuum-disk plus disk-wind model calculations.
The calculations of the intensity distributions of the Brγ-emitting region and corresponding interferometric model quantities (i.e., visibilities, wavelength-differential phases, and closure phases of the model images) show that they are very sensitive to the geometrical and kinematical parameters of the disk-wind model. Furthermore, they also depend on the disk inclination. We used the following approach to find models that can approximately reproduce the observations:
-
1)
to select the most appropriate the disk parameters, we calculatethe continuum intensity of the disk,Id, at wavelengths near Brγ and compare it with the stellar intensity I∗. A good solution has to reproduce the observed ratio Id/I∗, the observed K-band flux, and the observed visibilities;
-
2)
we determine the velocity and density distribution along each streamline corresponding to the wind geometry and kinematics parameters (see Sect. 4 and Appendix A);
-
3)
using the velocity and density distribution, and choosing the temperature law along each streamline (we use a constant electron temperature of 8000 K), we solve the equations of the statistical equilibrium for the hydrogen atoms and compute the population of the hydrogen atomic levels and the ionization degree along each streamline;
-
4)
we then calculate the Brγ line profile and compare it with the observed line profile. The solution is good if the theoretical line profile is in good agreement with the intensity and shape of the observed one;
-
5)
for each disk-continuum and disk-wind model (see Table 3), we compute the two-dimensional intensity distribution map for several inclination angles. We calculate all model intensity distributions for 15 different wavelengths across the Brγ line and the continuum. The spectral resolution of AMBER of R = 12 000 is modeled in the final model intensity distributions (see discussion on the importance of modeling AMBER’s spectral resolution by convolution in Sect. A.3 and Fig. A.3);
-
6)
finally, we compute visibilities, wavelength-differential phases, and closure phases of the obtained 2-D model intensity distributions, which are needed for the comparison with the observations.
4.4. Comparison of the models with the observations
Using this method, we found that model 5 (see Tables A.1 and 3) provides the closest agreement with the AMBER data (see Figs. 7, A.4, and A.5) and the K-band continuum flux, as discussed below. The inner radius of the disk-wind ejection region of model 5 is 0.5 AU (ω1 = 17.5 r∗) and the half-opening angle of the disk wind is 80°. The disk-wind half-opening angle is defined as the angle between the rotation axis and the innermost wind streamline (see Fig. A.1). Figure 7 shows flux, visibilities, wavelength-differential phases, and closure phases of model 5 for the same interferometric baselines as the AMBER observations presented in Fig. 1.
The spectral energy distribution of model 5 predicts that log λFλ[erg cm-2 s-1] = −7.13 in the K-band continuum near Brγ for a distance of 250 pc, which is in good agreement with the dereddened SED of MWC 297 from Acke et al. (2008) and Alonso-Albi et al. (2009). The model ratio Id/I∗ = 10 also agrees with the observations.
 |
Fig. 7 Comparison of the observations (left panel; see Fig. 1) with the corresponding model quantities of model 5 for two different PAs of the model image (middle and right panel; the model quantities are calculated for AMBER’s spectral resolution of 12 000, as discussed in Sect. A.3 and Fig. A.3). The middle and right panels show the dependence of the interferometric observables (spectrum, visibilities, wavelength-differential phases, and closure phases) of our best-fit disk-wind model 5 (disk-wind emitting region, continuum accretion disk, plus central star; Tables 3 and A.1) on the wavelength across the Brγ line for an inclination angle of i = 20°, clock-wise motion of the disk wind, and for two different PAs of the projected disk polar axis on the sky: 65° (middle) and 300° (right). Several other PAs that are also approximately in agreement with the observations are discussed in the text and Figs. A.4 and A.5. The detailed dependence of the interferometric observables on the PA is presented in Figs. A.4 and A.5. |
Since the position angle of MWC 297’s projected polar disk axis on the sky is unknown, the interferometric observables of the best-fit model 5 (spectrum, visibilities, wavelength-differential phases, and closure phases) were calculated for all PAs in steps of 10° (see Sect. A.3). Figure 7 compares the observations (left panel) with two of the models that are approximately in agreement with all observables (clockwise motion, i = 20°, middle: PA = 65°, right: PA = 300°). A similar agreement can also be obtained for some smaller inclination angles (see Fig. 8).
The detailed PA dependence is presented in Sect. A.3 and Figs. A.4 and A.5, which show the following results. For models with clockwise motion of the disk wind and i ~ 20° (i.e., almost pole-on), we obtained the closest agreement between model and observations for the PAs of approximately 65, 120, 245, and 300° (±5°; see Fig. A.4). For the models with anti-clockwise motion and i ~ 20°, we obtained the best agreement for the PAs of approximately 15, 70, 195, and 250° (see Fig. A.5).
 |
Fig. 8 Dependence of the interferometric quantities (visibilities, wavelength-differencial phases, and closure phases) of our best-fit disk-wind model 5 (see Table A.1) on the inclination angle i: 10, 15, and 20° from left to right for the PA 300° of the disk (see Fig. 7). In contrast to Fig. 7, the Brγ line profiles are given without convolution with the instrumental profile of the AMBER spectrograph for clearer visibility of the theoretical line profiles. |
5. Discussion
Our disk-wind model allows us to approximately reproduce all interferometric observables, including the remarkably strong differential and closure phases measured in our AMBER/VLTI observations of MWC 297 and to draw several conclusions:
-
1)
the AMBER continuum visibili-ties confirm previous results (Monnieret al. 2005; Malbetet al. 2007; Ackeet al. 2008; Krauset al. 2008a) that the continuum-emitting region is remarkably compact. We used geometricmodels consisting of a stellar point source, an extended halo, anda dominant compact Gaussian or ring to characterize its size. Forthe compact ring component, we obtained an inner ring-fit radiusof ~ 2.2 mas (~0.56 AU). This compactring radius is about 5.4 times smaller than the3 AU dust sublimation radius expected for silicategrains, if there is no radiation-shielding material between the starand the dust rim;
-
2)
the Brγemission line region is far more extended than the compact continuum-emitting region. The strong and wavelength-dependent closure phase reveals that the line-emitting region is very asymmetric along our measured interferometric position angle and the asymmetry dramatically changes across the Brγ line. At the center of the Brγ line, we derived a Gaussian fit HWHM radius of ~6.8 mas (1.6 AU), which is ~2.7 times larger than the compact 0.56 AU continuum Gaussian. The diameters of the Brγ-line-emitting region shown in Fig. 3 are derived from continuum-compensated visibilities. Therefore, they are the diameters of the Brγ-line-emitting region (not of the emission region of both line and continuum);
-
3)
to interpret our AMBER observations, we employed a magneto-centrifugally driven disk-wind model. This model consists of an accretion disk, which emits the observed continuum radiation, and a disk wind, which emits the Brγ line. The disk wind starts at a distance of ~0.5 AU from the star, which is further out than the typical value of 0.07 AU suggested for the inner radius of T Tauri star disk winds (Safier 1993; Ferreira 2007). The required large half-opening angle (~80°) of the wind in our model is much larger than the typical value (30–45°) considered for T Tauri stars (see, e.g., Safier 1993; Ferreira 2007). Both of these features of the model are likely to be caused by the strong influence of the radiation pressure of the star (Drew et al. 1998). The model images of the disk wind are highly asymmetric and their photocenter shift and shape strongly change across the line profile, resulting in a strong wavelength dependence of the visibilities, wavelength-differential phases, and closure phase. This asymmetry of the model images is a result of the Doppler shift of the radiation caused by the gas motion in the emitting region. The Doppler shift strongly depends on the position within the disk and the disk inclination angle. The properties of the inner region of the circumstellar environment of MWC 297 are remarkable in many respects. In the NIR, it radiates at temperatures of Td ≤ 2000 K at a distance of only ≥ 0.5 AU from the star. If the disk is optically thick between the star and the sublimation zone (i.e., the disk is able to shield the radiation from the cental star), the radius of this zone, Rsub, will be smaller than for the optically thin limit. Using the model of optically thick and geometrically thin disks (Adams & Shu 1986) heated by the central star, one obtains Rsub ~ 0.8 AU for MWC 297, which is comparable to the inner disk radius of the best-fit model 5. The mass-loss rate of the disk wind of the best-fit model 5 is 10-7 M⊙ yr-1 (Table A.1). The theory of magneto-centrifugal disk winds predicts a typical ratio Ṁw/Ṁacc on the order of 0.1 (Königl & Pudritz 2000). In this case, the mass accretion rate in the disk of MWC 297, Ṁacc, is ~10-6 M⊙ yr-1. According to Muzerolle et al. (2004), such a disk is optically thick between the star and the sublimation zone because of the gas opacity. What type of matter radiates in this compact inner disk inside the dust sublimation radius? We assume that it is a mixture of the warm, mostly neutral molecular gas plus refractory (e.g. graphite) grains. Similar properties of the inner compact material were found by Benisty et al. (2010) for the HAeBe star HD 163296. Interaction of the dust grains with the stellar radiation possibly plays an important role in the acceleration of dust and gas and the formation of the disk wind. As shown above, an inner gap in the disk of MWC 297 is needed to explain the observations. This gap region may be filled with material that is either fully transparent or semi-transparent in the infrared (e.g., Tannirkulam et al. 2008). The formation of this gap could be a result of binarity (Artymowicz & Lubow 1994). Another possibility for gap formation is the interaction of stellar radiation and wind with the inner disk. The strong radiation pressure and the stellar wind can blow away the disk atmosphere (Drew et al. 1998). As a result, the disk can partially or fully dissipate in the vicinity of the star;
-
4)
the critical rotation velocity
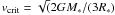 (Maeder & Meynet 2000) of MWC 297 would be 450 km s-1 for R∗ = 6 R⊙ and M∗ = 10 M⊙, as adopted in our paper. For our determined inclination angle i = 20 ± 10°, the maximum value of vrot sini would be 150 ± 80 km s-1 for vrot < vcrit. This is in clear contradiction with the value of vrot sini = 350 ± 50 km s-1 obtained by Drew et al. (1997) for MWC 297. What is the cause of this discrepancy? Is it our poor knowledge of either mass or radius, the inclination angle of 20 ± 10°, or the observed vrot sini = 350 ± 50 km s-1? The value of i is constrained not only by our modeling but also by the recent interferometric studies reported by Malbet et al. (2007) and Acke et al. (2008). Nevertheless, further studies of i will be required to constrain i more reliably. Furthermore, it cannot be excluded that the value of vrot sini = 350 ± 50 km s-1 is overestimated, since it is difficult to derive the exact rotational velocity from the width of the observed absorption lines because of the medium spectral resolution employed and the quite low SNR of the Drew et al. spectrum caused by the relatively faint magnitude of V = 12.2. Moreover, the absorption lines in MWC 297 might be: a) contaminated by emission from outflowing material, as is often the case in massive young stars; or b) formed at a certain distance from the photosphere, where the broadening of the spectral line would be dominated by the outflow kinematics. Nevertheless, this question is far from being solved, and we encourage independent determinations of vrot sini using, for instance, high-resolution spectroscopy and state-of-the-art atmospheric modeling. Future multi-wavelength observations of MWC 297 using high spectral and spatial resolutions, combined with non-LTE radiative transfer modeling of the stellar atmosphere, will be essential to improve our knowledge of the stellar parameters such as the rotational velocity;
(Maeder & Meynet 2000) of MWC 297 would be 450 km s-1 for R∗ = 6 R⊙ and M∗ = 10 M⊙, as adopted in our paper. For our determined inclination angle i = 20 ± 10°, the maximum value of vrot sini would be 150 ± 80 km s-1 for vrot < vcrit. This is in clear contradiction with the value of vrot sini = 350 ± 50 km s-1 obtained by Drew et al. (1997) for MWC 297. What is the cause of this discrepancy? Is it our poor knowledge of either mass or radius, the inclination angle of 20 ± 10°, or the observed vrot sini = 350 ± 50 km s-1? The value of i is constrained not only by our modeling but also by the recent interferometric studies reported by Malbet et al. (2007) and Acke et al. (2008). Nevertheless, further studies of i will be required to constrain i more reliably. Furthermore, it cannot be excluded that the value of vrot sini = 350 ± 50 km s-1 is overestimated, since it is difficult to derive the exact rotational velocity from the width of the observed absorption lines because of the medium spectral resolution employed and the quite low SNR of the Drew et al. spectrum caused by the relatively faint magnitude of V = 12.2. Moreover, the absorption lines in MWC 297 might be: a) contaminated by emission from outflowing material, as is often the case in massive young stars; or b) formed at a certain distance from the photosphere, where the broadening of the spectral line would be dominated by the outflow kinematics. Nevertheless, this question is far from being solved, and we encourage independent determinations of vrot sini using, for instance, high-resolution spectroscopy and state-of-the-art atmospheric modeling. Future multi-wavelength observations of MWC 297 using high spectral and spatial resolutions, combined with non-LTE radiative transfer modeling of the stellar atmosphere, will be essential to improve our knowledge of the stellar parameters such as the rotational velocity; -
5)
according to our data, the Brγ line has a low redshift in the LSR frame (but not in the heliocentric system), in contrast to the model spectrum. However, it is not yet known whether the Brγ- emitting region is really redshifted with respect to the star, since the small observed redshift could simply be caused by the (unknown) radial velocity of the star (see Appendix D).
The model of the emitting region of MWC 297 proposed in this paper needs to be improved. In particular, we need to investigate the dynamics of the magneto-centrifugal disk wind in the presence of the strong radiation field of the star. It is also necessary to investigate the effect on the thermal regime of the wind of both stellar radiation and ambipolar diffusion.
Additional information about the properties of the emitting region can be obtained by analyzing other hydrogen lines, first of all the Hα line. The observations by Drew et al. (1997) show that in the spectrum of MWC 297, this line is broader than the Brα line and has symmetric, extended wings up to 400–500 km s-1. The Brγ line is also much narrower than Hα. Our preliminary test calculations show that this difference can be the result of opacity effects (τ (Hα) ≫ τ (Brγ)) in addition to Stark broadening. A more detailed discussion of the Hα line properties as well as those of other Balmer lines will be presented in a forthcoming paper.
6. Conclusions
We have presented VLTI/AMBER observations of the Herbig Be star MWC 297 with a spectral resolution of 12 000. This high spectral resolution has allowed us to study the structure and kinematics of the inner sub-AU accretion-ejection region in approximately ~10 different spectral channels (radial velocities) across the resolved Brγ emission line and compare the observations with disk-wind models.
The K-band continuum observations confirm that MWC 297’s continuum emitting region is remarkably compact. We measured a ring-fit radius of ~2.2 mas (~0.56 AU) for the dominant compact component. At all Doppler velocities across the Brγ line, the line-emitting region is both asymmetric (as indicated by the strong closure phase) and more extended than the compact continuum-emitting region. At the center of the Brγ line, we derived a Gaussian continuum-compensated radius (HWHM) of 6.3 ± 0.4 mas (1.6 ± 0.1 AU) for the line-emitting region, which is ~3 times larger than the 0.58 AU HWHM of the compact continuum-emitting Gaussian component.
To interpret our AMBER observations, we employed a magneto-centrifugally driven disk-wind model consisting of an accretion disk, which emits the observed continuum radiation, and a disk wind, which emits the Brγ line. We have demonstrated that all observables, i.e., the observed Brγ line profile, K-band continuum flux, visibilities, wavelength-differential phases, and remarkably strong closure phases, can simultaneously be reproduced by our disk-wind model. The modeling also shows that disk-wind models developed for T Tauri stars can be used to interpret Herbig Be star observations if suitable modifications are applied. The modification has to take into account the higher radiation pressure from hot stars, which can change the inclination angle of the streamlines of the disk wind and cause a flatter disk wind than in T Tauri stars. The disk wind of MWC 297 starts at a distance of ~0.5 AU (~17.5 stellar radii) from the star, which is a larger distance than the typical value of 0.07 AU predicted for T Tauri stars.
Acknowledgments
We thank the ESO VLTI team on Paranal for the excellent collaboration. The data presented here were reduced using the publicly available data-reduction software package amdlib kindly provided by the Jean-Marie Mariotti Center (http://www.jmmc.fr/data_processing_amber.htm). The telluric spectra used in this work for spectral calibration of the AMBER data were created from data that was kindly made available by the NSO/Kitt Peak Observatory. A.M., V.G., and L.T. thank the Max-Planck-Society for support during their stay in Bonn. This publication makes use of the SIMBAD database operated at CDS, Strasbourg, France. We are grateful to Rene Oudmaijer and Bram Acke for sharing their spectroscopic data. Finally, we thank the referee for his comments that helped to improve the manuscript.
References
- Acke, B., van den Ancker, M. E., & Dullemond, C. P. 2005, A&A, 436, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Acke, B., Verhoelst, T., van den Ancker, M. E., et al. 2008, A&A, 485, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adams, F. C., & Shu, F. H. 1986, ApJ, 308, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Albi, T., Fuente, A., Bachiller, R., et al. 2009, A&A, 497, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrillat, Y., & Jaschek, C. 1998, A&AS, 131, 479 [Google Scholar]
- Artymowicz, P., & Lubow, S. H. 1994, in Circumstellar Dust Disks and Planet Formation, ed. R. Ferlet, & A. Vidal-Madjar, 339 [Google Scholar]
- Benisty, M., Natta, A., Isella, A., et al. 2010, A&A, 511, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N., Hartmann, L., & Strom, S. E. 2000, Protostars and Planets IV, 377 [Google Scholar]
- de Kool, M., & Begelman, M. C. 1995, ApJ, 455, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Drew, J. E., Busfield, G., Hoare, M. G., et al. 1997, MNRAS, 286, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Drew, J. E., Proga, D., & Stone, J. M. 1998, MNRAS, 296, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Eisner, J. A., Lane, B. F., Hillenbrand, L. A., Akeson, R. L., & Sargent, A. I. 2004, ApJ, 613, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Everett, J. E., Königl, A., & Kartje, J. F. 2001, in Probing the Physics of Active Galactic Nuclei, ed. B. M. Peterson, R. W. Pogge, & R. S. Polidan, ASP Conf. Ser., 224, 441 [Google Scholar]
- Ferreira, J. 2007, in Lecture Notes in Physics (Berlin: Springer Verlag), ed. J. Ferreira, C. Dougados, & E. Whelan, 723, 181 [Google Scholar]
- Gorti, U., & Hollenbach, D. 2009, ApJ, 690, 1539 [Google Scholar]
- Grachev, S. I., & Grinin, V. P. 1975, Astrophysics, 11, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Grinin, V. P., & Mitskevich, A. S. 1990, Astrofizika, 32, 383 [NASA ADS] [Google Scholar]
- Harmanec, P., Habuda, P., Štefl, S., et al. 2000, A&A, 364, L85 [NASA ADS] [Google Scholar]
- Humphreys, R. M., Lamers, H. J. G. M., Hoekzema, N., & Cassatella, A. 1989, A&A, 218, L17 [NASA ADS] [Google Scholar]
- Israelian, G., Friedjung, M., Graham, J., et al. 1996, A&A, 311, 643 [NASA ADS] [Google Scholar]
- Johnson, L. C. 1972, ApJ, 174, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Königl, A., & Pudritz, R. E. 2000, Protostars and Planets IV, 759 [Google Scholar]
- Kraus, S., Hofmann, K., Benisty, M., et al. 2008a, A&A, 489, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, S., Preibisch, T., & Ohnaka, K. 2008b, ApJ, 676, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Kurosawa, R., Harries, T. J., & Symington, N. H. 2006, MNRAS, 370, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 2000, A&A, 361, 159 [NASA ADS] [Google Scholar]
- Malbet, F., Benisty, M., de Wit, W.-J., et al. 2007, A&A, 464, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannings, V., & Sargent, A. I. 1997, ApJ, 490, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Mérand, A., Bordé, P., & Coudé du Foresto, V. 2005, A&A, 433, 1155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Millan-Gabet, R., Schloerb, F. P., & Traub, W. A. 2001, ApJ, 546, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Millour, F., Petrov, R. G., Vannier, M., & Kraus, S. 2008, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conf. Ser., 7013, [Google Scholar]
- Miroshnichenko, A. S., Klochkova, V. G., Bjorkman, K. S., & Panchuk, V. E. 2002, A&A, 390, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monnier, J. D., Millan-Gabet, R., Billmeier, R., et al. 2005, ApJ, 624, 832 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., Berger, J.-P., Millan-Gabet, R., et al. 2006, ApJ, 647, 444 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, N., & Chiang, J. 1997, ApJ, 474, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., D’Alessio, P., Calvet, N., & Hartmann, L. 2004, ApJ, 617, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Okazaki, A. T. 1991, PASJ, 43, 75 [NASA ADS] [Google Scholar]
- Petrov, R. G., Malbet, F., Weigelt, G., et al. 2007, A&A, 464, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pudritz, R. E., & Banerjee, R. 2005, in Massive Star Birth: A Crossroads of Astrophysics, ed. R. Cesaroni, M. Felli, E. Churchwell, & M. Walmsley, IAU Symp., 227, 163 [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1978, ApJ, 219, 654 [NASA ADS] [CrossRef] [Google Scholar]
- Safier, P. N. 1993, ApJ, 408, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Scholz, T. T., Walters, H. R. J., Burke, P. J., & Scott, M. P. 1990, MNRAS, 242, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Shlosman, I., & Vitello, P. 1993, ApJ, 409, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Sobolev, V. V. 1960, Moving envelopes of stars (Cambridge: Harvard University Press) [Google Scholar]
- Stee, P., & de Araujo, F. X. 1994, A&A, 292, 221 [NASA ADS] [Google Scholar]
- Stee, P., de Araujo, F. X., Vakili, F., et al. 1995, A&A, 300, 219 [NASA ADS] [Google Scholar]
- Tambovtseva, L. V., Grinin, V. P., Rodgers, B., & Kozlova, O. V. 2001, Astron. Rep., 45, 442 [NASA ADS] [CrossRef] [Google Scholar]
- Tannirkulam, A., Monnier, J. D., Harries, T. J., et al. 2008, ApJ, 689, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Tatulli, E., Millour, F., Chelli, A., et al. 2007, A&A, 464, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vieira, S. L. A., Corradi, W. J. B., Alencar, S. H. P., et al. 2003, AJ, 126, 2971 [NASA ADS] [CrossRef] [Google Scholar]
- Weigelt, G., Kraus, S., Driebe, T., et al. 2007, A&A, 464, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zickgraf, F.-J. 2003, A&A, 408, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Description of the model calculations
A.1. Disk wind
For the description of the disk wind, we use a coordinate system (l, θ, ω) centered at point S located on the rotation axis (see the sketch in Fig. A.1). In MHD models of the disk wind, the inclination angle of the first streamline with respect to the disk plane is typically assumed to be around 60° (Blandford & Payne 1982). However, in the case of Herbig Be stars, the strong stellar radiation pressure possibly bends down the streamlines and makes the disk wind flatter. Therefore, in our models we use a smaller inclination angle for the innermost streamline (e.g., between 10° and 30°). This effect influences the characteristic size of the wind-launching region.
 |
Fig. A.1 Sketch of the geometry of the disk-wind model adopted. |
 |
Fig. A.2 Left: radial velocity of the outflow along the different streamlines as a function of l; numbers 1–6 denote the number of the streamline. Right: the same for the rotational velocity; the dashed line shows the Keplerian velocity in the disk. |
As mentioned in Sect. 4, the tangential velocity of the wind changes along streamlines as 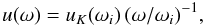 (A.1)where ω = l sinθ is the distance of the point (l,θ) from the rotation axis, ωi = li sinθ, and uK (ωi) = (G M∗/ωi)1/2 at the point (ωi) at the base of streamline i.
(A.1)where ω = l sinθ is the distance of the point (l,θ) from the rotation axis, ωi = li sinθ, and uK (ωi) = (G M∗/ωi)1/2 at the point (ωi) at the base of streamline i.
The radial velocity v increases along the streamlines as  (A.2)where v0 and v∞ are the initial and terminal values of the radial velocity and β is a parameter.
(A.2)where v0 and v∞ are the initial and terminal values of the radial velocity and β is a parameter.
We adopt v∞ = f uK(ωi), where uK(ωi) is the Keplerian velocity at distance ωi from the disk axis and f is the scale factor of the asymptotic terminal velocity to the local Keplerian velocity at the wind emerging point (see Kurosawa et al. 2006). The parameter f can change with distance ω because the magnetic field in the accretion disk decreases with ω. An example of the velocity field of one of the models considered below is shown in Fig. A.2.
The kinematical model described above is typical of disk-wind models adopted for different astrophysical objects with accretion disks including T Tauri stars (Kurosawa et al. 2006), cataclysmic variables (Shlosman & Vitello 1993), and even active galactic nuclei (Murray & Chiang 1997). In these models, the gas streams that start in the innermost regions of the disk-wind launching region have the highest radial velocities. These kinematical models are characterized by non-local radiative coupling between distant parts of the moving media (see, e.g., Grachev & Grinin 1975; Rybicki & Hummer 1978), which complicate the radiative transfer problem. In our calculations, we neglect the influence of the non-local radiative coupling since its effect on the radiative excitation in the flattened emitting regions (such as accretion disks or disk winds with large opening angles) is small.
For the calculation of the density distribution ρ in the disk wind, we use the mass-loss rate per unit solid angle, Ṁw(θ)/4π. One can show that Ṁw(θ) and the mass-loss rate per unit area of the disk, ṁw, are related by 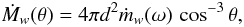 (A.3)where d is the distance between point S and the star. The total mass-loss rate is then
(A.3)where d is the distance between point S and the star. The total mass-loss rate is then  (A.4)In this case, we can write the continuity equation in its usual form
(A.4)In this case, we can write the continuity equation in its usual form  (A.5)Using this equation, one can calculate the distribution of the number density at each point in the disk wind.
(A.5)Using this equation, one can calculate the distribution of the number density at each point in the disk wind.
 |
Fig. A.3 Comparison of the theoretical interferometric quantities of model 5 obtained with (left) and without (right) modeling of AMBER’s spectral resolution of 12 000. In both cases, position and inclination angles are identical (PA = 300°, i = 20°). |
A.2. Calculation of the model intensity distributions
For the calculations of the 2-D intensity distributions (maps) of the emitting region, we use the coordinate system (x,y,z) centered on the star. The (x,y) plane coincides with the sky plane, the x axis is the intersection of the disk plane with the sky plane, and the z axis is parallel to the line-of-sight. In this case, the intensity of radiation at a frequency ν within a spectral line is 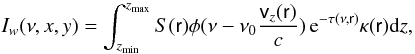 (A.6)where r is a vector, | r | = (x2 + y2 + z2)1/2, vz(r) is the projection of the velocity at point r on the line-of-sight, and S is a source function for a transition between energy levels i and j
(A.6)where r is a vector, | r | = (x2 + y2 + z2)1/2, vz(r) is the projection of the velocity at point r on the line-of-sight, and S is a source function for a transition between energy levels i and j (A.7)κis the integrated line opacity in the considered spectral line, τ(ν,r) is the line optical depth at point r and for the frequency ν in the direction to an observer, and ni is the number density of atoms in the ith state
(A.7)κis the integrated line opacity in the considered spectral line, τ(ν,r) is the line optical depth at point r and for the frequency ν in the direction to an observer, and ni is the number density of atoms in the ith state 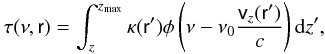 (A.8)where φ is the profile function normalized to unity, r′ is the vector with coordinates (x,y,z′), and z′ changes from the current value z in Eq. (A.6) to the outer boundary value zmax.
(A.8)where φ is the profile function normalized to unity, r′ is the vector with coordinates (x,y,z′), and z′ changes from the current value z in Eq. (A.6) to the outer boundary value zmax.
The optical depth of the disk wind in the line frequencies in the direction toward the star is τ∗(ν) = τ(ν,r = 0). We assume that there is a complete redistribution of the line frequencies in the reference frame of the atom and use the Doppler profile φ in the calculations of the Brγ and the Voigt profile for the Hα line (with the same constants as in Kurosawa et al. 2006).
The calculations of the ionization state and the number densities of the atomic levels were performed in a cylinder with a radius rc up to 300 R∗ and a height hc = 600 R∗ divided into grid cells in l,θ coordinates. In each cell, we solved the equations of the statistical equilibrium for the 15-level hydrogen atom + continuum, taking into account both collision and radiative processes of excitation and ionization (see Grinin & Mitskevich 1990 for more details). We assumed that the distribution of the atomic sub-levels follows their statistical weights. Johnson collision rates (Johnson 1972) were used for all transitions except 1–2; for the latter, we used those from Scholz et al. (1990).
The main sources of continuum radiation near the Brγ line are: i) the circumstellar disk; ii) the stellar atmosphere; and iii) the free-free and free-bound radiation of the disk wind. If the radiation of the star (I∗) intersects the disk wind in the line of sight, it has to be corrected for the absorption in the wind and we observe I∗ exp( − τ∗(ν)). In the adopted coordinate system, we obtain for the observed disk intensity distribution  (A.9)where R = (x2 + y2/cos2i)1/2, τw(ν,x,y) is the optical thickness of the disk wind at frequency ν between an observer and the point in the disk with the coordinates x′ = x and y′ = y/cosi, and i is the inclination angle (i = 0 corresponds to the pole-on orientation). It is assumed that the disk is flat and optically thick; each elementary area of the disk radiates as a black body with the local temperature Td(ω).
(A.9)where R = (x2 + y2/cos2i)1/2, τw(ν,x,y) is the optical thickness of the disk wind at frequency ν between an observer and the point in the disk with the coordinates x′ = x and y′ = y/cosi, and i is the inclination angle (i = 0 corresponds to the pole-on orientation). It is assumed that the disk is flat and optically thick; each elementary area of the disk radiates as a black body with the local temperature Td(ω).
The total intensity map of the object at frequency ν is the sum 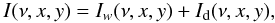 (A.10)where Iw(ν,x,y) is the intensity of the disk wind at the point x,y at an emission line frequency ν, and Id is the disk intensity distribution.
(A.10)where Iw(ν,x,y) is the intensity of the disk wind at the point x,y at an emission line frequency ν, and Id is the disk intensity distribution.
At the central part of the map where x2 + y2 ≤ r∗, we have to add the intensity of the stellar radiation I∗(ν)exp( − τ∗(ν)) to this sum. Our calculations have shown that the contribution of the free-bound and free-free radiation of the disk wind at the wavelength of the Brγ line is small compared with the disk radiation.
To model observations with a spectral resolution lower than the theoretical one, the intensity maps have to be convolved with the instrumental profile 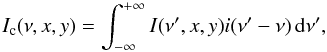 (A.11)where i(ν) is the normalized instrumental profile of AMBER.
(A.11)where i(ν) is the normalized instrumental profile of AMBER.
In our case, the spectral resolution is quite high (~25 km s-1). The calculations of the theoretical maps (Fig. 5) and the interferometric model quantities (Figs. 7, A.4, and A.5) were made using Eq. (A.11). A comparison of the results obtained with and without spectral convolution shows (see Sect. A.3) that noticeable differences in the interferometric quantities exist even at this high spectral resolution.
The flux at distance D from the object is an integral over the entire area in the x, y-plane of the emitting region  (A.12)To summarize, the model assumptions are:
(A.12)To summarize, the model assumptions are:
-
the disk wind is launched from the accretion disk surface in therange from distance ω1 (the starting point of the innermoststreamline) to ωN (starting point of the outermost streamline). Thehalf-opening angle (which is the angle between the rotation axisand the innermost streamline) is θ1 (see Fig. A1);
-
the wind is assumed to be isothermal with an electron temperature of 8000 K (for all models in Table A.1);
-
the disk wind possesses both radial and tangential (rotation) motion;
-
the number density distribution is calculated from the mass continuity equation for each streamline using the local mass-loss rate per unit area;
-
the atomic level populations were computed in the Sobolev approximation; a 15-level hydrogen atom has been considered. The 3–D radiative problem (exact integration) has been solved in a cylinder with a radius of 300 R∗ and a height 600 R∗.
A.3. Interferometric model quantities
 |
Fig. A.4 Dependence of the visibilities and phases of model 5 (see Tables 3 and A.1) on both the wavelength across the Brγ line and the PA of the model on the sky for an inclination angle of i = 20° and clockwise motion of the disk wind (the corresponding anti-clockwise plots are shown in Fig. A.5). Top: PAs from 0 to 80° in steps of 10° from left to right; bottom: PAs = 90 to 170°. Closest agreement between observation and model is obtained for PAs of 65, 120, 245, and 300°, as discussed in Sect. A.3. |
 |
Fig. A.5 Same as Fig. A.4, but for anti-clockwise motion. The best agreement between model and observations is obtained for the PAs of approximately 15, 70, 195, and 250° (see figure caption A.4). |
 |
Fig. A.6 Disk-wind model profiles of the Brγ line for different inclination angles (from top to bottom: 20, 40, and 60°). From left to right, the profiles correspond to models 1, 2, 3, and 4 in Table A.1 (model 5 is discussed in Fig. 6). |
Five examples of the computed disk-wind models.
Using the theoretical intensity distribution maps of the emitting regions, one can calculate the interferometric quantities of the model: spectrum, visibilities, wavelength-differential phases, and closure phases for the same interferometric baseline lengths and position angles as the AMBER observations. Examples of interferometric quantities of disk-wind model 5 (see Table A.1) are shown in Figs. 7, 8, A.3, A.4, and A.5.
In Figure A.3, we show the interferometric model quantities of the Brγ line calculated for model 5 with and without convolution of the theoretical intensity maps with the spectral AMBER profile corresponding to spectral resolution 12 000 (see Eq. (A.11)). One can see that in both cases, the visibilities inside the line profiles are very similar for all three baselines. However, the differential phases for the largest baseline (42 m) and the closure phases are quite different.
In Figs. A.4 and A.5, we show the detailed dependence of the visibilities and phases of model 5 (see Tables 3 and A.1) on both the wavelength across the Brγ line and the PA of the model on the sky for both an inclination angle of i = 20° and clockwise (Fig. A.4) and anti-clockwise (Fig. A.5) motion of the disk wind (the PA is counted from north to east with north up and east to the left). In Fig. A.4, the closest agreement between observation and model is obtained for PAs of 65 and 120°. The different sign of the phase at the PA = 120° does not disagree with the AMBER observations since the sign is unknown. The plots for the PAs of 180 to 350° are not shown since they give the same results as the PAs from 0 to 170°, except an opposite sign of the differential and closure phases, since a 180° rotation leads to a conjugate complex Fourier transform. Therefore, the PAs of 65 + 180 = 245° and 120 + 180 = 300° agree with the observations in addition to the PAs of 65 and 120°. For anti-clockwise motion (Fig. A.5), the closest agreement between model and observations is obtained for the PAs of approximately 15, 70, 195, and 250°.
A.4. Brγ line as a function of the model parameters
Examples of the theoretical Brγ line profiles calculated for the models listed in Table A.1 are presented in Fig. A.6. It shows that even for large inclination angles i, the profiles are quite narrow. This is due to the large radius of the disk-wind launching region. Except for a small range of i values close to pole-on view (i ≤ 20°), all orientations of the disk result in a double-peaked Brγ line. In observations, the double-peaked structure can, of course, appear single-lined if the line is narrow and the spectral resolution is too low.
A single-peaked Brγ emission line can also be obtained if a weak, narrow emission component is added to the model. Such emission can arise at large distances from the star, as discussed in the following Sect. A.4.1.
A.4.1. Low-velocity component of the disk wind
A low-velocity outflow from circumstellar disks can be caused by the heating of the upper layers of the disk atmosphere by EUV (hν > 13.6 eV) radiation from the central star. As a result, the thermal velocity of atoms and ions in the outer part of the disk can exceed the escape velocity. This is the region where the disk can evaporate (Hollenbach et al. 1994). The inner radius of this zone is rg =  , where vs is the sound speed. For ionized gas and M∗ = 10 M⊙, rg is ~7 × 104/Te ≈ 70 AU (Gorti & Hollenbach 2009). This value exceeds the radius of the AMBER FOV (~120 mas or ~30 AU at the distance of MWC 297), meaning that the photo-evaporated disk wind cannot contribute to the emission observed with VLTI. However, in the extended region of the disk between the outer radius of the MHD wind ejection region (~1 AU) and rg, the EUV photons ionize the upper layers of the disk atmosphere and produce a mini-H II region. This part of the disk does not evaporate, but can radiate in the Brγ and other lines. This emission is broadened by the Keplerian rotation and thermal motion of atoms. Its contribution to the total emission may be small, but potentially enough to fill in the small depression in the cental part of the double-peaked Brγ line profile formed by the disk wind. We simulated this profile (Fig. A.7) by changing the parameter f from f = 3 at ω1 to 0.5 at ωN. A more detailed modeling of this narrow emission is beyond the scope of this paper and will be presented in a separate one.
, where vs is the sound speed. For ionized gas and M∗ = 10 M⊙, rg is ~7 × 104/Te ≈ 70 AU (Gorti & Hollenbach 2009). This value exceeds the radius of the AMBER FOV (~120 mas or ~30 AU at the distance of MWC 297), meaning that the photo-evaporated disk wind cannot contribute to the emission observed with VLTI. However, in the extended region of the disk between the outer radius of the MHD wind ejection region (~1 AU) and rg, the EUV photons ionize the upper layers of the disk atmosphere and produce a mini-H II region. This part of the disk does not evaporate, but can radiate in the Brγ and other lines. This emission is broadened by the Keplerian rotation and thermal motion of atoms. Its contribution to the total emission may be small, but potentially enough to fill in the small depression in the cental part of the double-peaked Brγ line profile formed by the disk wind. We simulated this profile (Fig. A.7) by changing the parameter f from f = 3 at ω1 to 0.5 at ωN. A more detailed modeling of this narrow emission is beyond the scope of this paper and will be presented in a separate one.
 |
Fig. A.7 Brγ line profile of model 4 with constant a) and outward decreasing b) parameter f (i = 20°; see Sect. A.4.1 for details). |
A.4.2. Screening effects
As noted above, the optically thick part of the disk may screen some parts of the disk wind. This could lead to a red-shift of emission lines (depending on i, see Fig. A.8). The calculations show that this effect strongly depends on the opening angle θ1 of the disk wind.
At large i, the approaching part of the disk wind can be screened from an observer by optically thick layers of the flared disk. We simulated this screening effect by introducing a screen with a sharp upper boundary at some distance from the center. The angular size θ of the screen seen from the stellar position is the parameter that we introduced. The calculations show (see Fig. A.8) that for some θ (depending on the disk-wind parameters) and i ≃ 70°, the screening effect leads to a red-shifted emission line. It is likely that this mechanism is not important in our case, since the observations suggest that MWC 297’s inclination angle is small (10 to 20°).
 |
Fig. A.8 Dependence of the Brγ line profile on screening caused by an optically thick, dusty disk wind. The solid line represents the unscreened line profile of model 2 (see Table A.1) with f = 5, while the long-dashed (Hd = 100 R∗; θ = 20°) and dot-dashed (Hd = 130 R∗, θ = 25°) lines show models with screening. For all models shown, the inclination angle is i = 70°. See text for further details. |
Appendix B: Wavelength calibration
 |
Fig. B.1 Wavelength calibration of the AMBER data. Top: raw AMBER spectrum of MWC 297 (solid blue line) compared to a telluric spectrum from the Kitt Peak Observatory. The green line shows the original Kitt Peak spectrum with a spectral resolution of 60 000, while the red line displays the telluric spectrum that has been convolved to the same spectral resolution as the AMBER data (R = 12 000). For clarity, the red curve has been shifted down by 0.4. As the figure reveals, after the wavelength calibration, the AMBER raw spectrum of MWC 297 matches several telluric features. Bottom: same as top panel, but just for the wavelength region around the Brγ line. |
 |
Fig. B.2 Top: calibration between the pixel and wavelength values of the VLTI/AMBER observations of MWC 297. A least-square polynomial fit of the data is also shown (red line). Bottom: residuals between the measured position of the telluric line spectrum obtained from the wavelength calibration of the AMBER data and the expected position from the reference telluric spectrum provided by NOAO. The root-mean square value is of the order of 2.5 km s-1. |
Appendix C: Beam commutation device
 |
Fig. C.1 Differential phases and closure phases derived from the data obtained without (left, BCD OUT) and with (right, BCD IN) the beam commutation device. The shown signals are not yet corrected using the calibrator data. After we corrected the sign changes introduced by the BCD device, the two data sets yield the shown signals, which are nearly identical and demonstrate the high accuracy of the measured phase signals. |
 |
Fig. C.2 BCD-calibrated closure phase signal obtained by subtracting the calibrated closure phases obtained from the BCD IN and BCD OUT data. The blue line is the fit of a constant to the continuum (2.147–2.194 μm) closure phase outside the Brγ line. |
To optimize the calibration accuracy, we employed the AMBER Beam Commutation Device (BCD, Petrov et al. 2007), as described in Sect. 2. This device is located very early in the optical path of the AMBER instrument and allows us to exchange two of the three telescope beams within a few seconds. Performing this beam commutation between two subsequent exposures, allows one to correct potential instrumental drifts. The insertion of the BCD causes a sign change in one of the three differential phases and the CP signal (Millour et al. 2008). Our BCD OUT/BCD IN data sets precisely showed these expected sign changes. The differential phases and closure phases derived from both independent data sets (BCD OUT/BCD IN) are shown in Fig. C.1. Subtraction of the closure phases obtained with and without BCD cancels potential instrumental phase drifts. Figure C.2 presents the derived closure phase and a fit of a constant to the continuum closure phases. The obtained averaged continuum closure phase is − 1.28 ± 0.42°.
Appendix D: Optical spectroscopy
MWC 297 has been rarely observed spectroscopically mostly because of its relative faintness (V ~ 12.2 mag) and high reddening (B − V ~ 2.1 mag). Only two spectra that cover almost the entire optical range, although with a low resolution of 0.8 Å, have ever been published (Drew et al. 1997; Andrillat & Jaschek 1998). Higher-resolution spectroscopy was obtained for a few regions, mainly centered on strong emission or absorption lines (He i 5876 Å, Na i D-lines, [O i] 6300 Å, and Hα, Zickgraf 2003; Acke et al. 2005). A summary of the published optical spectroscopic data is presented in Table D.1.
Summary of published optical spectroscopic observations of MWC 297.
A detailed study of the object’s spectrum is beyond the scope of this paper. Thus, we only focus on the details that are relevant to the modeling of our interferometric results. One important issue for this purpose is the geometry of the circumstellar environment. The strongest emission-line profiles exhibit a double-peaked structure, which can only be revealed at a resolving power of R ≥ 30 000 (see Zickgraf 2003; Acke et al. 2005). This prompted Zickgraf (2003) to suggest that MWC 297 might be surrounded by a disk that is viewed at an intermediate inclination with respect to the line-of-sight.
Another crucial parameter is the systemic (stellar) radial velocity. Since this had never been carefully discussed, we critically examined possible methods to derive this quantity and performed an independent study of the published spectra. Absorption lines of the photospheric origin are only seen in the spectra obtained by Drew et al. (1997). They include a few He i lines blueward of 5800 Å and those of C iii and N iii in the 4500–4700 Å range. All of them are broad, which was interpreted to be caused by a high stellar rotation rate (Drew et al. 1997). Additionally, the residual intensities of the carbon and nitrogen lines are within ~5% of the continuum, hampering high accuracy measurements even at the SNR of ~120 achieved in the spectrum. The average LSR radial velocity, which we derived from five He i absorption lines at 4009, 4026, 4143, 4471, and 4713 Å, is −7 ± 7 km s-1. However, He i lines in the spectra of B-type emission-line stars are known to be strongly affected by the circumstellar material in the dense regions close to the star. Even pure absorption lines can exhibit variations that result in the observed shifts from the photospheric positions (see Israelian et al. 1996). Therefore, these lines cannot be considered as a reliable source of the systemic velocity. The most clearly recognized non-helium photospheric line is the C iii 4650.16 Å line, which however, forms a blend with two N iii lines at 4640.64 and 4641.90 Å. This line gives a more negative LSR radial velocity of − 29 km s-1. The accuracy of this value is at least of the order of 15 km s-1. The line can also be affected by the circumstellar material, which also ensures that this measurement is unreliable.
An alternative method for deriving the systemic velocity can be used if photospheric lines are not seen in the spectrum or there are no data of sufficient quality for these lines. It employs centroid radial velocities of emission lines, such as those of Fe ii. It has been successfully tested on complex objects, such as LBVs (e.g., Humphreys et al. 1989) and stars that exhibit the B[e] phenomenon (e.g., Miroshnichenko et al. 2002). The resulting systemic velocity is used to determine a kinematical distance and luminosity of the object that are in general good agreement with those found by other methods (e.g., spectroscopic parallax, interstellar extinction versus distance relationship). The method seems to work for any type of centrally symmetric circumstellar envelopes. Moreover, it has been shown to trace the central star motion even in binary Be stars (e.g., Harmanec et al. 2000), whose disks may contain asymmetric density perturbations (see Okazaki 1991).
Drew et al. (1997) comment that the centroid LSR radial velocities of the Hα, Hβ, and the He i 5876 Å lines are located between +2 and +20 km s-1. Other measurements, including those we made in the optical spectra and which we have at our disposal, are listed in Table D.1. The average value is + 8 ± 1 km s-1, similar to + 10 ± 2 km s-1 from Acke et al. (2008). We note that the formal statistical uncertainty of these velocities may be larger, because the number of lines used is relatively small. In addition, a systematic error due to, for instance, a slight asymmetry in the line profiles (see those shown by Zickgraf 2003) cannot be excluded. Therefore, we assume that the real uncertainty in the systemic velocity estimated with this method might be as large as ~5 km s-1.
To summarize the above discussion, we conclude that the positions of the emission lines suggest a systemic radial velocity of MWC 297 of + 8 ± 5 km s-1. In contrast, the He i absorption lines give − 7 km s-1 with an even larger uncertainty, because of their possible displacement from the photospheric position due to processing by the circumstellar material. The value derived from the emission lines seems to be more reliable because it is based on data from several spectra obtained over a period of 15 years. Nevertheless, it still needs to be confirmed using high-resolution data of more lines.
All Tables
Geometric model fit diameters of MWC 297 in the continuum and the center of the Brγ emission line.
Range of parameter variations for our continuum-disk plus disk-wind model calculations.
All Figures
 |
Fig. 1 AMBER observations of MWC 297 with spectral resolution of 12 000: (from top to bottom) wavelength dependence of flux, visibilities, wavelength-differential phases (for better visibility, the differential phases of the shortest and longest baselines are shifted by +40 and − 40°, respectively), and closure phase observed at projected baselines of 14.0, 28.0, and 42.1 m along the position angle (PA) of 68.0° on the sky. The wavelength scale at the bottom is the directly observed one, i.e. without heliocentric or LSR correction (see text). However, the radial velocity scale at the top, gives spectrum, visibilities, and phases as a function of the Brγ Doppler shift in the Local Standard of Rest (LSR) frame. The dashed vertical line indicates the centroid Brγ vacuum wavelength (2.1661 μm) in the LSR frame. |
| In the text | |
 |
Fig. 2 Left: fit of a two-component Gaussian plus a point source with a 10% flux contribution to the wavelength-averaged (2.147–2.194 μm) K-band continuum visibilities near Brγ. Right: fit of a compact ring plus Gaussian halo plus a point source with a 10% flux contribution to the K-band continuum visibilities. |
| In the text | |
 |
Fig. 3 Left: Gaussian FWHM fit diameters of the Brγ line-emitting region for several individual spectral channels (in the center and the line wings) across the Brγ emission line (red bullets). The diameters are derived from continuum-compensated visibilities. Therefore, they are the diameters of the Brγ line-emitting region and not of the emission region of both line plus continuum. The AMBER spectrum of MWC 297 is shown for comparison (green curve). Right: Gaussian fit to the continuum-compensated AMBER visibilities at the peak intensity of the Brγ emission line. |
| In the text | |
 |
Fig. 4 Sketch of the MWC 297 disk-wind model adopted in this paper. |
| In the text | |
 |
Fig. 5 Intensity distributions of our best-fit disk-wind model 5 (i.e., intensity distribution of the continuum disk plus the disk wind; the central star is not shown; see Tables 3 and A.1) at the center of the Brγ line (v = 0 km s-1) and at 14 other velocities (the labels give the velocity in km s-1). For the calculation of the model images in this figure, a clockwise motion of the disk wind was assumed. Therefore, in the blue-shifted images (left panels), mainly the disk regions on the right hand side of the star are bright. The radius of the inner edge of the disk wind ejection region (i.e., radius of the inner hole) is ω1 = 17.5 R∗ (~0.3 AU). The inclination angle (angle between the polar axis and the viewing direction) of the model is i = 20° (i.e., almost pole-on). The colors represent the intensity in erg ster-1 s-1 Å-1 cm-2. In these images, AMBER’s spectral resolution of 12 000 was modeled, as described in Sect. A.3. |
| In the text | |
 |
Fig. 6 Normalized Brγ line profiles of the disk-wind model 5 from Table A.1 at the inclination angles i = 10° (dotted line), 20° (solid), 40° (dashed), and 60° (dashed-dotted; high spectral resolution, not degraded to the spectral resolution of AMBER). |
| In the text | |
 |
Fig. 7 Comparison of the observations (left panel; see Fig. 1) with the corresponding model quantities of model 5 for two different PAs of the model image (middle and right panel; the model quantities are calculated for AMBER’s spectral resolution of 12 000, as discussed in Sect. A.3 and Fig. A.3). The middle and right panels show the dependence of the interferometric observables (spectrum, visibilities, wavelength-differential phases, and closure phases) of our best-fit disk-wind model 5 (disk-wind emitting region, continuum accretion disk, plus central star; Tables 3 and A.1) on the wavelength across the Brγ line for an inclination angle of i = 20°, clock-wise motion of the disk wind, and for two different PAs of the projected disk polar axis on the sky: 65° (middle) and 300° (right). Several other PAs that are also approximately in agreement with the observations are discussed in the text and Figs. A.4 and A.5. The detailed dependence of the interferometric observables on the PA is presented in Figs. A.4 and A.5. |
| In the text | |
 |
Fig. 8 Dependence of the interferometric quantities (visibilities, wavelength-differencial phases, and closure phases) of our best-fit disk-wind model 5 (see Table A.1) on the inclination angle i: 10, 15, and 20° from left to right for the PA 300° of the disk (see Fig. 7). In contrast to Fig. 7, the Brγ line profiles are given without convolution with the instrumental profile of the AMBER spectrograph for clearer visibility of the theoretical line profiles. |
| In the text | |
 |
Fig. A.1 Sketch of the geometry of the disk-wind model adopted. |
| In the text | |
 |
Fig. A.2 Left: radial velocity of the outflow along the different streamlines as a function of l; numbers 1–6 denote the number of the streamline. Right: the same for the rotational velocity; the dashed line shows the Keplerian velocity in the disk. |
| In the text | |
 |
Fig. A.3 Comparison of the theoretical interferometric quantities of model 5 obtained with (left) and without (right) modeling of AMBER’s spectral resolution of 12 000. In both cases, position and inclination angles are identical (PA = 300°, i = 20°). |
| In the text | |
 |
Fig. A.4 Dependence of the visibilities and phases of model 5 (see Tables 3 and A.1) on both the wavelength across the Brγ line and the PA of the model on the sky for an inclination angle of i = 20° and clockwise motion of the disk wind (the corresponding anti-clockwise plots are shown in Fig. A.5). Top: PAs from 0 to 80° in steps of 10° from left to right; bottom: PAs = 90 to 170°. Closest agreement between observation and model is obtained for PAs of 65, 120, 245, and 300°, as discussed in Sect. A.3. |
| In the text | |
 |
Fig. A.5 Same as Fig. A.4, but for anti-clockwise motion. The best agreement between model and observations is obtained for the PAs of approximately 15, 70, 195, and 250° (see figure caption A.4). |
| In the text | |
 |
Fig. A.6 Disk-wind model profiles of the Brγ line for different inclination angles (from top to bottom: 20, 40, and 60°). From left to right, the profiles correspond to models 1, 2, 3, and 4 in Table A.1 (model 5 is discussed in Fig. 6). |
| In the text | |
 |
Fig. A.7 Brγ line profile of model 4 with constant a) and outward decreasing b) parameter f (i = 20°; see Sect. A.4.1 for details). |
| In the text | |
 |
Fig. A.8 Dependence of the Brγ line profile on screening caused by an optically thick, dusty disk wind. The solid line represents the unscreened line profile of model 2 (see Table A.1) with f = 5, while the long-dashed (Hd = 100 R∗; θ = 20°) and dot-dashed (Hd = 130 R∗, θ = 25°) lines show models with screening. For all models shown, the inclination angle is i = 70°. See text for further details. |
| In the text | |
 |
Fig. B.1 Wavelength calibration of the AMBER data. Top: raw AMBER spectrum of MWC 297 (solid blue line) compared to a telluric spectrum from the Kitt Peak Observatory. The green line shows the original Kitt Peak spectrum with a spectral resolution of 60 000, while the red line displays the telluric spectrum that has been convolved to the same spectral resolution as the AMBER data (R = 12 000). For clarity, the red curve has been shifted down by 0.4. As the figure reveals, after the wavelength calibration, the AMBER raw spectrum of MWC 297 matches several telluric features. Bottom: same as top panel, but just for the wavelength region around the Brγ line. |
| In the text | |
 |
Fig. B.2 Top: calibration between the pixel and wavelength values of the VLTI/AMBER observations of MWC 297. A least-square polynomial fit of the data is also shown (red line). Bottom: residuals between the measured position of the telluric line spectrum obtained from the wavelength calibration of the AMBER data and the expected position from the reference telluric spectrum provided by NOAO. The root-mean square value is of the order of 2.5 km s-1. |
| In the text | |
 |
Fig. C.1 Differential phases and closure phases derived from the data obtained without (left, BCD OUT) and with (right, BCD IN) the beam commutation device. The shown signals are not yet corrected using the calibrator data. After we corrected the sign changes introduced by the BCD device, the two data sets yield the shown signals, which are nearly identical and demonstrate the high accuracy of the measured phase signals. |
| In the text | |
 |
Fig. C.2 BCD-calibrated closure phase signal obtained by subtracting the calibrated closure phases obtained from the BCD IN and BCD OUT data. The blue line is the fit of a constant to the continuum (2.147–2.194 μm) closure phase outside the Brγ line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


