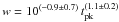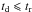| Issue |
A&A
Volume 526, February 2011
|
|
|---|---|---|
| Article Number | A27 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201015703 | |
| Published online | 16 December 2010 | |
Gamma-ray burst long lasting X-ray flaring activity⋆
1
INAF – Osservatorio Astronomico di Brera,
via Bianchi 46, 23807
Merate ( LC), Italy
e-mail: grazia.bernardini@brera.inaf.it
2
ICRANet, p.le
della Repubblica 10, 65100
Pescara,
Italy
3
University of Milano Bicocca, Physics Dept., P.zza della Scienza 3,
Milano
20126,
Italy
4
University of Ferrara, Physics Dept., via Saragat 1, 44122
Ferrara,
Italy
5
Yunnan Observatory & Key Laboratory for the Structure
and Evolution of Celestial Objects, Chinese Academy of Sciences,
Kunming,
Yunnan Province
650011, PR
China
Received: 6 September 2010
Accepted: 2 October 2010
Context. One of the most intriguing features revealed by the Swift satellite are flares that are superimposed on the gamma-ray burst (GRB) X-ray light curves. The vast majority of flares occurs before 1000 s, but some of them can be found up to 106 s after the main event.
Aims. We shed light on late-time (i.e. with peak time tpk ≳ 1000 s) flaring activity. We address the morphology and energetic of flares in the window ~103−106 s to put constraints on the temporal evolution of the flare properties and to identify possible differences in the mechanism producing the early and late-time flaring emission, if any. This requires the complete understanding of the observational biases affecting the detection of X-ray flares superimposed on a fading continuum at t > 1000 s.
Methods. We consider all Swift GRBs that exhibit late-time flares. Our sample consists of 36 flares, 14 with redshift measurements. We inherit the strategy of data analysis from Chincarini et al. (2010) in order to make a direct comparison with the early-time flare properties.
Results. The morphology of the flare light curve is the same for both early-time and late-time flares, but they differ energetically. The width of late-time flares increases with time similarly to the early-time flares. Simulations confirmed that the increase of the width with time is not owing to the decaying statistics, at least up to 104 s. The energy output of late-time flares is one order of magnitude lower than the early-time flare one,and is ~1%Eprompt. The evolution of the peak luminosity as well as the distribution of the peak-flux-to-continuum ratio for late-time flares indicate that the flaring emission is decoupled from the underlying continuum, differently from early-time flares/steep decay. A sizable fraction of late-time flares are compatible with afterglow variability.
Conclusions. The internal shock origin seems the most promising explanation for flares. However, some differences that emerge between late- and early-time flares suggest that there could be no unique explanation about the nature of late-time flares.
Key words: radiation mechanisms: non-thermal / gamma-rays: general / X-rays: general
Tables 1 and 2 are only available in electronic form at http://www.aanda.org
© ESO, 2010
1. Introduction
One of the most intriguing and unexpected features revealed by the X-Ray Telescope (XRT, Burrows et al. 2005a) on board the Swift satellite (Gehrels et al. 2004) are flares superimposed on the gamma-ray burst (GRB) X-ray light curves (Burrows et al. 2005b; Falcone et al. 2006; Chincarini et al. 2007; Falcone et al. 2007). The vast majority of flares occurs before 1000 s (Chincarini et al. 2007), but some of them can be found up to 106 s after the main event.
Recent analyses of the flare temporal and spectral properties (Chincarini et al. 2010, hereafter C10; Margutti et al. 2010c) of a large sample of early time (i.e. with peak time tpk ≲ 1000 s) flares and of a subsample of bright flares revealed close similarities between them and the prompt emission pulses, pointing to an internal origin of their emission (Chincarini et al. 2007, 2010). Therefore, the central engine itself should remain active and variable for long time. Alternatively, flaring emission can be powered by delayed magnetic dissipation during the deceleration of the ejecta (Giannios 2006). Despite many efforts from both the observational and the theoretical point of view, a clear explanation of the X-ray flares is still lacking (C10).
In this paper we shed light on late-time (i.e. tpk ≳ 1000 s) flaring activity observed by XRT in the 0.3−10 keV energy band. Its existence poses constraints on the theoretical models because late-time flares require huge releases of energy (~1050 erg) up to one month after the main event. A previous work on late-time X-ray flares has been presented by Curran et al. (2008). These authors analysed a sample of 7 GRBs that exhibit flares after 104 s by fitting them with a Gaussian profile plus power-law underlying continuum. The purpose was to compare the temporal and spectral properties of the underlying continuum and of the temporal and flux amplitude variability of these flares with the results found in Chincarini et al. (2007) and with the prescription of the internal and external shock models. They concluded that late-time flares are not different from the early-time ones. However, owing to the small number of flares in their sample, this statement needed further investigation.
The present work addresses the morphology of flares in the temporal window ~103−106 s of a larger sample than in Curran et al. (2008). The good fraction of flares of the sample with redshift measurement allows us also to characterise the energetic properties at very late times. We inherit the C10 strategy of data analysis to make a direct comparison with the results obtained for early-time flares and put stringent constraints on the temporal evolution of the flare properties. The aim is to identify possible differences in the mechanism producing the observed early- and late-time flare emission, if any. This requires the complete understanding of the observational biases affecting the detection of X-ray flares superimposed on a fading continuum at t > 1000 s.
In Sect. 2 we present the late-time flare sample and we describe the fitting procedure. In Sect. 3 we show the main results of the present analysis of the late-time flares temporal profiles and compare them with those obtained from the C10 sample. In Sect. 4 we discuss our findings. In Sect. 5 we summarize the results obtained and draw our main conclusions. We adopt standard values of the cosmological parameters: H0 = 70 km s-1 Mpc-1, ΩM = 0.27 and ΩΛ = 0.73. Errors are given at 1σ confidence level unless otherwise stated.
2. Sample and fitting procedure
We consider all Swift GRBs observed between April 2005 and December 2009 that exhibit late-time (i.e. tpk ≳ 1000 s) flares. Among all X-ray light curves observed by XRT, we include in our sample only those that contain a flaring activity with a relatively complete structure: rise, peak, and decay phase. The present data set consists of 22 long GRBs (LGRB) and 1 short GRB (SGRB), GRB050724, with 36 flares (see Table 1). Nine GRBs (14 flares) have measured redshift1. These flares and their underlying continuum have been analysed in the 0.3−10 keV energy band. For a full description of the data reduction we refer to C10.
The flare properties were investigated by fitting the 0.3−10 keV light curve with an empirical function proposed by Norris et al. (2005, hereafter Norris05): 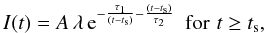 (1)where μ = (τ1/τ2)1/2 and λ = e2μ. The intensity peaks at tpk = τpk + ts = (τ1τ2)1/2 + ts. The pulse width is measured between the two 1/e intensity points,
(1)where μ = (τ1/τ2)1/2 and λ = e2μ. The intensity peaks at tpk = τpk + ts = (τ1τ2)1/2 + ts. The pulse width is measured between the two 1/e intensity points, 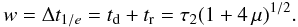 (2)The pulse asymmetry is
(2)The pulse asymmetry is 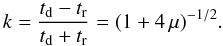 (3)The decay time td and the rise time tr are expressed in terms of w and k as
(3)The decay time td and the rise time tr are expressed in terms of w and k as 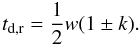 (4)The choice of the Norris05 profile allows us to perform a direct comparison of the properties of late and early-time flares.
(4)The choice of the Norris05 profile allows us to perform a direct comparison of the properties of late and early-time flares.
We simultaneously fitted the underlying continuum and the flares by adopting a multiple broken power-law plus an appropriate number of Norris05 functions. As a measure of the quality of the fit we used the χ2 statistics. The results of the fitting procedure are listed in Tables 1 and 2. The errors on the derived quantities are obtained by accounting for the entire covariance matrix of the fitting parameters. The flare fluence S is calculated by integrating the corresponding Norris05 function over the entire duration. The count-to-flux conversion factor was computed from a spectrum extracted during the entire duration of the burst (Evans et al. 2007, 2009; Margutti et al. 2010b).
3. Analysis and results
Below we characterise the late-time flare emission by investigating those flare morphology and energetics, which the theoretical models most commonly address. The morphology of the flare light curves is presented in the observer frame, while the energetic properties are investigated in the source rest frame.
3.1. Morphology
 |
Fig. 1 Width vs. peak time for the sample of late-time flares (blue squares) compared with early-time flare sample (red stars). Green line: linear (w = 10. + 0.2 tpk) behaviour found in the early flare sample. Pink line: best-fit for the late flares sample, |
Flares are an erratic emission of a huge amount of energy on a relatively short timescale. The median of the distribution of the ratio between the width w and the time tpk at which flares occur is ⟨ w/tpk ⟩ = 0.28, which is similar to the one of the population of early-time flares (0.23). However, late-time flares have a much broader distribution (σ = 0.33 compared with σ = 0.14). The highest w/tpk occurs for the flare belonging to the only SGRB of our sample (GRB050724).
In Fig. 1 we show the evolution of w with time for late-time flares. The width depends on time as 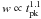 . The increase of the flare duration with time observed in this sample as well as in the early-time flare sample is one of the main differences from the prompt emission pulses: while w is almost constant with time for the BATSE pulses belonging to the Norris05 sample, it linearly increases for the early-time flare sample (see Fig. 3 in C10).
. The increase of the flare duration with time observed in this sample as well as in the early-time flare sample is one of the main differences from the prompt emission pulses: while w is almost constant with time for the BATSE pulses belonging to the Norris05 sample, it linearly increases for the early-time flare sample (see Fig. 3 in C10).
An important issue is whether this increasing trend is a real feature or if it is caused by the progressive widening of the light curve temporal bins: as the time proceeds, the decaying light curve is built by integrating the observed counts over larger time intervals in order to keep the signal-to-noise ratio constant. Therefore, an intense and narrow flare would be spread into a less intense and wider one, thus resulting in a possible bias for the correlation. Simulations in Chincarini et al. (2007) revealed indeed that very short duration flares (up to a factor 10-2 with respect to the best-fit relation shown in Fig. 1) could be in principle detected at 105 s at 90% confidence level. This result was obtained by generating flares with any possible luminosity, width, and temporal occurrence. The real situation is slightly different, because flares become dimmer as the time proceeds (see Sect. 3.2). This motivated us to perform simulations that reproduce the observed scenario in more detail.
We simulate for each flare of the sample a set of fake flares by adding different Norris05 profiles to the best fit of the continuum that have the same peak intensity and peak time of the original flare, but different decreasing widths. Then, we rebin each simulated light curve as the corresponding observed one, and we fit the results with a new Norris05 profile plus the underlying continuum. In this way we define a minimum observable width for each time interval as the width calculated with the best-fit Norris05 parameters of the shortest simulated flare occurring in that time interval that we can identify after the rebinning procedure. Low-significance fluctuations (number of σ ≲ 2) were not classified as flares. The result is shown in Fig. 1: the grey area represents the forbidden region for flare detection, namely a flare having these values of width and peak time would be classified as a non significant fluctuation around the underlying continuum. We found that the w − tpk best-fit relation is unbiased up to 104 s because the forbidden region is at least one order of magnitude below the best-fit relation, consistently with Chincarini et al. (2007). After ~104 s the range of detectable widths progressively reduces, and is only 24% of the observed value at 106 s. This is because of the progressively lower statistics of the GRB afterglows with time, which possibly causes a departure from the best-fit w − tpk relation found at early times.
Another source of bias affecting the late-time flare sample in some cases is the difficulty to distinguish blended structures. The integration of the observed counts over progressively larger time intervals makes it harder and harder to distinguish wether the observed excess is caused by one single flare or if it comes from the contribution of many overlapping flares. Therefore in some cases the width obtained with our fitting procedure could be overestimated, but only by a factor of a few. This factor will be not so different from the average number of flares observed in a temporal interval Δt ~ t of the early-time sample, that is ~1.5.
 |
Fig. 2 Decay time vs. rise time for the sample of late-time flares (blue squares) compared with the early-time flare sample (red stars). The best linear fitting for the two samples is td = (−0.1 ± 0.6) + (2.15 ± 0.04) tr (pink line). Grey area: |
A remarkable property of the flare profile is a self-similar behaviour, which is the rise over decay time constant in time. This feature is found in the present sample of late-time flares as well as in the C10 analysis, with the same best-fit relation td ~ 2 tr and a distribution of tr/td (see Fig. 2) and of asymmetry k (median value 0.31 with standard deviation 0.22) with a similar central tendency and dispersion. The K-S test on the two distributions of tr/td for early-time and late-time flares gives a 60% probability that they belong to the same population. Still, there is no flare with tr > td (grey area in Fig. 2).
3.2. Energy and luminosity
 |
Fig. 3 Isotropic energy emitted in the observer 0.3−10 keV energy band vs. rest frame peak time for the sample of late-time flares (blue squares) compared with the early-time flare sample (red stars). The absence of energetic late-time flares is manifest. Inset: distribution of the logarithm of the isotropic energy emitted in the 0.3−10 keV energy band of late-time flares (blue rectangles) compared with the early-time flare one (red rectangles). The late-time flares are clearly less energetic than the early-time ones, with a median for the distribution of the energy 1.4 × 1050 erg and standard deviation σ = 3.2 × 1050 erg. |
 |
Fig. 4 Peak luminosity vs. peak time measured in the rest frame for the 14 late-time flares with measured redshift (blue squares) compared with the early-time flare sample (red stars). The best fit for the whole sample accounting for the extrinsic scatter is Log [Lpk] = (53.2 ± 0.3) + (−1.8 ± 0.1) Log [tpk] with σext = (0.72 ± 0.07) (pink line). The best fit for early-time flares accounting for the extrinsic scatter Log [Lpk] = (54.8 ± 4.0) + (−2.7 ± 0.5) Log [tpk] with σext = (0.73 ± 0.08) (green line) is shown for comparison. The thinner lines indicate the 2σ regions for the two best-fit relations. |
In Fig. 3 we show in the inset the distribution of the logarithm of the isotropic energy emitted in the observer frame 0.3−10 keV energy band of late-time flares, compared with that obtained in C10 for early-time flares. Late flares are less energetic, with a median value of 1.4 × 1050 erg, one order of magnitude lower than the early-time flare sample. As stated in C10, the distribution function of the isotropic energy emitted is likely incomplete at the low-energy tail. On the other hand it is evident that high energetic flares are not detected at late times (see Fig. 3).
One of the most important clues for understanding X-ray flares is the evolution of the peak luminosity Lpk versus time. In Fig. 4 we compare the behaviour 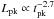 found in C10 with our sample: the flares with
found in C10 with our sample: the flares with 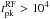 s differ from this relation for more than 2σ. The best fit of the late-time flare luminosity-time relation leads to
s differ from this relation for more than 2σ. The best fit of the late-time flare luminosity-time relation leads to 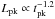 . This result is consistent with the average luminosity behaviour after 1000 s found in Margutti et al. (2010a, hereafter M10). In M10 is clearly shown that at this epoch the average luminosity function of flares tracks the detectability threshold. Therefore, the unbiassed luminosity-time relation for late flares is likely steeper. If we perform a joined fitting of the early and late-time flare data, we find
. This result is consistent with the average luminosity behaviour after 1000 s found in Margutti et al. (2010a, hereafter M10). In M10 is clearly shown that at this epoch the average luminosity function of flares tracks the detectability threshold. Therefore, the unbiassed luminosity-time relation for late flares is likely steeper. If we perform a joined fitting of the early and late-time flare data, we find 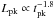 . If we account for an extra-variance of the sample (D’Agostini 2005), this best-fitting relation has a χ2/d.o.f. = 58.1/55 and a p-value of 40%.
. If we account for an extra-variance of the sample (D’Agostini 2005), this best-fitting relation has a χ2/d.o.f. = 58.1/55 and a p-value of 40%.
 |
Fig. 5 Distribution of the logarithm of the peak-flux-to-continuum ratio of late-time X-ray flares (blue rectangles) compared with the early-time flare one (red rectangles). The late-time flares clearly have a lower ΔF/F than early-time ones, with a median for the distribution of the logarithm 0.04 compared with 0.60 for the early-time flares, and standard deviation σ = 0.75 compared with σ = 0.73. |
In M10 we reported that the distribution of the peak-flux-to-continuum ratio ΔF/F of the C10 early-time flare sample can be fitted by the superposition of two Gaussian profiles. If we include the late-time flares of the present sample, we obtain that they all lie in the “fainter” part of the distribution (see Fig. 5). A K-S test performed on the two distributions gives a 2 × 10-5 probability that they belong to the same population.
The lower ratio at late times can be ascribed to two occurrences: a) the peak flux of flares decreases with time, then at late-times flares are fainter (see also Fig. 4); b) after 1000 s in 80% of the light curves of our sample the underlying continuum changes its behaviour and becomes shallower. To investigate these two effects, we calculate how the ΔF/F of a late-time flare would appear at early times. The ratio ΔF/F is substituted for the equivalent peak-luminosity-to-continuum ratio ΔL/L. We assume that the peak luminosity of flare evolves as t-2.7 for 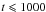 s and t − α for t > 1000 s, while the continuum evolves as t-2.7 for
s and t − α for t > 1000 s, while the continuum evolves as t-2.7 for 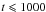 s (M10) and t-1 for t > 1000 s, this index is the average behaviour between 1000 s and 104 s of the light curves of our sample. We leave α as a free parameter owing to the impossibility to quantitatively evaluate the luminosity-time relation for late-time flares. However, it is reasonably between the value of the detection threshold found in M10 and the value found for early-time flares,
s (M10) and t-1 for t > 1000 s, this index is the average behaviour between 1000 s and 104 s of the light curves of our sample. We leave α as a free parameter owing to the impossibility to quantitatively evaluate the luminosity-time relation for late-time flares. However, it is reasonably between the value of the detection threshold found in M10 and the value found for early-time flares, 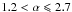 . We consider a flare with ΔL/L = 1, equal to the median value for the late flare sample distribution, at 104 s. Extrapolating backwards, we find that depending on α, the corresponding ΔL/L at 102 s would be higher by up to 50, within the range of values observed for the early-time sample. This simple calculation reveals that the discrepancy in the ΔL/L values for late-time and early-time flares depends on the shallower behaviour of the continuum after 1000 s that results in a bias for the flare detection (M10).
. We consider a flare with ΔL/L = 1, equal to the median value for the late flare sample distribution, at 104 s. Extrapolating backwards, we find that depending on α, the corresponding ΔL/L at 102 s would be higher by up to 50, within the range of values observed for the early-time sample. This simple calculation reveals that the discrepancy in the ΔL/L values for late-time and early-time flares depends on the shallower behaviour of the continuum after 1000 s that results in a bias for the flare detection (M10).
4. Discussion
The existence of flares at 106 s after the trigger poses several constraints on GRB central engines. Many authors pointed out that late-time flares must require a late ejection of shells rather than late collisions of prompt emission shells (Zhang et al. 2006; Lazzati & Perna 2007; Maxham & Zhang 2009). This conclusion, based on the constraints imposed by the observed duration of flares (Lazzati & Perna 2007), implies that the collisions producing flares occur in the same conditions as those producing the prompt emission pulses, but the ejection time is comparable to the flare observational time (Lazzati & Perna 2007). Therefore, the differences observed in flares with respect to the prompt emission pulses entirely depend on intrinsic differences in the shells ejected by the central engine and not on their evolution (Maxham & Zhang 2009). More important, the central engine itself should remain active up to 106 s.
Late-time flares are less energetic than early flares by at least one order of magnitude (see Fig. 3, Inset). In Fig. 3 it is manifest that early-time flares from C10 span a wide range of energies, and a hint of bimodality appears in their energy distribution (see C10, Fig. 8, Inset). Late-time flares mainly belong to the low-energy tail of the distribution. This translates, within the internal shock model, into less energetic collisions at late times (Lazzati et al. 2008; Maxham & Zhang 2009), and that corresponds to less energetic shells ejected at late times from the central engine (Lazzati et al. 2008).
The peak luminosity of early-time flares decreases with time as a power-law 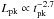 , as found in C10 (see Fig. 4) and obtained also in M10 with a different method. The late-time flares of the present sample observed at 103 ≲ t ≲ 104 s are slightly brighter with respect to the expectations based on the early-time flares, but are still consistent within the dispersion (see Fig. 4). This is mainly a result of the bias introduced by the underlying continuum: at t ~ 1000 s we observe in 90% of the X-ray light curves of our subsample of GRBs that show late-time flares and with a redshift measurement the transition from a steep decay to a shallow decay phase (Evans et al. 2009), and this prevents the flares belonging to the faint tail of the distribution from being detected.
, as found in C10 (see Fig. 4) and obtained also in M10 with a different method. The late-time flares of the present sample observed at 103 ≲ t ≲ 104 s are slightly brighter with respect to the expectations based on the early-time flares, but are still consistent within the dispersion (see Fig. 4). This is mainly a result of the bias introduced by the underlying continuum: at t ~ 1000 s we observe in 90% of the X-ray light curves of our subsample of GRBs that show late-time flares and with a redshift measurement the transition from a steep decay to a shallow decay phase (Evans et al. 2009), and this prevents the flares belonging to the faint tail of the distribution from being detected.
A different situation occurs for the three flares2 observed at t ≳ 105 s that are well above the extrapolation of the t-2.7 behaviour. To understand the nature of these flares we estimate the probability that they are compatible with the distribution of the observed early-time flares around the extrapolated fitting Lpk ∝ t-2.7 with the same extra-variance of the sample σext = 0.73. We compute the logarithmic average X-ray luminosity light curve of the underlying continuum of the GRBs of our sample, and we define the minimum luminosity for a flare at a given time as the one that can be detected at 2σ over the average continuum light curve. At t = 105 s the probability that a flare belonging to that distribution has a luminosity higher than the minimum one is less than 10-5. At t = 106 s this probability is even much lower, <10-9.
Conversely, we could assume that all flares of the C10 and of the present sample follow the same luminosity-time relation, but it is not the one found in C10 (and, we recall, also in M10 with a different method). In this case for the joined sample of early-time and late-time flares it reads: Log [L] = 53.2−1.8 Log [t] , with an extrinsic scatter σext = 0.72. This is an acceptable fit (χ2/d.o.f. = 58.1/55, p-value = 40%). However, in M10 we showed that the early-time flare average luminosity between 60 s and 400 s is steeper than t-1.8 at 90% confidence level. Moreover the continuum after 1000 s introduces a severe bias for the detectability of faint late-time flares: probably only the brightest flares can overshine the continuum at late times (M10). Therefore, the best fit t-1.8 likely overestimates the peak luminosity of flares.
If we consider the distribution of the peak-flux-to-continuum ratio ΔF/F for late-time and early-time flares, we find that the two datasets differ significantly, with a K-S probability that they belong to the same population of 2 × 10-5. The faintness of the ΔF/F for late-time flares can be ascribed to the shallower behaviour of the underlying continuum after 1000 s: with a simple calculation we show that the same flare with ΔF/F ~ 1 at 104 s would have a ΔF/F ~ 50 at 102 s because of the steeper continuum. This under the crucial assumption that the evolution of the peak luminosity of late-time flares is decoupled from the underlying continuum, different from what has been found for early-time flares. In M10 we found that the average luminosity of flares at t ≲ 400 s decreases with time with a power-law index that is linearly correlated to the one of the underlying steep decay. This points to a deep connection between the mechanisms that produce the two components. If this connection is not established at late times, it is natural to expect that late-time flares are so rare, because only the brightest ones are able to overshine the continuum (M10).
In the framework of accretion models, the long-lasting accretion up to late times can be caused either by a very small viscosity parameter α ≲ 0.01, or by a continued mass fall-back (Kumar et al. 2008). The first possibility seems to be disfavored since it predicts temporal indices for the initial and final decays of the whole light curve less steep than the observed ones (Kumar et al. 2008). In the second scenario, in a very short timescale a quasi steady-state is established with ṁacc ~ ṁfb, where ṁacc and ṁfb are the accretion rate and the mass fall-back rate respectively; therefore the observed luminosity tracks the mass fall-back rate fairly well (Kumar et al. 2008). The fall-back radius is rfb > 1000 rs, where rs is the corresponding Schwarzschild radius (for a central black hole mass MBH = 5 M⊙), and an accretion timescale of ~104 s is not unreasonable for very low accretion rates (Perna et al. 2006), that is the case of Kumar et al. (2008), Fig. 7.
In this context, the presence of flares in the light curve is caused by sudden changes in the accretion rate (Kumar et al. 2008). The duration of each accretion episode, which corresponds to the duration of the flare, is of the order of the accretion time (Perna et al. 2006) with tacc/t often less than unity (see Kumar et al. 2008, Figs. 6, 7). Disc instabilities could in principle lead to large variations in the accretion rate. A promising possibility are gravitation instabilities (we refer to M10 for a discussion of thermal and viscous instabilities in the context of early-time flares): these instabilities may occur in the outer regions of the disc (r > 100 rs) if the angular momentum is high. This requirement is more likely fulfilled in collapsars than in the merging of compact objects (Perna et al. 2006). Alternatively, the fall-back material can fragment into bound objects, producing a modulation in the accretion rate (Kumar et al. 2008; see Rosswog 2007, in the context of the merging of compact objects). If fragments form, their initial mass depends strongly on the local properties. However, their estimated mass is Mfrag ~ 1050 erg for fragmentation taking place at very large radii/times (Perna et al. 2006, Eq. (5)), which corresponds to the median energy observed for late-time flares (see Fig. 3, Inset).
A different process of fragmentation can occur in the collapse of a rapidly rotating stellar core, with the formation of more than one compact object (King et al. 2005). These subsequently coalesce under the effect of gravitational radiation releasing an energy ~2% of the main event with a delay of hundreds of seconds (Davies et al. 2002; King et al. 2005). The reactivated burst has a jet axis close to the first one, thus it expands in a cleaner environment with lower baryonic contamination and consequently with an higher Lorentz factor (King et al. 2005). This can explain why flares are softer than the main event.
Many GRBs have X-ray light curves without flares. Indeed, a flaring activity is observed in ~33% of XRT light curves. The conditions for fragmentation in the outer layer of the disc are uncertain, but high rotation is generally required (Perna et al. 2006). Rotation plays an important role in shaping the X-ray light curve at very early stages (Kumar et al. 2008): Fig. 5 of Kumar et al. (2008) clearly shows that lowering the rotation rate of the central object, results in a light curve that exhibits a longer and fainter prompt duration with a steeper decline. However, the rotation rate cannot be very low (less than 8 times lower than the model in Fig. 2 of Kumar et al. 2008) otherwise the entire core directly collapses to a black hole preventing the occurrence of the GRB. We noted in M10 that GRBs with multiple flares have generally a much flatter steep decay light curve. A flatter decay can be produced by a higher rotation rate for these GRB central objects, which allows them to produce more suitable conditions for fragmentation.
For a late-time X-ray light curve the angular momentum of the fall-back material is crucial to shape the transition between the shallow decay phase and the subsequent normal decay. If the angular momentum is low, this transition results in a sudden drop of the light curve. In the opposite case the transition is smooth. In our sample of GRBs with late-time flares, only three cases show a final decay steeper than 1.5. This is consistent with the expectations of high angular momentum for the fall-back material, and to the leading role that it has in favouring the fragmentation. The complete analysis of the light curves without flares needed in order to confirm this scenario is beyond the scope of the present work and will be presented elsewhere.
Magnetic fields strongly modify the dynamics of accretion (see e.g. Proga & Begelman 2003). In particular the energy release can be repeatedly stopped and restarted by the magnetic flux accumulated around the central object, giving origin to the observed X-ray flares, if the mass supply rate decreases with time (Proga & Begelman 2003; Proga & Zhang 2006). In this context a flaring episode depends on the strength of the magnetic field, namely when the magnetic stress provides support against gravity: 2BRBZ/4π ~ GMΣ/r2, where B is the magnetic field, M the mass of the central object, r the radius and Σ the surface density. A magnetic flux of the order of φ = πr2B(r) ~ 1029 cm2 G is necessary to stop an accretion with the rate 10-3 M⊙ s-1 around a 3 M⊙ central object at r = 300 rs, which is representative of the late-time evolution (Proga & Zhang 2006). Simple estimates show for the emission episodes that they are less energetic by one or two orders of magnitude than the prompt emission, and the duration of each episode is coupled with the time of occurrence (Proga & Zhang 2006), thus reproducing the main observational features of flares.
Despite the similarity with the early-time flares and the prompt emission pulses that point to an internal-shock origin of late-time flares, thus favouring accretion models, there are different promising possibilities such as the magnetic reconnection model (Lyutikov 2006; Giannios 2006; Lazar et al. 2009) that do not require a long lasting activity of the central engine. Indeed, in this model the emission takes place immediately before the deceleration radius. Within this context, flares originate from delayed magnetic dissipations during the deceleration of the ejecta (Giannios 2006). For a constant variability (which is indeed the case of flares) the isotropic energy emitted is proportional to the energy in the forward shock (Giannios 2006). This is consistent with late-time flares being on average less energetic than early-time ones. However, the time dependence of the width can be recovered only with ad-hoc assumptions on the characteristic length scales of the reconnection regions (Giannios 2006; Lazar et al. 2009).
The linear evolution of the decay time as a function of the rise time is present in the early as well as in the late-time flare sample, and is td ~ 2 td (see Fig. 2). This is a result that is valid over 5 orders of magnitude, and it is also a property common to the prompt emission pulses as shown in C10. This is a very stringent requirement for any theoretical model, because the rise and decay times depend either on the dynamic of the shocks within the internal shock model (Kobayashi et al. 1997), or on the motion of turbulent eddies or mini-jets (Narayan & Kumar 2009; Lazar et al. 2009).
4.1. Flares associated to variability in the GRB afterglow: the case of GRB050724
 |
Fig. 6 Increase of the flux with respect to the underlying continuum vs. temporal variability for the sample of late flares (blue squares) compared with the early flare sample (red stars). The black stars and square correspond to the SGRB early-time and late-time flares, respectively. The solid lines limit the kinematically allowed regions for density fluctuations on-axis (blue line) and off-axis (red line), for off-axis multiple regions density fluctuations (green line), for patchy shell model (black line) and for refreshed shocks (pink line), see Ioka et al. (2005) for details. |
In the above discussion we focused mainly on an internal origin of flares. However, it is of some interest to investigate late-time flares in the context of variability of the GRB afterglow. A useful tool in this respect is the plot proposed by Ioka et al. (2005) where they trace the regions of allowance for the increase of the flux with respect to the continuum as a function of the temporal variability for bumps in the afterglow on the basis of kinematic arguments. In Fig. 6 we present our sample of late-time flares in a “Ioka plot”, compared with the results presented in Fig. 13 of C10. As stated in Sect. 3.1 the range of observed w/tpk of the two sample is comparable, while as we noted in Fig. 5 the flux increase with respect to the continuum covers a different range for late-time flares.
All late-time flares of our sample, with the exception of GRB050724, fulfill the general requirement for internal shocks Δt/t < 1. However, ~14% are compatible with an internal-shock origin only. Differently from the early-time flares, ~25% of late-time flares are compatible also with bumps owing to on-axis density fluctuations. This reveals that although the internal-shock origin is the most promising explanation for flares, a sizable fraction of late-time flares can have a different origin from early-time ones. Therefore, there could be no unique explanation for the nature of late-time flares. Similar results were found by Curran et al. (2008), who compared the flare-to-continuum flux versus variability of the eight flares of their sample3 with the sample of Chincarini et al. (2007). They found that one flare (i.e. ~12% of their sample) can be explained only with internal shocks, and all the other flares can be interpreted both by internal and by external shocks. However, they do not have any flare compatible with on-axis density fluctuations.
The flare of the short GRB050724 is the most challenging. As pointed out in Sect. 3.1 it has the longest duration among the flares of the joined early and late sample, w/tpk ~ 1.4. This translates in the Ioka plot into being the only case compatible with the geometrical constraint for the multicomponent jet model, the refreshed shock model and marginally with the density fluctuation of many regions.
GRB050724 has also been observed at the epoch of the flare in the optical and radio frequencies (Malesani et al. 2007, and references therein). The simultaneous analysis of X-ray and optical data led Malesani et al. (2007) to conclude that they likely belong to the same spectral component (with βOX = (0.72 ± 0.04)) which implies a similar temporal behaviour. Therefore, despite the poor sampling of the optical light curve, they identify the presence of a simultaneous flare in the optical energy band (Malesani et al. 2007). A rebrightening in the radio light curve is also present, but it is delayed with respect to the X-ray and optical peaks (Malesani et al. 2007).
The association of this flaring emission in different energy bands with the afterglow has been tested by Panaitescu (2006). He included the flare in the forward shock emission in an interstellar medium environment as an episode of energy injection and simulated the observed X-ray, optical, and radio light curves. He found agreement with the observations, but with different assumptions and a smaller dataset than in Malesani et al. (2007). In the same context of the external shock model, the observed duration of the flare and spectral index can be accommodated in the adiabatic shock propagating in a wind environment (Lazzati & Perna 2007, Fig. 2).
The simultaneous detection of a flare at different wavelengths is not a feature common to all X-ray flares (see e.g. C10). Moreover, Margutti et al. (2010c) found in two cases of very bright flares that during the emission episode, the peak energy crosses the X-ray energy band with a temporal dependence very close to the temporal decay of the observed flux. Although this has not been demonstrated to be a common property of all flares, the optical-X-ray SED reported by Malesani et al. (2007) seems to exclude that the peak frequency crosses the X-ray band.
The above reasoning reveals indeed that the flare observed in the X-ray light curve of the short GRB050724 can be interpreted within different frameworks. Also the early-time flares associated to SGRBs included in the C10 sample are all compatible with afterglow variability (see Fig. 6). While consensus has been reached about the origin of flares associated to long GRBs, there is no overwhelming evidence on the nature of the flares in SGRBs. A devoted study is necessary in order to increase our knowledge on the SGRB progenitors and their environment.
5. Summary and conclusions
We analysed 23 GRB X-ray light curves observed by XRT that exhibit late-time (i.e. tpk ≳ 1000 s) flares. The present work inherits the C10 strategy of data analysis but extends the temporal window of investigation by three orders of magnitude, from 103 s to 106 s, with a larger sample than in previous works on late-time flares (Curran et al. 2008). We found that late-time flares are similar to early-time flares for the following reasons:
-
the width of late-time flares increases with time similarly to theearly-time flares. This is a real property of flares, at least up to104 s;
-
the self-similar behaviour of the flare profile, which is the decay proportional to the rise time, is also a property shared by both early-time and late-time flares. This is a more stringent requirement than being simply “asymmetrical pulses”.
However, they differ in the following characteristics:
-
the median energy output of late-time flares is one order ofmagnitude lower than the early-time flare one, whichis ~1%Eprompt;
-
the bias introduced by the shallower underlying continuum after 1000 s allows the detection of only the brightest flares. However it seems unlikely that the flares observed at t ≳ 105 s are compatible with the extrapolation of the behaviour t-2.7 found for early-time flares;
-
the decoupling of the evolution of the peak luminosity of late-time flares from the underlying continuum can account for the fainter distribution of the peak-flux-to-continuum ratio ΔF/F of late-time flares;
-
a sizable fraction of late-time flares are compatible with variability in the GRB afterglow.
The global pictures that emerges is that the morphology of the flare light curve is the same for both early and late-time flares, but that they differ energetically. The similarities of late-time flares with the early-time ones and with the prompt emission pulses as well as their energetic can be fairly well explained in the framework of the accretion models. The existence of flares in this context is ascribed to instabilities either in the disc (Perna et al. 2006) or in the fall-back material (Kumar et al. 2008; Rosswog 2007). This fragmentation can in principle account for the observed energetic and the longer duration of the accretion episodes at later times (Perna et al. 2006). Intermittence can be achieved also with magnetic fields (Proga & Begelman 2003; Proga & Zhang 2006). Different explanations are provided by the magnetic reconnection model (Lyutikov 2006; Giannios 2006; Lazar et al. 2009) which does not require a long-lasting activity of the central engine. However, the ~86% of the late-time flares of our sample that can be ascribed to variability in the GRB afterglow emission leads us to conclude that there could be no unique explanation about the nature of late-time flares.
Online material
Table of the best-fitting parameters and of the derived physical quantities.
Table of the best-fitting parameters and of the derived physical quantities of the underlying continuum.
For the redshift values we refer to http://www.mpe.mpg.de/~jcg/grbgen.html.
We recall that the width in the Norris05 profile is measured at ~37% of the maximum. If we consider the corresponding width measured on a Gaussian profile, it is wGauss = 2.83σ, while the Full Width at Half Maximum (FWHM) is wFWHM = 2.35σ. Therefore, the position on the x axis of the flares in the Ioka plot crucially depends on the profile adopted and on the definition of the duration. In the work of Curran et al. (2008) the duration of flares is the FWHM.
Acknowledgments
We thank the referee J. Norris for valuable comments and suggestions. MGB thanks P. D’Avanzo, E. Zaninoni and A. Melandri for useful discussions. This work is supported by ASI grant SWIFT I/011/07/0, by the Ministry of University and Research of Italy (PRIN MIUR 2007TNYZXL), by MAE and by the University of Milano Bicocca (Italy). This work made use of data supplied by the UK Swift Science Data Centre at the University of Leicester.
References
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005a, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, D. N., Romano, P., Falcone, A., et al. 2005b, Science, 309, 1833 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chincarini, G., Moretti, A., Romano, P., et al. 2007, ApJ, 671, 1903 [NASA ADS] [CrossRef] [Google Scholar]
- Chincarini, G., Mao, J., Margutti, R., et al. 2010, MNRAS, 406, 2113 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, P. A., Starling, R. L. C., O’Brien, P. T., et al. 2008, A&A, 487, 533 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Agostini, G. 2005, unpublished [arXiv:physics/0511182] [Google Scholar]
- Davies, M. B., King, A., Rosswog, S., & Wynn, G. 2002, ApJ, 579, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2007, A&A, 469, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Falcone, A. D., Burrows, D. N., Lazzati, D., et al. 2006, ApJ, 641, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Falcone, A. D., Morris, D., Racusin, J., et al. 2007, ApJ, 671, 1921 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Giannios, D. 2006, A&A, 455, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ioka, K., Kobayashi, S., & Zhang, B. 2005, ApJ, 631, 429 [NASA ADS] [CrossRef] [Google Scholar]
- King, A., O’Brien, P. T., Goad, M. R., et al. 2005, ApJ, 630, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, S., Piran, T., & Sari, R. 1997, ApJ, 490, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., Narayan, R., & Johnson, J. L. 2008, MNRAS, 388, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Lazar, A., Nakar, E., & Piran, T. 2009, ApJ, 695, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Lazzati, D., & Perna, R. 2007, MNRAS, 375, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Lazzati, D., Perna, R., & Begelman, M. C. 2008, MNRAS, 388, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Lyutikov, M. 2006, MNRAS, 369, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Malesani, D., Covino, S., D’Avanzo, P., et al. 2007, A&A, 473, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Margutti, R., Bernardini, G., Barniol Duran, R., et al. 2010a, MNRAS, in press [arXiv:1009.0172] [Google Scholar]
- Margutti, R., Genet, F., Granot, J., et al. 2010b, MNRAS, 402, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Margutti, R., Guidorzi, C., Chincarini, G., et al. 2010c, MNRAS, 406, 2149 [NASA ADS] [CrossRef] [Google Scholar]
- Maxham, A., & Zhang, B. 2009, ApJ, 707, 1623 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Kumar, P. 2009, MNRAS, 394, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. P., Bonnell, J. T., Kazanas, D., et al. 2005, ApJ, 627, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Panaitescu, A. 2006, MNRAS, 367, L42 [NASA ADS] [Google Scholar]
- Perna, R., Armitage, P. J., & Zhang, B. 2006, ApJ, 636, L29 [Google Scholar]
- Proga, D., & Begelman, M. C. 2003, ApJ, 592, 767 [NASA ADS] [CrossRef] [Google Scholar]
- Proga, D., & Zhang, B. 2006, MNRAS, 370, L61 [NASA ADS] [Google Scholar]
- Rosswog, S. 2007, MNRAS, 376, L48 [NASA ADS] [Google Scholar]
- Zhang, B., Fan, Y. Z., Dyks, J., et al. 2006, ApJ, 642, 354 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Table of the best-fitting parameters and of the derived physical quantities of the underlying continuum.
All Figures
 |
Fig. 1 Width vs. peak time for the sample of late-time flares (blue squares) compared with early-time flare sample (red stars). Green line: linear (w = 10. + 0.2 tpk) behaviour found in the early flare sample. Pink line: best-fit for the late flares sample, |
| In the text | |
 |
Fig. 2 Decay time vs. rise time for the sample of late-time flares (blue squares) compared with the early-time flare sample (red stars). The best linear fitting for the two samples is td = (−0.1 ± 0.6) + (2.15 ± 0.04) tr (pink line). Grey area: |
| In the text | |
 |
Fig. 3 Isotropic energy emitted in the observer 0.3−10 keV energy band vs. rest frame peak time for the sample of late-time flares (blue squares) compared with the early-time flare sample (red stars). The absence of energetic late-time flares is manifest. Inset: distribution of the logarithm of the isotropic energy emitted in the 0.3−10 keV energy band of late-time flares (blue rectangles) compared with the early-time flare one (red rectangles). The late-time flares are clearly less energetic than the early-time ones, with a median for the distribution of the energy 1.4 × 1050 erg and standard deviation σ = 3.2 × 1050 erg. |
| In the text | |
 |
Fig. 4 Peak luminosity vs. peak time measured in the rest frame for the 14 late-time flares with measured redshift (blue squares) compared with the early-time flare sample (red stars). The best fit for the whole sample accounting for the extrinsic scatter is Log [Lpk] = (53.2 ± 0.3) + (−1.8 ± 0.1) Log [tpk] with σext = (0.72 ± 0.07) (pink line). The best fit for early-time flares accounting for the extrinsic scatter Log [Lpk] = (54.8 ± 4.0) + (−2.7 ± 0.5) Log [tpk] with σext = (0.73 ± 0.08) (green line) is shown for comparison. The thinner lines indicate the 2σ regions for the two best-fit relations. |
| In the text | |
 |
Fig. 5 Distribution of the logarithm of the peak-flux-to-continuum ratio of late-time X-ray flares (blue rectangles) compared with the early-time flare one (red rectangles). The late-time flares clearly have a lower ΔF/F than early-time ones, with a median for the distribution of the logarithm 0.04 compared with 0.60 for the early-time flares, and standard deviation σ = 0.75 compared with σ = 0.73. |
| In the text | |
 |
Fig. 6 Increase of the flux with respect to the underlying continuum vs. temporal variability for the sample of late flares (blue squares) compared with the early flare sample (red stars). The black stars and square correspond to the SGRB early-time and late-time flares, respectively. The solid lines limit the kinematically allowed regions for density fluctuations on-axis (blue line) and off-axis (red line), for off-axis multiple regions density fluctuations (green line), for patchy shell model (black line) and for refreshed shocks (pink line), see Ioka et al. (2005) for details. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.