| Issue |
A&A
Volume 523, November-December 2010
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200811446 | |
| Published online | 15 November 2010 | |
Total solar irradiance since 1996: is there a long-term variation unrelated to solar surface magnetic phenomena?
Swiss Federal Institute of Aquatic Science and
Technology, Eawag, 8600 Dübendorf, Switzerland
e-mail: friedhelm.steinhilber@eawag.ch
Received:
29
November
2008
Accepted:
24
August
2010
Context. Total solar irradiance (TSI) has been measured with space-based instruments since 1978. The TSI during the recent solar minimum in 2009 has been lower than the two former minima around the years 1986 and 1996, which points to a long-term decrease.
Aims. In this study, we address the question of whether the observed decrease in the TSI is the result of evolving solar surface magnetism (sunspots and faculae).
Methods. We use a TSI model that is solely based on solar surface magnetic phenomena (sunspots and faculae including network). The information needed for this model is derived from Carrington rotation magnetogram and photogram synoptic charts measured with the Michelson Doppler Imager (MDI) instrument on-board the Solar and Heliospheric Observatory (SOHO). By combining these data with solar atmosphere calculations, TSI is reconstructed.
Results. The TSI is reconstructed from June 1996 to May 2010. From the solar minimum of 1996 to the solar maximum of 2004 the model reproduces the observations well, but it fails to explain the observed decrease in TSI in the solar minimum of 2009 and the very recent data of 2010.
Conclusions. The difference between modeled and observed TSI might be the result of underrepresented weak magnetic fields in the Carrington rotation synoptic charts, an uncertainty in the TSI measurement, or a decline of the global temperature of the photosphere. If latter were true, this would have important implications for reconstructions of TSI in the past. In order to study if an underrepresentation of weak magnetic fields in the Carrington rotation synoptic charts is the explanation for the difference between our model and the observation, full-disk images with higher spatial and temporal resolution should be analyzed in future.
Key words: solar-terrestrial relations / Sun: activity / Sun: magnetic fields / Sun: faculae, plages / sunspots / Sun: rotation
© ESO, 2010
1. Introduction
Total solar irradiance (TSI) has been continuously measured with space-based instruments since 1978. The TSI records from several missions have to be composed to obtain a continuous time series over the whole period (1978 to today). Three different TSI composites exist: 1. ACRIM composite (Willson & Mordvinov 2003), mainly using the irradiance measurements of the Active Cavity Radiometer Irradiance Monitors 1–3, 2. IRMB composite (Institut Royal Météorologique Belgique) (Dewitte et al. 2004), 3. PMOD composite (Physikalisch-Meteorologisches Observatorium Davos) (Fröhlich 2006) As is discussed in Fröhlich (2006, 2009a), the ACRIM and the IRMB composites show unreasonable behavior in time, whereas the PMOD composite does not. Therefore we restrict ourselves in this study on the PMOD composite. The PMOD composite includes three periods of high solar activity called solar maxima (around the years 1980, 1991, 2002) and low solar activity called solar minima (around the years 1986, 1996, 2009). While TSI during the first two solar minima (1986 and 1996) was practically constant, it dropped significantly from the minimum level as observed in 1996 by about 0.2 W m2 (140 ppm) in the solar minimum of 2009 (Fröhlich 2009a).
For the period 1996 to the present day the PMOD composite is mainly based on TSI measured with the VIRGO instrument (Fröhlich et al. 1997) on-board the Solar Heliospheric Observatory (SOHO). Because VIRGO has been in space over a relative long period, the observed drop in the TSI could be due to aging of the VIRGO instrument. However, this is not the case as emphasized in Fröhlich (2009a). The author compares the ratio of TSI measured by VIRGO with TSI measured by TIM (Kopp & Lawrence 2005) on-board the NASA Earth Observing System Solar Radiation and Climate Experiment. While VIRGO was launched in 1996, TIM has only been in space since 2003. Because TIM has not been as long in space as VIRGO, it should show another long-term trend than VIRGO if VIRGO were substantially affected by its age. However, the ratio TIM/VIRGO has been fairly stable, showing a slight upward trend of about 50 ppm per decade. This is by far less than the observed change of 140 ppm in VIRGO TSI between 1996 and 2008, which is therefore significant at the 1.5-σ level as pointed out by Fröhlich (2009a).
One kind of the TSI reconstruction models called SATIRE (Spectral And Total Irradiance REconstructions, Solanki et al. 2005, and references therein) is based on manifestations of solar surface magnetism such as sunspots, faculae, and network. TSI is reconstructed in this model by using the area fractions of the different solar surface phenomena together with their individual spectral intensity functions from solar atmosphere calculations. The SATIRE model very successfully reconstructs the TSI variations on time scales from days to solar cycles (Fligge et al. 2000; Wenzler et al. 2005; Krivova et al. 2003). So far, no results are available for the period after 2003, which raises the question whether these models are also capable to reproduce the observed decrease in the TSI since 2005.
Another type of model is also based on solar surface magnetic phenomena. But instead of solar surface area fractions of the phenomena it uses the MgII-index for faculae and the photometric sunspot index for sunspots (Fröhlich & Lean 2004, and references therein). This model is very successful in reproducing the observed TSI variations from 1978 to 2004, but it fails to explain the decrease observed since 2005 (Fröhlich 2009b). An additional component in the form of a linear decreasing trend has to be added in order to match the observations. Fröhlich (2009b) attributes the additional component to the global temperature of the photosphere and not to magnetic phenomena.
We investigate here whether the SATIRE model can explain the recently observed negative trend in the TSI, or if an additional component as proposed in Fröhlich (2009b) is needed. For this purpose we extended the work of Krivova et al. (2003) from 2002 to the present day, i.e. we reconstructed the TSI for the period 1996−2010. Following the procedure of Krivova et al. (2003) we analyzed magnetograms and photograms from the same instrument (Michelson Doppler Imager (MDI) on-board SOHO, Scherrer et al. 1995), but used synoptic charts (each covering one Carrington rotation) instead of individual full-disk images.
The paper is structured as follows. In Sect. 2 we introduce the model, which is used in Sect. 3 to reconstruct the TSI from June 1996 to May 2010. The discussion is in Sect. 4, and the conclusions are drawn in Sect. 5.
2. Method
2.1. Model
We used the same four components as in the SATIRE model of Krivova et al. (2003). The four components are: Faculae (subscript F) including also the network, sunspots divided into penumbra (P) and umbra (U), and the quiet sun (Q) as background.
Different intensity functions (spectral fluxes at the solar surface), Ix(λ), for each component are considered. x stands for F, P, U, and Q. These intensity functions depend on the spectral wavelength, λ. We used the intensity functions derived by Unruh et al. (1999), which have also been used in the TSI reconstruction by Krivova et al. (2003). Additionally to the intensities Ix we need to know what fraction of the solar disk is covered by each component. These surface fractions are called filling factors αx(t), which are functions of time.
The filling factors of penumbra and umbra are extracted from photograms (“continuum images”) and the filling factors of the faculae are derived from magnetograms. The solar surface, which is not covered by faculae and sunspots, is considered as quiet sun ![\begin{equation} \alpha_{\rm Q}(t) = 1 - \left[\alpha_{\rm F}(t) + \alpha_{\rm P}(t) + \alpha_{\rm U}(t)\right]. \end{equation}](/articles/aa/full_html/2010/15/aa11446-08/aa11446-08-eq10.png) (1)Knowing the intensity functions and the filling factors, the solar spectral irradiance is calculated by summing up over all four components
(1)Knowing the intensity functions and the filling factors, the solar spectral irradiance is calculated by summing up over all four components 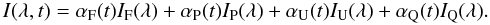 (2)Then, the TSI is the integral of the solar spectral irradiance over all wavelengths
(2)Then, the TSI is the integral of the solar spectral irradiance over all wavelengths 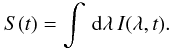 (3)Note that our study is similar to Krivova et al. (2003), except that we restricted ourselves on “global” filling factors and intensity functions, i.e. functions of time only, whereas in Krivova et al. (2003) the filling factors and intensity functions are functions of time and position on the solar disk.
(3)Note that our study is similar to Krivova et al. (2003), except that we restricted ourselves on “global” filling factors and intensity functions, i.e. functions of time only, whereas in Krivova et al. (2003) the filling factors and intensity functions are functions of time and position on the solar disk.
2.2. Data
We analyzed synoptic charts1 produced from full-disk measurements by the MDI instrument on-board the SOHO satellite. A synoptic chart represents the solar surface for one Carrington rotation (CR), which lasts about 27.28 days.
Below we briefly describe the procedure to produce the CR synoptic charts applied by the MDI team. Full-disk magnetograms of the line-of-sight magnetic field have been measured every 96 min. Photograms have been observed 2−4 times a day. Both photograms and magnetograms are composed to synoptic charts by remapping them onto a CR grid. Before their composition the photograms are corrected for limb darkening, flat field, orbital and instrumental variations. The synoptic charts of magnetograms are built by taking the mean of pixels from a selective window with a width of maximal 80° around the central meridian (Y. Liu, pers. comm.). For photograms a similar procedure is applied, but instead of the mean value the median value of pixels in a selective window of also maximal 80° near the central meridian is calculated. The synoptic charts are interpolated to a disk-center resolution of 3600 pixel × 1080 pixel (Carrington longitude × sine latitude). In this projection each pixel in both magnetograms and photograms represents the same surface area on the solar disk.
All available synoptic charts were analyzed covering the period from June 1996 to May 2010 (CR 1910 to 2097). Owing to SOHO “vacations” there are data gaps in the years 1998 and 1999, i.e. the synoptic charts of CRs 1937–1946 are not used.
2.3. Extraction of filling factors
Firstly, we identified sunspot regions from the photograms using contrast masks. The contrast masks were determined by matching the resulting filling factors with those found by Krivova et al. (2003) during the overlapping period from 1996 to 2002. We distinguished between penumbra and umbra regions. Umbra regions are those areas where the intensity is lower than 60% of the median intensity. Penumbra regions are regions where the intensity is lower than 90% compared to the median intensity, but which have not yet been identified as umbra regions. The median intensity was calculated for circles of contrast at a distance from the center μ = cosθ, where θ is the heliocentric angle. For all identified sunspot pixels the position was cross-checked in magnetograms. Each pixel fulfilling the contrast condition gets a filling factor α = 1. The same contrast masks were used for the entire period.
To identify faculae regions magnetograms of the radial magnetic field, B/μ, are analyzed. To suppress the noise, pixels were only considered as magnetically active if the magnetic signal was larger than a noise threshold, BNoise. The noise level in the original full-disk magnetograms depends on the position (Ortiz et al. 2002). But in the synoptic charts this dependence is smoothed out and, therefore, was kept constant at BNoise = 50 G, which is 10 times the value given at the MDI web page. The pixels that were identified as magnetically active pixels, but which had been already identified as sunspots, were removed. The filling factor of a facular of a single pixel is a linear function of the magnetic field strength until a saturation limit, Bsat, is reached. A pixel with a magnetic field strength higher than Bsat has a filling factor αF = 1. Bsat is principally the only free parameter in our model. This parameter was found in such a way that our faculae filling factors agree best with the found filling factors of Krivova et al. (2003) during the overlapping period 1996 to 2002, and that the resulting reconstruction of the TSI best matches the observed TSI. We found a saturation limit of Bsat = 450 G, which is about 30% higher than in Krivova et al. (2003). The newly determined Bsat was kept constant over the whole period of the analysis.
The MDI instrument measures the line-of-sight magnetic field from which the radial component has to be calculated. Hence artifacts could occur at the limb. We suppress the artifacts at the limb by considering only filling factors with μ ≥ 0.43 corresponding to a heliocentric angle, θ, of about 65°. On synoptic charts this is only a restriction for high latitudes and does not change the results because the active part on the Sun is limited to latitudes between about ± 40°. We note that we also extracted the filling factors for the high latitudes, i.e. for μ < 0.43. The resulting filling factors (not shown) did not differ much from those without considering the high latitudes. Thus the artifacts at high latitudes have only a small impact on the results. Nevertheless below we used the filling factors from low latitudes (μ ≥ 0.43).
Degradation effects of the MDI photograms may lead to uncertainties in the determination of the sunspot areas, which could have influenced the filling factors of faculae. As a worst-case scenario we assumed uncertainties of the umbra and penumbra filling factors equal to their mean values during the solar minimum of 1996. The resulting uncertainties integrated over all latitudes are ΔαP = 100 ppm for penumbra and ΔαU = 50 ppm for umbra. As a consequence the uncertainty range of the filling factors is rather large during the solar minima, with a relative uncertainty in umbra and penumbra area of about 100%, but less than 10% during solar maximum. All parameters used for extracting the filling factors are summarized in Table 1.
Parameters used for extracting the filling factors of the umbra and penumbra and of faculae from SOHO-MDI synoptic charts of photograms and magnetograms.
3. Results
In Fig. 1 the filling factors extracted from synoptic charts are compared with those extracted from full-disk images by Krivova et al. (2003). Except for the penumbra filling factors during the solar minimum in 1996, the relative differences are about 10%. Because we cannot identify any drift in the absolute relative differences of the faculae regions between solar minimum of 1996 and solar maximum in 2002, we conclude that the extraction of filling factors from MDI synoptic charts has been successful.
 |
Fig. 1 Comparison of our filling factors with those of Krivova et al. (2003) (Kr03). The data gap around 1998/1999 is due to SOHO “vacations”. a) Filling factors. b) Absolute relative differences, |Our Work - Kr03| / Our Work. |
 |
Fig. 2 Results of filling factors (FF) for Carrington rotations 1910−2097 (June 1996–May 2010). The data gap around 1998/1999 is due to SOHO “vacations”. a) Sum of penumbra and umbra pixels as a function of latitude and time. b) Faculae as a function of latitude and time. c) Filling factors of faculae summed up over all latitudes. The red and green horizontal bars indicate the faculae filling factors in February 2010 and the solar minimum 2009, respectively. d) Filling factors of penumbra and umbra summed up over all latitudes. On the right hand side the estimated uncertainties for the penumbra and umbra are given as red and green bars. |
The extracted filling factors from the synoptic charts for the entire period of June 1996 to May 2010 are shown in Fig. 2. The relative coverage by active regions (sum of faculae and sunspots) varies between about 1000 ppm at solar minimum and about 30 000 ppm at solar maximum. As expected from sunspot number observations, the filling factors of umbra and penumbra regions are slightly lower in the solar minimum of 2009 compared to the solar minimum of 1996. Note that considering the assumed uncertainties (as given in Table 1 and on the right side of Fig. 2d) the differences between these solar minima are not significant. The filling factors of faculae have decreased on average by 50% from 2000 ppm to 1000 ppm between the solar minima of 1996 and 2009. The decrease from 2000 ppm to 1000 ppm lasts longer than 20 CRs from about October 2007 to November 2009. The lowest value is found for CR 2087, when the faculae filling factor is only 700 ppm.
 |
Fig. 3 Relative number of magnetogram pixels of synoptic charts. Lines from top to bottom are pixel numbers of CRs 1982 (October 2001, solar maximum), 1926 (August 1997, similar to CR 2093), 2093 (February 2010) 1912 (July 1996, solar minimum), and 2087 (August 2009, lowest values in solar minimum 2009)0. Only pixels with magnetic field strengths above the noise threshold at B/μ = 50 G (marked with vertical line) are considered to obtain filling factors. a) B/μ: 0−100 G, b) B/μ: 0–1000 G. |
The red horizontal bar in Fig. 2c clearly shows that in February 2010 the filling factors for faculae have already recovered from the very low values of the solar minimum 2009 (green horizontal bar) to values similar to those in August 1997. They are approximately higher by a factor of 2 compared to the solar minimum of 1996. The very recent values of April and May 2010 are slightly lower than in February 2010 and are at the same level as observed in the solar minimum of 1996. The variation of the magnetic field in time is studied in more detail in Fig. 3. There the relative number of MDI synoptic magnetogram pixels is plotted as a function of the radial magnetic field, B/μ. This is done for five selected CRs: 1912 (July 1996, solar minimum), 1982 (October 2001, solar maximum), 2087 (August 2009, lowest values found in solar minimum 2009), 2093 (February 2010), and 1926 (August 1997, similar to CR 2093). Not shown are pixel numbers for CRs of April and May 2010. These are very similar to those of CR 1912. From Fig. 3 it is obvious that in the lowest part of the solar minimum 2009 (CR 2087) there are less pixels with strong magnetic field strengths compared to the former solar minimum represented by CR 1912. The pixel numbers for CR 2093 are very similar to those of the CR 1926. From that it is expected that TSI in February 2010 (CR 2093) is similar to TSI in August 1997 (CR 1926). This will be studied below.
 |
Fig. 4 Comparison of our TSI reconstruction based on Carrington rotation SOHO-MDI magnetograms and photograms with the observation (VIRGO TSI). The thin red lines show the upper and lower limits of our reconstruction considering the estimated uncertainties of the filling factors for sunspots and faculae. The data gap around 1998/1999 is due to SOHO “vacations”. a) Absolute values normalized to observation in 1996 marked with horizontal black dashed line. b) Difference between observation and the model. A zoom-in of the period 2004−2010 is plotted in Fig. 5. The differences between observation and the reconstructions of Krivova et al. (2003) (based on SOHO-MDI full-disk magnetograms and photograms) and Fröhlich (2009b) (based on MgII and photospheric sunspot indices) are also displayed. |
 |
Fig. 5 a) Zoom-in of Fig. 4b. b) Zoom-in of faculae filling factors (FF) of Fig. 2c. The horizontal bar at 2000 ppm marks the average level of faculae filling factors in the solar minimum of 1996. |
TSI was calculated from Eqs. (2) and (3) using the extracted filling factors as shown in Fig. 2. We normalized our reconstructed TSI to the average value of observed TSI in 1996. In Fig. 4a our reconstruction is compared with the observation (VIRGO TSI)2. Figure 4b shows the differences between our model and the observation, and Fig. 5 is a zoom-in on the period 2004−2010.
During the period 1996−2002 our reconstruction agrees fairly well with the observations. It reproduces the increase from the solar minimum in 1996 to solar maximum in 2002 as well as the observed variability of the TSI from 2002 to 2004. Especially the darkening effect of a large sunspot group, which appeared in November 2003, is very well reproduced. However, from 2005 to 2009 our reconstruction fails to show the observed decline and the very recent increase in TSI in 2010. This is emphasized by Fig. 4b, where the differences between observed TSI and the model are displayed. In addition the resulting differences between the observation and the reconstructions of Krivova et al. (2003) and Fröhlich (2009b) are plotted, showing a similar behavior. Before 2004 the difference to the observation is consistent with 0, but after 2004 the differences are significantly below 0, indicating a different long-term behavior of the models and the observation. The zoom-in on the period 2004–2010 as shown in Fig. 5 clearly illustrates that firstly although the filling factors in solar minimum 2009 are 50% lower than in solar minimum 1996 the model cannot reproduce the large drop in the observation. Secondly although the filling factors in 2010 are already recovered to similar or higher values as in solar minimum of 1996, the observed TSI is still lower than the model, or in other words the modeled TSI is too high.
The different long-term behavior of the model and the observation can also be seen in the scatter plot in Fig. 6. There each individual data point obtained for the period 1996−2010 (CRs 1910−2097) with the model is plotted versus the corresponding CR average of the observed TSI. While almost all points before the year 2005 lie on the 1:1 line, the points after the year 2005 lie above, i.e. the model gives too high values of TSI in the period after 2005.
 |
Fig. 6 Our TSI reconstruction versus the observation (VIRGO TSI). The colors indicate the date. Black dashed is the 1:1 line. Our model represents the observed TSI before 2005, including the solar minimum in 1996, the solar maximum in 2002, and the decrease due to the large sunspot region in November 2003. The modeled values for the solar minimum in 2009 and for 2010 are higher than the observation. |
To summarize, our results in Figs. 2–6 show that the SATIRE model using filling factors based on MDI CR synoptic charts cannot reproduce the observed TSI.
4. Discussion
The basic assumption of the SATIRE model is that the entire variation of TSI can be ascribed to evolving manifestations of solar surface magnetism. During solar minima sunspots appear only very rarely on the solar disk, and therefore, they cannot be responsible for the observed difference in TSI between the solar minima 1996 and 2009. Thus, the only remaining candidate are faculae. Indeed, we find that the faculae filling factors are smaller during the solar minimum in 2009 compared to the minimum in 1996. However, they can only explain parts of the observed drop in the TSI. To explain the full change the faculae filling factors during the minimum of 2009 should be smaller by a factor of about 5 compared to those determined. How to explain such a large discrepancy?
The first explanation for the discrepancy between the modeled and observed TSI, could be uncertainty in the observation itself. However, the difference between the solar minima 1996 and 2009 is significant at the 1.5−σ level (Fröhlich 2009a). Of course this does not exclude that parts of the discrepancy are owing to an uncertainty in the observation. But the difference between the model and the observation in the years 2008−2010 is about 0.2 W m-2 (see Fig. 5a), which is too much to be reasonably explained by an uncertainty in the observation.
Hence the model itself or the data used in the model must be mainly responsible for the discrepancy. It could be that in CR synoptic charts the background or ephemeral regions of the Sun are underrepresented as discussed in Krivova & Solanki (2004). Because the ephemeral regions are small regions with weak and signed magnetic fields, averaging several magnetograms to produce a CR synoptic chart zeroes out these weak magnetic fields. This effect could be even more amplified by the relatively high magnetic threshold of 50 G which is used to suppress the noise. Thus if the background magnetic field below the magnetic threshold in the solar minimum 2009 were weaker than in the former solar minimum, this is not resolved by using CR synoptic charts. In order to study if the magnetic fields below 50 G changed between 1996 and 2010, full-disk magnetograms and photograms with higher spatial and temporal resolution should be analyzed. Still, underrepresented weak magnetic fields are probably not the explanation because of the following points: First, we note that the observed TSI in February 2010 is equal to TSI in June 1996, but lower than in August 1997. This is unexpected, because the extracted filling factors of faculae in February 2010 are similar to those found in August 1997 and higher by a factor of 2 compared to June 1996 (see Fig. 2c). So, even if the ephemeral regions were probably underrepresented in the CR synoptic charts in the solar minimum in 2009, the extracted filling factors of February 2010 should be “normal” again, implying also that the model should be able to reconstruct the observed TSI for February 2010. Second, the model successfully reproduces the variations over several solar rotations and the amplitude from solar minimum in 1996 to maximum in 2002. In addition the model is even able to reconstruct the influence of short-lived phenomena on the TSI like the occurrence of a large sunspot group in November 2003 (see e.g. Fig. 6). Third, a frequency analysis (not shown) of the difference between the observed TSI and our reconstruction does not give a peak at the periodicity of one Carrington rotation. Thus, our reconstruction considers all solar surface phenomena, which rotate on the solar surface, producing the Carrington rotation variation in the TSI. This means that at least those ephemeral regions which occur next to the active regions (sunspots and faculae) and, therefore, corotate with them are implicitly considered in our study. Fourth, another model (Fröhlich 2009b) using different data (MgII and photospheric sunspot indices), but the same assumption, namely that the entire variation of the TSI is caused by the evolving surface magnetism, is also not able to reproduce the observed decline in the TSI. Moreover, the results of Fröhlich (2009b) agree with ours as shown in Figs. 4b and 5a.
Besides an underrepresentation of the weak magnetic field as discussed above, explanations for the drop in the TSI could be a change in the solar radius or the global temperature of the photosphere. Measurements of the solar radius are very difficult and up to date it is not known whether the solar radius is subject to variations (Thuillier et al. 2005). The other possibility for the observed decrease could be a change of the global temperature of the photosphere as suggested by Fröhlich (2009b). A change in temperature is not considered in the SATIRE model and might be the missing mechanism. Assuming that the difference between the model and the observation can be entirely ascribed to a change in global temperature, the temperature change can be calculated with the Stefan-Boltzmann law. Only a small change by about 0.25 K would be needed to explain the discrepancy in the TSI of about 0.2 W/m2 between the model and observation in the solar minimum of 2009. We also found that the global temperature of the photosphere has to be lower by about 0.1−0.2 K to explain the difference between the modeled TSI and the observation of February–May 2010. Our results support the findings of Fröhlich (2009a) who finds that the different solar indices for UV irradiance (such as MgII, CaII hk-index, sunspots, 10.7 cm solar radio flux, Lyman-α) do not show any change within the uncertainty range in the solar cycle minima. Because these indices are very sensitive to changes of the solar surface magnetic field but not of the temperature, a strong decrease in these datasets would be expected if solar surface magnetic fields were the cause for the found decrease.
As discussed the filling factors of faculae during the solar minimum of 2009 are about 50% smaller compared to the minimum in 1996 which is not enough to explain the observed change in TSI. In the past, sunspots (Hoyt & Schatten 1998) and faculae (Foukal 2002) show long-term trends of the amplitude, but hardly of the level of solar minima. However, other proxies of solar magnetic activity like geomagnetic indices (e.g. Lockwood et al. 1999; Rouillard et al. 2007) and cosmogenic radionuclides (e.g. Beer et al. 1998; Usoskin et al. 2007; Steinhilber et al. 2010) clearly show a long-term variation of the solar minima values. Thus, maybe the postulated decrease in temperature is indirectly the result of solar magnetism. If correct this raises several interesting questions: How is the global temperature of the photosphere related to solar magnetic activity? What is the physics behind the relationship?
5. Conclusions
Total solar irradiance (here we used the TSI measured with VIRGO on-board SOHO) has been significantly lower in the solar minimum of 2009 compared to the solar minimum of 1996. We studied if the widely accepted mechanism of TSI variation based on evolving phenomena of solar surface magnetism (sunspots and faculae) is responsible for all variations in the TSI, i.e. also for the observed decrease in the solar minimum of 2009 compared to the solar minimum in 1996. Solar surface area fractions of these phenomena were extracted from CR synoptic charts (magnetograms and photograms) measured with MDI on-board SOHO, covering the period from June 1996 to May 2010 (CRs 1910–2097). The main findings are:
-
1.
Sunspots have covered similar fractions of the solar disk duringthe solar minima of 1996 and 2009.
-
2.
Faculae covered on average 1000 ppm of the solar disk in the solar minimum of 2009, which is 50% less than the area covered by faculae during the solar minimum of 1996. The lowest value is 700 ppm in August 2009 (Carrington rotation 2087). In February 2010 the faculae areas have already recovered from the very low values in 2009 to values similar to those found in August 1997, which are higher by a factor of 2 than found in the solar minimum of 1996.
-
3.
The time series of sunspot and faculae areas were used to reconstruct the TSI. The reconstructed TSI agrees well with the observation in the period 1996 to 2004, but not after 2004. The model results in TSI values that are too high compared to the observation during the solar minimum of 2009, and also for the most recent period of 2010. The observed TSI in February 2010 is similar to the one of June 1996, but the model gives a higher TSI similar to August 1997.
-
4.
Because the model is not able to reconstruct the observed TSI for the solar minimum of 2009 and also for 2010, we conclude that the TSI observation cannot be described by evolving manifestations of solar surface magnetism as obtained from MDI CR synoptic magnetograms and photograms.
-
5.
Explanations for the discrepancy between model and observation could be due to an uncertainty in the TSI observation, to an underrepresentation of weak magnetic fields in CR synoptic charts, or to a drop of the global temperature of the photosphere by about 0.2 K during the past solar cycle. If this last were the reason, it would have important implications for reconstructions of the TSI. This should be studied with full-disk magnetograms and photograms with higher spatial and temporal resolution in future.
Images with level 1.8.2 calibration from http://soi.stanford.edu/magnetic/index6.html
Acknowledgments
Very helpful discussions with Claus Fröhlich, José Abreu, and Jürg Beer are gratefully acknowledged as well as the comments of an anonymous reviewer. This work was financially supported by NCCR Climate – Swiss Climate Research. We also would like to thank the Stanford Solar Group for making the MDI synoptic charts available for public use and for unpublished irradiance data (version 6.2) from the VIRGO experiment on the cooperative ESA/NASA mission SOHO.
References
- Beer, J., Tobias, S., & Weiss, N. 1998, Sol. Phys., 181, 237 [Google Scholar]
- Dewitte, S., Crommelynck, D., & Joukoff, A. 2004, J. Geophys. Res. (Space Phys.), 109 [Google Scholar]
- Fligge, M., Solanki, S. K., & Unruh, Y. C. 2000, Space Sci. Rev., 94, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Foukal, P. 2002, Geophys. Res. Lett., 29, 230000 [Google Scholar]
- Fröhlich, C. 2006, Space Sci. Rev., 125, 53 [Google Scholar]
- Fröhlich, C. 2009a, A&A, 501, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fröhlich, C. 2009b, Proc. CAWSES Symp., October, 23−27 2007, Kyoto, Japan, 217 [Google Scholar]
- Fröhlich, C., & Lean, J. 2004, A&A Rev., 12, 273 [CrossRef] [Google Scholar]
- Fröhlich, C., Crommelynck, D. A., Wehrli, C., et al. 1997, Sol. Phys., 175, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyt, D. V., & Schatten, K. H. 1998, Sol. Phys., 181, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Kopp, G., & Lawrence, G. 2005, Sol. Phys., 230, 91 [Google Scholar]
- Krivova, N. A., & Solanki, S. K. 2004, A&A, 417, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivova, N. A., Solanki, S. K., Fligge, M., & Unruh, Y. C. 2003, A&A, 399, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lockwood, M., Stamper, R., & Wild, M. N. 1999, Nature, 399, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz, A., Solanki, S. K., Domingo, V., Fligge, M., & Sanahuja, B. 2002, A&A, 388, 1036 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rouillard, A. P., Lockwood, M., & Finch, I. 2007, J. Geophys. Res.(Space Phys.), 112, 5103 [Google Scholar]
- Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [Google Scholar]
- Solanki, S. K., Krivova, N. A., & Wenzler, T. 2005, Adv. Space Res., 35, 376 [Google Scholar]
- Steinhilber, F., Abreu, J. A., Beer, J., & McCracken, K. G. 2010, J. Geophys. Res. (Space Phys.), 115 [Google Scholar]
- Thuillier, G., Sofia, S., & Haberreiter, M. 2005, Adv. Space Res., 35, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Unruh, Y. C., Solanki, S. K., & Fligge, M. 1999, A&A, 345, 635 [NASA ADS] [Google Scholar]
- Usoskin, I. G., Solanki, S. K., & Kovaltsov, G. A. 2007, A&A, 471, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wenzler, T., Solanki, S. K., & Krivova, N. A. 2005, A&A, 432, 1057 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willson, R. C., & Mordvinov, A. V. 2003, Geophys. Res. Lett., 30, 050000 [Google Scholar]
All Tables
Parameters used for extracting the filling factors of the umbra and penumbra and of faculae from SOHO-MDI synoptic charts of photograms and magnetograms.
All Figures
 |
Fig. 1 Comparison of our filling factors with those of Krivova et al. (2003) (Kr03). The data gap around 1998/1999 is due to SOHO “vacations”. a) Filling factors. b) Absolute relative differences, |Our Work - Kr03| / Our Work. |
| In the text | |
 |
Fig. 2 Results of filling factors (FF) for Carrington rotations 1910−2097 (June 1996–May 2010). The data gap around 1998/1999 is due to SOHO “vacations”. a) Sum of penumbra and umbra pixels as a function of latitude and time. b) Faculae as a function of latitude and time. c) Filling factors of faculae summed up over all latitudes. The red and green horizontal bars indicate the faculae filling factors in February 2010 and the solar minimum 2009, respectively. d) Filling factors of penumbra and umbra summed up over all latitudes. On the right hand side the estimated uncertainties for the penumbra and umbra are given as red and green bars. |
| In the text | |
 |
Fig. 3 Relative number of magnetogram pixels of synoptic charts. Lines from top to bottom are pixel numbers of CRs 1982 (October 2001, solar maximum), 1926 (August 1997, similar to CR 2093), 2093 (February 2010) 1912 (July 1996, solar minimum), and 2087 (August 2009, lowest values in solar minimum 2009)0. Only pixels with magnetic field strengths above the noise threshold at B/μ = 50 G (marked with vertical line) are considered to obtain filling factors. a) B/μ: 0−100 G, b) B/μ: 0–1000 G. |
| In the text | |
 |
Fig. 4 Comparison of our TSI reconstruction based on Carrington rotation SOHO-MDI magnetograms and photograms with the observation (VIRGO TSI). The thin red lines show the upper and lower limits of our reconstruction considering the estimated uncertainties of the filling factors for sunspots and faculae. The data gap around 1998/1999 is due to SOHO “vacations”. a) Absolute values normalized to observation in 1996 marked with horizontal black dashed line. b) Difference between observation and the model. A zoom-in of the period 2004−2010 is plotted in Fig. 5. The differences between observation and the reconstructions of Krivova et al. (2003) (based on SOHO-MDI full-disk magnetograms and photograms) and Fröhlich (2009b) (based on MgII and photospheric sunspot indices) are also displayed. |
| In the text | |
 |
Fig. 5 a) Zoom-in of Fig. 4b. b) Zoom-in of faculae filling factors (FF) of Fig. 2c. The horizontal bar at 2000 ppm marks the average level of faculae filling factors in the solar minimum of 1996. |
| In the text | |
 |
Fig. 6 Our TSI reconstruction versus the observation (VIRGO TSI). The colors indicate the date. Black dashed is the 1:1 line. Our model represents the observed TSI before 2005, including the solar minimum in 1996, the solar maximum in 2002, and the decrease due to the large sunspot region in November 2003. The modeled values for the solar minimum in 2009 and for 2010 are higher than the observation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


