| Issue |
A&A
Volume 522, November 2010
|
|
|---|---|---|
| Article Number | A5 | |
| Number of page(s) | 6 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201014113 | |
| Published online | 26 October 2010 | |
A kinematic study of the compact jet in quasar B3 1633+382
1
Key Laboratory for Research in Galaxies and Cosmology, Shanghai
Astronomical Observatory, Chinese Academy of Sciences, 80 Nandan Road, Shanghai
200030, PR
China
e-mail: yliu@shao.ac.cn
2
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
Received:
21
January
2010
Accepted:
2
June
2010
We present a study of the motion of compact jet components in quasar B3 1633+382. Through analyzing 14 epochs of VLBI observations of three components (B1, B2, and B3) at 22 GHz, we find two different possibilities of component classification. Thus two corresponding kinematical models can be adopted to explain the evolutionary track of components. One is a linear motion, while another is a helical model. Future observations are needed to provide new kinematical constraints for the motion of these components in this source.
Key words: galaxies: jets / galaxies: nuclei / quasars: individual: B3 1633+382 / quasars: general / radio continuum: galaxies
© ESO, 2010
1. Introduction
Associated with a redshift of z = 1.814 (Strittmatter et al. 1974), the radio source B3 1633+382 (4C 38.41) was identified as a quasar (Pauliny-Toth et al. 1973) and has been frequently observed at different wavelengths across the electromagnetic spectrum during the past decades. A nearly flat spectrum has been derived from 1.5 to 90 GHz contemporaneous measurements (Landau et al. 1986). Strong variability at both long and short radio wavelengths has also been detected (Spangler & Cotton 1981; Aller et al. 1992; Seielstad et al. 1985; Kühr et al. 1981). This quasar has been classified as an optically violent variable (OVV) (Mattox et al. 1993) because of its strong optical variability. Both infrared and X-ray fluxes have been obtained with the IRAS and the Einstein Observatory respectively (Neugebauer et al. 1986; Ku et al. 1980). As one of the most powerful extragalactic objects detected by the Energetic Gamma Ray Experiment Telescope (EGRET) on the Compton Gamma Ray Observatory (Fichtel et al. 1994; Thompson et al. 1995; Hartman et al. 1999), its γ-ray power is two orders of magnitude higher than the typical value at any longer wavelength (Mattox et al. 1993). This source is also included in the Fermi-LAT 3-month bright AGN list (Abdo et al 2009).
Very Large Array (VLA) observations of B3 1633+382 have shown a triple structure with an overall size of 12'' along the north-south direction. This is a misaligned source, with its VLA jet at almost 90 degrees position angle to the Very Long Baseline Array (VLBA) jet (Murphy et al. 1993; Britzen et al. 2007). A jet in the western direction with a sharp bend to the south at about 50 mas was detected by Polatidis et al. (1995) with 1.7 GHz Very Long Baseline Interferometer (VLBI) observations. Superluminal proper motion μ = 0.16 ± 0.03 masyr-1 (4.4 ± 0.8 c) was detected on the basis of three epochs of VLBI observations at 5 GHz (Barthel et al. 1995). It has also been observed with the VLBA at dual-frequency (Fey & Charlot 1997). The VLBI space observatory programme (VSOP) mission, using the HALCA satellite along with a global array of earth-based telescopes, has detected a faint core with sub-milliarcsec resolution (Lister et al. 2001; Scott et al. 2004). Jorstad et al. (2001) presented results of their multi-frequency monitoring program with the VLBA during six epochs between 1994 and 1996. A prominent jet at a position angle (PA) ~−87°, extending out to 1.5 mas with three components, has been detected at 22 GHz. The authors found that the proper motions of components B1 and B3 are 0.20 and 0.14 masyr-1 (5.5 c and 3.9 c), respectively. Component B2 was shown to be quasi-stationary at a distance of ~0.5 mas from the core.
 |
Fig. 1 Model-fitted image of the quasar B3 1633+382 at 22 GHz, observed on 2000 March 1. The restoring beam is 0.737 × 0.319 mas at PA = − 1.6°. The contour levels are ( − 1, 1 ,2, 4, 8, 16, 32, 64, 128, 256) × 2.93 mJy beam-1. The peak brightness is 0.992 Jy beam-1. |
In our 22 GHz VLBA observation preformed on 2000 March 1 (see Fig. 1), there are four jet components (in this work, we name them components B1, B2, and B3 following Jorstad et al. 2001) loacted in a western direction with 0.51, 1.33 and 2.15 mas separation from the core respectively. Component B4 is the newest one at 0.15 mas from the core. This result is consistent with another VLBA observation at 43 GHz in 1999 (Lister & Smith 2000). However, after combining their proper motion with Jorstad et al. (2001) and ours (see Fig. 2a), we find it hard to distinguish the evolutionary track of the two internal components owing to the lack of observations from 1997 to 2000. In order to study the kinematic in quasar B3 1633+382, more observation epochs are needed. Thus we additionally collected and analyzed seven more VLBA epochs at the same 22 GHz frequency from the National Radio Astronomy Observatory (NRAO) archive data (see Table 1). Combined with these seven archive observed data, one observation of our own, and six other observations obtained from literature, we have 14 epochs of VLBA observations at 22 GHz for this source.
Gaussian models of VLBI observation.
 |
Fig. 2 Core separation as a function of time for the individual jet component. The data combined are from the Jorstad et al. (2001) (open symbols), archive data, and our observation (solid symbols). Stars show the components from the VSOP observations by Lister et al. (2001). The first panel plots the proper motion with Jorstad et al. (2001) and our own observation (purple pentagon). The second shows a simple linear proper motion to fit the evolution track of components of 14 epochs. The last one displays a simple helical fit to the evolution track of components depending on a different classification of the components. |
We study the kinematics of the compact jet in quasar B3 1633+382. The paper is organized as follows. In Sect. 2 the data reduction is described. The motions of components are detailed in Sect. 3, followed by our conclusions in Sect. 4. We adopt the spectral index convention fν ∝ ν−α and a cosmology with H0 = 70 km s-1 Mpc-1, ΩM = 0.3, ΩΛ = 0.7.
2. Data reduction
Our 22 GHz VLBA observation of B3 1633+382 was performed on 2000 March 1. The signals were recorded in four intermediate frequency (IF) bands for a total bandwidth of 32 MHz with 2 bit sampling. The recorded data were first correlated at the VLBA correlator in Socorro (New Mexico) and then calibrated and fringe-fitted using the NRAO astronomical image processing system (AIPS) software. Initial amplitude calibration was done using system temperature measurements and the NRAO-supplied gain curves. The data were corrected for 2 bit sampling errors and atmospheric opacity. The imaging and self-calibration were carried out in the DIFMAP package (Shepherd et al. 1994). Of the seven epochs from the NRAO archived data, four were observed at 8, 15, 22 and 43 GHz, one at both 22 and 43 GHz, and two at 22 GHz only. All archive data were processed with the steps described above. However, we encountered a problem with the correction for atmospheric opacity for the data of 1998 January 2. We used the simultaneously observed 15 GHz data instead to replace the 22 GHz data in our study, which might introduce a less than 0.1 mas position shift.
After obtaining images in DIFMAP, we performed the model fitting to the self-calibrated visibility data using circular Gaussian components. For all model fits we assumed the brightest component to be stationary and used it as a reference point. The other components were measured relative to it. Uniform weighting of the uυ data was used to ensure the highest resolution. Figure 1 shows the naturally weighted image of our observation with the model-fitted circular Gaussian components. During the model-fitting procedure of components, we found that inner component B3 (see Fig. 1) was consistently detected in all seven archive data and our own observation (see Table 1). At the same time, component B3 had about half as much flux density as core when it was ejected from the core. Because this was similar to a situation of the innermost component B4, it was continuously detected in at last two observations. Component B4 also displays a flux density comparable to that of the bright core when it is ejected from the core. That means we could consider those components B3 and B4 as real and rule out the possibility that they are just noise on the fringes of the strong core component. Table 1 is a summary of the model-fitting parameters. We used data from the VSOP observations by Lister et al. (2001) for our component identification. A maximum uncertainty of 15% in the flux density was calculated from the uncertainties of the amplitude calibration and from the formal errors of the model fitting. Fomalont (1989) presented a method to estimate the position error as 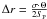 , where σ is the residual noise of the image after the subtraction of the model, Θ is the full width at half maximum (FWHM) of the component, and SP is the peak flux density. However, this formula might underestimate the actual position error if the peak flux density SP is very high or the width Θ of component is small. Therefore we derived our position error from the formula
, where σ is the residual noise of the image after the subtraction of the model, Θ is the full width at half maximum (FWHM) of the component, and SP is the peak flux density. However, this formula might underestimate the actual position error if the peak flux density SP is very high or the width Θ of component is small. Therefore we derived our position error from the formula 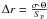 . Figure 2 presents the core separation (the radial distance from the core) as a function of time for the individual model components (open symbols denote the data at 22 GHz from published literature, solid symbols show our model-fitting results in Table 1; stars display components from the VSOP survey by Lister et al. 2001, which is used for our component identification), where circle, triangle, and square symbols denote the B1, B2, and B3 components, respectively.
. Figure 2 presents the core separation (the radial distance from the core) as a function of time for the individual model components (open symbols denote the data at 22 GHz from published literature, solid symbols show our model-fitting results in Table 1; stars display components from the VSOP survey by Lister et al. 2001, which is used for our component identification), where circle, triangle, and square symbols denote the B1, B2, and B3 components, respectively.
3. Kinematic motion of the jet
After combining all 14 epochs VLBA observations, we found there are two different possibilities to classify the components. The first one is related to a simple linear proper motion (see Fig. 2b). The linear proper motion of component B1 is found to be 0.21 mas yr-1, consistent with Jorstad et al. (2001). It is also roughly consistent with the result of Kellermann et al. (2004), who found a smaller proper motion of 0.15 mas yr-1 (4.1 c) from a simple linear fit. As for component B3, we found a linear proper motion of 0.32 mas yr-1, which is about 50% higher than that of component B1. Then we found that is always one blob ~0.5 mas away from the core at different epochs. If those blobs were responding to the same component, it would mean that component B2 is quasi-stationary at distances of ~0.5 mas away from the core, at least during the observation interval. However, we note that there is an abrupt transition from the year of 1996 September to 1997 June for both components B2 and B3. Component B2 experiences a sudden rapid fallback to the core at an apparent velocity of 0.39 mas yr-1 between these six months, while B2 is modeled to be in a quasi-stationary motion. Meanwhile, component B3 undergoes a fast acceleration with 0.78 mas yr-1 during the same time interval. This proper motion is much higher than that fitted from all observed data points of component B3. However, we note that because of the rarity of observations, the apparent acceleration when component B3 passes through or gets ahead of component B2, could also be a result of the observations’ accuracy. More observations are needed in the future.
Parameters of the helical model.
Although a linear fit can explain the motion of components, there is another possibility, depending on the different classification of the components (see Fig. 2c). In this case, component B2 seems to remain almost stationary at a core separation of ~0.5 mas during the period 1994 − 1997. Subsequently component B2 accelerates to 0.20 mas yr-1 (5.5 c), a velocity comparable to that of component B1. This kind of accelerated motion has sometime been interpreted as a change of the angle between the jet direction and the line of sight (Hough et al. 1996; Vicente et al. 1996; Homan et al. 2001; Wang et al. 2001). Meanwhile, component B3 moves with a similar apparent velocity to component B1 before reaching a core separation of ~0.5 mas. When component B3 is ~0.5 mas away from the core, its speed is significantly low. Thus, it is likely that the two inner jet components (B2 and B3) show a similar proper motion mode; both appear stationary at a core-separation of ~0.5 mas, but when they leave the region of ~0.5 mas from the core, they both display velocities on the order of 0.2 mas yr-1 (5.5 c). Then the linear motion is not enough to explain both the core separation evolution and the overall path of the components. Therefore we adopt a simple helical model presented by Steffen et al. (1995) to fit the evolution track of the components.
In the helical model, the jet can be described by four physical parameters, the jet’s kinematic energy Ekin, the opening half-angle ψ of helix (hereafter called opening angle), the angular momentum Lz, and the momentum along the jet axis Pz. Keeping three of these four physical parameters constant, four possible cases were studied. We found only one case (where Ekin, Lz, and ψ are conserved) that was physically plausible for our kinematic study of B3 1633+382. To fully determine the curved trajectory with the helical model, 10 free parameters are required (for an illustration see Fig. 1. in Steffen et al. 1995). These are: three parameters corresponding to the orientation of the coordinates (the viewing angle between the jet axis and the observer’s line of sight θ; the phase angle of the helix φ0; the position angle of the jet axis in the sky plane χ), two parameters describing the initial point of the jet ejection (the ejecting time tej and the distance from the jet axis r0), two parameters accounting for the offset of the observed VLBI-core from the ejection of the helix in right ascension ( △ α) and declination ( △ δ), and three parameters of conservation (the initial value for the Lorentz factor γ of a component, the angular velocity ω0, and the opening angle ψ). The best parameters derived from this simple helical fit are listed in Table 2.
There are several constraints derived by using the same methods as Steffen et al. (1995): the Lorentz factor (γ ≳ 10), the opening angle (ψ ≲ 5°), the initial radius (r0 ≲ 0.1 mas), the time of appearance for component B3 (tejt1995.2), and the offset 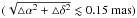 . We plot the result of model fits to the observed trajectory for each component in the left panels of Fig. 3. Points with error-bars are observed data, whereas the solid lines are from model calculation.
. We plot the result of model fits to the observed trajectory for each component in the left panels of Fig. 3. Points with error-bars are observed data, whereas the solid lines are from model calculation.
 |
Fig. 3 Results of helical model fit to the observed trajectory and the comparisons of model-calculated apparent velocities |
The apparent velocity βapp is related to the proper motion μ by 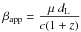 (1)(Pearson & Zensus 1987), where dL is the luminosity distance, c is the speed of light, and z is the redshift. Proper motion calculated from two neighboring data points are assigned to be measured at the middle of these two observations. With parameters γ and θ derived from the helical model fitting for each jet component, we can calculate the predicted apparent velocity
(1)(Pearson & Zensus 1987), where dL is the luminosity distance, c is the speed of light, and z is the redshift. Proper motion calculated from two neighboring data points are assigned to be measured at the middle of these two observations. With parameters γ and θ derived from the helical model fitting for each jet component, we can calculate the predicted apparent velocity 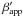 using
using 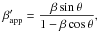 (2)where
(2)where 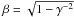 is the velocity of the bulk motion.
is the velocity of the bulk motion. 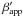 can be compared to the observed βapp, in order to evaluate the correctness of this fit. In the right panels of Fig. 3 we show a comparison of the apparent velocity
can be compared to the observed βapp, in order to evaluate the correctness of this fit. In the right panels of Fig. 3 we show a comparison of the apparent velocity 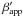 , calculated with the helical model, and the apparent velocity βapp estimated from observations. Points with error-bars and solid lines are corresponding to the observed data and helical model calculation, respectively.
, calculated with the helical model, and the apparent velocity βapp estimated from observations. Points with error-bars and solid lines are corresponding to the observed data and helical model calculation, respectively.
The model parameters of the helical fitting (e.g., γ, ω, φ) listed in Table 2 are consistent for the three components. Moreover, the single dish radio flux monitoring of this source at 22 GHz, reported by Teraesranta et al. (1998, 2004), lasting nearly twenty years from 1981 to 2000, shows three prominent peaks at about 1986.7, 1991.4 and 1995.3 in its light curve (Britzen et al. 1999; Turler et al. 1999). They can be considered as the ejection time tej for each corresponding component, assuming that each new component appearance is accompanied by an outburst in the total intensity. The ejection times derived by the helical model for these three components are 1986.6, 1990.1, and 1994.1. If component B1 moves along a linear path, the tej derived from proper motion extrapolation would be around 1989.7, three years later than the flaring time 1986.7. Compared with the extrapolated ejection times from a linear fit, it seems that the ejection times derived from the helical model are more consistent.
After combining the 14 epoch observations of this source, we find the kinematical motions of B3 1633+382 can be reasonably explained with both a simple linear and helical mode. In the linear kinematical motion, the component B2 moves at significantly slower apparent velocity than the other two components in this compact jet. These low-pattern velocity or even stationary features have sometimes been explained as standing recollimation shocks in an initially over-pressurized outflow, which have been reproduced in numerical simulations of AGN jets (e.g., Gómez et al. 1995; Perucho & Martí 2007; Lister et al. 2009). Alternatively, it is possible that the quasi-stationary motion of the component is due to an extremely small viewing angle of the specific geometry (Alberdi et al. 2000). We roughly estimate a Doppler factor of approximately several tens by using both the average flux density and the average size of the core. Taking the apparent velocities into account, this implies that the jet is aligned at ~1° to our line of sight, and the Lorentz factor corresponding to the pattern velocity is Γ ∼ 18. Although it is an approximate estimation, the direction of the jet from our line of sight and the Lorentz factor fitted from linear model are consistent with the parameters from the helical model calculation. As for the helical fitting, on the other hand, it has been applied for fitting both the projected trajectory and the apparent velocity of components in the compact jet of quasar B3 1633+382. The model-calculated projected trajectories also well fit the significantly low apparent velocity for components B2 and B3 around a core-separation of ~0.5 mas. Helical motions combined with indications of a time-dependent ejection angle can be explained in the context of a binary core. Binary black hole (BBH) models have been employed to explain similar component motions in other sources (e.g., 1803+784, Britzen et al. 2010; Roland et al. 2008; 3C 345, Lobanov & Roland 2005). The component B3 1633+382 has been shown to exhibit periodicities in the radio (Fan et al. 2007) and in the optical (Bozyan et al. 1990) lightcurves, while also being variable in the γ-rays (Fan et al. 2002). Quasi-periodic variability across the spectrum is a further argument in favor of a BBH in the nucleus of this object (Karouzos et al. 2010; e.g., OJ 287, Sillanpaa et al. 1988; Lehto & Valtonen 1996; 3C 454.3, Qian et al. 2007). Helicity and precession of the jet can be explained in terms of Kelvin-Helmholtz instabilities (e.g., Camenzind & Krochenberger 1992; Perucho et al. 2006), precession of the accretion disk (e.g., Caproni et al. 2006), or magnetic torques (Lai 2003). Although the stationary proper motion of components in B3 1633+382 can also be explained with both linear and helical model in this study, the long-term VLBA study has indicated that the standing components may be in temporarily quiescent states (Lister et al. 2009). Future observations will provide new kinematical constraints.
4. Conclusions
The quasar B3 1633+382 shows two different kinds of proper motion for its components. We note that it could be explained as two kinds of kinematical models when we use different classifications for the components. In the first case, if component B1 and B3 move outwards with a linear speed, then component B2 stays at a quasi-stationary state ~0.5 mas from the core for the whole observation interval. Component B1 has a proper motion of 0.21 mas yr-1, which is roughly similar to previous observations. In the meantime, component B3 also experienes a linear expansion with an apparent velocity of 0.32 mas yr-1. Although this model can explain the motion of the components, there is another possibility. In the second case, component B2 was accelerated after remaining almost stationary at a core-separation of about 0.5 mas for several years, while component B3 decelerates to a significantly low velocity at the same core separation of about 0.5 mas. Then we applied a helical model under the assumption of three conservative quantities (the jet’s kinematic energy, angular momentum, and the momentum along the jet axis; Steffen et al. 1995) to interpret the kinematics of the components. The solutions for each component can be used to explain the projected trajectories and the apparent velocity with time as well as to demonstrate in particular the low apparent velocity of the two components B2 and B3. Based on the predictions from the helical model, the components may have the same mode of motion. Future observations are needed to provide new kinematical constraints for the motion of these three components in this source.
Acknowledgments
We thank the anonymous referee for insightful comments and constructive suggestions. We are grateful to Thomas Krichbaum and Richard Porcas for helpful discussions and proofreading that improved the presentation of this work. Research Supported by the CAS/SAFEA International Partnership Program for Creative Research Teams. This work is supported by NSFC under grants 10803015, 10625314, 10633010, 10821302, 10978009 and supported by the Ministry of Science and Technology of China (Grant No. 2009CB824900). Yi Liu also thanks the support from the Knowledge Innovation Program of Chinese Academy of Sciences. M. Karouzos was supported for this research through a stipend from the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics. The VLBA is operated by the National Radio Astronomy Observatory which is managed by Associated Universities, Inc., under cooperative agreement with the National Science Foundation. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. This paper has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 700, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Alberdi, A., Gómez, J. L., Marcaide, J. M., Marscher, A. P., & Pérez-Torres, M. A. 2000, A&A, 361, 529 [NASA ADS] [Google Scholar]
- Aller, M. F., Aller, H. D., & Hughes, P. A. 1992, ApJ, 399, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Barthel, P. D., Conway, J. E., Myers, S. T., Pearson, T. J., & Readhead, A. C. S. 1995, ApJ, 444, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Bozyan, E. P., Hemenway, P. D., & Argue, A. N. 1990, AJ, 99, 1421 [NASA ADS] [CrossRef] [Google Scholar]
- Britzen, S., Witzel, A., Krichbaum, T. P., Qian, S. J., & Campbell, R. M. 1999, A&A, 341, 418 [NASA ADS] [Google Scholar]
- Britzen, S., Brinkmann, W., Campbell, R. M., et al. 2007, A&A, 476, 759 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Britzen, S., Kudryavtseva, N. A., Witzel, A., et al. 2010, A&A, 511, 57 [Google Scholar]
- Camenzing, M., & Krockenberger, M. 1992, A&A, 255, 59 [NASA ADS] [Google Scholar]
- Caproni, A., Livio, M., Abraham, Z., & Mosquera Cuesta, H. J. 2006, ApJ, 653, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, J. H., Cheng, K. S., & Zhang, L. 2002, PASJ, 54, 533 [NASA ADS] [Google Scholar]
- Fan, J. H., Liu, Y., Yuan, Y. H., et al. 2007, A&A, 462, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fey, A. L., & Charlot, P. 1997, ApJS, 111, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Fichtel, C. E., Bertsch, D. L., Chiang, J., et al. 1994, ApJS, 94, 551 [Google Scholar]
- Fomalont, E. B. 1989, in Synthesis Imaging in Radio Astronomy, ed. R. A. Perley, F. R. Schwab, & A. H. Bridle (San Francisco, CA: ASP), ASP Conf. Ser., 6, 213 [Google Scholar]
- Gómez, J. L., Martí, J. M. A., Marscher, A. P., Ibáñez, J. M. A., & Marcaide, J. M. 1995, ApJ, 449, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, R. C., Bertsch, D. L., Bloom, S. D., et al. 1999, ApJS, 123, 9 [Google Scholar]
- Homan, D. C., Ojha, R., Wardle, J. F. C., et al. 2001, ApJ, 549, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Hough, D. H., Zensus, J. A., & Porcas, R. W. 1996, ApJ, 464, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Mattox, J. R., et al. 2001, ApJS, 134, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Karouzos, M., Britzen, S., Eckart, A., & Zensus, J. A. 2010, A&A, 519, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kellermann, K. I., Lister, M. L., Homan, D. C., et al. 2004, ApJ, 609, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Ku, W. H. M., Helfand, D. J., & Lucy, L. B. 1980, Nature, 288, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhr, H., Witzel, A., Pauliny-Toth, I. I. K., & Nauber, U. 1981, A&AS, 45, 367 [NASA ADS] [Google Scholar]
- Lai, D. 2003, ApJ, 591, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Landau, R., Golisch, B., Jones, T. J., et al. 1986, ApJ, 308, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Lehto, H. J., & Valtonen, M. J. 1996, ApJ, 460, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., & Smith, P. S. 2000, ApJ, 541, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Tingay, S. J., Murphy, D. W., et al. 2001, ApJ, 554, L948 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Cohen, M. H., Homan, D. C., et al. 2009, AJ, 138, 1874L [NASA ADS] [CrossRef] [Google Scholar]
- Lobanov, A. P., & Roland, J. 2005, A&A, 431, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1993, ApJ, 410, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, D. W., Browne, I. W. A., & Perley, R. A. 1993, MNRAS, 264, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Neugebauer, G., Miley, G. K., Soifer, B. T., & Clegg, P. E. 1986, ApJ, 308, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Pauliny-Toth, I. I. K., Preuss, E., Witzel, A., et al. 1973, A&A, 27, 475 [NASA ADS] [Google Scholar]
- Pearson, T. J., & Zensus, J. A. 1987, in Superluminal Radio Sources, ed. J. A. Zensus, & T. J. Pearson (San Francisco, CA: ASP), 1 [Google Scholar]
- Perucho, M., & Martí, J. M. 2007, MNRAS, 382, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Perucho, M., Lobanov, A. P., Martí, J. M., & Hardee, P. E. 2006, A&A, 456, 493 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polatidis, A. G., Wilkinson, P. N., Xu, W., et al. 1995, ApJS, 98, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, S. J., Kudryavtseva, N. A., Britzen, S., et al. 2007, ChJAA, 7, 364 [Google Scholar]
- Roland, J., Britzen, S., Kudryavtseva, N. A., Witzel, A., & Karouzos, M. 2008, A&A, 483, 125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scott, W. K., Fomalont, E. B., Horiuchi, S., et al. 2004, ApJS, 155, 33 [Google Scholar]
- Seielstad, G. A., Pearson, T. J., & Readhead, A. C. S. 1985, PASP, 95, 842 [Google Scholar]
- Shepherd, M. C., Pearson, T. J., & Taylor, G. B. 1994, BAAS, 26, 987 [NASA ADS] [Google Scholar]
- Sillanpaa, A., Haarala, S., Valtonen, M. J., Sundelius, B., & Byrd, G. G. 1988, ApJ, 325, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Spangler, S. R., & Cotton, W. D. 1981, AJ, 86, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, W., Zensus, J. A., Krichbaum, T. P., Witzel, A., & Qian, S. J. 1995, A&A, 302, 335 [Google Scholar]
- Strittmatter, P. A., Carswell, R. F., Gilbert, G., & Burbidge, E. M. 1974, ApJ, 190, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Teraesranta, H., Tornikoski, M., Mujunen, A., et al. 1998, A&AS, 132, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teraesranta, H., Achren, J., Hanski, M., et al. 2004, A&A, 427, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thompson, D. J., Bertsch, D. L., Dingus, B. L., et al. 1995, ApJS, 101, 259 [Google Scholar]
- Turler, M., Courvoisier, T. J.-L., & Paltani, S. 1999, A&A, 349, 45 [NASA ADS] [Google Scholar]
- Vicente, L., Charlot, P., & Sol, H. 1996, A&A, 312, 727 [NASA ADS] [Google Scholar]
- Wang, W. H., Hong, X. Y., Jiang, D. R., et al. 2001, A&A, 380, 123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Model-fitted image of the quasar B3 1633+382 at 22 GHz, observed on 2000 March 1. The restoring beam is 0.737 × 0.319 mas at PA = − 1.6°. The contour levels are ( − 1, 1 ,2, 4, 8, 16, 32, 64, 128, 256) × 2.93 mJy beam-1. The peak brightness is 0.992 Jy beam-1. |
| In the text | |
 |
Fig. 2 Core separation as a function of time for the individual jet component. The data combined are from the Jorstad et al. (2001) (open symbols), archive data, and our observation (solid symbols). Stars show the components from the VSOP observations by Lister et al. (2001). The first panel plots the proper motion with Jorstad et al. (2001) and our own observation (purple pentagon). The second shows a simple linear proper motion to fit the evolution track of components of 14 epochs. The last one displays a simple helical fit to the evolution track of components depending on a different classification of the components. |
| In the text | |
 |
Fig. 3 Results of helical model fit to the observed trajectory and the comparisons of model-calculated apparent velocities |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


