EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 511 (February 2010) A&A, 511 (2010) A74 Full HTML
Free Access
Issue
A&A
Volume 511, February 2010
Article Number A74
Number of page(s) 14
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/200912898
Published online 12 March 2010
A&A 511, A74 (2010)

Strong near-infrared emission in the sub-AU disk of the Herbig Ae star HD 163296: evidence of refractory dust?[*]

M. Benisty 1,2 - A. Natta1 - A. Isella3 - J-P. Berger2 - F. Massi1 - J-B. Le Bouquin4 - A. Mérand4 - G. Duvert2 - S. Kraus5 - F. Malbet2,3 - J. Olofsson2 - S. Robbe-Dubois6 - L. Testi7 - M. Vannier6 - G. Weigelt5

1 - INAF-Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
2 - Laboratoire d'Astrophysique de Grenoble, CNRS-UJF UMR 5571, 414 rue de la piscine, 38400 St Martin d'Hères, France
3 - Caltech, MC 249-17, 1200 East California Blvd, Pasadena, CA 91125, USA
4 - European Southern Observatory, Casilla 19001, Santiago 19, Chile
5 - Max Planck Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
6 - Laboratoire A. H. Fizeau, UMR 6525, Université de Nice-Sophia Antipolis, Parc Valrose, 06108 Nice Cedex 02, France
7 - European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching, Germany

Received 15 July 2009 / Accepted 3 November 2009

Abstract
We present new long-baseline spectro-interferometric observations of the Herbig Ae star HD 163296 (MWC 275) obtained in the H and K bands with the AMBER instrument at the VLTI. The observations cover a range of spatial resolutions between $\sim $3 and $\sim $12 milliarcseconds, with a spectral resolution of $\sim $30. With a total of 1481 visibilities and 432 closure phases, they represent the most comprehensive (u,v) coverage achieved so far for a young star. The circumstellar material is resolved at the sub-AU spatial scale and closure phase measurements indicate a small but significant deviation from point-symmetry. We discuss the results assuming that the near-infrared excess in HD 163296 is dominated by the emission of a circumstellar disk. A successful fit to the spectral energy distribution, near-infrared visibilities and closure phases is found with a model in which a dominant contribution to the H and K band emission originates in an optically thin, smooth and point-symmetric region extending from about 0.1 to 0.45 AU. At a distance of 0.45 AU from the star, silicates condense, the disk becomes optically thick and develops a puffed-up rim, whose skewed emission can account for the non-zero closure phases. We discuss the source of the inner disk emission and tentatively exclude dense molecular gas as well as optically thin atomic or ionized gas as its possible origin. We propose instead that the smooth inner emission is produced by very refractory grains in a partially cleared region, extending to at least $\sim $0.5 AU. If so, we may be observing the disk of HD 163296 just before it reaches the transition disk phase. However, we note that the nature of the refractory grains or, in fact, even the possibility of any grain surviving at the very high temperatures we require ($\sim $ 2100-2300 K at 0.1 AU from the star) is unclear and should be investigated further.

Key words: protoplanetary disks - methods: observational - techniques: interferometric - stars: pre-main sequence

1 Introduction

Herbig AeBe stars (HAeBe) are intermediate-mass young stars, surrounded by large amounts of dust and gas. The distribution of this circumstellar material remains actively debated. Various types of models can reproduce the spectral energy distribution (SED) by considering material in geometrically thin accretion disks (Hillenbrand et al. 1992), in a spherical envelope (Miroshnichenko et al. 1997), a puffed-up inner disk rim (Isella & Natta 2005; Dullemond et al. 2001) or a disk plus a halo (Vinkovic et al. 2006). Fitting the SED alone is therefore highly ambiguous.

Near-infrared (NIR) long baseline interferometry has allowed us to directly probe the properties of matter within the innermost astronomical unit (AU), where key quantities for the star-disk-protoplanets interactions are set. The first interferometric studies of HAeBe showed that the NIR characteristic sizes were larger than expected by classical accretion disk models (Millan-Gabet et al. 2001), and were found to be correlated with the stellar luminosity (Monnier & Millan-Gabet 2002). This supports the idea that the NIR emission is dominated by the thermal emission of hot dust heated by stellar radiation. Natta et al. (2001) suggested that an inner, optically thin cavity produced by dust sublimation exists inside the disk. At the edge of this region, where dust condensates, the disk is expected to puff up because of the direct illumination from the star (Isella & Natta 2005; Dullemond et al. 2001), explaining the size-luminosity law derived for Herbig Ae (and late Be) stars by Monnier & Millan-Gabet (2002). Based on a small number of interferometric observations, simple geometrical models were proposed to explain the global morphology of these regions (Millan-Gabet et al. 2001; Monnier et al. 2005; Eisner et al. 2004; Monnier et al. 2006). However, when larger sets of data became available, it became clear that the regions probed by NIR interferometry are much more complex and that a deeper understanding requires the combination of photometric and multi wavelength interferometric measurements at the milli-arcsecond resolution and more sophisticated models.

In this study, we present an analysis of the inner disk surrounding the HAe star HD 163296 (MWC275). This isolated Herbig Ae star is described well by a spectral type of A1, a $\sim $30 $L_\odot$luminosity, and a $\sim $2.3 $M_\odot$ mass (Montesinos et al. 2009; van den Ancker et al. 1998; Natta et al. 2004). It is is located at 122 +17-13 pc and exhibits a NIR excess interpreted as the emission from a circumstellar disk (Hillenbrand et al. 1992). A large-scale disk was detected in scattered light (Grady et al. 2000), as well as at millimeter wavelengths (Mannings & Sargent 1997). This inclined disk, traced out to 540 AU, was found to be in Keplerian rotation, and probably evolving towards a debris disk phase (Isella et al. 2007). In addition, it also exhibits an asymmetric outflow on large scales ($\geq$27'') perpendicular to the disk, with a chain of six Herbig-Haro knots (HH409) that traces the history of mass loss (Devine et al. 2000; Wassell et al. 2006). The spectrophotometric observations that probe the intermediate and small spatial scales are also compatible with the presence of a disk. Doucet et al. (2006) studied the warm dust emitting in the mid-infrared, located in the surface layers of the intermediate regions of the disk (30-100 AU) and concluded that the emission was consistent with a disk that has little flaring. This conclusion is consistent with the classification of HD 163296 by Meeus et al. (2001) in their Group II, whose SED can be explained by assuming that the inner part of the disk shields the outer part from stellar radiation. In the innermost regions, the far-UV emission lines have been attributed to optically thin gas accreting onto the stellar surface, a magnetically confined wind, or shocks at the base of the jet (Swartz et al. 2005; Deleuil et al. 2005). Weak X-ray emission ($L_{\rm x}$/ $L_\star \sim 5\times 10^{-6}$) was detected on large scales and attributed to the jet (Günther & Schmitt 2009). In the NIR, the SED time variability was interpreted to be due to changes in the inner disk structure, on timescales similar to the generation of the HH objects (Sitko et al. 2008).

With a disk, signs of accretion, and a bipolar outflow, HD 163296 provides an excellent case study to understand how circumstellar material is distributed on the sub-AU scale. Its NIR disk was resolved by IOTA, PTI, and Keck-Interferometer (Monnier et al. 2005; Millan-Gabet et al. 2001; Eisner et al. 2009), and at milli-arcsecond (mas) resolution with the long CHARA baselines (Tannirkulam et al. 2008) (T08, hereafter). T08 found that their observations could not be reproduced using models where the majority of the K band emission originates in a dust rim, but that an additional NIR emission inside the dust sublimation radius could explain the visibilities and the SED. They interpreted this additional emission as being produced by gas, as suggested for other Herbig AeBe stars (Eisner et al. 2007; Isella et al. 2008; Kraus et al. 2008b). The advent of spectro-interferometry, as provided by the AMBER instrument at VLTI, allows us to simultaneously measure the emission at various NIR wavelengths and consequently, to derive temperature profiles for the emission, bringing additional constraints on its nature. In this paper, we present an observational study of the circumstellar disk around HD 163296 at the sub-AU scale, using the largest interferometric dataset obtained for a young star so far. The paper is organized as follows: in Sect. 2, we describe the spectro-interferometric observations obtained at AMBER/VLTI and the data processing; in Sect. 3, we present the obtained visibilities and closure phases. In Sect. 4, we outline a successful disk model that reproduces all observables and we discuss its physical origin. We summarize our results in Sect. 5.

Table 1:   Log of the interferometric observations.

2 Observations and data reduction

2.1 Observations at VLTI

HD 163296 was observed in the NIR with the AMBER instrument (Petrov et al. 2007), at the Very Large Telescope Interferometer (VLTI; Schöller 2007), located at Cerro Paranal, Chile and operated by the European Southern Observatory (ESO). The AMBER instrument allows the simultaneous combination of three beams in the H and K bands (i.e., from 1.6 to 2.5 $\mu$m) with spatial filtering. The instrument delivers spectrally dispersed interferometric observables (e.g., visibilities, closure phases, differential phases) at spectral resolutions of up to 12 000.

In the following, we present observations taken at the low spectral resolution mode ($R\sim 30$) with the 1.8 m Auxiliary Telescopes (AT) and the 8.2 m Unit Telescopes (UTs). The data were obtained within programs of both guaranteed time and open time observations (081.C-0794; 081.C-0098; 081.C-0124; 081.C-0851). HD 163296 was observed with 14 different baselines of 5 VLTI telescope configurations, during 8 nights from May to July 2008. The longest baseline is $\sim $128 m corresponding to a maximum resolution of 3.5 mas in the K band, and of 2.7 mas in the H band. In this paper, we use the VLTI nomenclature to identify the different configurations. A summary of the observations can be found in Table 1, including the weather conditions, the average baseline position angles ( $B_{\rm {PA}}$), and projected lengths ( $B_{\rm {L}}$). The projected baseline is obtained when the vector between the two telescopes is projected onto the plane of the sky. Because of the Earth rotation, measurements with the same physical baseline but at different hour angles correspond to different projected baselines.

All the observations were performed with three telescopes, except during the night of the 2008 May 26 when only two were available. In addition to HD 163296, three calibrator stars (HD 156897, HD 160915, HD 163955) were observed before and after each measurement on the scientific target to correct for instrumental effects. Their stellar parameters, including their diameters, can be found in Table 2. About 25% of the observations were performed using the VLTI fringe-tracker FINITO that uses 70% of the H band flux to measure the relative optical path difference between the light beams (Le Bouquin et al. 2008).

2.2 Photometry

In addition to this interferometric dataset, we collected photometric data from the literature (Tannirkulam et al. 2008; Sitko et al. 2008).

2.3 Data reduction

The interferometric data reduction was performed following Tatulli et al. (2007), using the amdlib package (release 2.1) and the yorick interface provided by the Jean-Marie Mariotti Center (JMMC). This led to spectrally dispersed raw visibilities and closure phases for all exposures of each observing file. Not all exposures turned out to provide useful data. In several cases, instrumental jitter, insufficient fringe tracking, and unsatisfactory light injection into the instrument led to low contrast interferograms of our rather faint source, and we had to select the good exposures. Various selection thresholds were examined based on the fringe signal-to-noise ratio (SNR) criterion and led to the same absolute values for the interferometric observables. On the other hand, their accuracy changes with varying selections, and the optimal case (i.e., with the smallest errors) was obtained with a 20% and 80% best exposure selections for the squared visibilities and the closure phases, respectively. In addition, data obtained at very high airmass with unstable fringe tracking were removed. No selection based on the optical path difference (i.e., piston) was performed, since the numbers of useful exposures could have been a possible source of bias.

Table 2:   Star and calibrator properties.

\begin{figure} \par\includegraphics[width=7.5cm,clip]{12898fg1.eps} \end{figure} Figure 1:

(u,v) plane coverage of the observations in spatial frequencies. The observing nights are plotted with different symbols and the corresponding telescope configurations are reported in the figure.

Open with DEXTER
For each night, special care was given to the calibration and stability of the AMBER+VLTI instrumental transfer function throughout the whole observing period. Measurements of HD 163296 were encircled with observations of targets of known diameters (see Table 2) and the transfer function was interpolated along all calibrations of the night. The errors in the calibrated spectral visibilities and closure phases include the statistical errors obtained when averaging the individual exposures as well as the errors in the calibration star diameters. To account for the variation in the transfer function with time, we quadratically added the dispersion over the calibrator measurements to the errors. The latter is the effect that dominates the error budget.

With 8 to 14 spectral channels in the K band and 5 to 8 in the H band, the total data set (after processing) consists of 1000 and 304 spectrally dispersed K band visibilities and closure phases, respectively, and 481 and 128 H band visibilities and closure phases, respectively. The processed data will be made available for the community in the OI-FITS format (Pauls et al. 2005) on the OLBIN website[*] in January 2010.

\begin{figure} \par\includegraphics[width=8cm,clip]{12898fg2.eps}\hspace*{4mm} \includegraphics[width=8cm,clip]{12898fg3.eps} \end{figure} Figure 2:

Squared visibilities against spatial frequencies B/$\lambda $ in the K band ( left panel) and the H band ( right panel). Different symbols correspond to different configurations, that are reported in the upper right corner of the left panel.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{12898fg4.eps}\hspace*{4mm} \includegraphics[width=8cm,clip]{12898fg5.eps} \end{figure} Figure 3:

Broad-band squared visibilities against spatial frequencies B/$\lambda $ in the K band ( left panel) and the H band ( right panel). Different symbols and colors correspond to different configurations that are given in Fig. 2. The IOTA points are overplotted in the right panel (empty circles).

Open with DEXTER

3 Results

The set of interferometric data presented in this paper is by far the largest for a single pre-main sequence star. The corresponding (u,v) plane coverage is shown in Fig. 1. In this section, we present a summary of the results and describe the main characteristics of the inner region of HD 163296 as measured by NIR interferometry. For the sake of clarity, we separate the H and K band results in most of the figures below.

3.1 Visibilities

Figure 2 presents the spectral visibilities as a function of the spatial frequency (i.e., the ratio of the projected baseline length to the wavelength of the observation). Figure 3 similarly shows broad-band visibilities, obtained when averaging over all spectral channels, for the K band (left) and the H band (right). One can immediately see from the figures that at these spatial resolutions, the circumstellar matter around HD 163296 is resolved. Within the error bars, the H band visibilities vary with baseline qualitatively in the same way as those of the K band. However, at spatial frequencies higher than 20 m/$\mu$m, the H band V2 are at least 25% higher than those in the K band.

The errors in individual points vary significantly from night to night. However, some of the scatter is not caused by the uncertainties in individual measurements, since different observations were performed with baselines of similar projected baselines (equivalently, at similar spatial frequencies) but different position angles, therefore sampling distinct orientations on the sky. This effect means that the source geometry deviates from a circular one, and can instead present an elongated shape, as expected for an inclined disk.

We note that in the H band, at the shortest spatial frequencies (below 10 m/$\mu$m), the AMBER visibilities do not reach unity. This can be due to flux from an extended halo as suggested by Monnier et al. (2006) from their IOTA H band measurements. All the IOTA points, except one, are consistent with our measurements (see Fig. 3, right). On the other hand, this effect is not clearly seen in the K band, where visibilities are close to unity at short baselines (e.g., $V^{2}=0.94 \pm0.03$ at a 13.8 m baseline).

The observations show that V2 also depends on wavelength (Fig. 2). This can be related to the physical extension of the emitting region at various wavelengths and the existence of temperature gradients within it. Since the interferometer resolution also changes with wavelength, it is natural to visualize this dependence using a geometrical model to convert the measurements in angular sizes while taking this effect into account. With this aim, we fit the V2 in each spectral channel for each measurement, using a ring of uniform brightness (with a 20% thickness). Although the circumstellar material is mainly responsible for the emission in the H and K bands, the star also contributes to the measured fluxes and visibilities. We estimate a contribution from the stellar photosphere of $\sim $33% in H and $\sim $14% in K (see Sect. 4.1 for details). The flux from the circumstellar matter was then computed for each AMBER channel as the difference between the observed NIR flux (T08) and the photospheric flux. Figure 4 gives an example of the wavelength dependence of the size obtained on the three baselines of the A0-D0-H0 configuration, in the two extremes cases (observed maximum and minimum variations with wavelength).

For the majority of the measurements (except those obtained at very small baselines with the E0-G0-H0 configuration), the size of the circumstellar matter slightly increases with wavelength. To quantify the wavelength dependence of the visibility, we studied its variation over only the K band, H band, and over both bands together. Across the K and H band separately, 24% and 31%, respectively, of the measurements show a chromaticity above the 2-$\sigma$ level. Over the entire spectral range, a stronger effect is expected due to the greater wavelength interval, 62% of the data show a chromaticity greater than the 2-$\sigma$ level. This is consistent with the case shown in Fig. 4, where the characteristic size of the emitting region increases between the Hand K bands. This trend is also observed in the spectrally dispersed measurements across the Br$_{\gamma}$ emission line obtained with the Keck-Interferometer (Eisner et al. 2009).

\begin{figure} \par\includegraphics[width=8.5cm,clip]{12898fg6.eps} \end{figure} Figure 4:

Example of wavelength dependence for the squared visibilities obtained on the three baselines during observations with the A0-D0-H0 configuration. In each panel, the characteristic size of the emission is given at each wavelength across the H and K band. These sizes are derived from a ring model of uniform brightness to account for the change of resolution with wavelength. The triangles show the maximum chromaticity over the whole wavelength range, while the circles give the minimum variation. For each measurement, the corresponding projected baseline length and position angle are indicated in the top right corner.

Open with DEXTER

\begin{figure} \par\begin{tabular}{ccc} \includegraphics[width=0.31\textwidth]{1... ...cludegraphics[width=0.30\textwidth]{12898fg11.ps}\\ \end{tabular} \end{figure} Figure 5:

Measured closure phases for each configuration (reported in the top left corners) plotted versus maximum spatial frequency. In all panels, except for U1-U2-U4 for which only K band data were useful, the measurements include both the H and K bands.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7cm,clip]{12898fg12.eps}\hspace*{4mm} \includegraphics[width=7cm,clip]{12898fg13.eps} \end{figure} Figure 6:

Broad-band closure phases plotted against the maximum spatial resolution achieved for all telescope configurations (K band, left; H band, right). The configurations and the corresponding symbols are reported at the bottom of the left panel.

Open with DEXTER

3.2 Closure phases

The closure phase is a quantity that can be derived from interferometric observations with at least 3 telescopes. By combining up the phases of the fringes obtained with 3 telescopes, the atmospheric disturbances are cancelled out. Consequently, the sum of the three phases (the closure phase) is atmosphere-free, i.e., independent of the phase fluctuations. It is related to the degree of asymmetry of the observed brightness distribution: a point-symmetric object will have zero closure phases, while a non-zero measurement is indicative of a deviation from point-symmetry. The sign of the CP is derived from the way that it is calculated (clockwise or counterclockwise). Physically, the CP depends on the directions that are sampled by the individual baselines of the configuration since they probe different asymmetries of the brightness distribution, which in turn strongly depend on the ratio of the star to circumstellar matter flux.

One or more closure phase (CP) measurements were obtained for each observing night, except for the night of 2008 May 26. In total, we obtained 304 CP in the K band, and 128 in the H band. This is an enormous improvement over the existing datasets for a young star. The full set of measured CP across the K and H bands is shown in Fig. 5, plotted against the maximum spatial frequency $B_{\rm {max}}/\lambda$, where $B_{\rm {max}}$ refers to the projected length of the longest baseline in the corresponding configuration.

The CP signal depends on the spatial resolution achieved by the interferometer (unresolved sources are centro-symmetric). Figure 6 show the broad-band CP in K and Hplotted against the maximum spatial resolution $\lambda/{B}_{\rm {max}}$, achieved with the corresponding three-telescope configuration. It can be seen that the level of the CP signal increases with the power of resolution (see, for example, the configurations of aligned telescopes along the same $B_{\rm {PA}}$, E0-G0-H0, and A0-D0-H0). Table 3 gives the corresponding broad-band CP averaged over all the measurements as well as the achieved maximum spatial resolution for each telescope configuration. Since we checked that all the CP were calculated in the same way, the relative signs between measurements obtained with various configurations are relevant and should be reproduced by model fitting.

The CP is close to zero for the short linear array (E0-G0-H0): we do not detect any meaningful deviations from zero (i.e., any flux asymmetries) at these low spatial resolutions (10.8 and 8.5 mas in the K and H band, respectively). Monnier et al. (2006) detected CP signals below $\leq$$5^\circ$ for 12 Herbig AeBe stars with the IOTA-3T interferometer, including HD 163296 for which they derived  $0.6 \pm 0.4^\circ$at a resolution of 11.8 mas. Our observations at similar resolution provide comparable results.

At higher resolutions, we found that the CP signal is not zero, i.e., that the emission is no longer centro-symmetric. However, the departure of the closure phase signals from zero is small, with a maximum average CP in K band of $11.7 \pm 2.9^\circ$ and in H band of $-5.8 \pm 2.5^\circ$ (see Table 3). As we discuss in the following section, this level of asymmetry is not compatible with strongly skewed distributions for the circumstellar material in the innermost regions surrounding the star.

Except in one case (A0-K0-G1), the CP does not vary much with varying hour angle (see Fig. 12). This means that, considering the change in maximum resolution and position angle that occurs when varying the hour angle (i.e., when changing the direction and the projected baseline length $B_{\rm {L}}$), the level of asymmetry does not change much. Consequently, the circumstellar matter must have a rather smooth azimuthal brightness distribution.

The H band CP are slightly lower than those measured in the K band, as expected since the emission in H probably originates in a more compact region, as most of our data suggest, than the one emitting the K band flux. However, considering the large error bars, this effect is hardly significant. Over the K band and H band separately, 12% and 15% of the CP, respectively, show a variation above the 1-$\sigma$ level and all measurements are consistent with variations within the 2-$\sigma$ level. Considering the entire range of wavelength (H and K together), 45% of the CP show a variation with wavelength above the 2-$\sigma$ level.

Table 3:   Values of the closure phase as averaged over all the measurements.

4 Modelling the interferometry results

The analysis of visibilities and closure phases requires the assumption of a model for the brightness distribution on the plane of the sky to be compared with the observations. Even when the comparison is successful, it is impossible to know if the solution is unique, and because models are difficult to compute, it is practically impossible to explore all possibilities. Here, we are guided by the current paradigm that the NIR emission in excess of the photospheric one is produced by the inner parts of a circumstellar disk.

4.1 Stellar parameters

To model the interferometry results, one needs to know the unresolved contribution of the star to the total flux at the wavelength of interest. We compute it from the observed magnitude in the I band (i.e., $6.71 \pm 0.026$, with very little variability over a period of about 20 years (Tannirkulam et al. 2008; de Winter et al. 2001), assuming ZAMS colors for a A1 star and an extinction AV=0.25. The resulting stellar fluxes are about 1.4 Jy in K and 2.2 Jy in H. The observed NIR fluxes display a moderate variability (Sitko et al. 2008), so that the stellar contribution may be in the interval 14-18% in K and 33-37% in H, respectively. The effect of variability on the interferometry results and the desirability of performing simultaneous photometry were discussed by Sitko et al. (2008). This, unfortunately, is practically impossible with AMBER/VLTI, and we do not know the values of the total flux at the time of the observations. In this paper, we adopt a stellar contribution of $\sim $14% and $\sim $33% to the observed K and H band fluxes, respectively, i.e., on the lower side of the estimates. These numbers are in agreement with the CHARA and AMBER measurements at long baselines, where all the circumstellar matter appears to be resolved, and are similar to the values adopted by Tannirkulam et al. (2008). The HD 163296 SED is shown in Figs. 8 and 9.

\begin{figure} \par\includegraphics[width=7.8cm,clip]{12898fg14.eps}\hspace*{4mm} \includegraphics[width=7.8cm,clip]{12898fg15.eps}\ \end{figure} Figure 7:

Model visibilities when considering a rim alone, located at 0.23, 0.36, and 0.45 AU (dashed red, dotted blue, and full black lines respectively), versus effective spatial frequency $B_{\rm {eff}}/\lambda $, compared to the measured broad-band visibilities (blue full squares) in the K band ( left) and the H band ( right). The predictions of the model described in T08, which includes an additional inner component interpreted as gas, is given in red (T08; dash-dot-dot). The K band measurements obtained at CHARA and Keck-I are overplotted (circles and triangles respectively) in the left panel, as well as the IOTA Hband data (triangles) in the right panel. An incoherent flux contributing to $\sim $8% of the total H and K band fluxes is considered.

Open with DEXTER

4.2 Incoherent flux

In our models, we consider incoherent flux possibly emitted by an extended halo, as first suggested by Monnier et al. (2006). They estimated its contribution to be 5% of the total H band fluxes (i.e., 10% in V2), a value that T08 also used when modelling their K band data. Our H band data suggest a slightly higher value of $\sim $8% (i.e., $\sim $15% in V2). We adopt this value when fitting both the H and K band interferometric observations. The precise origin of this emission is unknown and discussing it is beyond the scope of this paper.

4.3 Disk position angle and inclination

Values of inclination (i) and position angle (PA) of the HD 163296 disk (i.e., its major axis) have been derived at different wavelengths with a variety of techniques and tend to agree: Wassell et al. (2006) (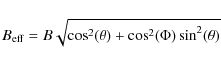 $i=51^\circ$$^{+11^\circ}_{-9^\circ}$; PA = 139 $^\circ\pm15^\circ$), Isella et al. (2007) ( $i=46^\circ\pm4^\circ$; PA = 128 $^\circ\pm4^\circ$) and T08 ( $i=48^\circ\pm2^\circ$; PA = 136 $^\circ\pm2^\circ$). They are also consistent with our visibility data, which infer an inclination of $40^\circ \pm 10^\circ$ and a position angle of $140^\circ \pm 15^\circ$, when fitted with geometrical models of uniform brightness ring. Since we do not constrain these parameters better, in the following, we adopt the values derived by T08, i.e., $i=48^\circ$ and PA = 136$^\circ$. In the following sections, we use the effective baseline, which is defined by:

\begin{displaymath}B_{\rm {eff}}= B\sqrt{\cos^{2}(\theta) + \cos^{2}(\Phi)\sin^{2}(\theta)}\end{displaymath}

where $\theta$ is the angle between the baseline direction and the major axis of the disk, and $\Phi$ is the disk inclination (T08). This representation allows us to show the data in a concise way once the inclination and position angle of the disk are known.

4.4 A disk rim

Early NIR interferometric studies of Herbig Ae stars have shown that standard accretion disks, extending up to the dust sublimation radius do not fit the observations (Millan-Gabet et al. 2007) and that superior fits are obtained by assuming that the disk develops a curved rim, probably (but not necessarily) controlled by dust sublimation and its dependence on gas density (Isella & Natta 2005; Tannirkulam et al. 2007). Not only the disk rim hypothesis is supported by physical calculations (Isella & Natta 2005; Dullemond et al. 2001): the overall properties of HD 163296 are also consistent with this model. The SED appears to be consistent with a rim emission up to 7-8 $\mu$m and a disk in the shade at longer wavelengths (Isella et al. 2007; Dullemond et al. 2001). In addition, our measured visibilities show a dependence on hour angle (or similarly on baseline position angle $B_{\rm {PA}}$) consistent with an elliptical shape, as expected in either a rim or any axisymmetrical distribution seen at high inclination. Finally, the detection of non-zero closure phases supports the idea that an asymmetric brightness distribution - such as the disk inner rim - contributes to the NIR emission.

As in the NIR, the contribution of the disk outside the rim can be neglected (Isella et al. 2007), we begin by examining a star + rim system to model the NIR emission following Isella & Natta (2005). We adopt a stellar luminosity and mass of 30 $L_\odot$ and 2.3 $M_\odot$, respectively, and an effective temperature of 9250 K. The disk is assumed to be in hydrostatic equilibrium. The dust consists of silicates with optical properties given by Weingartner & Draine (2001). The evaporation temperature, of around 1500 K, depends on the local gas density as in Pollack et al. (1994). Since the shape of the rim is controlled by the largest grains, we consider a single size for the silicate dust, which is therefore the only free parameter in the model. The dependence of the evaporation temperature on z implies that the distance from the star at which dust evaporates increases with z, i.e., that the rim is curved.

As can clearly be seen in Fig. 7, our interferometric measurements are inconsistent with a circumstellar emission produced by a rim only, regardless of its location. This figure shows the AMBER broad-band visibilities as a function of the effective spatial frequency $B_{\rm {eff}}/\lambda $. In addition to the AMBER data, we include the K band visibilities obtained at CHARA (circles; Tannirkulam et al. 2008) and at Keck-I (triangles; Monnier et al. 2005) as well as the H band IOTA data (upside down triangles; Monnier et al. 2006). We emphasize that all measurements from these four interferometers are compatible with each other within their error bars. The results for three rim models computed by assuming a 30 $L_\odot$ stellar luminosity and silicate grain sizes of 3, 0.6, or 0.3 $\mu$m, corresponding to inner rim radii at 0.23, 0.36, and 0.45 AU, respectively, are overplotted. These models produce an emission that does not exceed the observed flux at any wavelength, and, contributes respectively, to about 80, 50, and 28% of the observed emission in H, and 91, 86, and 66% in K. All models show large departures from the observations. In addition, all these models have very asymmetric emission, and produce a closure phase signal greater than observed (see Fig. 12, red dashed lines). Our large data sets, which include H and K visibilities and closure phases, reinforce the conclusions of other authors, namely that there should be an additional, symmetric emission closer to the star (T08).

\begin{figure} \par\includegraphics[width=8cm,clip]{12898fg16.eps}\hspace*{4mm} \includegraphics[width=8cm,clip]{12898fg17.eps} \end{figure} Figure 8:

SED of HD 163296 (Tannirkulam et al. 2008; Sitko et al. 2008) with the predictions of gaseous disk models. The flux emitted by the rim located at 0.45 AU (cyan dashed line) as well as the additional inner disk emission (black dotted line) are added in both panels to allow direct comparisons. Left: the predictions for optically thick and dense layers of gas in LTE (Muzerolle et al. 2004) are overplotted (red full line). In this case, the gas is mostly in a molecular state. Right: the continuum emission as predicted by thin disks of gas in non-LTE, heated from the top by the stellar radiation, are shown. The gas extends from 0.1 to 0.45 AU and has constant surface densities of 0.1, 1, and 6 g/cm2 (red line with squares, blue line with triangles and green line with diamonds, respectively). In these conditions, the gas is mostly atomic. The predictions of a fully ionized layer of gas at 8000 K with a constant surface density of 0.06 g/cm2 are also reported (magenta curve with diamonds). As long as the disk remains optically thin, the emission is proportional to the surface density, and this value was chosen only to display its wavelength dependence.

Open with DEXTER

4.5 A bright inner disk

A rim alone cannot reproduce our observations. As a matter of fact, the lack of bounces in the visibilities suggests a continuous and smooth distribution of matter in the inner regions of HD 163296, and a low contribution of the rim to the NIR emission. In the following, we explore the effect of adding emission from an inner disk (inside the rim) to both the star and rim contributions. We fix the rim location to be $R_{\rm {rim}}=0.45$ AU. This large radius is implied by the results of our three-component models, as we show in the following. It can, for example, be obtained by considering small silicate grains (from 0.05 to 0.5 $\mu$m) in a high-density dusty disk, or micron-sized grains in a low-density region, where the evaporation temperature is lower. In both cases, the rim effective temperature is quite low ( $T_{\rm {eff}}\sim1000$ K) and accounts for the total observed flux in the wavelength range 4-8 $\mu$m, but not at shorter wavelengths (see Fig. 8, cyan dashed line). The SED of the proposed additional inner disk can be computed by subtracting both the stellar and disk rim fluxes from the observed ones. As shown in Fig. 8 (dotted line), it peaks in the H band and is higher than the rim emission at all wavelengths shorter than about 2.5 $\mu$m. Therefore, the NIR emission is dominated by the inner disk component rather than the rim.

We obtain a first estimate of the emission properties of the inner disk by modeling it as a region of constant surface brightness between an inner and outer radius. The surface brightness is constrained by the condition that the integrated flux must be equal to the flux derived from the SED for the additional component. We compute visibilities and find that these three-component models reproduce the H and K band observations quite well over the entire range of baselines if the smooth, inner emission extends between $\sim $0.10 and $\sim $0.45 AU. The emission can be roughly described as that of a diluted black-body with temperature $\sim $1600 K and optical depth $\sim $0.2, which decreases as $\lambda^{-1.6}$with increasing wavelength. A natural interpretation is that the emission originates in an optically thin region inside the rim. In the following sections, we discuss the physical nature of this component.

\begin{figure} \par\includegraphics[width=8cm,clip]{12898fg18.eps}\hspace*{4mm} \includegraphics[width=8cm,clip]{12898fg19.eps} \end{figure} Figure 9:

Left: radial temperature profiles for graphite (green line with triangles), corundum (red line with crosses), or iron (blue line with squares). The prediction from a black body (i.e., large grains) is overplotted to allow comparisons. The vertical dotted line indicates 0.10 AU. Right: SED of HD 163296 together with the predictions of three models that include an inner disk made of dust in addition to the star and the rim. The additional disk component has structural characteristics that are reported in Table 5 and is made of a single refractory species - either graphite, corundum, or iron. The dotted lines represent the corresponding emission, while the full lines show the total flux.

Open with DEXTER

4.5.1 An inner gaseous disk?

Several authors have suggested that NIR interferometers detect the emission of gas within the dust evaporation radius (Isella et al. 2008; Eisner et al. 2007; Kraus et al. 2008b; Tannirkulam et al. 2008). This interpretation presents several difficulties in the case of HD 163296, where the additional component dominates the emission in H and K, and where good observations of high spectral resolution exist over a wide range of wavelengths.

Models of the emission of purely gaseous disks inside the dust sublimation radius were computed by Muzerolle et al. (2004) for HAe stars assuming LTE opacities. For typical HAe accretion rates ($\sim $ $10^{-7}~M_{\odot}$ yr-1), the inner, dust-free, disk gas surface density is higher than 103 g/cm2, the gas temperature ranges from a few thousand to a few hundred K, and the gas is fully molecular. The NIR emission is sufficiently strong to, in principle, account for the observations. However, as has been pointed out by several authors, the models also predict many strong molecular bands (mostly water and CO overtone transitions) that are absent in the HD 163296 spectrum (see Fig. 8, left) (Najita et al. 2000,2007). This problem is also discussed in Najita et al. (2009), in connection with the non-detection of CO overtone and water emission in the Herbig Ae star, MWC480, that also exhibits a hot compact NIR excess previously detected with interferometry and interpreted as resulting from water (Eisner 2007).

The assumption that the gas is in LTE, however, is certainly inappropriate at least in the upper disk layers, where the stellar radiation can penetrate, ionize, and dissociate matter well above the LTE predictions. However, these thin gas layers are unlikely to contribute significantly to the broadband observed fluxes. We computed the emission from thin layers of gas, using the code Cloudy (Ferland et al. 1998). We assumed that the region inside the rim can be described as a geometrically thin disk, heated from the outside by the star. The disk extends from 0.1 to 0.45 AU and has a constant surface density. In these conditions, as long as the disk is optically thin to the stellar radiation, the gas is mostly atomic and the ionization fraction is low (e.g., <0.01). In the NIR, H- dominates the emission. We show in Fig. 8, right, that for surface density values of 0.1, 1, and 6 g/cm2 (all much lower than predicted by the viscous accreting disks modelled by Muzerolle et al. 2004), the continuum emission is always too weak to be significant. Increasing it further would require higher surface densities, in which case LTE conditions would very likely be reached. In fact, for $\Sigma=6$ g/cm2, the mean optical depth to the stellar radiation is already of order unity. Moreover, we note that the wavelength dependence of the non-LTE continuum is inconsistent with the observations. In particular, the H-bound-free emission produces a sharp drop at 1.6 $\mu$m corresponding to its activation energy, which would be seen in the HD 163296 high resolution spectra (Sitko et al. 2008) if the gas emission was higher.

T08 suggested that hot gas is the physical origin of the additional inner component. We note that their models cannot reproduce our AMBER/VLTI data, mostly because of their small inner rim radius. However, we examined the possibility that the gas is heated to higher temperatures by additional energy sources. We computed the properties of the same disk model but after fixing the temperature to 8000 K. In this case, the ionization fraction is high ($\gg$0.5) and the emission is dominated by bound-free processes. The emission can be very high, but its wavelength dependence is inconsistent with the observations (see Fig. 8, right).

Based on these crude considerations, we tend to exclude that the NIR flux detected by the interferometers is dominated by the emission of hot gas inside the dust sublimation radius. However, it is clear that, before this can be definitely ruled out, one needs more realistic, non-LTE models that treat the transition from optically thin to optically thick layers, i.e., from atomic to molecular gas in a dust-free environment. These models would also be important for the interpretation of the hydrogen and helium recombination lines, which appear very strong in the models. Atomic lines - mostly hydrogen and helium ones - are often interpreted as being emitted in magnetospheric accretion columns of gas. This, however, is unlikely to be true for most Herbig Ae stars, based on the results obtained with spectro-interferometry around the Br$_{\gamma}$ emission line (Kraus et al. 2008a; Eisner et al. 2009), since this line seems to be formed in most cases, in disk material closer to the star than the silicate dust sublimation radius but outside the corotation radius.

\begin{figure} \par\includegraphics[width=7.8cm,clip]{12898fg20.eps}\hspace*{4mm} \includegraphics[width=7.8cm,clip]{12898fg21.eps} \end{figure} Figure 10:

Left: visibilities produced by our model that assumes that iron grains are responsible for the additional dusty inner disk emission, in K band ( left) and H band ( right) compared to the observations. The AMBER/VLTI observations (blue full squares) as well as the Keck-I (triangles) and the CHARA (circles) are added. The IOTA H band data (upside down triangles) are plotted together with the AMBER visibilities.

Open with DEXTER

4.5.2 An inner dusty disk?

Inside the silicate sublimation radius, not only gas but also more refractory grains can exist and contribute to the observed NIR emission. In this section, we explore the possibility that a layer of refractory grains, extending between an inner and an outer radius (inside the rim), accounts for the interferometric and photometric observations of HD 163296. We assume that the layer is optically thin in the vertical direction with surface density profile $\Sigma_{\rm {dust}}$ and that its vertical optical depth is proportional to 1/r, where r is the distance from the star (D'Alessio et al. 1999). We compute grain temperatures and emissivity in the H and K bands, and vary the inner and outer radii ( $R_{\rm {in}}$and $R_{\rm {out}}$, respectively) as well as the optical depth of the layer. We then computed the emission, visibilities, and closure phases for models that include this inner layer, the star, and the rim. We consider separately three grain species known to be refractory: iron, graphite, and corundum (aluminium oxides). The iron and corundum grain cross-sections are computed for spherical grains from the optical constants tabulated in Pollack et al. (1994), Koike et al. (1995), and Begemann et al. (1997). We use the graphite cross sections tabulated by B. Draine[*], based on the optical constants of Laor & Draine (1993). For relatively small grains, the radial temperature profile follows $\propto r^{-0.4}$ (Fig. 9, left). For comparison, we also show the temperature profile of very large grains (which behave as blackbodies), which have flat opacity from the UV to the IR ( $T \propto r^{-0.5}$).

These models are very simple, but probably not unrealistic. The strongest approximation concerns the dust temperature, which we compute by assuming that each grain is heated by the stellar radiation, and attenuated by an average optical depth $\tau_{\rm star}\propto 0.25$. In fact, the attenuation is not constant, since the optical path toward any individual grain varies not only with r but also with the incident angle of the stellar radiation. Once the temperature of the grains is known, then the emission is computed at all NIR wavelengths using a ray-tracing algorithm. As discussed in the following, a rim caused by silicate condensation can form in the low density region that we propose and its properties may also be affected by refractory grains in the inner disk, which absorb a small fraction of the stellar radiation. However, a self-consistent calculation of the rim properties is beyond the purpose of this paper. In this section, we model the rim following Isella & Natta (2005) and Isella et al. (2006), assuming micron-size silicates, an evaporation temperature of $\sim $1250 K, and an effective stellar luminosity of 75% $L_\star$ to account for the shielding by the inner disk. The rim radius is about 0.45 AU and its effective temperature is about 1000 K.

Table 4:   Refractory dust model parameters.

We obtain a good fit to the SED, as shown in Fig. 9 (right), for $R_{\rm {in}}=0.10$ AU and $R_{\rm {out}}=0.45$ AU, and an optical depth in the H band at $R_{\rm {in}}$ of 0.31, 0.2, and 0.25 for iron, graphite, and corundum, respectively. Table 4 indicates the grains properties used in these models. For each species, the optical depths in H and K bands at 0.10 AU ( $R_{\rm {in}}$) are reported as well as the minimum and maximum grain sizes considered in the calculations. The resulting surface density $\Sigma_{\rm {dust}}$ and the total mass of dust grains within 0.45 AU are also given. The latter is always very low ($\leq$ $10^{-6}~M_{\oplus}$). Although we have not tried to constrain the grain parameters in any detail, we note that very large refractory grains do not provide an equally good fit to the SED, as the ratio of the H to the K emission is always too high.

\begin{figure} \par\includegraphics[width=7.2cm,clip]{12898fg22.eps}\hspace*{4mm} \includegraphics[width=7.25cm,clip]{12898fg23.ps} \end{figure} Figure 11:

Model images of the circumstellar matter surrounding HD 163296, in the case where the inner disk is consists of refractory iron grains and a rim (outer ring). The colors represent the flux in W s/m2.

Open with DEXTER
These models successfully reproduce the interferometric data, in terms of both visibilities and CP. Since all three models produce similar results, we present the case for iron grains. Figure 10 shows the broad-band visibilities compared with the predictions of such a model. Figure 12 presents the broadband closure phases plotted versus hour angle and the model predictions calculated for each telescope configuration. We overplot the predictions of the rim-alone models (red, dashed line) to show how adding the optically thin dusty, inner disk emission smoothes out the asymmetry induced by the rim by the correct amount. Table 5 summarizes the structural parameters of this model, as inferred from SED and interferometric data fitting. The table reports in addition, for both bands, the ratio of the stellar, rim, and inner disk contributions (F*, $F_{\rm {rim}}$, and F respectively) to the total flux in the model ( $F_{\rm {tot}}$). Figure 11 shows the corresponding H and K band images.

The gas density of the inner disk can be derived from the values of $\Sigma_{\rm {dust}}$, once the abundances of iron, carbon, and aluminium in the solid species are known. Assuming, for example, that 50% of the iron is in grains, the gas surface density at 0.10 AU will be 0.2 g/cm2 (0.02 g/cm2 if 30% of carbon is in graphite, or 1.3 g/cm2 if all aluminium is in corundum). The gas density can be higher if a lower fraction of the metals is condensed. However, it seems likely, from the considerations of Sect. 4.5.1, that the gas density cannot be too high. A density only a few times higher than the above lower limits is inferred by the properties of the rim in HD 163296. In particular, both the large rim radius and its low effective temperature can be reproduced in a low density disk by silicates of micron size, as inferred in several HAe stars (Isella et al. 2006), and do not require very small grains. Assuming that the rim is produced by the evaporation of silicates and that all the silicon is in olivine of $\sim $$1~\mu$m size, we analyzed the rim properties in disks of increasing (but still low) surface density. For $\Sigma= 5(r/0.1~{\rm AU})^{-1}$ g/cm2, the vertical optical depth to the stellar radiation is $\sim $10 for a gas surface density of 1 g/cm2 at $R_{\rm rim}$, large enough to allow the formation of an optically thick rim that can be modelled following Isella & Natta (2005). The low gas density, and the correspondingly low evaporation temperature, moves the rim radius further from the star. Assuming a reasonable scale height of 10-3-10-2 AU, the gas density is $\sim $10-11 g/cm3, and the silicate evaporation temperature of the order of 1150 K. The corresponding rim radius is $\sim $0.4-0.5 AU, and its effective temperature is about 1000-1100 K, as required to fit the HD 163296 SED and interferometric data.

The only difficulty in assuming that the inner disk emission originates in grains within the silicate sublimation radius, is the need for them to survive at temperatures much higher than is generally assumed. The three types of grains that we examined reach temperatures of 2100-2300 K at $\sim $0.10 AU (Fig. 9, left). While similar values are possible for graphite (Krugel 2003), they are too high for both iron and corundum in the pressure of our inner disk (Pollack et al. 1994; Kama et al. 2009; Posch et al. 2003). However, there is room for discussion (Najita et al. 2009), as the balance between gas and dust in the conditions of the inner disk should be reconsidered in detail (Duschl et al. 1999). We emphasize that only a small amount of refractory grains need to survive these high temperatures, i.e., probably a minor fraction of the original population. The grains that we have considered are likely candidates, but if other, more refractory species can form, they would certainly fit the observations equally well.

\begin{figure} \par\begin{tabular}{ccc} \par\includegraphics[width=0.31\textwidt... ...=0.31\textwidth]{12898fg32.ps}\\ \par\end{tabular} \vspace*{1mm} \end{figure} Figure 12:

Closure phases versus hour angle. In each panel, the predictions of the disk rim model (dashed red lines) and our model that includes iron grains (full black line) are overplotted. The corresponding telescope configuration and wavelength band are indicated in the upper, left corners. The K band and H band measurements are plotted with circles and triangles, respectively.

Open with DEXTER

5 Summary and conclusions

This paper had discussed the largest set of NIR interferometric data collected so far for a young star. HD 163296 has a well studied disk at large spatial scale, which motivated our interpretation of the NIR interferometry using a star + inner disk model. Both interferometric and photometric data can be accounted for by an inclined disk with a low density inner region. The NIR continuum emission is then not dominated by the thermal emission from the dusty disk rim located at the sublimation radius of astronomical silicates, but by the additional optically thin component located inside. This component emits about 32% of the stellar luminosity, but 54% (50%) of the observed radiation in H (K) band. Because of the silicate condensation and the strong increase in opacity, the disk rim forms in this low-density region at $\sim $0.45 AU from the star and emits about 16% (36%) of the H (K) band flux. The combination of the unresolved stellar radiation, the smooth and point-symmetric emission of the inner disk region, and the skewed disk rim emission can successfully explain the visibilities and non-zero closure phases measured in both bands.

The nature of the emission in the inner disk remains a matter of discussion. We argue against gas being mainly responsible for this continuum emission. A dense, cold disk, as expected for viscous accretion models (Muzerolle et al. 2004), would produce strong molecular lines that are not seen in high-resolution spectra. Non-LTE tenuous gas layers, in an atomic state if only heating by the star is assumed, or fully ionized by additional sources of energy, cannot account for the observed properties of the NIR continuum. However, we emphasize that self-consistent models of dust-free gaseous disks are not currently available, but are needed to exploit the full potential of the interferometric observations.

We suggest instead that a small fraction of refractory grains survive very close to the star. We propose models for the optically thin emission of the innermost region, using various kinds of refractory grains, distributed from 0.10 AU to 0.45 AU. The dust surface density provides only a lower limit to the gas surface density, as we do know neither the exact nature of the grains nor their abundance. However, we find that a low density region is consistent with the location and properties of the rim, as condensation of silicates will occur, and with the lack of molecular features in the spectrum of HD 163296. We expect the gas in the inner disk indeed to be mostly atomic, in non-LTE, and although its continuum emission will be weak, hydrogen lines can be strong. The models used in Sect. 4.5.2 to argue for the presence of refractory grains, make a number of crude assumptions, and improved models that self-consistently compute the grain temperature and emission in the thin disk as well as the properties of the rim are being developed. Our study indicates that the inner region of HD 163296 is quite empty, with a very low surface density that is inconsistent with a dense accretion disk. For comparison, a surface density of 1 g/cm2 at $\sim $0.10 AU corresponds, in a standard accretion disk ( $\alpha=0.01$), to an accretion rate of $\sim $ $ 10^{-11}~M_{\odot}$ yr-1, much lower than typical values for Herbig Ae stars (Garcia Lopez et al. 2006). With our data, we do not constrain the outer radius of this low density region, which can be larger than 0.5 AU. However, we know that at large radii the HD 163296 disk is massive and dense, as shown by the millimeter interferometric observations of Isella et al. (2007). It seems likely that HD 163296 has a dense disk with an inner cavity, and that we observe it just before it reaches the transition disk phase, as suggested by Sitko et al. (2008).

Table 5:   Parameters of our model with iron grains.

It is fair to emphasize that we make no claim that our interpretation is unique. As stated at the beginning of Sect. 4, we assumed that the NIR emission of HD 163296, at spatial scales of less than 0.5 AU, is dominated by the emission of a circumstellar disk. Moreover, we interpreted the non-zero values of the CP as evidence of the asymmetric emission of a disk rim. While the properties that we derived for the smooth inner emission are probably robust, the existence of the rim is less so. In particular, the lack of visibility bounces at large baselines argues against the presence of a rim. In this case, the observed closure phases may possibly be caused by any asymmetric brightness distribution, such as a symmetric flared disk with a stellar contribution that is off-centered by a few percent of the inner disk radius with respect to the disk (Malbet et al. 2001), by a hot spot on the disk, or by a density discontinuity. Only a larger (u,v) coverage, providing access to more details of the morphology could solve this ambiguity.

Our interpretation of the smooth, inner emission as originating in refractory grains requires their survival at very high temperatures ($\sim $ 2100-2300 K), much higher than expected, even for the most refractory grains, at the pressure of the low-density inner disk (Pollack et al. 1994; Kama et al. 2009). However, clearing the innermost regions and optically thin emission from left-over refractory grains could be a common phenomenon in Herbig Ae stars. Their presence within the first few tenths of an AU is a promising interpretation of the observed depletions in refractory dust species - such as iron - in jets of young stars that are launched from this region (Nisini et al. 2005; Podio et al. 2006). Similar interferometric studies, with a large number of measurements in various wavelength bands simultaneously, should be performed for a large sample of stars. A higher level of complexity in models is also needed to account for both the dust and the gas emission in a self-consistent way. Finally, the advent of the next-generation of imaging instruments will hopefully provide unambiguous constraints on these complex environments.

Acknowledgements
We acknowledge fundings from CNRS and INAF (grant ASI-INAF I/016/07/0). This work was in part performed under contract with the Jet Propulsion Laboratory (JPL) funded by NASA through the Michelson Fellowship Program. JPL is managed for NASA by the California Institute of Technology. We thank A. Sargent and T. Ray for hosting part of this research, and the VLTI team at Paranal for the help in obtaining these data. We thank J.D. Monnier who provided with the IOTA data, and M. Sitko for discussions about the photometric measurements. We are greatful to A. Crida, M. Desort and S. Renard for fruitful discussions. We acknowledge the anonymous referee for his comments that improved the clarity of the paper.

References

  1. Begemann, B., Dorschner, J., Henning, T., et al. 1997, ApJ, 476, 199 [NASA ADS] [CrossRef] [Google Scholar]
  2. D'Alessio, P., Calvet, N., & Hartmann, L. E. A. 1999, ApJ, 527, 893 [NASA ADS] [CrossRef] [Google Scholar]
  3. de Winter, D., van den Ancker, M. E., Maira, A., et al. 2001, A&A, 380, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Deleuil, M., Bouret, J.-C., Catala, C., et al. 2005, A&A, 429, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Devine, D., Grady, C. A., Kimble, R. A., et al. 2000, ApJ, 542, L115 [NASA ADS] [CrossRef] [Google Scholar]
  6. Doucet, C., Pantin, E., Lagage, P. O., & Dullemond, C. P. 2006, A&A, 460, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
  8. Duschl, W. J., Gail, H.-P., Keller, C., & Tscharnuter, W. M. 1999, in Astronomische Gesellschaft Meeting Abstracts, ed. R. E. Schielicke, 15, 14 [Google Scholar]
  9. Eisner, J. A. 2007, Nature, 447, 562 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  10. Eisner, J. A., Lane, B. F., & Hillenbrand, L. A. E. A. 2004, ApJ, 613, 1049 [NASA ADS] [CrossRef] [Google Scholar]
  11. Eisner, J. A., Chiang, E. I., Lane, B. F., & Akeson, R. L. 2007, ApJ, 657, 347 [NASA ADS] [CrossRef] [Google Scholar]
  12. Eisner, J. A., Graham, J. R., Akeson, R. L., & Najita, J. 2009, ApJ, 692, 309 [NASA ADS] [CrossRef] [Google Scholar]
  13. Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
  14. Garcia Lopez, R., Natta, A., Testi, L., & Habart, E. 2006, A&A, 459, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Grady, C. A., Devine, D., Woodgate, B., et al. 2000, ApJ, 544, 895 [Google Scholar]
  16. Günther, H. M., & Schmitt, J. H. M. M. 2009, A&A, 494, 1041 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Hillenbrand, L. A., Strom, S. E., Vrba, F. J., & Keene, J. 1992, ApJ, 397, 613 [NASA ADS] [CrossRef] [Google Scholar]
  18. Isella, A., & Natta, A. 2005, A&A, 438, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Isella, A., Testi, L., & Natta, A. 2006, A&A, 451, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Isella, A., Testi, L., Natta, A., et al. 2007, A&A, 469, 213 [CrossRef] [EDP Sciences] [Google Scholar]
  21. Isella, A., Tatulli, E., Natta, A., & Testi, L. 2008, A&A, 483, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Kama, M., Min, M., & Dominik, C. 2009, A&A, 506, 1199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Koike, C., Kaito, C., Yamamoto, T., et al. 1995, Icarus, 114, 203 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kraus, S., Hofmann, K.-H., Benisty, M., et al. 2008a, A&A, 489, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Kraus, S., Preibisch, T., & Ohnaka, K. 2008b, ApJ, 676, 490 [NASA ADS] [CrossRef] [Google Scholar]
  26. Krugel, E. 2003, Astron. Geophys., 44, 35 [Google Scholar]
  27. Laor, A., & Draine, B. T. 1993, ApJ, 402, 441 [NASA ADS] [CrossRef] [Google Scholar]
  28. Le Bouquin, J.-B., Bauvir, B., Haguenauer, P., et al. 2008, A&A, 481, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Malbet, F., Lachaume, R., & Monin, J.-L. 2001, A&A, 379, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Mannings, V., & Sargent, A. I. 1997, ApJ, 490, 792 [NASA ADS] [CrossRef] [Google Scholar]
  31. Meeus, G., Waters, L. B. F. M., Bouwman, J., et al. 2001, A&A, 365, 476 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Millan-Gabet, R., Schloerb, F. P., & Traub, W. A. 2001, ApJ, 546, 358 [NASA ADS] [CrossRef] [Google Scholar]
  33. Millan-Gabet, R., Malbet, F., Akeson, R., et al. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 539 [Google Scholar]
  34. Miroshnichenko, A., Ivezic, Z., & Elitzur, M. 1997, ApJ, 475, L41 [NASA ADS] [CrossRef] [Google Scholar]
  35. Monnier, J. D., & Millan-Gabet, R. 2002, ApJ, 579, 694 [NASA ADS] [CrossRef] [Google Scholar]
  36. Monnier, J. D., Millan-Gabet, R., Billmeier, R., et al. 2005, ApJ, 624, 832 [NASA ADS] [CrossRef] [Google Scholar]
  37. Monnier, J. D., Berger, J.-P., Millan-Gabet, R., et al. 2006, ApJ, 647, 444 [NASA ADS] [CrossRef] [Google Scholar]
  38. Montesinos, B., Eiroa, C., Mora, A., & Merín, B. 2009, A&A, 495, 901 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Muzerolle, J., D'Alessio, P., Calvet, N., & Hartmann, L. 2004, ApJ, 617, 406 [NASA ADS] [CrossRef] [Google Scholar]
  40. Najita, J. R., Edwards, S., Basri, G., & Carr, J. 2000, Protostars and Planets IV, 457 [Google Scholar]
  41. Najita, J. R., Carr, J. S., Glassgold, A. E., & Valenti, J. A. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 507 [Google Scholar]
  42. Najita, J. R., Doppmann, G. W., & Carr, J. S. E. A. 2009, ApJ, 691, 738 [NASA ADS] [CrossRef] [Google Scholar]
  43. Natta, A., Prusti, T., Neri, R., et al. 2001, A&A, 371, 186 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Natta, A., Testi, L., Neri, R., Shepherd, D., & Wilner, D. 2004, A&A, 416, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Nisini, B., Bacciotti, F., Giannini, T., et al. 2005, A&A, 441, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Pauls, T. A., Young, J. S., Cotton, W. D., & Monnier, J. D. 2005, PASP, 117, 1255 [NASA ADS] [CrossRef] [Google Scholar]
  47. Petrov, R. G., Malbet, F., Weigelt, G., et al. 2007, A&A, 464, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Podio, L., Bacciotti, F., Nisini, B., et al. 2006, A&A, 456, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Pollack, J. B., Hollenbach, D., Beckwith, S., et al. 1994, ApJ, 421, 615 [NASA ADS] [CrossRef] [Google Scholar]
  50. Posch, T., Kerschbaum, F., Fabian, D., et al. 2003, ApJS, 149, 437 [NASA ADS] [CrossRef] [Google Scholar]
  51. Schöller, M. 2007, New Astron. Rev., 51, 628 [NASA ADS] [CrossRef] [Google Scholar]
  52. Sitko, M. L., Carpenter, W. J., Kimes, R. L., et al. 2008, ApJ, 678, 1070 [NASA ADS] [CrossRef] [Google Scholar]
  53. Swartz, D. A., Drake, J. J., Elsner, R. F., et al. 2005, ApJ, 628, 811 [NASA ADS] [CrossRef] [Google Scholar]
  54. Tannirkulam, A., Harries, T. J., & Monnier, J. D. 2007, ApJ, 661, 374 [NASA ADS] [CrossRef] [Google Scholar]
  55. Tannirkulam, A., Monnier, J. D., Harries, T. J., et al. 2008, ApJ, 689, 513 [NASA ADS] [CrossRef] [Google Scholar]
  56. Tatulli, E., Millour, F., Chelli, A., et al. 2007, A&A, 464, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. van den Ancker, M., de Winter, D., & Tjin A Djie, H. 1998, A&A, 330, 145 [NASA ADS] [Google Scholar]
  58. Vinkovic, D., Ivezic, Z., Jurkic, T., & Elitzur, M. 2006, ApJ, 636, 348 [NASA ADS] [CrossRef] [Google Scholar]
  59. Wassell, E. J., Grady, C. A., & Woodgate, B. E. A. 2006, ApJ, 650, 985 [NASA ADS] [CrossRef] [Google Scholar]
  60. Weingartner, J. C., & Draine, B. T. 2001, ApJ, 563, 842 [Google Scholar]

Footnotes

... dust?[*]
Based on AMBER observations collected at the VLTI (European Southern Observatory, Paranal, Chile) with Arcetri Guaranteed Time program 081.C-0124, LAOG Guaranteed Time program 081.C-0794 and open time programs 081.C-0851, 081.C-0098.
... website[*]
http://olbin.jpl.nasa.gov
... B. Draine[*]
http://www.astro.princeton.edu/ draine/dust/dust.diel.html

All Tables

Table 1:   Log of the interferometric observations.

Table 2:   Star and calibrator properties.

Table 3:   Values of the closure phase as averaged over all the measurements.

Table 4:   Refractory dust model parameters.

Table 5:   Parameters of our model with iron grains.

All Figures

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{12898fg1.eps} \end{figure} Figure 1:

(u,v) plane coverage of the observations in spatial frequencies. The observing nights are plotted with different symbols and the corresponding telescope configurations are reported in the figure.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{12898fg2.eps}\hspace*{4mm} \includegraphics[width=8cm,clip]{12898fg3.eps} \end{figure} Figure 2:

Squared visibilities against spatial frequencies B/$\lambda $ in the K band ( left panel) and the H band ( right panel). Different symbols correspond to different configurations, that are reported in the upper right corner of the left panel.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{12898fg4.eps}\hspace*{4mm} \includegraphics[width=8cm,clip]{12898fg5.eps} \end{figure} Figure 3:

Broad-band squared visibilities against spatial frequencies B/$\lambda $ in the K band ( left panel) and the H band ( right panel). Different symbols and colors correspond to different configurations that are given in Fig. 2. The IOTA points are overplotted in the right panel (empty circles).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{12898fg6.eps} \end{figure} Figure 4:

Example of wavelength dependence for the squared visibilities obtained on the three baselines during observations with the A0-D0-H0 configuration. In each panel, the characteristic size of the emission is given at each wavelength across the H and K band. These sizes are derived from a ring model of uniform brightness to account for the change of resolution with wavelength. The triangles show the maximum chromaticity over the whole wavelength range, while the circles give the minimum variation. For each measurement, the corresponding projected baseline length and position angle are indicated in the top right corner.

Open with DEXTER
In the text

  \begin{figure} \par\begin{tabular}{ccc} \includegraphics[width=0.31\textwidth]{1... ...cludegraphics[width=0.30\textwidth]{12898fg11.ps}\\ \end{tabular} \end{figure} Figure 5:

Measured closure phases for each configuration (reported in the top left corners) plotted versus maximum spatial frequency. In all panels, except for U1-U2-U4 for which only K band data were useful, the measurements include both the H and K bands.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{12898fg12.eps}\hspace*{4mm} \includegraphics[width=7cm,clip]{12898fg13.eps} \end{figure} Figure 6:

Broad-band closure phases plotted against the maximum spatial resolution achieved for all telescope configurations (K band, left; H band, right). The configurations and the corresponding symbols are reported at the bottom of the left panel.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm,clip]{12898fg14.eps}\hspace*{4mm} \includegraphics[width=7.8cm,clip]{12898fg15.eps}\ \end{figure} Figure 7:

Model visibilities when considering a rim alone, located at 0.23, 0.36, and 0.45 AU (dashed red, dotted blue, and full black lines respectively), versus effective spatial frequency $B_{\rm {eff}}/\lambda $, compared to the measured broad-band visibilities (blue full squares) in the K band ( left) and the H band ( right). The predictions of the model described in T08, which includes an additional inner component interpreted as gas, is given in red (T08; dash-dot-dot). The K band measurements obtained at CHARA and Keck-I are overplotted (circles and triangles respectively) in the left panel, as well as the IOTA Hband data (triangles) in the right panel. An incoherent flux contributing to $\sim $8% of the total H and K band fluxes is considered.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{12898fg16.eps}\hspace*{4mm} \includegraphics[width=8cm,clip]{12898fg17.eps} \end{figure} Figure 8:

SED of HD 163296 (Tannirkulam et al. 2008; Sitko et al. 2008) with the predictions of gaseous disk models. The flux emitted by the rim located at 0.45 AU (cyan dashed line) as well as the additional inner disk emission (black dotted line) are added in both panels to allow direct comparisons. Left: the predictions for optically thick and dense layers of gas in LTE (Muzerolle et al. 2004) are overplotted (red full line). In this case, the gas is mostly in a molecular state. Right: the continuum emission as predicted by thin disks of gas in non-LTE, heated from the top by the stellar radiation, are shown. The gas extends from 0.1 to 0.45 AU and has constant surface densities of 0.1, 1, and 6 g/cm2 (red line with squares, blue line with triangles and green line with diamonds, respectively). In these conditions, the gas is mostly atomic. The predictions of a fully ionized layer of gas at 8000 K with a constant surface density of 0.06 g/cm2 are also reported (magenta curve with diamonds). As long as the disk remains optically thin, the emission is proportional to the surface density, and this value was chosen only to display its wavelength dependence.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{12898fg18.eps}\hspace*{4mm} \includegraphics[width=8cm,clip]{12898fg19.eps} \end{figure} Figure 9:

Left: radial temperature profiles for graphite (green line with triangles), corundum (red line with crosses), or iron (blue line with squares). The prediction from a black body (i.e., large grains) is overplotted to allow comparisons. The vertical dotted line indicates 0.10 AU. Right: SED of HD 163296 together with the predictions of three models that include an inner disk made of dust in addition to the star and the rim. The additional disk component has structural characteristics that are reported in Table 5 and is made of a single refractory species - either graphite, corundum, or iron. The dotted lines represent the corresponding emission, while the full lines show the total flux.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm,clip]{12898fg20.eps}\hspace*{4mm} \includegraphics[width=7.8cm,clip]{12898fg21.eps} \end{figure} Figure 10:

Left: visibilities produced by our model that assumes that iron grains are responsible for the additional dusty inner disk emission, in K band ( left) and H band ( right) compared to the observations. The AMBER/VLTI observations (blue full squares) as well as the Keck-I (triangles) and the CHARA (circles) are added. The IOTA H band data (upside down triangles) are plotted together with the AMBER visibilities.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.2cm,clip]{12898fg22.eps}\hspace*{4mm} \includegraphics[width=7.25cm,clip]{12898fg23.ps} \end{figure} Figure 11:

Model images of the circumstellar matter surrounding HD 163296, in the case where the inner disk is consists of refractory iron grains and a rim (outer ring). The colors represent the flux in W s/m2.

Open with DEXTER
In the text

  \begin{figure} \par\begin{tabular}{ccc} \par\includegraphics[width=0.31\textwidt... ...=0.31\textwidth]{12898fg32.ps}\\ \par\end{tabular} \vspace*{1mm} \end{figure} Figure 12:

Closure phases versus hour angle. In each panel, the predictions of the disk rim model (dashed red lines) and our model that includes iron grains (full black line) are overplotted. The corresponding telescope configuration and wavelength band are indicated in the upper, left corners. The K band and H band measurements are plotted with circles and triangles, respectively.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.