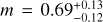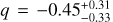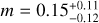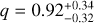| Issue |
A&A
Volume 695, March 2025
|
|
|---|---|---|
| Article Number | A257 | |
| Number of page(s) | 17 | |
| Section | Planets, planetary systems, and small bodies | |
| DOI | https://doi.org/10.1051/0004-6361/202452287 | |
| Published online | 25 March 2025 | |
Survey of Orion Disks with ALMA (SODA)
III. Disks in wide binary systems in L1641 and L1647
1
European Southern Observatory,
Karl-Schwarzschild-Str 2,
85748
Garching, Germany
2
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg, Germany
3
Università di Pisa, Physics Department E. Fermi,
Largo Bruno Pontecorvo 3,
56127
Pisa, Italy
4
Space Research Institute, Austrian Academy of Sciences,
Schmiedlstr. 6,
8042
Graz, Austria
5
Alma Mater Studiorum, Università di Bologna, Dipartimento di Fisica e Astronomia (DIFA),
Via Gobetti 93/2,
40129
Bologna, Italy
6
INAF-Osservatorio Astrofisico di Arcetri,
Largo E. Fermi 5,
50125
Firenze, Italy
7
Department of Astrophysics, University of Vienna,
Türkenschanzstraße 17 (Sternwarte),
1180
Wien, Austria
8
INFN, Sezione di Pisa,
Largo Bruno Pontecorvo 3,
56127
Pisa, Italy
★ Corresponding author; giulia.ricciardi@eso.org
Received:
17
September
2024
Accepted:
18
February
2025
Context. Observations of protoplanetary disks within multiple systems in nearby star-forming regions (SFRs) have shown that the presence of a neighboring object influences the evolution of dust in disks. However, the size of the available sample and the separation range covered are insufficient to fully understand the dust evolution in binary systems.
Aims. The goal of this work, based on the Survey of Orion Disks with ALMA (SODA), is to comprehensively characterize the impact of stellar multiplicity on Class II disks in the L1641 and L1647 regions of Orion A (∼1–3 Myr). We characterized the protostellar multiplicity using the Atacama Large Millimeter/submillimeter Array (ALMA), the ESO-VISTA, and the Hubble Space Telescope. The resulting sample of 65 multiple systems is the largest catalog of wide binary systems to date (projected separation ≥1000 AU) and enables a more robust statistical characterization of the evolution and properties of protoplanetary disks.
Methods. The disk population was observed in the continuum with ALMA at 225 GHz, with a median rms of 1.5 M⊕. We combined these data (resolution of ∼1.1″) with the ESO-VISTA near-infrared survey of the Orion A cloud (resolution of ∼0.7″). From this dataset, multiple-star systems were selected using an iterative inside-out search in projected separation (≥1000 AU).
Results. We identify 61 binary systems, 3 triple systems, and 1 quadruple system. The separation range is between 1000 and 104 AU. The dust mass distributions inferred via the Kaplan-Meier estimator yield a median mass of 3.23−0.4+0.6 M⊕ for primary disks and 3.88−0.3+0.3 M⊕ for secondary disks.
Conclusions. Combining our data with those available for the Lupus and Taurus disks, we identify a threshold separation of about 130 AU, beyond which the previously observed positive correlation between millimeter flux (and hence dust mass) and projected separation is lost. Recent theoretical models confirm that pre- and post-threshold systems are the result of different star formation processes, such as the fragmentation of gravitationally unstable circumstellar disks, the thermal fragmentation of infalling cores, or the turbulent fragmentation of molecular clouds. We can rule out the dependence on different SFRs: the cumulative mass distributions of multiples in SFRs of similar ages are statistically indistinguishable. This result strengthens the hypothesis that there is a universal initial mass distribution for disks.
Key words: methods: statistical / protoplanetary disks / binaries: general / stars: pre-main sequence
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Multiple systems are a common outcome of the star formation process (Bate 2018; Duchêne & Kraus 2013; Larson 2001), especially in the early stages (Tobin et al. 2016; Reipurth et al. 2014). The occurrence of binary systems is ~50% in the local solar neighborhood (Raghavan et al. 2010), and the occurrence of multiple systems is about 30–50% in the field (Raghavan et al. 2010) and up to about 70% in young clusters (Kraus et al. 2011). Some studies even discuss the possibility that all stars may have formed in some kind of multiple configuration at the very beginning of their lifetimes (Kroupa 1995; Marks et al. 2014). In addition, multiplicity studies of pre-main-sequence stars (Class II and Class III sources) have derived multiplicity fractions comparable to or exceeding those of main sequence stars (Moe & Di Stefano 2017; Kraus et al. 2011; Reipurth et al. 2007). This prevalence across different class types and their close separation suggest that the origin of multiplicity is a direct consequence of the physical conditions of star formation.
Multiple-star systems can be formed through various processes (and combinations thereof): (1) turbulent fragmentation of the molecular cloud (Kawasaki & Machida 2023), (2) thermal fragmentation of a strongly perturbed, rotating, and infalling core (e.g., Boss & Keiser 2014, 2013), and (3) fragmentation of a gravitationally unstable circumstellar disk (e.g., Longarini et al. 2023; Stamatellos & Whitworth 2009; Machida et al. 2008). The first two scenarios will lead to multiples that are initially separated by several hundred to several thousand AU, while scenario (3) leads to the formation of companions with separations of ≤100 AU (e.g., Tobin et al. 2013; Takakuwa et al. 2012; Rodríguez et al. 1998). The separation of companions is therefore an important signature of the physics of star formation.
It is not clear how much the multiplicity of stars hinders planet formation and evolution. Numerical simulations have shown that in a given binary system there are some regions of orbit where planets are unstable (Holman & Wiegert 1999). Specifically, if the planet is orbiting one of the two stars, there is a maximum semimajor axis beyond which the planet’s orbit is unstable; if the planet is instead orbiting both stars, there is a minimum semimajor axis below which the planet is unstable. Observations have shown that planets and protoplanetary disks easily form and survive around binary systems (Duchêne 2010; Bonavita & Desidera 2007). It should also be noted that in a star-forming environment, binaries have the added complication that they present a larger cross-section for encounters with other stars, and consequently the likelihood of interactions that could potentially destabilize the planetary system is higher than for systems orbiting a single star (Adams et al. 2006). Therefore, it is crucial to better understand the effect of stellar multiplicity on the circumstellar disk structure, as this has a direct impact on the process of planet formation.
Ongoing improvements to observational techniques and hydrodynamic simulations have shed new light on the evolution of isolated protoplanetary disks, such as the mechanisms responsible for mass accretion (Espaillat et al. 2022) or the existence of multiphase instabilities and dynamical phenomena that can increase planet formation rates (Lesur et al. 2022). The presence of companion stars can significantly influence the dynamics and evolution of protoplanetary disks (Pinte et al. 2023). On the one hand, companion stars can exert gravitational forces on the disk, leading to perturbations in the dust and gas distribution and in the orbital dynamics. On the other hand, tidal forces from the companions can induce gas flows or create regions of increased gas density, affecting the overall mass distribution and accretion rates within the disk, or affecting dust evolution processes such as grain growth and fragmentation. All of these aspects have implications for the subsequent evolution of the disk and the formation of planetary systems.
In the last decade, observations of the gas and dust in disks of multiple-star systems have detected compact disks (<100 AU; e.g., Rota et al. 2022; Zagaria et al. 2021; Zurlo et al. 2021; Akeson et al. 2020; Manara et al. 2019; Cox et al. 2017; Harris et al. 2012). The results confirm that the size and properties of the disks depend on the presence of companions. More recently, studies by Zagaria et al. (2023, 2021) and Zhang et al. (2023) have shown that the evolution and lifetimes of disks around binary or multiple-star systems differ from those of single stars. Nevertheless, the effects of stellar multiplicity on disk evolution are still poorly constrained: the available samples and the separation range do not provide a complete picture of disk evolution.
In this study we focused on the dust to better constrain its evolution in disks in multiple-star systems. Specifically, we used the Survey of Orion Disks with ALMA1 (SODA) (van Terwisga et al. 2022), which, with an angular resolution of ~1.1″, explores a broader disk population of 873 Class II disks around low-mass stars in Orion A below −6° declination. This survey is based on the Spitzer survey by Megeath et al. (2012), later updated to its final version by Megeath et al. (2016).
To characterize the evolution of circumstellar dust around stars in multiple systems, we included in our analysis the optical and near-infrared (NIR) data collected by the VISION survey (Meingast et al. 2016). The angular resolution ranges from 2″−5″ for Spitzer to ~0.7″ for VISION, so we can detect more dusty young stellar objects (YSOs) in the same coverage area, down to sizes about 3–7 times smaller than what can be detected by Spitzer (in Spitzer observations, excess sources would be blended).
In this paper we present a new catalog of multiple systems in the L1641 and L1647 regions of Orion A constructed by combining the SODA sample (van Terwisga et al. 2022) with ancillary ESO-VISTA (Meingast et al. 2016; Großschedl et al. 2019) and Hubble Space Telescope (Kounkel et al. 2016) observations. The final sample consists only of Class II YSOs: 61 binary systems, 3 triple systems, and 1 quadruple system with separations ranging from 100 to 104 AU.
The sample selection and the statistical method used to associate the multiple systems are described in Section 2. The results are presented and discussed in Section 3 and 4 respectively
2 Sample characterization
The focus of this paper is young dusty sources and their evolution within multiple configurations, so careful selection of an appropriate and unbiased sample was required. Megeath et al. (2012) presented a survey of dusty YSOs identified in the Orion A and B clouds using the Infra-Red Array Camera (IRAC) and MIPS instruments on board the Spitzer Space Telescope, mapping 9 deg2 in five MIR bands from 3–24 µm, with a resolution of 2″−5″. The photometric classification of sources is based on IR or MIR excess colors, with MIPS and IRAC data merged with the 2MASS point source catalog to generate an eight-band photometric catalog. Among the 298 405 point sources identified in the Orion molecular clouds, 3479 sources have been classified as Class II objects (dusty YSOs), with a MIR emission above that expected for a reddened photosphere. Megeath et al. (2016) slightly updated the sample, including about 10 new dusty sources. Using the Atacama Large Millimeter/submillimeter Array (ALMA), SODA (van Terwisga et al. 2022) observed all disks in these previous Spitzer catalogs located in Orion A below -6° degrees in declination. The sample of 873 protoplanetary disks was observed with ALMA at 225 GHz, with a median rms of 1.5 M⊕ (or 0.08 mJy beam−1) − assuming Tdust=20 K and kv=2.3 cm2 g−1 − and a typical synthesized beam full width at half maximum of ~1.1″. Further details can be found in van Terwisga et al. (2022) (Paper I).
Due to the resolution of Spitzer, close companions (projected separation ≤5″) are likely to be missing from the infrared catalog. Großschedl et al. (2019) combined archival mid- to far- infrared (Megeath et al. 2012, 2016; Furlan et al. 2016; Lewis & Lada 2016) and the VISTA telescope data to extend and redefine the catalog of YSOs in Orion A. The updated catalog has the deep seeing-limited resolution of ~0.7″ and the sensitivity KS < 19 mag of the ESO-VISTA NIR survey of the Orion A cloud, which is called VISION (Meingast et al. 2016), and it covers an extended spatial region of ~950 pc2 (or 18.3 deg2). This allows us to construct the largest catalog of dusty YSOs in the Orion A molecular cloud to date. Compared to 2MASS, the sensitivity of VISTA is 4–5 magnitudes better and its resolution is improved by a factor of about 3. Therefore, the VISION catalog contains more sources in the same coverage area, resulting in an improved YSO classification and a better discrimination of background galaxies or extended nebulous IR emission from YSO candidates. In this way, VISION allows the assembly of the multiplicity sample, while SODA provides the corresponding millimeter data to characterize the structure and evolution of the dust in the circumstellar disk.
2.1 Catalog completeness
The VISION and SODA surveys discuss their catalog completeness with reference to Megeath et al. (2016). The main factor to consider for the completeness of the Spitzer-selected sample is the confusion between the nebular background and the sources, which is estimated from the route median square deviations of the pixels surrounding each YSO candidate in an IRAC image (Fazio et al. 2004). This provides an estimate of the incompleteness due to the local MIR background emission, which varies spatially and increases with stellar density. Thus, Spitzer is less sensitive to fainter (or low-mass) stars in regions with non-negligible background emission. This can lead to a bias in our observations: the lower the mass of the star, the fainter and less massive the disk, but with non-negligible dispersion (e.g., Ansdell et al. 2016; Pascucci et al. 2016). However, this completeness is greatly enhanced in regions where the background emission is faint and the stellar density is low, such as L1641 and L1647. In addition, the VISION survey achieves ≳90% completeness of 20.4, 19.9, and 19.0 mag in J, H, and Ks, which allows the observation of a spatially extended sample of YSOs.
Given the average distance of Orion A of between 388 pc and 414 pc (Großschedl et al. 2018) and the spatial resolution of VISION and SODA of ~0.7″ and ~1.1″, respectively, we cannot resolve individual components in multiple systems with separations of less than 1000 AU. For example, in Figure A.9 (Appendix A) we note that source Vis2868 seems to be a double system that was not classified as such in either the SODA or VISION catalogs, due to observational limitations.
Kounkel et al. (2016) presented a NIR survey (1.6 µm) aimed at observing visual multiple systems in Orion at separations between 100 and 1000 AU. Of the 201 protostars and 198 premain-sequence stars with disks observed by these authors, they found 29 candidate binary systems and 1 candidate triple system around protostars, and 27 candidate binary systems and 1 candidate triple system around pre-main-sequence stars. In the region of interest (i.e., Orion A below −6° declination) this NIR survey allows us to identify 7 closer binary systems, which were added to our catalog and included in our analysis (see Table D.1). These double systems have all been observed by SODA, and they are all visible in the 225 GHz continuum ALMA images (see Figures A.16 and A.17 in Appendix A), although they were not resolved as a binary system and were therefore classified as single disks in the original VISION and SODA catalogs.
Raghavan et al. (2010) presented one of the most comprehensive surveys on the multiplicity of solar-type stars, covering stars within 25 parsecs of the Sun. The main conclusion is that the distribution of binary separations ranges from a few AU to over 104 AU, with a peak around 30–50 AU, suggesting that solartype stars are commonly found in binary systems with moderate separations, rather than being tightly bound or extremely wide. They also found that ~44% of solar-type stars have at least one companion, making the occurrence of binary and multiple systems quite common. Therefore, even including the Kounkel et al. (2016) visual binaries, our sample is likely to miss half of the binary systems.
2.2 Multiple system associations
We took a probabilistic approach to identifying multiple systems since detailed stellar masses and kinematics cannot be obtained for most of the sample. The probability that two objects are physically associated, indicating a true multiple system, decreases with the square of the distance between them.
To investigate the stellar multiplicity in our sample, we employed the iterative inside-out search method presented by Tobin et al. (2022). Starting from an initial search radius of 1000 AU, which by observational limitations represents the minimum observable separation in our sample, we iteratively searched for companions with an increasing separation up to 104 AU. Beyond this upper limit, we consider the probability of finding a physically bound system negligible (Tobin et al. 2022). Therefore, we searched in the VISION catalog (Grossschedl et al. 2020) for the nearest Class II neighbor to each Class II source identified by Spitzer in regions L1641 and L1647 using the k-nearest neighbors algorithm.
When two sources are associated by the algorithm, they are considered as a candidate binary system. Their individual catalog entries are replaced with a new single one, whose coordinates corresponds to the geometric midpoint of the newly formed system without any weighting. These multiple systems can be further associated with other individual sources or multiple systems. By removing the individual entries, we ensured that each component is associated with only one multiple system, avoiding multiple assignments. Since the only imposed condition is on distance, there is no upper limit on the number of potential associations.
It is important to note that the algorithm only checks the separation between the two objects forming the multiple system at a given step, but not the distance between the individual objects within the multiple systems. This means that if, for example, we consider a triple system, the distance between the three individual objects can be greater than the chosen limit, as long as the separation between the binary system and the single source forming the triple is less than 104 AU.
This method is not limited to a specific observation wavelength and offers simplicity in replication, but in order to distinguish the bound pairs from chance alignments, it is necessary to find a way to assign a measure to each system to distinguish between the two cases. We chose to consider the probability of random alignments by considering the local surface density. The procedure is described in Section 2.3.
2.3 Multiple system selection
Chance alignments with other YSOs can introduce contamination into the observed multiple systems within the sample. This likelihood of contamination generally rises with larger separations and higher local surface densities of YSOs. To address this issue, it is necessary to assess the local surface density around each target in the sample and the probability of detecting an unassociated source.
The local surface density σYSO is computed employing the k- nearest neighbors algorithm. This involves dividing the arbitrary number of neighbors by the area of the circle with a radius equal to the distance (in parsecs) between the central object and the farthest selected object. The resulting value provides an estimate of the expected number of YSOs within a given area surrounding the central target. Following Megeath et al. (2016), we selected ten neighbors, obtaining:
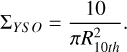 (1)
(1)
In principle, this approach can cause problems along the edges of the entire sample region. For objects along the periphery, the i-th neighbor may not represent the true i-th companion, since elements outside the region may not be considered. As a result, the local density may be underestimated. However, our SODA sample is mainly located in L1641 and L1647 (with a field of view of ~50″), while VISION (i.e., the catalog we use to identify multiple systems) has a larger spatial footprint (~19.8 deg2), and it is therefore complete when searching for our nearest companions.
In our framework, we used the following statements:
D: The object i is within the area A.
C: The object i is the companion (secondary) of the object k.
I: The primary object j is detected (background information).
The probability of whether a detected source is a companion or not is determined by Bayes’ theorem
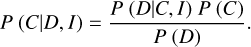 (2)
(2)
In our notation, P(D|C, I) is the probability of detecting a companion if this is actually present. We assumed the NIR catalog is complete for Class II sources and thus P(D|C, I) = 1.
P(D|1) is the combined probability of detecting a source, whether it is a companion or an unassociated source, within a given research radius d. To derive these terms, we followed the process outlined in Tobin et al. (2022). The detection probability is modeled as a Poisson distribution,
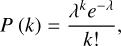 (3)
(3)
where λ = ΣYSO πd2, d the search radius employed in the density calculation and k = 10 is the number of expected YSOs within this radius. Therefore, the probability of detecting at least one unassociated source is
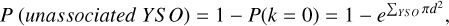 (4)
(4)
the overall probability of detecting an object, regardless of its state of association, is
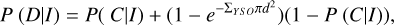 (5)
(5)
and the probability that this object is the secondary of a binary system depends only on the separation and the local surface density of YSOs:
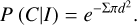 (6)
(6)
For each candidate, we computed the probability of it being a multiple system, including in our final catalog only those that passed the threshold value of 0.9. If we are missing any other information (such as the relative velocity) and as such are unable to test the robustness of this approach, the best choice is to consider a high threshold (P > 0.9), which minimizes false positives while maintaining a high true positive rate.
3 Results
Our final catalog counts 61 binary systems, 3 triple systems, and 1 quadruple system, located in the regions L1641 and L1647 of Orion A. Figure 1a shows the sample distribution of our binary systems in Orion A color coded according to the system mean disk dust mass, whereas Figure 1b shows the distribution of the same sample color coded according to the system separation. It appears that the lower mass binaries are mainly located at lower longitudes, while the higher mass ones are at higher longitudes. On the other hand, systems with separations smaller than about 3 kAU are evenly distributed along the Orion A filament, while those with the largest separations are mainly located in L1641-S and L1641-N. van Terwisga & Hacar (2023) have demonstrated that L1641-S and L1641-N contain the most irradiated disks in Orion A. Therefore, our separation distribution could be a result of the external far-ultraviolet (FUV) radiation: the presence of massive stars could influence the system formation process or its very early evolution.
In this study we focused primarily on disk dust mass in multiple systems. Further comments and analysis on system separation are presented in Appendix B.
The quadruple configuration is rarely observed in the other nearby star-forming regions (SFRs). Figure 2 shows the only quadruple system in our analysis, consisting of 4 young stars (ages ~1–3 Myr), each of which is surrounded by a disk detected in the mid- to far-infrared by the VISION survey, but not always detected and resolved at 225 GHz with ALMA (van Terwisga et al. 2022). Such a configuration provides a rare opportunity to better constrain the possible effects of gravitational interactions between disks within the same system. For reference, some of the assembled multiple systems are shown in Appendix A.
3.1 Disk dust mass
As discussed in Section 2, the sample was assembled considering the VISION data. This choice allows us to construct a more complete sample down to smaller separations. Nevertheless, more compact systems (separation ≤1000 AU) cannot be resolved in our sample and are usually classified as single objects. To solve this problem, our analyses include 7 new closer binaries, with separations between 100 and 1000 AU, resolved by Kounkel et al. (2016). All of these sources are visible, but not always resolved, in the continuum ALMA images at 225 GHz. We estimated the disk masses based on their ALMA continuum using the same procedure presented in Paper I (van Terwisga et al. 2022).
We assumed that the continuum millimeter flux is optically thin. Knowing the distance, d, and the opacity, kv, the millimeter continuum flux, Fv, can be related to the mass of the dust emitting the radiation via the equation:
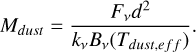 (7)
(7)
For opacity and dust effective temperature, we used the constant values of kv=2.3 cm2 g−1 and Tdust,eff=20 K, respectively, chosen in Paper I. We also used the disk distances from Paper I and the resulting range, between 380 and 455 parsecs.
Table D.1 lists average distances, projected separations and mean dust masses of our multiple systems. It should be noted, however, that the assumptions of optically thin emission and constant opacity introduce an unquantifiable source of uncertainty. There is increasing evidence that a fraction of the millimeter part of the disk structure may be optically thick (e.g., Xin et al. 2023; Zhu et al. 2019), and that the assumed opacity value of millimeter grains along the disk structure may not always be valid or constant (e.g., Krapp et al. 2022; Macías et al. 2021; Zhu et al. 2019). As a result, the disk dust masses may be underestimated. However, if the disk emission is (mostly) optically thick at these wavelengths, the millimeter continuum flux is instead tracing the radial extent of the dust in these sources.
 |
Fig. 1 Top: spatial distribution of binary systems in Orion A, color coded according to the system disk dust mass. Bottom: spatial distribution of binary systems in Orion A, color coded according to the system separation. Stars mark the position of the binary systems. Herschel SPIRE observations at 250, 300, and 500 µm (Soler 2019) form the background. |
 |
Fig. 2 Left: continuum ALMA image at 225 GHz from SODA (van Terwisga et al. 2022). The crosses mark the positions of the four sources in the quadruple system, identified by the source index in the VISION III catalog (Großschedl et al. 2020). The central pair [Vis 2570]-[Vis 2570b], has only been resolved by Kounkel et al. (2016). The beam is shown in black on the right. Right: image drawn from the ESO-VISTA NIR survey of the Orion A cloud of the same system as in the left-panel (Meingast et al. 2016). |
4 Discussion
In recent years, several surveys have been conducted in nearby SFRs to characterize the structure and better understand the evolution of protoplanetary disks through all phases of planetary formation (e.g., Tobin et al. 2022; van Terwisga et al. 2022; Zurlo et al. 2021; Manara et al. 2019). The results shed new light on key aspects such as the spatial distribution of gas and dust mass, the evolution and dynamics of the gas and dust components within the disk, or the links between the disk structure, the host star, and the planet system. Nevertheless, the available catalogs are not large enough and do not span a sufficiently large range in separations to study how multiplicity affects disk survival.
In this paper we present the largest catalog of Class II YSOs multiple systems in Orion A, about 94% of which are binary systems. Our analysis focuses on the disk dust masses, since this is undoubtedly one of the properties of crucial interest for disks, providing elementary constraints on the future content of planetary systems. Recent observations show that physical interactions within multiple systems (e.g., Zagaria et al. 2021; Manara et al. 2019; Cox et al. 2017) and (F)UV radiation (e.g., van Terwisga & Hacar 2023; Winter & Haworth 2022) significantly affect the disk masses.
In the following sections, we prove that there is a projected separation beyond which the millimeter flux (and hence the dust mass) and the separation are no longer correlated, which implies that at large separations the evolution of disks is independent of the presence of a companion. We obtain this conclusion by combining observations of protoplanetary disks in multiple systems in Orion, Lupus, and Taurus. We also show that the mass distribution of the disks in binary systems is the same in regions of similar age and that dust evolution can therefore be explained as a function of age. Finally, by focusing on the effects of stellar multiplicity on the individual components of binaries, we show that it is statistically impossible to distinguish between disks around single stars and disks around stars in multiple configurations in the SODA sample.
4.1 Flux-separation correlation
In the past decade, several (sub)millimeter surveys of protoplan- etary disks in multiple systems have focused on the relation between the radii and masses and their projected separations (e.g., Zagaria et al. 2021; Manara et al. 2019; Ansdell et al. 2016). Among these studies, Harris et al. (2012) presented a high angular resolution millimeter-wave dust continuum imaging survey of circumstellar material associated with the individual components of 23 multiple-star systems in the Taurus–Auriga young cluster, proving that the millimeter flux of the combined system positively relates to the projected separation of the stellar companion. Subsequently, Zagaria et al. (2021) proves that this same relation holds for a larger sample of Taurus disks, and if ρ Ophiuchus and Lupus samples are considered as well.
Comparing the properties of all the disks in Orion with those in Taurus and Lupus, we find essentially no difference in disk mass distribution or abundance (e.g., van Terwisga et al. 2022). Furthermore, all these regions are of similar age and have similar underlying stellar mass distributions (Da Rio et al. 2016). Thus, while the Orion sample is restricted to wide binaries, and the Lupus and Taurus samples to close binaries, the evidence suggests that the underlying populations have similar properties. It is therefore worth investigating what happens when the Orion region is included. In Fig. 3 we reproduce a plot from Zagaria et al. that includes the multiple samples from Lupus (Zurlo et al. 2021; Ansdell et al. 2018), Taurus (Akeson et al. 2020; Manara et al. 2019; Akeson & Jensen 2014; Harris et al. 2012), and the regions L1641 and L1647 of Orion A. As a guide, we show the linear regression from Zagaria et al. (2021) – performed using the hierarchical Bayes model Linmix2 (Kelly 2007) – which also includes the ρ Ophiuchus region (see Figures 1 and 3 of Zagaria et al. 2021), and the linear regression we obtain when also including our wider binary sample in Orion A. It is readily apparent that the latter trend deviates from the previous one, and that a global fit to all data is almost flat. Indeed, looking at Figure 3, it appears that at higher separations the data points are more evenly distributed across the graph, and so the previously observed flux-separation correlation may be lost.
To quantify this behavior, we performed an additional fit to the combined observations, including a separation threshold beyond which we assume a constant system dust mass. The fit is shown in Figure 4. Table 1 lists the best-fitting parameters of our two fits, and the respective corner plots are shown in Appendix C.
The plots were obtained using the UltraNest3 package by Buchner (2016), which allows the fitting and comparison of complex models and implements a Monte Carlo technique called nested sampling. Specifically for our case upper limits are treated as constraints on the parameter space. The UltraNest algorithm iteratively samples from a series of nested probability contours, gradually exploring the imposed parameter space. During each iteration, UltraNest calculates the marginal likelihood Z of the sampled parameter values based on the data and the imposed constraints, allowing the posterior distribution to be effectively explored. It is then possible to determine the relative predictive power of different models using Bayes factors (BF).
The linear regression in Figure 3 yields log Z = −20.831 ± 0.101, while the regression fit in Figure 4 yields log Z = −18.333 ± 0.109. Therefore, BF = e x p(log Z2 – log Z1) > 1, confirming that the second model is substantially favored (see Jeffreys 1998): we identify a threshold separation xedge = 127 ± 4 AU beyond which the previously observed positive correlation between pair millimeter flux and projected separation is lost.
Recent theoretical models and simulations show that multiple systems are formed mainly through three channels: turbulent fragmentation of the molecular cloud (e.g., Kawasaki & Machida 2023), thermal fragmentation of strongly perturbed, rotating, and infalling core (e.g., Boss & Keiser 2013, 2014), and fragmentation of a gravitationally unstable circumstellar disk (e.g., Longarini et al. 2023; Stamatellos & Whitworth 2009). The first two scenarios will lead to multiples that are initially separated by a few hundred to a few thousand AU, while the last one leads to the formation of companions with separation of ≤100 AU (e.g., Tobin et al. 2013; Takakuwa et al. 2012).
From this perspective, our results suggest that the systems before and after the threshold are the outcome of different formation processes. In particular, before the separation threshold we can consider the multiple system to be the result of the fragmentation of a gravitationally unstable circumstellar disk, while after this threshold, it is likely the result of the thermal fragmentation of an infalling core and the turbulent fragmentation of a molecular cloud.
In the following sections, we explore a number of alternative possible causes that could account for the different observed flux-separation correlations. First, we compared the mass distributions in the nearby SFRs aforementioned with those in Orion A (see Section 4.2), and then we analyzed what happens when we consider the components of the binary systems separately (see Section 4.3). However, the results obtained cannot explain the behavior highlighted in Figure 3.
The broken flux-separation correlation may imply that the mechanisms behind the formation of multiple systems at fixed ages are affected by external environmental influences, with dramatic effects on planet formation. van Terwisga & Hacar (2023) show that FUV radiation from the A0 and B massive stars, mainly located in the Orion Nebula Cluster (the northern part of Orion A), significantly reduces the mass of the disks, with the disks losing a factor of ∼2 in mass over two orders of magnitude in FUV field strength. However, we do not observe a significant mass-separation trend in the SODA sources alone, and the similarity of the cumulative disk mass distributions suggests that the FUV radiation does not dominate the results.
The effect of FUV on the multiplicity properties of YSOs has not been well studied, and we do not have the data to test this in more detail. In addition, the results of our analysis are inherently limited by the observed systems: the observational resolution allows us to observe only systems with large separations. A closer comparison between systems of the same age and separation with the Taurus and Lupus data is possible with ad hoc spectroscopic surveys or direct imaging.
 |
Fig. 3 Pair millimeter flux (rescaled to a distance of d = 140 pc) and dust mass of binary systems located in Orion A, Lupus (Zurlo et al. 2021; Ansdell et al. 2018), and Taurus (Akeson et al. 2020; Manara et al. 2019; Akeson & Jensen 2014; Harris et al. 2012) as a function of their projected separation. Crosses represent detections and triangles non-detections: in accordance with to Akeson et al. (2020), we consider a binary pair to be detected only if both disk components were detected. The linear regression (slope |
 |
Fig. 4 Regression best fit of the logarithm of flux over the logarithm of separation. Free parameters are the slope (m), the intercept (q), and the separation threshold (xedge). Crosses indicate detected systems and triangles upper limits. The binary systems are color coded as in Figure 3. |
4.2 Mass distribution of multiple systems in nearby SFRs
The result presented in the previous section was obtained by considering three different SFRs. Therefore, the new trend observed could be due to environmental differences in different regions. To clarify this, in this section, we compare the disk mass distributions of binaries in the four nearby SFRs Lupus, Taurus, Orion A, and Upper Scorpius.
We followed other studies (e.g., Zurlo et al. 2021; Testi et al. 2022; van Terwisga et al. 2022; Grant et al. 2021; Cazzoletti et al. 2019) in using the Kaplan–Meier estimator to infer the distribution of disk masses. We used the implementation of this estimator in the lifelines package (Davidson-Pilon et al. 2020). This nonparametric tool for assessing censored random variables, relying on the assumption that the censoring is unrelated to the variable of interest, is robust in describing these distributions and facilitates their comparison.
Figure 5 shows the inferred cumulative mass distribution for the approximately same-age Lupus, Taurus, and Orion A (age≃1–3 Myr), and the older Upper Scorpius (age≃5–11 Myr). Looking at regions of similar and different ages allows us to address the dependence between the region’s age and the evolution of the disks within it.
The cumulative trends in Figure 5 show a consistent disk evolution across the whole mass range for the younger regions. To quantify this similarity, we used the log-rank correlation test (Feigelson & Nelson 1985), which states that a significant difference between samples can only be detected when the p-value is p ≤ 0.05. Since lifelines only supports right censored data for this test, we subtracted our data from a constant before running the test. For our comparison, we find a p-value ≥0.05 for each pair combination, indicating that the cumulative distributions for Lupus, Taurus, and Orion A are not statistically distinguishable. On the contrary, the log-rank test confirms that the distribution of Upper Scorpius is statistically different from the distributions observed in the younger SFRs: the disks in the older region have lower dust masses, confirming that dust evolution is even more advanced in this region. This result is consistent with what has already been observed: recent surveys prove that if disks are optically thin at millimeter wavelengths, they typically hold just a few Earth masses of dust available for potential planet formation within the first 1–3 Myr (e.g., Ansdell et al. 2018; Andrews et al. 2013), while in later stages the dust evolution proceeds even further, resulting in even lower median disk (e.g., Barenfeld et al. 2016).
 |
Fig. 5 Dust mass distributions inferred with the Kaplan-Meier estimator for the binary systems located in Orion A, Lupus, Taurus, and Upper Scorpius. For the last three regions, we used the available data from the literature (Zurlo et al. 2021; Ansdell et al. 2018; Akeson et al. 2020; Manara et al. 2019; Akeson & Jensen 2014; Harris et al. 2012; Barenfeld et al. 2019). |
4.3 Mass distribution in Orion A: Separate system components
The results shown in Section 4.1 and 4.2 were obtained by considering the binary systems as a whole (i.e., the analyses consider the sum of the fluxes and masses of the two components of the systems). In this section, we look at how stellar multiplicity affects the individual components of binary systems. Our multiple sample results in mainly binary systems. For each of these systems, the primary disk is selected as the brightest: the disk with the lowest magnitude is selected as the primary based on the J magnitude in VISION III, or the H and K magnitudes if the J magnitude is not available.
Figure 6 shows the cumulative distributions of the primary, secondary, and single disk dust masses. As a comparison, Figure 7 shows the cumulative mass distributions for the binary systems as a whole (i.e., we considered the unweighted average mass of the dust in the two disks, and the single disk systems). This comparison suggests that the most massive disks surround single stars and that the derived distributions for binary and single systems are different. Although the two distributions are compatible within the 1 σ confidence intervals, they differ both in the region ≤102 M⊕, where the binary systems are more likely to have a higher mean mass, and in the region ≥102 M⊕, where the distribution of the pairs ends. The log-rank test yields a p-value of ∼0.023, which suggests a (weak but significant) difference in the underlying distributions, and thus the disk evolution depends on the presence of a companion and the resulting physical interactions with it. For Figure 6, on the other hand, the log-rank test proves that only the primary and the single disk distributions are statistically distinguishable (p ∼ 0.036). Given the relatively low significance of the log-rank tests and the limited sample sizes, we prefer a more robust statistical comparison between the mass distributions in Figure 6. We expect primary stars to be more massive on average than secondary stars, by definition. Spectroscopy-based stellar mass estimates are not available yet for the majority of the multiple system candidates: from the Sloan Digital Sky Survey (SDSS) APOGEE INfrared Spectroscopy of Young Nebulous Clusters program (IN-SYNC) of the Orion A molecular cloud (Da Rio et al. 2016) we obtained information for both components for only 6 pairs and information for only one component for 19 systems. From these stellar parameters, which are listed in Table D.2, we computed a mean age of 1.2 Myr for our binary sample. To ensure a more robust comparison, we adopted a bootstrap testing approach to validate the results. Specifically, we selected identical-size subsets of disks from the reference single-disk sample with similar J-band magnitude distribution of primary and secondary disks. For each resampled subset, we compared the dust mass distributions with the original distributions using the log-rank test. We repeated this procedure 104 times to generate a bootstrap distribution ofp- values. The results are shown in Figure 8. The median p-value for the primary and secondary disks is about 0.07 and 0.16, respectively, proving that the simulated and original mass distributions are statistically indistinguishable. This means that in our sample there are no significant differences between the disks in isolated and multiple systems for the separation range considered. We expect such differences for more compact multiple YSOs, but due to the limitations of our observations, we cannot reach these lowest separation ranges.
 |
Fig. 6 System mean dust mass distributions inferred with the KaplanMeier estimator for primaries, secondaries, and single Class II disks in L1641 and L1647. |
 |
Fig. 7 System mean dust mass distributions inferred with the Kaplan- Meier estimator for binary and single systems in L1641 and L1647. |
 |
Fig. 8 Cumulative distributions of p-values to compare the mass distribution of the primary and secondary disks with an equal-sized sample of randomly selected single disks with similar J-band magnitude distribution. The distributions were made by repeating the test 104 times. The median p-values for the primary sample (0.071) and the secondary sample (0.166) are shown for reference. |
5 Conclusions
We have characterized the stellar multiplicity of regions L1641 and L1647 in Orion A. The resulting catalog contains all Class II disks: 61 binary systems, 3 triple systems, and 1 quadruple system. Separations range covered is from 100 to 104 AU. This is the largest sample assembled in the literature to date. We characterized the dust mass distributions for single disk and multiple systems. Our statistical analyses allowed us to quantify the differences between these two samples and compare the disk evolution we obtain for the multiple sample with the disk evolution obtained for the multiples in other nearby SFRs.
Our main findings are as follows:
Recent studies (e.g., Harris et al. 2012; Zagaria et al. 2021) show a positive correlation between the millimeter flux (and hence the dust mass) and the projected separation of binary systems in the nearby SFRs Lupus and Taurus. Our data of Orion A alone, however, suggest a weaker correlation and are consistent with no correlation within the confidence interval: although the regression fit is inconclusive since we cannot exclude a slope equal to zero, the positive correlation within the 2 sigma range physically suggests that as the separation increases, the physical interaction between the system components becomes negligible;
When considering the joint data of Lupus, Taurus, and Orion A, the positive flux–separation correlation is lost at a threshold separation of about 130 AU;
Recent simulations and theoretical models have confirmed that different star formation processes lead to multiple systems with different separations. Our result suggests that before a threshold of 130 AU there is fragmentation of a gravitationally unstable circumstellar disk, and that beyond 130 AU there is thermal or turbulent fragmentation, respectively;
The cumulative distributions for binaries in the younger regions of Orion A, Lupus, Taurus, and the older Upper Scorpius prove that the disk evolution within regions of the same age is consistent across the mass range: a log-rank test confirms that the only statistically distinguishable distribution is Upper Scorpius, the oldest SFR, strengthening the idea that there is a universal initial mass distribution for disks;
A comparison of the mass distributions of the primary and secondary disks with an equal-sized sample of randomly selected single disks with similar J-band magnitude distributions confirms that it is not possible to statistically distinguish the dust evolution of the disk in single- and multiple-star systems for the separations considered in this study (103–104 AU);
We found a unique system: a quadruple system in which the four stars are surrounded by a protoplanetary disk detected in the mid- to far-infrared by the VISION survey, but not always detected and resolved at 225 GHz with ALMA (van Terwisga et al. 2022). Such a system has never been studied in the literature, and such an analysis would allow us to better understand the effects of the gravitational interaction between companions on the structure and the evolution of the disks, and to better constrain the typical tidal interaction that occurs in a multiple system.
Acknowledgements
The authors would like to thank the support of the Italian National Institute of Astrophysics (INAF) through the INAF GTO Grant ERIS & SHARK GTO data exploitation and the European Union’s Horizon 2020 research and innovation program and the European Research Council via the ERC Synergy Grant ECOGAL (project ID 855130). This paper makes use of the following ALMA data: ADS/JAO.ALMA#2019.1.01813.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), NSTC (U.S.) ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. We also want to sincerely thank Steven N. Shore and Riccardo Franceschi for helpful discussions, and Stefano Rinaldi for reading the first draft of this article.
Appendix A Multiple systems in ALMA and VISION (JHKs) data
In this section, we present some continuum ALMA images at 225 GHz from SODA (van Terwisga et al. 2022) in which our multiple systems are visible. For each image, the source at the center indicates the primary disk, that is, the brightest disk in the multiple system according to JHKs magnitudes in VISION III (Großschedl et al. 2019).
 |
Fig. A.1 Continuum ALMA image at 225 GHz of binary system MGM 143–MGM 144 from SODA (van Terwisga et al. 2022). The crosses mark the positions of the sources within the multiple system, identified by the index in either the VISION III catalog (Großschedl et al. 2020) or in the Megeath et al. (2012) catalog. The beam is shown in black on the right. |
Appendix B System separation
This work focuses mainly on the dust mass of the Class II disk, which is directly proportional to the millimeter flux of the disk itself. Among the analyses performed, special attention has been given to deriving the relationship between the system mean mass, the system flux, and the system separation.
In this appendix, we focus on the separation of multiple systems. Figure B.1 shows the cumulative distribution of the projected separation of our binary systems. Closer binary systems (projected separation between 100 and 1000 au) resolved by Kounkel et al. (2016), were also considered.
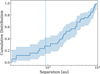 |
Fig. B.1 Cumulative distribution of the system separation inferred with the Kaplan-Meier estimator for binary systems in L1641 and L1647. The closer systems resolved by Kounkel et al. (2016) are located before the vertical blue line. |
Since the separation between companions can provide information about the formation process of the multiple system, it is interesting to consider objects of different ages. Our catalog only includes Class II disks, and the observations we used for our analyses of Taurus and Lupus are only of Class II YSOs. Tobin et al. (2022) characterize protostellar multiplicity in Orion considering younger and more embedded sources: Class 0, I, and flat spectrum (FT) YSOs. Considering all the binary systems in these surveys, in Figure B.2 we again show the pair millimeter flux as a function of the system separation, while in Figure B.3 we show the flux density ratio over systems separation for the binary disk systems located in Orion and Taurus. We note that in Figure B.2, the flux of each system is corrected for the frequency difference and rescaled at the same distance. Indeed, the Class II sample is observed at 1.3 mm, while Tobin et al. (2022) have observations at 0.85 or 9 mm. To convert the fluxes into 1.3 mm, we assumed Fv ∝ v−3, which is valid under the assumption of optically thin emission with a dust opacity spectral index β ≃ 1. To rescale the fluxes at 140 pc, we assumed F ∝ d−2. In Figure B.3, the flux ratio considered is instead simply equal to the ratio between the minor and major fluxes. This is because Tobin et al. (2022) do not denote the primary and secondary disks within their binary systems.
Figure B.2 shows that the pair flux of embedded double systems tends to be higher. Although the envelope of gas and dust surrounding these YSOs is more prominent at submillimeter and beyond wavelengths, it can still contribute to the millimeter-wavelength emission and hence to the observed millimeter flux. However, according to Figure B.3, if we look at the flux density ratio, there is no obvious distinction between the different stages. The plot is uniformly populated and there is no correlation between the flux ratio and the separation.
 |
Fig. B.2 Millimeter flux in binary systems located in Orion, Lupus, and Taurus as a function of their projected separation. The flux of each system is rescaled at 140 pc, i.e., the average distance of Taurus. The Class II sources are Orion A (this work), Lupus (Zurlo et al. 2021; Ansdell et al. 2018), and Taurus (Akeson et al. 2020; Manara et al. 2019; Akeson & Jensen 2014; Harris et al. 2012). The Class 0, I, and FT sources are Orion (Tobin et al. 2022). We only considered systems detected by ALMA (0.87 mm). |
 |
Fig. B.3 Flux density ratio vs. separation for binaries in Orion (the sample of multiple Class 0, I, and FS disks from Tobin et al. 2022 and our multiple Class II disks) and Taurus (multiple systems presented by Akeson et al. 2020, Manara et al. 2019, and Akeson & Jensen 2014). |
Appendix C Flux-separation correlation: Corner plots
In this appendix we present corner plots of the data shown in Figures 3 and 4
 |
Fig. C.1 Corner plot of the data presented in Fig. 3: the posterior parameter distribution and the correlations between the free parameters slope (m) and intercept (q). |
 |
Fig. C.2 Corner plot of the data presented in Fig. 4: the posterior parameter distribution and the correlations between the free parameters slope (m), intercept (q), and separation threshold (xedge). |
Appendix D Additional tables
Multiple systems in the L1641 and L1647 regions of Orion A. In Col. 1, the first index indicates the primary disk.
Stellar masses
References
- Adams, F. C., Proszkow, E. M., Fatuzzo, M., & Myers, P. C. 2006, ApJ, 641, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Akeson, R. L., & Jensen, E. L. N. 2014, ApJ, 784, 62 [Google Scholar]
- Akeson, R. L., Jensen, E. L. N., Carpenter, J., et al. 2020, VizieR Online Data Catalog, J/ApJ/872/158 [Google Scholar]
- Andrews, S. M., Rosenfeld, K. A., Kraus, A. L., & Wilner, D. J. 2013, ApJ, 771, 129 [Google Scholar]
- Ansdell, M., Williams, J. P., van der Marel, N., et al. 2016, ApJ, 828, 46 [Google Scholar]
- Ansdell, M., Williams, J. P., Trapman, L., et al. 2018, ApJ, 859, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Barenfeld, S. A., Carpenter, J. M., Ricci, L., & Isella, A. 2016, ApJ, 827, 142 [Google Scholar]
- Barenfeld, S. A., Carpenter, J. M., Sargent, A. I., et al. 2019, ApJ, 878, 45 [Google Scholar]
- Bate, M. R. 2018, MNRAS, 475, 5618 [Google Scholar]
- Bonavita, M., & Desidera, S. 2007, A&A, 468, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boss, A. P., & Keiser, S. A. 2013, ApJ, 764, 136 [Google Scholar]
- Boss, A. P., & Keiser, S. A. 2014, in Dense Cores: Origin, Evolution, and Collapse, 4, 108.01 [Google Scholar]
- Buchner, J. 2016, Statist. Comput., 26, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Cazzoletti, P., Manara, C. F., Liu, H. B., et al. 2019, A&A 626, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, E. G., Harris, R. J., Looney, L. W., et al. 2017, ApJ, 851, 83 [Google Scholar]
- Da Rio, N., Tan, J. C., Covey, K. R., et al. 2016, ApJ, 818, 59 [Google Scholar]
- Davidson-Pilon, C., Kalderstam, J., Zivich, P., et al. 2020, https://doi.org/10.5281/zenodo.3629409 [Google Scholar]
- Duchêne, G. 2010, ApJ, 709, L114 [Google Scholar]
- Duchêne, G., & Kraus, A. 2013, ARA&A, 51, 269 [Google Scholar]
- Espaillat, C. C., Herczeg, G. J., Thanathibodee, T., et al. 2022, AJ, 163, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [Google Scholar]
- Feigelson, E. D., & Nelson, P. I. 1985, ApJ, 293, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Furlan, E., Fischer, W. J., Ali, B., et al. 2016, ApJS, 224, 5 [Google Scholar]
- Grant, S. L., Espaillat, C. C., Wendeborn, J., et al. 2021, ApJ, 913, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Großschedl, J. E., Alves, J., Meingast, S., et al. 2018, A&A, 619, A106 [Google Scholar]
- Großschedl, J. E., Alves, J., Teixeira, P. S., et al. 2019, A&A, 622, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grossschedl, J. E., Alves, J., Teixeira, P. S., et al. 2020, VizieR Online Data Catalog: Vienna survey in Orion. III. (Grossschedl+, 2019), VizieR On-line Data Catalog: J/A+A/622/A149. Originally published in: 2019A&A…622A.149G [Google Scholar]
- Großschedl, J. E., Alves, J., Teixeira, P. S., et al. 2020, VizieR Online Data Catalog, J/A+A/622/A149 [Google Scholar]
- Harris, R. J., Andrews, S. M., Wilner, D. J., & Kraus, A. L. 2012, ApJ, 751, 115 [Google Scholar]
- Holman, M. J., & Wiegert, P. A. 1999, AJ, 117, 621 [Google Scholar]
- Jeffreys, H. 1998, The Theory of Probability, Oxford Classic Texts in the Physical Sciences (OUP Oxford) [Google Scholar]
- Kawasaki, Y., & Machida, M. N. 2023, MNRAS, 522, 3679 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, B. C. 2007, ApJ, 665, 1489 [Google Scholar]
- Kounkel, M., Megeath, S. T., Poteet, C. A., Fischer, W. J., & Hartmann, L. 2016, ApJ, 821, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Krapp, L., Kratter, K. M., & Youdin, A. N. 2022, ApJ, 928, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, A. L., Ireland, M. J., Martinache, F., & Hillenbrand, L. A. 2011, ApJ, 731, 8 [Google Scholar]
- Kroupa, P. 1995, MNRAS, 277, 1491 [Google Scholar]
- Larson, R. B. 2001, in The Formation of Binary Stars, 200, eds. H. Zinnecker, & R. Mathieu, 93 [Google Scholar]
- Lesur, G., Ercolano, B., Flock, M., et al. 2022, arXiv e-prints [arXiv:2203.09821] [Google Scholar]
- Lewis, J. A., & Lada, C. J. 2016, ApJ, 825, 91 [Google Scholar]
- Longarini, C., Armitage, P. J., Lodato, G., Price, D. J., & Ceppi, S. 2023, MNRAS, 522, 6217 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Omukai, K., Matsumoto, T., & Inutsuka, S.-I. 2008, ApJ, 677, 813 [NASA ADS] [Google Scholar]
- Macías, E., Guerra-Alvarado, O., Carrasco-González, C., et al. 2021, A&A, 648, A33 [EDP Sciences] [Google Scholar]
- Manara, C. F., Tazzari, M., Long, F., et al. 2019, A&A, 628, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marks, M., Leigh, N., Giersz, M., et al. 2014, MNRAS, 441, 3503 [NASA ADS] [CrossRef] [Google Scholar]
- Megeath, S. T., Gutermuth, R., Muzerolle, J., et al. 2012, AJ, 144, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Megeath, S. T., Gutermuth, R., Muzerolle, J., et al. 2016, AJ, 151, 5 [Google Scholar]
- Meingast, S., Alves, J., Mardones, D., et al. 2016, A&A, 587, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moe, M., & Di Stefano, R. 2017, ApJS, 230, 15 [Google Scholar]
- Pascucci, I., Testi, L., Herczeg, G. J., et al. 2016, ApJ, 831, 125 [Google Scholar]
- Pinte, C., Teague, R., Flaherty, K., et al. 2023, in Astronomical Society of the Pacific Conference Series, 534, Protostars and Planets VII, eds. S. Inutsuka, Y. Aikawa, T. Muto, K. Tomida, & M. Tamura, 645 [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [Google Scholar]
- Reipurth, B., Guimarães, M. M., Connelley, M. S., & Bally, J. 2007, AJ, 134, 2272 [NASA ADS] [CrossRef] [Google Scholar]
- Reipurth, B., Clarke, C. J., Boss, A. P., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 267 [Google Scholar]
- Rodríguez, L. F., D’Alessio, P., Wilner, D. J., et al. 1998, Nature, 395, 355 [CrossRef] [Google Scholar]
- Rota, A. A., Manara, C. F., Miotello, A., et al. 2022, A&A, 662, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soler, J. D. 2019, A&A, 629, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stamatellos, D., & Whitworth, A. P. 2009, MNRAS, 400, 1563 [CrossRef] [Google Scholar]
- Takakuwa, S., Saito, M., Lim, J., et al. 2012, ApJ, 754, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., Natta, A., Manara, C. F., et al. 2022, A&A, 663, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tobin, J. J., Chandler, C. J., Wilner, D. J., et al. 2013, ApJ, 779, 93 [Google Scholar]
- Tobin, J. J., Looney, L. W., Li, Z.-Y., et al. 2016, ApJ, 818, 73 [CrossRef] [Google Scholar]
- Tobin, J. J., Offner, S. S. R., Kratter, K. M., et al. 2022, ApJ, 925, 39 [NASA ADS] [CrossRef] [Google Scholar]
- van Terwisga, S. E., & Hacar, A. 2023, A&A, 673, L2 [CrossRef] [EDP Sciences] [Google Scholar]
- van Terwisga, S. E., Hacar, A., van Dishoeck, E. F., Oonk, R., & Portegies Zwart, S. 2022, A&A, 661, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winter, A. J., & Haworth, T. J. 2022, Eur. Phys. J. Plus, 137, 1132 [NASA ADS] [CrossRef] [Google Scholar]
- Xin, Z., Espaillat, C. C., Rilinger, A. M., Ribas, Á., & Macías, E. 2023, ApJ, 942, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Zagaria, F., Rosotti, G. P., & Lodato, G. 2021, MNRAS, 507, 2531 [NASA ADS] [CrossRef] [Google Scholar]
- Zagaria, F., Rosotti, G. P., Alexander, R. D., & Clarke, C. J. 2023, Eur. Phys. J. Plus, 138, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Ginski, C., Huang, J., et al. 2023, A&A, 672, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhu, Z., Zhang, S., Jiang, Y.-F., et al. 2019, ApJ, 877, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Zurlo, A., Cieza, L. A., Ansdell, M., et al. 2021, MNRAS, 501, 2305 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Multiple systems in the L1641 and L1647 regions of Orion A. In Col. 1, the first index indicates the primary disk.
All Figures
 |
Fig. 1 Top: spatial distribution of binary systems in Orion A, color coded according to the system disk dust mass. Bottom: spatial distribution of binary systems in Orion A, color coded according to the system separation. Stars mark the position of the binary systems. Herschel SPIRE observations at 250, 300, and 500 µm (Soler 2019) form the background. |
| In the text | |
 |
Fig. 2 Left: continuum ALMA image at 225 GHz from SODA (van Terwisga et al. 2022). The crosses mark the positions of the four sources in the quadruple system, identified by the source index in the VISION III catalog (Großschedl et al. 2020). The central pair [Vis 2570]-[Vis 2570b], has only been resolved by Kounkel et al. (2016). The beam is shown in black on the right. Right: image drawn from the ESO-VISTA NIR survey of the Orion A cloud of the same system as in the left-panel (Meingast et al. 2016). |
| In the text | |
 |
Fig. 3 Pair millimeter flux (rescaled to a distance of d = 140 pc) and dust mass of binary systems located in Orion A, Lupus (Zurlo et al. 2021; Ansdell et al. 2018), and Taurus (Akeson et al. 2020; Manara et al. 2019; Akeson & Jensen 2014; Harris et al. 2012) as a function of their projected separation. Crosses represent detections and triangles non-detections: in accordance with to Akeson et al. (2020), we consider a binary pair to be detected only if both disk components were detected. The linear regression (slope |
| In the text | |
 |
Fig. 4 Regression best fit of the logarithm of flux over the logarithm of separation. Free parameters are the slope (m), the intercept (q), and the separation threshold (xedge). Crosses indicate detected systems and triangles upper limits. The binary systems are color coded as in Figure 3. |
| In the text | |
 |
Fig. 5 Dust mass distributions inferred with the Kaplan-Meier estimator for the binary systems located in Orion A, Lupus, Taurus, and Upper Scorpius. For the last three regions, we used the available data from the literature (Zurlo et al. 2021; Ansdell et al. 2018; Akeson et al. 2020; Manara et al. 2019; Akeson & Jensen 2014; Harris et al. 2012; Barenfeld et al. 2019). |
| In the text | |
 |
Fig. 6 System mean dust mass distributions inferred with the KaplanMeier estimator for primaries, secondaries, and single Class II disks in L1641 and L1647. |
| In the text | |
 |
Fig. 7 System mean dust mass distributions inferred with the Kaplan- Meier estimator for binary and single systems in L1641 and L1647. |
| In the text | |
 |
Fig. 8 Cumulative distributions of p-values to compare the mass distribution of the primary and secondary disks with an equal-sized sample of randomly selected single disks with similar J-band magnitude distribution. The distributions were made by repeating the test 104 times. The median p-values for the primary sample (0.071) and the secondary sample (0.166) are shown for reference. |
| In the text | |
 |
Fig. A.1 Continuum ALMA image at 225 GHz of binary system MGM 143–MGM 144 from SODA (van Terwisga et al. 2022). The crosses mark the positions of the sources within the multiple system, identified by the index in either the VISION III catalog (Großschedl et al. 2020) or in the Megeath et al. (2012) catalog. The beam is shown in black on the right. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1 but for the triple system MGM 192 -MGM 191 - MGM 193. |
| In the text | |
 |
Fig. A.3 Same as Fig. A.1 but for the binary system MGM 227 -Vis 3009. |
| In the text | |
 |
Fig. A.4 Same as Fig. A.1 but for the binary system MGM 230 -MGM 229. |
| In the text | |
 |
Fig. A.5 Same as Fig. A.1 but for the binary system MGM 241 -MGM 243. |
| In the text | |
 |
Fig. A.6 Same as Fig. A.1 but for the binary system MGM 355 -Vis 2635. |
| In the text | |
 |
Fig. A.7 Same as Fig. A.1 but for the binary system MGM 378 -MGM 379. |
| In the text | |
 |
Fig. A.8 Same as Fig. A.1 but for the binary system MGM 407 - MGM 405. |
| In the text | |
 |
Fig. A.9 Same as Fig. A.1 but for the binary system MGM 43 -Vis 2868. |
| In the text | |
 |
Fig. A.10 Same as Fig. A.1 but for the triple system MGM 55 -MGM 56 - Vis 2858. |
| In the text | |
 |
Fig. A.11 Same as Fig. A.1 but for the binary system MGM 597 -MGM 591. |
| In the text | |
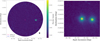 |
Fig. A.12 Same as Fig. A.1 but for the binary system MGM 70 -Vis 3035. |
| In the text | |
 |
Fig. A.13 Same as Fig. A.1 but for the binary system MGM 704 - MGM 705. |
| In the text | |
 |
Fig. A.14 Same as Fig. A.1 but for the binary system MGM 802 -MGM 803. |
| In the text | |
 |
Fig. A.15 Same as Fig. A.1 but for the binary system MGM 994 -MGM 995. |
| In the text | |
 |
Fig. A.16 Same as Fig. A.1 but for the binary system MGM 950 -MGM 950b. |
| In the text | |
 |
Fig. A.17 Same as Fig. A.1 but for the binary system MGM 523 -MGM 523b. |
| In the text | |
 |
Fig. B.1 Cumulative distribution of the system separation inferred with the Kaplan-Meier estimator for binary systems in L1641 and L1647. The closer systems resolved by Kounkel et al. (2016) are located before the vertical blue line. |
| In the text | |
 |
Fig. B.2 Millimeter flux in binary systems located in Orion, Lupus, and Taurus as a function of their projected separation. The flux of each system is rescaled at 140 pc, i.e., the average distance of Taurus. The Class II sources are Orion A (this work), Lupus (Zurlo et al. 2021; Ansdell et al. 2018), and Taurus (Akeson et al. 2020; Manara et al. 2019; Akeson & Jensen 2014; Harris et al. 2012). The Class 0, I, and FT sources are Orion (Tobin et al. 2022). We only considered systems detected by ALMA (0.87 mm). |
| In the text | |
 |
Fig. B.3 Flux density ratio vs. separation for binaries in Orion (the sample of multiple Class 0, I, and FS disks from Tobin et al. 2022 and our multiple Class II disks) and Taurus (multiple systems presented by Akeson et al. 2020, Manara et al. 2019, and Akeson & Jensen 2014). |
| In the text | |
 |
Fig. C.1 Corner plot of the data presented in Fig. 3: the posterior parameter distribution and the correlations between the free parameters slope (m) and intercept (q). |
| In the text | |
 |
Fig. C.2 Corner plot of the data presented in Fig. 4: the posterior parameter distribution and the correlations between the free parameters slope (m), intercept (q), and separation threshold (xedge). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.