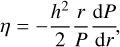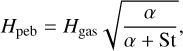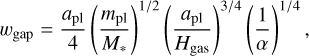| Issue |
A&A
Volume 686, June 2024
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202347605 | |
| Published online | 31 May 2024 | |
Planetesimal and planet formation in transient dust traps
1
ELTE Eötvös Loránd University, Institute of Physics and Astronomy, Department of Astronomy,
1117
Budapest,
Pázmány Péter sétány 1/A,
Hungary
e-mail: Zs.Sandor@astro.elte.hu
2
Konkoly Observatory, HUN-REN Research Centre for Astronomy and Earth Sciences,
Konkoly-Thege Miklós út 15-17,
1121
Budapest,
Hungary
3
CSFK, MTA Centre of Excellence,
Konkoly-Thege Miklós út 15-17,
1121
Budapest,
Hungary
e-mail: regaly.zsolt@csfk.org
4
Astrophysical Institute of La Plata, National Scientific and Technical Research Council and National University of La Plata,
Paseo del Bosque s/n,
1900 La
Plata,
Argentina
e-mail: oguilera@fcaglp.unlp.edu.ar
5
Millennium Nucleus of Planetary Formation (NPF),
Chile
6
New Mexico State University, Department of Astronomy,
PO Box 30001
MSC 4500,
Las Cruces,
NM
88001,
USA
Received:
30
July
2023
Accepted:
16
February
2024
Context. The ring-like structures in protoplanetary discs that are observed in the cold dust emission by ALMA might be explained by dust aggregates trapped aerodynamically in pressure maxima.
Aims. We investigate the effect of a transient pressure maximum that develops between two regimes with different turbulent levels. We study how such a pressure maximum collects dust aggregates and transforms them into large planetesimals and Moon-mass cores that can further grow into a few Earth-mass planets by pebble accretion, and eventually into giant planets by accreting a gaseous envelope.
Methods. We developed a numerical model, incorporating the evolution of a gaseous disc, the growth and transport of pebbles, N-body interactions of growing planetary cores, and their backreaction to a gas disc by opening a partial gap. Planetesimal formation by streaming instability is parametrised in our model.
Results. A transient pressure maximum efficiently accumulates dust particles that can grow larger than millimetre-sized. If this happens, dust aggregates can be transformed by the streaming instability process into large planetesimals, which can grow further by pebble accretion according to our assumptions. As the gas evolves towards a steady state, the pressure maximum vanishes, and the concentrated pebbles not transformed into planetesimals and accreted by the growing planet drift inward. During this inward drift, if the conditions of the streaming instability are met, planetesimals are formed in the disc within a wide radial range.
Conclusions. A transient pressure maximum is a favourable place for planetesimal and planet formation during its lifetime and the concentration of pebbles induces continuous formation of planetesimals even after its disappearance. In addition, the formation of a planet can trigger the formation of planetesimals over a wide area of the protoplanetary disc.
Key words: planets and satellites: formation / protoplanetary disks / planet-disk interactions
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The concept of planet formation in the pressure maxima of pro-toplanetary discs has been proposed to avoid the quick loss and destruction of solid material by rapid inward drift and high-velocity collisions a problem commonly known as the ‘metre-size barrier’ (Blum & Wurm 2008). As a possible it has been assumed that there are preferential places for dust and planet growth where the aerodynamical drag acting on dust particles and torques that lead to planet migration vanish or significantly decrease. These places are named dust and planet traps, respectively. Of particular interest are the moments when a density maximum generates a planet trap, because a pressure maximum may also develop in connection. Pressure maxima act as dust traps, collecting grains, and helping their further growth into planetesimals, or even into embryo sizes via either coagulation (Brauer et al. 2008) or drag-induced instabilities (Youdin & Shu 2002; Johansen et al. 2009). If massive embryos form in a pressure maximum due to the subsequent accretion processes, they might be locked in the nearby developed planet trap. Many authors have investigated the combined effect of a planet trap and a pressure maximum in the formation of larger bodies with sizes ranging between Mars and Jupiter (e.g. Lyra et al. 2008, 2009; Sándor et al. 2011; Regály et al. 2013; Guilera & Sándor 2017; Guilera et al. 2020; Morbidelli 2020; Chambers 2021; Sándor & Regály 2021, among many others).
Pressure traps are naturally expected to develop in disc locations where accretion flow transitions occur. An ideal candidate for such a transition could be the boundary between an accretion-ally active region, in which magnetorotational instability (MRI) plays the central role (Balbus & Hawley 1991), and an inactive region, where the low ionisation fraction of the disc causes gas to accrete on a residual level. On the other hand, the role of MRI in protoplanetary discs has been questioned over the last decade. As recent results indicate, the structure of the dead zone is relatively complex: the Ohmic dead zone, whose existence was suggested by Gammie (1996), is followed by a region in which the Hall effect is dominant – that is, a region that is prone to Hall shear instability –, which itself is then followed by a region where ambipolar diffusion is the most important effect, suppressing the MRI, and enabling the magnetic breaking by the disc wind (Lesur et al. 2014); see a recent review by Lyra & Umurhan (2019). Despite these developments in our understanding of the ionisation structure of the outer disc, the existence of a transition between regions with different accretion strengths is still generally assumed (Delage et al. 2022; Lesur et al. 2022). It is important to note that if the accretionally weaker disc region is followed by an accretionally stronger one, both the gas surface density maximum and the pressure maximum developed at the boundary of these regions will vanish as the disc adapts to its steady state (Guilera & Sándor 2017). For this reason, such maxima have limited lifetimes and can be considered as transient.
A key element of our proposed scenario is the development of such transient surface density and pressure maxima in the gas of the disc, because the high concentration of dust grains in pressure maxima may lead to planetesimal formation via streaming instability (SI), a mechanism first proposed by Youdin & Goodman (2005). The investigations of Carrera et al. (2021) show that SI is triggered for centimetre-sized dust aggregates in pressure bumps. Subsequently, Carrera & Simon (2022) found that triggering the SI in pressure bumps may be problematic for dust particles in the millimetre regime, which are the most accessible to (sub)millimetre observations with ALMA. The observations carried out by ALMA revealed ring structures of dust in protoplanetary discs. These ring structures are associated with pressure maxima that are considered to be preferential places of planet formation (e.g. Dullemond et al. 2018). Nevertheless, the formation of planetesimals by SI or by direct gravitational collapse in such pressure maxima is still an open question and the subject of active research (e.g. Carrera et al. 2021; Carrera & Simon 2022; Xu & Bai 2022a,b).
In the case of a static pressure maximum, if the SI is triggered, planetesimal formation is localised to the vicinity of the pressure maximum. This is contradicted by the fact that plan-etesimals are distributed throughout the disc, as seen in the Solar System for example (main belt of asteroids, Kuiper belt objects, etc).
There are other places where planetesimal formation can be triggered. For instance, the disc’s solid material can accumulate at the water snowline: inside the snowline, water ice evaporates, but water vapour can penetrate the low-temperature region (beyond the snowline) by outer diffusion, where it freezes out to solid dust aggregates, increasing the surface density of the solid material (see e.g. Stevenson & Lunine 1988). This enhancement of the solid particles has been investigated in the context of planetesimal formation more recently by Drążkowska & Alibert (2017). In one of the initially high-metallicity disc models (Z = 0.05) of these latter authors, the outer boundary of planetesimals can extend to 16 AU; however, in the lower metal-licity (and more realistic) cases, the outer boundary extends out to 7 AU. In addition, Drążkowska & Dullemond (2018, 2023) showed that migration of the water snowline due to the infalling material during disc formation can extend the region of plan-etesimal formation. More recently, Guilera et al. (2020) and Lau et al. (2022) showed that static pressure bumps are also preferential locations for the local formation of planetesimals because of the efficient dust accumulation at such locations. Moreover, Lau et al. (2022) showed that gravitational stirring between planetes-imals and the embryos that can form at the pressure bump can disperse planetesimals to broader regions. Finally, the works of Shibaike & Alibert (2020, 2023) should also be mentioned; these authors show that planetesimal formation happens in a pressure maximum developed at the outer edge of a migrating planet in a wide range of radii of the protoplanetary disc. In the present work, we suggest a new mechanism that triggers the formation of planetesimals at large distances from the central star and in broad regions of a few tens of astronomical units (au).
The paper is organised as follows: first, we briefly describe our code, whose detailed description is given in the Appendices, and then the particular disc model we use. Our results are presented in Sect. 3. We first show that a modest jump in the α viscosity parameter results in only a dust trap due to a traffic jam. The effect of larger jumps in the α viscosity parameter is also discussed. These large jumps result in real pressure maxima, in which solids are trapped for a long time while the pressure maxima exist due to the disc’s viscous evolution. In the subsequent subsections, for the modest and stronger jumps in viscosity, we also assume the formation of a massive planetesimal that grows due to pebble accretion and then by gas accretion. The paper closes with a summary and discussion of our results.
2 Our numerical code and disc model
To study the various effects at work at a transient density and pressure maximum, we developed a numerical model that incorporates the following processes:
Gas evolution code in the vertically integrated and axisym-metric case (Lynden-Bell & Pringle 1974).
N-body code using the Bulirsch-Stoer scheme, incorporating the mutual gravitational interactions, as well as the planet-disc interactions to follow the motion of the initially Moon-mass embryos (Sándor et al. 2011), whose masses grow by pebble accretion (Venturini et al. 2020a,b).
Partial gap opening in the gas surface density due to the growing planets (Chambers 2021), which, by altering the gas surface density profile, has a non-negligible impact on dust transport and evolution.
The two-population model for dust transport and evolution (Birnstiel et al. 2012) in the time-evolving disc, including sink terms due to pebble accretion by the growing solid planetary core and planetesimal formation via SI (as follows).
Parametrised planetesimal formation via SI, adopting various values of the planetesimal formation efficiency ζ (Drążkowska et al. 2016).
Onset of giant planet formation and the collapse of the gaseous envelope to form a giant planet (Ikoma et al. 2000).
The equations describing the above phenomena are detailed in the Appendices. We note that in this particular work, only the formation, growth, and dynamical evolution of a single planet are investigated.
A usual way to mimic the transitions between the regions of different turbulence is to apply an α viscosity parameter that is given as the function of the distance to the star:
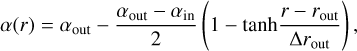 (1)
(1)
which is a smoothed step function, where rout is the radial location where the jump in viscosity occurs; see Fig. 1. The width of the transition region between the two regimes characterised by αout (for r > rout) and αin (for r < rout) is denoted by Δrout. To characterise the magnitude of the viscosity transition, we introduce
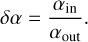 (2)
(2)
If δα = 1, there is no transition in viscosity, while a decreasing value of δα means a gradually stronger transition.
The initial condition of the gas evolution equation is
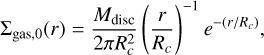 (3)
(3)
which is parametrised with the disc mass Mdisc and critical radius Rc for the disc compactness, with a viscosity prescription given by Eq. (1). Additionally, we use the following (fixed) temperature profile throughout our simulations:
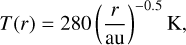 (4)
(4)
assuming a locally isothermal equation of state.
The initial condition for the dust transport equation is derived from Eq. (3):
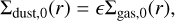 (5)
(5)
where ϵ is the solid-to-gas mass ratio, sometimes also referred to as the disc metallicity.
In our simulations, the following parameters are kept fixed: the initial dust-to-gas ratio ϵ = 0.01, and the initial size and density of dust grains, s0 = 1 µm and ρdust = 1.6 g cm−3. For the fragmentation threshold velocity of dusty ice particles, we use ufrag = 10 m s−1, which has historically been used in the literature (Gundlach & Blum 2015). However, the sticking and fragmenting properties of the ice-coated dust aggregates are extremely important for resolving the so-called bouncing barrier (Zsom et al. 2010), and are therefore the subject of intense research. The laboratory experiments of Musiolik & Wurm (2019) suggest that the water-ice-coated dust particles behave similarly to silicates, which appears to invalidate the use of the value 10 m s−1. More recently, Musiolik (2021) found that the UV-irradiated ices of various volatile molecules on the surface of dust aggregates behave like liquids, therefore increasing their sticking properties and enabling higher velocity collisions that do not lead to the fragmentation of ice-coated dust aggregates.
We apply a planetesimal formation efficiency in the interval ζ ∈ [10−6, 10−3]. In the main part of the paper, we present results that incorporate the highest value of ζ = 10−3, which is the value proposed by Drążkowska & Alibert (2017). However, Krapp et al. (2019) showed that the efficiency of planetesimal formation might be lower if the size distribution of pebbles is also considered. In a more recent paper, while applying a similar prescription for planetesimal formation, Izidoro et al. (2022) used a formation efficiency in the interval of ζ ∈ [10−6, 10−4].
In the MRI dead region, we use the viscosity parameter αin = 0.0003. This choice is motivated by the fact that even in the low-ionisation disc regions, the vertical shear instability (Stoll & Kley 2014) generates turbulent transport of gas at a similar level. In our simulations, we keep this value fixed, while we change the value of a outside the MRI dead region in the interval [7.5 × 10−4, 6 × 10−3] to control the strength of the viscosity jump, whose magnitude is an essential parameter of our study. These values, ranging between 3 × 10−4 and 3 × 10−3, or even higher, are consistent with those estimated to reproduce the observed accretion rates from recent surveys; see Ribas et al. (2020) and Rosotti (2023) and references therein. Additionally, the disc mass is Mdisc = 0.06 M⊙, the critical radius is Rc = 50 au, and the viscosity transition happens at rout = 45 au, with a width of Δrout = 2.25 au, corresponding to the disc’s scale height. The disc extends between 1 and 300 au divided by 5000 grid points placed equidistantly.
 |
Fig. 1 Viscosity jump when αin = 0.0003, δα = 0.2, rout = 45 au, and Δrout = 2.25 au. |
3 Results
3.1 Dust trap due to a traffic jam
Here, we present the outcome of our simulations when the changes in α viscosity are relatively modest, falling within the interval of
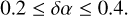 (6)
(6)
The following values are considered in our simulations: δα = 0.2, 0.25, 0.3, and 0.35. In the first simulation, δα = 0.2, and therefore αout = 0.0015. In this case, as the disc evolves, a temporary maximum in Σgas develops (see panel a of Fig. 2); however, a corresponding maximum in P(r) does not form as its derivative remains below zero dP/dr < 0. (We recall that the gas pressure P is given by Eq. (E.3).) On the other hand, the value of dP/dr is very close to zero (see panel b of Fig. 2) around the viscosity transition, and therefore the inward drift of solids is slowed down considerably, and as a consequence, dust particles are accumulated there and a ‘traffic jam’ develops, as shown in panel c. At a certain point, dust particles grow to pebble sizes; that is, their Stokes numbers become larger than our assumed threshold of St ≥ 0.01 for SI to be triggered. When the condition given by Eq. (F.3) is also fulfilled, planetesimals begin to form according to Eq. (F.4) assuming ζ = 10−3 efficiency. As |dP/dr| grows as r → 0, the inward drift of pebbles becomes gradually faster, and planetesimals form in a wide range of radii of the protoplanetary disc as the ring of concentrated pebbles rapidly drifts inward. This phenomenon is shown in panel d of Fig. 2.
To constrain the viscosity transition that still results in the formation of a visible number of planetesimals, we run a few additional simulations with fixed αinn = 0.0003 and slightly increasing δα = 0.25, 0.3, 0.35, and 0.4 values, meaning gradually decreasing differences in the turbulence between the neighbouring layers. We find that some number of planetesimals could still be formed for δα = 0.35, but not for δα = 0.4. On the other hand, the radial region in which planetesimals form is shrinking with increasing δα. Figure 3 shows the surface density of planetesimals formed for the different values of δα.
A final remark on our simulations is that even a short-living (~104 yr) transient dust trap can trigger planetesimal formation in a broad region of the protoplanetary disc. In our case, the short-living dust trap is formed due to a traffic jam triggered by a modest jump in the α viscosity parameter. Nevertheless, the existence of other mechanisms with similar outcomes cannot be excluded (e.g. Jiang & Ormel 2023).
 |
Fig. 2 Disc evolution with δα = 0.2 until the end of planetesimal formation. Panel a shows the Σgas(r) profiles for different epochs. Panels b–d show the dP(r)/dr, Σpeb(r), and Σplts(r) profiles at the same epochs as in panel a. |
3.2 Dust trap due to a pressure maximum
To see the effect of a pressure maximum on the formation of planetesimals, we describe in this section the outcomes of two simulations, in which we use viscosity transitions of δα = 0.15 and δα = 0.05. In the simulation shown here, δα = 0.15 is close to the value at which no pressure maximum develops. However, we note that the pressure maximum is transient in our presented simulations. The evolution of the Σgas(r), dP(r)/dr, Σpeb(r), and Σplts(r) profiles as a function of time is shown in panels a–d of Fig. 4. We see that during the viscous evolution of the disc, a pressure maximum develops at those radial locations where dP(r)/dr = 0 and dP(r)/dr is a strictly monotonically decreasing function of the distance r. The lifetime of the pressure maximum can therefore be constrained within the epochs 1.8 × 104 < t < 7 × 104 yr, as seen in panel b of Fig. 4. During this time interval, pebbles accumulate at the pressure maximum, forming a narrow ring-like structure. In this ring of pebbles, the SI is triggered as pebbles grow up to St > 0.01 in size and the condition given by Eq. (F.3) is fulfilled. As the pressure maximum gradually vanishes, the SI is terminated; however, due to their inward radial drift, pebbles form another sharp peak (narrow ring) in which the SI starts again. The rapidly inward-drifting ring of pebbles creates planetesimals until reaching the semi-major axis at ~3 au, corresponding to the epoch t ~ 105 yr. In this way, planetesimals form in a wide radial range of the disc quite rapidly, except for an empty ring within 34 au < r < 37 au, (see panel d of Fig. 4). When comparing the radial region of planetesimal formation, one can see that planetesimals are formed in a wider region than in our previous simulations with δα > 0.2. The reason for this result is not particularly surprising: even a short-living pressure maximum can efficiently collect pebbles that form a massive ring that can survive for a longer time as its drifts closer to the star.
To see the effect of the parameter δα on the formation of planetesimals, we redo the above simulation using δα = 0.05, which represents a stronger jump in viscosity. The results of this simulation are displayed in Fig. 5. Similarly to the previous case with δα = 0.15, a pressure maximum develops but survives for a much longer time, of namely ~2 × 105 yr. During this time, pebbles are assembled in a ring-like structure around the pressure maximum and a number of them are transformed into planetes-imals. When the pressure maximum is terminated, the ring of pebbles drifts inwards and planetesimals still form in a narrow ring, as shown by the corresponding peaks in panel c of Fig. 5. In panel d, the surface density of planetesimals is shown at the epochs displayed in the panels. In this case, there is no gap in the surface density of planetesimals formed, and they form in a larger quantity. A larger jump in viscosity results in a larger overall mass of planetesimals.
During this relatively long lifetime of the pressure maximum, the formation of a larger body (planetesimal or planetary core) can also be assumed that can further grow by pebble accretion. In what follows, we describe our results for the case where the formation of a more massive planetesimal or an embryo is considered in the ring of pebbles and planetesimals.
 |
Fig. 3 Surface density of planetesimals and the radial extent of their formation sites for different values of the viscosity transition δα. The larger the value of δα, the narrower the radial region in which planetes-imals form. |
 |
Fig. 4 Same as in Fig. 2 but with δα = 0.15. In this case, a temporary pressure maximum develops. The Σgas(r) profiles are shown for different epochs in panel a. In panel b, the curves of the pressure gradient dP/dr are displayed at the same epochs as in the upper panel. Some of the curves of the pressure gradient cross the horizontal axis at zero, and therefore a temporary pressure trap forms within the following range of epochs: 1.8 × 104 < t < 7 × 104 yr. |
3.3 Effects of a growing embryo
If a sufficiently massive body (planetesimal or planetary embryo) can form in the concentrated ring of pebbles, it might be able to further grow by pebble accretion (Lambrechts & Johansen 2012). It has been shown that the fast growth of such a body can lead to the formation of a giant planet (see Guilera et al. 2020). In another study, Chambers (2021) used bodies with an initial mass of 10−4M⊕ in his simulations to grow further via pebble accretion. In a more recent investigation, Lau et al. (2022) ran self-consistent simulations on the formation of multiple planetary cores and planetesimals in a relatively wide region around the outer edge of a gap. These authors found ~3 × 10−3M⊕ to be a characteristic planetesimal mass. Inspired by the above works, in our simulations, we insert one body with the following initial masses into the pressure maximum: (i) 10−2M⊕, (ii) 3 × 10−3M⊕, and (iii) 10−4M⊕, each one corresponding to a separate simulation. Conservatively, we inserted this body when the overall mass of planetesimals exceeded 5 × 10−2M⊕ at the pressure maximum.
We are aware that more than one planetesimal is likely to form in the pressure trap (see Lau et al. 2022); however, here we assume that one body is more massive, and grows faster than the others.
As pebble accretion is assumed here to be the main mechanism responsible for the growth of the large planetesi-mals or planetary cores, it is important to check whether the inserted body is in the Bondi (headwind) or Hill (shear) regime (Lambrechts & Johansen 2012; Ormel 2017; Lyra et al. 2023). Usually, pebble accretion in the Hill regime is more efficient; however, as shown by a recent study of Lyra et al. (2023), the 3D polydisperse (using all sizes from the size distribution of pebbles) Bondi accretion could also be quite efficient. Therefore, we checked the mass of the inserted body to find out in which regime it is.
For pebble accretion in the Hill regime, the mass of the inserted body should be larger than the transition mass between the Bondi and Hill regimes (MHB), which is given by Ormel (2017):
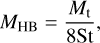 (7)
(7)
where St is the Stokes number of the particle and Mt can be written as
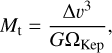 (8)
(8)
where G is the constant of gravity, ΩKep the angular velocity for the circular Keplerian orbit, and Δυ the relative velocity between pebbles and the growing body. This relative velocity can be easily calculated as
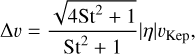 (9)
(9)
with h being the aspect ratio of the gas disc and P the gas pressure.
The limit for the 3D polydisperse Bondi accretion (Lyra et al. 2023), which can also be very effective is
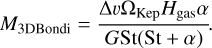 (11)
(11)
As the relative velocity Δυ tends to zero when approaching the radial position of the pressure maximum, the transition mass can also be arbitrarily small there. On the other hand, the radial position of the pressure maximum is moving slightly inwards, and therefore it is important to identify the most convenient radial position where the massive planetesimal or embryo should be inserted to be in the Hill regime of pebble accretion. To determine the optimal location of the embryo, we plot the transition masses as functions of the distance from the star in that region when planetesimal formation took place until the overall mass of planetesimals reached a value of 5 × 10−2M⊕; see panels a–c of Fig. 6.
We can see that even in the case of the traffic jam, the inserted body with a mass of 10−4M⊕ is in the Hill regime of pebble accretion; however, according to Eq. (11), it can also be in a regime of 3D polydisperse Bondi accretion. In the other two cases shown, this mass is above M3DBondi, albeit in a relatively narrow region. The other two masses, 3 × 10−3M⊕ and 10−2M⊕ are reassuringly in the Hill regime of pebble accretion. In the main part of our paper, we present those simulations that correspond to this latter case; namely a Moon-mass core is inserted when the overall mass of planetesimals rises above 5 × 10−2M⊕. The results of our simulations using bodies of smaller masses are shown in the appendix.
As a final remark, we should note that the growth process leading to the formation of this core is not modelled in our simulations; however, based on earlier investigations, we assume that the formation of such a body might physically be reasonable by runaway growth of planetesimals (Liu et al. 2019), formation of large planetesimals (Lau et al. 2022), or by gravitational collapse of the ring of pebbles (Takahashi et al. 2023).
 |
Fig. 5 Same as in Fig. 4 but with δα = 0.05. This is another case where a temporary pressure maximum develops. The Σgas(r) profiles are shown for different epochs in panel a. In panel b, the curves of the pressure gradient dP/dr are displayed at the same epochs as in the upper panel. Some of the curves of the pressure gradient cross the horizontal axis at zero, and therefore a temporary pressure trap forms between the epochs 2 × 103 < t < 2.4 × 105 yr. |
 |
Fig. 6 Transition masses (MHB and M3DBondi) as functions of the radial distance around the dust traps. In panel a, δα = 0.2 when the accumulation of solids occurs due to a traffic jam. Panels b and c show the cases in which pressure maxima are developed when δα = 0.15 and δα = 0. 05, respectively. The horizontal line displays the minimum mass of the inserted embryo in our simulations (10−4M⊕). |
3.3.1 Formation of a planet in the ‘traffic jam’ (δα = 0.2) by pebble accretion
The massive planetary body corresponding to case (i) is inserted into the initially assembled ring of pebbles around r ≈ 40 au.
The mass of this planetary core is growing further by pebble accretion, and when the maximum in Σgas is gradually diminishing and the planet trap is terminated, the planetary core begins to migrate towards the star. During the one-million-year numerical simulation with δα = 0.2, the core migrated to a distance of 7 au from the star and reached the mass of a super-Earth, mpl = 3 M⊕, which is less than the critical core mass – given by Eq. (G.1) – that would lead to the formation of a giant planet.
Figure 7 also shows the result of using gradually growing viscosity jump parameters δα. The larger the value of δα (meaning a more modest jump), the smaller the mass of the planet formed. From our simulations, we find planets masses to be in the range of 1.5–3 M⊕. As a consequence, the smaller-mass planet does not migrate as close to the central star as the more massive one. In the appendix, we present how the mass and migration history of the planet formed depend on the initial mass of the inserted body into the pressure trap.
 |
Fig. 7 Inward migration (panel a) and mass growth of the planet due to pebble accretion (panel b) during the whole length of the numerical simulation for various values of δα. The evolution of the mass and the semi-major axis of the planet for each value of δα is shown with different colours. |
3.3.2 Formation of a planet in the pressure maximum (δα = 0.15) by pebble accretion
The various effects leading to the formation of planetesimals as well as a mini-Neptune mass planet are shown in the panels of Fig. 8, where the red line shows the surface density of gas Σgas(r), the green line the surface density of solids Σpeb(r) (mostly pebbles in our case), and the blue line the surface density of planetesimals formed Σplts(r). The black dot denotes the planet and the black line is its evolutionary track on the semi-major axis-planet mass plane.
As our simulations show, immediately after the development of a density maximum in Σgas(r), a maximum in Pgas(r) develops as well. This pressure maximum traps dust particles very efficiently and these grow rapidly to sizes above St ≥ 0.01; when the condition given by Eq. (F.3) is fulfilled, SI is triggered and planetesimals begin to form. Around the epoch of t ~ 37 000 yr, displayed in panel a, when the overall mass of planetesimals formed exceeds 5 Moon masses, we insert a Moon-mass planetary core that grows further by pebble accretion; see Eqs. (C.1) and (C.4). The initial Moon-mass core grows rapidly and at t ~ 105 yr its mass is about 12.6 M⊕; see panel b. Up until this epoch, the planet has already migrated slightly inward from its place of formation following the disc’s viscous evolution and, according to Eq. (D.4), a partial gap in Σgas(r) has already been opened. The peak in the surface density of pebbles Σpeb(r) is trapped at the outer edge of this gap and moves together with the planet. At the epoch of t ~ 2 × 105 yr, the gap is deepened and widened as the planet’s mass grows up to 13.3 M⊕, as shown in panel c. Finally, at the epoch of t ~ 2.5 × 105 yr, shown in panel d, the planet’s mass is mpl ~ 13.8 M⊕, and it has migrated to apl ~ 7.6 au. As the partial gap migrates with the planet, the peak in Σpeb(r) follows the planet, and as the conditions of the SI are fulfilled, planetesimals still form, as can be seen in the Σplts(r) curve.
The mass growth and the migration history of the planet are shown in panels a and b of Fig. 9, respectively. Around the epoch of t ~ 1.17 × 105 yr, the flux of pebbles is drastically reduced, and therefore the planet reaches the critical mass given by Eq. (G.1), as no heating mechanism can support the gaseous envelope in hydrostatic equilibrium. This sudden reduction in the flux of pebbles also means that the planet reaches the pebble isolation mass (Lambrechts et al. 2014). In our work, pebble isolation is obtained self-consistently; only the gap opened by the planet regulates the flux of pebbles onto the planet. From this epoch, the mass of the planet grows solely due to gas accretion by the already existing envelope, which grows exponentially on a Kelvin-Helmholtz timescale; see Eqs. (G.4) and (G.2). Instead of solving the equations for the structure and evolution of the initial gaseous envelope,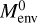 is assumed to be 10% of the total planet mass (Schneider & Bitsch 2021) and is formed mainly by evaporated pebbles, as shown by the black curve in panel b of Fig. 9. Although the mass growth of the envelope is exponential, during the planet’s migration there is not enough time for the formation of a giant planet. As the total mass of the planet at the end of its migration does not exceed 20 M⊕, we assume type I migration throughout the simulation. While the planet has been acquiring the mass of a mini Neptune-like planet, during its inward migration, planetesimals have still been forming at the outer edge of the gap, as seen in panel b of Fig. 8.
is assumed to be 10% of the total planet mass (Schneider & Bitsch 2021) and is formed mainly by evaporated pebbles, as shown by the black curve in panel b of Fig. 9. Although the mass growth of the envelope is exponential, during the planet’s migration there is not enough time for the formation of a giant planet. As the total mass of the planet at the end of its migration does not exceed 20 M⊕, we assume type I migration throughout the simulation. While the planet has been acquiring the mass of a mini Neptune-like planet, during its inward migration, planetesimals have still been forming at the outer edge of the gap, as seen in panel b of Fig. 8.
 |
Fig. 8 Episodes of mass growth and inward migration of a planet that forms at the boundary of two regions with a viscosity transition of δα = 0.15. The evolution of Σgas(r), Σpeb(r), and Σplts(r) are shown together with the migration and mass growth of the planet. The large black dot, and the black line indicate the planet’s position and its track in the apl − mpl plane. |
 |
Fig. 9 Inward migration (panel a) and mass growth of the planet due to pebble accretion and formation of a massive gaseous envelope (panel b) for δα = 0.15. Theblack line in the bottom panel reflects the assumption that the envelope’s mass is 10% of the total mass until the exponential growth of the envelope is shown with the blue line. |
3.3.3 Formation of a planet in the pressure maximum (δα = 0.05) by pebble accretion
To investigate how the value of δα affects the outcome of the above-described scenario, we also ran a simulation with δα = 0.05. In this case, the various formation episodes of planetes-imals and Neptune-mass planets (with final mass ~20 M⊕) are displayed in the panels of Fig. 10. However, the overall scenario is very similar to the case of δα = 0.15. By comparing Figs. 9 to 11, we see that in the simulation with δα = 0.15 a Neptune-mass planet forms with a mass of ~15 M⊕. However, this planet migrates closer to the star in a shorter time. This behaviour can be explained by the more modest jump in the viscosity, which results in the termination of the planet trap in a shorter time than in the simulation with δα = 0.05. Being trapped for a shorter time in the pebble-rich environment, the planet acquires a lower mass. Due to the earlier release from the planet trap, the planet also gets closer to the star. Moreover, as the accretion rate of the gaseous envelope depends on the core’s mass when the pebble accretion almost stops, the gaseous envelope is also less massive than in the case of δα = 0.05. These simulations support the conjecture that the smaller the value of δα = 0.05 (e.g. the stronger the jump of viscosities), the larger the mass of the formed planet.
Contrary to the previous simulations with δα ≥ 0.2 presented in Sects. 3.1, the solid core forms first, which is followed by the formation of planetesimals in a wide radial range of the disc at later epochs. In this sense, planetesimals are byproducts of the formation of a (mini) Neptune-like planet during its inward migration. We note that planetesimal formation at the outer edge of the gas gap opened by a migrating planet has already been proposed by Shibaike & Alibert (2020, 2023); however, in our work, the formation and growth of the planet are modelled in a more comprehensive physical model.
4 Effects of the planetesimal formation efficiency and the migration speed of the planet
In this part, we show how the final surface density of plan-etesimals and the mass of the formed planet depend on the planetesimal formation efficiency ζ and the migration speed of the planet.
4.1 The number of planetesimals formed without planet formation
Similar to in Sects. 3.1 and 3.2, here we present the results of our simulations for lower values of the planetesimal formation efficiency ζ. We ran several simulations for ζ = 10−4, 10−5, and 10−6 in cases with a traffic jam (δα = 0.2) and dust traps due to pressure maxima (δα = 0.15, 0.05). We note that, in these cases, we do not enable the formation of a large planetesimal or small planetary core due to pebble accretion from the ring of pebbles accumulating at the viscosity transition.
In Fig. 12, we present the case of δα = 0.2 with ζ ∈ [10−5, 10−3]. We note that, in this case, no pressure maximum develops in gas, and pebbles are accumulated due to a traffic jam. In agreement with our expectations, the overall mass of plan-etesimals decreases with lower values of ζ. On the other hand, planetesimal formation is triggered, and happens in the same radial extent of the disc, as the condition given by Eq. (F.3) does not depend on ζ.
In Figs. 13 and 14, the surface density of planetesimals is shown for those cases with δα = 0.15 and 0.05, in which a real pressure maximum develops at the viscosity transition. We note that the orange lines correspond to the cases of ζ = 10−3 already shown in Figs. 4 and 5. From these figures, one can immediately see that lower ζ values result in fewer planetesimals.
 |
Fig. 12 Surface density of planetesimals for different values of planetesimal formation efficiency ζ = 10−3, 10−4, and 10−5 when δα = 0.2. The larger the value of ζ, the larger the overall mass of planetesimals formed. |
 |
Fig. 13 Surface density of planetesimals for different values of planetesimal formation efficiency: ζ = 10−3, 10−4, 10−5, and 10−6 when δα = 0. 15. The larger the value of ζ, the larger the mass of planetes-imals formed. |
4.2 The number of planetesimals and the mass of the formed planet
In this part, the number of planetesimals and the mass of the planet are investigated for gradually decreasing values of the parameter ζ. Contrary to the case presented in the previous subsection, here we insert a massive planetesimal (or a relatively low-mass planetary core) into the pressure maximum when the overall mass of planetesimals formed around the pressure maximum exceeds the mass of the Moon (10−2M⊕). We use two values for the mass of the inserted body, namely 10−3M⊕ and 10−4M⊕, which are one tenth and one hundredth of the mass of the Moon, respectively. The mass of the inserted body does not affect the outcome of our simulations.
In Fig. 15, the surface density of planetesimals formed is shown when using various planetesimal formation efficiencies. The pressure maximum develops due to the viscosity jump δα = 0.15, in which a massive planetesimal is inserted. The smaller the parameter ζ, the smaller the overall mass of planetesimals formed. We also examined how the change in ζ affects the final mass of the planet formed. Interestingly, this value is not particularly sensitive to ζ: for ζ = 10−3, the mass is 14.86 M⊕; and in the interval ζ ∈ [10−6, 10−4], the mass of the planet ranges between 15.24 and 15.46 M⊕. An explanation for this slight change could be that, due to the reduced planetesimal formation efficiency, there are more pebbles for small ζ in the pressure maximum, and therefore the pebble-accretion rate is also slightly higher, leading to a higher solid core mass. When the massive planetesimal is inserted into the pressure maximum that forms due to the viscosity jump δα = 0.05, the mass of the planet formed ranges between 21.26 and 21.56 M⊕ for ζ ∈ [10−6, 10−3], while the surface density of planetesimals changes in a very similar way to the case shown in Fig. 15; we therefore we do not display this case here.
Our simulations show that, in agreement with our expectations, the reduction in planetesimal accretion efficiency leads to a lower overall mass of formed planetesimals, while in those cases where planet formation is also assumed and investigated, the final mass of the planet formed is almost insensitive to ζ.
 |
Fig. 14 Surface density of planetesimals for different values of planetesimal formation efficiency: ζ = 10−3, 10−4, 10−5, and 10−6 when δα = 0.05. The larger the value of ζ, the larger the mass of planetes-imals formed. |
4.3 The effect of the migration speed on the mass of planetesimals and the mass of the planet formed
In our simulations, due to the present capability of our model, we use a locally isothermal equation of state, meaning that the radial profile of the disc temperature is kept stationary. To keep our model simple, we therefore implemented the prescription of Tanaka et al. (2002) for migration and that of Tanaka & Ward (2004) for damping the planet’s eccentricity and inclination. However, this prescription may result in excessively fast inward migration, and so instead of considering more elaborate models for migration in the present study, we investigated a few cases in which the migration timescale is artificially increased. In this way, we can study the effects of reduced migration rates on the formation of planetesimals and the mass of the planet.
We ran several simulations with artificially increased migration times to mimic the effect of a slower inward migration. We find that, generally, a slower inward migration results in a larger final planetary mass. The reason for this result is two-fold: first, as it stays for longer at the planet trap in the vicinity of the accumulated pebbles, the solid core can grow larger, and moreover, the growing planet spends a longer time in the disc, and therefore its gaseous envelope can grow larger too. In Fig. 16, we see that the increase in the original migration timescale by a factor of two and three results in final masses of 33 M⊕ (panel b) and 60 M⊕ (panel c), respectively, while the final planetary mass after the migration of unmodified timescale is 20 M⊕ (panel a). We also checked whether or not the massive 60 M⊕ planet is subject to rapid III-type migration. As both the mass of the planet (Mp) and the Toomre Q parameter (Toomre 1964) depend on the distance from the star, we can plot the path of the planet in the Mp − Q parameter plane. In this plane, we can already identify the region in which the runaway migration occurs; see Fig. 14 in (Masset & Papaloizou 2003). We find that although the planetary mass can approach close to the region where runaway migration is possible, it always remains outside.
From Fig. 16, we also conclude that the slower inward migration also affects the overall mass of planetesimals: an increase can be seen at the onset of migration. This behaviour can be explained by the fact that the overdense ring of pebbles that follows the planet also spends more time in the region of the disc where the migration of the planet happens allowing the formation of more planetesimals. At later times, this effect cannot be seen because of the faster inward migration of the more massive planet.
Our results obtained in this section suggest that a slower inward migration indeed has implications for the final mass of the planet and planetesimals formed. In future work, we will carry out a more detailed investigation in this direction using more elaborate migration prescriptions (e.g. Paardekooper et al. 2011; Jiménez & Masset 2017) in which the heating (e.g. Guilera et al. 2019, 2021) and pebble torques are also incorporated (e.g. Guilera et al. 2023).
 |
Fig. 15 Surface density of planetesimals for different values of planetesimal formation efficiency: ζ = 10−3, 10−4, 10−5, and 10−6 when a massive planetesimal is inserted into the pressure maximum, which develops as the result of the viscosity jump δα = 0.15. The larger the value of ζ, the larger the overall mass of planetesimals formed. |
 |
Fig. 16 Results of our simulations using parameters δα = 0.05, ζ = 10−4, and reduced migration speed for planet migration. Panel a shows the reference run with unmodified migration speed. Panel b shows the same run but with twice the migration timescale (e.g. with half of the migration speed), while in panel c the migration timescale is three times resulting in third of the migration speed that displayed in panel a. All simulations are run until the planet reaches 3.7 au (which is chosen arbitrarily). The large black dot and the black line in each panel indicate the planet’s position and its track in the apl − mpl plane. |
5 Discussion and summary
Solar System examples, such as the main belt asteroids and Kuiper-belt objects, suggest that a large number of planetesimals should also form in the outer region of protoplanetary discs. In the present work, we propose a mechanism that can trigger plan-etesimal formation far from the inner disc and independently of the effect of the water snowline (Drążkowska & Alibert 2017; Drążkowska & Dullemond 2018). Planetesimal formation has also been studied in a static pressure bump by Guilera et al. (2020) and Lau et al. (2022). In the latter work, planetesimals could be dispersed in a broader region due to the gravitational interactions with the growing embryos formed in the pressure maximum. Formation of planetesimals in a broad, belt-like region has also been investigated by Shibaike & Alibert (2020, 2023), who consider an inward-migrating planet; this planet opens a gas gap and, similarly to our findings in the pressure maximum at the outer edge of the gap, planetesimals form during the migration of the planet. However, the origin of the migrating planet was not considered by these authors.
Our study shows similarities to the works of Lau et al. (2022), Shibaike & Alibert (2020, 2023), who also investigate the formation of planetesimals and a planet in a pressure trap and the formation of planetesimals in an inward-moving ring of pebbles. A significant difference is that we introduce the idea of a transient dust (and planet) trap that may develop at the boundary between two regions characterised by different accretion strengths. Due to the still limited knowledge of the exact location of such regions, we use an arbitrarily chosen boundary at 45 au, and the accretion rate of the two regions is characterised by a jump in the α viscosity parameter. It is very important to note that this bump in surface density diminishes as the disc evolves to a steady state.
If the jump in the disc’s viscosity is modest, no pressure maximum appears at the surface density maximum; however, in our particular cases, the pressure gradient becomes very close to zero, and therefore the inward drift of solids significantly slows down. Due to this slowdown, dust particles accumulate, forming an overdense ring, and planetesimals begin to form when the conditions for SI are fulfilled. As there is nothing to stop the inward drift of the ring of pebbles, it drifts more and more rapidly towards the star, because the absolute value of the (negative) pressure gradient increases as it reaches the inner region of the disc. In our particular simulations, the conditions of SI are met in a broad radial range of the disc; but this range shrinks as δα increases. Additionally, we enable the growth of a large planetesimal with a mass ranging within 10−4M⊕ ≤ mpl ≤ 10−2M⊕ when the overall mass of planetesimals exceeds 5 Moon masses at the location of the viscosity transition. This body, depending on its initial mass, can grow up to 3 M⊕ by accreting pebbles arriving from the outer realms of the protoplanetary disc and migrating inward.
In the case of a larger jump in disc viscosity, a pressure maximum also develops in connection with the surface-density maximum. In the pressure maximum, the solid particles get trapped, grow, and sediment towards the disc’s midplane, triggering SI. Similarly to the previous cases with the modest jumps in viscosity, we also enable the growth of a large planetesimal or small protoplanet (10−4M⊕ ≤ mpl ≤ 10−2M⊕) when the overall mass of planetesimals exceeds 5 Moon masses at the location of the viscosity transition. This body grows very quickly up to a planet with 10 Earth masses while partly consuming pebbles accumulated at the pressure maximum. The planet gradually opens a partial gap in the gas that traps solid particles arriving from the outer disc. These particles also form a ring ofpebbles in which planetesimals form via SI. As the planet trap vanishes, the planet migrates inwards, and the ring of pebbles moves together with it. In our simulations, planetesimals still form in this ring of pebbles during the planet’s migration. At the end of these simulations, a Neptune-mass planet is usually formed.
We show that a transition between an accretionally more active outer region and less active inner region promotes the formation of both planets and planetesimals. Planetesimals play an important role in planet formation, being the building blocks of planets. Depending on their sizes, planetesimals can further grow either by consecutive collisions or by pebble accretion, which in turn may result in the formation of the solid core of a giant planet. In the scenario presented here, the planetesimal population is not affected gravitationally by the migrating planet; this effect, which certainly results in the spreading of planetesi-mals throughout the disc, will be studied in a forthcoming work. This latter investigation may help us to understand the formation of the ancient population of minor bodies that evolve further collisionally and dynamically into the presently observed population of asteroids in the Solar System, and perhaps those in planetary systems in general.
In future work, the formation of planetary cores from the wide sea of planetesimals should also be investigated, which certainly opens a broad way for the formation of diverse planetary systems, and merits more detailed investigations.
Acknowledgements
Zs.S. acknowledges the support of the National Research, Development and Innovation Office (NKFIH, grant number MEC_R 141396) for funding his participation in the Protostars and Planets VII conference, which significantly contributed to the research presented in this paper. O.M.G. is partially supported by PIP-2971 from CONICET (Argentina) and by PICT 2020-03316 from Agencia I+D+i (Argentina). The authors thank the anonymous reviewer for the useful comments and suggestions that helped us considerably improve the manuscript.
Appendix A Gas evolution equation
To follow the gas evolution, we use the diffusion-like equation presented by Lynden-Bell & Pringle (1974):
![${{\partial {\Sigma _{{\rm{gas }}}}} \over {\partial t}} = {3 \over r}{\partial \over {\partial r}}\left[ {{r^{1/2}}{\partial \over {\partial r}}\left( {v{\Sigma _{{\rm{gas }}}}{r^{1/2}}} \right)} \right],$](/articles/aa/full_html/2024/06/aa47605-23/aa47605-23-eq13.png) (A.1)
(A.1)
where Σgas is the surface density of gas, and v is the kinematic viscosity, which according to Shakura & Sunyaev (1973) is approximated as 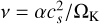 , where cs = ΩKHgas is the sound speed, Hgas is the disc’s scale height, and ΩK is the Keplerian angular velocity. The parameter α is dimensionless, embodying the strength of the turbulence. To numerically solve the above partial differential equation, we provide an initial condition Σgas,0(r) with appropriate boundary conditions: outflow at rmin, and Σgas(rmax) = 10−15M⊙au−2, where rmax = 300 au. Moreover, a temperature profile T(r) is also provided.
, where cs = ΩKHgas is the sound speed, Hgas is the disc’s scale height, and ΩK is the Keplerian angular velocity. The parameter α is dimensionless, embodying the strength of the turbulence. To numerically solve the above partial differential equation, we provide an initial condition Σgas,0(r) with appropriate boundary conditions: outflow at rmin, and Σgas(rmax) = 10−15M⊙au−2, where rmax = 300 au. Moreover, a temperature profile T(r) is also provided.
Appendix B N-Body integration including forces from the ambient disc
To solve the N-body problem, in which the planetary bodies are embedded in the protoplanetary disc, in addition to the mutual gravitational forces, forces arising from the ambient disc should also be calculated. The force (per unit mass) acting on the ith planet is given by the following system of differential equations (Cresswell & Nelson 2008):
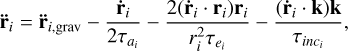 (B.1)
(B.1)
where 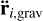 the gravitational force, r and ṙ are the position and velocity vector of the ith planet, respectively,
the gravitational force, r and ṙ are the position and velocity vector of the ith planet, respectively, 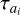 is the migration time,
is the migration time, 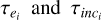 are the eccentricity and inclination damping times, respectively, and k is the unit vector in z-direction. The migration and damping timescales are calculated based on the prescription of Tanaka et al. (2002) and Tanaka & Ward (2004) for the local isothermal case using the gradients of the gas surface density and temperature. The N-body integration is done using a Bulirsch-Stoer scheme (Press et al. 1989) that we developed and proved to be efficient and accurate in our earlier investigations (Sándor et al. 2011; Horn et al. 2012).
are the eccentricity and inclination damping times, respectively, and k is the unit vector in z-direction. The migration and damping timescales are calculated based on the prescription of Tanaka et al. (2002) and Tanaka & Ward (2004) for the local isothermal case using the gradients of the gas surface density and temperature. The N-body integration is done using a Bulirsch-Stoer scheme (Press et al. 1989) that we developed and proved to be efficient and accurate in our earlier investigations (Sándor et al. 2011; Horn et al. 2012).
Appendix C Planet growth by pebble accretion
In our model, pebble accretion is incorporated following the work of Venturini et al. (2020a,b). One can distinguish between 2D and 3D accretion. Pebble accretion is in 2D if pebbles sediment at approximately the disc’s midplane and happens for low α values or high Stokes-numbers. In this case, when St < 0.1, the pebble-accretion rate of a growing planetary core is (Lambrechts & Johansen 2014):
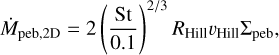 (C.1)
(C.1)
where RHill is the Hill radius of the planet, and υHill is the Hill velocity, e.g. the orbital velocity around the planetary core at the Hill radius. If 0.1 < St < 1, the above expression should be evaluated with St = 0.1. If, due to the stronger turbulence, pebbles are stirred up from the disc’s midplane, pebble accretion happens in 3D. The condition for 3D accretion is:
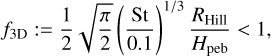 (C.2)
(C.2)
is the scale height of pebbles, given by Youdin & Lithwick (2007). In this case, the pebble accretion rate is
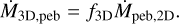 (C.4)
(C.4)
Appendix D Gap opening by the growing planet
A growing core exerts a torque on the ambient gaseous material in its region of corotation, pushing gas away. On the other hand, due to the turbulent viscosity, gas is replenished at a certain level. As a net effect, planetary cores more massive than a few times the Earth’s mass open a partial gap that is almost fully cleared if the planet reaches the Jupiter-mass regime. In our model, gap opening is modelled by the analytic formula provided by Chambers (2021), which is based on the work of Kanagawa et al. (2018). According to the latter, the depth of the gap is given by
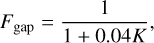 (D.1)
(D.1)
where apl and mpl are the semi-major axes and mass of the growing planet, respectively, Hgas is the scale height of the gas, M* is the mass of the star, and
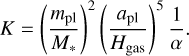 (D.3)
(D.3)
Having defined the depth and the width of the gap, the surface density profile Σgas(a) is given by
![${{{\Sigma _{{\rm{gas }}}}(a)} \over {{\Sigma _{{\rm{un }},{\rm{ gap }}}}(a)}} = 1 - \left( {1 - {F_{{\rm{gap }}}}} \right)\exp \left[ { - {1 \over 4}{{\left( {{{a - {a_p}} \over {{w_{{\rm{gap }}}}}}} \right)}^4}} \right],$](/articles/aa/full_html/2024/06/aa47605-23/aa47605-23-eq26.png) (D.4)
(D.4)
where Σun,gap(a) is the unperturbed surface density profile around the position of the planetary core. This profile approximately mimics the shape of the gap calculated by Duffell (2020).
Appendix E Dust evolution and dynamics
In protoplanetary discs, the solid-to-gas mass ratio (or metallic-ity) is assumed to be ε = 0.01, and therefore dust transport can be described by an advection-diffusion equation. In our simulations, we use the two-population model of Birnstiel et al. (2012) for the evolution of the dust surface density, in which the solid material is treated as large grains and µm-sized dust particles. The overall transport of dust particles can be investigated by solving the transport equation
![$\eqalign{ & {{\partial {\Sigma _{{\rm{dust }}}}} \over {\partial t}} + {1 \over r}{\partial \over {\partial r}}\left( {r{\Sigma _{{\rm{dust }}}}\tilde u} \right) - \cr & & {1 \over r}{\partial \over {\partial r}}\left[ {r{\Sigma _{{\rm{gas }}}}{D^*}{\partial \over {\partial r}}\left( {{{{\Sigma _{{\rm{dust }}}}} \over {{\Sigma _{{\rm{gas }}}}}}} \right)} \right] - {{\cal S}_{{\rm{acc }}}}(r,t) - {{\cal S}_{{\rm{plts }}}}(r,t) = 0, \cr} $](/articles/aa/full_html/2024/06/aa47605-23/aa47605-23-eq27.png) (E.1)
(E.1)
where Σdust is the surface density of dust particles, with the mass-weighted radial drift velocity for advection ũ and diffusion coefficient D*, whose definitions can be found in Birnstiel et al. (2012). The third term S(r, t)acc is a sink term due to the pebble accretion by the growing planetary core, while the fourth term, S(r, t)plts takes into account the loss of pebbles due to SI. We note that for Σdust, the initial and boundary conditions applied are similar to those for Σgas, apart from the multiplicative factor ϵ = 0.01.
The radial velocity u of a dust particle depends mainly on its size and the radial pressure gradient of gas (Weidenschilling 1977):
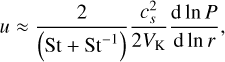 (E.2)
(E.2)
where VK is the circular Keplerian velocity, P is the pressure of the gas, and cs is the sound speed of the gas at the given location. The Stokes-number (dimensionless friction time) St of a dust particle with radius s and physical density ρp can be easily calculated both in the Epstein or Stokes/quadratic drag regimes (Rafikov 2004; Chambers 2008). The gas pressure P in the disc’s midplane can be calculated as:
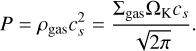 (E.3)
(E.3)
Initially, dust particles with size s0 (set to 1 µm in our simulations) grow by coagulation on the timescale
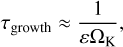 (E.4)
(E.4)
until the maximum value of
![${s_{\max }}(r,t) = \min \left[ {{s_{{\rm{frag }}}},{s_{{\rm{drift }}}},{s_{{\rm{df}}}},{s_0}\exp \left( {{t \over {{\tau _{{\rm{growth }}}}}}} \right)} \right]$](/articles/aa/full_html/2024/06/aa47605-23/aa47605-23-eq31.png) (E.5)
(E.5)
is reached, where sfrag is the fragmentation size limit, depending on the fragmentation threshold velocity of dust aggregates ufrag and the turbulence of gas, sdrift is the dust size limit due to the fast radial drift of particles, and sdf is the dust size limit due to the radial drift-induced fragmentation; see Birnstiel et al. (2012) for more details. It is commonly assumed that the fragmentation threshold velocity ufrag of dust particles varies within 1 – 10 m/s for aggregates depending on whether they are formed by silicates (lowest value) or ices (highest value); see for example Gundlach & Blum (2015).
Appendix F Planetesimal formation via streaming instability
As the pressure maximum is formed inside an accretionally less active region characterised by relatively low values of α = 10−4 − 10−3, dust particles can grow relatively quickly until they are sedimented at approximately the disc’s midplane and the (volumetric) density of pebbles, ρdust, is comparable to that of the gas ρgas. Analogously to the density of gas in the disc’s midplane,
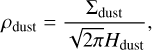 (F.1)
(F.1)
where the scale height of dust Hdust, in the presence of a turbulence characterised by the parameter α, is given by Youdin & Lithwick (2007) as
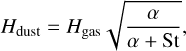 (F.2)
(F.2)
where Hgas is the scale height of gas. The condition of the onset of SI is fulfilled when
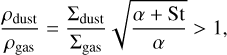 (F.3)
(F.3)
for particles with Stokes number St > 0.01 (Drążkowska et al. 2016). We note that a recent study Li & Youdin (2021) found a less restrictive condition for the SI; however, in our work, we still use the above, more conservative approach. Whenever the condition given by Equation (F.3) holds, pebbles accumulated in the pressure maximum are transformed to large planetesimals (assumed to be insensitive to drag force) with the rate:
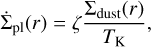 (F.4)
(F.4)
where ζ is the efficiency parameter of planetesimal formation and 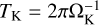 is the Keplerian orbital period at r.
is the Keplerian orbital period at r.
Appendix G Onset of giant planet formation and accretion of a gaseous envelope
A planetary core can maintain a massive gaseous envelope in hydrostatic equilibrium if there is a mechanism that assures a continuous heat release at the core’s surface. Assuming that the gaseous envelope is optically thick, the increased temperature supplies the extra pressure that counteracts the gravity of the envelope. The heat release is due to pebble or planetesimal accretion when the gravitational potential energy of solid material is converted to heat when reaching the core’s surface. If the envelope becomes massive enough at a given solid accretion rate, this extra pressure cannot counterbalance gravity and the envelope will collapse on a Kelvin-Helmholtz timescale leading to the formation of a gas giant planet. According to the numerical integrations of the equations for evolution and structure, Ikoma et al. (2000) find that the critical core mass until the gaseous envelope is in hydrostatic equilibrium. If the mass of the core is bigger than this critical mass, the gaseous envelope collapses and a giant planet forms. The critical core mass is given by:
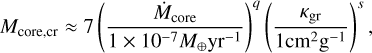 (G.1)
(G.1)
depending on the accretion rate of solids Ṁcore and the dust opacity κgr, while the exponents q and s range between 0.2 and 0.3. We note that in the outer disc, κgr = 1g/cm2 (see Guilera et al. 2020; Venturini et al. 2020a), and therefore in our simulations the exponent s does not enter into the formula of the critical core mass.
Once the mass of the planetary core becomes larger than the critical mass mpl > Mcore,cr, the gaseous envelope begins to collapse on a Kelvin-Helmholtz timescale τenv that depends on the core’s mass and the grain opacity κgr as given by Ikoma et al. (2000):
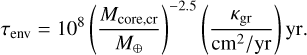 (G.2)
(G.2)
 |
Fig. H.1 Migration (upper panel) and the mass growth (bottom panel) of the planet in the three simulations using three different initial masses; see the text for the details. The curves are coloured corresponding to the initial masses. |
The growth of the envelope is then governed by τenv, as
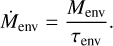 (G.3)
(G.3)
The initial condition to the above differential equation is 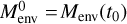 , where t0 is the time when the collapse of the envelope begins. With this initial condition, the growth of the envelope is purely exponential:
, where t0 is the time when the collapse of the envelope begins. With this initial condition, the growth of the envelope is purely exponential:
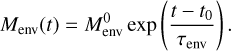 (G.4)
(G.4)
Appendix H Dependence of the mass and migration history of the planet on the initial mass of the inserted massive planetesimal
We present our results on how the mass of the large planetesi-mal affects the mass and migration history of the planet formed. We use three mass values for the planetesimal inserted in the pressure trap, namely 10−4M⊕, 3 • 10−3M⊕, and 10−2M⊕; see our detailed explanation in Section 3.3. We assume that these bodies are indeed formed in the pressure traps developed in our simulations. We also verified that even the body with the smallest mass (10−4M⊕) is in the Hill regime of pebble accretion as its mass is above the transition mass between Bondi and Hill regimes.
First, we show our results when the dust traps form in transient pressure maxima (δα ≤ 0.15). In these cases, the large planetesimal stays for a sufficiently long time in a pebble-rich region, and therefore the initial mass difference disappears in a very short time. Results for δα = 0.15 are shown in Figure H.1 in which the mass growth (bottom panel) and migration history (upper panel) of the planet formed are almost indistinguishable between simulations with different initial masses.
In the case where δα ≥ 0.2, no pressure maximum develops, and therefore the ring of pebbles is continuously drifting inwards. As a consequence, planetesimals formed are exposed to the high pebble flux for a significantly shorter time than in the cases where δα ≤ 0.15; see Figure H.2. Therefore, their initial mass differences do not disappear. As a consequence, smaller-mass planetesimals grow into smaller-mass planets.
 |
Fig. H.2 Ring of pebbles rapidly drifting away from the formation place of the large planetesimal, denoted by the black dot. |
References
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blum, J., & Wurm, G. 2008, ARA&A, 46, 21 [Google Scholar]
- Brauer, F., Henning, T., & Dullemond, C. P. 2008, A&A, 487, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carrera, D., & Simon, J. B. 2022, ApJ, 933, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Carrera, D., Simon, J. B., Li, R., Kretke, K. A., & Klahr, H. 2021, AJ, 161, 96 [Google Scholar]
- Chambers, J. 2008, Icarus, 198, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. 2021, ApJ, 914, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Cresswell, P., & Nelson, R. P. 2008, A&A, 482, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delage, T. N., Okuzumi, S., Flock, M., Pinilla, P., & Dzyurkevich, N. 2022, A&A, 658, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drążkowska, J., & Alibert, Y. 2017, A&A, 608, A92 [Google Scholar]
- Drążkowska, J., & Dullemond, C. P. 2018, A&A, 614, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drążkowska, J., & Dullemond, C. P. 2023, A&A, 671, C10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drążkowska, J., Alibert, Y., & Moore, B. 2016, A&A, 594, A105 [Google Scholar]
- Duffell, P. C. 2020, ApJ, 889, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., Birnstiel, T., Huang, J., et al. 2018, ApJ, 869, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C. F. 1996, ApJ, 457, 355 [Google Scholar]
- Guilera, O. M., & Sándor, Z. 2017, A&A, 604, A10 [Google Scholar]
- Guilera, O. M., Cuello, N., Montesinos, M., et al. 2019, MNRAS, 486, 5690 [NASA ADS] [CrossRef] [Google Scholar]
- Guilera, O. M., Sándor, Z., Ronco, M. P., Venturini, J., & Miller Bertolami, M. M. 2020, A&A, 642, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guilera, O. M., Miller Bertolami, M. M., Masset, F., et al. 2021, MNRAS, 507, 3638 [NASA ADS] [CrossRef] [Google Scholar]
- Guilera, O. M., Benitez-Llambay, P., Miller Bertolami, M. M., & Pessah, M. E. 2023, ApJ, 953, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Gundlach, B., & Blum, J. 2015, ApJ, 798, 34 [Google Scholar]
- Horn, B., Lyra, W., Mac Low, M.-M., & Sándor, Z. 2012, ApJ, 750, 34 [Google Scholar]
- Ikoma, M., Nakazawa, K., & Emori, H. 2000, ApJ, 537, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Izidoro, A., Dasgupta, R., Raymond, S. N., et al. 2022, Nat. Astron., 6, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, H., & Ormel, C. W. 2023, MNRAS, 518, 3877 [Google Scholar]
- Jiménez, M. A., & Masset, F. S. 2017, MNRAS, 471, 4917 [Google Scholar]
- Johansen, A., Youdin, A., & Mac Low, M.-M. 2009, ApJ, 704, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Kanagawa, K. D., Tanaka, H., & Szuszkiewicz, E. 2018, ApJ, 861, 140 [Google Scholar]
- Krapp, L., Benítez-Llambay, P., Gressel, O., & Pessah, M. E. 2019, ApJ, 878, L30 [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A&A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lau, T. C. H., Drazkowska, J., Stammler, S. M., Birnstiel, T., & Dullemond, C. P. 2022, A&A, 668, A170 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesur, G., Kunz, M. W., & Fromang, S. 2014, A&A, 566, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesur, G., Ercolano, B., Flock, M., et al. 2022, arXiv e-prints [arXiv:2203.09821] [Google Scholar]
- Li, R., & Youdin, A. N. 2021, ApJ, 919, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, B., Ormel, C. W., & Johansen, A. 2019, A&A, 624, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [Google Scholar]
- Lyra, W., & Umurhan, O. M. 2019, PASP, 131, 072001 [Google Scholar]
- Lyra, W., Johansen, A., Klahr, H., & Piskunov, N. 2008, A&A, 491, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyra, W., Johansen, A., Zsom, A., Klahr, H., & Piskunov, N. 2009, A&A, 497, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyra, W., Johansen, A., Cañas, M. H., & Yang, C.-C. 2023, ApJ, 946, 60 [CrossRef] [Google Scholar]
- Masset, F. S., & Papaloizou, J. C. B. 2003, ApJ, 588, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A. 2020, A&A, 638, A1 [Google Scholar]
- Musiolik, G. 2021, MNRAS, 506, 5153 [CrossRef] [Google Scholar]
- Musiolik, G., & Wurm, G. 2019, ApJ, 873, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W. 2017, Astrophys. Space Sci. Lib., 445, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S. J., Baruteau, C., & Kley, W. 2011, MNRAS, 410, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Flannery, B. P., Teukolsky, S. A., & Vetterling, W. T. 1989, Numerical Recipes in C. The art of Scientific Computing (Cambridge: Cambridge University Press) [Google Scholar]
- Rafikov, R. R. 2004, AJ, 128, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Regály, Z., Sándor, Z., Csomós, P., & Ataiee, S. 2013, MNRAS, 433, 2626 [CrossRef] [Google Scholar]
- Ribas, Á., Espaillat, C. C., Macías, E., & Sarro, L. M. 2020, A&A, 642, A171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosotti, G. P. 2023, New A Rev., 96, 101674 [NASA ADS] [CrossRef] [Google Scholar]
- Sándor, Z., & Regály, Z. 2021, MNRAS, 503, L67 [CrossRef] [Google Scholar]
- Sándor, Z., Lyra, W., & Dullemond, C. P. 2011, ApJ, 728, L9 [CrossRef] [Google Scholar]
- Schneider, A. D., & Bitsch, B. 2021, A&A, 654, A71 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shibaike, Y., & Alibert, Y. 2020, A&A, 644, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shibaike, Y., & Alibert, Y. 2023, A&A, 678, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stevenson, D. J., & Lunine, J. I. 1988, Icarus, 75, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Stoll, M. H. R., & Kley, W. 2014, A&A, 572, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takahashi, S. Z., Kokubo, E., & Inutsuka, S.-i. 2023, ApJ, 945, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., & Ward, W. R. 2004, ApJ, 602, 388 [Google Scholar]
- Tanaka, H., Takeuchi, T., & Ward, W. R. 2002, ApJ, 565, 1257 [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [Google Scholar]
- Venturini, J., Guilera, O. M., Haldemann, J., Ronco, M. P., & Mordasini, C. 2020a, A&A, 643, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturini, J., Guilera, O. M., Ronco, M. P., & Mordasini, C. 2020b, A&A, 644, A174 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [Google Scholar]
- Xu, Z., & Bai, X.-N. 2022a, ApJ, 924, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Z., & Bai, X.-N. 2022b, ApJ, 937, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [Google Scholar]
- Youdin, A. N., & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Shu, F. H. 2002, ApJ, 580, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Zsom, A., Ormel, C. W., Güttler, C., Blum, J., & Dullemond, C. P. 2010, A&A, 513, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Viscosity jump when αin = 0.0003, δα = 0.2, rout = 45 au, and Δrout = 2.25 au. |
| In the text | |
 |
Fig. 2 Disc evolution with δα = 0.2 until the end of planetesimal formation. Panel a shows the Σgas(r) profiles for different epochs. Panels b–d show the dP(r)/dr, Σpeb(r), and Σplts(r) profiles at the same epochs as in panel a. |
| In the text | |
 |
Fig. 3 Surface density of planetesimals and the radial extent of their formation sites for different values of the viscosity transition δα. The larger the value of δα, the narrower the radial region in which planetes-imals form. |
| In the text | |
 |
Fig. 4 Same as in Fig. 2 but with δα = 0.15. In this case, a temporary pressure maximum develops. The Σgas(r) profiles are shown for different epochs in panel a. In panel b, the curves of the pressure gradient dP/dr are displayed at the same epochs as in the upper panel. Some of the curves of the pressure gradient cross the horizontal axis at zero, and therefore a temporary pressure trap forms within the following range of epochs: 1.8 × 104 < t < 7 × 104 yr. |
| In the text | |
 |
Fig. 5 Same as in Fig. 4 but with δα = 0.05. This is another case where a temporary pressure maximum develops. The Σgas(r) profiles are shown for different epochs in panel a. In panel b, the curves of the pressure gradient dP/dr are displayed at the same epochs as in the upper panel. Some of the curves of the pressure gradient cross the horizontal axis at zero, and therefore a temporary pressure trap forms between the epochs 2 × 103 < t < 2.4 × 105 yr. |
| In the text | |
 |
Fig. 6 Transition masses (MHB and M3DBondi) as functions of the radial distance around the dust traps. In panel a, δα = 0.2 when the accumulation of solids occurs due to a traffic jam. Panels b and c show the cases in which pressure maxima are developed when δα = 0.15 and δα = 0. 05, respectively. The horizontal line displays the minimum mass of the inserted embryo in our simulations (10−4M⊕). |
| In the text | |
 |
Fig. 7 Inward migration (panel a) and mass growth of the planet due to pebble accretion (panel b) during the whole length of the numerical simulation for various values of δα. The evolution of the mass and the semi-major axis of the planet for each value of δα is shown with different colours. |
| In the text | |
 |
Fig. 8 Episodes of mass growth and inward migration of a planet that forms at the boundary of two regions with a viscosity transition of δα = 0.15. The evolution of Σgas(r), Σpeb(r), and Σplts(r) are shown together with the migration and mass growth of the planet. The large black dot, and the black line indicate the planet’s position and its track in the apl − mpl plane. |
| In the text | |
 |
Fig. 9 Inward migration (panel a) and mass growth of the planet due to pebble accretion and formation of a massive gaseous envelope (panel b) for δα = 0.15. Theblack line in the bottom panel reflects the assumption that the envelope’s mass is 10% of the total mass until the exponential growth of the envelope is shown with the blue line. |
| In the text | |
 |
Fig. 10 Same as in Fig. 8 but with a viscosity transition of δα = 0.05. |
| In the text | |
 |
Fig. 11 Same as in Fig. 9 but with a viscosity transition of δα = 0.05. |
| In the text | |
 |
Fig. 12 Surface density of planetesimals for different values of planetesimal formation efficiency ζ = 10−3, 10−4, and 10−5 when δα = 0.2. The larger the value of ζ, the larger the overall mass of planetesimals formed. |
| In the text | |
 |
Fig. 13 Surface density of planetesimals for different values of planetesimal formation efficiency: ζ = 10−3, 10−4, 10−5, and 10−6 when δα = 0. 15. The larger the value of ζ, the larger the mass of planetes-imals formed. |
| In the text | |
 |
Fig. 14 Surface density of planetesimals for different values of planetesimal formation efficiency: ζ = 10−3, 10−4, 10−5, and 10−6 when δα = 0.05. The larger the value of ζ, the larger the mass of planetes-imals formed. |
| In the text | |
 |
Fig. 15 Surface density of planetesimals for different values of planetesimal formation efficiency: ζ = 10−3, 10−4, 10−5, and 10−6 when a massive planetesimal is inserted into the pressure maximum, which develops as the result of the viscosity jump δα = 0.15. The larger the value of ζ, the larger the overall mass of planetesimals formed. |
| In the text | |
 |
Fig. 16 Results of our simulations using parameters δα = 0.05, ζ = 10−4, and reduced migration speed for planet migration. Panel a shows the reference run with unmodified migration speed. Panel b shows the same run but with twice the migration timescale (e.g. with half of the migration speed), while in panel c the migration timescale is three times resulting in third of the migration speed that displayed in panel a. All simulations are run until the planet reaches 3.7 au (which is chosen arbitrarily). The large black dot and the black line in each panel indicate the planet’s position and its track in the apl − mpl plane. |
| In the text | |
 |
Fig. H.1 Migration (upper panel) and the mass growth (bottom panel) of the planet in the three simulations using three different initial masses; see the text for the details. The curves are coloured corresponding to the initial masses. |
| In the text | |
 |
Fig. H.2 Ring of pebbles rapidly drifting away from the formation place of the large planetesimal, denoted by the black dot. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.