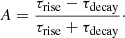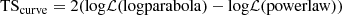EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 649 (May 2021) A&A, 649 (2021) A77 Full HTML
Free Access
Issue
A&A
Volume 649, May 2021
Article Number A77
Number of page(s) 16
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202039378
Published online 13 May 2021

© ESO 2021

1. Introduction

Narrow-line Seyfert 1 (NLSy 1) objects are typically located in the centres of spiral galaxies. They differ from normal Seyfert 1 galaxies through their unusual narrow lines originating from the broad line region (FWHM (Hβ) ≤ 2000 km s−1; Osterbrock & Pogge 1985). These lines are proportionally strong with regard to the forbidden [O III] λ5007 Å line, with a flux ratio of [O III]/Hβ ≤ 3. Surprisingly, a small percentage (<7%) of NLSy 1 galaxies are found to be radio-loud (e.g., Komossa et al. 2006; Singh & Chand 2018). When the Fermi Large Area Telescope (LAT) detected γ-ray emission from the NLSy 1 galaxy PMN J0948+0022 (Abdo et al. 2009a) in 2009, these objects became the third class of active galactic nuclei (AGNs) to be detected at γ-ray energies. This discovery was soon followed by the detection of three more γ-NLSy 1 galaxies based on data accumulated over one year (Abdo et al. 2009b).

The second data release (DR2)1 of the Fourth Fermi/LAT source catalogue (4FGL; Abdollahi et al. 2020) reports nine γ-ray detected NLSy1 galaxies, though a few other studies have proposed more identifications (see, e.g., Ciprini & Fermi-LAT Collaboration 2018; Romano et al. 2018; Paliya et al. 2018). To distinguish them from non-γ-ray detected NLSy 1s, we refer to them as γ-NLSy 1s. Among the small sample of γ-NLSy 1 galaxies, four sources have shown at least one GeV flare with a luminosity comparable to blazar flares in the first 11 years of Fermi observations. These sources are 1H 0323+342 (Paliya et al. 2014), SBS 0846+513 (D’Ammando et al. 2012), PMN J0948+0022 (Foschini et al. 2011; D’Ammando et al. 2015), and PKS 1502+036 (Paliya & Stalin 2016; D’Ammando et al. 2016). Γ-ray variability of days or weeks is a common feature of blazars (e.g., Abdo et al. 2010). Furthermore, the more powerful blazar class of flat-spectrum radio quasars (FSRQs) appears to be more variable than the less luminous BL Lacs (Rajput et al. 2020). Flaring γ-NLSy 1 galaxies therefore constitute a very interesting target for observations during states of high activity since they seem to be scarce and so rarely show flares.

As postulated, for example by Peterson et al. (2000), central black holes in NLSy 1 galaxies exhibit high accretion rates for radio-quiet and radio-loud NLSy 1 galaxies alike; however, there is an ongoing debate about the mass of their central engines. While deriving the mass via virial methods results in fairly low black hole masses of MBH < 108 M⊙ (e.g., Grupe & Mathur 2004; Deo et al. 2006; Järvelä et al. 2017), other methods suggest that black hole masses of NLSy 1s are comparable to those in FSRQs (e.g., Decarli et al. 2008; Marconi et al. 2008; Viswanath et al. 2019). Detailed discussions on this topic have recently been summarised by D’Ammando (2019) and Paliya et al. (2019).

Because Seyfert galaxies generally belong to the class of radio-quiet AGNs and are not detected in γ-rays, γ-NLSy 1s seem to contradict the AGN unification scheme (Urry & Padovani 1995). Their radio and γ-ray emission suggests that relativistic jets are present in these systems, indicating possible evolutionary processes within these sources. Additionally, the nature of their host galaxies remains an open question. D’Ammando et al. (2018), for instance, found indications for an elliptical host galaxy for the γ-NLSy 1 PKS 1502+036, although Olguín-Iglesias et al. (2020) stated that a disk-like host fits their observation better. A systematic study by the latter authors indicates that the hosts of radio-loud NLSy 1s are preferentially disk galaxies, with a spiral galaxy suggested as the host for PKS 2004−447. Furthermore, high-resolution near-infrared imaging of some of the NLSy 1s has also revealed ongoing galaxy mergers, thus suggesting a pivotal role played by such mergers in triggering the jet launching (see, e.g., Paliya et al. 2020). Therefore, given the small sample of known γ-ray NLSy 1 galaxies and their unclear nature, each new study of one of these objects can help improve our understanding of the underlying physical properties both in regard to their probable link to AGN evolution and to their role within the unified scheme of AGNs.

The most recent γ-ray flare was detected from PKS 2004−447 (Gokus 2019). This is the first gigaelectronvolt flare observed from this AGN at redshift z = 0.24 (Drinkwater et al. 1997). The source showed a γ-ray flux of (1.1 ± 0.2) × 10−6 ph cm−2 s−1 in the 0.1−300 GeV energy range on 2019 October 25 and continued to stay at a high activity level on the following day. Its flux during the flare was a factor of ∼55 higher than its average flux as reported in the 4FGL catalogue. PKS 2004−447 was one of the first γ-NLSy 1 galaxies seen by Fermi/LAT but has never before shown an outburst comparable to blazar flares. Additionally, this AGN is of a somewhat mysterious nature as it does not show typical features compared to other similarly classified sources. In the X-rays it lacks a soft excess (see e.g., Gallo et al. 2006; Orienti et al. 2015; Kreikenbohm et al. 2016), which is usually common in the spectra of NLSy 1 galaxies. In the radio band, PKS 2004−447 shows only a little extended emission and a steep spectrum, suggestive of a compact-steep-spectrum (CSS) object (Oshlack et al. 2001; Gallo et al. 2006; Schulz et al. 2016). As shown by Schulz et al. (2016), this behaviour is unique among the small γ-NLSy 1 sample, and it is also extremely rare for γ-loud AGNs. There are only five CSS sources reported in the Fourth Fermi/LAT AGN catalogue (4LAC; Ajello et al. 2020).

We have carried out a multi-frequency campaign to study this first γ-ray flaring event from PKS 2004−447, including observations from NuSTAR, Swift, XMM-Newton, and the Australia Telescope Compact Array (ATCA). In this paper we present the findings and conclusions of this dataset. We describe the data reduction in Sect. 2. We present the results of our variability analysis in Sect. 3.1 and the results of the X-ray analysis in Sect. 3.2, and we describe the model for the spectral energy distribution (SED) in Sect. 3.3. We discuss our findings in Sect. 4 and conclude in Sect. 5. We adopt a flat cosmology of H0 = 67.8 km s−1 Mpc−1, Ωλ = 0.692, and ΩM = 0.308 (Planck Collaboration XIII 2016).

2. Observations and data reduction

2.1. Fermi Large Area Telescope observations

The LAT on board the Fermi satellite is a pair-conversion telescope. It has been in operation since 2008 (Atwood et al. 2009). LAT’s all-sky monitoring strategy provides a full coverage of the γ-ray sky every 3.2 h, that is two Fermi orbits. Our reduction of the Fermi/LAT data follows the standard data reduction process2 and uses the Science Tools v11r04p00. We extract those events suitable for an analysis3 with energies in the range from 100 MeV to 300 GeV in a region of interest (ROI) of 15° centred at the 4FGL position of PKS 2004−447. We ignore all events with zenith angles ≥90°, in order to exclude γ-rays originating from Earth-limb effects. We use the post-launch instrument response function P8R3_SOURCE_V2, gll_iem_v07 as the Galactic diffuse model and iso_P8R3_SOURCE_V2_v1 to model the isotropic diffusion emission4. We use a maximum likelihood analysis to optimise our model parameters and determine the significance of the modelled γ-ray signal via the test statistic TS = 2Δlog(ℒ), where ℒ is the likelihood function that represents the difference between models with and without a point source at the source coordinates (Mattox et al. 1996). Our model includes all 4FGL sources within 20° of PKS 2004−447. Following the 4FGL, we model the spectrum of PKS 2004−447 with a logarithmic parabola and discuss the significance of the spectral curvature during the time of the flare in Sect. 3.1. For all sources within 3° that have TS ≥ 10, as well as for the isotropic and Galactic diffuse components, we leave the normalisation free to vary but keep the spectral parameters as reported in the 4FGL. For the sources not fulfilling these requirements, the normalisation is set to their respective 4FGL value as well.

Data used for compiling the low-state SED are centred in time on Swift and XMM-Newton observations performed in 2012 March and May, respectively (see Kreikenbohm et al. 2016). They cover 24 months from 2011 May 1 through 2013 May 1.

We compute a daily-binned light curve from 2019 September 26 to 2019 November 19, shown in Fig. 1, and keep the parameters of all sources in the ROI fixed to the values derived by the analysis over this time range. For a deeper investigation of the γ-ray variability in the source around the time of the γ-ray flare, we go to smaller time binnings (12 h, 6 h, and 3 h). We generate these light curves similarly to the daily binned light curve, but over a slightly shorter time range, from 2019 October 10 to 2019 November 14. Uncertainties for all Fermi/LAT light curves are shown at the 1σ level.

thumbnail Fig. 1.

Light curves in the γ-ray (top), X-ray (middle), and UV/optical (bottom) regimes from 2019 September 27 until 2019 November 19. The Fermi/LAT light curve shows the daily binned flux of the bins with TS ≥ 1. LAT light curve bins with TS < 1 are represented as 2σ upper limit arrows. All errors represent the 1σ uncertainties. For NuSTAR, the flux is interpolated down to 0.5 keV. The dark-grey shadowed region marks the time range that is used for the flare SED, while the pre- and post-flare time ranges are shown in light grey.

2.2. Neil Gehrels Swift Observatory observations

Following our detection of the flare of PKS 2004−447 on 2019 October 25 (Gokus 2019), we triggered a target of opportunity observation with the Swift satellite (Gehrels et al. 2004), which was performed on 2019 October 27 (D’Ammando et al. 2019). This observation was followed by several follow-up observations on 2019 October 28 and 30 and 2019 November 4, 6, 9, and 13. The Swift observations were performed in photon-counting mode. In order to clean the data and create calibrated event files we used the standard filtering methods and xrtpipeline, as distributed in the HEASOFT (v6.26) package. The spectrum of the source was accumulated from a circular region with a radius of 35″. The background region was defined by an annulus with an inner radius of 50″ and an outer radius of 150″ at the same coordinates as the source region.

To derive the source fluxes and describe the spectral shape, we use the Interactive Spectral Interpretation System (ISIS, Version 1.6.2-40, Houck & Denicola 2000). Throughout this paper, we describe the absorption in the interstellar medium using vern cross sections (Verner et al. 1996) and wilm abundances (Wilms et al. 2000). We use C-statistics (Cash 1979) and estimate all uncertainties at 68% confidence (1σ). The source spectra are binned after the algorithm described by Kaastra & Bleeker (2016) in order to ensure optimal binning. We adopt an absorbed power law (tbabs*powerlaw) to model each spectrum. The Galactic H I column density, NH, Gal = 2.97 × 1020 cm−2, is taken from the H I 4π survey (HI4PI; HI4PI Collaboration 2016), modelled with tbabs (Wilms et al. 2000), and kept fixed during the fit. The observations confirm a high state of the X-ray flux compared to previous X-ray observations (an overview of all X-ray observations between 2004 and 2012 is given by Kreikenbohm et al. 2016). The results are listed in Table 1 together with the results from the XMM-Newton and NuSTAR data analysed in this work. For the X-ray light curve we analyse each Swift/XRT observation individually. For building SEDs we stack all Swift observations that fall into the time interval considered.

Table 1.

Results from the analysis of the individual X-ray observations by Swift/XRT (S), XMM-Newton/MOS+pn (X), and NuSTAR/FPMA+B (N).

Simultaneously to the XRT, the Ultraviolet/Optical Telescope (UVOT) on board Swift was also observing the source. We use this instrument to derive optical and ultraviolet fluxes. The data are reduced using the standard procedures with a source region of 5″ and a background annulus with an inner radius of 7″ and an outer radius of 21″. The optical-UV fluxes shown in this paper are dereddened via the E(B − V) correction using the Fitzpatrick parametrisation (Fitzpatrick 1999). The magnitude values are converted to flux units using the unfolding procedure implemented in ISIS, which is a model-independent approach described by Nowak et al. (2005). The optical-UV light curve is shown in Fig. 1.

2.3. XMM-Newton observations

In addition to the Swift monitoring, we performed an XMM-Newton ToO observation on 2019 October 31 with an exposure time of 11 ks (ObsID: 0853980701). Archival data taken during the low state of the source were obtained from an observation in 2012 May, which has been discussed in detail by Kreikenbohm et al. (2016). The observations by XMM-Newton (Jansen et al. 2001) were performed with both the PN (Strüder et al. 2001) and the MOS (Turner et al. 2001) CCD arrays of the European Photon Imaging Camera (EPIC). The observation of optical-UV emission was conducted with the Optical Monitor (OM; Mason et al. 2001).

The observation with the EPIC was performed in the Small Window Mode with a thin filter. We use standard methods of the XMM-Newton Science Analysis System (SAS, Version 18.0) to process the observation data files, and to create calibrated event lists and images. We extract the source spectrum and a light curve for an energy range from 0.5 keV to 10 keV from a circular region of 35″ radius around the source. The background is taken from a circle with a radius of 60″. For both the source and the background spectra we extract the single and double event patterns for the EPIC-pn detector and all events for the EPIC-MOS detectors. Pile-up is negligible in the observation. We fit the spectra of the EPIC-MOS and EPIC-pn detectors simultaneously with an absorbed power law, while using the optimal binning approach. The result is listed in Table 1 together with the results from the analysis of Swift/XRT and NuSTAR observations. The X-ray flux of PKS 2004−447 seen by XMM-Newton shortly after the flare is also part of the X-ray light curve in Fig. 1.

The OM observed the source in the v, b, u, w1, and m2 filters in imaging mode with an exposure time of 1200 s, 1200 s, 1200 s, 1780 s, and 2200 s, respectively. The data were processed using the SAS task omichain and omsource. For the count rate to flux conversion we used the conversion factors given in the SAS watchout dedicated page5. The optical/UV fluxes were dereddened via E(B − V) correction, using the same approach as for Swift, and are included in the light curve shown in Fig. 1.

2.4. NuSTAR observation

We performed a ToO observation with the Nuclear Spectroscopic Telescope Array (NuSTAR; Harrison et al. 2013) with an exposure of 30 ks on 2019 November 1 (ObsID: 90501649002). We use standard methods of the software package NUSTARDAS (Version v1.8.0) distributed in HEASOFT and the calibration database (CALDB) 20190812 to reduce and extract the data for both Focal Plane Modules A and B (FPMA, FPMB). We use nuproducts to create spectra and response files. We choose a circular region with 50″ radius for the source region, and a circle with 120″ radius in a source-free region as the background region. We use the same binning method as we used for the Swift/XRT and XMM-Newton spectra and fit the spectra from FPMA and FPMB simultaneously with an absorbed power law from 3 to 79 keV. The result is given in Table 3. In order to compare the flux directly with the other X-ray observations in the light curve in Fig. 1, we extrapolate the flux down to 0.5 keV and list this value for the flux in Table 1. Initial modelling of the data shows a slight indication for a spectral hardening at higher energies that is, however, also compatible with residuals caused by slight variations of the background level at the ∼10% level. In our final fits we therefore vary the normalisation of the background by introducing a multiplicative constant that accounts for this variation.

2.5. ATCA observations

As part of the TANAMI blazar monitoring programme, ATCA has been observing PKS 2004−447 at multiple radio frequencies since 2009 (Stevens et al. 2012). The ATCA is an array of six 22 m diameter radio antennas located in northern New South Wales, at a latitude of −30° and altitude 237 m above sea level. Its baselines can be adjusted and its configuration is typically changed every few weeks. The longest possible baseline is 6 km. ATCA receivers can be quickly switched enabling observations to be made over a large range of frequencies in a short period of time. For our study, monitoring data between 5.5 GHz and 40 GHz are collected for the pre-flare and the flaring states6. The data consist of snapshot observations of PKS 2004−447 covering a duration of several minutes, which were calibrated against the ATCA primary flux calibrator PKS 1934−638. Data reduction is carried out in the standard manner with the MIRIAD software package7.

3. Results

3.1. Variability

Figure 1 shows the light curves for PKS 2004−447 based on the daily-binned γ-ray emission, and individual X-ray observations by Swift/XRT and XMM-Newton/EPIC, and optical-UV observations by Swift/UVOT and XMM-Newton/OM. The γ-ray flux started to rise on 2019 October 23 (MJD 58779). It reached a daily-averaged maximum of (1.2 ± 0.2) × 10−6 ph cm−2 s−1, which was maintained over about two days. After that, the flux decreased within two days, returning to the same flux level as before the flare. In the 3 h binned γ-ray light curves, on 2019 October 26 (MJD 58782.6), we find a maximum flux of (2.7 ± 0.6) × 10−6 ph cm−2 s−1. This is the highest γ-ray flux ever measured for PKS 2004−447. Together with the spectral index of Γ0.1−300 GeV = 2.42 ± 0.09 measured during the flare, we derive an isotropic γ-ray luminosity of (2.9 ± 0.8) × 1047 erg s−1. The light curves binned on different timescales are shown in Fig. 2. For all analyses that follow, we do not include any time bins with TS < 4, but, for visual purposes, we plot these data points as upper limits in Figs. 1 and 2.

thumbnail Fig. 2.

γ-ray light curves of PKS 2004−447 during the 2019 GeV flare for the different time binnings of the LAT data. Time bins with TS < 1 have an estimated error that was derived using their 1σ upper limit value. For those bins we show the 2σ upper limits in grey to visually show how many bins would have been rejected from the analysis otherwise. The Bayesian blocks are shown in red, while the baseline (average flux during the time range from 2019 October 10 to 2019 November 14) is shown in yellow. The dashed lines mark the time range chosen to construct the broadband SED of the flaring state.

At X-ray energies (0.5−10 keV), the flux was highest on 2019 October 30 (MJD 58786), with a flux of 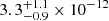3 . 3 − 0.9 + 1.1 × 10 − 12 $ 3.3^{+1.1}_{-0.9}\times10^{-12} $ erg cm−2 s−1 and a power law index of 0.8 ± 0.3. The short exposure time of this observation results in poor constraints on the spectral parameters. The optical emission in the V, B, and U bands shows strong variations. The maximum flux occured on 2019 October 27 (MJD 58783), which coincides with the time of the γ-ray flare.

To quantify the variability, we first apply a χ2 test against the null hypothesis that the emission from PKS 2004−447 is constant in each energy band. In the γ-ray band, we find a null-hypothesis probability of p < 0.006 for each of the light curves, regardless of their time binning, thus confirming variability. With a p-value < 0.00001, the X-ray light curve shown in Fig. 1 exhibits significant variability as well. On shorter timescales, however, no significant variability is detected in either the XMM-Newton (p = 0.06) or the NuSTAR (p ∼ 1) data. In the optical-UV band, strong variability (p < 0.03) at a level of up to a factor of five compared to the flux before the flare is observed with the maximum roughly coinciding with the γ-ray flare.

Variability is also seen in the ATCA radio light curves (see Fig. 3). This is in agreement with earlier work by Schulz et al. (2016), who discussed the radio variability of PKS 2004−447 based on TANAMI/ATCA observations between 2010 and 2014 and found moderate variability. Given that only two observations are located in the time range in which we analysed the γ- and X-ray variability, we do not conduct the chi-squared test on these. Following the ATCA calibrator database documentation8, we have flagged several epochs that were plotted in Schulz et al. (2016). We show an updated version of the PKS 2004−447 radio light curve, including data up to early 2020. These data are presented in Table A.1. The uncertainties reported are statistical only and do not include any systematic errors, which in general are known to be smaller than 5% in the centimetre bands (Tingay et al. 2003).

thumbnail Fig. 3.

ATCA light curves taken from 2010−2020 in the λ4 cm (5.5 GHz, 9 GHz), λ15 mm (16.8 GHz, 17 GHz, 19 GHz, and 21.2 GHz) and λ7 mm band (38 GHz, 40 GHz). The time of the flare is marked by a dashed grey line.

The radio emission of PKS 2004−447 through 2018 until early 2020 can be characterised by an overall rising trend in all radio bands. In the months prior to the γ-ray flare (marked by the dashed grey line in Fig. 3), PKS 2004−447 showed a relatively constant flux-density level of about 440 mJy at 5.5 GHz and 350 mJy at 9 GHz. Full broadband radio spectra of PKS 2004−447 were taken on 2019 October 4 and 2019 November 22, namely about 21 days before and 28 days after the 2019 October 25 γ-ray flare. Figure 4 shows a difference spectrum, which illustrates the difference between the spectra derived during each of these two epochs. While the higher frequencies show only a mild increase in radio emission after the flare, the 5.5 GHz emission increased by about 25 mJy (∼6%). It is not possible to determine whether this increase is related to the γ-ray flare. For other AGNs, delays of a few months have been reported between γ-ray flares and subsequent radio flux density increases (e.g., Fuhrmann et al. 2014; Ramakrishnan et al. 2015).

thumbnail Fig. 4.

Difference spectrum derived from the radio observations 21 days before (t1) and 28 days after (t2) the flare. The dashed line marks the zero change of the flux.

To look further into the flare behaviour in γ-rays, the Bayesian-block algorithm is applied (Scargle et al. 2013). According to Meyer et al. (2019), a flare can be described as a group of blocks, which is determined by applying the HOP9 algorithm. In this algorithm, each Bayesian block that surpasses a certain baseline is assigned to belong to its highest adjacent block. For this work, we chose the mean flux of each light curve to represent the baseline flux, as illustrated in yellow in Fig. 2. The total duration of the flare can then be defined as the time range between the beginning of the first block and the end of the last block above the baseline, while the peak is assumed to be located at the centre of the maximum block. This time range is defined as a HOP group10, for which we measure the rise time τrise from the beginning of the HOP-group to the peak, and the decay time τdecay from the peak to the end of the HOP-group. We conservatively estimate the error on the edge of each Bayesian block to be as big as the binning of each respective light curve (e.g., ±1 d in daily binning). To apply this method to the Fermi light curves of PKS 2004−447, we calculate the Bayesian blocks as described by Scargle et al. (2013), and set the parameter ncp_prior = 2.

A source is not necessarily detected significantly in each light curve bin, hence upper limits on the flux are usually reported (see e.g., the Fermi/LAT light curve in Fig. 1) in order to give an indication about the trend of the flux of a source. In a standard LAT light-curve analysis, it is not straightforward to deal with data bins that have a low test statistic. Moreover, the number of such low-significance flux bins typically increases for a finer binning. Specifically, this is problematic for the Bayesian-block point algorithm which assumes that the flux in each bin follows Gaussian statistics. For a low source significance this assumption is not valid. A common approach is to ignore the upper limits altogether as upper limits cannot be inserted as such in the Bayesian-block algorithm, and therefore waive the information contained in data points with low significance, thus biasing the analysis results. To avoid this, we take all data into account and calculate best-possible flux values also in the case of low-significance data bins following the standard analysis procedure. For light-curve bins that have a low significance, a problem that occurs in the determination of the fluxes and their corresponding uncertainties with the Likelihood calculation is that the Likelihood fit does not converge and this can then yield unreasonably small values for the flux uncertainties. This can have a strong influence on the Bayesian-block algorithm. Hence, to avoid this issue, rather than relying on the Likelihood to provide the uncertainties on the flux values, we calculate the 1-sigma upper limits for the flux in the low-flux bins and use the difference between these upper-limit values and the flux returned by the Likelihood as a conservative proxy for the magnitude of the flux uncertainties. In this way our light curve does not exhibit gaps and the Bayesian-block algorithm can be applied to a continuous dataset.

The results from the Bayesian-block algorithm are shown in red in Fig. 2. Following Meyer et al. (2019) we define the flare asymmetry via

A = τ rise − τ decay τ rise + τ decay · $$ \begin{aligned} A = \frac{\tau _{\mathrm{rise} }-\tau _{\mathrm{decay} }}{\tau _{\mathrm{rise} }+\tau _{\mathrm{decay} }}\cdot \end{aligned} $$(1)

Uncertainties are obtained using Gaussian error propagation. The results are shown in Table 2.

Table 2.

Flare lengths in days for the different binnings of the Fermi light curves.

The asymmetry values depend on the binning size chosen for the light curve. For the daily-binned light curve, the procedure yields an asymmetry value A < 0, indicating a faster rise than decay of the flare. The 12 h binned light curve resolves more structure and a local dip at MJD 58785 followed by an increased flux level separated from the flare. Due to this the resulting Bayesian blocks indicate a slightly faster decay than rise (A > 0). The 6 and 3 h binning, in turn, resolve this to consist of a very short and a longer symmetric flare. We focus on the latter, which lies within the time range chosen to construct the SED of the flaring state as indicated with dashed lines in Fig. 2. The properties of this flare and the corresponding higher binnings are reported in Table 2, but it is important to note that the 6 and 3 h flares only represent a fraction of the daily and 12 h one. Furthermore, the 6 and 3 h binned flares consist of one block only which, by definition, results in A = 0. Thus, the perceived flare symmetry is most likely due to the analysis procedure and limited sensitivity rather than actual symmetry of the flux behaviour and the true flare shape remains unknown. Interestingly, nine days after the main flare a second, shorter flare is identified by the Bayesian-block algorithm in all light curves but the daily-binned one. This demonstrates that the γ-ray variability of the source takes place on sub-day scales. What appears to be one flare in daily binning is shown to consist of three independent flares in 6 and 3 h binning. Unfortunately, the sensitivity of the instrument is not high enough to fully resolve this structure. In general, care has to be taken in the interpretation of Bayesian flare-duration studies by considering and testing different bin sizes.

To quantify this sub-dayscale variability, we scan all Fermi light curves for significant jumps in flux between adjacent data points and calculate the minimum doubling and halving times. The most significant flux difference (∼2.88σ) between adjacent data points is found in the 6 h binned light curve at MJD 58792.0, during the second, shorter flare. We compute a flux-doubling timescale of τd = 2.2 ± 0.8 h, assuming an exponential rise (Zhang et al. 1999).

We search for the presence of spectral curvature in the γ-ray spectrum of the brightest state during the flare (MJD 58781–58784) and obtain the curvature via

TS curve = 2 ( log L ( logparabola ) − log L ( powerlaw ) ) $$ \begin{aligned} \mathrm{TS}_{\rm curve} = 2({\log }\mathcal{L} (\mathrm{logparabola})-{\log }\mathcal{L} (\mathrm{powerlaw})) \end{aligned} $$(2)

from Nolan et al. (2012). Our analysis yields TScurve = 11.66, providing tentative evidence for the presence of curvature in the γ-ray spectrum. Although the photon index of 2.42 ± 0.09 measured during the flare is marginally harder than the average photon index of 2.60 ± 0.05 reported in 4FGL (Abdollahi et al. 2020), the difference is not large enough to claim that spectral hardening has taken place during the flare. PKS 2004−447 is significantly detected up to an energy of 3 GeV during the flare. The slight curvature of the spectrum and the increasing flux threshold for detection are responsible for the non-detection at higher energies. Attenuation of the γ-ray emission seen by Fermi/LAT due to pair production with the extragalactic background light (EBL) is negligible at these energies for the redshift (z = 0.24) of PKS 2004−447.

3.2. Analysis of the X-ray spectra

A feature often seen in X-ray spectra of NLSy 1 galaxies is a soft excess below 2 keV (Vaughan et al. 1999; Grupe 2004). Previously, Gallo et al. (2006) found an indication of a soft excess in PKS 2004−447 in XMM-Newton data from 2004, while the source was in a higher state. However, Orienti et al. (2015) and Kreikenbohm et al. (2016) did not find an excess for PKS 2004−447 during its low state in 2012, and Kreikenbohm et al. (2016) could not confirm the excess in the data from 2004.

Given that the source showed its brightest X-ray flux compared to previous observations during the γ-ray flare reported here, we search for an excess below 2 keV in the XMM-Newton spectrum. We apply a simple, unbroken power law model with Galactic H I absorption. Similar to the analysis of the individual X-ray spectra, we use C-statistics (Cash 1979) and estimate all uncertainties at 1σ confidence. All spectra are binned following the optimal binning procedure of Kaastra & Bleeker (2016). Modelling both the spectra obtained with XMM-Newton and NuSTAR individually between 3 and 10 keV with a power law yields compatible values for the power-law indices for both instruments (Γ3−10 keV = 1.33 ± 0.09 for XMM-Newton vs. 1.37 ± 0.10 for NuSTAR). Although the observations are separated by one day, this result justifies the use of the spectra from both instruments for a combined analysis.

First, we fitted the data in the full energy range from 0.5 keV to 79 keV with a fixed NH, which yields a good fit with 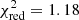χ red 2 =1.18 $ \chi^2_{\mathrm{red}}=1.18 $ (721.1/608) and a best-fit power-law index of Γ = 1.45 ± 0.02. Freeing the NH parameter, we find an upper limit of ≤0.75 times the Galactic value for the absorption, meaning there is no evidence for significant intrinsic absorption in PKS 2004−447. Therefore, we kept this parameter fixed at the Galactic value in the further analysis.

To search for a soft excess, we fitted the spectra again, but only for the 2−79 keV band, and extrapolated the best fit down to 0.5 keV. We show the EPIC-pn and EPIC-MOS spectra in Fig. 5, where the fits to the full and the hard energy range are shown as a solid and a dashed line, respectively. For plotting purposes, the XMM-Newton spectra are binned with a signal-to-noise (S/N) ratio of 5 per energy bin, and the NuSTAR spectra with a S/N ratio of 3. The fit results in χ red 2 =1.17 $ \chi^2_{\rm red}=1.17 $ (595.3/508) and Γ = 1 . 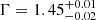45 − 0.02 + 0.01 $ \Gamma=1.45^{+0.01}_{-0.02} $. This power-law index agrees with that obtained from modelling the full fitted energy range. Describing the data with a broken power law also yields no evidence for a soft excess. We therefore conclude that there is no evidence for a soft excess in the X-ray spectrum of PKS 2004−447 during the 2019 October outburst as the fits are indistinguishable.

thumbnail Fig. 5.

XMM-Newton and NuSTAR spectra with the best-fit results of an absorbed power-law model. For plotting purposed only the spectra are binned to a S/N of 5 and 3 for XMM-Newton and NuSTAR, respectively. Bins from the NuSTAR spectrum are only shown up to 50 keV, because at energies above this, no significant bin for the given S/N value is found. Upper panel: EPIC pn (blue), MOS (red) and FPMA/FPMB (yellow) data together with the best fits for the full (0.5−80 keV) energy range (solid line) as well as the hard (2−80 keV) energy range (dashed line). The zoom window shows small deviations between the fits of the full and the hard energy range. Middle panel: data-to-model ratio for the best fit to the full energy range. Lower panel: data-to-model ratio for the best-fit to the hard energy range with extrapolating the model down to 0.5 keV.

The presence of an iron Kα line at 6.4 keV is also a common feature in NLSy 1 galaxies. Among the small γ-NLSy 1 sample, however, only 1H 0323+342 shows an indication for an Iron-line feature. For our data, adding an unresolved Gaussian line at 6.4 keV does not improve the fit statistics. We determine an upper limit for the equivalent width of EW6.4 keV ≤ 73 eV at the 90% confidence level. This limit is slightly less constraining than what has been reported for this source in previous analyses (Gallo et al. 2006; Orienti et al. 2015; Kreikenbohm et al. 2016).

The photon index derived from the XMM-Newton observation is harder compared to the values derived from the low state analysed by Orienti et al. (2015) and Kreikenbohm et al. (2016), This fits into the ‘harder-when-brighter’ behaviour of blazars, more precisely BL Lacs (e.g., Giommi et al. 1990; Wang et al. 2018). During an XMM-Newton observation in 2004, and also at the end of 2013 during a monitoring campaign with Swift, PKS 2004−447 was in a bright state as well. However, a spectral hardening was not observed at these times (Gallo et al. 2006; Kreikenbohm et al. 2016), which suggests that different processes might be responsible for the X-ray variability that is present on monthly and yearly timescales.

3.3. Spectral energy distribution

Due to X-ray and optical-UV observations ∼20 days before, during, and after the flare, we can construct the broadband SEDs for PKS 2004−447 and study the evolution of the SEDs over the flaring period. We construct three SEDs, covering the time spans of a pre-flare state of the source (MJD 58754–58770), the flaring period (MJD 58781–58784), and the post-flare period right after the γ-ray flare (MJD 58787–58789). These time ranges are marked in Fig. 1. We also consider a low activity state of this source for comparison, adopting the period from Kreikenbohm et al. (2016). The Fermi/LAT data used for the low-state SED are centred on XMM-Newton and Swift observations in 2012 May and March, respectively, and cover 24 months from 2011 May 1 through 2013 May 1.

We can describe the broadband SEDs of PKS 2004−447 for all four activity states with a simple synchrotron inverse Compton radiative model (see, e.g., Sikora et al. 2009; Dermer & Menon 2009; Ghisellini & Tavecchio 2009). In particular, the emission region is assumed to be spherical (radius Rblob), moving along the jet axis with the bulk Lorentz factor Γb. The emission region is also considered to cover the entire cross-section of the jet whose semi-opening angle is assumed to be 0.1 radian. We have assumed a viewing angle of 2°, similar to that adopted in the modelling of beamed AGNs (cf. Ghisellini & Tavecchio 2015). Considering a significantly larger viewing angle would drastically reduce the Doppler boosting (e.g., Dermer 1995). Indeed, the observation of the large-amplitude γ-ray flare from the source indicates a significant Doppler boosting as explained in the next section, hence supporting a small viewing angle.

In our model, a relativistic population of electrons fills the emission region and emits synchrotron and inverse Compton radiation in the presence of a uniform but tangled magnetic field B. The energy distribution of the electrons, with minimum and maximum energies of γmin and γmax, respectively, follows a smooth broken power law of the type

Q ( γ ) = Q 0 γ b − s 1 ( γ / γ b ) s 1 + ( γ / γ b ) s 2 , $$ \begin{aligned} Q(\gamma ) = Q_0\,\frac{\gamma _{\rm b}^{-s_1}}{(\gamma /\gamma _{\rm b})^{s_1} + (\gamma /\gamma _{\rm b})^{s_2}}, \end{aligned} $$(3)

where γb is the break Lorentz factor, s1 and s2 are the spectral indices of the power law below and above γb, and Q0 is a normalisation constant.

We include various sources of seed photons in the computation of the inverse Compton radiation caused by the relativistic electrons present in the jet. Sources include the synchrotron photons produced within the emission region (synchrotron self Compton or SSC, see, e.g., Finke et al. 2008; van den Berg et al. 2019) and thermal emission originating outside the jet (so-called external Compton or EC process; e.g., Sikora et al. 1994; Błażejowski et al. 2000). For the latter, we adopt radiation emitted by the accretion disk, X-ray corona, broad line region (BLR), and the dusty torus. The comoving-frame radiative energy densities of these AGN components have been adopted following the prescriptions of Ghisellini & Tavecchio (2009) and are used to derive the EC flux. Jet powers are calculated assuming a two-sided jet and equal number density of electrons and protons, meaning we do not consider the presence of pairs in the jet (see, e.g., Pjanka et al. 2017). Protons are assumed to be cold and to participate only in carrying the jet’s momentum.

We generate the broadband SEDs following the methodology described in Sect. 2 and reproduce them using the model outlined above. The results are shown in Fig. 6 and the associated spectral flux values and SED parameters are presented in Tables 3 and 4.

thumbnail Fig. 6.

Spectral energy distribution of PKS 2004−447 for four stages modelled with a simple leptonic emission model. Open green circles refer to the archival measurements taken from the SSDC SED builder (https://tools.ssdc.asi.it/), whereas filled black circles represent the data analysed by us. The thin solid pink line shows the synchrotron emission. Dashed green and dash-dash-dot orange lines correspond to the synchrotron self Compton and external Compton processes, respectively. The dotted black line shows the thermal emission from the accretion disk and dusty torus. The thick solid blue line is the sum of all radiative components. The SEDs are sorted from left to right as follows: low (MJD 55682–56413), pre-flare (MJD 58754–58770), flaring (MJD 58781–58784), and post-flare activity states (MJD 58787–58789), as defined in the text. The model parameters are listed in Table 3.

Table 3.

Summary of the analysis of each individual energy range for each SED.

4. Discussion

4.1. Variability

The detection of a γ-ray flare from PKS 2004−447 provides more observational evidence supporting the blazar-like behaviour of γ-NLSy 1 galaxies (see also e.g., Baldi et al. 2016). In general, γ-ray variability is an indicator for the presence of a closely aligned, relativistic jet. For blazars variability on timescales as short has minutes is commonly observed at TeV energies (e.g., Rieger & Volpe 2010; Aleksić et al. 2011), but such short timescales have only been observed in few sources at GeV energies (e.g., Meyer et al. 2019).

It has been proposed that γ-NLSy 1s represent the start of the life of an AGN, when the central black hole mass is still below 108 M⊙ and the source appears not as bright as a full-grown FSRQ (Mathur 2000; Foschini 2017; Paliya 2019). Nevertheless, the detection of blazar-like short-term variability in γ-NLSy 1 galaxies, which has been seen previously in 1H 0323+342 (flux doubling timescales of ∼3 h; Paliya et al. 2014) and PKS 1502+036 (variability on 12 h timescales; D’Ammando et al. 2016), suggests that the physical mechanisms operating in the relativistic jet of γ-NLSy 1s are similar to those working in blazar jets resulting in fast γ-ray variability (e.g., Shukla & Mannheim 2020). For PKS 2004−447, we find indications for sub-daily variability with flux doubling times as short as 2.2 h at a 2.8σ level.

We note that if we consider only GeV flares with fluxes above 10−6 ph cm−2 s−1, the few observed flares by γ-NLSy 1 galaxies lasted roughly 1−4 days. Blazar flares reported from single sources at γ-ray energies have a tendency to be brighter, last longer, and for some sources occur more often, but a strong bias towards the most luminous and extreme detections exists due to the different sensitivities and observing constraints of space-based and ground-based γ-ray telescopes: While the large field of view and observing strategy of Fermi/LAT offers unbiased all-sky observations of many blazars in the GeV energy regime, its relatively small collection area renders it less sensitive to weak flares. In the TeV energy range Cherenkov telescopes have large collection areas giving them good sensitivity to short time variability, but with their relatively small fields of view and low duty cycles, their observations are limited to a smaller sub-sample of targeted observations on blazars. Even though observing programmes often include scheduled observations on a selection of blazars during the parts of the year that they are visible from the ground, many blazar observations are triggered and therefore take place during a particularly active period. This leads to an under-reporting of short, less luminous blazar flares, which could in turn belong to a class of less luminous blazars that might be missing in the AGN evolution scenario.

4.2. Physical interpretation of the SED parameters

We now turn to the interpretation of the SED of PKS 2004−447. We first discuss the low activity state SED of the source before considering the γ-ray flaring epochs. The motivation is to first derive the quiescent-level SED parameters and then to explain the flaring-state SEDs while changing the minimum number of input parameters. This approach may permit us to understand the primary factors responsible for the γ-ray flare.

We have used the Hβ emission line dispersion (1869 km s−1) and luminosity (1.62 × 1042 erg s−1) reported in Foschini et al. (2015, 2017), which were calculated from the optical spectrum of PKS 2004−447 published in Drinkwater et al. (1997) to derive a value of the mass of the black hole of MBH = 7 × 107 M⊙. This value is similar to that usually determined for radio-loud NLSy 1 galaxies (Foschini et al. 2017) but lower than typical blazars (e.g., Shaw et al. 2012). Interestingly, Baldi et al. (2016) have reported a MBH of 6 × 108 M⊙ from the spectropolarimetric observation of PKS 2004−447. Furthermore, the accretion disk luminosity reported in Foschini et al. (2017, Ldisk = 4.8 × 1044 erg s−1) is not supported by the shape of the low activity state optical-UV spectrum of PKS 2004−447. This is because the radiation from such a luminous accretion disk should be detectable in the form of a strong big blue bump at optical-UV frequencies, especially during the low jet activity state. As can be seen in the top left panel of Fig. 6, no such feature was observed. Rather, by reproducing the observed optical-UV emission with the combined synchrotron and accretion disk spectra, we have constrained the Ldisk value to 2 × 1043 erg s−1. A larger Ldisk value would be in disagreement with the data. For the adopted values of MBH and Ldisk, the accretion rate in Eddington units is ∼0.4% of the Eddington one. This is lower than ∼1%, which is typically found for radiatively efficient accreting systems, that is AGNs exhibiting broad emission lines (e.g., Ghisellini et al. 2017; Paliya et al. 2019). This observation indicates that PKS 2004−447 could be one of the rare AGNs where the accretion process can be radiatively efficient even with such a low level of accretion activity (see, e.g., Fig. 6 of Best & Heckman 2012).

For a look at the evolution of the SED we start with the low activity state. There, the infrared-to-ultraviolet (IR-to-UV) spectrum of PKS 2004−447 is well explained by the synchrotron emission. We note that the emission from a giant elliptical galaxy could explain part of the observed IR-optical SED. Though the wavelength at which the host galaxy emission peaks (∼1.5 micron) is not covered in our multi-band follow-up campaign, the observed flux variability and the overall shape of the optical-UV spectrum (Figs. 1 and 6) point to the synchrotron origin of the observed emission.

The shape of the steeply falling optical-to-UV SED enables us to constrain the high-energy spectral index of the particle spectrum, s2, and also the break, γb, and maximum energy of the emitting electron population, γmax. On the other hand, we use the shape of the X-ray spectrum to constrain the low-energy particle spectral index, s1. The model fails to explain the low-frequency radio data because compact emission regions are synchrotron-self absorbed at low radio frequencies. Additional emission components on larger scales (approaching parsec scales and beyond) dominate the observed radio emission, but are not included in the model.

In the low activity state, the X-ray emission is mainly due to SSC. The level of SSC along with the constrained synchrotron emission allows us to derive the size of the emission region and the magnetic field (see Table 3). The γ-ray emission is explained with the external Compton process with seed photons provided by the dusty torus. This sets the location of the emission region outside the BLR but inside the dusty torus. The shape of the γ-ray spectrum provides further constraints to s2. Overall, the derived SED parameters during the low activity state are similar to previous studies (Paliya et al. 2013; Orienti et al. 2015). There are a few minor differences, for example the large bulk Lorentz factor reported by Orienti et al. (2015), which could be mainly due to datasets taken at different epochs and underlying assumptions associated with the adopted leptonic models. In particular, and in contrast to what we do here, the X-ray part of the SED during a different low activity state of the source was modelled by Orienti et al. (2015) with the EC of seed photons from the dusty torus.

During the pre-flare phase, Swift-UVOT shows that the level of the optical-UV emission, and hence the synchrotron radiation, remains comparable to that measured during the quiescent state (Fig. 6). In addition to the X-ray flux increase, a significant spectral hardening is observed in the 0.5−10 keV energy range (see Table 3). We explain the X-ray spectrum with a combination of the SSC and EC processes. There is a slight decrease in the magnetic field (from 0.4 G to 0.3 G) causing an enhancement of both SSC and EC fluxes since the level of the synchrotron emission remains the same. This is because a decrease in the magnetic field strength requires an increase in the number of electrons to produce the same level of the synchrotron flux, which ultimately enhances the inverse Compton flux (e.g., Dermer et al. 2009). Above a few keV, the modelled pre-flare SED includes a significant contribution from EC photons. The different electron populations of SSC and EC producing electrons is responsible for the flattening of the X-ray spectrum. Furthermore, the increase in the γ-ray flux is even larger compared to that seen in the X-ray band. The ratio of the inverse Compton to synchrotron peak luminosities, meaning Compton dominance (see, e.g., Finke 2013) significantly increases with respect to the low activity state. We explain this observation with an increase in the bulk Lorentz factor and, hence, a larger Doppler boosting.

At the peak of the flare, the enhancement of the γ-ray flux is largest with respect to that observed at lower frequencies (Fig. 6). There is an increase in the optical-UV flux level indicating an elevated electron energy, possibly due to a fresh supply of energetic electrons within the emission region. Accordingly, the synchrotron energy density gets enhanced, leading to the brightening of the SSC radiation, as observed in the X-ray band. However, the larger amplitude of the flux variations seen at γ-rays indicates an even stronger boosting. Since we explain the γ-ray spectrum with the EC process, this can be understood as follows: In addition to the usual beaming due to the relativistic motion of the plasma towards the observer, the external photon field receives an additional boosting due to motion of the emission region with respect to the photon fields external to the jet (see Dermer 1995). This phenomenon causes the radiation pattern of the external Compton emission to be anisotropic even in the comoving frame, making it more sensitive to Doppler boosting with respect to the synchrotron and SSC mechanisms. The relatively large enhancement of the γ-ray flux could therefore be due to increased Doppler boosting. This conjecture is confirmed by the SED modelling, where we find the bulk Lorentz factor to increase considerably during the flare. This also makes the EC peak much more luminous than the synchrotron peak, thus indicating a Compton dominated SED, which is observed (see Fig. 6).

The data from PKS 2004−447 taken after the peak of the γ-ray flare reveal a decrease in the optical-UV and X-ray fluxes, similar to that found during the pre-flare state, while the source remains bright in the γ-rays, indicating a still large Doppler beaming, albeit a bit lower than that at the flare peak (see Table 4). Comparing the photon indices derived from the individual XMM-Newton and NuSTAR data during the post-flare period (see Table 3), a slight spectral hardening is visible at hard X-ray energies, even when we consider the influence of the background. As discussed above, this observation implies a dominance of the SSC mechanism at softer X-rays (<10 keV). At higher energies, the EC process takes over, leading to the observation of the flatter NuSTAR spectrum. These findings reveal the crucial role of data taken above 10 keV in disentangling various radiative mechanisms at work during the flare.

Table 4.

Summary of the parameters used for and derived from the modelling of the multi-epoch SEDs of PKS 2004−447 shown in Fig. 6.

When we compared various jet powers estimated during different activity states, an interesting pattern was noticed. Compared to the low state, the jet powers increase during the pre-flare phase, particularly the radiative and kinetic powers, Pr and Pp, in which a change of about one order of magnitude more is found. During the main flare, there is a significant enhancement of Pr; however, the kinetic luminosity decreases. This behaviour suggests an efficient conversion of Pp into radiation during the flare since Pp has increased in the post-flare state, again. This presence of radiatively efficient jets during γ-ray flares has also been reported for blazars (see, e.g., Tanaka et al. 2011; Saito et al. 2013; Paliya et al. 2015). Interestingly, the observed radiative power exceeds the total available accretion power. Given the fact that this is the first GeV outburst detected from PKS 2004−447 in more than a decade of Fermi/LAT operation, such extraordinary events can be considered rather rare and short-lived (e.g., Tavecchio et al. 2010).

4.3. Comparison with flares from other γ-NLSy 1 galaxies

Since the sample of flaring γ-NLSy 1 galaxies is so small, not much is known about their typical flaring behaviour nor about their possible differences. We compare the flaring state broadband SED of PKS 2004−447 with four γ-NLSy 1 galaxies that have shown a GeV flare in the past. The data for 1H 0323+342, PMN J0948+0022, and PKS 1502+036 are taken from Paliya & Stalin (2016). Although the brightest flare of SBS 0846+513, which happened in 2011, is not covered by multi-wavelength data, this source showed high γ-ray activity in May 2012 as well. During that time, the γ-ray emission was slightly below the flare of 2011, but X-ray and optical-UV data are available. We take data of SBS 0846+513 from D’Ammando et al. (2013). All SEDs obtained from data throughout their respective flares are plotted in Fig. 7. The parameters discussed in this comparison are also listed in Table 5.

thumbnail Fig. 7.

Comparison of the rest-frame SEDs of γ-ray flaring NLSy 1 galaxies covering their GeV flaring epochs. The epochs of the flares are given in their labels. Except for PKS 2004−447, data taken for this comparison were analysed by Paliya & Stalin (2016) and D’Ammando et al. (2013).

Table 5.

Comparison of chosen SED model parameters of the flaring γ-NLSy 1 galaxies.

The shape of the optical-UV emission from PKS 2004−447 is similar to that of SBS 0846+513, but differs from the other three sources: Although the level of luminosity is different for 1H 0323+342, PMN J0948+0022, and PKS 1502+036, their observed optical-UV spectra could all be explained with a combination of the synchrotron and accretion disk emission (Paliya et al. 2014). For 1H 0323+342, the optical-UV emission remains disk dominated even during the GeV flare. Such thermal emission, however, is not observed in PKS 2004−447 (see also Fig. 6). Taken together with SED modelling, this indicates that emission from the accretion disk is negligible compared to the synchrotron emission.

In the X-rays, the luminosity of PKS 2004−447 is similar to that of PKS 1502+036 and 1H 0323+342. Within the soft X-rays, models predict a transition from SSC to EC emission. During flaring states, the EC can become dominant over SSC, as it is the case for 1H 0323+342, PMN J0948+0022 and PKS 1502+036. The EC component of PKS 2004−447, however, starts at higher energies compared to the other γ-NLSy 1 galaxies; therefore most of its soft X-ray emission originates from SSC. The spectral shapes of γ-NLSy 1 galaxies behave similarly by showing a harder spectral index during a flare compared to low states. All sources, including PKS 2004−447, show photon indices of ∼1.3−1.6.

In the γ-rays, PKS 2004−447 reaches about the same luminosity as PKS 1502+036, and is about one order of magnitude more luminous than 1H 0323+342 (see Fig. 7). SBS 0846+513 showed a slightly higher luminosity, while PMN J0948+0022 presents the highest luminosity ever observed for a γ-ray flare of a NLSy 1 galaxy, exceeding the luminosity of PKS 2004−447 by a factor of ten. The γ-ray photon indices during the flaring state are ∼2.5, with the exception of SBS 0846+513, which shows a significantly harder spectrum. Both PKS 2004−447 and PKS 1502+036 exhibit a similar luminosity and bulk Lorentz factor (PKS 1502+036 has Γ = 25; Paliya & Stalin 2016). The mass of their central black holes is similar as well. However, the accretion disk luminosity of the latter is a factor of ∼30 larger indicating a higher accretion rate in Eddington units. Since the sizes of the BLR and the torus adjust to the luminosity of the accretion disk, they are likely ten times larger as well for PKS 1502+036. For PKS 2004−447, in order to be able to produce a similar γ-ray luminosity, a higher particle density is required.

The γ-ray emission of PKS 2004−447 is explained by the EC process with seed photons provided by the dusty torus, as already reported for SBS 0846+513, PMN J0948+0022, and PKS 1502+036 during flaring episodes (D’Ammando et al. 2013; D’Ammando et al. 2015; D’Ammando et al. 2016). As is observed for PKS 2004−447, a high Compton dominance has also been seen in these sources at the peak of the activity, confirming that the EC emission is the main mechanism for producing γ-rays, similar to several FSRQs. This result confirms the similarities between γ-NLSy 1s and FSRQs. In contrast to PKS 2004−447, for which an increase in the bulk Lorentz factor is the driver of the change in the SED for different activity states, comparing low and flaring activity states, the SEDs of SBS 0846+513, PMN J0948+0022, and PKS 1502+036 can be described satisfactorily by changing the electron distribution parameters as well as the magnetic field. In the same way, a significant shift of the synchrotron peak has been observed during the flaring states of SBS 0846+513 and PMN J0948+0022, while it was not observed for PKS 2004−447.

5. Summary

In this paper we presented the analysis of the first GeV flare from the γ-NLSy 1 galaxy PKS 2004−447. We created daily and sub-daily binned Fermi/LAT light curves and used the method of Meyer et al. (2019) to derive the temporal behaviour of the flare. We built SEDs containing (quasi-)simultaneous datasets, and modelled the emission of the source during a low state, as well as before, during and after the flare, with a one-zone, leptonic model. Our main results are the following:

  1. Short-term variability on timescales of hours to weeks is found in the γ-rays. The X-ray and optical-UV light curves show flux changes within days. The ATCA light curves show a steady rise since 2018. Observations before and after the flare revealed a slight increase, which seemed to be strongest at 5.5 GHz. We find indications for γ-ray flux-doubling times as short as ∼2.2 h at the ∼3σ level.

  2. The soft excess frequently observed in the X-ray spectra of NLSy 1 galaxies is not found in the XMM-Newton spectrum of PKS 2004−447 during the flare, which is in agreement with the 2012 low-state analysis of Kreikenbohm et al. (2016).

  3. The simultaneous multi-wavelength data can be well described with a one-zone leptonic model. The emission region from where the flare possibly originated lies outside the BLR, but within the dusty torus. The γ-ray emission is dominated by EC processes, while the SEDs of the flaring, pre-, and post-flare state exhibit strong Compton dominance. During the GeV flare, the source was in an elevated activity state at lower frequencies as well. However, the amplitude of the flux variability was the highest in the γ-ray band. SED modelling explains this behaviour with an increase in the bulk Lorentz factor of the jet, similar to that typically seen in powerful FSRQs.

We conclude that all of the observations of PKS 2004−447, and γ-NLSy1 in general, point to a scenario in which these objects could be considered to belong to the blazar sub-class of radio-loud emitters.

3

We use SOURCE class events and set the following flags: (DATA_QUAL > 0)&&(LAT_CONFIG==1).

6

Supplementary data from the C 007 ATCA calibrator programme were used.

9

The name HOP is not an acronym, but taken from the verb ‘to hop’ to each data element’s highest neighbour (Eisenstein & Hut 1998).

10

Meyer et al. (2019) added an additional criterion requiring that the maximum block is at least five times above the average flux in order to single out only the brightest flares, which we drop in our analysis.

Acknowledgments

We are grateful to the journal referee for a constructive criticism. We thank the Fermi/LAT Collaboration members E. Ros, D. Horan, D. J. Thompson, and G. Johannesson for their comments, which helped to improve the manuscript. A. Gokus was partially funded by the Bundesministerium für Wirtschaft und Technologie under Deutsches Zentrum für Luft- und Raumfahrt (DLR grant number 50OR1607O) and by the German Science Foundation (DFG grant number KR 3338/4-1). V.S.P.’s work was supported by the Initiative and Networking Fund of the Helmholtz Association. S.M.W. acknowledges support by the Stiftung der deutschen Wirtschaft (sdw). F.D. acknowledges financial contribution from the agreement ASI-INAF n. 2017-14-H.0. We are grateful to the ATCA, Swift, XMM-Newton, and NuSTAR PIs for approving the ToO observations, and to the mission operation teams for quickly executing them. The Fermi LAT Collaboration acknowledges generous ongoing support from a number of agencies and institutes that have supported both the development and the operation of the LAT as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat à l’Energie Atomique and the Centre National de la Recherche Scientifique/Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana and the Istituto Nazionale di Fisica Nucleare in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K.A. Wallenberg Foundation, the Swedish Research Council and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase is gratefully acknowledged from the Istituto Nazionale di Astrofisica in Italy and the Centre National d’Études Spatiales in France. This work was performed in part under DOE Contract DE-AC02-76SF00515. This work made use of data from the NuSTAR mission, a project led by the California Institute of Technology, managed by the Jet Propulsion Laboratory, and funded by the National Aeronautics and Space Administration. We thank the NuSTAR Operations, Software, and Calibration teams for support with the execution and analysis of these observations. This research has made use of the NuSTAR Data Analysis Software (NuSTARDAS) jointly developed by the ASI Science Data Center (ASDC, Italy) and the California Institute of Technology (USA). We acknowledge the use of public data from the Swift data archive. The Australia Telescope Compact Array is part of the Australia Telescope National Facility which is funded by the Australian Government for operation as a National Facility managed by CSIRO. This research has made use of a collection of ISIS functions (ISISscripts) provided by ECAP/Remeis observatory and MIT (http://www.sternwarte.uni-erlangen.de/isis/). The colours in Figs. 1, 2, 3, and 5 were taken from Paul Tol’s colour schemes and templates (https://personal.sron.nl/~pault/).

References

  1. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009a, ApJ, 699, 976 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009b, ApJ, 707, L142 [NASA ADS] [CrossRef] [Google Scholar]
  3. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 722, 520 [NASA ADS] [CrossRef] [Google Scholar]
  4. Abdollahi, S., Acero, F., Ackermann, M., et al. 2020, ApJS, 247, 33 [NASA ADS] [CrossRef] [Google Scholar]
  5. Ajello, M., Angioni, R., Axelsson, M., et al. 2020, ApJ, 892, 105 [CrossRef] [Google Scholar]
  6. Aleksić, J., Antonelli, L. A., Antoranz, P., et al. 2011, ApJ, 730, L8 [NASA ADS] [CrossRef] [Google Scholar]
  7. Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
  8. Baldi, R. D., Capetti, A., Robinson, A., Laor, A., & Behar, E. 2016, MNRAS, 458, L69 [NASA ADS] [CrossRef] [Google Scholar]
  9. Best, P. N., & Heckman, T. M. 2012, MNRAS, 421, 1569 [NASA ADS] [CrossRef] [Google Scholar]
  10. Błażejowski, M., Sikora, M., Moderski, R., & Madejski, G. M. 2000, ApJ, 545, 107 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
  12. Ciprini, S., & Fermi-LAT Collaboration 2018, Revisiting Narrow-Line Seyfert 1 Galaxies and their Place in the Universe, 20 [Google Scholar]
  13. D’Ammando, F. 2019, Galaxies, 7, 87 [Google Scholar]
  14. D’Ammando, F., Orienti, M., Finke, J., et al. 2012, MNRAS, 426, 317 [NASA ADS] [CrossRef] [Google Scholar]
  15. D’Ammando, F., Orienti, M., Finke, J., et al. 2013, MNRAS, 436, 191 [NASA ADS] [CrossRef] [Google Scholar]
  16. D’Ammando, F., Orienti, M., Finke, J., et al. 2015, MNRAS, 446, 2456 [NASA ADS] [CrossRef] [Google Scholar]
  17. D’Ammando, F., Orienti, M., Finke, J., et al. 2016, MNRAS, 463, 4469 [NASA ADS] [CrossRef] [Google Scholar]
  18. D’Ammando, F., Acosta-Pulido, J. A., Capetti, A., et al. 2018, MNRAS, 478, L66 [NASA ADS] [Google Scholar]
  19. D’Ammando, F., Gokus, A., Kadler, M., & Ojha, R. 2019, ATel, 13233, 1 [Google Scholar]
  20. Decarli, R., Dotti, M., Fontana, M., & Haardt, F. 2008, MNRAS, 386, L15 [NASA ADS] [Google Scholar]
  21. Deo, R. P., Crenshaw, D. M., & Kraemer, S. B. 2006, AJ, 132, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Dermer, C. D. 1995, ApJ, 446, L63 [NASA ADS] [CrossRef] [Google Scholar]
  23. Dermer, C. D., & Menon, G. 2009, High Energy Radiation from Black Holes: Gamma Rays, Cosmic Rays, and Neutrinos (Princeton: Princeton University Press) [Google Scholar]
  24. Dermer, C. D., Finke, J. D., Krug, H., & Böttcher, M. 2009, ApJ, 692, 32 [NASA ADS] [CrossRef] [Google Scholar]
  25. Drinkwater, M. J., Webster, R. L., Francis, P. J., et al. 1997, MNRAS, 284, 85 [NASA ADS] [Google Scholar]
  26. Eisenstein, D. J., & Hut, P. 1998, ApJ, 498, 137 [NASA ADS] [CrossRef] [Google Scholar]
  27. Finke, J. D. 2013, ApJ, 763, 134 [NASA ADS] [CrossRef] [Google Scholar]
  28. Finke, J. D., Dermer, C. D., & Böttcher, M. 2008, ApJ, 686, 181 [NASA ADS] [CrossRef] [Google Scholar]
  29. Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
  30. Foschini, L. 2017, Front. Astron. Space Sci., 4, 6 [Google Scholar]
  31. Foschini, L., Ghisellini, G., Kovalev, Y. Y., et al. 2011, MNRAS, 413, 1671 [NASA ADS] [CrossRef] [Google Scholar]
  32. Foschini, L., Berton, M., Caccianiga, A., et al. 2015, A&A, 575, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Foschini, L., Berton, M., Caccianiga, A., et al. 2017, A&A, 603, C1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Fuhrmann, L., Larsson, S., Chiang, J., et al. 2014, MNRAS, 441, 1899 [NASA ADS] [CrossRef] [Google Scholar]
  35. Gallo, L. C., Edwards, P. G., Ferrero, E., et al. 2006, MNRAS, 370, 245 [NASA ADS] [CrossRef] [Google Scholar]
  36. Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
  37. Ghisellini, G., & Tavecchio, F. 2009, MNRAS, 397, 985 [NASA ADS] [CrossRef] [Google Scholar]
  38. Ghisellini, G., & Tavecchio, F. 2015, MNRAS, 448, 1060 [NASA ADS] [CrossRef] [Google Scholar]
  39. Ghisellini, G., Righi, C., Costamante, L., & Tavecchio, F. 2017, MNRAS, 469, 255 [Google Scholar]
  40. Giommi, P., Barr, P., Garilli, B., Maccagni, D., & Pollock, A. M. T. 1990, ApJ, 356, 432 [NASA ADS] [CrossRef] [Google Scholar]
  41. Gokus, A. 2019, ATel, 13229, 1 [NASA ADS] [Google Scholar]
  42. Grupe, D. 2004, AJ, 127, 1799 [NASA ADS] [CrossRef] [Google Scholar]
  43. Grupe, D., & Mathur, S. 2004, ApJ, 606, L41 [NASA ADS] [CrossRef] [Google Scholar]
  44. Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [Google Scholar]
  45. HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Houck, J. C., & Denicola, L. A. 2000, in Astronomical Data Analysis Software and Systems IX, eds. N. Manset, C. Veillet, & D. Crabtree (San Francisco: Astronomical Society of the Pacific), ASP Conf. Ser., 216, 591 [Google Scholar]
  47. Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Järvelä, E., Lähteenmäki, A., Lietzen, H., et al. 2017, A&A, 606, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Kaastra, J. S., & Bleeker, J. A. M. 2016, A&A, 587, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Komossa, S., Voges, W., Xu, D., et al. 2006, AJ, 132, 531 [NASA ADS] [CrossRef] [Google Scholar]
  51. Kreikenbohm, A., Schulz, R., Kadler, M., et al. 2016, A&A, 585, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Marconi, A., Axon, D. J., Maiolino, R., et al. 2008, ApJ, 678, 693 [NASA ADS] [CrossRef] [Google Scholar]
  53. Mason, K. O., Breeveld, A., Much, R., et al. 2001, A&A, 365, L36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Mathur, S. 2000, MNRAS, 314, L17 [NASA ADS] [CrossRef] [Google Scholar]
  55. Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [NASA ADS] [CrossRef] [Google Scholar]
  56. Meyer, M., Scargle, J. D., & Blandford, R. D. 2019, ApJ, 877, 39 [NASA ADS] [CrossRef] [Google Scholar]
  57. Nolan, P. L., Abdo, A. A., Ackermann, M., et al. 2012, ApJS, 199, 31 [NASA ADS] [CrossRef] [Google Scholar]
  58. Nowak, M. A., Wilms, J., Heinz, S., et al. 2005, ApJ, 626, 1006 [NASA ADS] [CrossRef] [Google Scholar]
  59. Olguín-Iglesias, A., Kotilainen, J., & Chavushyan, V. 2020, MNRAS, 492, 1450 [NASA ADS] [CrossRef] [Google Scholar]
  60. Orienti, M., D’Ammando, F., Larsson, J., et al. 2015, MNRAS, 453, 4037 [NASA ADS] [CrossRef] [Google Scholar]
  61. Oshlack, A. Y. K. N., Webster, R. L., & Whiting, M. T. 2001, ApJ, 558, 578 [NASA ADS] [CrossRef] [Google Scholar]
  62. Osterbrock, D. E., & Pogge, R. W. 1985, ApJ, 297, 166 [NASA ADS] [CrossRef] [Google Scholar]
  63. Paliya, V. S. 2019, J. Astrophys. Astron., 40, 39 [NASA ADS] [CrossRef] [Google Scholar]
  64. Paliya, V. S., & Stalin, C. S. 2016, ApJ, 820, 52 [NASA ADS] [CrossRef] [Google Scholar]
  65. Paliya, V. S., Stalin, C. S., Shukla, A., & Sahayanathan, S. 2013, ApJ, 768, 52 [NASA ADS] [CrossRef] [Google Scholar]
  66. Paliya, V. S., Sahayanathan, S., Parker, M. L., et al. 2014, ApJ, 789, 143 [NASA ADS] [CrossRef] [Google Scholar]
  67. Paliya, V. S., Sahayanathan, S., & Stalin, C. S. 2015, ApJ, 803, 15 [NASA ADS] [CrossRef] [Google Scholar]
  68. Paliya, V. S., Ajello, M., Rakshit, S., et al. 2018, ApJ, 853, L2 [NASA ADS] [CrossRef] [Google Scholar]
  69. Paliya, V. S., Parker, M. L., Jiang, J., et al. 2019, ApJ, 872, 169 [NASA ADS] [CrossRef] [Google Scholar]
  70. Paliya, V. S., Pérez, E., García-Benito, R., et al. 2020, ApJ, 892, 133 [CrossRef] [Google Scholar]
  71. Peterson, B. M., McHardy, I. M., Wilkes, B. J., et al. 2000, ApJ, 542, 161 [NASA ADS] [CrossRef] [Google Scholar]
  72. Pjanka, P., Zdziarski, A. A., & Sikora, M. 2017, MNRAS, 465, 3506 [CrossRef] [Google Scholar]
  73. Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Rajput, B., Stalin, C. S., & Rakshit, S. 2020, A&A, 634, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Ramakrishnan, V., Hovatta, T., Nieppola, E., et al. 2015, MNRAS, 452, 1280 [CrossRef] [Google Scholar]
  76. Rieger, F. M., & Volpe, F. 2010, A&A, 520, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Romano, P., Vercellone, S., Foschini, L., et al. 2018, MNRAS, 481, 5046 [NASA ADS] [CrossRef] [Google Scholar]
  78. Saito, S., Stawarz, Ł., Tanaka, Y. T., et al. 2013, ApJ, 766, L11 [NASA ADS] [CrossRef] [Google Scholar]
  79. Scargle, J. D., Norris, J. P., Jackson, B., & Chiang, J. 2013, ApJ, 764, 167 [NASA ADS] [CrossRef] [Google Scholar]
  80. Schulz, R., Kreikenbohm, A., Kadler, M., et al. 2016, A&A, 588, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Shaw, M. S., Romani, R. W., Cotter, G., et al. 2012, ApJ, 748, 49 [CrossRef] [Google Scholar]
  82. Shukla, A., & Mannheim, K. 2020, Nat. Commun., 11, 4176 [CrossRef] [Google Scholar]
  83. Sikora, M., Begelman, M. C., & Rees, M. J. 1994, ApJ, 421, 153 [Google Scholar]
  84. Sikora, M., Stawarz, Ł., Moderski, R., Nalewajko, K., & Madejski, G. M. 2009, ApJ, 704, 38 [NASA ADS] [CrossRef] [Google Scholar]
  85. Singh, V., & Chand, H. 2018, MNRAS, 480, 1796 [NASA ADS] [CrossRef] [Google Scholar]
  86. Stevens, J., Edwards, P. G., Ojha, R., et al. 2012, ArXiv e-prints [arXiv:1205.2403] [Google Scholar]
  87. Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Tanaka, Y. T., Stawarz, Ł., Thompson, D. J., et al. 2011, ApJ, 733, 19 [NASA ADS] [CrossRef] [Google Scholar]
  89. Tavecchio, F., Ghisellini, G., Bonnoli, G., & Ghirlanda, G. 2010, MNRAS, 405, L94 [NASA ADS] [CrossRef] [Google Scholar]
  90. Tingay, S. J., Jauncey, D. L., King, E. A., et al. 2003, PASJ, 55, 351 [NASA ADS] [Google Scholar]
  91. Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [Google Scholar]
  93. van den Berg, J. P., Böttcher, M., Domínguez, A., & López-Moya, M. 2019, ApJ, 874, 47 [Google Scholar]
  94. Vaughan, S., Reeves, J., Warwick, R., & Edelson, R. 1999, MNRAS, 309, 113 [Google Scholar]
  95. Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [Google Scholar]
  96. Viswanath, G., Stalin, C. S., Rakshit, S., et al. 2019, ApJ, 881, L24 [NASA ADS] [CrossRef] [Google Scholar]
  97. Wang, Y., Xue, Y., Zhu, S., & Fan, J. 2018, ApJ, 867, 68 [CrossRef] [Google Scholar]
  98. Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [Google Scholar]
  99. Zhang, Y. H., Celotti, A., Treves, A., et al. 1999, ApJ, 527, 719 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Flux densities measured with ATCA

The radio data in Table A.1 cover ATCA observations from 2010 up to early 2020 of PKS 2004−447 and are taken in three different bands (λ4 cm, λ15 mm, and λ7 mm).

Table A.1.

ATCA flux densities taken in the λ4 cm (5.5 GHz, 9 GHz), λ15 mm (16.8 GHz, 17 GHz, 19 GHz, 21.2 GHz), and λ7 mm band (38 GHz, 40 GHz).

All Tables

Table 1.

Results from the analysis of the individual X-ray observations by Swift/XRT (S), XMM-Newton/MOS+pn (X), and NuSTAR/FPMA+B (N).

In the text
Table 2.

Flare lengths in days for the different binnings of the Fermi light curves.

In the text
Table 3.

Summary of the analysis of each individual energy range for each SED.

In the text
Table 4.

Summary of the parameters used for and derived from the modelling of the multi-epoch SEDs of PKS 2004−447 shown in Fig. 6.

In the text
Table 5.

Comparison of chosen SED model parameters of the flaring γ-NLSy 1 galaxies.

In the text
Table A.1.

ATCA flux densities taken in the λ4 cm (5.5 GHz, 9 GHz), λ15 mm (16.8 GHz, 17 GHz, 19 GHz, 21.2 GHz), and λ7 mm band (38 GHz, 40 GHz).

In the text

All Figures

thumbnail Fig. 1.

Light curves in the γ-ray (top), X-ray (middle), and UV/optical (bottom) regimes from 2019 September 27 until 2019 November 19. The Fermi/LAT light curve shows the daily binned flux of the bins with TS ≥ 1. LAT light curve bins with TS < 1 are represented as 2σ upper limit arrows. All errors represent the 1σ uncertainties. For NuSTAR, the flux is interpolated down to 0.5 keV. The dark-grey shadowed region marks the time range that is used for the flare SED, while the pre- and post-flare time ranges are shown in light grey.
In the text
thumbnail Fig. 2.

γ-ray light curves of PKS 2004−447 during the 2019 GeV flare for the different time binnings of the LAT data. Time bins with TS < 1 have an estimated error that was derived using their 1σ upper limit value. For those bins we show the 2σ upper limits in grey to visually show how many bins would have been rejected from the analysis otherwise. The Bayesian blocks are shown in red, while the baseline (average flux during the time range from 2019 October 10 to 2019 November 14) is shown in yellow. The dashed lines mark the time range chosen to construct the broadband SED of the flaring state.
In the text
thumbnail Fig. 3.

ATCA light curves taken from 2010−2020 in the λ4 cm (5.5 GHz, 9 GHz), λ15 mm (16.8 GHz, 17 GHz, 19 GHz, and 21.2 GHz) and λ7 mm band (38 GHz, 40 GHz). The time of the flare is marked by a dashed grey line.
In the text
thumbnail Fig. 4.

Difference spectrum derived from the radio observations 21 days before (t1) and 28 days after (t2) the flare. The dashed line marks the zero change of the flux.
In the text
thumbnail Fig. 5.

XMM-Newton and NuSTAR spectra with the best-fit results of an absorbed power-law model. For plotting purposed only the spectra are binned to a S/N of 5 and 3 for XMM-Newton and NuSTAR, respectively. Bins from the NuSTAR spectrum are only shown up to 50 keV, because at energies above this, no significant bin for the given S/N value is found. Upper panel: EPIC pn (blue), MOS (red) and FPMA/FPMB (yellow) data together with the best fits for the full (0.5−80 keV) energy range (solid line) as well as the hard (2−80 keV) energy range (dashed line). The zoom window shows small deviations between the fits of the full and the hard energy range. Middle panel: data-to-model ratio for the best fit to the full energy range. Lower panel: data-to-model ratio for the best-fit to the hard energy range with extrapolating the model down to 0.5 keV.
In the text
thumbnail Fig. 6.

Spectral energy distribution of PKS 2004−447 for four stages modelled with a simple leptonic emission model. Open green circles refer to the archival measurements taken from the SSDC SED builder (https://tools.ssdc.asi.it/), whereas filled black circles represent the data analysed by us. The thin solid pink line shows the synchrotron emission. Dashed green and dash-dash-dot orange lines correspond to the synchrotron self Compton and external Compton processes, respectively. The dotted black line shows the thermal emission from the accretion disk and dusty torus. The thick solid blue line is the sum of all radiative components. The SEDs are sorted from left to right as follows: low (MJD 55682–56413), pre-flare (MJD 58754–58770), flaring (MJD 58781–58784), and post-flare activity states (MJD 58787–58789), as defined in the text. The model parameters are listed in Table 3.
In the text
thumbnail Fig. 7.

Comparison of the rest-frame SEDs of γ-ray flaring NLSy 1 galaxies covering their GeV flaring epochs. The epochs of the flares are given in their labels. Except for PKS 2004−447, data taken for this comparison were analysed by Paliya & Stalin (2016) and D’Ammando et al. (2013).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.