| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202347919 | |
| Published online | 15 December 2023 | |
Investigating Gaia EDR3 parallax systematics using asteroseismology of cool giant stars observed by Kepler, K2, and TESS
II. Deciphering Gaia parallax systematics using red clump stars
1
Institute of Physics, École Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
e-mail: saniya.khan@epfl.ch
2
Dipartimento di Fisica e Astronomia, Universitá degli Studi di Bologna, Via Gobetti 93/2, 40129 Bologna, Italy
3
INAF – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Gobetti 93/3, 40129 Bologna, Italy
4
School of Physics and Astronomy, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK
5
LESIA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Université, Université Paris Diderot, 92195 Meudon, France
Received:
8
September
2023
Accepted:
13
October
2023
We analyse Gaia EDR3 parallax systematics as a function of magnitude and sky location using a recently published catalogue of 12 500 asteroseismic red-giant star distances. We selected ∼3500 red clump (RC) stars of similar chemical composition as the optimal subsample for this purpose because (1) their similar luminosity allows for straightforward interpretation of trends with apparent magnitude; (2) RC stars are the most distant stars in our sample at a given apparent magnitude, so uncertainties related to asteroseismic radii and distances are the smallest; (3) and they provide the largest sample of intrinsically similar stars. We performed a detailed assessment of systematic uncertainties relevant for parallax offset estimation based on the asteroseismic distances. Specifically, we investigated (1) the impact of measuring the basic asteroseismic quantities νmax and ⟨Δν⟩ using different pipelines, (2) uncertainties related to extinction, (3) the impact of adopting spectroscopic information from different surveys, and (4) blending issues related to photometry. Following this assessment, we adopted for our baseline analysis the asteroseismic parameters measured in Elsworth et al. (2020, Res. Notes Am. Astron. Soc., 4, 177) and spectroscopy from the Apache Point Observatory Galactic Evolution Experiment (DR17), and we further restricted the sample to low-extinction (AV ≤ 0.5 mag) RC stars with quality astrometric solutions from Gaia EDR3, as indicated by RUWE < 1.4. We then investigated both the parallax offset relative to the published Gaia EDR3 parallaxes and the residual parallax offset after correcting Gaia EDR3 parallaxes following Lindegren et al. (2021, A&A, 649, A4). We found residual parallax offsets very close to zero (−1.6 ± 0.5 (stat.)±10 (syst.) μas) for stars fainter than G > 11 mag in the initial Kepler field, suggesting that the Lindegren parallax offset corrections are adequate in this magnitude range. For 17 K2 campaigns in the same magnitude range, the residual parallax offset is +16.5 ± 1.7 (stat.)±10 (syst.) μas. At brighter magnitudes (G ≤ 11 mag), we found inconsistent residual parallax offsets between the Kepler field, 17 K2 campaigns, and the TESS southern continuous viewing zone, with differences of up to 60 μas. This contradicts the studies that suggest a monotonic trend between magnitude and residual parallax offsets and instead suggests a significant dependence on sky location at bright magnitudes due to a lack of bright physical pairs being available to determine the parallax offset corrections. Inspection of the 17 K2 campaigns allowed for investigation of parallax offsets as a function of ecliptic longitude and revealed a possible signal. Finally, we estimated the absolute magnitude of the red clump and obtained MKsRC = −1.650 ± 0.025 mag in the 2MASS Ks band and MGRC = (0.432 ± 0.004) − (0.821 ± 0.033) · (Teff [K]−4800 K)/1000 K [mag] in the Gaia G-band.
Key words: asteroseismology / astrometry / distance scale / parallaxes / stars: distances / stars: low-mass
© ESO 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Gaia EDR3 has provided unprecedented data that generate a large amount of interest in the astrophysical community. It is also known that there exists a residual parallax offset at the level of ∼10 μas that is an issue for distances beyond 1 kpc (Gaia Collaboration 2021). Lindegren et al. (2021, hereafter L21), estimated the parallax bias as a function of magnitude, colour, and ecliptic latitude. The bias corrections by L21 were determined using quasars, Large Magellanic Cloud (LMC) sources, and physical pairs.
Many studies have reported parallax offsets (Δϖ=ϖEDR3 − ϖother) and residuals (Δϖcorr = (ϖEDR3 − Z5)−ϖother) to complement the work done by L21, where ϖother is the parallax measured through an independent method and Z5 is the L21 offset for five-parameter astrometric solutions. These methods are based on direct comparisons where the parallaxes are either known or measured independently (e.g., quasars, detached eclipsing binaries, asteroseismology), jointly determined as part of the calibration of period-luminosity relations (e.g., Cepheids, RR Lyrae), or known through differential methods (e.g., binary systems, open and globular clusters). We refer the reader to the introduction of Paper I (Khan et al. 2023) and to Fig. 7 for a review of residual parallax offsets that have been measured in the literature. Existing compilations of literature results have showed that parallax offset residuals potentially follow a trend with magnitude. At the brightest magnitudes (6 < G < 13 mag), L21 corrections would overcorrect parallaxes by +10–20 μas, while as one moves to fainter magnitudes (G > 13 mag), the residuals decrease to about ∼ + 5 μas (see e.g., Fig. 1 in Li et al. 2022; Fig. 2 in Riess et al. 2022; Fig. 10 in Molinaro et al. 2023; where Δϖcorr is defined with the opposite sign).
In Paper I, we presented distance measurements for red-giant stars in the original Kepler mission (Borucki et al. 2010), 17 K2 campaigns (Howell et al. 2014), and the Transiting Exoplanet Survey Satellite (TESS) southern continuous viewing zone (TESS-SCVZ; Ricker et al. 2015) fields, with a first comparison to Gaia parallaxes. Kepler and K2 correspond to the same telescope but have very different baselines (four years and 80 days, respectively). The TESS telescope is smaller and has an intermediate baseline in the continuous viewing zones (one year). The asteroseismic distance is determined by assuming the luminosity of a stellar model that produces the observed asteroseismic observables. In the current paper, we seek to specifically address the best way to determine parallax systematics based on that dataset and to determine the limitations of this approach based on asteroseismology.
We refer the reader to Paper I for the description of the datasets and of the methods to derive distances based on asteroseismic and spectroscopic constraints. Section 2 discusses the key role of red clump (RC) stars as distance indicators. In Sect. 3, we explore and quantify systematics that may affect the estimation of the parallax offset, such as the asteroseismic method, the extinction, the spectroscopic survey, and the photometric bands. This allows us to compute a total systematic uncertainty on the parallax zero-point estimate, as well as to define the most suitable sample to characterise the Gaia offset. Section 4 presents our final comparison of Gaia EDR3 and asteroseismic parallaxes and especially comparison of the resulting offsets with those predicted by L21. We also discuss distinctions that need to be made between Kepler and K2 observations, trends that appear when we consider K2 campaigns individually, the distribution of bright calibrators in the L21 model, and the possibility of deriving the magnitude of the red clump based on Kepler results in Sect. 5. Conclusions are given in Sect. 6.
2. Red clump stars as key distance indicators
After the helium flash event, low-mass stars settle in what is known as the red clump, where helium burning proceeds in the core. At this stage, stars share very similar helium core masses and hence luminosities on the horizontal branch. They are thus located in a confined region of the Hertzsprung–Russell diagram (HRD), with a small dependence on effective temperature owing to their total mass (lower masses being slightly hotter) and composition (higher metallicities being cooler). For this reason, RC stars are known as standard candles, as their apparent brightness relates directly to their distance. They also have applications in, for example, estimating extinctions (e.g., Skowron et al. 2021; Sanders et al. 2022), mapping the Galactic bulge (e.g., Paterson et al. 2020; Johnson et al. 2022), and constraining stellar physics processes (e.g., Bossini et al. 2015, 2017). We refer the reader to Girardi (2016) for an extensive review about the red clump phase.
Based on the HRD shown in Fig. 1, we observed that among the most luminous giants in our sample, RC stars are more common than first-ascent red-giant branch (RGB) stars. For a given apparent magnitude, this means that RC stars will in general be at further distances compared to RGB stars. This has at least two benefits for parallax offset estimates: (1) asteroseismic distances have a relative uncertainty (≲5%) that will transform into a smaller absolute error for more distant stars (smaller parallaxes) compared to nearby ones (larger parallaxes; see Sect. 5.3 in Paper I); (2) the red clump alone is a rather homogeneous population compared to the whole sample of giants, which may help to reduce dispersion among the asteroseismic parallaxes. Some studies have shown that radii and masses of old metal-poor red horizontal branch (RHB) stars are likely to be biased (see, e.g., Tailo et al. 2022; Matteuzzi et al. 2023), but we can assert that very few RHB stars are included in our datasets (if any; see also Sect. 5.1). Besides, we emphasise that our asteroseismic parallaxes are model-dependent. In this regard, homogeneity is important because it ensures that the systematics affecting our stars are similar throughout the sample. This allows us to obtain the most precise relative parallax differences (e.g., between asteroseismic pipelines in Sect. 3.1) as a function of magnitude or sky position.
 |
Fig. 1. Diagrams illustrating our two-step selection method to have a RC star population as homogeneous as possible among the Kepler (left), K2 (middle), and TESS-SCVZ fields (right) using E20 and APOGEE DR17. Top: Teff vs. [Fe/H] diagrams. The red box indicates the first selection of the bulk of the RGB and RC stars to make sure that our sample is chemically similar. Bottom: Hertzsprung–Russell diagrams (Teff vs. absolute magnitude from Gaia in the G-band) after the first selection was applied. We draw a region in the HRD to select RC stars (red rectangles). |
We strive to have an RC star selection as homogeneous as possible among our Kepler, K2, and TESS-SCVZ datasets. These surveys cover different areas on the sky, so we wanted to limit the impact of sample differences as much as possible. As a first step, we selected the bulk of RGB and RC stars in the Teff–[Fe/H] plane with the following corner coordinates: {(4832, 0.416), (4432, 0.366), (4750, −0.827), (5150, −0.777)}. This ensures that our giant stars are chemically comparable and that we do not include any RHB stars. Then, we selected stars within the range defined by the following (Teff, MG) coordinates: {(4990, −0.160), (4510, 0.280), (4510, 0.930), (4990, 0.490)} (see Fig. 1), where MG is computed using Gaia parallaxes (without L21 corrections) and extinctions AV from PARAM. Given the impact that a parallax offset would have on MG and the height of the box, it does not need to be considered at this stage of the analysis. In the Kepler field, core-helium burning stars have been identified using the evolutionary-dependent signature of gravity modes in the oscillation spectra (Bedding et al. 2011; Elsworth et al. 2017); hence, we used this classification to prevent any contamination from RGB stars. For K2 and TESS, we know that there could still be some contamination due to RGB stars as well as secondary clump stars (see, e.g., Sect. 3.5 in Schonhut-Stasik et al. 2023). Some studies have provided a classification for K2 campaigns (K2 GAP, Zinn et al. 2022; K2-APO, Schonhut-Stasik et al. 2023) and TESS continuous viewing zones (HD-TESS, Hon et al. 2022), although it is not as robust as in Kepler’s dataset. The original Kepler field remains unmatched in its asteroseismic detail due to the long temporal baseline of four years and its larger telescope aperture, compared to TESS. A crossmatch between our RC stars and those of previous catalogues led to lower statistics and does not affect our results; hence, we continued with our selection, relying on Teff, [Fe/H], and MG. Without the classification as RGB or RC for the Kepler field, we would find a contamination of about 15% by RGB stars.
Based on the above discussion, we therefore investigated parallax systematics primarily using RC stars. In total, we selected 3422 RC stars after cuts on AV and RUWE (see Table 1 and beginning of Sect. 4). Where useful, we considered other RGB stars as well (Sects. 3.2.1 and 3.3). General information about the RC stars we selected is provided in Table 1.
Summary information for the RC stars selected in each field.
3. Quantifying systematic uncertainties related to asteroseismic parallaxes
Asteroseismic parallaxes were estimated with the Bayesian tool PARAM (Rodrigues et al. 2017). The code requires observational parameters as inputs, namely, νmax, ⟨Δν⟩, Teff, log g, [Fe/H], and [α/Fe] (when available), as well as magnitudes in various photometric systems. Observations were then compared with a grid of stellar evolutionary tracks in order to predict the best-fitting stellar properties, such as radii, masses, distances, total extinctions.
3.1. Differences among asteroseismic methods
The global asteroseismic parameters that are used to determine the model luminosity can differ according to the way that they are measured. In our study, we have access to asteroseismic observables determined by Elsworth et al. (2020, hereafter E20), and Mosser & Appourchaux (2009, hereafter MA09). We used RC stars to assess how using one pipeline or the other affects our results.
As the relative uncertainty on the seismic distance is constant (≲5%), we expected that the resulting absolute error on parallax would be larger for nearby stars (large parallaxes) compared to distant stars (small parallaxes; see also discussion in Sect. 5.3 in Paper I). Because of the very restricted range of absolute magnitudes in the red clump, there is a tight relation between distance and apparent magnitude, namely, nearby stars are bright, while more distant stars are fainter.
Figure 2 shows that E20’s pipeline yields greater consistency between RGB and RC stars, differences are on the order of a few microarcseconds at most. By contrast, with MA09’s asteroseismic constraints, discrepancies cover a wide range of values between 10 μas and 40 μas at the brightest magnitudes. Owing to the greater agreement based on the E20 pipeline, we used their asteroseismic quantities for the remainder of this study. We adopted the difference of the two pipelines as the asteroseismic contribution to the total systematic uncertainty.
 |
Fig. 2. Parallax difference binned as a function of magnitude for the Kepler field with RC (solid) and RGB stars (dotted line) shown separately. Results from E20 and MA09 are shown in orange and green, respectively. The black arrows show the difference used to measure the systematic error due to using different asteroseismic methods. |
As illustrated in Fig. 2, we estimated the bias due to asteroseismic methods as the absolute mean difference between the parallax offsets measured using E20 and MA09 but also considering how it evolves as a function of magnitude. For Kepler, it decreases from 15 to 5 μas; for K2, the values are rather stable and stay around 5–10 μas at most; and for TESS, it is around 8 μas. It is clear that the bias is of greater importance at the brightest magnitudes, and it decreases when moving towards fainter stars. This is also in accordance with the above discussion. The absolute parallax uncertainty of Gaia parallaxes is lower than asteroseismic parallax uncertainties at G ≲ 10 − 11 mag for a fiducial RC star of MG = 0.5 mag with Teff = 4750 K. Overall, the difference between the E20 and MA09 parallax offsets, which we adopt as an asteroseismic systematic uncertainty, we measure can be approximated by
This relation is valid for G ∈ [9, 13] mag.
3.2. Impact of extinction
Extinction is an important quantity to consider for at least two aspects: its determination is often quite uncertain, and reddening is such that the observed colour is different from the star’s intrinsic colour. In PARAM, extinction coefficients are computed adopting the Cardelli et al. (1989) and O’Donnell (1994) reddening laws with RV = 3.1. It is then assumed that extinctions in all filters Aλ are related by a single interstellar extinction curve expressed in terms of its V-band value, that is, Aλ(AV). The total extinction AV and the distance d can then be derived simultaneously. Hence, uncertainties come from both the reddening law (dust composition) and the match of the assumed, reddened spectral energy distribution (SED) to the observed SED.
3.2.1. K2 fields: Galactic plane versus halo
Figure 3 shows the relation between the parallax difference and the G magnitude for three of the most populated campaigns in our K2 sample with both RGB and RC stars. Notably, C4 is located close to the Galactic plane and has a median extinction of AV ∼ 0.8 mag, while C3 and C5 are in the halo and show much milder extinction (AV ∼ 0.15 mag). It appears that at magnitudes brighter than G = 11.5 mag, the parallax difference of C4 stars decreases towards more negative offsets with a steeper slope than the other two campaigns. This colour-dependent effect could be an illustration of a reddening systematic (given that C4 contains more red stars with respect to C3 and C5). We also note that the brightest magnitude bin is missing in C4, and thus a lack of bright red stars potentially points towards dust attenuation. The brightest RC stars in the different K2 campaigns are similarly distant due to similar spatial distribution. Hence, an RC star in the plane at the same distance as one in the halo would be fainter.
 |
Fig. 3. Parallax difference binned as a function of magnitude for three K2 campaigns selected for their large number of stars and low or high extinction. C3 (light pink) and C5 (light green), which are located in the halo (|b|> 30°), and C4 (magenta) is closer to the Galactic plane (|b|< 30°). |
3.2.2. Examining whether there is a need to rescale the extinction
An error in the extinction correction would more readily affect stars at bright magnitudes than at faint magnitudes. Since Fig. 3 indicates such a trend, we considered whether a small adjustment to the extinction estimate in PARAM could lead to better agreement. We tested the impact that a different RV value would have on the following relationship AV = RV E(B − V). This implies modifying the asteroseismic parallax as follows:
where f is the correction factor applied to the total extinction in the V-band. A factor f > 1 is equivalent to RV > 3.1, and f < 1 corresponds to RV < 3.1. We also initially considered a correction in the form of an additive term, namely, AV + δAV, but two significant issues arise in this case: the corrections derived would often lead to negative extinctions (which are non-physical), and there is no way to tell whether an additive term corrects the extinction, magnitude, or any other quantity involved in the computation of the parallax. Hence, we did not explore this avenue further.
Our rescaling test was done using RC stars only. We first defined a reference low-extinction sample containing the 30% of stars with the lowest extinctions. Then, for each G magnitude bin (ranging from [9,13], [9,15], and [9,11] with a bin size varying between 0.2 and 0.5 mag for Kepler, K2, and TESS, respectively), we derived mean estimates for the asteroseismic and Gaia parallaxes and computed a parallax offset – which would be our expected value. Then, we kept the remaining 70% of stars as individual. We estimated χ2 for each f value in the range [0.8, 1.2] as follows:
where Δϖind and Δϖexp are the individual and expected parallax offsets after applying the extinction rescaling factor f, while σΔϖind and σΔϖexp are their respective uncertainties. All individual χ2 values were added together so that we would have a single χ2 estimate for a given f and magnitude bin. The best-fitting correction factor f is the one at which the χ2 distribution finds its minimum, and the corresponding uncertainty is obtained by looking at how much f varies if we were to consider min(χ2)+1.
Whether it be for Kepler, K2, or TESS, the χ2 distributions suggest that f is close to unity (fKepler ∼ 1.01 ± 0.11, fK2 ∼ 0.99 ± 0.06, and fTESS ∼ 0.96 ± 0.08 where the two values quoted are the mean and standard deviation), and we did not find any significant correction that should be applied to extinction values from PARAM (Fig. 4). Despite this, we know that low-extinction stars are nevertheless more reliable because any uncertainties of the extinction correction would impact the results less. Hence, we applied the following criterion for all fields:
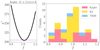 |
Fig. 4. Derivation of the best-fitting correction factor f on the total extinction AV per magnitude bin and per field. Left panel: example of a χ2 distribution for a given magnitude bin in the Kepler field. The purple dashed line corresponds to min(χ2)+1. Right panel: stacked distribution of f values in all magnitude bins for Kepler, K2, and TESS. |
We also looked at whether we could characterise the sightline extinction as a function of Galactic latitude. In order to do this, we split our Kepler and K2 datasets between the low-extinction reference and other stars, as done above. We looked at K2 campaigns individually and did not bin in magnitude, as the statistics would be too low. We computed a rescaling factor f for Kepler and each K2 campaign with enough low-extinction stars (fields with |b|< 30° were thus excluded), and we studied the relation with Galactic latitude. We did not observe any clear trend. Considering Kepler and K2 campaigns together, we measured a mean value of f ∼ 0.9, with a standard deviation of about 0.15. We estimated the impact that f = 0.9 would have on Kepler and K2 parallax differences, restricting the sample to AV < 0.5 mag. We found that the systematic bias due to extinction can be approximated by an exponential with a base ten function:
This relation is valid for G ∈ [9, 15] mag.
3.3. Spectroscopic surveys
In terms of spectroscopy, PARAM uses Teff, [Fe/H], and [α/Fe] (when available) to derive distances and, hence, parallaxes. Parameters from different spectroscopic surveys may differ depending on the wavelength in which observations were taken, the region of the sky they focused on, and the spectral resolution. The survey APOGEE DR17 is a near-infrared (NIR) all-sky spectroscopic survey (Abdurro’uf et al. 2022) with a resolution of R ∼ 22 500, while GALAH DR3 focused on the southern hemisphere in the optical and NIR and with R ∼ 28 000 (Buder et al. 2021). We estimated the systematic uncertainty of the parallaxes by comparing the difference among datasets for the same stars. We considered K2 stars with observations from both catalogues, leaving us with nearly 2800 RGB and RC stars. As done in Sect. 3.1, the bias due to the choice of spectroscopic constraints was computed as the absolute mean difference between the offsets measured using APOGEE and GALAH data. The bias shows small oscillations as a function of magnitude, but overall we found that the spectroscopic systematic uncertainty is about
We adopted APOGEE DR17 as the largest sample measured homogeneously across all Kepler, K2, and TESS fields.
3.4. Photometric data used by PARAM
The distances in Paper I used data from different photometric surveys as available. This resulted in different sets of multi-band photometry being employed for different fields (Kepler, individual K2 campaigns, TESS-SCVZ). Those photometric sets are shown in Table 2 and could lead to slight differences in the homogeneity of the outputs generated by the Bayesian code. In particular, the photometry used for Kepler and TESS goes deeper in the infrared with respect to K2, notably with the addition of WISE bands.
Photometric bands used for the different fields.
We also considered the fact that the angular resolution achieved by some of these surveys is not at the level of Gaia’s. For instance, it is of the order of 2.5″ for 2MASS and ∼6″ for W1–3. This means that the magnitudes measured in these bands could potentially be affected by blending issues, because nearby contaminants would not be resolved due to the limited angular resolution.
To test this, we performed a multi-cone search within the Gaia catalogue in order to list all the sources within a 6″ search radius of our targets in Kepler, K2, and TESS. We found that 574, 108, and 106 targets have potential stellar contaminants in each field, respectively. We measured the magnitude contrast between those contaminants and the main source of interest. We considered that blending effects can be considered negligible with a magnitude contrast above 5 mag, which would correspond to a 1/100 flux ratio. We removed stars with at least one nearby source that could contribute significantly to blending, and they amounted to 97, 24, and 7 in Kepler, K2, and TESS respectively. If we wanted to decrease the magnitude contrast threshold to 2 mag, it would only remove 6, 0, and 1 stars. In both cases, when we repeated our analysis with the reduced samples, the differences were barely noticeable. Hence, potential blending issues do not affect our results, and we did not have to consider them further in our investigation.
Table 3 provides average estimates for the asteroseismic, extinction, spectroscopic, and total systematic uncertainty in microarcseconds for different G-magnitude ranges. We also provide the corresponding systematic error that would apply to the distance modulus, in magnitude.
Average systematic uncertainty for the asteroseismic, extinction, and spectroscopic components and the total systematic uncertainty.
4. Analysis of the Gaia EDR3 parallax zero-point
As described above, we selected the following sample to obtain the most detailed view of Gaia’s parallax systematics using asteroseismic parallaxes: RC stars selected according to temperature, iron abundance, and absolute magnitude (cf. Fig. 1); asteroseismic constraints from E20, as the pipeline gives more consistent results between RGB and RC stars, and we do not expect the parallax offset to depend on the evolutionary stage (see Fig. 2); spectroscopic properties from APOGEE DR17; low-extinction stars (AV ≤ 0.5 mag); and Gaia EDR3 sources with good astrometric quality (RUWE < 1.4). With these choices, we were left with 1560, 1227, and 635 RC stars from Kepler, K2, and TESS, respectively.
The top panels of Fig. 5 show Δϖ=ϖEDR3 − ϖPARAM as a function of magnitude for Kepler, K2, and TESS RC star targets. The background stars in grey show the entire sample with both RGB and RC stars, while the purple ones correspond to RC stars only. The running mean was calculated based on RC stars and more evidently shows the trend with magnitude. The non-linear trend with G is very much apparent in Kepler, as already discussed in Sect. 4.1 of Paper I. We did not see it in K2, possibly because of the larger uncertainties or the fact that K2 fields are scattered along the ecliptic, which might average out some systematics, while the TESS targets are too bright. Overall, Δϖ values are mostly negative, but they do approach zero, for example, for G ≤ 10 mag in Kepler, and at G ∼ 12.5 mag for K2.
 |
Fig. 5. Parallax difference before (top) and after correction (bottom) as a function of G magnitude for Kepler (left), K2 (middle), and TESS (right). The grey scatter corresponds to the entire sample of RGB and RC stars. Our best sample with low-extinction RC stars is shown with purple points, and the colour scale indicates their density (increasing from dark purple to white). The red, yellow, and blue lines show the running mean and its uncertainty for each field. |
The bottom panels of Fig. 5 show Δϖcorr = (ϖEDR3 − Z5)−ϖPARAM as a function of magnitude. For Kepler stars, the magnitude-dependent non-linear systematics are very effectively removed by the L21 corrections. The parallax offset residuals become very close to zero for G ≥ 11 mag. For K2 stars, they seem to be shifted globally towards slightly positive residuals, that is, L21 corrections are a bit too large. And TESS stars are shifted by a very small amount, which is far from being enough to reach zero; in other words, L21 offsets are underestimated in this case.
Figure 6 gathers the residuals obtained for Kepler, K2, and TESS together as a function of magnitude. At bright magnitudes (G ≤ 11 mag), the picture is not that clear. For Kepler, L21 overcorrects the Gaia parallaxes. This is also the case for K2 fields, despite a decrease towards zero at the brightest end. This result goes in the same direction as those from the literature in this magnitude regime (see, e.g., Li et al. 2022; Molinaro et al. 2023). However, TESS exhibits the opposite trend, that is, L21 undercorrects the parallaxes. For TESS, Z5 is of the order of ∼10 μas, and it is ∼25 μas for Kepler. Given the similarity of the stars and the homogeneous methodology, we consider a dependence on sky location in Sect. 5.2. But whether it be for Kepler or TESS, L21 either corrects too much or not enough, potentially highlighting a drawback in the L21 zero-point correction model. There also does not seem to be a link between the trend suggested by Fig. 6 and the fact that we have varying observation lengths in Kepler (4 years), TESS-SCVZ (1 year), and finally K2 (80 days), in descending order (see Sect. 5.1 for a discussion about how observing conditions may affect the target selection and asteroseismic properties). All of this means that one cannot simply apply the same offset at bright magnitudes.
 |
Fig. 6. Parallax offset residual (after correcting using L21) as a function of magnitude for Kepler (red), K2 (yellow), and TESS (blue). The points show the mean values, while the shaded areas indicate the corresponding uncertainty (given as the error on the mean per bin). |
Figure 7 shows our results in the context of other recent findings related to Gaia parallax systematics. These literature offsets were determined in different regions of the sky using astrophysically different objects and different methods. There is no clear trend with magnitude, although the majority of the residuals are positive. A summary of the median parallax offsets and residuals obtained for each field in the bright and faint magnitude ranges is given in Table 4.
 |
Fig. 7. Comparison of our results, Δϖcorr = (ϖGEDR3 − Z5)−ϖPARAM, to a compilation of Gaia parallax offset residuals from the literature as a function of the magnitude in the G-band. Results displayed as open circles with vertical error bars are from the literature. Our findings for Kepler, K2, and TESS are shown as red, yellow, and blue shaded areas, respectively. Different literature sources used very astrophysically different objects and methods. Here we used the same methodology applied to a rather intrinsically homogeneous group of stars. The sign convention we use is such that positive values correspond to an overcorrection of parallaxes and negative values to an underestimation of parallaxes by L21. |
Median parallax offsets before and after applying L21 in the faint (11 ≤ G ≤ 13 mag) and bright magnitude ranges (G ≤ 10 mag).
We also considered the possibility of applying additional Gaia photometric quality flags in order to remove stars likely to be blended by nearby sources (see Sect. 9.3 in Riello et al. 2021). These include: β = (phot_bp_n_blended_transits + phot_rp_n_blended_transits)*1.0/(phot_bp_n_obs + phot_rp_n_obs) < 0.1 (blending fraction); ipd_frac_multi_peak < 7 (Gaia EDR3 percent of successful-IPD windows with more than one peak); ipd_frac_odd_win < 7 (Gaia EDR3 percent of transits with truncated windows or multiple gates); and C* < 1σ (Gaia EDR3 corrected BP/RP excess factor). The number of stars in each field then becomes 1314, 1051, and 474. This affects the median values computed at the level of ±2 μas at most, so it is not significant.
5. Discussion
5.1. How to interpret differences between Kepler and K2
At faint magnitudes (G > 11 mag), Kepler and K2 lead to different conclusions regarding the suitability of the L21 zero-point model. The latter works well for Kepler targets where the residual offset is almost zero. However, for K2 fields, Z5 overcorrects Gaia parallaxes.
Even if the asteroseismic pipeline leading to the measurement of νmax and ⟨Δν⟩ is the same for both Kepler and K2, the two surveys still have significant differences observation-wise. Kepler is a high ecliptic latitude field with observations taken continuously for four years. K2 campaigns cover 17 different locations (in our study), and their observations span a much shorter duration of 80 days. So their comparison should account for the larger uncertainties in K2, and we cannot interpret our results in the sense that K2 contradicts Kepler.
The difference in the observation duration leads to differences in the seismic performance index (Mosser et al. 2019). This index depends on νmax, the height-to-background ratio, and the observation duration. It is naturally lower for shorter observations, as in K2. Hence, measurements are likely to be biased towards red-giant stars with a high enough signal and amplitude. For a given magnitude, the signal ratio between observations spanning either several years or a couple of months can reach ten or more (see, e.g., Fig. 3 in Mosser et al. 2019). Population effects associated with different magnitude distributions, for instance, can also affect the seismic signal. Fainter targets, which K2 contains a larger fraction of, are increasingly harder to detect asteroseismically. We note that our selection of RC stars in K2 (cf. bottom middle panel of Fig. 1) effectively removes metal-poor RHB stars that could be biased in their ⟨Δν⟩, hence radius and mass, determination (Tailo et al. 2022; Matteuzzi et al. 2023). As a sanity check, we also excluded α-rich stars ([α/Fe] > 0.15 dex) from our K2 RC star sample, and this brought the residual offset to ∼ + 14 μas (for G ∈ [11, 13] mag), so nothing was significantly different.
All of these aspects go in the same direction such that Kepler’s observing conditions are more favourable to the detection of oscillations and to a greater quality of asteroseismic measurements. However, K2 also provides invaluable information regarding spatial variations of the parallax zero-point that could go beyond the only latitudinal dependence considered in L21, which we discuss in the next section. The shorter baseline of K2 compared to Kepler results in a much-reduced density (number of stars over the sky area) of red-giant stars with determined asteroseismic parameters. Despite the fact that K2 goes fainter and has approximately 15 times the total area of Kepler, thanks to the many different campaigns, the number of stars in the Kepler and K2 samples are similar. This means that the K2 stars could be a biased selection of the population that make up the Kepler sample. Hence, there is a small chance that some of the differences between Kepler and K2 come from population differences that cannot be conclusively assessed here. Yet, a comparison between the different K2 campaigns is valid because the conditions are the same for each campaign (baseline, area, magnitude range).
5.2. Exploring variations among K2 campaigns
As a follow-up to Kepler, K2’s survey design probes different ecliptic longitudes at zero ecliptic latitude. This allows for investigation of a dependence of the residuals on ecliptic longitude, as shown in Fig. 8. To this end, we evaluated the median parallax offset for each K2 campaign in the magnitude range G ∈ [11, 13] mag. We also added the Kepler field for comparison. Campaigns with similar longitude taken years apart yield similar results, which excludes significant temporal evolution of the instrument as a source of the variations. There are some intriguing features that we highlight: (1) most campaigns are near +10 or +20 μas; (2) adjacent campaigns (in lecl) can differ greatly (cf. near 180°); (3) maximum variations are seen near 180° and 360°; (4) there are campaigns at near-identical lecl (C6 and C17, C5 and C16). Since the analysis is done exactly in the same way using astrophysically very similar objects, we considered the variations to be real. We observed that there are two clear outliers with a residual offset ≳ + 40 μas: C10 at lecl ∼ 180° and C12 at lecl ∼ 360°. All the other campaigns lie below ∼ + 30 μas. Including the extinction and RUWE flags slightly decreases the overall scatter among the different K2 campaigns, as one would expect since that restricts the sample to stars with better photometry and astrometry.
 |
Fig. 8. Median residual offset as a function of ecliptic longitude for the individual K2 campaigns and Kepler. Open and filled circles show the results before and after applying the extinction and RUWE cuts. For clarity, error bars are only shown for the offsets where the cuts were applied. |
Hence, K2 campaigns provide a spatial dependence hint along the ecliptic longitude – which is currently not considered in the L21 correction model. When combining all K2 fields together, this longitudinal dependence is averaged over, and data from very different regions of the sky are combined, which is not the case for the original Kepler field and TESS-SCVZ. This stresses the point that analyses must still solve the residual parallax offset and cannot simply adopt offsets from the literature if these were not determined on similar samples with respect to sky location, magnitude, and colour. So it is likely that the ∼ + 16 μas (+13 μas, when the two greatest outliers C10 and C12 are removed) residual offset observed in the G ∈ [11, 13] mag range could be caused by systematic uncertainties related to both the quality of asteroseismic observations (Sect. 5.1) and the need to resolve positional variations within K2 (which requires higher statistics).
5.3. Coverage of bright physical pairs in L21 model
The L21 zero-point correction is based on quasars, physical pairs, and stars in the LMC. What is missing is thus a good determination of this bias for brighter stars, as quasars only cover the faint end of magnitudes (G > 14 mag), very few LMC sources have G < 13 mag (1457), and physical pairs constitute a major part of calibrators in the bright regime (6 < G < 14 mag), with nearly 70 000 sources but only ∼4000 with G < 11 mag. Hence, the bright component of the correction relies quite heavily on the sky coverage by physical pairs. We reproduced Fig. 1 from Khan et al. (2023), overlaying the location of the physical pairs with G < 11 mag that have been used within the L21 correction (list of sources shared through priv. comm. by Lindegren; see Fig. 9). Among the initial list of nearly 121 000 physical pairs, only 4374 are brighter than G = 11 mag. The coverage provided by these bright physical pairs is rather sparse over the entire sky, and most of them are located on the Galactic disc, while the asteroseismic fields probe many off-disc locations. Given the limited overlap and low statistics at the bright end, we considered that our reported differences indicate true shortcomings of the L21 model that originate from the limited spatial coverage by physical pairs. This also demonstrates how asteroseismology can effectively complement Gaia in certain regions of the sky.
 |
Fig. 9. Skymap in Galactic coordinates showing the location and coverage resulting from the crossmatch between the various asteroseismic fields considered in this study and APOGEE DR17. Galactic longitude increases from right to left. The yellow crosses correspond to the location of the bright physical pairs (G < 11 mag) that have been used in the process of deriving the zero-point correction model from L21. This figure was generated using the python package mw-plot (http://milkyway-plot.readthedocs.io/). The background image comes from ESA/Gaia/DPAC. |
5.4. Estimation of the red clump magnitude
In Sect. 4, we found a robust result for the Kepler field, namely, that the residual parallax offset (after applying L21 corrections) is nearly null for 11 < G < 13 mag. We used this opportunity to compute the absolute magnitude of the red clump in this magnitude range in the Ks and G bands. Absolute magnitudes and uncertainties were computed for individual RC stars as follows:
where ϖEDR3 and Z5 are in arcseconds, and Aλ is calculated from the AV estimate computed by PARAM. Taking the median value, we found the absolute magnitude of the clump to be
in the Ks band. The uncertainties were computed in a conservative way such that we considered the total systematic uncertainty from Table 3 (0.025 mag) and the formal error on the median (0.002–0.003 mag). The latter is fairly negligible, while the systematic error completely dominates in this case. Unlike 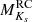 , which is relatively independent of Teff,
, which is relatively independent of Teff, 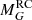 can vary quite significantly over the Teff range we considered here. Hence, we instead stated the absolute magnitude in the G-band as a function of Teff:
can vary quite significantly over the Teff range we considered here. Hence, we instead stated the absolute magnitude in the G-band as a function of Teff:
where the average dispersion around the fit is of ∼0.12 mag. Figure 10 shows the HRD for the final sample of Kepler stars used to estimate 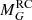 and the fit derived as a function of Teff (Eq. (6)). As discussed in Sect. 5.1 of Paper I, the red clump magnitude is also subject to population effects related to the age and metallicity spread, so the conservative estimate of the uncertainty reflects that intrinsic scatter as well. Values for the Ks band in the literature have been found to range between −1.53 and −1.62 mag before the Gaia era (see Table 1 in Girardi 2016). With Gaia DR1, Hawkins et al. (2017) derived
and the fit derived as a function of Teff (Eq. (6)). As discussed in Sect. 5.1 of Paper I, the red clump magnitude is also subject to population effects related to the age and metallicity spread, so the conservative estimate of the uncertainty reflects that intrinsic scatter as well. Values for the Ks band in the literature have been found to range between −1.53 and −1.62 mag before the Gaia era (see Table 1 in Girardi 2016). With Gaia DR1, Hawkins et al. (2017) derived 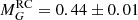 mag and
mag and 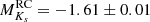 mag. Using Gaia DR2 parallaxes, Hall et al. (2019) measured
mag. Using Gaia DR2 parallaxes, Hall et al. (2019) measured 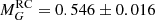 mag and
mag and 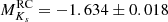 mag, while Chan & Bovy (2020) found
mag, while Chan & Bovy (2020) found 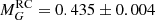 mag and
mag and 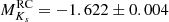 mag.
mag.
 |
Fig. 10. Hertzsprung–Russell diagram for our final set of Kepler RC stars where the G-band absolute magnitude is computed using L21-corrected Gaia parallaxes (black points). The sample is restricted to G ∈ [11, 13] mag, where we found the residual parallax offset to be approximately zero. The pink dashed line shows the fit given by Eq. (6), and the brown shaded region illustrates how the fit could vary given the uncertainties on the slope and the intercept. |
Our red clump absolute magnitude estimates are in reasonably good agreement with the literature values, within the uncertainties. For the G-band red clump magnitude, our estimate agrees with Hawkins et al. (2017) and Chan & Bovy (2020) for Teff ∼ 4800 K, while a cooler Teff (4650 K) is required to obtain a good agreement with the results from Hall et al. (2019). We acknowledge that the red clump absolute magnitude determination presented here is slightly circular because the same RC stars that determine the absolute magnitude were used to demonstrate the absence of a residual zero-point in the magnitude range used to determine 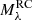 . Additionally, the extinction estimates were obtained by PARAM and rely on known SEDs and bolometric corrections. However, because the parallax offset residual is zero and extinction corrections are low by selection, it is still valid to present this approach despite its circularity.
. Additionally, the extinction estimates were obtained by PARAM and rely on known SEDs and bolometric corrections. However, because the parallax offset residual is zero and extinction corrections are low by selection, it is still valid to present this approach despite its circularity.
6. Conclusions
This study provides the most in-depth asteroseismic view of Gaia parallax systematics based on the most informative subset of stars in our sample, namely, RC stars observed by Kepler, K2, and TESS-SCVZ, together with a detailed analysis of uncertainties affecting the asteroseismic parallaxes. It builds upon the asteroseismic datasets and methods presented in Paper I (Khan et al. 2023).
We presented detailed results for parallax offsets as a function of magnitude in Kepler, K2, and TESS-SCVZ fields, both before and after applying L21 corrections. Each field leads to different conclusions regarding the parallax systematics residuals. For magnitudes fainter than G = 11 mag, the residuals are very close to zero in Kepler. However, in the bright regime (G ≤ 11 mag), the L21 correction model overcorrects parallaxes for Kepler targets by ∼ + 15 μas and undercorrects those of TESS sources by ∼ − 25 μas, on average. For K2 fields, L21 offsets are slightly overestimated independently of magnitude (by ∼ + 12 μas). Previous literature compilations have led to the general finding that parallax residuals follow a trend with G magnitude, meaning that the L21 model significantly overcorrects parallaxes for G ≤ 13 mag and that this effect would decrease on the fainter side (Li et al. 2022; Molinaro et al. 2023). Our findings show that the final picture is actually not as straightforward. In the same bright magnitude regime (G ≤ 11 mag), Kepler, K2, and TESS demonstrate that the L21 model either overestimates or underestimates the parallax systematics. Hence, it could be that the L21 offsets do not fully account for the positional dependence of the systematics. Moreover, studies should not apply magnitude-dependent residual parallax offset corrections nor rely on residual parallax offsets derived from objects covering different parameter spaces (e.g., sky location, magnitude). This is particularly true for objects brighter than G = 11 mag, where we consider our results to indicate real shortcomings of the L21 model related to the sparsity of physical pairs. For the time being, studies seeking parallax accuracy better than 15 μas should solve for the residual parallax offset as it applies to the sample under study.
We also explored K2 campaigns in more detail by checking individual parallax offsets against ecliptic longitude. We potentially found interesting variations where two campaigns stand out with significantly more positive offsets at lecl ∼ 180° and 360°. The ∼ + 16 μas residual offset in the faint magnitude regime (G ∈ [11, 13] mag), where Kepler agrees very well with L21, could also in part be related to this longitudinal dependence not being resolved when considering the K2 dataset as a whole. There is certainly room for improvement, as TESS observations will potentially continue for another decade, and the ESA PLAnetary Transits and Oscillations of stars (PLATO) mission will observe thousands of solar-like oscillators in a field of view approximately 20 times larger than Kepler and is expected to launch by the end of 2026 (Rauer et al. 2014). Moreover, High-precision AsteroseismologY of DeNse stellar fields (HAYDN), one of five potential candidates for the next ESA medium-class mission, would offer the possibility of probing much denser fields, such as globular clusters; its potential launch would be in the late 2030s (Miglio et al. 2021).
Finally, we computed the absolute magnitude of the red clump in the KS and G bands using Kepler RC stars with 11 < G < 13 mag and whose residual offset we found to be basically zero. These are the first measurements using Gaia EDR3 parallaxes, and they are in close agreement with previous results from the literature, within the uncertainties.
Acknowledgments
We warmly thank Lennart Lindegren for providing information regarding the Gaia parallax zero-point correction model. We also wish to thank the referee whose comments helped clarify and improve the paper. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. R.I.A. and S.K. are funded by the Swiss National Science Foundation (SNSF) through an Eccellenza Professorial Fellowship (award PCEFP2_194638). A.M. acknowledges support from the ERC Consolidator Grant funding scheme (project ASTEROCHRONOMETRY, G.A. n. 772293). This research was supported by the International Space Science Institute (ISSI) in Bern, through ISSI International Team project #490, SHoT: The Stellar Path to the Ho Tension in the Gaia, TESS, LSST and JWST Era.
References
- Abdurro’uf, AccettaK., AertsC., et al. 2022, ApJ, 259, 35 [Google Scholar]
- Bedding, T. R., Mosser, B., Huber, D., et al. 2011, Nature, 471, 608 [Google Scholar]
- Bhardwaj, A., Rejkuba, M., de Grijs, R., et al. 2021, ApJ, 909, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
- Bossini, D., Miglio, A., Salaris, M., et al. 2015, MNRAS, 453, 2290 [Google Scholar]
- Bossini, D., Miglio, A., Salaris, M., et al. 2017, MNRAS, 469, 4718 [Google Scholar]
- Buder, S., Sharma, S., Kos, J., et al. 2021, MNRAS, 506, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Chan, V. C., & Bovy, J. 2020, MNRAS, 493, 4367 [Google Scholar]
- Cruz Reyes, M., & Anderson, R. I. 2023, A&A, 672, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elsworth, Y., Hekker, S., Basu, S., & Davies, G. R. 2017, MNRAS, 466, 3344 [NASA ADS] [CrossRef] [Google Scholar]
- Elsworth, Y., Themeßl, N., Hekker, S., & Chaplin, W. 2020, Res. Notes Am. Astron. Soc., 4, 177 [Google Scholar]
- Fabricius, C., Luri, X., Arenou, F., et al. 2021, A&A, 649, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilligan, C. K., Chaboyer, B., Marengo, M., et al. 2021, MNRAS, 503, 4719 [Google Scholar]
- Girardi, L. 2016, ARA&A, 54, 95 [Google Scholar]
- Hall, O. J., Davies, G. R., Elsworth, Y. P., et al. 2019, MNRAS, 486, 3569 [Google Scholar]
- Hawkins, K., Leistedt, B., Bovy, J., & Hogg, D. W. 2017, MNRAS, 471, 722 [Google Scholar]
- Hon, M., Kuszlewicz, J. S., Huber, D., Stello, D., & Reyes, C. 2022, AJ, 164, 135 [CrossRef] [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [Google Scholar]
- Huang, Y., Yuan, H., Beers, T. C., & Zhang, H. 2021, ApJ, 910, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, C. I., Rich, R. M., Simion, I. T., et al. 2022, MNRAS, 515, 1469 [NASA ADS] [CrossRef] [Google Scholar]
- Khan, S., Miglio, A., Willett, E., et al. 2023, A&A, 677, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, S., Casertano, S., & Riess, A. G. 2022, ApJ, 939, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Bastian, U., Biermann, M., et al. 2021, A&A, 649, A4 [EDP Sciences] [Google Scholar]
- Matteuzzi, M., Montalbán, J., Miglio, A., et al. 2023, A&A, 671, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miglio, A., Girardi, L., Grundahl, F., et al. 2021, Exp. Astron., 51, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Molinaro, R., Ripepi, V., Marconi, M., et al. 2023, MNRAS, 520, 4154 [NASA ADS] [CrossRef] [Google Scholar]
- Mosser, B., & Appourchaux, T. 2009, A&A, 508, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Michel, E., Samadi, R., et al. 2019, A&A, 622, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Donnell, J. E. 1994, ApJ, 422, 158 [Google Scholar]
- Paterson, D., Coleman, B., & Gordon, C. 2020, MNRAS, 499, 1937 [NASA ADS] [CrossRef] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [Google Scholar]
- Ren, F., Chen, X., Zhang, H., et al. 2021, ApJ, 911, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Riello, M., De Angeli, F., Evans, D. W., et al. 2021, A&A, 649, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2021, ApJ, 908, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Breuval, L., Yuan, W., et al. 2022, ApJ, 938, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Rodrigues, T. S., Bossini, D., Miglio, A., et al. 2017, MNRAS, 467, 1433 [NASA ADS] [Google Scholar]
- Sanders, J. L., Smith, L., González-Fernández, C., Lucas, P., & Minniti, D. 2022, MNRAS, 514, 2407 [CrossRef] [Google Scholar]
- Schonhut-Stasik, J., Zinn, J. C., Stassun, K. G., et al. 2023, AJ, submitted [arXiv:2304.10654] [Google Scholar]
- Skowron, D. M., Skowron, J., Udalski, A., et al. 2021, ApJ, 252, 23 [NASA ADS] [Google Scholar]
- Stassun, K. G., & Torres, G. 2021, ApJ, 907, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Tailo, M., Corsaro, E., Miglio, A., et al. 2022, A&A, 662, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasiliev, E., & Baumgardt, H. 2021, MNRAS, 505, 5978 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, C., Yuan, H., & Huang, Y. 2022, AJ, 163, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Zinn, J. C. 2021, AJ, 161, 214 [Google Scholar]
- Zinn, J. C., Stello, D., Elsworth, Y., et al. 2022, ApJ, 926, 191 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Average systematic uncertainty for the asteroseismic, extinction, and spectroscopic components and the total systematic uncertainty.
Median parallax offsets before and after applying L21 in the faint (11 ≤ G ≤ 13 mag) and bright magnitude ranges (G ≤ 10 mag).
All Figures
 |
Fig. 1. Diagrams illustrating our two-step selection method to have a RC star population as homogeneous as possible among the Kepler (left), K2 (middle), and TESS-SCVZ fields (right) using E20 and APOGEE DR17. Top: Teff vs. [Fe/H] diagrams. The red box indicates the first selection of the bulk of the RGB and RC stars to make sure that our sample is chemically similar. Bottom: Hertzsprung–Russell diagrams (Teff vs. absolute magnitude from Gaia in the G-band) after the first selection was applied. We draw a region in the HRD to select RC stars (red rectangles). |
| In the text | |
 |
Fig. 2. Parallax difference binned as a function of magnitude for the Kepler field with RC (solid) and RGB stars (dotted line) shown separately. Results from E20 and MA09 are shown in orange and green, respectively. The black arrows show the difference used to measure the systematic error due to using different asteroseismic methods. |
| In the text | |
 |
Fig. 3. Parallax difference binned as a function of magnitude for three K2 campaigns selected for their large number of stars and low or high extinction. C3 (light pink) and C5 (light green), which are located in the halo (|b|> 30°), and C4 (magenta) is closer to the Galactic plane (|b|< 30°). |
| In the text | |
 |
Fig. 4. Derivation of the best-fitting correction factor f on the total extinction AV per magnitude bin and per field. Left panel: example of a χ2 distribution for a given magnitude bin in the Kepler field. The purple dashed line corresponds to min(χ2)+1. Right panel: stacked distribution of f values in all magnitude bins for Kepler, K2, and TESS. |
| In the text | |
 |
Fig. 5. Parallax difference before (top) and after correction (bottom) as a function of G magnitude for Kepler (left), K2 (middle), and TESS (right). The grey scatter corresponds to the entire sample of RGB and RC stars. Our best sample with low-extinction RC stars is shown with purple points, and the colour scale indicates their density (increasing from dark purple to white). The red, yellow, and blue lines show the running mean and its uncertainty for each field. |
| In the text | |
 |
Fig. 6. Parallax offset residual (after correcting using L21) as a function of magnitude for Kepler (red), K2 (yellow), and TESS (blue). The points show the mean values, while the shaded areas indicate the corresponding uncertainty (given as the error on the mean per bin). |
| In the text | |
 |
Fig. 7. Comparison of our results, Δϖcorr = (ϖGEDR3 − Z5)−ϖPARAM, to a compilation of Gaia parallax offset residuals from the literature as a function of the magnitude in the G-band. Results displayed as open circles with vertical error bars are from the literature. Our findings for Kepler, K2, and TESS are shown as red, yellow, and blue shaded areas, respectively. Different literature sources used very astrophysically different objects and methods. Here we used the same methodology applied to a rather intrinsically homogeneous group of stars. The sign convention we use is such that positive values correspond to an overcorrection of parallaxes and negative values to an underestimation of parallaxes by L21. |
| In the text | |
 |
Fig. 8. Median residual offset as a function of ecliptic longitude for the individual K2 campaigns and Kepler. Open and filled circles show the results before and after applying the extinction and RUWE cuts. For clarity, error bars are only shown for the offsets where the cuts were applied. |
| In the text | |
 |
Fig. 9. Skymap in Galactic coordinates showing the location and coverage resulting from the crossmatch between the various asteroseismic fields considered in this study and APOGEE DR17. Galactic longitude increases from right to left. The yellow crosses correspond to the location of the bright physical pairs (G < 11 mag) that have been used in the process of deriving the zero-point correction model from L21. This figure was generated using the python package mw-plot (http://milkyway-plot.readthedocs.io/). The background image comes from ESA/Gaia/DPAC. |
| In the text | |
 |
Fig. 10. Hertzsprung–Russell diagram for our final set of Kepler RC stars where the G-band absolute magnitude is computed using L21-corrected Gaia parallaxes (black points). The sample is restricted to G ∈ [11, 13] mag, where we found the residual parallax offset to be approximately zero. The pink dashed line shows the fit given by Eq. (6), and the brown shaded region illustrates how the fit could vary given the uncertainties on the slope and the intercept. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



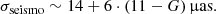
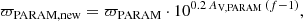
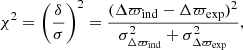
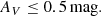
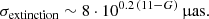
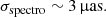
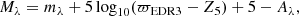
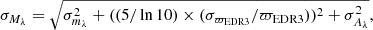
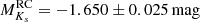
![$$ \begin{aligned} M_{G}^\mathrm{RC}&= (0.432 \pm 0.004) \nonumber \\&\quad - (0.821 \pm 0.033) \cdot (T_{\rm eff}\,[\mathrm{K}] - 4800\,\mathrm{K})/1000\,\mathrm{K} \, \mathrm{[mag]}, \end{aligned} $$](/articles/aa/full_html/2023/12/aa47919-23/aa47919-23-eq14.gif)