| Issue |
A&A
Volume 582, October 2015
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526832 | |
| Published online | 20 October 2015 | |
Online material
Appendix A: MmD with an absorbed extended continuum
We consider a line profile where absorption is present. We write 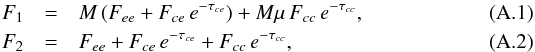 where Fce represents the flux from an extended source of continuum, which is only macrolensed as the emission line flux Fee, Fcc ≠ 0 is the flux from the source of continuum compact enough to be microlensed, and τcc (τce) is the optical depth of the absorber in front of cc (ce). Using these relations in Eqs. (3) and (4) with A = Mμ, we obtain
where Fce represents the flux from an extended source of continuum, which is only macrolensed as the emission line flux Fee, Fcc ≠ 0 is the flux from the source of continuum compact enough to be microlensed, and τcc (τce) is the optical depth of the absorber in front of cc (ce). Using these relations in Eqs. (3) and (4) with A = Mμ, we obtain  In these equations, A′ and M′ are parameters tuned to satisfy constraints on FM and FMμ. The constraint FMμ = 0 at wavelengths where Fcce−τcc = 0 and Fee ≠ 0 can only be satisfied with M′ = M. If M is correctly estimated, FMμ = Fcce−τcc ≥ 0 independently of the existence of a nonmicrolensed extended continuum.
In these equations, A′ and M′ are parameters tuned to satisfy constraints on FM and FMμ. The constraint FMμ = 0 at wavelengths where Fcce−τcc = 0 and Fee ≠ 0 can only be satisfied with M′ = M. If M is correctly estimated, FMμ = Fcce−τcc ≥ 0 independently of the existence of a nonmicrolensed extended continuum.
In the absence of a nonmicrolensed extended continuum (i.e., Fce = 0), making FM = 0 at wavelengths where Fee = 0 and τcc = τce = 0 (i.e., in the unabsorbed continuum) gives A′ = A. In the presence of a nonmicrolensed extended continuum, making FM = 0 in the unabsorbed continuum gives A′ ≠ A. In this case, FM = Fce (e−τce − e−τcc) at wavelengths where the continuum is absorbed and Fee = 0, which can result in either positive or negative values for FM whether τce<τcc or τce > τcc, respectively. Making FM ≥ 0 allows the detection of the extended continuum in the latter case (τce > τcc), but A′ = A is derived only if e−τce = 0 at some wavelengths where Fee = 0 and e−τcc ≠ 0. Without absorption (i.e., τce = τcc = 0), such a nonmicrolensed extended continuum would remain unnoticed.
Note that μ′ = A′/M, determined by making FM = 0 in the unabsorbed continuum, can be seen as the average microamplification of the whole continuum source, while μ = A/M refers to the microamplification of the compact continuum source. They are related by  (A.5)
(A.5)
Appendix B: Equivalent width in the absorption trough
In order to understand how microlensing affects the EW, we can write Eq. (5), with more explicit expression of Fλ and of the continuum flux ℱ. We assume that the latter is constant over the emission line and the absorption trough and is well approximated by the continuum flux measured in the vicinity of the line. We consider a broad emission line characterized by a flux Fλ,E, and a continuum originating from two regions, a compact region cc, compact enough to be microlensed, and a more extended region ce, which is not microlensed. We can specialize Eq. (5) in the presence of absorption. For a lensed image i, we obtain 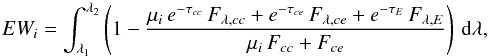 (B.1)where μi is the amplitude of micromagnification of the compact continuum cc, and τcc, τce, and τE are the optical depths of the gas absorbing the compact continuum, the extended continuum, and the broad emission line, respectively. Contrary to Appendix A, we make explicit the fact that the emission line can be absorbed (i.e., Fee = e−τEFλ,E).
(B.1)where μi is the amplitude of micromagnification of the compact continuum cc, and τcc, τce, and τE are the optical depths of the gas absorbing the compact continuum, the extended continuum, and the broad emission line, respectively. Contrary to Appendix A, we make explicit the fact that the emission line can be absorbed (i.e., Fee = e−τEFλ,E).
Equation (B.1) clearly shows that if Fλ,ce = Fλ,E = 0 (i.e., no extended continuum or emission line), and if the continuum does not vary over the range [λ1,λ2] (i.e., Fλ,cc ≈ Fcc), then the EW is independent of the amplitude of microlensing μi. In the following, we compare the difference of equivalent widths ΔEW = EWD − EWA, between image D, characterized by microlensing μ, and image A, unaffected by microlensing, in the presence of flux from the emission line and/or from an extended continuum region.
Appendix B.1: Compact continuum+emission line
We first consider the situation where there is only the compact source of continuum Fcc and the emission line over the wavelength range [λ1,λ2]. We then have Fλ,ce = 0 in (B.1). Assuming that the continuum flux does not vary over the range [λ1,λ2] such that Fλ,cc = Fcc, we can rewrite (B.1):  The difference of equivalent width, ΔEW = EWD − EWA, can be derived from the above equation specialized for the pair of images, i.e.,
The difference of equivalent width, ΔEW = EWD − EWA, can be derived from the above equation specialized for the pair of images, i.e., 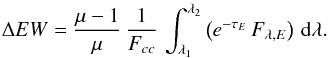 (B.4)It results from this equation that when μ > 1, one may only observe EWD > EWA.
(B.4)It results from this equation that when μ > 1, one may only observe EWD > EWA.
Appendix B.2: Compact + extended continua
We now consider that there is no flux from the emission line (Fλ,E = 0) over the wavelength range [λ1,λ2], but two sources of continuum: a compact continuum microlensed by a factor μi and an extended continuum Fce which is not microlensed. Assuming that the continuum flux is constant over the range [λ1,λ2] such that Fλ,cc = Fcc and Fλ,ce = Fce, we obtain  where we defined ℱi = μiFcc + Fce, the flux in the unabsorbed continuum.
where we defined ℱi = μiFcc + Fce, the flux in the unabsorbed continuum.
The difference of equivalent width ΔEW = EWD − EWA, is then  (B.7)We clearly see that a difference of equivalent width is only detected if there is a difference of opacity between the absorbers covering the extended and the compact continua, i.e., τcc ≠ τce. If μ > 1, we find ΔEW > 0 (EWD > EWA), and if τcc > τce, and conversely ΔEW < 0 (EWA > EWD) if τcc<τce.
(B.7)We clearly see that a difference of equivalent width is only detected if there is a difference of opacity between the absorbers covering the extended and the compact continua, i.e., τcc ≠ τce. If μ > 1, we find ΔEW > 0 (EWD > EWA), and if τcc > τce, and conversely ΔEW < 0 (EWA > EWD) if τcc<τce.
Appendix B.3: Compact + extended continua + emission line
The situation where the source of light under the absorption is the sum of a compact and an extended continuum and of an emission line, directly results from the two previous cases. If we define the flux of the unabsorbed continuum of image A and D, ℱA = Fcc + Fce, and ℱD = μFcc + Fce, then we can write the following difference of equivalent width ΔEW = EWD − EWA between images D and A: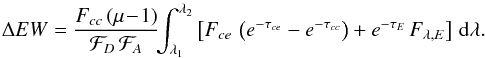 (B.8)
(B.8)
From this equation, we see that when μ > 1 and τcc > τce (i.e., when the compact continuum is more absorbed than the extended continuum), ΔEW > 0. Conversely, ΔEW < 0 can only be obtained if τcc<τce, i.e., when the compact continuum is less absorbed than the extended continuum. Positive value of ΔEW may also occur depending on the absorption rate of the different components, and on the relative contribution of the extended continuum and of the emission line.
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


