| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A137 | |
| Number of page(s) | 23 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201424924 | |
| Published online | 14 January 2015 | |
Online material
Appendix A: Detection limits
We computed the detection limits in the z − L2 − 10 plane for highly obscured sources, assuming two different spectral models, one with NH= 7 × 1023 for CTN sources and the other with NH= 1.6 × 1024 cm-2 for CTK sources. We then estimated the maximum redshift at which a CTN or CTK source can be detected, with >30 net counts in full band, for a given intrinsic luminosity, given the flux limit of the XMM-COSMOS survey (red and green dashed lines in Fig. A.1), and compare this with the one computed for a typical unobscured AGN spectrum i.e. assuming as model an unabsorbed power-law with γ = 1.9 (black dashed line). Red (green) circles represent CTKf (CTNf) sources. Gray points represent the 1073 hard (2−10 keV) band detected XMM-COSMOS sources (hard band undetected sources suffer from larger uncertainties in the L2 − 10, because an extrapolation from the soft band have to be made). We stress that the shape of the X-ray spectrum of CT AGN is responsible for a positive K-correction, which shift the X-ray flux of the very hard (>7−10 keV) unobscured part of the spectrum in the observing band and favors the detection of high z CT with respect to low redshift (relatively to the flux limit of the survey). This can be clearly seen in Fig. A.1: the red (CT) detection limit line is flatter than the black one for the full hard detected sources. Using these curves we computed the weight to be applied to each source (CTK or CTN) of a given L2 − 10, defined as the ratio between the maximum volume sampled for an unobscured source of the same intrinsic L2 − 10 and the maximum volume sampled for a CTK or CTN source. From the plot is clear that the weights are larger for low luminosity sources, and slightly larger for CTK sources with respect to CTN.
 |
Fig. A.1
Redshift vs. L2 − 10 distribution for CTKf (red) and CTNf (green) sources. Gray squares represent the 2−10 keV band detected XMM-COSMOS sources. The black dashed line represents the detection limit computed for an unabsorbed power-law with Γ = 1.9, while the red (green) dashed line show the detection limit computed for a CTK (CTN) source. |
| Open with DEXTER | |
Appendix B: Model comparison
As described in Sect. 3, we used two different models to reproduce the observed spectra of highly obscured sources in XMM-COSMOS: one makes use of the TORUS table developed in Brightman & Nandra (2012), which was specifically developed to model CT sources, while the second is built in order to mimic as much as possible the first one, with the advantage of having as output the Fe Kα line EW. Therefore, we are interested in testing how the two models agree in determining the two main parameters involved in our analysis, namely the NH and the absorption corrected 2−10 keV luminosity. Figure B.1 (left) shows a comparison of the best fit values obtained for NH from the Tor and Pl models, respectively. In red are shown the ten CTKi sources, in green the 29 CTNi sources. In blue we highlighted 5 sources that are border-line: they are either seen as CT from one model but not the other, or they are very close to the dividing line (NH= 1024 cm-2) and with large error bars, that makes them fully consistent with being CT (see Table 1). Several CTKi sources are shown with their lower limit in NH, because their NH is consistent with the model upper boundaries, which is NH= 1025 cm-2 for the Tor model and NH= 1026 cm-2 for the Pl model. The Pl model typically slightly overestimates the NH with respect to the Tor model, in both Compton thin and thick regimes. However, all the measurements are perfectly consistent within the large error-bars. Figure B.1 (right) shows a comparison of the 2−10 keV, absorption corrected luminosity, obtained from the Pl and Tor model. The intrinsic luminosity obtained from the Tor model is systematically slightly higher (~ 0.1 − 0.2 dex) than the one obtained from the power-law model. The small differences in NH and L2 − 10 between the two models are probably related to the different reflection modelization, that slightly underestimate the primary power-law normalization in the Pl case with respect to Tor, to reproduce the same data points (see the different levels of the continuum above 10 keV in Fig. 3 left and right).
|
Fig. B.1
Left panel: comparison of the NH best fit obtained from the Pl (y-axis) and Tor (x-axis) models. Right panel: comparison of the 2−10 keV, absorption corrected luminosity, obtained from the same two models. In both panels we show CTNi sources in green, CTKi sources in red and border-line sources in blue, and the solid line represents the 1:1 relation. |
|
| Open with DEXTER | |
Appendix C: Unfolded spectrum plus model
Figure C.1 shows the unfoled, co-added spectrum of one of the sources in the CTKf sample (namely XID 54514), togheter with the best fit model obtained from the Tor model. The presence of the best fit model helps in interpreting the spectral features observed in this as in all the CTK spectra shown in Fig. 4: the sharp flux drop below 7−10 keV due to absorption, the soft emission arising below 1−2 keV, the presence of the Fe Kα line, and the strong feature at ~ 7 keV due to the absorption edge.
However, we believe that, given the limited quality of these spectra, adding the best fit model in these plots would be a very strong guide for the eye, while we do not want to impose a bias to the reader. Furthermore it would be misleading, since we are not fitting our models to these co-added spectra, but rather to the single XMM-Newton pn, MOS and Chandra spectra simultaneously. Even if the model parameters are the same for all the spectra, and therefore there is no conceptual difference between fitting the sum of the spectra or simultaneously fit all of them, there is a subtle practical difference in the two approach, since there are a number of unavoidable approximation that have to be made to produce the co-added spectrum, and therefore the simultaneous fit is always preferable. Given all these considerations, we decided to show in Fig. 4 only the co-added spectra, and to show only here, as an example, one unfolded spectrum plus best fit model.
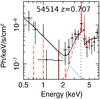 |
Fig. C.1
Unfolded, merged pn+MOS+Chandra spectrum of one of the sources in the CTKf sample, shown as an example. The best fit model is shown with the black solid curve. The TORUS component is shown with the red dashed curve, while the scattered component is shown with the black dotted curve. The XMM source ID and redshift are labeled. The dashed line marks the expected location of the 6.4 keV Fe Kα line. |
| Open with DEXTER | |
Appendix D: Comparison with Brightman et al. (2014)
Brightman et al. (2014, B14) reported a search for CT sources in the Chandra data of the COSMOS, CDFS and AEGIS fields, using a similar approach to the one presented here: they used a simple model comprising a Torus component and a scattered component, with the Cstat statistic applied to lightly grouped spectra (1 counts per bin). The main differences are in the set of models adopted: three different models are built with the Torus component having 60°, 30° and 0° half opening angle respectively (models A, B and C, with the C having no scattered component), plus a model with a simple power-law without absorption (model D). The photon index is fixed to 1.7 for sources with fewer than 600 counts, but for each model, if the fit with a free Γ is significantly better, then this parameter is left free to vary even for sources with fewer than 600 counts. No cut in minimum number of counts is used.
We compared our results on NH distribution in the entire XMM-Newton catalog with the ones published in B14, for the sources in common. There are 644 Chandra counterparts from B14 of our XMM-Newton catalog sources. We excluded from the comparison 111 sources that are not detected in the hard band in the XMM-Newton catalog: the Chandra data are much deeper in both soft and hard bands (see Sect. 2.1), and the lack of hard band detection in the XMM-Newton catalog make it impossible to correctly estimate the amount of obscuration for highly obscured sources (the source is detected in XMM-Newton only in the soft band thanks to the scattered light).
Because we are interested in comparing the NH distribution, we also excluded 70 sources that have a best fit photon index outside the range 1.5−2.5 that was used in our analysis: these very steep (up to Γ = 3) or flat (down to Γ = 0) spectra may indicate interesting sources, e.g. reflection dominated CT candidates, but are not useful for the comparison on NH results. Indeed 23 sources that are obscured in our analysis, are best fitted in B14 with an unabsorbed power-law with Γ < 1. Finally we excluded 30 sources with fewer than 30 counts in the Chandra spectrum: the associated error bars are too large, and below this threshold, the method used to determine which model is preferred is shown not to work properly in B14.
We are left with 433 sources for the comparison. The distribution of NH vs. NH is shown in Fig. D.1. There is a global good agreement between the two measurements, within the large uncertainties (the average error-bar is shown in the top left corner). However only 1 out of 4 CT candidates from our analysis is found to be CT also in B14. The remaining 3 show a slightly lower NH, below the CT limit, and there is a general trend of having lower NH values in B14 for sources above 1023 cm-2. This is due to the different fixed Γ adopted (1.7 in B14 instead of 1.9): we tested that the use of Γ = 1.7 gives results consistent with B14 for these sources.
There are two sources (namely XID 2210 and 272, shown with blue diamonds) that are found to be heavily CT in B14 (NH> 6 × 1024 cm-2). The XMM-Newton spectra of both this sources have a factor of 2−3 more counts with respect to the Chandra ones, and no indication of strong absorption can be
found. We conclude that these two sources are misclassified in the Chandra spectral analysis. On the other hand, in red are shown two sources for which the fit of the XMM-Newton spectra shows a primary minimum of the probability distribution of the NH at Compton thin values, while a strong secondary minimum is found at CT values, in agreement with what is found from the Chandra spectra. In this case is not possible to exclude that these are indeed CT sources, and a simultaneous fit of Chandra and XMM-Newton data would give a more constrained result.
 |
Fig. D.1
Comparison between of the best fit NH from B14 and this work, for the 433 sources in common. The star show the location of source XID 2608. With cyan diamonds are marked two sources for which the nature of CT sources from Chandra data is not confirmed with better XMM-Newton spectra. In red are shown two sources for which the fit of the XMM-Newton spectrum shows a secondary minimum at CT values. The average error-bar is shown in the top left corner. |
| Open with DEXTER | |
A similar case is for XID 2608, the best CT candidate in the sample, and the only one being CT both from our analysis and from B14 (marked with a star in Fig. D.1): the fit of the XMM-Newton data alone gives as best fit an NH of only 1.06 × 1024 cm-2 (see Table 1), while the fit of Chandra data alone gives an NH> 1025 cm-2 from both our analysis and B14. The joint fit of all the data (including also MOS) give an intermediate and well constrained value (see Table 2).
There is finally a large population of sources for which we measure a moderate obscuration, while B14 found that an obscured model is not required for these sources, and the best fit is a simple power law (possibly with free Γ). The much higher effective area of XMM-Newton below 1 keV, extending down to 0.3 keV (instead of 0.5 keV as in Chandra) clearly plays a role in determining what is the minimum NH that can be constrained for each spectrum (depending on the number of counts and the source redshift).
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


