| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 10 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201322134 | |
| Published online | 01 November 2013 | |
Online material
Appendix A: Dependence on initial conditions
In the following we demonstrate that the initial conditions chosen in model LK 1 represent the best fit to the observational data in the investigated parameter range.
 |
Fig. A.1
Same as Fig. 3, but here for model LK1 only the simulation results for 30% SFE are shown (solid line). Those are compared to the results obtained using a larger initial radius (models LK 2 and LK 5 – dash-dotted line). For model LK 2 the cases of 20% (dotted line) and 30% (dashed line) SFE are depicted. |
| Open with DEXTER | |
 |
Fig. A.2
Same as Fig. 3, but this time varying the initial cluster mass (model LK 1 – solid, model LK 3 – dashed, and model LK 4 – dotted). This corresponds to the models containing 30 000, 45 000, and 15 000 stars, respectively. Only the simulation results for 30% SFE are shown. |
| Open with DEXTER | |
Appendix A.1: Initial cluster size
First we investigate the sensitivity of our results on the initial cluster radius. The mean cluster radius of the six youngest loose clusters is 6.1 pc. Since it is unlikely that the massive exposed clusters presented here are observed exactly at the end of the gas expulsion phase, we set up clusters with ~1/4, 1/2, and 3/4 of this size and followed the cluster dynamics after gas expulsion.
In model LK 1 the initial radius was 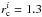 pc. In models LK 5 and LK 2 we use larger initial radii of
pc. In models LK 5 and LK 2 we use larger initial radii of 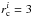 pc and
pc and 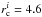 pc, respectively. Figure A.1 shows that for
pc, respectively. Figure A.1 shows that for 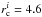 pc and 30% SFE, the radius development fits the data quite well up to ~10 Myr. In the later stages (>10 Myr) LK 1 (solid) matches only the two smaller observed clusters, whereas LK 2 (dashed) fits the two bigger ones better. From the size-age relation alone, no clear distinction can thus be made as to which of the models gives the better fit.
pc and 30% SFE, the radius development fits the data quite well up to ~10 Myr. In the later stages (>10 Myr) LK 1 (solid) matches only the two smaller observed clusters, whereas LK 2 (dashed) fits the two bigger ones better. From the size-age relation alone, no clear distinction can thus be made as to which of the models gives the better fit.
Looking at the mass development (Fig. A.1b), the first impression is that LK 2 would fit the results as well. However, closer inspection reveals that in the timespan 4–10 Myr the fit is relatively bad and, what is more severe, the curve partly fits the masses at the wrong cluster ages. Or in other words, the line fits but not the colour. The physical explanation is that larger initial cluster sizes lead to a slower cluster expansion resulting in too high a cluster mass at ages 4–10 Myr. Similar problems are found for 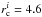 pc and 20% SFE. Although the cluster mass now fits better at 4–10 Myr, at ages >10 Myr the obtained cluster masses are far too low and the mismatch in cluster age still remains and would not be remedied by using any other SFE either.
pc and 20% SFE. Although the cluster mass now fits better at 4–10 Myr, at ages >10 Myr the obtained cluster masses are far too low and the mismatch in cluster age still remains and would not be remedied by using any other SFE either.
The best fit to the cluster data is obtained for an initial cluster radius of 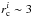 pc (dash-dotted line). However, the effects of binaries and stellar evolution neglected here likely lead to additional cluster expansion without much additional mass loss. Thus we conclude that the radius of these clusters was likely in the range 1–3 pc at the end of the star formation process.
pc (dash-dotted line). However, the effects of binaries and stellar evolution neglected here likely lead to additional cluster expansion without much additional mass loss. Thus we conclude that the radius of these clusters was likely in the range 1–3 pc at the end of the star formation process.
Appendix A.2: Initial cluster mass
So far we have modelled clusters with 30 000 stars that, for the IMF used here, is equivalent to a cluster mass Mc ~ 18 000 M⊙. This approximately corresponds to the average mass of the observed young clusters in the sequence. However, clusters form with a wide variety of masses. Figure A.2 shows the temporal development of clusters with initially 15 000, 30 000, and 45 000 stars, corresponding to cluster masses of roughly 9000 M⊙, 18 000 M⊙, and 27 000 M⊙. The comparison of the simulation results of these clusters of different initial mass shows that for initial cluster masses 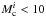 000 M⊙, the clusters never reach a sufficient size that they could be the predecessors of the clusters observed at 10–20 Myr. These clusters end up with radii well below l5 pc and masses lower than 2000 M⊙ at an age of 20 Myr (see Fig. A.2a).
000 M⊙, the clusters never reach a sufficient size that they could be the predecessors of the clusters observed at 10–20 Myr. These clusters end up with radii well below l5 pc and masses lower than 2000 M⊙ at an age of 20 Myr (see Fig. A.2a).
This means clusters with 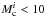 000 M⊙ do not develop along the observed cluster sequence – at least for ages older than 10 Myr – but follow their own sequence that is located at lower masses and radii. This has consequences for our statistical estimate in Sect. 3: it is only the three most massive clusters of the youngest age group that have the capacity to develop into the older observed population. This means in our crude sample statistics that >50% of all observed clusters with Mc > 10 000 M⊙ develop in a way that corresponds to simulations with 30% ± 5% SFE and an initial cluster radius in the range of 1–3 pc. So for such massive clusters, it is the rule rather than the exception to follow the observed loose cluster sequence.
000 M⊙ do not develop along the observed cluster sequence – at least for ages older than 10 Myr – but follow their own sequence that is located at lower masses and radii. This has consequences for our statistical estimate in Sect. 3: it is only the three most massive clusters of the youngest age group that have the capacity to develop into the older observed population. This means in our crude sample statistics that >50% of all observed clusters with Mc > 10 000 M⊙ develop in a way that corresponds to simulations with 30% ± 5% SFE and an initial cluster radius in the range of 1–3 pc. So for such massive clusters, it is the rule rather than the exception to follow the observed loose cluster sequence.
Appendix B: (In)sensitivity of the sequences to the radius definition
 |
Fig. B.1
Development of the radius of the bound cluster mass over time for the case of 30% and 70% SFE. The solid lines give the results for clusters with |
| Open with DEXTER | |
As mentioned above, the loose cluster sequence is based on a homogeneous sample. The cluster sizes are all determined in the same way as the average distance of the B-type stars to the cluster centre. More commonly the cluster definitions used are the half-mass radius, the core radius, and the radius where the cluster density equals the background density. Obviously the latter is unsuitable for a comparison of clusters in very different environments (solar neighbourhood, Galactic centre, spiral arms) as done here.
The core radius, i.e. the inner radius at which the surface density distribution flattens, is also not really suitable to measure the cluster expansion in these early phases. The reason is twofold: i) the clusters are not in equilibrium; and ii) the mixture of bound and unbound stars results in a cluster profile that is rather complex, so that the definition of a core can be an artefact of the current distribution of bound and unbound stars. For the compact clusters, the situation is additionally complicated by the possibility that the real core radius is less than 0.1 pc, which is for the more distant clusters very difficult to resolve.
Figure B.1 shows the development of the radii, which contain the innermost 5% and 10% of stars – 5% and 10% Lagrange radius – and the half-mass radius for models LK 1 and CK 1, being representative for loose and compact clusters. The core radius typically starts out close to the 10% Lagrange radius and drops to approximately the 5% Lagrange radius (Kroupa et al. 2001). The different expansion histories of compact and loose clusters can be clearly distinguished for the half-mass radii, whereas this is more complex for the core radii: the core radius might even decrease for some time as seen in Fig. B1. Although the core radius at 20 Myr is larger than at 1 Myr in both cases, the temporal development in between is not so straight forward. For example, the core radius in model LK 1 at 10 Myr is smaller than at 5 Myr. For the compact clusters the situation is even more complex: for a given half-mass radius the corresponding core radii of the youngest clusters in the sample should be ≪0.1 pc which could be difficult to resolve in many cases.
Thus, only the half-mass radius or the definition of the mean distance of the B stars used here are suitable to monitor the cluster expansion phase. If there is no mass segregation in the cluster, both definitions lead to the same result. However, when the cluster expands, the more massive stars remain bound more easily. As a result the half-mass radius is slightly smaller than the radius defined via the B stars at the end of the expansion process (see Fig. B.1). However, the difference is less than 10%. For initially mass-segregated clusters, the situation is probably more complex, which we plan to investigate in a future study.
A short remark on the data for the compact cluster. They come from different sources. The data for Arches, NGC 3603, Trumpler 14, Westerlung 1, 2, RSGC1, 2, and Quintuplett are from Figer (2008), the data for DBS2003 from Borissava et al. (2008), and the data for χ and h Per from Wolff et al. (2007). The last define the radius as used above, whereas in Figer (2008) the radius is determined as the average projected separation from the centroid position. Given that most of these clusters are at distances where A or B stars are predominantly resolved, this means that very similar radius measures have been used in these two studies. The only definition that differs considerably is that of Borissava et al. (2008), since there the radius was interpreted as the distance where the density distribution exceeds twice the standard deviation of the surface density in the surrounding. Apart from the data point by Borissava et al., the used radius definitions are all very consistent for the sequence of compact clusters as well.
Appendix C: Massive cluster candidates
Properties of recently discovered massive clusters with Mc > 104M⊙.
For determinating the cluster expansion and mass loss after gas expulsion, a large data base of the properties would be desirable. However, in the Milky Way the number of massive young compact and loose clusters with known masses and sizes is currently rather limited, basically restricted to the clusters displayed in Fig. 1. However, during the last few years a number of candidates of massive young clusters have been detected. Examples are given in Table C.1. This list is far from complete, but shows that at least a doubling of the data points could be achieved in the near future. For these candidate massive clusters either the mass or cluster radius are currently unknown. This knowledge would help answer the question of whether a real size gap exists
between loose and compact clusters or whether this region is just sparsely populated. Whether a definite answer to this question is possible depends on the total number of masive young clusters in the Milky Way. Currently it is estimated that this number is well below 100.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.