| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A125 | |
| Number of page(s) | 23 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321393 | |
| Published online | 16 October 2013 | |
Online material
Appendix A: Flux extraction and SED fittings
SED results.
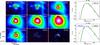 |
Fig. A.1
Left: results of the source extraction by getsources in CygX-N3. All images cover the same angular scale. The detections of getsources at 1.3 mm are used to extract the fluxes at 24 μm, 70 μm, 1.3 mm, and 3.5 mm (even though we study only sources 1 and 2, in black). The getsources detections at 24 μm are used to retrieve the flux of the MDC in the remaining bands (MDC shown in black). These MDC fluxes are divided by the 3 fragments detected at 1.3 mm. Right: SEDs of CygX-N3 MM1 (top) and MM2 (bottom). The black curves (and top-right parameters) are the grey-body fits to the cold component. The green line shows the grey-body curve of the cold component assuming fixed parameters (from Bontemps et al. 2010). When applicable, the best SED fit of a warm component is shown as a dotted blue curve and top-left parameters. The sum of the cold and warm components is plotted with dashed lines (light blue for the sum of best SED fit, and yellow for the sum of the warm component with the fixed-parameters SED). |
| Open with DEXTER | |
To estimate the mass, bolometric luminosity, and dust temperatures of our sample of nine high-mass fragments, we have constructed SEDs using the emission from 24 μm to 3.5 mm. Since our sample of sources consists of IR-quiet cores, the flux bellow 8 μm is in fact negligible, and integrating the SEDs down to 24 μm is enough to get a good estimate of the bolometric luminosity. We used the 24 μm from Spitzer MIPS (6′′ resolution), the 70, 160, 250, 350, and 500 μm from Herschel PACS and SPIRE (8.4′′, 13.5′′, 18.2′′, 24.9′′, and 36.3′′ resolution, respectively) observed as part of the HOBYS programme (Hennemann et al. 2012; in prep.), the 1.2 mm from MAMBO (11′′ resolution, Motte et al. 2007), and the 1.3 mm and 3.5 mm emission from PdBI (1′′ and 2.4′′ resolution respectively, Bontemps et al. 2010).
 |
Fig. A.2
Left: results of the source extraction by getsources in CygX-N12. The MDC fluxes are divided by the 2 fragments detected at 1.3 mm. Right: SEDs of CygX-N12 MM1 (top) and MM2 (bottom). Curves are the same as in Fig. A.1. |
| Open with DEXTER | |
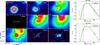 |
Fig. A.3
Left: results of the source extraction by getsources in CygX-N48. The 250 μm image is unusable since it is saturated. In this case, because the 24 μm emission does not trace the millimetre sources, we have used the combined detections at 350 μm and 1.2 mm for estimating the emission from the MDC, whose flux is then divided by 5 fragments. The flux extraction at 500 μm is not very well constrained to the MDC only, and therefore the flux measurement at 500 μm is likely overestimated. Right: SEDs of CygX-N48 MM1 (top) and MM2 (bottom). Curves are the same as in Fig. A.1. |
| Open with DEXTER | |
The extractions of the fluxes were made using the getsources code (v1.120126, Men’shchikov et al. 2012). Because the PdBI 1.3 mm emission filters out the more extended emission, we cannot derive precise envelope/core sizes. However, since the mean separation between the high-mass fragments detected by Bontemps et al. (2010) varies between 3000 AU and 5000 AU, we take 4000 AU (i.e. ~3′′ resolution) as the size for estimating the properties of the individual high-mass collapsing cores. Therefore, owing to the different resolutions of the datasets, two separate extractions were made.
For resolutions worse than 10′′ (i.e. physical scales greater than 14 000 AU), which is the case for the 160 μm, 250 μm, 350 μm, 500 μm, and 1.2 mm images, we are no longer able to separate the emission from the different fragments, and therefore we have estimated the flux correspondent to the MDC as a whole. For these five wavelengths, we used the 24 μm emission as the detection wavelength, in order to give an idea of the position of the MDC (black ellipses, labelled with “MDC” in Figs. A.1 to A.5), plus the existence of other nearby 24 μm sources that could be blended within the coarser resolutions. Because getsources uses the positional information coming from the detection wavelength to make the best deblended flux estimates at the other wavelengths (see Men’shchikov et al. 2012, for details on how the deblending is made), the flux we retrieve should represent the flux of the entire MDC, deblended for any nearby sources. We then assume that the contribution of each individual fragment to the continuum is similar, and therefore we divided the MDC flux by the number of PdBI 1.3 mm fragments as an estimate of their individual fluxes. Since this method only provides a rough estimate of the individual fluxes, we increased the uncertainties associated with these measurements accordingly. (We assume uncertainties of ~60–70% on the individual fluxes.) The lower weight we associate to these points on the SEDs implies that the SED fittings do not strongtly rely on the actual fluxes from 160 μm–1.2 mm, and these only provide a trend in the behaviour of the peak of the SEDs, useful to help constrain the temperature.
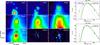 |
Fig. A.4
Left: results of the source extraction by getsources in CygX-N53. The emission from the MDC is then divided by 2 fragments. Right: SED of CygX-N53 MM1 and MM2. Curves are the same as in Fig. A.1. The extraction from getsources assigned a significant flux to MM2 at 70 μm even though this emission is mostly centred on MM1. Therefore, we believe that the 70 μm flux measurement is slightly overestimated for MM2. For MM1 we can see that a temperature of 20 K (green curves), as assumed by Bontemps et al. (2010), greatly overestimates the emission around the peak of the SED. |
| Open with DEXTER | |
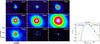 |
Fig. A.5
Left: results of the source extraction by getsources in CygX-N63, where all the emission arises from MM1 (not sub-fragmented). Right: SED of CygX-N53 MM1. Curves are the same as in Fig. A.1. Similar to CygX-N53 MM1, the temperature of 20 K (green curves) for CygX-N63 MM1, as assumed by Bontemps et al. (2010), overestimates the emission around the peak of the SED. |
| Open with DEXTER | |
The most reliable measurements are those whose resolution is enough to separate the individual fragments. That is the case for the 24 μm, 70 μm, 1.3 mm, and 3.5 mm. For these four wavelengths, we extracted the fluxes using getsources detections at 1.3 mm. Even though at 24 μm and 70 μm the sources are still blended, in most cases the peak is centred well on one of the mm sources, allowing getsources to properly assign the flux arising from the individual fragments. Since the emission at 24 μm (and 70 μm) arises from the inner warm regions around a protostar, they are expected to correspond to sizes of <7000 AU. Therefore, even though the area where the flux is measured is larger than this, we need no rescaling of the fluxes because all the inner emission is recovered in the beam. For the 3.5 mm emission we also do not need to rescale, since getsources extracts the flux from fragments using the beam size, i.e. 3′′, which corresponds to regions of ~4000 AU size. For the 1.3 mm, however, with a resolution of 1′′, the PdBI filters out all extended emission and is only sensitive to the inner ~1000–2000 AU. Therefore, to construct the SEDs we used the PdBI 1.3 mm fluxes as measured by Bontemps et al. (2010) that correspond to deconvolved sizes in the range of 800–1500 AU (for a distance of 1.4 kpc), and rescaled these to more realistic envelope sizes by assuming a density profile as ρ ∝ r-2 outside the central ~1000 AU (as in Bontemps et al. 2010). Density profiles close to ρ ∝ r-2 have been observed for individual protostars (e.g., Motte & André 2001; Mueller et al. 2002), and even though studies of starless/prestellar cores have suggested shallower slopes (e.g., Butler & Tan 2012), these studies also suggest that steepening of these profiles could be expected with the evolution and contraction of such cores. In fact, if using a shallower density profile, we would very quickly recover all the single-dish emission. For instance, for the isolated CygX-N63 MM1, the most massive core of our sample, all the single dish 1.2 mm emission is in fact recovered by rescaling the PdBI 1.3 mm flux to simply ~2500 AU using a steep r-2 density profile. Using a shallower profile would imply that this core contained all its mass within a mere thousand AU, and it would require a sharp edge after that. Therefore, we have taken a profile as r-2, because our sample of cores already show important outflow activity, indicative of on-going star formation, and we rescaled the PdBI 1.3 mm emission to envelope sizes of ~4000 AU FWHM for all sources, except for CygX-N63 MM1 where we used 2500 AU. Despite the small errors retrieved by the flux extraction by getsources, we assumed conservative uncertainties of the flux measurements for these four wavelengths, as being 30% of the flux extracted. This is meant to account for biases linked to the flux extraction (using different parameters for the getsources extraction), the assumptions on the need for rescaling and observational uncertainties.
Using these flux measurements, we constructed the SEDs for the nine high-mass fragments of our sample. Each SED was fit with a grey-body curve, assuming an opacity law as in Hildebrand (1983) with β = 2, assuming a dust emissivity of 1.0 cm2 g-1 at 1.3 mm (Ossenkopf & Henning 1994) and a dust-to-gas ratio of 100. For sources with 24 μm emission, two-temperature grey-body fits were made with both a cold and a warm component. The SEDs and their grey-body fittings can be seen in Figs. A.1 to A.5. We have estimated the bolometric luminosities using three methods: 1) integrating the best SED curve fitting; 2) integrating the SED fitting retrieved from assuming the mass from Bontemps et al. (2010) estimated using a dust temperature of 20 K for all sources, and corrected for the new distance of Cygnus-X; 3) integrating the SED points (without any fitting), and estimating the uncertainties on the bolometric luminosity by using the maximum and minimum points from the error bars. The results from the three methods agree nicely, and therefore we take the masses and bolometric luminosities estimated from the best SED fitting. The uncertainties on the bolometric luminosity were estimated as the difference between methods 1) and the minimum estimate of method 3). It is worth noting that despite the rough method for determining the fluxes for the unresolved wavelengths, the bolometric luminosity is most sensitive to the flux estimates at 24 and 70 μm. Since the flux extraction for these two wavelengths is relatively well constrained, we consider that the errors we provide are adequate. The results from these SED fittings are summarised in Table A.1.
Appendix B: Areas for momentum flux estimates
Outflow energetics.
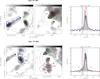 |
Fig. B.1
Left: blue and red CO emission in grey scale and contours for CygX-N3 MM1 (top) and MM2 (bottom). For clarity purposes only, the shown integrated intensity for MM2 red emission covers a narrower velocity range than used for the actual estimation. The intersection between the polygons and rings are the areas taken to measure the respective momentum flux for each wing. The blue and red crosses show the positions of the spectra shown on the right panel. Right: spectra at the position of the source in grey (CygX-N3 MM1 in the top panel and MM2 in the lower), with the spectra at the peak of the blue and red emission (SB1 and SR1 for MM1, SB2 and SR2 for MM2). The vertical dashed lines constrain the systemic velocities of the cloud excluded for the momentum flux calculations. The shaded area shows the velocity range affected by a cloud in front, also excluded. |
| Open with DEXTER | |
As mentioned in Sect. 4.5, to estimate the energetics of the outflows from this sample of sources, we used an approach similar to what Bontemps et al. (1996) used for a sample of low-mass protostellar objects. This method assumes that the momentum flux is conserved along the outflow direction, and it consists of estimating the momentum flux of the outflows on a ring centred on the driving source. The velocity ranges used to integrate the red and blue emission had been estimated using the average spectrum over each region, and they are illustrated in the right-hand panels of Figs. B.1 to B.6 (with vertical dashed lines). In these panels we show the spectrum at the position of each source, as well as an example of a blue and red-shifted spectra (whose positions are shown in the left-hand panels).
We then estimated the momentum fluxes by integrating across an annulus of fixed width,
Δr, of 1.15′′ (i.e. chosen to correspond to the beam FWHM). The inner
and outer radii of the annulus, however, are source and lobe-dependent: they are chosen
so that the ring comprises the peak of integrated intensity of the respective outflow in
the respective lobe (blue or red). The choice of using a variable inner and outer radius
aims at maximising the momentum flux estimate, by covering the surroundings of the
protostar, which are likely to harbour the most powerful impact of such outflows. To
avoid an increase in noise due to non-outflowing gas and contamination from neighbour
outflows within the annulus, we defined polygons based on the integrated intensity maps
of the blue and the red-shifted emission, to constrain the spacial extent of individual
outflows. The areas (rings and polygons) used for each source, and each lobe, are shown
in Figs. B.1 to B.6. The momentum flux is then estimated for each outflow wing inside the
intersection between the rings and the polygon, as 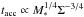 (B.1)\newpage\noindentwhere T
is the main beam intensity (in K) and vo the velocity of the
ambient cloud. For these calculations, we assumed a distance of 1.4 kpc, a fractional
abundance of CO to H2 of 104, a temperature of 20 K, a molecular
weight of 2.33 and an average correction factor of 3.5 for the opacities of
12CO wings (Cabrit & Bertout
1992). At this point we do not, however, correct for any inclination effect of
the outflow direction against the line of sight.
(B.1)\newpage\noindentwhere T
is the main beam intensity (in K) and vo the velocity of the
ambient cloud. For these calculations, we assumed a distance of 1.4 kpc, a fractional
abundance of CO to H2 of 104, a temperature of 20 K, a molecular
weight of 2.33 and an average correction factor of 3.5 for the opacities of
12CO wings (Cabrit & Bertout
1992). At this point we do not, however, correct for any inclination effect of
the outflow direction against the line of sight.
The results from these estimates are summarised on Table B.1, where vo is the ambient velocity of the cloud (as from the N2H+ from Motte et al. 2007; Bontemps et al. 2010), v range is the velocity range used for estimating the momentum flux (chosen using the Gaussian fittings, and excluding velocities where there was emission from another cloud), rin is the inner radius of the annulus taken for flux measurements, and Fco is the momentum flux calculated for the blue and red wing emission. Assuming that the outflows are symmetrically bipolar and that the amount of momentum released through one lobe is the same as released on the other, our best estimate of the total momentum flux ejected is not the sum of the two lobes, but twice the estimate of the wing with the highest momentum flux. Such estimates of the total momentum flux of individual outflows are shown as the total Fco (last column of Table B.1), now corrected by a possible effect of the inclination angle (factor 2.9 from a random distribution of angles, Cabrit & Bertout 1992). Also worth noting is that we may be missing some momentum flux since we do not necessarily pick up the highest velocity material likely carrying a significant part of the momentum flux. Given all the assumptions on estimating the momentum flux, the uncertainties can easily be as high as a factor 2.
 |
Fig. B.2
Same as Fig. B.1, for CygX-N12 MM1 (top) and MM2 (bottom). |
| Open with DEXTER | |
 |
Fig. B.3
Same as Fig. B.1, for CygX-N40 MM1. |
| Open with DEXTER | |
 |
Fig. B.4
Same as Fig. B.1, for CygX-N48 MM1 (top) and MM2 (bottom). |
| Open with DEXTER | |
 |
Fig. B.5
Same as Fig. B.1, for CygX-N53 MM1 (top) and MM2 (bottom). |
| Open with DEXTER | |
 |
Fig. B.6
Same as Fig. B.1, for CygX-N63 MM1. |
| Open with DEXTER | |
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


