Calibrating the fundamental plane with SDSS DR8 data

Home

All issues

Volume 557 (September 2013)

A&A, 557 (2013) A21

Online Material

Free Access

Issue		A&A Volume 557, September 2013


Article Number		A21
Number of page(s)		36
Section		Extragalactic astronomy
DOI		https://doi.org/10.1051/0004-6361/201321466
Published online		14 August 2013

Online material

Table 1

List of previous publications (we do not claim completeness) of fundamental plane coefficients, based on the list of Magoulas et al. (2012), which is itself based on the lists of Bernardi et al. (2003c) and Colless et al. (2001).

Appendix A: Redshift correction for the motion relative to the CMB

The observed redshift z is in the rest frame of our solar system, but for cosmological and extragalactic application, one requires a corrected redshift z_cor, which is in the same rest frame as the CMB. 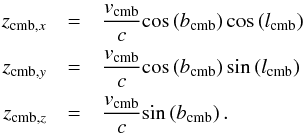(A.1)The solar system moves into the direction of l_cmb = 263.99° ± 0.14°b_cmb = 48.26° ± 0.03° (galactic coordinates) with a velocity of v_cmb = (369.0 ± 0.9) km s^-1 (Hinshaw et al. 2009). The first step required for this correction is to calculate the redshift space vector of our motion relative to the CMB 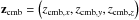. 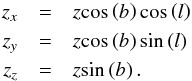(A.2)Then we translate the coordinates (l, b, z) of the observed galaxies into Cartesian coordinates into redshift space 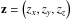. In the next step, we perform a vector addition,

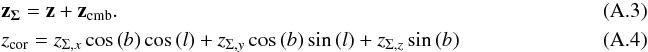Now we project the vector 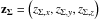onto the line of sight and obtain the corrected (for our motion relative to the CMB) redshift z_cor. The corrected redshifts z_cor are in the same rest frame as the CMB and can be used to calculate distances using the Hubble relation.

Appendix B: Additional figures

	Fig. B.1 Malmquist bias in the u band for the c model parameters is indicated by the black solid line of our fit. Due to the larger scatter in the u band, the fit is not as tight as for the other filters.
Open with DEXTER

	Fig. B.2 Malmquist bias in the g band for the c model parameters is indicated by the black solid line of our fit.
Open with DEXTER

	Fig. B.3 Malmquist bias in the r band for the c model parameters is indicated by the black solid line of our fit.
Open with DEXTER

	Fig. B.4 Malmquist bias in the i band for the c model parameters is indicated by the black solid line of our fit.
Open with DEXTER

	Fig. B.5 Malmquist bias in the z band for the c model parameters is indicated by the black solid line of our fit.
Open with DEXTER

	Fig. B.6 Malmquist bias in the u band for the dV model parameters is indicated by the black solid line of our fit. Due to the larger scatter in the u band, the fit is not as tight as for the other filters.
Open with DEXTER

	Fig. B.7 Malmquist bias in the g band for the dV model parameters is indicated by the black solid line of our fit.
Open with DEXTER

	Fig. B.8 Malmquist bias in the r band for the dV model parameters is indicated by the black solid line of our fit.
Open with DEXTER

	Fig. B.9 Malmquist bias in the i band for the dV model parameters is indicated by the black solid line of our fit.
Open with DEXTER

	Fig. B.10 Malmquist bias in the z band for the dV model parameters is indicated by the black solid line of our fit.
Open with DEXTER

	Fig. B.11 Malmquist bias in the u band for the p model parameters is indicated by the black solid line of our fit. Due to the larger scatter in the u band, the fit is not as tight as for the other filters.
Open with DEXTER

	Fig. B.12 Malmquist bias in the g band for the p model parameters is indicated by the black solid line of our fit.
Open with DEXTER

	Fig. B.13 Malmquist bias in the r band for the p model parameters is indicated by the black solid line of our fit.
Open with DEXTER

	Fig. B.14 Malmquist bias in the i band for the p model parameters is indicated by the black solid line of our fit.
Open with DEXTER

	Fig. B.15 Malmquist bias in the z band for the p model parameters is indicated by the black solid line of our fit.
Open with DEXTER

	Fig. B.16 Luminosity function for our sample in the u band for the c model. We split it into different subsamples (within different redshift bins) and compared the expected unbiased luminosity function and the total observed luminosity function. Our sample is almost complete at the luminous end, but we are missing many of the fainter galaxies due to the Malmquist bias.
Open with DEXTER

	Fig. B.17 Luminosity function for our sample in the g band for the c model. We split it into different subsamples (within different redshift bins) and compared the expected unbiased luminosity function and the total observed luminosity function. Our sample is almost complete at the luminous end, but we are missing many of the fainter galaxies due to the Malmquist bias.
Open with DEXTER

	Fig. B.18 Luminosity function for our sample in the r band for the c model. We split it into different subsamples (within different redshift bins) and compared the expected unbiased luminosity function and the total observed luminosity function. Our sample is almost complete at the luminous end, but we are missing many of the fainter galaxies due to the Malmquist bias.
Open with DEXTER

	Fig. B.19 Luminosity function for our sample in the i band for the c model. We split it into different subsamples (within different redshift bins) and compared the expected unbiased luminosity function and the total observed luminosity function. Our sample is almost complete at the luminous end, but we are missing many of the fainter galaxies due to the Malmquist bias.
Open with DEXTER

	Fig. B.20 Luminosity function for our sample in the z band for the c model. We split it into different subsamples (within different redshift bins) and compared the expected unbiased luminosity function and the total observed luminosity function. Our sample is almost complete at the luminous end, but we are missing many of the fainter galaxies due to the Malmquist bias.
Open with DEXTER

	Fig. B.21 Luminosity function for our sample in the u band for the dV model. We split it into different subsamples (within different redshift bins) and compared the expected unbiased luminosity function and the total observed luminosity function. Our sample is almost complete at the luminous end, but we are missing many of the fainter galaxies due to the Malmquist bias.
Open with DEXTER

	Fig. B.22 Luminosity function for our sample in the g band for the dV model. We split it into different subsamples (within different redshift bins) and compared the expected unbiased luminosity function and the total observed luminosity function. Our sample is almost complete at the luminous end, but we are missing many of the fainter galaxies due to the Malmquist bias.
Open with DEXTER

	Fig. B.23 Luminosity function for our sample in the i band for the dV model. We split it into different subsamples (within different redshift bins) and compared the expected unbiased luminosity function and the total observed luminosity function. Our sample is almost complete at the luminous end, but we are missing many of the fainter galaxies due to the Malmquist bias.
Open with DEXTER

	Fig. B.24 Luminosity function for our sample in the z band for the dV model. We split it into different subsamples (within different redshift bins) and compared the expected unbiased luminosity function and the total observed luminosity function. Our sample is almost complete at the luminous end, but we are missing many of the fainter galaxies due to the Malmquist bias.
Open with DEXTER

	Fig. B.25 Luminosity function for our sample in the u band for the p model. We split it into different subsamples (within different redshift bins) and compared the expected unbiased luminosity function and the total observed luminosity function. Our sample is almost complete at the luminous end, but we are missing many of the fainter galaxies due to the Malmquist bias.
Open with DEXTER

	Fig. B.26 Luminosity function for our sample in the g band for the p model. We split it into different subsamples (within different redshift bins) and compared the expected unbiased luminosity function and the total observed luminosity function. Our sample is almost complete at the luminous end, but we are missing many of the fainter galaxies due to the Malmquist bias.
Open with DEXTER

	Fig. B.27 Luminosity function for our sample in the r band for the p model. We split it into different subsamples (within different redshift bins) and compared the expected unbiased luminosity function and the total observed luminosity function. Our sample is almost complete at the luminous end, but we are missing many of the fainter galaxies due to the Malmquist bias.
Open with DEXTER

	Fig. B.28 Luminosity function for our sample in the i band for the p model. We split it into different subsamples (within different redshift bins) and compared the expected unbiased luminosity function and the total observed luminosity function. Our sample is almost complete at the luminous end, but we are missing many of the fainter galaxies due to the Malmquist bias.
Open with DEXTER

	Fig. B.29 Luminosity function for our sample in the z band for the p model. We split it into different subsamples (within different redshift bins) and compared the expected unbiased luminosity function and the total observed luminosity function. Our sample is almost complete at the luminous end, but we are missing many of the fainter galaxies due to the Malmquist bias.
Open with DEXTER

	Fig. B.30 Comparison of the luminosity functions in different filters for the c model. Although their shapes stay approximately the same, the peaks move to higher luminosities with redder filters. The short lines in the upper part of the plot indicate the Malmquist-bias-corrected mean magnitudes of our sample in the corresponding filters.
Open with DEXTER

	Fig. B.31 Comparison of the luminosity functions in different filters for the dV model. Although their shapes stay approximately the same, the peaks move to higher luminosities with redder filters. The short lines in the upper part of the plot indicate the Malmquist-bias-corrected mean magnitudes of our sample in the corresponding filters.
Open with DEXTER

	Fig. B.32 Comparison of the luminosity functions in different filters for the p model. Although their shapes stay approximately the same, the peaks move to higher luminosities with redder filters. The short lines in the upper part of the plot indicate the Malmquist-bias-corrected mean magnitudes of our sample in the corresponding filters.
Open with DEXTER

	Fig. B.33 Distribution of the apparent corrected radius r_cor is displayed in different filters for the p model. The measured radii of this model are clearly larger than those of the dV model. Furthermore, the distribution is extremely spread out in the u band due to known problems in this filter.
Open with DEXTER

	Fig. B.34 Central velocity dispersion σ₀ for different filters (only slightly different in all of them due to the small correction for the fixed fibre diameters) for the c and the dV model. One can clearly see the cut-off of at 100 km s^-1, which has been introduced to avoid the contamination of our sample.
Open with DEXTER

	Fig. B.35 Central velocity dispersion σ₀ for different filters (only slightly different in all of them due to the small correction for the fixed fibre diameters) for the p model. One can clearly see the cut-off of at 100 km s^-1, which has been introduced to avoid the contamination of our sample.
Open with DEXTER

	Fig. B.36 Distribution of extinction- and K-corrected apparent magnitudes m_app in different filters for the c model, showing a steady increase in numbers until the steep cut-off at the sample’s limiting magnitudes, which are listed in Table 3.
Open with DEXTER

	Fig. B.37 Distribution of extinction- and K-corrected apparent magnitudes m_app in different filters for the dV model, showing a steady increase in numbers until the steep cut-off at the sample’s limiting magnitudes, which are listed in Table 3.
Open with DEXTER

	Fig. B.38 Distribution of extinction- and K-corrected apparent magnitudes m_app in different filters for the p model, showing a steady increase in numbers until the steep cut-off at the sample’s limiting magnitudes, which are listed in Table 3.
Open with DEXTER

	Fig. B.39 Distribution of the surface brightness μ₀ in different filters for the c model showing an almost Gaussian shape. For the u band, the distribution is wider and shows a small bump at the faint end.
Open with DEXTER

	Fig. B.40 Distribution of the surface brightness μ₀ in different filters for the p model shows some peculiar features in the u band and to some smaller extent in z band as well. In these two filters, one can see a clear second peak on the faint side of the main Gaussian.
Open with DEXTER

	Fig. B.41 Distributions of the logarithm of the physical radius log ₁₀(R₀) in different filters for the c model are well described by sharp Gaussian with their peaks almost exactly at the same value. Only the u band shows some digressive behaviour. In this case the peak is smaller and set apart from the other. Furthermore, the distribution is wider and shows a small bump at the larger end.
Open with DEXTER

Fig. B.42

Distributions of the logarithm of the physical radius log ₁₀(R₀) in different filters for the p model are well described by sharp Gaussian with their peaks almost exactly at the same value. However, the u band shows a peculiar second peak aside the consequently smaller (in comparison to the other filters) main one. In addition to this deviation, the z band distribution has a small bump at its larger end.

Open with DEXTER

	Fig. B.43 Distributions of the logarithm of the central velocity dispersion log ₁₀(R₀) in different filters for the p model are almost exactly the same for all filters. They show an general abundance (compared with a perfect Gaussian) of galaxies at the lower end, which might indicate some residual contamination of the sample.
Open with DEXTER

	Fig. B.44 Projection of the fundamental plane for the u band of the c model.
Open with DEXTER

	Fig. B.45 Projection of the fundamental plane for the g band of the c model.
Open with DEXTER

	Fig. B.46 Projection of the fundamental plane for the r band of the c model.
Open with DEXTER

	Fig. B.47 Projection of the fundamental plane for the i band of the c model.
Open with DEXTER

	Fig. B.48 Projection of the fundamental plane for the z band of the c model.
Open with DEXTER

	Fig. B.49 Projection of the fundamental plane for the u band of the dV model.
Open with DEXTER

	Fig. B.50 Projection of the fundamental plane for the g band of the dV model.
Open with DEXTER

	Fig. B.51 Projection of the fundamental plane for the r band of the dV model.
Open with DEXTER

	Fig. B.52 Projection of the fundamental plane for the u band of the p model.
Open with DEXTER

	Fig. B.53 Projection of the fundamental plane for the g band of the p model.
Open with DEXTER

	Fig. B.54 Projection of the fundamental plane for the r band of the p model.
Open with DEXTER

	Fig. B.55 Projection of the fundamental plane for the i band of the p model.
Open with DEXTER

	Fig. B.56 Projection of the fundamental plane for the z band of the p model.
Open with DEXTER

	Fig. B.57 Redshift evolution of the surface brightness in the u band of dV model indicated by the solid black line. The solid red line shows the Malmquist-bias-corrected average value of the surface brightness for this particular filter and model.
Open with DEXTER

	Fig. B.58 Redshift evolution of the surface brightness in the g band of dV model indicated by the solid black line. The solid red line shows the Malmquist-bias-corrected average value of the surface brightness for this particular filter and model.
Open with DEXTER

	Fig. B.59 Redshift evolution of the surface brightness in the r band of dV model indicated by the solid black line. The solid red line shows the Malmquist-bias-corrected average value of the surface brightness for this particular filter and model.
Open with DEXTER

	Fig. B.60 Redshift evolution of the surface brightness in the i band of dV model indicated by the solid black line. The solid red line shows the Malmquist-bias-corrected average value of the surface brightness for this particular filter and model.
Open with DEXTER

	Fig. B.61 Redshift evolution of the surface brightness in the z band of dV model indicated by the solid black line. The solid red line shows the Malmquist-bias-corrected average value of the surface brightness for this particular filter and model.
Open with DEXTER

	Fig. B.62 Corrected angular radii plotted against the apparent magnitudes, showing some grouping in the u band for the p model.
Open with DEXTER

	Fig. B.63 Corrected angular radii plotted against the apparent magnitudes, not showing any peculiar features in the r band for the p model.
Open with DEXTER

	Fig. B.64 Corrected angular radii plotted against the apparent magnitudes, showing some small grouping in the z band for the p model.
Open with DEXTER

	Fig. B.65 Logarithm of the physical radii against the redshift, clearly showing band-like structures in the u band for the p model.
Open with DEXTER

	Fig. B.66 Logarithm of the physical radii against the redshift, showing band-like structures in the z band for the p model.
Open with DEXTER

	Fig. B.67 Colour-magnitude diagram of the red sequence for the c model. The solid black line represents our best fit and the two solid red lines indicate the 3-σ confidence limits beyond which we clipped the sample.
Open with DEXTER

	Fig. B.68 Colour-magnitude diagram of the red sequence for the dV model. The solid black line represents our best fit and the two solid red lines indicate the 3-σ confidence limits beyond which we clipped the sample.
Open with DEXTER

	Fig. B.69 Colour-magnitude diagram of the red sequence for the p model. The solid black line represents our best fit and the two solid red lines indicate the 3-σ confidence limits beyond which we clipped the sample.
Open with DEXTER

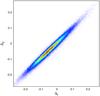	Fig. B.70 Tight correlation between the residuals of the fundamental plane in the r band Δ_r and of those in the z band Δ_z. This plot uses the fundamental-plane fit for the dV model.
Open with DEXTER

	Fig. B.71 Strong correlation between the residuals of the fundamental plane in the g band Δ_g and of those in the z band Δ_z, however the correlation is visible weaker than for previous plots, due to the larger difference in the wavelength between the two filters. This plot uses the fundamental-plane fit for the dV model.
Open with DEXTER

	Fig. B.72 Correlation between the residuals of the fundamental plane in the u band Δ_u and of those in the z band Δ_z. Due to the larger scatter in the u band, the correlation is significantly weaker than for all other filters. This plot uses the fundamental-plane fit for the dV model.
Open with DEXTER

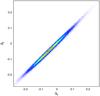	Fig. B.73 Tight correlation between the residuals of the fundamental plane in the r band Δ_r and of those in the z band Δ_i. This plot uses the fundamental-plane fit for the dV model.
Open with DEXTER

	Fig. B.74 Strong correlation between the residuals of the fundamental plane in the g band Δ_g and of those in the i band Δ_i. This plot uses the fundamental-plane fit for the dV model.
Open with DEXTER

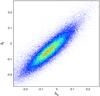	Fig. B.75 Correlation between the residuals of the fundamental plane in the u band Δ_u and of those in the i band Δ_i. Due to the larger scatter in the u band, the correlation is significantly weaker than for all other filters. This plot uses the fundamental-plane fit for the dV model.
Open with DEXTER

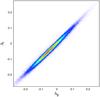	Fig. B.76 Strong correlation between the residuals of the fundamental plane in the g band Δ_g and of those in the r band Δ_r. This plot uses the fundamental-plane fit for the dV model.
Open with DEXTER

	Fig. B.77 Correlation between the residuals of the fundamental plane in the u band Δ_u and of those in the r band Δ_r. Due to the larger scatter in the u band, the correlation is significantly weaker than for all other filters. This plot uses the fundamental-plane fit for the dV model.
Open with DEXTER

	Fig. B.78 Correlation between the residuals of the fundamental plane in the u band Δ_u and of those in the g band Δ_g. Due to the larger scatter in the u band, the correlation is significantly weaker than for all other filters. This plot uses the fundamental-plane fit for the dV model.
Open with DEXTER

Appendix C: Additional tables

Table C.1

Coefficients for the K-correction in the u band using u − r colours.

Table C.2

Coefficients for the K-correction in the g band using g − r colours.

Table C.3

Coefficients for the K-correction in the r band using g − r colours.

Table C.4

Coefficients for the K-correction in the i band using g − i colours.

Table C.5

Coefficients for the K-correction in the z band using g − z colours.

Table C.6

Coefficients and the root mean square of the best fit for the red sequence using our sample.

Table C.7

Quality of the fundamental plane as a distance indicator using our selected sample of 94 922 elliptical galaxies, but with the direct-fit coefficients of Bernardi et al. (2003c) or Hyde & Bernardi (2009), respectively (the coefficients are listed in Table 1 of this paper).

Table C.8

Mean values and standard deviations of several different parameters that have to be calculated or measured for the calibration of the fundamental plane.

Table C.9

Best fits for the fundamental-plane coefficients in all filters and for all models with the 3-σ clipping disabled.

Table C.10

Best fits for the fundamental-plane coefficients in all filters and for all models with the volume weights disabled.

Table C.11

Best fits for the fundamental-plane coefficients in all filters and for all models with the correction for redshift evolution completely disabled.

Table C.12

Best fits for the fundamental-plane coefficients in all filters and for all models with volume weights and 3-σ clipping and a filter-dependend redshift evolution derived from the redshift evolution of the surface brightness (see Table C.13).

Table C.13

Redshift evolution derived from changes in the surface brightness using non-evolution-corrected magnitudes.

Table C.14

Fundamental-plane coefficients in all filters and for all models derived from the volume-limited subsample, which is to 95,45% (2-σ) completed.

Table C.15

Fundamental-plane coefficients in all filters and for all models derived from an extended sample up to a redshift of 0.3.

© ESO, 2013

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.