| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201321826 | |
| Published online | 05 August 2013 | |
Online material
Appendix A: Lower limit for the strand diameter
The typical length scale perpendicular to the magnetic field through whatever process places a lower limit for the strand diameter d. If d were smaller than this length scale, the neighboring strand would interact through this process and consequently the strands would no longer be individual structures but one common entity. This discussion is of interest, because if this lower limit for the strand diameter were larger than the upper limit derived from observations in Sect. 3.3, the loops would have to be monolithic structures.
Reconnection.
Most probably reconnection is the basis of the heating process. For reconnection to happen the inductive term and the dissipative term in the induction equation have to be on the same order of magnitude, or in other words, the magnetic Reynolds number has to be of order unity; i.e., Rm = U ℓ/η ≈ 1. Here U is the typical velocity and η the magnetic diffusivity. The length scale ℓ would represent the thickness of the resulting current sheet. This ℓ is then a lower limit for the strand diameter. If strands were thinner, they would be part of the same reconnection region and thus not distinguishable.
Following Spitzer (1962) one can derive the electric conductivity σ from classical transport theory, which then provides η = (μ0 σ)-1. In the corona at 106 K, the value is η ≈ 1 m2 s-1. For Rm ≈ 1 the length scale is given by ℓ ≈ η/U. For a low value of U ≈ 1 km s-1 (certainly there are much faster flows in the corona), we find a value of 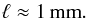 (A.1)Arguments along this line of thought can be found in e.g. Boyd & Sanderson (2003) or in the preface of Ulmschneider et al. (1991). This value must be a vast underestimation, because it is much less than the ion (and even the electron) gyro radius.
(A.1)Arguments along this line of thought can be found in e.g. Boyd & Sanderson (2003) or in the preface of Ulmschneider et al. (1991). This value must be a vast underestimation, because it is much less than the ion (and even the electron) gyro radius.
Gyration.
Another relevant length scale is the Larmor or gyro radius of the gyration of the ions and electrons in the corona. This is given by rL = m v⊥(e B)-1 , with mass m and charge e of the particles and the magnetic field B. Assuming that the perpendicular velocity is given by the thermal speed, v⊥ = (3kT/m)1/2, one finds 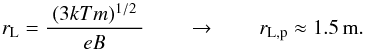 (A.2)Thus in the corona at temperatures of about T ≈ 106 K and for B ≈ 10 G, the Larmor radius of the protons is on the order of 1 m.
(A.2)Thus in the corona at temperatures of about T ≈ 106 K and for B ≈ 10 G, the Larmor radius of the protons is on the order of 1 m.
Heat conduction.
The head conduction perpendicular to the magnetic field is much less efficient than the parallel conduction, but if the temperature gradients across the field become large enough it might become non-negligible. For the coefficient of the perpendicular heat conduction one can derive (e.g. Priest 1982, Sect. 2.3.2) 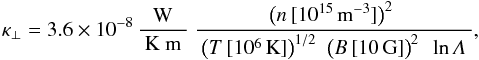 (A.3)where n is the particle density and in the corona the Coulomb logarithm is roughly lnΛ ≈ 13.
(A.3)where n is the particle density and in the corona the Coulomb logarithm is roughly lnΛ ≈ 13.
We now consider the minimum diameter d of a strand with length L. For this we assume that the energy lost by heat conduction perpendicular to the magnetic field, κ⊥ ∇T, through the mantle surface of the strand, L πd, is balanced by the energy input FH through the two footpoints of the strand with cross section πd2/4, 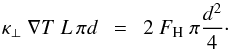 (A.4)Using expression (A.3) one finds
(A.4)Using expression (A.3) one finds 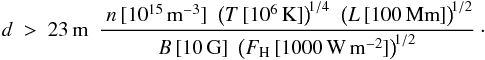 (A.5)For typical coronal values and an energy flux density into the corona of 1000 W m-2, we find a diameter of the order of 20 m. This is a lower limit for the strand diameter. If the strand were thinner, the temperature gradient to the neighboring (cold) strand would be higher, and thus the energy loss by perpendicular heat conduction would be stronger than the energy input. Consequently the strand would start to dissolve into the neighboring strands, thereby increasing its diameter.
(A.5)For typical coronal values and an energy flux density into the corona of 1000 W m-2, we find a diameter of the order of 20 m. This is a lower limit for the strand diameter. If the strand were thinner, the temperature gradient to the neighboring (cold) strand would be higher, and thus the energy loss by perpendicular heat conduction would be stronger than the energy input. Consequently the strand would start to dissolve into the neighboring strands, thereby increasing its diameter.
Other processes.
From the above discussion we find that the strands should be at least some 10 m to 50 m in diameter, set by the perpendicular heat conduction. However, this lower limit might be on the low side. Other processes, in particular MHD turbulence, might increase the length scale perpendicular to the magnetic field considerably. Then the reconnection process will effectively operate on larger length scales, and also the heat conduction perpendicular to the magnetic field will be more effective, ensuring smaller temperature gradients and thus larger length scales perpendicular to the magnetic field. The MHD turbulence simulations of Rappazzo et al. (2008) show elongated current concentrations aligned with the magnetic field, which could be interpreted as the strands in a loop. However, because of the lack of heat conduction and radiative losses in their model, which would have been beyond the scope of their study, one cannot say much about the diameter of the potentially developing strands.
Future theoretical investigations might place a better lower limit to the strand diameter and thus further limit the range of possible strand diameters given by the relations (7) and (A.5). Finally such studies would help in deciding whether loops are monolithic or multi-stranded.
Appendix B: Size of the loops seen in Hi-C
 |
Fig. B.1
Size of the loop structures in Hi-C. Shown are the power spectra of the cross-sectional cuts of the loops in Fig. 6, for the original data (top panel, red here and in Fig. 6) and the data averaged over 21 pixels along the loop (bottom panel green here and in Fig. 6). The horizontal dashed lines shows the noise level (21 in top panel, 1 in bottom panel). The diagonal blue line is a by-eye fit to the power spectrum at low spatial frequencies, the vertical line indicated the intersection of this fit with the respective noise level. The numbers in the panels give the corresponding spatial scale. See Appendix B. |
| Open with DEXTER | |
To obtain a quantitative estimate for the size of the loop structures discussed in Sect. 3.2 we performed a Fourier transform of the spatial variation shown in Fig. 6. We did this for the original profile across the loop (red with bars in Fig. 6), as well as for the data-averaged 21 pixels along the loops (in green). After subtracting the linear trend and apodizing using a Welsh filter we performed a Fourier transform to obtain the power spectrum as a function of spatial frequency. The resulting power spectra are shown in Fig. B.1. The top panel shows the power spectrum for the original profile, the bottom panel shows the power spectrum for the averaged data.
We calculated the noise level in the power spectrum by equating the square of the error in the data integrated over space to the noise in the power integrated over spatial frequency. For the data averaged aver 21 pixels along the loop, we assumed the error to be given by the original errors scaled down by 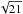 . We have overplotted these noise levels for the original and the spatially averaged data in Fig. B.1.
. We have overplotted these noise levels for the original and the spatially averaged data in Fig. B.1.
From the power spectra in Fig. B.1, it is clear that all structures on scales below 1.2′′ are consistent with noise (i.e., right of the vertical blue lines). The corresponding frequency of 0.8 1/′′ is far from the Nyquist frequency of about 3.4 1/′′. The results are similar for the original and the averaged Hi-C data. Based on the averaged Hi-C data, which show less noise, the structures on scales below 1.2′′ represent less than 1% of the power. If there were significant power from (sub-)structures in the loops investigated in Fig. 6, it should show up somewhere in the frequency range from 1 1/′′ to 3.4 1/′′, where Hi-C would be sensitive.
In other parts of the field-of-view for different structures, e.g. in moss areas or for the miniature loop discussed in Sect. 3.1, Hi-C shows much smaller structures basically down to its resolution limit. However, the loop structures investigated in Sect. 3.2 and Fig. 6, which have widths of about 2′′, do not show any substructure on scales below 1.2′′. This is equivalent to saying that the long 2′′ wide coronal loops as seen in Hi-C have no substructure.
Appendix C: Appearance of multi-stranded loops
 |
Fig. C.1
Numerical experiments for the cross-sectional profile of multi-stranded loops. The top panels show the loop cross-section for four experiments with about 7500 strands where about 750 are bright. They differ only by the random selection of which strands are bright. Each strand has a diameter of 15 km. The bottom panels show the respective cross-sectional profiles (i.e., integration along Y) as would be observed by AIA (blue, diamonds) and Hi-C (red). The height of the bars for Hi-C correspond to 10% of the counts. See Appendix C. |
| Open with DEXTER | |
To visualize the analytical results in Sect. 3.3 on the upper limit for the strand diameter and the lower limit for the number of
bright strands in the loop, we conducted a simple numerical experiment. In the following all variables have the same meaning as in Sect. 3.3.
For the experiment we assumed each individual strand has a Gaussian cross-sectional profile (in intensity), where the full width at half maximum is used to define the strand diameter d. We then filled the circular loop cross section with a most dense packing of circles, which provides us with the total number of strands Nt. For the numerical experiment we randomly selected which of the loops are bright, with a fraction fb of all loops being bright, Nb = Nt fb.
We then integrated along a line-of-sight perpendicular to the loop, which provides the cross-sectional intensity profile of the loop. This profile was folded with a point spread function for AIA and Hi-C (where for simplicity we assumed a Gaussian profile, which is sufficient for the purpose at hand).
In Fig. C.1 we visualize the results for the parameters as found in Sect. 3.3, i.e., a total of Nt = 7500 strands of which a fraction of fb = 0.1 or Nb = 750 is bright with a diameter of d = 15 km. These fit into a circular loop with a diameter D corresponding to 2′′ or 1500 km.
In the top panels of Fig. C.1 we show the cross section of the loop for four different random selections of which loops are bright. The respective lower panel shows the cross-sectional profile if it were observed with AIA or Hi-C. It is clear that the limited spatial resolution of AIA of slightly worse than 1′′ does not allow any features to be seen. We instead see a smooth profile that is basically identical for all four cases.
The Hi-C data show some variation in the cross-sectional profile. In Sect. 3.3 we used the variability ε to derive the upper limit of the strand diameter. Here we plot the variability ε as bars on top of the profile. We see that the variability in the simulated cross-sectional profile for the four cases in Fig. C.1 is roughly comparable with the variability ε we used in Sect. 3.3. If we used a significantly larger (smaller) number of individual strands, we would find a smoother (rougher) cross sectional profile, which confirms the derivation of the limit for the strand diameter in Sect. 3.3. Actually, the cross sectional profiles shown in Fig. C.1 look quite similar to the profiles of the loops seen in observations in Fig. 6.
This numerical experiment also elucidates the interpretation of substructures in loops. In the four examples we show in Fig. C.1 only one (d) shows a perfectly smooth profile. One might be tempted to conclude from a cross-sectional profile, as in case (c), that this loop shows only two major substructures. In cases (a) and (b) one might underestimate the diameter of the loop. Looking at more randomly generated distributions of bright strands, one finds a wide variety of cross-sectional profiles. This shows that one has to be careful when analyzing single loops, because the (random) distribution of a large number of loops might mimic the existence of structures that are not present in reality.
These numerical experiments confirm our conclusions based on the analytical analysis in Sect. 3.3 that the strand diameter should be on the order of about 15 km or less (in particular when conducting experiments for loops with different numbers of strands, which we do not show here for brevity). Of course, this does not exclude the possibility that there is no substructure at all, but rather that the loop is a monolithic structure, as noted in Sect. 3.3.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


