| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220885 | |
| Published online | 27 June 2013 | |
Online material
Appendix A: Two dimensional RT grid
 |
Fig. A.1
Gas density and velocity field for Model 3 at t/tacc = 0.13 and 0.28 within 1500 AU. The density contours start from log (n/cm-3) = 5.5 and increase by steps of 0.5 up to log (n/cm-3) = 9. There are vertical and radial motions in the disk, which are not captured in this figure. |
| Open with DEXTER | |
 |
Fig. A.2
Example of the gridding used in the Stage 0 phase to resolve the small extent of the outflow cavity and to resolve the density and velocity gradient from the disk midplane to the envelope. The color contours are the same as in Fig. A.1. The structure shown is for Model 1 at t/tacc = 0.13. |
| Open with DEXTER | |
The grid needs to resolve the steep density and velocity gradients at the boundaries between adjacent components as shown in Fig. A.1. Improper gridding can lead to order-of-magnitude difference in the high-J (J ≥ 6) line fluxes. The escape probability code begins with a set of regularly spaced cells on a logarithmic grid to resolve both small and large scales. Any cells where the abundance or density at the corners differs by more than a factor of 5, or where the temperature at the corners differs by more than a factor of 1.5, are split into smaller cells until the conditions across each cell are roughly constant. The full non-LTE excitation calculation takes about five minutes for a typical number of cells of 15 000 (Stage I)−25 000 (Stage 0).
Figure A.2 presents an example of the gridding in our models. Such gridding is most important for early time steps where the outflow cavity opening angle is small. The refining ensures that the non-LTE population calculation converges and high-J emission which comes from the inner region can escape.
Appendix B: FIR and submm lines
Figure B.1 shows the mass evolution of the evolutionary models which indicates the times at which the models enter various evolutionary stages. Figure B.2 presents the C18O 9−8 lines for the three different evolutionary models convolved to a 9″ beam. Most of the line is emitted from the inner envelope region. The line is generally broader in later stages due to a combination of thermal, turbulent width and velocity structure. However, the width of the line depends on whether the emitting region is infall or rotation dominated. Figures B.3 and B.4 shows the Ju = 3, 6 and 9 line profiles for the different models and how they change within different beams. The disk contribution to the observed lines within a 9″ beam is presented in Fig. B.5 which is close to negligible for the low-J lines.
 |
Fig. B.1
Evolution of the envelope, disk and stellar mass (top), effective stellar temperature (middle) and stellar luminosity (bottom) for the three different models as function of time (in units of tacc). The solid circles show the time steps (roughly around t/tacc ~ 10-3,0.1,0.5,0.75,0.89,0.99) used for rendering the molecular lines. The adopted time steps vary per model in order to cover properly the time when the model enters Stage 1 (Menv < M⋆) and when the Md = Menv as indicated by the vertical dotted lines. |
| Open with DEXTER | |
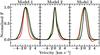 |
Fig. B.2
C18O 9 − 8 line profiles convolved to a 9″ beam for the three models at t/tacc = 0.13 (red), 0.50 (green) and 0.96 (black). |
| Open with DEXTER | |
 |
Fig. B.3
Normalized C18O and 13CO line profiles as functions of evolution for Ju = 3, 6 and 9 at t/tacc = 0.13 (red), 0.50 (green) and 0.96 (black) for i = 5° orientation for Model 1. The lines are convolved to beams of 20″ (top), 9″ (middle) and 1″ (bottom). |
| Open with DEXTER | |
 |
Fig. B.4
As Fig. 3, but for Models 2 and 3. |
| Open with DEXTER | |
 |
Fig. B.5
Disk contribution to total emission as a function of Ju within a 9″ beam (1260 AU at 140 pc) for the three different models. The different colors correspond to different time steps: t/tacc ~ 0.50 (red), 0.75 (blue), 0.96 (black). |
| Open with DEXTER | |
Appendix C: NIR molecular lines
Appendix C.1: Inner disk
The formation of NIR continuum and the region where absorption happens depend on the physical structure in the inner few AU as will discussed extensively in the next section. Figure C.2 shows the inner 5 AU structure of the three different models. In both Models 1 and 3, the 104.5 cm-3 density contour extends up to the line of sight of 45° due to the presence of compact disk and massive disk, respectively. On the other hand, the density structure is flatter in Model 2. Thus, the NIR continuum emission is emitted through the high temperature region (mostly the red region in the temperature plot) and encounters more material along the line of sight to an observer in Models 1 and 3. Consequently, the emission from the region close to the midplane of the disk will not contribute to the NIR continuum. Figure 13 presents an example of the radial contribution to the column density along a line of sight from the star. At viewing angles <45°, most of the warm material is located at 10−40 AU from the star along the line of sight while most of the cold material is located >50 AU. The inner disk and high density region (< 1 AU) is only accessible through i ≥ 75° in our models.
Appendix C.2: Radiative transfer effects
Section 4 discusses the RADLite results with respect to the predicted observables. In this section, we present the comparison between RADLite and a simple calculation using the integrated column density (column method, Eq. (3)) to examine the radiative transfer effects in particular where the 4.7 μm continuum is formed and its affect on the simulated absorption lines.
Figure C.4 illustrates the difference in line center optical depth between the formal solution of the radiative transfer equation and the column density approach at i = 45° (Eq. (3)). This particular model and time was chosen as an example that clearly shows the difference. The difference in τ0 between the methods generally increases with Jl and are largest for Jl ~ 10. Figure C.3 shows the 4.7 μm continuum flux due to dust only (i.e., no stellar contribution) as function of radius at various viewing angles. The continuum is point-like for low inclinations but it is generally off-center for high inclinations. Thus, larger τ0 differences between the two methods are expected for larger inclinations since the absorption does not take place directly along the line of sight to the star. The implication is that the column method overestimates τ0 of the high-J absorptions as this method takes the full line of sight through the warm material into account.
What are the implications for translating observed optical depths to column densities and excitation temperatures? The differences are largest for J ≥ 5 lines which result in lower derived warm temperature and column densities in the full treatment. Consequently, the direct transformation from the observed optical depth to column density requires additional information on where the absorption arises, i.e., the NIR continuum image. One way is to construct the physical structure and assess the NIR continuum image. Observationally, a comparison between interferometric submm and NIR continuum should result in different continuum position if the NIR continuum arises from scattered light. Observationally driven constraint is likely more useful in practice since modelling of the NIR continuum requires a sophisticated inner disk and envelope physical structure. For systems with an off-centered NIR continuum, the derived column densities and temperature of the warm component are lower limits.
 |
Fig. C.1
Example of the two-temperature fitting of the NIR lines. The column densities are derived from a curve-of-growth analysis performed on the simulated spectra using RADLite. The different symbols correspond to 12CO (circle), 13CO (triangles) and C18O (squares). The solid lines are the combination of the cold and warm components. |
| Open with DEXTER | |
 |
Fig. C.2
Density structure in the inner 10 AU (starting from n(H2) = 104.5 cm-3) and temperature structure (starting from 60 K) of the three models. The three viewing angles are shown by dotted lines. |
| Open with DEXTER | |
 |
Fig. C.3
Normalized continuum flux without the stellar photosphere as function of distance from the center along one direction. The figure is constructed from a NIR image of Model 1 at t/tacc = 0.7 as an example. The general trend is similar for t/tacc > 0.5 independent of evolutionary models. The normalized continuum is similar for the various evolutionary models for t/tacc > 0.5. The continuum is shown to arise in the inner few AU region and to fall off very quickly for i < 60°. However, significant contributions from larger radii are expected for relatively high inclination. |
| Open with DEXTER | |
 |
Fig. C.4
Comparison of the line center optical depth obtained from a simple integration of the column density along the line of sight (circles) and the radiative transfer calculation (triangles). The P and R branches are shown in black and red, respectively. The horizontal line indicates the current observation limit with CRIRES at τ ~ 3 × 10-3. The 13CO lines are shown for Model 1 at t/tacc = 0.76 for i = 45°. |
| Open with DEXTER | |
Appendix C.3: Non-LTE effects
 |
Fig. C.5
Comparison between LTE (squares) and non-LTE (triangles) line center optical depth obtained from RADLite for Model 3 at an inclination of 45°. The different colors correspond to the P (black) and R (red) branches. |
| Open with DEXTER | |
The effects of non-LTE excitation in the vibrational ground state are studied by either using the level populations calculated with the full non-LTE escape probability method (Sect. 3) or assuming LTE populations. The LTE level population is calculated using the partition functions provided by the HITRAN database (Rothman et al. 2005).
Figure C.5 compares LTE and non-LTE line center opacities of C18O for Model 3 at an inclination of 45° (other isotopologs are shown in Fig. C.6). Model 3 was chosen as an example; in general, the non-LTE effects are most apparent for the higher levels independent of isotopologs and evolutionary models. This reflects the findings of Sect. 3: lower pure rotational levels are more easy to thermalize due to lower critical densities. The difference between LTE and non-LTE is independent of inclination while radiative transfer effects do. Thus, it is more important to treat the radiative transfer correctly in the NIR to derive observables.
 |
Fig. C.6
Similar to Fig. C.5 for 12CO (diamonds and circles) and 13CO (squares and triangles). |
| Open with DEXTER | |
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


