| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201219567 | |
| Published online | 20 March 2013 | |
Online material
Appendix A: Derivation of used formulas
Appendix A.1: Rotation and kinetic temperature
As described in Sect. 3, the hyperfine fit routine returns the best fit parameters of the brightness temperature, Tmb, optical depth, τ, velocity of rest, Vlsr, and line width FWHM, Δv, (with errors).
The brightness temperature Tmb describes the brightness temperature of a source and depends on the beam this source is observed with by returning the mean value over this beam. It is needed to calculate the excitation temperature.
The excitation temperature Tex is no physical
temperature, but describes the ratio between two population levels
u(p) and l(ow) via 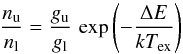 (A.1)where
ni is the numbers of particles in the state i and
gi its statistical weight. ΔE
represents the energy difference between the states and k the
Boltzmann constant. For the IRDCs temperatures above 10 K are expected. Thus, (by
applying the Rayleigh-Jeans law) the brightness and excitation temperatures are
simplified connected by
(A.1)where
ni is the numbers of particles in the state i and
gi its statistical weight. ΔE
represents the energy difference between the states and k the
Boltzmann constant. For the IRDCs temperatures above 10 K are expected. Thus, (by
applying the Rayleigh-Jeans law) the brightness and excitation temperatures are
simplified connected by  (A.2)with
τ being the source’s optical depth and
TBG the background temperature (being about 2.7 K).
ηf represents the beam-filling factor. It describes the
fraction of the antenna pattern being received from the source. In the case of
extended and not clumpy sources, the beam-filling factor is equal to 1. We assume this
case for the sample. The excitation temperatures are calculated for both transition
lines.
(A.2)with
τ being the source’s optical depth and
TBG the background temperature (being about 2.7 K).
ηf represents the beam-filling factor. It describes the
fraction of the antenna pattern being received from the source. In the case of
extended and not clumpy sources, the beam-filling factor is equal to 1. We assume this
case for the sample. The excitation temperatures are calculated for both transition
lines.
The rotation temperature Trot is defined similar to the
excitation temperature by  (A.3)But in contrast to
the excitation temperature, the rotation temperature does not describes the ratio
between different levels being split by inversion, but between the levels of quantum
numbers J and K (total angular momentum and its
absolute projection along the z-axis). We are interested in the
rotation temperatures of the metastable inversion levels with
J = K (non-metastable inversion levels:
J > K). These levels
cannot be populated or depopulated by radiation. Therefore, their population numbers
are high enough to emit measurable line intensities. Furthermore, metastable levels
interact only via collisions (Ho & Townes
1983; Schilke 1989) and are useful for
the calculation of gas temperatures.
(A.3)But in contrast to
the excitation temperature, the rotation temperature does not describes the ratio
between different levels being split by inversion, but between the levels of quantum
numbers J and K (total angular momentum and its
absolute projection along the z-axis). We are interested in the
rotation temperatures of the metastable inversion levels with
J = K (non-metastable inversion levels:
J > K). These levels
cannot be populated or depopulated by radiation. Therefore, their population numbers
are high enough to emit measurable line intensities. Furthermore, metastable levels
interact only via collisions (Ho & Townes
1983; Schilke 1989) and are useful for
the calculation of gas temperatures.
The remaining problem is that we do not know the exact population numbers and have to
approximate them by the column densities. For lines being observed in the same region
the ratio of the population numbers should be equal to the ratio between the
corresponding column densities depending on the ratio of the lines’ optical depths:
 (A.4)where
τJK is the optical depth of the
(J,K)-inversion line,
ΔvJ its line width FWHM,
Nl(J,K) its column density and
(A.4)where
τJK is the optical depth of the
(J,K)-inversion line,
ΔvJ its line width FWHM,
Nl(J,K) its column density and
 its excitation
temperature. Because only the (1,1)- and (2,2)-inversion lines have been studied, it
is J = K = 2 and
J′ = K′ = 1 in the following
calculations.
its excitation
temperature. Because only the (1,1)- and (2,2)-inversion lines have been studied, it
is J = K = 2 and
J′ = K′ = 1 in the following
calculations.
Inserting this into Eq. (A.3), one
gets:  (A.5)where
(A.5)where
 K (Ho & Townes 1983) and
K (Ho & Townes 1983) and  (A.6)Following the
instruction of Schilke (1989) and Ho & Townes (1983), there are four cases
one has to consider for calculating the rotation temperature. These cases differ in
the optical depth of each inversion line:
(A.6)Following the
instruction of Schilke (1989) and Ho & Townes (1983), there are four cases
one has to consider for calculating the rotation temperature. These cases differ in
the optical depth of each inversion line:
-
1.
both inversion lines are optical thick:
 (A.7)where
τii is the optical depth of the (i, i)-inversion
line and fi is the relative
intensity of the main hyperfine component. For the given transitions, there is
f1 = 0.5 and
f2 = 0.796 (Ho
& Townes 1983).
(A.7)where
τii is the optical depth of the (i, i)-inversion
line and fi is the relative
intensity of the main hyperfine component. For the given transitions, there is
f1 = 0.5 and
f2 = 0.796 (Ho
& Townes 1983). -
2.
only the (1,1)-inversion line is optical thick and the (2,2)-inversion line is optical thin:
 (A.8)
(A.8) -
3.
both inversion lines are optical thin:
 (A.9)where
(A.9)where
 represents the brightness temperature of the (i, i)-inversion line.
represents the brightness temperature of the (i, i)-inversion line. -
4.
only the (1,1)-inversion line is detected, the (2,2)-inversion line is not:
 (A.10)In this case,
the (2,2)-inversion line lies within the noise. To be able to continue with the
calculations,
(A.10)In this case,
the (2,2)-inversion line lies within the noise. To be able to continue with the
calculations,  has
been given the triple value of the average root-mean-square noise (rms = 0.0925
K). It is important to emphasise that in this case it is not possible to derive
exact rotation temperatures, but only upper limit estimations!
has
been given the triple value of the average root-mean-square noise (rms = 0.0925
K). It is important to emphasise that in this case it is not possible to derive
exact rotation temperatures, but only upper limit estimations!
Having the rotation temperature of ammonia, we were able to calculate the kinetic
temperature of a source’s gas by using the approximation of Tafalla et al. (2004):
 (A.11)This approximation
has been derived with Monte Carlo models and gives an accuracy of 5% in the range
between 5 and 20 K. Because the majority of the sample IRDCs are within this range,
their errors are set to this.
(A.11)This approximation
has been derived with Monte Carlo models and gives an accuracy of 5% in the range
between 5 and 20 K. Because the majority of the sample IRDCs are within this range,
their errors are set to this.
Appendix A.2: Column density
As mentioned before in Sect. A.1, the column
density is related to a source’s optical depth (Schilke 1989). If one neglects the background radiation and expresses the
excitation temperature in terms of the optical depth, following Schilke (1989), the column density of the (1,1)-inversion level
N11 can by calculated by  (A.12)where
μ = 1.476 Debye is the electric dipole moment and
ν1 = 23 694.496 MHz the laboratory frequency of the
NH3 (1,1)-inversion transition. To derive the total column density,
(A.12)where
μ = 1.476 Debye is the electric dipole moment and
ν1 = 23 694.496 MHz the laboratory frequency of the
NH3 (1,1)-inversion transition. To derive the total column density,
NNH3, we assumed that the sources are in
thermal equilibrium. In this case, the column density follows a Boltzmann
distribution. Additionally, we took into account that Eq. (A.12) calculates the column density of
para-NH3 being the ammonia inversion levels with
K ≠ 3n (n being an integer) where
the hydrogen spins are not parallel. In contrast, the states with parallel hydrogen
spins are called ortho-NH3 (with K = 3n).
The statistical weight gJK of
ortho-NH3 is twice the one of para-NH3. Therefore, for
calculating the total column density of ammonia, one has to take the triple of column
density of para-NH3 (cf. Schilke
1989):  (A.13)
(A.13)
 |
Fig. B.1
ATLASGAL dust emission map with indicated sample IRDCs in the range of l = 27° to 51° (Schuller et al. 2009). The red triangles indicate the IRDCs with detected ammonia lines, the green triangles the ones without detected ammonia lines. |
| Open with DEXTER | |
 |
Fig. B.2
ATLASGAL dust emission map with indicated sample IRDCs in the range of l = 12° to 27° (Schuller et al. 2009). The red triangles indicate the IRDCs with detected ammonia lines, the green triangles the ones without detected ammonia lines. |
| Open with DEXTER | |
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


