Building merger trees from cosmological N-body simulations - Towards improving galaxy formation models using subhaloes

Free Access

Issue		A&A Volume 506, Number 2, November I 2009


Page(s)		647 - 660
Section		Cosmology (including clusters of galaxies)
DOI		https://doi.org/10.1051/0004-6361/200911787
Published online		27 August 2009

Online Material

Appendix A: Comparing halo finders: AdaptaHOP and FOF

We first proceed in Sect. A.1 of this appendix to compare AdaptaHOP haloes as defined at the end Sect. 2.1 to haloes identified using the popular FOF algorithm with a standard value of b=0.2for the linking length parameter. To be consistent, we also choose 20 as the minimum number of particles a halo detected by the FOF algorithm can contain. The halo finder algorithms are then run on the same N-body simulation described in paper GalICS I (Hatton et al. 2003). We also find necessary to compare the haloes and subhaloes obtained with AdaptaHOP using the MSM method to the halos detected using the FOF algorithm, this task is summarised in Sect. A.2.

A.1 Comparing halos

A.1.1 Individual examples

Our first goal is to ``calibrate'' AdaptaHOP. To do so, we simply collapse the node structure tree onto its first node to define a single halo as a group of particles with a density above the $\rho_{\rm t}$ threshold.

In this appendix we refer to objects detected with AdaptaHOP and whose hierarchy of inner local density maxima has been collapsed as described in Sect. 2.1 as AdaptaHOP haloes. Similarly FOF haloes are objects detected using the FOF algorithm.

Intuitively, we expect haloes detected with FOF and AdaptaHOP to resemble one another, provided they are fairly relaxed and well resolved, i.e. they are close to spherical in shape and contain a large enough number of particles. This is the case for the halo represented in Fig. A.1. The projected positions of dark matter particles belonging to this halo in the (xy) plane are shown in both panels of this figure, with the centre of the halo located at point (0,0). On the left hand side panel we can see the FOF halo, on the right hand side panel, we can see the AdaptaHOP halo. At first glance, one can easily be convinced that they are mostly the same halo, but, looking a bit closer, one gets the impression that the AdaptaHOP halo contains a few small overdensities which are not included in the FOF halo.

This impression is confirmed by going to the next halo example displayed in Fig. A.2. This one is ``peanut'' shaped as it has just undergone a merger. Again both haloes are quite similar but the AdaptaHOP halo clearly shows overdensities which are not part of the FOF halo.

From these two examples, we conclude that haloes detected by the two algorithms do not seem to be very sensitive to the dynamical state the halo is in. This is understandable since both methods rely on particle positions only to define haloes. However, the smoothing process used by algorithms which compute the density field (AdaptaHOP in our case) seems responsible for the systematic inclusion of more overdensities within the haloes than percolation algorithms (FOF here), especially when haloes are less relaxed. Even though this last point seems minor, it is more important than it seems: if we wished to compare the SUBFIND and AdaptaHOP subhalo distribution for instance, SUBFIND would not detect these extra AdaptaHOP overdensities since it performs a FOF first step, and this would, in turn, influence the computation of the potential energy of the particles that SUBFIND performs, possibly resulting in a different stripping of particles not bound to the halo.

A.1.2 Comparing halo finders: statistics

$\begin{figure} \par\includegraphics[width=9cm,clip]{11787fA1.eps} \end{figure}$	Figure A.1: Example of a ``relaxed'' halo detected in our test simulation, the left panel is the halo detected using friend-of-friend (FOF) algorithm, the right panel is the same halo detected using AdaptaHOP. The left panel corresponds to the example shown in the top right panel of Fig. 3 before the subhalo decomposition of the AdaptaHOP halo.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm,clip]{11787fA2.eps} \end{figure}$	Figure A.2: Example of a ``merging'' halo detected in our test simulation, the left panel is the halo detected using friend-of-friend (FOF) algorithm, the right panel is the same halo detected using AdaptaHOP. The left panel corresponds to the example shown in the top right panel of Fig. 4 before the subhalo decomposition of the AdaptaHOP halo.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm,clip]{11787fA3.eps} \end{figure}$

Figure A.3:

For both halo finders, haloes detected at redshift 0 were sorted into 25 mass bins. The top panel shows the number of haloes detected with FOF (triangles) and AdaptaHOP (squares) in each mass bin. Using their particle content, we then cross-identify FOF haloes with their AdaptaHOP counterparts, as described in the text (Sect. 2.1.3). In other words, we enforce that each FOF halo is identified with at most one AdaptaHOP halo and that the identification yields the same result when performed in the reverse order. The bottom panel displays the percentage of haloes per mass bin thus cross identified. The error bars correspond to Poisson uncertainties. The vertical dotted line present on both panels corresponds to the 20 particle detection threshold.

Open with DEXTER

The two individual halo examples discussed in the previous section naturally lead us to wonder about how general the conclusions we have drawn really are. In other words:

How well does the mass distribution of resolved haloes obtained with both halo finders agree?
How frequent is the splitting of single AdaptaHOP haloes into several FOF haloes? Does it depend on resolution/mass? Are all pieces detected?
How do the smallest, poorly resolved, AdaptaHOP and FOF halo (which do not show internal overdensities) populations compare?

The mass distributions of haloes at redshift 0 are shown in Fig. A.3. In both panels squares correspond to the FOF halo distribution and triangles to the AdaptaHOP halo distribution. The mass threshold of 20 particles is represented by a vertical dashed line. The first impression one gets from the top panel of the figure is that the mass distributions of haloes are very close indeed. Looking a bit closer, we find that the number of FOF haloes is more than 5% higher than the number of AdaptaHOP haloes in the first 5 bins, with about 15 000 FOF haloes against 11600 AdaptaHOP haloes of a mass lower than $2.67\times 10^{11}$ $M_{\odot }$ . For masses above $4.5\times 10^{11}$ $M_{\odot }$ , both algorithms converge within 0.5%, as we count 1842 FOF haloes and 1856 AdaptaHOP haloes.

To compare FOF haloes to their AdaptaHOP counterparts, we simply use the list of particles belonging to each halo as follows: (i) an AdaptaHOP halo is identified with at most one FOF halo, the one which contains the highest fraction of its particles (ii) the same procedure is applied to identify a FOF halo to its one and only AdaptaHOP counterpart. A FOF halo and its AdaptaHOP counterpart are then deemed to be the same object when both the highest fraction of the AdaptaHOP halo particles are found in the FOF halo, and the highest fraction of the FOF halo particles are found in the AdaptaHOP halo. For each mass bin we then compute the number of haloes which are found to be ``identical'' in that sense. The curves in the bottom panel are obtained by dividing this number by the number of FOF haloes in the bin (triangles) or by the number of AdaptaHOP haloes in the bin (square), for each mass bin. This yields the percentage of haloes from each algorithm (FOF or AdaptaHOP) also identified as single haloes by the other. In the case of the least resolved haloes, 90% of AdaptaHOP haloes are identified as FOF haloes, but this percentage drops to 77% for FOF haloes identified as AdaptaHOP haloes. Also in the former case, the percentage hits the 100% mark from $5\times 10^{12}$ $M_{\odot }$ onward, whereas for the latter the percentage rises more slowly, reaching 90% for haloes around $5\times 10^{12}$ $M_{\odot }$ , and 100% for haloes of 10¹⁴ $M_{\odot }$ only.

$\begin{figure} \par\includegraphics[width=9cm,clip]{11787fA4.eps} \end{figure}$	Figure A.4: Percentage per bin (of width 1 particle) of haloes with less than 50 particles which are not detected in two consecutive snapshots between redshifts 0 and 10, i.e. among a total of 70 snapshots. The error bars correspond to Poisson uncertainties. The vertical dotted line corresponds to the 20 particle detection threshold.
Open with DEXTER

Whilst one can argue that the comparison of the two algorithms is irrelevant in a regime where results should not be trusted because of a too small number of particles per halo, we believe it is nevertheless important for two reasons: (i) it better underlines the differences between the algorithms and (ii) semi-analytic models of galaxy formation do populate such low resolution haloes with galaxies (e.g. Hatton et al. 2003; Springel et al. 2005). The consequent discrepancy at the low mass end is quite worrisome, and while it is well known that all halo finders will be incomplete when the number of neighbours used to smooth the density field is close to the minimum number of particles per halo, one may wonder whether a significant fraction of these haloes is in any case marginally bound.

A good indicator of this (other than the measure of the total energy of the halo which has quite a large error bar attached to it) is their stability in time. This data is shown in Fig. A.4. We find that 27% of the haloes containing 20 particles detected by FOF at a given time output are not found at the next. This number drops to 17% for AdaptaHOP haloes. For both halo finders this fraction decreases quickly when the number of particles per halo increases. In other words, when using the FOF, we need to reach a resolution of at least 34 particles to lose less than 1% of the haloes between time outputs. In the case of AdaptaHOP, with a resolution of 24 particles or more, less than 1% of haloes are lost. From these numbers, we conjecture that only a small part of the discrepancy between the two algorithms at the low mass end of the halo mass function comes from the fact that AdaptaHOP (and in general algorithms using density criteria) is more efficient than FOF (i.e. algorithms using percolation criteria) for selecting bound objects.

$\begin{figure} \par\includegraphics[width=9cm,clip]{11787fA5.eps} \end{figure}$

Figure A.5:

Every FOF halo detected at redshift 0, with less than 100 particles, is identified with its AdaptaHOP counterpart using the method described in the text (Sect. 2.1.3). Solid curves show the case where we enforce that a unique FOF halo (the one which contains the largest number of particles of its AdaptaHOP counterpart) be identified with its best AdaptaHOP counterpart (the one which contains the highest fraction of the FOF halo particles), as in Fig. A.3. Dashed curves show what happens when we relax this constraint, and allow several FOF haloes to be identified with the same AdaptaHOP counterpart. The error bars correspond to Poisson uncertainties. The vertical dotted line corresponds to the 20 particles detection threshold.

Open with DEXTER

To further substantiate this claim, we now proceed to check the other possible source of discrepancy, i.e. we address the issue of how many of the smallest FOF haloes are not identified as individual haloes by AdaptaHOP, but simply detected as parts of other (larger) haloes. We therefore apply the same technique we used to produce Fig. A.3 but only to FOF haloes with less than 100 particles since we are interested in the low mass end, and relaxing the constraint that an AdaptaHOP halo must necessarily have a unique FOF counterpart.

Results of this experiment are shown as dotted curves in Fig. A.5. Examination of this figure reveals that:

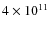
when the constraint of unicity is enforced (solid curve), the percentage of FOF haloes identified as individual AdaptaHOP haloes never reaches 100%, even for haloes containing 100 particles. Instead, this percentage rises slowly from 68% for FOF haloes in the first (20-24 particles) mass bin to reach 90% (+/-1%) for FOF haloes more massive than 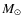$4\times 10^{11}$ $M_{\odot }$ (44 particles or so);
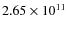
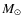when the constraint of unicity is relaxed (dashed curve) - meaning that one AdaptaHOP halo can have several FOF counterparts -, only 14% of FOF haloes in the first mass bin (20-24 particles) are not identified at all by AdaptaHOP as being part of a halo, and this percentage drops to less than 1% in the next mass bin (24-28 particles). Furthermore, from a FOF halo mass of $2.65\times 10^{11}$ $M_{\odot }$ (32 particles) onward, not a single FOF halo remains undetected by AdaptaHOP.

These numbers lead us to conclude that most of the discrepancy of the halo mass function between halo finders at the low mass end can indeed be attributed to a different integration of small objects into larger ones, i.e. to different numbers of small overdensities being included in FOF haloes and their AdaptaHOP counterparts.

$\begin{figure} \par\includegraphics[width=9cm,clip]{11787fA6.eps} \end{figure}$	Figure A.6: Average number of FOF haloes at redshift 0 per AdaptaHOP halo. The error bars correspond to the mean quadratic dispersion. The vertical dotted line corresponds to the 20 particles detection threshold. The diamond and the square correspond to the 2 example haloes shown in Figs. A.1 and A.2 respectively.
Open with DEXTER

One cannot help to wonder how mass dependent such a statement is, i.e. if these small haloes preferentially get included in the outskirts of large clusters, or if their ``mis''-classification happens uniformly across the whole halo mass range spanned by the N-body simulation. This information is presented in Fig. A.6, where we counted the number of FOF haloes detected at the last time output (z=0) inside each halo found by AdaptaHOP. The AdaptaHOP halo population was then split into 25 mass bins, and for each of these bins we computed the average number (and associated mean quadratic dispersion) of FOF haloes detected as counterparts of the AdaptaHOP haloes. For smallish, galaxy size AdaptaHOP haloes (less massive than $4\times 10^{12}$ $M_{\odot }$ or about 400 particles), we find that the average number of FOF haloes per AdaptaHOP halo stays close to the minimal value of one, but starts increasing quite steeply as a function of AdaptaHOP halo mass after that, scaling as $N \propto M^{3/4}$ . This implies that cluster size haloes detected by AdaptaHOP with masses comprised between 10¹⁴ and 10¹⁵ $M_{\odot }$ contain up to several tens of FOF haloes. Since the halo mass function decays as $N \propto M^{-1}$ (see Fig. A.3) in this mass range, this means that cluster size AdaptaHOP haloes get in total roughly the same number of small ``undetected'' FOF haloes as galaxy/group size AdaptaHOP haloes, only they are redistributed over a smaller number of objects. As an illustration of the scatter around the average value, the two example haloes of similar masses displayed in Figs. A.1 and A.2 are marked with a diamond and a square in Fig. A.6 respectively, with the diamond AdaptaHOP halo containing 3 FOF haloes and the square one 16. Note that this explains why in those two cases, most, if not all the extra ``clumps'' of particles seen in the AdaptaHOP halo are not present in the FOF halo to which it was identified, but are detected by FOF as stand alone haloes.

The two group finding algorithms we have studied (FOF and AdaptaHOP) give similar results. The discrepancies measured between them occur principally at the low mass end of the halo mass function and can be brought down to the percent level when one considers that haloes detected using AdaptaHOP generally contain several FOF haloes. Alternatively, one could use (as in the HOP algorithm, see Eisenstein & Hut 1998), multiple/adaptive density thresholds to separate haloes from the background to reduce discrepancies with percolation algorithms. However it is unclear that the various thresholds to use can be determined using physical arguments, so we believe it makes more sense to limit the number of ``free'' parameters and use a single density threshold, as implemented in AdaptaHOP. One can then take advantage of the embedded hierarchy of density maxima within each of the haloes identified that way to define subhaloes. Finally, we emphasise that it is hard to decide which of the algorithms (percolation or density based) is closer to the ``true'' gravitationally bound halo, as poorly resolved substructures located in the outskirts of massive haloes are neither isolated, nor fully relaxed objects, and as such, a reliable estimate of their total energy is not easy to achieve, making it very difficult to decide whether they are bound to the larger halo.

A.2 Comparing halo finder MSM vs. FOF

A.2.1 Individual example

$\begin{figure} \par\includegraphics[width=9cm,clip]{11787fA7.eps} \end{figure}$	Figure A.7: Top right panel: AdaptaHOP halo shown in the right panel of Fig. A.2. Top left panel: the 16 FOF haloes whose particles are found in this AdaptaHOP halo (the best FOF halo match is shown in the left panel of Fig. A.2). Bottom left panel: virial regions of the 16 FOF haloes. Bottom right panel: virial regions of the MSM halo and subhaloes as detailed in Fig. 4.
Open with DEXTER

As mentioned in the previous subsection of this appendix, by mapping particles contained in an AdaptaHOP halo onto the FOF halo distribution, one realises that these particles often belong to several FOF haloes. This is illustrated in Fig. A.7, where we see in the top left panel the 16 FOF haloes which contain particles from the single AdaptaHOP halo plotted in the top right panel. Recall that this means that for each of these 16 FOF haloes most of their particles are cross identified as particles belonging to the AdaptaHOP halo. Each circle in the bottom left panel represents the virial sphere of one of these 16 FOF haloes. The circles on the bottom right panel represent the virial sphere of the main halo and its subhaloes defined using the MSM method. We point out that the largest FOF halo in the cluster (shown in Fig. A.2) includes both the main MSM halo and its largest subhalo. It means that from the FOF point of view the major merger between halo and largest subhalo has occurred as well. We also see that the 15 extra FOF haloes are detected as MSM subhaloes of the main halo. As a matter of fact this cluster of 16 FOF haloes is identified with a single structure tree containing 23 subhaloes by AdaptaHOP/MSM.

A.2.2 Statistics

Turning now to the issue of the identification of several FOF haloes with a single AdaptaHOP halo, we use the MSM method to check how often FOF haloes are detected as subhaloes rather than main haloes.

$\begin{figure} \par\includegraphics[width=9cm,clip]{11787fA8.eps} \end{figure}$

Figure A.8:

Cross identification of FOF haloes with less than 100 particles at z=0 and MSM haloes or subhaloes (see text Sect. 2.1.3 for details). In the first case (solid curves), only one FOF halo is allowed to be identified with a MSM halo or subhalo. In the second case (dashed curves), several FOF haloes can be identified with a single MSM halo or subhalo. The error bars correspond to Poisson uncertainties. The vertical dotted line corresponds to the 20 particles detection threshold.

Open with DEXTER

As we did in Sect. A.1.2 of this appendix, we now proceed to check that the conclusions we have just drawn for a single, well resolved halo are valid for the whole distribution of haloes, and especially for the poorly resolved ones. In order to do so, for each time output of the N-body simulation, we check whether each halo detected by the FOF is detected either as a halo or as a subhalo with the MSM. This data is presented in Fig. A.8 for all haloes between $1.66\times 10^{11}$ $M_{\odot }$ and $8.33\times 10^{11}$ $M_{\odot }$ (i.e. 20 to 100 particles). The solid curves in this figure are obtained when we allow only one FOF halo to be cross-identified with a MSM halo or subhalo. The percentage of FOF haloes identified as AdaptaHOP haloes (i.e. containing their subhaloes) is the same as in Fig. A.5, but the main difference is that now the smallest FOF haloes can be identified as subhaloes of larger haloes instead of having to be cross-identified with a single small AdaptaHOP halo. So the new information that we get from this figure, as compared to Fig. A.5 is that the percentage of FOF haloes identified as MSM subhaloes (triangles) is quite small (5%) at the 20 particles mass threshold, increases until $3\times 10^{11}$ $M_{\odot }$ and remains steady around the 10% level up to $8\times 10^{11}$ $M_{\odot }$ . When we allow for the fact that several FOF haloes can be found in one MSM halo or subhalo we obtain the dashed curves, i.e. if one MSM halo or subhalo was cross-identified with at most one FOF halo the dashed and solid curves would perfectly match. The interesting result here is that this actually happens to be the case for all but the lowest FOF halo mass bins for MSM subhaloes (triangles), but not for MSM main haloes (diamonds) which means that small FOF haloes are preferentially fused into the smooth component of the main halo found by the MSM method rather than with MSM subhaloes.

To quantify this behaviour a bit further, we plot in Fig. A.9, the average number of FOF haloes per MSM main halo. This figure was obtained in the same way as Fig. A.6 except that we excluded FOF haloes cross-identified with MSM subhaloes. We notice that the average number of FOF haloes per MSM halo is close to 1 until we consider MSM haloes with masses greater than 10¹³ $M_{\odot }$ . Then the average number of FOF haloes per MSM halo rises quickly as a function of MSM halo mass. At $4\times 10^{14}$ $M_{\odot }$ we obtain on average 17.6 FOF haloes per MSM haloes. This means that small FOF haloes (less than 50 particles or so) are preferentially blended with the smooth main halo component of group to cluster size main MSM haloes: they are not dense enough to be detected as separate local maxima which is the necessary condition to be identified as subhaloes.

$\begin{figure} \par\includegraphics[width=8.6cm,clip]{11787fA9.eps} \end{figure}$	Figure A.9: Number of FOF haloes at redshift 0 whose particles are found in a single main MSM halo (i.e. in an AdaptaHOP halo without its MSM subhaloes). The error bars correspond to the mean quadratic dispersion. The vertical dotted line corresponds to the 20 particles detection threshold. The diamond and the square correspond to the examples shown in Figs. A.1 and A.2 respectively.
Open with DEXTER

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.