Table B.1.
36 MBBH Candidates results
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) |
|---|---|---|---|---|---|---|---|---|---|---|
| Identifier | Fitted | 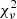 |
G.L.S. | Ar | Ag | Estimated | z | Log M | Pr | R |
| Period | (d.o.f) | Period / p-value | (mag) | (mag) | separation | (M⊙) | (days) | |||
| (days) | (days) | (mpc) | ||||||||
| J141425+171811 | 2017 ± 43 | 4.4 (112) | 2017 / 0.06 | 0.25 ± 0.01 | 0.40 ± 0.02 | 6.0 | 0.41 | 8.1 ± 0.4 | 1994 ± 180 | 7.84 |
| QNZ3:54 | 1765 ± 34 | 2.9 (132) | 1765 / 0.09 | 0.15 ± 0.01 | 0.18 ± 0.02 | 8.3 | 1.4 | 9.1 ± 0.1 | 1724 ± 123 | 3.49 |
| J133654+171040 | 1278 ± 16 | 5.3 (159) | 1278 / 0.002 | 0.13 ± 0.01 | 0.15 ± 0.01 | 7.6 | 1.23 | 9.2 ± 0.1 | 1262 ± 62 | 3.12 |
| J122616+504205 | 1508 ± 55 | 1.6 (192) | 1508 / 0.003 | 0.17 ± 0.02 | 0.21 ± 0.02 | 2.9 | 0.75 | 7.6 ± 1.2 | 1515 ± 110 | 1.95 |
| J092911+203708 | 1768 ± 27 | 2.6 (140) | 1768 / 0.007 | 0.17 ± 0.02 | 0.18 ± 0.02 | 10.9 | 1.84 | 9.6 ± 0.2 | 1755 ± 167 | 1.36 |
| J152157+181018 | 2093 ± 78 | 2.7 (151) | 2092 / 0.19 | 0.12 ± 0.01 | 0.12 ± 0.01 | 4.6 | 0.73 | 7.9 ± 1.3 | 2186 ± 238 | 1.11 |
| J133807+360220 | 2073 ± 42 | 9.5 (128) | 2072 / 0.32 | 0.19 ± 0.01 | 0.25 ± 0.01 | 9.9 | 1.19 | 9.1 ± 0.1 | 2037 ± 253 | 0.65 |
| J114857+160023 | 1748 ± 40 | 2.5 (144) | 1749 / 0.144 | 0.10 ± 0.01 | 0.11 ± 0.01 | 12.8 | 1.22 | 9.6 ± 0.2 | 1774 ± 162 | 0.57 |
| J130040+172758 | 2068 ± 53 | 3.0 (136) | 2068 / 0.16 | 0.27 ± 0.03 | 0.29 ± 0.03 | 9.4 | 0.86 | 8.9 ± 0.1 | 2129 ± 407 | 0.40 |
| J131626+390752 | 1532 ± 50 | 2.2 (217) | 1531 / 0.07 | 0.17 ± 0.02 | 0.18 ± 0.02 | 5.1 | 2.42 | 8.9 ± 0.1 | 1529 ± 136 | 0.27 |
| J124838+364453 | 1700 ± 50 | 1.8 (206) | 1699 / 0.07 | 0.20 ± 0.03 | 0.24 ± 0.03 | 8.7 | 2.44 | 9.5 ± 0.2 | 1704 ± 154 | 0.26 |
| J082716+490534 | 1646 ± 20 | 4.1 (138) | 1645 / 0.001 | 0.41 ± 0.02 | 0.37 ± 0.02 | 10.1 | 0.68 | 9.1 ± 0.2 | 1632 ± 227 | 0.25 |
| J172656+600348 | 1924 ± 66 | 8.2 (109) | 1925 / 0.66 | 0.1 ± 0.01 | 0.1 ± 0.01 | 13.6 | 0.99 | 9.5 ± 0.7 | 1813 ± 129 | 0.22 |
| J160730+144904 | 1577 ± 22 | 8.8 (160) | 1576 / 0.08 | 0.1 ± 0.01 | 0.14 ± 0.01 | 11.0 | 1.8 | 9.7 ± 0.1 | 1584 ± 177 | 0.18 |
| J104941+085548 | 1263 ± 15 | 4.1 (171) | 1263 / 0.12 | 0.10 ± 0.01 | 0.10 ± 0.01 | 8.3 | 1.18 | 9.3 ± 0.1 | 1291 ± 91 | 0.18 |
| J131909+090814 | 1057 ± 13 | 3.3 (144) | 1057 / 0.0001 | 0.13 ± 0.01 | 0.15 ± 0.01 | 4.8 | 0.88 | 8.6 ± 0.3 | 1379 ± 96 | 0.17 |
| UM211 | 2162 ± 54 | 5.7 (123) | 2165 / 0.08 | 0.12 ± 0.01 | 0.14 ± 0.01 | 1.99 | 2207 ± 324 | 0.17 | ||
| J121457+132024 | 2405 ± 73 | 4.7 (139) | 2404 / 0.44 | 0.16 ± 0.02 | 0.17 ± 0.02 | 12.6 | 1.49 | 9.4 ± 0.2 | 2394 ± 688 | 0.15 |
| J091501+460937 | 1793 ± 51 | 1.7 (190) | 1792 / 0.04 | 0.16 ± 0.03 | 0.21 ± 0.03 | 6.6 | 1.77 | 8.9 ± 0.1 | 1825 ± 535 | 0.14 |
| J115445+244646 | 1548 ± 34 | 2.6 (200) | 1548 / 0.007 | 0.22 ± 0.02 | 0.23 ± 0.02 | 11.7 | 0.8 | 9.4 ± 0.3 | 1310 ± 190 | 0.10 |
| J082926+180020 | 1652 ± 45 | 2.2 (141) | 1651 / 0.34 | 0.15 ± 0.02 | 0.17 ± 0.02 | 6.1 | 0.81 | 8.5 ± 0.1 | 1639 ± 333 | 0.06 |
| J083349+232809 | 1243 ± 15 | 11.2 (182) | 1243 / 0.30 | 0.10 ± 0.01 | 0.12 ± 0.01 | 8.3 | 1.15 | 9.3 ± 0.2 | 1270 ± 103 | 0.06 |
| J134855-032141 | 2101 ± 72 | 3.2 (136) | 2100 / 0.09 | 0.10 ± 0.01 | 0.10 ± 0.01 | 12.5 | 2.1 | 9.7 ± 0.1 | 2112 ± 495 | 0.05 |
| J102255+172155 | 1336 ± 22 | 3.4 (164) | 1336 / 0.05 | 0.11 ± 0.01 | 0.13 ± 0.02 | 5.6 | 1.06 | 8.7 ± 0.3 | 1929 ± 393 | 0.05 |
| UM234 | 2375 ± 86 | 8.3 (110) | 2323 / 0.32 | 0.15 ± 0.01 | 0.15 ± 0.01 | 12.7 | 0.73 | 9.1 ± 0.1 | 1696 ± 273 | 0.04 |
| J155449+084204 | 1647 ± 25 | 7.2 (155) | 1646 / 0.29 | 0.10 ± 0.01 | 0.10 ± 0.01 | 7.1 | 0.79 | 8.7 ± 0.2 | 1679 ± 129 | 0.04 |
| J081133+065558 | 1335 ± 22 | 3.9 (146) | 1335 / 0.19 | 0.15 ± 0.01 | 0.19 ± 0.02 | 9.1 | 1.27 | 9.4 ± 0.1 | 1385 ± 225 | 0.03 |
| J100641+253110 | 1851 ± 182 | 2.1 (200) | 1857 / 0.46 | 0.11 ± 0.03 | 0.15 ± 0.03 | 10.9 | 1.13 | 9.3 ± 0.5 | 2053 ± 491 | 0.03 |
| J115141+142156 | 1332 ± 26 | 3.5 (134) | 1331 / 0.13 | 0.11 ± 0.01 | 0.12 ± 0.01 | 6.7 | 1.00 | 8.9 ± 0.2 | 1310 ± 191 | 0.02 |
| J155647+181531 | 1370 ± 29 | 3.0 (153) | 1370 / 0.24 | 0.1 ± 0.01 | 0.15 ± 0.02 | 7.4 | 1.50 | 9.2 ± 0.1 | 1392 ± 176 | 0.02 |
| J123527+392824 | 1863 ± 77 | 3.5 (203) | 1861 / 0.13 | 0.16 ± 0.01 | 0.18 ± 0.01 | 6.2 | 2.15 | 8.9 ± 0.1 | 2008 ± 412 | 0.014 |
| J113142+304139 | 1604 ± 71 | 1.8 (216) | 1603 / 0.41 | 0.10 ± 0.02 | 0.11 ± 0.02 | 7.9 | 2.34 | 9.4 ± 0.3 | 1609 ± 161 | 0.012 |
| J102625+295907 | 1634 ± 63 | 1.6 (213) | 1633 / 0.15 | 0.10 ± 0.01 | 0.11 ± 0.01 | 8.4 | 3.39 | 9.7 ± 0.1 | 1667 ± 300 | 0.01 |
| PKS 0157+011 | 1127 ± 26 | 4.0 (165) | 1127 / 0.53 | 0.05 ± 0.01 | 0.06 ± 0.01 | 5.7 | 1.16 | 8.9 ± 0.1 | 1137 ± 239 | 0.008 |
| J043526-164346 | 1304 ± 12 | 14.3 (127) | 1304 / 0.10 | 0.17 ± 0.01 | 0.18 ± 0.01 | 0.01 | 1300 ± 250 | 0.008 | ||
| J122728+322508 | 1655 ± 86 | 2.4 (189) | 1652 / 0.48 | 0.06 ± 0.01 | 0.06 ± 0.01 | 5.3 | 0.75 | 8.3 ± 0.3 | 1694 ± 284 | 0.007 |
Notes. 36 good massive black hole binary candidates showing a similar periodicity in both CRTS and ZTF observations. Columns show: (1): The identifier of the sources. (2): The fitted periodicity to combined CRTS and ZTF data and the 3σ error. (3): The reduced chi-squared value of the fitted periodicity to combined CRTS and ZTF data (and the number of degrees of freedom). (4): The period corresponding to the maximum peak in the Generalized Lomb-Scargle periodogram and the p-value computed using the method described in 2.6 (5): The fitted amplitude of the ZTF periodicity in the r-band and the 3σ error. (6): The fitted amplitude of the ZTF modulation in the g-band and the 3σ error. (7): The estimated separation of the sources calculated from the periodicity corrected with redshift and mass estimate (assuming it corresponds to the total MBBH mass and that the two black holes are of similar mass). (8): the redshift z of the candidates. (9): Logarithm of the mass estimated for the central black hole(s) (Rakshit et al. 2020). (10): The period estimated using sinusoidal variability modulated by a red noise model. Uncertainties are given in a 3σ confidence interval. Also, VanderPlas (2018) explains that Gaussian error bars should be avoided in the context of a periodogram analysis, so uncertainties of identified Lomb-Scargle periods are not specified. (11) Bayes ratio comparing the DRW+Sine model to the DRW model.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


