EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 698 (June 2025) A&A, 698 (2025) A216 Full HTML
Open Access
Issue
A&A
Volume 698, June 2025
Article Number A216
Number of page(s) 9
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202554461
Published online 17 June 2025

© The Authors 2025

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Massive stars are responsible for the production of roughly half of the solar abundances of the elements in the periodic table (see, e.g., Prantzos et al. 2018; Kobayashi et al. 2020). During their lives, they transform their initial chemical composition, mostly dominated by H and He, into increasingly heavy nuclear species by means of nuclear reactions, until a compact Fe core forms surrounded by layers of materials with variable chemical composition. Massive stars evolve by alternating contraction phases of the core, in which the temperature rises, to central burning phases, where an element is converted into a heavier species. Once a given fuel is exhausted in the center of the star, the contraction resumes, the burning of that fuel shifts outward in mass (shell burning), and a heavier fuel is ignited in the center (e.g., Woosley et al. 2002). During the spectacular end of their lives as core-collapse supernovae (CCSNe) the products of the hydrostatic evolution contained in these layers are partly reprocessed by explosive nucleosynthesis, therefore, the CCSN ejecta contain the contribution from the nuclear burning that occurred both during the presupernova evolution and during the explosion itself (Rauscher et al. 2002; Pignatari et al. 2016; Limongi & Chieffi 2018; Roberti et al. 2024a; Boccioli & Roberti 2024).

In the last days of their lives, massive stars can experience the ingestion of carbon (C) and neon (Ne) into the oxygen (O) burning shell, where convection, in the form of turbulent motions, vigorously mixes out the burning products and brings in further fuel (Rauscher et al. 2002; Meakin & Arnett 2006; Ritter et al. 2018a; Andrassy et al. 2020; Rizzuti et al. 2024). This convective-reactive event is referred to as a “C-O shell merger” and can result in the formation of a large mixed convective region, where C-rich material is exposed to the high temperatures typical of O burning. The resulting peculiar nucleosynthetic signature of this merger has been shown to survive reprocessing by explosive nucleosynthesis (Rauscher et al. 2002; Chieffi & Limongi 2017; Ritter et al. 2018b; Roberti et al. 2023, 2024b). The variety of products from the C-O shell merger are thus ejected into the stellar surroundings, and contribute to the chemical enrichment of the interstellar medium. Furthermore, this peculiar merger event may create asymmetries in the stellar structure of the supernova progenitor and cause a significant drop in density at the interface between the Si and O layers. These effects could potentially facilitate the CCSN explosion and influence the oscillation modes of gravitational waves emitted during the explosion (see, e.g., Couch & Ott 2013; Müller et al. 2016; Boccioli et al. 2023; Torres-Forné et al. 2019; Zha et al. 2024; Laplace et al. 2025).

Carbon-oxygen shell mergers have been found in theoretical, spherically symmetric (1D) stellar models, independently from the code used to produce the simulations, generally in massive stars with an initial mass 12≤Mini(M⊙)≤25. Their occurrence is also supported by the rather few multidimensional simulations of the final stages of the evolution of massive stars (see, e.g., Meakin & Arnett 2006; Mocák et al. 2018; Andrassy et al. 2020; Yadav et al. 2020). For example, Rizzuti et al. (2022, 2023) showed that O and Ne convective shells in a 3D model naturally tend to entrain some material from the layers at the edges of the convective zone. This process facilitates the ingestion of material from the adjacent burning shell and may trigger a convective-reactive event (Rizzuti et al. 2024). However, direct, or even indirect, observational evidence of the existence in nature of C-O shell mergers is still lacking. Ritter et al. (2018b) suggest that a fraction of massive stars in a stellar population is required to undergo C-O mergers to reproduce the Galactic abundances of the odd-Z elements, such as P, K, and Sc. However, this analysis was limited to a parametric study based on the ejecta of a single nonrotating 15 M⊙ stellar model of solar metallicity.

Here we present a study that provides us with a new method to predict the occurrence of C-O shell merger in 1D stellar models. Furthermore, we demonstrate that observations of old stars from the early Universe show the effect of the C-O mergers that occurred in the first generation of massive stars.

2. Conditions for C-O mergers

The advanced burning stages of a massive star are controlled by the extension in mass of the He-exhausted core, rich in C and O (the CO core mass, or MCO), and the 12C mass fraction left in the center of the star (XC12) after the central He burning phase (Chieffi & Limongi 2013; Limongi & Chieffi 2018). The CO core mass has the same role in the advanced burning phases as the initial mass does in the main sequence of the star. Since all the following burning phases take place within the CO core, its size (both in mass and in radius) determines the region available for the development and evolution of the various C, Ne, O, and Si burning shells. In a smaller CO core, these burning shells are closer to each other than that in a larger CO core. The 12C abundance controls the amount of fuel available for core C burning and, more importantly, the number and the extent of the C-burning shells that contribute to sculpt the final density and entropy profiles at the moment of the core collapse. In particular, a lower 12C abundance left by He burning results in a lower 20Ne abundance1 and, eventually, in a smaller entropy discontinuity at the interfaces between the O, Ne, and C convective shells (Roberti et al. 2024b). In general, an entropy discontinuity acts as a barrier sustained by nuclear burning, which prevents the underlying shell from penetrating into the overlying one. As the C (and Ne) abundance decreases, the strength of this barrier decreases accordingly. It follows that a small CO core together with a low 12C abundance at the end of He burning would, in principle, favor the penetration of the O-burning region into the C-rich layers.

To systematically study this prediction on the occurrence of C-O shell mergers in theoretical calculations, we collected 209 published 1D models with initial masses between 9.2 and 25 M⊙, initial metallicity between 0 and 0.05, and initial rotation velocity between 0 and 800 km s−1 (Rauscher et al. 2002; Pignatari et al. 2016; Sieverding et al. 2018; Ritter et al. 2018a; Limongi & Chieffi 2018; Brinkman et al. 2019, 2021; Limongi et al. 2024; Jeena et al. 2024; Roberti et al. 2024a, b, see Appendix A for a brief overview of the main properties of the sets of models considered), and present their MCO and XC12 in Fig. 1. Out of 209 models, 41 present a C-O shell merger. While this number constitutes a representative percentage of massive star models with a C-O merger in the literature, it is not necessarily representative of a real stellar population because it is not weighted over an initial mass function, nor over an initial rotation velocity and metallicity distribution. Significantly, we find that the majority of the models with a C-O merger fall in an identifiable region of the MCO-XC12 diagram, the gray area in Fig. 1. Most of the models without a C-O shell merger are not located in this area (77%, 132 out of 172). Some exceptions are present, which is not surprising and mostly due to the large uncertainty introduced by the adoption of a different physics input (e.g., reaction rates, opacity, mass loss prescriptions) and mixing treatments (e.g., convection and semi-convection parameters, definition of convective boundary mixing, rotational mixing) in every set of models, which can affect the exact parameter space for C-O shell merger events. For example, using the Schwarzschild criterion to define the convective O-shell boundary permits a deeper penetration into the Ne-C region, whereas the Ledoux criterion would limit the extent of the convective zone at the chemical discontinuity (Clayton 1968; Kippenhahn & Weigert 1990). As another example, the adoption of a larger 12C(α,γ)16O rate would result in a lower XC12, but approximately the same MCO. The quantitative impact of these uncertainties can only be assessed by running large grids of models, each varying a single input parameter, all of which approaches are extremely costly both in terms of time and resources.

thumbnail Fig. 1.

Carbon-oxygen core mass (MCO) versus the central 12C mass fraction abundance (XC12) at the end of central He burning phase. The different colors identify the different sets of models (see side legend) where RAU is Rauscher et al. (2002); PGN is Pignatari et al. (2016); SIE is Sieverding et al. (2018); RIT is Ritter et al. (2018a); L&C is Limongi & Chieffi (2018); BRI is Brinkman et al. (2019, 2021); LIM is Limongi et al. (2024); RLC is Roberti et al. (2024a); ROB is Roberti et al. (2024b); and KEP is Jeena et al. (2024). Different symbols identify different initial masses (see top legend). Models with and without a C-O shell merger are represented by filled and empty symbols, respectively. The two gray shaded areas represent the covariant confidence ellipses relative to the models with C-O mergers within one and two standard deviations, σ, centred at MCO = 4.02 and XC12 = 0.176.

Figure 1 demonstrates that the occurrence of a C-O shell merger depends on the outcomes of the central He burning phase (specifically, MCO and XC12), and only indirectly on initial mass and metallicity. We find that 90% of models that undergo a C-O merger have XC12 <0.277 and MCO <4.90 M⊙, with average values MCO = 4.02 M⊙ and XC12 = 0.176. Within this parameter space, we identify 79 models in total, of which 38 do not exhibit a C-O merger. This indicates that the threshold values for XC12 and MCO are a necessary but not sufficient condition to determine whether the merger occurs and that, even when the CO core mass and central carbon abundance fall within the expected range, the likelihood of a merger remains around 50%, which suggests that additional mechanisms may play a role in triggering the merger.

While both rotating and nonrotating models are included in the figure, this is not a criterium for the merger. In fact, rotationally induced secular instabilities do not have enough time to affect the latest stages of evolution. Consequently, because of the timescales, the rotation does not influence the mixing coefficient at the interface of the two shells and thus does not directly cause the shell interaction, although it affects it indirectly via changing MCO and XC12 (e.g., Chieffi & Limongi 2013), similarly to other stellar parameters such as the initial mass and metallicity.

3. Nuclear reactions and nucleosynthesis in a C-O merger

During a C-O shell merger, C-burning products are transported to the base of the O-burning shell, where they interact with the products of O burning at temperatures significantly higher than those typical of C burning. This interaction leads to a slight reduction in the final abundances of the C-burning products (such as 23Na, 24Mg, and 27Al) and an enhancement of those of the O-burning products (such as 28Si, 31P, and 32S). Fig. 2 shows this occurrence in the case of a 15 M⊙ star at solar metallicity. The injection of 12C and fresh 16O at approximately 2.6–2.8 GK (typical temperature of O-shell burning) leads to the activation of heavy ion fusion reactions (such as 12C+12C, 12C+16O, and 16O+16O) together with the 20Ne+γ reaction, which suddenly release a large number of light particles, mostly p and α. The O-burning products capture the free p and α particles, leading to a substantial production of intermediate odd-Z elements (such as Cl, K, and Sc). For example, in these models 34S is the seed for p and α captures that produce 35Cl, 39K, and 45Sc via 34S(p,γ)35Cl, 34S(α,γ)38Ar and 38Ar(α,γ)42Ca(α,p)45Sc, or 38Ar(p,γ)39K. The enhanced number of α captures may also lead to the production of 44Ti, which is considered to be mostly produced in explosive conditions, with a significant contribution coming from neutrino-driven explosions (see, e.g., Tur et al. 2010; Chieffi & Limongi 2017; Sieverding et al. 2023; Wang & Burrows 2024). The production of these nuclei is independent from the metallicity, being predominantly primary, that is, the result of the interaction of direct products of the O- and C-burning processes. Additionally, under these conditions, the efficient activation of the proton captures (such as those leading to the production of 35Cl and 39K) can significantly impact the nuclear energy generation at the base of the O-burning shell. Therefore, the use of an appropriately detailed nuclear network is mandatory when calculating the evolution of models experiencing C-O shell mergers.

thumbnail Fig. 2.

Comparison between the abundances before (dashed lines) and after the C-O shell merger (solid lines) in the RIT 15 M⊙ model at solar metallicity (see Ritter et al. 2018a, for a detailed description of the model). The upper panel shows the effect of the merger on the major fuels. The lower panel shows instead the effect of the merger on some key C- and O-burning products and selected odd-Z isotopes (see text). The vertical dotted lines represent the location of the edges of the shells before the C-O shell merger. The light gray area is the region modified by the merger, the dark gray area represents the untouched deeper layers of the star after the merger, i.e., the Fe core and the Si shell.

At these high temperatures, the reactions start tending to an equilibrium and therefore the inverse reactions start to be efficient, in particular the photodissociation processes. As a consequence, some secondary processes (i.e., depending on pre-existing seeds in the initial composition of the star) may occur. This is the case for the production of p-nuclei (35 neutron-deficient isotopes beyond iron, like 92Mo and 130Ba) via the γ–process, and weak s-process peak elements (such as Sr, Y, and Zr) from photodisintegrations of heavier isotopes, both previously produced by the s–process in He core and C-shell burning or from the unburned pristine material (Rauscher et al. 2002; Ritter et al. 2018b; Roberti et al. 2023, 2024b). This unique nucleosynthetic signature is mostly preserved, even after the explosive nucleosynthesis, due to the extensive radius of the mixed convective zone created by the merger (see Fig. 3, Roberti et al. 2023, 2024b, and references therein)2.

thumbnail Fig. 3.

As Fig. 2, but for the presupernova (dashed lines) and postsupernova (solid lines) stages, with the inclusion of 56Ni. The supernova explosion was modeled with a semianalytical approach, using the Sedov blast wave (SBW) solution for the determination of the peak velocity of the shock throughout the stellar structure and the remnant mass prescription from Fryer et al. (2012) (see Pignatari et al. 2016; Ritter et al. 2018a; Roberti et al. 2024c, for a detailed description of the explosion method). The gray bands in the plots mark each explosive burning stage in the corresponding mass coordinate (i.e., complete and incomplete Si burning, explosive O, Ne, and C burning). The vertical dotted line represents the mass-cut that divides the supernova ejecta from the remnant mass. The variation of 24Mg and 32S in the He shell represents the activation of the α capture chain in the explosive He burning (Pignatari et al. 2023).

4. Stellar archaeology

As demonstrated above, the occurrence of C-O shell mergers is independent from the metallicity. Therefore we can use the observations of the earliest generation of low-mass stars to look for traces of pollution from C-O merger events in primordial massive stars. This is allowed because the interstellar cloud where most of the metal poor stars that we can still observe today were born, is thought to have experienced pollution by one or very few core-collapse supernova explosions. Therefore the observation of the surface abundances of metal poor stars still reflect the pristine composition of the gas enriched by the first supernovae.

We explored the use of [K/Mg] and [Sc/Mg]3 as tracers for C-O mergers. As mentioned above, K and Sc are two odd-Z elements abundantly produced in a C-O shell merger, and which can be observed even at extremely low metallicity (Ritter et al. 2018b). Mg, an α element typically produced by massive stars, can also be observed at low metallicity, but it is not significantly affected by the C-O merger. Figure 4 presents the [K/Mg] and [Sc/Mg] ratios as a function of the initial metallicity for most of the models shown in Fig. 1, that is, those that provided CCSN yields. We furthermore included two other sets of models (NOM Nomoto et al. 2013 and PUSH Curtis et al. 2019; Ebinger et al. 2020), which, conversely, did not appear in Fig. 1 because the MCO and XC12 values are not available. In most of the models with C-O shell mergers, both the [K/Mg] and [Sc/Mg] are positive (i.e., their absolute ratios have from solar to super-solar values), while in most of the models without C-O shell mergers, they are negative instead (i.e., their absolute ratios have sub-solar values), especially at low metallicity, where the initial abundances of these elements are negligible. The only exceptions are the [Sc/Mg] ratios of the PUSH models, which include neutrino interactions in the explosion. The impact of neutrinos is particularly important for the α-rich freeze out and explosive Si burning and allows these models to reach [Sc/Mg] ≳0 without a C-O shell merger. For further discussion of this dataset, see Appendix B.

thumbnail Fig. 4.

[K/Mg] (upper panel) and [Sc/Mg] (lower panel) versus the initial metallicity. The adopted solar reference is from Asplund et al. (2009). The different colored labels identify each set of models (see bottom legend): RAU Rauscher et al. (2002); NOM Nomoto et al. (2013); RIT Ritter et al. (2018a); L&C Limongi & Chieffi (2018); PUSH Ebinger et al. (2020); ROB Roberti et al. (2024b); RLC Roberti et al. (2024a); KEP Jeena et al. (2024). Different symbols identify different initial masses (see top legend). Models with and without a C-O shell merger are represented by a filled and an empty symbol, respectively.

Figure 5 shows a comparison between the model predictions and the observations at extremely low metallicity (with [Fe/H] ≤−3, taken from JINAbase (Abohalima & Frebel 2018), see Appendix C). To ensure a meaningful comparison between the observations and progenitor candidates from the sample presented in Fig. 4, we only included models with a C-O shell merger (in which the nucleosynthesis of Mg, K, and Sc is primary) and models with an initial metallicity lower than 10−5 (corresponding to [Fe/H]≈−3). In other words, we did not include higher metallicity models without a merger, as their ratios would be close to solar primarily due to their initial composition rather than the effects of nucleosynthesis. The observations show that the [K/Mg] ratio is centered around the solar value, whereas the [Sc/Mg] ratio is slightly sub-solar. In the plot, the gray shaded area represents the average [K/Mg] and [Sc/Mg] ratios, including an error band. This average data point divides the models into three subclasses: models without a C-O shell merger in the lower left quadrant, models with a C-O shell merger in the upper right quadrant, and models without C-O shell mergers but incorporating neutrino physics in the explosion, in the upper left quadrant. The observed data fall in a junction region between these three populations, making it difficult to identify any single population as the definitive progenitor of these second-generation stars. However, it becomes clear that a single component alone cannot reproduce the observations, suggesting that a nucleosynthetic contribution from C-O shell mergers is essential even at extremely low metallicity. Currently, it is challenging to estimate the required fraction of C-O merger ejecta needed to align the interstellar cloud composition with the observed values, as this may heavily depend on the selection of progenitors without C-O shell mergers or even on the galactic chemical evolution (GCE). Nevertheless, this analysis emphasizes the need for more extensive low-metallicity observations and provides a framework for interpreting the chemical signatures of extremely low-metallicity stars based on their position within the quadrants.

thumbnail Fig. 5.

Ratios of [K/Mg] versus [Sc/Mg] from those models selected from Fig. 4 that have either a C-O shell merger or initial metallicity Zini<10−5. The adopted solar reference is from Asplund et al. (2009). The different colored labels identify each set of models as in Fig. 4 (see side legend). Different symbols identify different initial masses (see top legend). Models with and without a C-O shell merger are represented by a filled and empty symbol, respectively. The blue star symbols are observations of low-mass stars of low metallicity taken from JINAbase (Abohalima & Frebel 2018) with [Fe/H] < −3. A representative error bar for the observation data is shown, as taken from Roederer et al. (2014). The dashed vertical and horizontal lines represent the average [K/Mg] and [Sc/Mg] ratios from the observations. The gray shaded area represents the representative error bar for the average data point.

5. Discussion

One of the largest sources of uncertainty in stellar models is the treatment of convection and the definition of convective borders. In this context, constraints from asteroseismology (Aerts et al. 2003; Aerts 2021; Burssens et al. 2023; Brinkman et al. 2024) and indications from multidimensional simulations of burning shells (Rizzuti et al. 2022, 2023, 2024) are starting to provide valuable tools to improve the future generation of 1D stellar modeling. At first glance, both seem to lead to the conclusion that mixing is more efficient at the edges of convection zones than current 1D models predict. This suggests that C-O shell mergers are a relevant feature of massive stars, and more frequent than expected.

Another significant source of uncertainty is the determination of the reaction rates that govern the latest stages of the evolution, and in particular the 12C(α,γ)16O,12C+12C, and, in the case of C-O shell mergers, 12C+16O and light particle capture reaction rates. The 12C(α,γ)16O rate is already rather well constrained by current extrapolations of available experimental data, with an estimated uncertainty of approximately 20% (deBoer et al. 2017). The 12C+12C reaction rate is much more uncertain than the 12C(α,γ)16O rate and its variation can drastically change the convective history of the C-burning shell and thus even affect the final fate of the star (see, e.g., Pignatari et al. 2013; Chieffi et al. 2021). The 12C+16O reaction rate can significantly contribute to the energy generation during a C-O shell merger, especially for a low rate of C ingestion in the O shell, and, as the 12C+12C reaction rate, it is still rather uncertain (Andrassy et al. 2020). Future and ongoing measures of the 12C(α,γ)16O and the heavy ion fusion rates as in the case of the 12C+12C reaction at the Laboratory for Underground Nuclear Astrophysics (LUNA, Ananna et al. 2024) and the Jinping Underground Nuclear Astrophysics (JUNA, Kajino 2023), and of the 12C+16O reaction at the Laboratori Nazionali del Sud (INFN-LNS, Oliva et al. 2023), will help to constrain the evolutionary properties of stars approaching the CCSN stage.

While it is estimated that most massive stars are part of binary or even multiple systems, current modeling of massive star binaries is challenging and relies on significant approximations (e.g., Laplace et al. 2021; Brinkman et al. 2023). Still, we can use a simplified approach to discuss C-O shell mergers in binary systems. The primary effect of binarity is a significantly larger mass loss, which can reduce the size of the helium cores and, consequently, result in smaller MCO and higher XC12 compared to single stars (e.g., Brinkman et al. 2023). As demonstrated in Sect. 2, a higher XC12 would increase the entropy barriers between C-, Ne-, and O-burning shells, thereby hindering the penetration of the convective O shell into the C- and Ne-rich zones. Therefore, we can predict that binary stars will probably move outside to the right of the gray area of Fig. 1 and have less C-O shell mergers.

The GCE effects of C-O shell mergers on odd-Z elements have been indirectly confirmed by Prantzos et al. (2018), who utilized the yield set from Limongi & Chieffi (2018). In that dataset, all C-O shell mergers but one are found within rotating models (see Appendix A.3). The difference between the GCE results obtained without and with the inclusion of massive star rotating models reflects the effect of both rotation and C-O shell merger nucleosynthesis. In particular, the GCE with rotating massive stars improved the fit to observations for many elements compared to nonrotating models alone. Although it is challenging to disentangle the individual contributions of rotation and C-O shell mergers to the production of odd-Z elements like K and Sc, the role of C-O mergers in their synthesis is undoubtedly as important as the effect of rotation. Notably, their GCE results for Mg, K, and Sc at extremely low metallicity align with the gray shaded area in our Fig. 5, highlighting the significant contribution of C-O mergers in matching observed values.

6. Summary and conclusions

We studied the occurrence of C-O shell mergers in a large set of models published in the literature, with a wide range of initial mass, metallicity, and rotation velocity conditions. We found that, in spite of all the current uncertainties, the occurrence of C-O mergers does not depend on the initial mass, rotational velocity, or metallicity of the star; instead, it is influenced by the intrinsic properties of the star at the end of the He-burning phase, and the representative values of MCO and XC12 for models with a C-O merger are MCO <4.90 M⊙ and XC12 <0.277. This provides a method to predict the occurrence of these events from the first evolutionary phases with a likelihood of about 50%.

We furthermore showed that the nucleosynthesis during a C-O shell merger is dominated by the light particle captures, leading to a large production of odd-Z nuclear species, such as 31P, 39K, 45Sc, and of the radioactive species 44Ti, whose Galactic origin is still unclear and debated (e.g., Chieffi & Limongi 2017; Ritter et al. 2018b; Maas et al. 2022; Sieverding et al. 2023, and references therein). These reactions also have a significant impact on nuclear energy generation and they even dominate over the energy generated by the heavy ion fusions, such as 16O+16O and 12C+16O reactions.

Finally, using observational data from stellar archaeology, we have demonstrated that the impact of C-O shell mergers on nucleosynthesis was already visible in the early Universe. This highlights the significant contribution of these events to the chemical enrichment processes of galaxies and the origin of solar matter and the need to investigate them further. C-O shell mergers likely contributed to enrich the pre-Solar System material with odd-Z isotopes, such as the radioactive 40K, a fundamental heat source in the evolution of rocky planets like the Earth (Turcotte & Schubert 2002; Lugaro et al. 2018).

Data availability

The data of the models used to produce Fig. 1 and Fig. 5 are available on Zenodo (https://zenodo.org/records/15286771).

Acknowledgments

We thank the support from the NKFI via K-project 138031 and the Lendület Program LP2023-10 of the Hungarian Academy of Sciences. LR and MP acknowledge the support to NuGrid from JINA-CEE (NSF Grant PHY-1430152) and STFC (through the University of Hull’s Consolidated Grant ST/R000840/1), and ongoing access to viper, the University of Hull High Performance Computing Facility. LR acknowledges the support from the ChETEC-INFRA – Transnational Access Projects 22102724-ST and 23103142-ST and the PRIN URKA Grant Number prin_2022rjlwhn. This work was supported by the European Union’s Horizon 2020 research and innovation programme (ChETEC-INFRA – Project no. 101008324), and the IReNA network supported by US NSF AccelNet (Grant No. OISE-1927130). AS acknowledges this work performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. HEB has received funding from the KU Leuven Research Council (grant C16/18/005: PARADISE), from the Research Foundation Flanders (FWO) under grant agreement G089422N. This work has been partially supported by the Theory Grant “Evolution, nucleosynthesis and final fate of stars in the transition between AGB and Massive Stars” (1.05.12.06.04, PI M. Limongi) and by the Theroy Grant “Massive stars as cosmic clocks: shaping the evolution of infant galaxies” (1.05.24.05.07, PI M. Limongi) of the INAF Fundamental Astrophysics Funding Program 2022–2023. M. Limongi has also been partially supported by the World Premier International Research Center Initiative (WPI), MEXT, Japan. We acknowledge support from PRIN MUR 2022 (20224MNC5A), “Life, death and after-death of massive stars”, funded by European Union – Next Generation EU. M. Lugaro was also supported by the NKFIH excellence grant TKP2021-NKTA-64.

1

We note that 20Ne is the main product of C burning via 12C(12C,α)20Ne, 12C(12C,p)23Na(p,α)20Ne, and 16O(α,γ)20Ne.

2

Note that the peak temperature of the shock scales as T peak ∝ R * − 3 / 4 $ {\rm T_{peak}\propto R_*^{-3/4}} $, with R* radial coordinate of the star.

3

[X/Y] = log10(X/Y)-log10(X/Y)⊙.

References

  1. Abohalima, A., & Frebel, A. 2018, ApJS, 238, 36 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aerts, C. 2021, Rev. Mod. Phys., 93, 015001 [Google Scholar]
  3. Aerts, C., Thoul, A., Daszyńska, J., et al. 2003, Science, 300, 1926 [Google Scholar]
  4. Ananna, C., Barbieri, L., Boeltzig, A., et al. 2024, Universe, 10, 228 [Google Scholar]
  5. Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
  6. Andrassy, R., Herwig, F., Woodward, P., & Ritter, C. 2020, MNRAS, 491, 972 [NASA ADS] [CrossRef] [Google Scholar]
  7. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  8. Boccioli, L., & Roberti, L. 2024, Universe, 10, 148 [NASA ADS] [CrossRef] [Google Scholar]
  9. Boccioli, L., Roberti, L., Limongi, M., Mathews, G. J., & Chieffi, A. 2023, ApJ, 949, 17 [CrossRef] [Google Scholar]
  10. Brinkman, H. E., Doherty, C. L., Pols, O. R., et al. 2019, ApJ, 884, 38 [NASA ADS] [CrossRef] [Google Scholar]
  11. Brinkman, H. E., den Hartogh, J. W., Doherty, C. L., Pignatari, M., & Lugaro, M. 2021, ApJ, 923, 47 [NASA ADS] [CrossRef] [Google Scholar]
  12. Brinkman, H. E., Doherty, C., Pignatari, M., Pols, O., & Lugaro, M. 2023, ApJ, 951, 110 [CrossRef] [Google Scholar]
  13. Brinkman, H. E., Roberti, L., Kemp, A., et al. 2024, A&A, 689, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Buchmann, L. 1996, ApJ, 468, L127 [Google Scholar]
  15. Burssens, S., Bowman, D. M., Michielsen, M., et al. 2023, Nat. Astron., 7, 913 [NASA ADS] [CrossRef] [Google Scholar]
  16. Casey, A. R., & Schlaufman, K. C. 2015, ApJ, 809, 110 [Google Scholar]
  17. Caughlan, G. R., & Fowler, W. A. 1988, Atom. Data Nucl. Data Tables, 40, 283 [CrossRef] [Google Scholar]
  18. Chieffi, A., & Limongi, M. 2013, ApJ, 764, 21 [Google Scholar]
  19. Chieffi, A., & Limongi, M. 2017, ApJ, 836, 79 [NASA ADS] [CrossRef] [Google Scholar]
  20. Chieffi, A., Roberti, L., Limongi, M., et al. 2021, ApJ, 916, 79 [NASA ADS] [CrossRef] [Google Scholar]
  21. Clayton, D. D. 1968, Principles of Stellar Evolution and Nucleosynthesis (The University of Chicago Press) [Google Scholar]
  22. Cohen, J. G., Christlieb, N., Thompson, I., et al. 2013, ApJ, 778, 56 [Google Scholar]
  23. Couch, S. M., & Ott, C. D. 2013, ApJ, 778, L7 [NASA ADS] [CrossRef] [Google Scholar]
  24. Curtis, S., Ebinger, K., Fröhlich, C., et al. 2019, ApJ, 870, 2 [Google Scholar]
  25. Cyburt, R. H., Fields, B. D., & Olive, K. A. 2002, Astropart. Phys., 17, 87 [Google Scholar]
  26. deBoer, R. J., Görres, J., Wiescher, M., et al. 2017, Rev. Mod. Phys., 89, 035007 [NASA ADS] [CrossRef] [Google Scholar]
  27. Ebinger, K., Curtis, S., Ghosh, S., et al. 2020, ApJ, 888, 91 [NASA ADS] [CrossRef] [Google Scholar]
  28. Eggenberger, P., Meynet, G., Maeder, A., et al. 2008, Astrophys. Space Sci., 316, 43 [NASA ADS] [CrossRef] [Google Scholar]
  29. Freytag, B., Ludwig, H. G., & Steffen, M. 1996, A&A, 313, 497 [NASA ADS] [Google Scholar]
  30. Fröhlich, C., Hix, W. R., Martínez-Pinedo, G., et al. 2006a, New Astron. Rev., 50, 496 [CrossRef] [Google Scholar]
  31. Fröhlich, C., Hauser, P., Liebendörfer, M., et al. 2006b, ApJ, 637, 415 [Google Scholar]
  32. Fryer, C. L., Belczynski, K., Wiktorowicz, G., et al. 2012, ApJ, 749, 91 [Google Scholar]
  33. Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, eds. N. Prantzos, E. Vangioni-Flam, & M. Casse, 15 [Google Scholar]
  34. Heger, A., & Woosley, S. E. 2010, ApJ, 724, 341 [Google Scholar]
  35. Howes, L. M., Casey, A. R., Asplund, M., et al. 2015, Nature, 527, 484 [NASA ADS] [CrossRef] [Google Scholar]
  36. Howes, L. M., Asplund, M., Keller, S. C., et al. 2016, MNRAS, 460, 884 [NASA ADS] [CrossRef] [Google Scholar]
  37. Jeena, S. K., Banerjee, P., & Heger, A. 2024, MNRAS, 527, 4790 [Google Scholar]
  38. Kajino, T. 2023, Nucl. Sci. Tech., 34, 42 [Google Scholar]
  39. Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution (Berlin: Springer) [Google Scholar]
  40. Kobayashi, C., Leung, S. -C., & Nomoto, K. 2020, ApJ, 895, 138 [CrossRef] [Google Scholar]
  41. Kunz, R., Fey, M., Jaeger, M., et al. 2002, ApJ, 567, 643 [CrossRef] [Google Scholar]
  42. Laplace, E., Justham, S., Renzo, M., et al. 2021, A&A, 656, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Laplace, E., Schneider, F. R. N., & Podsiadlowski, P. 2025, A&A, 695, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Li, H. -N., Zhao, G., Christlieb, N., et al. 2015, ApJ, 798, 110 [NASA ADS] [CrossRef] [Google Scholar]
  45. Limongi, M., & Chieffi, A. 2018, ApJS, 237, 13 [NASA ADS] [CrossRef] [Google Scholar]
  46. Limongi, M., Roberti, L., Chieffi, A., & Nomoto, K. 2024, ApJS, 270, 29 [NASA ADS] [CrossRef] [Google Scholar]
  47. Lugaro, M., Ott, U., & Kereszturi, Á. 2018, Prog. Part. Nucl. Phys., 102, 1 [Google Scholar]
  48. Maas, Z. G., Hawkins, K., Hinkel, N. R., et al. 2022, AJ, 164, 61 [NASA ADS] [CrossRef] [Google Scholar]
  49. Meakin, C. A., & Arnett, D. 2006, ApJ, 637, L53 [CrossRef] [Google Scholar]
  50. Mocák, M., Meakin, C., Campbell, S. W., & Arnett, W. D. 2018, MNRAS, 481, 2918 [CrossRef] [Google Scholar]
  51. Müller, B., Viallet, M., Heger, A., & Janka, H. -T. 2016, ApJ, 833, 124 [CrossRef] [Google Scholar]
  52. Nomoto, K., Kobayashi, C., & Tominaga, N. 2013, ARA&A, 51, 457 [CrossRef] [Google Scholar]
  53. Oliva, A. A., Tumino, A., Soic, N., et al. 2023, Eur. Phys. J. Web Conf., 275, 02010 [Google Scholar]
  54. Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
  55. Pignatari, M., Hirschi, R., Wiescher, M., et al. 2013, ApJ, 762, 31 [NASA ADS] [CrossRef] [Google Scholar]
  56. Pignatari, M., Göbel, K., Reifarth, R., & Travaglio, C. 2016, Int. J. Mod. Phys. E, 25, 1630003 [NASA ADS] [CrossRef] [Google Scholar]
  57. Pignatari, M., Trueman, T. C. L., Womack, K. A., et al. 2023, MNRAS, 524, 6295 [Google Scholar]
  58. Placco, V. M., Frebel, A., Beers, T. C., et al. 2014, ApJ, 781, 40 [Google Scholar]
  59. Placco, V. M., Beers, T. C., Ivans, I. I., et al. 2015, ApJ, 812, 109 [NASA ADS] [CrossRef] [Google Scholar]
  60. Prantzos, N., Abia, C., Limongi, M., Chieffi, A., & Cristallo, S. 2018, MNRAS, 476, 3432 [Google Scholar]
  61. Rauscher, T., Heger, A., Hoffman, R. D., & Woosley, S. E. 2002, ApJ, 576, 323 [Google Scholar]
  62. Ritter, C., Herwig, F., Jones, S., et al. 2018a, MNRAS, 480, 538 [NASA ADS] [CrossRef] [Google Scholar]
  63. Ritter, C., Andrassy, R., Côté, B., et al. 2018b, MNRAS, 474, L1 [NASA ADS] [CrossRef] [Google Scholar]
  64. Rizzuti, F., Hirschi, R., Georgy, C., et al. 2022, MNRAS, 515, 4013 [NASA ADS] [CrossRef] [Google Scholar]
  65. Rizzuti, F., Hirschi, R., Arnett, W. D., et al. 2023, MNRAS, 523, 2317 [NASA ADS] [CrossRef] [Google Scholar]
  66. Rizzuti, F., Hirschi, R., Varma, V., et al. 2024, MNRAS, 533, 687 [Google Scholar]
  67. Roberti, L., Pignatari, M., Psaltis, A., et al. 2023, A&A, 677, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Roberti, L., Limongi, M., & Chieffi, A. 2024a, ApJS, 272, 15 [Google Scholar]
  69. Roberti, L., Limongi, M., & Chieffi, A. 2024b, ApJS, 270, 28 [NASA ADS] [CrossRef] [Google Scholar]
  70. Roberti, L., Pignatari, M., Fryer, C., & Lugaro, M. 2024c, A&A, 686, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Roederer, I. U., Sneden, C., Thompson, I. B., Preston, G. W., & Shectman, S. A. 2010, ApJ, 711, 573 [NASA ADS] [CrossRef] [Google Scholar]
  72. Roederer, I. U., Preston, G. W., Thompson, I. B., et al. 2014, AJ, 147, 136 [Google Scholar]
  73. Sieverding, A., Martínez-Pinedo, G., Huther, L., Langanke, K., & Heger, A. 2018, ApJ, 865, 143 [NASA ADS] [CrossRef] [Google Scholar]
  74. Sieverding, A., Müller, B., & Qian, Y. Z. 2020, ApJ, 904, 163 [NASA ADS] [CrossRef] [Google Scholar]
  75. Sieverding, A., Kresse, D., & Janka, H. -T. 2023, ApJ, 957, L25 [NASA ADS] [CrossRef] [Google Scholar]
  76. Siqueira Mello, C., Hill, V., Barbuy, B., et al. 2014, A&A, 565, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Skúladóttir, Á., Tolstoy, E., Salvadori, S., et al. 2015, A&A, 574, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Torres-Forné, A., Cerdá-Durán, P., Obergaulinger, M., Müller, B., & Font, J. A. 2019, Phys. Rev. Lett., 123, 051102 [CrossRef] [Google Scholar]
  79. Tur, C., Heger, A., & Austin, S. M. 2010, ApJ, 718, 357 [NASA ADS] [CrossRef] [Google Scholar]
  80. Turcotte, D. L., & Schubert, G. 2002, Geodynamics (Cambridge University Press) [CrossRef] [Google Scholar]
  81. Wang, T., & Burrows, A. 2024, ApJ, 962, 71 [NASA ADS] [CrossRef] [Google Scholar]
  82. Weaver, T. A., Zimmerman, G. B., & Woosley, S. E. 1978, ApJ, 225, 1021 [NASA ADS] [CrossRef] [Google Scholar]
  83. Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
  84. Xu, Y., Takahashi, K., Goriely, S., et al. 2013, Nucl. Phys. A, 918, 61 [Google Scholar]
  85. Yadav, N., Müller, B., Janka, H. T., Melson, T., & Heger, A. 2020, ApJ, 890, 94 [NASA ADS] [CrossRef] [Google Scholar]
  86. Zha, S., Eggenberger Andersen, O., & O’Connor, E. P. 2024, Phys. Rev. D, 109, 083023 [Google Scholar]

Appendix A: Models used in Figure 1

In the following, we list the prescriptions used for convection and for the 12C(α,γ)16O rate in the 209 models shown in Fig. 1. The adopted 12C+12C rate is instead the same for all the models and it is the one provided by Caughlan & Fowler (1988). We refer the reader to the cited papers for a more detailed description of each set of models.

A.1. The KEPLER models (RAU, SIE, KEP)

We considered models calculated with the KEPLER code from Rauscher et al. (2002) (RAU) and Sieverding et al. (2018) (SIE), with initial mass equal to 15, 20, and 25 M⊙ and solar metallicity (Anders & Grevesse 1989, with Z = 0.02). Convective borders are defined by the Ledoux criterion, as in Weaver et al. (1978). The adopted 12C(α,γ)16O rate is from Buchmann (1996), multiplied by a factor of 1.2. In addition to RAU and SIE sets, we also consider the KEPLER models by Jeena et al. (2024) (KEP). The KEP set includes 76 models between 12 and 30 M⊙ at zero metallicity, with the primordial Big Bang nucleosynthesis (BBN) initial composition from Cyburt et al. (2002). For consistency with most of the other sets having initial masses up to 25 M⊙, we only consider the 66 KEP models with an initial mass Mini≤25 M⊙. The convection and mixing criteria are the same as in Heger & Woosley (2010) and consist in Ledoux with a semiconvective diffusion coefficient that is roughly 10% of the radiative diffusion coefficient, plus a small amount of convective overshooting included by forcing convective boundary zones to be semiconvective. The 12C(α,γ)16O rate is the same as adopted by RAU and SIE.

We note that the 12C(α,γ)16O rate of Buchmann (1996) is a factor of 2-3 higher than that of Kunz et al. (2002), adopted by most of the other sets of models (see below), in the typical He-burning temperature range (T9 = 0.2−0.5, where T9=T/109 K, Fig. A.1.). As a consequence, the MCO versus XC12 datapoints from the for KEPLER models are shifted toward lower XC12 values than the other models in Fig. 1.

thumbnail Fig. A.1.

The different 12C(α,γ)16O reaction rates normalized to the Kunz et al. (2002) reaction rate in the typical He burning temperature range.

A.2. GENEC models (PGN)

We include the 15, 20, and 25 M⊙ models with solar metallicity (Z = 0.02, Grevesse & Noels 1993) presented in Pignatari et al. (2016) (PGN), computed using the GENEC stellar evolutionary code Eggenberger et al. (2008). The evolution of these models is calculated up to the end of central Si burning phase, while the birth of the Si burning shell and the pre-collapse phase are not included. For this reason, we do not know if these models may experience a C-O shell merger in their final stages, while the structure of these models at the end of the calculated evolution suggest that a C-O shell merger is very unlikely, as the external border of the O-burning shell is rather distant in mass from the base of the C-burning shell. The adopted convection criterion is Schwarzschild, with core overshooting included only in the central H and He burning phases (with an overshooting parameter αov = 0.2Hp). The 12C(α,γ)16O rate is from Kunz et al. (2002).

A.3. FRANEC models (L&C, RLC, LIM, ROB)

We include several sets of models calculated with the FRANEC code (Chieffi & Limongi 2013; Limongi & Chieffi 2018). The L&C (Limongi & Chieffi 2018) and RLC (Roberti et al. 2024a) models are part of a large set of rotating massive stars, with initial masses between 13 and 120 M⊙ and spanning 5 different initial metallicities, [Fe/H] = 0.3,0,−1,−2,−3. In this work, we considered only the models up to Mini≤25 M⊙ (i.e., Mini = 13, 15, 20, and 25 M⊙), at the three available rotation velocities (0, 150, and 300 km/s), and at all the metallicities, for a total of 60 models, 12 of which present C-O shell mergers. In these sets, the borders of the convective zones are defined according to the Ledoux criterion. In addition, 0.2Hp of overshooting is included at the outer edge of the convective core only during the core H-burning phase. The 12C(α,γ)16O rate is taken from Kunz et al. (2002). The LIM set (Limongi et al. 2024) includes models at solar metallicity in the range between 7 and 12 M⊙. Since we are interested in the CCSN progenitor evolution, we consider only the models that evolve to the formation of a Fe core, corresponding to models from Mini = 9.22 M⊙. In this set, the convective borders are determined according to the Ledoux criterion in the H-rich layers and according to the Schwarzschild criterion elsewhere. Core overshooting is included during core H burning with αov = 0.2Hp. The adopted 12C(α,γ)16O rate is from Xu et al. (2013), a re-analysis that also includes the experimental points from Kunz et al. (2002). In typical He burning conditions it is very similar to the Kunz et al. (2002) rate (Fig. A.1.). None of these models undergo C-O shell mergers. The same prescriptions for convection and 12C(α,γ)16O reaction rate are also adopted in the ROB set Roberti et al. (2024b). This set includes 34 models of 15 and 25 M⊙ stars at zero and extremely low metallicity ([Fe/H]≤−4) spanning a wide range of initial rotation velocity (from 0 to 800 km s−1). All but two of the rotating 15 M⊙ models undergo C-O shell mergers.

A.4. MESA models (RIT, BRI)

We include two sets of models calculated with the MESA code Paxton et al. (2018). The RIT set Ritter et al. (2018a) includes massive star models of 12, 15, 20, 25 M⊙, at 5 different metallicities: Z = 0.02, 0.01, 0.006, 0.001, 0.0001. The exponential diffusion model of Freytag et al. (1996) defines all the external convective boundaries from the pre-main sequence up to the end of core He burning. The reaction rate database is the same as used in PGN models. Five RIT models experience C-O shell mergers. The BRI set (Brinkman et al. 2019, 2021) includes non-rotating and rotating massive star models at solar metallicity with Mini between 10 and 80 M⊙ and vini = 0, 150, and 300 km s−1, calculated up to the collapse of the Fe core. Again, we only considered models up to 25 M⊙ (i.e., 10, 15, 20, and 25 M⊙). The convective boundaries are determined using the Ledoux criterion, with overshooting included only for the central burning stages (αov = 0.2Hp) and in the H burning shell (αov = 0.1Hp). The adopted 12C(α,γ)16O rate is Kunz et al. (2002). None of these models experience C-O shell mergers.

Appendix B: Models used in Figures 4 and 5

Figure 4 shows the distribution of [K/Mg] and [Sc/Mg] from several sets of CCSN yields, with progenitor initial mass between 11 and 25 M⊙ and initial metallicity between 0 and 0.05. As discussed in Sect. 4, some of the models shown in Fig. 1 are not in Fig. 4 and vice versa, because not all the sets provided both the MCO and XC12 at the end of He burning and the explosive yields. Among the models used in Fig. 1, those from the SIE, PGN, LIM, and BRI sets do not have C-O shell mergers, nor metallicity different than solar. Therefore, as discussed in the text, we did not include them in our comparison with observations of stars of low metallicity in Fig. 5. We added instead the NOM yield set of zero metallicity (Nomoto et al. 2013) and the PUSH set (Curtis et al. 2019; Ebinger et al. 2020) of zero (z-series) and 10−4Z⊙ metallicity (u-series). From the NOM set, we considered 6 CCSNe from progenitors with initial masses between 11 and 25 M⊙  and 2 hypernova models with initial masses equal to 20 and 25 M⊙. From the PUSH set we considered 12 models of the u-series, with initial masses between 11 and 25 M⊙, and 13 models of the z-series, with initial masses between 11 and 23 M⊙. The PUSH models only includes the composition of the inner part of the explosion which reaches temperatures above 1.75 GK. However, about 50% of the total Mg yield is produced outside of this regions and neither Sc nor K are significantly produced outside this region. Thus, we do not expect a significant impact on the [X/Mg] values. The production of the only stable isotope of Sc, 45Sc, is a signature of proton-rich, neutrino-processed supernova ejecta Fröhlich et al. (2006a,b) and recent multi-dimensional simulations have confirmed an enhancement of Sc compared to parameterized explosion models Sieverding et al. (2020), Wang & Burrows (2024). While this enhancement of Sc could be up to a factor 10 Sieverding et al. (2020), it is not accompanied by an enhancement in the production of K. Therefore, we expect that the effects of multi-dimensional dynamics and neutrinos could improve the agreement with the observations, the effects alone are unlikely to be able to explain cases with an enhancement in both elements, Sc and K. Nonetheless, self-consistent simulations of metal-poor progenitor stars are needed to confirm the impact of multi-dimensional dynamics and neutrinos on the production of Sc and K.

Appendix C: Observations

In Fig. 5 we compare the theoretical yield predictions with 37 observations of extremely metal poor (EMP, [Fe/H]≤−3) stars taken from the JINAbase database Abohalima & Frebel (2018) (as detailed in Table C.1.). The full database contains 121 stars with [K/Mg] and [Sc/Mg] observations, with initial metallicity in the range −4.12≤[Fe/H]≤−1.51. More specifically, the data extracted from JINAbase is from Roederer et al. (2010, 2014), Cohen et al. (2013), Siqueira Mello et al. (2014), Placco et al. (2014, 2015), Li et al. (2015), Casey & Schlaufman (2015), Skúladóttir et al. (2015), Howes et al. (2015, 2016). A large number of the observations (≃50%) are below [Fe/H]=–3, as indicated by the pink bars in Fig. C.1., also showing that the distribution peaks at [Fe/H]=–2.8. The majority of these stars likely did not experience pollution from multiple generations of CCSNe, making them suitable candidates to establish the composition of the ejecta of single or few CCSNe. The average values for the full sample are 〈[K/Mg]〉=−0.006 and 〈[Sc/Mg]〉=−0.410, while the subsample used for comparison with the models has slightly lower average values of 〈[K/Mg]〉=−0.047 and 〈[Sc/Mg]〉=−0.523. Since the JINAbase does not provide an error bar for the observed values, in Fig. 5 we show a typical error bar from Roederer et al. (2014), the largest sample from which the data was extracted. With this error bar, we see that the EMP sample effectively represents the broader set of 121 stars.

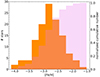thumbnail Fig. C.1.

Metallicity histogram (orange bars) and normalized cumulative number of stars (pink bars) of the observational sample of 121 stars taken from JINAbase.

Table C.1.

Observations used in Fig. 5.

All Tables

Table C.1.

Observations used in Fig. 5.

In the text

All Figures

thumbnail Fig. 1.

Carbon-oxygen core mass (MCO) versus the central 12C mass fraction abundance (XC12) at the end of central He burning phase. The different colors identify the different sets of models (see side legend) where RAU is Rauscher et al. (2002); PGN is Pignatari et al. (2016); SIE is Sieverding et al. (2018); RIT is Ritter et al. (2018a); L&C is Limongi & Chieffi (2018); BRI is Brinkman et al. (2019, 2021); LIM is Limongi et al. (2024); RLC is Roberti et al. (2024a); ROB is Roberti et al. (2024b); and KEP is Jeena et al. (2024). Different symbols identify different initial masses (see top legend). Models with and without a C-O shell merger are represented by filled and empty symbols, respectively. The two gray shaded areas represent the covariant confidence ellipses relative to the models with C-O mergers within one and two standard deviations, σ, centred at MCO = 4.02 and XC12 = 0.176.
In the text
thumbnail Fig. 2.

Comparison between the abundances before (dashed lines) and after the C-O shell merger (solid lines) in the RIT 15 M⊙ model at solar metallicity (see Ritter et al. 2018a, for a detailed description of the model). The upper panel shows the effect of the merger on the major fuels. The lower panel shows instead the effect of the merger on some key C- and O-burning products and selected odd-Z isotopes (see text). The vertical dotted lines represent the location of the edges of the shells before the C-O shell merger. The light gray area is the region modified by the merger, the dark gray area represents the untouched deeper layers of the star after the merger, i.e., the Fe core and the Si shell.
In the text
thumbnail Fig. 3.

As Fig. 2, but for the presupernova (dashed lines) and postsupernova (solid lines) stages, with the inclusion of 56Ni. The supernova explosion was modeled with a semianalytical approach, using the Sedov blast wave (SBW) solution for the determination of the peak velocity of the shock throughout the stellar structure and the remnant mass prescription from Fryer et al. (2012) (see Pignatari et al. 2016; Ritter et al. 2018a; Roberti et al. 2024c, for a detailed description of the explosion method). The gray bands in the plots mark each explosive burning stage in the corresponding mass coordinate (i.e., complete and incomplete Si burning, explosive O, Ne, and C burning). The vertical dotted line represents the mass-cut that divides the supernova ejecta from the remnant mass. The variation of 24Mg and 32S in the He shell represents the activation of the α capture chain in the explosive He burning (Pignatari et al. 2023).
In the text
thumbnail Fig. 4.

[K/Mg] (upper panel) and [Sc/Mg] (lower panel) versus the initial metallicity. The adopted solar reference is from Asplund et al. (2009). The different colored labels identify each set of models (see bottom legend): RAU Rauscher et al. (2002); NOM Nomoto et al. (2013); RIT Ritter et al. (2018a); L&C Limongi & Chieffi (2018); PUSH Ebinger et al. (2020); ROB Roberti et al. (2024b); RLC Roberti et al. (2024a); KEP Jeena et al. (2024). Different symbols identify different initial masses (see top legend). Models with and without a C-O shell merger are represented by a filled and an empty symbol, respectively.
In the text
thumbnail Fig. 5.

Ratios of [K/Mg] versus [Sc/Mg] from those models selected from Fig. 4 that have either a C-O shell merger or initial metallicity Zini<10−5. The adopted solar reference is from Asplund et al. (2009). The different colored labels identify each set of models as in Fig. 4 (see side legend). Different symbols identify different initial masses (see top legend). Models with and without a C-O shell merger are represented by a filled and empty symbol, respectively. The blue star symbols are observations of low-mass stars of low metallicity taken from JINAbase (Abohalima & Frebel 2018) with [Fe/H] < −3. A representative error bar for the observation data is shown, as taken from Roederer et al. (2014). The dashed vertical and horizontal lines represent the average [K/Mg] and [Sc/Mg] ratios from the observations. The gray shaded area represents the representative error bar for the average data point.
In the text
thumbnail Fig. A.1.

The different 12C(α,γ)16O reaction rates normalized to the Kunz et al. (2002) reaction rate in the typical He burning temperature range.
In the text
thumbnail Fig. C.1.

Metallicity histogram (orange bars) and normalized cumulative number of stars (pink bars) of the observational sample of 121 stars taken from JINAbase.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.