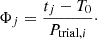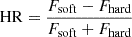EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 692 (December 2024) A&A, 692 (2024) A19 Full HTML
Open Access
Issue
A&A
Volume 692, December 2024
Article Number A19
Number of page(s) 8
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/202452031
Published online 29 November 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Symbiotic binaries1 are systems consisting of a red giant star and a compact object (Muerset et al. 1997), which typically is a white dwarf (Tutukov & Iungelson 1976). In a handful of cases, however, the compact object has been confirmed to be a neutron star. These systems can be observed to emit in X-rays and are called symbiotic X-ray binaries (SyXRBs) (Masetti et al. 2006). At the time of writing, only five such systems have been confirmed (see, e.g., Bozzo et al. 2022 and references therein). While these systems are a subclass of low-mass X-ray binaries (LMXBs), they exhibit characteristics that are often found in high-mass X-ray binaries (HMXB) instead, such as long pulse periods (up to hours), strong X-ray variability (factors of 10–20), and extremely long orbital periods of up to thousands of days (Bozzo et al. 2022). Because these systems are rare and show a multitude of peculiar characteristics, they are prime candidates for further studies.

One of these rare objects is the SyXRB GX 1+4, which was first discovered in X-rays during balloon-borne experiments in 1970 (Lewin et al. 1971) in the form of a new variable source with a pulsation period of ∼135 s. Three years later, the optical counterpart of the source was identified by Glass & Feast (1973) as V2116 Oph, a bright infrared source. This allowed Davidsen et al. (1977) to classify GX 1+4 as an SyXRB containing an M-giant mass donor. This made GX 1+4 the first of this class of SyXRBs. It is understood today that the system consists of a neutron star and a giant star companion (Davidsen et al. 1977) that does not fill its Roche lobe (Hinkle et al. 2006), with evidence for an accretion disk in the system that is either persistent (Jablonski et al. 1997; Chakrabarty & Roche 1997; Chakrabarty et al. 1998) or transient (Serim et al. 2017). The spectral type of the donor is either M6 III (Davidsen et al. 1977) or M5 III (Chakrabarty & Roche 1997). The constituent masses of the binary system are not conclusively determined, but Hinkle et al. (2006) suggested a maximum mass of the optical companion of 1.22 M⊙ based on radial velocity measurements and adopting a typical neutron star mass of 1.35 M⊙. The neutron star showed a strong spin-up trend since its discovery. The spin period decreased from the initial value to ∼110 s until 1980 (Ricketts et al. 1982). The system then entered a faint state and remained undetectable (Hall & Davelaar 1983) until 1986, when it was again detected after undergoing a torque reversal during the faint state and showed a spin-down trend with ̇P ∼ 4.5 ⋅ 10−8s s−1, which has stayed roughly constant since then (see González-Galán et al. 2012 and references therein for a comprehensive overview of the spin history evolution). Newer measurements by Luna (2023) suggested a spin-down of ̇P ∼ 1.61 ⋅ 10−7s s−1 based on data from the Kepler/K2 space telescope from observations carried out in 2016.

Multiple attempts have been made over the years to determine the orbital period of the system. Initially, Cutler et al. (1986) found a periodicity of ∼304 d based on epochs of enhanced spin-up in the spin-derivative history. Adopting an analogous approach, Pereira et al. (1999) inferred similar periodicities based on the residuals of the spin-frequency derivative history of the neutron star and connected it to the orbital period based on an increase in torque exerted by the accretion disk on the neutron star magnetosphere near the periastron passages, which would therefore cause regular variations in the spin-down trend. A few years later, Dieters et al. (2005) searched for the orbital period using data from the Rossi X-Ray Timing Explorer (RXTE) and the Burst and Transient Source Experiment (BATSE), but were unable to confirm the previous findings of 304 d. They instead reported a tentative detection of a 420–460 d orbital period. Following this, an analysis of infrared radial velocities of the optical companion conducted by Hinkle et al. (2006) ruled out the candidate period of 304 d and instead reported strong evidence for an orbital period of ∼1161 d alongside an eccentricity of e = 0.101. In addition to this, Hinkle et al. (2006) proposed an upper limit of M = 1.22 M⊙ of the companion, which would correspond to an inclination of the system of up to 90°. They also ruled out a near face-on inclination of the system, mentioning that an eclipse of the neutron star is theoretically possible. Corbet et al. (2008) searched for orbital periodicity using a relatively small time interval of Swift Burst Alert Telescope (Swift/BAT) data spanning approximately 200 days and RXTE All-Sky Monitor (RXTE/ASM) data covering about 4000 days. They reported no significant detection of either the 304 d, 420–460 d, or 1161 d period, however. Analysis of optical I-band data from the Optical Gravitational Lensing Experiment (OGLE) conducted by Majczyna et al. (2016) was similarly unable to verify the detection of the 1161 d orbital period. Instead, Majczyna et al. reported a clear detection of a 295 ± 70 d period, which therefore would support the findings of Cutler et al. (1986) and Pereira et al. (1999). In the following year, Iłkiewicz et al. (2017) conducted a multi-wavelength study of the system using optical data from the Klein Karoo Observatory as well as observations from the International Gamma-Ray Astrophysics Laboratory (INTEGRAL) using data from the Optical Monitoring Camera (OMC) and the INTEGRAL Soft Gamma-Ray Imager (ISGRI) as well as RXTE observations, where no detection of any of the previously mentioned periods was made. Instead, Iłkiewicz et al. argued that the flaring behaviour of the source, which would increase in activity near the periastron passages, supports the 1161 d period reported by Hinkle et al. (2006). To our knowledge, the most recent work supporting the 1161 d period reported by Hinkle et al. and Iłkiewicz et al. was reported by Serim et al. (2017). In this work, the authors found long-term variations of the torque-luminosity correlation of the source at timescales similar to the 1161 d orbital period. Additionally, their timing analysis indicated a strong noise level at the orbital timescales that can even dominate the frequency residuals for the suggested orbital semi-major axis. The period of the system is today generally accepted as 1160.8 ± 12.4 d following the radial velocity measurements of Hinkle et al. (2006) because they provided more compelling evidence for orbital motions than other methods. A conclusive detection of the orbital period in X-rays still remains to be made, however.

We use multiple long-baseline X-ray observations of GX 1+4 from different missions in order to independently determine the orbital period of the system. To do this, we make use of Lomb-Scargle and epoch-folding periodograms and search directly for periodicity in light-curve and spin-frequency data of the source. Furthermore, we support our findings using folded light curves and hardness ratios as well as images of the source during the predicted eclipse.

2. Observations and data selection

We used all available public INTEGRAL/ISGRI observations from 52698 MJD to 59694 MJD with an off-axis angle of ≤10° in the energy range of 28 to 40 keV, and all INTEGRAL Joint European X-Ray Monitor (INTEGRAL/JEM-X) observations from 53052 MJD to 60009 MJD with an off-axis angle of ≤3.5° in the energy ranges from 4–10 keV and 10–20 keV, respectively. The data were reduced using the Multi-Messenger Online Data Analysis (MMODA) service2 on OSA, version 11.2. The time bin for the ISGRI and JEM-X data reduction was set to 1000 s. Since the two JEM-X telescopes do not always operate simultaneously, data from the two detector units were combined. Since the JEM-X data were not suitable for direct analysis due to numerous gaps in the data and a low number of data points that resulted in a poor coverage of the orbit, we instead only used it to support our findings on multiple occasions throughout the analysis.

Additionally, we used Swift/BAT daily light curves in the 15–50 keV energy range between 53419 MJD and 59142 MJD that were taken directly from the web-archive3 (see also Krimm et al. 2013). Data points after 59142 MJD were excluded due to strong noise that was likely caused by instrument degradation.

Furthermore, we used light curves from the Monitor of All-sky X-ray Image (MAXI) (Matsuoka et al. 2009) in the energy ranges of 5–10 keV, 10–20 keV, and 5–20 keV from 55054 MJD to 59885 MJD. We decided to deviate from the standard MAXI light curves, which usually start at 4 keV, due to an apparent excess in background radiation below 5 keV visible in the MAXI spectra, and we excluded data below this value. The data reduction was performed using the MAXI on-demand processing4 online service.

To supplement the light-curve data, we used all available pulse frequency measurements of the neutron star in the spin-down regime between 46885 MJD and 59864 MJD. These measurements consist of data that were taken by multiple missions and can be found in Appendix B in González-Galán et al. (2012) in addition to spin-frequency measurements from Serim et al. (2017), Cui & Smith (2004) and the Fermi Gamma-ray Burst Monitor (Fermi/GBM) archive5.

3. Data analysis and results

3.1. Orbital period

3.1.1. Light curves

For each of the available data sets, we calculated the Lomb-Scargle periodogram using the LombScargle routine implemented through the astropy6 (Astropy Collaboration 2022) package in Python 3.9, taking measurement uncertainties into account (see VanderPlas et al. (2012), VanderPlas & Ivezić (2015) for the methods used in the astropy package). The period corresponding to the highest power in the periodogram are considered to be an indicator of the orbital periodicity Porb.

We then calculated the false-alarm level corresponding to a false-alarm probability of 0.1%. The false-alarm level indicates the probability that a peak of the corresponding power was caused by random fluctuations in the data set, under the assumption that the data follow a purely Gaussian distribution (i.e. do not contain a signal) (see VanderPlas 2018). While this is a common way to ensure the significance of a peak, other peaks would also be significant, such as harmonics at fractions of the periodicity, or periodicities caused by other factors that might be artificially enhanced by red noise at lower frequencies. Furthermore, the false-alarm probability prevented us from drawing conclusions regarding the uncertainty on the associated period. One way to do this would be to employ a bootstrapping approach. However, the Lomb-Scargle periodogram was not sensitive enough to the changes introduced by a bootstrapping approach, likely due to the strong inherent variability of the data, which interplays with any periodic signal. We therefore needed to use a different approach to determine the uncertainties on the found periods. This was done by first folding the light curve using the found period and then calculating the orbital phase of each point in the data set. The reference epoch T0 for the folding was chosen to be 54557.5 MJD, which was extrapolated based on the time of the predicted eclipse (Tconj = 52235.3 MJD) provided by Hinkle et al. (2006) to be closer to the beginning of our data sets. Following this, we interpolated over the folded profile to obtain the expected amplitude of the signal corresponding to each data point and subtracted this expected signal from the original data set. We then confirmed that the peak in the periodogram created from the subtracted data set corresponding to the previously found period had vanished or was below the detection threshold.

Next, we generated signals with a number of trial periods Ptrial, i in a range of ±200 d around the previously found period. For each trial period Ptrial, i, we calculated the phases Φj of each data point in our data set as

Φ j = t j − T 0 P trial , i · $$ \begin{aligned} \Phi _j = \frac{t_j - T_0}{P_{\mathrm{trial} ,i}}\cdot \end{aligned} $$(1)

We then calculated the expected rate rj for each point in phase Φj using the interpolation we obtained earlier, and we replicated the shape of the original signal in this way, but with a varying periodicity. Based on our assumption of the intrinsic variability of the data shifting the peak of the periodogram, this new signal was then re-added to the subtracted data set with a random phase shift Δϕ. The Lomb-Scargle periodogram was then calculated, and the period corresponding to the peak with the highest power was saved. This process was repeated 1000 times for each trial period in order to create a distribution of found periods for each inserted signal with a fixed trial period. We then calculated the differences between the periodicity of the inserted signal and the detected periods. The resulting distributions do not resemble a normal distribution in all cases, which means that the standard deviation cannot be used as a 68% confidence interval. Instead, we chose to iteratively calculate the intervals of each distribution centred around the mean value, which contains 34% of the periods to the left and right of the mean value, respectively, which then represent the asymmetric uncertainties on the obtained periods.

Next, we searched for a periodicity in the data using epoch-folding. This approach relies on folding the data over a range of trial periods and maximising the resulting χ2 statistic. Profiles were obtained by applying good time interval (GTI) exposure correction prior to folding. We applied this technique to the available light curves and summarise the results in Table 1, alongside the results of the Lomb-Scargle periodograms. In this case, the uncertainties were obtained by bootstrapping.

The Lomb-Scargle and epoch-folding periodograms are shown in Fig. 1 and Fig. 2, respectively. Light curves folded with the Lomb-Scargle period, the epoch-folding period, and the radial velocity period from Hinkle et al. (2006) are shown in Fig. 3. As the reference epoch T0 for the folding, we again used 54557.5 MJD. Since this time was extrapolated based on the radial velocity ephemerides by Hinkle et al. (2006) and corresponds to the time of the predicted eclipse, it is important to note that the phase bin around phase zero of the folded profiles therefore likewise represents the phase bin of the predicted eclipse.

thumbnail Fig. 1.

Lomb-Scargle periodograms of the light curves. Swift (top), MAXI (middle), and ISGRI (bottom).

thumbnail Fig. 2.

Epoch-folding periodograms of the light curves. Swift (top), MAXI (middle), and ISGRI (bottom).

thumbnail Fig. 3.

Folded light curves. We show folded Swift (first row), MAXI (second row), and ISGRI (third row) light curves with the folding periods being the corresponding Lomb-Scargle (LS) period PLS (left column), the epoch-folding (EF) period PEF (centre column), and the radial velocity (RV) period PRV (right column) from Hinkle et al. (2006). The phase bin around phase 0 corresponds to the phase bin of the predicted eclipse.

3.1.2. Hardness ratio

In addition to analysing the light curves, we also calculated the hardness ratio, which we defined as

HR = F soft − F hard F soft + F hard $$ \begin{aligned} \mathrm{HR} = \frac{F_\mathrm{soft} -F_\mathrm{hard} }{F_\mathrm{soft} +F_\mathrm{hard} } \end{aligned} $$(2)

for the 5–10 keV and 10–20 keV bands of MAXI and JEM-X data. Then, we searched for periodicities in the hardness ratios using the methods outlined in the previous section. The JEM-X data were only used to fold the obtained hardness ratio with the candidate periods in order to check for consistency with the results obtained using MAXI data. The MAXI period is listed in Table 1. Following this, we folded the hardness ratios with the obtained periods as well as the 1160.8 d radial velocity period PRV from Hinkle et al. (2006), and we compare the results in Fig.4. For consistency with the folded light curves in the previous section, the reference epoch T0 for the folding was also chosen to be 54557.5 MJD.

thumbnail Fig. 4.

Folded hardness ratios. We show MAXI (first row) and JEM-X (second row) hardness ratios folded with the Lomb-Scargle (LS) period PLS (left column), the epoch-folding (EF) period PEF (centre column), and the radial velocity (RV) period PRV (right column) from Hinkle et al. (2006). The phase bin around phase zero corresponds to the phase bin of the predicted eclipse.

The results presented in Fig. 4 suggest that the hardness ratio changes periodically and shows a minimum at the predicted eclipse, which could be due to a modulation in the column density NH along the line of sight. We attempted to perform orbital-phase resolved spectroscopy of the system using INTEGRAL as well as MAXI spectra in order to investigate whether the spectral parameters change with the orbital phase, as the hardness ratio suggests. However, due to the degeneracy between the column density and photon index, we were unable to draw definitive conclusions. We then performed a spectral analysis on archival Swift/XRT data in PC mode around the orbital phases 0 (OBSIDs 00050750001, 00050751001, 00050751002, 00050751003, 00050751004, 00050752001, 00050752002, and 00050752003 for a combined 57 ks), 0.15 (OBSID 00081653001 with 1.7 ks) and 0.35 (OBSID 00089914001 with 1.9 ks) using a simple absorbed power-law model (TBabs*powerlaw in XSPEC), which was sufficient to fit the spectra well7. The results of this analysis are presented in Table 2. We find that the column density increases by a factor of 10 near the expected eclipse.

3.1.3. Spin-frequency and spin-frequency derivative evolution

Lastly, we analysed the spin frequency and spin-frequency derivative evolution of the source to search for a possible periodicity, for example caused by the orbital modulation of the spin frequency or a change in the accretion behaviour near periastron. While this has previously been attempted using BATSE data covering about 3000 days by Pereira et al. (1999), we instead achieved a baseline of about 12000 days using the combined data from multiple missions, shown in Fig. 5, which would correspond to a coverage of about ten orbital cycles of the source based on the radial velocity period derived by Hinkle et al. (2006). We first subtracted a linear long-term trend from the spin-frequency evolution of the source and then calculated the Lomb-Scargle periodogram of the subtracted spin-frequency evolution. Similar to the previous sections, we also applied the epoch-folding technique to the data. The results of the two approaches are summarised in Table 3.

thumbnail Fig. 5.

Spin-frequency history of GX 1+4. The data were taken from multiple missions. The solid line represents the linear fit to the data. We searched for periodicity in the residuals in the lower plot.

Although the Lomb-Scargle periodogram of the data suggests a periodicity that is consistent with the radial velocity period, the corresponding peak lies below the 0.1% false-alarm level threshold, and we furthermore could not apply the approach to determine the uncertainties outlined in the previous section since removing the folded signal did not remove the peak in the periodogram. There is an inherent variability in the spin evolution that is associated with variations in accretion torques, which might be the cause for the above. Therefore, we cannot report any uncertainty on the Lomb-Scargle period and only used this data set to support our claims. In addition to the spin-frequency history, we also searched for a periodicity in the spin-frequency derivatives of the source. To do this, we restricted our analysis to data from Fermi/GBM between 54704 MJD and 59864 MJD because the coverage is better, since measuring a single frequency derivative corresponding to large gaps may smear out the periodic signals. We employed a sliding-window approach where we selected ten consecutive data points to which we fit a linear function with the slope corresponding to the spin frequency derivative. We then moved the window one data point forward in time and repeated the fit until we reached the end of the data set. Since the Lomb-Scargle periodogram of the spin-frequency derivatives showed a strong peak at around 3600 days, we fit a quadratic function to the data, which we considered to be a part of the long-term intrinsic evolution due to accretion (shown in Fig.6), and subtracted it from the spin-frequency derivatives to remove the underlying trend and performed the analysis on the subtracted data set. As before, we also analysed the spin-frequency derivatives using the epoch-folding technique and summarise the results in Table 3.

thumbnail Fig. 6.

Spin-frequency derivatives of GX 1+4 using Fermi/GBM data. The data points were obtained using a sliding-window approach, and a long-term trend was subtracted (solid orange line; see text).

3.2. INTEGRAL images

In contrast to the periodicities that are deduced from X-ray variabilities through periodograms, the radial velocity measurements from Hinkle et al. (2006) provide a total orbital solution, including the amplitude of the semi-major axis and the time of periastron passages, as well as the time T0 of a possible eclipse of the neutron star. Therefore, we used this information to search for an eclipse in the X-ray data.

To do this, we created ISGRI and JEM-X mosaic images for the orbital phase bin around the orbital phase corresponding to the expected position of the eclipse as predicted by Hinkle et al. (2006). Since we extrapolated the reference epoch for folding from the radial velocity ephemerides, eclipses should in principle repeat at each passage n ⋅ T0, leading to a minimum in the folded profile when folded with the given ephemeris. However, since the uncertainty projection after many orbital cycles leads to an ambiguity in the arrival times of the eclipses and because we folded the profiles at a resolution of eight bins (corresponding to a coverage of 145.125 d each), we also considered the possibility of an occurrence of the eclipse in adjacent phase bins. In addition to the phase-resolved imaging of the source, we also performed imaging on an orbit-by-orbit basis. We did not find any evidence for a complete eclipse of the neutron star by the companion, however, because the source was clearly detected in every image.

4. Discussion and conclusions

The orbital period of GX 1+4 has been a point of contention for a long time and until radial velocity measurements suggested the 1161 d period as the orbital period of the system (Hinkle et al. 2006), which has generally been accepted because the radial velocity measurements provide compelling evidence. This detection has not been reproduced in X-rays so far.

Based on their assumptions on the mass of the neutron star and the value of the mass function, Hinkle et al. (2006) suggested a maximum mass of the companion of 1.22 M⊙ for a neutron star mass of MNS = 1.35 M⊙, which requires a corresponding inclination of the system of ∼90° and provides ephemerides for a predicted total eclipse. This means that even in X-rays, a periodic decrease in brightness of the source can be expected, which should be detectable in the long-term light curves of the source. Furthermore, the orbit of the system is eccentric, and changes in the accretion torque at periastron could therefore have an effect on the spin-frequency history.

We searched for a periodicity of GX 1+4 using different approaches and data sets. Lomb-Scargle and epoch-folding periodograms were calculated from the light curves, hardness ratios, and spin-frequency derivative history of the source. An overview of the results is presented in Fig.7, and detailed results are presented in Table 1 and Table 3. The results obtained using these two independent methods agree with the radial velocity period proposed by Hinkle et al. (2006) within the 68% confidence interval.

thumbnail Fig. 7.

Visual summary of the analysis results. The blue circles represent the results obtained with the epoch-folding approach, and the results obtained with the Lomb-Scargle technique are shown as orange squares. The data sets are Swift, MAXI, ISGRI, MAXI hardness ratio, and spin-frequency derivative evolution, as indicated by the labels in the figure. The solid red line indicates the 1160.8 d radial velocity period obtained by Hinkle et al. (2006), and the dashed lines mark the corresponding 12.4 d uncertainty on this value.

Table 1.

Orbital periods from light curves and hardness ratios.

This implies that the light curves of the source show behaviours that occur periodically on the same timescale as the proposed orbital period, which is consistent with the assumption of an increase in accretion rate, and consequently, the luminosity, near periastron and a decrease in luminosity near the predicted eclipse.

Furthermore, we folded the light curves and hardness ratios with the radial velocity period and obtained profiles with features that are consistent with the expectations from the radial velocity ephemerides. The light curves folded with the radial velocity period in the rightmost column of Fig.3 show an excellent agreement between Swift and ISGRI data. The minima of the profiles coincide within the statistical uncertainties with the predicted eclipse, but are not consistent with zero. This suggests the absence of a complete eclipse and may instead be caused by an increase in column density in the line of sight, possibly due to the outer layers of the M-type giant companion entering the line of sight between the neutron star and the observer, leading to an increase in absorption. This is further supported by the folded hardness ratios, which are at a minimum at the expected eclipse, suggesting either an increase in hard X-rays or a decrease in soft X-ray emission via increased absorption due to the companion. The results of the spectral analysis using Swift/XRT data, summarised in Table 2, support this assumption of an increased column density NH as they show an increase by a factor of 10 near the expected eclipse. However, the results of the spectral analysis do not show a hardening of the spectral shape at the predicted eclipse (orbital phase Φ = 0). On the contrary, we observe a slight softening. We also do not observe the typical appearance of a bright iron line complex (see e.g. Naik & Paul 2011). Additionally, we found pulsations in the light curves of the source in some of the observations taken near the eclipse, suggesting that the neutron star is observed directly. The images obtained with INTEGRAL likewise support the absence of a complete eclipse as the source is consistently detected with a high detection significance (⪆20σ) throughout all the phasevintervals that we analysed. The folded light curves obtained using MAXI data (rightmost column of Fig. 3) show a secondary peak at Φ ∼ 0 that is not seen with Swift/BAT and ISGRI. This might be caused by the different energy ranges of MAXI with respect to Swift and INTEGRAL, suggesting an energy dependence of the MAXI profiles. Since we do not see this secondary peak in the folded JEM-X light curve, another reason could be contamination of MAXI data from two neighbouring LMXBs GX 3+1 and SLX 1735–269 due to the large point spread function (PSF) of 1.5° of the instrument.

Table 2.

Results of the spectral analysis using Swift/XRT data.

Table 3.

Orbital periods obtained from the spin frequency and spin-frequency derivative history.

Since the orbit of the neutron star has a non-zero eccentricity, the accretion torque is likely to vary over the course of the orbit. These changes would therefore be reflected in the spin frequency and spin-frequency derivative history. We find periodicities in the spin frequency and spin-frequency derivative history of the source that would agree with the proposed radial velocity period and could therefore be indicative of these changes in accretion torque.

The lack of the eclipse emerging from our analysis implies that the binary system is not observed edge-on (i ≠ 90°). We show that this result, together with other information obtained by Hinkle et al. (2006), allows us to place constraints on the inclination i of the orbital plane and the mass of the neutron star. We first calculated the red giant radius as a function of the red giant mass using the surface gravity provided by Hinkle et al. (2006) (log(g) = 0.5 ± 0.3). The resulting region of allowed masses and radii is represented by the blue line and light blue region in Fig. 8. Furthermore, based on the abundances of 17O and 16O, Hinkle et al. (2006) determined a range of allowed masses for the red giant ranging from ∼1 M⊙ to ∼1.3 M⊙. This is represented by the grey region in Fig. 8. The region in which the grey and blue regions overlap represents the possible solutions for the mass and radius of the red giant.

thumbnail Fig. 8.

Companion radius as function of mass. The solid lines indicate the limits placed on the radius of the companion at different inclinations for a given neutron star mass. The mass-radius relation of M giants from the results by Dumm & Schild (1998) is indicated by the green dots. M5- and M6-type giants from this sample are represented by blue diamonds and black stars, respectively. The solid blue line represents the radius calculated from the gravitational acceleration log(g) as determined by Hinkle et al. (2006) for a given red giant mass, and the area shaded in light blue indicates the corresponding uncertainty. The area shaded in grey indicates the mass limits of the red giant as determined by Hinkle et al. (2006) through a spectroscopic analysis of the oxygen isotopic abundances of 17O and 16O.

Following this, we calculated the resulting masses of the companion and the semi-major axes of the system for a number of different neutron star masses and inclinations between 40° and 90° using the results for orbital period and the mass function of the system provided by the radial velocity measurements of Hinkle et al. (2006). By calculating the separation of the companion and the neutron star at the time of the predicted eclipse (orbital phase Φ = 0), we were able to obtain a maximum radius that the red giant can have in order to not eclipse the neutron star for different neutron star masses and inclinations. This is shown in Fig. 8. Since we do not find any evidence for a complete eclipse of the system, the radius of the red giant must be smaller than the value indicated for the red giant in Fig. 8, corresponding to the given inclination for any specified MNS (i.e. below the red, orange, or yellow lines). The intersection of the grey area with the light blue area in Fig. 8 furthermore allows us to place constraints on the neutron star mass and the inclination of the system. Based on this intersection, we find a range of neutron star masses of ∼1.23 M⊙ to ∼1.45 M⊙ and inclinations of the system in the range of ∼76° to ∼84°.

Considering that the spectral type of the companion in the system was determined to be either M6 III (Davidsen et al. 1977), or M5 III (Chakrabarty & Roche 1997), we can compare our results to the findings of Dumm & Schild (1998) for masses and radii of nearby M giants. This is represented by the green dots in Fig. 8, where M5 and M6 giants are distinguished from this sample by blue diamonds and black stars, respectively. Since all allowed solutions for the red giant in the system have to be contained within the overlap region between the grey and blue regions, we can immediately see that some of the red giants from the sample by Dumm & Schild (1998) fall within that area.

However, the calculations leading to this result assumed that in the low state at the predicted eclipse, the hard X-ray emission originates directly from the neutron star rather than being scattered by an intervening medium such as the wind of the red giant, in which case we would expect to observe spectral variability and characteristic emission lines (see e.g. Naik & Paul 2011, Wojdowski et al. 2003). The sparse Swift/XRT data indicate an increase in the column density around the expected eclipse (orbital phase Φ = 0), which could be a possible cause for the observed hardness ratio modulation, but it remains unclear whether the spectral continuum is also periodically variable. Future observations of the entire orbit, covering both soft (< 1 keV) and hard X-ray energies, are crucial to fully understand the implications of the spectral analysis and the consequences of the absence of an eclipse in the system.

1

For a comprehensive compilation of symbiotic variables see https://sirrah.troja.mff.cuni.cz/~merc/nodsv/

7

The XRT analysis was done using the Swift-XRT builder: https://www.swift.ac.uk/user_objects/, which processed the data using HEASOFT v6.32.

Acknowledgments

Based on observations with INTEGRAL, an ESA project with instruments and science data centre funded by ESA member states (especially the PI countries: Denmark, France, Germany, Italy, Switzerland, Spain), and with the participation of the Russian Federation and the USA. We acknowledge the use of public data from the Swift data archive. This research has made use of MAXI data provided by RIKEN, JAXA and the MAXI team. This paper is supported by European Union’s 2020 research and innovation programme under grant agreement No.871158, project AHEAD2020.

References

  1. Astropy Collaboration (Price-Whelan, A. M., et al.) 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bozzo, E., Romano, P., Ferrigno, C., & Oskinova, L. 2022, MNRAS, 513, 42 [CrossRef] [Google Scholar]
  3. Chakrabarty, D., & Roche, P. 1997, ApJ, 489, 254 [Google Scholar]
  4. Chakrabarty, D., van Kerkwijk, M. H., & Larkin, J. E. 1998, ApJ, 497, L39 [NASA ADS] [CrossRef] [Google Scholar]
  5. Corbet, R. H. D., Sokoloski, J. L., Mukai, K., Markwardt, C. B., & Tueller, J. 2008, ApJ, 675, 1424 [NASA ADS] [CrossRef] [Google Scholar]
  6. Cui, W., & Smith, B. 2004, ApJ, 602, 320 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cutler, E. P., Dennis, B. R., & Dolan, J. F. 1986, ApJ, 300, 551 [NASA ADS] [CrossRef] [Google Scholar]
  8. Davidsen, A., Malina, R., & Bowyer, S. 1977, ApJ, 211, 866 [NASA ADS] [CrossRef] [Google Scholar]
  9. Dieters, S., O’Neill, P., Farrell, S., & Sood, R. 2005, Adv. Space Res., 35, 1185 [NASA ADS] [CrossRef] [Google Scholar]
  10. Dumm, T., & Schild, H. 1998, New Astron., 3, 137 [NASA ADS] [CrossRef] [Google Scholar]
  11. Glass, I. S., & Feast, M. W. 1973, Nat. Phys. Sci., 245, 39 [NASA ADS] [CrossRef] [Google Scholar]
  12. González-Galán, A., Kuulkers, E., Kretschmar, P., et al. 2012, A&A, 537, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Hall, R., & Davelaar, J. 1983, IAU Circ., 3872, 1 [NASA ADS] [Google Scholar]
  14. Hinkle, K. H., Fekel, F. C., Joyce, R. R., et al. 2006, ApJ, 641, 479 [NASA ADS] [CrossRef] [Google Scholar]
  15. Iłkiewicz, K., Mikołajewska, J., & Monard, B. 2017, A&A, 601, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Jablonski, F. J., Pereira, M. G., Braga, J., & Gneiding, C. D. 1997, ApJ, 482, L171 [CrossRef] [Google Scholar]
  17. Krimm, H. A., Holland, S. T., Corbet, R. H. D., et al. 2013, ApJS, 209, 14 [NASA ADS] [CrossRef] [Google Scholar]
  18. Lewin, W. H. G., Ricker, G. R., & McClintock, J. E. 1971, ApJ, 169, L17 [NASA ADS] [CrossRef] [Google Scholar]
  19. Luna, G. J. M. 2023, A&A, 676, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Majczyna, A., Madej, J., Należyty, M., Różańska, A., & Udalski, A. 2016, in 37th Meet. Pol. Astron. Soc., 3, 133 [NASA ADS] [Google Scholar]
  21. Masetti, N., Orlandini, M., Palazzi, E., Amati, L., & Frontera, F. 2006, A&A, 453, 295 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Matsuoka, M., Kawasaki, K., Ueno, S., et al. 2009, PASJ, 61, 999 [Google Scholar]
  23. Muerset, U., Wolff, B., & Jordan, S. 1997, A&A, 319, 201 [Google Scholar]
  24. Naik, S., & Paul, B. 2011, in Astron. Soc. India Conf. Ser., 3, 138 [NASA ADS] [Google Scholar]
  25. Pereira, M. G., Braga, J., & Jablonski, F. 1999, ApJ, 526, L105 [NASA ADS] [CrossRef] [Google Scholar]
  26. Ricketts, M. J., Hall, R., Page, C. G., Whitford, C. H., & Pounds, K. A. 1982, MNRAS, 201, 759 [NASA ADS] [Google Scholar]
  27. Serim, M. M., Şahiner, Ş., Çerri-Serim, D., İnam, S. Ç., & Baykal, A. 2017, MNRAS, 469, 2509 [CrossRef] [Google Scholar]
  28. Tutukov, A. V., & Iungelson, L. R. 1976, Astrofizika, 12, 521 [NASA ADS] [Google Scholar]
  29. VanderPlas, J. T. 2018, ApJS, 236, 16 [Google Scholar]
  30. VanderPlas, J. T., & Ivezić, Ž. 2015, ApJ, 812, 18 [Google Scholar]
  31. VanderPlas, J., Connolly, A. J., Ivezic, Z., Gray, A., et al. 2012, Proc. CIDE, 47, 20.02 [Google Scholar]
  32. Wojdowski, P. S., Liedahl, D. A., Sako, M., Kahn, S. M., & Paerels, F. 2003, ApJ, 582, 959 [Google Scholar]

All Tables

Table 1.

Orbital periods from light curves and hardness ratios.

In the text
Table 2.

Results of the spectral analysis using Swift/XRT data.

In the text
Table 3.

Orbital periods obtained from the spin frequency and spin-frequency derivative history.

In the text

All Figures

thumbnail Fig. 1.

Lomb-Scargle periodograms of the light curves. Swift (top), MAXI (middle), and ISGRI (bottom).
In the text
thumbnail Fig. 2.

Epoch-folding periodograms of the light curves. Swift (top), MAXI (middle), and ISGRI (bottom).
In the text
thumbnail Fig. 3.

Folded light curves. We show folded Swift (first row), MAXI (second row), and ISGRI (third row) light curves with the folding periods being the corresponding Lomb-Scargle (LS) period PLS (left column), the epoch-folding (EF) period PEF (centre column), and the radial velocity (RV) period PRV (right column) from Hinkle et al. (2006). The phase bin around phase 0 corresponds to the phase bin of the predicted eclipse.
In the text
thumbnail Fig. 4.

Folded hardness ratios. We show MAXI (first row) and JEM-X (second row) hardness ratios folded with the Lomb-Scargle (LS) period PLS (left column), the epoch-folding (EF) period PEF (centre column), and the radial velocity (RV) period PRV (right column) from Hinkle et al. (2006). The phase bin around phase zero corresponds to the phase bin of the predicted eclipse.
In the text
thumbnail Fig. 5.

Spin-frequency history of GX 1+4. The data were taken from multiple missions. The solid line represents the linear fit to the data. We searched for periodicity in the residuals in the lower plot.
In the text
thumbnail Fig. 6.

Spin-frequency derivatives of GX 1+4 using Fermi/GBM data. The data points were obtained using a sliding-window approach, and a long-term trend was subtracted (solid orange line; see text).
In the text
thumbnail Fig. 7.

Visual summary of the analysis results. The blue circles represent the results obtained with the epoch-folding approach, and the results obtained with the Lomb-Scargle technique are shown as orange squares. The data sets are Swift, MAXI, ISGRI, MAXI hardness ratio, and spin-frequency derivative evolution, as indicated by the labels in the figure. The solid red line indicates the 1160.8 d radial velocity period obtained by Hinkle et al. (2006), and the dashed lines mark the corresponding 12.4 d uncertainty on this value.
In the text
thumbnail Fig. 8.

Companion radius as function of mass. The solid lines indicate the limits placed on the radius of the companion at different inclinations for a given neutron star mass. The mass-radius relation of M giants from the results by Dumm & Schild (1998) is indicated by the green dots. M5- and M6-type giants from this sample are represented by blue diamonds and black stars, respectively. The solid blue line represents the radius calculated from the gravitational acceleration log(g) as determined by Hinkle et al. (2006) for a given red giant mass, and the area shaded in light blue indicates the corresponding uncertainty. The area shaded in grey indicates the mass limits of the red giant as determined by Hinkle et al. (2006) through a spectroscopic analysis of the oxygen isotopic abundances of 17O and 16O.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.