EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 691 (November 2024) A&A, 691 (2024) A275 Full HTML
Open Access
Issue
A&A
Volume 691, November 2024
Article Number A275
Number of page(s) 12
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202450879
Published online 18 November 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

The origin of water on the Moon and terrestrial planets remains a matter of debate. One hypothesis posits that water sources from C-type asteroids and comets were dominant in the past. The ubiquitous presence of water in lunar soil, associated with solar wind, was recently confirmed through analyses of remote sensing and lunar samples (Clark 2009; Li & Milliken 2017; Liu et al. 2012; Pieters et al. 2009; Stephant & Robert 2014; Sunshine et al. 2009; Tian et al. 2024; Xu et al. 2022; Zhou et al. 2022). Water produced by solar wind has also been identified in interplanetary dust particles (IDPs) and regolith grains from the S-type asteroid Itokawa (Bradley et al. 2014; Daly et al. 2021). The interaction of solar wind protons with oxygen-containing materials is considered a significant mechanism of water formation on the surface of the Moon and other airless bodies in the Solar System (Farrell et al. 2017; Jones et al. 2020; Wöhler et al. 2017; Zhu et al. 2020). This process is thought to have played an essential role in the early formation of water in terrestrial planets (Daly et al. 2021; Djouadi et al. 2011; Jin & Bose 2021; King et al. 2010). According to this proposed mechanism, during the solar nebula and debris disk period, water was produced through hydrogen diffusion and implanted in dust grains, which were subsequently transported to the planetary interior via the accretion of micrometre-sized dust particles and planetesimals.

Understanding the formation and preservation of solar-wind-produced water is crucial for assessing its contributions to water on the Moon and terrestrial planets. Previous analyses of lunar samples and simulation experiments have confirmed the formation of solar-wind-produced water and determined its occurrence state, generation mechanism, and influencing factors (Ichimura et al. 2012; Liu et al. 2012; Schaible & Baragiola 2014; Stephant & Robert 2014; Tang et al. 2021; Xu et al. 2022; Zeller et al. 1966; Zeng et al. 2021; Zhou et al. 2022; Zhu et al. 2019). However, the depth profile characteristics of solar wind protons implanted in minerals have not been examined in detail. Moreover, there is still a lack of systematic analyses on the activities of solar wind protons implanted in minerals, including collisions, sputtering, and diffusion. Consequently, our understanding of the occurrence and chemical location of implanted protons in minerals remains limited, which in turn limits our knowledge of the escape and preservation of solar-wind-produced water.

According to previous studies of the Apollo and Chang’E-5 samples, as well as simulation experiments, solar wind protons are predicted to exist within a depth range of 20 to 200 nm in samples after implantation, which corresponds to the amorphous rims produced by solar wind (Blanford et al. 1986; Bradley et al. 2014; Keller & Berger 2014; Keller & McKay 1997; Leich et al. 1973; Xu et al. 2022; Zeng et al. 2021; Zhou et al. 2022). During NASA’s Genesis mission, solar wind particles were collected, and the hydrogen depth distribution was recorded using synthetic materials (Huss et al. 2020). However, due to their different chemical compositions and structures, these samples do not represent lunar silicate minerals. Recently, Daly et al. (2021) analysed the profile distribution of hydrogen species in Itokawa olivine grains and deuterium (D) in irradiated olivine using atom-probe tomography and transmission electron microscopy (TEM). They primarily discuss the occurrence and relative contents of implanted particles in the shallow region (40–180 nm) without focusing on the distribution in the interior region. Given the limited sensitivity of analytical instruments to detect low abundances of H and D, it remains challenging to identify the implanted solar wind protons within the interior of minerals. Consequently, the distribution and retention of implanted protons from the surface to the interior of various minerals remain unclear. The structure and crystal planes of different minerals may influence the implantation depth of solar wind protons and the distribution of OH and H2O (Li et al. 2013). The highly mobile H readily diffuses to interior breaks or defects in the crystal structure, forming chemically bound hydroxyl (−OH) and even water (H2O), which are more stable than at the surface (McCord et al. 2011). Understanding the relationship between the surface profile of solar wind protons and the structural modifications of silicate minerals should clarify how OH and H2O are generated via solar wind proton implantation.

To elucidate the distribution of implanted solar wind in silicate minerals and the contribution of solar-wind-produced water on the Moon and terrestrial planets, we conducted simulation experiments by implanting deuterium ions (D+) in samples of olivine, pyroxene, and plagioclase. A combination of Fourier transform infrared (FTIR) spectroscopy, nanoscale secondary ion mass spectrometry (NanoSIMS), and TEM was utilised to determine the occurrence state and depth profile distribution of D, as well as its relationship with the irradiation-induced damage in the structure of the implanted silicates.

2 Materials and methods

2.1 Sample preparation

Olivine, pyroxene, and plagioclase are abundant in lunar regolith. Terrestrial single-crystal samples of these minerals were selected to simulate solar wind implantation on the lunar surface. The olivine and pyroxene samples were sourced from peridotite and pyroxenite, respectively, in the Damaping volcanic field in Hebei, China. Plagioclase was obtained from the Damiao Anorthosite, also in Hebei, China. The composition of all three samples was quantitatively analysed using a JOEL JXA 8230 electron probe microanalyser (Tokyo, Japan) at the Institute of Geochemistry, Chinese Academy of Sciences (IG-CAS).

Detailed analytical methods and chemical compositions are provided in Appendix A and Table A.1, respectively. Each silicate sample was prepared as a double-sided polished section, approximately 0.5 × 0.5 cm2 in size and 200 ± 10 µm thick. All polished samples were soaked in acetone for 24 h and then alternately cleaned three times with ethanol and pure water. Finally, sections were fixed onto an aluminium alloy holder with metal clips and baked at 110 °C for 24 h to remove absorbed water.

2.2 Ion irradiation

The D+ implantation experiment was performed using an ion implanter at the IG-CAS. This instrument comprises an ion source, an accelerator, a magnetic deflection system, a vacuum system, a sample chamber, and a control system. Before irradiation, the holder containing the prepared samples was placed in the sample chamber. The entire system was purged with pure nitrogen gas (99.999%) and then evacuated to maintain a pressure of approximately 2 × 10−7 Torr. Molecular deuterium ions (D2+) were generated by ionising high-purity molecular deuterium gas (D2; 99.999%) and then accelerated in an electric field. The filtered D2+ flow was implanted in the samples via the magnetic field. The three silicate minerals were exposed to 3 keV D2+ with a total fluence of 1.4 ± 0.1 × 1017 ions/cm2. This is equivalent to 1.5 keV D+ and corresponds to D implantation with a total fluence of 2.8 ± 0.2 × 1017 ions/cm2 (Kato et al. 2015), which approximates exposure times of nearly 50–90 years on the Moon (Hansteen & Velli 2012). The irradiation temperature was maintained at 21 ± 1 °C, monitored using an infrared thermometer during the implantation process. The areas in the samples covered by metal clips were not irradiated and were used as control samples, ensuring that the background level of D was retained in these regions.

2.3 Fourier transform infrared spectroscopy

All transmission FTIR data were collected before and after irradiation using a Thermo IS50 FTIR (Thermo Fisher Scientific, Waltham, MA, USA) coupled with a Continuum infrared microscope (Thermo Fisher Scientific) at the IG-CAS in a high-purity nitrogen environment. The implanted samples were transferred between the ion implanter and FTIR spectrometer, exposing them to air for a few minutes. After measurements, the samples were restored under dry conditions. Spectra in the range of 4500–1000 cm−1 were collected with 256 scans and a spectral resolution of 4 cm−1 using a mercury-cadmium-telluride detector. The same positions before and after D+ implantation in each sample were measured to compare the effects of D+ implantation on the minerals. Approximately 50 × 50 µm2 measurement spots were chosen from clean, crack-free areas of the three silicate minerals.

2.4 Nanometre-scale secondary ion mass spectrometry

The hydrogen isotopes in the D-irradiated and unirradiated areas of the three samples were measured with a Cameca NanoSIMS 50 L at the Institute of Geology and Geophysics, Chinese Academy of Sciences. The samples and standards were fixed in an indium holder and baked at approximately 40 °C in a NanoSIMS airlock for 12 h. The sample holder was then transferred to a NanoSIMS sample chamber to improve vacuum quality and minimise the H background (Hu et al. 2020a,b) (for details, see Appendix B). To determine the H isotope abundance from the surface to the interior, each 8 × 8 µm analysis area was directly measured using a 50-pA primary caesium ion (Cs+) beam without pre-sputtering. The secondary ions 1H−, 2D−,13 C−, and16 O− were simultaneously counted using electron multipliers from the central 2 × 2 µm area (93.75% blanking). According to Hu et al. (2015), the high blanking improves the accuracy of analysis results and significantly reduces the influence of lateral signals. The distributions of the four ions in the shallow and deeper regions of the implanted samples were counted using two methods. The first method aimed to determine the D trend from the surface to the interior: (1) using a 50 pA Cs+ beam to measure 4000 cycles; (2) sputtering for 2 min with a 6 nA beam; (3) using a 50 pA beam to measure 160 cycles; and (4) repeating steps (2)–(3) five times. The second method used a 50 pA Cs+ beam to measure 4000 cycles, verifying the consistency of the surface distribution of the four ions in different positions on the same sample and calculating the sputtering speed of the 50 pA beam. Finally, two measuring pits of each irradiated mineral were left: deep and shallow. The unirradiated areas in each mineral sample covered by metal clips were measured in two pits with 400 cycles.

thumbnail Fig. 1

FTIR spectra. (a) Unirradiated and D+-irradiated olivine. (b) Unirradiated and D+-irradiated pyroxene. (c) Unirradiated and D+-irradiated plagioclase. (d, e, and f) Difference (D+-irradiation minus unirradiated) between a D+-irradiation spectrum and an unirradiated spectrum in olivine, pyroxene, and plagioclase, respectively. (g, h, and i) FTIR spectra of the reference blank unirradiated region in each sample, taken before and after the experiment. Panels (g, h, and i) show that the changes in the spectra shown in panels (a, b, and, c) result from the D implantation rather than environmental conditions.

2.5 Transmission electron microscopy

To measure the depth of the pits produced via NanoSIMS and prepare samples for TEM analysis, four thin slices of each silicate mineral were prepared using an FEI Scios dual-beam focused ion beam scanning electron microscope (Hillsboro, OR, USA) at IG-CAS (for details, see Text S3). Structural and chemical analyses of the three irradiated samples (including high-resolution images, bright-field/dark-field images, electron diffraction data, and energy dispersive spectroscopy) were performed using a Talos F200S TEM (Thermo Fisher Scientific) at the Guangdong University of Technology. The instrument was operated at an accelerating voltage of 200 kV and beam current of 1 nA.

3 Results

Figure 1 shows the FTIR absorption spectra in the 2400–4000 cm−1 range for olivine, pyroxene, and plagioclase before and after D+ implantation. The absorption range of 3000–3800 cm−1 primarily represents O–H vibrations in nominally anhydrous minerals (Johnson & Rossman 2004; Koga et al. 2003). Plagioclase exhibited the strongest hydroxyl absorption among the three samples, with the most significant decrease following D+ implantation. In contrast, olivine and pyroxene showed almost no OH absorption peaks, and no substantial changes were observed in the 3000–3800 cm−1 range after the implantation experiment. D+ implantation introduced a new broad band at 2400–2800 cm−1 for each silicate mineral, representing the O–D stretching vibration of deuterated silanol groups (Burneau & Gallas 1998; Ichimura et al. 2012). The central absorption peaks for OD in olivine, pyroxene, and plagioclase were 2624 ± 8, 2608 ± 10, and 2620 ± 10 cm−1, respectively. The OD absorption strength increased most significantly in plagioclase, followed by olivine and pyroxene, with integrated absorption area increases of 0.15 ± 0.06, 0.12 ± 0.03, and 0.04 ± 0.01 cm−1, respectively.

The D/16O ratio, obtained from the NanoSIMS analysis, reflects the abundance of implanted D in the profiles of olivine, pyroxene, and plagioclase (Fig. 2) minerals. The D/16O ratios of irradiated samples show similar variation trends at shallow depths, as shown in Figs. 2a, 2c, and 2e. Initially, the D/16O ratio rose rapidly, reached a peak, and then declined sharply. Although the peak values of the D/16O ratio were comparable in olivine and pyroxene, they were much lower in plagioclase. Subsequently, the D/16O ratio gradually decreased until stabilising at depths of approximately 160 nm for olivine, 175 nm for pyroxene, and 200 nm for plagioclase. This depth range is broader than that predicted by the Stopping and Range of Ions in Matter (SRIM) program (see Ziegler et al. 2010 and our Appendix C and Fig. C.1). In the shallow region, the total D/16O ratio at depths of 266–280 for olivine, 369–388 for pyroxene, and 415–437 nm for plagioclase decreased steadily to 1.65 ± 0.05 × 10−5, 1.94 ± 0.06 × 10−5, and 7.09 ± 0.38 × 10−6, respectively. Moreover, the deeper profiles showed that the D/16O ratio could persist several micrometres deep in all three minerals (Fig. 2b, 2d, and 2f). The variation trends of D/16O with depth in the three minerals are consistent with Fick’s second law and fit an exponential function. The intersection of the fitted curve with the baseline indicates the maximum depth of implanted D. Among the three evaluated silicates, plagioclase exhibited the deepest penetration of implanted D at 4855 ± 263 nm, followed by pyroxene at 4049 ± 50 nm, and olivine at 3619 ± 112 nm.

The surface microstructures of olivine, pyroxene, and plagioclase after D+ implantation are shown in Fig. 3. Except for the conductive coating layers covering the silicate samples, distinct structural features were observed from the mineral surface to the interior. The top layer of the three D-irradiated silicates showed an absence of diffraction spots, indicating complete amorphisation, with thicknesses of 45–65 nm for olivine, 57–70 nm for pyroxene, and 65–70 nm for plagioclase. Additionally, numerous nanoscale bubble-like features developed in the olivine and pyroxene areas, while fewer were present in plagioclase. Below the completely amorphous rim of each sample, the structure gradually transitioned to a partially amorphous state, whose diffraction pattern displayed diffraction rings and blurred lattice spots. The depth of this partially amorphous state varied among the three silicates, extending up to 160 nm in olivine, 180 nm in pyroxene, and 190 nm in plagioclase. The bottom region of the three TEM images revealed the crystalline matrix of the silicates. Compared to the crystal matrix and the partially amorphous area, the arrangement of diffraction patterns remained similar despite some partially missing patterns. This observation indicates that the implanted D particles destroyed the mineral structure without generating new crystals.

The profile changes of major elements in olivine, pyroxene, and plagioclase after D+ implantation are shown in Fig. 4. In olivine, the counts of oxygen (O), magnesium (Mg), and silicon (Si) generally increased with depth up to approximately 65 nm near the boundary of the amorphous rim, after which they gradually stabilised. In contrast, iron (Fe) signals exhibited minimal variation throughout the profile. For pyroxene, the O, Si, Mg, and calcium (Ca) counts increased from the surface to the interior, with a stable plateau occurring deeper than in olivine. The counts for aluminium (Al) and Fe showed only minor changes with depth. In plagioclase, only O exhibited an increasing trend with depth. The counts of Si and Al fluctuated noticeably within 20 nm on the surface, and the changes in the Ca and sodium (Na) were minimal. Notably, major elements in the three silicates exhibited local decreases or abnormalities when crossing the bubble-like features in the amorphous rim, indicating the presence of vesicles. Overall, after deuterium implantation, the elemental counts on the surface of silicate samples generally decreased, particularly the major elements constituting the crystal structure, such as O and Si. The depth of this variation generally corresponds to the extent of the completely amorphous rim.

thumbnail Fig. 2

Depth profiles of the D/16O ratio determined using NanoSIMS for D-irradiated samples on the surface (a, c, and e) and in the interior (b, d, and, f). Depth measurement methods and interior data calibration methods are described in Appendices D and E. The upper x-axis gives the raster cycle number, and the lower x-axis the depths according to the NanoSIMS analysis pits. Each data point in panels a, c, and e corresponds to one cycle at one depth. Each data point in panels b, d, and f is the sum analysis result of 160 cycles. The grey region in panels b, d, and f represents the D/16O ratio of backgrounds for each mineral (less than 9.7 ± 6.8 × 10−9 for olivine; less than 1.9 ± 0.8 × 10−8 for pyroxene; and less than 2.3 ± 1.3 × 10−8 for plagioclase). The error bars represent the standard error of the mean. The dashed red line in panels b, d, and f represents the fitting curve for the decreasing trend of D/16O. The intersection of the fitting curve with the background value for each silicate indicates the deepest penetration of implanted D: 3619 ± 112 nm in olivine, 4049 ± 50 nm in pyroxene, and 4855 ± 263 nm in plagioclase.
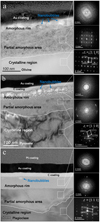thumbnail Fig. 3

Microstructural characteristics of D-irradiated silicates as revealed by TEM images: olivine (a), pyroxene (b), and plagioclase (c). The three images to the right of the main TEM images show diffraction patterns from selected white areas. The absence of diffraction spots in the top image of each set indicates the presence of an amorphous rim. The middle image for each silicate features both diffraction rings and blurred spots, suggesting a partial amorphous state. The distinct crystal diffraction pattern in the bottom image of each set represents the crystalline matrix; the zone axis superimposed on the image aligns with [110] in olivine and pyroxene, and [111] in plagioclase.
thumbnail Fig. 4

Major element profile of a D-irradiated silicate surface, measured via energy dispersive spectroscopy in TEM. (a) High-angle annular dark-field (HAADF) image of olivine. (b) Element profile of olivine obtained from the green arrow in panel (a). (c) HAADF image of pyroxene. (d) Element profile of pyroxene obtained from the green arrow in panel (c). (e) HAADF image of plagioclase. (f) Element profile of plagioclase obtained from the green arrow in panel (e). The dotted black line in the images to the right (b, d, and e) indicates the boundary of completely amorphous rims, measured from the TEM image shown in Fig. 3.

4 Discussion

4.1 Distribution of implanted deuterium in silicates

The FTIR data suggest that the implanted D can destroy the original OH groups in silicate minerals, producing a new broad band at 2400–2800 cm−1, indicative of the OD stretch of deuterated silanol groups (Si O–D; Burneau & Gallas 1998; Chumaevskii et al. 1999). Since the natural abundance of D in terrestrial mineral is too low to be detected by FTIR, all newly formed OD groups were attributed to the combination between the implanted D particles and oxygen atoms in silicates, consistent with experiments involving D+ implantation in lunar regolith (Ichimura et al. 2012). The variation in OD absorption density across the three minerals suggests that the type of silicate minerals can influence the efficiency of OD generation. Plagioclase exhibits the highest capacity for forming OD, followed by olivine, with pyroxene showing the least conversion of implanted D in OD species. This observation aligns with that reported by Tang et al. (2021), which reported that the H-irradiated plagioclase exhibits the highest OH generation efficiency among different silicate minerals. They associated this efficiency with the high content of Si–O tetrahedra in plagioclase. Implanted D (or H) particles can break the bonds within Si–O tetrahedra and M–O (where M represents a metal cation) octahedra in silicates, binding to the suspended oxygen in these structures to form OD (or OH) groups. Pla-gioclase, with its higher density of silica tetrahedra compared to olivine and pyroxene, captures more implanted D particles. Additionally, implanted D particles may also enter structural defects or vacancies, potentially forming new bonds such as Si–D, although these were not detected in our FTIR analysis.

By comparing the D depth profiles obtained from NanoSIMS with the microstructural observations gathered from TEM analysis, we identified that the retention sites of implanted D are closely correlated with the radiation-induced damage on the mineral surface. Table 1 shows the proportions of implanted D signals from different regional ranges relative to the total amounts in the three silicate samples (see the calculation method in Appendix F). The majority of the implanted D is concentrated in the fully amorphous rims, amounting to ~92.8% in olivine, ~87.8% in pyroxene, and ~72.7% in plagioclase. Here, the D concentration exhibits a precipitous decline from a high value at the surface to a relatively low plateau. As depth increases, the D signals gradually decrease further, and the structure transitions from being completely amorphous to discontinuously partially amorphous. In the partially amorphous region, D content accounts for approximately 6%, 10.7%, and 25.3%, of the total implanted signals in olivine, pyroxene, and plagioclase, respectively. When the depth increases to the crystallisation region, only a few implanted D signals were measured, and the D ratio of total implantation is about 1.2% in olivine, 1.5% in pyroxene, and 2.0% in plagioclase. These results indicate that implanted D primarily accumulates in the radiation-damaged areas, with smaller amounts distributed in the crystalline regions. Interestingly, at depths beyond 1 micron, between 0.17% and 0.48% of the total implanted D signals are still detectable. Furthermore, the distribution of D differs among the three minerals. In the radiation-damaged regions, olivine has the highest proportion of implanted D, followed by pyroxene and plagioclase. Conversely, in the deeper crystalline regions, the proportion of D is greater in plagioclase compared to pyroxene and olivine.

4.2 Mechanism of deuterium ion implantation

According to the profile characteristics of D/16O and microstructure, four main mechanisms may determine the distribution of implanted D in the minerals: (1) the collision process between implanted D and atoms in the minerals, (2) the diffusion of D from high to low concentrations, (3) the sputtering of implanted D on the mineral surface, and (4) the exchange of D for original H in the minerals (Shelby 1977; Stone 1987). Considering that the exchange process mainly occurs in environments above 300°C (Shelby 1977), which is not applicable in our experiment, only collision, sputtering, and diffusion processes are described below.

At an implantation energy of 1.5 keV of D and D+, the interaction between the implanted D particles and lattice atoms in the minerals was expressed as elastic and inelastic collisions. As reported by Zhu et al. (2019), the impact from D can cause lattice atoms to shift or sputter, leading to the creation of dislocations, vacancies and broken bonds. The implanted D gradually loses energy and eventually becomes embedded in the lattice, resulting in a significant accumulation of D in the radiation damage layer on the mineral surface. Simultaneously, this implanted D may combine with the O ions of broken bonds to form OD. A high dose of implanted D can cause local defect regions to merge, forming an amorphous layer. If the dose exceeds a certain threshold, vesicles or nanocracks could develop in a completely amorphous layer (Cerofolini et al. 2000; Terreault 2007). In this study, we observed a completely amorphous rim with vesicles on the surfaces of olivine, pyroxene, and plagioclase. The key distinction lies in the rim of plagioclase, which is thicker and contains fewer vesicles compared to those on olivine and pyroxene. Consequently, implanted D appears to penetrate the interior of plagioclase more easily than in pyroxene and olivine. This observation is supported by data showing that the proportion of implanted D in the completely amorphous rim is highest in olivine (~92.8%), followed by pyroxene (~87.8%) and lowest in plagioclase (~72.7%). Moreover, due to cascade collisions and channel effects, some implanted D can enter deeper into the interior, leading to partial amorphisation in the lower region. According to the TEM images, the partial amorphous layers observed in the three silicates are irregular and can extend up to approximately 200 nanometres, which consists of the second decline trend observed in the depth profile of D in the NanoSIMS data. Contrary to the completely amorphous rim, the proportion of implanted D in partially amorphous region was the largest in plagioclase (~25.3%), following to pyroxene (~10.7%) and the smallest in olivine (~6%). Overall, these results indicate that the collision process was the dominant mechanism for D retention and OD formation in the implanted samples. Due to the varying properties of mineral structures, three silicates demonstrate varying degrees of resistance to the implantation of D ions. Notably, plagioclase is the most susceptible to damage, which enhances the penetration of D ions into deeper layers.

Deuterium, like hydrogen, has favourable diffusion properties in minerals (Ingrin & Blanchard 2006). Diffusion process is the most likely mechanism for the small amount of D observed in the crystalline regions of the three minerals. In the D-irradiated olivine, pyroxene, and plagioclase samples, the diffusion of D species includes both outward and inward processes. While outwardly diffusing D particles may potentially escape the sample surface, analytical results indicate that approximately 1.3% to 2% of the total implanted deuterium remains distributed in the crystallisation region below the radiation damage rim. Notably, the D signals in the irradiated silicates at depths beyond 1 micron remain above the baseline of the blank sample and display an exponentially decreasing trend consistent with the diffusion equation. Given the absence of structural damage, these results suggest that inward diffusion is the primary mechanism facilitating the migration of implanted D particles to deeper sites within the mineral, following particle collision processes. During diffusion, temperature and concentration gradients are critical factors driving particle migration within solids (Higashi et al. 2017). In our implantation experiment, there was only a slight temperature increase of 2°C. Consequently, the concentration gradient played a dominant role in influencing the distribution of the implanted deuterium (D) within the interior region. Among the three D-irradiated silicates, plagioclase exhibits the highest proportion of interior signals relative to the total amount of D implantation and the greatest penetration depth, indicating superior inward migration efficiency of implanted D particles in plagioclase. Regardless of the type of silicate mineral, these inward diffusing D particles could become trapped in the defects and vacancies of the silicate structure, allowing them to be retained more stably in the interior than in the surface region.

Based on inelastic collisions, the implanted D transferred energy to surface atoms, enabling light atoms on the surface to acquire a higher kinetic energy that exceeds their binding energy, leading to sputtering out of the surface (Barghouty et al. 2011). In the amorphous rim, mostly crystal framework elements showed significant reductions, particularly O, Si, and Al, whereas other coordinating cation elements such as Mg, Fe, and Ca showed smaller changes. These results are consistent with studies that demonstrate the depletion of chemical elements such as oxygen (O) and silicon (Si) on the surface of lunar minerals (Keller & McKay 1997; Zhou et al. 2022). Overall, sputtering by solar wind provides an important pathway for the origin of ions in the lunar exosphere.

Table 1

Proportion of implanted D in different depth regions of olivine, pyroxene, and plagioclase.

4.3 Implications for the contribution of solar-wind-induced water

Under the effects of collision and diffusion processes, implanted D particles are ultimately trapped within the silicates, with some forming OD groups by bonding with oxygen. The implanted D was primarily concentrated within approximately 80 nm of the mineral surface, but the final retention depth was significantly larger than that discussed in previous studies (Blanford et al. 1986; Bradley et al. 2014; Keller & Berger 2014; Keller & McKay 1997; Leich et al. 1973). Similarly, following decades of exposure on the lunar surface, implanted protons from the solar wind can be deposited at depths ranging from over 200 nm to several micrometres within the mineral interior. This is crucial for understanding the contribution of solar-wind-induced protons to the origins of water on the Moon and terrestrial planets.

The influence of solar wind must be carefully considered when determining the ratio of hydrogen isotopes and the variation of water content in lunar minerals, especially in regolith grains with high water content on the surface. According to Zhou et al. (2022), the water content of the Chang’E 5 lunar olivine, pyroxene, and plagioclase within 200 nm is up to 4483 ± 314, 5962 ± 335, and 4476 ± 142 ppm, respectively, with very low hydrogen isotope ratios ranging from −773 ± 188 to 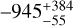−945−55+384$ - 945_{ - 55}^{ + 384}$ ‰, indicating a solar wind radiation source. Based on the proportion of implanted D calculated in this study, it can be estimated that nearly 60 ± 4 ppm, 101 ± 5 ppm, and 124 ± 3 ppm of solar-wind-induced water can be preserved at depths ranging from 200 nm to several micrometres in olivine, pyroxene, and plagioclase, respectively. Correspondingly, small amounts of water (8 ppm in olivine, 22 ppm in pyroxene, and 29 ppm in plagioclase) from solar wind implantation may diffuse to depths exceeding 1 to 5 µm. Hence, solar wind protons could significantly affect the isotopic composition of hydrogen and the water abundance in the micrometre range of silicate grains, especially in discussions of magma-derived water. Moreover, the lunar regolith has generally been exposed to solar wind for prolonged periods, resulting in a fluence much larger than that in our experiment, which simulates exposure over several decades. Consequently, the diffusion depth and amount of hydrogen could be more significant than those observed in our study. Given the influence of solar-wind-induced water on the depth profile of the lunar samples collected by the Apollo, Chang’E-5, and Chang’E-6 missions, it is essential to carefully distinguish the sources when analysing the characteristics of water derived from lunar magma in the fine-grain surface within the micrometre range.

Additionally, our experimental findings have improved the understanding of the contribution of solar wind implantation to the water content in IDPs (mainly silicates), which relates to the accretion of early terrestrial bodies (Djouadi et al. 2011; Bradley et al. 2014). Daly et al. (2021) detected water in the solar-wind-irradiated rim (within 200 nm) of an olivine grain from the S-type asteroid Itokawa and discussed that the implantation of solar wind into fine-grained silicates serves as a crucial pathway for providing a light water reservoir. The results of our study suggest that the implanted solar wind protons not only accumulated in the amorphous rim but could also continue to diffuse into the crystalline interior, reaching depths exceeding 200 nm to several micrometres. Moreover, solar wind implantation was more intense in the early stages of the Solar System, exhibiting higher energy and flux (Wood et al. 2002; Vidotto 2021). This led to stronger hydrogen fixation and greater water accumulation on the surfaces of IDPs, potentially driving deeper diffusion of hydrogen ions due to concentration gradients. These diffused hydrogen particles, which are more stable within the crystal structure than on the amorphous surface of silicate grains, contribute to providing a primitive hydrogen reservoir for terrestrial bodies during the early accretion period of the Solar System (Jin & Bose 2021).

5 Conclusions

We have examined the current understanding that solar wind protons implanted in silicates and combined with oxygen are important mechanisms for the formation of OH/H2O on the Moon and other airless bodies in the Solar System, primarily at the nanometre-surface scale of minerals. To investigate the detailed ion penetration profiles of solar wind protons, three types of silicates (olivine, pyroxene, and plagioclase) were implanted with 3 keV D2+ to simulate solar wind irradiation. We analysed the active mechanism of implanted D to characterise the occurrence, distribution, and modification of these three silicates.

A new OD bond was produced in olivine, pyroxene, and plagioclase after D implantation, accompanied by a decrease in the original OH/H2O. The OD bond absorption exhibited the largest increase in plagioclase, followed by olivine and pyroxene, respectively. The profile trends of implanted D were similar across all three silicate samples, although the specific retention depths varied. More than 73% of implanted D was retained in amorphous rims within 70 nm, whereas less than 25% reached deeper into partially amorphous areas to approximately 190 nm. Small amounts of the total implanted D (about 1.3% in olivine, 1.5% in pyroxene, and 2% in plagioclase) were detected within a depth of several micrometres in the crystalline region. This result suggests that the collision process is the main mechanism controlling the distribution of implanted D. However, diffusion processes within the crystal structure allowed implanted D particles to penetrate deeper into the interior, with a range significantly larger than that calculated from SRIM simulations. Overall, the effects of both collision and diffusion cannot be ignored in the process of implanted particle migration, especially in anhydrous minerals.

We have determined the general depth-profile distribution of implanted D in three typical silicates found on airless bodies in the Solar System and have demonstrated that solar wind protons can affect more than just the surface layers, penetrating to depths greater than 200 nanometres. The influence of solar wind protons on hydrogen isotopes must be carefully considered when analysing extraterrestrial samples with long-term exposure to Sun irradiation, particularly minerals that originally contained almost no water. Deeper implanted solar wind protons can also stably remain in minerals and may enter the interior of the planet with the accretion of silicates, providing an important source of planetary water.

Acknowledgements

This work was supported by the National Natural Science Foundation of China [grant number 41931077]; the Strategic Priority Research Program of the Chinese Academy of Sciences [grant number XDB 41000000]; and the Youth Innovation Promotion Association of the Chinese Academy of Sciences, with an award to Hong Tang [grant number Y2022099]. Additional funding was provided by the Innovation and Development Fund of Science and Technology of Geochemistry, Chinese Academy of Sciences [grant number 2024-1]. We extend our gratitude to Kate Burgess for her valuable review suggestions and to Jialong Hao and Ziliang Jin for their technical support.

Appendix B Chemical compositions of samples

Quantitative compositional analyses of the three samples were performed using a JOEL JXA 8230 electron probe microanalyser at the State Key Laboratory of Ore Deposit Geochemistry, Institute of Geochemistry, Chinese Academy of Sciences. The analytical conditions were set with an accelerating voltage of 25 kv and a beam current of 10 nA. Mineral standards for olivine, diopside, and plagioclase were used for calibration. Matrix corrections were performed using the ZAF (atomic number, absorption, fluorescence) program. The detection limits for the major elements were below 0.01 wt%. The chemical analysis data are shown in Table A.1.

Table A.1

Major and minor compositions of the studied minerals.

Appendix B NanoSIMS background and methods

San Carlos olivine was used for H background corrections according to the following relationship: H/Obg =(Hcounts−Hbg)/Ocounts) and D/Hmeasured = (1−f) × D/Hreal + f × D/Hbg, where f is the proportion of H from the instrument background (Hu et al. 2020a,b), D/Hbg = (2.17 ± 0.73) × 10−4, and Hbg = (9.23 ± 0.24) × 103 (2SD, N = 4). Instrumental mass fractionation and matrix effects on water content were established by measuring two apatite standards: Durango apatite (0.0478 wt% H2O) (Greenwood et al. 2008, 2011) and Kovdor apatite (0.98 ± 0.07 wt% H2O and δ D = −66 ± 21‰) (Nadeau et al. 1999), along with a mid-ocean ridge basalt (MORB) glass reference material (SWIFT MORB glass; 0.258 wt% H2O and δD = −73 ± 2 ‰). Hydrogen isotopic compositions are presented in delta notation δD = ((D/H)sample/(D/H)SMOW) −1) × 1000‰, where SMOW is the standard mean ocean water with a D/H ratio of 1.5576×10−4. All data are reported at 2σ uncertainties, including reproducibility of D/H measurements on reference materials, uncertainty of H2O background subtraction on San Carlos olivine, and internal precision of each analysis (Hu et al. 2020a,b).

We measured the irradiated and unirradiated areas on the experimental silicates (olivine, pyroxene, and plagioclase). Secondary anions 1H−, 2D−, and 12C− were counted simultaneously using electron multipliers, and 16O− were collected using a Faraday cup, as an internal reference for calibration. Thus, the D/16O ratio provides a more accurate reflection of implanted D trends in minerals than direct D counts.

Appendix C D+ implantation profiles from SRIM

Figure C.1 shows the calculated implantation profiles of 1.5 keV implanted D+ in olivine, pyroxene, and plagioclase using SRIM. The enrichment of D peaked at depths of 25, 27, and 31 nm for olivine, pyroxene, and plagioclase, respectively. In addition, the maximum penetration ranges of implanted D were 60, 63, and 75 nm for olivine, pyroxene, and plagioclase, respectively. The peak enrichment of implanted D ions generally corresponded to the maximum values in the NanoSIMS data (olivine: 8 ± 2 nm, pyroxene: 10 ± 3 nm, and plagioclase: 15 ± 3 nm). However, the penetration ranges observed in the NanoSIMS profiles are significantly deeper than the calculated results from SRIM.

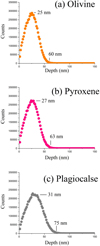thumbnail Fig. C.1

Calculated implantation profiles from SRIM simulations for 1.5 keV D+ into olivine (a), pyroxene (b), and plagioclase (c).

Appendix D Depth measurement methods and TEM preparation

After NanoSIMS analysis, measurement pits were observed on the sample surfaces. To determine the depth of these pits, slices of both deep and shallow pits from each silicate mineral were prepared using focused ion beam scanning electron microscopy (FIB/SEM), and the distance from the pit bottom to the surface was measured. The depths of the deep pits were approximately ~7.5, ~7.9, and ~8.5 µm, while the shallow pits measured ~280, ~389, and ~437 nm for olivine, pyroxene, and plagioclase, respectively. For TEM analysis, 70 nm-thick sections from both the un-implanted and implanted regions of each sample were also prepared using FIB/SEM.

Appendix E Depth D signals calibration method

To confirm and mitigate the influence of D re-deposition during NanoSIMS analysis in the depth region, we conducted depth NanoSIMS analysis on the irradiated minerals (olivine, pyroxene, and plagioclase) from both the front and back directions (Fig. E.1 ) to obtain a calibration equation. The front analysis was performed as follows: (1) sputtering for 4 min using a 2 nA beam from the irradiation surface; (2) measuring 160 cycles with a 50 pA beam; and (3) repeating steps (1)-(2) five times. Signals 1H−, 2D−, 13C−, and 18O−) were collected from the central 2.5 × 2.5 µm area of the 5 × 5 µm sputtering region (with 75% blanking). For the back NanoSIMS analysis, 20 × 20 × 8 µm slices were extracted from the irradiated surface using FIB, and the analysis was performed similarly to the front, but the sputtering and measuring direction was from the unirradiated side. Several interior D/18O data points at comparable depths were then used to fit the calibration equation via Origin software (Table E.1 , Fig. E.2 ). Based on the three derived calibration curves, the re-deposition influence on D signals was effectively eliminated from the original D/16O data of the deeper regions in olivine, pyroxene, and plagioclase, respectively.

Table E.1

D/18O of the front and back NanoSIMS analysis at different depths in implanted olivine, pyroxene, and plagioclase.

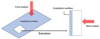thumbnail Fig. E.1

Schematic diagram of front and back NanoSIMS analysis methods in deep D signal validation experiments.
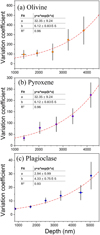thumbnail Fig. E.2

Variation coefficient between the front and back analysis data calculated using the following formula: (D/18O(front) )/( D/18O(back)). (a) Olivine. (b) Pyroxene. (c) Plagioclase. Both the front and back data exhibited a diffusion feature that increased with depth. Thus, the variation trend of the coefficient follows an exponential function. For olivine, pyroxene, and plagioclase, three distinct calibration curves were produced through exponential fitting. Utilising these three sets of equations allows for the effective removal of influence of D particle re-deposition during the deep NanoSIMS analysis from the original D/16O data.

Appendix F Method for calculating the proportion of D signals in different depth regions

To determine the proportion of implanted D signals in different depth regions of olivine, pyroxene, and plagioclase, we performed the following calculations: First, we fit the decreasing trend of the D/16O in the interior region and identified the intersection points between the fitting curve and the blank D/16O value for each silicate (see panels b, d, and fofFig. 2). This intersection point represents the maximum penetration depth (Rm) of the implanted D. Second, the D/16O variation trend (f(x)) was integrated from the surface depth of 0 to Rm to obtain the total D signal value. The D signal value in each respective region (including the completely amorphous region, the partially amorphous region, and the diffusion-affected region) was calculated by integrating f(x) from the beginning depth (Rb) to the ending depth (Re) of each region. Finally, the relative proportion (P) of D signals was determined by dividing the D signal value in the corresponding region by the total D signal value, as shown in the following equation: 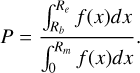P = ∫RbRef(x)dx∫0Rmf(x)dx.$P\, = \,{{\int_{{R_b}}^{{R_e}} {f\left( x \right)dx} } \over {\int_0^{{R_m}} {f\left( x \right)dx} }}.$(F.1)

This estimation process for the relative proportion of D signals involves data derived from average values obtained through detection or simulation results. The calculations were completed using Origin software.

References

  1. Barghouty, A., Meyer, F. W., Harris, P. R., & Adams Jr, J. 2011, Nucl. Instrum. Methods Phys. Res. B, 269, 1310 [NASA ADS] [CrossRef] [Google Scholar]
  2. Blanford, G., Børgesen, P., Maurette, M., Möller, W., & Monart, B. 1986, J. Geophys. Res. Solid Earth, 91, 467 [CrossRef] [Google Scholar]
  3. Bradley, J. P., Ishii, H. A., Gillis-Davis, J. J., et al. 2014, PNAS, 111, 1732 [NASA ADS] [CrossRef] [Google Scholar]
  4. Burneau, A., & Gallas, J. 1998, Hydroxyl groups on silica surfaces (Wiley New York) [Google Scholar]
  5. Cerofolini, G., Corni, F., Frabboni, S., et al. 2000, Mater. Sci. Eng. R: Rep., 27, 1 [CrossRef] [Google Scholar]
  6. Chumaevskii, N., Rodnikova, M., & Sirotkin, D. 1999, J. Mol. Liquids, 82, 39 [CrossRef] [Google Scholar]
  7. Clark, R. N. 2009, Science, 326, 562 [NASA ADS] [CrossRef] [Google Scholar]
  8. Daly, L., Lee, M. R., Hallis, L. J., et al. 2021, Nat. Astron., 5, 1275 [NASA ADS] [CrossRef] [Google Scholar]
  9. Djouadi, Z., Robert, F., d’Hendecourt, L. L. S., et al. 2011, A&A, 531, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Farrell, W., Hurley, D., Esposito, V., McLain, J., & Zimmerman, M. 2017, J. Geophys. Res. Planets, 122, 269 [NASA ADS] [CrossRef] [Google Scholar]
  11. Greenwood, J. P., Itoh, S., Sakamoto, N., Vicenzi, E. P., & Yurimoto, H. 2008, Geophys. Res. Lett., 35, L05203 [NASA ADS] [CrossRef] [Google Scholar]
  12. Greenwood, J. P., Itoh, S., Sakamoto, N., et al. 2011, Nat. Geosci., 4, 79 [NASA ADS] [CrossRef] [Google Scholar]
  13. Hansteen, V. H., & Velli, M. 2012, Space Sci. Rev., 172, 89 [Google Scholar]
  14. Higashi, Y., Itoh, S., Hashiguchi, M., et al. 2017, Geochem. J., 51, 115 [NASA ADS] [CrossRef] [Google Scholar]
  15. Hu, S., Lin, Y., Zhang, J., et al. 2015, J. Analyt. At. Spectrom., 30, 967 [CrossRef] [Google Scholar]
  16. Hu, S., Lin, Y., Anand, M., et al. 2020a, J. Geophys. Res. Planets, 125, e2020JE006537 [CrossRef] [Google Scholar]
  17. Hu, S., Lin, Y., Zhang, J., et al. 2020b, Earth Planet. Sci. Lett., 530, 115902 [CrossRef] [Google Scholar]
  18. Huss, G. R., Koeman-Shields, E., Jurewicz, A. J., et al. 2020, Meteor. Planet. Sci., 55, 326 [NASA ADS] [CrossRef] [Google Scholar]
  19. Ichimura, A., Zent, A., Quinn, R., Sanchez, M., & Taylor, L. 2012, Earth Planet. Sci. Lett., 345, 90 [CrossRef] [Google Scholar]
  20. Ingrin, J., & Blanchard, M. 2006, Rev. Mineral. Geochem., 62, 291 [NASA ADS] [CrossRef] [Google Scholar]
  21. Jin, Z., & Bose, M. 2021, ApJ, 913, 116 [NASA ADS] [CrossRef] [Google Scholar]
  22. Johnson, E. A., & Rossman, G. R. 2004, Am. Mineralogist, 89, 586 [NASA ADS] [CrossRef] [Google Scholar]
  23. Jones, B., Sarantos, M., & Orlando, T. 2020, ApJ, 891, L43 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kato, S., Tanaka, N., Sasao, M., et al. 2015, J. Nucl. Mater., 463, 351 [NASA ADS] [CrossRef] [Google Scholar]
  25. Keller, L. P., & Berger, E. L. 2014, Earth Planets Space, 66, 1 [CrossRef] [Google Scholar]
  26. Keller, L. P., & McKay, D. S. 1997, Geochim. Cosmochim. Acta, 61, 2331 [NASA ADS] [CrossRef] [Google Scholar]
  27. King, H., Stimpfl, M., Deymier, P., et al. 2010, Earth Planet. Sci. Lett., 300, 11 [CrossRef] [Google Scholar]
  28. Koga, K., Hauri, E., Hirschmann, M., & Bell, D. 2003, Geochem. Geophys. Geosyst., 4, 1019 [NASA ADS] [CrossRef] [Google Scholar]
  29. Leich, D., Tombrello, T., & Burnett, D. 1973, in Proceedings of the Lunar Science Conference, 4, 1597 [NASA ADS] [Google Scholar]
  30. Li, S., & Milliken, R. E. 2017, Sci. Adv., 3, e1701471 [Google Scholar]
  31. Li, Y., Li, X., Wang, S., et al. 2013, J. Geophys. Res.: Planets, 118, 1974 [NASA ADS] [CrossRef] [Google Scholar]
  32. Liu, Y., Guan, Y., Zhang, Y., et al. 2012, Nat. Geosci., 5, 779 [NASA ADS] [CrossRef] [Google Scholar]
  33. McCord, T., Taylor, L., Combe, J.-P., et al. 2011, J. Geophys. Res. Planets, 116, E00G05 [CrossRef] [Google Scholar]
  34. Nadeau, S. L., Epstein, S., & Stolper, E. 1999, Geochim. Cosmochim. Acta, 63, 1837 [NASA ADS] [CrossRef] [Google Scholar]
  35. Pieters, C. M., Goswami, J., Clark, R., et al. 2009, Science, 326, 568 [NASA ADS] [CrossRef] [Google Scholar]
  36. Schaible, M. J., & Baragiola, R. A. 2014, J. Geophys. Res.: Planets, 119, 2017 [NASA ADS] [CrossRef] [Google Scholar]
  37. Shelby, J. 1977, J. Appl. Phys., 48, 3387 [NASA ADS] [CrossRef] [Google Scholar]
  38. Stephant, A., & Robert, F. 2014, PNAS, 111, 15007 [NASA ADS] [CrossRef] [Google Scholar]
  39. Stone, J. 1987, J. Lightwave Technol., 5, 712 [NASA ADS] [CrossRef] [Google Scholar]
  40. Sunshine, J. M., Farnham, T. L., Feaga, L. M., et al. 2009, Science, 326, 565 [CrossRef] [Google Scholar]
  41. Tang, H., Li, X., Zeng, X., et al. 2021, Icarus, 359, 114322 [NASA ADS] [CrossRef] [Google Scholar]
  42. Terreault, B. 2007, Physica status solidi (a), 204, 2129 [CrossRef] [Google Scholar]
  43. Tian, H.-C., Hao, J., Lin, Y., et al. 2024, Geophys. Res. Lett., 51, e2023GL107005 [Google Scholar]
  44. Vidotto, A. A. 2021, Liv. Rev. Solar Phys., 18, 3 [NASA ADS] [CrossRef] [Google Scholar]
  45. Wöhler, C., Grumpe, A., Berezhnoy, A. A., & Shevchenko, V. V. 2017, Sci. Adv., 3, e1701286 [CrossRef] [Google Scholar]
  46. Wood, B. E., Müller, H.-R., Zank, G. P., & Linsky, J. L. 2002, ApJ, 574, 412 [NASA ADS] [CrossRef] [Google Scholar]
  47. Xu, Y., Tian, H.-C., Zhang, C., et al. 2022, PNAS, 119, e2214395119 [NASA ADS] [CrossRef] [Google Scholar]
  48. Zeller, E. J., Ronca, L. B., & Levy, P. 1966, J. Geophys. Res., 71, 4855 [NASA ADS] [CrossRef] [Google Scholar]
  49. Zeng, X., Tang, H., Li, X., et al. 2021, Earth Planet. Sci. Lett., 560, 116806 [CrossRef] [Google Scholar]
  50. Zhou, C., Tang, H., Li, X., et al. 2022, Nat. Commun., 13, 5336 [Google Scholar]
  51. Zhu, C., Crandall, P. B., Gillis-Davis, J. J., et al. 2019, PNAS, 116, 11165 [NASA ADS] [CrossRef] [Google Scholar]
  52. Zhu, C., Góbi, S., Abplanalp, M. J., et al. 2020, Nat. Astron., 4, 45 [Google Scholar]
  53. Ziegler, J. F., Ziegler, M. D., & Biersack, J. P. 2010, Nucl. Instrum. Methods Phys. Res. B, 268, 1818 [Google Scholar]

All Tables

Table 1

Proportion of implanted D in different depth regions of olivine, pyroxene, and plagioclase.

In the text
Table A.1

Major and minor compositions of the studied minerals.

In the text
Table E.1

D/18O of the front and back NanoSIMS analysis at different depths in implanted olivine, pyroxene, and plagioclase.

In the text

All Figures

thumbnail Fig. 1

FTIR spectra. (a) Unirradiated and D+-irradiated olivine. (b) Unirradiated and D+-irradiated pyroxene. (c) Unirradiated and D+-irradiated plagioclase. (d, e, and f) Difference (D+-irradiation minus unirradiated) between a D+-irradiation spectrum and an unirradiated spectrum in olivine, pyroxene, and plagioclase, respectively. (g, h, and i) FTIR spectra of the reference blank unirradiated region in each sample, taken before and after the experiment. Panels (g, h, and i) show that the changes in the spectra shown in panels (a, b, and, c) result from the D implantation rather than environmental conditions.
In the text
thumbnail Fig. 2

Depth profiles of the D/16O ratio determined using NanoSIMS for D-irradiated samples on the surface (a, c, and e) and in the interior (b, d, and, f). Depth measurement methods and interior data calibration methods are described in Appendices D and E. The upper x-axis gives the raster cycle number, and the lower x-axis the depths according to the NanoSIMS analysis pits. Each data point in panels a, c, and e corresponds to one cycle at one depth. Each data point in panels b, d, and f is the sum analysis result of 160 cycles. The grey region in panels b, d, and f represents the D/16O ratio of backgrounds for each mineral (less than 9.7 ± 6.8 × 10−9 for olivine; less than 1.9 ± 0.8 × 10−8 for pyroxene; and less than 2.3 ± 1.3 × 10−8 for plagioclase). The error bars represent the standard error of the mean. The dashed red line in panels b, d, and f represents the fitting curve for the decreasing trend of D/16O. The intersection of the fitting curve with the background value for each silicate indicates the deepest penetration of implanted D: 3619 ± 112 nm in olivine, 4049 ± 50 nm in pyroxene, and 4855 ± 263 nm in plagioclase.
In the text
thumbnail Fig. 3

Microstructural characteristics of D-irradiated silicates as revealed by TEM images: olivine (a), pyroxene (b), and plagioclase (c). The three images to the right of the main TEM images show diffraction patterns from selected white areas. The absence of diffraction spots in the top image of each set indicates the presence of an amorphous rim. The middle image for each silicate features both diffraction rings and blurred spots, suggesting a partial amorphous state. The distinct crystal diffraction pattern in the bottom image of each set represents the crystalline matrix; the zone axis superimposed on the image aligns with [110] in olivine and pyroxene, and [111] in plagioclase.
In the text
thumbnail Fig. 4

Major element profile of a D-irradiated silicate surface, measured via energy dispersive spectroscopy in TEM. (a) High-angle annular dark-field (HAADF) image of olivine. (b) Element profile of olivine obtained from the green arrow in panel (a). (c) HAADF image of pyroxene. (d) Element profile of pyroxene obtained from the green arrow in panel (c). (e) HAADF image of plagioclase. (f) Element profile of plagioclase obtained from the green arrow in panel (e). The dotted black line in the images to the right (b, d, and e) indicates the boundary of completely amorphous rims, measured from the TEM image shown in Fig. 3.
In the text
thumbnail Fig. C.1

Calculated implantation profiles from SRIM simulations for 1.5 keV D+ into olivine (a), pyroxene (b), and plagioclase (c).
In the text
thumbnail Fig. E.1

Schematic diagram of front and back NanoSIMS analysis methods in deep D signal validation experiments.
In the text
thumbnail Fig. E.2

Variation coefficient between the front and back analysis data calculated using the following formula: (D/18O(front) )/( D/18O(back)). (a) Olivine. (b) Pyroxene. (c) Plagioclase. Both the front and back data exhibited a diffusion feature that increased with depth. Thus, the variation trend of the coefficient follows an exponential function. For olivine, pyroxene, and plagioclase, three distinct calibration curves were produced through exponential fitting. Utilising these three sets of equations allows for the effective removal of influence of D particle re-deposition during the deep NanoSIMS analysis from the original D/16O data.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.