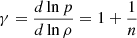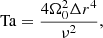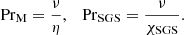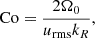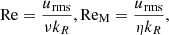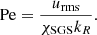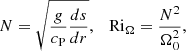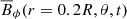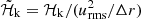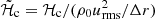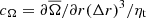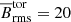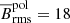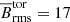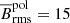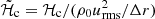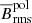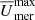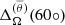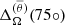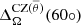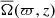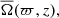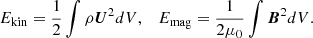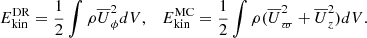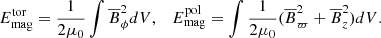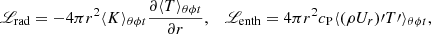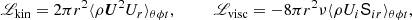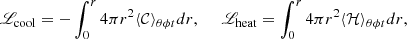| Issue |
A&A
Volume 691, November 2024
|
|
|---|---|---|
| Article Number | A326 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202449977 | |
| Published online | 22 November 2024 | |
Magnetohydrodynamic simulations of A-type stars: Long-term evolution of core dynamo cycles
1
Departamento de Astronomía, Facultad Ciencias Físicas y Matemáticas, Universidad de Concepción, Av. Esteban Iturra s/n, Barrio Universitario, Concepción, Chile
2
Institut für Sonnenphysik (KIS), Georges-Köhler-Allee 401a, 79110 Freiburg, Germany
3
Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
4
Institute of Space Sciences (ICE-CSIC), Campus UAB, Carrer de Can Magrans s/n, 08193 Barcelona, Spain
5
Institut d’Estudis Espacials de Catalunya (IEEC), Carrer Gran Capità 2–4, 08034 Barcelona, Spain
⋆ Corresponding author; jhidalgo2018@udec.cl
Received:
14
March
2024
Accepted:
24
September
2024
Context. Early-type stars have convective cores due to a steep temperature gradient produced by the CNO cycle. These cores can host dynamos and the generated magnetic fields may be relevant in explaining the magnetism observed in Ap/Bp stars.
Aims. Our main objective is to characterise the convective core dynamos and differential rotation. We aim to carry out the first quantitative analysis of the relation between magnetic activity cycle and rotation period.
Methods. We used numerical 3D star-in-a-box simulations of a 2.2 M⊙ A-type star with a convective core of roughly 20% of the stellar radius surrounded by a radiative envelope. We explored rotation rates from 8 to 20 days and used two models of the whole star, along with an additional zoom set where 50% of the radius was retained.
Results. The simulations produce hemispheric core dynamos with cycles and typical magnetic field strengths around 60 kG. However, only a very small fraction of the magnetic energy is able to reach the surface. The cores have solar-like differential rotation and a substantial part of the radiative envelope has a quasi-rigid rotation. In the most rapidly rotating cases, the magnetic energy in the core is roughly 40% of the kinetic energy. Finally, we find that the magnetic cycle period, Pcyc, increases with decreasing the rotation period, Prot, which has also been observed in many simulations of solar-type stars.
Conclusions. Our simulations indicate that a strong hemispherical core dynamo arises routinely, but that it is not enough the explain the surface magnetism of Ap/Bp stars. Nevertheless, since the core dynamo produces dynamically relevant magnetic fields, it should not be neglected even when other mechanisms are being explored.
Key words: dynamo / magnetic fields / magnetohydrodynamics (MHD) / stars: chemically peculiar / stars: early-type / stars: magnetic field
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Magnetic fields can be found in a wide variety of stars and there is a general consensus that most of them are amplified and maintained via self-excited dynamos. In this context, these processes typically require rotation and fluid motions; therefore, they are most likely to occur inside convection zones (see Brandenburg & Subramanian 2005; Brun & Browning 2017). The most obvious example is the Sun, which has a cyclic large-scale magnetic field driven by a self-excited dynamo operating in its convective envelope (see e.g. Charbonneau 2020). Like the Sun, other late-type stars (M, K, F) have convective envelopes and the observed magnetic fields in these stars are also very likely to be convective in terms of origin. Numerical simulations targeting a wide variety of rotating fully or partially convective stars yield dynamos of various sorts (see e.g. Käpylä et al. 2023, and references therein).
Early-type main sequence (MS) stars exhibit masses of M > 1.5 M⊙ and effective temperatures of Teff ≳ 104 K. Roughly 10% of early-type stars are magnetic (see e.g. Kochukhov & Bagnulo 2006; Landstreet et al. 2007, 2008; Grunhut et al. 2017; Shultz et al. 2019). According to our understanding of stellar evolution, these stars have radiative and, therefore, stably stratified, envelopes. This might explain why a dynamo cannot usually operate near the surfaces of these stars, since vigorous fluid motions are absent. However, some stars in the range of 1.5 M⊙ to 6 M⊙ host observable large-scale magnetic fields. The best example is the sub-group of chemically peculiar MS stars, classified as Ap/Bp. These stars host magnetic fields with mean field strengths ranging from 200 G to 30 kG (Aurière et al. 2007), the strongest field being 34 kG in HD 215441 (Babcock 1960). Roughly 10% of A-type stars belong to the sub-classification Ap and have detectable strong magnetic fields (Moss 2001). The non-magnetised population (‘normal’ A-type stars) usually have very weak fields below the detection limit. Nevertheless, weak magnetic fields have been detected in the normal population; for example, in Sirius and Vega. In the case of Vega, Zeeman polarimetry gives a magnetic field strength of 0.6 ± 0.3 G (Lignières et al. 2009; Petit et al. 2010, 2022), and 0.2 ± 0.1 G for Sirius (Petit et al. 2011). Normal A stars are typically rapid rotators (Royer et al. 2007), whereas Ap stars are slower rotators than their non-magnetic counterparts (Abt & Morrell 1995). Indeed, Mathys (2008) have shown that non-magnetic A stars have rotation periods ranging from a few hours to a day, while most Ap stars have periods of between one and ten days. This could be an indication of magnetic braking, although there is no clear correlation between rotation and magnetic fields (Kochukhov & Bagnulo 2006).
The origin of the large-scale magnetic fields in Ap/Bp stars remains uncertain, although several theories have been proposed. The fossil field theory suggests that these magnetic fields originate from the protostellar phase of the star. The Ohmic diffusion time in radiative zones is very long (e.g. 1010 years in the context of the Sun, Cowling 1945), and therefore, a magnetic field in equilibrium in a radiative zone could survive the whole MS lifetime of the star. Stable magnetic configurations in fully radiative A-type stars have been reported in numerical simulations (Braithwaite & Spruit 2004; Braithwaite & Nordlund 2006; Braithwaite 2008; Becerra et al. 2022). In principle, the fossil magnetic field has to survive the convective protostellar phase as the star descends the Hayashi track (Hayashi et al. 1962; Siess et al. 2000). This appears to be very unlikely assuming a fully convective evolution, but a transition to a radiative phase could counterbalance this problem and preserve a significant part of the initial magnetic flux (Schleicher et al. 2023). For instance, such protostellar models have been proposed by Palla & Stahler (1992, 1993).
Alternatively, it has been proposed that radiative envelopes can host dynamos, as a result of the interaction between a magnetic instability (e.g. Tayler 1973) and differential rotation. This is the Tayler-Spruit dynamo scenario (Spruit 2002). Recently, Petitdemange et al. (2023, 2024) performed global simulations of a magnetised stably stratified fluid with differential rotation in a spherical shell, reporting the first numerical demonstration of the Tayler-Spruit dynamo.
Another alternative is a strong core dynamo. Early-type stars have convective cores due to the temperature sensitivity of the dominant nuclear reaction (CNO cycle) such that energy production is highly concentrated in the centre of the star, leading to a steep temperature gradient that drives convection. It has long been suspected that the convective cores in A stars host dynamos (Krause & Oetken 1976). Simulations by Browning et al. (2004) showed that such convective cores have differential rotation that is beneficial for dynamo action. This was reported by Brun et al. (2005), who performed numerical simulations of the inner 30% by radius (half of which was convective) of a 2 M⊙ A-type star, obtaining magnetic fields with typical strengths around equipartition with kinetic energy. Interestingly, the inclusion of a fossil field in the radiative envelope might affect the nature of the core dynamo (see, e.g. Boyer & Levy 1984, in the context of the Sun). Featherstone et al. (2009) performed simulations of the core dynamo from a 2 M⊙ A-type star, reporting an equipartition magnetic field. However, the inclusion of a twisted toroidal fossil field can lead to a superequipartition state in the core, where the magnetic energy is roughly ten times stronger than the kinetic energy. In B-type stars, dynamos have been found as well. Simulations by Augustson et al. (2016) of the core of a 10 M⊙ B-type star, showed vigorous dynamo action and generated superequipartition magnetic fields with peak values exceeding a megagauss in the rapid rotators. However, although these studies show that a convective core can lead to strong dynamo action, the nature of these dynamos has not been explored in detail. For example, no cyclic solutions or a relation between the magnetic cycle period to rotation period of the core dynamo have been reported.
A natural question is whether the magnetic fields generated in the core can reach the surface of the star. This could happen under the action of buoyancy. Stellar structure models predict convection zones close to the surface of early-type stars (Richard et al. 2001; Cantiello et al. 2009) due to bumps in the stellar opacities from iron (Iglesias et al. 1992), hydrogen and helium ionisation. These layers can host dynamos and the resulting magnetic field, could easily rise to the surface due to magnetic buoyancy, creating surface magnetic fields of order a few Gauss (Cantiello & Braithwaite 2019). In principle, the same could happen in the context of a core dynamo. However, the timescale of this process has been estimated to be longer than the MS lifetime of these stars (Schuessler & Paehler 1978; Parker 1979; Moss 1989), unless the magnetic structures are very small. This was reported by MacGregor & Cassinelli (2003), who modelled a buoyant magnetic flux ring in the radiative interior of an early-type star (with M < 10 M⊙), and found transport timescales that were shorter than the MS lifetime of the star. Nonetheless, MacDonald & Mullan (2004) re-examined the conclusions of MacGregor & Cassinelli (2003) with more realistic models including differential rotation and realistic strong compositional gradients in the radiative layers. This slows down the buoyancy process considerably, and magnetic fields higher than the equipartition values are required to make this process feasible. One mechanism that could counter this situation is convective overshooting. This could allow for mixing in the stably stratified zone above the convective core, thereby reducing the compositional gradient. Also, the field that penetrates the radiative envelope might be strengthened by the shearing produced by the differential rotation, making it strong enough to reach the surface due to buoyancy.
Core dynamo simulations often include the convective core and only a part of the radiative envelope of the star (e.g. Brun et al. 2005; Augustson et al. 2016). In the current study, we perform simulations of a MS A-type star using the star-in-a-box model. This set-up allows us to explore dynamo action generated by convection in the core of the star (including r = 0) and study the resulting magnetic field, not only in the core but also on the stellar surface, modelling the entire star for the first time through 3D numerical simulations. Another point of interest is to study magnetic cycles and their relation to the rotation period. The relation between these quantities has been studied before in simulations of other types of stars (see e.g. Warnecke 2018; Strugarek et al. 2018, for solar-like stars), but such a relation has not been presented before in the context of A-type stars. The models and methods are described in Sect. 2. The analysis and results of the simulations are provided in Sect. 3. The discussion and conclusions of this study are presented in Sect. 4.
2. Numerical models and methods
2.1. Full star set-up
The model used here is based on the star-in-a-box set-up presented by Käpylä (2021), which is based on the set-up by Dobler et al. (2006). The computational domain corresponds to a box of side l = 2.2R, where R is the stellar radius and all coordinates (x, y, z) range from −l/2 to l/2. The following non-ideal fully compressible MHD equation set is solved:
where A is the magnetic vector potential, U is the flow velocity, B = ∇ × A is the magnetic field, η is the magnetic diffusivity, μ0 is the magnetic permeability of vacuum, J = ∇ × B/μ0 is the current density given by Ampère’s law, D/Dt = ∂/∂t + U⋅∇ is the advective (or material) derivative, ρ is the mass density, p is the pressure, Φ is the fixed gravitational potential, given by the Padé approximation obtained from 1D stellar structure model:
where r′=r/R is the fractional radius, G is the gravitational constant, M is the mass of the star. For an A0-type star the coefficients are given by a0 = 4.3641, a2 = −1.5612, a3 = 0.4841, b2 = 4.0678, and b3 = 1.2548. ν is the kinematic viscosity, [BOLD]S is the traceless rate-of-strain tensor, given by
where δij is the Kronecker delta. Ω = (0, 0, Ω0) is the rotation vector and fd describes damping of flows exterior to the star, given by
where τdamp = 0.2τff ≈ 1.5 days is the damping timescale and 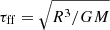 is the freefall time. The function fe(r) is defined as
is the freefall time. The function fe(r) is defined as
where rdamp = 1.03R is the damping radius and wdamp = 0.02R is its width. T is the temperature, s is the specific entropy, Frad is the radiative flux and FSGS is the sub-grid-scale (SGS) entropy flux. Radiation inside the star is approximated as a diffusion process. Therefore, the radiative flux is given by
where K is the radiative heat conductivity, a quantity that is assumed to be constant. In addition, it is convenient to introduce a SGS entropy diffusion that does not contribute to the net energy transport, but damps fluctuations near the grid scale. This is given by the SGS entropy flux,
where χSGS is the SGS diffusion coefficient, and
is the fluctuating entropy, where ⟨s⟩t(x) is a running temporal mean of the specific entropy. Also, ℋ and 𝒞 describe additional heating and cooling, respectively, and we adopted similar expressions as in Dobler et al. (2006) and Käpylä (2021), where
is a normalised Gaussian profile that parameterises the nuclear energy production inside the core of the star, where Lsim is the luminosity in the simulation, and wL = 0.1R is the width of the Gaussian. Furthermore, 𝒞(x) models the radiative losses above the stellar surface. This is given by
where cP is the heat capacity at constant pressure, Tsurf = T(R) is the temperature at the surface of the star, τcool = τdamp is a cooling timescale, and fe(r) is given by Eq. (8), with the same parameters, rcool = rdamp and wcool = wdamp. The ideal gas equation of state p = ℛρT is assumed, where ℛ = cP − cV is the ideal gas constant, and cV is the heat capacity at constant volume.
To avoid a diffusive spreading of magnetic fields and flows from the core to the envelope, we followed Käpylä (2022) and used radial profiles for the diffusivities, ν and η, where the radiative layers have values that are 102 times smaller than the core. The magnetic diffusivity has to be already rather low in the core to excite a dynamo (see Sect. 3). Therefore, the diffusivities in the radiative envelope are even lower, making it hard to resolve the flows and magnetic fields there. To cope with this issue, we added artificial sixth-order hyperdiffusivity terms in the dynamical equations. The hyperdiffusive terms smooth small-scale oscillation to avoid numerical instabilities near grid scale (see e.g. Brandenburg & Sarson 2002; Johansen & Klahr 2005). Here, we used the resolution-independent mesh hyper-Reynolds number method described in Appendix A of Lyra et al. (2017) for ν and η, in all sets of simulations. Furthermore, the advective terms of Eqs. (1) and (4) are written in terms of fifth-order upwinding derivatives, with a sixth-order hyperdiffusive correction and a flow dependent diffusion coefficient. More details are given in Appendix B of Dobler et al. (2006).
2.2. Zoom set-up
Modelling the whole star allows us to study the convective core all the way to the surface of the star. However, this also reduces the number of grid points available to resolve convection inside the core. To test the robustness of the results and to increase the spatial resolution in the core, we ran a few simulations using a zoom model, which is otherwise the same as the full star model, but the box has a side of l = 1.1R. Therefore, we excluded the surface of the star and focus exclusively in the convective core with higher resolution.
The flow damping radius was changed to rdamp = 0.45R with τdamp = 0.02τff ≈ 0.15 days, and wdamp = 0.01R, and the cooling was set to start at rcool = 0.52R, with wcool = 0.02R and τcool = 0.2τff ≈ 1.5 days. These choices were made more out of numerical convenience rather than physical arguments. However, as explained in Sect. 3, the main results remain unaffected.
2.3. Physical units and initial and boundary conditions
The stellar parameters were extracted from a 2.2 M⊙ MS one dimensional (1D) stellar model. This model was obtained using the MESA code (see Paxton et al. 2019, and the references therein). The radius, mass density and temperature of the stellar centre, and luminosity averaged from t = 2.5 ⋅ 106 years to t = 4.5 ⋅ 108 years are given by R* = 2.1 R⊙, ρ0 = 5.5 ⋅ 104 kg m−3, T0 = 2.3 ⋅ 107 K and L* = 23.5 L⊙, where L⊙ = 3.83 ⋅ 1026 W is the solar luminosity, respectively. Furthermore, the surface gravity is:
where g⊙ = 274 m s−2. Using realistic parameters in fully compressible simulations of stars is infeasible due to the huge gap between the acoustic (dynamic) and Kelvin-Helmholtz (thermal) timescales. A solution to this problem was originally pointed out by Chan & Sofia (1986), and it consists of exaggerating the luminosity in numerical simulations. Here we follow the notation of Dobler et al. (2006) and define a dimensionless luminosity,
with which we define the luminosity ratio between the simulation and the target star:
Now, the gap between acoustic and Kelvin-Helmholtz timescales is reduced by a cumulative factor of Lratio4/3 (see Käpylä 2021, for a detailed discussion).
The units of length and time are given by the radius of the star [x]=R and the free-fall time [t]=τff respectively. Furthermore, the unit of magnetic field is obtained from the equipartition field strength as ![$ [B] = \sqrt{\mu_0 \rho_0} [x]/[t] $](/articles/aa/full_html/2024/11/aa49977-24/aa49977-24-eq18.gif) , and the unit of entropy is [s]=cP. The conversion factors between simulation and physical units are (for example, x = xfacxsim, see Käpylä et al. 2020)
, and the unit of entropy is [s]=cP. The conversion factors between simulation and physical units are (for example, x = xfacxsim, see Käpylä et al. 2020)
where the sub-script ‘sim’ represents the quantity in simulation units. Furthermore, since the convective velocity scales with luminosity as uconv ∝ L1/3 (Jones et al. 2017; Käpylä et al. 2020; Baraffe et al. 2023; Käpylä 2024), the rotation rate needs to be enhanced by the same factor (Lratio1/3) to have a consistent rotational influence on the flow. Following Appendix A of Käpylä et al. (2020), we obtain
The convective core is assumed to encompass 20% of the stellar radius. To set such a configuration, we must assume a piecewise polytropic initial state. A polytrope is defined via:
where K0 is a constant, and
is the adiabatic index written in terms of the polytropic index n. We choose n = nad = 1.5 in the convectively unstable layer (r < 0.2R), and n = nrad = 3.25 in the stable layer (r > 0.2R) with a smooth transition between them. Here, nad corresponds to a marginally stable stratification whereas nrad arises in a hydrostatic solution of a radiative atmosphere with Kramers opacity law (e.g. Barekat & Brandenburg 2014).
The boundary conditions are impenetrable and stress-free conditions for flow and the magnetic field is assumed to be perpendicular to the boundary. We further assume a vanishing second derivative for lnρ, and vanishing temperature gradient across the exterior boundaries of the box. For the initial conditions of the flow and magnetic field, we considered low amplitude Gaussian noise with initial amplitudes of 2 ⋅ 10−3 m/s and 1 G, respectively. The simulations were run with the PENCIL CODE1 (Brandenburg & Dobler 2002; Pencil Code Collaboration 2021), which is a highly modular high-order finite-difference code for solving partial differential equations.
2.4. Dimensionless parameters
To characterise our simulations, the following dimensionless numbers are computed. The effect of rotation relative to viscous forces is measured by the Taylor number
where Δr = 0.2R is the depth of the convective zone. The magnetic and SGS Prandtl numbers are
The influence of rotation on the flow is measured by the Coriolis number,
where urms is the root-mean-square (rms) velocity averaged over the convective zone (r < Δr) and kR = 2π/Δr is the scale of the largest convective eddies. The fluid and magnetic Reynolds numbers are defined as:
and the SGS Péclet number is
Furthermore, the Brunt-Väisälä (or buoyancy) frequency and the Richardson number related to rotation in the radiative zone are defined as
respectively. If N2 > 0, then the layer will be stable against buoyancy fluctuations.
3. Results
We present three sets of simulations exploring rotation periods from 8 to 20 days. All simulations have ν = 5.45 ⋅ 107 m2/s, η = 7.78 ⋅ 107 m2/s, and χSGS = 2.61 ⋅ 108 m2/s in the core; therefore, PrM = 0.7 and PrSGS ≈ 0.21. In the first set of simulations (group MHD), ν and η have radial jumps around 0.35R, with a smooth transition over a width of 0.06R. Above the jump, diffusivities are 102 times smaller. In the second set (group MHD*), the jump is at 0.3R and its width is 0.03R. Simulations in this group start from already saturated snapshots of the respective simulation with the same rotation rate in the MHD group. The third set corresponds to the zoom set-up (group zMHD) described in Sect. 2.2. The radial profiles are the same as those in group MHD. The runs, as well as the diagnostic quantities are listed in Table 1. All simulations were run on a grid of 2003 uniformly distributed grid points.
Figure 1 shows the radial profiles of density, temperature, and specific entropy from representative runs, where the overlines denote horizontal (ϕθ) averaging. The density stratification between the centre and the surface of the star (r = R) is 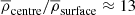 in the full star runs. Furthermore, the stratification between the centre and the surface of the convective core (r = 0.2R) is
in the full star runs. Furthermore, the stratification between the centre and the surface of the convective core (r = 0.2R) is 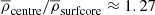 , which is close to that from the MESA model
, which is close to that from the MESA model 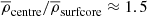 . The same ratios for the temperature are
. The same ratios for the temperature are 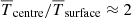 and
and 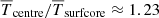 . From the lower panel of Fig. 1, we can infer a negative entropy gradient in the convective core and a positive gradient at the rest of the star, which is the expected configuration for a A-type MS star. The surface cooling becomes effective above rcool and relaxes the regions exterior to the star toward a constant temperature, Tsurf. Therefore the density drops nearly exponentially above r = rcool. Radiation transports all of the energy in the stellar envelope all the way to the surface; see Sect. 3.3.2. This means that the photosphere at the stellar surface is modelled in a very simplistic way where the energy transport mechanism switches from radiative diffusion to the cooling flux which mimics radiative losses in the optically thin exterior. This approach avoids detailed physics that would involve such effects as thin convection zones near the surface. Since the focus in the current study is in the core dynamo, this simplification is justified.
. From the lower panel of Fig. 1, we can infer a negative entropy gradient in the convective core and a positive gradient at the rest of the star, which is the expected configuration for a A-type MS star. The surface cooling becomes effective above rcool and relaxes the regions exterior to the star toward a constant temperature, Tsurf. Therefore the density drops nearly exponentially above r = rcool. Radiation transports all of the energy in the stellar envelope all the way to the surface; see Sect. 3.3.2. This means that the photosphere at the stellar surface is modelled in a very simplistic way where the energy transport mechanism switches from radiative diffusion to the cooling flux which mimics radiative losses in the optically thin exterior. This approach avoids detailed physics that would involve such effects as thin convection zones near the surface. Since the focus in the current study is in the core dynamo, this simplification is justified.
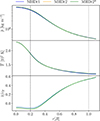 |
Fig. 1. Density profiles as functions of radius from MHDr1, MHDr2, and MHDr2* (top). Temperature profiles for the same runs (middle). Specific entropy profiles from the same runs (bottom). The black dashed line indicates the surface of the convective core (r = 0.2R) and the grey dashed line the stellar surface (r = R). The quantities are time-averaged over the thermally relaxed phase. |
Finally, the stratification in the cores of the simulations in group zMHD is similar to those in the full star models. The density and temperature ratios between the centre of the star and the outer edge of the radiative zone (r = 0.55R) are 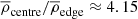 and
and 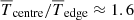 .
.
3.1. Dynamo solutions
All of our runs, except for MHDr1, host a dynamo. In the corresponding run zMHDr1 the magnetic field grows but the dynamo is very close to marginal, and it is impractical to run it to saturation.
3.1.1. Core dynamos
The azimuthally averaged toroidal magnetic fields at r = 0.2R as functions of time and latitude of the full star simulations are shown in Fig. 2. All of the magnetic field solutions are cyclic and hemispheric. These are the first cyclic solutions reported from core dynamos of early-type stars. Cyclic solutions have been reported in simulations of fully convective stars where the geometry of the dynamo region is similar to that of the current models with similar Coriolis number, Co ≈ 9 (Käpylä 2021; Ortiz-Rodríguez et al. 2023). The main difference is the hemispheric nature of the current simulations, although during limited periods a run in Käpylä (2021) shows a predominantly hemispheric magnetic field as well (see their Fig. 10). Here, all the simulations show hemispheric fields most of the running time, with equally strong fields on both hemispheres only rarely (in particular, runs MHDr2, MHDr4*, and zMHDr2). Hemispheric dynamo solutions have been also found in Boussinesq (Landeau & Aubert 2011; Simitev & Busse 2012) and anelastic spherical shells models (Raynaud et al. 2014; Raynaud & Tobias 2016). In runs MHDr2 and MHDr3 the magnetic field is concentrated in the southern hemisphere, while in MHDr4 the magnetic activity is located in the northern hemisphere. In MHDr2*, the magnetic field starts in the southern hemisphere, same as in MHDr2, but then it moves to the northern hemisphere. This is a unique behaviour in this run and it is unclear why it happens. Similar behaviour was also found by Brown et al. (2020) in spherical simulations of fully convective M dwarfs, with no conclusive explanation either. The rest of the MHD* runs are very similar to their MHD counterparts, as shown in Fig. 2. The dynamo of MHDr3* is essentially the same as that of MHDr3. MHDr4* has a cyclic dynamo on both hemispheres in the early part of the simulation, but the activity in the southern hemisphere vanishes after ∼23 years, and the resulting magnetic field is similar to MHDr4. Something similar was found by Brown et al. (2020), where their hemispheric dynamos are initially symmetric on both hemispheres, but after some time strong southern-hemisphere fields replace the original symmetric configuration. The rms-magnetic fields from group MHD* are somewhat weaker than in group MHD; see Table 1.
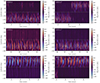 |
Fig. 2. Time-latitude diagrams of the azimuthally averaged toroidal magnetic field |
Figure 3 shows 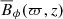 for two of the zMHD runs. These dynamos are also very similar to their MHD group counterparts. zMHDr2 shows a dynamo in the southern hemisphere. However, roughly between 75 and 85 years, it exhibits some activity in the northern hemisphere as well, which slightly reduces the activity in the southern hemisphere. This behaviour is also somewhat more frequently visible in MHDr2, and it is possibly related with the switch of active hemisphere seen in MHDr2*. The activity is almost completely hemispherical in all of the other simulations in the zMHD group. The toroidal magnetic field of zMHDr3 is not shown because it is almost identical to its full star counterparts, although, the mean intensity is somewhat weaker. Fourth column of Table 1 shows that a similar trend is present in all of the zMHD runs, so that Brms is about 10 kG weaker than in the full star MHD counterparts. As mentioned, the dynamo from zMHDr4 is very similar to that of MHDr4. However, their magnetic cycles does not seem to match and Pcyc from zMHDr4 is significantly shorter (2.50 yr) than that of MHDr4 (3.14 yr). The strengths of the toroidal and radial magnetic fields at the surface of the convective core (r = 0.2R) for the full star runs are
for two of the zMHD runs. These dynamos are also very similar to their MHD group counterparts. zMHDr2 shows a dynamo in the southern hemisphere. However, roughly between 75 and 85 years, it exhibits some activity in the northern hemisphere as well, which slightly reduces the activity in the southern hemisphere. This behaviour is also somewhat more frequently visible in MHDr2, and it is possibly related with the switch of active hemisphere seen in MHDr2*. The activity is almost completely hemispherical in all of the other simulations in the zMHD group. The toroidal magnetic field of zMHDr3 is not shown because it is almost identical to its full star counterparts, although, the mean intensity is somewhat weaker. Fourth column of Table 1 shows that a similar trend is present in all of the zMHD runs, so that Brms is about 10 kG weaker than in the full star MHD counterparts. As mentioned, the dynamo from zMHDr4 is very similar to that of MHDr4. However, their magnetic cycles does not seem to match and Pcyc from zMHDr4 is significantly shorter (2.50 yr) than that of MHDr4 (3.14 yr). The strengths of the toroidal and radial magnetic fields at the surface of the convective core (r = 0.2R) for the full star runs are 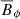 kG and
kG and 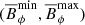 kG, while the zoom have
kG, while the zoom have 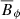 kG and
kG and 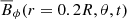 kG, respectively.
kG, respectively.
Summary of the simulations.
The meridional distribution of the azimuthally averaged magnetic field of MHDr3* is shown in Fig. 4. The amplitude of the mean toroidal component is typically larger than that of the mean poloidal component. In the core the full star runs have rms values of 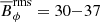 –25 kG and
–25 kG and 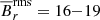 –22 kG, while the zoom models have
–22 kG, while the zoom models have 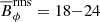 –20 kG and
–20 kG and 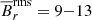 –17 kG. Although the magnetic activity in the core is hemispheric, there is still some magnetic field in the radiative zone above the non-active hemisphere of the core. From Fig. 4, we can see that this magnetic field might be coming from the core dynamo. At the beginning of the cycle (t = 48.1 yr), the northern hemisphere of the core is almost free of magnetic activity. Briefly after, at t = 48.7 yr, some of the magnetism from the core dynamo migrates through the northern hemisphere. This magnetism reaches the lower part of the radiative envelope while the core dynamo changes its polarity. Once the cycle finishes, the northern hemisphere of the core gets almost devoid of magnetic activity again. The zone where the magnetic field is concentrated in the radiative zone starts around r ≈ 0.6R, which is roughly the radius where the radial jumps of the diffusivities occur in the MHD* group. Therefore, due to the low diffusivities in these layers, the magnetic field can stay and evolve in long timescales compared to the period of the core dynamo. These magnetic fields might be transported from the core to the bottom of the radiative envelope by the columnar flows produced by the Taylor-Proudman theorem, due to the high Coriolis numbers in our simulations (see Sect. 3.2). The reason of why these vertical flows can penetrate the stable stratification of the radiative envelope could be the unrealistically low Richardson number computed in such layers (see Table 1). These low values are a direct consequence of the low Brunt-Väisälä frequencies achieved by our simulations, as in real stars these values are expected to be several of orders of magnitudes higher. In the southern hemisphere the situation is similar, but the magnetic field has a different polarity than in the north.
–17 kG. Although the magnetic activity in the core is hemispheric, there is still some magnetic field in the radiative zone above the non-active hemisphere of the core. From Fig. 4, we can see that this magnetic field might be coming from the core dynamo. At the beginning of the cycle (t = 48.1 yr), the northern hemisphere of the core is almost free of magnetic activity. Briefly after, at t = 48.7 yr, some of the magnetism from the core dynamo migrates through the northern hemisphere. This magnetism reaches the lower part of the radiative envelope while the core dynamo changes its polarity. Once the cycle finishes, the northern hemisphere of the core gets almost devoid of magnetic activity again. The zone where the magnetic field is concentrated in the radiative zone starts around r ≈ 0.6R, which is roughly the radius where the radial jumps of the diffusivities occur in the MHD* group. Therefore, due to the low diffusivities in these layers, the magnetic field can stay and evolve in long timescales compared to the period of the core dynamo. These magnetic fields might be transported from the core to the bottom of the radiative envelope by the columnar flows produced by the Taylor-Proudman theorem, due to the high Coriolis numbers in our simulations (see Sect. 3.2). The reason of why these vertical flows can penetrate the stable stratification of the radiative envelope could be the unrealistically low Richardson number computed in such layers (see Table 1). These low values are a direct consequence of the low Brunt-Väisälä frequencies achieved by our simulations, as in real stars these values are expected to be several of orders of magnitudes higher. In the southern hemisphere the situation is similar, but the magnetic field has a different polarity than in the north.
 |
Fig. 4. Azimuthally averaged toroidal magnetic field |
To understand the origin of the dynamos in the simulations we make estimates of commonly used dynamo numbers in mean-field dynamo theory (e.g. Krause & Rädler 1980). This involves computing the α effect which is proportional to the kinetic helicity of the flow (Steenbeck et al. 1966). The fluctuating kinetic and current helicities are
respectively, where ω = ∇ × U is the vorticity. Furthermore, to quantify the α and the Ω effects, it is convenient to introduce the following dynamo parameters (Käpylä et al. 2013)
where ηt = τurms2/3 is an estimate of the turbulent diffusivity and τ = Δr/urms is the convective turnover time. Furthermore, the non-linear α effect is given by (Pouquet et al. 1976)
Finally, 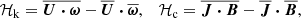 is the time- and azimuthally averaged rotation rate.
is the time- and azimuthally averaged rotation rate.
The normalised fluctuating kinetic helicity 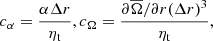 and current helicity
and current helicity 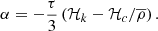 of MHDr3*, as well as the dynamo parameters (Eq. (28)) are shown in Fig. 5. The kinetic helicity is negative (positive) in the northern (southern) hemisphere. The current helicity has less large-scale coherence and a much lower amplitude. Together with the solar-like differential rotation of the core, which is discussed in Sect. 3.2, a poleward propagation of dynamo waves is expected in the αΩ dynamo approximation (e.g. Parker 1955; Yoshimura 1975). This is consistent with Figs. 2 and 4. Furthermore, as shown in the rightmost panels of Fig. 5, the values of cΩ inside the core, are larger than those of cα. Although the difference between
of MHDr3*, as well as the dynamo parameters (Eq. (28)) are shown in Fig. 5. The kinetic helicity is negative (positive) in the northern (southern) hemisphere. The current helicity has less large-scale coherence and a much lower amplitude. Together with the solar-like differential rotation of the core, which is discussed in Sect. 3.2, a poleward propagation of dynamo waves is expected in the αΩ dynamo approximation (e.g. Parker 1955; Yoshimura 1975). This is consistent with Figs. 2 and 4. Furthermore, as shown in the rightmost panels of Fig. 5, the values of cΩ inside the core, are larger than those of cα. Although the difference between 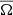 and
and 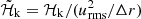 is not very large, we nevertheless interpret the dynamos in our simulations to be of some αΩ or α2Ω flavour. We note that cα is close to zero at the base of the radiative zone between z = 0.25R and z = 0.5R, which suggests lack of dynamo action there. In the southern hemisphere between z = −0.5R and z = −0.25R, cα has non-zero values, but these do not overlap significantly with the non-zero values of cΩ, suggesting dynamo action unlikely as well. Therefore, the interpretation that the magnetic field in the radiation zone, as seen in Fig. 4, is transported there from the core dynamo remains plausible. The rest of the simulations have very similar kinetic helicity and dynamo coefficient profiles regardless of the location of the core dynamo.
is not very large, we nevertheless interpret the dynamos in our simulations to be of some αΩ or α2Ω flavour. We note that cα is close to zero at the base of the radiative zone between z = 0.25R and z = 0.5R, which suggests lack of dynamo action there. In the southern hemisphere between z = −0.5R and z = −0.25R, cα has non-zero values, but these do not overlap significantly with the non-zero values of cΩ, suggesting dynamo action unlikely as well. Therefore, the interpretation that the magnetic field in the radiation zone, as seen in Fig. 4, is transported there from the core dynamo remains plausible. The rest of the simulations have very similar kinetic helicity and dynamo coefficient profiles regardless of the location of the core dynamo.
 |
Fig. 5. Time-averaged helicities and dynamo parameters from MHDr3*. From left to right the panels correspond to the normalised fluctuating kinetic helicity |
Magnetic helicity conservation has profound consequences for large-scale dynamos. If magnetic helicity cannot exit the system, the α effect can be catastrophically quenched leading to resistively slow large-scale magnetic field growth (e.g. Brandenburg 2001). In solar-like stars the dynamo-active region can shed magnetic helicity to the surrounding interstellar space via coronal mass ejections and other eruptive events. No such possibility exists for massive stars where the core dynamo is isolated from the stellar surface. A plausible possibility in this case is a diffusive magnetic helicity flux toward the equator where oppositely signed helicity can cancel. Such a scenario has been demonstrated in simpler forced turbulence simulations, where the kinetic helicity changes sign at the equator similarly as in the current models (e.g. Mitra et al. 2010). However, we have postponed any further investigation of this issue to future studies.
3.1.2. Surface magnetic fields
Figure 6 shows the rms magnetic field Brms at the surface of the star for the MHD and MHD* simulations. As expected, the magnetic field generated by the core dynamo is unable to create strong large-scale magnetic structures at the surface of the star. In all simulations the magnetic field is nearly zero on almost the whole surface of the star, except at the poles. The Brms from latitudes between −90 and −75 degrees and from 75 to 90 degrees, that is near the poles, have the order of 0.1 kG in the MHD group, and 10−3 kG in the MHD* group. While the magnetic fields from the rest of latitudes in both groups have values of the order of 10−5 kG. Additionally, there does not seem to be any correlation between the amount of magnetic flux that reaches the surface and the rotation period of the star. The highest rms value averaged over the poles in the MHD group comes from MHDr3 with 0.47 kG, and in the MHD* group from MHDr3*, with 6.8 ⋅ 10−3 kG. Similarly to what happens in the bottom radiative envelope, the magnetic field are probably transported from the core to the surface near the poles by the combination of unrealistic Richardson numbers and axially aligned flows due to the high rotation of the simulations.
 |
Fig. 6. Time-averaged rms magnetic field at the surface of the star r = R as a function of latitude from the runs in groups MHD and MHD*. |
Although the radial profiles of the diffusivities in the MHD* group reduce the intensity of these flows and therefore, the magnetic field in the poles, they are still two orders of magnitude stronger than the magnetic fields in the rest of the stellar surface. In principle, increasing the Brunt-Väisälä frequency closer to realistic values should reduce the spreading of flows from the core to the envelope (see e.g. Korre & Featherstone 2024). However, increasing this frequency is numerically very expensive, therefore with the current resolution of our simulations these results at the stellar surface should be taken with caution.
Finally, the magnetic field that reaches the poles is not only located at the pole corresponding to the active hemisphere despite the hemispheric nature of the core dynamo. This can be a consequence of the distribution seen in Fig. 4, as the flows might be transporting a fraction of the magnetic flux from the base of the bottom radiative envelope. The local rms velocity urms(ϖ, z) averaged from ϖ = 0 to ϖ = 0.2R, that is, close to the axis of rotation, has comparable values from z = 0.2R to z = R and from z = −0.2R to z = −R. Therefore a fraction of the magnetic field in the radiative zone seen in Fig. 4 is transported to the corresponding pole. From Fig. 6 is visible that the pole over the inactive hemisphere has a Brms typically an order of magnitude weaker than that of the other pole, but it is still significantly higher than the rest of the latitudes. The relatively high values of urms(ϖ, z) close to the axis of rotation are likely due to the combination of much higher diffusion coefficients and lower Richardson number in our simulations than in real stars. The advection timescales of the vertical flows are estimated to be around 100 yr in the MHD group and 300 yr in the MHD* group, while diffusion timescales are around 20 yr in both groups. Therefore, the magnetic field is transported to the surface most likely due to turbulent diffusion.
3.2. Large-scale flows
The time- and azimuthally averaged rotation rate is given by:
where ϖ = r sin θ is the cylindrical radius. Furthermore, the averaged meridional flow is:
We use the same parameters as in Käpylä et al. (2013), Käpylä (2021), and Ortiz-Rodríguez et al. (2023) to quantify the amplitude of the radial and latitudinal differential rotation. These are given by:
where rtop = 0.9R and rbot = 0.1R are the radius near the surface and centre of the star, respectively. θeq corresponds to the latitude at the equator, and 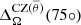 is an average of
is an average of 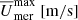 between latitudes −θ and θ. Additionally, it is relevant to also analyse the differential rotation of the convective core. Therefore, we introduce ΔΩCZ(r) and
between latitudes −θ and θ. Additionally, it is relevant to also analyse the differential rotation of the convective core. Therefore, we introduce ΔΩCZ(r) and 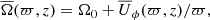 , which are the same as Eqs. (32) and (33), but with rtop = 0.2R and rbot = 0.05R.
, which are the same as Eqs. (32) and (33), but with rtop = 0.2R and rbot = 0.05R.
The differential rotation parameters are summarised in Table 2. From columns two to four of Table 2, we can conclude that the stellar surface rotates nearly rigidly, because 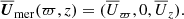 is ∼10−4 for θ = 60° and θ = 70°. This implies negligible difference between the averaged rotation at the chosen latitudes and the equator. Figure 7 shows that in run MHDr3*, rigid rotation extends from the surface to a significant part of the radiative envelope between r ≈ 0.5R and r = R. This is similar to the radiative interior of the Sun, which has approximately rigid rotation (see Howe 2009). This behaviour is present in all the simulations from this study. Unlike the simulations by Augustson et al. (2016) whose radiative envelopes are almost completely rigid (see their Fig. 7), the current runs show a stronger differential rotation in the regions closest to the core.
is ∼10−4 for θ = 60° and θ = 70°. This implies negligible difference between the averaged rotation at the chosen latitudes and the equator. Figure 7 shows that in run MHDr3*, rigid rotation extends from the surface to a significant part of the radiative envelope between r ≈ 0.5R and r = R. This is similar to the radiative interior of the Sun, which has approximately rigid rotation (see Howe 2009). This behaviour is present in all the simulations from this study. Unlike the simulations by Augustson et al. (2016) whose radiative envelopes are almost completely rigid (see their Fig. 7), the current runs show a stronger differential rotation in the regions closest to the core.
Differential rotation parameters and the maximum meridional flow 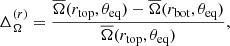 from all the simulations.
from all the simulations.
 |
Fig. 7. Profile of the temporally and azimuthally averaged rotation rate |
All runs have positive ΔΩ(r) because the innermost part of the core is rotating slower than the stellar surface, as shown in Fig. 7. In Fig. 8 the rotation profiles of other representative simulations are shown. The radial extent is now limited to 0.5R, allowing for a better display of the flows from the core and the portion of the radiative envelope with non-rigid rotation. The convective cores from all the runs have solar-like differential rotation, similar to the solar-like state reported by Brown et al. (2020), and the hydrodynamic case H4 of Augustson et al. (2016). This is also shown by the positive values of 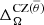 in Table 2, which indicate that the convective core is rotating faster at the equator than at other latitudes. Furthermore, we can see vertical structures that are parallel to the axis of rotation due to the Taylor-Proudman theorem. This is similar to the fast rotator from Brun et al. (2005) (see their Fig. 9). As mentioned in Sect. 3.1.2, these flows penetrate the radiative zone probably as a consequence of the low Brunt-Väisälä frequencies in our simulations. We estimate that RiΩ in a real A0 star is of the order of 104 which is five to six orders of magnitude higher than in the current simulations (see the tenth column in Table 1). Higher values of N would also increase the ratio between the Eddington-Sweet and viscous timescales (e.g. Wood & Brummell 2012), and the mean flows would only penetrate a small distance outside the core (see, e.g. Fig. 5 of Korre & Featherstone 2024). Therefore, although high rotation rates influence the efficiency of angular momentum transport in massive stars (Aerts et al. 2019), we would not expect differential rotation to spread in such a significant part of the radiative envelope if realistic stellar parameters were used.
in Table 2, which indicate that the convective core is rotating faster at the equator than at other latitudes. Furthermore, we can see vertical structures that are parallel to the axis of rotation due to the Taylor-Proudman theorem. This is similar to the fast rotator from Brun et al. (2005) (see their Fig. 9). As mentioned in Sect. 3.1.2, these flows penetrate the radiative zone probably as a consequence of the low Brunt-Väisälä frequencies in our simulations. We estimate that RiΩ in a real A0 star is of the order of 104 which is five to six orders of magnitude higher than in the current simulations (see the tenth column in Table 1). Higher values of N would also increase the ratio between the Eddington-Sweet and viscous timescales (e.g. Wood & Brummell 2012), and the mean flows would only penetrate a small distance outside the core (see, e.g. Fig. 5 of Korre & Featherstone 2024). Therefore, although high rotation rates influence the efficiency of angular momentum transport in massive stars (Aerts et al. 2019), we would not expect differential rotation to spread in such a significant part of the radiative envelope if realistic stellar parameters were used.
 |
Fig. 8. Profiles of the temporally and azimuthally averaged rotation rate, |
Run MHDr1 without a dynamo has the largest differential rotation in the core (for details, see columns five to seven in Table 2). The rotation profile is symmetric with respect to the equator; see the left lower panel of Fig. 8. On the other hand, MHDr2 and MHDr4 are asymmetric with respect to the equator. This is due to the presence of strong hemispheric dynamos, which quench the differential rotation where the magnetic fields are strong. Magnetic quenching of differential rotation has been reported by various other numerical simulations (e.g. Brun et al. 2004; Käpylä et al. 2017; Bice & Toomre 2023). Run MHDr3 behaves similarly to MHDr2. MHD* group shows similar behaviour. The rotation profile of MHDr2* shown in Fig. 8 is averaged between 13 and 60 years, that is, before the dynamo moves from the southern to the northern hemisphere. As a consequence, the rotation profile is asymmetric with respect to the equator and very similar to that of MHDr2. After the dynamo migration (t > 60 yr) the rotation profile is inverted with respect to the equator and resembles that of MHDr4. The rest of the runs in the MHD* group are almost identical to their MHD counterparts, which is shown for runs MHDr4* and MHDr4 in the lower panels of Fig. 8. We note that the maximum meridional velocities 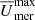 are always smaller in the MHD* group (see last column of Table 2). Here the meridional flow amplitude is not monotonic in the rotation rate as the value of MHDr4* is slightly higher than that of MHDr3*, whereas in the MHD group the meridional flow amplitude decreases with increasing rotation rate.
are always smaller in the MHD* group (see last column of Table 2). Here the meridional flow amplitude is not monotonic in the rotation rate as the value of MHDr4* is slightly higher than that of MHDr3*, whereas in the MHD group the meridional flow amplitude decreases with increasing rotation rate.
The rotation profiles from group zMHD are very similar to their MHD counterparts, with similar maximum and minimum values of  , and slightly higher maximum values of the averaged meridional flow, as shown for zMHDr2 in the upper right panel of Fig. 8. zMHDr1 has
, and slightly higher maximum values of the averaged meridional flow, as shown for zMHDr2 in the upper right panel of Fig. 8. zMHDr1 has 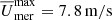 being the highest value of the simulations. In the rotation profile of zMHDr2, we can clearly distinguish more structures than in that of MHDr2. This is due to the increase of grid points inside the convective core, allowing flows to be resolved on smaller scales. The same happens with all the runs from the zMHD group, but the main results remain the same, and therefore they are not included in the plot. In this set of simulations
being the highest value of the simulations. In the rotation profile of zMHDr2, we can clearly distinguish more structures than in that of MHDr2. This is due to the increase of grid points inside the convective core, allowing flows to be resolved on smaller scales. The same happens with all the runs from the zMHD group, but the main results remain the same, and therefore they are not included in the plot. In this set of simulations 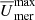 decreases with increasing Ω0, similar to the MHD group.
decreases with increasing Ω0, similar to the MHD group.
3.3. Energy analysis
3.3.1. Global and core energies
The total kinetic and magnetic energies, respectively, are given by
The energies for the differential rotation (DR) and meridional circulation (MC), are
Furthermore, the toroidal and poloidal magnetic energies are defined as
These expressions (34–36) were integrated over the volume of the star (r < R), or over the convective core (r < Δr), to study the energies in the entire star and in core, respectively. The obtained values are listed in Table 3.
Kinetic and magnetic energies.
The slowest rotators have the highest kinetic energies and Ekin is seen to decrease with Ω0. This is a consequence of high rotation rates reducing the intensity of the flows, as visible from urms in Table 1 and the differential rotation parameters in Table 2. We note that MHDr1 has a significantly higher value of Ekin than the rest of the simulations. This is a consequence of the absence of dynamo in this run. Earlier simulations (e.g. Brown et al. 2008; Viviani et al. 2018) and theoretical considerations (e.g. Kitchatinov & Rüdiger 1999) suggest that differential rotation and meridional circulation decrease when the rotation rate increases. Our results are mostly in agreement with these results, although the most rapidly rotating runs in each group deviate from this trend. A possible explanation is that the flows penetrate deeper in the radiative layer in these simulations due to the higher rotation rate and smaller Richardson numbers.
The magnetic and kinetic energies of the entire star are always larger in the group MHD* than in group MHD. This is because of the different diffusivity profiles between groups. In Fig. 9 is visible from the Brms profile that runs from group MHD* have a secondary maxima closer to the core than those of group MHD. These maxima above the core envelope interface around 0.36R lead to higher overall values of Brms in the MHD* group even though the fields in the radiative envelope are weaker in these cases. However, this behavior disappears in the core, as shown in the last rows of Table 3. With r < Δr the values of the magnetic energy in group MHD* are smaller than in group MHD, while the values of the kinetic energy, although quite close, do not seem to show any tendency between groups. Similarly to the differential rotation energies, the toroidal magnetic energies are very similar, with values of Emagtor/Emag between 0.229 and 0.3 for r < R, and between 0.132 and 0.189 for r < Δr. In both cases, the highest value occurs in MHDr4, same as with the poloidal magnetic energy. However, the maximum Emag occurs in MHDr3* for the entire star, and in MHDr3 for the core. This is consistent with Table 1, as these runs show the highest Brms. In the core, toroidal magnetic energies are somewhat larger than the poloidal energies, with typically Emagtor ≈ 1.5Emagpol. This is consistent with the discussion about the nature of the core dynamo; see Sect. 3.1.1.
 |
Fig. 9. Radial profiles of the horizontally averaged Brms (top) and urms (bottom) from representative runs. |
The magnetic energies in all of the current simulations are below equipartition even in the most rapidly rotating cases, typically with Emag/Ekin ≈ 0.4, and only when considering the energies in the whole star the magnetic energy is near or at equipartition; see Fig. 10. We therefore do not reach the near equipartition regime in the dynamo region that was found by Brun et al. (2005). This is likely because of the relatively laminar parameter regime explored in the current study. The kinetic energies in the zMHD group are comparable to the corresponding full star runs. However, as with Brms, the total magnetic energy in the zMHD runs are lower than in the rest of simulations.
 |
Fig. 10. Temporal evolution of the magnetic (blue) and kinetic (orange) energies in the full star of the runs MHDr2 (top) and MHDr4 (bottom). |
3.3.2. Energy fluxes and luminosities
The luminosities related to the radiative, enthalpy, kinetic energy, and viscous fluxes, and the additional cooling and heating, are defined as (Käpylä 2021):
where primes indicates fluctuations from the horizontal (θϕ) average, r denotes the radial component in spherical coordinates, and ⟨.⟩θϕt horizontal and temporal averaging.
The contributions to the total luminosity from runs MHDr3 and MHDr2* are shown in Fig. 11. ℒvisc is not shown because it is negligible, reaching maximally 0.02% of the total flux at r ≈ 0.22R. The convective luminosity ℒconv = ℒkin + ℒenth is dominated by a positive ℒenth in the convection zone (0 < r ≤ 0.2R). The kinetic energy flux is negligible, which is expected in the rapid rotation regime; for example, as reported by Käpylä (2024). In the majority of the star, the contribution due to the radiative energy flux dominates. This is due to the internal structure of the star, where the main energy transfer mechanism is radiation (the radiative zone is roughly 80% of the radial extent). Near the surface of the star, the cooling becomes effective and it dominates the total luminosity. The rest of the runs from groups MHD and MHD* have almost identical luminosity profiles. These profiles are similar to those of Augustson et al. (2016) and Brun et al. (2005); in particular, evident in their Figs. 3 and 13, respectively. The contribution of ℒenth in the core is about 10% which is somewhat smaller than in Brun et al. (2005) (≈25%), and in Augustson et al. (2016) (≈40%). In the zMHD group the luminosity profiles are very similar to those shown in Fig. 11, with the obvious differences that these profiles extend only to r = 0.55R and the cooling becomes effective around r = 0.5R.
 |
Fig. 11. Luminosity contributions from kinetic energy, enthalpy, radiative, cooling and heating fluxes from MHDr2* (top) and MHDr3 (bottom). |
3.4. Rotational scaling of magnetic cycles
As discussed in Sect. 3.1.1, the averaged toroidal magnetic fields in the core show clear cycles. To estimate the magnetic cycle period Pcyc of the core dynamo we computed the spectral density of the magnetic field at different latitudes from the active hemisphere using Welch’s method (Welch 1967). The peak value of the power spectrum corresponds to the frequency of the magnetic cycle, and its inverse gives the cycle period. The mean value of Pcyc obtained from the considered latitudes with the respective standard error is listed in the last column of Table 1. In the full star models there is a clear trend that Pcyc increases with decreasing Prot. This is visible in left panel of Fig. 12. Furthermore, our best power-law fit shows Pcyc ∝ Prot−0.89 ± 0.06 in the MHD group, and Pcyc ∝ Prot−0.77 ± 0.16 in the MHD* group. The relation between the magnetic cycle of the core dynamo and rotation has not been studied before. However, simulations of solar-like stars have shown similar results. Data from Warnecke (2018) indicate Pcyc ∝ Prot−1.06, which is a relation steeper than those found in our simulations. In the zMHD group the magnetic cycle period seems to be less sensitive to rotation. Our best fit shows Pcyc ∝ Prot−0.36 ± 0.25, which is less steep than in the full star models. This relation is similar to the Pcyc ∝ Prot−0.33 ± 0.05 reported in Strugarek et al. (2017).
 |
Fig. 12. Magnetic cycle period Pcyc as a function of the rotation period Prot (left). Ratios of rotation to cycle period as a function of the Coriolis number (right). Additional data are from Strugarek et al. (2018, red), Warnecke (2018, purple) and Käpylä (2022, brown). The dashed lines are the best power-law fits to the data. |
Observations of chromospheric activity suggest that the stellar magnetic activity cycles are distributed in active and inactive branches (see e.g. Brandenburg et al. 1998; Böhm-Vitense 2007). These studies suggest a relation Prot/Pcyc ∝ Coβ with β > 0. However, the exact nature of these branches and the relation between stellar cycles and rotation are still under debate (e.g. Brandenburg et al. 2017; Boro Saikia et al. 2018; Bonanno & Corsaro 2022). We present this relation in the core dynamo of an A-type star for the first time, with β ≈ −1 in all the sets. Our results are shown in the right panel of Fig. 12. Furthermore, our best power law fits are summarised in Table 4. Data from other authors from observations and numerical simulations is also added for comparison purposes. From Table 4 it is visible that our results are usually in agreement with solar-like simulations. However, as discussed in Sect. 3.1.1, the expulsion of the magnetic helicity has direct consequences in the cycle period, and the mechanism responsible is expected to differ between core and envelope dynamos. One possible explanation of why the scaling laws appear to be in agreement is that all the solar-like simulations reported in Sect. 3.1.1 have been done at relatively modest magnetic Reynolds numbers; therefore, the direct effects of the magnetic helicity conservation might not be immediately evident.
Comparison of β values.
4. Summary and conclusions
We present results from star-in-a-box simulations (see Dobler et al. 2006; Käpylä 2021) of a 2.2 M⊙ A-type star with a convective core of roughly 20% of the stellar radius. We have explored rotation periods ranging from 8 to 20 days in three sets of simulations. The full star sets MHD and MHD* have somewhat different radial profiles of the kinematic viscosity and the magnetic diffusivity. The third set (zMHD) consists of zoom-in versions of the MHD group, where we modelled the convective core and a part of the radiative envelope at higher resolution.
All of the core dynamos are hemispheric and cyclic with rms values of around 60 kG. Observational constrains of the internal magnetic field strength of early-type stars can be obtained via asteroseismology. Lecoanet et al. (2022) estimated an upper limit of Br ≈ 500 kG at r = 0.18R for the B star HD 43317, based on the g-mode frequencies from Buysschaert et al. (2018). Our results are one order of magnitude lower than this (at r = 0.20R we find 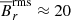 kG). However, in B-type stars the convective velocities in the core are expected to be roughly ten times higher than in A-type stars (Browning et al. 2004). Therefore we would expect correspondingly stronger magnetic fields in the former; see, for example Augustson et al. (2016). The dynamos in our simulations remain hemispheric throughout the simulation time, except in MHDr2*, where the magnetic activity migrated from the southern to the northern hemisphere. A similar behaviour was reported by Brown et al. (2020) in fully convective M dwarfs, but the reason behind it is not clear. Some magnetic fields reach the surface of the star in our simulations. However, these fields are very weak everywhere except at the poles, where the maximum rms value averaged over the poles (−90° > θ > −75°, and 75° < θ < 90°) was seen in run MHDr3 with ∼0.47 kG. In the group MHD*, the surface magnetic fields are significantly weaker due to the different radial profiles of diffusivities, with maximum values around 10−4 kG. These weak surface magnetic fields might be a consequence of the flows aligned with the rotation axis because of the Taylor-Proudman theorem, due to the high Coriolis numbers in our simulations. Such flows could penetrate the radiative layers due to the unrealistically low Richardson number there.
kG). However, in B-type stars the convective velocities in the core are expected to be roughly ten times higher than in A-type stars (Browning et al. 2004). Therefore we would expect correspondingly stronger magnetic fields in the former; see, for example Augustson et al. (2016). The dynamos in our simulations remain hemispheric throughout the simulation time, except in MHDr2*, where the magnetic activity migrated from the southern to the northern hemisphere. A similar behaviour was reported by Brown et al. (2020) in fully convective M dwarfs, but the reason behind it is not clear. Some magnetic fields reach the surface of the star in our simulations. However, these fields are very weak everywhere except at the poles, where the maximum rms value averaged over the poles (−90° > θ > −75°, and 75° < θ < 90°) was seen in run MHDr3 with ∼0.47 kG. In the group MHD*, the surface magnetic fields are significantly weaker due to the different radial profiles of diffusivities, with maximum values around 10−4 kG. These weak surface magnetic fields might be a consequence of the flows aligned with the rotation axis because of the Taylor-Proudman theorem, due to the high Coriolis numbers in our simulations. Such flows could penetrate the radiative layers due to the unrealistically low Richardson number there.
All the simulations have approximately rigid rotation in a significant part of their radiative envelope, and a solar-like differential rotation in the convective core. On average, the core is rotating slightly slower than the envelope. Run MHDr1 has 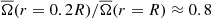 , while the runs with dynamos have ratios very close to unity. Differential rotation has been observed in early-type stars via asteroseismology (see Bowman 2021, 2023, and the references therein). Kurtz et al. (2014) reported the surface-to-core rotation of the MS A-type star KIC 11145123, finding that the star is almost a rigid rotator, but the surface rotates slightly faster than the core in agreement with our simulations. Furthermore, most of the observed intermediate-mass MS stars have nearly rigid rotation, based on the average near-core and envelope rotation rates (see Fig. 4 of Bowman 2023). In massive stars (M > 9 M⊙), the near-core rotation rate is typically larger than that of the envelope. For example, Burssens et al. (2023) recently deduced the core-to-surface radial rotation profile of the B star HD 192575, finding that the convective core is rotating between 1.4 and 6.3 times faster than the radiative envelope.
, while the runs with dynamos have ratios very close to unity. Differential rotation has been observed in early-type stars via asteroseismology (see Bowman 2021, 2023, and the references therein). Kurtz et al. (2014) reported the surface-to-core rotation of the MS A-type star KIC 11145123, finding that the star is almost a rigid rotator, but the surface rotates slightly faster than the core in agreement with our simulations. Furthermore, most of the observed intermediate-mass MS stars have nearly rigid rotation, based on the average near-core and envelope rotation rates (see Fig. 4 of Bowman 2023). In massive stars (M > 9 M⊙), the near-core rotation rate is typically larger than that of the envelope. For example, Burssens et al. (2023) recently deduced the core-to-surface radial rotation profile of the B star HD 192575, finding that the convective core is rotating between 1.4 and 6.3 times faster than the radiative envelope.
The hemispheric dynamos imprint an asymmetry also on the rotation profile via magnetic quenching of the differential rotation. There is no clear difference between groups in their rotation profiles. As we increase the rotation rate, the magnetic energy gets closer to the equipartition values with the kinetic energy. The magnetic energy inside the core reaches Emag ≈ 0.4Ekin in the fast rotators MHDr4 and MHDr4*, while in the full star both energies are comparable. Unlike the fast rotators in Augustson et al. (2016), none of our runs reached super-equipartition values. This might be a consequence of the different values of the dimensionless diagnostic parameters in their simulations; for example, the fluid Reynolds number (computed as Re′/2π for a proper comparison, see Appendix A of Käpylä et al. 2017) are in the range of 81-132, while those in our study range between 25 and 52. Furthermore, the ReM (Rm′/2π) values in their work range from 324 to 490; these values are significantly higher than what we have obtained in the current study (17–36).
All groups have very similar luminosity profiles, which are also similar to those in Brun et al. (2005) and Augustson et al. (2016). In general, the zoom models show very similar results compared to the full star models. However, in the zoom models the magnetic fields are slightly weaker (see Tables 1 and 3). This is possibly a resolution effect. Nevertheless, the changes are not drastic and the large-scale structures are very similar giving us confidence in the robustness of the results.
We found the following relation: Pcyc ∝ Protα with α = −0.89 ± 0.06, α = −0.77 ± 0.16, and α = −0.36 ± 0.25 in the groups MHD, MHD*, and zMHD, respectively. Furthermore, we present a scaling of Prot/Pcyc ∝ Coβ, with β = −1.22 ± 0.05 in the MHD group, β = −1.13 ± 0.11 in the MHD* group and β = −0.83 ± 0.16 in the zMHD group; noting that this is the first time that this has been found with the core dynamo cycles of A-type stars. Similar results with β ≈ −1 were recently reported by Irving et al. (2023) and have been found in data from simulations of other types of stars (e.g. Warnecke 2018; Strugarek et al. 2018; Viviani et al. 2018; Ortiz-Rodríguez et al. 2023). Furthermore, Bonanno & Corsaro (2022) reported a dichotomy in the relation Pcyc ∝ Protα, in terms of ωcyc = 2π/Pcyc and Ω = 2π/Prot, where our results (α < 0) agree with one of the reported branches (Group 2 in their Fig. 1). This branch is attributed to having older stars with higher metallicities than the other. The reason of why our simulations fit with this group is currently unclear. However, there is considerable debate regarding the scaling of stellar cycles as a function of rotation both from observations as well as simulations (see, e.g. Käpylä et al. 2023, and references therein).
Our simulations indicate that the magnetic field created by a core dynamo is not enough to explain the large-scale structures observed at the surface of Ap/Bp stars, in accordance with earlier analytical studies (e.g. MacGregor & Cassinelli 2003). This makes sense considering the wide range of magnetic field strengths observed at the surfaces of stars whose convective cores are predicted to be of similar size. Moreover, the surface magnetic fields of Ap/Bp stars often have simple geometries, for example, dipoles with a magnetic axis misaligned with the rotational axis, supporting the fossil field theory (see Keszthelyi 2023, and the references therein). Interestingly, the internal magnetic field inferred by Lecoanet et al. (2022) seems to be unlikely to reach exclusively with fossil fields, supporting the evidence of a strong core dynamo inside early-type stars. In future studies, different mechanisms (e.g. fossil fields, Tayler-Spruit dynamo) should be included, while the strong core dynamo is present. A logical step to follow in the future is to add a fossil field into our model and to study how these magnetic configurations affect the nature of the hemispheric dynamo that was obtained in all the magnetic runs. Different initial configurations can be implemented as a way to test their stability and how they interact with an existing core dynamo, similarly to Featherstone et al. (2009). Also modelling the entire star and seeing how the resulting magnetic field behaves at the stellar surface could offer promising insights. Furthermore, more rotation rates can be explored, although it is true that Ap stars can rotate very slowly (Prot = 300 years), most of them have rotation periods between 1 and 10 days (Braithwaite & Spruit 2017), so the ‘fast rotator regime’ of between 1 to 8 days remains unexplored.
Data availability
Movie associated to Fig. 4 is available at https://www.aanda.org
Acknowledgments
We thank the anonymous referee for providing useful comments on the manuscript. JPH and DRGS gratefully acknowledge support by the ANID BASAL projects ACE210002 and FB21003, as well as via Fondecyt Regular (project code 1201280) and via ANID Fondo 2022 QUIMAL 220002. The simulations were performed with resources provided by the Kultrun Astronomy Hybrid Cluster via the projects Conicyt Quimal #170001, Conicyt PIA ACT172033, and Fondecyt Iniciacion 11170268. PJK was supported in part by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) Heisenberg programme (grant No. KA 4825/4-1), and by the Munich Institute for Astro-, Particle and BioPhysics (MIAPbP) which is funded by the DFG under Germany’s Excellence Strategy –EXC-2094 – 390783311. CAOR acknowledges financial support from ANID (DOCTORADO DAAD-BECAS CHILE/62220030) as well as financial support from DAAD (DAAD/BECAS Chile, 2023 – 57636841 ). FHN acknowledges funding from the program Unidad de Excelencia María Maeztu, reference CEX2020-001058-M.
References
- Abt, H. A., & Morrell, N. I. 1995, ApJS, 99, 135 [Google Scholar]
- Aerts, C., Mathis, S., & Rogers, T. M. 2019, ARA&A, 57, 35 [Google Scholar]
- Augustson, K. C., Brun, A. S., & Toomre, J. 2016, ApJ, 829, 92 [Google Scholar]
- Aurière, M., Wade, G. A., Silvester, J., et al. 2007, A&A, 475, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Babcock, H. W. 1960, ApJ, 132, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Clarke, J., Morison, A., et al. 2023, MNRAS, 519, 5333 [NASA ADS] [CrossRef] [Google Scholar]
- Barekat, A., & Brandenburg, A. 2014, A&A, 571, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Becerra, L., Reisenegger, A., Valdivia, J. A., & Gusakov, M. E. 2022, MNRAS, 511, 732 [NASA ADS] [CrossRef] [Google Scholar]
- Bice, C. P., & Toomre, J. 2023, ApJ, 947, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 2007, ApJ, 657, 486 [CrossRef] [Google Scholar]
- Bonanno, A., & Corsaro, E. 2022, ApJ, 939, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Boro Saikia, S., Marvin, C. J., Jeffers, S. V., et al. 2018, A&A, 616, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bowman, D. M. 2021, OBA Stars: Variability and Magnetic Fields, 27 [Google Scholar]
- Bowman, D. M. 2023, Ap&SS, 368, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Boyer, D. W., & Levy, E. H. 1984, ApJ, 277, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Braithwaite, J. 2008, MNRAS, 386, 1947 [Google Scholar]
- Braithwaite, J., & Nordlund, Å. 2006, A&A, 450, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braithwaite, J., & Spruit, H. C. 2004, Nature, 431, 819 [Google Scholar]
- Braithwaite, J., & Spruit, H. C. 2017, R. Soc. Open Sci., 4, 160271 [Google Scholar]
- Brandenburg, A. 2001, ApJ, 550, 824 [Google Scholar]
- Brandenburg, A., & Dobler, W. 2002, Comput. Phys. Commun., 147, 471 [Google Scholar]
- Brandenburg, A., & Sarson, G. R. 2002, Phys. Rev. Lett., 88, 055003 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Saar, S. H., & Turpin, C. R. 1998, ApJ, 498, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Mathur, S., & Metcalfe, T. S. 2017, ApJ, 845, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, B. P., Browning, M. K., Brun, A. S., Miesch, M. S., & Toomre, J. 2008, ApJ, 689, 1354 [CrossRef] [Google Scholar]
- Brown, B. P., Oishi, J. S., Vasil, G. M., Lecoanet, D., & Burns, K. J. 2020, ApJ, 902, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Browning, M. K., Brun, A. S., & Toomre, J. 2004, ApJ, 601, 512 [Google Scholar]
- Brun, A. S., & Browning, M. K. 2017, Liv. Rev. Sol. Phys., 14, 4 [Google Scholar]
- Brun, A. S., Miesch, M. S., & Toomre, J. 2004, ApJ, 614, 1073 [Google Scholar]
- Brun, A. S., Browning, M. K., & Toomre, J. 2005, ApJ, 629, 461 [Google Scholar]
- Burssens, S., Bowman, D. M., Michielsen, M., et al. 2023, Nat. Astron., 7, 913 [NASA ADS] [CrossRef] [Google Scholar]
- Buysschaert, B., Aerts, C., Bowman, D. M., et al. 2018, A&A, 616, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantiello, M., & Braithwaite, J. 2019, ApJ, 883, 106 [Google Scholar]
- Cantiello, M., Langer, N., Brott, I., et al. 2009, A&A, 499, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chan, K. L., & Sofia, S. 1986, ApJ, 307, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, P. 2020, Liv. Rev. Sol. Phys., 17, 4 [Google Scholar]
- Cowling, T. G. 1945, MNRAS, 105, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, W., Stix, M., & Brandenburg, A. 2006, ApJ, 638, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Featherstone, N. A., Browning, M. K., Brun, A. S., & Toomre, J. 2009, ApJ, 705, 1000 [Google Scholar]
- Grunhut, J. H., Wade, G. A., Neiner, C., et al. 2017, MNRAS, 465, 2432 [NASA ADS] [CrossRef] [Google Scholar]
- Guerrero, G., Zaire, B., Smolarkiewicz, P. K., et al. 2019, ApJ, 880, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C., Hōshi, R., & Sugimoto, D. 1962, Prog. Theor. Phys. Suppl., 22, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Howe, R. 2009, Liv. Rev. Sol. Phys., 6, 1 [Google Scholar]
- Iglesias, C. A., Rogers, F. J., & Wilson, B. G. 1992, ApJ, 397, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Irving, Z. A., Saar, S. H., Wargelin, B. J., & do Nascimento, J. D. 2023, ApJ, 949, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., & Klahr, H. 2005, ApJ, 634, 1353 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, S., Andrassy, R., Sandalski, S., et al. 2017, MNRAS, 465, 2991 [NASA ADS] [CrossRef] [Google Scholar]
- Käpylä, P. J. 2021, A&A, 651, A66 [Google Scholar]
- Käpylä, P. J. 2022, ApJ, 931, L17 [CrossRef] [Google Scholar]
- Käpylä, P. J. 2024, A&A, 683, A221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Mantere, M. J., Cole, E., Warnecke, J., & Brandenburg, A. 2013, ApJ, 778, 41 [CrossRef] [Google Scholar]
- Käpylä, P. J., Käpylä, M. J., Olspert, N., Warnecke, J., & Brandenburg, A. 2017, A&A, 599, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Gent, F. A., Olspert, N., Käpylä, M. J., & Brandenburg, A. 2020, Geophys. Astrophys. Fluid Dyn., 114, 8 [CrossRef] [Google Scholar]
- Käpylä, P. J., Browning, M. K., Brun, A. S., Guerrero, G., & Warnecke, J. 2023, Space Sci. Rev., 219, 58 [CrossRef] [Google Scholar]
- Keszthelyi, Z. 2023, Galaxies, 11, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Kitchatinov, L. L., & Rüdiger, G. 1999, A&A, 344, 911 [NASA ADS] [Google Scholar]
- Kochukhov, O., & Bagnulo, S. 2006, A&A, 450, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korre, L., & Featherstone, N. A. 2024, ApJ, 964, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, F., & Oetken, L. 1976, in IAU Colloq. 32: Physics of Ap Stars, eds. W. W. Weiss, H. Jenkner, & H. J. Wood, 29 [Google Scholar]
- Krause, F., & Rädler, K.-H. 1980, Mean-field Magnetohydrodynamics and Dynamo Theory (Oxford: Pergamon Press) [Google Scholar]
- Kurtz, D. W., Saio, H., & Takata, M. 2014, MNRAS, 444, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Landeau, M., & Aubert, J. 2011, Phys. Earth Planet. Inter., 185, 61 [CrossRef] [Google Scholar]
- Landstreet, J. D., Bagnulo, S., Andretta, V., et al. 2007, A&A, 470, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landstreet, J. D., Silaj, J., Andretta, V., et al. 2008, A&A, 481, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lecoanet, D., Bowman, D. M., & Van Reeth, T. 2022, MNRAS, 512, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Lignières, F., Petit, P., Böhm, T., & Aurière, M. 2009, A&A, 500, L41 [CrossRef] [EDP Sciences] [Google Scholar]
- Lyra, W., McNally, C. P., Heinemann, T., & Masset, F. 2017, AJ, 154, 146 [NASA ADS] [CrossRef] [Google Scholar]
- MacDonald, J., & Mullan, D. J. 2004, MNRAS, 348, 702 [NASA ADS] [CrossRef] [Google Scholar]
- MacGregor, K. B., & Cassinelli, J. P. 2003, ApJ, 586, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Mathys, G. 2008, Contrib. Astron. Obs. Skalnate Pleso, 38, 217 [NASA ADS] [Google Scholar]
- Mitra, D., Candelaresi, S., Chatterjee, P., Tavakol, R., & Brandenburg, A. 2010, Astron. Nachr., 331, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D. 1989, MNRAS, 236, 629 [NASA ADS] [Google Scholar]
- Moss, D. 2001, ASP Conf. Ser., 248, 305 [Google Scholar]
- Ortiz-Rodríguez, C. A., Käpylä, P. J., Navarrete, F. H., et al. 2023, A&A, 678, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palla, F., & Stahler, S. W. 1992, ApJ, 392, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, F., & Stahler, S. W. 1993, ApJ, 418, 414 [Google Scholar]
- Parker, E. N. 1955, ApJ, 122, 293 [Google Scholar]
- Parker, E. N. 1979, Ap&SS, 62, 135 [NASA ADS] [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
- Pencil Code Collaboration (Brandenburg, A., et al.) 2021, J. Open Source Software, 6, 2807 [CrossRef] [Google Scholar]
- Petit, P., Lignières, F., Wade, G. A., et al. 2010, A&A, 523, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petit, P., Lignières, F., Aurière, M., et al. 2011, A&A, 532, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petit, P., Böhm, T., Folsom, C. P., Lignières, F., & Cang, T. 2022, A&A, 666, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petitdemange, L., Marcotte, F., & Gissinger, C. 2023, Science, 379, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Petitdemange, L., Marcotte, F., Gissinger, C., & Daniel, F. 2024, A&A, 681, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pouquet, A., Frisch, U., & Léorat, J. 1976, J. Fluid Mech., 77, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Raynaud, R., & Tobias, S. M. 2016, J. Fluid Mech., 799, R6 [NASA ADS] [CrossRef] [Google Scholar]
- Raynaud, R., Petitdemange, L., & Dormy, E. 2014, A&A, 567, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richard, O., Michaud, G., & Richer, J. 2001, ApJ, 558, 377 [Google Scholar]
- Royer, F., Zorec, J., & Gómez, A. E. 2007, A&A, 463, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saar, S. H., & Brandenburg, A. 1999, ApJ, 524, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. R. G., Hidalgo, J. P., & Galli, D. 2023, A&A, 678, A204 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuessler, M., & Paehler, A. 1978, A&A, 68, 57 [NASA ADS] [Google Scholar]
- Shultz, M. E., Wade, G. A., Rivinius, T., et al. 2019, MNRAS, 490, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [Google Scholar]
- Simitev, R. D., & Busse, F. H. 2012, Phys. Scr., 86, 018407 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [CrossRef] [EDP Sciences] [Google Scholar]
- Steenbeck, M., Krause, F., & Rädler, K.-H. 1966, Z. Naturforsch. Teil A, 21, 369 [Google Scholar]
- Strugarek, A., Beaudoin, P., Charbonneau, P., Brun, A. S., & do Nascimento, J. D. 2017, Science, 357, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Strugarek, A., Beaudoin, P., Charbonneau, P., & Brun, A. S. 2018, ApJ, 863, 35 [Google Scholar]
- Tayler, R. J. 1973, MNRAS, 161, 365 [CrossRef] [Google Scholar]
- Viviani, M., Warnecke, J., Käpylä, M. J., et al. 2018, A&A, 616, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warnecke, J. 2018, A&A, 616, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Welch, P. 1967, IEEE Trans. Audio Electroacoust., 15, 70 [Google Scholar]
- Wood, T. S., & Brummell, N. H. 2012, ApJ, 755, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshimura, H. 1975, ApJ, 201, 740 [Google Scholar]
All Tables
Differential rotation parameters and the maximum meridional flow 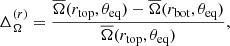 from all the simulations.
from all the simulations.
All Figures
 |
Fig. 1. Density profiles as functions of radius from MHDr1, MHDr2, and MHDr2* (top). Temperature profiles for the same runs (middle). Specific entropy profiles from the same runs (bottom). The black dashed line indicates the surface of the convective core (r = 0.2R) and the grey dashed line the stellar surface (r = R). The quantities are time-averaged over the thermally relaxed phase. |
| In the text | |
 |
Fig. 2. Time-latitude diagrams of the azimuthally averaged toroidal magnetic field |
| In the text | |
 |
Fig. 3. Same as Fig. 2 but for the zoom models zMHDr2 and zMHDr4. |
| In the text | |
 |
Fig. 4. Azimuthally averaged toroidal magnetic field |
| In the text | |
 |
Fig. 5. Time-averaged helicities and dynamo parameters from MHDr3*. From left to right the panels correspond to the normalised fluctuating kinetic helicity |
| In the text | |
 |
Fig. 6. Time-averaged rms magnetic field at the surface of the star r = R as a function of latitude from the runs in groups MHD and MHD*. |
| In the text | |
 |
Fig. 7. Profile of the temporally and azimuthally averaged rotation rate |
| In the text | |
 |
Fig. 8. Profiles of the temporally and azimuthally averaged rotation rate, |
| In the text | |
 |
Fig. 9. Radial profiles of the horizontally averaged Brms (top) and urms (bottom) from representative runs. |
| In the text | |
 |
Fig. 10. Temporal evolution of the magnetic (blue) and kinetic (orange) energies in the full star of the runs MHDr2 (top) and MHDr4 (bottom). |
| In the text | |
 |
Fig. 11. Luminosity contributions from kinetic energy, enthalpy, radiative, cooling and heating fluxes from MHDr2* (top) and MHDr3 (bottom). |
| In the text | |
 |
Fig. 12. Magnetic cycle period Pcyc as a function of the rotation period Prot (left). Ratios of rotation to cycle period as a function of the Coriolis number (right). Additional data are from Strugarek et al. (2018, red), Warnecke (2018, purple) and Käpylä (2022, brown). The dashed lines are the best power-law fits to the data. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



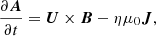
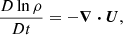
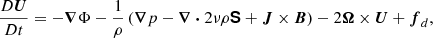
![$$ \begin{aligned} T \frac{Ds}{Dt}&= - \frac{1}{\rho } \left[ \boldsymbol{\nabla } \boldsymbol{\cdot } (\boldsymbol{F}_\text{ rad} + \boldsymbol{F}_\text{ SGS}) + \mathcal{H} - \mathcal{C} + \mu _0 \eta \boldsymbol{J}^2 \right] + 2 \nu \boldsymbol{\mathsf{S}}^2, \end{aligned} $$](/articles/aa/full_html/2024/11/aa49977-24/aa49977-24-eq4.gif)
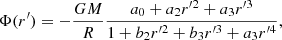
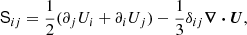
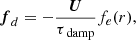
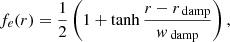
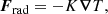
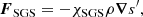
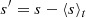
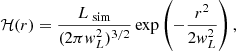
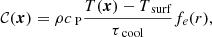
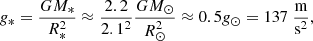
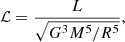
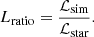
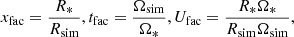
![$$ \begin{aligned}&\rho _\mathrm{fac} = \frac{\rho _0}{\rho _\mathrm{0,sim} }, B_\mathrm{fac} = \left[ \frac{\mu _0 \rho _0 (\Omega _* R_*)^2}{\mu _\mathrm{0,sim} \rho _\mathrm{0,sim} (\Omega _\mathrm{sim} R_\mathrm{sim} )^2}\right]^{1/2}, \end{aligned} $$](/articles/aa/full_html/2024/11/aa49977-24/aa49977-24-eq20.gif)