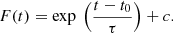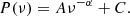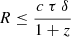| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A223 | |
| Number of page(s) | 7 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202449888 | |
| Published online | 10 October 2024 | |
Rapid optical flare in the extreme teraelectronvolt blazar 1ES 0229+200 on intraday timescales with the Transiting Exoplanet Survey Satellite
1
Aryabhatta Research Institute of Observational Sciences (ARIES), Manora Peak, Nainital 263001, India
e-mail: amp700151@gmail.com; acgupta30@gmail.come-mail: wiitap@tcnj.edu
2
Department of Physics, DDU Gorakhpur University, Gorakhpur 273009, India
3
Xinjiang Astronomical Observatory, Chinese Academy of Sciences (CAS), 150 Science-1 Street, Urumqi 830011, PR China
4
Department of Physics, The College of New Jersey, 2000 Pennington Rd., Ewing, NJ 08628-0718, USA
e-mail: wiitap@tcnj.edu
Received:
7
March
2024
Accepted:
27
April
2024
Context. The extreme teraelectronvolt (TeV) blazar 1ES 0229+200 is a high-frequency-peaked BL Lacertae object. It has not shown intraday variability in extensive optical and X-ray observations, nor has it shown any significant variability on any measurable timescale in the 1–100 GeV energy range over a 14-year span; however, variations in the source flux around its average are present in the energy range above 200 GeV.
Aims. We aim to search for intraday optical variability in 1ES 0229+200 as part of an ongoing project to search for variability and quasi-periodic oscillations in the high-cadence (2 min), nearly uniformly sampled optical light curves of blazars provided by the Transiting Exoplanet Survey Satellite (TESS).
Methods. 1ES 0229+200 was monitored by TESS in its Sectors 42, 43, and 44. We analysed the data of all these three sectors both with the TESS-provided lightkurve software and the eleanor reduction pipeline. We detected a strong, essentially symmetric flare that lasted about 6 h in Sector 42. We fitted the flare’s rising and declining phases to exponential functions. We also analysed the light curve of Sector 42 using the Lomb-Scargle periodogram (LSP) and continuous auto-regressive moving average (CARMA) methods.
Results. The optical light curve of Sector 42 of the TESS observations displayed in the present work provides the first evidence of a strong, rapid, short-lived optical flare on the intraday timescale in the TeV blazar 1ES 0229+200. The variability timescale of the flare provides the upper limit for the size of the emission region to be within (3.3 ± 0.2–8.3 ± 0.5)×1015 cm. Away from the flare, the slope of the periodogram’s power spectrum is fairly typical of many blazars (α < 2), but the nominal slopes for the flaring regions are very steep (α ∼ 4.3), which may indicate that the electron distribution undergoes a sudden change. We discuss possible emission mechanisms that could explain this substantial and rapid flare.
Key words: galaxies: active / BL Lacertae objects: general / BL Lacertae objects: individual: 1ES 0229+200 / galaxies: jets
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The investigation of rapid flux variability offers considerable insight into the physical mechanisms of the innermost regions of active galactic nuclei (AGNs). The blazar subclass of AGNs has stochastic flux variations in the light curves (LCs), which exhibit the largest magnitude changes, as well as those over the shortest timescales. The observed variation in blazars’ LCs have been used to deduce several parameters of underlying physical processes that are not directly perceivable (e.g., Zhang et al. 2021; Roy et al. 2023; Raiteri et al. 2023; Dhiman et al. 2024, and references therein). However, it can be quite difficult to explain the physical and astrophysical processes associated with the normally aperiodic nature of the LCs of a blazar since they have been seen to vary on all timescales, ranging from a few minutes to several years, in all observable electromagnetic (EM) bands. Blazar variability from GeV observations with Fermi-LAT can often be characterised by the exponential Ornstein-Uhlenbeck process (Burd et al. 2021). Perhaps the most puzzling blazar variability is that which occurs on timescales ranging from a few minutes to less than a day, often called intraday variability (IDV; Wagner & Witzel 1995). Multiple methods, including determination of variability timescales, power spectrum density (PSD) analysis, regression methods, correlation methods, and so on, have been used to gain insight into these objects (e.g., Tarnopolski et al. 2020; Raiteri et al. 2023; Gupta et al. 2023, and references therein). In this context, it generally appears that the sub-class of high-energy peaking (HBLs), or high synchrotron peaking (HSPs), blazars show lower amplitude variability with a lower duty cycle (DC) in the optical bands (e.g., Gaur et al. 2012a,c; Gupta et al. 2016; Pandey et al. 2019, 2020a,b; Dhiman et al. 2023, 2024, and references therein). The opposite seems to be usually true for the low-energy peaking blazars (LBLs), or low-energy synchrotron-peaking blazars (LSPs; e.g., Miller et al. 1989; Heidt & Wagner 1996; Sagar et al. 1999; Gupta et al. 2008; Poon et al. 2009; Rani et al. 2011; Bachev et al. 2012, 2023; Gaur et al. 2012b; Tripathi et al. 2024, and references therein).
The blazar 1ES 0229+200 was first detected in the Einstein Imaging Proportional Counter (IPC) Slew Survey (Elvis et al. 1992) and subsequently classified as a BL Lacertae object (Schachter et al. 1993). It has a redshift of z = 0.1396, and the mass of its central supermassive black hole (SMBH) has been estimated to be ∼4.8 × 108 M⊙ (Woo et al. 2005). Based on its high X-ray-to-radio flux ratio, it was classified as an HBL (Giommi et al. 1995). 1ES 0229+200 is among a few blazars that were extensively observed in the first 5.5 months of observations by the Fermi-LAT (Abdo et al. 2009). It is listed in the catalogue of teraelectronvolt (TeV) emitting sources1. The VLA radio observations of this blazar demonstrate curved jets and found a core flux of 51.8 mJy at 5 GHz (Rector et al. 2003). On 184 nights of optical observations over ∼5 years (2007–2012), its brightness varied only slightly (within ≈0.2 magnitudes), and no clear colour magnitude correlation was found (Wierzcholska et al. 2015). In a recent X-ray polarisation study of the source in the 2–8 keV energy range with the Imaging X-ray Polarimetry Explorer (IXPE), a degree of polarisation of 17.9% ± 2.8% and an electric-vector position angle of 25°.0 ± 4°.6 were found (Ehlert et al. 2023).
The blazar 1ES 0229+200 has shown some very peculiar behaviour. Very high energy (VHE) TeV γ-ray emission from the source was detected, with a spectrum characterised by a hard power law in the energy range of 0.5–15 TeV (Aharonian et al. 2007). While those early data showed no evidence for significant TeV variability, additional VHE observations have shown variations in flux on timescales of months (see Acciari et al. 2023). It is considered as an extreme TeV-emitting blazar in both its synchrotron and Compton emissions in the sense that its X-ray emission is detected up to ∼100 keV, with a very hard spectrum (with photon index Γ ∼ 1.8) showing an excess absorption above the Galactic value (Kaufmann et al. 2011). Kaufmann et al. (2011) also mention it as having one of the highest inverse Compton (IC) peak frequencies known at that time. The multi-wavelength (MW) spectral energy distribution (SED) of 1ES 0229+200 is well fitted by a synchrotron self Compton (SSC) model with a very high Doppler factor in the range of 40–100 (Tavecchio et al. 2009; Kaufmann et al. 2011; Aliu et al. 2014). Over 14 nights of optical R-band monitoring from 2016–2019, no IDV was detected on any of the nights (Pandey et al. 2020a). In several X-ray LCs (three made with NuStar and two with XMM-Newton), all of which have substantial good time intervals (GTIs) in the range of ∼16–21 ks, no IDV was detected (Pandey et al. 2017; Devanand et al. 2022).
To better understand blazars’ optical flux variabilities on IDV timescales, we have begun using data from the Transiting Exoplanet Survey Satellite (TESS2; Ricker et al. 2014) to search for strong flaring, stochastic variability, and quasi-periodic oscillations (QPOs) in the essentially evenly sampled LCs with high cadence (down to 2 min) that TESS allows. Recently, we reported the detection of several QPOs with periods in the range of 0.6–2.5 days in the optical emission of the blazar S4 0954+658 (Kishore et al. 2023). We also reported on two exceptional optical flares in the blazar OJ 287, with fluxes nearly doubling and then nearly tripling over two days (Kishore et al. 2024). In the present work, we report the detection of a strong optical flare on an IDV timescale in the blazar 1ES 0229+200 for the first time. As described above, until now, observations of this source have not shown much variability on IDV timescales in any EM band.
In Sect. 2 of this paper, we briefly describe our TESS data analysis. In Sect. 3, we describe the LC analysis and results. A discussion and our conclusions are given in Sect. 4.
2. Observations and data reduction
The Transiting Exoplanet Survey Satellite observed the blazar 1ES 0229+200 for the first time in three consecutive sectors (42, 43, and 44) spanning 2021 August 21 to 2021 November 05 at a cadence of two minutes. Each sector typically lasts 27 days, and there are 1–3 day inter- and intra-sectorial gaps in the data, during which the satellite sends the observed data to Earth or waits for any commands to be uploaded.
We used and reduced the PDCSAP_FLUX (Jenkins et al. 2016) data for our analysis, which is provided by TESS with a cadence of two minutes, in the same manner as in Kishore et al. (2023, 2024). We refer the reader to these papers for details of this approach that uses cotrending basis vectors (CBV) and a discussion of the reduction procedure using the TESS lightkurve software. The goal here is to have the highest possible values of both overfitting and underfitting metrics consistent with a low value of the regularisation parameter α. Table 1 includes the values of the fitting parameters obtained during the reduction of PDCSAP_FLUX of our object for each of the sectors, indicating that this goal was achieved for each of these observations of 1ES 0229+200. Figure 1 shows these data in all three sectors reduced in this fashion.
Flux-calibration details.
 |
Fig. 1. Sectoral TESS LCs of 1ES 0229+200 after data reduction (in 30-min bins for better visualisation). |
Other groups have designed reduction pipelines for TESS data that aim to produce LCs for AGNs that take better account of the variable backgrounds and instrumental noise. These pipelines include eleanor (Feinstein et al. 2019; Brasseur et al. 2019) and quaver (Smith & Sartori 2023). Recently, Poore et al. (2024) conducted a careful comparison of three methods based on the lightkurve package (CBV, regression, and pixel level decorrelation) as well as the eleanor (Feinstein et al. 2019) and quaver (Smith & Sartori 2023) pipelines and the simple-differential-photometry-reduction method. The key result of this comparison is that the latter three methods provide better matches to simultaneous ground-based observations of several blazars. While the direct methods using lightkurve usually show the same types of variations in the LCs as the pipelines, they tend to squash the amplitude of the variability.
Therefore, we also used the eleanor python package to check the results produced with lightkurve where the reduced pca_flux was used for analysis. The baseline flux for the eleanor LC was found to be shifted higher by ∼40 e− s−1, and we note that eleanor uses the longer cadence of ten minutes. A comparison of the LCs produced with these two different methods is shown in Fig. 2. The variation of the baseline could be due to differences in background estimation, which hence leads to the visual long-term variation. Although we do not have simultaneous ground-based observations that could decide which approach is better here, we note that the flare is clearly seen in both LCs. Contra Poore et al. (2024), in this case the relative amplitude of the flare is actually smaller for eleanor.
 |
Fig. 2. Reduced LCs showing the fast variability in Sector 42. The upper plot includes the complete reduced LC using lightkurve, where the inset shows a zoomed-in view of the flare period. The red curve in the subplot is the model fitted by Eq. (1). The lower plot presents a comparison between the LCs produced using lightkurve and eleanor. The eleanor LC in this plot has been shifted down by 40 e− s−1. A zoomed-in view of the flare with the eleanor reduction is plotted in the inset. |
3. Light-curve analysis and results
Visual inspection of the LC of Sector 42 of the blazar 1ES 0229+200 in Fig. 1 gives clear evidence of strong, but short-lived, rapid variability. On the other hand, the LCs of two other epochs observed in Sectors 43 and 44 do not show any obvious variation. To confirm the genuine nature of the variability in the LC of Sector 42, we used the TESS LCs of comparison stars ‘3’ and ‘4’ from the USNO 2.0 Catalogue (Monet 1998)3 to investigate the LC behaviours near the epoch of apparent high variability of the source in the same manner as in Kishore et al. (2024). To perform this comparison, we took a 10 × 10 cutout of the full-frame images of the source blazar and the noted comparison stars. Using the aperture module available in the lightkurve package, we extracted the median flux LC of all these objects. A background of ∼151 e− s−1 in the cutouts was found around the time of the flare. We plot the background-subtracted median flux LCs of these objects in Fig. 3. The increased flux of the blazar over many consecutive data points, along with simultaneous relatively quiescent behaviour of the comparison objects (COs; with all nominal variations spanning very few points) clearly indicates an intrinsic variability of the blazar. A zoomed-in view of a portion of this high-variability region is shown in Fig. 2, revealing a rapid flare centred at BTJD 2448.20. It should be noted that these median flux values have only been used here to make the presence of the flare clear.
 |
Fig. 3. Partial Sector 42 median flux LCs of 1ES 0229+200 (blue) and comparison objects (CO) ‘3’ (orange) and ‘4’ (green). It should be emphasised that this plot provides a preliminary version of the LC (obtained from the targetpixelfile created using TESSCUT for each of the individual objects indicated). While this provides a useful visual comparison, the more fully reduced version of PDCSAP_flux from the already created lightcurvefile was used in our actual analysis. The comparison had to be conducted this way as there were no lightcurvefile outputs available for the COs. |
Our detailed analysis requires the determination of the baseline flux both before and after the flare, the starting and ending epochs, and the e-folding timescales. The latter were separately fitted for both the rising and declining phases of the flare, using the least-squares method, with the model found to be
Here, c is the baseline flux, and τ gives the e-folding timescale. In the rising phase of the flare, t0 gives the time of onset of the flare, while in the declining phase, it is the flare ending time; with this set of parameters, no additional normalisation is required for the exponential terms. Table 2 includes the parameters individually found for the two phases of the flare using our direct lightkurve CBV approach, and the upper panel of Fig. 2 explicitly shows the flaring spans along with the model fit. These indicate that the flare is essentially symmetric. The flare reaches a maximum flux of ∼60 e− s−1 at the epoch ∼2448.201 d with an associated uncertainty (which happens to be maximum during nearby epochs) of ∼5 e− s−1. Taking a mean baseline of 27 e− s−1 from the obtained values and using the maximum local uncertainty, this flare exhibits a ∼6.6σ (max. flux – baseline/uncertainty) significance level detection, making it quite an interesting phenomenon for 1ES 0229+200, which has otherwise been observed to be quiet on short timescales.
Flare characteristics.
We also show the LC from eleanor in the lower panel of Fig. 2 and note the excellent agreement of the timescales obtained for the rising part of the flare, which is 0.8 ± 0.1 h here. However, when using eleanor, the LC showed a more relaxed decay timescale of ∼1.9 h. The confirmation of the rising timescale is helpful in determining the size of the emission region, assuming this value for the most probable shortest variability timescale (see e.g., Kishore et al. 2024).
3.1. Temporal analysis
The periodogram of an LC gives an estimate of the strengths of various temporal frequencies in the LC. Typical blazar periodograms are characterised by a red-noise power-law spectrum at lower frequencies, which at high frequencies becomes asymptotic to white noise (e.g., see Revalski et al. 2014; Wehrle et al. 2019; Kishore et al. 2024, and references therein). A highly dominant frequency compared to the background spectrum implies a periodic or quasi-periodic component in the signal; however, even in the absence of such peaks in the periodogram, its spectral index may yield information about the source of variability since different physical models naturally produce distinct ranges of the spectral index.
The parameters shown in Table 2, obtained from fitting Eq. (1), were used to separate the flaring region from the rest of the first segment of Sector 42 LC, as shown in Fig. 2. Both the post-flare and flare portions of that LC were then individually analysed to estimate the spectral index in the frequency domain using a Lomb-Scargle periodogram (LSP) with ‘HorneBaliunas’ normalisation (Lomb 1976; Scargle 1982; Horne & Baliunas 1986). As always, there is a sparsity of data points in the low-frequency range of the LSP, and this can substantially affect the fitting of the periodogram; so, we employed an oversampling factor of ten while calculating the LSPs. The two LSPs were fitted using a log-likelihood method (see Eq. (17) of Vaughan 2010), with a simple power-law model as well as the associated white noise:
The upper panel of Fig. 4 shows the two LSPs obtained and their corresponding model fits for our standard approach, while the LSP fitting parameters are listed in the first two rows of Table 3. The parameter of interest here is α, which is ∼0.04 (the only simple power law preferred) for the post-flare bulk of the segment’s LC, but it is nominally very steep (∼4.3) for the flare portion. We do note, however, that the flare PSD is being fitted over quite a limited range in frequency thanks to the modest duration of the flare, so this steep α is a tentative result. In the lower panel of Fig. 4, we show the PSDs found using the eleanor LC. The long-term variation visible (probably due to a different background subtraction) in the lower plot of Fig. 2 may well account for the greater power in the lower frequency range of this LSP (lower plot of Fig. 4), which leads to a steeper slope of ∼1.9. The nominal value for the flare’s PSD slope was ∼4.3, which is in agreement with the steep slope obtained with lightkurve. To investigate the impact of any uncertainty in the appropriate length of flare on the PSD plots, we considered several different temporal extents for the flare and corresponding different lengths for the post-flare dataset using our lightkurve reduction. In all cases, the flare PSD slopes exceeded four, while the post-flare slopes were less than one. Though our primary focus is on the first segment of the Sector 42 LC we analysed other segments of other sectors also made using the lightkurve reduction and found that their LSPs are all consistent with just white noise.
 |
Fig. 4. LSP plots of flaring and post-flaring portions of first segment of Sector 42 LC. The upper plot shows LSP corresponding to the LC achieved with lightkurve, while the lower plot corresponds to the eleanor one. In these plots, the LSPs are plotted correspondingly to the over-samplings (OS) indicated. The normal LSPs with no over-sampling are over-plotted to demonstrate the unreliability of their fitting due to the scarcity of available data points. The LSP fits correspond to OS = 10. |
Comparison of flaring and post-flaring LSP parameters.
3.2. CARMA analysis
A somewhat more sophisticated method to analyse the LC makes the initial assumption that it is a manifestation of a Gaussian noise process. The continuous, autoregressive moving-average (CARMA) method, based on this assumption, describes the LC and its first p derivatives in terms of the underlying noise and its first q derivatives with respect to time. It is hence characterised by two parameters, p and q, and denoted as CARMA (p, q; e.g., Kelly et al. 2014). The CARMA models essentially describe the connection between the short-term memory of the process and the behaviour of random fluctuations on different timescales.
We also analysed the flaring and non-flaring portions of the Sector 42 LC reduced with the CBV approach using CARMA, following the method of Yu & Richards (2022). We considered all the (p, q) pairs with 1 ≤ p ≤ 5 and q < p for the CARMA fittings, and the best (p, q) set was estimated by minimising the negative of the log-likelihood found for all those (p, q) sets. We found that both portions were preferably fitted with the simplest CARMA (1,0) model; however, the likelihood of a CARMA (2,0) model was very similar to that of the CARMA (1,0) model for the non-flaring portion.
4. Discussion and conclusions
In this work, we considered the LC of three sectors (42–44) of the TESS observations of the blazar 1ES 0229+200. The object shows almost no optical variations during that period, except for a flare in the first segment of Sector 42. We find that the flare is highly symmetric, exhibiting identical e-folding timescales within errors. This is evidence that this variability is regulated by the radiation or disturbance crossing time through the emission region instead of the acceleration or energy-loss timescales of the radiating electrons (see Chiaberge & Ghisellini 1999; Roy et al. 2019). Multiple examples of evidence of sharp hour-timescale flares, with rises and decays that are approximately linear or exponential, have been found over the past years for different blazars in different EM-bands (e.g., Wagner et al. 1993; Marscher et al. 2008; Chatterjee et al. 2012; Saito et al. 2013; Kushwaha et al. 2014; Kishore et al. 2024, and references therein).
The simple causality constraint given as
can be utilised to limit the size of the emission region, R, where c, τ, δ, and z are the speed of light, variability timescale, Doppler factor, and redshift, respectively. Very high Doppler factors with a large range of 40–100 for 1ES 0229+200 have been estimated via MW SED modelling (Tavecchio et al. 2009; Kaufmann et al. 2011; Aliu et al. 2014). Taking z = 0.1396 and considering an average e-folding timescale (∼0.036 ± 0.002 d, or ∼0.88 ± 0.05 h) as the variability timescale, for this range of δ, we find the upper limit to the size of the emission region to be within (3.3 ± 0.2 − 8.3 ± 0.5)×1015 cm, assuming that the uncertainty is propagated via a variability timescale only.
Properties of the variability, such as the timescale and periodogram, can provide significant insight into the driving process. Different proposed models spontaneously result in specific variability timescales and the spectral indices of their PSDs. A strong, rapid, and rare flare, such as that seen here for 1ES 0229+200, indicates that some extreme change has occurred in the emission region. The periodogram analysis of the flare in Sector 42 suggests a very steep PSD index, α ∼ 4.3, regardless of the reduction method, compared to values typically seen (1.4 − 3.0) for optical variability from most blazars (e.g., see Chatterjee et al. 2012; Nilsson et al. 2018; Wehrle et al. 2019, 2023; Carini et al. 2020; Goyal 2021, and references therein). The weak variations in the post-flare portion of that sector have shallower PSD slopes (α ∼ 0.04 or 1.9, depending on the reduction method), indicating a sudden change in electron distribution during the flare. Previously, Wehrle et al. (2019) found nominal PSD slopes of three (out of 9 studied) γ-ray detected blazars in the 3–4 range for K2 extended Kepler emission LCs, but they were measured on ∼2–3 month timescales. A subsequent reanalysis of those and additional data from 40 K2 LCs measured for 29 AGNs (including 16 BL Lacs) found only one slope steeper than 3, while the vast majority were between 1.6 and 2.6 (Wehrle et al. 2023). A study of the power spectra of the intranight LCs of 14 bright blazars found a wide range of best-fitting PSD slopes and a rather steep average of 2.9 ± 0.3 on those short timescales (Goyal 2021). Over multi-year time frames, Nilsson et al. (2018) found generally shallower PSD slopes for their sample of 31 γ-ray-emitting blazar LCs, with a range from 1.0 to 1.9 and an average of 1.46 ± 0.18. So, we are unaware of any previous clear case for such steep PSD slopes of optical LC for blazars on timescales of a few hours. We note that we performed separate PSD analyses of the flare and post-flare LCs of 1ES 0229+200 while these other studies analysed the entire LCs.
The EM emission in blazars is generated in relativistic jets that are beamed and Doppler-boosted towards the observer’s line of sight, which dominates the thermal emission from the accretion disc; so, any blazar variability observed on any timescale is more likely to be explained using relativistic jet-based models. However, as there are situations where flat-spectrum radio quasars in their low states show features of disc thermal emission in their SEDs, the variability can arise from hotspots on (or instabilities in) the accretion discs (e.g., Mangalam & Wiita 1993; Chakrabarti & Wiita 1993). Since 1ES 0229+200 is an HBL, the possibility of significant variability from the disc region can be discarded. Several jet-based models have been proposed for blazar flux variability observed on different timescales. These include shock-in-jet scenarios (e.g., Marscher & Gear 1985), turbulence behind the shocks in a relativistic jet (e.g., Marscher 2014; Pollack et al. 2016), ultra-relativistic mini-jets (e.g., Ghisellini et al. 2009; Giannios et al. 2009), and turbulence produced by magnetic reconnection (e.g., Guo et al. 2021; Kadowaki 2021).
Since 1ES 0229+200 is a BL Lac, a disc emission contribution is unlikely; so, the LC in Fig. 2 can be interpreted as a superimposition of a short-term flare in a compact magnetic reconnection region that arises from instabilities over a barely varying envelope of non-thermal jet emission. In a similar study of γ-ray flares, Shukla & Mannheim (2020) found a peak-in-peak behaviour in two of the three detected fast flares of the FSRQ 3C 279, where the fast flares were superimposed on the more slowly varying envelope emission; they attributed this rapid variation to a mini-jet scenario. Although their study included multiple flares, this scenario can still produce an isolated flare. Hence, we suggest this jet-in-jet or mini-jet model as a likely way to produce a rapid change in electron distribution and an increased local Doppler factor that could engender the outburst seen in 1ES 0229+200 during Sector 42 of these TESS observations.
Acknowledgments
This paper includes data collected with the TESS mission, obtained from the MAST data archive at the Space Telescope Science Institute (STScI). Funding for the TESS mission is provided by the NASA Explorer Program. STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 526555. ACG’s work is partially supported by the CAS “Light of West” China Program (No. 2021-XBQNXZ-005) and the Xinjiang Tianshan Talents Program. Facility: Transiting Exoplanet Survey Satellite (TESS) – The dataset used in this paper can be found in MAST: https://mast.stsci.edu/portal/Mashup/Clients/Mast/Portal.html?searchQuery=%7B%22service%22:%22DOIOBS%22,%22inputText%22:%2210.17909/b3et-af14%22%7D. Software: lightkurve (Lightkurve Collaboration 2018), SciPy (Virtanen et al. 2020), eleanor (Feinstein et al. 2019), EzTao (Yu & Richards 2022).
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 707, 1310 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Agudo, I., Aniello, T., et al. 2023, A&A, 670, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. 2007, A&A, 475, L9 [CrossRef] [EDP Sciences] [Google Scholar]
- Aliu, E., Archambault, S., Arlen, T., et al. 2014, ApJ, 782, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Bachev, R., Semkov, E., Strigachev, A., et al. 2012, MNRAS, 424, 2625 [CrossRef] [Google Scholar]
- Bachev, R., Tripathi, T., Gupta, A. C., et al. 2023, MNRAS, 522, 3018 [NASA ADS] [CrossRef] [Google Scholar]
- Brasseur, C. E., Phillip, C., Fleming, S. W., Mullally, S. E., & White, R. L. 2019, Astrophysics Source Code Library [record ascl:1905.007] [Google Scholar]
- Burd, P. R., Kohlhepp, L., Wagner, S. M., et al. 2021, A&A, 645, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carini, M., Wehrle, A. E., Wiita, P. J., Ward, Z., & Pendleton, K. 2020, ApJ, 903, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Chakrabarti, S. K., & Wiita, P. J. 1993, ApJ, 411, 602 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, R., Bailyn, C. D., Bonning, E. W., et al. 2012, ApJ, 749, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Chiaberge, M., & Ghisellini, G. 1999, MNRAS, 306, 551 [Google Scholar]
- Devanand, P. U., Gupta, A. C., Jithesh, V., & Wiita, P. J. 2022, ApJ, 939, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Dhiman, V., Gupta, A. C., Kurtanidze, S. O., et al. 2023, MNRAS, 519, 2796 [Google Scholar]
- Dhiman, V., Gupta, A. C., Bachev, R., et al. 2024, MNRAS, 527, 1344 [Google Scholar]
- Ehlert, S. R., Liodakis, I., Middei, R., et al. 2023, ApJ, 959, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M., Plummer, D., Schachter, J., & Fabbiano, G. 1992, ApJS, 80, 257 [CrossRef] [Google Scholar]
- Feinstein, A. D., Montet, B. T., Foreman-Mackey, D., et al. 2019, PASP, 131, 094502 [Google Scholar]
- Gaur, H., Gupta, A. C., Strigachev, A., et al. 2012a, MNRAS, 420, 3147 [CrossRef] [Google Scholar]
- Gaur, H., Gupta, A. C., Strigachev, A., et al. 2012b, MNRAS, 425, 3002 [NASA ADS] [CrossRef] [Google Scholar]
- Gaur, H., Gupta, A. C., & Wiita, P. J. 2012c, AJ, 143, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Tavecchio, F., Bodo, G., & Celotti, A. 2009, MNRAS, 393, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Giannios, D., Uzdensky, D. A., & Begelman, M. C. 2009, MNRAS, 395, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Giommi, P., Ansari, S. G., & Micol, A. 1995, A&AS, 109, 267 [NASA ADS] [Google Scholar]
- Goyal, A. 2021, ApJ, 909, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, F., Li, X., Daughton, W., et al. 2021, ApJ, 919, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A. C., Fan, J. H., Bai, J. M., & Wagner, S. J. 2008, AJ, 135, 1384 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A. C., Agarwal, A., Bhagwan, J., et al. 2016, MNRAS, 458, 1127 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A. C., Kushwaha, P., Valtonen, M. J., et al. 2023, ApJ, 957, L11 [CrossRef] [Google Scholar]
- Heidt, J., & Wagner, S. J. 1996, A&A, 305, 42 [NASA ADS] [Google Scholar]
- Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [Google Scholar]
- Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, in Software and Cyberinfrastructure for Astronomy IV, eds. G. Chiozzi, & J. C. Guzman, SPIE Conf. Ser., 9913, 99133E [Google Scholar]
- Kadowaki, L. H. S., de Gouveia Dal Pino, E. M., Medina-Torrejón, T. E., Mizuno, Y., & Kushwaha, P., 2021, ApJ, 912, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufmann, S., Wagner, S. J., Tibolla, O., & Hauser, M. 2011, A&A, 534, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kelly, B. C., Becker, A. C., Sobolewska, M., Siemiginowska, A., & Uttley, P. 2014, ApJ, 788, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Kishore, S., Gupta, A. C., & Wiita, P. J. 2023, ApJ, 943, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Kishore, S., Gupta, A. C., & Wiita, P. J. 2024, ApJ, 960, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Kushwaha, P., Singh, K. P., & Sahayanathan, S. 2014, ApJ, 796, 61 [NASA ADS] [Google Scholar]
- Lightkurve Collaboration (Cardoso, J. V. D. M., et al) 2018, Astrophysics Source Code Library [record ascl:1812.013] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
- Mangalam, A. V., & Wiita, P. J. 1993, ApJ, 406, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P. 2014, ApJ, 780, 87 [Google Scholar]
- Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114 [Google Scholar]
- Marscher, A. P., Jorstad, S. G., D’Arcangelo, F. D., et al. 2008, Nature, 452, 966 [Google Scholar]
- Miller, H. R., Carini, M. T., & Goodrich, B. D. 1989, Nature, 337, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Monet, D. G. 1998, Am. Astron. Soc. Meet. Abstr., 193, 120.03 [NASA ADS] [Google Scholar]
- Nilsson, K., Lindfors, E., Takalo, L. O., et al. 2018, A&A, 620, A185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pandey, A., Gupta, A. C., & Wiita, P. J. 2017, ApJ, 841, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Pandey, A., Gupta, A. C., Wiita, P. J., & Tiwari, S. N. 2019, ApJ, 871, 192 [CrossRef] [Google Scholar]
- Pandey, A., Gupta, A. C., Damljanovic, G., et al. 2020a, MNRAS, 496, 1430 [NASA ADS] [CrossRef] [Google Scholar]
- Pandey, A., Gupta, A. C., Kurtanidze, S. O., et al. 2020b, ApJ, 890, 72 [CrossRef] [Google Scholar]
- Pollack, M., Pauls, D., & Wiita, P. J. 2016, ApJ, 820, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Poon, H., Fan, J. H., & Fu, J. N. 2009, ApJS, 185, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Poore, E., Carini, M., Dingler, R., Wehrle, A. E., & Wiita, P. J. 2024, ApJ, 966, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Raiteri, C. M., Villata, M., Jorstad, S. G., et al. 2023, MNRAS, 522, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Rani, B., Gupta, A. C., Joshi, U. C., Ganesh, S., & Wiita, P. J. 2011, MNRAS, 413, 2157 [CrossRef] [Google Scholar]
- Rector, T. A., Gabuzda, D. C., & Stocke, J. T. 2003, AJ, 125, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Revalski, M., Nowak, D., Wiita, P. J., Wehrle, A. E., & Unwin, S. C. 2014, ApJ, 785, 60 [NASA ADS] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, in Space Telescopes and Instrumentation 2014: Optical, Infrared, and Millimeter Wave, eds. J. Oschmann, M. Jacobus, M. Clampin, G. G. Fazio, & H. A. MacEwen, SPIE Conf. Ser., 9143, 914320 [Google Scholar]
- Roy, N., Chatterjee, R., Joshi, M., & Ghosh, A. 2019, MNRAS, 482, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Roy, A., Gupta, A. C., Chitnis, V. R., et al. 2023, ApJS, 265, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Sagar, R., Gopal, K., Mohan, V., et al. 1999, A&AS, 134, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saito, S., Stawarz, Ł., Tanaka, Y. T., et al. 2013, ApJ, 766, L11 [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
- Schachter, J. F., Stocke, J. T., Perlman, E., et al. 1993, ApJ, 412, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Shukla, A., & Mannheim, K. 2020, Nat. Commun., 11, 4176 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, K. L., & Sartori, L. F. 2023, ApJ, 958, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Tarnopolski, M., Żywucka, N., Marchenko, V., & Pascual-Granado, J. 2020, ApJS, 250, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., Ghisellini, G., Ghirlanda, G., Costamante, L., & Franceschini, A. 2009, MNRAS, 399, L59 [CrossRef] [Google Scholar]
- Tripathi, T., Gupta, A. C., Takey, A., et al. 2024, MNRAS, 527, 5220 [Google Scholar]
- Vaughan, S. 2010, MNRAS, 402, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Wagner, S. J., & Witzel, A. 1995, ARA&A, 33, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, S. J., Witzel, A., Krichbaum, T. P., et al. 1993, A&A, 271, 344 [NASA ADS] [Google Scholar]
- Wehrle, A. E., Carini, M., & Wiita, P. J. 2019, ApJ, 877, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Wehrle, A. E., Carini, M., Wiita, P. J., et al. 2023, ApJ, 951, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Wierzcholska, A., Ostrowski, M., Stawarz, Ł., Wagner, S., & Hauser, M. 2015, A&A, 573, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woo, J.-H., Urry, C. M., van der Marel, R. P., Lira, P., & Maza, J. 2005, ApJ, 631, 762 [Google Scholar]
- Yu, W., & Richards, G. T. 2022, Astrophysics Source Code Library [record ascl:2201.001] [Google Scholar]
- Zhang, Z., Gupta, A. C., Gaur, H., et al. 2021, ApJ, 909, 103 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Sectoral TESS LCs of 1ES 0229+200 after data reduction (in 30-min bins for better visualisation). |
| In the text | |
 |
Fig. 2. Reduced LCs showing the fast variability in Sector 42. The upper plot includes the complete reduced LC using lightkurve, where the inset shows a zoomed-in view of the flare period. The red curve in the subplot is the model fitted by Eq. (1). The lower plot presents a comparison between the LCs produced using lightkurve and eleanor. The eleanor LC in this plot has been shifted down by 40 e− s−1. A zoomed-in view of the flare with the eleanor reduction is plotted in the inset. |
| In the text | |
 |
Fig. 3. Partial Sector 42 median flux LCs of 1ES 0229+200 (blue) and comparison objects (CO) ‘3’ (orange) and ‘4’ (green). It should be emphasised that this plot provides a preliminary version of the LC (obtained from the targetpixelfile created using TESSCUT for each of the individual objects indicated). While this provides a useful visual comparison, the more fully reduced version of PDCSAP_flux from the already created lightcurvefile was used in our actual analysis. The comparison had to be conducted this way as there were no lightcurvefile outputs available for the COs. |
| In the text | |
 |
Fig. 4. LSP plots of flaring and post-flaring portions of first segment of Sector 42 LC. The upper plot shows LSP corresponding to the LC achieved with lightkurve, while the lower plot corresponds to the eleanor one. In these plots, the LSPs are plotted correspondingly to the over-samplings (OS) indicated. The normal LSPs with no over-sampling are over-plotted to demonstrate the unreliability of their fitting due to the scarcity of available data points. The LSP fits correspond to OS = 10. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.