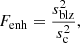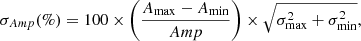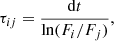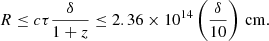| Issue |
A&A
Volume 679, November 2023
|
|
|---|---|---|
| Article Number | A28 | |
| Number of page(s) | 27 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202347545 | |
| Published online | 31 October 2023 | |
Investigating the origin of optical flares from the TeV blazar S4 0954+65
1
Center for Theoretical Physics, Polish Academy of Sciences, Al. Lotnikov 32/46, 02-668 Warsaw, Poland
e-mail: ashwanitapan@gmail.com
2
Institute of Astronomy and NAO, Bulgarian Academy of Sciences, 72 Tsarigradsko Shosse Blvd., 1784 Sofia, Bulgaria
3
Department of Physics, The College of New Jersey, 2000 Pennington Road, Ewing, NJ 08628-0718, USA
4
Aryabhatta Research Institute of Observational Sciences (ARIES), Manora Peak, Nainital 263001, India
5
Faculty of Automatic Control, Electronics and Computer Science, Akademicka 16, 44-100 Gliwice, Poland
Received:
24
July
2023
Accepted:
13
September
2023
Aims. We aim to investigate the extreme variability properties of the TeV blazar S4 0954+65 using optical photometric and polarisation observations carried out between 2017 and 2023 using three ground-based telescopes.
Methods. We examined an extensive dataset comprised of 138 intraday (observing duration shorter than a day) light curves (LCs) of S4 0954+65 for flux, spectral, and polarisation variations on diverse timescales. For the variable LCs, we computed the minimum variability timescales. We investigated flux–flux correlations and colour variations to look for spectral variations on long (several weeks to years) timescales. Additionally, we looked for connections between optical R-band flux and polarisation degree.
Results. We found significant variations in 59 out of 138 intraday LCs. We detected a maximum change of 0.58 ± 0.11 in V-band magnitude within ∼2.64 h and a corresponding minimum variability timescale of 18.21 ± 4.87 mins on 2017 March 25. During the course of our observing campaign, the source brightness changed by ∼4 magnitudes in V and R bands; however, we did not find any strong spectral variations. The slope of the relative spectral energy distribution was 1.37 ± 0.04. The degree of polarisation varied from ∼3% to 39% during our monitoring. We observed a change of ∼120 degrees in polarisation angle (PA) within ∼3 h on 2022 April 13. No clear correlation was found between optical flux and the degree of polarisation.
Conclusions. The results of our optical flux, colour, and polarisation study provide hints that turbulence in the relativistic jet could be responsible for the intraday optical variations in the blazar S4 0954+65. However, the long-term flux variations may be caused by changes in the Doppler factor.
Key words: galaxies: active / BL Lacertae objects: general / BL Lacertae objects: individual: S4 0954+65
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
According to the traditional orientation-based classification scheme of active galactic nuclei (AGN), blazars are radio-loud sources with relativistic jets pointing in a direction that is very close to our line of sight (Urry & Padovani 1995). Depending on the strength of their optical/ultraviolet (UV) emission lines, blazars are further classified as BL Lacertae objects (BLLs; EW1rest < 5 Å) and flat-spectrum radio quasars (FSRQs; EWrest > 5 Å; Stocke et al. 1991; Marcha et al. 1996). The primary characteristics of blazars are high-amplitude flux variations throughout the whole electromagnetic spectrum, significant polarisations in all bands in which it can be measured, and the double-humped shape of their broad-band spectral energy distributions (SEDs; Wagner & Witzel 1995; Fossati et al. 1998; Pandey et al. 2022; Liodakis et al. 2022). The low-energy hump of the SED is attributed to the synchrotron emission from relativistic electrons within the jet, while the high-energy component is usually explained by inverse Compton emission (Sikora et al. 1994; Bloom & Marscher 1996). However, models dominated by hadronic processes have also been proposed to explain the high-energy hump (e.g. Böttcher et al. 2013).
The blazar S4 0954+65 was discovered as a radio source and its optical counterpart was identified by Cohen et al. (1977). It was classified as a BL Lac object by Walsh et al. (1984) and its redshift was first measured to be z = 0.368 (Lawrence et al. 1986; Stickel et al. 1993). Landoni et al. (2015) challenged this value of the redshift and suggested a lower limit of z ≥ 0.45. However, Becerra González et al. (2021) recently ruled out this lower limit and determined the redshift of S4 0954+65 to be z = 0.3694 ± 0.0011 using the Mg II line during its low-flux state.
S4 0954+65 has been studied several times for flux variations on diverse timescales (Wagner et al. 1993; Raiteri et al. 1999; Morozova et al. 2014). The source exhibited extreme optical intraday variability (IDV) of ∼0.7 mag within 7 h and ∼1.0 mag within 5 h on 2011 March 9 and April 24, respectively, accompanied by changes in the fractional polarisation (Morozova et al. 2014). During its 2015 February outburst, Bachev (2015) observed rapid intranight flux variability with a change of ∼0.7 mag in optical brightness within about 5 h. During the same epoch, the source was detected for the first time at very high energies (E≥ 100 GeV) by the MAGIC telescopes (MAGIC Collaboration 2018b). Recently, Raiteri et al. (2021b) investigated the nature of the complex variability of S4 0954+65 using data from the Whole Earth Blazar Telescope (WEBT) Collaboration and the Transiting Exoplanet Survey Satellite (TESS). These authors observed extreme flux variability with an increase of 1 mag in brightness in 24 h followed by a decrease of 0.8 mag in brightness in 23 h. They also found strong variations in optical polarisation degree (PD) and electric vector polarisation angle (PA). However, they did not find any correlation between optical PD and flux.
Variability timescales in blazars span from years to minutes, indicating a variety of underlying physical processes (e.g. Wagner & Witzel 1995; Pandey et al. 2020b; Pandey & Stalin 2022; Raiteri et al. 2023, and references therein). These emission mechanisms can be intrinsic; for example, the interaction of shocks with turbulent plasma and magnetic reconnection in localised jet regions (e.g. Marscher & Gear 1985; Marscher 2014; Pollack et al. 2016), and/or extrinsic geometrical effects, such as a change in viewing angle and therefore also in the Doppler boosting (e.g. Camenzind & Krockenberger 1992; Raiteri et al. 2017). Polarisation variations are also often observed in blazars on a variety of timescales. Observed variable polarisation provides crucial information about the magnitude and direction of the magnetic field inside the jets. A number of investigations have been carried out of the connections between optical flux and polarisation variations. Authors have observed correlations, anti-correlations, and no correlations between optical flux and PD (e.g. Hagen-Thorn et al. 2002; Jorstad et al. 2006; Pandey et al. 2022; Rajput et al. 2022). It is crucial to investigate the relationship between optical flux and PD variations in order to comprehend how the magnetic field affects blazar jet emission processes.
With this motivation, we investigate the multi-band optical variability properties of TeV blazar S4 0954+65 on diverse timescales during 2017–2023. We also examine the optical polarisation variability and the correlation between optical flux and PD to probe the origin of low-energy emissions from S4 0954+65.
The paper is structured as follows. Details of the observations and description of the data reduction are given in Sect. 2. The results of our optical photometry and polarimetry study are presented in Sect. 3. A discussion of our results and conclusions is provided in Sect. 4. Finally, we summarise our findings in Sect. 5.
2. Observations and data reduction
We carried out optical photometric monitoring of the TeV blazar S4 0954+65 from 2017 March 21 to 2023 April 28 using three ground-based optical telescopes in Bulgaria and Spain listed in Table 1. We spent a total of 89 nights observing the blazar, gathering a total of 5005 image frames in the B, V, R, and I optical bands. A detailed log of our optical photometric monitoring is given in Table A.1.
Telescopes used for observations.
For data reduction, we performed the conventional steps, which include cleaning (bias-subtraction, flat-fielding, and cosmic ray removal) of raw images in IRAF, followed by the aperture photometry of cleaned images in DAOPHOT II to get the instrumental magnitudes. Detailed descriptions of the data reduction procedure are given in Pandey et al. (2019; 2020a,b, and references therein). In addition to the source, each image frame also contains three comparison stars (S2, S3, and S4 from Fig. 1 of Raiteri et al. 1999). We generated differential light curves (DLCs) of the blazar S4 0954+65 relative to the comparison stars as well as DLCs of the comparison stars. The standard deviation of DLCs between comparison stars indicates the observational uncertainties on that particular night, whereas the DLC of the blazar with respect to the comparison stars shows the blazar’s intrinsic variability. First, we selected a steady (having minimum standard deviation) pair of comparison stars. We then used the comparison star (S4) from that pair – which has a magnitude and colour comparable to those of the blazar – to obtain the calibrated magnitudes. The calibrated magnitudes were dereddened by subtracting the Galactic extinction, Aλ2, and converted into flux densities. The observations in different bands (BVRI) on a particular night were carried out quasi-simultaneously (within 20 min) using the same telescope.
In addition, we also performed optical (R-band) polarimetry observations using the 60 cm telescope of the Belogradchik observatory between 2022 March 15 and 2023 April 28. To obtain the polarimetric parameters, the PD and the electric vector PA, we used photometric measurements of the blazar S4 0954+65 with respect to the ambient field stars through three polarising filters (in addition to the R-band filter). The polarising filters are oriented at 0–180, 60–240, and 120–300 degrees with respect to North. This approach cannot employ the standard Stokes parameters and requires solving three equations for three unknowns instead; details are given in Bachev et al. (2023). The location of S4 0954+65 in the sky implies the presence of interstellar absorption in that direction of Av ≃ 0.33 mag (Schlafly & Finkbeiner 2011). The dichroic polarisation due to the interstellar dust can then be estimated following Whittet (1992) as PDdust, max < 3Av %, which is equivalent to PDdust, max < 1%. Therefore, for the purposes of our study, the ISM dichroic polarisation can be neglected.
To resolve the 180° ambiguity in the PA measurements, we employed the standard procedure wherein the value 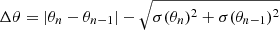 is minimised for consecutive measurements (e.g. Blinov & Pavlidou 2019). Here, θn and σ(θn) are respectively the nth measurement of PA and its uncertainty. For Δθ > 90°, θn is shifted by ±n × 180°, where the integer n is selected to minimise the value of Δθ. For Δθ ≤ 90°, θn remains the same.
is minimised for consecutive measurements (e.g. Blinov & Pavlidou 2019). Here, θn and σ(θn) are respectively the nth measurement of PA and its uncertainty. For Δθ > 90°, θn is shifted by ±n × 180°, where the integer n is selected to minimise the value of Δθ. For Δθ ≤ 90°, θn remains the same.
3. Results
3.1. Optical flux variability
3.1.1. Intraday flux variability
In order to ensure that there were enough photometric points available to characterise IDV, we chose DLCs with at least ten data points in a given filter on each night. By applying this criterion, we were able to consider 138 IDV DLCs, a sample of which is shown in Fig. 1. The calibrated light curves for the DLCs shown in Fig. 1 are plotted in Fig. 2.
 |
Fig. 1. Sample DLCs of the TeV blazar S4 0954+65. Here, S2, S3, and S4 refer to the comparison stars and Blz refers to the blazar. The observation date and the filter name are mentioned at the top of each plot. All 138 DLCs are shown in Fig. C.1. |
We examined the DLCs of TeV blazar S4 0954+65 for IDV using the power-enhanced F-test, which is one of the most powerful and reliable statistical tests to detect microvariability in blazars (de Diego 2014). In the power-enhanced F-test, the variance of the DLC of a blazar is compared with the combined variance of more than one comparison star to detect flux variations. A detailed description of the power-enhanced F-test is provided in our previous papers (Pandey et al. 2019, 2020a). Here, we briefly discuss its main steps. First, we estimate the power-enhanced F-test statistics, which is given by
where 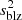 is the variance of the source DLC and
is the variance of the source DLC and 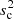 is the combined variance of k comparison stars DLCs. The value of
is the combined variance of k comparison stars DLCs. The value of 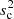 is calculated using Eq. (2) of Pandey et al. (2019). The number of degrees of freedom in the numerator and denominator of the F-statistics are ν1 = N − 1 and ν2 = k(N − 1), respectively, where N is the number of data points. We then compare the value of Fenh with the critical value (Fc) at α = 0.01 (99% confidence level). If Fenh ≥ Fc, we refer to the light curve as variable (V); otherwise, we refer to it as non-variable (NV). The Fenh test results are given in Table B.1. Using this criterion we find that S4 0954+65 displays IDV variability on 59 of the 138 nights of our observations.
is calculated using Eq. (2) of Pandey et al. (2019). The number of degrees of freedom in the numerator and denominator of the F-statistics are ν1 = N − 1 and ν2 = k(N − 1), respectively, where N is the number of data points. We then compare the value of Fenh with the critical value (Fc) at α = 0.01 (99% confidence level). If Fenh ≥ Fc, we refer to the light curve as variable (V); otherwise, we refer to it as non-variable (NV). The Fenh test results are given in Table B.1. Using this criterion we find that S4 0954+65 displays IDV variability on 59 of the 138 nights of our observations.
3.1.2. Flux variability amplitude
To quantify the amplitude of variations in the variable IDV light curves, we estimated the variability amplitude, Amp, which is defined as (Heidt & Wagner 1996)
where Amax and Amin are the maximum and minimum magnitudes of the calibrated light curve, respectively, while σ is the measurement error. The error in the variability amplitude is calculated using the error propagation as
where σmin and σmax are the uncertainties in the minimum (Amin) and maximum (Amax) calibrated magnitudes, respectively. The values of the variability amplitude and its error are given in Table B.1 for the variable light curves; a dash in the table signifies a non-variable light curve.
3.1.3. Variability timescale
For each variable light curve, we also determined the variability timescale following Burbidge et al. (1974),
where dt represents the time interval between two separate flux measurements Fi and Fj such that |Fi − Fj|> σFi + σFj. The minimum flux variability timescale is estimated as τvar = min(τij). The uncertainties in τij were obtained by standard error propagation (Bevington & Robinson 1992). The value of τvar and its uncertainty σ(τvar) are given for the variable light curves in Table B.1 whenever τvar ≥ σ (τvar), otherwise a dash is used. We noticed four occasions when the estimated timescale was more than the length of the light curve; we signal these with an asterisk in Table B.1.
3.1.4. Long-term multi-band flux variability
The daily averaged optical multi-band (BVRI) LCs of the TeV blazar S4 0954+65 for the entire monitoring period are shown in Fig. 3. The source showed clear variations in all the bands. The minimum, maximum, and averaged magnitudes of the source are listed in Table 2, together with the change in magnitude (Δmag) and the minimum variability timescale in each optical band. During our observing campaign, the brightest state we observed the source to be in was Rmag = 13.11 on 2023 March 29, while the faintest state, with Rmag = 17.08, was recorded on 2017 March 28. The V and R band light curves showed the greatest fluctuations (Δmag ∼ 4) and the shortest variability timescales (∼21 h). The significantly higher variability timescale and the smaller values of Δ mag for the B band are almost certainly due to the fewer observations in the B band.
 |
Fig. 3. Long-term light curves of S4 0954+65 in B, V, R, and I bands. Here, the observations performed with telescopes A, B, and C are indicated in black, magenta, and red, respectively. The vertical lines indicate the epochs of flaring events F1, F2, F3, F4, and F5. |
Results of LTV analysis of S4 0954+65.
3.2. Optical spectral variability
To study the spectral variability of the blazar S4 0954+65 for our entire monitoring period, we adopted the technique used by Hagen-Thorn et al. (2008), which is based on the assumption that the radiation has two components, one constant and one variable, and that the variable component causes all the changes in the flux. This method involves plotting the flux–flux diagrams for pairs of bands. If the spectral properties of the variable component remain unchanged during a given time interval, the flux–flux diagrams will follow a linear relationship. The slopes of these lines are the flux ratios for the respective pairs of bands. The reverse is also true, with a few limitations: a linear relationship between fluxes at two separate bands during a period of flux variability implies that the slope (flux ratio) remains constant. Such a linear relation for multiple bands would indicate that the mean relative SED of the variable component remains unchanged for the entire period and can be determined from the slopes of these lines.
The flux–flux diagrams for S4 0954+65 are plotted in Fig. 4. As can be seen from the figure, a straight line fits all the flux–flux plots very well. Using the slopes (log(FB/FR) = − 0.24, log(FV/FR) = − 0.10, log(FR/FR) ≡ 0.0, log(FI/FR) = 0.12) of the lines, we constructed the mean relative SED of S4 0954+65, which is shown in Fig. 5. The SED follows a power law (Fv ∝ ν−α) with a spectral index of α = 1.37 ± 0.04, which is consistent with the value (1.32 ± 0.05) obtained by Hagen-Thorn et al. (2015) during 2008–2012. It is important to note that, here we are only using optical data in BVRI bands, which cover a relatively narrow spectral range. In a few cases, flux–flux plots have been found to deviate from the linear relationship in the infrared (IR) bands (Larionov et al. 2010; Liodakis et al. 2020). However, Hagen-Thorn et al. (2015) observed that for S4 0954+65, the flux–flux plots followed a linear relationship even in the IR bands.
 |
Fig. 4. Flux–flux diagrams of S4 0954+65 for optical wavelengths. The solid red line represents the straight-line fit indicating that the fluxes are correlated. |
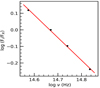 |
Fig. 5. Mean observed relative SED of S4 0954+65 for the entire monitoring period. |
In addition, we also estimated the colour indices for the total observing period in order to examine colour variations with time and magnitude. We acquired 38 B–V, 40 B–R, 38 B–I, 86 V–R, 82 V–I, and 86 R–I colour indices with average values of 0.646 ± 0.014, 1.146 ± 0.014, 1.811 ± 0.014, 0.503 ± 0.003, 1.187 ± 0.002, and 0.679 ± 0.003, respectively. The V–I colour indices, having the highest average value among the frequently measured indices, are plotted against time and I band magnitude in Fig. 6. The correlation coefficient is just 0.23 (p-value > 0.05) and the slope of the linear fit is 0.01, indicating that there was an insignificant relationship between the V–I colour indices and I magnitude.
 |
Fig. 6. Variations of V–I colour indices with time (top panel) and I-band magnitude (bottom panel). The horizontal blue line denotes the average value of the V–I colour indices, while the red solid line in the bottom panel represents a linear fit. |
3.3. Optical flares
The source exhibited several high-flux stages during the course of our monitoring period, as seen in Fig. 3. We identified five such flaring epochs (F1, F2, F3, F4, and F5) each having at least three data points in each filter. The duration of these epochs, the observed changes in R-mag, and the minimum variability timescales are given in Table 3. The maximum change in R-mag, Δmag = 2.69, was recorded during flare F5, which also has the shortest variability timescale of ∼21 h.
Results of the flux and spectral variability analysis of optical flares.
For each of these flaring epochs, we generated the relative SED shown in Fig. 7 in order to investigate the spectral variability. The large uncertainty in the data point corresponding to the B-band in each SED is due to the smaller number of observations in the B-band. The derived optical spectral indices for these periods are listed in Table 3. The spectral indices are comparable within the uncertainties.
 |
Fig. 7. Relative SEDs for different flaring epochs. |
3.4. Polarisation variability
The magnetic field almost certainly plays an important role in the flux variability of blazars. To obtain information on the magnetic field, we also performed optical R-band polarimetric observations of S4 0954+65 from 2022 March 15 to 2023 April 28 using the 60 cm telescope at the Belogradchik Observatory (telescope A in Table 1). The log of our polarimetry observations is given in Table 4. We can see fluctuations in both PD and PA despite the noisy and sparse nature of the data on IDV timescales; see Fig. 8. The minimum and maximum values of PD and PA for each night are given in Table 4.
 |
Fig. 8. Sample plot showing variation of PD and PA with optical flux on an intraday timescale. All such IDV plots are shown in Fig. D.1. |
Polarisation observation log of S4 0954+65.
We found significant changes in the PD over the course of a night (ΔPD > 3 σΔPD) on 5 of the 22 nights. The maximum significant change in PD was 10 ± 1% observed on 2022 April 11. We also noticed a change in PA by ∼120 deg in ∼3 h on 2022 April 13 (see Fig. 8). For the full monitoring period, the values of PD range from ∼3% to 39%, while the PA varied between ∼11° and ∼169°.
3.5. Correlation between optical flux and polarisation
For the nights when we had more than five polarimetry readings, we display both PD and PA with R-band flux (in mJy) in Fig. D.1. We see no obvious correlations or trends between the optical flux and polarisation on IDV timescales. However, this is unsurprising as our IDV polarisation data are sparse and have large error bars.
For the entire span of our observations, we plotted PD against optical flux in Fig. 9 to investigate their potential correlation. We found no correlation between PD and optical flux, as is evident from the plot, and this is quantified through the values of the correlation coefficient, r = −0.01, and the null hypothesis, p = 0.97. Raiteri et al. (2021b) also observed no correlation between optical brightness and PD for S4 0954+65 using data limited to 2019 and 2020. The absence of correlation between optical flux and PD has also been reported in several other blazars (e.g. Ikejiri et al. 2009; Jermak et al. 2016).
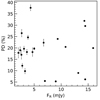 |
Fig. 9. Degree of polarisation versus optical R-band flux. |
4. Discussion and conclusions
The blazar S4 0954+65 is well recognised for its extremely variable optical properties over a range of periods. In this study, we used optical photometry and polarisation measurements spanning approximately 6 years to further explore its optical flares. During our monitoring campaign, the blazar S4 0954+65 exhibited fluctuations in optical flux and PD over a range of timescales. We found statistically significant variations in 59 out of 138 IDV light curves. The variability amplitudes varied from ∼6% to ∼57% on IDV timescales. On 2017 March 25, we observed violent optical variability with a magnitude change of 0.58 within 2.64 h and the corresponding minimum variability timescale of 18.21 ± 4.87 min, which is similar to the variability timescale of 17.10 ± 6.18 min reported by Bhatta et al. (2023). Accepting the black hole mass estimate for S4 0954+65 of 3.3 × 108 M⊙ (Fan & Cao 2004), the corresponding event horizon crossing timescale is ∼27 min. The detected variability timescale is therefore less than the event horizon crossing timescale, supporting the expectation that substructures within the jet are responsible for the fastest changes. Using the minimum variability timescale, we can constrain the size of the emission region as
Here, δ is the Doppler factor, which depends on the viewing angle, θ, and the velocity, βc, of the jet as δ = 1/(Γ[1 − β cos θ]), where the bulk Lorentz factor 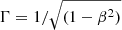 .
.
Assuming a typical value of δ = 10 (Weaver et al. 2022), the size of the emitting region R ≤ 2.36 × 1014 cm. Such a compact (< 10−3 pc) optical emission region has also been reported for the blazar S5 0716+714 by Raiteri et al. (2021a).
This indicates that the IDV fluctuations originate from very compact (R < 10−3 pc) regions. We also noticed variations in PD and PA on IDV timescales. The maximum variation in PD was ∼10% and the PA changed over different ranges. We detected a rapid PA rotation of ∼120 degrees within ∼3 h on 2022 April 13. In the literature, the fastest PA rotation to date was reported by MAGIC Collaboration (2018a) in blazar S5 0716+714, with a change of 300 degrees in PA in just 3.6 h.
The stochastic acceleration of particles in a turbulent region within the jet can account for such rapid fluctuations originating from relatively compact regions (Marscher 2014; Pollack et al. 2016; Kadowaki et al. 2021). In such scenarios, the randomness of the magnetic field direction within turbulent cells would produce random PA rotations. Variant models such as the ‘striped blazar jet’ scenario of Zhang & Giannios (2021) can also produce rapid particle acceleration in small volumes that yield flux changes similar to the observed IDV.
Throughout the course of our observations, the maximum change in the source brightness was ∼4 magnitudes. These flux variations on longer timescales in blazars depend on a number of parameters, including propagating shocks and changes in the injected spectral index, magnetic field, Doppler factor, and/or the density of particles within the emission region. The linear relationship we observed between different waveband light curves showed that the SED of the variable component remains constant during the monitoring period, which is further confirmed by the lack of a significant correlation between V–I colour and I-mag. To investigate the role of the magnetic field in these longer-term optical variations, we examined the correlation between PD and optical flux for the entire duration of these observations. The lack of a substantial relationship between these quantities indicates that the flux changes in S4 0954+65 are not primarily caused by the magnetic field.
The long-term flux variations in blazar S4 0954+65 can very possibly be explained by changes in the viewing angle, and hence in the Doppler factor, using a helical jet model (e.g. Villata & Raiteri 1999; Raiteri et al. 2021b). In this scenario, the relativistic plasma flows continuously in an inhomogeneous helical jet such that each part of the jet, located at a given distance from the jet apex, produces a constant flux controlled by its local physical parameters such as magnetic field, optical depth, and particle density. The twisting of the helical jet causes flux variations over time, while all other jet parameters are considered to remain constant. The observed flux depends on the Doppler factor as 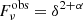
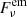 , where α is the power-law spectral index and
, where α is the power-law spectral index and 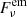 is the emitted flux. Therefore, whenever the emitting region aligns closely to the observer’s line of sight there is an increase in the δ and hence a flare (increased flux) is observed.
is the emitted flux. Therefore, whenever the emitting region aligns closely to the observer’s line of sight there is an increase in the δ and hence a flare (increased flux) is observed.
If the long-term variations in the optical light curve of S4 0954+65 are only due to geometrical factors such as a change in the orientation of the emitting region and a consequent change in the Doppler factor, δ, then δ = δmax(Fν/Fν,max)1/2+α. Taking α = 1.37 as obtained in Sect. 3.2 and a tentative value of δmax = 16 (Raiteri et al. 2021b), the Doppler factor should vary from δmin ∼ 7 to δmax = 16 to explain the variations in the weekly binned R-band light curve (see Fig. 10). Using the definition of δ, the corresponding change in the viewing angle can also be estimated as follows:
 |
Fig. 10. Temporal variation of the weekly binned R-band flux (top panel) together with the corresponding variation in the Doppler factor (middle panel), and the viewing angle (bottom panel) of the emission region based on the model of Raiteri et al. (2021b). |
Adopting Γ = 38.8 from Weaver et al. (2022), we find θmin ∼ 2.9° for δmax = 16 and θmax ∼ 4.7° for δmin = 7 (Fig. 10). This helical jet model has been previously used to explain the long-term optical flux variations in S4 0954+65 (Raiteri et al. 2021b).
In the present work, we investigated the physical mechanisms causing the optical flux and polarisation fluctuations of the TeV blazar S4 0954+65 on IDV and LTV timescales. By analysing an extensive IDV data set, we found that the IDV flux and polarisation variations could be explained by the acceleration of the particles in the turbulent medium within the relativistic jet. On LTV timescales, the spectral variability and correlation between optical brightness and PD provided hints that the changes in the spectral index and magnetic field are not the primary factors responsible for the long-term flux variations in S4 0954+65. We discuss the change in the Doppler factor as a possible cause for the LTV variations and estimate the corresponding variations in the viewing angle of the emitting region. However, in order to fully comprehend the long-term flux variations of S4 0954+65, further study employing a multi-wavelength data set is necessary, which will be the subject of our future work.
5. Summary
We studied the flux, colour, and polarisation fluctuations of blazar S4 0954+65 on diverse timescales from 2017 to 2023 using multi-band optical photometry and R-band polarimetry observations. Our key findings are summarised as follows:
-
On IDV timescales, we find significant flux variation in 59 out of 138 light curves. The variability amplitudes range from 5.7 ± 0.4 to 56.5 ± 11.4%.
-
The observed minimum variability timescale is 18.21 ± 4.87 min, indicating a compact (10−4 pc) emitting region.
-
The acceleration of particles by shock in a turbulent plasma may cause flux variations on IDV timescales.
-
On longer timescales, the brightness of S4 0954+65 varied by ∼4 mag, while no spectral variability was detected. We find the power-law spectral index for relative SED to be 1.37 ± 0.04.
-
We observed a PA rotation of ∼120 degrees in ∼3 h.
-
No correlation was detected between the optical flux and PD.
-
Long-term flux variations may be caused by the change in the Doppler factor of the emission region.
Taken from https://ned.ipac.caltech.edu/
Acknowledgments
We thank the anonymous referee for their thoughtful comments that helped improve the manuscript. Part of this work was supported by the Polish Funding Agency National Science Centre, project 2017/26/A/ST9/00756 (MAESTRO 9). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. [951549]). This research was partially supported by the Bulgarian National Science Fund of the Ministry of Education and Science under grants KP-06-H38/4 (2019), KP-06-KITAJ/2 (2020) and KP-06-H68/4 (2022).
References
- Bachev, R. 2015, MNRAS, 451, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Bachev, R., Tripathi, T., Gupta, A. C., et al. 2023, MNRAS, 522, 3018 [NASA ADS] [CrossRef] [Google Scholar]
- Becerra González, J., Acosta-Pulido, J. A., Boschin, W., et al. 2021, MNRAS, 504, 5258 [CrossRef] [Google Scholar]
- Bevington, P. R., & Robinson, D. K. 1992, Data Reduction and Error Analysis for the Physical Sciences (New York: McGraw-Hill) [Google Scholar]
- Bhatta, G., Zola, S., Drozdz, M., et al. 2023, MNRAS, 520, 2633 [NASA ADS] [CrossRef] [Google Scholar]
- Blinov, D., & Pavlidou, V. 2019, Galaxies, 7, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, S. D., & Marscher, A. P. 1996, ApJ, 461, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Böttcher, M., Reimer, A., Sweeney, K., & Prakash, A. 2013, ApJ, 768, 54 [Google Scholar]
- Burbidge, G. R., Jones, T. W., & Odell, S. L. 1974, ApJ, 193, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Camenzind, M., & Krockenberger, M. 1992, A&A, 255, 59 [NASA ADS] [Google Scholar]
- Cohen, A. M., Porcas, R. W., Browne, I. W. A., Daintree, E. J., & Walsh, D. 1977, MmRAS, 84, 1 [NASA ADS] [Google Scholar]
- de Diego, J. A. 2014, AJ, 148, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Z.-H., & Cao, X. 2004, ApJ, 602, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, G., Maraschi, L., Celotti, A., Comastri, A., & Ghisellini, G. 1998, MNRAS, 299, 433 [Google Scholar]
- Hagen-Thorn, V. A., Larionova, E. G., Jorstad, S. G., Björnsson, C. I., & Larionov, V. M. 2002, A&A, 385, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hagen-Thorn, V. A., Larionov, V. M., Jorstad, S. G., et al. 2008, ApJ, 672, 40 [CrossRef] [Google Scholar]
- Hagen-Thorn, V. A., Larionov, V. M., Arkharov, A. A., et al. 2015, Astron. Rep., 59, 551 [CrossRef] [Google Scholar]
- Heidt, J., & Wagner, S. J. 1996, A&A, 305, 42 [NASA ADS] [Google Scholar]
- Ikejiri, Y., Uemura, M., Sasada, M., et al. 2009, ArXiv e-prints [arXiv:0912.3664] [Google Scholar]
- Jermak, H., Steele, I. A., Lindfors, E., et al. 2016, MNRAS, 462, 4267 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S., Marscher, A., Stevens, J., et al. 2006, Chin. J. Astron. Astrophys. Suppl., 6, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Kadowaki, L. H. S., de Gouveia Dal Pino, E. M., Medina-Torrejón, T. E., Mizuno, Y., & Kushwaha, P. 2021, ApJ, 912, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Landoni, M., Falomo, R., Treves, A., Scarpa, R., & Reverte Payá, D. 2015, AJ, 150, 181 [CrossRef] [Google Scholar]
- Larionov, V. M., Villata, M., & Raiteri, C. M. 2010, A&A, 510, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lawrence, C. R., Pearson, T. J., Readhead, A. C. S., & Unwin, S. C. 1986, AJ, 91, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Liodakis, I., Blinov, D., Jorstad, S. G., et al. 2020, ApJ, 902, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Liodakis, I., Marscher, A. P., Agudo, I., et al. 2022, Nature, 611, 677 [CrossRef] [Google Scholar]
- MAGIC Collaboration (Ahnen, M. L., et al.) 2018a, A&A, 617, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MAGIC Collaboration (Ahnen, M. L., et al.) 2018b, A&A, 619, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marcha, M. J. M., Browne, I. W. A., Impey, C. D., & Smith, P. S. 1996, MNRAS, 281, 425 [CrossRef] [Google Scholar]
- Marscher, A. P. 2014, ApJ, 780, 87 [Google Scholar]
- Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114 [Google Scholar]
- Morozova, D. A., Larionov, V. M., Troitsky, I. S., et al. 2014, AJ, 148, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Pandey, A., & Stalin, C. S. 2022, A&A, 668, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pandey, A., Gupta, A. C., Wiita, P. J., & Tiwari, S. N. 2019, ApJ, 871, 192 [CrossRef] [Google Scholar]
- Pandey, A., Gupta, A. C., Kurtanidze, S. O., et al. 2020a, ApJ, 890, 72 [CrossRef] [Google Scholar]
- Pandey, A., Gupta, A. C., Damljanovic, G., et al. 2020b, MNRAS, 496, 1430 [NASA ADS] [CrossRef] [Google Scholar]
- Pandey, A., Rajput, B., & Stalin, C. S. 2022, MNRAS, 510, 1809 [Google Scholar]
- Pollack, M., Pauls, D., & Wiita, P. J. 2016, ApJ, 820, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Raiteri, C. M., Villata, M., Tosti, G., et al. 1999, A&A, 352, 19 [NASA ADS] [Google Scholar]
- Raiteri, C. M., Villata, M., Acosta-Pulido, J. A., et al. 2017, Nature, 552, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Raiteri, C. M., Villata, M., Carosati, D., et al. 2021a, MNRAS, 501, 1100 [Google Scholar]
- Raiteri, C. M., Villata, M., Larionov, V. M., et al. 2021b, MNRAS, 504, 5629 [NASA ADS] [CrossRef] [Google Scholar]
- Raiteri, C. M., Villata, M., Jorstad, S. G., et al. 2023, MNRAS, 522, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Rajput, B., Pandey, A., Stalin, C. S., & Mathew, B. 2022, MNRAS, 517, 3236 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Sikora, M., Begelman, M. C., & Rees, M. J. 1994, ApJ, 421, 153 [Google Scholar]
- Stickel, M., Fried, J. W., & Kuehr, H. 1993, A&AS, 98, 393 [NASA ADS] [Google Scholar]
- Stocke, J. T., Morris, S. L., Gioia, I. M., et al. 1991, ApJS, 76, 813 [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Villata, M., & Raiteri, C. M. 1999, A&A, 347, 30 [NASA ADS] [Google Scholar]
- Wagner, S. J., & Witzel, A. 1995, ARA&A, 33, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, S. J., Witzel, A., Krichbaum, T. P., et al. 1993, A&A, 271, 344 [NASA ADS] [Google Scholar]
- Walsh, D., Beckers, J. M., Carswell, R. F., & Weymann, R. J. 1984, MNRAS, 211, 105 [NASA ADS] [Google Scholar]
- Weaver, Z. R., Jorstad, S. G., Marscher, A. P., et al. 2022, ApJS, 260, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. C. B. 1992, Dust in the Galactic Environment (Philadelphia: A. Hilger) [CrossRef] [Google Scholar]
- Zhang, H., & Giannios, D. 2021, MNRAS, 502, 1145 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Observation log
Optical photometric observation log.
Appendix B: Results of variability analyses.
Results of IDV analyses of the TeV blazar S4 0954+65. The values of variability amplitude, Δmag, and τvar are only mentioned for the variable light curves. For non-variable light curves, we put a ’-’. Also, when τvar < σ (τvar) we use a ’-’ for τvar. A * denotes that the detected variability timescale is greater than the duration of the light curve.
Appendix C: Intraday differential light curves of S4 0954+65.
 |
Fig. C.1. DLCs of the TeV blazar S4 0954+65. Here, S2, S3 and S4 refer to the comparison stars and Blz refers to the blazar. The observation date and the filter name are mentioned at the top of each plot. |
 |
Fig. C.1. continued. |
 |
Fig. C.1. continued. |
 |
Fig. C.1. continued. |
 |
Fig. C.1. continued. |
 |
Fig. C.1. continued. |
 |
Fig. C.1. continued. |
 |
Fig. C.1. continued. |
 |
Fig. C.1. continued. |
 |
Fig. C.1. continued. |
 |
Fig. C.1. continued. |
 |
Fig. C.1. continued. |
Appendix D: Intraday optical and polarisation light curves.
 |
Fig. D.1. Intraday R-band light curves (in mJy) along with polarisation measurements. The observation date and the name of the filter used are given at the top of each plot. |
All Tables
Results of IDV analyses of the TeV blazar S4 0954+65. The values of variability amplitude, Δmag, and τvar are only mentioned for the variable light curves. For non-variable light curves, we put a ’-’. Also, when τvar < σ (τvar) we use a ’-’ for τvar. A * denotes that the detected variability timescale is greater than the duration of the light curve.
All Figures
 |
Fig. 1. Sample DLCs of the TeV blazar S4 0954+65. Here, S2, S3, and S4 refer to the comparison stars and Blz refers to the blazar. The observation date and the filter name are mentioned at the top of each plot. All 138 DLCs are shown in Fig. C.1. |
| In the text | |
 |
Fig. 2. Calibrated light curves for the DLCs shown in Fig. 1. |
| In the text | |
 |
Fig. 3. Long-term light curves of S4 0954+65 in B, V, R, and I bands. Here, the observations performed with telescopes A, B, and C are indicated in black, magenta, and red, respectively. The vertical lines indicate the epochs of flaring events F1, F2, F3, F4, and F5. |
| In the text | |
 |
Fig. 4. Flux–flux diagrams of S4 0954+65 for optical wavelengths. The solid red line represents the straight-line fit indicating that the fluxes are correlated. |
| In the text | |
 |
Fig. 5. Mean observed relative SED of S4 0954+65 for the entire monitoring period. |
| In the text | |
 |
Fig. 6. Variations of V–I colour indices with time (top panel) and I-band magnitude (bottom panel). The horizontal blue line denotes the average value of the V–I colour indices, while the red solid line in the bottom panel represents a linear fit. |
| In the text | |
 |
Fig. 7. Relative SEDs for different flaring epochs. |
| In the text | |
 |
Fig. 8. Sample plot showing variation of PD and PA with optical flux on an intraday timescale. All such IDV plots are shown in Fig. D.1. |
| In the text | |
 |
Fig. 9. Degree of polarisation versus optical R-band flux. |
| In the text | |
 |
Fig. 10. Temporal variation of the weekly binned R-band flux (top panel) together with the corresponding variation in the Doppler factor (middle panel), and the viewing angle (bottom panel) of the emission region based on the model of Raiteri et al. (2021b). |
| In the text | |
 |
Fig. C.1. DLCs of the TeV blazar S4 0954+65. Here, S2, S3 and S4 refer to the comparison stars and Blz refers to the blazar. The observation date and the filter name are mentioned at the top of each plot. |
| In the text | |
 |
Fig. C.1. continued. |
| In the text | |
 |
Fig. C.1. continued. |
| In the text | |
 |
Fig. C.1. continued. |
| In the text | |
 |
Fig. C.1. continued. |
| In the text | |
 |
Fig. C.1. continued. |
| In the text | |
 |
Fig. C.1. continued. |
| In the text | |
 |
Fig. C.1. continued. |
| In the text | |
 |
Fig. C.1. continued. |
| In the text | |
 |
Fig. C.1. continued. |
| In the text | |
 |
Fig. C.1. continued. |
| In the text | |
 |
Fig. C.1. continued. |
| In the text | |
 |
Fig. D.1. Intraday R-band light curves (in mJy) along with polarisation measurements. The observation date and the name of the filter used are given at the top of each plot. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.