| Issue |
A&A
Volume 689, September 2024
|
|
|---|---|---|
| Article Number | A134 | |
| Number of page(s) | 23 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202142081 | |
| Published online | 13 September 2024 | |
The impact of improved estimates of radio star astrometric models on the alignment of the Gaia bright reference frame to ICRF3
1
Technische Universität Berlin, Chair of Satellite Geodesy,
Kaiserin-Augusta-Allee 104-106,
10553
Berlin,
Germany
2
GFZ German Research Centre for Geosciences,
14473
Potsdam,
Germany
e-mail: susanne.lunz@gfz-potsdam.de
3
Aalto University Metsähovi Radio Observatory,
Metsähovintie 114,
02540
Kylmälä,
Finland
4
Aalto University Department of Electronics and Nanoengineering,
PL15500,
00076
Aalto,
Finland
5
Geoscience Australia,
PO Box 378,
Canberra
2601,
Australia
6
LERMA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités,
UPMC Univ. Paris 06,
75014
Paris,
France
7
United States Naval Observatory (USNO),
3450 Massachusets Ave NW,
Washington,
DC
20392,
USA
8
Shanghai Astronomical Observatory,
80 Nandan Road,
Shanghai,
200030,
China
9
Yunnan Observatories,
Yangfangwang 396th, Kunming
650011,
Yunnan,
China
10
University of Tasmania,
Private Bag 37, Hobart,
Tasmania,
7001,
Australia
11
Observatorio de Yebes (IGN),
Cerro de la Palera S/N,
19141,
Guadalajara,
Spain
Received:
24
August
2021
Accepted:
20
June
2024
Aims. We investigated the residual orientation offset and spin between the bright (G ≤ 13 mag) frame of the Gaia Early Data Release 3 (Gaia EDR3) and the third realization of the International Celestial Reference Frame (ICRF3). For this purpose, six rotation parameters (orientation offset and its time derivative, the spin), as well as corrections to the Gaia astrometric model for each star involved, are fitted to the differences in the astrometric models derived from very long baseline interferometry (VLBI) and Gaia. This study aims to find reliable estimates for the rotation parameters between the two frames.
Methods. We reprocessed our previous analyses while taking into account the effect of Galactocentric acceleration on the VLBI observations. Furthermore, we replaced VLBI data for 12 stars by improved estimates of models of stellar motion from combining historical data with the new positions, rather than including the new observations directly as single-epoch positions in the analysis of the rotation parameters. Additionally, we replaced the model positions by positions obtained without correcting the calibrator data for source structure whenever possible to better reference the star position to ICRF3. In the same fashion, the VLBI proper motion and parallax were included for two of the stars for the first time, and data for five new stars were added.
Results. The iterative solutions for the spin parameters show less scatter in the X component when the new models of stellar motion from VLBI are applied. The mean formal errors of the spin parameters decrease by about 15%, whereas those of the orientation offsets increase by about 15%. Small additional improvements in the mean formal error were achieved by including new VLBI data and by excluding stars that produce offsets in the iterative rotation parameter estimates from the beginning. The orientation offset [ϵX(T),ϵY(T),ϵZ(T)] and the spin [ωX,ωY,ωZ] of the final baseline solution of this work were found to be (+0.322, +0.228, +0.163)±(0.203, 0.251, 0.155) mas and (+0.034, +0.072, −0.026)±(0.023, 0.025, 0.023) mas yr−1. As a consequence, no significant orientation offset of Gaia EDR3 toward ICRF3 is detected; however, the spin ωY is statistically significant at the 3σ level. The rotation parameters between the Gaia and VLBI frames in the Y direction remain the least well determined in terms of formal errors. The impact of Galactocentric acceleration on the rotation parameter analysis was found to be negligible with the currently available VLBI data. As a result, it was found that the uncorrected bright Gaia frame exhibits a closer alignment with ICRF3 compared to the corrected frame.
Key words: techniques: interferometric / astrometry / reference systems / radio continuum: stars
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
In December 2020 the third data release (Early Data Release 3; EDR3; Gaia Collaboration 2021a) of the Gaia spacecraft (Gaia Collaboration 2016), operated by the European Space Agency (ESA), was published online. It contains astrometric and photometric data of about 1.8 billion objects in the Milky Way and Local Group and therefore is the largest catalog of this kind to date. Since 01 January 2022, the celestial reference frame of Gaia EDR3, Gaia-CRF3 (Gaia Collaboration 2022), has become the fundamental realization of the International Celestial Reference System (ICRS; Arias et al. 1995) in the optical domain (IAU resolution B3, 2021). The counterpart in the radio domain is the third realization of the International Celestial Reference Frame (ICRF3; Charlot et al. 2020), which has been in use since 01 January 2019 (IAU resolution B2, 2018). The ICRF3 was produced from very long baseline interferometry (VLBI) observations of extragalactic radio sources at radio wavelengths (S/X, K, and X/Ka). The Gaia-CRF3 is aligned to the ICRF3 with an uncertainty of 10 µas at epoch T = 2016.0 and it is nonrotating with respect to the ICRF3 and the All-WISE (mid-infrared) active galactic nucleus catalog (Secrest et al. 2015, 2016) with a spin of less than ±10 µas yr−1 (Gaia Collaboration 2021a). The alignment of the Gaia catalog to ICRF3 is known to be G magnitude dependent due to the Gaia internal calibration strategies, and thus, the above numbers are only valid for the optical magnitude G = 19 since the counterparts used for calculations lie mostly around this magnitude (Lindegren et al. 2021b). None of the ICRF3 sources that were detected by Gaia have optical magnitudes G ≤ 13 mag. As a result, the spin correction for the Gaia EDR3 bright frame (G ≤ 13 mag) was derived by comparing proper motions of bright sources calculated from the position differences between Gaia Data Release 2 (DR2; Gaia Collaboration 2018) and HIPPARCOS (van Leeuwen 2007; ESA 1997), divided by the epoch difference of 24.25 yr, and from Gaia EDR3. It was then applied to the Gaia bright frame in EDR3. Thus no residual spin should be present between the Gaia bright frame and ICRS after the correction, and therefore also no residual spin should be present between the Gaia bright frame and the Gaia faint frame. Using this approach, the orientation offset (to the HIPPARCOS reference frame) was assumed to be zero (Lindegren et al. 2021b). However, HIPPARCOS positions and the ICRS at epoch J1991.25 are aligned to no better than 0.6 mas in each axis (Kovalevsky et al. 1997), which introduces a systematic uncertainty of 24 µas yr−1 for Gaia EDR3. This is above the expected uncertainties for bright objects with G ≤ 13 mag, which are predicted to be less than 6 µas for positions and less than 2 µas yr−1 for proper motions in the final Gaia data release1. Because the error budget with this approach cannot be reduced by enhanced Gaia data and obviously no improvements of the HIPPARCOS positions are to be expected, the alignment to ICRS needs to be tested by other methods for the final Gaia data release.
Such an alternative method for the verification of the alignment is by using VLBI observations of optically bright radio stars, as introduced by Lindegren (2020a). Positions, proper motions, and parallaxes from VLBI are compared to those from Gaia. From the differences in these astrometric parameters, residual rotations (orientation offsets ϵX, ϵY, and ϵZ and spins ωX, ωY, and ωZ) about the three orthogonal axes X, Y, and Z and adjustments to the Gaia 5-parameter astrometric models for the individual stars are determined in a combined fit. With this method, not only do the proper motions contribute to the spin parameter adjustment, but also position offsets at a common epoch divided by the epoch difference between VLBI and Gaia positions. In Lunz et al. (2023) this method was adopted and the dataset provided by Lindegren (2020a) was homogenized to consistently reference historical VLBI positions of radio stars to ICRF3 at epoch 2015.0. Furthermore, a realistic error budget was applied to the positions. The main concern for increasing the uncertainties was the difference in the observational method for radio-bright extragalactic objects used to create the ICRF3 (absolute geodetic VLBI based on dual-frequency group delays) and the observational method for radio stars. The latter radio stars are bright at optical frequencies but faint at radio frequencies, thus, only the technique of phase referencing, which allows for the determination of relative star positions with respect to radio-bright calibrators in the ICRF3 based on phase delays, can be used. New single-epoch positions for 32 stars, observed in January 2020 in project UL005 with the Very Long Baseline Array (VLBA) at X and C bands, were added in Lunz et al. (2023) to enhance the fit of orientation and spin parameters. However, the analysis showed that the realistic single-epoch position uncertainties were too large for the new positions to have a significant effect on the spin determination.
In this study, we replace the data for 12 stars that were detected in January 2020 with improved models of stellar motion. These models were derived from a fit of the five astro-metric parameters to a combined position time series consisting of data found in literature and the January 2020 position for each star. In addition, data from five stars recently observed with other VLBI networks have been incorporated into the analysis.
In ICRF3 the effect of Galactocentric acceleration was taken into account for the first time in ICRF history (Charlot et al. 2020). In Gaia EDR3 the Galactocentric acceleration has also been detected due to reduced internal systematics (Gaia Collaboration 2021b). Thus, the impact of this effect on the models of stellar motion, and therefore also on the rotation parameter analysis, must be addressed.
In Sect. 2 we consider the effect of Galactocentric acceleration and investigate its impact on the phase referencing results. Section 3 describes the algorithm used to fit models of stellar motions to VLBI position time series, the reprocessing of the phase referencing observations from January 2020, and the new model estimates including comparisons to literature for each of the respective stars. The choice of the absolute VLBI positions to be used for comparison with the Gaia positions is also discussed. Section 4 presents rotation parameter results for various scenarios that test different aspects of the analysis, including the impact of Galactocentric acceleration, the impact of single stars on the analysis, the impact of the new estimates for models of stellar motion, and the impact of the additional data of the five new stars. Finally, in Sect. 5 we evaluate the results and in Sect. 6 conclusions are drawn.
2 Impact of Galactocentric acceleration on phase referencing results
To account for the global systematic effect of Galactocentric acceleration in ICRF3, a time-dependent correction in the shape of a dipole pattern of magnitude |D| =5.8 µas yr−1 in the Galactocentric direction (αD = 266.4°, δD = −29.0°) was added for the first time to the definition of the ICRF positions, which are given for the epoch 2015.0 (Charlot et al. 2020). While for comparison of the VLBI results to Gaia DR2 it was sufficient to neglect this effect because internal systematics of the Gaia DR2 dataset were well above its magnitude, it is appropriate to investigate the impact when comparing to Gaia EDR3. Using Gaia EDR3, the effect was detected to have a magnitude |D| = 5.05 ± 0.35 µas yr−1 indirection αD = 269.1° ± 5.1°, δD = −31.6° ± 4.1° solely from the proper motions of extragalac-tic compact objects (Gaia Collaboration 2021b). These results match the VLBI-based result within the error bounds.
In Lunz et al. (2023) all star positions were homogeneously referenced to the calibrator positions in ICRF3 at epoch 2015.0. To investigate the effect of Galactocentric acceleration on the phase referencing results, we distinguish between the correction for absolute positions and for proper motions: The absolute position of a star is determined relative to the catalog position of its phase calibrator in ICRF3. Therefore, if this position accounts for the effect of Galactocentric acceleration, the star position also includes this effect. Considering this relation, the homogenized star positions in ICRF3 at epoch 2015.0 can be corrected for the effect of Galactocentric acceleration (see e.g., Titov et al. 2011; MacMillan et al. 2019) by
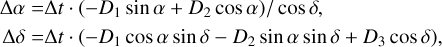 (1)
(1)
where D1 = |D| · cos δD cos αD, D2 = |D| · cos δD sin αD, D3 = |D| · sin δD and ∆t = tB − 2015.0, where tB is the epoch of the star position, and α and δ are the calibrator coordinates. The correction needs to be added to the star position.
At the same time, the proper motions of the stars from position time series are also systematically biased by not accounting for the effect of Galactocentric acceleration in the calibrator positions. Calibrator positions in phase referencing analysis have never been corrected for the effect of Galactocentric acceleration before, since the catalogs used for deriving positions for the phase calibrators never accounted for this effect prior to ICRF3. Therefore, the historical absolute positions of the stars also do not account for the effect of Galactocentric acceleration. The effect needs to be considered for VLBI results because also the Gaia proper motions include it. The corrections
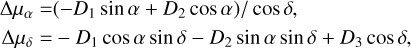 (2)
(2)
need to be added to the star proper motions µα and µδ to correct for the time-varying calibrator coordinates that should have been used during the data processing with respect to ICRF3. In this work, all α · cos(δ) terms are abbreviated by α*.
3 Fitting models of stellar motion to multi-epoch star positions
In this section, we first describe the fitting process of the main astrometric parameters (Sect. 3.1). Since the structure corrected absolute positions of the stars to their calibrators are needed for the model-fitting, the corresponding data processing for the January 2020 positions is also outlined (Sect. 3.2). Then, for each star, a detailed description of input positions and estimated model parameters is given along with a comparison to astro-metric models from the literature and Gaia EDR3 (Sect. 3.3). Finally, only the proper motions and parallaxes are selected from the newly derived models as input for the computation of the rotation parameters in the following section. To be consistent with ICRF3, the absolute positions as determined in Lunz et al. (2023) are used instead of the fitted model positions. These single-epoch absolute positions are corrected for the parallax effect.
3.1 Functional models and fitting procedure
The new estimates for models of stellar motion for each star were determined by fitting its single-epoch coordinates α(t) and δ(t) at observation epoch t to the functional model as, for example, described in Loinard et al. (2007):
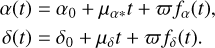 (3)
(3)
The model consists of positions α0 and δ0 at a reference epoch t0, parallax ϖ, as well as linear proper motion terms µα* and µδ. The terms fα(t) and ƒδ(t) are the projections of the parallactic ellipse over α and δ (Seidelmann 1992), calculated as
![$\matrix{ {{f_\alpha }(t) = \left[ {{X_E}(t)\sin {\alpha _1} - {Y_E}(t)\cos {\alpha _1}} \right]/\cos {\delta _1},} \hfill \cr {{f_\delta }(t) = {X_E}(t)\cos {\alpha _1}\sin {\delta _1} + {Y_E}(t)\sin {\alpha _1}\sin {\delta _1} - {Z_E}(t)\cos {\delta _1},} \hfill \cr } $](/articles/aa/full_html/2024/09/aa42081-21/aa42081-21-eq4.png) (4)
(4)
where α1 = α(t) − ϖƒα(t), δ1 = δ(t) − ϖƒδ(t), and (XE (t), YE(t), ZE(t)) is the vector between the solar system barycenter and Earth in units of AU. The equations therefore depend on a prior knowledge of ет and need to be solved iteratively. Using Eq. (3) a linear least squares fit was performed to the data. According to Loinard et al. (2007), it gives identical results as if using singular value decomposition. Additional variances 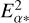 and
and 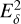 are added to the variances of the individual positions for weighting so that the reduced χ2 values per coordinate direction approximate unity in the fit, yielding realistic uncertainty estimates for the parameters.
are added to the variances of the individual positions for weighting so that the reduced χ2 values per coordinate direction approximate unity in the fit, yielding realistic uncertainty estimates for the parameters.
3.2 Analysis of phase referencing observations
We used the single-epoch observations of 32 stars detected in phase referencing mode at X and C bands (8.11225 GHz and 4.61175 GHz) with the VLBA in project UL005. The observation setup, the data calibration, and the analysis are described in Lunz et al. (2023). In that work, absolute positions for stars were derived from a fringe fit of the calibrator with a point-like calibrator model for its structure. This scheme is consistent with that used for ICRF3 where source structure was not considered. However, because of systematic errors, including the unknown difference between group-delay and phase delay positions, the error budget of the absolute star position was inflated.
For the present analysis, which aims at fitting models of stellar motions to the position time series, the calibrator fringe fits were repeated by applying self-calibrated images of the phase calibrators, instead of a point source model. The self-calibrated images were derived from the same data. This reanalysis minimizes the potential star position jitter coming from the calibrator structure and yields better consistency with positions from other studies, where the same procedure was applied. The positions of the stars α(t) and δ(t) at the observation epoch t, which is the mean of the first and last scans involved, were determined using the task modelfit in the Caltech Difmap imaging package (Shepherd 1997). Their uncertainties σα*,random and σδ, random are due to thermal noise and are derived from the beam shape and the root mean square (RMS) noise of the image based on formulas for elliptical Gaussians in Condon (1997). The new positions are listed in Table 1.
In the January 2020 data, the RMS of the differences in the positions of the 32 stars using one or the other method for fringe-fitting (i.e., based on a point-source model or a self-calibrated image for the calibrator structure) were only on the order of 19 µas in α* and 35 µas in δ. The deviation in coordinates is at most 112 µas in δ for the star HD 283572. All other coordinate deviations are within ±75 µas. Therefore, the impact of the calibrator structure on the results remains small. The differences in the dynamic range are negligible.
3.3 New estimates for models of stellar motion
For all stars in Lunz et al. (2023), we searched the literature for single-epoch positions and added to this list the positions we derived in January 2020 (Sect. 3.2). New estimates for models of stellar motion, obtained through the scheme presented in Sect. 3.1, were then computed for each star when the data allowed. This computation was possible for 15 stars.
Each star position was corrected to be referenced to the calibrator position in ICRF3 by accounting for the difference between the calibrator position in ICRF3 and the calibrator position used in the literature. Except where noted, all positions are free from systematic errors due to the calibrator structure, which was corrected as described in Sect. 3.2. Variances based on thermal noise σrandom were used to weight the individual positions. The new estimates for models of stellar motion obtained in this study are listed in Table A.1 along with estimates found in the literature. The corresponding sky motions are shown in Fig. A.1. The estimates for the models of the five astrometric parameters α0, δ0, ϖ, µα*, and µδ derived using only data from the literature are denoted Mold, while the estimates for the models containing the 2020 positions are labeled Mnew. The table also provides information on the additional uncertainties Eα* and Eδ. The RMS of the post-fit residuals v is denoted by RMSv, specifically RMSv,α* and RMSv,δ for the two coordinate directions. The epoch of α0 and δ0 was chosen as the mean epoch t0 of all observation epochs t to minimize the correlations between the parameters. For the projection of the parallax ellipse in Eq. (4), the barycen-tric coordinates of the Earth’s center of mass at the observation epoch were derived from the DE 421 ephemeris (Folkner et al. 2009).
Because of the presence of systematic errors, special attention should be paid to the combination of star positions referenced to different phase calibrators. For the VLBA observations in 2020, position differences with an RMS of 0.28 mas in α* and 0.69 mas in δ were determined from referencing seven stars to two different phase calibrators (Lunz et al. 2023). To account for this effect, all observations not referenced to a primary phase calibrator have been down-weighted by adding the respective additional uncertainties to the star position uncertainties through variance propagation. A mean value of 0.5 mas in both directions was adopted and assumed to be not too pessimistic in the presence of different uv-coverage, source structure, differences between group- and phase delay positions, and residual delay model errors in the historical observations. The resulting models are denoted “w0.5”. Details of the data and analysis for each star are discussed in the following subsections.
Absolute positions in ICRF3 for 14 stars based on observations conducted in January 2020 and analysis including the modeling of the phase calibrator structure.
3.3.1 HD 283572
The star HD 283572 (HDE283572) was observed relative to J0429+2724 at 6 epochs from September 2004 to December 2005 at 8.4 GHz (Torres et al. 2007). These data were reprocessed in Galli et al. (2018) using the same scheme as that described in Sect. 3.2. Observations in the same band and using the same primary calibrator were carried out in project UL005. The shifts of −0.1333 mas in α and 0.1413 mas in δ (as given in Table E.1 of Lunz et al. 2023) were subtracted from the single-epoch star positions from Galli et al. (2018) to reference them to ICRF3.
The work of Galli et al. (2018) does not report a model position, whereas Lindegren (2020a) determined a full five-parameter model for the star using the single-epoch positions of Galli et al. (2018). The solution Mold is not significantly different from that of Galli et al. (2018) – however, the formal errors of Mold are larger. Adding the 2020 position to the analysis (Mnew) reduces the formal errors by 10% to 20% for α0, δ0, and ϖ, and by about 90% for µα* and µδ compared to Mold. The latter is due to the much longer time span involved for the estimation. The additional uncertainties Eα* and Eδ decrease by 10% to 15%, while the values of RMSv do not change significantly. The differences in model estimates between Mnew and Galli et al. (2018) are not significant.
3.3.2 V410 Tau
The 2020 position of V410 Tau (HD 283518) was added to the 9 epochs listed in Galli et al. (2018). These epochs span from November 2013 to September 2017 and used the same antenna network as the January 2020 observations. The first 5 epochs were observed at 8.4 GHz, whereas the last 4 epochs were observed at 5.0 GHz, consistent with the January 2020 observation at 4.6 GHz. The same phase calibrator, J0429+2724, was used. The shifts of 0.0167 mas in α and 0.1813 mas in δ (as given in Table E.1 of Lunz et al. 2023) were subtracted from the star positions from Galli et al. (2018) to reference them to ICRF3.
The formal errors are not improved between Mold and Mnew. The additional observation uncertainties increase from Eα* = 116 µas and Eδ = 79 µas to Eα* = 199 µas and Eδ = 93 µas when the January 2020 position is included in the analysis, and the scatter of the residuals increases. The residuals at the X band and C band do not differ. Since V410 Tau is a multiple star, this difference and the increase in the residuals may be due to the signature of orbital motion, even though only one component is detected at radio frequencies (Harris et al. 2012). However, we defer the testing of this hypothesis to when further observations (at more epochs) are acquired.
3.3.3 SS Cyg
SS Cyg was observed by Miller-Jones et al. (2013) from April 2010 to October 2012 in 7 epochs with the VLBA at 8.4 GHz and in 2 epochs at 5 GHz with the European VLBI Network (EVN). In the publication, the phase calibrator position of the EVN observations was already corrected to match that used by the VLBA. The 2020 position was referenced to the same phase calibrator, J2136+4301, and observed at 8.1 GHz. All star positions used in our analysis were referred to the ICRF3 position of this calibrator by subtracting 0.4542 mas in α and −0.5418 mas in δ to the positions (at 9 epochs) reported by Miller-Jones et al. (2013). As previously, these corrections come from Table E.3 of Lunz et al. (2023).
For Mnew, the formal errors are reduced by 10% to 20% (for α and δ), 40% (for ϖ) and by 70% (for µα* and µδ) compared to Mold. The additional observation uncertainty Eα* is 184 µas, while in the δ direction no uncertainty was added, since the reduced χ2 was already below 1. For this star, the correlations between all parameters decrease when the new epoch in 2020 is included, especially those between α and δ, and between µα* and µδ. Only the correlation between parallax and proper motion increases slightly. This indicates that further observations sensitive to the parallax determination are still needed to decorrelate those two parameters. This behavior contrasts with that for the other stars where adding the new epoch did not change the correlations significantly. The residuals at the X band and C band do not differ.
3.3.4 Brun 334
Brun 334 (VLBA 19, Parenago 1540) was observed by Kounkel et al. (2017) using the VLBA in 5 epochs between March 2014 and March 2016 at 5 GHz. The publication only gives the observation epochs to the precision of a full day. Therefore, the positions could be imprecise by up to 0.005 mas, considering the proper motion in Gaia EDR3 of 3.840 mas yr−1. The star was observed in one epoch in January 2020 at 4.6 GHz relative to the same phase calibrator, J0529–0519. The shifts of −0.7522 mas in α and 0.1458 mas in δ from Lunz et al. (2023) were subtracted from the star positions from Kounkel et al. (2017) to reference them to ICRF3.
When the January 2020 position is included in the analysis, the formal errors of µα* and µδ improve by 60% and 40%, respectively, while those of the position and parallax degrade, especially for the δ coordinate, which has a formal error 50% higher. Additionally, the residual scatter in each coordinate direction doubles and the additive variances (mostly in δ) need to be increased to obtain χ2 equal one. Although Brun 334 is a spectroscopic binary (Marschall & Mathieu 1988), the short-term orbital parameters, which may explain the degradation, were not considered in this work. Comparing our model estimates with those from Gaia EDR3 shows good agreement, except for µδ where the difference is at the 2σ level.
3.3.5 TYC 5346-538-1
Star TYC 5346-538-1 (VLBA 45) was observed in 5 epochs between March 2014 and March 2016 by Kounkel et al. (2017) at 5 GHz. The new observation in January 2020 was conducted at 4.6GHz and the same phase calibrator calibrator as in the historical observations, J0542–0913, was used. The shifts of −0.9450 mas in α and −1.0675 mas in δ were subtracted to the star positions from Kounkel et al. (2017) to reference them to ICRF3. In addition, Kounkel et al. (2017) applied corrections of 0.256 mas in α and 0.771 mas in δ to the positions of the first epoch and of 0.204 mas in α and 0.659 mas in δ to the positions of the fourth epoch. It is believed that the reason is a pointing error due to calibration. These corrections were also applied in our analysis to obtain positions consistent with those shown in Fig. 4 in Kounkel et al. (2017).
The reduced χ2 in the α direction is already 0.07 without adding additional weights to the data in model Mold. The formal errors for µα* and µδ in Mnew decrease by about 40 % compared to the formal errors in Mold, whereas those for α*, δ, and ϖ increase by 50% to 70%. Mold and Mnew differ by (0.299 ± 0.142) mas yr−1 in µδ, which is about 60% of its value, and by (−0.102 ± 0.049)mas yr−1 in µα*. Both parameters are closer to the Gaia EDR3 solution when Mnew is considered. Mold,orig and Mnew,orig are solutions without applying the above corrections from Kounkel et al. (2017). The corresponding model estimates agree with those from solutions Mold, Mnew, and Gaia EDR3 within the uncertainty bounds, except for µδ for which the difference between Mold and Mold,orig is at the 1.4σ level.
3.3.6 BH CVn
Star BH CVn (HR5110) was observed at 15 epochs from May 1987 to May 1994 relative to J1317+3425 or relative to J1340+3754 in Lestrade et al. (1999). The 6 sessions relative to J1340+3754 (observed after 01 January 1992) were conducted at 8.4 GHz, while the frequency of the observations on J1340+3754 was 5.0 GHz for the four sessions before 01 January 1992 and 8.4 GHz for the sessions thereafter. The star was observed in January 2020 at 8.1 GHz relative to J1340+3754 and J1324+3622. A second reference source was chosen because J1340+3754 has significant structure and is relatively faint considering the sensitivity of the observations at this frequency band. J1324+3622 is closer to the target star than the second historical calibrator J1317+3425, though also relatively faint, and served as a backup calibrator. In Lestrade et al. (1999) the phase calibrator data were corrected for source structure only for J1340+3754 because of the significant structure of this source. Following the scheme described in Sect. 3.2, correction for the structure was applied to both calibrators (i.e., J1340+3754 and J1324+3622) in our 2020 data. The star positions were referenced to the ICRF3 position of the respective calibrators at all epochs. To this end, shifts of −0.0414 mas in α and 0.1481 mas in δ were subtracted from the star positions from Lestrade et al. (1999) referenced to J1317+3425, while for those referenced to J1340+3754, the subtracted shifts were −0.8662 mas in α and 1.3768 mas in δ.
As with the other stars in this study, several solutions with five astrometric parameters were determined based on three different selections of observations to show the reliability of the final solution. Mold and Mnew are based on the observations relative to all calibrators, whereas MJ1340+3754 contains only positions relative to calibrator J1340+3754 and Mothers contains only positions referenced to the other two calibrators. Because MJ1340+3754 has the least residual scatter, J1340+3754 was used as the primary calibrator in solution Mw0.5,new, while J1317+3425 and J1324+3622 were considered as secondary calibrators. As noted above, the star positions relative to these two calibrators were thus down-weighted in the analysis. Comparing the various solutions, no significant differences can be found for µα*. On the other hand, the estimate for parameter µδ varies when the 2020 position is added. The formal error of both parameters decreases by 80% when the 2020 position is added. Looking at specific solutions, the decrease is by more than 90% for solution MJ1340+3754, but only by 60% to 70% for solution Mothers. Examination of the post-fit residuals, RMSv,α* and RMSα,δ, indicates that even though J1340+3754 suffers from source structure, the individual absolute positions for BH CVn appear to be more consistent when using only this calibrator (and correcting for its structure), as in solution M_J1340+3754, than when referencing to several more compact calibrators (without consistent calibration of their structure), as in solution Mnew, Mw0.5,new, and Mothers.
The latter is the solution that determines the parallax worst in terms of formal error. Solution Mw0.5,new is not significantly different from MJ1340+3754 and Mnew, but MJ1340+3754 clearly has the lowest formal errors in all parameters. Thus, it was adopted for the analysis of the rotation parameters in Sect. 4.3 below, and the observations relative to the two other calibrators are thereby neglected. This is only possible due to the many positions available for BH CVn, allowing for a selection among these, which in general is not the case for the other stars in our sample, where solutions deteriorate if neglecting a subset of the positions.
3.3.7 Haro1-6
Star Haro 1-6 (DoAr 21) was observed in 9 epochs from September 2005 to August 2006 relative to J1625–2527 at 8.42 GHz, and where 7 epochs were analyzed and published in Loinard et al. (2008). Another 8 epochs were conducted at the same frequency from July 2007 to September 2007, also relative to J1625–2527. In total, five of these epochs were discarded due to the influence of bad weather, thus leaving data for 12 epochs (Ortiz-León et al. 2017). Then Ortiz-León et al. (2017) observed the star in 2 epochs at 8 GHz and in 5 epochs at 5 GHz from August 2012 to October 2015 relative to J1627–24262. In the following, the reprocessed data from Ortiz-León et al. (2017), where all positions of Haro 1-6 were referenced to the position of a unique calibrator, J1627–2426, is used. In January 2020, the star was observed at 4.6 GHz relative to J1633–2557, since J1627–2426 is not in ICRF3 and probably too faint for the observation mode, and J1625–2527 has developed structure in the meantime.
To reference the star positions to the ICRF3 position of J1633–2557 at all epochs, the shifts of −0.345 mas in α and −1.2 mas in δ between J1627–2426 and J1625–2527, as determined by Ortiz-León et al. (2017) from observations between 2005 and 2007, were first subtracted from the star positions in Ortiz-León et al. (2017). Another shift of −0.03 mas in α and 0.06 mas in δ was further subtracted, corresponding to the offset between the positions of J1625–2527 from Ortiz-León et al. (2017) and from the rfc_2018b catalog used in the 2020 observation. Finally, a third shift of 0.7550 mas in α and −0.0207 mas in δ was subtracted, which represents the difference between the observed position of J1625–2527 in the 2020 experiment (when phase referenced to J1633–2557) and the rfc_2018b catalog position. This workaround is not ideal; however, it reduces the RMSv,δ by 10%. Calibrator J1627–2426 would need to be observed with global astrometry and added to the next ICRF realization to resolve this issue.
To show the robustness of the final solution, several solutions based on three different subsets of the positions were obtained. Mall includes all the above-mentioned positions as input data to the fitting process, while Mwo7 excludes the position at the seventh epoch since that position showed the largest residuals (about 6 mas for α*) and was considered as an outlier. M>2012 includes only the latest more precise observations, similar to what was used for the final selection in Ortiz-León et al. (2017). For each of the three different selections, a solution with (new) or without (old) the January 2020 position was obtained. Down-weighting the 2020 position by 0.5 mas, because it is relative to a different calibrator (similar to what was tested for the observations of BH CVn), does not change the results significantly, which is to be expected as the positions for the different calibrators were previously homogenized.
Comparing the model estimates Mall with Mwo7, the additional noise required to achieve a χ2 of 1 and the scatter of residuals decrease significantly in α*. The proper motion estimates do not change, but the formal errors of µα* decrease by 60%. Furthermore, ϖ decreases by 8% and its formal error by 60%. While the parallax for the M_all solution is consistent with that from Gaia EDR3, the estimate from the Mw07 solution instead deviates significantly due to the decreased formal error. Employing only the more precise positions in M>2012 reduces the residual scatter by more than half. The estimate of ϖ in this solution matches the Gaia EDR3 result. On the other hand, µδ is found to deviate significantly compared to the Gaia EDR3 value, even though the observation selection is closest in time to the Gaia EDR3 observations compared to the other solutions. Since the formal error in proper motion parameters is smallest for the Mwo7,new solution due to the long time interval between the first and last observation employed, this solution was adopted for the subsequent analysis in Sect. 4.3.
3.3.8 σ2CrB
Star σ2 CrB was observed at 14 epochs from May 1987 to November 1994 relative to J1613+3412 in Lestrade et al. (1999). The observing frequency was 5.0 GHz for the first three epochs and 8.4 GHz thereafter. Of these data, only 12 epochs were found in the archive and thus used in our analysis. In January 2020 the star was observed at 8.1 GHz relative to the same calibrator with position in ICRF3. For the calculation of the new estimates for the model of stellar motion, the position of the phase calibrator uncorrected for source structure was employed, since the correction was also not made in Lestrade et al. (1999). The subtraction of 0.1017mas in α and 0.1965 mas in δ is required to reference the star positions from the historical observations to ICRF3.
Additional weights are only needed in case of Mnew. Due to the large time difference between the historical observations and the 2020 position, small but significant linear acceleration terms (for parameterization see Loinard et al. 2007) are needed to properly model the star motion. This is evidenced by the large reduction of residual scatter between solutions Mnew and Mnew,a (see Table A.1). The derived acceleration terms are (−0.046 ± 0.004) mas yr−2 in α* and (−0.018 ± 0.004) mas yr−2 in δ. The estimates for Mold and Mnewa differ by (−1.137 ± 0.060) mas yr−1 in µα* and (−0.451 ± 0.061) mas yr−1 in µδ, while the formal errors for these parameters decrease by more than 20%. On the other hand, the formal error of ϖ increases by about 15% and those of the coordinates double. This could be due to the reference epoch (2016.0) being away from the bulk of the observations. In all, the estimated proper motion and parallax parameters for Mnew,a are found to be closer to those from Gaia EDR3 compared to values in Lestrade et al. (1999) or Mnew.
3.3.9 HD 199178
Star HD 199178 was observed at 8 epochs from September 1992 to September 1994 relative to J2102+4702 by Lestrade et al. (1999) at 8.4 GHz. However, the source was too weak for detection at two epochs, thus leaving 6 epochs for analysis. In January 2020, the star was observed at 8.1 GHz relative to the same calibrator with position in ICRF3. For the calculation of the new estimates for the model of stellar motion, the position of the phase calibrator uncorrected for source structure was employed, since the correction was also not made in Lestrade et al. (1999). The subtraction of 0.3760 mas in α and 1.3861 mas in δ is required to reference the star positions from the historical observations to ICRF3.
The scatter of the residuals does not change comparing Mold and Mnew. This shows that the observations fit each other well. Moreover, the formal errors decrease by about 97% for proper motion and by 30% for ϖ. The estimates from Mnew are closer to the Gaia EDR3 parameters than the ones from Lestrade et al. (1999); however, because of the smaller formal errors, the differences are significant for Mnew, whereas they are not for the Lestrade et al. (1999) solution. No additional weights were added in either solution, and the χ2 was 0.5. This suggests that uncertainties for the individual positions were perhaps too large.
3.3.10 AR Lac
Star AR Lac was observed at 7 epochs from April 1989 to May 1994 relative to J2202+4216 in Lestrade et al. (1999), at 5.0 GHz in the first three epochs and at 8.4 GHz thereafter. However, the data from the first epoch was not available in the archive, thus leaving 6 epochs for our analysis. In January 2020, the star was observed at 8.1 GHz relative to the same calibrator with position in ICRF3. Additionally, the star was observed relative to J2153+4322 because J2202+4216 shows a lot of structure and future observations could benefit from a more compact calibrator, which can nowadays be used due to the increased sensitivity of the antenna network compared to historical observations. The position of the phase calibrator uncorrected for source structure was employed because the correction was also not made in Lestrade et al. (1999). The subtraction of 0.1730mas in α and 0.0837 mas in δ is required to reference the star positions from the historical observations to ICRF3.
Adding the new position in 2020 to all available observations relative to J2202+4216, the formal errors of the proper motions decrease by 90% compared to solution Mold. Furthermore, leaving out the epoch in July 1990, which was affected by poor uv-coverage, was found to reduce the residual scatter and formal errors of all parameters by about 50%, compared to a solution including this epoch (see solution M_wo90J2202+4216,new in Table A.1). Adding the star position relative to J2153+4322 in 2020 in solution Mwo90,w0.5,new with an additional uncertainty of 0.5 mas in quadrature, has almost no influence on the estimates, which is verified by the position with respect to J2202+4216 having residuals of zero, while the position with respect to J2153+4322 has residuals of about ±0.28 mas. If no additional uncertainty was added, the uncertainties of the model parameters would double. Solution Mwo90,w0.5,new was selected for the analysis of the rotation parameters in Sect. 4.3. Compared to the solution from Lestrade et al. (1999), µα* from Mwo90,w0.5,new is closer to the value from Gaia EDR3. However, its formal error is considerably smaller, which is why the selected solution shows an offset relative to Gaia EDR3 that is larger than 3σ, while it is less than 2σ in the solution of Lestrade et al. (1999). The same applies to µδ. In contrast, the parallax from solution Mwo90,w0.5,new is significantly off that from Gaia EDR3, while the value from Lestrade et al. (1999) agrees with that fromGaia EDR3 within about 1 σ.
3.3.11 IM Peg
Star IM Peg was observed at 4 epochs from December 1991 to July 1994 relative to J2253+1608 in Lestrade et al. (1999) at 5.0 GHz in the first epoch and at 8.4 GHz thereafter. The subtraction of −0.0318 mas in α and −0.0005 mas in δ is required to reference the star positions to ICRF3. In addition, 35 positions between January 1997 and July 2005 from the Gravity Probe B experiment at 8.3 GHz could be used (Ratner et al. 2012). They are referenced to point C1 in J2253+1608 with coordinates α = 22h53m57s.7479573, δ = 16°8′53″.561281 (Bartel et al. 2012), and the calibrator structure was corrected during the fringe-fit (Lebach et al. 2012). The subtraction of 0.2577 mas in α* and 0.4005 mas in δ is needed for these star positions to be referenced to ICRF3. To weigh this set of positions relative to the other data sets used in our study, the 0.06 mas WRMS scatter of residuals of the astrometric check source determined in Ratner et al. (2012) was used as position uncertainty in α* and δ for the star at each individual epoch. In January 2020, IM Peg was observed at 8.1 GHz relative to the same calibrator.
Adding the 2020 position, the formal errors of the proper motions in α* and δ decreased by 30%, while the formal error in σ remained stable. The radio emission from star IM Peg has an orbital motion with a semi-major axis of 0.89 mas and an axis ratio of 0.30 (Ratner et al. 2012). The orbital motion has a period of 24.64877 days (Marsden et al. 2005). The reduction of the orbital pattern in the positions by subtracting the model values derived from the functional model for the linear orbital parameters in Table 3 of Ratner et al. (2012) resulted in a decrease in RMSv,α* of about 0.15 mas and in RMSv,δ of about 0.05 mas in the corresponding solution (labeled Morb,new in Table A.1). Smaller additive errors were needed for this solution and thus the formal errors of all parameters decreased. However, the astrometric parameters did not change significantly (they remain within 1 σ). Since the binary cannot be resolved by Gaia, the determination of the rotation parameters in Sect. 4.3 will use the estimates for the model without correction for the binary orbit trajectory, Mnew. The new model estimates are not significantly different from those presented in previous studies, but the formal error of the proper motion values is significantly smaller.
3.3.12 HD 22468
Star HD 22468 (HR 1099) was observed at 8 epochs from March 1991 to August 1994 relative to J0339–0146 in Lestrade et al. (1999), at 5.0 GHz in the first 3 sessions and at 8.4 GHz thereafter. The subtraction of −0.0200 mas in α and 0.2792 mas in δ is required for these star positions to be referenced to ICRF3. In addition, one position was obtained during experiment V515C (July 2018) relative to the same calibrator by the Long Baseline Array (LBA) supported by the ATNF (CSIRO), by Russian antennas operated by the Institute of Applied Astronomy of Russian Academy of Sciences (Shuygina et al. 2019), and by the HartRAO antenna in South Africa as described in Titov et al. (2020). The calibrator position was in ICRF3. Three additional positions in ICRF3 between May 2015 and July 2016 from absolute astrometry in S/X mode are published in Titov et al. (2020). Further details are given in Table A.2. In January 2020, the star was observed at 8.1 GHz relative to the same calibrator, J0339–0146, with the VLBA. For the calculation of the new estimates for the model of stellar motion, the position determined without correcting the phases of the calibrator for structure was employed, since the correction was not applied in the observations from the archive.
Several estimates of the astrometric model for HD 22468 were produced to test the impact of the new data compared to using only the Lestrade et al. (1999) data through solution Mold. The addition of the 2018 and 2020 positions (solution Mnew) leads to a reduction in the formal errors of the proper motions of more than 90%, but also to a decrease of 40% of the formal error of ϖ. The latter can be explained by the two positions being located at the local minimum and local maximum of the parallax pattern of the star.
As a final test, the three positions from absolute astrometry were included in the analysis, thus all 13 epochs were used. However, the first two such experiments (AOV003, AUA011) had to be discarded (Mabs,wo9&10,new) because they show residuals several milliarcseconds large. Only the third experiment, AOV010, provides a good fit to the phase referenced data. The number of observations in the latter is 56 compared to 6 and 10 for the two rejected experiments (Titov et al. 2020). Adding this position to the phase referencing dataset does not change the results within the error bounds, but improves the formal errors by another 5% to 10% for all parameters. This solution was selected for comparison with Gaia and the determination of the rotation parameters in Sect. 4.3 below.
3.3.13 CoKu HP Tau G2
Star CoKu HP Tau G2 (HP Tau/G2) was observed at 8 epochs between September 2005 and December 2007 with the VLBA at 8.42 GHz by Torres et al. (2009) relative to the calibrator J0426+2327. In addition, Galli et al. (2018) detected the star in 5 epochs at 8.4GHz and in 4 epochs at 5.0GHz between December 2012 and October 2017 relative to J0438+2153. They corrected the 8 epochs from Torres et al. (2009) for the shift of the calibrator position and combined the time series. The homogenized data are used for astrometric fitting and the star position obtained relative to J0438+2153 at 4.6 GHz in January 2020, including correction for source structure, is added. The star positions from Galli et al. (2018) were corrected by subtracting −0.4287 mas in α and −0.0492 mas in δ, to refer them to the calibrator position in ICRF3, as also the case for the position from UL005.
The young star is the primary star in a gravitationally bound system with HP Tau G3 AB, which has a separation of about 10” (Harris et al. 2012; Nguyen et al. 2012). HP Tau G3 AB itself is a close binary (Richichi et al. 1994). Linear terms appear to be not sufficient to model the trajectory of CoKu HP Tau G2 given the above observations, as can be seen from the large residual scatter and the deviation of the estimated proper motion from the Gaia EDR3 values for the solution including all observations (Mnew).
A nonlinear model is supported by the RUWE parameter (renormalized unit weight error, calculated from Gaia data; Lindegren et al. 2018) in Gaia EDR3, which is 3.85 for this star. A value larger than about 1.4 indicates that the star is not a single star as seen by Gaia. Galli et al. (2018) estimated orbital parameters in addition to position, proper motion, and parallax. In this work, orbital parameters are not considered. To compare the proper motion with Gaia EDR3, the VLBI time series were therefore trimmed to match the Gaia EDR3 observations between 25 July 2014 and 28 May 2017 (solution labeled MGaia in Table A.1). In this solution, the residuals for X band and C band do not differ; therefore frequency dependent position offsets do not need to be considered. In order to best match the Gaia EDR3 model parameterization, MGaia will be further used for the subsequent rotation parameter analysis in Sect. 4.4.
3.3.14 del Lib
Star del Lib (HD 132742) was observed at 3 epochs from July 2016 to July 2020. The positions in experiment UL005 (January 2020) were obtained relative to two different calibrators, J1456–0617 and J1510–0843, at 8.1 GHz. During experiment AOV010 (July 2016) it was observed relative to J1456–0617 with the Asia-Oceania VLBI network (AOV) and during experiment V583B (July 2020) it was observed relative to J1512–0905 by the LBA, both at about 8.4 GHz. The positions are listed in Table A.2. The star position derived without correcting the calibrator phases for structure was used for this fit because the other experiments did not use it either. To reference all observations to ICRF3, shifts of −0.4572 mas in α and −0.2092 mas in δ were subtracted from the position of J1512-0905, which was originally α = 15h12m50s.5329, δ = −9°5′59″.830. All observations relative to J1456–0617 were already in ICRF3 and no correction was thus necessary.
As mentioned above, an additional uncertainty of 0.5 mas was applied to the star positions that are not relative to J1456–0617 (considered as the primary calibrator) to account for systematic errors. The resulting solution, labeled Mw0.5,new, is not significantly different from the solution without the additional uncertainties Mnew. However, the VLBI model estimates do differ largely from those of Gaia EDR3, but for comparison, those of Gaia DR2 (also listed in Table A.1) are again different. Solution Mw0.5,new was adopted for the subsequent analysis in Sect. 4.4.
3.3.15 HD 142184
Star HD 142184 (HR 5907, 1550–238) was not in the sample of sources observed by the VLBA in January 2020 because it is a Be-type star and therefore may exhibit radio emission from stellar winds leading to radio-optical offsets. It is one of the fastest rotating stars. Data from absolute astrometry performed with the LBA, VLBA, AOV, and other networks were collected.
During experiment V583B (July 2020) HD 142184 was further observed relative to J1553−2422 with the LBA at about 8.4 GHz. To reference the observation to ICRF3, shifts of −0.2098 mas in α and 0.0491 mas in δ were subtracted from the position of J1553−2422, which was originally α = 15h53m31s.6278, δ = −24º22′6″.036. All positions collected or derived from this work are listed in Table A.2.
The proper motion and parallax (solution Mnew in Table A.1) are in agreement with the Gaia EDR3 values within the error bounds. Because most of the data (i.e., the absolute positions) is not referenced to ICRF3 but to the aus2020b3 reference frame, the position information was not included in the analysis of the rotation parameters in Sect. 4.4 below, and only the proper motion and parallax were used4.
3.3.16 Additional single-epoch positions
For four additional stars (HD 167971, V 479 Sct, EI Eri, YY Men), observations at one or two epochs are available from experiments conducted at 8.4 GHz by the LBA, as listed in Table A.2. In experiments V583A (March 2020) and V583B (July 2020), star HD 167971 was observed, but relative to two different calibrators. Shifts of 42.8062 mas in α and −10.2367 mas in δ were subtracted for the star position relative to J1818−1108 and shifts of 1.0813mas in α and 0.5267 mas in δ were subtracted for the star position relative to J1832−1035 to transfer them to ICRF3. Because the time interval between the first and last scans on HD 167971 in experiment V583A was only about 20–30 min, the uv-coverage was sparse. Thus, the side lobes were large and the uncertainty of the position was high. The same is true for stars V479 Sct and EI Eri, which were also observed in experiment V583A. For these stars, the shifts subtracted to reference positions to ICRF3 were −0.5414 mas in α and −0.4250 mas in δ (for V479 Sct) and −0.6007 mas in α and 0.4208 mas in δ (for EI Eri). Star YY Men was observed in absolute geodetic mode in two single-baseline experiments in 1990 and 1991, from which the position in 1990 could be determined. In addition, it was detected in experiment V583B relative to J0529–7245. In that case, shifts of 0.3641 mas in α and 0.5004 mas in δ were subtracted to reference the position to ICRF3.
3.3.17 Recapitulation
The RMS of the residual scatter shows that modern phase referencing observations can reach levels of 0.1 mas to 0.2 mas and below, whereas the inclusion of historical observations from around the 1990s (case of BH CVn, HD 199178, AR Lac, IM Peg, HD 22468) yields RMS levels of 0.2 mas to about 1.0 mas. At the present stage, accelerations are not considered in the rotation parameter analysis. However, six stars were found to have signs of nonlinear proper motion from their VLBI data verified by Student’s t-test with a significance level of 5% (V410 Tau, Brun 334, σ2 CrB, HD 22468, CoKu HP Tau G2, and HD 142184). For some stars, the model estimates better fit the values of the astro-metric Gaia model when the same parameterization is applied (i.e., with no acceleration terms). This is usually the case when the VLBI mean epoch is close in time to the Gaia observations, such as for V410 Tau, Brun 334, and HD 142184. In the case of σ2 CrB, the proper motion estimates are closer to the Gaia estimates when linear accelerations are also estimated. This star is part of those objects for which the mean epoch of the VLBI observations is more distant from the Gaia observation time interval. Star CoKu HP Tau G2 has a more complicated trajectory. Restricting the VLBI time interval to the time interval of the Gaia EDR3 observations provides a better match to the Gaia data; however, there are no significant proper motion differences between models with and without acceleration terms. Star HD 22468 is a close binary with a period of about 2.8 days (Fekel 1983; García-Alvarez et al. 2003). It is located in another binary system ADS 2644A with an orbital period of 2101 yr and 6″.2 orbital diameter (Lestrade et al. 1999). For this star, the acceleration terms were not found significant according to Student’s t-test. The greater agreement of the parameter estimates with the Gaia EDR3 parameters and the reduction in Eα* as well as RMSv,α* however suggests that a long-term acceleration in α should be tested again when more observations have been acquired in the future. The detailed investigation of the various star time series showed that for some stars more observations would help to prove the existence of long-term accelerations (V410 Tau, Brun 334, HD 22468), decorrelating the model parameters (SS Cyg, Haro1-6), or investigating the reason for significant model differences between VLBI and Gaia (AR Lac).
Other reasons, such as orbital jitter (see Lestrade et al. 1999), may account for the differences between the estimated VLBI and Gaia models as well. This effect is specific to each source. For the present study, it is not considered, since long-term linear proper motions are of interest.
3.4 Absolute positions from VLBI and correction of parallax effect
In the calculations above, the absolute star position was lost by the application of source structure corrections during the fringe fit of the phase referencing calibrator data, as explained in Sect. 3.2. Thus, the mean positions α0 and δ0 from the five parameter fit at the mean epoch of the respective star time series have also no absolute reference. For this reason, the absolute single-epoch positions from Table 4 in Lunz et al. (2023) have been used instead for the frame tie. They are based on calibrator data that is not corrected for source structure, in agreement with the scheme used to derive the ICRF3 source positions. These single-epoch positions must be corrected for the parallax effect at the epoch of the observation, and the epoch t of the observation itself must be corrected for the Römer delay to match the barycentric time (Lindegren 2020a). For the stars considered in this study, the corrections employed the newly determined parallaxes listed in Table A.1. For the other stars, such as the additional stars in Sect. 3.3.16, the corrected Gaia parallax (Lindegren et al. 2021a) was used. All corrections are listed in Table 2. They are based on the barycentric coordinates of the Earth’s center at the time of observation from the DE 421 ephemeris (Folkner et al. 2009) using the VLBI software VieVS@GFZ developed by GFZ in Potsdam, Germany.
The random position errors that come out from the phase referencing analysis are based on the beam shape and dynamic range of the image. However, these are only applicable to the relative calibrator-star positions. They do not represent a full error budget for an absolute star position from phase referencing at a single epoch. To this end, we consider a more realistic error budget by combining the random errors with additional uncertainties, using the same formulas as in Lunz et al. (2023). This comprises the celestial reference frame position uncertainty from the phase calibrator and an average for a combination of several types of errors (delay model errors, source structure errors, and the difference between positions obtained from phase and group-delays). The latter is about 0.28 mas in α* or 0.69 mas in δ from measurements to two different calibrators for a subset of the January 2020 VLBA positions in Lunz et al. (2023). Such more realistic uncertainties are given in Table 3 for the additional stars considered in this study (see Sect. 3.3.16). The positional uncertainty from absolute geodetic observations, such as that for YY Men in the last line of Table 3, remains unchanged.
Römer delay, position corrections due to parallax effect, and radial velocity for the single-epoch positions used for the rotation parameter analysis.
4 Results
This section presents the results of the rotation parameter analysis for different scenarios in which the changes to the VLBI dataset described in the previous sections were tested. The analysis was done in the same way as in Lunz et al. (2023). In particular, correction of the Gaia EDR3 parallaxes was performed using the functions provided in Lindegren et al. (2021a). For details see Lunz et al. (2023) and Lindegren (2020a,b). The weighted mean WM, the weighted root mean square WRMS, nd the mean standard deviation ME of the rotation parameters using a representative range of iterations were used to assess the solutions and are listed in Table 4 for each scenario. These quantities were derived as described in Lunz et al. (2023). Similar to Lunz et al. (2023), the significance of the change in WM values between two scenarios is determined by a two-sample t-test with the null hypothesis that the mean values are equal (5% significance level). It is assumed that the rotation parameters are normally distributed with unknown and unequal variances (Behrens-Fisher problem). If the probability value is smaller than the significance level, the difference in the WM between the two scenarios is significant as the test cannot be accepted. Furthermore, as in Lindegren (2020a,b) and Lunz et al. (2023), an iteration solution was selected that best represents the rotation parameters of the respective scenario. It is referred to as the “baseline solution.” Table 5 summarizes the baseline solutions for the various scenarios
Realistic error budget for the single-epoch positions of the additional stars.
4.1 Rotation parameters including Galactocentric acceleration effect on positions and proper motions
We first reprocessed the results “55,EDR3” (where “55” represents the number of stars in the sample and “EDR3” represents the Gaia data release employed) from Lunz et al. (2023). The new solution includes the effect of Galactocentric acceleration as introduced in Sect. 2. The new rotation parameter results “55,EDR3,GA” (where “GA” indicates that the effect of Galac-tocentric acceleration was corrected) are presented in Fig. 1. Taking into account the effect of Galactocentric acceleration did not significantly change the WM, WRMS, and ME statistics of the rotation parameters (see Table 4). The baseline solution for scenario “55,EDR3,GA” was chosen at k = 13 number of rejected stars as for scenario “55,EDR3” because both orientation and spin parameters are stable for some iterations thereafter. The rotation parameters from this solution are very close to those of “55,EDR3”, both of which are reported in Table 5. Correlation coefficients for k =13 and T = 2016.0 are
![$\matrix{ {corr\left[ {{_X}(T),{_Y}(T),{_Z}(T),{\omega _X},{\omega _Y},{\omega _Z}} \right]} \cr {\quad = \left[ {\matrix{ { + 1.000} & { + 0.225} & { + 0.212} & { + 0.200} & { + 0.024} & { - 0.003} \cr \ldots & { + 1.000} & { + 0.177} & { + 0.021} & { + 0.177} & { + 0.010} \cr \cdots & \cdots & { + 1.000} & { - - .007} & { + 0.039} & { + 0.023} \cr \ldots & \cdots & \cdots & { + 1.000} & { + 0.044} & { + 0.326} \cr \ldots & \cdots & \cdots & \cdots & { + 1.000} & { + 0.018} \cr \ldots & \cdots & \ldots & \ldots & \ldots & { + 1.000} \cr } } \right]} \cr } .$](/articles/aa/full_html/2024/09/aa42081-21/aa42081-21-eq7.png) (5)
(5)
These coefficients are identical to those in solution “55,EDR3” (see Lunz et al. 2023). In all, the baseline solution is very close to that of “55,EDR3”, hence meaning that adding Galactocentric acceleration has almost no impact on the results.
WM, WRMS, and ME of the rotation parameters for various scenarios.
4.2 Impact of individual stars on rotation parameters
From Fig. 1, it can be seen that some stars that are not in the group of the first few stars that get rejected have a large impact on the spin parameters. Offsets of up to 0.03 mas yr−1 are visible when just one star is rejected. This is the case for σ2 CrB (k = 12), V410 Tau (k = 19), HD 22468 (k = 23) and LS I + 61 303 (k = 24). All of these stars are in multiple star systems. As an example, V410 Tau has one of the lowest uncertainties in the VLBI proper motions in this scenario, with values of 0.017masyr−1 in µα* and 0.020masyr−1 in µδ, and at the same time it is a star in a multiple star system. Excluding that star from the solution shows that the spin parameter in X becomes 0.025 mas yr−1 higher after the rejection at k = 19, hence reflecting the large impact of this one star on the entire analysis. Inflating the uncertainty in the proper motion of V410 Tau to about 0.10 mas yr−1 in each direction is required to achieve a similar effect as if the star were completely excluded from the analysis. This suggests that the proper motion uncertainties for this star were too optimistic or that acceleration parameters are significant and must be accounted for in the analysis.
In a similar way, an offset of about 0.15 mas appears in the orientation parameters along the Y and Z directions when DoAr 51 gets rejected (k = 13). On the other hand, no offset in the spin parameters is visible. This star is an unresolved binary as seen by Gaia, while it shows two closeby components in the VLBI images (see Lunz et al. 2023). Since the offset appears only in the orientation parameters, it must be investigated which of the center of luminosity or barycenter works better as a counterpart to the Gaia position, which is equal to the photocenter. A solution where the barycenter was used instead of the center of luminosity changed the offset only by up to 2µas per rotation axis, which is insignificant. Looking at the residuals of the January 2020 position for such a solution did not shed light on this question either, because the magnitude of the residuals is smaller in α* for the center of luminosity and smaller in δ for the barycenter. The other two close binaries in our sample, HD 283447 and UX Ari (see Lunz et al. 2023), are rejected within the first few iterations anyway – so they have no bearing on this analysis.
The statistics for a scenario excluding the five stars producing offsets in the rotation parameters are reported in Tables 4 and 5 under the label “50,EDR3,GA”. The WRMS of the orientation parameters in X and Y in that scenario is reduced by 40% compared to WRMS55,EDR3,GA. The WRMS in Z remained similar. For ωY, the decrease is by 50% and the difference in the parameter values was also found to be significant. For the other spin parameters, the decrease is by about 10%. The mean standard deviations slightly deteriorate (by less than 10%), which can be explained by the reduced number of objects in the dataset.
Baseline solutions for various scenarios.
 |
Fig. 1 Results for scenario “55,EDR3,GA”, when using the VLBI data and Gaia EDR3 as in Fig. 3 in Lunz et al. (2023) but correcting for the effect of Galactocentric acceleration. The orientation and spin parameters for 51 different adjustment solutions are shown in the upper row. For each adjustment solution the star with the largest (Qi/ni) (which indicates the quality of the fit of the star data to a five parameter astrometric model, see Lindegren 2020a) was rejected in the following iteration. The respective (Qi/ni) along with the star name are shown in the lower left plot, whereas the lower right plot shows the quality of the overall fit Q/n, equivalent to χ2 of the adjustment. |
4.3 Rotation parameters including the new models instead of one-epoch observations
In this section, we replace the VLBI data for 12 stars (HD283572, V410Tau, SSCyg, Brun334, TYC 5346-538-1, BHCVn, Haro 1-6, σ2 CrB, HD 199178, AR Lac, IM Peg, and HD 22468) by the new models of stellar motion determined in Sect. 3.3 for these stars and replicate the rotation parameter analysis “55,EDR3,GA”. This way, the change of the rotation parameters due to the new model estimates can be directly assessed. In the analysis, absolute positions determined from the fringe fit of the calibrator to a point source model and corrected as described in Sect. 3.4, were used in place of the positions derived from the models of stellar motions to best connect to ICRF3. Furthermore, the new data was also corrected for the effect of Galactocentric acceleration as in described Sect. 4.1 and no stars were excluded. The resulting rotation parameter estimates for this scenario, denoted “55,EDR3,GA,NM” (where “NM” indicates that star data was replaced with the new models of stellar motion), are shown in Fig. A.2.
The new scenario still shows some offsets for iterations 10 ≤ k ≤ 35 in both the orientation and spin parameters (as for “55,EDR3,GA”). This indicates that data from individual stars still has an impact on the derived rotation parameters. Small offsets in orientation occur at iterations 12, 22, and 24 when DoAr 51, LS I + 61 303, and HD 283641 are rejected. Offsets in spin appear for the iterations when stars HD 22468 (k = 21), LSI + 61 303 (k = 22), V410 Tau (k = 28), and AR Lac (k = 32) are rejected. Among these stars, only LSI+61 303 had no new model considered due to the complexity of its trajectory. It is worth noting that the introduction of the new stellar motion models reduced the offsets caused by σ2 CrB. On the other hand, a new offset, not present before, was introduced for AR Lac. This suggests that more emphasis has to be put on the details of the VLBI-Gaia comparison for these objects.
When comparing “55,EDR3,GA,NM” to “55,EDR3,GA”, the largest deviations in WM occur in the Y direction (for both orientation and spin). The new estimates for models of stellar motion reduce the scatter in ωX and increase it in ϵX and ϵY (Figs. 1 and A.2), which is also reflected by the WRMS statistics (Table 4). On average, the ME decreased by about 15% for the spin, while for the orientation parameters it increased by about 15%. The “55,EDR3,GA” scenario has a lower ME for the orientation parameters because more VLBI positions are involved in the adjustment than in the “55,EDR3,GA,NM” scenario. At the same time, the uncertainties of the spin parameters are lower for the “55,EDR3,GA,NM” scenario because improved VLBI proper motion estimates were used.
The new baseline solution is chosen to be at k = 12 rejected stars because both orientation and spin parameters are stable for some iterations thereafter. The corresponding rotation parameters are given in Table 5. The spin tends to be larger compared to the baseline solution of “55,EDR3,GA”. Correlation coefficients for k = 12 and T = 2016.0 are
![$\matrix{ {corr\left[ {{_X}(T),{_Y}(T),{_Z}(T),{\omega _X},{\omega _Y},{\omega _Z}} \right]} \cr {\quad = \left[ {\matrix{ { + 1.000} & { + 0.199} & { + 0.193} & { + 0.001} & { + 0.004} & { - 0.050} \cr \cdots & { + 1.000} & { + 0.161} & { - 0.002} & { - 0.030} & { - 0.018} \cr \cdots & \cdots & { + 1.000} & { - 0.052} & { + 0.007} & { - 0.093} \cr \cdots & \cdots & \cdots & { + 1.000} & { - - 0.034} & { + 0.334} \cr \cdots & \cdots & \cdots & \cdots & { + 1.000} & { - 0.098} \cr \cdots & \cdots & \cdots & \cdots & \cdots & { + 1.000} \cr } } \right],} \cr } $](/articles/aa/full_html/2024/09/aa42081-21/aa42081-21-eq15.png) (6)
(6)
which shows that no strong correlations are present. Compared to the scenario with the old models, “55,EDR3,GA”, the correlation coefficients between the orientation and spin parameters in each axis have now vanished. Only a weak correlation between the X and Z spin components exists.
Another scenario “49,EDR3,GA,NM” was tested where the four stars HD 22468, LSI +61 303, V410 Tau, and AR Lac, which produce jumps in the iterative results of the spin parameters, and the two stars DoAr 51 and HD 283641, which produce jumps in the iterative results of the orientation parameters, were excluded from the beginning. The WRMS statistics for all parameters dropped by 5% to 65% compared to those for the scenario “55,EDR3,GA,NM”. At the same time, the WM values changed significantly for ωY and ωZ. The six rotation parameters of a new baseline solution at k = 13 based on this scenario are provided in Table 5. As for the WM, some parameters changed significantly, namely ϵY, ωY and ωZ. In particular, the spin parameter along the Y direction was cut by half. Correlation coefficients for k = 13 and T = 2016.0 are
![$\matrix{ {{\rm{corr}}\left[ {{_X}(T),{_Y}(T),{_Z}(T),{\omega _X},{\omega _Y},{\omega _Z}} \right]} \cr {\quad = \left[ {\matrix{ { + 1.000} & { + 0.180} & { + 0.104} & { - 0.021} & { - 0.015} & { - 0.041} \cr \cdots & { + 1.000} & { + 0.093} & { - 0.009} & { - 0.117} & { + 0.031} \cr \cdots & \cdots & { + 1.000} & { - 0.054} & { + 0.030} & { - 0.093} \cr \cdots & \cdots & \cdots & { + 1.000} & { - 0.044} & { + 0.258} \cr \cdots & \cdots & \cdots & \cdots & { + 1.000} & { - 0.257} \cr \ldots & \ldots & \ldots & \ldots & \ldots & { + 1.000} \cr } } \right],} \cr } $](/articles/aa/full_html/2024/09/aa42081-21/aa42081-21-eq16.png) (7)
(7)
which shows that the correlation coefficients between the orientation parameters decrease compared to scenario “55,EDR3,GA,NM”. Also, the correlation coefficient between ωX and ωZ decreases, while it increases (in the absolute sense) between ωY and ωZ.
4.4 Rotation parameters including the new models and additional observations
In another test, observations from five stars, HD 142184, EI Eri, HD 167971, V479 Sct, and YY Men, were added to the previous dataset. Furthermore, proper motion and parallax information was added to the two 2020 positions of CoKu HP Tau G2 and del Lib, respectively. The resulting plots for this scenario, labeled “60,EDR3,GA,NM”, are shown in Fig. A.3.
Star EI Eri is rejected at k = 7, star HD 167971 at k = 8, star V479 Sct at k = 10, and star YY Men at k = 17. For the first three stars and CoKu HP Tau G2 (rejected at k = 14), small shifts occur in both orientation and spin when they are excluded. Star delLib is rejected at k = 25, and no shift can be identified. Star HD 142184 gets excluded as one of the last stars. Furthermore, the offsets in orientation for DoAr 51, LSI +61303, and HD 283641 and in spin for HD 22468, LSI +61 303, V410 Tau, and ARLac remain similar to those in scenario “55,EDR3,GA,NM”.
Comparing “60,EDR3,GA,NM” to “55,EDR3,GA,NM”, the MEs are slightly improved. The WMs and WRMSs do not significantly change, except for the WRMS of ϵX, which almost doubles (increasing from 0.062 mas to 0.114 mas). This increase can be explained by CoKu HP Tau G2 now being included in the statistics.
The new baseline solution is chosen to be at k = 15 rejected stars because both orientation and spin parameters remain stable for some iterations thereafter. The results of the rotation parameters for this scenario (see Table 5) are very close to those of the baseline solution for scenario “55,EDR3,GA,NM”.
Correlation coefficients for k =15 and T = 2016.0 are not significantly different than for the baseline solution of scenario “55,EDR3,GA,NM”.
Another scenario “53,EDR3,GA,NM” was tested where the four stars HD 22468, LSI +61 303, V410 Tau, and AR Lac, which produce jumps in the iterative results of the spin parameters, and the three stars DoAr 51, CoKu HP Tau G2, and HD 283641, which produce jumps in the iterative results of the orientation parameters, were excluded at the beginning. The iterative solutions are shown in Fig. A.4. The WRMS statistics dropped by 20% to 60% for all parameters except for ϵz compared to “60,EDR3,GA,NM”. Otherwise, the same conclusions can be drawn as when comparing “55,EDR3,GA,NM” and “49,EDR3,GA,NM”, so they are not repeated here. This shows that the new data has little impact on the results. The six rotation parameters of the corresponding baseline solution at k = 12 are listed in Table 5. The correlation coefficients are similar to those of “49,EDR3,GA,NM”.
5 Discussion
The different scenarios considered in the previous section characterize the changes in the analysis of the rotation parameters between ICRF3 and Gaia EDR3 due to the improved VLBI data. In all of them, the Y component of the rotation parameters is still less well determined than the X and Z components, as indicated by the formal errors. The χ2 of the iterative solutions in scenarios “50,EDR3,GA” and “55,EDR3,GA” drops to below unity when there are 15 stars left in the sample, and for “49,EDR3,GA,NM” and “55,EDR3,GA,NM” when there are 16 stars left. For “53,EDR3,GA,NM” and “60,EDR3,GA,NM”, the χ2 drops to below unity when 17 stars are still in the sample. This suggests that systematic errors were not reduced in the new solutions compared to scenario “55,EDR3” in Lunz et al. (2023), where the threshold was 16 stars. The addition of new data in scenario “60,EDR3,GA,NM” has little impact on the rotation parameter analysis as the additional noise that was required to be added to make the error budget realistic is currently too large.
All scenarios in which the stars that lead to offsets in the iterative rotation parameter results were excluded a priori (“50,EDR3,GA”, “49,EDR3,GA,NM”, and “53,EDR3,GA,NM”) show smaller ωY values compared to those from the scenarios in which all stars were included. To test the impact of the exclusion of other stars on the results, additional test scenarios were created in which the 11 most deviating stars of the “60,EDR3,GA,NM” scenario were excluded from the beginning. Then, a random selection of four other stars was excluded, so that in total 15 stars, as in the baseline solution of this scenario, are excluded. All possible combinations of four stars from the data set were tested. From each of the 211 876 individual scenarios, iterative solutions for the rotation parameters were obtained and the WM, WRMS, and ME statistics were calculated, discarding the last 10 iterations because otherwise, the formal errors become too large due to the small sample. The orientation offset WMs range from (0.117, 0.109, −0.030)mas to (0.550, 0.551, 0.222)mas, and the spin WMs range from (0.000, 0.021, −0.043) mas yr−1 to (0.106, 0.097, 0.014) mas yr−1. Their mean values ((0.339, 0.354, 0.069) mas for the orientation offset and (0.033, 0.095, −0.016) mas yr−1 for the spin) are close to the WM values for scenario “60,EDR3,GA,NM” in Table4. The Q/n for the first iteration in these scenarios (without rejecting further stars) varies between 6.43 and 14.66, with a median of 13.46. The scenario where the sum of all Q/n considered in the calculation of the WMs (i.e., including 35 stars) is minimum is the scenario where TLep, DoAr51, CoKuHPTauG2, and SZ Psc were the four additional excluded stars. These are the same stars that were excluded in the baseline solution of “60,EDR3,GA,NM”, proving that the rejection process is sound. The four stars have RUWE parameters greater than 1.4, indicating that the Gaia data do not fit the standard model of stellar motion well.
The minimum magnitudes5 of the WRMSs are 0.100mas for the orientation offset and 0.009 mas yr−1 for the spin, and the minimum magnitudes of the MEs are 0.164mas and 0.018 mas yr−1, respectively. For the orientation offset, the minimum WRMS magnitude is reached when LSI+61303, HD 283641, DoAr51, and CoKu HP Tau G2 are excluded, while for the spin, it is reached when LSI+61303, HD22468, CoKuHPTauG2, and ARLac are rejected. Except LSI+61303 for the orientation offset and CoKuHPTauG2 for the spin they are the same stars as from the manual selection in “53,EDR3,GA,NM”. This overlap was expected because the stars that were rejected manually in the latter produce jumps and this also deteriorates the WRMSs. From the scatter of these results and the minimum MEs and WRMSs, it is concluded that the minimum uncertainty of WM is ~0.2 mas/ 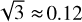 mas for each of the three orientation offset components and ~0.02 mas yr−1/
mas for each of the three orientation offset components and ~0.02 mas yr−1/ 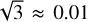 mas yr−1 for each of the three spin components for “60,EDR3,GA,NM”.
mas yr−1 for each of the three spin components for “60,EDR3,GA,NM”.
The solution adopted for this work is the baseline solution of scenario “60,EDR3,GA,NM”. This solution includes the most complete dataset and, as noted above, has the lowest sum of Q/n, thus indicating that it is superior to the other solutions. However, the value of Q/n in this solution (6.43) remains larger than unity, meaning that the uncertainties of the input data are underestimated. To account for this, the formal errors of the rotation parameters have been multiplied by a factor of 2.5 (corresponding to 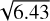 ), resulting in more realistic uncertainties. The rotation parameters then become (+0.322, +0.228, +0.163, +0.034, +0.072, −0.026)±(0.203, 0.251, 0.155, 0.023, 0.025, 0.023) mas or mas yr−1. Comparing with the baseline solution of the best scenario in Lunz et al. (2023) ((+0.226, +0.327, +0.168, +0.022, +0.065, −0.016) ± (0.165, 0.215, 0.128, 0.024, 0.026, 0.024) mas or mas yr−1, after scaling the uncertainties by
), resulting in more realistic uncertainties. The rotation parameters then become (+0.322, +0.228, +0.163, +0.034, +0.072, −0.026)±(0.203, 0.251, 0.155, 0.023, 0.025, 0.023) mas or mas yr−1. Comparing with the baseline solution of the best scenario in Lunz et al. (2023) ((+0.226, +0.327, +0.168, +0.022, +0.065, −0.016) ± (0.165, 0.215, 0.128, 0.024, 0.026, 0.024) mas or mas yr−1, after scaling the uncertainties by 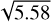 ), the values then do not differ significantly. In these solutions, the spin in the Y direction is the only parameter that is found significant at the 3σ level.
), the values then do not differ significantly. In these solutions, the spin in the Y direction is the only parameter that is found significant at the 3σ level.
For the bright Gaia EDR3 reference frame, a correction was applied to its spin in one of the middle iterations of the processing, as explained in Sect. 1. The applied spin correction was (−0.0166, −0.0950, +0.0283) mas yr−1 with an uncertainty of 0.024 mas yr−1 per axis, and no orientation offset was considered. Reversing the applied correction by adding it back to the baseline solution from scenario “60,EDR3,GA,NM” results in an original, uncorrected spin in Gaia EDR3 of (0.016, −0.023, +0.002) ± (0.023, 0.025, 0.023) mas yr−1. The spin in Y is then reduced to 1-σ, which suggests that the uncorrected Gaia EDR3 bright frame is more consistent with the ICRF3 than the corrected frame. The results also show that the current level of accuracy in aligning the bright Gaia reference frame spin to ICRF3 is the same as when employing the HIPPARCOS positions.
The results for the residual spin for the scenarios “55,EDR3,GA”, “55,EDR3,GA,NM”, and “60,EDR3,GA,NM” (i.e., without manually excluding stars before the iterative adjustment process starts), align with the independent estimates of 80 µas yr−1 for the total spin in the magnitude range G = 11– 13 mag from Cantat-Gaudin & Brandt (2021), with the main component being the rotation about the Y axis with a value of 60 µas yr−1 to 77 µas yr−1. Their analysis is based on Gaia EDR3 data from open clusters and binaries with a bright and faint component, taking also into account a magnitude dependence of the optically bright frame. Furthermore, the results for the residual spin for the scenarios “50,EDR3,GA”, “49,EDR3,GA,NM”, and “53,EDR3,GA,NM” (with manually excluding stars that produce offsets in the rotation parameters before the iterative adjustment process starts), align with the independent spin estimates in the magnitude range G ≤ 10.5 mag of about 40 µas yr−1 from the same authors. The largest component in these solutions, of 31 µas yr−1 to 36 µas yr−1, still is the rotation about the Y axis. The stars DoAr 51, CoKu HP Tau G2, and HD 283641, which were excluded a priori because they lead to offsets in the iterative orientation offset parameter results, are fainter than the threshold of G = 10.5 mag. This may indicate that the alignment results in this work are also sensitive to the magnitude. On the other hand, the RUWE parameters of these stars are also larger than 1.4, which means that the standard model of stellar motion does not fit their Gaia data well. Therefore, the effect seen could also well be a consequence of excluding the stars from the analysis. Fifteen stars in the sample have G ≥ 10.5 mag, and 28 stars have a RUWE ≥ 1.4, almost 50%. The stars producing the offsets in spin do not show any conspicuousness from the Gaia data but show acceleration or orbital motion from the VLBI data. In all, it is difficult to test the magnitude dependence of the alignment between Gaia and VLBI because the current VLBI dataset only includes 15 stars with G ≥ 10.5.
Orbital motion and accelerations should be considered in future work in order to properly model the trajectories of some of the stars. More accurate and precise VLBI data will help to refine the model estimates, identify outliers (i.e., problematic stars), and improve the overall reliability of the results. The addition of only a few positions and model estimates of a few new stars (Sect. 4.4) did not significantly improve the rotation parameter analysis as systematic errors dominate over the thermal errors. Furthermore, for some stars in our sample, the correlations between the astrometric parameters in the model of stellar motion were large. This means these stars need additional geometrically sensitive observations to decorrelate the parameters.
The comparisons presented in this study show that the alignment of Gaia EDR3 with ICRF3 using VLBI observations of radio stars will require more effort from the VLBI community to reach the level of uncertainties expected for the final Gaia data release (see Sect. 1). It should be emphasized that the alignment between VLBI and Gaia for individual objects is only as good as shown by the comparison between the various VLBI models and the astrometric Gaia model with five parameters, as listed in Table A.1. The model values may differ due to, among other things, orbital motions, differences between the barycen-ter and center of luminosity of unresolved binary stars as seen by Gaia, and radio-optical offsets (Brosche & Schuh 1999; Lunz et al. 2023).
6 Conclusions
This study focused on further improving the determination of residual orientation offsets and spin between the Gaia EDR3 bright (G ≤ 13 mag) frame and the ICRF3. VLBI observations of radio stars consistently referenced to ICRF3 were used for the alignment. It was shown that the influence of Galactocen-tric acceleration on the rotation parameter analysis is negligible with the currently available data.
In this work, new observations from January 2020 were added to the historical time series whenever possible, allowing large improvements in the stellar motion model estimates due to the longer time span between the first and last observations. Thanks to this additional data, it was possible to obtain improved estimates for 12 stars and new estimates for three stars. Replacing the proper motion and parallax information of these 12 stars in the sample of 55 stars from Lunz et al. (2023) and using the January 2020 positions derived based on a point source model for the calibrators reduced the mean standard deviation for the spin parameters in the iterative rotation parameter analysis by 10% to 20% and the scatter of the spin parameter in the x direction by 35%. At the same time, the orientation offsets are less well determined, with an increase of the mean standard deviation by about 15% for these parameters, because a smaller number of VLBI positions and not the more precise model positions are used in the adjustment. Adding positions for four new stars and model estimates for three stars reduced the mean formal errors in the orientation offset parameters slightly, as expected.
We tested different scenarios in which selected stars were excluded a priori. This test showed that excluding only a few stars (namely 6 stars) besides the obvious outliers has a large impact on the rotation parameter estimates.
A possible direction for further studies is to determine whether the stars producing offsets in the iterative solution results should be excluded from the analysis, differently weighted, or have their modeling extended (e.g., adding orbital motion). New VLBI observations carried out in parallel with the Gaia observations would clearly help to improve the analysis and increase confidence in the estimated parameters. Additionally, more stars in common between VLBI and Gaia would be desirable to also study the possible magnitude dependence of the rotation parameters. Finally, the systematic effects that lead to inflating the error budget would need to be investigated as well, and, if possible, reduced to give absolute positions a greater influence on the determination of the spin.
The adopted scenario is the one that makes the sum of Q/n over the representative range of the iterative spin solutions minimum. The selected baseline solution for this scenario shows orientation offsets between Gaia EDR3 and ICRF3 on the order of 0.2 mas to 0.3 mas and spins of about 0.03 mas yr−1 in X and Z and about 0.07 mas yr−1 in Y. Among these, only the spin component in Y is statistically significant (at the 3σ level).
Acknowledgements
We deeply thank the anonymous reviewer for the thorough feedback on our work. The authors acknowledge the use of the Very Long Baseline Array under the US Naval Observatory’s time allocation. This work supports USNO’s ongoing research into the celestial reference frame and geodesy. We thank also the Socorro correlator for reliably and quickly providing the correlated data. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. We acknowledge the use of two large radio telescopes: Tianma65 and Parkes. The Parkes radio telescope is part of the Australia Telescope National Facility which is funded by the Australian Government for operation as a National Facility managed by CSIRO. The observations of radio stars were coordinated within the framework of the Asia-Oceania VLBI Group for Geodesy and Astrometry (AOV). The scheduling and data correlation were supported by three AOV member institutes which include Shanghai Astronomical Observatory of Chinese Academy of Sciences, University of Tasmania in Australia and Geospa-tial Information Authority of Japan. Experiments V515C and AUA020 were done with participation of the Scientific Equipment Sharing Center of the Quasar VLBI Network of the Institute of Applied Astronomy of the Russian Academy of Sciences (IAA RAS). We further thank Belén Tercero and Chris Phillips for their contribution. This project is supported by the DFG Grant Nos. SCHU 1103/7-2 and HE 5937/2-2. M.H. Xu was supported by the ERC StG Grant No. 101076060. This work has made use of the data from the European Space Agency (ESA) mission Gaia processed by the Gaia Data Processing and Analysis Consortium as well as from the mission HIPPARCOS. Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. Calibrators were selected using the NRAO VLBA calibrator search tool (www.vlba.nrao.edu/astro/calib/), the RFC calibrator search tool (http://astrogeo.org/calib/search.html) and the Astrogeo VLBI FITS image database (http://astrogeo.org/vlbi_images/). This research has made use of the VizieR catalog access tool and the SIMBAD database (Wenger et al. 2000), operated at CDS, Strasbourg, France. Calculations were made in MATLAB by The MathWorks, Inc.
Appendix A Tables and Figures
Newly derived astrometric models of stellar motion for 15 stars.
Star positions from absolute astrometry and alternate observations used in this study.
 |
Fig. A.1 Sky motion for the 15 stars with astrometric models reported in Table A.1. The observed positions are marked with the red stars and their uncertainties are visualized by the black ellipses. The adjusted positions are labeled by the black dots and their uncertainties by the blue ellipses. The model is indicated by a black line. |
 |
Fig. A.2 Results for scenario “55,EDR3,GA,NM”, using the VLBI data and Gaia EDR3 as in Fig. 1, but replacing the VLBI data of stars HD 283572, V410Tau, SS Cyg, Brun 334, TYC 5346-538-1, Haro 1-6, BHCVn, σ2 CrB, HD 199178, AR Lac, IM Peg, and HD 22468 with newly determined models of stellar motion and newly corrected absolute positions as described in Sect. 4.3. |
 |
Fig. A.3 Results for scenario “60,EDR3,GA,NM”, using the VLBI data and Gaia EDR3 as in Fig. A.2, but adding the data of five new stars and astrometric information as described in Sect. 4.4. |
 |
Fig. A.4 Results for scenario “53,EDR3,GA,NM”, using the VLBI data and Gaia EDR3 as in Fig. A.3, but excluding seven stars (HD 22468, LSI +61 303, V410 Tau, AR Lac, DoAr 51, CoKu HP Tau G2, and HD 283641) from the beginning. |
References
- Arias, E. F., Chariot, P., Feissel, M., & Lestrade, J. F. 1995, A&A, 303, 604 [NASA ADS] [Google Scholar]
- Bartel, N., Bietenholz, M. F., Lebach, D. E., et al. 2012, ApJS, 201, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Brosche, P., & Schuh, H. 1999, ZFV – Zeitsch. Geodasie Geoinform. Land-manag., 124, 343 [Google Scholar]
- Cantat-Gaudin, T., & Brandt, T. D. 2021, A&A, 649, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charlot, P., Jacobs, C. S., Gordon, D., et al. 2020, A&A, 644, A159 [EDP Sciences] [Google Scholar]
- Condon, J. J. 1997, PASP, 109, 166 [NASA ADS] [CrossRef] [Google Scholar]
- ESA 1997, ESA Special Publication, 1200, The HIPPARCOS and TYCHO catalogues. Astrometric and photometric star catalogues derived from the ESA HIPPARCOS Space Astrometry Mission [Google Scholar]
- Fekel, F. C., J. 1983, ApJ, 268, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Folkner, W. M., Williams, J. G., & Boggs, D. H. 2009, IPN Progress Report, 178 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021a, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Klioner, S. A., et al.) 2021b, A&A, 649, A9 [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Klioner, S. A., et al.) 2022, A&A, 667, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galli, P. A. B., Loinard, L., Ortiz-Léon, G. N., et al. 2018, ApJ, 859, 33 [Google Scholar]
- García-Alvarez, D., Foing, B. H., Montes, D., et al. 2003, A&A, 397, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, R. J., Andrews, S. M., Wilner, D. J., & Kraus, A. L. 2012, ApJ, 751, 115 [Google Scholar]
- Kounkel, M., Hartmann, L., Loinard, L., et al. 2017, ApJ, 834, 142 [Google Scholar]
- Kovalevsky, J., Lindegren, L., Perryman, M. A. C., et al. 1997, A&A, 323, 620 [NASA ADS] [Google Scholar]
- Lebach, D. E., Bartel, N., Bietenholz, M. F., et al. 2012, ApJS, 201, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Lestrade, J. F., Preston, R. A., Jones, D. L., et al. 1999, A&A, 344, 1014 [NASA ADS] [Google Scholar]
- Lindegren, L. 2020a, A&A, 633, A1 [Google Scholar]
- Lindegren, L. 2020b, A&A, 637, C5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Bastian, U., Biermann, M., et al. 2021a, A&A, 649, A4 [EDP Sciences] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021b, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Loinard, L., Torres, R. M., Mioduszewski, A. J., et al. 2007, ApJ, 671, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Loinard, L., Torres, R. M., Mioduszewski, A. J., & Rodriguez, L. F. 2008, ApJ, 675, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Lunz, S., Anderson, J. M., Xu, M. H., et al. 2023, A&A, 676, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacMillan, D. S., Fey, A., Gipson, J. M., et al. 2019, A&A, 630, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marschall, L. A., & Mathieu, R. D. 1988, AJ, 96, 1956 [Google Scholar]
- Marsden, S. C., Berdyugina, S. V., Donati, J.-F., et al. 2005, ApJ, 634, L173 [Google Scholar]
- Miller-Jones, J. C. A., Sivakoff, G. R., Knigge, C., et al. 2013, Science, 340, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen, D. C., Brandeker, A., van Kerkwijk, M. H., & Jayawardhana, R. 2012, ApJ, 745, 119 [Google Scholar]
- Ortiz-León, G. N., Loinard, L., Kounkel, M. A., et al. 2017, ApJ, 834, 141 [Google Scholar]
- Ratner, M. I., Bartel, N., Bietenholz, M. F., et al. 2012, ApJS, 201, 5 [CrossRef] [Google Scholar]
- Richichi, A., Leinert, C., Jameson, R., & Zinnecker, H. 1994, A&A, 287, 145 [Google Scholar]
- Secrest, N. J., Dudik, R. P., Dorland, B. N., et al. 2015, ApJS, 221, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Secrest, N. J., Dudik, R. P., Dorland, B. N., et al. 2016, VizieR Online Data Catalog: J/ApJS/221/12 [Google Scholar]
- Seidelmann, P. K. 1992, Explanatory supplement to the Astronomical almanac., rev. edn. (Mill Valley: University Science Books) [Google Scholar]
- Shepherd, M. C. 1997, in Astronomical Society of the Pacific Conference Series, 125, Astronomical Data Analysis Software and Systems VI, eds. G. Hunt, & H. Payne, 77 [NASA ADS] [Google Scholar]
- Shuygina, N., Ivanov, D., Ipatov, A., et al. 2019, Geodesy Geodyn., 10, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Titov, O., Lambert, S. B., & Gontier, A. M. 2011, A&A, 529, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Titov, O., Shu, F., & Chen, W. 2020, in Astrometry, Earth Rotation, and Reference Systems in the GAIA era, ed. C. Bizouard, 173 [Google Scholar]
- Torres, R. M., Loinard, L., Mioduszewski, A. J., & Rodriguez, L. F. 2007, ApJ, 671, 1813 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, R. M., Loinard, L., Mioduszewski, A. J., & Rodríguez, L. F. 2009, ApJ, 698, 242 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [CrossRef] [EDP Sciences] [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Absolute positions in ICRF3 for 14 stars based on observations conducted in January 2020 and analysis including the modeling of the phase calibrator structure.
Römer delay, position corrections due to parallax effect, and radial velocity for the single-epoch positions used for the rotation parameter analysis.
Star positions from absolute astrometry and alternate observations used in this study.
All Figures
 |
Fig. 1 Results for scenario “55,EDR3,GA”, when using the VLBI data and Gaia EDR3 as in Fig. 3 in Lunz et al. (2023) but correcting for the effect of Galactocentric acceleration. The orientation and spin parameters for 51 different adjustment solutions are shown in the upper row. For each adjustment solution the star with the largest (Qi/ni) (which indicates the quality of the fit of the star data to a five parameter astrometric model, see Lindegren 2020a) was rejected in the following iteration. The respective (Qi/ni) along with the star name are shown in the lower left plot, whereas the lower right plot shows the quality of the overall fit Q/n, equivalent to χ2 of the adjustment. |
| In the text | |
 |
Fig. A.1 Sky motion for the 15 stars with astrometric models reported in Table A.1. The observed positions are marked with the red stars and their uncertainties are visualized by the black ellipses. The adjusted positions are labeled by the black dots and their uncertainties by the blue ellipses. The model is indicated by a black line. |
| In the text | |
 |
Fig. A.2 Results for scenario “55,EDR3,GA,NM”, using the VLBI data and Gaia EDR3 as in Fig. 1, but replacing the VLBI data of stars HD 283572, V410Tau, SS Cyg, Brun 334, TYC 5346-538-1, Haro 1-6, BHCVn, σ2 CrB, HD 199178, AR Lac, IM Peg, and HD 22468 with newly determined models of stellar motion and newly corrected absolute positions as described in Sect. 4.3. |
| In the text | |
 |
Fig. A.3 Results for scenario “60,EDR3,GA,NM”, using the VLBI data and Gaia EDR3 as in Fig. A.2, but adding the data of five new stars and astrometric information as described in Sect. 4.4. |
| In the text | |
 |
Fig. A.4 Results for scenario “53,EDR3,GA,NM”, using the VLBI data and Gaia EDR3 as in Fig. A.3, but excluding seven stars (HD 22468, LSI +61 303, V410 Tau, AR Lac, DoAr 51, CoKu HP Tau G2, and HD 283641) from the beginning. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


