| Issue |
A&A
Volume 687, July 2024
|
|
|---|---|---|
| Article Number | A248 | |
| Number of page(s) | 16 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202449504 | |
| Published online | 22 July 2024 | |
Catalogue of dual-field interferometric binary calibrators
1
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge
CB3 0HA,
UK
e-mail: mcn35@cam.ac.uk
2
Kavli Institute for Cosmology, University of Cambridge,
Madingley Road,
Cambridge
CB3 0HA,
UK
3
LESIA, Observatoire de Paris, PSL, CNRS, Sorbonne Université, Université de Paris,
5 place Janssen,
92195
Meudon,
France
4
European Southern Observatory,
Karl-Schwarzschild-Straße 2,
85748
Garching,
Germany
5
Universidade de Lisboa – Faculdade de Ciências,
Campo Grande,
1749-016
Lisboa,
Portugal
6
CENTRA – Centro de Astrofísica e Gravitação, IST, Universidade de Lisboa,
1049-001
Lisboa,
Portugal
7
Max Planck Institute for Astronomy,
Königstuhl 17,
69117
Heidelberg,
Germany
8
Department of Physics & Astronomy, Johns Hopkins University,
3400 N. Charles Street,
Baltimore,
MD
21218,
USA
9
Space Telescope Science Institute,
3700 San Martin Drive,
Baltimore,
MD
21218,
USA
10
Univ. Grenoble Alpes, CNRS, IPAG,
38000
Grenoble,
France
11
Center for Interdisciplinary Exploration and Research in Astrophysics (CIERA) and Department of Physics and Astronomy, Northwestern University,
Evanston,
IL
60208,
USA
12
Max Planck Institute for extraterrestrial Physics,
Giessenbach-straße 1,
85748
Garching,
Germany
13
Aix Marseille Univ, CNRS, CNES, LAM,
Marseille,
France
14
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange,
France
15
STAR Institute, Université de Liège,
Allée du Six Août 19c,
4000
Liège,
Belgium
16
Leiden Observatory, Leiden University,
PO Box 9513,
2300 RA
Leiden,
The Netherlands
17
Department of Astrophysical & Planetary Sciences, JILA,
Duane Physics Bldg., 2000 Colorado Ave, University of Colorado,
Boulder,
CO
80309,
USA
18
Institute of Physics, University of Cologne,
Zülpicher Straße 77,
50937
Cologne,
Germany
19
Max Planck Institute for Radio Astronomy,
Auf dem Hügel 69,
53121
Bonn,
Germany
20
Universidade do Porto, Faculdade de Engenharia,
Rua Dr. RobertoRua Dr. Roberto Frias,
4200-465
Porto,
Portugal
21
School of Physics, University College Dublin,
Belfield,
Dublin 4,
Ireland
22
Astrophysics Group, Department of Physics & Astronomy, University of Exeter,
Stocker Road,
Exeter
EX4 4QL,
UK
23
Departments of Physics and Astronomy, Le Conte Hall, University of California,
Berkeley,
CA
94720,
USA
24
European Southern Observatory,
Casilla 19001,
Santiago 19,
Chile
25
Advanced Concepts Team, European Space Agency, TEC-SF, ESTEC,
Keplerlaan 1, NL-2201,
AZ Noordwijk,
The Netherlands
26
University of Exeter,
Physics Building, Stocker Road,
Exeter
EX4 4QL,
UK
27
Fakultät für Physik, Universität Duisburg-Essen,
Lotharstraße 1,
47057
Duisburg,
Germany
28
Institüt für Astronomie und Astrophysik, Universität Tübingen,
Auf der Morgenstelle 10,
72076
Tübingen,
Germany
29
Center for Space and Habitability, Universität Bern,
Gesellschaftsstrasse 6,
3012
Bern,
Switzerland
30
Astronomy Department, University of Michigan,
Ann Arbor,
MI
48109,
USA
31
Academia Sinica, Institute of Astronomy and Astrophysics,
11F Astronomy-Mathematics Building, NTU/AS campus, No. 1, Section 4, Roosevelt Rd.,
Taipei
10617,
Taiwan
32
European Space Agency, ESA Office, Space Telescope Science Institute,
3700 San Martin Drive,
Baltimore,
MD
21218,
USA
33
Department of Earth & Planetary Sciences, Johns Hopkins University,
Baltimore,
MD,
USA
34
Max Planck Institute for Astrophysics,
Karl-Schwarzschild-Str. 1,
85741
Garching,
Germany
35
Excellence Cluster ORIGINS,
Boltzmannstraße 2,
85748
Garching bei München,
Germany
Received:
6
February
2024
Accepted:
18
April
2024
Context. Dual-field interferometric observations with VLTI/GRAVITY sometimes require the use of a binary calibrator. This is a binary star whose individual components remain unresolved by the interferometer, with a separation between 400 and 2000 mas for observations with the Unit Telescopes (UTs), or 1200–3000 mas for the Auxiliary Telescopes (ATs). The separation vector also needs to be predictable to within 10 mas for a proper pointing of the instrument.
Aims. No list of properly vetted calibrators was available so far for dual-field observations with VLTI/GRAVITY on the UTs. Our objective is to compile such a list and make it available to the community.
Methods. We identified a list of candidates from the Washington Double Star (WDS) catalogue, all with appropriate separations and brightness, scattered over the southern sky. We observed them as part of a dedicated calibration programme, determined whether these objects were true binaries (excluding higher multiplicities resolved interferometrically, but unseen by imaging), and extracted measurements of the separation vectors. We combined these new measurements with those available in the WDS to determine updated orbital parameters for all our vetted calibrators.
Results. We compiled a list of 13 vetted binary calibrators for observations with VLTI/GRAVITY on the UTs, and we provide orbital estimates and astrometric predictions for each of them. We show that our list guarantees that there are always two binary calibrators at least at an airmass < 2 in the sky over the Paranal observatory at any point in time.
Conclusions. Any principal investigator wishing to use the dual-field mode of VLTI/GRAVITY with the UTs can now refer to this list to select an appropriate calibrator. We encourage the use of whereistheplanet to predict the astrometry of these calibrators, which seamlessly integrates with p2Gravity for VLTI/GRAVITY dual-field observing material preparation.
Key words: instrumentation: high angular resolution / instrumentation: interferometers / techniques: interferometric / catalogs / binaries: visual
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Long-baseline optical interferometry is a powerful tool for high-angular resolution astronomy, and the GRAVITY instrument (GRAVITY Collaboration 2017) on the Very Large Telescope Interferometer (VLTI) has proven to be extremely useful for the study of many objects, ranging from the centre of our Galaxy (GRAVITY Collaboration 2022) and its supermassive black hole (GRAVITY Collaboration 2020a,b,d, 2018a,b, 2019a) to active galactic nuclei (GRAVITY Collaboration 2020d) or exoplanets (GRAVITY Collaboration 2019b, 2020c; Nowak et al. 2020).
All these recent achievements have benefited from the unique capability of GRAVITY to obtain high-precision astrometric measurement beyond the diffraction limit of a single telescope of the array, that is, in the so-called dual-field mode. In this mode, the two channels of the instrument simultaneously observe two targets: the science target, and a close-by fringe-tracking target. An internal laser metrology system is used to track and correct the non-common path errors between the two channels, so that the relative astrometry between the two targets can be measured accurately. This mode, among other feats, has made GRAVITY successful in high-contrast imaging of exoplanets and in the astrometric monitoring of stars orbiting Sgr A* in the centre of the Milky Way.
However, in order to derive accurate astrometric measurements from dual-field interferometric observations, a calibration of the metrology reference is needed, which in some situations requires the observation of a dedicated binary calibrator. In the absence of a catalogue of vetted binary calibrators, options were initially very limited. This was a main source of concern during the early days of the ExoGRAVITY Large Programme (1104.C-0651; PI Lacour), and it triggered a series of efforts to assemble such a catalogue, in particular, through a dedicated calibration programme (106.21S5.001; PI Nowak).
This paper reports on those efforts and presents the first catalogue of vetted binary calibrators covering the southern sky (Fig. 1) for VLTI/GRAVITY dual-field observations on the Unit Telescopes (UTs). In Sect. 2, we give some general background on dual-field astrometry with GRAVITY and explain why these binary calibrators are needed in this peculiar observing mode. Section 3 details the procedure we followed to assemble and observe our initial list of targets, and Sect. 4 explains how the data were reduced and the calibrators vetted. In Sect. 5 we present the final catalogue, which contains a total of 13 entries. We also report on the numerous astrometric measurements obtained on these targets and provide orbital parameter estimates and astrometric predictions that can be used for pointing the instrument during observations. Section 6 gives our final conclusions.
 |
Fig. 1 Map representing the on-sky coverage provided by the 13 vetted binary calibrators presented in this work. The shaded regions show the number of available calibrators within 45deg. |
2 GRAVITY dual-field astrometry, and why we need binary calibrators
2.1 Optical path, fringe-tracking, and metrology in the GRAVITY instrument
The GRAVITY instrument is built around two different inter-ferometric combiners. The science (SC) combiner records the coherent flux at low to medium spectral resolution (R = 50 to 4000), usually with a relatively long integration time (up to 300 s for faint targets). The fringe-tracker (FT) combiner enables these long integrations by actively compensating for the atmospheric turbulence. This second combiner records the coherent flux at a much lower resolution and with a short integration time. It actively measures and records the phase of the coherent flux and controls a set of actuators to keep the interferometric signal stable (Lacour et al. 2019; Nowak et al. 2024).
The use of two beam combiners is one of the strengths of GRAVITY, but it also makes it difficult to keep track of the different optical path lengths (OPL) in the instrument. When we assume that both the FT and the SC are pointed towards two different close-by target stars SFT and SSC, then for a baseline (j, k) linking telescope Tj to Tk, the recorded coherent fluxes in both channels as a function of time and wavelength are given by
![${\rm{\Gamma }}_{j,k}^{{\rm{FT}}}(t,\lambda ) = T(t,\lambda ){I_{{S_{{\rm{FT}}}}}}(\lambda )\exp \left[ { - i{{2\pi } \over \lambda }{\rm{OPD}}_{j,k}^{{\rm{FT}}}(t)} \right],$](/articles/aa/full_html/2024/07/aa49504-24/aa49504-24-eq1.png) (1)
(1)
![${\rm{\Gamma }}_{j,k}^{{\rm{SC}}}(t,\lambda ) = T(t,\lambda ){I_{{S_{{\rm{Sc}}}}}}(\lambda )\exp \left[ { - i{{2\pi } \over \lambda }{\rm{OPD}}_{j,k}^{{\rm{SC}}}(t)} \right].$](/articles/aa/full_html/2024/07/aa49504-24/aa49504-24-eq2.png) (2)
(2)
In these equations, I(λ) represents the spectrum of the target, T is the transmission (of the atmosphere and instrument), and  refers to the effective optical path difference on baseline (j, k) for the given channel.
refers to the effective optical path difference on baseline (j, k) for the given channel.
The OPD terms in Eqs. (1) and (2) include contributions from very different elements, which are summarized in the block diagram presented in Fig. 2. From the target to the FT or SC channel via telescope Tk, the total optical path is the sum of the items listed below.
- 1.
The in-vacuum OPL from the FT or SC target to telescope Tk,
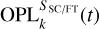 . This OP depends on the time through the rotation of the Earth.
. This OP depends on the time through the rotation of the Earth. - 2.
An additional time-dependent contribution from the atmosphere above the telescope Tk, OPLatm,k(t).
- 3.
A contribution representing the path from the telescope Tk through the VLTI delay lines (DL) and up to the GRAVITY injection unit (where the beam is split between the two channels). This can be represented as a single-telescope dependent quantity OPLDL,k(t), and it is the quantity actively controlled by the FT.
- 4.
A channel-dependent contribution that represents the path from the injection unit for the beam coming from Tk to the detector through the given channel (SC/FT):
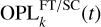 .
.
The total OPL from the target to the detector of the channel FT or SC is therefore written
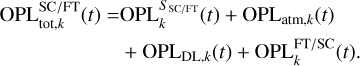 (3)
(3)
Using this expression, the OPDs on baseline ( j, k) seen by the two beam combiners are given by
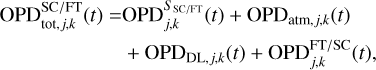 (4)
(4)
where any OPDj,k term is to be understood as the difference OPLk − OPLj.
From an astrophysical perspective, the quantity of interest in Eq. (4) is the in-vacuum term 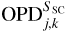 , which is directly related to the astrometric position of the science target SSC. To extract this astrometry, one of the main steps performed during the data reduction is to reference the science channel to the FT channel. This means that the phase of the FT coherent flux is extracted, interpolated onto the SC wavelength grid, and subtracted from the SC measurements, according to
, which is directly related to the astrometric position of the science target SSC. To extract this astrometry, one of the main steps performed during the data reduction is to reference the science channel to the FT channel. This means that the phase of the FT coherent flux is extracted, interpolated onto the SC wavelength grid, and subtracted from the SC measurements, according to
![$\eqalign{ & \tilde \Gamma _{j,k}^{{\rm{SC}}}(t,\lambda ) = \Gamma _{j,k}^{{\rm{SC}}}(t,\lambda ) \times \exp \left\{ {i\arg \left[ {\Gamma _{j,k}^{{\rm{FT}}}(t,\lambda )} \right]} \right\} \cr & & \,\,\,\,\, = T(t,\lambda ){I_{{S_{{\rm{Sc}}}}}}(\lambda ) \cr & & \,\,\,\,\,\,\,\,\, \times \exp \left( { - i{{2\pi } \over \lambda }\left[ {{\rm{OPD}}_{j,k}^{{{\rm{S}}_{{\rm{SC}}}}}(t) - {\rm{OPD}}_{j,k}^{{S_{{\rm{FT}}}}}(t)} \right]} \right) \cr & & \,\,\,\,\,\,\,\,\,\,\, \times \exp \left( { - i{{2\pi } \over \lambda }\left[ {{\rm{OPD}}_{j,k}^{{\rm{SC}}}(t) - {\rm{OPD}}_{j,k}^{{\rm{FT}}}(t)} \right]} \right). \cr} $](/articles/aa/full_html/2024/07/aa49504-24/aa49504-24-eq9.png) (5)
(5)
The expression of 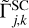 shows two remaining differential OPD terms. The first term is the difference between the in-vacuum OPD on baseline (j, k) for the SC target and the FT target. This is a purely astrophysical quantity, which is directly related to the differential astrometry ΔRA and ΔDec between the SC and FT targets, and to the baseline (u, υ) coordinates,
shows two remaining differential OPD terms. The first term is the difference between the in-vacuum OPD on baseline (j, k) for the SC target and the FT target. This is a purely astrophysical quantity, which is directly related to the differential astrometry ΔRA and ΔDec between the SC and FT targets, and to the baseline (u, υ) coordinates,
![$\left[ {{\rm{OPD}}_{j,k}^{{S_{{\rm{SC}}}}}(t) - {\rm{OPD}}_{j,k}^{{S_{{\rm{FT}}}}}(t)} \right] = [\Delta {\rm{RA}} \times u(t) + \Delta {\rm{Dec}} \times v(t)].$](/articles/aa/full_html/2024/07/aa49504-24/aa49504-24-eq11.png) (6)
(6)
Conversely, the second differential term is a purely instrumental quantity. It is better understood by reordering the terms in the difference, using
![$\eqalign{ & \left[ {{\rm{OPD}}_{j,k}^{{\rm{SC}}} - {\rm{OPD}}_{j,k}^{{\rm{FT}}}} \right] = \left( {{\rm{OPL}}_k^{{\rm{SC}}} - {\rm{OPL}}_j^{{\rm{SC}}}} \right) - \left( {{\rm{OPL}}_k^{{\rm{FT}}} - {\rm{OPL}}_j^{{\rm{FT}}}} \right) \cr & & & \,\,\,\,\,\,\,\,\, = \left( {{\rm{OPL}}_k^{{\rm{SC}}} - {\rm{OPL}}_k^{{\rm{FT}}}} \right) - \left( {{\rm{OPL}}_j^{{\rm{FT}}} - {\rm{OPL}}_j^{{\rm{SC}}}} \right), \cr & & & \,\,\,\,\,\,\,\,\, = \Delta {\rm{OPL}}_k^{{\rm{SC}} - {\rm{FT}}} - \Delta {\rm{OPL}}_j^{{\rm{SC}} - {\rm{FT}}} \cr} $](/articles/aa/full_html/2024/07/aa49504-24/aa49504-24-eq12.png) (7)
(7)
which demonstrates that this instrumental part stems from a non-common-path error between the FT and SC channels.
In GRAVITY, this non-common-path error is measured by a laser-metrology system (Gillessen et al. 2012). To do this, a laser beam is sent backwards in the optical train from the beam-combiner to the telescopes. In the pupil-plane of each telescope, the laser light from the SC and FT channels interferes to create fringes, which are recorded by a set of diodes on the telescope spider. From this, each of the four ΔOPLSC–FT terms (one per telescope) can be extracted. This allows for the correction of this term up to an unknown wavelength-dependent metrology zero-point ϕZP(λ), which stems from the uncontrolled injection phase of the laser beam. During the data reduction, for any baseline (j, k), both 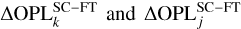 can be computed and removed from the SC coherent flux. This leaves the metrology-corrected coherent flux, expressed as
can be computed and removed from the SC coherent flux. This leaves the metrology-corrected coherent flux, expressed as
![$\eqalign{ & {\Gamma ^{{\rm{metcorr }}}}j,k(t,\lambda ) = T(t,\lambda ){I_{{S_{{\rm{SC}}}}}}(\lambda ) \cr & & & \,\,\,\,\,\,\,\, \times {{\rm{e}}^{ - i{{2\pi } \over \lambda }[\Delta {\mathop{\rm RA}\nolimits} \times u(t) + \Delta {\mathop{\rm Dec}\nolimits} \times v(t)] - i\phi _{j,k}^{{\rm{ZP}}}(\lambda )}}. \cr} $](/articles/aa/full_html/2024/07/aa49504-24/aa49504-24-eq14.png) (8)
(8)
Equation (8) shows that the metrology zero-point can interfere with the measurement of the astrometry of the target. One of the main concerns of the dual-field observing strategy and the astrometric extraction therefore is to find a way to determine and correct for this unknown term ϕZP(λ).
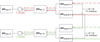 |
Fig. 2 Block diagram showing the different elements contributing to the total OPL within the two channels of the GRAVITY when used in dual-field mode. |
2.2 First observing strategy: On-axis
A first option to determine the metrology zero-point (also known as the phase reference) is to point the SC and FT channels at the same target. In this case, the relative astrometry between the channels is zero, and the terms ΔRA and ΔDec vanish from Eq. (8). The coherent flux on the SC channel after correction from the FT phase and the metrology is almost a direct measurement of ϕZP,
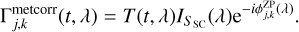 (9)
(9)
This forms the basis of the on-axis observing strategy, which consists of interleaving observations with the SC channel pointed on the science target and observations with the SC channel pointed at the FT target (see Fig. 3). For an on-science observation obtained at time t, the phase zero-point is obtained from the average of the on-FT observation obtained just before (at t1 < t), and the on-FT observation obtained just after (at t2 > t) according to
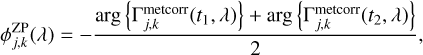 (10)
(10)
and the phase-referenced coherent flux is calculated using
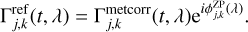 (11)
(11)
The amplitude of this phase-referenced coherent flux is only determined by the spectrum of the science target and by the combined atmosphere-instrument transmission, whereas its phase is only determined by the relative astrometry with respect to the FT target. In other words, we have
![$\Gamma _{j,k}^{{\rm{ref}}}(t,\lambda ) = T(t,\lambda ){S_{{S_{{\rm{SC}}}}}}(\lambda ){{\rm{e}}^{ - i{{2\pi } \over \lambda }[\Delta {\rm{RA}} \times u(t) + \Delta {\rm{Dec}} \times \upsilon (t)]}}.$](/articles/aa/full_html/2024/07/aa49504-24/aa49504-24-eq18.png) (12)
(12)
From a technical perspective, pointing the FT and SC channels simultaneously towards the same target to extract the metrology zero-point requires the use of a beam-splitter to separate the beam in amplitude. The phase-reference remains valid as long as the instrumental setup does not change, which means that the beam-splitter must also be used for the on-science observations. In GRAVITY, the beam-splitter can only accommodate a maximum separation between the FT and SC fibres of ∽500 mas, and thus, beyond this, a different strategy is required. The beamsplitter also reduces the flux by a factor of 2, which might not be ideal for fainter targets.
 |
Fig. 3 Illustration of the dual-field on-axis observing strategy. This strategy is used to measure the astrometry of a scientific target relative to a fringe-tracking target. The left panel illustrates the position of the two fibres in the instrument, with the use of a beam-splitter to separate the field. The right panel illustrates the resulting position of the two fibres on-sky. |
2.3 Second observing strategy: Off-axis swap
When the separation between the fringe-tracking and science targets is too large to use the beam-splitter, the only remaining option in GRAVITY is to use a roof-mirror to split the field between the SC and FT channels. However, in this case, the two channels cannot physically be pointed simultaneously at the same target to obtain the metrology zero-point. Another strategy must therefore be used to determine the metrology zero-point in Eq. (8).
If the science target itself is suitable for fringe-tracking, a possibility is to perform a swap observation. In this case, the two fibres are swapped. This reverses the differential astrometry in Eq. (8), and results in the measurement of two coherent fluxes (at t− before the swap, and t+ after the swap), given by
![$\Gamma _{j,k}^{{\rm{metcorr }}}\left( {{t_ - },\lambda } \right) = T\left( {{t_ - },\lambda } \right)S(\lambda ){{\rm{e}}^{ - i{{i\pi } \over \lambda }\left[ {u\left( {{t_ - }} \right)\Delta {\rm{RA}} + \upsilon \left( {{t_ - }} \right)\Delta {\rm{Dec}}} \right] - i\phi _{jk}^{{\rm{ZP}}}(\lambda )}},$](/articles/aa/full_html/2024/07/aa49504-24/aa49504-24-eq19.png) (13)
(13)
![$\Gamma _{j,k}^{{\rm{metcorr }}}\left( {{t_ + },\lambda } \right) = T\left( {{t_ + },\lambda } \right)S(\lambda ){{\rm{e}}^{ + i{{2\pi } \over \lambda }\left[ {u\left( {{t_ + }} \right)\Delta {\rm{RA}}\upsilon \left( {{t_ + }} \right) + \Delta {\rm{Dec}}} \right] - i\phi _{jk}^{{\rm{ZP}}}(\lambda )}},$](/articles/aa/full_html/2024/07/aa49504-24/aa49504-24-eq20.png) (14)
(14)
and from which the metrology zero-point can be extracted using
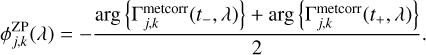 (15)
(15)
The coherent flux at both t+ and t− can then be corrected for this zero-point to yield a phase-referenced coherent flux similar to Eq. (12). In this scenario, represented in Fig. 4, half of the observations measure the astrometry of the science target relative to the FT target, whereas the other half measures the astrometry of the FT target relative to the main scientific target.
2.4 Need for binary calibrators, and their requirements
For the off-axis swap strategy to work, the science target itself needs to be suitable for fringe-tracking. When this is not the case (it is too faint, e.g.), the swap strategy cannot be performed on the FT–SC pair. In this case, the remaining option is to perform dedicated dual-field calibration observations. This involves moving the telescopes towards a binary calibrator and performing the swap observation on this binary target. The metrology zero-point is extracted from the calibration observation and is subtracted from the science observations.
To perform this separate calibration observation, a suitable binary calibrator must be available. A proper binary calibrator for an observation with GRAVITY on the UTs is typically defined as a visual binary with a separation ranging from ∽ 400 mas (to easily separate the two components with the individual telescopes) to 2000 mas (to stay within the available field of view of GRAVITY), for which the two components must have a magnitude 8.5 at least in K band (for fringe-tracking in even poor conditions) and must be unresolved by the interferometer.
The separation vector between the two components of the binary calibrator must be known in advance, for two main reasons. Firstly, this separation is used to point the instrument at the two components. The typical field of view of the single-mode fibres used in GRAVITY is ≃60 mas on the UTs, but the coupling starts to decrease significantly at around 30 mas (Pourré et al. 2024). To ensure that most of the flux of the two components is properly injected in the fibre, the separation of the binary should therefore be known at a precision better than 30 mas. Secondly, even though a fibre pointing error on its own does not bias the astrometry, the coupling between the offset of the metrology beam induced by such a fibre mispointing and pupil-tracking errors will result in an error on the astrometry and metrology phase measurements (Lacour et al. 2014). The design of the pupil tracking in GRAVITY ensures that a 10 mas pointing error of the fibre generates a 2 nm error on the OPD at most (equivalent to a 4 µas astrometric error on a 100 m baseline). This defines our most stringent requirement on the knowledge of the separation of the binary: To ensure that the calibration observation itself does not dominate the error on the astrometry of the science target, the separation vector should be known at a precision of 10 mas at least.
 |
Fig. 4 Similar to Fig. 3, but illustrating the dual-field off-axis observing strategy. In this case, a roof-mirror is used to separate the field, and two sequences are required. In the science sequence, the FT fibre is positioned on an appropriately selected FT target, whereas the SC fibre is centred on the science target. In the calibration sequence, a binary star is observed multiple times while swapping the position of the two fibres. If the science target is appropriate for fringe-tracking, the calibration can be performed on the science target itself. If this is not the case, the calibration sequence must be performed on a separate binary calibrator. |
3 Assembling the catalogue: Target selection and observations
Three binary calibrators were known at the start of the Exo-GRAVITY Large Program: WDSJ04021-3429, WDSJ14077-4952, and WDSJ20399+1115. They did not cover the entire southern sky, and in an effort to expand on this very limited list, we searched for more candidates in the Washington Double Star (WDS) catalogue.
We assembled a list of binary calibrator candidates by selecting targets from the WDS catalogue using specific criteria. These criteria included a separation ranging from 400 mas to 2000 mas and a K band magnitude below 8 to ensure that a good SNR can be reached with minimum observing time. We also searched for targets with available orbit predictions for a proper pointing of the single-mode fibres during observations, and we selected a sample covering the entire southern sky. We did not aim for completeness in our selection.
From the pool of potential targets, a subset of 21 binaries was chosen to provide broad coverage across the southern sky. A calibration program was submitted to ESO, and the selected targets were observed with the Auxiliary Telescopes (ATs). The original observation plan spanning P106 to P107 was adjusted due to COVID-19 disruptions, leading to observations being conducted exclusively during the Chilean summer (P106 and P108, from October to March). Consequently, most targets within RA range of 10 h 00 min 00 s to 20 h 00 min were regrettably not observed (see Table 1). One of the three original calibrators is fortunately located at 14 h of RA, which limits the impact of this disruption.
Observations were conducted using the GRAVITY instrument on the ATs in its dual-field on-axis mode (see Sect. 2.2 and Fig. 3). In addition to these observations, dual-field calibration observations from the ExoGRAVITY Large Program and other related programmes were also incorporated in an effort to improve the orbital parameter estimates. These calibration observations were originally acquired using the GRAVITY instrument on the UTs in the off-axis dual-field mode with the swap strategy (see Sect. 2.3 and Fig. 4). The observing logs describing the data included in this study are given in Appendix A.
4 Data reduction
4.1 Pipeline reduction and general steps
The first step in our data reduction was to use the ESO GRAVITY pipeline (Lapeyrere et al. 2014) to create the intermediate astroreduced files, in which the individual detector integrations (DITs) are not averaged. The GRAVITY pipeline can also produce fully reduced dualscivis files in which the DITs are averaged. However, as we explain in Sect. 4.3.2, averaging coherent flux without blurring the signal requires some careful considerations about the astrometry of the targets. The GRAVITY pipeline assumes that the fibre is well centred on the target, and uses the coordinates of the fibre as the assumption on the astrometry required to calculate the average. In many of our observations, the coordinates of the secondary were poorly known, so this assumption was not always valid. Therefore, in all this work, we decided to keep the astroreduced data and to perform any required DITs averaging manually in our own astrometry extraction routines.
As a note, the FT referencing and metrology correction described in Eqs. (5) and (8) are not performed by the pipeline on the astroreduced data product. Therefore, we included these steps in our own routines, using the algorithms described in the GRAVITY Pipeline User manual (VLT-MAN-ESO-19500-XXXX).
Initial list of target selected from the WDS catalogue.
4.2 Vetting of the AT observations
Our analysis of the binary calibrator candidates started by a check for potential systems with higher multiplicity. A binary calibrator needs to be a proper binary for it to be useful for extracting the metrology zero-point, otherwise, the phase of Eq. (8) is affected by an additional term coming from the resolved system, which cannot be easily accounted for in all the subsequent calculations.
To determine whether the two components of any given target binary are seen as point sources (i.e. are unresolved) by the VLTI, we treated each of them independently, in a similar fashion as if these were single-field observations, and performed a χ2-test. This started by calculating the interferometric visibility, defined by
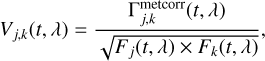 (16)
(16)
where Fi refers to the flux on telescope i. In theory, for an unresolved component, the amplitude of this visibility should remain constant and equal to 1, and the closure phase calculated from this visibility should remain equal to 0. In practice, however, the amplitude of the visibility is never equal to 1 and needs to be calibrated with the observation of a known unresolved point-source (a so-called interferometric calibrator). As we did not obtain such calibrations during our observations, we focused on the closure-phase to determine whether the individual components of our target binaries are unresolved.
For a given triangle of three telescopes (j, k, l), we calculated the bispectrum using
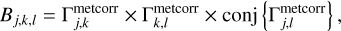 (17)
(17)
and we then extracted the closure phase, defined as the argument of this bispectrum,
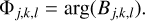 (18)
(18)
The error bars σj,k,l on the closure phase were propagated from the error bars reported by the pipeline on the coherent fluxes. We then performed a detrending step by fitting and subtracting a second-order polynomial in wavelength for each exposure and triangle. If the component is truly unresolved, the resulting closure phase should be 0 within the error bars. Therefore, we calculate the reduced χ2 under this null-hypothesis,
![$\chi _{{\rm{red }}}^2 = {1 \over {{\rm{ d}}{\rm{.o}}{\rm{.f}}{\rm{. }}}}\sum\limits_{\scriptstyle \lambda ,t \atop \scriptstyle (j,k,l)} {{{\left[ {{{{\Phi _{j,k,l}}(t,\lambda )} \over {{\sigma _{j,k,l}}(t,\lambda )}}} \right]}^2}} .$](/articles/aa/full_html/2024/07/aa49504-24/aa49504-24-eq25.png) (19)
(19)
In this equation, d.o.f. stands for the number of degrees of freedom and is given by
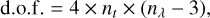 (20)
(20)
since 4 corresponds to the number of independent triangles with six baselines, nλ to the number of wavelength channels, nt to the number of exposures, and “minus 3” accounts for the three coefficients of the detrending polynomial.
The values of these reduced 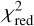 are reported in Table 2. Their distribution shows a very clear separation between the unresolved sources, with values close to 1.3–1.8, and resolved sources, where the
are reported in Table 2. Their distribution shows a very clear separation between the unresolved sources, with values close to 1.3–1.8, and resolved sources, where the 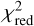 spikes to values of >7. We adopted a threshold of 2 and rejected any candidate binary with one component resulting in a
spikes to values of >7. We adopted a threshold of 2 and rejected any candidate binary with one component resulting in a 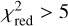 from our list.
from our list.
Results of the 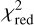 multiplicity test performed on the closure-phase for the first epoch of each target part of the calibration programme.
multiplicity test performed on the closure-phase for the first epoch of each target part of the calibration programme.
4.3 Extracting the astrometry
4.3.1 On-axis observations
The extraction of astrometric measurements from a sequence of on-axis observations with exposures on the science target interleaved with exposures on the FT target has been described extensively in the frame of exoplanet observations (GRAVITY Collaboration 2020d; Nowak et al. 2020). In the case of the binary stars presented in this work, a few minor differences need consideration. First, at the level of contrasts and separations considered in this work, the contamination of on-science observations with FT star residuals is not really an issue, meaning that when the SC fibre is centred on one of the two components, the other component does not significantly contribute to the coherent flux. Second, we are only interested in extracting the astrometry and not the contrast spectrum between the two components.
With these differences in mind, we followed a similar set of steps as were described in the above-mentioned papers. We first combined all the on-FT coherent fluxes to extract the metrology zero-point,
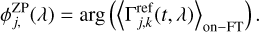 (21)
(21)
Since we were not interested in extracting a proper contrast spectrum, and because only one component contributes to the coherent flux in these low-contrast observation, the amplitude reference was simply taken as the modulus of the coherent flux, using
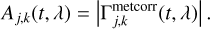 (22)
(22)
From this, we defined a simple binary star model using the metrology zero-point, the amplitude reference, and the binary astrometry (ΔRA, ΔDec),
![$\eqalign{ & \Gamma _{j,k}^{{\rm{model}}}(\Delta {\rm{RA}},\Delta {\rm{Dec}},t,\lambda ) = {A_{j,k}}(t,\lambda ){{\rm{e}}^{i\phi jk}}(\lambda ) \cr & & & & & \times {{\rm{e}}^{ - i{{2\pi } \over \lambda }[u(t)\Delta {\rm{RA}} + v(t)\Delta {\rm{Dec}}]}}, \cr} $](/articles/aa/full_html/2024/07/aa49504-24/aa49504-24-eq34.png) (23)
(23)
and defined the χ2 associated with an on-science exposure as
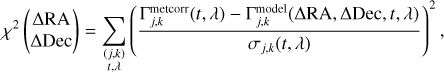 (24)
(24)
where the summation runs over all baselines (j, k), all wavelength channels λ, and all DITs t within the exposure file.
The corresponding best estimate of the astrometry was taken as the location of the minimum χ2. This resulted in a series of measurements 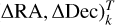 , with 1 < k < nexp, nexp being the number of observations taken with the SC fibre on the secondary component (on-science observations as opposed to on-FT, where the SC fibre is on the same component as the FT fibre). The final best estimate of the astrometry, its associated covariance matrix, was taken as the mean and covariance of the series of individual measurements,
, with 1 < k < nexp, nexp being the number of observations taken with the SC fibre on the secondary component (on-science observations as opposed to on-FT, where the SC fibre is on the same component as the FT fibre). The final best estimate of the astrometry, its associated covariance matrix, was taken as the mean and covariance of the series of individual measurements,
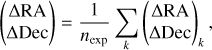 (25)
(25)
![$W = \left[ {\matrix{ {\sigma _{\Delta {\rm{RA}}}^2} & {\rho {\sigma _{\Delta {\rm{RA}}}}{\sigma _{\Delta {\rm{Dec}}}}} \cr {\rho {\sigma _{\Delta {\rm{RA}}}}{\sigma _{\Delta {\rm{Dec}}}}} & {\sigma _{\Delta {\rm{Dec}}}^2} \cr } } \right] = {1 \over {{n_{\exp }}}}{\mathop{\rm cov}} \left\{ {{{\left( \matrix{ \Delta {\rm{RA}} \cr \Delta {\rm{Dec}} \cr} \right)}_k}} \right\}.$](/articles/aa/full_html/2024/07/aa49504-24/aa49504-24-eq38.png) (26)
(26)
4.3.2 Off-axis swap observations
In contrast to the on-axis observations, extracting the metrology zero-point from the swap observations takes slightly more care. The overall method described in Sect. 2.3 holds, and the metrology zero-point can be extracted by combining the arguments of the swapped and non-swapped observations according to Eq. (15). The main difficulty lies in the fact that all DITs are not acquired simultaneously, which causes some problems with how the individual DIT measurements are averaged and how the two swap positions are combined.
First, to avoid large errors on the phase, the coherent fluxes should be averaged before extracting the arguments. Due to the time-dependence of the baseline coordinates u(t), υ(t), however, this coherent flux average cannot be calculated simply by taking the average of all DITs, as this would blur the signal. Instead, the proper way to average the coherent fluxes is to do it at zero-OPD by first shifting them in the target reference frame, then calculating the average, and finally moving the result back to the initial frame. In mathematical terms, this would be written
![$\eqalign{ & \Gamma _{j,k}^{{\rm{metcorr }}}\left( {{t_{{\rm{mean }}}},\lambda } \right) = \left\langle {\Gamma _{j,k}^{{\rm{metcorr }}}(t,\lambda ) \times {{\rm{e}}^{i{{2\pi } \over \lambda }[u(t)\Delta {\rm{RA}} + \upsilon (t)\Delta {\rm{Dec}}]}}} \right\rangle \cr & & & \,\,\,\,\,\,\,\, \times {{\rm{e}}^{ - i{{2\pi } \over \lambda }\left[ {u\left( {{t_{{\rm{mean }}}}} \right)\Delta {\rm{RA}} + \upsilon \left( {{t_{{\rm{mean }}}}} \right)\Delta {\rm{Dec}}} \right]}}. \cr} $](/articles/aa/full_html/2024/07/aa49504-24/aa49504-24-eq39.png) (27)
(27)
Then, because the swapped and non-swapped observations are not acquired simultaneously, Eq. (15) is not exactly correct, as it would in practice introduce an error on the phase in the form of 2πΔRA [u(t+) − u(t−)]/λ, plus a similar term for ΔDec. Therefore, the zero-point is in practice calculated directly in the zero-OPD frame using
![$\eqalign{ & \phi _{j,k}^{{\rm{ZP}}} = {1 \over 2}{\left\langle {\Gamma _{j,k}^{{\rm{metcorrr}}}{{\rm{e}}^{i{{2\pi } \over \lambda }[u\Delta {\rm{RA}} + \upsilon \Delta {\rm{Dec}}]}}} \right\rangle _{{\rm{swapped }}}} \cr & & + {1 \over 2}{\left\langle {\Gamma _{j,k}^{{\rm{metcorr}}}{{\rm{e}}^{i{{2\pi } \over \lambda }[u\Delta {\rm{RA}} + \upsilon \Delta {\rm{Dec}}]}}} \right\rangle _{{\rm{unswapped }}}}. \cr} $](/articles/aa/full_html/2024/07/aa49504-24/aa49504-24-eq40.png) (28)
(28)
The problem in Eqs. (27) and (28) is that they require an a priori knowledge of the astrometry of the target. If this astrome-try is known in advance, it can be used to average the swapped and non-swapped observations, and then to calculate the metrology zero-point. This is typically the case when observing a known binary calibrator for an off-axis science target, but it was not the case for our binary targets, for which we tried to determine the best estimate of the astrometry.
To circumvent this issue, we resorted to a grid of astrometry, in a similar fashion as for the on-axis observations described in Sect. 2.2. For any point ΔRA, ΔDec on our grid, we combined the averaged coherent fluxes of the two swap positions using
![$\eqalign{ & {\Gamma _{j,k}}(\Delta {\rm{RA}},\Delta {\rm{Dec}}) = \left\langle {\Gamma _{j,k}^{{\rm{metcorr }}}{{\rm{e}}^{i{{2\pi } \over \lambda }[u\Delta {\rm{RA}} + \upsilon \Delta {\rm{Dec}}]}}} \right\rangle _{{\rm{swapped }}}^{{1 \over 2}} \cr & & & \,\,\,\,\,\,\,\,\,\,\,\, \times {\mathop{\rm conj}\nolimits} {\left[ {{{\left\langle {\Gamma _{j,k}^{{\rm{metcorr }}}{{\rm{e}}^{i{{2\pi } \over \lambda }[u\Delta {\rm{RA}} + \upsilon \Delta {\rm{Dec}}]}}} \right\rangle }_{{\rm{unswapped }}}}} \right]^{{1 \over 2}}}. \cr} $](/articles/aa/full_html/2024/07/aa49504-24/aa49504-24-eq41.png) (29)
(29)
Through the use of the complex-conjugate for the second element, the metrology zero-point vanishes. For the correct astrom-etry, this quantity should be a purely real number. We therefore calculated an associated χ2 quantity from the imaginary part of this coherent flux,
![${\chi ^2}(\Delta {\rm{RA}},\Delta {\rm{Dec}}) = \sum\limits_{(j,k),\lambda } {{{{\mathop{\rm Im}\nolimits} \left[ {{\Gamma _{j,k}}(\Delta {\rm{RA}},\Delta {\rm{Dec}})(\lambda )} \right]} \over {{\sigma _{j,k}}(\Delta {\rm{RA}},\Delta {\rm{Dec}})(\lambda )}}} ,$](/articles/aa/full_html/2024/07/aa49504-24/aa49504-24-eq42.png) (30)
(30)
with σj,k (ΔRA, ΔDec) the error bar on the imaginary part of Γ propagated from the pipeline-reported error bars. The best astrometric guess was then taken as the location of the χ2 minimum,
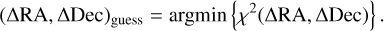 (31)
(31)
The metrology zero-point was then calculated using Eq. (28), using this best guess to re-centre and average the coherent fluxes. When the zero-point was known, we subtracted it from each individual exposure, and the remaining data reduction followed the same steps as for the on-axis case, keeping in mind that the sign of all astrometric measurements from the swapped observations is reversed to account for the fact that these observations measure the position of the FT target relative to the SC target. This yielded one astrometric measurement per exposure file, and the final astrometric estimate was taken as the mean of the series, with the associated error bars calculated from the empirical covariance using Eq. (26).
5 Results
5.1 Vetted selection of binary calibrators
Twelve of the 21 targets that were parts of the AT calibration programme to find new potential binary calibrators were observed (see Table 1). Our χ2 closure-phase tests excluded WDSJ02407+2637 and WDSJ05417-0254, with respective maximum 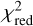 values of 63 and 7.8 among their two visual components. These values are clear signs of a higher multiplicity, which justifies their exclusion from the final list.
values of 63 and 7.8 among their two visual components. These values are clear signs of a higher multiplicity, which justifies their exclusion from the final list.
Overall, the calibration programme provided a set of 10 new binary calibrators. With the addition of the 3 calibrators already known at the start of the ExoGRAVITY Large Programme, this means that 13 binary calibrators in total are available for dual-field or off-axis observations with VLTI/GRAVITY on the UTs. The complete list of vetted binary calibrators with coordinates and magnitudes, is provided in Table 2.
In Fig. 5, we show the evolution of the elevation of these vetted calibrators as a function of sidereal time for a complete rotation of the Earth (24h). We also give the evolution of the number of calibrators at an elevation of at least 30 deg, which shows that our list always guarantees that two calibrators at least are available at an elevation >30deg (airmass < 2) at any point in time. This should guarantee the feasibility of all upcoming programmes using the dual-field mode of GRAVITY on the UTs.
5.2 Astrometry
The astrometric measurements obtained on the vetted binaries with the ATs and UTs are presented in Table B.1. To obtain the best possible constraints on the orbits of our binaries, and to be able to provide estimates of the separation vector for the next few years, we added a series of measurements taken from the WDS catalogue to our GRAVITY astrometric measurements.
Our vetted binaries are all present in the catalogue, which provides astrometric measurements obtained with a mixture of instruments, some dating back to the nineteenth century. The catalogue does not provide the error bars on the individual measurements, but it does provide the best estimate of the orbit of the binary obtained from the individual astrometric measurements.
We used this best estimate of the orbit to extract an estimate of the error bars on the individual WDS data points. To do this, we first calculated the WDS astrometric residuals for all our vetted binaries, which we defined as the difference between each individual astrometric measurement available in the catalogue and position along the best estimate of the orbit at the corresponding epoch. Combining our 13 targets, we obtained a total of 1078 residuals in RA and Dec, corresponding to epochs ranging from 1843 to late 2021. We then adopted a simple linear model to describe the error bars, given by
 (32)
(32)
with t0 = 1843 the year of the first observation, and in which a was a positive coefficient describing the improvement in astro-metric precision made over the years. We assumed that a residual δRA(t) or δDec(t) obtained at epoch t in the catalogue followed a normal distribution of mean 0 (unbiased), and variance σ(t)2.
Based on this, we combined all the 1078 epochs gathered from the WDS catalogue to calculate a likelihood associated with our model of σ,
![${\cal L}[\sigma (t)] = \prod\limits_t {{1 \over {2\pi \sigma {{(t)}^2}}}} \exp \left( { - {{\delta {\rm{R}}{{\rm{A}}^2} + \delta {\mathop{\rm Dec}\nolimits} {{(t)}^2}} \over {2\sigma {{(t)}^2}}}} \right)$](/articles/aa/full_html/2024/07/aa49504-24/aa49504-24-eq46.png) (33)
(33)
and ignoring the 2π factors in the normalization, we calculated the log-likelihood of the model using
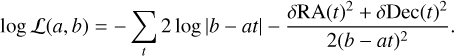 (34)
(34)
We maximised this log-likelihood to obtain the best estimates of the parameters a and b, which in turn provided our linear rule to calculate a value of σ for all the individual measurements. We obtained
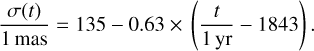 (35)
(35)
 |
Fig. 5 Observability of the dual-field calibrators as a function of mean sidereal time at Paranal. The red curves (left axis) show the elevation for each vetted binary calibrator from Table 2. The blue curve (right axis) shows the number of calibrators at above 30 deg of elevation. |
5.3 Orbit fit and astrometric predictions
We used orbitize! (Blunt et al. 2020) to fit the relative motion of our vetted binaries. For each of them, we gathered all the astrometric measurements available in the WDS catalogue, to which we associated error bars using Eq. (35). We also added our own GRAVITY astrometric measurements, as reported in Table B.1. Table 3 gives a brief overview of the measurements available on each target.
We used the parallel-tempering affine-invariant (Foreman-Mackey et al. 2013; Vousden et al. 2016) MCMC sampler available in orbitize! to determine the posterior distributions of the orbital parameters. Except for the total mass of the system Mtot and the parallax π, we used the default priors in orbitize!. The system masses estimated from the combination of the orbital parameters available in the WDS catalogue and the Gaia parallax measurements typically range from 2 to 5 M⊙, except for WDJ05055+1948, for which the mass reaches 200 M⊙, likely because the poor orbital coverage leads to an extremely eccentric orbital solution (e = 0.97). Consequently, we ignored the value of WDJ05055+1948, which is most probably highly uncertain, and set relatively loose Gaussian priors of Mtot = 4 ± 4 for all targets. Our resulting posteriors, including for WDJ05055+1948, are all better constrained than this prior, which should therefore not be a cause of bias in our orbit fits. For the parallax, we based our priors on the Gaia DR3 measurements Gaia Collaboration (2021). For systems that remained unresolved with Gaia and for which only one value of the parallax was available, we adopted a Gaussian prior centred on the Gaia measurement, and with a standard-deviation corresponding to the reported measurement error. For systems on which measurements were available for each component, we took the average of the two as our mean value for the Gaussian prior, and we used the half difference of the two components as our prior standard deviation.
The MCMC runs were all set up with 100 walkers and 20 temperatures for a burn-in phase of 300 000 steps, followed by an additional 600 000 steps to approximate the posterior distributions, keeping only one-tenth of the samples. The resulting orbital parameter estimates are reported in Table C.1, and Fig. C.1 gives a visual overview of these posteriors for each target. In particular, Fig. C.1 clearly illustrate the very large disparities in terms of orbital coverage, which inevitably results in very large disparities in terms of orbital constraints.
From these orbital posteriors, we also calculated a set of astrometric predictions that can be used for future observations. To obtain these predictions, we calculated the predicted astrom-etry for each orbit of our posteriors at the beginning of 2024, 2025, and 2026. We report the mean values and the error estimates in Table 4, but we strongly encourage the use of the tool whereistheplanet1 to calculate predicted separations, as we plan to update the orbit posteriors to improve predictions when new observations become available. This tool also seamlessly integrates with p2Gravity2 to further simplify the process of preparing observing material for VLTI/GRAVITY. All the vetted calibrators of Table 2 were integrated in whereistheplanet.
Summary of the astrometric measurements used in our orbit fits.
Predicted astrometry from 2024 to 2026 for the vetted binary calibrators.
6 Conclusion
We have assembled a catalogue of 13 visual binary stars that can be used as calibrators for dual-field interferometric observations with VLTI/GRAVITY on the UTs. This catalogue guarantees that there are always two vetted calibrators at least up in the sky above Paranal.
Using a combination of our own recent high-precision astro-metric measurements together with archival measurements from the WDS catalogue, we also obtained updated orbital elements for the 13 binaries of the catalogue. From these updated orbital elements, we derived a set of predictions for the binary separation vector that can be used to point the instrument during calibration observations. The level of precision obtained on these astrometric predictions will ensure that the calibration process itself stays within the GRAVITY astrometric error budget, which allows for a pointing error of 10 mas (resulting in a 2 nm OPD error, or ≃4 µas astrometric error on a 100 m baseline; see Sect. 2.4).
Our predictions are available in Table 4 for a period from 2024 to 2026, and in whereistheplanet, which can be used to obtain a prediction at any epoch. We will endeavour to maintain the predictions generated by whereistheplanet up to date as new observations are added, and we strongly recommend the use of this tool, together with p2Gravity, for the preparation of VLTI/GRAVITY dual-field observing material.
Acknowledgements
This work is based on observations collected at the European Southern Observatory under ESO programmes 1103.B-0626, 1104.C-0651, 106.21S5.001, 108.226K.002, 108.22MY.001, 112.25GE.001, 111.24MN.001, 2104.C-5040. 5102.C-0122. SL acknowledges the support of the French Agence Nationale de la Recherche (ANR), under grant ANR-21-CE31-0017 (project Exo-VLTI). G-DM acknowledges the support of the DFG priority program SPP 1992 “Exploring the Diversity of Extrasolar Planets” (MA 9185/1) and from the Swiss National Science Foundation under grant 200021_204847 “PlanetsInTime”. Parts of this work have been carried out within the framework of the NCCR PlanetS supported by the Swiss National Science Foundation. A.A. and P.G. were supported by Fundação para a Ciência e a Tecnologia, with grants reference UIDB/00099/2020 and PTDC/FIS-AST/7002/2020. This research has made use of the Jean-Marie Mariotti Center Aspro service (http://www.jminc.fr/aspro).
Appendix A Observing logs
Observing log with the Auxiliary Telescopes.
Observing log with the Unit Telescopes.
Appendix B Astrometry
Astrometric measurements on the vetted binary calibrators.
Appendix C Orbit estimates
Orbital parameters for our 13 UT binary calibrators. Notes: For each parameter, we give the best estimate, which corre sponds to the mode of the posterior distribution, as well as the 68% confidence interval reported by orbitize!. The time of periapsis (tau) is given in units of orbital period from the reference epoch 58849 MJD.
 |
Fig. C.1 Posterior orbits for each of the 13 vetted calibrators from Table 2. Each panel illustrates a set of 20 orbits drawn from our posterior distributions of orbital parameters (in blue), as well as the coverage offered by our combined WDS (yellow bubbles) and GRAVITY (red crosses) astrometry. The grey star provides a visual reference of the (0, 0) coordinate origin. For each target, an inset shows the details of the GRAVITY measurements. |
References
- Blunt, S., Wang, J. J., Angelo, I., et al. 2020, AJ, 159, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillessen, S., Lippa, M., Eisenhauer, F., et al. 2012, in Optical and Infrared Interferometry III, 8445 (International Society for Optics and Photonics), 84451O [NASA ADS] [CrossRef] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2017, A&A, 602, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2018a, A&A, 615, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2018b, A&A, 618, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2019a, A&A, 625, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Lacour, S., et al.) 2019b, A&A, 623, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2020a, A&A, 636, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Bauböck, M., et al.) 2020b, A&A, 635, A143 [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Nowak, M., et al.) 2020c, A&A, 633, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Pfuhl, O., et al.) 2020d, A&A, 634, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2022, A&A, 657, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacour, S., Eisenhauer, F., Gillessen, S., et al. 2014, A&A, 567, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacour, S., Dembet, R., Abuter, R., et al. 2019, A&A, 624, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lapeyrere, V., Kervella, P., Lacour, S., et al. 2014, in Optical and Infrared Interferometry IV, 9146 (SPIE), 735 [Google Scholar]
- Nowak, M., Lacour, S., Lagrange, A.-M., et al. 2020, A&A, 642, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nowak, M., Lacour, S., Abuter, R., et al. 2024, A&A, 684, A184 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pourré, N., Winterhalder, T. O., Le Bouquin, J.-B., et al. 2024, A&A, 686, A258 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vousden, W. D., Farr, W. M., & Mandel, I. 2016, MNRAS, 455, 1919 [NASA ADS] [CrossRef] [Google Scholar]
Available at https://github.com/semaphoreP/whereistheplanet
Available at https://github.com/f4hzg/p2Gravity
All Tables
Results of the  multiplicity test performed on the closure-phase for the first epoch of each target part of the calibration programme.
multiplicity test performed on the closure-phase for the first epoch of each target part of the calibration programme.
Orbital parameters for our 13 UT binary calibrators. Notes: For each parameter, we give the best estimate, which corre sponds to the mode of the posterior distribution, as well as the 68% confidence interval reported by orbitize!. The time of periapsis (tau) is given in units of orbital period from the reference epoch 58849 MJD.
All Figures
 |
Fig. 1 Map representing the on-sky coverage provided by the 13 vetted binary calibrators presented in this work. The shaded regions show the number of available calibrators within 45deg. |
| In the text | |
 |
Fig. 2 Block diagram showing the different elements contributing to the total OPL within the two channels of the GRAVITY when used in dual-field mode. |
| In the text | |
 |
Fig. 3 Illustration of the dual-field on-axis observing strategy. This strategy is used to measure the astrometry of a scientific target relative to a fringe-tracking target. The left panel illustrates the position of the two fibres in the instrument, with the use of a beam-splitter to separate the field. The right panel illustrates the resulting position of the two fibres on-sky. |
| In the text | |
 |
Fig. 4 Similar to Fig. 3, but illustrating the dual-field off-axis observing strategy. In this case, a roof-mirror is used to separate the field, and two sequences are required. In the science sequence, the FT fibre is positioned on an appropriately selected FT target, whereas the SC fibre is centred on the science target. In the calibration sequence, a binary star is observed multiple times while swapping the position of the two fibres. If the science target is appropriate for fringe-tracking, the calibration can be performed on the science target itself. If this is not the case, the calibration sequence must be performed on a separate binary calibrator. |
| In the text | |
 |
Fig. 5 Observability of the dual-field calibrators as a function of mean sidereal time at Paranal. The red curves (left axis) show the elevation for each vetted binary calibrator from Table 2. The blue curve (right axis) shows the number of calibrators at above 30 deg of elevation. |
| In the text | |
 |
Fig. C.1 Posterior orbits for each of the 13 vetted calibrators from Table 2. Each panel illustrates a set of 20 orbits drawn from our posterior distributions of orbital parameters (in blue), as well as the coverage offered by our combined WDS (yellow bubbles) and GRAVITY (red crosses) astrometry. The grey star provides a visual reference of the (0, 0) coordinate origin. For each target, an inset shows the details of the GRAVITY measurements. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


