| Issue |
A&A
Volume 687, July 2024
|
|
|---|---|---|
| Article Number | A262 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202349137 | |
| Published online | 22 July 2024 | |
How planets grow by pebble accretion
V. Silicate rainout delays the contraction of sub-Neptunes
1
Astrophysics Research Center (ARCO), Department of Natural Sciences, The Open University of Israel,
Raanana
4353701,
Israel
e-mail: vazan@openu.ac.il
2
Department of Astronomy, Tsinghua University,
30 Shuangqing Rd,
100084
Beijing,
PR
China
3
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge
CB3 0HA,
UK
Received:
31
December
2023
Accepted:
16
May
2024
The characterization of super-Earth- to Neptune-sized exoplanets relies heavily on our understanding of their formation and evolution. In this study, we link a model of planet formation by pebble accretion to the planets’ long-term observational properties by calculating the interior evolution, starting from the dissipation of the protoplanetary disk. We investigate the evolution of the interior structure in 5–20 M⊕ planets, accounting for silicate redistribution caused by convective mixing, rainout (condensation and settling), and mass loss. Specifically, we have followed the fate of the hot silicate vapor that remained in the planet’s envelope after planet formation as the planet cools. We find that disk dissipation is followed by a rapid contraction of the envelope from the Hill or Bondi radius to about one-tenth of that size within 10 Myr. Subsequent cooling leads to substantial growth of the planetary core through silicate rainout accompanied by inflated radii, in comparison to the standard models of planets that formed with core-envelope structure. We examined the dependence of rainout on the planet’s envelope mass, on the distance from its host star, on its silicate mass, and on the atmospheric opacity. We find that the population of planets that formed with polluted envelopes can be roughly divided into three groups based on the mass of their gas envelopes: bare rocky cores that have shed their envelopes, super-Earth planets with a core-envelope structure, and Neptune-like planets with diluted cores that undergo gradual rainout. For polluted planets that formed with envelope masses below 0.4 M⊕, we anticipate that the inflation of the planet’s radius caused by rainout will enhance the mass loss by a factor of 2–8 compared to planets with unpolluted envelopes. Our model bridges the gap between the predicted composition gradients in massive planets and the core-envelope structure in smaller planets.
Key words: planets and satellites: atmospheres / planets and satellites: composition / planets and satellites: formation / planets and satellites: interiors / planets and satellites: physical evolution
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The mass-radius relation of exoplanets (i.e., the bulk density) depends on their composition, but also on the distribution of the composition in the interior. Here, the mixtures of elements are usually more compact than in the separate composition layers (e.g., Baraffe et al. 2008; Fortney et al. 2013; Dorn & Lichtenberg 2021). In particular, the mass-radius relation of silicate-dominated planets with only a few percent of gas is more sensitive to the thermal evolution of the metal-rich interior (Lopez & Fortney 2014; Vazan et al. 2018a,b) and to the mean molecular weight (pollution) of the gas envelope.
Observations from online and upcoming facilities such as the James Webb Space Telescope (JWST, Greene et al. 2016), PLATO (Planetary Transits and Oscillations of stars, Rauer et al. 2014), and ARIEL (Atmospheric Remote-sensing Infrared Exoplanet Large-survey, Tinetti et al. 2018) space telescopes are expected to provide high-quality data as well as improved statistics for stellar ages (PLATO) and atmospheric compositions (ARIEL and JWST). One way to shed light on the nature of these planets is to study the sequence of planet formation and long-term thermal evolution. While planet formation sets the initial mass and composition of the planet, the long-term evolution connects it to the observed properties.
Planet formation models that follow the solid deposition in the interior show that most of the accreted metals are distributed in the gas envelope when the planet exceeds about 2 M⊕ as a result of solid-gas interaction in the growing envelope (Bodenheimer et al. 2018; Brouwers et al. 2018; Valletta & Helled 2019; Brouwers & Ormel 2020; Ormel et al. 2021; Steinmeyer et al. 2023). Thus, the formation-evolution of 5–20 M⊕ rocky planets involves the evolution of polluted envelopes, usually with a nonuniform distribution of metals in it.
The question arises whether this nonuniform structure is stable on the timescales at which these planets are observed, that is, several billion years, or whether the internal state has been rearranged into a standard core-envelope structure (“standard” refers to how these planets are typically perceived) or something in between (i.e., compositional layers). Processes in the interior such as mixing or settling redistribute matter along with the thermal evolution of the planet. If convection is vigorous convective-mixing can erode the initial metal distribution and homogenize it (Vazan et al. 2015). Alternatively, progressive cooling can lead to oversaturation in the polluted envelope and rainout (condensation and settling) of silicate droplets to deeper, hotter layers (Brouwers & Ormel 2020). Thus, the planetary structure directly after formation is not necessarily the present-day structure1.
Evolution models commonly use arbitrary initial conditions. While this is a fair assumption for interior models with two to three homogeneous composition layers, it cannot hold for the evolution of planets with a nonuniform distribution of the composition. When the composition in planets after their formation is not uniformly distributed, evolution is not adiabatic (Ledoux 1947; Rosenblum et al. 2011), and hence, thermal evolution is sensitive to the initial conditions (i.e., formation outcomes).
In Ormel et al. (2021), we found that rocky 5–20 M⊕ planets formed by pebble accretion typically have the structure of a small rocky core that is surrounded by a silicate vapor composition gradient and a vapor-rich (>40%) convective envelope on top of it. In that work, Phase IV was defined as the phase in which the protoplanetary disk dissipates, the outer layers of the atmosphere may evaporate, and in which progressive cooling may cause the vapor to rain out. Here, we aim to model this phase.
In a recent letter of Vazan & Ormel (2023), we showed that condensation and settling (rainout) of silicates in the envelope of sub-Neptune planets have a noticeable effect on their observed radii. In this paper, we generalize this study to a wider range of planetary masses and conditions, and we denote the trends in the evolution of polluted envelopes. We calculate the long-term properties of 5–20 M⊕ rocky planets composed of silicate, hydrogen, and helium that formed via pebble accretion. The model contains (1) the initial interior structure from the planet formation model, (2) the thermal evolution, including relevant heat transport mechanisms and energy sources, (3) the structural evolution (material transports) by convective mixing and settling, and (4) gas mass-loss from young atmospheres.
 |
Fig. 1 Post-formation outcome of the interior structure of planets assembled by pebble accretion (Ormel et al. 2021). We show the silicate mass fraction distribution (black) and the envelope temperature profile (red) in planets of 5 M⊕ (left), 10 M⊕ (middle), and 20 M⊕ (right), formed at 0.2 AU from a Sun-like star. |
2 Method
2.1 Formation-evolution interface
Our initial models are the resulting interior models of Ormel et al. (2021) for planet formation by rocky pebble accretion. At the end of the formation phase, the young planet is embedded in the disk, and its radius is about 100 Earth radii (Bondi radius / Hill radius). The interior of the young planet is typically structured in four stable layers: a small rocky core (1–2 M⊕), a silicate vapor composition gradient, a uniform silicate-rich convective envelope, and a thin silicate-poor saturated atmosphere.
In Fig. 1 we present the silicate distribution (Z) and temperature profile of planets at the end of their formation phase. The formation models in the figure were calculated for accretion of 1 mm rocky (SiO2) pebbles at a solid accretion rate of 10−5 M⊕ yr−1, where opacity in the formation phase is of gas and pebbles. In Sec. 3.6 we discuss the effect of varying these parameters on the results. The parameters from the formation model that we used to calculate the evolution were the interior profile of temperature, density, luminosity, entropy, and composition (species mass fraction).
In our simulation, the transition from disk phase to postdisk long-term evolution is sharp because the formation outcome model is the input of the evolution model. Specifically, the pressure at the outer boundary is now given by the photospheric conditions, which is significantly lower than the disk pressure. The temperature at the outer boundary is determined by the distance from the (Sun-like) star, which is unchanged between formation and evolution.
For consistency of the thermal evolution model with the planet formation model, we used the same set of equations of state for hydrogen and helium (Saumon et al. 1995) and SiO2 rock (Faik et al. 2018). Irradiation by the parent star is for the same location as in the disk phase (i.e., no migration). We evolved formation models of planets at distances of 0.2 and 1 AU from a Sun-like star2. The number of mass grid points was reduced by interpolation to 500, which is optimal for the thermal evolution code runs.
2.2 Thermal evolution model
The interior thermal evolution code is a Henyey-like3 code that solves the set of structure-evolution equations simultaneously on an adaptive grid of mass from the center to the surface (Kovetz et al. 2009). Thus, the thermal state of the deep silicate core, including its compression and cooling, is an integral part of the evolution scheme. At each mass grid-point, we obtained a solution for the equations of continuity (Eq. (1)), hydrostatic equilibrium (Eq. (2)), energy transport via convection, radiation, and conduction (Eq. (3a)), energy balance (Eq. (5)), and composition flux (Eq. (5)),
![$\[\frac{\partial}{\partial m} \frac{4 \pi}{3} r^3=\frac{1}{\rho}\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq1.png) (1)
(1)
![$\[\frac{\partial p}{\partial m}=-\frac{G m}{4 \pi r^4}\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq2.png) (2)
(2)
![$\[\frac{\partial \ln T}{\partial m}=\nabla \frac{\partial \ln p}{\partial m},\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq3.png) (3a)
(3a)
where the symbols r, m, ρ, p, and T are the radius, mass, density, pressure, and temperature, respectively. ∇ = d ln T/d ln P is the temperature gradient determined by the heat transport mechanism according to the Ledoux convection criterion (Ledoux 1947),
![$\[\nabla=\left\{\begin{array}{ll}\nabla_{\mathrm{R}} & \text { for } \nabla_{\mathrm{R}} \leq \nabla_{\mathrm{ad}}+\nabla_{\mathrm{X}} \\\nabla_{\mathrm{MLR}} & \text { for } \nabla_{\mathrm{R}}>\nabla_{\mathrm{ad}}+\nabla_{\mathrm{X}}\end{array}\right. \text {. }\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq4.png) (3b)
(3b)
∇ad is the adiabatic gradient,
![$\[\nabla_{\mathrm{ad}}=\left.\frac{\mathrm{d} \ln T}{\mathrm{~d} \ln p}\right|_s,\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq5.png) (3c)
(3c)
∇X is the composition-dependent gradient,
![$\[\nabla_X=\sum_j \frac{\partial \ln T}{\partial X_j} \frac{\mathrm{d} X_j}{\mathrm{~d} \ln p},\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq6.png) (3d)
(3d)
where Xj is mass fraction of the jth species.
∇R is the radiative (and/or conductive) temperature gradient,
![$\[\nabla_{\mathrm{R}}=\frac{\kappa_{\mathrm{op}} L}{4 \pi c G m} \frac{p}{4 p_R},\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq7.png) (3e)
(3e)
pR is the radiation pressure, L is the luminosity, and κop is the harmonic mean of the radiative (κrad) and conductive (κcond) opacities,
![$\[\kappa_{\mathrm{op}}=\left(\frac{1}{\kappa_{\mathrm{rad}}}+\frac{1}{\kappa_{\text {cond }}}\right)^{-1}.\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq8.png) (3f)
(3f)
Grains or pebbles are not expected to remain in the upper envelope after the formation phase (Brouwers et al. 2021; Movshovitz et al. 2010; Ormel 2014; Mordasini 2014), and therefore, we used the radiative opacity of Freedman et al. (2014) for grain-free atmospheres. The opacity in each layer was calculated for the given pressure, temperature, and metallicity values of the layer. However, because in practice, the atmospheric metallicity is composed of various elements and not solely of the silicate vapor that we consider in this work, we applied the condition
![$\[Z_{\text {radiative }}=\max \left(Z, Z_{\text {min }}\right)\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq9.png) (4)
(4)
as the metallicity for which the Freedman opacities were calculated. We took Zmin to be equal to the solar metallicity by default. While Zmin was fixed throughout the simulation, Z was calculated based on the L-V curve (Eq. (9)). Thus, in layers in which the silicate vapor fraction drops below solar, the solar metallicity was adopted to calculate the opacity. Conduction is governed by the silicate component because molecular hydrogen is a poor conductor (French et al. 2012), and the pressure temperature in the interiors of super-Earths is below the metallic hydrogen level. A conductive opacity was obtained by extrapolation of Earth rock parameters to high pressure and temperature, as described in the Appendix B.
∇MLR is the temperature gradient calculated by the mixing-length recipe (MLR) (Mihalas 1978; Kippenhahn et al. 2013), where turbulent Rayleigh-Bénard convection is simulated in 1D. We took the size of a convective cell to be half the local scale height4.
The energy balance in the interior was
![$\[\frac{\partial u}{\partial t}+p \frac{\partial}{\partial t} \frac{1}{\rho}=q-\frac{\partial L}{\partial m},\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq10.png) (5)
(5)
where specific energy (u), contraction, and contribution of radiogenic heating in the rock (q) were considered.
Material transport by convective mixing was calculated as a diffusive-convective flux of particles (Kippenhahn et al. 2013),
![$\[\frac{\partial Y_j}{\partial t}=\frac{\partial}{\partial m} F_j,\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq11.png) (6a)
(6a)
where Yj = Xj/Aj is the number fraction of the jth element, namely, the mass fractions divided by the atomic mass of the element, and Fj is the particle flux of the jth element,
![$\[F_j=\sigma_j \frac{\partial Y_j}{\partial m}\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq12.png) (6b)
(6b)
![$\[\sigma_j=\left(\frac{\mathrm{d} m}{\mathrm{~d} r}\right)^2 v_c l_c.\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq13.png) (6c)
(6c)
The particle flux was determined by a diffusive coefficient σj that depends on the convection velocity υc and mixing length lc.
At every mass layer and time step, the equation of state for a mixture of the three materials (hydrogen, helium (H, He), and silicate (SiO2)) was calculated according to the additive volume law,
![$\[\rho=\left(\sum_j \frac{X_j}{\rho_j}\right)^{-1},\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq14.png) (7)
(7)
where ρj is the density of the jth species, obtained from the equation of state (H and He from Saumon et al. 1995, and SiO2 from Faik et al. 2018). The other thermodynamic properties of the mixture were calculated as described in Vazan et al. (2013).
2.2.1 Rainout model
As the planet cools, the vapor in the envelope becomes oversaturated, and part of it condensates and settles down to deeper hotter (undersaturated) layers. The process sweeps the silicate from the outer layers downward and gives rise to late core growth. The rainout phase terminates when all silicates have settled into a silicate core surrounded by a metal-poor hydrogen-helium envelope5. When the core-envelope structure was established, the structure was static, and further cooling did not affect the distribution of the composition. We defined the rainout timescale train as the time from disk dissipation until all silicates have settled and a core-envelope structure has been established.
Settling from an supersaturated layer into a deeper undersaturated layer is assumed to be instantaneous because the settling timescale of a silicate droplet is orders of magnitude shorter than the evolution timescale (see Sec. 2.4 below). For the same reason, we excluded the possibility of supersaturation. We modeled rainout numerically by removing the excess of silicate (the amount above the saturation metallicity) from a layer i to the layer below it i − 1. Between time steps t and t + 1, whenever the pressure temperature in the layer (pi, Ti) is such that ![$\[Z_i>Z_{\text {sat }\left(p_i, T_i\right)}\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq15.png) we took
we took
![$\[Z_i^{t+1}=Z_{\mathrm{sat}\left(p_i, T_i\right)},\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq16.png) (8a)
(8a)
and the excess amount of silicate ![$\[\Delta m_Z=\left(Z_i-Z_{\mathrm{sat}\left(\mathrm{p}_{\mathrm{i}}, \mathrm{T}_{\mathrm{i}}\right)}\right) m_i\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq17.png) was moved from layer i to the layer below it, enhancing its metallicity,
was moved from layer i to the layer below it, enhancing its metallicity,
![$\[Z_{i-1}^{t+1}=\frac{Z_{i-1}^t m_{i-1}+\Delta m_Z}{m_{i-1}}.\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq18.png) (8b)
(8b)
The rainout of silicate releases energy, that is, latent heat of condensation and gravitational energy of settling. An additional energy source is the late release of the heat from the formation that is liberated after the compositional gradient has been erased. This energy is more difficult to estimate as it varies with the formation conditions. The energy change by rainout is included in our equation scheme: The energy of condensation (latent heat) was part of the equation of state, the energy of settling (gravitational energy) was obtained by the structure equations, and the release of heat from formation was calculated self-consistently by the evolution model. A schematic sketch of the rainout process and its energetic contribution to the thermal evolution appear in Fig. 2.
The saturation criterion is defined by silicate liquid-vapor (L-V) curve (e.g. Podolak et al. 1988; Bodenheimer et al. 2018; Stevenson et al. 2022). For consistency with our formation model (Ormel et al. 2021), we used the fit of the L-V curve (lower branch) of Kraus et al. (2012),
![$\[\rho_{\text {sat }}=\exp \left(a-\frac{b}{T}+\left(\frac{T}{T_{\mathrm{c}}}\right)^c\right) \text {, }\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq19.png) (9)
(9)
in cgs units, where a = 9.0945, b = 5.630 × 104 K, c = 13.26, and Tc = 5130 K.
 |
Fig. 2 Schematic picture of the rainout process in a polluted envelope. Cooling (from left to right) leads to condensation of silicate in an oversaturated outer envelope and settling of the condensed silicates to deeper undersaturated layers. Condensation and settling release energy (curly arrows), which leads to envelope extension and an inflated radius in comparison to a planet with the same composition in the core-envelope structure. Rainout ends when the planet reaches a core-envelope structure, and the radius inflation is diminished. The axes in the figure are not to scale. |
2.2.2 Atmosphere model and mass-loss estimate
The atmosphere in our model is gray and plane-parallel, and the temperature distribution was calculated for a vertical (maximal) irradiation flux, without an angle dependence of the incident flux (e.g., Guillot 2010). The temperature in the atmosphere follows
![$\[\sigma_{\mathrm{SB}} T^4(\tau)=\left(\frac{3}{4} \tau+\frac{1}{4}\right) F_E+g(\tau) \sigma_{\mathrm{SB}} T_{\mathrm{irr}}^4,\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq20.png) (10)
(10)
where τ is the optical depth, FE is the outgoing energy flux, ![$\[g(\tau)=\frac{3}{2}\left(1-\frac{1}{2} e^{-\tau}\right)\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq21.png) (Kaniel & Kovetz 1967), and σSB is Stefan-Boltzmann’s constant.
(Kaniel & Kovetz 1967), and σSB is Stefan-Boltzmann’s constant.
The atmospheric boundary is the planetary photosphere, with an optical depth τs = 1. The net outward luminosity Ls from the surface of the planet Rp is
![$\[L_s=4 \pi R_p^2 F_E=4 \pi R_p^2 \sigma_{\mathrm{SB}}\left[T^4-g\left(\tau_S\right) T_{\mathrm{irr}}^4\right].\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq22.png) (11)
(11)
The irradiation temperature as a function of the distance from the star is
![$\[T_{\mathrm{irr}}=\left(\frac{L_{\star}(1-A)}{16 \pi \sigma d^2}\right)^{1 / 4},\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq23.png) (12)
(12)
where L* is the stellar luminosity, here taken to be solar, d is the planet-star orbital separation, and A is the Bond albedo.
Mass loss was simulated as material escape from the outermost layer at a given rate. The outermost layer is poor in silicate vapor due to efficient rainout and atmospheric temperatures well below silicate evaporation (Tevap ≈ 2500 K). Therefore, the mass loss (removal) was assumed to be of hydrogen and helium.
2.3 Analytical estimate for the rainout timescale
Brouwers & Ormel (2020) analytically estimated rainout timescales for super-Earth planets. Their calculation assumed an ideal gas equation of state, constant opacity and luminosity, and adiabatic cooling. It was calculated for a three layers structure of a constant density core, an intermediate uniform polluted envelope, and an outer hydrogen envelope.
We adopted a slightly modified form of the estimate of Brouwers & Ormel (2020) for the sedimentation timescale. We estimated the energy available for rainout as
![$\[U_{\text {rain }}=\left(\frac{3 G}{5} \max \left[\frac{M_c}{r_c}, \frac{M_z}{r_z}\right]+u_{\text {lat }}\right)\left(M_z-M_c\right),\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq24.png) (13)
(13)
where Mc and Mz are the core mass and total heavy element mass, respectively, rc and rz are the radii corresponding to these masses, and ulat is the latent heat per unit mass of silicate (SiO2) condensation. Brouwers et al. (2018) and Ormel et al. (2021) showed that Mc = 2 M⊕ is an appropriate choice for the (solid) core mass after formation; the heavy element mass above this point (Mz − Mc) will be vaporized. In Eq. (13) the two cases correspond to the limits where Mz is low, in which case, the gravitational potential is determined by Mc, and where Mz is high, respectively. The sedimentation luminosity follows Brouwers & Ormel (2020)
![$\[L_{\text {rain }}=\frac{64 \pi \sigma T_{\mathrm{rcb}}^3 T_{\text {vap }}}{\kappa \rho_c} r_c^{\frac{\gamma-2}{\gamma-1}} r_B^{\frac{1}{\gamma-1}} \frac{M_c}{M_{\mathrm{xy}}} \text {, }\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq25.png) (14)
(14)
where Trcb is the radiative-convective boundary (RCB) temperature, set to be the evaporation temperature Tvap, κ is the radiative opacity at the radiative atmosphere, ρc is the core density, and Mxy is the gas (H and He) mass. r’B is the modified Bondi radius
![$\[r_B^{\prime}=\frac{\gamma-1}{\gamma} \frac{G M_p \mu}{k_{\mathrm{B}} T},\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq26.png) (15)
(15)
where γ and μ are the gas adiabatic index and mean molecular weight, respectively, and kB is Boltzmann’s constant.
From this, we calculated a rainout time
![$\[t_{\text {rain }}=\frac{U_{\text {rain }}}{L_{\text {rain }}}.\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq27.png) (16)
(16)
The values of the model parameters appear in Table 1.
Values of the parameters we used in the analytical calculations in Sect. 2.3, based on Brouwers & Ormel (2020) and Ormel et al. (2021).
2.4 Timescales of the interior evolution
To give an impression of the thermal evolution of nonuniform polluted envelopes, we provide order-of-magnitude estimates of the relevant timescales below.
Settling: for silicate vapor condensation, we assumed rain droplets sizes of ad = 0.01–1 mm, which based on Movshovitz & Podolak (2008) provides a sedimentation velocity of υsed =
![$\[10^{11} \times a_d^2\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq28.png) [m s−1], resulting in a sedimentation time (τsed = Rp/υsed) of up to 200 yr, which is orders of magnitude shorter than the Kelvin-Helmholtz times in the evolution model. Thus, it is reasonable to take settling to be an instantaneous process in our simulation.
[m s−1], resulting in a sedimentation time (τsed = Rp/υsed) of up to 200 yr, which is orders of magnitude shorter than the Kelvin-Helmholtz times in the evolution model. Thus, it is reasonable to take settling to be an instantaneous process in our simulation.Mass loss: the average mass-loss rate by XUV radiation from planets at 0.2 AU is about 10−3−10−1 M⊕ Myr−1, using a standard photoevaporation model (e.g., Owen & Wu 2013). An estimated mass-loss timescale of
![$\[\tau_{\mathrm{ML}}=M_{\mathrm{env}} / \dot{M}\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq29.png) results in a timescale of 108−1010 yr, indicating that polluted planets in the lower mass range can lose their entire envelopes.
results in a timescale of 108−1010 yr, indicating that polluted planets in the lower mass range can lose their entire envelopes.Conduction: suppression of convection in the deep interior can form thermal boundaries in which heat is transported by conduction / layered convection, where conductive transport is slower and therefore is the lower bound for heat transport. The timescale for conduction in a layer of thickness X, density ρ, and thermal conductivity K is approximately τcond = X2cpρ/K. For the heat capacity cp = 1 [KJ kg−1 K−1] and values for the density and thermal conductivity from our simulations, we obtain τcond = 10−2 × (X[m])2 [yr]. Thus, an effective thermal boundary (i.e., τcond > 109 yr) has a conductive layer of about 300 km in order to keep most of the heat from formation in the deep interior within billions of years.
Material diffusion: diffusion in the composition boundaries can be approximated by a Brownian motion with a timescale τdiff = L2/2D, where L is the length scale of the change in particle position, and D is the diffusivity. An estimate of the diffusivity by the Stokes-Einstein equation
![$\[D=\frac{k_{\mathrm{B}} T}{6 \pi \eta a}\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq30.png) for a temperature T = 5 × 103 [K], viscosity of η = 1 [Pas], and silicate (SiO2) molecular size of a = 10−9 [m] provides D ~ 10−12 [m−2 s−1]. Hence, diffusion can transport particles within τdiff = 1 Gyr to about 0.5 km. Since this upper bound of the diffusion length-scale is smaller than the conductive boundary, diffusion is expected to be negligible in the interior evolution of rock-dominated planets. A higher viscosity (than 1 Pas) and/or larger particles (than 10−9 m) result in an even slower diffusion.
for a temperature T = 5 × 103 [K], viscosity of η = 1 [Pas], and silicate (SiO2) molecular size of a = 10−9 [m] provides D ~ 10−12 [m−2 s−1]. Hence, diffusion can transport particles within τdiff = 1 Gyr to about 0.5 km. Since this upper bound of the diffusion length-scale is smaller than the conductive boundary, diffusion is expected to be negligible in the interior evolution of rock-dominated planets. A higher viscosity (than 1 Pas) and/or larger particles (than 10−9 m) result in an even slower diffusion.
3 Results
3.1 From formation to evolution
The evolution calculation started at the disk dissipation. We find that the decrease in the pressure of the outermost envelope at disk dissipation does not lead to mass loss by Roche-lobe overflow, unless the atmospheric metallicity (opacity) is unrealistically high. If the upper atmosphere maintains a high opacity for some reason, this would lead to an envelope expansion and to mass loss (Ginzburg et al. 2016). However, the efficient grain settling expected in planetary atmospheres (Brouwers et al. 2021; Movshovitz & Podolak 2008; Ormel 2014; Mordasini 2014) leads to grain-free atmospheres, and thus, to a low atmospheric metallicity. The grain-free opacity tables of Freedman et al. (2014) result in efficient cooling and no mass loss at the disk dissipation stage (see also Appendix A.2 in Vazan et al. 2018b). This finding holds for all models we tested.
After the disk dissipates, the young planet enters a phase of rapid contraction of the outer diluted envelope, in which the formed planet contracts from its Bondi / Hill radius to about a tenth of it. In Fig. 3 we show the radius contraction of the planets from Fig. 1 at 0.2 AU. For comparison, we show planets with the same composition that formed with a core-envelope structure. The initial models for the core-envelope cases are an isentropic core and envelope, with the same central temperature as in our formation models. The evolution time is shown in log scale to emphasize the early evolution right after the end of planet formation. In general, the early rapid contraction of planets with polluted envelopes is faster than that of similar planets with a core-envelope structure. The higher mean molecular weight of the polluted envelope and the slower heat transport due to the deep composition gradient (suppressed convection) lead to an accelerated early contraction of the polluted envelopes6, where the difference is greater for smaller more strongly polluted planets. The timescale for the contraction from the formation radius to about one-tenth of it varies from a few 104 years for the 5 M⊕ planets to a few 107 yr for 20 M⊕ planets. A higher opacity could potentially prolong the contraction time, but we find the required opacity increase unrealistically high.
3.2 Thermal and structural evolution
After the rapid contraction that heats up the outer envelope, the planet starts to cool. The cooling of the uniform metal-rich envelope is governed by large-scale convection, while the heat transport from the deeper interior, where the composition gradient acts as a thermal boundary, is less efficient. Consequently, the temperatures in the metal-rich envelope decreases to below the saturation level, and silicate condensates and settles (rains out) to deeper undersaturated layer (see Fig. 2). The process of rainout is a top-to-bottom process, in which a complete rainout leads to a core-envelope structure.
The core erosion and mixing upward of the silicates by convection (convective mixing) are found to be negligible in all the planets we explored in this work, for two reasons. First, the deep composition gradients from the formation are relatively steep in metal-dominated planets and are therefore stable against convection (Vazan et al. 2022). Second, inhibition of convection by composition gradients in the saturation pressure-temperature profile suppresses the redistribution of elements in saturated layers (Guillot 1995; Markham et al. 2022).
In Fig. 4 we show the silicate mass fraction (Z) profile and the temperature profile of 5 M⊕ (left), 10 M⊕ (middle), and 20 M⊕ (right) planets located at 0.2 AU. It shows that the early rapid contraction phase has only a small effect on the distribution of the composition (dotted). Despite the strong change in radius, the deep interior (composition gradient and below) stays almost unchanged in this early evolution phase. In the long-term cooling phase the distribution of the composition changes significantly through rainout. Rainout in the 10 M⊕ and 5 M⊕ planets results in a core-envelope structure before 5 Gyr and 1 Gyr, respectively. In the more massive and gas-rich 20 M⊕ planet, rainout depletes the outer layers from silicates, but a significant composition gradient is still maintained in the deep interior even after 10 Gyr.
The structure evolution (redistribution of silicate in time) by the rainout is shown in Fig. 5. The rainout of silicate in the 5 M⊕ planet starts almost immediately after disk dissipation and ends (the planet reaches core-envelope structure) after 0.38 Gyr. The process is much slower in the gas-rich 20 M⊕ planet, where silicate rainout starts after 10 Myr and is still ongoing after 10 Gyr. The 10 M⊕ planet is an intermediate case, in which the core-envelope structure is reached after 4.25 Gyr.
 |
Fig. 3 Radius evolution from disk dissipation of planets with a polluted envelope (solid) and planets with the same composition and core-envelope structure (dashed). The planets have a static interior structure (no rainout) and are located at 0.2 AU from a Sun-like star. |
3.3 Rainout dependence on envelope mass and metal mass
Planets with different envelope masses experience rainout at different times and strengths (Vazan & Ormel 2023). Consequently, the strength and duration of the radius inflation that is caused by the rainout energy release varies. When rainout is faster, the energy release is on a shorter timescale, and therefore, the radius expansion is larger. Rainout is faster and earlier in smaller planets because their envelope mass is lower, their envelope metallicity is higher, and their gravity is lower. In Fig. 6 we show the radius evolution corresponding to the 5 M⊕, 10 M⊕ and 20 M⊕ planets shown in Fig. 5. For comparison, we also plot the radius evolution of planets of the same composition, but that start off with a core-envelope structure from the outset. The 5 M⊕ planet has an early and large radius inflation by rainout, after which it becomes identical to its core-envelope twin. The 10 M⊕ and 20 M⊕ keep a moderate radius inflation in comparison to their core-envelope analog due to post-rainout heat release (10 M⊕) and ongoing rainout (20 M⊕).
Misener & Schlichting (2022) calculated a structure model for planets with polluted envelopes and found that a silicate vapor layer decreases the total radius of a planet compared to a similar planet with pure H and He envelope. While mean molecular weight and composition gradient (suppression of convection) arguments indeed lead to a smaller radius, as suggested by these authors, including the structure evolution and specifically the rainout process in thermal evolution can result in a larger radius, which is caused by the release of rainout energy: latent heat, gravitational energy, and a late release of locked formation energy.
The envelope mass, more specifically, the pressure temperature at the bottom of the envelope, plays a key role for the rainout time. Planets with light envelopes experience shorter and earlier rainout than planets with massive envelopes. In Vazan & Ormel (2023), we found that an envelope mass of approximately 0.75 M⊕ is an upper limit for sub-Neptunes to reach the core-envelope structure within 1 Gyr. This result was found for planets with 6.7 M⊕ of silicates. We repeated this calculation here for planets with different silicate masses.
In Fig. 7 we show the simulation results (points) of the rainout timescale with gas (H and He) mass for three different cases of total silicate mass (MZ): 4.3 M⊕ (blue), 6.7 M⊕ (red), and 8.9 M⊕ (green). The lines are for analytical fits and are discussed in the next section. We find that the rainout timescale increases with the total silicate mass (for the same envelope mass), and therefore, rainout takes longer in more massive planets with the same gas mass. The simulation results indicate that the change in rainout time with silicate mass is especially noticeable in planets with a low gas-to-silicate ratio. For example, rainout in a gas envelope of 1.2 M⊕ H and He takes 0.81 Gyr in a 5.5 M⊕ planet, 1.23 Gyr in an ~8 M⊕ planet, and 2.1 Gyr in an ~10 M⊕ planet. The reason is that the higher gravity in more massive planet leads to denser and hotter deep envelopes, in which silicate are undersaturated for longer times. However, when the gas mass is comparable to the metal mass, the differences between the cases diminishes. This is probably the result of the larger heat capacity of hydrogen and helium in comparison to rock.
3.4 Comparison to an analytical calculation
We next used our detailed simulation to examine the validity of the analytical results of Brouwers & Ormel (2020) on the rainout timescale. As described in Sec. 2.3, the analytical model contains assumptions on the structure (three-layer model) and its properties (ideal gas and constant parameters), and is obtained by assuming low-mass envelopes (to neglect the gravity of gas). The free parameter values were set as in Brouwers & Ormel (2020), and appear in Table 1. The fit of the analytical calculation (Eq. (16)) to the simulation results was found to be poor for planets with a significant gas fraction. The poor fit may be the result of the neglected envelope gravity, the oversimplification of gas compression (ideal gas), and constants such as opacity, core density, and evaporation temperature. However, we obtain a much better fit to the simulation data for
![$\[t_{\text {rain }}=\frac{U_{\text {rain }}}{L_{\text {rain }}} \times 0.0251\left(1+\frac{M_{x y}}{M_z}\right)^{5.2}.\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq31.png) (17)
(17)
The improved fit of Eq. (17) to the simulations is achieved by the additional term of the gas-to-silicate mass ratio, which leads to a steeper dependence of the rainout timescale on the envelope mass Mxy in comparison to the old calculation (Eq. (16)). The inverse dependence on silicate mass is less significant than the envelope mass because Mz also appears in the numerator of Eq. (16). Thus, the rainout timescale increases steeply with envelope mass and only moderately with metal mass, as found in the simulations. In Fig. 7 we also show the rainout time versus planetary gas mass calculated by the analytical approximation in Eq. (17) (curves) for the three cases of silicate mass from the numerical simulations.
An important source of the difference between the simulation and the analytical calculation is the use of ideal gas in the analytical calculation, an approximation that suffers from the overestimated compressibility and constant heat capacity. In Appendix A we present a comparison between ideal and nonideal (tabular) hydrogen and helium EoS in formation-evolution models.
Next, we derived an empirical approximation based on our simulations for a relation between the rainout time (the time from formation to a core-envelope structure) and the radius inflation at the end of the rainout time, which is the maximum radius inflation. We define the radius inflation ΔR as the excess radius of a planet undergoing rainout compared to a planet of similar mass, composition, and age that formed with a classical core-envelope structure. We find that the maximum radius inflation is approximately proportional to the inverse square-root of the rainout timescale,
![$\[\left(\frac{\Delta R}{R}\right)_{\max } \simeq A\left(\frac{t_{\mathrm{rain}}}{1 \mathrm{~Gyr}}\right)^{-0.5}.\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq32.png) (18)
(18)
For planets with a silicate mass of 4.3 M⊕, a proportion factor of A = 0.14 fits the simulation results.
We then use Eqs. (17) and (18) to obtain the maximum normalized radius inflation as a function of envelope mass in time (age). The radius inflation difference between a raining-out planet (R) and a core-envelope planet (RCE) with the same composition ![$\[\left(\frac{\Delta R}{R}=\frac{R-R_{\mathrm{CE}}}{R_{\mathrm{CE}}}\right)\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq33.png) is time dependent. For the time dependence, we fit the simulation results with a Gaussian, in which the standard deviation is the inverse of the maximum radius inflation, and the mean is the rainout timescale. The results (ΔR/R) for planets with 4.3 M⊕ of silicates are presented in Fig. 8. As we show, the radius inflation is larger and earlier for planets with lighter envelopes.
is time dependent. For the time dependence, we fit the simulation results with a Gaussian, in which the standard deviation is the inverse of the maximum radius inflation, and the mean is the rainout timescale. The results (ΔR/R) for planets with 4.3 M⊕ of silicates are presented in Fig. 8. As we show, the radius inflation is larger and earlier for planets with lighter envelopes.
 |
Fig. 4 Interior silicate mass fraction (top) and temperature profile (bottom) of 5 M⊕ (left), 10 M⊕ (middle) and 20 M⊕ (right) planets. The profiles are shown at the end of formation (dashed), after the rapid contraction (dotted), and after 1, 5, 10 Gyr (solid) for an evolution at 0.2 AU. The early contraction (from a Hill sphere to about one-tenth of it) is the cause of the gas temperature increase between the formation and the million-year curves. The increase in the central temperatures is the result of core contraction due to the constant core density assumption in the formation model. The dashed and dotted lines of the 20 M⊕ model overlap in the top right panel. |
 |
Fig. 5 Silicate mass fraction (color) distribution in radius (y-axis) and time (x-axis). The evolution is shown for 5 M⊕ (left), 10 M⊕ (middle), and 20 M⊕ (right). The x-axis has different ranges (1 Gyr, 5 Gyr, and 10 Gyr). The dotted black curves indicate Z = 0.98 and Z = 0.02 silicate mass fraction levels. The dashed red curve signifies the boundary between saturated and undersaturated regions, according to Eq. (9). A core-envelope boundary is approximately indicated by the Z = 0.98 curve. Because of the high temperatures at the core-envelope boundary, the (saturated) envelope is characterized by a silicate mass fraction of a few percent. |
 |
Fig. 6 Radius evolution of planets formed with a polluted envelope (solid) and planets with the same bulk composition, but starting with a core-envelope (CE) structure from the outset (dashed). The measured rainout time is determined by the time at which the classical core-envelope structure is established (dotted vertical line). Rainout in the polluted envelopes causes radius inflation in comparison to planets formed with a core envelope. The radius inflation is shorter and more prominent in smaller planets. All planets are located at 0.2 AU from a Sun-like star. |
 |
Fig. 7 Rainout time as a function of gas (H and He) mass for three cases of silicate mass: MZ = 4.3 M⊕ (blue), MZ = 6.7 M⊕ (red), and MZ = 8.9 M⊕ (green). We show numerical simulations (points) and analytical calculation (curves). The analytical model is according to Eq. (17), and the parameters appear in Table 1. |
 |
Fig. 8 Radius inflation, ΔR/R = (R − RCE)/RCE, as a function of age (x-axis) and envelope mass (y-axis) for planets with 4.3 M⊕ of silicates. For illustrative clarity, we limited the scale of ΔR/R to 0.25 (red), but in reality, ΔR/R reaches values up to 1. The dashed curve signifies the maximum radius inflation for each envelope mass. |
3.5 Gas escape enhancement by rainout: sedimentation-powered mass loss
In the case of a static (nonevolving) interior, the polluted envelopes may diminish mass loss by photoevaporation because of the higher envelope density and smaller radius. However, in an evolving interior, the energy release by the rainout processes enhances the mass loss through radius inflation. Mass loss by photoevaporation is commonly modeled by the energy-limited approach (e.g. Lammer et al. 2003; Owen & Wu 2013; Lopez & Fortney 2013), where planetary evaporation depends on the radius to the third power. From Rogers & Owen (2021),
![$\[\dot{M}=\eta \frac{\pi R_p^3 L_{\mathrm{XUV}}}{4 \pi d^2 G M_p},\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq34.png) (19)
(19)
where η = 0.17(υesc/25 [km s−1])−0.4 is the efficiency coefficient, depending on the escape velocity (υesc), and the XUV luminosity LXUV from a Sun-like star is
![$\[L_{\mathrm{XUV}}= \begin{cases}10^{-3.5} L_{\odot} & \text { for } t<100 \mathrm{~Myr} \\ 10^{-3.5} L_{\odot}\left(\frac{t}{100 \mathrm{~Myr}}\right)^{-1.5} & \text { for } t \geq 100 \mathrm{~Myr}.\end{cases}\]$](/articles/aa/full_html/2024/07/aa49137-23/aa49137-23-eq35.png) (20)
(20)
According to the equations above, a larger radius as a result of radius inflation by rainout is expected to significantly increase the mass-loss rate, especially when the inflation takes place early on. The other way around also holds, however: the loss of hydrogen from the surface of planets with polluted envelopes accelerates rainout via two channels. It increases the silicate-to-gas ratio in the outer envelope and thus increasing oversaturation, and it removes part of the gas blanket and thus hastens the cooling. Therefore, when the rainout timescale overlaps with the period of strong stellar XUV radiation, the mass loss by photoevaporation, which is proportional to radius cube (Eq. (19)), grows significantly, boosting more radius inflation, which in turn enhances the mass loss. Consequently, close-in and less massive planets with polluted envelopes are more vulnerable to enhanced mass loss by photoevaporation.
Figure 9 is a zoom-in of the first 1 Gyr of Fig. 8 in log time (x-axis). Clearly, super-Earth planets with envelope masses below 0.4 M⊕ experience a major envelope expansion by rainout during the first 100 million years. This is when the XUV-driven photoevaporation rates peak, then enhanced by sedimentation-powered mass loss. The radius inflation of raining polluted envelopes that is larger by 0.25 (ΔR/R = 0.25) doubles the mass-loss rate, and a larger radius inflation of ΔR/R = 1 translates into eight times more mass loss in comparison to a similar planet with an initial core-envelope structure. The enhanced sedimentation-powered mass loss caused by the mutual effects of mass loss and rainout may end in a complete strip of the gas envelope in planets that were born with polluted low-mass envelopes. A further investigation would require coupling the two processes to examine the mutual effect in detail.
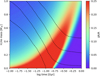 |
Fig. 9 Zoom-in on Fig. 8 in the first 1 Gyr in log timescale. Planets with significant radius inflation in the first 0.1 Gyr are vulnerable to mass loss by photoevaporation. As in Fig. 8, red signifies ΔR/R in the range of 0.25–1. The dashed curves show examples of estimated mass-loss tracks at 0.2 AU. |
3.6 Model parameter dependence
Atmospheric metallicity has a major role in the cooling of gaseous envelopes by changing the radiative opacity in the outer envelope, which acts as the bottleneck for the planet cooling. Consequently, it influences the silicate rainout timescale. The higher the atmospheric opacity, the longer the rainout time. Opacity can be affected by atmospheric phenomena such as cloud formation or haze formation (Ormel & Min 2019; Poser & Redmer 2024). To explore the dependence of the atmospheric opacity on our results, we modified the outer atmospheric radiative metallicity. Specifically, we obtained the radiative opacity change by adjusting the Zmin parameter in Eq. (4) to values between 0.1 andc10 times solar. As is shown in Fig. 10, changing the atmosphere metallicity by two orders of magnitude (between 0.1 and 10 times solar) changes the rainout time by an order of magnitude. We remark that although we formulated the opacity in terms of a metallicity Zradiative, adjusting the opacity by changing the value of Zmin has no bearing on the actual metallicity (composition) and overall equation of state. In this way, adjusting Zmin will directly inform us how the opacity affects the rainout timescale.
The effect of the distance from the star on the results is weak and varies with mass. In massive planets and/or massive envelopes, the distance from the parent star has a negligible effect on the interior evolution and on the rainout process because the compressed gas density is mainly determined by gravity. In planets with light envelopes, the irradiation effect can be noticeable. We find that the 5 M⊕ planet shown in Fig. 5 experiences a 10% shorter rainout phase at 1 AU than at 0.2 AU. This comparison is for the same planetary mass and composition. The indirect effect of irradiation via mass loss is ignored in this comparison (see Sec. 3.5 for mass-loss effects).
We next examined the effect of planet formation conditions on the results, such as the pebble accretion rate and the pebble size. The conditions of planet formation shape the initial temperature profile and metal distribution, but varying the formation parameters within the range of the Ormel et al. (2021) model has only a weak effect on the long-term evolution. The reason is that planet formation parameters, unlike opacity and distance from the star, influence the long-term cooling rate only very little.
 |
Fig. 10 Rainout time as a function of atmospheric radiative opacity (Zmin in Eq. (4)) based on the opacity formalism of Freedman et al. (2014). The cases show a 5 M⊕ planet with 4.3 M⊕ of silicates and 0.7 M⊕ gas. The points are simulations results, and the larger point is the standard (solar metallicity) case. |
3.7 Overview and implications for the interpretation of observations
Our results indicate that rocky exoplanets with a super-Earth-to-Neptune mass can be classified into three groups regarding their interior structures, mainly depending on their mass and in particular, their gas (H and He) mass, as listed below.
Planets that lost their H and He envelope due to sedimentation-powered mass loss and/or other mass-loss mechanisms.
Planets that retain a few percent of gas (by mass) after the mass-loss stage, whose interiors have since evolved to a core-envelope structure.
Planets with thick envelopes whose interiors are still characterized by a composition gradient(s).
In Fig. 11 we show a schematic picture of the thermal and structural evolution of the planets that retain (part of) their primordial envelopes. The time and mass axes are for our standard set of parameters, and they can vary with parameters as described in Sec. 3.6.
The evolution of planets with polluted envelopes and the subsequent radius inflation by the rainout provides an alternative for the interpretation of the planet radius-mass relation. The observed mass-radius relation when the planet is raining out is overestimated in the standard model (see Vazan & Ormel 2023 for exoplanet examples). The main parameter that determines whether rainout takes place in an observed planet is its age. Although currently, many of the observed planets lack good age estimates, in a few years, a much larger and precise database of stellar ages will be available due to the PLATO mission (Rauer et al. 2014), which will allow us to examine the temporal dimension of the mass-radius relation.
The heat flux generated by the interior of a planet experiencing rainout is significantly higher than in the standard (unpolluted) case because of the release of rainout energy (potential energy, latent heat, and formation energy). Certain chemical abundances, such as the C/H ratio in the visible atmosphere of a planet, may provide clues about the cooling history of the planet and its effective temperature (Fortney et al. 2020). Observations by JWST (Greene et al. 2016) and ARIEL (Tinetti et al. 2018) are expected to obtain spectra of a wide range of planetary atmospheres, and will help us identify planets that formed with polluted envelopes.
The radius inflation caused by the rainout from polluted envelopes can explain the puffiness of observed close-in young planets in certain conditions, such as the 0.5 Gyr old Kepler-51 system (Masuda 2014; Libby-Roberts et al. 2020). In this scenario, the mutual effect of mass loss and rainout results in a significant radius inflation that peaks at the observed age. The conditions to preform such evolutionary tracks require relatively high atmospheric metallicity and a significant initial gas content. Moreover, if rainout is the dominant mechanism for puffing close-in young planets, then the current estimate of the gas content of these planets is an overestimate.
 |
Fig. 11 Summary sketch. Interior evolution (x-axis) for different planetary masses (y-axis) formed with polluted envelopes. Planets can be classified into three groups regarding their interior structure: planets with massive gas envelopes that maintain part or all of their composition gradients, planets with low-mass envelopes that completed their rainout and have a core-envelope structure, and planets that lost all of their gas (not shown). See Sec. 3.7 for details. The phases of rainout and mass loss are marked in droplets and wave-arrows symbols, respectively. The values in this schematic picture can vary with additional parameters such as atmospheric opacity and envelope-to-core mass. |
4 Discussion
The formation models of Ormel et al. (2021) stop at the crossover mass, before the planet enters the runaway gas accretion phase. We showed that planets with massive envelopes (i.e., slow rainout) preserve their formation composition gradient. Massive (runaway) gas accretion in addition to the planets we explored would keep the deep interior undersaturated on timescales of billions of years. This result is consistent with the indications of the diluted core in Jupiter and Saturn (Vazan et al. 2016; Wahl et al. 2017; Debras & Chabrier 2019; Mankovich & Fuller 2021) and implies that the Z-gradient may arise perhaps from the formation in the interior, although other mechanisms can also redistribute the metals7.
We find that the envelope mass is the key factor that determines the timing and duration of the silicate rainout. However, the initial envelope mass is an uncertain parameter that varies with the planet formation model assumptions. The initial envelope masses found in Ormel et al. (2021) are broadly within the range of other planet formation works (e.g., Mordasini 2020; Lee & Chiang 2015), but they can vary with additional processes that potentially slow or halt gas accretion, such as envelope recycling (Ormel et al. 2015; Kuwahara et al. 2019; Moldenhauer et al. 2021), which are not included in our formation model. Moreover, atmospheric boil-off (Owen & Wu 2016; Rogers et al. 2024) can remove a significant part of the envelope at a very early evolution stage. We therefore varied the envelope masses resulting from the planet formation model mainly to lower values than in the original model.
Although the work presented here assumes that planets are formed by pebble accretion, some of the findings may also hold for planets formed by planetesimal accretion. Bodenheimer et al. (2018) and Valletta & Helled (2020) showed that formation of sub-Neptune planets by planetesimal accretion also terminates with composition gradients, although steeper than in the pebble accretion case (Ormel et al. 2021). Further investigation is required to explore the silicate rainout processes in these planets.
The envelope metallicity follows the saturation L-V curve, in which the silicate content increases with pressure and temperature, forming a composition gradient along the saturated envelope. For simplicity, we ignored the effect of this saturated outer composition gradient on the thermal evolution. Nevertheless, this additional composition gradient is expected to inhibit convection and to slow the cooling of the planet in this region (Guillot et al. 1995; Leconte et al. 2017). Markham et al. (2022) suggested this mechanism to lower the heat flux from deep interiors of sub-Neptunes, keeping the core in a high-entropy supercritical state for billions of years, and permitting the dissolution of large quantities of hydrogen into the core. We anticipate that this process prolongs the rainout timescales we find here. In this context, our result therefore provides a lower bound for the rainout timescale.
We used the liquid-vapor curve as the sole criterion for the silicate redistribution, as in Podolak et al. (1988); Bodenheimer et al. (2018); Stevenson et al. (2022). We ignored any chemical interaction between the silicates and hydrogen. However, chemical interaction between species is expected to produce elements, such as water and silane, that are not included in our study (Schaefer & Fegley 2009; Misener et al. 2023; Horn et al. 2023). Dissociation of SiO2 molecules in the deep interior at a temperature of about 5000 K and above (Melosh 2007) is another mechanism that influences our results. Hydrogen dissolution in the rocky deep interior and outgassing of hydrogen as the planet cools (Chachan & Stevenson 2018; Kite et al. 2019) may affect planets with a low gas content.
We used the Freedman et al. (2014) radiative opacities as a function of pressure, temperature, and metallicity. The original tables are valid in the range of up to 0.03 GPa in pressure, 4000 K in temperature, and 50X solar in metallicity. For higher values, we extrapolated the radiative opacity based on the analytical expressions provided in Freedman et al. (2014) as a function of pressure, temperature, and metallicity. The higher opacity obtained by the extrapolation leads to more convection in the outer composition gradient and upper envelope, thus, not necessarily to slower cooling. Moreover, the radiative opacity effect is limited as the clean atmosphere (on top of the rainout boundary) is mainly convective, while the heat transport in the extrapolated high-pressure layers (>0.1 GPa), for example, in the deep composition gradient, is mainly conductive. We also note that the Freedman et al. (2014) opacity was calculated for a solar ratio composition, in which the contribution of species to the opacity is related to their solar abundances. An atmospheric metallicity that is based on L-V curves and a cloud model (Poser & Redmer 2024; Ormel & Min 2019; Min et al. 2020) requires an opacity calculation for other ratios, which may affect the rainout timescales we find here.
The planets we studied are rocky (dry) planets. Our results cannot be directly applied to planets containing a large fraction of volatiles (wet planets) for two main reasons. First, volatiles evaporate in the outer atmosphere and not in the deep interior. This affects the outer envelope properties and thus the planet formation and evolution process (Hori & Ikoma 2011; Venturini et al. 2016, 2020; Kurosaki & Ikoma 2017). Second, perhaps more fundamental to our work, the miscibility of rock in water at high pressure (Nisr et al. 2020; Kim et al. 2021) may prohibit the silicate settling, leaving the rock mixed with the water on a timescale of billions of years (Vazan et al. 2022; Dorn & Lichtenberg 2021). We therefore expect rainout and its consequent effects to be less remarkable in wet planets.
The thermodynamic properties of H and He were derived from the equation of state (EoS) of Saumon et al. (1995) for consistency with the planet formation calculation (Ormel et al. 2021). A newer EoS for a hydrogen and helium mixture (Chabrier et al. 2019) indicates a higher compressibility than Saumon et al. (1995) for a density above 0.1 g cm−3. Based on the results of Chabrier et al. (2019), we estimate a difference of up to 15% in envelope density-pressures relation for the planets in this work. Consequently, the thermal evolution and rainout rimescale are expected to be similar for the super-Earth planets in our sample, but longer for the more massive Neptune-like planets. Together with the convection inhibition described above, the rainout timescales presented in this work are a lower bound.
5 Conclusions
By linking a planet formation model to a nonadiabatic structure-evolution model, we have calculated the post-formation structure and thermal evolution of rocky planets formed by pebble accretion. Specifically, we followed for the first time the fate of the hot silicate vapor that remained in the planet’s envelope after pebbles sublimated as the planet cools. The model includes heat transport by radiation, convection, and conduction, and mass redistribution by rainout (condensation and settling) and by convective mixing. We find that the interior structure of silicate-rich planets that formed with polluted envelopes can be roughly divided into three groups, based on their envelope (H and He) mass: bare rocky cores that have lost their envelopes, super-Earth planets with core-envelope structure, and Neptune-like planets with diluted cores that slowly rain out. Our findings bridge the gap between the indications for the composition gradients in massive planets (e.g., Solar System gas giants) and the core-envelope structure in small planets. We list our main conclusions below.
The formation of sub-Neptune planets by pebble accretion (and to a lesser extent, planetesimal accretion) results in a strong composition gradient within the envelope that is due to the thermal ablation of the pebbles (planetesimals). This composition gradient cannot be overturned by convection, but its metals can be redistributed by rainout.
The cooling of polluted envelopes leads to silicate rainout and late core growth. The interior structure of rocky sub-Neptunes is therefore determined by the time over which rainout proceeds (train), which mainly depends on the envelope mass, but also on the planet mass and atmospheric opacity. Specific formation conditions (e.g., the pebble size or the pebble accretion rate) are insignificant for the rainout process.
The energy release that accompanies rainout,gravitational (settling) and to a lesser extent latent heat (condensation), as well as stored formation energy,act to inflate the planet radius in comparison to a core-envelope analog. Radius inflation is inversely proportional to the rainout timescale. Lower-mass planets have a shorter rainout time and larger radius inflation. We provided an analytical estimate for the rainout timescale and radius inflation (Sec. 2.3). Accurate age determinations are therefore key in order to properly interpret mass-radius relations for planets with a significant gas content.
Young planets with envelopes lighter than 0.4 M⊕ experience their maximum radius inflation by rainout in the first 100 million years, during which they are prone to mass loss by photoevaporation. The mutually enforcing processes of radius inflation and mass loss in this period result in enhanced (sedimentation-powered) loss of envelopes for these planets.
Planets with massive envelopes preserve their primordial composition gradients due to the blanketing effect of the envelope. Thus, billion-year-old Neptune-like planets are expected to have a gradual distribution of metals in their interiors.
Acknowledgements
We thank the referee for their constructive comments. We thank Tristan Guillot, Steve Markham, Masahiro Ikoma, Jonathan Fortney, and Re’em Sari for useful discussions. A.V. acknowledges support by ISF grants 770/21 and 773/21. C.W.O. acknowledge support by the National Natural Science Foundation of China (grant no. 12250610189 and no. 12233004). Figures were plotted using Matplotlib (Hunter 2007).
Appendix A Comparison between the ideal and nonideal gas equations of state
A very common approximation in planet formation and evolution studies is that the gas is ideal. Its deviation from the more realistic EoS is usually not considered. One of the differences between our simulations and the analytical model in section 3.4 is the use of a tabular EoS in the simulations, while in the analytical calculation, the gas is assumed to be ideal. To explore the difference, we compare the ideal gas EoS against the tabular pressure, temperature, and density relation of a H and He mixture. The ideal gas we used for the comparison was calculated for a hydrogen and helium mass fraction of 0.7 and 0.3, respectively. The mean molecular weight of the H and He mixture was 2.35, the adiabatic index was 1.45, and the adiabatic gradient was 0.31, as in Ormel et al. (2021).
In figure A.1 we plot the properties of the H and He mixture as a function of density and temperature from the tabular EoS of Saumon et al. (1995). The H and He mixture was calculated according to the additive volume law, as in Vazan et al. (2013). We show the pressure normalized to the ideal gas pressure (top) and the related adiabatic temperature gradients (bottom). The upper panel of figure A.1 indicates that the gas density-pressure agrees fairly well with ideal gas up to a density of about 0.1 g/cm3. The ideal gas prefactor of 1/(μ =2.35) is shown as the red curve. At higher density, the real gas diverges from the ideal gas and is significantly less compressible than the ideal gas. The pressure-temperature profiles of the planets we modeled here indicate that most of the gas is at a density higher than 0.1 g/cm3 for most of the evolution time. In general, sub-Neptune planets with more than a few percent of gas have a large fraction of their gas at high density, in which the ideal gas assumption no longer holds. Consequently, when planets that have more than a few percent of gas are modeled by using ideal gas, the envelopes are unrealistically hotter and the radii are smaller.
Another phenomenon that is ignored in the ideal gas calculation is the ionization and dissociation of molecules, which affects the heat capacity and thus the temperature profile and evolution. In the bottom panel of figure A.1, the grayscale represents the adiabatic temperature gradient (nabla) parameter, where the ideal gas value is shown as the orange curve. The ideal gas value of 0.31 (2/7 for H and 2/5 for He) is higher than of the real gas for a gas density above 0.1 g/cm3, leading to a too sharp temperature-pressure slope in models that use ideal gas.
Appendix B Harmonic mean of the radiative and conductive opacity
The conductive opacities were calculated from the thermal conductivity of silicate because the hydrogen-helium conductivity is negligible in the pressure-temperature range of interest (French et al. 2012). We took the thermal conductivity of Earth, 4 Wm−1 K−1 (Stevenson et al. 1983), to be our reference value and scaled it with pressure and temperature according to Stamenković et al. (2011). Then, the harmonic mean of the radiative and conductive opacities was calculated according to equation 3f. In figure B.1 we present the values of the radiative opacity (solid) and the harmonic mean of the radiative and conductive opacity (dashed) as a function of temperature for three metallicity values (color) in three pressures (panels). The conduction scales linearly with the silicate mass fraction in a given layer. The conduction clearly dominates the heat transport as temperature and pressure increase.
 |
Fig. A.1 Hydrogen-helium mixture of 0.7 H and 0.3 He (in mass fraction) from the equations of state of Saumon et al. (1995). We show the pressure normalized to ideal gas (top) and the adiabatic gradient (bottom). The red curve (top) fits the ideal gas prefactor of 1/(μ =2.35), and the orange curve (bottom) signifies the ideal gas constant value of ∇ad = 0.31. |
 |
Fig. B.1 Radiative opacity, based on the Freedman et al. (2014) calculation (solid), and the harmonic mean of the radiative and conduction opacity (dashed) as a function of temperature. Color represents different metallicities, and each panel shows a different pressure. |
References
- Baraffe, I., Chabrier, G., & Barman, T. 2008, A&A, 482, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bodenheimer, P., Stevenson, D. J., Lissauer, J. J., & D’Angelo, G. 2018, ApJ, 868, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Brouwers, M. G., & Ormel, C. W. 2020, A&A, 634, A15 [Google Scholar]
- Brouwers, M. G., Vazan, A., & Ormel, C. W. 2018, A&A, 611, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brouwers, M. G., Ormel, C. W., Bonsor, A., & Vazan, A. 2021, A&A, 653, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G., Mazevet, S., & Soubiran, F. 2019, ApJ, 872, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Chachan, Y., & Stevenson, D. J. 2018, ApJ, 854, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Debras, F., & Chabrier, G. 2019, ApJ, 872, 100 [Google Scholar]
- Dorn, C., & Lichtenberg, T. 2021, ApJ, 922, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Faik, S., Tauschwitz, A., & Iosilevskiy, I. 2018, Comput. Phys. Commun., 227, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Mordasini, C., Nettelmann, N., et al. 2013, ApJ, 775, 80 [Google Scholar]
- Fortney, J. J., Visscher, C., Marley, M. S., et al. 2020, AJ, 160, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, R. S., Lustig-Yaeger, J., Fortney, J. J., et al. 2014, ApJS, 214, 25 [CrossRef] [Google Scholar]
- French, M., Becker, A., Lorenzen, W., et al. 2012, ApJS, 202, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Ginzburg, S., Schlichting, H. E., & Sari, R. 2016, ApJ, 825, 29 [Google Scholar]
- Greene, T. P., Line, M. R., Montero, C., et al. 2016, ApJ, 817, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T. 1995, Science, 269, 1697 [CrossRef] [Google Scholar]
- Guillot, T. 2010, A&A, 520, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T., Chabrier, G., Gautier, D., & Morel, P. 1995, ApJ, 450, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Henyey, L. G., Forbes, J. E., & Gould, N. L. 1964, ApJ, 139, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Hori, Y., & Ikoma, M. 2011, MNRAS, 416, 1419 [NASA ADS] [CrossRef] [Google Scholar]
- Horn, H. W., Prakapenka, V., Chariton, S., Speziale, S., & Shim, S. H. 2023, Planet. Sci. J., 4, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Kaniel, S., & Kovetz, A. 1967, Phys. Fluids, 10, 1186 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, T., Chariton, S., Prakapenka, V., et al. 2021, Nat. Astron., 5, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., Weigert, A., & Weiss, A. 2013, Stellar Structure and Evolution (Berlin: Springer) [Google Scholar]
- Kite, E. S., Fegley, Bruce, J., Schaefer, L., & Ford, E. B. 2019, ApJ, 887, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Kovetz, A., Yaron, O., & Prialnik, D. 2009, MNRAS, 395, 1857 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, R. G., Stewart, S. T., Swift, D. C., et al. 2012, J. Geophys. Res. Planets, 117, E09009 [Google Scholar]
- Kurosaki, K., & Ikoma, M. 2017, AJ, 153, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Kuwahara, A., Kurokawa, H., & Ida, S. 2019, A&A, 623, A179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lammer, H., Selsis, F., Ribas, I., et al. 2003, ApJ, 598, L121 [Google Scholar]
- Leconte, J., Selsis, F., Hersant, F., & Guillot, T. 2017, A&A, 598, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ledoux, P. 1947, ApJ, 105, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, E. J., & Chiang, E. 2015, ApJ, 811, 41 [Google Scholar]
- Libby-Roberts, J. E., Berta-Thompson, Z. K., Désert, J.-M., et al. 2020, AJ, 159, 57 [Google Scholar]
- Lopez, E. D., & Fortney, J. J. 2013, ApJ, 776, 2 [Google Scholar]
- Lopez, E. D., & Fortney, J. J. 2014, ApJ, 792, 1 [Google Scholar]
- Mankovich, C. R., & Fuller, J. 2021, Nat. Astron., 5, 1103 [NASA ADS] [CrossRef] [Google Scholar]
- Markham, S., Guillot, T., & Stevenson, D. 2022, A&A, 665, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masuda, K. 2014, ApJ, 783, 53 [Google Scholar]
- Melosh, H. J. 2007, Meteor. Planet. Sci., 42, 2079 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D. 1978, Stellar Atmospheres, 2nd edn. (San Francisco: W. H. Freeman and Co.) [Google Scholar]
- Min, M., Ormel, C. W., Chubb, K., Helling, C., & Kawashima, Y. 2020, A&A, 642, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Misener, W., & Schlichting, H. E. 2022, MNRAS, 514, 6025 [CrossRef] [Google Scholar]
- Misener, W., Schlichting, H. E., & Young, E. D. 2023, MNRAS, 524, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Moldenhauer, T. W., Kuiper, R., Kley, W., & Ormel, C. W. 2021, A&A, 646, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C. 2014, A&A, 572, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C. 2020, A&A, 638, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Movshovitz, N., & Podolak, M. 2008, Icarus, 194, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Movshovitz, N., Bodenheimer, P., Podolak, M., & Lissauer, J. J. 2010, Icarus, 209, 616 [Google Scholar]
- Müller, S., Helled, R., & Cumming, A. 2020, A&A, 638, A121 [Google Scholar]
- Nisr, C., Chen, H., Leinenweber, K., et al. 2020, Proc. Natl. Acad. Sci., 117, 9747 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W. 2014, ApJ, 789, L18 [Google Scholar]
- Ormel, C. W., & Min, M. 2019, A&A, 622, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., Shi, J.-M., & Kuiper, R. 2015, MNRAS, 447, 3512 [Google Scholar]
- Ormel, C. W., Vazan, A., & Brouwers, M. G. 2021, A&A, 647, A175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owen, J. E., & Wu, Y. 2013, ApJ, 775, 105 [Google Scholar]
- Owen, J. E., & Wu, Y. 2016, ApJ, 817, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Podolak, M., Pollack, J. B., & Reynolds, R. T. 1988, Icarus, 73, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Poser, A. J., & Redmer, R. 2024, MNRAS, 529, 2242 [NASA ADS] [CrossRef] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [Google Scholar]
- Rogers, J. G., & Owen, J. E. 2021, MNRAS, 503, 1526 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, J. G., Owen, J. E., & Schlichting, H. E. 2024, MNRAS, 529, 2716 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenblum, E., Garaud, P., Traxler, A., & Stellmach, S. 2011, ApJ, 731, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Saumon, D., Chabrier, G., & van Horn, H. M. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Schaefer, L., & Fegley, B. 2009, ApJ, 703, L113 [CrossRef] [Google Scholar]
- Soubiran, F., Militzer, B., Driver, K. P., & Zhang, S. 2017, Phys. Plasmas, 24, 041401 [NASA ADS] [CrossRef] [Google Scholar]
- Stamenković, V., Breuer, D., & Spohn, T. 2011, Icarus, 216, 572 [Google Scholar]
- Steinmeyer, M.-L., Woitke, P., & Johansen, A. 2023, A&A, 677, A181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stevenson, D. J., Spohn, T., & Schubert, G. 1983, Icarus, 54, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Stevenson, D. J., Bodenheimer, P., Lissauer, J. J., & D’Angelo, G. 2022, Planet. Sci. J., 3, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Tinetti, G., Drossart, P., Eccleston, P., et al. 2018, Exp. Astron., 46, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Valletta, C., & Helled, R. 2019, ApJ, 871, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Valletta, C., & Helled, R. 2020, ApJ, 900, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Vazan, A., & Ormel, C. W. 2023, A&A, 676, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazan, A., Kovetz, A., Podolak, M., & Helled, R. 2013, MNRAS, 434, 3283 [NASA ADS] [CrossRef] [Google Scholar]
- Vazan, A., Helled, R., Kovetz, A., & Podolak, M. 2015, ApJ, 803, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Vazan, A., Helled, R., Podolak, M., & Kovetz, A. 2016, ApJ, 829, 118 [Google Scholar]
- Vazan, A., Ormel, C. W., & Dominik, C. 2018a, A&A, 610, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazan, A., Ormel, C. W., Noack, L., & Dominik, C. 2018b, ApJ, 869, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Vazan, A., Sari, R., & Kessel, R. 2022, ApJ, 926, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Venturini, J., Alibert, Y., & Benz, W. 2016, A&A, 596, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturini, J., Guilera, O. M., Haldemann, J., Ronco, M. P., & Mordasini, C. 2020, A&A, 643, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wahl, S. M., Hubbard, W. B., Militzer, B., et al. 2017, Geophys. Res. Lett., 44, 4649 [CrossRef] [Google Scholar]
- Wilson, H. F., & Militzer, B. 2012, Phys. Rev. Lett., 108, 111101 [CrossRef] [Google Scholar]
Compositional diffusion might also change the planetary structure, but is found to be negligible in comparison to convective-mixing and rainout, as is shown in Sect. 2.4.
An iterative implicit integration method for boundary value problems, in which the structure equations are solved together with the evolution equations (Henyey et al. 1964).
See Vazan et al. (2015) for more details on the MLR model and on the effect of its parameters on results.
In giant planets, other processes such as miscibility of rock in metallic hydrogen (Wilson & Militzer 2012; Soubiran et al. 2017, e.g.) and/or convective mixing (Vazan et al. 2015; Müller et al. 2020) can change the long-term interior structure.
All Tables
Values of the parameters we used in the analytical calculations in Sect. 2.3, based on Brouwers & Ormel (2020) and Ormel et al. (2021).
All Figures
 |
Fig. 1 Post-formation outcome of the interior structure of planets assembled by pebble accretion (Ormel et al. 2021). We show the silicate mass fraction distribution (black) and the envelope temperature profile (red) in planets of 5 M⊕ (left), 10 M⊕ (middle), and 20 M⊕ (right), formed at 0.2 AU from a Sun-like star. |
| In the text | |
 |
Fig. 2 Schematic picture of the rainout process in a polluted envelope. Cooling (from left to right) leads to condensation of silicate in an oversaturated outer envelope and settling of the condensed silicates to deeper undersaturated layers. Condensation and settling release energy (curly arrows), which leads to envelope extension and an inflated radius in comparison to a planet with the same composition in the core-envelope structure. Rainout ends when the planet reaches a core-envelope structure, and the radius inflation is diminished. The axes in the figure are not to scale. |
| In the text | |
 |
Fig. 3 Radius evolution from disk dissipation of planets with a polluted envelope (solid) and planets with the same composition and core-envelope structure (dashed). The planets have a static interior structure (no rainout) and are located at 0.2 AU from a Sun-like star. |
| In the text | |
 |
Fig. 4 Interior silicate mass fraction (top) and temperature profile (bottom) of 5 M⊕ (left), 10 M⊕ (middle) and 20 M⊕ (right) planets. The profiles are shown at the end of formation (dashed), after the rapid contraction (dotted), and after 1, 5, 10 Gyr (solid) for an evolution at 0.2 AU. The early contraction (from a Hill sphere to about one-tenth of it) is the cause of the gas temperature increase between the formation and the million-year curves. The increase in the central temperatures is the result of core contraction due to the constant core density assumption in the formation model. The dashed and dotted lines of the 20 M⊕ model overlap in the top right panel. |
| In the text | |
 |
Fig. 5 Silicate mass fraction (color) distribution in radius (y-axis) and time (x-axis). The evolution is shown for 5 M⊕ (left), 10 M⊕ (middle), and 20 M⊕ (right). The x-axis has different ranges (1 Gyr, 5 Gyr, and 10 Gyr). The dotted black curves indicate Z = 0.98 and Z = 0.02 silicate mass fraction levels. The dashed red curve signifies the boundary between saturated and undersaturated regions, according to Eq. (9). A core-envelope boundary is approximately indicated by the Z = 0.98 curve. Because of the high temperatures at the core-envelope boundary, the (saturated) envelope is characterized by a silicate mass fraction of a few percent. |
| In the text | |
 |
Fig. 6 Radius evolution of planets formed with a polluted envelope (solid) and planets with the same bulk composition, but starting with a core-envelope (CE) structure from the outset (dashed). The measured rainout time is determined by the time at which the classical core-envelope structure is established (dotted vertical line). Rainout in the polluted envelopes causes radius inflation in comparison to planets formed with a core envelope. The radius inflation is shorter and more prominent in smaller planets. All planets are located at 0.2 AU from a Sun-like star. |
| In the text | |
 |
Fig. 7 Rainout time as a function of gas (H and He) mass for three cases of silicate mass: MZ = 4.3 M⊕ (blue), MZ = 6.7 M⊕ (red), and MZ = 8.9 M⊕ (green). We show numerical simulations (points) and analytical calculation (curves). The analytical model is according to Eq. (17), and the parameters appear in Table 1. |
| In the text | |
 |
Fig. 8 Radius inflation, ΔR/R = (R − RCE)/RCE, as a function of age (x-axis) and envelope mass (y-axis) for planets with 4.3 M⊕ of silicates. For illustrative clarity, we limited the scale of ΔR/R to 0.25 (red), but in reality, ΔR/R reaches values up to 1. The dashed curve signifies the maximum radius inflation for each envelope mass. |
| In the text | |
 |
Fig. 9 Zoom-in on Fig. 8 in the first 1 Gyr in log timescale. Planets with significant radius inflation in the first 0.1 Gyr are vulnerable to mass loss by photoevaporation. As in Fig. 8, red signifies ΔR/R in the range of 0.25–1. The dashed curves show examples of estimated mass-loss tracks at 0.2 AU. |
| In the text | |
 |
Fig. 10 Rainout time as a function of atmospheric radiative opacity (Zmin in Eq. (4)) based on the opacity formalism of Freedman et al. (2014). The cases show a 5 M⊕ planet with 4.3 M⊕ of silicates and 0.7 M⊕ gas. The points are simulations results, and the larger point is the standard (solar metallicity) case. |
| In the text | |
 |
Fig. 11 Summary sketch. Interior evolution (x-axis) for different planetary masses (y-axis) formed with polluted envelopes. Planets can be classified into three groups regarding their interior structure: planets with massive gas envelopes that maintain part or all of their composition gradients, planets with low-mass envelopes that completed their rainout and have a core-envelope structure, and planets that lost all of their gas (not shown). See Sec. 3.7 for details. The phases of rainout and mass loss are marked in droplets and wave-arrows symbols, respectively. The values in this schematic picture can vary with additional parameters such as atmospheric opacity and envelope-to-core mass. |
| In the text | |
 |
Fig. A.1 Hydrogen-helium mixture of 0.7 H and 0.3 He (in mass fraction) from the equations of state of Saumon et al. (1995). We show the pressure normalized to ideal gas (top) and the adiabatic gradient (bottom). The red curve (top) fits the ideal gas prefactor of 1/(μ =2.35), and the orange curve (bottom) signifies the ideal gas constant value of ∇ad = 0.31. |
| In the text | |
 |
Fig. B.1 Radiative opacity, based on the Freedman et al. (2014) calculation (solid), and the harmonic mean of the radiative and conduction opacity (dashed) as a function of temperature. Color represents different metallicities, and each panel shows a different pressure. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


