| Issue |
A&A
Volume 686, June 2024
|
|
|---|---|---|
| Article Number | A222 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202347661 | |
| Published online | 14 June 2024 | |
Infrared colours and bolometric corrections of SiO masing stars in the inner Milky Way
1
Dipartimento di Fisica e Astronomia “Augusto Righi”, Alma Mater Studiorum, Università di Bologna,
Via Gobetti 93/2,
40129
Bologna,
Italy
e-mail: maria.messineo2@unibo.it
2
INAF – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna,
Via Gobetti 93/3,
40129
Bologna,
Italy
Received:
5
August
2023
Accepted:
20
March
2024
Aims. We analysed a sample of SiO-masing late-type stars located in the inner Galaxy with the goal of setting better constraints on their obscuration.
Methods. This reference sample has allowed us to define mathematical relations between their dereddened infrared colours and the observed colours (e.g. Ks-[8], Ks-[24]).
Results. The derived equations define a property (the locus) of these late-type stars. Therefore, they enable us to derive the interstellar extinction. With estimated spectral types, it is possible to decompose the total extinction in the two components (interstellar and envelope extinction).
Conclusions. These relations are useful for classifying extremely obscured late-type stars located in the inner Galaxy. Estimating the two extinction components can be performed on an individual late-type star, independently of its surroundings and even when few mid-infrared measurements are available.
Key words: methods: data analysis / circumstellar matter / stars: late-type / Galaxy: stellar content / infrared: stars
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Typically, SiO masing stars have late spectral types, namely, later than M4-M5. Dusty circumstellar envelopes surround the central star, where maser emission from SiO, OH, and H2O molecules may originate. The starlight is absorbed, reprocessed, and re-emitted at infrared wavelengths by the dusty envelope. In other words, the envelope represents a deforming and transforming mirror of the original stellar energy distribution (SED). The effect is dependent on both the interstellar absorption caused by a diffuse medium along the line of sight and on the optical depth of the envelope, which can range from zero to an equivalent of about AV = 100 mag. In the inner Galaxy, the interstellar extinction can likewise reach AV = 30–40 mag. Due to the severe dust obscuration and the patchy interstellar extinction, the reddening, distances, and luminosities of late-type stars cannot easily be inferred.
To characterize the SED of an asymptotic giant branch (AGB) star, a decomposition of its total extinction into the interstellar component and the circumstellar component is required. Messineo et al. (2005) measured the total extinction (![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq1.png) ) for a sample of masing AGB stars and broke it down into
) for a sample of masing AGB stars and broke it down into ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq2.png) (int) for the interstellar medium (ISM) and
(int) for the interstellar medium (ISM) and ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq3.png) (env) for the envelope. Their method was straightforward and relied on multi-wavelength (single-epoch) photometric measurements of the targeted AGB star, covering the near- and mid-infrared window. They assumed that the median extinction of nearby giants could be used to approximate the interstellar extinction.
(env) for the envelope. Their method was straightforward and relied on multi-wavelength (single-epoch) photometric measurements of the targeted AGB star, covering the near- and mid-infrared window. They assumed that the median extinction of nearby giants could be used to approximate the interstellar extinction.
Stellar colours and bolometric corrections (BC) of an AGB star vary depending on the properties of its envelope, namely, the extent, density, and mass loss rate. Here, we present correlations between stellar colours, bolometric corrections, and envelope types obtained for the sample of SiO masing stars from Messineo et al. (2018). The advantage of this sample is that it covers a wide range of interstellar extinction and infrared stellar colours. We used it to elaborate on the intrinsic colours of cold stars in Messineo (2004) and Messineo et al. (2005, 2012). This time, we have used this reference sample to develop a new technique. We have established correlations between the intrinsic infrared colours and the observed infrared colours and envelope types, assuming that we know the Galactic interstellar absorption curve. By solving a system of equations, it is then technically possible to decompose the extinction into the interstellar and envelope components, independently of the star's surroundings. It is possible to model the BCs as a function of the intrinsic stellar colours and to determine the apparent bolometric magnitudes.
This idea is especially helpful in the innermost obscured regions of the Milky Way, where it is not possible to study the entire SED, and individual measurements in the mid-infrared are often of poor quality (e.g., because of confusion). If the nature of the star is known, for example, because of its maser emission, we can use the established equations for the Ks-[24] or Ks-[8] colours to determine the extinction, characterize the SED of the star, and estimate the apparent bolometric magnitude.
We describe the stellar sample and the available parameters in Sec. 2. Extinction-free colours are defined and the relationships between them and the dereddened colours are described in Sec. 3. The existence of these relations allows us to determine the interstellar extinction. Using an average spectral type (such as M6), we can also estimate the envelope extinction given the interstellar extinction. Synthetic infrared colours derived from the DUSTY models are shown and compared with the observational data in Sec. 4. The empirical estimates of extinction are compared with previously published estimates in Sec. 5.
2 Sample
The sample consists of 572 late-type stars in the process of losing mass, which we searched to find SiO maser emission (Messineo et al. 2002, 2018). The sources are located at low latitudes (|b| < 0.5°). The sample had been created using near- and mid-infrared photometric measurements. The collected measurements cover from 0.9 μm to 24 μm and come from the publicly available surveys 2MASS, MSX, WISE, and GLIMPSE1 (Messineo et al. 2018). Each photometric data point is from a single epoch. Several stellar parameters were estimated by Messineo et al. (2005, 2018).
Total ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq4.png) determination. The total extinction was estimated by Messineo et al. (2005, 2018) in the Ks versus J-Ks or H-Ks diagram, by shifting the SiO masing stars onto the 47 Tuc giant branch along the reddening vector – which implies a late M type (M4-M5) star. The values of
determination. The total extinction was estimated by Messineo et al. (2005, 2018) in the Ks versus J-Ks or H-Ks diagram, by shifting the SiO masing stars onto the 47 Tuc giant branch along the reddening vector – which implies a late M type (M4-M5) star. The values of ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq5.png) (tot) span from 0 to 5.5 mag.
(tot) span from 0 to 5.5 mag.
Interstellar ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq6.png) determination. The mean of surrounding stars is used as a proxy for
determination. The mean of surrounding stars is used as a proxy for ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq7.png) (int) (Messineo et al. 2005, 2018). This assumption relies on the strong hypotheses that red giants and AGBs share the same Galactic distribution and that the target star is situated at the peak of the stellar density along the line of sight. Masing AGB stars are good tracers of the thin central bar, as shown by Habing et al. (2006). The thin disk population and the thick disk population do, in fact, cohabit in the disk; however, at low latitudes, the thick disk's contribution is less than 10% (Lee et al. 2011).
(int) (Messineo et al. 2005, 2018). This assumption relies on the strong hypotheses that red giants and AGBs share the same Galactic distribution and that the target star is situated at the peak of the stellar density along the line of sight. Masing AGB stars are good tracers of the thin central bar, as shown by Habing et al. (2006). The thin disk population and the thick disk population do, in fact, cohabit in the disk; however, at low latitudes, the thick disk's contribution is less than 10% (Lee et al. 2011).
Apparent bolometric magnitudes. Messineo et al. (2018) computed apparent bolometric magnitudes by directly integrating under the stellar SEDs from 0.9 μm to 24 μm. At longer wavelengths, the flux was linearly extrapolated to zero. At short wavelengths, the flux was estimated with a blackbody of 3000 K.
Infrared bolometric corrections (BC). For a given photometric band, the BC represents the correction to be added to the dereddened apparent magnitude in order to estimate the stellar apparent bolometric magnitude, (mbol), BCλ=mbol-mλ. There is a tight relation between the infrared ![$\[\mathrm{BC}_{K_S}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq8.png) values and the intrinsic stellar colours of Messineo et al. (2018). Second-order polynomial fits to the data are given in the appendix.
values and the intrinsic stellar colours of Messineo et al. (2018). Second-order polynomial fits to the data are given in the appendix.
Large-amplitude variables. The sample from Messineo et al. (2005) is made up of Mira-like stars. The average photometric measurements should ideally be used to infer average colours and luminosities due to large periodic light variations. Amplitudes of Miras in the Ks band can reach up to 2 mag, whereas at longer wavelengths, they are substantially smaller (e.g. at 15 μm they are about 50% than those in Ks). Nevertheless, average quantities of the entire sample generate quantities typical of the actual average value (Messineo et al. 2004), based on the random phase of each star (absence of synchronous pulsations). Using DENIS, 2MASS, MSX, and WISE photometric flags, Messineo et al. (2018) found that at least 74% of the sample is made of long-period variables (LPV).
There are 282 out of 572 stars with matches in the Gaia DR3 main catalog (Gaia Collaboration 2023), 249 have a measured G-band magnitude; of those, 72% (179) are classified as variables; the G-band values range from 9 to 20 mag; there are from 10 to 62 G-band observations per star, from 2 to 60 BP-band observations, and from 7 to 65 RP-observations. So far, Gaia DR3 has released photometric data covering 34 months of observations (Eyer et al. 2023). Two scanning laws were used; the ecliptic pole scanning law (EPSL) during the first 28 days and the nominal scanning law (NSL) afterward; the observational cadence depends on the period of the spin axis (6 h) and the precession around the Sun (63 days); the scanning law favours the Ecliptic poles. At the end of the 6-yr mission, each star is supposed to have an average of ≈70 usable photometric transits.
For the targets recognised as Gaia variables, the differences between the highest and lowest G-band measurements range from 0.12 mag to 3.54 mag (Eyer et al. 2023). Those marked as 'NOT_AVAILABLE' regarding variability are fainter (mostly from G = 18 to 21 mag), with a peak at G = 20 mag and have from 0 to 43 G-band observations, from 0 to 19 BP-band observations, and from 0 to 38 RP-observations. The differences between the highest and lowest G-band magnitudes range from 0.0 mag to 0.67 mag. A fraction of 55% of Gaia matches are variables in Gaia and also in Messineo et al. (2018) based on infrared measurements. Gaia adds 16% of new variables (not detected via infrared flags).
The amplitude, or the difference between the minimum and maximum, is typically more than G = 0.8 mag for Mira AGBs (e.g. Lebzelter et al. 2023; Messineo 2022). With variations greater than 0.8 mag, 74% of the Gaia variables are most likely Miras. However, only 86 of these 179 Gaia variables – whose amplitudes and periods range from 0.12 mag to 3.34 mag and their periods from 42 days to 808 days – are currently listed in the Gaia catalog of classified LPVs (Lebzelter et al. 2023). The Gaia catalog of LPVs includes only stars with a 5–95% quantile range larger than 0.1 mag in the G-band.
Since there is no discernible difference between the population of Gaia-identified LPVs and those not designated as variables for the purposes and diagrams displayed in this study, the fits and diagrams presented in this paper employ the whole sample of stars in Messineo et al. (2018).
3 Extinction
Messineo et al. (2012) used the interstellar extinction-free parameters Q1 and Q2, where Q1 = (J − H) − 1.8 × (H − Ks), and Q2 = (J − Ks) − 2.69 × (Ks − [8.0])2 to study the properties of different types of late-type stars. The extinction-free colours can be calculated directly from the observations.
Messineo et al. (2012) showed that the intrinsic MSX Ks−[A] colours, (Ks−[A])o, of SiO masing stars are well correlated with the Q1 parameter, as well as with their BC([A]) values. The Q1 parameter spans a quite narrow range (1.5 mag), while the Q2 parameter spans more than 10 mag (from 0 to 12 mag) and is a very sensitive meter of circumstellar obscuration.
This correlation is of great advantage because it allows us to decompose the total ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq9.png) in the envelope component,
in the envelope component, ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq10.png) (env), and the interstellar component,
(env), and the interstellar component, ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq11.png) (int), and to obtain estimates of the stellar bolometric magnitudes. In this exercise, we revisit this idea to determine
(int), and to obtain estimates of the stellar bolometric magnitudes. In this exercise, we revisit this idea to determine ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq12.png) (int) and
(int) and ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq13.png) (env) quantitatively by taking the following steps.
(env) quantitatively by taking the following steps.
By having adopted an interstellar extinction curve, we determine the Qλ values for stars in Messineo et al. (2005) that have ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq20.png) (int) values. Then, we verify the existence of mathematical relations between the Qλ values and independently obtained, intrinsic colours. For stars with unknown
(int) values. Then, we verify the existence of mathematical relations between the Qλ values and independently obtained, intrinsic colours. For stars with unknown ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq21.png) (int), we use these relations plus the observed Qλ values to estimate the intrinsic colours and
(int), we use these relations plus the observed Qλ values to estimate the intrinsic colours and ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq22.png) (int). By using
(int). By using ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq23.png) (tot) and AK (int), we also estimate the circumstellar extinction,
(tot) and AK (int), we also estimate the circumstellar extinction, ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq24.png) (env). Eventually, we obtain some constraints on the circumstellar extinction curve, as suggested by the kind referee.
(env). Eventually, we obtain some constraints on the circumstellar extinction curve, as suggested by the kind referee.
MIR interstellar effective extinction, ![$\[\langle A\rangle / A_{K_S}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq14.png) .
.
3.1 Adopted interstellar extinction ratios
3.1.1 NIR extinction power law
At near-infrared (NIR) wavelengths, the Galactic extinction curve is usually approximated with a power law, Aλ ∝ λ−α, and it appears the same in every direction. α determinations in the literature range from 1.61 to 2.2. A value of α = 1.61 was measured by Rieke & Lebofsky (1985). A model with α = 1.9 was favored in Messineo et al. (2005) based on an analysis of the 2MASS colours of late-type stars in the inner Galaxy. α measurements larger than 2.0 were published in a number of works between 2006 and 2011 (e.g., Nishiyama et al. 2006; Stead & Hoare 2009). In the nuclear disk, Fritz et al. (2011) reported a value of 2.1. For late-type stars at the Galactic center, which suffer about 2 mag of reddening in bands H-Ks, the increase of α from 1.61 to 1.9 implies a decrease of ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq25.png) of 0.7 mag. A change in α from 1.9 to 2.1 implies another decrease of about 0.35 mag. A higher α decreases the extinction and makes the stars fainter.
of 0.7 mag. A change in α from 1.9 to 2.1 implies another decrease of about 0.35 mag. A higher α decreases the extinction and makes the stars fainter.
In Messineo et al. (2005), an α of 1.9 was adopted, ![$\[A_{K_{\mathrm{S}}} / E(J-K s)=0.537\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq26.png) and
and ![$\[A_{K_{\mathrm{s}}} / E(H-K s)=1.493\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq27.png) , and, AJ:AH:
, and, AJ:AH:![$\[A_{K s}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq28.png) =2.86:1.66:1.00. Using the same calculation performed in Messineo et al. (2005), for α=2.1, it is found that
=2.86:1.66:1.00. Using the same calculation performed in Messineo et al. (2005), for α=2.1, it is found that ![$\[A_{K_{\mathrm{s}}} / E(J-K s)=0.455\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq29.png) and
and ![$\[A_{K_{\mathrm{s}}} / E(H-K s)=1.311\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq30.png) , and, AJ:AH:
, and, AJ:AH:![$\[A_{K s}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq31.png) =3.208:1.766:1.000. Within errors, the latter ratios are consistent with the empirical measurements of Wang & Chen (2019): AJ:AH:
=3.208:1.766:1.000. Within errors, the latter ratios are consistent with the empirical measurements of Wang & Chen (2019): AJ:AH:![$\[A_{K s}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq32.png) =3.115:1.679:1.000.
=3.115:1.679:1.000. ![$\[A_{K_{\mathrm{s}}} / E(J-K s)=0.473\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq33.png) and
and ![$\[A_{K_{\mathrm{s}}} / E(H-K s)=1.472\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq34.png) . At the Galactic center, Nogueras-Lara et al. (2020) measured AJ/AH = 1.87 ± 0.03 and AH/AK = 1.84 ± 0.03, the power law with α = 2.1 yields AJ/AH = 1.82 and AH/AKs = 1.77; while the Wang's ratios yield AJ/AH = 1.85 and AH/AKs = 1.68. Here, a single power law with index −α= −2.1 is adopted.
. At the Galactic center, Nogueras-Lara et al. (2020) measured AJ/AH = 1.87 ± 0.03 and AH/AK = 1.84 ± 0.03, the power law with α = 2.1 yields AJ/AH = 1.82 and AH/AKs = 1.77; while the Wang's ratios yield AJ/AH = 1.85 and AH/AKs = 1.68. Here, a single power law with index −α= −2.1 is adopted.
3.1.2 MIR extinction law
The average effective extinction values for the filters of the MSX, WISE, and GLIMPSE surveys were estimated by convolving the extinction curves with a 3200 K giant of Allard et al. (2011) and the filter response curves.
As in Messineo et al. (2005), the parametric extinction curve of Rosenthal et al. (2000), denoted as “curve 2,” obtained in the OMC-1 cloud with H2 observations, was used along with two other curves. Curve 3 is a modified version of the Rosenthal curve in the 3–8 μm region to incorporate the ratios from H-line observations in the Galactic center region of Fritz et al. (2011)3. Curve 4 was derived by Gordon et al. (2021) with Spitzer spectroscopic data of early-type stars located in the direction of a diffuse medium. The stars used by Gordon et al. (2021) are located at AV < 5 mag. The average effective extinction values from curve 2, curve 3, and curve 4 are listed in Table 1.
The effective extinction ratios may vary at mid-infrared wavelengths. The peak of the silicate feature around 8–9 μm ![$\[\frac{A_{9.7}}{A_{K_{\mathrm{S}}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq35.png) is 1–1.3 in the Galactic center, but it is only 0.7 in the solar neighbouring stars observed by Spitzer. The Gordon curve can be regarded as a lower limit curve, while the Galactic center curve represents an upper limit curve.
is 1–1.3 in the Galactic center, but it is only 0.7 in the solar neighbouring stars observed by Spitzer. The Gordon curve can be regarded as a lower limit curve, while the Galactic center curve represents an upper limit curve.
The effective extinction ratios for the WISE and GLIMPSE filters were also determined by Wang & Chen (2019) using broad-band photometry of red clump stars, which are primary indicators of distances due to their known luminosity and colours. These are also shown in the Table 1 and seem to agree with our predictions from the curves.
 |
Fig. 1 Correlations between intrinsec colours and between Q(λ) values and intrinsec colours. Left panel: Intrinsic (Ks−[D])o versus (H-Ks)o colours of Messineo et al. (2005), de-reddened using the median interstellar extinction of surrounding stars, shown in black. For comparison, in gray, we give the observed (Ks−[D]) versus (H-Ks) colours. Middle panel: Q(D) colours vs. (Ks−[D])o, for the MSX D-band. Right panel: Q(E) colours versus (Ks−[E])o, for the MSX E-band. The red dotted lines are fits to the data points. Error bars on the Q(D) and Q(E) are obtained by propagating the errors on the J, H, Ks, D, and E magnitudes. |
3.2 Definitions of the Qλ parameters
Based on parameters Q1 and Q2 of Messineo et al. (2012), we can analogously calculate an interstellar extinction-free parameter Qλ for each filter and each interstellar extinction curve (Table 1):
![$\[Q_\lambda^{J K s}=(J-K s)-C_\lambda^{J K s} \times(K s-[\lambda]),\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq36.png) (1)
(1)
By combining Eqs. (1) and (3), we obtain:
![$\[Q_\lambda=Q_\lambda^{H K s}+Q_\lambda^{J K s}=(J+H-2 K s)-\left(C_\lambda^{J K s}+C_\lambda^{H K s}\right) \times(K s-[\lambda]).\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq40.png) (5)
(5)
The constants can be estimated with an extinction curve. Curve 3 applies to highly obscured regions. The Gordon's curve (for a diffuse interstellar gas) can be regarded as the Galactic lower limit (smaller peak at 10 μm).
The filters GLIMPSE [8], WISE W3, and MSX A contain the 10 μm silicate emission. The MSX D and WISE W4 filters appear to be particularly useful as they are not affected by the silicate emission and show small variations of Cλ values in the three curves.
By definition, Eq. (5) yields an identical value when calculated with the observed magnitudes and the dereddened magnitudes (see Appendix). This allows us to estimate the intrinsic colours.
In principle, we can use separately Eqs. (1) and (3) and obtain two independent colour estimates. However, the ![$\[Q_\lambda^{H K s}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq41.png) values span a much smaller range (e.g.,
values span a much smaller range (e.g., ![$\[Q_D^{H K s}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq42.png) from −1 to −5 mag) than the
from −1 to −5 mag) than the ![$\[Q_\lambda^{J K s}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq43.png) values (e.g.,
values (e.g., ![$\[Q_D^{J K s}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq44.png) from −2 to −19 mag) and the interpolated colours have large errors. The combined Qλ =
from −2 to −19 mag) and the interpolated colours have large errors. The combined Qλ = ![$\[Q_\lambda^{H K s}+Q_\lambda^{J K s}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq45.png) colours span a wider range, for instance, QD ranges from −2 to −22 mag (see Fig. 1). The combined case is used in the following sections.
colours span a wider range, for instance, QD ranges from −2 to −22 mag (see Fig. 1). The combined case is used in the following sections.
3.3 Qλ-intrinsic-colours curves for stars with known ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq46.png) (int)
(int)
Using the stars by Messineo et al. (2018) as a reference sample, a series of equations is set up to express the intrinsic colours as a function of the Qλ parameters. The parameter Qλ is correlated with the dereddened (Ks − [λ]) colour, for instance, Q(D) ∝ (Ks − D)o (see Fig. 1). The fits are made with third-grade polynomial fits. It follows that:
![$\[(K s-\lambda)_o=\mathrm{c} 1 \times Q(\lambda)+\mathrm{c} 2 \times Q(\lambda)^2+\mathrm{c} 3 \times Q(\lambda)^3+\mathrm{c} 0.\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq47.png) (6)
(6)
The intrinsic colours are calculated with the median ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq48.png) (int) values of the surrounding stars (Messineo et al. 2005), which are rescaled to a power law with an index of −2.1, and the assumed effective extinction ratios. In Messineo et al. (2004, 2005), it is shown that the SiO masing stars are rare and the majority of the surrounding stars are normal giants. The large interval spanned by Qλ is due to the intrinsic colour range of the stars (stellar SEDs). These bright late-type stars are mostly mass-losing Mira AGBs with spectral types later than M4.
(int) values of the surrounding stars (Messineo et al. 2005), which are rescaled to a power law with an index of −2.1, and the assumed effective extinction ratios. In Messineo et al. (2004, 2005), it is shown that the SiO masing stars are rare and the majority of the surrounding stars are normal giants. The large interval spanned by Qλ is due to the intrinsic colour range of the stars (stellar SEDs). These bright late-type stars are mostly mass-losing Mira AGBs with spectral types later than M4.
For each filter, the constants of the fits are listed in Table 2, when using the revised curve 3 of Messineo et al. (2005) and in Table 3 for the extinction curve of Gordon et al. (2021).
Coefficients of the polynomial fits between (Ks−[λ])o colours and the Qλ parameters, using curve 3.
Coefficients of the polynomial fits between (Ks−[λ])o colours and the Qλ parameters, based on the interstellar extinction curve by Gordon et al. (2021).
3.4 AKs and (Ks−[λ]o) colours derived with Qλ and the Qλ-intrinsic-colours curves
The Qλ-intrinsic-colours curves derived in the above section can be used to obtain estimates of the (Ks−[λ])o colours for stars with unknown parameters.
The following formula can be used to estimate the interstellar ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq51.png) (int) as a function of the observed and dereddened colours once the intrinsic colours have been identified with Qλ:
(int) as a function of the observed and dereddened colours once the intrinsic colours have been identified with Qλ:
![$\[A_{K_{\mathrm{s}}}(\text {int})=\frac{(K s-[\lambda])-(K s-[\lambda])_o}{1-\frac{A_\lambda}{A_{K_{\mathrm{s}}}}} \text {. }\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq52.png) (7)
(7)
The term (Ks − [λ])o results from Eq. (6) and the coefficients from Tables 2 or 3 by entering the Qλ. The term (Ks − [λ]) is the observed colour. The extinction ratios are listed in Table 1.
The revised curve 3 of Messineo et al. (2005) was used first. The four independent ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq53.png) (int) obtained with the MSX magnitudes were averaged; σ = 0.05 mag. We repeated the calculation with the WISE dataset and the GLIMPSE dataset. The
(int) obtained with the MSX magnitudes were averaged; σ = 0.05 mag. We repeated the calculation with the WISE dataset and the GLIMPSE dataset. The ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq54.png) (int) values from the W3 and W4 WISE bands give σ = 0.03 mag, while the
(int) values from the W3 and W4 WISE bands give σ = 0.03 mag, while the ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq55.png) (int) values from GLIMPSE [5.8] and [8.0] data yield σ = 0.03 mag. There are 135 stars with good photometry and estimates of
(int) values from GLIMPSE [5.8] and [8.0] data yield σ = 0.03 mag. There are 135 stars with good photometry and estimates of ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq56.png) (int) with MSX and WISE datasets; the average difference is 0.04 mag and the σ is 0.20 mag, as shown in Fig. 2. The 111
(int) with MSX and WISE datasets; the average difference is 0.04 mag and the σ is 0.20 mag, as shown in Fig. 2. The 111 ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq57.png) (int) estimates of good photometric quality in common between the GLIMPSE and WISE estimates yield σ=0.15 mag.
(int) estimates of good photometric quality in common between the GLIMPSE and WISE estimates yield σ=0.15 mag.
Identical ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq58.png) (int) values are measured (within errors) after repeating the full computation using Gordon's effective ratios of Table 1. The same
(int) values are measured (within errors) after repeating the full computation using Gordon's effective ratios of Table 1. The same ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq59.png) values are obtained as long as the dereddened colours and the Qλ are performed consistently with the same interstellar curve. We measured
values are obtained as long as the dereddened colours and the Qλ are performed consistently with the same interstellar curve. We measured ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq60.png) (int) by analyzing the correlations between Qλ and the intrinsic colours. The
(int) by analyzing the correlations between Qλ and the intrinsic colours. The ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq61.png) (int) values of individual stars are obtained independently of the stellar environment, anywhere in the Galactic Disk.
(int) values of individual stars are obtained independently of the stellar environment, anywhere in the Galactic Disk.
In Fig. 3, we compare the original estimate of ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq62.png) (int) (via the surrounding stars) and the one obtained with the fits and Qλ. Using the MSX data, the average
(int) (via the surrounding stars) and the one obtained with the fits and Qλ. Using the MSX data, the average ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq63.png) (int)(fit)-
(int)(fit)-![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq64.png) (int)(surrounding)=0.14 mag with a σ = 0.36 mag and a median of 0.07 mag; using the WISE data the average
(int)(surrounding)=0.14 mag with a σ = 0.36 mag and a median of 0.07 mag; using the WISE data the average ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq65.png) (int)(fit)-
(int)(fit)-![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq66.png) (int)(surrounding)=0.04 mag with a σ = 0.32 mag and a median of 0.00 mag; using the GLIMPSE data
(int)(surrounding)=0.04 mag with a σ = 0.32 mag and a median of 0.00 mag; using the GLIMPSE data ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq67.png) (int)(fit)-
(int)(fit)-![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq68.png) (int)(surrounding)=0.05 mag with a σ = 0.33 mag and a median of 0.03 mag. The data points displayed in Fig. 3 were fitted with a Huber regression; for the GLIMPSE and the MSX data points, at
(int)(surrounding)=0.05 mag with a σ = 0.33 mag and a median of 0.03 mag. The data points displayed in Fig. 3 were fitted with a Huber regression; for the GLIMPSE and the MSX data points, at ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq69.png) = 2 mag the fits indicate values 0.2 mag larger than the equity line, suggesting that the new estimated
= 2 mag the fits indicate values 0.2 mag larger than the equity line, suggesting that the new estimated ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq70.png) magnitudes may be 0.2 mag larger than those estimated by Messineo et al. (2005). This systematic error could be corrected a posteriori. However, as shown in the discussion section, for Miras at the Galactic center the new method yields
magnitudes may be 0.2 mag larger than those estimated by Messineo et al. (2005). This systematic error could be corrected a posteriori. However, as shown in the discussion section, for Miras at the Galactic center the new method yields ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq71.png) values that are 0.1 mag smaller than comparison values from the literature. The regression line for the WISE dataset shows a larger offset from the equity line of 0.4 mag at
values that are 0.1 mag smaller than comparison values from the literature. The regression line for the WISE dataset shows a larger offset from the equity line of 0.4 mag at ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq72.png) = 2 mag. This method allows for an accuracy of ≈0.35 mag, which corresponds to the scatter of the data points in the diagram J-Ks versus Ks−D of Fig. 1 (the NIR and MIR measurements were not acquired simultaneously).
= 2 mag. This method allows for an accuracy of ≈0.35 mag, which corresponds to the scatter of the data points in the diagram J-Ks versus Ks−D of Fig. 1 (the NIR and MIR measurements were not acquired simultaneously).
 |
Fig. 2 Comparison of |
 |
Fig. 3 Comparison of the three |
3.5 Estimates of ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq84.png) (env) as
(env) as ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq85.png) (tot)−
(tot)−![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq86.png) (int)
(int)
The H-Ks colours of naked giants were calculated by synthetic photometry of theoretical spectra. For this purpose, the publicly available NextGen spectra of Allard et al. (2011) with Teff=3500, 3200, 2600 K, log10(g) = 1, and solar metallicity were used4. The synthetic spectra were generated with the PHOENIX atmospheric code considering spherical symmetry. The synthetic spectra reproduce the TiO and VO molecules, which dominate the optical spectrum, and water vapour and CO molecules in the infrared spectrum. The molecular list was refined to reproduce the atmospheric lines of brown dwarfs (Allard et al. 2011; Allard 2014). The infrared colours are obtained by convolving the spectrum with the filter and calculating the mean flux density. The adopted zero points come from Cohen et al. (2003, 2MASS), Egan et al. (2003, MSX), Jarrett et al. (2011, WISE), and Fazio et al. (2004, GLIMPSE). The synthetic infrared colours are listed in Table 4.
The average differences between the ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq87.png) (tot) calculated with the synthetic (H-Ks) colours and those obtained with the colours of Koornneef (1983) are +0.05 mag with σ=0.00 mag (M4) and +0.14 mag with σ=0.00 mag (M6). While the average differences between the
(tot) calculated with the synthetic (H-Ks) colours and those obtained with the colours of Koornneef (1983) are +0.05 mag with σ=0.00 mag (M4) and +0.14 mag with σ=0.00 mag (M6). While the average differences between the ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq88.png) (tot) calculated with the synthetic (H-Ks) colours for a 3500 K (M4) and a 3200 K (M5–6) star are +0.015 mag with σ=0.006 mag. The
(tot) calculated with the synthetic (H-Ks) colours for a 3500 K (M4) and a 3200 K (M5–6) star are +0.015 mag with σ=0.006 mag. The ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq89.png) (int) values were re-determined using the fiducial color sequences Qλ ∝ (KS − λ)o, as described in Sec. 3.
(int) values were re-determined using the fiducial color sequences Qλ ∝ (KS − λ)o, as described in Sec. 3.
Using the derived ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq90.png) (tot) and
(tot) and ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq91.png) (int), we could estimate the envelope extinction
(int), we could estimate the envelope extinction ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq92.png) (env) for 324 targets.
(env) for 324 targets. ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq93.png) (env)=
(env)=![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq94.png) (tot)−
(tot)−![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq95.png) (int) ranges from 0 to 2.5 mag, as shown in Fig. 4. The envelope's optical depth at 0.55 μm, τ0.55, ranges from 0 to 32 when estimating it as: ≈
(int) ranges from 0 to 2.5 mag, as shown in Fig. 4. The envelope's optical depth at 0.55 μm, τ0.55, ranges from 0 to 32 when estimating it as: ≈![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq96.png) (env)/0.0775.
(env)/0.0775.
Naked star colours.
3.6 Empirical circumstellar excess colors
The naked colours listed in Table 4 can be useful for determining the colour excess ratios and to set constraints on the circumstellar extinction curve.
A circumstellar colour excess is defined as
![$\[E(K s-[\lambda])_{\mathrm{env}}=(K s-[\lambda])_o-(K s-[\lambda])_{\text {naked }} \text{,}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq97.png) (8)
(8)
where (Ks − [λ])o is the interstellar-dereddened colour and (Ks −[λ])naked is the expected color for a star of similar parameters (e.g., gravity, metallicity, and temperature), but without an envelope. For the (Ks − [λ])naked values, the synthetic colors are taken from a stellar model with a temperature of 3200 K (Table 4).
In Fig. 5, the E(Ks − [D]) colour excess is plotted against the E(K − [A]), E(Ks − [C]), and E(Ks − [E]) color excess. Figures 6 and 7 show similar diagrams for the WISE and GLIMPSE filters. There is a tight correlation between the MSX excess colours, as well as between the E(Ks − [W4]) and E(Ks − [W3]) excess colors and the E(Ks − [8.0]) and E(Ks − [5.8]) excess colors. On the contrary, a large scatter appears in the diagrams showing the E(Ks − [W1]), E(Ks − [W2]), E(Ks − [3.6]), and E(Ks − [4.5]) excess colours in Figs. 6 and 7. Indeed, the stellar spectrum of cold stars at wavelengths shorter than 4 μm is dominated by strong molecular bands (Bedijn 1987). Furthermore, the data used here are from a single-epoch, and the NIR and MIR data were not taken simultaneously. The radial pulsation expands the atmosphere, and creates an extra layer of molecules (CO, H2O, CO2, and SiO) above the atmosphere. The region from 2.4 to 4 μm is dominated by strong water vapour, which is the main source of opacity. The water vapour absorption changes dramatically with the pulsation phase (Matsuura et al. 2002). This extended layer of molecules was analyzed in detail in the work of Matsuura et al. (2002) and Cami (2002). The larger scatter of data points shown in Figs. 6 and 7, with the filters W1 and W2, and with the filters [3.6] and [4.5], indicates the presence of strong absorption by water.
A tighter correlation of the colour excess E(Ks-D) with E(Ks-A), E(Ks-C), and E(Ks-E) confirms that the filters A, C, D, and E are dominated by dust emission, as well as W3, W4, [5.8], and [8.0]. As already reported by Volk & Kwok (1988) for the LRS spectra: “in the region from 8 to 23 μm the emergent spectrum will directly reflect the shape of the opacity function.”
Using Eq. (8), the excess ratios can also be calculated. The median excess ratios and standard deviations are tabulated in Tables 5 and 6. The excess ratios were calculated with the MSX bands, WISE W3 and W4, and GLIMPSE [8.0] bands. They appear to be described by constant values and can provide constraints on the circumstellar extinction curve of the sampled O-rich AGB stars (e.g., Bedijn 1987; Volk & Kwok 1988; Ossenkopf et al. 1992).
 |
Fig. 4 Histogram of the obtained interstellar AK values (black line). The envelope AK values ( |
4 A grid of blackbody models with mass loss
We assumed a fixed temperature of 3200 K (M6), the astronomical silicate grains of Ossenkopf et al. (1992) as well as the silicate grains of Suh (1999). We used the DUSTY code of Ivezic et al. (1999) to generate a set of SED models with optical depth, τ0.55μm, from 0 to 40. The model consists of a spherical shell with density decreasing with R−2. The dust condensation radius was set to 1000 K.
In the diagram depicting W1 − W4 versus Ks−W4, the models aptly describe the data points of Messineo et al. (2018), as shown in Fig. 8. In the diagram W3 − W4 versus Ks-W4, the models with the Ossenkopf's silicate grains display smaller W3 − W4 than the data points, while the models with the cold silicates by Suh (1999) reproduce the observed colours (Suh 2021). Indeed, the W3 filter encompasses the 10 μm, as well as the 13 μm, and the 18 μm dust features. SED models with Suh's silicates and models with Ossenkopf's silicates agree short-ward of 10 μm; but they disagree around 18 μm (Suh 1999). Suh's warm silicates generate a smaller emission feature at 18 μm than the cold silicates (Suh 1999). Suh's cold silicates generate a stronger absorption feature at 18 μm and a stronger continuum longward of 18 μm than Ossenkopf's silicates (Suh 1999) and generate larger W3-W4 colours.
Figure 8 shows how changing the τ results in a colour-colour track, given a stellar temperature and a dust type. Each point on the track represents a specific tau-point. However, when varying the dust size, the τ scale changes. This can be seen in Fig. 9, where the dereddened (Ks−W4)o is plotted against the τ envelope. A larger maximum size results in a larger τ for a given colour. In recent literature, the standard distribution of grain sizes, MNR, is usually adopted with maximum sizes from 0.1 to 1. μm (e.g., Olofsson et al. 2022; van Loon et al. 2005; Wang et al. 2021) or fixed sizes of 0.1–0.5 μm (e.g., Blommaert et al. 2018; Suh 2021).
Circumstellar effective extinction ratios are highly dependent on the maximum grain size. We estimated that τ2.2 = 2.48 × τ9.7 using the DUSTY code, the astronomical silicate grains by Ossenkopf et al. (1992), and an MNR distribution from 0.005 to 0.75 μm. For a maximum size of 0.45 μm, τ2.2 = 1.47 × τ9.7, and τ2.2 = 0.71 × τ9.7 when the maximum size is 0.25 μm. Four circumstellar extinction curves with the MNR distribution and maximum sizes of 2.00, 0.75, 0.45, and 0.25 μm are plotted in Fig. 10 to illustrate this. The curves show different peak values of the 9.7 feature (0.49–0.50, 0.44–0.46, 0.77–0.78, and 1.59–1.61, respectively) when normalizing at 2.12 μm. Compared to a curve with a maximum grain size of 0.25 μm, an extinction curve with a maximum grain size of 0.75 μm appears to have a lower 9.7 μm peak opacity. In the near-infrared, the same curve appears located above the curve with a maximum grain size of 0.25 μm, when normalized at 9.7 μm.
In Table 7, theoretical excess ratios are calculated by convolving the curves with a maximum grain size of 2.00 μm, 0.75 μm, and 0.25 μm with the filter profiles and a cool spectrum by Allard et al. (2011). A comparison of the theoretical excess ratios of Table 7 with those observationally measured (Table 5), suggests that an MNR distribution with a maximum grain size of 0.25 μm produces excess ratios that are incompatible with those observed ![$\[\left(\frac{E(K s-C)}{E(K s-D)}\right.\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq101.png) much lower than unity and
much lower than unity and ![$\[\frac{E(K s-W 2)}{E(K s-W 3)}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq102.png) above unity). An MNR distribution with a maximum grain size of 0.75 μm provides a better agreement with the data for the MSX data. An MNR distribution with a maximum grain size of 2.00 μm also reproduces the trends seen in Table 5 for the WISE and GLIMPSE filters short-ward of 8 μm (these filters are affected by molecular absorption).
above unity). An MNR distribution with a maximum grain size of 0.75 μm provides a better agreement with the data for the MSX data. An MNR distribution with a maximum grain size of 2.00 μm also reproduces the trends seen in Table 5 for the WISE and GLIMPSE filters short-ward of 8 μm (these filters are affected by molecular absorption).
In order to reproduce the observed colours, small values of the maximum grain sizes (0.1–0.25 μm) are frequently reported in the literature. For instance, Volk & Kwok (1988) estimated τ2.2 = 0.4 × τ9.7 for their sample of IRAS sources using dust grain sizes smaller than 0.25 μm. However, as David & Papoular (1990) points out, observational data (IRAS data) only constrains their opacity curve in the mid-infrared region; for the near-infrared curve, the theoretical model by Draine (1985) is used. Bedijn (1987) uses a power law with an index −1.5 for the opacity curve below 5 μm, yielding τ1.65 = 0.67 × τ9.7.
Recently, Maercker et al. (2022) preferred larger grain sizes (2 μm) to fit the far-infrared fluxes of Carbon AGB stars. Large dust grains with an average size of 0.5 μm were detected in the envelopes of VY Canis Majoris (Scicluna et al. 2015) and of W Hydrae (Ohnaka et al. 2016) with optical polarimetric imaging.
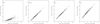 |
Fig. 5 Circumstellar color excess of the sample stars with 2MASS and MSX colours (based on the naked colours of a 3200 K star). |
 |
Fig. 6 Circumstellar color excess of the sample stars with 2MASS and WISE colours (based on the naked colours of a 3200 K star). |
 |
Fig. 7 The circumstellar colour excess of the sample stars with 2MASS and GLIMPSE colours (based on the naked colours of a 3200 K star). |
Observed circumstellar excess ratios, based on the naked colours of a 3200 K star.
Observed circumstellar excess ratios, based on the naked colors of a 2600 K star.
 |
Fig. 8 Dereddened (W3−W4)o vs. (Ks−W4)o (top). Dereddened (W1−W4)o vs. (Ks−W4)o (bottom). The panels on the left show the models obtained with blackbodies of 3200 K and 2000 K and the astronomical silicate of Ossenkopf et al. (1992) and Suh (1999). The panels on the right show the models with the synthetic spectra of 3200 K and 2600 K of Allard et al. (2011) and the astronomical silicate of Ossenkopf et al. (1992) and Suh (1999). It appears that the curves of stars of 3200 K and 2600 K are similar and that the main parameter is the dust type and the maximum grain size. A smaller maximum grain size increases the span of colours (extending the curve to redder colours). |
 |
Fig. 9 τ envelope (τ total minus τ interstellar) values of stars in Messineo et al. (2018) are plotted versus the dereddened (Ks−W4)o colours. Top panel: dusty models with a blackbody of 3200 K. Bottom panel shows dusty models of giant synthetic spectra with Teff of 2600 K (in orange) and 3200 K (in green), log = 1, and Z = 0 dex, from the NextGen library of Hauschildt et al. (1999). For every synthetic spectrum, three different curves obtained with DUSTY are over-plotted. The dashed-dotted model shows dust grains with a fixed size of 0.1 μm. The dotted model uses the MNR distribution with a minimum of 0.005 um and a maximum of 0.25 μm. The dashed model is based on the MNR distribution and has a maximum of 0.1 μm. |
5 Discussion
Relations between the de-reddened colours and the extinction-free colours Q1, Q2, QA, QC,... QW4 were constructed using a set of O-rich Mira-like stars with known interstellar extinction (Messineo et al. 2005). Such equations allow us to determine the interstellar extinction for every Mira-like star that has accessible near- and mid-infrared (NIR-MIR) colours.
In order to verify the applicability and reliability of the new methodology in determining interstellar extinction, we carried out an analysis of existing catalogs of Miras with available JHK and MIR measurements.
The most obscured Miras often exhibit OH maser emission and are therefore called OH/IR stars. Typically, their flux distribution is modeled with radiative transfer codes, and their interstellar extinction is derived from infrared extinction maps. For example, Olofsson et al. (2022) analyzed a sample of 22 AGB stars with OH masers near the Galactic center by using CO line observations taken with The Atacama large (sub-)millimeter array (Alma) array. The map of extinction by Gonzalez et al. (2018) and the extinction law by Nishiyama et al. (2009) were used. Archival JHK photometry (from the 2MASS, VVV, and UKIDSS surveys6, the catalogues of Nogueras-Lara et al. (2019, 2021) and mid-infrared photometry from GLIMPSE surveys (5.8 and 8.0 um) could be retrieved from the VIZIER database for 8 stars of the Olofsson's sample. The equations of Table 2 were used to make interstellar extinction estimates (![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq107.png) (int) from 0.90 to 2.0 mag). The two sets of
(int) from 0.90 to 2.0 mag). The two sets of ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq108.png) (int) linearly correlate with a standard deviation σ=0.49 mag and a mean difference (this work – Olofsson's values) of 0.09 mag (or 0.24 mag when rescaling the extinction to a power law with index = −2.1). The noncoevality of the near- and mid-infrared photometry accounts for the large σ; the OH/IR stars have typical Ks amplitudes ranging from 0.9 to 2.5 mag (Messineo et al. 2020).
(int) linearly correlate with a standard deviation σ=0.49 mag and a mean difference (this work – Olofsson's values) of 0.09 mag (or 0.24 mag when rescaling the extinction to a power law with index = −2.1). The noncoevality of the near- and mid-infrared photometry accounts for the large σ; the OH/IR stars have typical Ks amplitudes ranging from 0.9 to 2.5 mag (Messineo et al. 2020).
Using data from the ISOGAL survey (Omont et al. 2003), Ojha et al. (2003) determined interstellar extinction, mass loss rate, and luminosity values for 321 late-type stars located in Bulge fields at (|l| < 2°, |b| ≈ 1° − 4°). The majority of the sampled stars are AGB stars because they are brighter than the stars at the tip of the red giant branch. The authors used DENIS IJKs and ISOGAL photometry at 7 and 15 μm and the silicate models by Jeong et al. (2003). The new method was used to estimate AK (int) for 228 stars in this sample based on GLIMPSE and 2MASS data. The Ojha's AV values are converted to ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq109.png) using a factor of 0.089 (Ojha et al. 2003) and then compared with the
using a factor of 0.089 (Ojha et al. 2003) and then compared with the ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq110.png) obtained here. The mean difference is 0.09 mag and a σ = 0.20 mag.
obtained here. The mean difference is 0.09 mag and a σ = 0.20 mag.
Matsunaga et al. (2009) estimate the AK (int) values of 52 Mira stars at the Galactic center using average near-infrared measurements and the extinction law by Nishiyama et al. (2006). The average JHK measurements along with the GLIMPSE [5.8] and [8.0] magnitudes are used to compute the ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq111.png) (int) values for 30 stars using the new method. The
(int) values for 30 stars using the new method. The ![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq112.png) (HK) from Matsunaga were converted to a power law with index =−2.1 (by multiplying for 0.91) and range from 1.81 to 2.59 mag. An average difference between Matsunaga's extinction values and the here estimated values of +0.1 mag is obtained and σ = 0.16 mag.
(HK) from Matsunaga were converted to a power law with index =−2.1 (by multiplying for 0.91) and range from 1.81 to 2.59 mag. An average difference between Matsunaga's extinction values and the here estimated values of +0.1 mag is obtained and σ = 0.16 mag.
The established equations between intrinsic infrared colours and extinction-free colours (Qλ), which are listed in Table 2, are useful to automatically determine stellar obscuration. This set of equations can be used to select late-type stars in a given sky region, and to improve their estimates of luminosity.
Assuming a reasonable estimate of the total, the envelope extinction can be calculated as the difference between the total and the interstellar extinction. Mathematically, it is a straightforward calculation. In reality, estimating the circumstellar extinction is actually difficult because accurate spectral types are lacking, naked-star colours are unknown and affected by strong variable molecular absorption.
Future photometric multi-wavelengths and multi-epochs surveys and spectroscopic surveys, such as LSST, Gaia DR4, 4MOST, and GALAH, will enable us to obtain spectral types and temperatures, and their variations. As a result, we will be able to obtain more accurate extinction calculations.
 |
Fig. 10 Four circumstellar extinction curves were estimated with DUSTY using an MNR distribution and dust sizes from 0.005 to 0.25, 0.45, 0.75, and 2.00 μm, respectively. The curves are normalized to 9.7 μm in the left panels and 2.12 in the right panels. The astronomical silicate grains by Ossenkopf et al. (1992) for a maximum grain size of 0.25 μm (black), 0.45 μm (orange), 0.75 μm (cyan), and 2.00 μm (green) are used in the two upper panels; while in the two lower panels the silicate grains of Suh (1999) are used. The squares mark the circumstellar effective extinction ratios measured on SED models generated with the DUSTY code. The curves are obtained by interpolating the ratios to a finer grid (0.1 μm). |
Circumstellar model excess ratios.
Acknowledgements
This work has made use of data from the European Space Agency (ESA) mission Gaia (http://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, http://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center / California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This work is based on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. This research made use of data products from the Midcourse Space Experiment, the processing of which was funded by the Ballistic Missile Defense Organization with additional support from the NASA office of Space Science. This publication makes use of data products from WISE, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory / California Institute of Technology, funded by the National Aeronautics and Space Administration. This research has made use of the VizieR catalogue access tool, CDS, Strasbourg, France, and SIMBAD database. This research utilized the NASA's Astrophysics Data System Bibliographic Services. This work is based on the PhD thesis by Messineo M. (2004) which was supported by the Netherlands Research School for Astronomy (NOVA) through a netwerk 2, Ph.D. stipend. MM thanks Dr. Harm Habing and Dr. Frank Bertoldi for insightful discussions on interstellar extinction during her PhD thesis, and the anonymous referee for his constructive inputs.
Appendix A Qλ and the jolly equation
This is the definition of (Ks-λ) colour excess:
![$\[E(K s-\lambda)=A_{K s} \times\left(1-\frac{A_\lambda}{A_{K s}}\right),\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq113.png) (A.1)
(A.1)
![$\[A_{K s}(\text { interstellar })=\frac{[(K s-\lambda)-(K s-\lambda) o]}{\left(1-\frac{A_\lambda}{A_{K s}}\right)},\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq114.png) (A.2)
(A.2)
![$\[A_{K s}(\text { interstellar })=\frac{[(H-K s)-(H-K s) o]}{\left.\frac{A_H}{\left(A_{K s}\right.}-1\right)},\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq115.png) (A.3)
(A.3)
By combining Eq. A.2 and A.3, it is obtained
![$\[\frac{[(K s-\lambda)-(K s-\lambda) o]}{\left(1-\frac{A_\lambda}{A_{K s}}\right)}~~=\frac{[(H-K s)-(H-K s) o]}{\left(\frac{A_H}{A_{K s}}-1\right)},\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq116.png) (A.4)
(A.4)
The A.5 is the definition of the ![$\[Q_\lambda^{H K}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq119.png) parameter. The first member contains observed quantities, while the second term only contains intrinsic colours. This equivalence proves that
parameter. The first member contains observed quantities, while the second term only contains intrinsic colours. This equivalence proves that ![$\[Q_\lambda^{H K}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq120.png) does not depend on interstellar extinction. It is an intrinsic colour of the star. Analogously, a function
does not depend on interstellar extinction. It is an intrinsic colour of the star. Analogously, a function ![$\[Q_\lambda^{J K}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq121.png) can be defined with the J − Ks colour.
can be defined with the J − Ks colour.
Appendix B BC and intrinsic colours versus Qλ
In Messineo (2004), ![$\[\mathrm{BC}_{K_S}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq122.png) values as a function of infrared colours were obtained for the MSX filters. Mbol values and dereddened WISE and GLIMPSE magnitudes from the revised catalog of Messineo et al. (2018) are here used to extend the BC computation to the WISE and Glimpse filters. Polynomial fits are listed in Table B.1.
values as a function of infrared colours were obtained for the MSX filters. Mbol values and dereddened WISE and GLIMPSE magnitudes from the revised catalog of Messineo et al. (2018) are here used to extend the BC computation to the WISE and Glimpse filters. Polynomial fits are listed in Table B.1.
The ![$\[\mathrm{BC}_{K_S}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq123.png) values and the intrinsic colours are plotted versus the interstellar-extinction-free parameter Qλ in Figs. B.1, B.2, and B.3 for the MSX, WISE, and GLIMPSE filters.
values and the intrinsic colours are plotted versus the interstellar-extinction-free parameter Qλ in Figs. B.1, B.2, and B.3 for the MSX, WISE, and GLIMPSE filters.
Polynomial fits to the infrared BC values versus the dereddened colours.
Polynomial fits to the infrared BC values versus the dereddened colours.
 |
Fig. B.1 Correlations between the Qλ values and the BCλ and Ks−[λ] values. Left panel: BCλ values vs. Qλ, for the MSX bands (A, C, D, E). Right panel: De-reddened Ks−[λ] colours vs. Qλ. The red dotted lines are the fits given in Table 2. Stars with MSX A,C,D, and E magnitudes available are plotted. |
 |
Fig. B.2 BCλ values and Ks−[λ] colours vs. Qλ, for the WISE bands (W1, W2, W3, and W4). Stars with all four WISE magnitudes available are plotted. The red dotted lines are the fits given in Table 2. |
 |
Fig. B.3 BCλ values and Ks−[λ] colours vs. Qλ, for the GLIMPSE bands ([3.6], [4.5], [5.8], and [8.0]). Stars with all four GLIMPSE magnitudes available are plotted. The red dotted lines are the fits given in Table 2. |
References
- Allard, F. 2014, in Exploring the Formation and Evolution of Planetary Systems, 299, eds. M. Booth, B. C. Matthews, & J. R. Graham 271 [Google Scholar]
- Allard, F., Homeier, D., & Freytag, B. 2011, in Astronomical Society of the Pacific Conference Series, 448, 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. C. Johns-Krull, M. K. Browning, & A. A. West, 91 [Google Scholar]
- Bayo, A., Rodrigo, C., Barrado Y Navascués, D., et al. 2008, A&A, 492, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bedijn, P. J. 1987, A&A, 186, 136 [NASA ADS] [Google Scholar]
- Blommaert, J. A. D. L., Groenewegen, M. A. T., Justtanont, K., & Decin, L. 2018, MNRAS, 479, 3545 [CrossRef] [Google Scholar]
- Cami, J. 2002, PhD thesis, University of Amsterdam, The Netherlands [Google Scholar]
- Churchwell, E., Babler, B. L., Meade, M. R., et al. 2009, PASP, 121, 213 [Google Scholar]
- Cohen, M., Wheaton, W. A., & Megeath, S. T. 2003 AJ, 126, 1090 [Google Scholar]
- David, P., & Papoular, R. 1990, A&A, 237, 425 [NASA ADS] [Google Scholar]
- Draine, B. T. 1985, ApJS, 57, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Egan, M. P., Price, S. D., & Kraemer, K. E. 2003, in Air Force Research Laboratory Technical Report N. AFRL-VS-TR-2003-1589, 1, 1 [Google Scholar]
- Epchtein, N., de Batz, B., Copet, E., et al. 1994, Ap&SS, 217, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Eyer, L., Audard, M., Holl, B., et al. 2023, A&A, 674, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [Google Scholar]
- Fritz, T. K., Gillessen, S., Dodds-Eden, K., et al. 2011, ApJ, 737, 73 [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glass, I. S., & Schultheis, M. 2002, MNRAS, 337, 519 [CrossRef] [Google Scholar]
- Gonzalez, O. A., Minniti, D., Valenti, E., et al. 2018, MNRAS, 481, L130 [Google Scholar]
- Gordon, K. D., Misselt, K. A., Bouwman, J., et al. 2021, ApJ, 916, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Habing, H. J., Sevenster, M. N., Messineo, M., van de Ven, G., & Kuijken, K. 2006, A&A, 458, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hauschildt, P. H., Allard, F., Ferguson, J., Baron, E., & Alexander, D. R. 1999, ApJ, 525, 871 [Google Scholar]
- Indebetouw, R., Mathis, J. S., Babler, B. L., et al. 2005, ApJ, 619, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezic, Z., Nenkova, M., & Elitzur, M. 1999, arXiv e-prints, [arXiv:astro-ph/9910475] [Google Scholar]
- Jarrett, T. H., Cohen, M., Masci, F., et al. 2011, ApJ, 735, 112 [Google Scholar]
- Jeong, K. S., Winters, J. M., Le Bertre, T., & Sedlmayr, E. 2003, in Astrophysics and Space Science Library, 283, Mass-Losing Pulsating Stars and their Circumstellar Matter, eds. Y. Nakada, M. Honma, & M. Seki, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Koornneef, J. 1983, A&A, 128, 84 [NASA ADS] [Google Scholar]
- Lebzelter, T., Mowlavi, N., Lecoeur-Taibi, I., et al. 2023, A&A, 674, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, Y. S., Beers, T. C., An, D., et al. 2011, ApJ, 738, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Lucas, P. W., Hoare, M. G., Longmore, A., et al. 2008, MNRAS, 391, 136 [Google Scholar]
- Maercker, M., Khouri, T., Mecina, M., & De Beck, E. 2022, A&A, 663, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsuura, M., Yamamura, I., Cami, J., Onaka, T., & Murakami, H. 2002, A&A, 383, 972 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsunaga, N., Kawadu, T., Nishiyama, S., et al. 2009, MNRAS, 399, 1709 [NASA ADS] [CrossRef] [Google Scholar]
- Messineo, M. 2004, PhD thesis, Leiden Observatory, Leiden University, The Netherlands [Google Scholar]
- Messineo, M. 2022, PASJ, 74, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Messineo, M., Habing, H. J., Sjouwerman, L. O., Omont, A., & Menten, K. M. 2002, A&A, 393, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Messineo, M., Habing, H. J., Menten, K. M., Omont, A., & Sjouwerman, L. O. 2004, A&A, 418, 103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Messineo, M., Habing, H. J., Menten, K. M., et al. 2005, A&A, 435, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Messineo, M., Menten, K. M., Churchwell, E., & Habing, H. 2012, A&A, 537, A10 [Google Scholar]
- Messineo, M., Habing, H. J., Sjouwerman, L. O., Omont, A., & Menten, K. M. 2018, A&A, 619, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Messineo, M., Sjouwerman, L. O., Habing, H. J., & Omont, A. 2020, PASJ, 72, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Nagata, T., Kusakabe, N., et al. 2006, ApJ, 638, 839 [Google Scholar]
- Nishiyama, S., Tamura, M., Hatano, H., et al. 2009, ApJ, 696, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Nogueras-Lara, F., Schödel, R., Gallego-Calvente, A. T., et al. 2019, A&A, 631, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nogueras-Lara, F., Schödel, R., Neumayer, N., et al. 2020, A&A, 641, A141 [EDP Sciences] [Google Scholar]
- Nogueras-Lara, F., Schödel, R., & Neumayer, N. 2021, A&A, 653, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohnaka, K., Weigelt, G., & Hofmann, K. H. 2016, A&A, 589, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ojha, D. K., Omont, A., Schuller, F., et al. 2003, A&A, 403, 141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olofsson, H., Khouri, T., Sargent, B. A., et al. 2022, A&A, 665, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Omont, A., Gilmore, G. F., Alard, C., et al. 2003, A&A, 403, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V., Henning, T., & Mathis, J. S. 1992, A&A, 261, 567 [NASA ADS] [Google Scholar]
- Perrin, G., Coudé du Foresto, V., Ridgway, S. T., et al. 1998, A&A, 331, 619 [NASA ADS] [Google Scholar]
- Price, S. D., Egan, M. P., Carey, S. J., Mizuno, D. R., & Kuchar, T. A. 2001, AJ, 121, 2819 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [Google Scholar]
- Rosenthal, D., Bertoldi, F., & Drapatz, S. 2000, A&A, 356, 705 [NASA ADS] [Google Scholar]
- Scicluna, P., Siebenmorgen, R., Wesson, R., et al. 2015, A&A, 584, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Soto, M., Barbá, R., Gunthardt, G., et al. 2013, A&A, 552, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stead, J. J., & Hoare, M. G. 2009, MNRAS, 400, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Suh, K.-W. 1999, MNRAS, 304, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Suh, K.-W. 2021, ApJS, 256, 43 [NASA ADS] [CrossRef] [Google Scholar]
- van Belle, G. T., von Braun, K., Ciardi, D. R., et al. 2021, ApJ, 922, 163 [Google Scholar]
- van Loon, J. T., Marshall, J. R., & Zijlstra, A. A. 2005, A&A, 442, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Volk, K., & Kwok, S. 1988, ApJ, 331, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S., & Chen, X. 2019, ApJ, 877, 116 [Google Scholar]
- Wang, T., Jiang, B., Ren, Y., Yang, M., & Li, J. 2021, ApJ, 912, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
2MASS stands for Two Micron All Sky Survey (Skrutskie et al. 2006), DENIS for Deep Near Infrared Survey of the Southern Sky (Epchtein et al. 1994), MSX for Midcourse Space Experiment (Price et al. 2001), WISE for Wide-field Infrared Survey Explorer (Wright et al. 2010), and GLIMPSE for Galactic Legacy Infrared Mid-Plane Survey Extraordinaire (Churchwell et al. 2009).
The 2.69 coefficient is obtained using the effective extinction values of Indebetouw et al. (2005).
This is a revised version of curve 3 in Messineo et al. (2005), where the 3–8 μm opacity enhancement had been taken as a constant.
The spectra are distributed by the Virtual Observatory SED analyzer (Bayo et al. 2008). The bt-nextgen_agss2009 (gas only) were retrieved.
AV/![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq126.png) = 12.99 is appropriated for an interstellar infrared power law of index = −2.1 and RV = 3.1 (Messineo et al. 2005). This conversion factor is close to the 12.82 obtained by Wang & Chen (2019) for Galactic extinction. As shown in the next section, for a circumstellar extinction law, the actual A0.55/A2.2 ratio depends on the adopted grain sizes. It is 15.7 for a maximum size of 0.25 μm and 3.7 for a maximum size of 0.75 μm.
= 12.99 is appropriated for an interstellar infrared power law of index = −2.1 and RV = 3.1 (Messineo et al. 2005). This conversion factor is close to the 12.82 obtained by Wang & Chen (2019) for Galactic extinction. As shown in the next section, for a circumstellar extinction law, the actual A0.55/A2.2 ratio depends on the adopted grain sizes. It is 15.7 for a maximum size of 0.25 μm and 3.7 for a maximum size of 0.75 μm.
VVV stands for the VISTA Variables in the Via Lactea survey (Soto et al. 2013). The UKIDSS Galactic Plane Survey (GPS) is described in Lucas et al. (2008).
All Tables
Coefficients of the polynomial fits between (Ks−[λ])o colours and the Qλ parameters, using curve 3.
Coefficients of the polynomial fits between (Ks−[λ])o colours and the Qλ parameters, based on the interstellar extinction curve by Gordon et al. (2021).
Observed circumstellar excess ratios, based on the naked colours of a 3200 K star.
Observed circumstellar excess ratios, based on the naked colors of a 2600 K star.
All Figures
 |
Fig. 1 Correlations between intrinsec colours and between Q(λ) values and intrinsec colours. Left panel: Intrinsic (Ks−[D])o versus (H-Ks)o colours of Messineo et al. (2005), de-reddened using the median interstellar extinction of surrounding stars, shown in black. For comparison, in gray, we give the observed (Ks−[D]) versus (H-Ks) colours. Middle panel: Q(D) colours vs. (Ks−[D])o, for the MSX D-band. Right panel: Q(E) colours versus (Ks−[E])o, for the MSX E-band. The red dotted lines are fits to the data points. Error bars on the Q(D) and Q(E) are obtained by propagating the errors on the J, H, Ks, D, and E magnitudes. |
| In the text | |
 |
Fig. 2 Comparison of |
| In the text | |
 |
Fig. 3 Comparison of the three |
| In the text | |
 |
Fig. 4 Histogram of the obtained interstellar AK values (black line). The envelope AK values ( |
| In the text | |
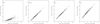 |
Fig. 5 Circumstellar color excess of the sample stars with 2MASS and MSX colours (based on the naked colours of a 3200 K star). |
| In the text | |
 |
Fig. 6 Circumstellar color excess of the sample stars with 2MASS and WISE colours (based on the naked colours of a 3200 K star). |
| In the text | |
 |
Fig. 7 The circumstellar colour excess of the sample stars with 2MASS and GLIMPSE colours (based on the naked colours of a 3200 K star). |
| In the text | |
 |
Fig. 8 Dereddened (W3−W4)o vs. (Ks−W4)o (top). Dereddened (W1−W4)o vs. (Ks−W4)o (bottom). The panels on the left show the models obtained with blackbodies of 3200 K and 2000 K and the astronomical silicate of Ossenkopf et al. (1992) and Suh (1999). The panels on the right show the models with the synthetic spectra of 3200 K and 2600 K of Allard et al. (2011) and the astronomical silicate of Ossenkopf et al. (1992) and Suh (1999). It appears that the curves of stars of 3200 K and 2600 K are similar and that the main parameter is the dust type and the maximum grain size. A smaller maximum grain size increases the span of colours (extending the curve to redder colours). |
| In the text | |
 |
Fig. 9 τ envelope (τ total minus τ interstellar) values of stars in Messineo et al. (2018) are plotted versus the dereddened (Ks−W4)o colours. Top panel: dusty models with a blackbody of 3200 K. Bottom panel shows dusty models of giant synthetic spectra with Teff of 2600 K (in orange) and 3200 K (in green), log = 1, and Z = 0 dex, from the NextGen library of Hauschildt et al. (1999). For every synthetic spectrum, three different curves obtained with DUSTY are over-plotted. The dashed-dotted model shows dust grains with a fixed size of 0.1 μm. The dotted model uses the MNR distribution with a minimum of 0.005 um and a maximum of 0.25 μm. The dashed model is based on the MNR distribution and has a maximum of 0.1 μm. |
| In the text | |
 |
Fig. 10 Four circumstellar extinction curves were estimated with DUSTY using an MNR distribution and dust sizes from 0.005 to 0.25, 0.45, 0.75, and 2.00 μm, respectively. The curves are normalized to 9.7 μm in the left panels and 2.12 in the right panels. The astronomical silicate grains by Ossenkopf et al. (1992) for a maximum grain size of 0.25 μm (black), 0.45 μm (orange), 0.75 μm (cyan), and 2.00 μm (green) are used in the two upper panels; while in the two lower panels the silicate grains of Suh (1999) are used. The squares mark the circumstellar effective extinction ratios measured on SED models generated with the DUSTY code. The curves are obtained by interpolating the ratios to a finer grid (0.1 μm). |
| In the text | |
 |
Fig. B.1 Correlations between the Qλ values and the BCλ and Ks−[λ] values. Left panel: BCλ values vs. Qλ, for the MSX bands (A, C, D, E). Right panel: De-reddened Ks−[λ] colours vs. Qλ. The red dotted lines are the fits given in Table 2. Stars with MSX A,C,D, and E magnitudes available are plotted. |
| In the text | |
 |
Fig. B.2 BCλ values and Ks−[λ] colours vs. Qλ, for the WISE bands (W1, W2, W3, and W4). Stars with all four WISE magnitudes available are plotted. The red dotted lines are the fits given in Table 2. |
| In the text | |
 |
Fig. B.3 BCλ values and Ks−[λ] colours vs. Qλ, for the GLIMPSE bands ([3.6], [4.5], [5.8], and [8.0]). Stars with all four GLIMPSE magnitudes available are plotted. The red dotted lines are the fits given in Table 2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\[C_\lambda^{J K s}=\frac{\frac{A_J}{A_{K \mathrm{~s}}}-1.}{1.-\frac{A_\lambda}{A_{K_{\mathrm{s}}}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq37.png)
![$\[Q_\lambda^{H K s}=(H-K s)-C_\lambda^{H K s} \times(K s-[\lambda]),\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq38.png)
![$\[C_\lambda^{H K s}=\frac{\frac{A_H}{A_{K_{\mathrm{s}}}}-1.}{1.-\frac{A_\lambda}{A_{K_{\mathrm{s}}}}}.\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq39.png)
![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq73.png)
![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq74.png)
![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq75.png)
![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq76.png)
![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq77.png)
![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq78.png)
![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq79.png)
![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq80.png)
![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq81.png)
![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq82.png)
![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq83.png)
![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq98.png)
![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq99.png)
![$\[A_{K_{\mathrm{s}}}\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq100.png)
![$\[(H-K s)-(K s-\lambda) * C o=(H-K s) o-(K s-\lambda) o * C o=Q_\lambda,\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq117.png)
![$\[C o=\frac{\left(\frac{A_H}{A_{K s}}-1\right)}{\left(1-\frac{A_\lambda}{A_{K s}}\right)} \text {. }\]$](/articles/aa/full_html/2024/06/aa47661-23/aa47661-23-eq118.png)