| Issue |
A&A
Volume 686, June 2024
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 29 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202347286 | |
| Published online | 30 May 2024 | |
The effect of lightning on the atmospheric chemistry of exoplanets and potential biosignatures
1
Space Research Institute, Austrian Academy of Sciences,
Schmiedlstrasse 6,
Graz
8042,
Austria
e-mail: patrick.barth@simtech.uni-stuttgart.de
2
Centre for Exoplanet Science, University of St Andrews, North Haugh, St Andrews
KY16 9SS,
UK
3
School of Earth & Environmental Sciences, University of St Andrews, Bute Building, Queen’s Terrace, St Andrews
KY16 9TS,
UK
4
SUPA, School of Physics & Astronomy, University of St Andrews, North Haugh, St Andrews
KY16 9SS,
UK
5
Stuttgart Center for Simulation Science, University of Stuttgart,
Pfaffenwaldring 5a,
70569
Stuttgart,
Germany
6
Fakultät für Mathematik, Physik und Geodäsie, TU Graz,
Petersgasse 16,
Graz
8010,
Austria
7
Department of Earth and Planetary Sciences, University of California,
Riverside,
CA,
USA
8
Blue Marble Space Institute of Science,
Seattle,
WA,
USA
9
School of Natural and Environmental Sciences, Newcastle University,
Newcastle upon Tyne
NE1 7RU,
UK
Received:
26
June
2023
Accepted:
19
February
2024
Context. Lightning has been suggested to play a role in triggering the occurrence of bio-ready chemical species. Future missions such as PLATO, ARIEL, HWO, and LIFE, as well as ground-based extremely large telescopes (ELTs), will carry out investigations of the atmospheres of potentially habitable exoplanets.
Aims. We aim to study the effect of lightning on the atmospheric chemistry. We also consider how it affects false-positive and false-negative biosignatures and whether these effects would be observable on exo-Earth and TRAPPIST-1 planets.
Methods. We utilised a combination of laboratory experiments and photochemical and radiative transfer modelling. We conducted spark discharge experiments in N2−CO2−H2 gas mixtures, representing a range of possible rocky-planet atmospheres. We investigated the production of potential lightning signatures (CO and NO), possible biosignature gases (N2O, NH3, and CH4), and important prebiotic precursors (HCN and urea). Using the measured CO and NO production rates, we conducted photochemical simulations for oxygen-rich and anoxic atmospheres for rocky planets orbiting in the habitable zones of the Sun and TRAPPIST-1 for a range of lightning flash rates. Synthetic spectra were calculated using SMART to study the atmosphere’s reflectance, along with the emission and transmission spectra.
Results. Lightning enhances the spectral features of NO, NO2, and (in some cases) CO through direct production; whereas CH4 and C2H6 may be enhanced indirectly. Lightning at a flash rate slightly higher than on modern-day Earth is able to mask the ozone features of an oxygen-rich, biotic atmosphere, making it harder to detect the biosphere of such a planet. Similarly, lightning at a flash rate at least ten times higher than on modern-day Earth is also able to mask the presence of ozone in the anoxic, abiotic atmosphere of a planet orbiting a late M dwarf, reducing the potential for a false-positive life detection.
Conclusions. The threshold lightning flash rates to eliminate oxygen (>0.1%) and ozone false positive biosignatures on planets orbiting ultra-cool dwarfs is up to ten times higher than the modern flash rate. This result indicates that lightning cannot always prevent these false-positive scenarios.
Key words: astrobiology / astrochemistry / methods: laboratory: molecular / techniques: spectroscopic / planets and satellites: atmospheres / planet-star interactions
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
In recent decades, more than 5500 extrasolar planets have been confirmed, the majority of which are located in the solar neighbourhood. Of these, 69 planets are potentially habitable1. These rocky planets orbit their host star at a distance where water may exist in liquid form, namely, the circumstellar habitable zone. When including the stellar and galactic environments, the number of potentially habitable known extrasolar planets decreases to just five (Spinelli et al. 2023). The limiting factor is high-energy radiation, which either enables or disables the necessary chemical pathways to form complex molecules. Since its launch in December 2021, JWST is the first telescope that enables detailed observations of exoplanet atmosphere composition through its infrared (IR) instruments. The first step towards detecting habitable planets, however, is the verification that a rocky planet has an atmosphere (e.g. Turbet et al. 2022; Ih et al. 2023). Based on the assumpton that an atmosphere is indeed present, extensive studies have been conducted to assess the detectability of the biosignature pairs, CO2−CH4 or CH4−O3 (Lin & Kaltenegger 2022; Rotman et al. 2023), with JWST and future extremely large telescopes (ELTs) in the atmosphere of the TRAPPIST-1 planets, for instance.
To interpret observations from present (JWST) and future missions and telescopes (PLAnetary Transits and Oscillations of stars, PLATO, Atmospheric Remote-sensing Infrared Exoplanet Large-survey, ARIEL, ELTs), so-called ‘biosignatures’ have been postulated. Biosignatures are gases or other planetary features that (singly or in combination) are potentially indicative of life (e.g. Seager et al. 2012; Grenfell 2017; Schwieterman et al. 2018). To avoid misinterpreting such signatures, other processes that can lead to an observable abundance of these gases need to be quantified. One such group of processes is electrostatic discharges in atmospheres, the largest of which is lightning. Lightning is expected to be present in various kinds of environments, including planetary atmospheres and planet-forming disks (e.g. Helling et al. 2016). Lightning in the cloudy atmosphere of a potentially habitable exoplanet is presenting a strong energy source for disequilibrium chemistry to take place. Lightning is a significant though small source of fixed nitrogen on modern Earth (Schumann & Huntrieser 2007, and references therein). Previous studies have shown that lightning can also produce fixed nitrogen in an N2−CO2 atmosphere, similar to the early Archean (Nna Mvondo et al. 2001; Navarro-González et al. 2001; Summers & Khare 2007; Barth et al. 2023), albeit Hu & Diaz (2019) suggest that lightning-fixed nitrogen will be quickly returned into to the atmosphere as N2. Further, lightning has also been postulated to have played an important role in the origin of life itself (Miller 1953).
The most abundant biologically produced gas on modern Earth and therefore prime candidate for a biosignature is O2 and its byproduct ozone O3 that is more easily detectable with a prominent absorption feature at 9.6 μm (O2 only has weak absorption features in the mid-infrared within the 6.3 μm water band; Segura et al. 2003; Meadows et al. 2018). On modern Earth, O2 is produced by photosynthesis, but in other circumstances, large amounts of O2 can be produced abiotically. For example when a rocky planet around an M dwarf loses a large part of its water inventory during the early, active phase of its host star. The selective escape of lighter H and retention of heavier O could overwhelm reductant sinks and cause O2 accumulation in the atmosphere (Ramirez & Kaltenegger 2014; Wordsworth & Pierrehumbert 2014; Luger et al. 2015; Meadows 2017; Wordsworth et al. 2018; Johnstone 2020; Barth et al. 2021a). In particular, on planets orbiting M dwarfs with a large atmospheric CO2 concentration, the increased intensity of the X-ray & UV (XUV) radiation can robustly dissociate the CO2 to produce CO and O, as we discuss below. The recombination of CO and O is restricted by deficient near UV (NUV) radiation from the M dwarf host star, which is key to generating photochemical catalysts that facilitate this reaction (the direct CO + O reaction is spin-forbidden), potentially producing a false positive O2 biosignature (Segura et al. 2007; Harman et al. 2015). Harman et al. (2018) suggested that lightning-produced NO might act as a catalyst to prevent the build-up of O2 in such an atmosphere. We discuss this possibility later in this work.
Nitrous oxide (N2O) has been stipulated as another potential biosignature (Rauer et al. 2011; Grenfell 2017; Schwieterman et al. 2022). In the Earth’s spectral energy distribution, N2O produces detectable peaks in the near-IR (NIR) and mid-IR (Sagan et al. 1993; Gordon et al. 2022). Further, N2O in the Earth’s atmosphere is mainly from biological origin and there are only a few abiotic sources. Mainly, stellar radiation or lightning can photochemically produce NO, which in an anoxic and weakly reducing atmosphere can undergo further reactions to produce N2O. To distinguish biotically from abiotically produced N2O, spectral discriminants can be used, such as HCN and NO2, which are abiotically produced together with the N2O (Airapetian et al. 2016, 2020; Schwieterman et al. 2022).
In many circumstances, the detection of a single biosignature gas such as O2 would be insufficient evidence to claim the detection of life. Extensive planetary context to rule out false positives (see Sousa-Silva et al. 2019 for PH3 or Thompson et al. 2022 for CH4) or additional biosignature gases would be required for a confident biosignature claim. An example is O2 in combination with CH4 (Lovelock et al. 1975; Sagan et al. 1993), which in equilibrium would react to CO2 and H2O (Segura et al. 2005). Another example would be the combination of N2 and O2, namely, modern Earth’s atmosphere, as this gas mixture would likely not be stable over geological timescales without the constant production of both O2 and N2 by life forms (Stüeken et al. 2016; Krissansen-Totton et al. 2018b; Lammer et al. 2019; Sproß et al. 2021). However, it still needs to be assessed whether photolysis of aqueous nitrite and nitrate could provide enough N2 to the atmosphere to stabilise the N2 concentration abiotically (Zafiriou & True 1979a,b; Carpenter & Nightingale 2015; Ranjan et al. 2019). Wogan & Catling (2020) discussed the potential of chemical disequilibria as biosignatures: only an ‘inedible’ disequilibrium, where a high activation energy is needed to move the system to equilibrium, can be considered a biosignature. Krissansen-Totton et al. (2018b; 2019) suggest the combination of CO2 and CH4, which was present in the Archean atmosphere, as such a disequilibrium biosignature. This biosignature would be strengthened by the absence of CO which has been suggested as an antibiosignature for exoplanets (Wang et al. 2016).
In contrast to a false-positive biosignature, where life may still be present on a planet, an antibiosignature suggests that the planet is not inhabited and is usually defined as the evidence for free energy not being exploited by life (Schwieterman et al. 2019). In this context, CO provides a source of chemical free energy and reduced carbon to life in metabolisms such as the Wood-Ljungdahl pathway (Ragsdale 2004). Previous simulations of the atmospheric chemistry during the early Archean represented several metabolisms that govern the concentration of CO in early Earth’s atmosphere (Kharecha et al. 2005): methanogens provide a source of CO, as the CH4 they produce will be photochemically oxidised to CO if irradiated by far UV (FUV) radiation. Acetogens, on the other hand, provide a biological sink of CO that is limited by the rate at which CO is deposited in the ocean (assuming immediate consumption of CO by acetogens). A major abiotic CO source is the photolysis of atmospheric CO2 and an abiotic sink is the oxidation of CO by hydroxyl radicals (OH), which are mainly produced by photochemical reactions (Schwieterman et al. 2019).
Past studies have demonstrated that many exoplanets will be covered in clouds for an extended period during their evolution such that it is reasonable to expect lightning to occur also in extrasolar planets (Woitke & Helling 2003; Helling et al. 2008, 2013a,b; Hodosán et al. 2021). Moreover, lightning will contribute to the formation of a global electric circuit (Helling 2019) and produce chemical tracers of a convectively active atmosphere of any planet (Hodosán et al. 2016b). However, the only planets where in situ measurements can be conducted are those within the Solar System, and the only planet for which lightning can be studied to a reasonable degree of completeness concerning flash density and energy range is modern Earth (Hodosán et al. 2016a). The global lightning flash rate on modern Earth is estimated to be 44 ± 5 s−1 (Christian et al. 2003) with an energy of 6.7 GJ per flash (Price et al. 1997), but much uncertainty remains for the lightning flash rate on the early Earth, terrestrial planets, and exoplanets in general (Hodosán et al. 2021).
Wong et al. (2017) used climate simulations and the convective available potential energy to estimate the lightning flash rate in potential Archean atmospheres with varying CO2 partial pressure. They found the lightning flash rate to peak at 3.4 times the modern Earth’s flash rate at 1 bar of CO2, with values lower than on modern Earth for CO2 partial pressures of 0.1 and 10 bar (with 1–2 bar of N2). Braam et al. (2022) suggested that the lightning flash rate on tidally locked exoplanets such as Proxima Centauri b is less than 10% of modern Earth’s. An additional factor that can influence the occurrence of lightning is cosmic rays. Planets orbiting M dwarfs will experience more frequent and intense stellar flares that are associated with flares of charged particles, known to enhance the ionisation in the planet’s atmosphere (Stozhkov 2003; Rimmer & Helling 2013; Grießmeier et al. 2015; Fraschetti et al. 2019; Scheucher et al. 2020; Barth et al. 2021b). Comparison between lightning flash rates and cosmic ray ionisation rates in Earth’s atmosphere has shown a strong correlation between these two quantities (Stozhkov 2003). However, the increased influx of charged particles into the atmospheres of planets orbiting M dwarfs is likely only more efficiently enabling lightning discharges in already existing electric fields in the clouds of these atmospheres. We might therefore only find a slightly enhanced lightning activity on these planets, but more detailed studies on the connection between cosmic ray ionisation and lightning are necessary to fully understand these processes.
This paper adopts an approach of combining laboratory experiments and modelling to investigate the impact of lightning on the atmospheric chemistry of exoplanets. We present results from spark-discharge experiments with different gas mixtures initially containing N2, CO2, and H2. The setup of the experiments and the photochemical model are described in Sect. 2. In Sect. 3, we present the results of our experiments and their implications. We apply our experimental results to two different hypothetical exoplanets and use photochemical simulations and calculated spectra to determine potentially observable signatures from lightning and the prospect for false-positive or false-negative biosignatures (Sect. 4). Due to the wide range of work presented in this paper and the large amount of results, we have decided to discuss the implications of individual results in the same sections. We discuss our assumptions on lightning flash rates and atmospheric composition in Sect. 5 and present our conclusions in Sect. 6.
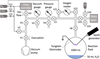 |
Fig. 1 Schematic of the experimental setup of the discharge experiment. First published in Barth et al. (2023) by Springer Nature. |
2 Methods
2.1 Spark experiments
All experiments were carried out at the University of St Andrews in the St Andrews Isotope Geochemistry lab (StAIG). We used the experimental setup (Fig. 1) described in Barth et al. (2023), similar to the one described by Parker et al. (2014). The spark discharge (generated by a BD-50E heavy-duty spark generator with a maximum voltage of 49 kV) was contained in the one-litre reaction flask (Pyrex glass), which contained 50 mL of water at the bottom and the spark electrodes (tungsten metal) secured in the headspace. The water was agitated with a magnetic stir bar. The system was evacuated and purged with N2 three times before adding the desired gas mixture and starting the experiment. To investigate the effect of water vapour in the gas phase on the final results, a set of dry experiments was run. For these, we added the water with a syringe through the septum port on the flask only after the spark had been turned off. The water was previously flushed with pure N2 (10 min at ~50 mL min−1) to remove dissolved oxygen. We then let the experiment with the water sit for 3 hours (with the spark still switched off) to allow for the gaseous and liquid phases to equilibrate. The water was continuously stirred with the magnetic stir bar to facilitate gas exchange between the headspace and the liquid phase.
Before and after each experiment, gas from the flask was analysed by a quadrupole mass spectrometer gas analyser. After the experiment, a gas sample was extracted from the flask with a gas-tight, lockable syringe to determine the concentration of CH4 and N2O with a gas chromatograph. From a limited sample of experiments, multiple gas samples were extracted for analyses of CO. The fluid phase was transferred into a 50 ml Falcon centrifuge tube for subsequent analyses of dissolved nitrite, nitrate, ammonium, urea, and cyanide (see below). The analytical methods used to determine the concentrations of these species are detailed in Appendix A. From these concentrations, the energy yield (molecules/J) can be calculated, using the energy of the spark E = 1/2U It with the applied voltage U = 49 kV, the current I = 1 mA, and the duration t of the spark. To extrapolate this yield to the annual, global production, we used an estimate for the global lightning flash rate on modern Earth of 44 ± 5 s−1 (Christian et al. 2003) with an energy of 6.7 GJ per flash (Price et al. 1997).
2.2 Photochemical simulations
We conducted photochemical simulations to calculate the mixing ratios of CO, NO, and NO2 in the atmosphere of different test planets for a range of NO and CO production rates, corresponding to a range of lightning flash rates. To conduct these tests, we used the photochemical model component of the Atmos coupled climate-photochemistry code (Arney et al. 2016; Lincowski et al. 2018)2. We conducted all simulations in uncoupled mode (no climate adjustment) to isolate the specific chemical impact of varying CO and NO fluxes from lightning. When simulating anoxic atmospheres, we adopt an Archean-Earth planet template with 74 chemical species and 392 photochemical reactions. For O2-rich atmospheres, we adopted a modern Earth-like template with 50 species and 239 reactions. We incorporated the latest H2O cross-sections and corrected sulfur reaction rate as recommended by Ranjan et al. (2020). The model normally includes the impact of Earth-like lightning by injecting NO into the troposphere (Harman et al. 2018); however, we have removed this feature and replaced it with a variable NO injection rate to assess the impact of varying NO production from lightning. The model includes diffusion-limited hydrogen escape (Harman et al. 2015).
We ran the simulations for an Earth-sized planet, orbiting the Sun at 1 au and the M dwarf TRAPPIST-1 at an instellation identical to that of TRAPPIST-1 e (Agol et al. 2021). The initial atmospheric composition was set to be similar to our high-CO2 experiments (4.6% CO2 with N2 as filler gas). We also calculated the CO and NO2 mixing ratios in a corresponding oxic atmosphere (21% O2, 4.6% CO2 with N2 as filler gas). In both cases, the CO2 concentration is fixed to the initial value of 4.6%. The tropospheric water vapour concentration is governed by the surface temperature of the planet: 0.5% H2O for T = 275 K, 1.2% H2O for T = 288 K, and 2.5% H2O for T = 300 K. The pressure-temperature profiles for the anoxic simulations assume surface temperatures of Tsurf = 275 K and Tsurf = 300 K, adiabatic cooling throughout the troposphere, and then an isothermal temperature of Tgas = 180 K. For the oxic simulations, the pressure-temperature profile of modern Earth is used, with a surface temperature of Tsurf = 288 K. The spectra of the Sun and TRAPPIST-1 (Fig. 2) are used for the photochemistry simulations and to simulate the planetary spectra. The spectrum of the Sun was sourced from Thuillier et al. (2004) while the TRAPPIST-1 spectrum represents an average of the three activity models presented in Peacock et al. (2019). Each spectrum is re-interpolated onto the standard Atmos base grid (Lgrid = 0 setting).
We ran the model for different scenarios. First, for the abiotic scenario: volcanic fluxes of CH4 (108 molecules cm−2 s−1), H2 (1010 molecules cm−2 s−1, deposition velocity into the ocean: υdep = 2.4 × 10−4 cm s−1), H2S (3.5 × 108 molecules cm−2 s−1, υdep = 2 × 10−2 cm s−1), and SO2 (3.5 × 109 molecules cm−2 s−1, υdep = 1 cm s−1) are included and distributed over the bottom 10 km of the atmosphere profile (as is the variable CO flux). The CO deposition velocity is υdep = 10−8 cm s−1, which is the limit for the abiotic formation of formate (Kharecha et al. 2005). For the biotic scenario: in addition to the volcanic sources of the abiotic scenario, a biological methane production of 1011 molecules cm−2 s−1 is included, which corresponds to the Earth’s current biogenic methane flux (Jackson et al. 2020). The CO deposition velocity in the biotic case is υdep = 1.2 × 10−4 cm s−1, which is the maximum deposition velocity for an ocean with a CO concentration of 0, namely, where all CO is immediately consumed by acetogens (Kharecha et al. 2005). A detailed table containing the parameters for all the different scenarios can be found in the appendix.
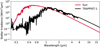 |
Fig. 2 Spectral energy distributions at the top of the planets’ atmospheres of the Sun (red) and TRAPPIST-1 (black) as used in the photochemical model and for the planetary spectra. |
2.3 Spectral simulations
To simulate the reflectance, emission, and transmission spectra we used the Spectral Mapping Atmospheric Radiative Transfer code (SMART; Meadows & Crisp 1996; Crisp 1997) with transit updates as described in Robinson (2017). SMART is a versatile and well validated line-by-line, multi-stream, multiple scattering, and absorption model that can produce planetary spectra from the far-UV to far-IR. SMART relies on the DISORT Fortran code (Stamnes et al. 1988) to solve the radiative transfer equation via the discrete ordinate method. SMART includes opacity data from HITRAN (Gordon et al. 2017) that are preprocessed by their Line-By-Line Absorption Coefficients (LBLABC) companion model. SMART has been used to simulate spectra of planets inside and outside of the Solar System including the TRAPPIST-1 planets (Tinetti et al. 2005; Robinson et al. 2011; Arney et al. 2014; Lustig-Yaeger et al. 2019). For the spectra presented in Sec. 4.4, we show reflectance spectra degraded to a spectral resolving power of R = 400, transmission spectra degraded to R = 200, and emission spectra with a spectra resolution of 1 cm−1.
3 Results and implications of experimental measurements
We performed spark discharge experiments in gas mixtures with different combinations of N2, CO2, and H2 to investigate the effect of lightning on the chemistry of lightly reducing gas mixtures with varying fractions of CO2. Our goal is to give a complete picture of the most abundant gaseous and aqueous compounds produced in spark discharge experiments in such gas mixtures. These compounds can be grouped into three categories: (1) CO and NO are (as we show later on) the most abundant products and are directly produced in the spark channel. Because of that, they might present signatures for lightning activity in exoplanetary atmospheres as we discuss in Sec. 4. (2) N2O, NH3, and CH4 are potential biosignatures (e.g. Seager et al. 2013b; Phillips et al. 2021; Huang et al. 2022; Schwieterman et al. 2022; Thompson et al. 2022) and we want to investigate whether lightning might present a significant source of these gases. (3) ![$\[\mathrm{NH}_4^{+}, ~\mathrm{NO}_2^{-}, ~\mathrm{NO}_3^{-},\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq1.png) HCN, and urea are important prebiotic compounds, either as precursors for the formation of biological macromolecules or as nutrients for early life forms (e.g. Miller 1957; Miller & Urey 1959; Abelson 1966; Sanchez et al. 1967; Miller & Schlesinger 1983; Schopf et al. 2007; Ducluzeau et al. 2009; Wong et al. 2017; Das et al. 2019). We investigated how the gas composition changes the yields of these products and what effect the presence of water vapor in the gas mixture has. We conducted a range of short, 120-min experiments as well as longer, overnight experiments to study the production of molecules with low yields that could not be detected in our short experiments. First, we present the results from our short experiments in individual sections for each compound and discuss their implications on the importance of lightning as a source of the specific molecule in the same section (Sects. 3.1–3.8). We then present and discuss the results from our overnight experiments (Sec. 3.9). The different gas compositions for all experiments are compiled in Table 1.
HCN, and urea are important prebiotic compounds, either as precursors for the formation of biological macromolecules or as nutrients for early life forms (e.g. Miller 1957; Miller & Urey 1959; Abelson 1966; Sanchez et al. 1967; Miller & Schlesinger 1983; Schopf et al. 2007; Ducluzeau et al. 2009; Wong et al. 2017; Das et al. 2019). We investigated how the gas composition changes the yields of these products and what effect the presence of water vapor in the gas mixture has. We conducted a range of short, 120-min experiments as well as longer, overnight experiments to study the production of molecules with low yields that could not be detected in our short experiments. First, we present the results from our short experiments in individual sections for each compound and discuss their implications on the importance of lightning as a source of the specific molecule in the same section (Sects. 3.1–3.8). We then present and discuss the results from our overnight experiments (Sec. 3.9). The different gas compositions for all experiments are compiled in Table 1.
For our short, 120-min experiments, we performed experiments both with (wet) and without water (dry) in the flask during the spark to investigate the effect of water vapor on the yields of our products. As described in Sec. 2, we added 50 mL of water to the dry experiments after turning off the spark. We then analysed the gas and water for the concentrations of NO, CO, N2O, CH4, ![$\[\mathrm{NH}_4^{+}, ~\mathrm{NO}_2^{-},\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq2.png) and
and ![$\[\mathrm{NO}_3^{-}\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq3.png) . Figure 3 shows the combined results from our short experiments. The individual measurements of each gas composition are averaged over 3–7 replicates (a detailed table with individual results is available online3), the results for wet and dry experiments are shown in different colors next to each other. As expected, one of the main results is that reduced nitrogen and carbon species (ammonium, ammonia, and methane) are more abundant in the pure N2−H2 and low-CO2 experiments. Oxidised forms of nitrogen (nitrate, nitrite, nitric oxide, and nitrous oxide) are more abundant in the high CO2 experiments where the dissociation of CO2 provides the necessary oxygen source for NO and subsequent nitrogen oxides.
. Figure 3 shows the combined results from our short experiments. The individual measurements of each gas composition are averaged over 3–7 replicates (a detailed table with individual results is available online3), the results for wet and dry experiments are shown in different colors next to each other. As expected, one of the main results is that reduced nitrogen and carbon species (ammonium, ammonia, and methane) are more abundant in the pure N2−H2 and low-CO2 experiments. Oxidised forms of nitrogen (nitrate, nitrite, nitric oxide, and nitrous oxide) are more abundant in the high CO2 experiments where the dissociation of CO2 provides the necessary oxygen source for NO and subsequent nitrogen oxides.
This follows the results from different studies in the past: Experiments with electric discharges in reducing CH4−NH3 and CH4−N2 gas mixtures produced a variety of reduced nitrogen and carbon products, including H2, NH3, hydrocarbons, and nitriles such as HCN (Toupance et al. 1975). Similar experiments simulating corona discharges in Titan’s reducing atmosphere (10% CH4 and 2% Ar in N2) have shown show the production of reduced nitrogen and carbon in the form of various hydrocarbons and nitriles (Reid Thompson et al. 1991; Navarro-González & Ramírez 1997; Navarro-González et al. 2001b). Spark experiments with different N2−CO2 gas mixtures have shown that predominantly oxidised forms of nitrogen and carbon are produced, such as NO, N2O, NO2, HNO3, or CO (e.g. Levine et al. 1982; Nna Mvondo et al. 2005; Heays et al. 2022). Navarro-González et al. (2001) and Nna Mvondo et al. (2001) studied the production of NO by lightning in gas mixtures with varying CO2 concentration and found a clear trend of decreasing nitrogen fixation efficiency with the decreasing availability of oxygen from CO2.
We found increased efficiency of nitrogen oxides production in the experiments that contained water in the flask during the spark. The presence of liquid water resulted in approximately 1% of water vapour in the gas phase at room temperature (Table 1), which was also dissociated in the spark, providing additional oxygen for the NO production. The individual products shown in Fig. 3 as well as CO are discussed in the following sections.
Initial gas compositions in our experiments in bar.
 |
Fig. 3 Final abundance of ammonium ( |
3.1 Ammonium (![$\[\mathrm{NH}_4^{+}\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq10.png) )
)
Ammonium is an important nutrient for microbial life on Earth and it was the product of the first developed pathways of biological nitrogen fixation (Schopf et al. 2007; Dodd et al. 2017). Lightning-produced ammonium would therefore present a potential nutrient source for life before the onset of biological nitrogen fixation. We found that maximum ammonium production happens in experiments with no or <1% of CO2. A higher CO2 concentration limits the efficiency of ammonium production. However, except for a few individual experiments, we found the final ammonium concentration to be lower than the concentration of nitrite and nitrate, in particular for the wet experiments. Our highest ammonium production rate (the wet, CO2-free case) is (3.8 ± 1.7) × 1012 molecules/J which, using the modern Earth flash rate, corresponds to a yearly production of (1.1 ± 0.5) × 10−3 Tg yr−1. With a higher CO2 concentration, more likely resembling early Earth’s atmosphere, this reduces to (1.8 ± 1.2) × 1012 molecules/J and (0.5 ± 0.3) × 10−3 Tg yr−1. This is much lower than the production of nitrite and nitrate (see below), though nitrite can subsequently be reduced to ammonium by Fe2+ and FeS in the ocean, while FeS can also reduce nitrate to ammonium albeit with a lower yield (Summers & Chang 1993; Summers 2005). Direct production of ammonium by lightning is therefore not significant on planets with a substantial concentration of CO2 or water vapour in the atmosphere.
3.2 Ammonia (NH3)
Ammonium is not directly produced by the spark. Instead, ammonia is the gaseous product of the spark discharge that then equilibrates with the water where it reacts to ammonium. Ammonia can be produced biologically and has been previously suggested as a biosignature for planets with a significant H2 fraction in the atmosphere (Seager et al. 2013a,b; Huang et al. 2022). Ranjan et al. (2022) describe a scenario where NH3 is produced in such high quantities that it saturates its photochemical sinks, such as O2 in modern Earth’s atmosphere, and goes into a runaway mode. The surface flux above which the NH3 concentration enters into this runaway state, depends on the level of UV-radiation. In their simulations of atmospheres with 10% H2 and 90% N2 (with 1% water vapour) on an Earth-sized planet orbiting an M dwarf, Ranjan et al. find this flux to be approximately 1011 cm−2 s−1, and as low as 108 cm−2 s−1 for an elevated stratospheric temperature (from Tstrat = 170 K to 210 K). The modern Earth NH3 flux is (1.1 − 1.8) × 1010 cm−2 s−1 (Bouwman et al. 1997) and the pre-industrial flux (2–9) × 109 cm−2 s−1 (Zhu et al. 2015). The maximum lightning-induced NH3 flux we can extrapolate from our experiments with an atmosphere of 1% H2 and 1% H2O (in N2), including the aqueous ![$\[\mathrm{NH}_4^{+}\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq11.png) , is approximately (2.2 ± 1.0) × 105 cm−2 s−1 (wet, pure N2−H2). This is many orders of magnitude below the flux necessary to enter into a runaway state, suggesting that lightning cannot be responsible for a false-positive biosignature detection with NH3.
, is approximately (2.2 ± 1.0) × 105 cm−2 s−1 (wet, pure N2−H2). This is many orders of magnitude below the flux necessary to enter into a runaway state, suggesting that lightning cannot be responsible for a false-positive biosignature detection with NH3.
3.3 Methane (CH4)
Methane is frequently discussed as a potential biosignature, in particular for Archean Earth-like worlds (e.g. Thompson et al. 2022). If lightning could produce significant amounts of methane in an early Earth-like atmosphere, this would present an important restriction on methane’s role as a biosignature. However, in our experiments, only small amounts of methane are produced. Most of the measurements are below the error of an individual measurement (0.6 ppm) which means that they are within 1σ of 0. We therefore assume 0.6 ppm (or a total production of 0.024 μmol) to be the upper limit for methane production in our experiments, as indicated by the red line in Fig. 3. This limit corresponds to an annual methane production with a modern lightning flash rate of less than 2 × 10−5 Tg yr−1 or 1.3 × 10−6 Tmol yr−1. The annual methane production on modern Earth is 37 Tmol yr−1 = 596 Tg yr−1, of which ~40% is natural (not anthropogenic; Jackson et al. 2020) while the possible Archean biological methane production was between 9 and 20 Tmol yr−1 (Sauterey et al. 2020). The upper limit for abiotic methane production by serpentinising systems (hydrothermal alteration of crustal mafic rocks) is between 0.02 and 10 Tmol yr−1 (Krissansen-Totton et al. 2018b). This suggests that in the atmospheric conditions explored in this study, methane production by lightning is negligible compared to other abiotic and biotic sources. The lightning flash rate in such an atmosphere would have to be 5–6 orders of magnitude higher than on modern Earth to produce a comparable amount of methane.
3.4 Carbon monoxide (CO)
In contrast to methane, carbon monoxide has been discussed as a potential antibiosignature (Wang et al. 2016; Schwieterman et al. 2019). If on an inhabited planet, lightning were to produce detectable amounts of CO by overwhelming biological sinks, this would provide a limitation on the use of CO as an antibiosignature. We analysed the CO concentrations of four experiments, each at three different points in time during the experiment (after 30, 60, and 120 min). These results are shown in Fig. 4. The CO production rate decreased with time, likely because CO concentration reaches equilibrium. We extrapolated the CO concentration to estimate the equilibrium concentration (Fig. 4). Following the equilibrium reaction A1 ⇌ A2 (A2 is CO in this case) with the reaction coefficients k1 and k2, the change in c2 (the concentration of A2) is given by:
![$\[\frac{\mathrm{d} c_2}{\mathrm{~d} t}=-k_2 c_2+k_1 c_1.\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq12.png) (1)
(1)
Starting with all molecules in A1 (c1,0 = ctot, c2,0 = 0), c2 increases with time:
![$\[c_2=\left(1-\frac{k_2+k_1 \cdot \exp \left(-\left(k_1+k_2\right) t\right)}{k_1+k_2}\right) \cdot c_{\text {tot }} \text {.}\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq14.png) (2)
(2)
The resulting equilibrium concentration of c2 (for t → ∞) is then given by:
![$\[c_{2, \mathrm{eq}}=\left(\frac{k_1}{k_1+k_2}\right) \cdot c_{\text {tot }}.\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq15.png) (3)
(3)
For our experiments, the estimates for CO equilibrium concentrations are 1.5% for the high-CO2 experiments (4.5–4.6% CO2) and 0.85% for the low-CO2 experiments (0.6–0.7% CO2).
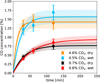 |
Fig. 4 CO concentration in 4 different spark experiments (high and low-CO2, wet and dry), measured at 3 different points in time during the experiment. Fitted lines give the CO concentration assuming CO is the product of an equilibrium reaction, following |
3.5 Extrapolating CO production to different atmospheres
In past studies, the lightning production rates of different gases such as NO have been determined by assuming the equilibrium concentration of said gases at the so-called ‘freeze-out temperature’ (e.g. Chameides et al. 1977; Hill et al. 1980; Borucki & Chameides 1984). The freeze-out temperature is the temperature at which the equilibrium timescale is larger than the cooling timescale of the gas mixture, freezing in the gas composition at that temperature. Every time a gas parcel has been heated up by a lightning strike and is cooling down again, the concentration of NO, CO, and other lightning products in the air parcel is increased to its equilibrium concentration at the respective freeze-out temperature. Comparison to experimental results of NO production rates by lightning show that this method is a valid approach to determine the production of NO etc. by lightning (see reviews by Schumann & Huntrieser 2007; Heays et al. 2022).
In this study, we used our experimental results and chemical equilibrium calculations to determine the freeze-out temperatures of NO and CO, allowing us in the next step to extrapolate our results to different gas compositions. To evaluate the effect of H2 on the CO and NO production, we carried out equilibrium calculations with GGChem (Fig. 5; Woitke et al. 2018). We used a subset of the species within GGChem with 87 charged and neutral species containing the elements H, C, N, and O, as well as electrons. We calculated the thermochemical equilibrium composition of gas mixtures with varying H2 fractions resembling our wet, high-CO2 experiments (4.6% CO2, 1% H2O, 0–10% H2, with the rest to 100% N2) for temperatures between 300 and 4000 K. By comparing our CO and NO measurements from the experiments with 0.9% H2 (red and blue shaded areas, respectively) to the corresponding calculations (dashed lines), we can estimate a minimum freeze-out temperature for the respective gas. Here, the CO measurement is from only one experiment, the NO concentration is the average of multiple experiments.
While the CO measurements with time allow us to estimate the equilibrium composition of CO in the flask (see Fig. 4), we only have one measurement of NO after the full 120 min run time of the experiment, which might increase slightly further. We therefore can only give a minimum estimate on the freeze-out temperature for NO. Our estimates are Tf(CO) = (2430 ± 65) K and Tf(NO) ≥ (3000 ± 160) K. The latter is similar to previous estimates by of Tf(NO) = 2300 K (Gilmore 1975; Chameides et al. 1977), 2660 K (Picone et al. 1981; Borucki & Chameides 1984), and 3500 K (Kasting & Walker 1981). These estimates are based on different methods and assumptions on the cooling timescale of the gas heated in the lightning channel, showing that extrapolating from lab experiments and theoretical calculations to real-world lightning strikes comes with large uncertainties. The errors we report with our freeze-out temperatures represent the range of temperatures necessary to explain the range of CO and NO concentrations in our experiments but do not include further uncertainties that arise when extrapolating our experimental conditions to real-world lightning strikes. Our estimate of the NO freeze-out temperature also allows us to determine a lower limit of the maximum temperature reached within the spark channel of approximately 3000 K.
There are much fewer estimates for the CO freeze-out temperature (compared to NO), with 3500 K when the CO is produced in the expanding shock front around the lightning channel (Levine et al. 1979; Chameides 1979) and 2000 K if the CO is produced in the inner core of the cooling channel (Chameides 1979). Hill et al. (1980) point out that the cooling channel is more important for the production of NO, CO, and other gases because of its larger volume compared to the expanding shock front. According to Stark et al. (1996), this is particularly true for spark experiments. Our estimate for the freeze-out temperature is thus slightly higher than the estimate of 2000 K for the cooling channel, potentially explained by an additional contribution of the higher freeze-out temperature of the shock front.
The estimates for the freeze-out temperatures allow us to extrapolate the CO and NO production to atmospheres with different H2 fractions. As the freeze-out temperature depends on the cooling timescale of the spark and the equilibrium timescale of the gas mixture, changing the gas composition can lead to a change in the freeze-out temperature. In our case, we only slightly vary the atmospheric composition, which allows us to assume a constant freeze-out temperature. Figure 5 shows additional equilibrium calculations for gas mixtures without H2 (solid lines), with 5% (dash-dotted) and with 10% H2 (dotted). The addition of H2 is increasing the abundance of CO in the lower temperature regime where (in the absence of H2) CO2 would be more stable. The H2 reacts with the atomic oxygen produced by the dissociation of the CO2 to form H2O, preventing the CO from recombining with the O to create CO2. Eventually, the abundance of CO is limited by the availability of C from the initial CO2. At the freeze-out temperature of ~2400 K this means an increase of the CO abundance by a factor of 2.5 when increasing the H2 fraction from 0.9% to 10% (in a background of 4.6% CO2 and in the context of the limited chemistry applied in these calculations). At the same time, the presence of H2 (and subsequent production of H2O) reduces the availability of oxygen for the production of NO. At 3000 K, we find that the NO concentration for 10% H2 is only 1/3 of the concentration expected in the 0.9%-H2 case.
From the initial slope of our fit to the CO concentration with time (Fig. 4) a global, annual production of (6–18) Tg yr−1 and a surface flux of (7.6–24) × 108 cm−2 s−1 can be estimated for the different H2 concentrations (assuming modern Earth’s lightning flash rate). Using those estimates for surface fluxes, a grid of photochemical simulations were performed, similar to those presented by Schwieterman et al. (2019). This allowed us to test under which conditions a lightning contribution to CO production could be observable (Sec. 4).
Previous experimental results and calculations for the CO production by lightning in modern Earth’s atmosphere are 0.01 Tg yr−1 (Green et al. 1973), 0.04 Tg yr−1 (Levine et al. 1979), and (0.004–0.2) Tg yr−1 (Chameides 1979). If we use the approach outlined above, using the equilibrium concentration of CO at 2430 K in a gas mixture resembling modern Earth’s atmosphere, our estimate for the global CO production by lightning is (0.01 ± 0.003) Tg yr−1 which is in agreement with the values presented in the literature.
 |
Fig. 5 CO and NO concentrations in chemical equilibrium as a function of gas temperature (with GGChem, Woitke et al. 2018) for high-CO2 gas mixtures. The different cases considered are: 0% (solid lines), 0.9% (dashed), 5% (dash dotted), and 10% (dotted) of H2. As H2 is binding free oxygen into H2O, increasing the H2 concentration prevents the recombination of CO to CO2 as well as the production of NO. CO (red) and NO (blue shaded area) measurements with uncertainties from wet 120 min experiments. Minimum freeze-out temperature estimates for CO (orange) and NO (green) with uncertainties. |
3.6 Nitrogen oxide (NO) production and extrapolation to different atmospheres
Barth et al. (2023) have shown that lightning can produce large amounts of nitrogen oxide in both N2−O2 and N2−CO2 atmospheres. This NO provides the precursor of other nitrogen oxides in the gas phase as well as nitrite and nitrate in the aqueous phase (see below). From our equilibrium calculations, we find that the maximum possible NO concentration (at ~3300 K) is only slightly higher than our measurement for the wet, high-CO2 experiments (Fig. 5). This suggests, that at the time we took the NO measurement, the NO concentration in the flask had (nearly) reached equilibrium. We cannot fit the production law we used for CO (Eq. (2)) to this single data point, but, assuming our data point represents the equilibrium NO concentration, we can find the slowest production that will reach equilibrium after 120 min (within 1%). The slope of this production curve at the origin provides a lower limit for the NO production rate. For the wet experiments with a high CO2 concentration, this returns a lower limit of (5.6 ± 1.0) × 1015 molecules/J or a yearly production of (2.6 ± 0.4) Tg yr−1 with modern Earth’s lightning flash rate.
For the other three sets of wet experiments (with N2, N2−H2, and low CO2 gas mixtures), the minimum NO production is independent from the CO2 and H2 fraction in the gas (3 ± 1) × 1015 molecules/J or (1.2 ± 0.3) × 10−2 Tg yr−1. In these experiments, water vapour in the gas mixture (1–1.4%) provides the necessary oxygen to oxidise nitrogen to NO. In the corresponding dry experiments, the NO production is lower than in the wet experiments, but not 0 due to traces of CO2 (in particular in the low-CO2 experiments), water vapour, and O2 being present in the gas mixture. Barth et al. (2023) found in their wet experiments with only trace amounts of O2 (0.06%) that ~3 × 1015 molecules/J of NO are produced. This production rate is similar to our wet experiments without any or with only small amounts of CO2, suggesting that dissociation of water vapour is the main production pathway for NO in all of these experiments where the concentration of CO2 and O2 is low.
From the high-CO2 experiments and subsequent equilibrium calculations (Fig. 5) we find that the presence of H2 in the gas mixture decreases the NO production. Instead, more H2O is produced. We used these results for the NO production rate as input for photochemical simulations of the NO2 concentration in the atmospheres of different potential exoplanets (Sec. 4). NO and NO2 are spectrally active at 5.3 μm and 6 μm, respectively, and therefore potential signatures for lightning activity in exoplanet atmospheres (Gordon et al. 2022).
3.7 Nitrous oxide (N2O)
Another potential biosignature is N2O, making an investigation of the possibility of a false-positive signature from lightning important. The maximum N2O production found in our experiments is 2.5 μmol, which corresponds to an energy yield of 8.5 × 1012 molecules/J or 1.3 × 10−4 Tmol yr−1 with modern Earth’s lightning flash rate (see Sec. 2). This value is similar to experimental results for Earth’s atmosphere (Levine et al. 1979; Hill et al. 1984; Chameides 1986). The total biological N2O emission on Earth is much larger with 0.45 Tmol yr−1 (Bouwman et al. 2002; Tian et al. 2020). This N2O is produced by incomplete denitrification of Nitrate to N2 (Schwieterman et al. 2022). In the Proterozoic, the N2O flux might have been significantly higher due to the limited availability of copper catalysts, preventing the last step of denitrification from N2O to N2 (Buick 2007).
In addition to the N2O directly produced by lightning, other forms of fixed nitrogen (e.g. NO, NO2, or HNO3) can be deposited into the ocean, converted to N2O by Fe2+ (Ranjan et al. 2019), and again outgassed into the atmosphere. If all lightning-produced NO (based on our experimental results) were to be converted to N2O eventually, that would correspond to an annual production of 0.09 Tmol yr−1. This would only be a factor of 5 lower than the modern Earth N2O flux and potentially detectable in the emission spectrum of an Earth-like planet orbiting a K dwarf (Schwieterman et al. 2022). This would be particularly true if the lightning flash rate in the atmosphere of such a planet is larger than that on modern Earth.
However, in the anoxic atmosphere of an Archean Earth-like planet, the N2O abundance will be reduced by the missing O2-shielding, decreasing the probability of a detectable signal and strengthening the case for the O2/O3 + N2O biosignature. Moreover, a O2-rich planet probably does not have Fe2+-rich oceans. In addition, UV photolysis of nitrate and nitrite, releasing nitrogen back into the atmosphere as N2 (Zafiriou & True 1979a,b; Carpenter & Nightingale 2015; Ranjan et al. 2019) would reduce the feed-stock to produce abiotic N2O. A detectable NO2 signature from lightning (see Sec. 4.4) might help to distinguish a lightning-produced N2O signature from a biogenic source (Schwieterman et al. 2022). We use our results from the photochemical simulations to estimate the maximum potential N2O production and compare it to the NO2 concentration (Sec. 4.3).
3.8 Nitrate (![$\[\mathrm{NO}_3^{-}\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq16.png) ) and nitrite (
) and nitrite (![$\[\mathrm{NO}_2^{-}\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq17.png) )
)
Lightning-produced nitrite and nitrate have been hypothesised as potential nutrients for life on early Earth before the onset of biological nitrogen fixation (e.g. Ducluzeau et al. 2009; Canfield et al. 2010; Nitschke & Russell 2013; Shibuya et al. 2016; Wong et al. 2017; Ranjan et al. 2019). Even though Barth et al. (2023) have shown that life likely became independent from lightning as a nutrient source very early, it might have still contributed to support Earth’s earliest biosphere. Further, this nitrate and nitrite could present a nutrient source for life on exoplanets.
We combined the concentrations of nitrate and nitrite (Fig. 3) because part of the nitrite will oxidise to nitrate in the solution during the experiment. The extent of this oxidation varies depending on the individual experiment setup. As was the case for NO, we find that in wet experiments, the production of nitrite and nitrate increases compared to the dry experiments. Also the experiments without CO2 show some nitrite and nitrate production: in the wet experiments, this is due to the presence of water, but also in the dry experiments, some nitrite and nitrate are present. This small residue may reflect the presence of trace amounts of gaseous H2O, CO2, or O2 in the initial gas mixture due to the limits of our vacuum. Overall, in the high-CO2 experiments the nitrite and nitrate yield is very similar to the NO yield, with a maximum production of ~400 μmol. With modern Earth’s lightning flash rate, that corresponds to ~0.02 Tmol yr−1 or ~0.3 TgN/yr of fixed nitrogen. This yield is very similar to the value presented by Barth et al. (2023) for a potential Archean atmosphere (0.16% CO2 in N2).
Our dry experiments suggest that the oxidation from lightning produced NO to NOx− takes place very fast, while the NO-and HNO-rich air (HNO is also a lightning product) and the droplets of the cloud deck are still in contact to each other, even at some time after the flash. This is in contradiction to Hu & Diaz (2019) who argue that the separation of HNO and NO before the equilibration with the ocean and the subsequent aqueous chemistry quickly return lightning-fixed nitrogen into to the atmosphere as N2.
3.9 Overnight experiments
In addition to the short 120-min experiments, we also conducted overnight experiments with an average total spark time of (925 ± 35) min to investigate the production of compounds that were not detectable in the short experiments or had only very small yields. Figure 6 shows the abundances of gaseous and aqueous products after the overnight experiments and linear fits to show the relation between CO2 concentration and the final abundance of the product. Again, the abundances of HCN and NH3 are calculated from the measured aqueous abundances of CN− and ![$\[\mathrm{NH}_4^{+}\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq18.png) , respectively, with their respective Henry’s law constants as described in Appendix A. Similar to the short experiments, we see an increasing production of oxidised nitrogen (NO, nitrate and nitrite) and a decreasing production of reduced nitrogen (ammonium) with increasing CO2 concentration. The maximum ammonium concentration (at 0% CO2) is only about 2–4 times the corresponding ammonium concentration in the short experiments, even though the spark was running for ~8 times as long, suggesting that the ammonium concentration reached equilibrium during the experiment. For a CO2 concentration of ≳5% basically no ammonium was produced. Instead, the dissociated nitrogen was likely oxidised to NO and eventually nitrite and nitrate. A higher H2 concentration might allow the production of ammonium at higher CO2 concentrations, but eventually, if there is significantly more CO2 (or a different oxygen source) than H2 in the gas mixture, the ammonium production would probably still be suppressed. As discussed above, significant amounts of ammonium can still be produced by subsequent reduction of nitrite by Fe2+ and FeS in the ocean, and to a lesser extent by reduction of nitrate by FeS (Summers & Chang 1993; Summers 2005).
, respectively, with their respective Henry’s law constants as described in Appendix A. Similar to the short experiments, we see an increasing production of oxidised nitrogen (NO, nitrate and nitrite) and a decreasing production of reduced nitrogen (ammonium) with increasing CO2 concentration. The maximum ammonium concentration (at 0% CO2) is only about 2–4 times the corresponding ammonium concentration in the short experiments, even though the spark was running for ~8 times as long, suggesting that the ammonium concentration reached equilibrium during the experiment. For a CO2 concentration of ≳5% basically no ammonium was produced. Instead, the dissociated nitrogen was likely oxidised to NO and eventually nitrite and nitrate. A higher H2 concentration might allow the production of ammonium at higher CO2 concentrations, but eventually, if there is significantly more CO2 (or a different oxygen source) than H2 in the gas mixture, the ammonium production would probably still be suppressed. As discussed above, significant amounts of ammonium can still be produced by subsequent reduction of nitrite by Fe2+ and FeS in the ocean, and to a lesser extent by reduction of nitrate by FeS (Summers & Chang 1993; Summers 2005).
The concentration of nitrite and nitrate as well as NO in our discharge experiments shows a very clear trend with CO2 concentration in the initial gas mixture. For CO2 concentrations around 0, water vapour in the gas mixture is a significant source of oxygen for the production of nitrogen oxides. The slightly increased scatter of measurements at that point can be explained by the additional uncertainty of the concentration of water vapour and other trace gases like O2. We also find the nitrite and nitrate concentration in the overnight experiments to be 5–10 times the concentration in the corresponding short experiments, suggesting that even though NO equilibrium in the gas phase is reached rather quickly (the final NO concentration in the overnight experiments is similar to the short experiments), the subsequent oxidation to NO2 and equilibration with the aqueous phase takes more time, in particular in the experiments where relatively small amounts of nitrite and nitrate are produced. All of these experiments were run with 50 mL of water in the flask, so even when the CO2 content is 0, there was sufficient oxygen available from the water to provide oxygen for the production of some NO and subsequently nitrite and nitrate. The presence of water as an oxygen source is likely also the reason that we again see only very small concentrations of methane, below the measurement error. Unlike the other forms of oxidised nitrogen, we do not see a clear trend in the production of N2O with CO2 concentration. This follows the trend in our short, wet experiments where also no clear trend was visible, suggesting that if enough oxygen is available, nitrogen oxides with a higher oxidation state are preferred. N2O has an oxidation state of +1 while NO, NO2, nitrite and nitrate have oxidation states of ≥2.
Urea (CO(NH2)2) is an important precursor for cyanamide (CH2N2) which itself is a precursor for RNA (Das et al. 2019). In our experiments, urea follows a similar trend as ammonium, with abundances of roughly one order of magnitude lower. However, because most measurements for CO2 concentrations above 1% were below the detection limit, we did not try to fit a line to the urea data. It thus seems that the production of (detectable levels of) urea is only possible under reducing conditions.
HCN is an important precursor molecule for the formation of RNA and has been hypothesised to be produced by lightning in reduced atmospheres (Miller 1957; Miller & Schlesinger 1983; Pearce et al. 2017, 2022). In our experiments, we can monitor the HCN production by its dissolved form, cyanide CN−. The cyanide abundance increases with increasing CO2 abundance, though much more slowly than the abundance of nitrite and nitrate. This follows the calculations performed by Chameides & Walker (1981), who predicted an increase in HCN production when decreasing the C/O-ratio (at constant H2 concentration), which is happening when increasing the CO2 concentration (without adding other forms of carbon this limits the C/O ratio to 1/2). Chameides & Walker (1981) predict an HCN production rate of ~3 × 109 to 4 × 1011 molecules/J for the range of C/O-ratios equivalent to our experiments (for a gas mixture with 0.9 bar N2 and 0.05 bar H2, C + O = 0.1 bar). We find our results for HCN production to be ~2 to 3 orders of magnitude larger than the values calculated by Chameides & Walker (1981). The reason for this might be that the water in our experiments acts as a buffer: produced HCN dissolves in the water, lowering the concentration in the gas phase and allowing for more HCN to be produced. This suggests that we over-predict the production of HCN even though lightning occurs in the water-saturated atmosphere (clouds). In real lightning conditions, HCN is produced with the chemical equilibrium composition at the specific freeze-out temperature. After the HCN is produced, equilibration with water droplets happens. The next lightning flash produces new HCN in a different air parcel. In contrast, in our experiments, we keep adding HCN to the same gas mixture which is constantly equilibrating with the water phase. For other gases, this is less of a problem as we are measuring most of them in the gas phase and their Henry’s law constants are orders of magnitude lower, meaning less of the gas is absorbed into the water. In conclusion, these experimental limitations suggest that our results do not apply to the real atmosphere for HCN. Chemical equilibrium calculations (Fig. 7) show that the concentration of HCN increases with CO2 concentration for gas temperatures above ~3000 K, while temperatures below ~2700 K the HCN concentration decreases. This suggests that the freeze-out temperature for HCN in our experiment is ≳3000 K. Other experiments studied the effect of Ch4 concentration on HCN production: an increase in CH4 increases the C/O-ratio, leading to a strong increase in HCN production (Chameides & Walker 1981; Tian et al. 2011; Pearce et al. 2022).
 |
Fig. 6 Final abundances of gaseous([g]; nitrous oxide (N2O), methane (CH4), hydrogen cyanide (HCN), nitric oxide (NO), and ammonia (NH3)) and aqueous products ([aq]; CN−, nitrite + nitrate, |
 |
Fig. 7 HCN concentration in chemical equilibrium (with GGChem, Woitke & Helling 2003) as function of gas temperature for different CO2 fractions in the gas mixture (other gases: 1% H2, 1% H2O, rest N2). For T ≳ 3000 K (right dashed grey line), HCN concentration increases with increasing CO2 concentration (until ~3–5% CO2). For T ≲ 2700 K HCN concentrations decreases with increasing CO2 concentration (except for 0.1% CO2). |
4 Results and implications of photochemical simulations
Now that we know the production rates for CO and NO, by far the most important direct products of lightning in N2−CO2 gas mixtures, we want to know how this influx of CO and NO changes the composition of different planetary atmospheres. We are particularly interested in whether lightning can produce observable signatures in transmission, emission, and reflected light spectroscopy. To answer these questions, we used the photochemical model of the Atmos coupled climate-photochemistry code (Arney et al. 2016; Lincowski et al. 2018, see Sec. 2) to calculate the atmospheric mixing ratio of CO, NO, NO2, and other gases for a large range of lightning flash rates. We modelled both oxygen-poor (anoxic) and oxygen-rich (oxic) atmospheres on Earth-sized planets orbiting the Sun (G-type star) and TRAPPIST-1 (M-type star) at the inner edge of their respective habitable zones.
4.1 Photochemistry in anoxic atmospheres
Figure 8 a, b shows the resulting CO mixing ratios for the anoxic atmosphere (4.6% CO2 in N2 filler gas), equivalent to our experiments and necessary to keep the surface of the investigated planets clement (Meadows et al. 2018a), for abiotic and biotic scenarios with different CH4 fluxes and CO deposition rates and a range of lightning flash rates (Table B1). Using equilibrium chemistry calculations as described in Sec. 3.5, we can estimate the production of CO and NO with modern Earth’s lightning flash rate to be 7.0 × 108 and 3.8 × 108 molecules cm−2 s−1, respectively, in this anoxic gas mixture. The results look very differently for the two different host stars with different spectra: On the planet orbiting the Sun, the CO mixing ratio in the biotic scenario is up to three orders of magnitude larger than in the abiotic scenario. On the planet orbiting TRAPPIST-1, this trend is reversed. The CO ratio in the biotic scenario is 100 times smaller than in the abiotic scenario for most of the CO flux range. the high CO concentrations in the TRAPPIST-1 simulations are due to efficient CO2 photolysis: The XUV flux is concentrated near the Ly-α line and the FUV continuum and therefore absorbed by the abundant CO2 molecules that are dissociated into CO and O. Thus, the CO2 is shielding water molecules from the XUV radiation and the photolysis of water in the atmosphere of a planet orbiting an M dwarf is less efficient and the concentration of the OH radical is lower (Segura et al. 2005; Schwieterman et al. 2019). Since the deposition velocity with which CO is deposited in the ocean is lower in the abiotic than in the biotic scenario where acetogens in the ocean consume the CO, the abiotic CO concentration remains higher than in the biotic case.
In the simulations for the planet irradiated by the Sun, the OH concentration in the atmosphere is higher and the CO lifetime is shorter. In the biotic scenario, the increased, biogenic flux of CH4 which is photo-oxidised to CO leads to a higher CO concentration than in the abiotic scenario. In a test case for the biotic scenario, where we assume no CO to be deposited into the ocean (dotted lines in Fig. 8), the final CO concentration is increased to well above 1% in all but one case despite OH being present. An increase in surface temperature increases the concentration of water vapour in the atmosphere and subsequently the concentration of OH, decreasing the lifetime of CO and its final concentration. This is especially apparent for the biotic planet around the Sun where we assume no CO deposition: while for a surface temperature of Tsurf = 275 K (blue) the CO concentration is enhanced to above 1%, for a slightly higher surface temperature of Tsurf = 300 K the subsequently higher water and OH concentrations allow for a more efficient removal of CO from the atmosphere (see Fig. 9 for comparison of mixing ratios). This suggests that for the biotic scenario for the Sun-orbiting planet with Tsurf = 300 K, recombination of CO with OH is the major CO sink. Overall, the major sink for CO in both biotic scenarios for TRAPPIST-1 and the biotic scenario with Tsurf = 275 K for the Sun is deposition in the ocean.
In nearly all anoxic simulations, the CO concentration is relatively high due to CO2 dissociation and CH4 photo-oxidation and additional contributions of CO by lightning are not able to further increase the CO concentration. Only for lightning flash rates around 1000 times the modern Earth lightning flash rate we can see the CO concentration increase slightly beyond the background level. The only scenario, where the background CO level is low enough to see an increase in CO concentration at lower flash rates, is the abiotic scenario for the planet orbiting the Sun. For CO production rates higher than ~1011 or ~1012 molecules cm−2 s−1 for Tsurf = 275 K and Tsurf = 300 K respectively, the atmosphere enters into a CO runaway: the CO flux overwhelms the CO deposition and the CO concentration jumps up to several per cent. Kasting (1990) showed that also an increased NO concentration (in our simulations, the NO flux and thus concentration increases with increasing flash rate) can lead to a longer lifetime of CO in the atmosphere and thus to a higher CO concentration. The CO flux where the atmosphere enters into a CO runaway is similar to the total CO emission on the modern Earth of ~2 × 1011 molecules cm−2 s−1 which is mainly from anthropogenic sources (68%) and wildfire and deforestation (32%; Zhong et al. 2017). However, on the uninhabited Archean Earth, the volcanic CO flux is estimated to be much lower at ~(1 − 2) × 108 molecules cm−2 s−1 (Kasting & Walker 1981). We also should note that for CO concentrations larger than the CO2 concentration (4.6%) which occur in our simulations only for extremely high lightning flash rates, our assumption of constant CO2 concentration might not be applicable anymore, as it would require very high volcanic fluxes of CO2 to replenish the CO2 dissociated by lightning and would greatly enhance the carbon budget in the atmosphere.
For the planet orbiting the Sun, we find a very similar trend for the NO2 concentration for all scenarios (Figs. 8e and f): Very low abundances (<10−8 for nearly all simulations), but a steady increase with increasing NO flux. For the planet orbiting TRAPPIST-1, this looks a bit different: in the biotic scenario with CO deposition, the NO2 concentration follows a very similar trend to the same case for the Sun-planet, but with slightly higher mixing ratios of up to 1 ppm for the highest NO fluxes. In the abiotic case, however, the NO2 abundance is more than six orders of magnitude higher for low NO fluxes compared to the biotic case, before it rapidly decreases, parallel to the CO abundance, at an NO input flux of ~3 × 109 molecules cm−2 s−1. At higher fluxes, the NO2 abundance increases again, very similar to the biotic scenario.
We can also observe this behaviour in the CO concentration for the abiotic scenario on the TRAPPIST-1 planet (Fig. 8b, solid lines): here the background CO concentration (for low CO lightning fluxes) is very high at approximately 1%. Once the CO and the corresponding NO flux cross a certain threshold (~1010 molecules cm−2 s−1), the CO concentration drops by more than two orders of magnitude before rapidly climbing again in a CO runaway. This drop in the CO and NO2 concentration is accompanied by a drop in O2 concentration and a strongly increasing NO concentration (Figs. 8c, d). In the anoxic gas mixture in our experiments as well as in lightning strikes in the anoxic Archean atmosphere, where NO and CO are produced from dissociated CO2 and N2, free oxygen is produced if not the same amount of NO and CO is produced to match the stoichiometric ratio of the split CO2 (Kasting 1990). When using the CO and NO production fluxes in our photochemical simulations, we included an additional O flux, which is variable alongside the NO and CO fluxes, to balance the ratio between the elements N, C, and O. Together, these three fluxes replace the lightning module originally included in Atmos (Harman et al. 2018) which we turned off for these simulations. The background concentrations of O2 and ozone as byproducts from CO2 photolysis are very high in this scenario and even slightly enhanced further by the addition of free oxygen from lightning, up to an O2 surface mixing ratio of 1.4 × 10−3 and a peak ozone concentration of ~5 ppm at a height of 32 km. The high concentration of oxygen allows for efficient oxidation of NO to NO2 (NO + O ⟶ NO2), resulting in a higher concentration of NO2 than NO. Other efficient destruction channels for NO and NO2 are NO + HCO ⟶ HNO + CO and NO2 + O ⟶ NO + O2, respectively. At high NO fluxes, the channels H + NO ⟶ HNO, NO + OH ⟶ HNO2, NO + O ⟶ NO2, and NO + HO2 ⟶ NO2 + OH become the limiting factors controlling the NO concentration, while NO2 photolysis and the reaction NO2 + H ⟶ NO + OH control the destruction of NO2. At high NO fluxes, the overall balance of the HOx reservoir shifts by decreasing steady-state HO2 while increasing steady-state OH. This shift allows for increased recombination of CO + OH ⟶ CO2 + H, leading to a sharp decrease in the concentration of CO and oxygen species, entering a different photochemical regime (Ranjan et al. 2022). We note that the HOx reservoir ultimately depends on H2O photolysis (Harman et al. 2015), and all NO-mediated catalytic cycles that net recombine CO and O to CO2 require the presence of HOx species (see Harman et al. 2018, their Table 1). For anoxic atmospheres with a Sun host, the dominant photochemical channels are more consistent throughout the range of NO fluxes, which is reflected in the lessened discontinuous behaviour in the flux-abundance relationships shown in the left panels of Fig. 8. For these atmospheres, NO is primarily destroyed by NO + O ⟶ NO2 and NO2 is primarily destroyed by NO2 photolysis.
This process was described by Harman et al. (2018) who suggested that lightning-produced NO can provide a catalyst for the recombination of CO and O to CO2, preventing a false-positive O2-biosignature. They assumed an NO production of ~6 × 108 molecules cm−2 s−1 (for modern Earth’s lightning flash rate) in an atmosphere with 5% CO2 and found this to strongly reduce the CO and O2 concentrations (for an M dwarf host star). This NO production rate is about 50% higher than what we assume for modern Earth’s lightning flash rate, but even if we correct for this difference, the additional production by lightning of CO and O in our model moves this behaviour to flash rates at least three times that of modern Earth. Using our assumption for the NO production per flash, a flash rate of more than six times modern Earth’s is necessary to prevent the build-up of significant amounts of oxygen in the atmosphere. This difference is likely due to differences in the UV spectrum used for the simulations. Larger stellar FUV/NUV flux ratios tend to drive higher abiotic O2 production rates (Harman et al. 2015) and TRAPPIST-1 (M8V) has a larger FUV/NUV ratio than the latest host star considered by Harman et al. (2018), an M4V dwarf. Importantly, this suggests that lightning may not eliminate all O2-false positive scenarios for CO2-rich terrestrial planets orbiting ultra-cool dwarf hosts, at least at the ~0.1% level. Figure B.6 shows the column density of the atmospheric constituents for the range of simulated CO and NO fluxes, Fig. B.1 (left panel) the atmospheric mixing ratio profiles for simulations before and after the drop in CO and O2 concentration for the scenario with Tsurf = 275 K. The spectra for these two cases are discussed below (Fig. 12, left panel).
 |
Fig. 8 Photochemically simulated CO (a, b), NO (c, d), and NO2 (e, f) mixing ratios in the anoxic atmosphere (4.6% CO2) of an Earth-sized planet orbiting the Sun (a, c, e) and TRAPPIST-1 (b, d, f) for varying CO and NO production rates and different scenarios: abiotic (solid), biotic with CO deposition (dashed), and biotic without CO deposition (dotted). The surface temperature (blue: Tsurf = 275 K, orange: Tsurf = 300 K) controls the water vapour concentration. The second x-axis gives the corresponding lightning flash rate (in units of modern Earth’s flash rate), as estimated for the respective atmospheric composition. |
 |
Fig. 9 Mixing ratios for biotic scenario (Sun) without CO deposition (CO flux ~107 molecules cm−2 s−1) for two different surface temperatures (solid lines: Tsurf = 275 K, dotted lines: Tsurf = 300 K) as result of a kinetic gas-phase calculation with photochemistry. |
 |
Fig. 10 Photochemically simulated CO (a, b), NO and NO2 (c, d) mixing ratios in the oxic atmosphere (4.6% CO2, 21% O2) of an Earth-sized planet orbiting the Sun (a, c) and TRAPPIST-1 (b, d) for varying CO and NO production rates and the biotic scenario with CO deposition (Tsurf = 288 K). The second x-axis gives the corresponding lightning flash rate (in units of modern Earth’s flash rate), as estimated for the respective atmospheric composition. |
4.2 Photochemistry in oxygen-rich atmospheres
Earth’s atmosphere was anoxic for the first ~2 Gyr of its evolution. After that, the oxygen concentration increased drastically, but it was only ~0.5 Gyr ago that the oxygen concentration reached today’s level (e.g. Catling & Zahnle 2020). Assuming that the evolution of oxygenic photosynthesis takes a similar amount of time on other worlds if it happens at all, it is therefore most likely that if we find an inhabited planet, it will have an anoxic or low-oxygen atmosphere (Krissansen-Totton et al. 2018b). However, as we have discussed in the introduction, photochemistry and hydrogen escape can lead to the abiotic build-up of O2 in an otherwise anoxic atmosphere. To fully investigate the impact of lightning on observable oxygen and ozone features, we therefore also conducted simulations for oxygen-rich atmospheres with a biosphere (4.6% CO2, 21% O2 in N2 filler gas; biotic scenario with maximum CO deposition; Fig. 10). In addition, the O2 and O3 features of an N2−O2 atmosphere are likely not detectable with JWST (Krissansen-Totton et al. 2018a). Thus, the atmosphere of a modern-Earth-like, inhabited planet might resemble the Archean Earth instead, with CH4 and CO2 features. In this case, it is important to understand the role of lightning in potentially producing a CO signature.
In such an oxic gas mixture, our estimate for the CO and NO production rates at modern Earth’s lightning flash rate are 1.5 × 108 and 2.5 × 109 molecules cm−2 s−1 respectively, using the method described in Sec. 3.5. Our simulations find, for both host stars, a significantly lower CO mixing ratio than in the anoxic atmospheres, independent from the CO deposition velocity. The high abundance of O2 in these atmospheres offers an additional sink for atmospheric CO: excited atomic oxygen from ozone photolysis increases the production of the OH radical: O3 + hv(λ < 320 nm) ⟶ O(1D) + O2 and H2O + O(1D) ⟶ 2 OH. Since the NUV radiation necessary for this pathway is lower for M dwarfs, the CO mixing ratio on the planet around TRAPPIST-1 is higher than on the planet around the Sun (Segura et al. 2005; Schwieterman et al. 2019). However, for CO fluxes >3 × 109 molecules cm−2 s−1 for the planet orbiting the Sun and >108 molecules cm−2 s−1 for the planet orbiting TRAPPIST-1 we find an increase of the CO mixing ratio. This corresponds to lightning flash rates of ~10 and ~0.7 times modern Earth’s flash rate, respectively. In the Sun case, the CO mixing ratio increases to ~10−7 for a CO flux of 3 × 109 molecules cm−2 s−1 and then steadily to ~10−4 for a CO flux of 5 × 1011 molecules cm−2 s−1. In the TRAPPIST-1 case, the CO mixing ratio increases to ~10−6 for a CO flux of 108 molecules cm−2 s−1 and then steadily to ~10−4 for a CO flux of 1011 molecules cm−2 s−1. To estimate the corresponding lightning flash rate, we used again equilibrium calculations to determine the CO concentration at the freeze-out temperature of 2430 K for the simulated, oxic gas mixture. We find that at modern Earth’s lightning flash rate, the CO concentration is approximately 6 and 2 orders of magnitude smaller than in the corresponding anoxic atmosphere for the Sun and TRAPPIST-1 planet, respectively (same CO2 concentration of 4.6%), as the abundant O2 increases the recombination of CO to CO2. This means lightning flash rates of 3000 and 500 times the modern Earth’s flash rate are needed to achieve CO concentrations similar to the corresponding anoxic scenarios (biotic with maximum CO deposition).
The NO2 concentration follows a very similar trend to the CO concentrations in the photochemical calculations with a sharp increase at CO fluxes of ~3 × 109 molecules cm−2 s−1 and ~108 molecules cm−2 s−1, and corresponding NO fluxes of ~6 × 1010 molecules cm−2 s−1 and ~2 × 109 molecules cm−2 s−1, for the Sun and TRAPPIST-1 case, respectively. The changes in the slope of the NO and NO2 abundances vs. NO flux are caused by shifts in their main photochemical destruction channels as these species overwhelm the photochemical sinks with the fastest kinetic rates. For NO, the NO + O3 ⟶ NO2 + O2 channel saturates near this threshold flux, and the slower NO + O ⟶ NO2 and NO + OH ⟶ HNO2 channels become comparable above it. This tracks with the depletion in O3 we also see in our photochemical simulations at increasing NO flux. For NO2, the NO2 + O ⟶ NO + O2 channel saturates, and NO2 photolysis becomes the dominant destruction channel. The flux-abundance relationships vary between host stars due to the different distributions of radical species generated by differences in stellar spectra. We also emphasise that these shifts in photochemical channels with increasing NO flux differ in the oxic vs. anoxic cases.
Similar to the anoxic case, in the oxic atmosphere, lightning will also produce free oxygen which we expect to mostly recombine to O2. However, it is hard to determine how much atomic oxygen is produced. Stoichiometrically, all NO and CO can be produced from dissociated N2, O2, and CO2 without any remaining O. To test whether the addition of free O might change the chemistry significantly, we ran simulations with an O flux similar to the lightning NO flux. We only found small enhancements in the final NO2 concentrations for the highest NO fluxes (>1012 molecules cm−2 s−1).
4.3 Nitrogen deposition into an ocean
To investigate the possibility of lightning-produced NO to be converted to N2O in the ocean, which could in return be outgassed into the atmosphere where it might produce a false-positive biosignature, we calculate the nitrogen deposition flux into the surface of the planet. In addition to NO, also NO2, HNO, and HNO3 are deposited from the atmosphere. The combined nitrogen deposition flux is shown in Fig. 11 in comparison to the NO production from lightning for the anoxic and abiotic scenario for the planet orbiting the Sun (Tsurf = 275 K). A large part of the introduced NO is deposited into the surface, mainly in the form of HNO: up to ~95% at NO fluxes of ~1010 molecules cm−2 s−1, decreasing to ~60% at NO fluxes of ~1012 molecules cm−2 s−1. This behaviour is similar to the other anoxic-abiotic scenarios. Even if all of this deposited nitrogen were to be converted to N2O and outgassed into the atmosphere, a lightning flash rate of more than 100 times modern Earth’s would be necessary to produce an N2O flux of 10 Tmol yr−1 which would still likely be not enough to be detectable with JWST (Schwieterman et al. 2022). On an Earth-like planet orbiting a K dwarf, an N2O flux of 1 Tmol yr−1 or even less might be detectable, though, potentially producing a false-positive biosignature. These calculations present an upper limit, assuming the whole surface is covered by an ocean, as is suggested for the exoplanet Kepler-138 d (Piaulet et al. 2023), but on a planet with a lower ocean-to-land surface ratio, deposition of nitrogen oxides into the ocean will be less efficient. This and other uncertainties that will likely decrease the N2O flux significantly, such as the efficiency of the conversion of deposited nitrogen into N2O, are the reasons why we are not further investigating this potential signature.
 |
Fig. 11 Deposition flux of fixed nitrogen into an ocean (red) for the anoxic, abiotic planet around the Sun (Tsurf = 275 K) for a range of lightning NO fluxes and corresponding lightning flash rates. For comparison, the total lightning-produced NO flux is shown (orange). The corresponding deposition rates in Tmol yr−1 are shown as black lines (converted into molecules cm−2 s−1). |
4.4 Observational signatures from lightning in transmission, emission, and reflected light
To investigate whether lightning produces observable signatures, we calculated the emission, transmission, and reflectance spectra for a selection of simulations. The most likely missions and observatories to directly image temperate terrestrial planets will either do so in the Vis/NIR range, such as NASA’s proposed Habitable Worlds Observatory, or the mid-IR (MIR), such as the proposed ESA Large Interferometer for Exoplanets (LIFE) mission. We have thus chosen the wavelength ranges and spectral resolving powers to accentuate features that would be plausibly detectable with these platforms.
Figure 12 shows the calculated transmission spectrum for two scenarios of the TRAPPIST-1 planets: The anoxic, abiotic scenario (Tsurf = 275 K) and the oxic, biotic scenario (Tsurf = 288 K). The different shapes of the CO2 feature around 15 μm in the emission spectra are due to the different atmospheric profiles we used: for the oxic atmosphere which is very similar to modern Earth’s atmosphere, we used Earth’s atmospheric profile with its stratospheric temperature inversion. Since the emission is probing different heights in the atmosphere it registers different temperatures, with the centre of the line at 15 μm probing furthest up in the atmosphere, where the temperature is higher than deeper in the atmosphere. For the anoxic atmosphere, we assumed an isothermal atmosphere above the convective troposphere, such that the absorption feature appears flat. The spectra are shown for two different CO fluxes, representing scenarios at lightning flash rates below and above where the atmospheric composition changes drastically: for the anoxic/abiotic scenario, these are CO fluxes of 109 molecules cm−2 s−1 (black), 2 × 1010 molecules cm−2 s−1 (magenta), and 1012 molecules cm−2 s−1 (blue), corresponding to lightning flash rates of ~2, ~35, and ~1500 times that of modern Earth, respectively. For the oxic and biotic scenario, CO fluxes of 108 molecules cm−2 s−1 (black) and 1011 molecules cm−2 s−1 (blue), corresponding to lightning flash rates of ~0.9 and ~680 times modern Earth’s, respectively, are shown. Most notable is how the increased concentration of NO and NO2 is reducing the ozone features at 9.6 μm (transmission and emission) and <0.65 μm (reflectance) in the scenario with the higher CO flux. The individual mixing ratio profiles for the two cases compared in Fig. 12 can be found in the appendix (Fig. B.1).
In the case of the anoxic planet, the removal of the ozone feature would prevent a possible false-positive detection of life. In contrast to the oxic scenario, the CO concentration is much higher here (for the low and high lightning flash rates), though, allowing for strong CO features in the transmission spectrum at 2.35 μm and 4.65 μm. This allows us to identify a CO2-rich atmosphere and for a correct interpretation of the ozone feature as potentially from an abiotic source. For the intermediate lightning flash rate (~35 times modern Earth’s) we find both the CO and the ozone features to be removed or very weak. However, in the absence of strong methane features, the missing CO feature should not be interpreted as a sign of life. However, if in this scenario, an increased CH4 feature from volcanism is observed it could be misinterpreted as a biosignature. In the corresponding biotic scenario (Fig. B.5), where the CO concentration is similarly low, the biotic methane flux produces strong features that should allow the detection of the present biosphere.
In the oxic and biotic scenarios, lightning is decreasing the ozone concentration in the atmosphere, reducing the spectral ozone feature used to identify an oxygen-rich atmosphere. In that case, other biosignatures are necessary to identify that the planet is inhabited, for example, the combination of CO2 and CH4 in the absence of CO, as suggested by Krissansen-Totton et al. (2018b). We find an increased concentration of CH4 for the higher CO flux, most notably in the reflected spectrum (1.6–1.8 μm), likely because the increased CO flux is taking up most of the available sinks (e.g. OH). We also find an NO2 feature at ~6 μm and a C2H6 feature at ~11 μm (both in transmission and emission spectra) to appear for the higher CO flux scenario, indicating the presence of lightning activity and helping to explain the absence of an ozone feature. This C2H6 feature is enhanced because other gases are soaking up the radical sinks that would otherwise destroy C2H6. In the reflected light, we find molecular oxygen features at 0.76 μm (O2 A-band) and 1.27 μm which are not affected by the lightning activity, potentially allowing for the identification of an oxygen-rich atmosphere if that wavelength range is observed. In any way, to enhance the CO concentration to a detectable level in the oxic scenario, significantly higher lightning flash rates are necessary.
Spectra for other scenarios and the corresponding atmospheric mixing ratio profiles are shown in Appendix B. For the oxic, biotic Sun scenario (Fig. B.2), the behaviour is very similar to the TRAPPIST-1 planet: with higher CO and NO fluxes, the ozone features are reduced but we find enhanced methane features. The spectra for the anoxic, abiotic Sun planet (Fig. B.3), however, look very different compared to the TRAPPIST-1 planet: because of the lower XUV radiation of the Sun, there is no abiotic ozone build-up in the atmosphere. Also, the CO concentration is much lower and the spectra mainly show CO2 features. Only the NO feature at 5.3 μm is stronger when the CO flux is increased.
For the anoxic, biotic scenarios, we are comparing the spectra for simulations with and without CO deposition (Figs. B.4 and B.5): as expected, the main difference is that without CO deposition, we find a strong CO feature at 4.65 μm. For the anoxic, biotic planet around the Sun without CO deposition, we calculated the spectra with individual species removed to show their individual impacts on the planetary spectrum (Fig. 13). In particular, we looked at the effect of removing methane (orange lines) and C2H6 (red). The complete spectra are shown in comparison (black dotted lines). As expected, we see many strong methane features in all three spectra, masking for example the 2.35 μm CO feature. For C2H6, we find a strong feature between 11 and 13 μm in the emitted (top panel) and transmitted spectra (bottom panel). Removing NO2 and HNO3 from the calculations did not change the spectra, suggesting features of these molecules are small and masked by other, more abundant molecules such as CH4.
Whether these spectral features are eventually detectable or not depends on many factors such as the wavelength range and resolving power of the instrument, the duration of the observation, or the variability of the stellar radiation. For example the ozone feature at 9.6 μm might not be detectable with JWST (Krissansen-Totton et al. 2018a). Future missions, dedicated to studying the atmospheres of terrestrial exoplanets will be better suited to detect atmospheric constituents of small planets, such as the Habitable Worlds Observatory (HWO) recommended by the US 2020 Astronomy & Astrophysics Decadal Survey (National Academies of Sciences & Medicine 2021) with capabilities informed by the Habitable Exoplanet Observatory (HabEx, Gaudi et al. 2020) and Large UltraViolet Optical and Infrared (LUVOIR, The LUVOIR Team 2019) mission concepts. This mission would be able to detect O3 and O2 features in the UV and visible and CH4 in the near-IR. The proposed Large Interferometer For Exoplanets (LIFE, Alei et al. 2022; Quanz et al. 2022) would be able to detect O3 and CH4 features in the MIR.
 |
Fig. 12 Simulated spectra for the TRAPPIST-1 planet: Emitted (top: MIR, R = 400), reflected (middle: NIR, R = 400), and transmitted light (bottom: NIR-MIR, R = 200). Note. MIR features in emission are not just dependent on the abundance of spectrally active gases, but also the temperature structure of the atmosphere. Left panel: anoxic, abiotic scenario (Tsurf = 275 K): CO flux of 109 (black), 1010 (magenta), and 1012 molecules cm−2 s−1 (blue), corresponding to lightning flash rates of ~2, ~35 and ~1500 times modern Earth’s, respectively. Right panel: oxic, biotic scenario (Tsurf = 288 K): CO flux of 108 (black) and 1011 molecules cm−2 s−1 (blue), corresponding to lightning flash rates of ~0.9 and ~680 times modern Earth’s, respectively. |
 |
Fig. 13 Simulated spectra for the planet orbiting the Sun: Anoxic, biotic scenario without CO deposition (CO flux ~109 molecules cm−2 s−1). Spectra with individual species removed are shown (without C2H6 in red, and without CH4 in orange) in comparison to the full spectrum (black dotted line). |
5 Discussion
When conducting our experiments and photochemical simulations, we encountered several unknowns and had to make assumptions that allowed us to simulate the atmospheric chemistry of terrestrial exoplanets. In this section, we want to discuss three of these uncertainties in more detail: the lightning flash rate on terrestrial exoplanets, the composition and stability of the atmosphere of Archean Earth and similar exoplanets, and the CO metabolism.
5.1 Lightning flash rate
In this work, we estimated the production rates of several gaseous and aqueous species by lightning in different atmospheric and planetary environments. To do so, at several points in the paper, we used the global lightning flash rate on modern Earth of 44 ± 5 s−1 (Christian et al. 2003) with an energy of 6.7 GJ per flash (Price et al. 1997) to extrapolate from our laboratory experiments to an annual, global production. Lightning rates and energies have been well studied on the modern Earth (Schumann & Huntrieser 2007; Hodosán et al. 2016a, and references therein). However, as discussed in the introduction, much uncertainty remains for the lightning flash rate on the early Earth, terrestrial planets, and exoplanets in general (Wong et al. 2017; Hodosán et al. 2021; Braam et al. 2022).
We therefore treat the lightning flash rate as an independent variable in our photochemical simulations (while always using an energy of 6.7 GJ per flash), simulating the atmospheric composition for a range of flash rates from less than 10% to more than 1000 times modern Earth’s flash rate (44 ± 5 s−1). This allowed us to analyse more plausible scenarios of flash rates similar to modern Earth’s but also to predict minimum flash rates for certain scenarios. In some scenarios, small changes in the flash rate have very little effect on the composition of the atmosphere and thus the observability of certain features, such as the biotic scenarios for the anoxic planets around TRAPPIST-1 and the Sun.
In other scenarios, small changes in the flash rate, close to that of modern Earth, can have a significant impact on the planetary spectrum. For example, our simulations of the anoxic, abiotic atmosphere of a planet orbiting TRAPPIST-1 show that lightning at modern Earth’s flash rate is not able to remove the abiotic ozone feature caused by the dissociation of CO2 due to the star’s strong XUV radiation. However, at a flash rate ten times higher, the additional NO input and subsequent oxidation to NO2 enhances the recombination of CO and oxygen to CO2, removing the abiotic ozone feature and preventing a false-positive biosignature detection. This shows how sensitive the atmospheric composition and planetary spectrum can be to the lightning flash rate.
In addition, the lightning flash rate at which this threshold appears depends on the individual XUV spectrum of the planet’s host star which is responsible for the CO2 dissociation and O2 production: Larger stellar FUV/NUV flux ratios tend to drive higher abiotic O2 production rates (Harman et al. 2015) and TRAPPIST-1 (M8V) has a larger FUV/NUV ratio than the latest host star considered by Harman et al. (2018), an M4V dwarf. Therefore, Harman et al. (2018) find a flash rate equal to modern Earth’s sufficient to remove the abiotic ozone feature in their simulations.
An additional factor that can influence the occurrence of lightning is cosmic rays, as planets orbiting M dwarfs will experience more frequent and intense stellar flares that are associated with flares of charged particles. In addition to their potential effect on the lightning flash rate, cosmic rays are also an important source of disequilibrium chemistry in the atmospheres of exoplanets. Studies of Earth-like planets orbiting M dwarfs have shown that the enhanced cosmic ray flux leads to increased production of nitrogen oxides (NO, NO2, HNO3) as well as a decreased concentration of ozone, similar to our results for lightning (Grenfell et al. 2012; Tabataba-Vakili et al. 2016; Scheucher et al. 2020).
Another uncertainty that is connected to the lightning flash rate is the effect of the flash properties. The freeze-out temperature of a specific gas, and thus its concentration in the air parcel cycled through the flash, depends on the cooling timescale of the flash. Therefore, the estimate of the freeze-out temperature depends on the properties of the flash considered in the experiment or calculations. In addition, the chemical timescales and thus the freeze-out temperature depend on the specific location in the discharge where the trace gas is produced: Trace gases produced in the expanding shock wave of a lightning strike where chemical timescales are shorter will freeze out at a higher temperature (Chameides 1979) than trace gases produced in the hot channel of the strike which is cooling more slowly (Hill et al. 1980). It has since been suggested that the latter process is more important (Uman & Rakov 2003), in particular in spark experiments (Stark et al. 1996), but a smaller contribution from the shock-wave could lead to an estimate of the freeze-out temperature somewhere between both extremes. The combination of these uncertainties explains the wide range of reported freeze-out temperatures for both NO (2300–3500 K; Gilmore 1975; Chameides et al. 1977; Kasting & Walker 1981; Picone et al. 1981; Borucki & Chameides 1984) and CO (2000–3500 K; Levine et al. 1979; Chameides 1979), placing our estimates of Tf(NO) ≳ 3000 K and Tf(CO) ≃ 2430 K within the range of these estimates.
5.2 Atmospheric stability
In our photochemical simulations, we studied the kinetic chemistry and photochemistry of terrestrial, habitable-zone planets around two different types of stars: the Sun and the M dwarf TRAPPIST-1. While we assumed a CO2 concentration of 4.6% in the atmosphere (for both the anoxic and oxic atmospheres), corresponding to our experiments and necessary to keep the surface of the planets clement (Meadows et al. 2018a), the CO2 partial pressure on the early Earth was likely higher (Lichtenegger et al. 2010; Johnstone et al. 2021b). Further, for planets around M dwarfs such as TRAPPIST-1, it will be much harder to hold on to their atmosphere because of the intense stellar wind and the enhanced and prolonged XUV activity of the host star (Lammer et al. 2011; Airapetian et al. 2017; Johnstone et al. 2021a). Recent observations with JWST have shown that the innermost planet of the TRAPPIST-1 system, TRAPPIST-1 b, is likely a bare rock without any atmosphere (Greene et al. 2023). Even if TRAPPIST-1 e has retained an atmosphere, the ongoing escape of hydrogen and nitrogen will continue to modify the atmosphere, potentially enhancing the oxygen fraction in the remaining atmosphere (Tian 2009; Johnstone et al. 2019). Connecting the upper atmosphere and the above-discussed escape processes to our photochemical model is beyond the scope of this study but should be investigated further in future studies.
To obtain our results, we used the TRAPPIST-1 spectrum from Peacock et al. (2019), though recent work has shown that photochemical results can differ when other versions of the TRAPPIST-1 spectrum are used (Cooke et al. 2023). The here presented simulations are therefore not specific predictions for the atmospheric composition of TRAPPIST-1 e but rather an example to investigate the effect of lightning on different atmospheres around different types of host stars. TRAPPIST-1 and the Sun are good end-members for several reasons, including the fact that TRAPPIST-1 is an immediate or near-term target, and terrestrial planets orbiting Sun-like stars are the targets for HWO. In case TRAPPIST-1 e, or similar exoplanets in the habitable zones of M dwarfs, can indeed retain an atmosphere that is similar to our simulations, this study informs us about atmospheric signatures that one may expect to observe.
5.3 Adapting CO metabolisms
In this study, we used biotic CO deposition and CH4 production rates that were independent of temperature, following previous work (Kharecha et al. 2005; Schwieterman et al. 2019). However, the metabolisms responsible for CH4 production and CO consumption might change depending on atmospheric composition, pressure, and temperature, and will likely vary substantially across a heterogeneous planetary surface. Taubner et al. (2023) show how the production of lipids and amino acids by methanogens can strongly depend on the temperature and nutrient supply. In addition, the productivity of a biosphere might be limited by the availability of other nutrients like phosphorus or fixed nitrogen, rather than CO or stellar irradiation, as is the case for modern Earth (Moore et al. 2013; Bristow et al. 2017). In particular, the availability of nickel can limit the CO consumption by acetogens (Dobbek et al. 2001). Throughout Earth’s history, the concentration of nickel in the oceans has varied, impacting the productivity of methanogens and acetogens (Konhauser et al. 2009, 2015). These uncertainties suggest that in realistic atmospheres the biotic CO deposition rate might be lower than assumed in this study. The biotic and abiotic deposition rates used here thus provide an upper and lower bound, respectively, on the efficiency of CO deposition.
6 Conclusions
We conducted spark discharge experiments to study the production of different gaseous and aqueous products, including potential (anti-)biosignatures, by lightning in atmospheres of N2, CO2, and H2. In contrast to previous studies that focused on individual or small numbers of products, we studied the production of a wide range of gaseous and aqueous compounds in a range of different atmospheres. This allowed us to investigate trends in our experiments concerning the oxidation state of lightning products and the influence of water vapour. In particular, we were interested in the effect of lightning on the production of potential (anti-)biosignatures in the context of current and upcoming observations of exoplanetary atmospheres.
Our results confirm that in a slightly reducing or oxidising atmosphere of a planet that has surface water and a habitable surface temperature, lightning will produce more oxidised nitrogen products than reduced ones. We confirm the predictions of Harman et al. (2018), stating that in the absence of other forms of oxygen, water vapour is responsible for a baseline production of NO and other oxidised forms of nitrogen by lightning. In return, this allows us to predict that for the kind of atmospheres studied here, lightning is not able to produce a false-positive NH3 or CH4 biosignature. It is also unlikely that lightning can produce a false-positive N2O biosignature.
We then used the CO and NO production rates determined in our experiments to calculate the atmospheric composition over a range of different lightning flash rates with a photochemical model. We applied this model to anoxic (CO2−N2) and oxic (O2−CO2−N2) atmospheres on Earth-sized planets in the habitable zone of the Sun and TRAPPIST-1. In particular, we conducted simulations with and without an assumed biosphere on the planet. We also calculated simulated spectra to identify signatures for the different scenarios.
We find that lightning is not able to produce a false-positive CO anti-biosignature on an inhabited planet. In an oxygen-rich atmosphere, however, lightning rates only a few times higher than modern Earth’s can mask the O3 biosignature. Enhanced NO, NO2, and C2H6 features might help to identify these oxygen-rich atmospheres with increased lightning activity.
Similarly, in an anoxic, abiotic atmosphere of a planet orbiting a late M dwarf, lightning at flash rates that are ten times or more that of modern Earth can remove the abiotic ozone feature produced by CO2 photolysis, preventing a false-positive biosignature detection. However, this also suggests that lightning might not be able to prevent all false-positive O2 scenarios for CO2-rich terrestrial planets orbiting ultracool M dwarfs. In summary, our work provides new constraints for the full characterisation of atmospheric and surface processes on exoplanets.
Acknowledgements
We thank Terry Smith, Nathan Rochelle-Bates, and Abu S. Bayida for support in analysing our data, and Helmut Lammer and Manuel Scherf for comments on the manuscript. P.B. acknowledges a St Leonard’s Interdisciplinary Doctoral Scholarship from the University of St Andrews. E.E.S. acknowledges funding from a Royal Society research grant (RGS\R1\211184) and from a NERC Frontiers grant (NE/V010824/1). Ch.H. is part of the CHAMELEON MC ITN EJD which received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement number 860470. E.W.S. acknowledges support from the NASA Interdisciplinary Consortia for Astrobiology Research (ICAR) program via the Alternative Earths team with funding issued under grant No. 80NSSC21K0594 and the CHAMPs (Consortium on Habitability and Atmospheres of M-dwarf Planets) team with funding issued under grant No. 80NSSC21K0905. E.W.S. additionally acknowledges support from the Virtual Planetary Laboratory, which is a member of the NASA Nexus for Exoplanet System Science and funded via NASA Astrobiology Program grant No. 80NSSC18K0829. In order to meet institutional and research funder open access requirements, any accepted manuscript arising shall be open access under a Creative Commons Attribution (CC BY) reuse licence with zero embargo. Machine-readable tables of the data presented in this work are available online at https://doi.org/10.17630/8b72510f-62a8-43dc-94f1-af9b7766f817.
Appendix A Analytical Methods
Appendix A.1 NO Gas Abundance Measurements
The gas in the flask was analysed with a quadrupole mass spectrometer (Hiden Analytical ExQ Quantitative Gas Analyser) in ‘multiple ions detection’ mode to monitor the abundance of several mass to charge ratios (m/z) (12, 14, 15, 16, 17, 18, 20, 28, 30, 32, 40, 46, 48) and thus detect N2, O2, CO2, NO, H2O, and O3, as described in Barth et al. (2023). Due to mass interferences, we were not able to measure CO at m/z 30 (same as NO), N2O at m/z 30 (same as NO) and m/z 44 (same as CO2), and NO2 at m/z 30 and 46 (the CO2 isotopologue 16O12C18O produces an m/z 46 peak).
Appendix A.2 CH4 and N2O Gas Abundance Measurements
Concentrations of methane (CH4) and nitrous oxide (N2O) were measured with a Thermo Fisher gas chromatograph (Trace Ultra) equipped with an electron capture detector (ECD) for N2O and a flame-ionisation detector (FID) for CH4. The packed column was held at 60°C, the ECD at a base temperature of 180°C and a central temperature of 330°C, and the FID at 300°C throughout the run. 10 mL of sample gas were extracted from the experiment with a gas-tight, lockable syringe through the septum, and this volume was injected undiluted into the GC to fill and flush out the 2 mL sample loop. Helium was used as a carrier gas at a pressure of 450 kPa. Auxiliary gases for the detectors were N2 (10 mL min−1), H2 (35 mL min−1) and zero air (350 mL min−1). Analysis of the measurements is limited by the availability of only one standard gas mixture (CH4: 10 ppm, N2O: 2.5 ppm). The lowest methane concentration that still produced a recognisable peak was about 0.2 ppm. However, this limit could not be tested with a low standard. Repeated measurements of the standard produced a standard deviation of 0.6 ppm, a relative error of 6%, which we assume for the error of each measurement.
Appendix A.3 CO Gas Abundance Measurements
A limited number of samples was analysed for their concentration of CO at the School of Natural and Environmental Sciences, Newcastle University, with an SRI 8610C gas chromatograph with a Hg reduction gas detector (RGD). The following run parameters were used: 25 psi N2 carrier gas at 20 mL min−1; column oven at 80°C; 5 min run time with the RGD at 280°C and in low sensitivity setting. All samples were diluted by a factor of 100 by adding 120 μL of the sample to an exetainer vial filled with 12 mL of N2. 3 mL of N2 were then injected into the diluted samples in the exetainer, the gas was mixed using a 5 mL gas-tight syringe, and then 3 mL of the gas were injected into a 0.5 mL sample loop on the GC. The sample loop then injected 0.5 mL of the gas into the column (molecular sieve 5A packed 60/80 mesh, 6 ft length). The centre of the CO peak leaves the column after approximately 3.0 to 3.1 minutes, depending on the concentration. No evidence of any interfering peaks in standards or samples was found. 1 ppm and 10 ppm standards were prepared by diluting a certified 100 ppm CO in N2 standard (Calgaz Ltd). A four-point calibration (0, 1, 10, 100 ppm) was performed. Multiple 100 ppm standard runs were conducted to determine the precision of the measurement to 3.5%. The error of both dilution steps is estimated to be 8.3%, giving a combined error of the CO concentration measurements of 12.3%.
Appendix A.4 Aqueous Nitrate and Nitrite Analyses
To determine the concentrations of nitrate (![$\[\mathrm{NO}_3^{-}\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq22.png) ) and nitrite (
) and nitrite (![$\[\mathrm{NO}_2^{-}\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq23.png) ) in our solutions, we used a Thermo Scientific Dionex ICS-6000 ion chromatograph equipped with a Dionex AS-AP autosampler, a 25 mm Dionex IonPac AS17-C separation column (2 mm bore), a 25 mm Dionex IonPac AG17-G guard column (2 mm bore), and a Dionex ADRS-600 2 mm suppressor. The flow rate was held constant at 0.5 mL min−1 while the concentration of the KOH eluent solution was ramped up from 1 mM to 40 mM over 20 minutes.
) in our solutions, we used a Thermo Scientific Dionex ICS-6000 ion chromatograph equipped with a Dionex AS-AP autosampler, a 25 mm Dionex IonPac AS17-C separation column (2 mm bore), a 25 mm Dionex IonPac AG17-G guard column (2 mm bore), and a Dionex ADRS-600 2 mm suppressor. The flow rate was held constant at 0.5 mL min−1 while the concentration of the KOH eluent solution was ramped up from 1 mM to 40 mM over 20 minutes.
Appendix A.5 Ammonium and Ammonia
We followed a colourimetric method (Solórzano 1969; Cleaves et al. 2008) to measure the ammonium concentration in our samples. Three stocks of reagents were prepared in larger quantities and stored for several months: (1) sodium citrate buffer (7.6 g trisodium citrate (Na3C6H5O7) and 0.4 g sodium hydroxide (NaOH) in 500 mL of water), (2) phenol alcohol (1 mL liquefied phenol (C6H5OH) in 90 mL of 100% ethanol (C2H5OH), brought up to 100 mL with water), and (3) aqueous sodium nitroprusside (0.15 g of sodium nitroprusside (C5FeN6Na2O) in 200 mL of water). Each day, an oxidising solution of 10 mL of the sodium citrate buffer with 0.1 mL of aqueous sodium hypochlorite (ClNaO, with 10–15% available chlorine) was prepared fresh (amount adjusted to number of samples). For our standards, we used a 1 mM stock of NH4Cl, diluted to 1, 2, 5, 10, 20, 50, and 100 μM. For analyses, 1 mL of sample or standard were transferred into a 15 mL Falcon centrifuge tube, followed by 0.5 mL phenol alcohol, 0.5 mL aqueous sodium nitroprusside, and 1 mL of the oxidising solution. The mixture is incubated for 60–80 minutes at room temperature, allowing it to develop a blue colour. Absorption was measured at 640 nm with a Thermo Fisher Evolution 220 UV-Vis spectrophotometer. According to Solórzano (1969), there is no interference between ammonium and other nitrogen compounds or seawater, which contains nitrate. From the ammonium concentration in the water, we can estimate the ammonia concentration in the gas phase. The ratio between the concentration of ammonium in the liquid phase and the pressure of ammonia gas is given by Henry’s law constant for NH3 which is H = (73 ± 5) M bar−1 for temperatures between 20 and 23°C (Edwards et al. 1978; Burkholder et al. 2019).
Appendix A.6 Urea
For the quantification of urea (CO(NH2)2) in solution, we followed the colourimetric method described by Cleaves et al. (2008). The following stocks of reagents were prepared: (1) Acidic ferric chloride (AFC, 0.208 g FeCl3•6H2O + 20 mL concentrated H2SO4 + 2.5 mL 85% H3PO4 in 250mL of DI-water), (2) diacetyl monoxime (DAM, 2.5 g in 100 mL DI-water), and (3) thiosemicarbazide (TSC, 0.25 g in 100 mL DI-water). Each day, 12 mL of DAM stock were combined with 5 mL of TSC stock and 33 mL DI-water. Then 8 mL of this combined DAMTSC stock were added to 40 mL AFC to prepare the color reagent. 2 mL of color reagent are added to 200 μL of sample in a 15 mL centrifuge tubes. The closed tubes are then heated in boiling water for 15 minutes and then analysed at 520 nm with the UV-Vis spectrophotometer. We found the detection limit of this method to be 1 μM. Analyses were calibrated with a 1 mM stock solution of urea, diluted to 1, 2, 5, 10, 20, 50, and 100 μM.
Appendix A.7 Cyanide and HCN
For the quantification of aqueous cyanide (CN−) we followed the method described by Cacace et al. (2007), which requires three stock solutions of reagents: (1) Borax buffer: 4.767 g of sodium tetraborate decahydrate are dissolved in 500 mL DI-water. The solution is then brought to a pH of 10.8 by adding approximately 2 mL of 10 M NaOH. This buffer can be stored in the fridge for several months. (2) Combined reagents: 0.2996 g copper(II) nitrate trihydrate are dissolved in 20 mL DI-water. Then, 0.1861 g ethylenediaminetetraacetic acid (EDTA) is added and dissolved (stir). Finally, 0.1777 g of phenolphthalin are added and the solution is topped up to 50 mL with DI-water. (3) Stabilising solution: 0.324 g triethanolamine hydrochloride and 1.25 g sodium sulfite are dissolved in 100 mL DI-water. Both the combined reagents and the stabilising solution should be made fresh every few weeks as the absorption efficiency will deteriorate. For the analysis, 0.2 mL of sample are added to 9 mL of borax buffer, followed by 0.2 mL of the combined reagents. After three minutes, 0.2 mL of stabilising solution are added. The sample was then analysed at 553 nm with the UV-Vis spectrophotometer. Measurements were calibrated with a 1000 ppm stock solution of KCN, diluted to 5, 8, 10, and 20 ppm. The detection limit was 5 ppm. Similar to ammonia, from the cyanide concentration in the water, we can estimate the HCN concentration in the gas phase using the respective Henry’s law constant. For HCN, this constant at 20 to 23°C is H = (13 ± 4) M bar−1 (Ma et al. 2010).
Appendix B Additional Results from Photochemical Simulations
This section includes a table with the detailed parameters of the photochemical model used (Table B1). It further contains the atmospheric mixing ratio profiles for the spectra shown in Fig. 12 (Fig. B.1) and further spectra for different scenarios with the corresponding atmospheric mixing ratio profiles (Figs. B.2 - B.5), as well as the column densities of the major atmospheric constituents for the whole range of CO fluxes and all scenarios presented in this paper (Figs. B.6 - B.9).
Input parameters for our photochemical model
 |
Fig. B.1 Atmospheric mixing ratios of most abundant species for scenarios shown in spectra in Fig. 12. Left panel: TRAPPIST-1, Anoxic, abiotic scenario (Tsurf = 275 K): CO flux of 109 (thick) and 1011 molecules cm−2 s−1 (thin), corresponding to lightning flash rates of ~2 and ~160 times modern Earth’s, respectively. Right panel: TRAPPIST-1, Oxic, biotic scenario (Tsurf = 288 K): CO flux of 108 (thick) and 1011 molecules cm−2 s−1 (thin), corresponding to lightning flash rates of ~0.9 and ~680 times modern Earth’s, respectively. |
 |
Fig. B.2 Oxic, biotic Sun scenario (Tsurf = 288 K): CO flux of 109 and 1011 molecules cm−2 s−1, corresponding to lightning flash rates of ~9 and ~680 times modern Earth’s, respectively. Left panel: Atmospheric mixing ratios of most abundant species. Right panel: Simulated spectra: Emitted (top, MIR, R = 400), reflected (middle, NIR, R = 400), and transmitted light (bottom, NIR-MIR, R = 200). |
 |
Fig. B.3 Anoxic, abiotic Sun scenario (Tsurf = 275 K): CO flux of 109 and 1011 molecules cm−2 s−1, corresponding to lightning flash rates of ~2 and ~160 times modern Earth’s, respectively. Left panel: Atmospheric mixing ratios of most abundant species. Right panel: Simulated spectra: Emitted (top, MIR, R = 400), reflected (middle, NDR R = 400), and transmitted light (bottom, NIR-MIR, R = 200). |
 |
Fig. B.4 Anoxic, biotic Sun scenario (Tsurf = 275 K) with CO flux of 109 molecules cm−2 s−1, corresponding to lightning flash rate of ~2 times modern Earth’s. Comparison between scenarios with and without CO deposition. Left panel: Atmospheric mixing ratios of most abundant species for the scenario with (thick) and without (thin) CO deposition. Right panel: Simulated spectra: Emitted (top, MIR, R = 400), reflected (middle, NIR, R = 400), and transmitted light (bottom, NIR-MIR, R = 200) for scenario with (red) and without (orange) CO deposition. |
 |
Fig. B.5 Anoxic, biotic TRAPPIST-1 scenario (Tsurf = 275 K) with CO flux of 109 molecules cm−2 s−1, corresponding to lightning flash rate of ~2 times modern Earth’s. Comparison between scenarios with and without CO deposition. Left panel: Atmospheric mixing ratios of most abundant species for the scenario with (thick) and without (thin) CO deposition. Right panel: Simulated spectra: Emitted (top, MIR, R = 400), reflected (middle, NIR, R = 400), and transmitted light (bottom, NIR-MIR, R = 200) for scenario with (black) and without (blue) CO deposition. |
 |
Fig. B.6 Column densities for a range of CO and NO fluxes. Anoxic abiotic cases. |
 |
Fig. B.7 Column densities for a range of CO and NO fluxes. Anoxic biotic cases. |
 |
Fig. B.8 Column densities for a range of CO and NO fluxes. Anoxic biotic (no CO deposition) cases. |
 |
Fig. B.9 Column densities for a range of CO and NO fluxes. Oxic biotic cases. |
References
- Abelson, P. H. 1966, PNAS, 55, 1365 [CrossRef] [Google Scholar]
- Agol, E., Dorn, C., Grimm, S. L., et al. 2021, The Planetary Science Journal, 2, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Airapetian, V. S., Glocer, A., Gronoff, G., Hébrard, E., & Danchi, W. 2016, Nat. Geosci., 9, 452 [Google Scholar]
- Airapetian, V. S., Glocer, A., Khazanov, G. V., et al. 2017, ApJ, 836, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Airapetian, V. S., Barnes, R., Cohen, O., et al. 2020, Int. J. Astrobiol., 19, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Alei, E., Konrad, B. S., Angerhausen, D., et al. 2022, A&A, 665, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arney, G., Meadows, V., Crisp, D., et al. 2014, J. Geophys. Res. Planets, 119, 1860 [NASA ADS] [CrossRef] [Google Scholar]
- Arney, G., Domagal-Goldman, S. D., Meadows, V. S., et al. 2016, Astrobiology, 16, 873 [Google Scholar]
- Barth, P., Carone, L., Barnes, R., et al. 2021a, Astrobiology, 21, 1325 [NASA ADS] [CrossRef] [Google Scholar]
- Barth, P., Helling, C., Stüeken, E. E., et al. 2021b, MNRAS, 502, 6201 [Google Scholar]
- Barth, P., Stüeken, E. E., Helling, C., et al. 2023, Nat. Geosci., 16, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., & Chameides, W. L. 1984, Rev. Geophys., 22, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwman, A. F., Lee, D. S., Asman, W. A. H., et al. 1997, Global Biogeochem. Cycles, 11, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwman, A. F., Boumans, L. J. M., & Batjes, N. H. 2002, Global Biogeochem. Cycles, 16, 6 [Google Scholar]
- Braam, M., Palmer, P. I., Decin, L., et al. 2022, MNRAS, 517, 2383 [NASA ADS] [CrossRef] [Google Scholar]
- Bristow, L. A., Mohr, W., Ahmerkamp, S., & Kuypers, M. M. 2017, Curr. Biol., 27, R474 [CrossRef] [Google Scholar]
- Buick, R. 2007, Geobiology, 5, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Burkholder, J., Sander, S., Abbatt, J., et al. 2019, in PL Publication 19-5 (Pasadena: Jet Propulsion Laboratory) [Google Scholar]
- Cacace, D., Ashbaugh, H., Kouri, N., et al. 2007, Analyt. Chim. Acta, 589, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Canfield, D. E., Glazer, A. N., & Falkowski, P. G. 2010, Science, 330, 192 [CrossRef] [PubMed] [Google Scholar]
- Carpenter, L. J., & Nightingale, P. D. 2015, Chem. Rev., 115, 4015 [CrossRef] [Google Scholar]
- Catling, D. C., & Zahnle, K. J. 2020, Sci. Adv., 6, 1420 [NASA ADS] [CrossRef] [Google Scholar]
- Chameides, W. L. 1979, Geophys. Res. Lett., 6, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Chameides, W. L. 1986, in The Earth’s Electrical Environment, eds. E. P. Krider, & R. G. Roble (Washington, DC: The National Academies Press), 70 [Google Scholar]
- Chameides, W. L., & Walker, J. C. G. 1981, Origins Life, 11, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Chameides, W. L., Stedman, D. H., Dickerson, R. R., et al. 1977, J. Atmos. Sci., 34, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Christian, H. J., Blakeslee, R. J., Boccippio, D. J., et al. 2003, J. Geophys. Res. Atmos., 108, ACL 4 [Google Scholar]
- Cleaves, H. J., Chalmers, J. H., Lazcano, A., Miller, S. L., & Bada, J. L. 2008, Origins Life Evol. Biospheres, 38, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Cooke, G. J., Marsh, D. R., Walsh, C., & Youngblood, A. 2023, ApJ, 959, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Crisp, D. 1997, Geophys. Res. Lett., 24, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Das, T., Ghule, S., & Vanka, K. 2019, ACS Central Sci., 5, 1532 [CrossRef] [Google Scholar]
- Dobbek, H., Svetlitchnyi, V., Gremer, L., Huber, R., & Meyer, O. 2001, Science, 293, 1281 [NASA ADS] [CrossRef] [Google Scholar]
- Dodd, M. S., Papineau, D., Grenne, T., et al. 2017, Nature, 543, 60 [CrossRef] [Google Scholar]
- Ducluzeau, A.-L., van Lis, R., Duval, S., et al. 2009, Trends Biochem. Sci., 34, 9 [CrossRef] [Google Scholar]
- Edwards, T. J., Maurer, G., Newman, J., & Prausnitz, J. M. 1978, AIChE J., 24, 966 [NASA ADS] [CrossRef] [Google Scholar]
- Fraschetti, F., Drake, J. J., Alvarado-Gómez, J. D., et al. 2019, Astrophys. J., 874, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Gaudi, B. S., Seager, S., Mennesson, B., et al. 2020, arXiv e-prints [arXiv:2001.06683] [Google Scholar]
- Gilmore, F. R. 1975, J. Geophys. Res., 80, 4553 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, I., Rothman, L., Hill, C., et al. 2017, HITRAN2016 Special Issue, 203, 3 [Google Scholar]
- Gordon, I., Rothman, L., Hargreaves, R., et al. 2022, J. Quant. Spectrosc. Radiative Transfer, 277, 107949 [NASA ADS] [CrossRef] [Google Scholar]
- Green, A. E. S., Sawada, T., Edgar, B. C., & Uman, M. A. 1973, J. Geophys. Res., 78, 5284 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, T. P., Bell, T. J., Ducrot, E., et al. 2023, Nature, 618, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Grenfell, J. L. 2017, Phys. Rep., 713, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Grenfell, J. L., Grießmeier, J.-M., von Paris, P., et al. 2012, Astrobiology, 12, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Grießmeier, J., Tabataba-Vakili, F., Stadelmann, A., Grenfell, J. L., & Atri, D. 2015, A&A, 581, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harman, C. E., Felton, R., Hu, R., et al. 2018, ApJ, 866, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Harman, C. E., Schwieterman, E. W., Schottelkotte, J. C., & Kasting, J. F. 2015, ApJ, 812, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Heays, A. N., Kaiserová, T., Rimmer, P. B., et al. 2022, J. Geophys. Res. Planets, 127, e2021JE006842 [CrossRef] [Google Scholar]
- Helling, C. 2019, J. Phys.: Conf. Ser., 1322, 012028 [NASA ADS] [CrossRef] [Google Scholar]
- Helling, C., Woitke, P., & Thi, W.-F. 2008, A&A, 485, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helling, C., Jardine, M., Diver, D., & Witte, S. 2013a, Planet. Space Sci., 77, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Helling, C., Jardine, M., Stark, C., & Diver, D. 2013b, ApJ, 767, 136 [Google Scholar]
- Helling, C., Harrison, R. G., Honary, F., et al. 2016, Surv. Geophys., 37, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, R. D., Rinker, R. G., & Wilson, H. D. 1980, J. Atmos. Sci., 37, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, R. D., Rinker, R. G., & Coucouvinos, A. 1984, J. Geophys. Res. Atmospheres, 89, 1411 [NASA ADS] [CrossRef] [Google Scholar]
- Hodosán, G., Helling, C., Asensio-Torres, R., Vorgul, I., & Rimmer, P. B. 2016a, MNRAS, 461, 3927 [Google Scholar]
- Hodosán, G., Rimmer, P. B., & Helling, C. 2016b, MNRAS, 461, 1222 [Google Scholar]
- Hodosán, G., Helling, C., & Vorgul, I. 2021, Planet. Space Sci., 204, 105247 [CrossRef] [Google Scholar]
- Hu, R., & Diaz, H. D. 2019, ApJ, 886, 126 [CrossRef] [Google Scholar]
- Huang, J., Seager, S., Petkowski, J. J., Ranjan, S., & Zhan, Z. 2022, Astrobiology, 22, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Ih, J., Kempton, E. M. R., Whittaker, E. A., & Lessard, M. 2023, ApJ, 952, L4 [CrossRef] [Google Scholar]
- Jackson, R. B., Saunois, M., Bousquet, P., et al. 2020, Environ. Res. Lett., 15, 071002 [NASA ADS] [CrossRef] [Google Scholar]
- Johnstone, C. P. 2020, ApJ, 890, 79 [Google Scholar]
- Johnstone, C. P., Khodachenko, M. L., Lüftinger, T., et al. 2019, A&A, 624, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnstone, C. P., Bartel, M., & Güdel, M. 2021a, A&A, 649, A96 [EDP Sciences] [Google Scholar]
- Johnstone, C. P., Lammer, H., Kislyakova, K. G., Scherf, M., & Güdel, M. 2021b, Earth Planet. Sci. Lett., 576, 117197 [CrossRef] [Google Scholar]
- Kasting, J. F. 1990, Origins Life Evol. Biosphere, 20, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Kasting, J. F., & Walker, J. C. G. 1981, J. Geophys. Res., 86, 1147 [NASA ADS] [CrossRef] [Google Scholar]
- Kharecha, P., Kasting, J., & Siefert, J. 2005, Geobiology, 3, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Konhauser, K. O., Pecoits, E., Lalonde, S. V., et al. 2009, Nature, 458, 750 [NASA ADS] [CrossRef] [Google Scholar]
- Konhauser, K. O., Robbins, L. J., Pecoits, E., et al. 2015, Astrobiology, 15, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Krissansen-Totton, J., Garland, R., Irwin, P., & Catling, D. C. 2018a, AJ, 156, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Krissansen-Totton, J., Olson, S., & Catling, D. C. 2018b, Sci. Adv., 4, 5747 [NASA ADS] [CrossRef] [Google Scholar]
- Krissansen-Totton, J., Arney, G. N., Catling, D. C., et al. 2019, BAAS, 51, 158 [Google Scholar]
- Lammer, H., Lichtenegger, H. I. M., Khodachenko, M. L., Kulikov, Y. N., & Griessmeier, J. 2011, in Molecules in the Atmospheres of Extrasolar Planets, eds. J. P. Beaulieu, S. Dieters, & G. Tinetti, Astronomical Society of the Pacific Conference Series, 450, 139 [NASA ADS] [Google Scholar]
- Lammer, H., Sproß, L., Grenfell, J. L., et al. 2019, Astrobiology, 19, 927 [NASA ADS] [CrossRef] [Google Scholar]
- Levine, J. S., Hughes, R. E., Chameides, W. L., & Howell, W. E. 1979, Geophys. Res. Lett., 6, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Levine, J. S., Gregory, G. L., Harvey, G. A., et al. 1982, Geophys. Res. Lett., 9, 893 [NASA ADS] [CrossRef] [Google Scholar]
- Lichtenegger, H., Lammer, H., Grießmeier, J.-M., et al. 2010, Icarus, 210, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Z., & Kaltenegger, L. 2022, MNRAS, 516, 3167 [NASA ADS] [CrossRef] [Google Scholar]
- Lincowski, A. P., Meadows, V. S., Crisp, D., et al. 2018, ApJ, 867, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Lovelock, J. E., Kaplan, I. R., & Pirie, N. W. 1975, Proc. Roy. Soc. Lond. Ser. B Biol.l Sci., 189, 167 [NASA ADS] [Google Scholar]
- Luger, R., Barnes, R., Lopez, E., et al. 2015, Astrobiology, 15, 57 [Google Scholar]
- Lustig-Yaeger, J., Meadows, V. S., & Lincowski, A. P. 2019, AJ, 158, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, J., Dasgupta, P. K., Blackledge, W., & Boss, G. R. 2010, Environ. Sci. Technol., 44, 3028 [NASA ADS] [CrossRef] [Google Scholar]
- Meadows, V. 2017, Astrobiology, 17, 1022 [CrossRef] [Google Scholar]
- Meadows, V. S., & Crisp, D. 1996, J. Geophys. Res. Planets, 101, 4595 [NASA ADS] [CrossRef] [Google Scholar]
- Meadows, V. S., Arney, G. N., Schwieterman, E. W., et al. 2018a, Astrobiology, 18, 133 [Google Scholar]
- Meadows, V. S., Reinhard, C. T., Arney, G. N., et al. 2018, Astrobiology, 18, 630 [Google Scholar]
- Miller, S. L. 1953, Science, 117, 528 [Google Scholar]
- Miller, S. L. 1957, Ann. N. Y. Acad. Sci., 69, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, S. L., & Schlesinger, G. 1983, Adv. Space Res., 3, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, S. L., & Urey, H. C. 1959, Science, 130, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, C. M., Mills, M. M., Arrigo, K. R., et al. 2013, Nat. Geosci., 6, 701 [Google Scholar]
- National Academies of Sciences, Engineering, and Medicine 2021, Pathways to Discovery in Astronomy and Astrophysics for the 2020s, Tech. Rep. (Washington, DC: National Academies Press) [Google Scholar]
- Navarro-González, R., & Ramírez, S. I. 1997, Proceedings of the F3.2 Symposium of COSPAR Scientific Commission F, 19, 1121 [Google Scholar]
- Navarro-González, R., McKay, C. P., & Mvondo, D. N. 2001a, Nature, 412, 61 [CrossRef] [Google Scholar]
- Navarro-González, R., Ramírez, S., de la Rosa, J., Coll, P., & Raulin, F. 2001b, Adv. Space Res., 27, 271 [CrossRef] [Google Scholar]
- Nitschke, W., & Russell, M. J. 2013, Philos. Trans. Royal Soc. B: Biol. Sci., 368, 20120258 [Google Scholar]
- Nna Mvondo, D., Navarro-González, R., McKay, C. P., Coll, P., & Raulin, F. 2001, Adv. Space Res., 27, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Nna Mvondo, D., Navarro-González, R., Raulin, F., & Coll, P. 2005, Origins Life Evol. Biospheres, 35, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. T., Cleaves, J. H., Burton, A. S., et al. 2014, J. Visual. Exp., e51039 [Google Scholar]
- Peacock, S., Barman, T., Shkolnik, E. L., Hauschildt, P. H., & Baron, E. 2019, ApJ, 871, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Pearce, B. K. D., Pudritz, R. E., Semenov, D. A., & Henning, T. K. 2017, PNAS, 114, 11327 [NASA ADS] [CrossRef] [Google Scholar]
- Pearce, B. K. D., He, C., & Hörst, S. M. 2022, ACS Earth Space Chem., 6, 2385 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, C. L., Wang, J., Kendrew, S., et al. 2021, ApJ, 923, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Piaulet, C., Benneke, B., Almenara, J. M., et al. 2023, Nat. Astron., 7, 206 [Google Scholar]
- Picone, J. M., Boris, J. P., Greig, J. R., Raleigh, M., & Fernsler, R. F. 1981, J. Atmos. Sci., 38, 2056 [NASA ADS] [CrossRef] [Google Scholar]
- Price, C., Penner, J., & Prather, M. 1997, J. Geophys. Res. Atmos., 102, 5929 [NASA ADS] [CrossRef] [Google Scholar]
- Quanz, S. P., Ottiger, M., Fontanet, E., et al. 2022, A&A, 664, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ragsdale, S. W. 2004, Crit. Rev. Biochem. Mol. Biol., 39, 165 [CrossRef] [Google Scholar]
- Ramirez, R. M., & Kaltenegger, L. 2014, ApJ, 797, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Ranjan, S., Todd, Z. R., Rimmer, P. B., Sasselov, D. D., & Babbin, A. R. 2019, Geochem. Geophys. Geosyst., 20, 2021 [NASA ADS] [CrossRef] [Google Scholar]
- Ranjan, S., Schwieterman, E. W., Harman, C., et al. 2020, ApJ, 896, 148 [Google Scholar]
- Ranjan, S., Seager, S., Zhan, Z., et al. 2022, ApJ, 930, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Rauer, H., Gebauer, S., Paris, P. v., et al. 2011, A&A, 529, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid Thompson, W., Henry, T. J., Schwartz, J. M., Khare, B., & Sagan, C. 1991, Icarus, 90, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Rimmer, P. B., & Helling, C. 2013, ApJ, 774, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, T. D. 2017, ApJ, 836, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, T. D., Meadows, V. S., Crisp, D., et al. 2011, Astrobiology, 11, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Rotman, Y., Komacek, T. D., Villanueva, G. L., Fauchez, T. J., & May, E. M. 2023, ApJ, 942, L4 [CrossRef] [Google Scholar]
- Sagan, C., Thompson, W. R., Carlson, R., Gurnett, D., & Hord, C. 1993, Nature, 365, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchez, R. A., Ferbis, J. P., & Orgel, L. E. 1967, J. Mol. Biol., 30, 223 [Google Scholar]
- Sauterey, B., Charnay, B., Affholder, A., Mazevet, S., & Ferrière, R. 2020, Nat. Commun., 11, 2705 [Google Scholar]
- Scheucher, M., Herbst, K., Schmidt, V., et al. 2020, ApJ, 893, 12 [Google Scholar]
- Schopf, J. W., Kudryavtsev, A. B., Czaja, A. D., & Tripathi, A. B. 2007, Precamb. Res., 158, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Schumann, U., & Huntrieser, H. 2007, Atmos. Chem. Phys., 7, 3823 [NASA ADS] [CrossRef] [Google Scholar]
- Schwieterman, E. W., Kiang, N. Y., Parenteau, M. N., et al. 2018, Astrobiology, 18, 663 [CrossRef] [Google Scholar]
- Schwieterman, E. W., Reinhard, C. T., Olson, S. L., et al. 2019, ApJ, 874, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Schwieterman, E. W., Olson, S. L., Pidhorodetska, D., et al. 2022, ApJ, 937, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S., Schrenk, M., & Bains, W. 2012, Astrobiology, 12, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S., Bains, W., & Hu, R. 2013a, ApJ, 775, 104 [Google Scholar]
- Seager, S., Bains, W., & Hu, R. 2013b, ApJ, 777, 95 [Google Scholar]
- Segura, A., Krelove, K., Kasting, J. F., et al. 2003, Astrobiology, 3, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Segura, A., Kasting, J. F., Meadows, V., et al. 2005, Astrobiology, 5, 706 [Google Scholar]
- Segura, A., Meadows, V. S., Kasting, J. F., Crisp, D., & Cohen, M. 2007, A&A, 472, 665 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shibuya, T., Russell, M. J., & Takai, K. 2016, Geochim. Cosmochim. Acta, 175, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Solórzano, L. 1969, Limnol. Oceanogr., 14, 799 [CrossRef] [Google Scholar]
- Sousa-Silva, C., Seager, S., Ranjan, S., et al. 2019, Astrobiology, 20, 235 [Google Scholar]
- Spinelli, R., Borsa, F., Ghirlanda, G., Ghisellini, G., & Haardt, F. 2023, MNRAS, 522, 1411 [NASA ADS] [CrossRef] [Google Scholar]
- Sproß, L., Scherf, M., Shematovich, V. I., Bisikalo, D. V., & Lammer, H. 2021, Astron. Rep., 65, 275 [CrossRef] [Google Scholar]
- Stamnes, K., Tsay, S.-C., Wiscombe, W., & Jayaweera, K. 1988, Appl. Opt., 27, 2502 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, M. S., Harrison, J. T. H., & Anastasi, C. 1996, J. Geophys. Res.: Atmospheres, 101, 6963 [NASA ADS] [CrossRef] [Google Scholar]
- Stozhkov, Y. I. 2003, J. Phys. G: Nucl. Part. Phys., 29, 913 [NASA ADS] [CrossRef] [Google Scholar]
- Stüeken, E., Kipp, M., Koehler, M., et al. 2016, Astrobiology, 16, 949 [Google Scholar]
- Summers, D. P. 2005, Origins Life Evol. Biospheres, 35, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Summers, D. P., & Chang, S. 1993, Nature, 365, 630 [NASA ADS] [CrossRef] [Google Scholar]
- Summers, D. P., & Khare, B. 2007, Astrobiology, 7, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Tabataba-Vakili, F., Grenfell, J. L., Grießmeier, J.-M., & Rauer, H. 2016, A&A, 585, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taubner, R.-S., Baumann, L. M. F., Steiner, M., et al. 2023, mSystems, 8, e01159 [CrossRef] [Google Scholar]
- The LUVOIR Team 2019, arXiv e-prints [arXiv:1912.06219] [Google Scholar]
- Thompson, M. A., Krissansen-Totton, J., Wogan, N., Telus, M., & Fortney, J. J. 2022, PNAS, 119, e2117933119 [NASA ADS] [CrossRef] [Google Scholar]
- Thuillier, G., Floyd, L., Woods, T., et al. 2004, Solar Variabil. Climate Change, 34, 256 [Google Scholar]
- Tian, F. 2009, ApJ, 703, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, F., Kasting, J. F., & Zahnle, K. 2011, Earth Planet. Sci. Lett., 308, 417 [CrossRef] [Google Scholar]
- Tian, H., Xu, R., Canadell, J. G., et al. 2020, Nature, 586, 248 [CrossRef] [Google Scholar]
- Tinetti, G., Meadows, V. S., Crisp, D., et al. 2005, Astrobiology, 5, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Toupance, G., Raulin, F., & Buvet, R. 1975, Origins life, 6, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Turbet, M., Fauchez, T. J., Sergeev, D. E., et al. 2022, PSJ, 3, 211 [NASA ADS] [Google Scholar]
- Uman, M. A., & Rakov, V. A. 2003, in Lightning: Physics and Effects, eds. M. A. Uman, & V. A. Rakov (Cambridge: Cambridge University Press), 507 [Google Scholar]
- Wang, Y., Tian, F., Li, T., & Hu, Y. 2016, Icarus, 266, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Wogan, N. F., & Catling, D. C. 2020, ApJ, 892, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Woitke, P., & Helling, C. 2003, A&A, 399, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., Helling, C., Hunter, G. H., et al. 2018, A&A, 614, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wong, M. L., Charnay, B. D., Gao, P., Yung, Y. L., & Russell, M. J. 2017, Astrobiology, 17, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Wordsworth, R., & Pierrehumbert, R. 2014, ApJ, 785, L20 [CrossRef] [Google Scholar]
- Wordsworth, R. D., Schaefer, L. K., & Fischer, R. A. 2018, AJ, 155, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Zafiriou, O. C. & True, M. B. 1979a, Marine Chemistry, 8, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Zafiriou, O. C., & True, M. B. 1979b, Geophys. Res. Lett., 6, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Zhong, Q., Huang, Y., Shen, H., et al. 2017, Environ. Sci. Pollut. Res., 24, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, L., Henze, D. K., Bash, J. O., et al. 2015, Curr. Pollut. Rep., 1, 95 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Schematic of the experimental setup of the discharge experiment. First published in Barth et al. (2023) by Springer Nature. |
| In the text | |
 |
Fig. 2 Spectral energy distributions at the top of the planets’ atmospheres of the Sun (red) and TRAPPIST-1 (black) as used in the photochemical model and for the planetary spectra. |
| In the text | |
 |
Fig. 3 Final abundance of ammonium ( |
| In the text | |
 |
Fig. 4 CO concentration in 4 different spark experiments (high and low-CO2, wet and dry), measured at 3 different points in time during the experiment. Fitted lines give the CO concentration assuming CO is the product of an equilibrium reaction, following |
| In the text | |
 |
Fig. 5 CO and NO concentrations in chemical equilibrium as a function of gas temperature (with GGChem, Woitke et al. 2018) for high-CO2 gas mixtures. The different cases considered are: 0% (solid lines), 0.9% (dashed), 5% (dash dotted), and 10% (dotted) of H2. As H2 is binding free oxygen into H2O, increasing the H2 concentration prevents the recombination of CO to CO2 as well as the production of NO. CO (red) and NO (blue shaded area) measurements with uncertainties from wet 120 min experiments. Minimum freeze-out temperature estimates for CO (orange) and NO (green) with uncertainties. |
| In the text | |
 |
Fig. 6 Final abundances of gaseous([g]; nitrous oxide (N2O), methane (CH4), hydrogen cyanide (HCN), nitric oxide (NO), and ammonia (NH3)) and aqueous products ([aq]; CN−, nitrite + nitrate, |
| In the text | |
 |
Fig. 7 HCN concentration in chemical equilibrium (with GGChem, Woitke & Helling 2003) as function of gas temperature for different CO2 fractions in the gas mixture (other gases: 1% H2, 1% H2O, rest N2). For T ≳ 3000 K (right dashed grey line), HCN concentration increases with increasing CO2 concentration (until ~3–5% CO2). For T ≲ 2700 K HCN concentrations decreases with increasing CO2 concentration (except for 0.1% CO2). |
| In the text | |
 |
Fig. 8 Photochemically simulated CO (a, b), NO (c, d), and NO2 (e, f) mixing ratios in the anoxic atmosphere (4.6% CO2) of an Earth-sized planet orbiting the Sun (a, c, e) and TRAPPIST-1 (b, d, f) for varying CO and NO production rates and different scenarios: abiotic (solid), biotic with CO deposition (dashed), and biotic without CO deposition (dotted). The surface temperature (blue: Tsurf = 275 K, orange: Tsurf = 300 K) controls the water vapour concentration. The second x-axis gives the corresponding lightning flash rate (in units of modern Earth’s flash rate), as estimated for the respective atmospheric composition. |
| In the text | |
 |
Fig. 9 Mixing ratios for biotic scenario (Sun) without CO deposition (CO flux ~107 molecules cm−2 s−1) for two different surface temperatures (solid lines: Tsurf = 275 K, dotted lines: Tsurf = 300 K) as result of a kinetic gas-phase calculation with photochemistry. |
| In the text | |
 |
Fig. 10 Photochemically simulated CO (a, b), NO and NO2 (c, d) mixing ratios in the oxic atmosphere (4.6% CO2, 21% O2) of an Earth-sized planet orbiting the Sun (a, c) and TRAPPIST-1 (b, d) for varying CO and NO production rates and the biotic scenario with CO deposition (Tsurf = 288 K). The second x-axis gives the corresponding lightning flash rate (in units of modern Earth’s flash rate), as estimated for the respective atmospheric composition. |
| In the text | |
 |
Fig. 11 Deposition flux of fixed nitrogen into an ocean (red) for the anoxic, abiotic planet around the Sun (Tsurf = 275 K) for a range of lightning NO fluxes and corresponding lightning flash rates. For comparison, the total lightning-produced NO flux is shown (orange). The corresponding deposition rates in Tmol yr−1 are shown as black lines (converted into molecules cm−2 s−1). |
| In the text | |
 |
Fig. 12 Simulated spectra for the TRAPPIST-1 planet: Emitted (top: MIR, R = 400), reflected (middle: NIR, R = 400), and transmitted light (bottom: NIR-MIR, R = 200). Note. MIR features in emission are not just dependent on the abundance of spectrally active gases, but also the temperature structure of the atmosphere. Left panel: anoxic, abiotic scenario (Tsurf = 275 K): CO flux of 109 (black), 1010 (magenta), and 1012 molecules cm−2 s−1 (blue), corresponding to lightning flash rates of ~2, ~35 and ~1500 times modern Earth’s, respectively. Right panel: oxic, biotic scenario (Tsurf = 288 K): CO flux of 108 (black) and 1011 molecules cm−2 s−1 (blue), corresponding to lightning flash rates of ~0.9 and ~680 times modern Earth’s, respectively. |
| In the text | |
 |
Fig. 13 Simulated spectra for the planet orbiting the Sun: Anoxic, biotic scenario without CO deposition (CO flux ~109 molecules cm−2 s−1). Spectra with individual species removed are shown (without C2H6 in red, and without CH4 in orange) in comparison to the full spectrum (black dotted line). |
| In the text | |
 |
Fig. B.1 Atmospheric mixing ratios of most abundant species for scenarios shown in spectra in Fig. 12. Left panel: TRAPPIST-1, Anoxic, abiotic scenario (Tsurf = 275 K): CO flux of 109 (thick) and 1011 molecules cm−2 s−1 (thin), corresponding to lightning flash rates of ~2 and ~160 times modern Earth’s, respectively. Right panel: TRAPPIST-1, Oxic, biotic scenario (Tsurf = 288 K): CO flux of 108 (thick) and 1011 molecules cm−2 s−1 (thin), corresponding to lightning flash rates of ~0.9 and ~680 times modern Earth’s, respectively. |
| In the text | |
 |
Fig. B.2 Oxic, biotic Sun scenario (Tsurf = 288 K): CO flux of 109 and 1011 molecules cm−2 s−1, corresponding to lightning flash rates of ~9 and ~680 times modern Earth’s, respectively. Left panel: Atmospheric mixing ratios of most abundant species. Right panel: Simulated spectra: Emitted (top, MIR, R = 400), reflected (middle, NIR, R = 400), and transmitted light (bottom, NIR-MIR, R = 200). |
| In the text | |
 |
Fig. B.3 Anoxic, abiotic Sun scenario (Tsurf = 275 K): CO flux of 109 and 1011 molecules cm−2 s−1, corresponding to lightning flash rates of ~2 and ~160 times modern Earth’s, respectively. Left panel: Atmospheric mixing ratios of most abundant species. Right panel: Simulated spectra: Emitted (top, MIR, R = 400), reflected (middle, NDR R = 400), and transmitted light (bottom, NIR-MIR, R = 200). |
| In the text | |
 |
Fig. B.4 Anoxic, biotic Sun scenario (Tsurf = 275 K) with CO flux of 109 molecules cm−2 s−1, corresponding to lightning flash rate of ~2 times modern Earth’s. Comparison between scenarios with and without CO deposition. Left panel: Atmospheric mixing ratios of most abundant species for the scenario with (thick) and without (thin) CO deposition. Right panel: Simulated spectra: Emitted (top, MIR, R = 400), reflected (middle, NIR, R = 400), and transmitted light (bottom, NIR-MIR, R = 200) for scenario with (red) and without (orange) CO deposition. |
| In the text | |
 |
Fig. B.5 Anoxic, biotic TRAPPIST-1 scenario (Tsurf = 275 K) with CO flux of 109 molecules cm−2 s−1, corresponding to lightning flash rate of ~2 times modern Earth’s. Comparison between scenarios with and without CO deposition. Left panel: Atmospheric mixing ratios of most abundant species for the scenario with (thick) and without (thin) CO deposition. Right panel: Simulated spectra: Emitted (top, MIR, R = 400), reflected (middle, NIR, R = 400), and transmitted light (bottom, NIR-MIR, R = 200) for scenario with (black) and without (blue) CO deposition. |
| In the text | |
 |
Fig. B.6 Column densities for a range of CO and NO fluxes. Anoxic abiotic cases. |
| In the text | |
 |
Fig. B.7 Column densities for a range of CO and NO fluxes. Anoxic biotic cases. |
| In the text | |
 |
Fig. B.8 Column densities for a range of CO and NO fluxes. Anoxic biotic (no CO deposition) cases. |
| In the text | |
 |
Fig. B.9 Column densities for a range of CO and NO fluxes. Oxic biotic cases. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\[\mathrm{NH}_4^{+}\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq5.png)
![$\[\mathrm{NO}_3^{-}\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq6.png)
![$\[\mathrm{NO}_2^{-}\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq7.png)
![$\[(\sigma / \sqrt{N})\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq8.png)
![$\[\mathrm{NH}_4^{+}\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq9.png)
![$\[c_{\mathrm{CO}_2}\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq13.png)
![$\[\mathrm{NH}_4^{+}\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq19.png)
![$\[\sqrt{2}\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq20.png)
![$\[\mathrm{NH}_4^{+}\]$](/articles/aa/full_html/2024/06/aa47286-23/aa47286-23-eq21.png)