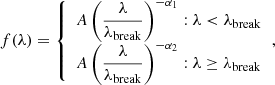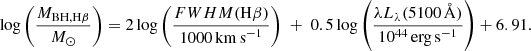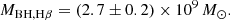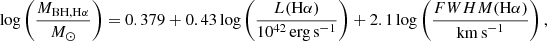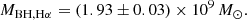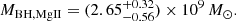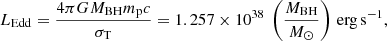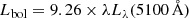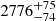EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 685 (May 2024) A&A, 685 (2024) A121 Full HTML
Highlight
Open Access
Issue
A&A
Volume 685, May 2024
Article Number A121
Number of page(s) 13
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202348535
Published online 15 May 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

High-redshift quasars are key laboratories for studying the early stages of galaxy evolution and black hole formation (see Fan et al. 2023, for a recent review). At z ≳ 6, that is, when the Universe was ≲1 Gyr old, they were often harbored by galaxies with a star formation rate (SFR) ∼100 − 4000 M⊙ yr−1, which is significantly higher than that of typical galaxies at similar redshifts with no nuclear activity (e.g., Vanzella et al. 2014; Bouwens et al. 2015; Salmon et al. 2015; Ota et al. 2017; Harikane et al. 2018; Walter et al. 2022). The central black holes can already have masses of 109 Ṁ (e.g., Yang et al. 2021; Farina et al. 2022; Mazzucchelli et al. 2023) and the molecular gas content of the host galaxy, which feeds both nuclear and star formation activity, can easily exceed 1010 Ṁ (e.g., Walter et al. 2003; Wang et al. 2008; Venemans et al. 2017). Accounting for the rapid growth of z ≳ 6 quasars poses important challenges to models of early black hole formation and evolution (see, e.g., the reviews by Inayoshi et al. 2020 and Volonteri et al. 2021).

Over the last years, significant effort has been invested to study z ≳ 6 quasars using the most advanced facilities. In particular, observations with the Atacama Large Millimeter/submillimeter Array (ALMA) and the Northern Extended Millimeter Array (NOEMA) have provided a detailed view of the rest-frame far-infrared emission in these sources. Submillimeter and millimeter data have enabled deep insights into several properties, such as the gas and dust content (Wang et al. 2008; Calura et al. 2014; Decarli et al. 2018, 2022; Venemans et al. 2018), kinematics (e.g., Willott et al. 2013, 2015; Venemans et al. 2016; Neeleman et al. 2019, 2021; Pensabene et al. 2020), and the physics of the interstellar medium (ISM; Walter et al. 2018; Novak et al. 2019; Li et al. 2020; Pensabene et al. 2021; Meyer et al. 2022a; Shao et al. 2022; Tripodi et al. 2022; Decarli et al. 2023) of quasar host galaxies. Observations at these wavelengths have revealed that z ≳ 6 quasars are often associated with companion galaxies from small to large distances, with overdensities exceeding the expectations for the field population of galaxies by several orders of magnitude (Aravena et al. 2016; Decarli et al. 2017; Meyer et al. 2022b; see also Zana et al. 2023 for the theoretical interpretation), even if there are also exceptions to this trend (Mazzucchelli et al. 2017a; Habouzit et al. 2019).

Observations with ground-based optical/near-infrared facilities have constrained the rest-frame ultraviolet (UV) emission from z ≳ 6 quasars (e.g., Kurk et al. 2007; Willott et al. 2010; Mazzucchelli et al. 2017b; Onoue et al. 2019; Schindler et al. 2020; Yang et al. 2021). For example, integral field data from the Multi Unit Spectroscopic Explorer (MUSE) show that quasars are often surrounded by Lyman α nebulae extending up to 10 − 30 kpc (e.g., Borisova et al. 2016; Farina et al. 2017, 2019; Drake et al. 2019). Using X-shooter detections of the Mg IIλ2799 and C IVλ1549 broad emission lines from quasars, Farina et al. (2022) provided estimates of black hole masses (see also De Rosa et al. 2014; Mazzucchelli et al. 2023), which enabled the study of the scaling relations between black hole and galaxy mass at z ≳ 6 (e.g., Willott et al. 2017; Izumi et al. 2019; see also Pensabene et al. 2020; Neeleman et al. 2021).

Despite the significant effort with the most advanced ground telescopes that has been invested over the last years, a number of questions remain unsolved. In particular, the rest-frame optical lines from z > 6 quasars, shifted to the near- and mid-infrared at these redshifts, represent uncharted territory due to the limits of the observing facilities in that window.

Now, with the James Webb Space Telescope (JWST; Gardner et al. 2023), it is finally possible to study the rest-frame optical emission from z > 6 quasars. Observations of emission lines originating from the broad line region (BLR; e.g., Hα and Hβ) provide robust estimates of the black hole mass based on local relations (Greene & Ho 2005; Vestergaard & Peterson 2006; Shen et al. 2011). In addition, the strength and ratios of nebular lines such as Hα, Hβ, [O III] λλ4959, 5007, [N II] λλ6548, 6584 offer a unique tool to characterize the ISM of the quasar host and companion galaxies, constraining important physical quantities (e.g., the ionization mechanism and the ionization parameter, metallicity and dust extinction) that are not accessible at these redshifts using UV spectra only. The first promising results on some of the z > 6 quasars observed with JWST come from the “A SPectroscopic survey of biased halos In the Reionization Era” (ASPIRE) project (Wang et al. 2023). Based on the ASPIRE data, Yang et al. (2023) studied the rest-frame emission at 4100 − 5100 Å in a sample of eight z > 6.5 quasars while Wang et al. (2023) discovered a filamentary structure tracing an overdensity around a luminous z ∼ 6.6 quasar (see also Kashino et al. 2023). Marshall et al. (2023) studied two other z ∼ 6.8 quasars, as well as their host galaxies and companion sources. These works also provide first estimates of black hole masses at z > 6 measured with the Hβ or Hα line (see also Bosman et al. 2023; Ding et al. 2023; Eilers et al. 2023; Yue et al. 2023).

PJ308-21 at z = 6.2342 stands out among the known quasars at z > 6 as a key laboratory to study quasar-galaxy interactions at cosmic dawn. This object was discovered by Bañados et al. (2016) (see also Mazzucchelli et al. 2017b) and intensively studied by Decarli et al. (2019) using high-resolution ALMA data, targeting the [C II] and dust continuum emission in this system. The ALMA observations reveal that the quasar host has two companion sources, respectively blueshifted (Δv[CII] ∼ −750 km s−1; Decarli et al. 2019) and redshifted (Δv[CII] ∼ +500 km s−1) from the quasar, located toward the western and eastern sides of the quasar at projected distances of ∼5 and ≳10 kpc, respectively. These two emission components are also detected in rest-frame UV images from the Hubble Space Telescope (HST), revealing light from young stars from both objects. As discussed by Decarli et al. (2019), the quasar host is possibly experiencing a merger with another galaxy that is tidally disturbed by the interaction and that accounts for the emission from the two companion sources. Deep MUSE observations reveal that the system is surrounded by a Lyman α halo (R ∼ 27 kpc) that overlaps with the eastern companion (Farina et al. 2019). Furthermore, Connor et al. (2019) found that PJ308-21 has an X-rays luminosity LX(2 − 10 keV)∼2 × 1045 erg s−1 while the western companion shows possible high-energy emission with no soft component, which may point to an active galactic nucleus (AGN) also in this object. Because of its complex and extended morphology, the PJ308-21 system is an ideal target for JWST/NIRSpec integral field spectroscopy, which allows us to probe rest-frame optical emission of the spatially resolved components of this object.

This work (Paper I) is the first of a series of papers studying the PJ308-21 system with NIRSpec data. In particular, it is devoted to the characterization of the quasar spectrum itself. Paper II (Decarli et al. 2024) studies the extended gas emission in the system. Paper III (Farina et al., in prep.) investigates the Lyman α and Hα halo. Yet another paper will focus on the kinematics of the system.

This paper is organized as follows: Sect. 2 deals with the NIRSpec observation and data reduction. Sect. 3 is devoted to the analysis of the quasar spectrum. In Sect. 4 we present the results of our analysis. Finally, we summarize our conclusions in Sect. 5. In this work we adopt a ΛCDM cosmology with ΩΛ = 0.7, ΩM = 0.3 and a Hubble constant H0 = 70 km s−1 Mpc−1.

2. Observations and data reduction

In this paper we analyze the data of the Cycle 1 General Observer (GO) program 1554 (PI: R. Decarli), which targets the PJ308-21 quasar system (see Table 1 of Decarli et al. 2019 for the properties of the system derived from ALMA and HST data). The observations were taken on September 22–23 2022 using the integral field unit (IFU) of JWST/NIRSpec (Jakobsen et al. 2022; Böker et al. 2022). The science observations consist of two separated fields (3″ × 3″ each), corresponding to the quasar and its western companion (PJ308-W), and to the eastern component (PJ308-E), respectively. A third field covered an empty region of the sky to estimate the background. We observed each field (background included) for 2 h and 30 min (including overheads), for a total execution time of 7.5 h (4.8 h on source). We used the NRSIRS2 readout in order to minimize the correlated noise and the data volume, and observed a total of 18 exposures (six per pointing applying a small-cycling dithering pattern), each of them consisting of 13 groups (i.e., integration elements). We also observed one leakage exposure of 87 s to remove the pattern introduced by the NIRSpec micro-shutter assembly (MSA). The data were taken in the high-resolution mode (spectral power R ∼ 2700) using the G395H/290LP grating/filter combination. This covers the wavelength range 2.87 − 5.27 μm with a gap due to the NRS1 and NRS2 detector separation corresponding to 4.1 − 4.3 μm.

We reduced the data using the JWST pipeline developed by the Space Telescope Science Institute (STScI). We used the 1.12.5 version of the pipeline combined with the Calibration Reference Data System (CRDS) context jwst_1183.pmap, which indicates the set of reference files necessary for calibrating the data. The reduction process consists of three stages, each of them involving several steps (see Fig. 1). Stage 1 processes the raw exposures (i.e., nondestructive readout ramps) correcting for detector effects such as bias, dark, and cosmic rays impact, and creates count rate images. During this stage, we introduced a further flagging of the ramps strongly affected by saturation, nonlinearity or cosmic rays (Further ramp flagging in Fig. 1). In particular, we excluded from the ramp fitting all the ramps containing only two useful groups (out of 13). This step resulted in a drop of the standard deviation in the rate files (i.e., 2D count rate images) by a factor ≲2 × 103. The rate files were affected by vertical stripes due to residual 1/f noise unremoved in stage 1 (see also Kashino et al. 2023; Perna et al. 2023; Rauscher 2024). We eliminated this pattern by subtracting from each spectral column in the 2D count rate images its median value, which provides a reasonable estimate of any spectrally dependent correlated noise (see Column median subtraction in Fig. 1).

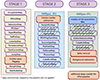thumbnail Fig. 1.

Scheme of the data reduction process for the NIRSpec data of PJ308-21. The data reduction is divided into three stages, each of them consisting of several steps. Stage 1 is independent from the JWST instrument and mode, unlike stage 2 and 3, for which we present the steps for NIRSpec/IFU. We skip some pipeline steps (boxes with gray tilted lines) and introduce additional steps (orange boxes) to improve the data reduction (see Sect. 2).

We thus processed the median-subtracted exposures through stage 2 of the reduction, where flat field correction, wavelength and flux calibration are applied to all the exposures. We skipped the BackgroundStep, as we applied the background subtraction at the end of stage 3. We also skipped the ImprintStep, which is meant to subtract the pattern created by the MSA, as we found that the subtraction of the dedicated leakage exposure results in a detrimental increase of the noise in the rate files.

We then performed stage 3, where all the exposures are combined into the final datacubes. We applied the OutlierDetectionStep, which is meant to remove the remaining outliers from the calibrated exposures, and which provides reliable results for our dataset from the 1.11.4 pipeline version.

The one-dimensional spectra extracted from random apertures in the final datacubes show several spikes, due to cosmic rays and possible wrong solutions for the ramp fitting. We filtered out these spikes by masking all the voxels that present a jump between contiguous channels persisting for less than four channels (corresponding to < 150 km s−1 at 4.0 μm), which is the typical width of the spikes. The procedure was applied to all the voxels of the datacubes (see Spike removal in Fig. 1). We carefully inspected the voxels corresponding to the science targets before and after applying this step to check that none of the emission lines is affected by the algorithm. Finally, we subtracted the background, which is higher for the spectral region sampled by the NRS2 detector (4.3 − 5.3 μm), as the NIR background grows with increasing wavelength (Rigby et al. 2023). We estimated the background from the median of spectra extracted from empty regions in the field of view as a function of wavelength. The median background was then subtracted from the datacubes channel by channel (see Background subtraction in Fig. 1).

In this paper, as we are interested in the quasar spectrum, we study the PJ308-W pointing only. A map showing an overlook on the system captured by the PJ308-W and PJ308-E reduced datacubes is shown in Fig. 2 (see Decarli et al. 2024, for more details).

thumbnail Fig. 2.

PJ308-21 system. The quasar has two companion sources, located to the western and eastern sides of the quasar, respectively. We show the Hα and the underlying continuum emission from the NIRSpec/IFU data (magenta) overimposed on the [C II] emission from ALMA high-resolution data (blue; Decarli et al. 2019). The yellow cross and circle show the aperture for the spectrum extraction (see Sect. 3.1).

3. Analysis

3.1. Spectrum extraction and aperture correction

We computed a wavelength-dependent aperture correction based on the observation of a point source (i.e., a star) using archival data. We used the uncalibrated exposures of the GSPC P330-E G–dwarf, observed in the 1538 calibration program (PI: K. Gordon). We opted for this star as it was observed with NIRSpec/IFU using the same grating/filter combination of our observation. We processed the data, applying the same steps described in Sect. 2. The final datacube was used for extracting one-dimensional spectra adopting circular apertures, with radii R ranging from R = 0.025″ to R = 1.2″ centered on the star. The growth curve asympotes at 1″, so we normalized the flux in each wavelength channel to the value at R = 1″ (see also Fig. A.1). We thus estimated the flux fraction for fixed aperture radii as a function of the wavelength (see Table 1 for representative wavelengths over the G395H/F290LP spectral range). We computed these values by fitting a second-order spline to the flux fractions. The enclosed flux fraction increases with increasing radius and, for fixed aperture, decreases with wavelength. The latter trend is less pronounced at larger radii, as most of the flux is also included for the redder part of the spectrum (see also Fig. A.1). For an aperture of 0.3″, the flux loss between the red and blue channels can be as high as ∼6%, while the difference is lower for larger apertures.

Table 1.

Flux fraction for fixed aperture radius R as a function of the wavelength (NIRSpec/IFU, G395H/F290LP).

The values reported in Table 1 can be used to correct the spectra extracted from apertures with radii R ∼ 0.3″ − 0.7″ to recover the total flux emitted by a point source. These values should provide reliable corrections when using the dataset observed using the NIRSpec/IFU with the G395H/F290LP grating/filter combination and the adopted version of the pipeline1. We adopted an extraction aperture of 0.3″ centered at the NIRSpec peak position of PJ308-21 (Fig. 2). We note that using a larger aperture, that is, 0.4″ − 0.7″, after applying the aperture correction gives perfectly consistent results, while using a smaller aperture (∼0.2″) cannot properly recover the quasar flux because of the undersampling of the NIRSpec point spread function (PSF; see Böker et al. 2022). We thus applied the 0.3″ aperture correction based on Table 1 to recover the total flux. The same correction was applied to the error spectrum. We obtained the noise spectrum by summing all the pixel variance over the 0.3″ aperture and extracting the square root of the summed total. We show in Fig. 3 the aperture-corrected spectrum together with the rest-frame UV spectra of PJ308-21 from the literature, obtained with MUSE (Farina et al. 2019) and X-shooter (Schindler et al. 2020). The signal-to-noise ratio (S/N) S/N of the NIRSpec spectrum per spectral element is 100 − 400. We show also the photometric data (see Bañados et al. 2016) from the first release of the Panoramic Survey Telescope and Rapid Response System (Pan-STARRS1, PS1; g, r, i, z, Y bands), the Gamma-ray Burst Optical/Near-infrared Detector (GROND; i, z, J bands), the VISTA Hemisphere Survey (VHS; Y, H, K bands), Spitzer (Ch1 = 3.5 μm, Ch2 = 4.5 μm), and the Wide-Field Infrared Survey Explorer (WISE; W1 = 3.3 μm, W2 = 4.6 μm). There is an overall agreement between the NIRSpec spectrum and the available photometry from Spitzer and WISE. The differences, in the order of ∼10%, are possibly due to systematics in the instruments zero-points. We note that the continuum slope changes between the NIRSpec data and the ground-based spectra. This is possibly due to both physical and instrumental effects. The power-law continuum in quasars is interpreted as the result of several black bodies, corresponding to layers in the accretion disk with different temperatures. The large black hole mass (see Sect. 4.1) yields a relatively large radius of the innermost ring, which corresponds to a peak in the continuum emission. Therefore, the quasar continuum is expected to change the slope from the rest-frame UV (where most of the disk emission is expected) to rest-frame optical. Second, the fluxes in the X-shooter spectrum are expected to be more extinguished from the dust in the quasar host in comparison to the near-infrared data, which can also influence the slope. Beyond these physical effects, possible systematics in the zero-points, potential slit losses in the X-shooter spectrum, and increased noise toward the red end of the X-shooter spectrum can also contribute to the slope variation.

thumbnail Fig. 3.

Rest-frame UV/optical spectroscopic and photometric data of PJ308-21. The main emission lines are indicated. The aperture-corrected NIRSpec spectrum is shown in red (see Sect. 3.1). The purple and blue lines show MUSE and X-shooter spectra from previous works (Farina et al. 2019; Schindler et al. 2020). We show in gray the X-shooter data affected by the atmosphere absorption. The photometric data from Pan-STARRS1 (PS1; g, r, i, z, Y bands), GROND (i, z, J bands), VHS (Y, H, K bands), Spitzer (Ch1 = 3.5 μm, Ch2 = 4.5 μm), and WISE (W1 = 3.3 μm, W2 = 4.6 μm) are shown with the associated errors (Bañados et al. 2016).

3.2. Spectral fitting

We converted the observed wavelength into the rest-frame using the [C II] based redshift (z = 6.2342, Decarli et al. 2019). The spectrum shows a strong quasar continuum and all the prominent Balmer lines (Hα, Hβ, Hγ, Hδ) due to the BLR. We also observe bright emission from the Fe II multiplets in the 4000 − 5500 Å range. The BLR dominates over the nebular emission of the narrow line region (NLR; i.e., [O III] λλ4959, 5007 and [N II] λλ6548, 6584 doublets). We do not detect a significant He IIλ4686 emission line, which can be used as a tracer of the nuclear activity (Tozzi et al. 2023), or significant [S II] λλ6716, 6732 emission. Also, we do not find absorption features over the spectrum.

3.2.1. Continuum subtraction

We performed a multicomponent fitting to reproduce the NIRSpec spectrum using a Markov chain Monte Carlo (MCMC) method with the Python package emcee (Foreman-Mackey et al. 2013). We first modeled the continuum emission, whereafter we modeled the iron and the nebular lines.

Quasar spectra often show a break in their shape, possibly due to the host galaxy contamination (see, for example, Vanden Berk et al. 2001). For this reason, we used a broken power-law to model the continuum emission, in the functional form of

f ( λ ) = { A ( λ λ break ) − α 1 : λ < λ break A ( λ λ break ) − α 2 : λ ≥ λ break , $$ \begin{aligned} f(\lambda ) = {\left\{ \begin{array}{ll} A \left( \dfrac{\lambda }{\lambda _{\rm break} } \right)^{-\alpha _1} : \lambda < \lambda _{\rm break} \\ A \left( \dfrac{\lambda }{\lambda _{\rm break}} \right)^{-\alpha _2} : \lambda \ge \lambda _{\rm break} \end{array}\right.}, \end{aligned} $$

where A is the normalization, λbreak is the break wavelength, and α1 and α2 are the power-law indices. Following Vanden Berk et al. (2001), we used the line-free regions of the spectra 6005 − 6035 Å and 7160 − 7180 Å with an additional region at 4000 − 4030 Å to constrain the bluest part of the spectrum, after have carefully checked that it is not contaminated by line emission (see the shaded regions in Fig. 4, top panel) to fit the continuum. The continuum model is shown in Fig. 4 (top panel), with the continuum-subtracted spectrum highlighted in orange (see also Table 2 for the fitted parameters). We do not discuss the physical meaning of the λbreak, A, α1, and α2 values, and compare with low-redshift quasars, as we find that the parameters are highly degenerate among themselves. We thus use the fit only to obtain a robust continuum-free spectrum for fitting the emission lines.

thumbnail Fig. 4.

JWST/NIRSpec rest-frame optical spectrum of the PJ308-21 quasar (black). Broad Balmer line emission (Hα, Hβ, Hγ, Hδ), strong Fe II, and [O III] emission is clearly seen. Top panel: quasar continuum fit (magenta curve). We highlight the line-free regions used for the continuum fit (pale blue). The orange curve shows the residuals. Bottom panel: Fe II line model (magenta). The fitted wavelengths are highlighted in pale blue. We fit the Fe II emission using the five multiplets template of Kovačević et al. (2010) and Shapovalova et al. (2012) (colored lines in the insets). The iron-subtracted spectrum (orange) was then used to fit the Balmer and nebular lines.

Table 2.

Continuum and iron fitted parameters.

3.2.2. Fe II subtraction

After subtracting the continuum, we modeled the Fe II multiplets in the spectral range 4000 − 5500 Å. Careful subtraction of the Fe II emission is indeed necessary for deriving an accurate Hβ-based black hole mass (see Sect. 4.1), as this line is partially contaminated by iron emission. We used the tool by Kovačević et al. (2010) and Shapovalova et al. (2012) to create an Fe II template consisting of five groups of lines (labeled as Zw I, S, F, P, G), using reasonable input parameters for an AGN spectrum (i.e., temperature T = 10 000 K, velocity width of 2500 km s−1 and no velocity shift). However, using a different set of input parameters does not change the fit results significantly. In particular, we verified that increasing the Fe II width, by smoothing it to match the width of other BLR lines, does not significantly impact the black hole mass derived from the broad Hβ full width at half maximum (FWHM; see Sect. 4.1). We fit the normalization of the five groups (labeled as IZwI, IS, IF, IP, IG, see Table 2) to properly rescale the templates using the spectral regions at 4150 − 4200 Å, 4430 − 4720 Å, and 5110 − 5520 Å (shaded regions in Fig. 4, bottom panel). The Fe II model is shown in Fig. 4 (bottom panel), with the iron-subtracted spectrum in orange (see also Table 2 for the fitted parameters). We used the templates of Kovačević et al. (2010) and Shapovalova et al. (2012), which secure reliable multiplets structure and intensity. However, the high S/N of our spectrum highlights the limits of the models. Introducing variable widths among the templates due to a velocity stratification of the BLR could possibly improve the fit compared to the simple case presented here.

3.2.3. Line fitting

After subtracting the continuum and Fe II model, we fit the line emission. In particular, we focused on the Hα and Hβ line complexes, since we used these lines to derive relevant physical quantities (e.g., black hole mass; see Sect. 4). We used two Lorentzian functions (one for each line) to model the Hα and Hβ lines from the BLR (Kollatschny & Zetzl 2013), leaving all parameters (i.e., normalization, width, and centroid) free. We also inserted six Gaussians to account for the nebular [O III] λλ4959, 5007, [N II] λλ6548, 6584, Hα, and Hβ lines from the NLR (referred to as “narrow” components in the rest of the paper). As the emission is completely dominated by the broad Hα and Hβ lines, we fixed the line centroids to the theoretical values to aid the fit, by assuming that the rest-frame velocity of the narrow lines is consistent with the [C II] velocity. We also required that all six narrow lines have the same velocity width and fixed the ratio of the amplitudes of [O III] λ4959 and [O III] λ5007 to the theoretical value (0.33), as well as for the [N II] λ6548 and [N II] λ6584 (0.33; e.g., Osterbrock & Ferland 2006). Thus, for the NLR lines, we fit only the normalization of [O III] λ5007, [N II] λ6584, Hα, Hβ, and the standard deviation (σ). Moreover, we added two further Gaussian components to reproduce the emission at 4900 − 5100 Å (the “broad” [O III] components discussed in Sect. 4.4). Under the assumption that this emission is due to [O III] λλ4959, 5007 blueshifted with respect to the systemic velocity, we required that the two Gaussians have the same velocity width and offset, and the theoretical ratio for the amplitudes. Therefore, in this case, the free parameters are the centroid, σ, and the normalization of the [O III] λ5007 component.

We adopted Maxwellian priors for all the fitted parameters except for the width of the narrow components. In this case we imposed that the FWHM can uniformly vary between 50 and 1000 km s−1 (a similar approach was adopted by Vietri et al. 2018). The fitted wavelength ranges are 4430 − 5520 Å and 6160 − 6900 Å. The fit is shown in Fig. 5 (see also Table 3).

thumbnail Fig. 5.

Fit of the Hβ + [O III] (left) and Hα + [N II] lines (right), after the continuum and iron subtraction. We modeled the BLR Hβ and Hα lines using two Lorentzian functions (one for each line). The nebular lines from the NLR ([O III], [N II], Hα, and Hβ narrow components) were each fitted with a Gaussian. We added two further Gaussian components (purple; “broad” components in the paper) to fit the emission around 5000 Å, likely associated with blueshifted [O III] (see also Sect. 4.4 and Fig. 8). The residuals are shown in orange.

Table 3.

Emission-line fitted parameters.

Our multicomponent fit nicely reproduces the line emission for both Hα and Hβ regions. The galactic contribution (i.e., NLR emission) is poorly constrained, as the BLR dominates the line emission. There are some residuals at 5000 − 5200 Å, possibly due to uncertainties in the iron modeling described in Sect. 3.2.2. However, this does not significantly impact the Hβ fit and the Hβ-based black hole mass estimates. Finally, we note that using a broken power-law rather than a Lorentzian curve to model the Hα and Hβ lines from the BLR also gives a consistent black hole mass. The BLR emission may have indeed asymmetric wings that are better reproduced by a broken power-law. A study of these features is however beyond the scope of this work. We also tested that adding a broad component for the Hα and Hβ lines, as done for the [O III] emission, does not affect the fit, as the component is in the order of the residuals for both lines.

4. Results

4.1. Black hole mass

A common way to estimate the black hole mass in quasars relies on the virial theorem. Assuming that the clouds of the BLR undergo pure gravitational motion around the black hole, we can write the black hole mass as 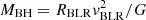M BH = R BLR v BLR 2 /G $ M_{\rm BH} = R_{\rm BLR} v^2_{\rm BLR}/G $, where G is the gravitational constant, vBLR the clouds’ velocity, and RBLR their distance from the black hole. Based on reverberation mapping studies in the low-z Universe, the continuum luminosity at 5100 Å is correlated with RBLR (e.g., Kaspi et al. 2005), while the FWHM of the BLR lines (e.g., Hβ, Hα, Mg II, C IV) provides the information for the velocity vBLR. Before the JWST launch, emission lines such as Mg II and, more rarely, C IV were commonly used to measure the black hole masses in high-z quasars (e.g., Jun et al. 2015; Lira et al. 2018; Onoue et al. 2019; Kaspi et al. 2021; Farina et al. 2022). However, the relations that employ these tracers are actually poorly constrained and uncertain, especially for the C IV line (Coatman et al. 2017; Marziani et al. 2019; Homayouni et al. 2020; Zuo et al. 2020). It is thus not clear if the black hole masses based on these lines are reliable. On the other hand, Hβ has been extensively studied to derive empirical calibrations for black hole mass at low redshift (e.g., Bentz et al. 2009; De Rosa et al. 2018; see Shen 2013, for a review), and it is thus considered the most robust tracer of this physical quantity. After the launch of JWST, we can now use this line for measuring the black hole mass even at high-redshift (see also Ding et al. 2023; Eilers et al. 2023; Marshall et al. 2023; Yang et al. 2023).

We estimate the black hole mass of PJ308-21 using the relation of Vestergaard & Peterson (2006), which uses the 5100 Å quasar continuum luminosity Lλ(5100 Å) and the FWHM of the Hβ

log ( M BH , H β M ⊙ ) = 2 log ( F W H M ( H β ) 1000 km s − 1 ) + 0.5 log ( λ L λ ( 5100 Å ) 10 44 erg s − 1 ) + 6.91 . $$ \begin{aligned} \log \left( \dfrac{M_{\rm BH, H\beta }}{M_{\odot }} \right) = 2 \log \left( \dfrac{FWHM(\mathrm{H}\beta )}{1000\,\mathrm{km\,s}^{-1}} \right) \ + \ 0.5 \log \left( \dfrac{\lambda L_{\lambda }(5100\,\AA )}{10^{44}\,\mathrm{erg\,s}^{-1}} \right) + 6.91. \end{aligned} $$(1)

We estimate the continuum monochromatic luminosity 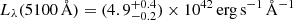L λ ( 5100 Å ) = ( 4 . 9 − 0.2 + 0.4 ) × 10 42 erg s − 1 Å − 1 $ L_{\lambda}(5100\,\AA) = (4.9^{+0.4}_{-0.2}) \times 10^{42}\,\mathrm{erg\,s}^{-1}\,\AA^{-1} $ from the power-law value at 5100 Å while the FWHM(Hβ) is 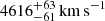4616 − 61 + 63 km s − 1 $ 4616^{+63}_{-61}\,\mathrm{km\,s}^{-1} $. The black hole mass is

M BH , H β = ( 2.7 ± 0.2 ) × 10 9 M ⊙ . $$ \begin{aligned} M_{\rm BH, H\beta } = (2.7 \pm 0.2) \times 10^{9}\,M_{\odot }. \end{aligned} $$

We note that the uncertainties on the black hole mass due to random errors from the MCMC fit are around the 7%. However, the adopted calibration has an intrinsic scatter of ∼0.5 dex, which thus represents the main source of uncertainty (Vestergaard & Peterson 2006).

Greene & Ho (2005) found that there is a correlation between the 5100 Å continuum luminosity and the Hα luminosity (see their Eq. (1)). A correlation is also present between the Hβ and HαFWHM (see their Eq. (3); see also Shen et al. 2011, Eq. (9)). Using these correlations and Eq. (1), it is thus possible to obtain a calibration for the black hole mass with the Hα line (Shen et al. 2011)

log ( M BH , H α M ⊙ ) = 0.379 + 0.43 log ( L ( H α ) 10 42 erg s − 1 ) + 2.1 log ( F W H M ( H α ) km s − 1 ) , $$ \begin{aligned} \log \left( \dfrac{M_{\rm BH, H\alpha }}{M_{\odot }} \right) = 0.379 + 0.43 \log \left( \dfrac{L(\mathrm H\alpha )}{10^{42}\,\mathrm{erg\,s}^{-1}} \right) + 2.1 \log \left( \dfrac{FWHM(\mathrm{H}\alpha )}{\mathrm{km\,s}^{-1}} \right), \end{aligned} $$(2)

where L(Hα) and FWHM(Hα) are the luminosity and FWHM of the Hα broad component. We estimate the former quantity L(Hα) = (1.84 ± 0.01) × 1045 erg s−1 by integrating the Hα Lorentzian component from 6300 Å to 6800 Å. The FWHM of the Lorentzian is FWHM(Hα) = 3739 ± 26 km s−1. The resulting Hα-based black hole mass is

M BH , H α = ( 1.93 ± 0.03 ) × 10 9 M ⊙ . $$ \begin{aligned} M_{\rm BH, H\alpha } = (1.93 \pm 0.03) \times 10^{9}\,M_{\odot }. \end{aligned} $$

We find that the MBH, Hβ and MBH, Hα values agree with each other within a factor of ≲1.5 (see also Table 4), as expected from the intrinsic scatter of the adopted correlations.

Table 4.

Physical quantities of PJ308-21 derived from line fitting.

We can compare our estimates of the black hole mass with the Mg II-based value for PJ308-21. Based on the relation of Shen et al. (2011), Farina et al. (2022) found

M BH , MgII = ( 2 . 65 − 0.56 + 0.32 ) × 10 9 M ⊙ . $$ \begin{aligned} M_{\rm BH, MgII} = (2.65^{+0.32}_{-0.56}) \times 10^{9}\,M_{\odot }. \end{aligned} $$

This value is consistent with the Hβ estimate. For this quasar Farina et al. (2022) also derived a C IV-based black hole mass using the relation of Coatman et al. (2017), that is, 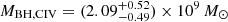M BH , C IV = ( 2 . 09 − 0.49 + 0.52 ) × 10 9 M ⊙ $ M_{\mathrm{BH,C IV}} = (2.09^{+0.52}_{-0.49}) \times 10^{9}\,M_{\odot} $, which is consistent with the estimates from the other lines.

Figure 6 compares the PJ308-21 black hole mass estimates with values from SDSS (Shen et al. 2011) and the other z > 6 quasars with both Mg II and Hβ or Hα black hole mass measurements from JWST data (Bosman et al. 2023; Eilers et al. 2023; Marshall et al. 2023; Yang et al. 2023; Yue et al. 2023). The Mg II masses are based on the Vestergaard & Osmer (2009) and Shen et al. (2011) calibration (see Pons et al. 2019; Reed et al. 2019; Shen et al. 2019; Wang et al. 2021; Yang et al. 2021; Farina et al. 2022; Mazzucchelli et al. 2023) while the Hβ and Hα measurements are based on Vestergaard & Peterson (2006) and Greene & Ho (2005). Overall, we see that the z > 6 quasars lie well inside the ∼0.5 dex scatter of the low-redshift estimates. Despite larger sample are necessary to constrain z > 6 black hole masses via Balmer lines targeting also less massive black holes (i.e., MBH ∼ 108 M⊙), these first findings suggest that the Mg II is a reliable mass tracer in distant quasars.

thumbnail Fig. 6.

Black hole masses from SDSS (Shen et al. 2011) and z > 6 quasars (Bosman et al. 2023; Eilers et al. 2023; Marshall et al. 2023; Yang et al. 2023; Yue et al. 2023), with both Mg II and Balmer line based measurements. The green line shows the one-to-one relation. PJ308-21 is indicated with blue diamonds (NIRSpec and X-shooter data). Overall, the z > 6 quasars show nice agreement between the Mg II and Hβ or Hα-based MBH, consistent with the ∼0.5 dex scatter of the low-redshift estimates (green region; Vestergaard & Peterson 2006). While a larger sample is needed to confirm these results, these first JWST estimates suggest that the Mg II is a reliable tracer of the black hole mass at both low and high-redshift.

4.2. Eddington ratio

We use the black hole mass to evaluate the Eddington ratio λEdd = Lbol/LEdd, that is, the ratio between the quasar bolometric luminosity Lbol and the Eddington luminosity LEdd (see Peterson 1997). Assuming spherical geometry, the latter quantity can be written as

L Edd = 4 π G M BH m p c σ T = 1.257 × 10 38 ( M BH M ⊙ ) erg s − 1 , $$ \begin{aligned} L_{\rm Edd} = \dfrac{4 \pi G M_{\rm BH} m_{\rm p} c}{\sigma _{\rm T}} = 1.257 \times 10^{38}\ \left( \dfrac{M_{\rm BH}}{M_{\odot }} \right)\,\mathrm{erg\,s}^{-1}, \end{aligned} $$

where σT is the cross-section for Thomson scattering, mp is the proton mass and c is the light speed in vacuum. Based on the MBH, Hβ estimate, we find for PJ308-21 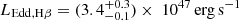L Edd , H β = ( 3 . 4 − 0.1 + 0.3 ) × 10 47 erg s − 1 $ L_{\mathrm{Edd, H\beta}} = (3.4^{+0.3}_{-0.1}) \times\ 10^{47}\,\mathrm{erg\,s}^{-1} $ (LEdd, Hα = (2.43 ± 0.04)× 1047 erg s−1). The bolometric luminosity Lbol can be estimated from the monochromatic luminosity Lλ(5100 Å) by assuming a bolometric correction. We use the relation from Richards et al. (2006), updated by Shen et al. (2011)

L bol = 9.26 × λ L λ ( 5100 Å ) $$ \begin{aligned} L_{\rm bol} = 9.26 \times \lambda L_{\lambda }(5100\,\AA ) \end{aligned} $$

based on 259 quasars from SDSS. This gives a bolometric luminosity of 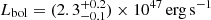L bol = ( 2 . 3 − 0.1 + 0.2 ) × 10 47 erg s − 1 $ L_{\mathrm{bol}} = (2.3^{+0.2}_{-0.1}) \times 10^{47}\,\mathrm{erg\,s}^{-1} $. Therefore, the Eddington ratio for PJ308-21 based on the Hβ line is 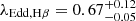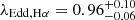λ Edd , H β = 0 . 67 − 0.05 + 0.12 $ \lambda_{\mathrm{Edd, H\beta}} = 0.67^{+0.12}_{-0.05} $ ( λ Edd , H α = 0 . 96 − 0.06 + 0.10 $ \lambda_{\mathrm{Edd, H\alpha}} = 0.96^{+0.10}_{-0.06} $ for Hα). We note that adopting a different bolometric correction would imply a lower Eddington ratio, in the range 0.32 < λEdd, Hβ < 0.47 (0.45 < λEdd, Hα < 0.66 for Hα; Shen et al. 2011; Krawczyk et al. 2013; Saccheo et al. 2023). We also note that the true uncertainty on λEdd is likely higher due to the statistical uncertainty, due to object-to-object differences, on the black hole mass calibrations and on the bolometric luminosity.

We can look at the high Eddington ratio of PJ308-21 in the context of the z ∼ 6 quasar population (see also Yang et al. 2023). Based on X-shooter spectra of 38 quasars at 5.8 < z < 7.5, Farina et al. (2022) found that these objects show higher values of λEdd than the low-redshift population at fixed Lbol (Shen et al. 2011). This suggests that in the early Universe quasars tended to accrete at higher rates than the low-z AGN, even if exceptions are present among low-luminosity quasars (Kim et al. 2018; Matsuoka et al. 2019). Besides, this trend can be affected by observational biases toward a selection of more massive black holes and higher bolometric luminosities (and thus higher Eddington ratios) at high redshift. PJ308-21 has an Eddington ratio based on Hβ and Hα above, but still consistent (given the statistical uncertainties in the black hole masses) with the median value 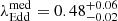λ Edd med = 0 . 48 − 0.02 + 0.06 $ \lambda_{\mathrm{Edd}}^{\mathrm{med}} = 0.48^{+0.06}_{-0.02} $ of the 5.8 < z < 7.5 quasar sample of Farina et al. (2022). The Hβ value is also in perfect agreement with the Mg II-based 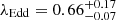λ Edd = 0 . 66 − 0.07 + 0.17 $ \lambda_{\mathrm{Edd}} = 0.66^{+0.17}_{-0.07} $ for PJ308-21 measured by Farina et al. (2022) adopting the bolometric correction for 3000 Å of Richards et al. (2006), updated by Shen et al. (2011).

4.3. Correlations between Fe II, [O III] and Hβ

As initially shown by Boroson & Green (1992), the strength of the Fe II and [O III] λ5007 emission is anticorrelated in low-redshift quasars. The so-called “Eigenvector 1 correlation” (EV1) was then confirmed by other papers (e.g., Sulentic et al. 2004, 2006; Kovačević et al. 2010; Runnoe et al. 2013; Pennell et al. 2017), comparing the Fe II strength, quantified by the ratio between the Fe II and Hβ rest-frame equivalent width, that is, RFe II = EWFe II/EWHβ, and the [O III] rest-frame equivalent width, EW[O III]. The physical origin of this relation is still poorly understood, although it may be related to the processes governing the black hole accretion (Shen 2016). At higher redshifts, Shen (2016) found that the anticorrelation is in place in 1.5 < z < 3.5 quasars, with slightly lower EW[O III] compared to low redshift (see also Sulentic et al. 2004, 2006). Before the JWST launch, it was not possible to investigate this relation for quasars at z > 6. First results using slitless JWST/NIRCam spectroscopy in eight z > 6 quasars by Yang et al. (2023) are consistent with low-redshift samples.

For PJ308-21 we find an [O III] λ5007 rest-frame equivalent width EW[O III] = 19 ± 2 Å. We measure this quantity including both the [O III] λ5007 narrow and broad component, following Shen et al. (2011). The EW of the Hβ broad component is 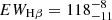E W H β = 118 − 11 − 8 $ EW_{\mathrm{H\beta }} = 118^{-8}_{-11} $ Å while the EWFe II is 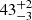43 − 3 + 2 $ 43^{+2}_{-3} $ Å. The latter quantity was obtained by directly integrating the continuum-subtracted Fe II emission in the range 4434 − 4684 Å (Shen et al. 2011). We integrate the data rather than the Fe II line fit in order to avoid uncertainties in the iron modeling (see Sect. 3.2.2 and Fig. 4, bottom panel). The resulting RFe II is 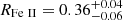R Fe II = 0 . 36 − 0.06 + 0.04 $ R_{\mathrm{Fe\ II}} = 0.36^{+0.04}_{-0.06} $. We note that the iron emission may be contaminated by the blue and red wing of the Hβ and Hγ BLR lines, respectively. We neglect this contribution when estimating the iron EW for consistency with Shen et al. (2011). We also test that subtracting the Hβ and Hγ emission does not significantly affect any of the results about the EV correlations for the quasar. In that case we obtain indeed EWFe II is 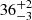36 − 3 + 2 $ 36^{+2}_{-3} $ Å and R Fe II = 0 . 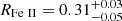31 − 0.05 + 0.03 $ R_{\mathrm{Fe\ II}} = 0.31^{+0.03}_{-0.05} $, which place PJ308-21 in a similar location in the two panels of Fig. 7.

thumbnail Fig. 7.

Anticorrelations between the Fe II strength, parametrized by RFe II, the [O III] EW, and HβFWHM. Top panel: the anticorrelation between RFe II and EW[O III] (EV1 relation). PJ308-21 (blue diamond) shows a value in agreement with both low-redshift (Shen et al. 2011), 1.5 < z < 3.5 (Shen 2016) and z > 6 quasars (Yang et al. 2023). Bottom panel: anticorrelation between RFe II and FWHM(Hβ) (2D EV1). Also in this case, the PJ308-21 value appears consistent with the findings of other studies.

In Fig. 7 (top panel), we compare PJ308-21 with the DR7 SDSS quasars from Shen et al. (2011) and a sample of 74 luminous (Lbol = 1046.2 − 48.2 erg s−1) 1.5 < z < 3.5 quasars (Shen 2016). We show also the eight z > 6 quasars from Yang et al. (2023). Our source is consistent with the values presented by both low-redshift and high-redshift quasars, showing a low RFe II corresponding to a high EW[O III].

We also explore the anticorrelation between RFe II and the HβFWHM (“2D EV1”, e.g., Boroson & Green 1992; Shen & Ho 2014); see Fig. 7, bottom panel). Compared to low-redshift objects, high-redshift quasars show a systematic offset in the HβFWHM up to z > 6 (Shen 2016; Yang et al. 2023). This is due to a selection effect as at high redshift we mainly sample the most massive black holes, which correspond to larger HβFWHM. We find that, for this relation as well, PJ308-21 shows values in line with the findings for the DR7 SDSS quasars and higher-redshift quasars.

4.4. Velocity shifts

Several papers have studied the bulk velocity shifts of the BLR gas (e.g., Gaskell 1982; Richards et al. 2002; Meyer et al. 2019; Onoue et al. 2020). In particular, high-ionization lines like C IVλ1549 and Si IVλ1397 have significantly higher velocity shifts relative to low-ionization broad lines, such as Mg II and Balmer lines. These velocity offsets are thought to be due to outflowing clouds from the BLR driven by winds or X-ray radiation (Murray & Chiang 1995).

According to Schindler et al. (2020), PJ308-21 displays a C IV blueshifted emission of 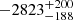− 2823 − 188 + 200 $ -2823^{+200}_{-188} $ km s−1 with respect to the [C II] systemic velocity. On the other hand, the low ionization Mg II line shows a blueshift of 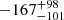− 167 − 101 + 98 $ -167^{+98}_{-101} $ km s−1. From the NIRSpec spectrum, we find that the Hα emission is blueshifted of ΔvHα = −149 ± 7 km s−1while the Hβ line is redshifted of ΔvHβ = 87 ± 15 km s−1. Shen et al. (2011) found no significant offset in Hα and Hβ relative to the narrow [O III] and [S II] lines in their SDSS DR7 sample of quasars. The overall small shifts found for the Mg II and Balmer lines in PJ308-21 suggest that the clouds these lines originate from are mostly dominated by virial motion around the black hole rather than outflowing material (Gaskell & Goosmann 2013), which is a required assumption for the validity of the single-epoch black hole mass estimates presented in Sect. 4.1. We also estimate the velocity shift of the [O III] broad components, which is commonly used as a tracer of ionized outflows (e.g., Cano-Díaz et al. 2012; Harrison et al. 2012, 2014; Carniani et al. 2015; Zakamska et al. 2016; Loiacono et al. 2019; Tozzi et al. 2021). These outflows are often found to extend to kpc-scales, well beyond the nuclear region, and thus can affect the host galaxy and its gas content. As discussed in Sect. 3.2, we fit the [O III] emission using four Gaussian functions, two narrow and two broad, with the former centered on the systemic velocity of the system (Fig. 5, left). The [O III] λ5007 broad line is blueshifted by Δv[O III] = −1922 ± 39 km s−1 relative to the systemic velocity traced by [C II]. The FWHM of the same line is FWHM([O III]) = 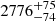2776 − 74 + 75 $ 2776^{+75}_{-74} $ km s−1. While this suggests significant outflowing ionized gas from the NLR of the quasar (see Fig. 8), we highlight that the [O III] modeling in this source is quite challenging, as this emission is strongly blended with the Hβ and iron lines from the BLR. This makes the errors on Δv[O III] and FWHM([O III]) likely underestimated. Strong blueshifted [O III] emission was also found in two out of z > 6.5 quasars studied by Yang et al. (2023). In their case, the velocity offsets are lower at ∼ − 630 km s−1 and ∼ − 1690 km s−1, and FWHM ∼ 1461 km s−1 and ∼3805 km s−1.

thumbnail Fig. 8.

Emission from the Hα and Hβ BLR lines, and the [O III] λ5007 broad component as a function of the velocity. Both the subtracted-data (solid lines) and the fitted models (semitransparent thick curves) are shown. The systemic velocity, set by the vertical gray line, is based on the [C II] redshift. The Hα and Hβ lines are offset of a small amount compared to the zero-reference point (ΔvHα = −149 ± 7 km s−1 and ΔvHβ = 87 ± 15 km s−1). On the other hand, the [O III] λ5007 broad component shows a velocity blueshift of Δv[O III] = −1922 ± 39 km s−1 and a FWHM([O III]) = 2776 − 74 + 75 $ 2776^{+75}_{-74} $ km s−1. This blueshifted emission highlights possible outflowing material from the quasar host galaxy.

High-velocity outflows in high-z sources are predicted by models to play a role in regulating both the black hole and galaxy growth (e.g., Di Matteo et al. 2005; Hopkins et al. 2016; Weinberger et al. 2017; Costa et al. 2022; Lupi et al. 2022). At intermediate and low redshift, several studies using optical/NIR, far-infrared, and submillimeter and millimeter facilities assessed the role of outflows in shaping the AGN host galaxies (e.g., Feruglio et al. 2010; Sturm et al. 2011; Liu et al. 2013; Zakamska & Greene 2014; Brusa et al. 2015a; Cresci et al. 2015; Nardini et al. 2015; Bischetti et al. 2017; Fiore et al. 2017; González-Alfonso et al. 2017). Outflows have been detected in only a small number of z ∼ 6 quasars (Stanley et al. 2019; Bischetti et al. 2022; Butler et al. 2023; Salak et al. 2024) and in some cases their presence is ambiguous (Maiolino et al. 2012; Cicone et al. 2015; Meyer et al. 2022a). The first JWST results suggest the existence of strong [O III] outflows at z > 6 for the first time, demonstrating the capabilities of JWST in detecting these features at the end of Reionization. With the uncertainties in mind, PJ308-21 shows remarkably large velocity offset and FWHM of the [O III] emission, significantly higher than typical values at lower redshift (Liu et al. 2013; Rodríguez Zaurín et al. 2013; Brusa et al. 2015b; Perna et al. 2015; Harrison et al. 2016; Bischetti et al. 2017).

Unfortunately, we cannot estimate the size of the outflowing [O III] component from the IFU data as it is outshone by the quasar emission. This quantity would enable indeed an estimate of the mass outflow rate, that is, the amount of ionized gas expelled per time unit (e.g., Cano-Díaz et al. 2012; Carniani et al. 2015). However, after PSF subtraction, Decarli et al. (2024) find a possible redshifted component located above the host galaxy, extending to the northwest with much lower velocity (∼115 km s−1), which may trace the receding cone of the outflow and can be related to the Lyman α nebula enshrouding the quasar Farina et al. (2022). Farina et al. (in prep.) will discuss this component in greater detail.

5. Conclusions

We presented the JWST/NIRSpec IFU spectrum of the z ∼ 6.23 quasar PJ308-21. The NIRSpec dataset shows the rest-frame optical emission in the 4000 − 7300 Å range. We briefly summarize the main results of this paper:

(i) We estimate the black hole mass using the Hβ and Hα broad lines. We find that PJ308-21 harbors a mature black hole, with MBH, Hβ = (2.7 ± 0.2)×109 M⊙. The Hα-based black hole mass is MBH, Hα = (1.93 ± 0.03)×109 M⊙. The two values are consistent within a factor ≲1.5, within the ∼0.5 dex statistical uncertainties of the mass calibrations. The Hβ value is also consistent with a previous estimate of the black hole mass 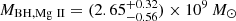M BH , Mg II = ( 2 . 65 − 0.56 + 0.32 ) × 10 9 M ⊙ $ M_{\mathrm{BH, Mg\ II}} = (2.65^{+0.32}_{-0.56}) \times 10^{9}\,M_{\odot} $ derived by Farina et al. (2022) using the Mg II line. All the estimates are consistent with the C IV based black hole mass by Farina et al. (2022).

(ii) PJ308-21 shows a high Eddington ratio 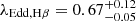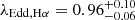λ Edd , H β = 0 . 67 − 0.05 + 0.12 $ \lambda_{\mathrm{Edd, H\beta}} = 0.67^{+0.12}_{-0.05} $ ( λ Edd , H α = 0 . 96 − 0.06 + 0.10 $ \lambda_{\mathrm{Edd, H\alpha}} = 0.96^{+0.10}_{-0.06} $), in line with the population of z ≳ 6 quasars (see Farina et al. 2022; Yang et al. 2023).

(iii) PJ308-21 shows values of EW(O III] and RFe II similar to those of low-z (Shen et al. 2011) and intermediate redshift quasars (1.5 < z < 3.5, Shen 2016). The same holds for the HβFWHM and RFe II anticorrelation (“2D EV1”).

(iv) We find evidence of a blueshifted and broad [O III] component, with a velocity shift Δv[O III]  =   − 1922 ± 39 km s−1 relative to the [C II]-based systemic velocity, and a FWHM([O III]) = 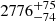2776 − 74 + 75 $ 2776^{+75}_{-74} $ km s−1. Both the FWHM and Δv[O III] are larger than in quasars at lower redshift. Despite the uncertainties affecting the line fitting, this could be one of the first detections of an [O III] outflow from a z ≳ 6 quasar.

Our study demonstrates the unique capabilities of JWST/NIRSpec in dissecting the emission from quasars at z ≳ 6 with modest amounts of telescope time (∼1.5 h on source in our case). Future NIRSpec campaigns on larger samples will be crucial to unveiling new and unparalleled insights on the quasar population at cosmic dawn.

1

We also tested the procedure on another unresolved source, IRAS 05248-7007, which was observed with the G395H/F290LP grating/filter setup in the NIRSpec calibration program 1492 (PI: T. Beck). For apertures of 0.3″ − 0.7″ we obtain flux fractions that differ from the values reported in Table 1 by less than 1%.

Acknowledgments

We thank the referee for their useful comments. L.F. acknowledges support from the INAF 2023 mini-grant “Exploiting the powerful capabilities of JWST/NIRSpec to unveil the distant Universe”. L.F. and R.D. acknowledge support from the INAF GO 2022 grant “The birth of the giants: JWST sheds light on the build-up of quasars at cosmic dawn”. L.B. acknowledges support from NSF award 2307171. SEIB is supported by the Deutsche Forschungsgemeinschaft (DFG) under Emmy Noether grant number BO 5771/1-1. R.A.M. acknowledges support from the Swiss National Science Foundation (SNSF) through project grant 200020_207349. A.P. acknowledges support from Fondazione Cariplo grant no. 2020-0902. J.T.S. is supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project number 518006966. B.T. acknowledges support from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement number 950533), and the Israel Science Foundation (grant number 1849/19). M.T. acknowledges support from the NWO grant 016.VIDI.189.162 (“ODIN”). M.V. gratefully acknowledges financial support from the Independent Research Fund Denmark via grant number DFF 8021-00130. This work is based on observations made with the NASA/ESA/CSA JamesWebb Space Telescope. The data were obtained from the Mikulski Archive for Space Telescopes at the Space Telescope Science Institute, which is operated by the Asssociation of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-03127 for JWST. These observations are associated with the GO program 1554.

References

  1. Aravena, M., Decarli, R., Walter, F., et al. 2016, ApJ, 833, 71 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bañados, E., Venemans, B. P., Decarli, R., et al. 2016, ApJS, 227, 11 [Google Scholar]
  3. Bentz, M. C., Walsh, J. L., Barth, A. J., et al. 2009, ApJ, 705, 199 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bischetti, M., Piconcelli, E., Vietri, G., et al. 2017, A&A, 598, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bischetti, M., Feruglio, C., D’Odorico, V., et al. 2022, Nature, 605, 244 [NASA ADS] [CrossRef] [Google Scholar]
  6. Böker, T., Arribas, S., Lützgendorf, N., et al. 2022, A&A, 661, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Borisova, E., Cantalupo, S., Lilly, S. J., et al. 2016, ApJ, 831, 39 [Google Scholar]
  8. Boroson, T. A., & Green, R. F. 1992, ApJS, 80, 109 [Google Scholar]
  9. Bosman, S. E. I., Álvarez-Márquez, J., Colina, L., et al. 2023, arXiv e-prints [arXiv:2307.14414] [Google Scholar]
  10. Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2015, ApJ, 803, 34 [Google Scholar]
  11. Brusa, M., Feruglio, C., Cresci, G., et al. 2015a, A&A, 578, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Brusa, M., Bongiorno, A., Cresci, G., et al. 2015b, MNRAS, 446, 2394 [NASA ADS] [CrossRef] [Google Scholar]
  13. Butler, K. M., van der Werf, P. P., Topkaras, T., et al. 2023, ApJ, 944, 134 [NASA ADS] [CrossRef] [Google Scholar]
  14. Calura, F., Gilli, R., Vignali, C., et al. 2014, MNRAS, 438, 2765 [NASA ADS] [CrossRef] [Google Scholar]
  15. Cano-Díaz, M., Maiolino, R., Marconi, A., et al. 2012, A&A, 537, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Carniani, S., Marconi, A., Maiolino, R., et al. 2015, A&A, 580, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Cicone, C., Maiolino, R., Gallerani, S., et al. 2015, A&A, 574, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Coatman, L., Hewett, P. C., Banerji, M., et al. 2017, MNRAS, 465, 2120 [Google Scholar]
  19. Connor, T., Bañados, E., Stern, D., et al. 2019, ApJ, 887, 171 [Google Scholar]
  20. Costa, T., Arrigoni Battaia, F., Farina, E. P., et al. 2022, MNRAS, 517, 1767 [NASA ADS] [CrossRef] [Google Scholar]
  21. Cresci, G., Mainieri, V., Brusa, M., et al. 2015, ApJ, 799, 82 [Google Scholar]
  22. Decarli, R., Walter, F., Venemans, B. P., et al. 2017, Nature, 545, 457 [Google Scholar]
  23. Decarli, R., Walter, F., Venemans, B. P., et al. 2018, ApJ, 854, 97 [Google Scholar]
  24. Decarli, R., Dotti, M., Bañados, E., et al. 2019, ApJ, 880, 157 [Google Scholar]
  25. Decarli, R., Pensabene, A., Venemans, B., et al. 2022, A&A, 662, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Decarli, R., Pensabene, A., Diaz-Santos, T., et al. 2023, A&A, 673, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Decarli, R., Loiacono, F., Farina, E. P., et al. 2024, A&A, submitted [Google Scholar]
  28. De Rosa, G., Venemans, B. P., Decarli, R., et al. 2014, ApJ, 790, 145 [Google Scholar]
  29. De Rosa, G., Fausnaugh, M. M., Grier, C. J., et al. 2018, ApJ, 866, 133 [NASA ADS] [CrossRef] [Google Scholar]
  30. Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [Google Scholar]
  31. Ding, X., Onoue, M., Silverman, J. D., et al. 2023, Nature, 621, 51 [NASA ADS] [CrossRef] [Google Scholar]
  32. Drake, A. B., Farina, E. P., Neeleman, M., et al. 2019, ApJ, 881, 131 [CrossRef] [Google Scholar]
  33. Eilers, A.-C., Simcoe, R. A., Yue, M., et al. 2023, ApJ, 950, 68 [CrossRef] [Google Scholar]
  34. Fan, X., Bañados, E., & Simcoe, R. A. 2023, ARA&A, 61, 373 [NASA ADS] [CrossRef] [Google Scholar]
  35. Farina, E. P., Venemans, B. P., Decarli, R., et al. 2017, ApJ, 848, 78 [NASA ADS] [CrossRef] [Google Scholar]
  36. Farina, E. P., Arrigoni-Battaia, F., Costa, T., et al. 2019, ApJ, 887, 196 [Google Scholar]
  37. Farina, E. P., Schindler, J.-T., Walter, F., et al. 2022, ApJ, 941, 106 [NASA ADS] [CrossRef] [Google Scholar]
  38. Feruglio, C., Maiolino, R., Piconcelli, E., et al. 2010, A&A, 518, L155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Fiore, F., Feruglio, C., Shankar, F., et al. 2017, A&A, 601, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  41. Gardner, J. P., Mather, J. C., Abbott, R., et al. 2023, PASP, 135, 068001 [NASA ADS] [CrossRef] [Google Scholar]
  42. Gaskell, C. M. 1982, ApJ, 263, 79 [NASA ADS] [CrossRef] [Google Scholar]
  43. Gaskell, C. M., & Goosmann, R. W. 2013, ApJ, 769, 30 [NASA ADS] [CrossRef] [Google Scholar]
  44. González-Alfonso, E., Fischer, J., Spoon, H. W. W., et al. 2017, ApJ, 836, 11 [Google Scholar]
  45. Greene, J. E., & Ho, L. C. 2005, ApJ, 630, 122 [NASA ADS] [CrossRef] [Google Scholar]
  46. Habouzit, M., Volonteri, M., Somerville, R. S., et al. 2019, MNRAS, 489, 1206 [CrossRef] [Google Scholar]
  47. Harikane, Y., Ouchi, M., Shibuya, T., et al. 2018, ApJ, 859, 84 [NASA ADS] [CrossRef] [Google Scholar]
  48. Harrison, C. M., Alexander, D. M., Swinbank, A. M., et al. 2012, MNRAS, 426, 1073 [NASA ADS] [CrossRef] [Google Scholar]
  49. Harrison, C. M., Alexander, D. M., Mullaney, J. R., & Swinbank, A. M. 2014, MNRAS, 441, 3306 [Google Scholar]
  50. Harrison, C. M., Alexander, D. M., Mullaney, J. R., et al. 2016, MNRAS, 456, 1195 [Google Scholar]
  51. Homayouni, Y., Trump, J. R., Grier, C. J., et al. 2020, ApJ, 901, 55 [Google Scholar]
  52. Hopkins, P. F., Torrey, P., Faucher-Giguère, C.-A., Quataert, E., & Murray, N. 2016, MNRAS, 458, 816 [NASA ADS] [CrossRef] [Google Scholar]
  53. Inayoshi, K., Visbal, E., & Haiman, Z. 2020, ARA&A, 58, 27 [NASA ADS] [CrossRef] [Google Scholar]
  54. Izumi, T., Onoue, M., Matsuoka, Y., et al. 2019, PASJ, 71, 111 [CrossRef] [Google Scholar]
  55. Jakobsen, P., Ferruit, P., Alves de Oliveira, C., et al. 2022, A&A, 661, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Jun, H. D., Im, M., Lee, H. M., et al. 2015, ApJ, 806, 109 [CrossRef] [Google Scholar]
  57. Kashino, D., Lilly, S. J., Matthee, J., et al. 2023, ApJ, 950, 66 [CrossRef] [Google Scholar]
  58. Kaspi, S., Maoz, D., Netzer, H., et al. 2005, ApJ, 629, 61 [Google Scholar]
  59. Kaspi, S., Brandt, W. N., Maoz, D., et al. 2021, ApJ, 915, 129 [NASA ADS] [CrossRef] [Google Scholar]
  60. Kim, Y., Im, M., Jeon, Y., et al. 2018, ApJ, 855, 138 [NASA ADS] [CrossRef] [Google Scholar]
  61. Kollatschny, W., & Zetzl, M. 2013, A&A, 549, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Kovačević, J., Popović, L. Č., & Dimitrijević, M. S. 2010, ApJS, 189, 15 [Google Scholar]
  63. Krawczyk, C. M., Richards, G. T., Mehta, S. S., et al. 2013, ApJS, 206, 4 [Google Scholar]
  64. Kurk, J. D., Walter, F., Fan, X., et al. 2007, ApJ, 669, 32 [NASA ADS] [CrossRef] [Google Scholar]
  65. Li, J., Wang, R., Cox, P., et al. 2020, ApJ, 900, 131 [NASA ADS] [CrossRef] [Google Scholar]
  66. Lira, P., Kaspi, S., Netzer, H., et al. 2018, ApJ, 865, 56 [NASA ADS] [CrossRef] [Google Scholar]
  67. Liu, G., Zakamska, N. L., Greene, J. E., Nesvadba, N. P. H., & Liu, X. 2013, MNRAS, 436, 2576 [NASA ADS] [CrossRef] [Google Scholar]
  68. Loiacono, F., Talia, M., Fraternali, F., et al. 2019, MNRAS, 489, 681 [Google Scholar]
  69. Lupi, A., Volonteri, M., Decarli, R., Bovino, S., & Silk, J. 2022, MNRAS, 510, 5760 [NASA ADS] [CrossRef] [Google Scholar]
  70. Maiolino, R., Gallerani, S., Neri, R., et al. 2012, MNRAS, 425, L66 [Google Scholar]
  71. Marshall, M. A., Perna, M., Willott, C. J., et al. 2023, A&A, 678, A191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Marziani, P., del Olmo, A., Martínez-Carballo, M. A., et al. 2019, A&A, 627, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Matsuoka, Y., Onoue, M., Kashikawa, N., et al. 2019, ApJ, 872, L2 [Google Scholar]
  74. Mazzucchelli, C., Bañados, E., Decarli, R., et al. 2017a, ApJ, 834, 83 [NASA ADS] [CrossRef] [Google Scholar]
  75. Mazzucchelli, C., Bañados, E., Venemans, B. P., et al. 2017b, ApJ, 849, 91 [Google Scholar]
  76. Mazzucchelli, C., Bischetti, M., D’Odorico, V., et al. 2023, A&A, 676, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Meyer, R. A., Bosman, S. E. I., & Ellis, R. S. 2019, MNRAS, 487, 3305 [Google Scholar]
  78. Meyer, R. A., Walter, F., Cicone, C., et al. 2022a, ApJ, 927, 152 [NASA ADS] [CrossRef] [Google Scholar]
  79. Meyer, R. A., Decarli, R., Walter, F., et al. 2022b, ApJ, 927, 141 [NASA ADS] [CrossRef] [Google Scholar]
  80. Murray, N., & Chiang, J. 1995, ApJ, 454, L105 [NASA ADS] [Google Scholar]
  81. Nardini, E., Reeves, J. N., Gofford, J., et al. 2015, Science, 347, 860 [Google Scholar]
  82. Neeleman, M., Bañados, E., Walter, F., et al. 2019, ApJ, 882, 10 [Google Scholar]
  83. Neeleman, M., Novak, M., Venemans, B. P., et al. 2021, ApJ, 911, 141 [NASA ADS] [CrossRef] [Google Scholar]
  84. Novak, M., Bañados, E., Decarli, R., et al. 2019, ApJ, 881, 63 [NASA ADS] [CrossRef] [Google Scholar]
  85. Onoue, M., Kashikawa, N., Matsuoka, Y., et al. 2019, ApJ, 880, 77 [Google Scholar]
  86. Onoue, M., Bañados, E., Mazzucchelli, C., et al. 2020, ApJ, 898, 105 [Google Scholar]
  87. Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (Sausalito, CA: University Science Books) [Google Scholar]
  88. Ota, K., Iye, M., Kashikawa, N., et al. 2017, ApJ, 844, 85 [Google Scholar]
  89. Pennell, A., Runnoe, J. C., & Brotherton, M. S. 2017, MNRAS, 468, 1433 [NASA ADS] [CrossRef] [Google Scholar]
  90. Pensabene, A., Carniani, S., Perna, M., et al. 2020, A&A, 637, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Pensabene, A., Decarli, R., Bañados, E., et al. 2021, A&A, 652, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Perna, M., Brusa, M., Cresci, G., et al. 2015, A&A, 574, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Perna, M., Arribas, S., Marshall, M., et al. 2023, A&A, 679, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Peterson, B. M. 1997, An Introduction to Active Galactic Nuclei (Cambridge, New York: Cambridge University Press), 238 [Google Scholar]
  95. Pons, E., McMahon, R. G., Simcoe, R. A., et al. 2019, MNRAS, 484, 5142 [NASA ADS] [CrossRef] [Google Scholar]
  96. Rauscher, B. J. 2024, PASP, 136, 015001 [CrossRef] [Google Scholar]
  97. Reed, S. L., Banerji, M., Becker, G. D., et al. 2019, MNRAS, 487, 1874 [Google Scholar]
  98. Richards, G. T., Vanden Berk, D. E., Reichard, T. A., et al. 2002, AJ, 124, 1 [NASA ADS] [CrossRef] [Google Scholar]
  99. Richards, G. T., Lacy, M., Storrie-Lombardi, L. J., et al. 2006, ApJS, 166, 470 [Google Scholar]
  100. Rigby, J. R., Lightsey, P. A., García Marín, M., et al. 2023, PASP, 135, 048002 [NASA ADS] [CrossRef] [Google Scholar]
  101. Rodríguez Zaurín, J., Tadhunter, C. N., Rose, M., & Holt, J. 2013, MNRAS, 432, 138 [CrossRef] [Google Scholar]
  102. Runnoe, J. C., Ganguly, R., Brotherton, M. S., & DiPompeo, M. A. 2013, MNRAS, 433, 1778 [NASA ADS] [CrossRef] [Google Scholar]
  103. Saccheo, I., Bongiorno, A., Piconcelli, E., et al. 2023, A&A, 671, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Salak, D., Hashimoto, T., Inoue, A. K., et al. 2024, ApJ, 962, 1 [NASA ADS] [CrossRef] [Google Scholar]
  105. Salmon, B., Papovich, C., Finkelstein, S. L., et al. 2015, ApJ, 799, 183 [NASA ADS] [CrossRef] [Google Scholar]
  106. Schindler, J.-T., Farina, E. P., Bañados, E., et al. 2020, ApJ, 905, 51 [Google Scholar]
  107. Shao, Y., Wang, R., Weiss, A., et al. 2022, A&A, 668, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  108. Shapovalova, A. I., Popović, L. Č., Burenkov, A. N., et al. 2012, ApJS, 202, 10 [NASA ADS] [CrossRef] [Google Scholar]
  109. Shen, Y. 2013, Bull Astron. Soc. India, 41, 61 [NASA ADS] [Google Scholar]
  110. Shen, Y. 2016, ApJ, 817, 55 [NASA ADS] [CrossRef] [Google Scholar]
  111. Shen, Y., & Ho, L. C. 2014, Nature, 513, 210 [NASA ADS] [CrossRef] [Google Scholar]
  112. Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [Google Scholar]
  113. Shen, Y., Wu, J., Jiang, L., et al. 2019, ApJ, 873, 35 [Google Scholar]
  114. Stanley, F., Jolly, J. B., König, S., & Knudsen, K. K. 2019, A&A, 631, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  115. Sturm, E., González-Alfonso, E., Veilleux, S., et al. 2011, ApJ, 733, L16 [NASA ADS] [CrossRef] [Google Scholar]
  116. Sulentic, J. W., Stirpe, G. M., Marziani, P., et al. 2004, A&A, 423, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  117. Sulentic, J. W., Repetto, P., Stirpe, G. M., et al. 2006, A&A, 456, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  118. Tozzi, G., Cresci, G., Marasco, A., et al. 2021, A&A, 648, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  119. Tozzi, G., Maiolino, R., Cresci, G., et al. 2023, MNRAS, 521, 1264 [NASA ADS] [CrossRef] [Google Scholar]
  120. Tripodi, R., Feruglio, C., Fiore, F., et al. 2022, A&A, 665, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  121. Vanden Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [Google Scholar]
  122. Vanzella, E., Fontana, A., Zitrin, A., et al. 2014, ApJ, 783, L12 [NASA ADS] [CrossRef] [Google Scholar]
  123. Venemans, B. P., Walter, F., Zschaechner, L., et al. 2016, ApJ, 816, 37 [Google Scholar]
  124. Venemans, B. P., Walter, F., Decarli, R., et al. 2017, ApJ, 851, L8 [NASA ADS] [CrossRef] [Google Scholar]
  125. Venemans, B. P., Decarli, R., Walter, F., et al. 2018, ApJ, 866, 159 [Google Scholar]
  126. Vestergaard, M., & Osmer, P. S. 2009, ApJ, 699, 800 [Google Scholar]
  127. Vestergaard, M., & Peterson, B. M. 2006, ApJ, 641, 689 [Google Scholar]
  128. Vietri, G., Piconcelli, E., Bischetti, M., et al. 2018, A&A, 617, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  129. Volonteri, M., Habouzit, M., & Colpi, M. 2021, Nat. Rev. Phys., 3, 732 [NASA ADS] [CrossRef] [Google Scholar]
  130. Walter, F., Bertoldi, F., Carilli, C., et al. 2003, Nature, 424, 406 [Google Scholar]
  131. Walter, F., Riechers, D., Novak, M., et al. 2018, ApJ, 869, L22 [NASA ADS] [CrossRef] [Google Scholar]
  132. Walter, F., Neeleman, M., Decarli, R., et al. 2022, ApJ, 927, 21 [NASA ADS] [CrossRef] [Google Scholar]
  133. Wang, R., Wagg, J., Carilli, C. L., et al. 2008, AJ, 135, 1201 [NASA ADS] [CrossRef] [Google Scholar]
  134. Wang, F., Yang, J., Fan, X., et al. 2021, ApJ, 907, L1 [Google Scholar]
  135. Wang, F., Yang, J., Hennawi, J. F., et al. 2023, ApJ, 951, L4 [NASA ADS] [CrossRef] [Google Scholar]
  136. Weinberger, R., Springel, V., Hernquist, L., et al. 2017, MNRAS, 465, 3291 [Google Scholar]
  137. Willott, C. J., Albert, L., Arzoumanian, D., et al. 2010, AJ, 140, 546 [NASA ADS] [CrossRef] [Google Scholar]
  138. Willott, C. J., Omont, A., & Bergeron, J. 2013, ApJ, 770, 13 [NASA ADS] [CrossRef] [Google Scholar]
  139. Willott, C. J., Bergeron, J., & Omont, A. 2015, ApJ, 801, 123 [NASA ADS] [CrossRef] [Google Scholar]
  140. Willott, C. J., Bergeron, J., & Omont, A. 2017, ApJ, 850, 108 [Google Scholar]
  141. Yang, J., Wang, F., Fan, X., et al. 2021, ApJ, 923, 262 [NASA ADS] [CrossRef] [Google Scholar]
  142. Yang, J., Wang, F., Fan, X., et al. 2023, ApJ, 951, L5 [NASA ADS] [CrossRef] [Google Scholar]
  143. Yue, M., Eilers, A. C., Simcoe, R. A., et al. 2023, ApJ, submitted [arXiv:2309.04614] [Google Scholar]
  144. Zakamska, N. L., & Greene, J. E. 2014, MNRAS, 442, 784 [Google Scholar]
  145. Zakamska, N. L., Hamann, F., Pâris, I., et al. 2016, MNRAS, 459, 3144 [NASA ADS] [CrossRef] [Google Scholar]
  146. Zana, T., Carniani, S., Prelogović, D., et al. 2023, A&A, 679, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  147. Zuo, W., Wu, X.-B., Fan, X., et al. 2020, ApJ, 896, 40 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Aperture correction

thumbnail Fig. A.1.

Aperture correction from the GSPC P330-E 220 G–dwarf. Left panel: flux fraction as a function of the aperture radius (NIRSpec/IFU, G395H/F290LP), that is, the cumulative PSF. Note that the PSF width increases going from blue to red wavelengths. The differences are larger for small radii, as the PSF profile is steeper. The curves are based on observations of the G-dwarf GSPC P330-E used for a Cycle 1 calibration program (ID: 1538). Right panel: Flux fractions for apertures with radii R = 0.1″ − 0.7″ as a function of the observed wavelength (NIRSpec/IFU, G395H/F290LP). The second-order spline fitted to the data is shown in yellow. The flux fraction decreases with increasing wavelength, especially at small radii.

All Tables

Table 1.

Flux fraction for fixed aperture radius R as a function of the wavelength (NIRSpec/IFU, G395H/F290LP).

In the text
Table 2.

Continuum and iron fitted parameters.

In the text
Table 3.

Emission-line fitted parameters.

In the text
Table 4.

Physical quantities of PJ308-21 derived from line fitting.

In the text

All Figures

thumbnail Fig. 1.

Scheme of the data reduction process for the NIRSpec data of PJ308-21. The data reduction is divided into three stages, each of them consisting of several steps. Stage 1 is independent from the JWST instrument and mode, unlike stage 2 and 3, for which we present the steps for NIRSpec/IFU. We skip some pipeline steps (boxes with gray tilted lines) and introduce additional steps (orange boxes) to improve the data reduction (see Sect. 2).
In the text
thumbnail Fig. 2.

PJ308-21 system. The quasar has two companion sources, located to the western and eastern sides of the quasar, respectively. We show the Hα and the underlying continuum emission from the NIRSpec/IFU data (magenta) overimposed on the [C II] emission from ALMA high-resolution data (blue; Decarli et al. 2019). The yellow cross and circle show the aperture for the spectrum extraction (see Sect. 3.1).
In the text
thumbnail Fig. 3.

Rest-frame UV/optical spectroscopic and photometric data of PJ308-21. The main emission lines are indicated. The aperture-corrected NIRSpec spectrum is shown in red (see Sect. 3.1). The purple and blue lines show MUSE and X-shooter spectra from previous works (Farina et al. 2019; Schindler et al. 2020). We show in gray the X-shooter data affected by the atmosphere absorption. The photometric data from Pan-STARRS1 (PS1; g, r, i, z, Y bands), GROND (i, z, J bands), VHS (Y, H, K bands), Spitzer (Ch1 = 3.5 μm, Ch2 = 4.5 μm), and WISE (W1 = 3.3 μm, W2 = 4.6 μm) are shown with the associated errors (Bañados et al. 2016).
In the text
thumbnail Fig. 4.

JWST/NIRSpec rest-frame optical spectrum of the PJ308-21 quasar (black). Broad Balmer line emission (Hα, Hβ, Hγ, Hδ), strong Fe II, and [O III] emission is clearly seen. Top panel: quasar continuum fit (magenta curve). We highlight the line-free regions used for the continuum fit (pale blue). The orange curve shows the residuals. Bottom panel: Fe II line model (magenta). The fitted wavelengths are highlighted in pale blue. We fit the Fe II emission using the five multiplets template of Kovačević et al. (2010) and Shapovalova et al. (2012) (colored lines in the insets). The iron-subtracted spectrum (orange) was then used to fit the Balmer and nebular lines.
In the text
thumbnail Fig. 5.

Fit of the Hβ + [O III] (left) and Hα + [N II] lines (right), after the continuum and iron subtraction. We modeled the BLR Hβ and Hα lines using two Lorentzian functions (one for each line). The nebular lines from the NLR ([O III], [N II], Hα, and Hβ narrow components) were each fitted with a Gaussian. We added two further Gaussian components (purple; “broad” components in the paper) to fit the emission around 5000 Å, likely associated with blueshifted [O III] (see also Sect. 4.4 and Fig. 8). The residuals are shown in orange.
In the text
thumbnail Fig. 6.

Black hole masses from SDSS (Shen et al. 2011) and z > 6 quasars (Bosman et al. 2023; Eilers et al. 2023; Marshall et al. 2023; Yang et al. 2023; Yue et al. 2023), with both Mg II and Balmer line based measurements. The green line shows the one-to-one relation. PJ308-21 is indicated with blue diamonds (NIRSpec and X-shooter data). Overall, the z > 6 quasars show nice agreement between the Mg II and Hβ or Hα-based MBH, consistent with the ∼0.5 dex scatter of the low-redshift estimates (green region; Vestergaard & Peterson 2006). While a larger sample is needed to confirm these results, these first JWST estimates suggest that the Mg II is a reliable tracer of the black hole mass at both low and high-redshift.
In the text
thumbnail Fig. 7.

Anticorrelations between the Fe II strength, parametrized by RFe II, the [O III] EW, and HβFWHM. Top panel: the anticorrelation between RFe II and EW[O III] (EV1 relation). PJ308-21 (blue diamond) shows a value in agreement with both low-redshift (Shen et al. 2011), 1.5 < z < 3.5 (Shen 2016) and z > 6 quasars (Yang et al. 2023). Bottom panel: anticorrelation between RFe II and FWHM(Hβ) (2D EV1). Also in this case, the PJ308-21 value appears consistent with the findings of other studies.
In the text
thumbnail Fig. 8.

Emission from the Hα and Hβ BLR lines, and the [O III] λ5007 broad component as a function of the velocity. Both the subtracted-data (solid lines) and the fitted models (semitransparent thick curves) are shown. The systemic velocity, set by the vertical gray line, is based on the [C II] redshift. The Hα and Hβ lines are offset of a small amount compared to the zero-reference point (ΔvHα = −149 ± 7 km s−1 and ΔvHβ = 87 ± 15 km s−1). On the other hand, the [O III] λ5007 broad component shows a velocity blueshift of Δv[O III] = −1922 ± 39 km s−1 and a FWHM([O III]) = 2776 − 74 + 75 $ 2776^{+75}_{-74} $ km s−1. This blueshifted emission highlights possible outflowing material from the quasar host galaxy.
In the text
thumbnail Fig. A.1.

Aperture correction from the GSPC P330-E 220 G–dwarf. Left panel: flux fraction as a function of the aperture radius (NIRSpec/IFU, G395H/F290LP), that is, the cumulative PSF. Note that the PSF width increases going from blue to red wavelengths. The differences are larger for small radii, as the PSF profile is steeper. The curves are based on observations of the G-dwarf GSPC P330-E used for a Cycle 1 calibration program (ID: 1538). Right panel: Flux fractions for apertures with radii R = 0.1″ − 0.7″ as a function of the observed wavelength (NIRSpec/IFU, G395H/F290LP). The second-order spline fitted to the data is shown in yellow. The flux fraction decreases with increasing wavelength, especially at small radii.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.