EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 685 (May 2024) A&A, 685 (2024) A72 Full HTML
Open Access
Issue
A&A
Volume 685, May 2024
Article Number A72
Number of page(s) 7
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/202348209
Published online 07 May 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Disks are almost ubiquitous in the star-forming galaxy (SFG) population of the local Universe. Somewhat surprisingly, recent observations (Ferreira et al. 2022; Kartaltepe et al. 2023; Robertson et al. 2023; Tohill et al. 2024; Pandya et al. 2024) using the James Webb Space Telescope (JWST) have unveiled their presence, in particular, in high stellar mass galaxies, even in the earliest epochs of the Universe, reaching back to z ∼ 9. However, these early disks might exhibit distinct dynamical characteristics when compared to their local counterparts.

Extensive observations with the kiloparsec-scale near-infrared Integral-Field-Unit (IFU) of SFGs around cosmic noon (1 ≤ z ≤ 3, e.g., Law et al. 2009; Stott et al. 2016; Förster Schreiber et al. 2018; Mieda et al. 2016; Mason et al. 2017; Turner et al. 2017; Wisnioski et al. 2019; Birkin et al. 2023) have found a significant increase in the gas velocity dispersion (∼50 − 100 km s−1) compared to local SFG values (∼20 − 25 km s−1, Andersen et al. 2006; Epinat et al. 2010). Notably, the rotation-to-dispersion ratio (Vrot/σ) for cosmic-noon disks typically falls in the range 1 − 10 (Law et al. 2009; Gnerucci et al. 2011; Genzel et al. 2011; Johnson et al. 2018; Birkin et al. 2023), in contrast to the value of 10 − 20 observed in Milky Way and other local spiral disks (Epinat et al. 2010). As a result, a significant conclusion drawn by these studies was that SFGs become dynamically hotter, featuring substantial pressure support, toward high-z.

In recent years, significant progress has been made in characterizing the dynamics of normal SFGs during cosmic high noon (3 ≤ z ≤ 6) and even into the epoch of reionization (EoR: z > 6) through far-infrared (FIR) emission line observations, in particular, [C II]-158 μm with the Atacama Large Millimeter/Submillimetre Array (ALMA; Jones et al. 2017; Smit et al. 2018; Bakx et al. 2020; Hashimoto et al. 2019; Harikane et al. 2020; Herrera-Camus et al. 2022; Le Fèvre et al. 2020; Romano et al. 2021; Fujimoto et al. 2021; Tokuoka et al. 2022; Parlanti et al. 2023; Posses et al. 2023). The estimated value of Vrot/σ for these galaxies falls in the ∼1 − 7.5 range. However, these observations are only marginally resolved, leading to a potential underestimate of Vrot/σ caused by beam-smearing effects (Kohandel et al. 2020; Rizzo et al. 2022).

Recent breakthrough observations (Rizzo et al. 2020; Lelli et al. 2021; Rizzo et al. 2021; Tsukui & Iguchi 2021; Roman-Oliveira et al. 2023) achieved a higher spatial resolution and sensitivity, robustly characterizing the dynamics of early galaxies. Massive, dusty starburst galaxies (M⋆ > 1010 M⊙) at z > 4 exhibit disk structures with Vrot/σ ∼ 10. Moreover, Pope et al. 2023 have recently revealed stable rotation-dominated disks (Vrot/σ = 5.3 ± 3.6) in relatively low-mass galaxies (M⋆ ∼ 109 M⊙) during cosmic high noon. Adding to this remarkable progress, Rowland et al. (in prep.) have recently discovered the most distant (z ∼ 7) massive (M⋆ > 1010 M⊙) dynamically cold disk (Vrot/σ ∼ 10) in REBELS-25 as part of an ALMA large program (Bouwens et al. 2022).

Finally, JWST/NIRspec multi-object spectroscopy of Hα and [O III] emission lines has started to shed light on the kinematics of ionized gas in EoR galaxies (de Graaff et al. 2024; Parlanti et al. 2024), indicating that early galaxies can settle into dynamically cold disks. This is somewhat surprising in contrast to previous findings from Hα surveys at cosmic noon (e.g. Wisnioski et al. 2019). Despite this progress, the statistical relevance of DCDs in early SFGs is uncertain because only a few deep spatially resolved observations are available.

From a theoretical standpoint, most studies (Dekel & Burkert 2014; Zolotov et al. 2015; Hayward & Hopkins 2017; Pillepich et al. 2019) struggle to explain the existence of DCDs at z > 4. For instance, TNG50 (Pillepich et al. 2019) showed an average Vrot/σ < 3 at z = 4, similarly to most cosmological simulations. Nonetheless, a few studies predicted that relatively massive galaxies (M⋆ ∼ 1010 M⊙) can temporarily sustain cold disks formed through intense accretion of coplanar corotating gas at z > 3 (Kretschmer et al. 2022). Kohandel et al. (2020) showed for EoR galaxies that moderate rotation support (Vrot/σ ∼ 7) can be achieved in M⋆ ∼ 1010 M⊙ galaxies as far back as z ∼ 6, but this conclusion was based on a relatively small sample of galaxies.

In this paper, we exploit the SERRA simulations (Pallottini et al. 2022) to investigate the kinematic properties of normal SFGs at 4 < z < 9 through the analysis of mock observations of the [C II] emission line at 158 μm, which is a tracer of cold (T ∼ 100 K) molecular or neutral gas, and of the Hα emission line, which is a tracer of warm (T ∼ 104 K) ionized gas.

2. SERRA simulations

2.1. Galaxy formation and evolution

The SERRA suite of simulations focuses on studying the formation and evolution of galaxies during the EoR (Pallottini et al. 2022). Gas and dark matter are evolved using a customized version of the adaptive mesh refinement code RAMSES (Teyssier 2002). KROME (Grassi et al. 2014) is employed to model the nonequilibrium chemical network that includes H, H+, H−, He, He+, He++, H2, H2+, electrons, and metals, encompassing ∼40 reactions (Bovino et al. 2016; Pallottini et al. 2017a). The tracking of metallicity (Z) involves summing heavy elements, assuming solar abundance ratios for different metal species (Asplund et al. 2009). Dust is approximated to scale with a fixed dust-to-metal ratio, denoted as 𝒟 = 𝒟⊙(Z/Z⊙), where 𝒟⊙/Z⊙ ≃ 0.3 for the Milky Way (Hirashita & Ferrara 2002). A Milky Way-like grain size distribution is adopted (Weingartner & Draine 2001). An initial metallicity floor of Zfloor = 10−3 Z⊙ is adopted, as expected from pre-enrichment of the intergalactic medium around density peaks (Madau et al. 2001; Pallottini et al. 2014a,b).

The conversion of molecular hydrogen into stars follows a Schmidt (1959)–Kennicutt (1998)-like relation (Pallottini et al. 2017a). These stars in turn act as sources of metals, mechanical energy, and radiation (Pallottini et al. 2017b). Feedback processes inject energy in thermal and turbulent (kinetic) forms. The former can cool via the thermo-chemical evolution modeled by KROME, while the latter dissipates (Teyssier et al. 2013) over an eddy turnover timescale (Mac Low 1999). The specific fractions depend on the process and the environment, as discussed in Appendix A of Pallottini et al. (2017b). For instance, supernovae exploding in a low-density medium typically exhibit a contribution of approximately 70% to thermal energy and 30% to turbulent energy during the Sedov-Taylor phase.

The interstellar radiation field (ISRF) is dynamically evolved on the fly using the moment-based solver from RAMSES-RT (Rosdahl et al. 2013), which is linked to the chemical evolution (Pallottini et al. 2019; Decataldo et al. 2019). To efficiently model radiation propagation, the speed of light is reduced by a factor of 103 in SERRA, leading to negligible deviations compared to a 102 reduction (Pallottini et al. 2019; Lupi et al. 2020). Simulations track radiation in five energy bins, with one bin partially covering the Habing band (6.0 < hν < 11.2), one bin dedicated to the Lyman-Werner band (11.2 < hν < 13.6) to address H2 photoevaporation, and the remaining three bins covering ionization processes from H to the first ionization level of He (13.6 < hν < 24.59).

Each run in the SERRA suite was initialized at z = 100 from cosmological conditions generated with MUSIC (Hahn & Abel 2011), and zoomed in on the target DM halos selected at around z ≃ 6. The cosmic volume considered was (20, Mpc/h)3, and it was evolved with a base grid of eight levels. The zoom-in region had a volume of about (2.1 Mpc/h)3 (approximately five times the virial radius of the target DM halo), and had three additional levels, resulting in a gas-mass resolution of mb = 1.2 × 104 M⊙. Additionally, six refinement levels were enabled in the zoom-in region based on a Lagrangian-like criterion, allowing the simulation to reach scales of lres ≃ 30 pc at z = 6 in the densest regions, similar to Galactic molecular clouds (Federrath & Klessen 2013).

2.2. Hyperspectral data cubes for [CII] and Hα emission lines

In SERRA, gas kinematics analyses involve two crucial postprocessing steps: 1) line emission modeling (Vallini et al. 2017; Pallottini et al. 2019), and 2) the generation of hyperspectral data cubes (HDCS, Kohandel et al. 2019, 2020).

Due to the coarse nature of the chemical network used in hydrodynamical simulations, precise emission computation requires postprocessing of the data to extract kinematic information. The line luminosity (Lem-line) for each gas cell was obtained using the spectral synthesis code CLOUDY (Ferland et al. 2017). This process took the interstellar radiation field into account, which is the turbulent and clumpy structure of the interstellar medium (ISM), which was parameterized as a function of the local gas Mach number (Vallini et al. 2018; Pallottini et al. 2022).

With information on Lem-line, position (x), velocity (v), and thermal+turbulent line broadening (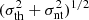) for each gas cell within a specified field of view (FOV)1 and along a line of sight direction, we constructed 3D HDCs. These cubes comprise two spatial dimensions and one spectral dimension, effectively mapping the 6D data to coordinates (x, y, vz). In HDCs, the surface brightness of the emission line is recorded for each voxel, providing valuable insights into the spatial and spectral distribution of the emission. The contribution of all gas cells within the FOV can be directly summed for optically thin emission lines. However, for optically thick lines, radiative transfer through dust needs to be considered when comparing with pre-dereddened observations (Behrens et al. 2018).

We modeled the [C II] 158 μm emission line as a tracer of cold neutral or molecular gas and the nebular Hα emission line as a tracer of warm ionized gas2. Different gas-phase tracers can yield different values of Vrot and σ (Kohandel et al. 2020; Ejdetjärn et al. 2022). We estimated the velocity dispersion of a galaxy separately using two tracers: [C II] observations (σ[CII]), and Hα (σHα). Following a similar approach to that of Kohandel et al. (2020), σem-line represents the luminosity-weighted average velocity dispersion, calculated using the moment-2 and moment-0 maps of the corresponding emission line. For the rotational velocity, we estimated3Vrot with the circular velocities of the galaxy, denoted as vc = (GMdyn/rd)1/2, where Mdyn = Mg + M⋆ is the dynamical mass within the desired FOV4, and rd is the disk effective radius, that is, where 50% of the gas mass is contained. In other words, we kept Vrot constant regardless of the tracer we used. Consequently, any differences observed in Vrot/σ for [C II] and Hα synthetic observations arose due to disparities in σ[CII] and σHα.

We focused on SERRA galaxies that exhibited a stellar mass of 108 M⊙ at least and covered the redshift range 4 ≤ z ≤ 9. Our sample includes 3218 galaxies with SFRs ranging from 0.04 to 128 M⊙yr−1 and stellar masses in 8 ≤ log M⋆/M⊙ ≤ 10.3. We refer to Table 1 for an overview of our sample.

Table 1.

Relevant properties of the simulated sample.

3. Rotation support in early galaxies

In Figs. 1 and 2, we present the kinematic characteristics of our sample within the M⋆-σ and Vrot/σ-z5 planes, respectively. In both cases, σ values were derived from [C II] 158 μm and Hα synthetic observations. In Fig. 2, along with SERRA galaxies, we plot the predictions from TNG50 simulations (Pillepich et al. 2019)6, as well as observed data of z > 4 galaxies through FIR [C II] emission line by ALMA and nebular Hα and [O III] lines by JWST/NIRspec.

thumbnail Fig. 1.

Relation of the velocity dispersion and stellar mass in the SERRA galaxy sample: Blue (red) contours show the 1, 2, and 3-sigma probability density function levels for the M⋆ − σ relation derived from synthetic [C II] (Hα) observations. Individual data points are represented by crosses.

thumbnail Fig. 2.

Redshift evolution of Vrot/σ in SERRA. The three stellar mass bins are distinguished by the line width; blue (red) markers represent σ from [C II] (Hα) synthetic observations. For comparison, predictions from TNG50 simulations (Pillepich et al. 2019) are shown with filled orange markers for z < 5. The gray triangles denote observational data points with [C II] line kinematics, including high-z DCDs (Rizzo et al. 2021; Lelli et al. 2021; Fraternali et al. 2021; Tsukui & Iguchi 2021; Roman-Oliveira et al. 2023; Pope et al. 2023; Rowland et al., in prep.), ALPINE disk galaxies (Jones et al. 2021), archival 4 < z < 7.7 [C II] data (Parlanti et al. 2023), the first discovered EoR disk galaxies (Smit et al. 2018), and the turbulent HZ4 system at z = 5.5 (Herrera-Camus et al. 2022). The gray squares represent data with nebular Hα and [OIII] kinematics (de Graaff et al. 2024; Parlanti et al. 2024). The filled (empty) markers distinguish spatially (barely) resolved observations.

Regarding the M⋆-σ relation, we find two distinct behaviors for the two tracers. Specifically, we find that σHα exhibits a steeper increase with M⋆ than σ[CII]. Interestingly, this trend is particularly pronounced in ∼40% of our high-mass bin galaxies and 30% of those in the intermediate-mass bin, where σHα > 2σ[CII]. This behavior is expected because even surveys of local galaxies (Levy et al. 2018; Girard et al. 2021) have highlighted systematic differences between hot ionized and neutral/molecular cold gas velocity dispersions. This disparity leads to a consistent difference between the results obtained using different tracers in SERRA, indicating that cold gas exhibits a higher degree of rotational support than warm ionized gas (see Table 1 and Fig. 2). We explore this point in more detail in Sect. 4.

As for the Vrot/σ-z, regardless of the kinematic tracer employed, we found no notable correlation even when different mass bins were considered. Nevertheless, a clear trend appears with the stellar mass of galaxies, indicating that most massive galaxies exhibit greater rotation support than the less massive ones. A milder version of this correlation was also predicted in TNG50 for z < 4 galaxies.

The most noteworthy finding of our analysis is that when we classify our galaxies based on their Vrot/σ ratio (as outlined in Table 2), not only do we identify supercold disks (Vrot/σ > 10 similar to SFGs observed at z ∼ 4 (Rizzo et al. 2021; Fraternali et al. 2021) and at z ∼ 7 at Rowland et al. in prep.) within our massive subsample (M⋆ > 1010 M⊙), we also ascertain that [C II] emitting gas in ∼60% of the whole sample is dynamically cold, having 4 < Vrot/σ < 10. This finding suggests that galactic disks can form as early as the EoR, and when deep ALMA observations targeting SFGs at z > 4 become available, more dynamically cold disks will likely be discovered. However, it is essential to note that the dynamical state of the stellar component in high-redshift galaxies may not align with simplistic axisymmetric disks, as indicated by prior HST observations (Ravindranath et al. 2006; van der Wel et al. 2014; Zhang et al. 2019), and as more recently confirmed by JWST observations (Pandya et al. 2024).

Table 2.

Dynamical categorization of SERRA galaxies.

For the majority of galaxies with [C II] observations, Vrot/σ values at z > 5 fall below the predicted mean values from SERRA simulations. This discrepancy can primarily be attributed to the marginal resolution of these observations (∼0.1 − 1.5 arcsecs), compared to our synthetic datacubes featuring a higher spatial resolution of 0.005 arcsecs. In Kohandel et al. (2020), we showed that the beam-smearing effect in low-resolution observations can lead to a substantial overestimate of the velocity dispersion, reaching up to ∼100% (see also Ejdetjärn et al. 2022; Rizzo et al. 2022). Another potential cause of this discrepancy is the challenge of accurately estimating disk inclination in high-z kinematic observations. This becomes crucial when determining kinematic properties, such as the velocity dispersion, from integrated spectra, where the shape is highly correlated with the disk inclination (Kohandel et al. 2019). Finally, galaxy mergers can also obscure disk rotational signatures of galaxies (Simons et al. 2019; Kohandel et al. 2019; Rizzo et al. 2022), further complicating their kinematic identification.

4. Discussion

To better clarify the above findings, we now focus on two representative galaxies in our massive subsample: “Hibiscus” with M⋆ = 1.5 × 1010 M⊙ and SFR = 16 M⊙ yr−1 at z = 4.5 and “Narcissus” with M⋆ = 1.2 × 1010 M⊙ and an SFR = 52 M⊙ yr−1 at z = 6.8. These galaxies have similar [C II] kinematics (i.e., Vrot/σ[CII] > 10), but their Hα kinematics is very different.

4.1. Why [CII] and Hα kinematics are different?

In Fig. 3 we show the synthetic [C II] and Hα maps and kinematics observables for a face-on and edge-on views of Hibiscus. The [C II] spectrum is characterized by a narrow and prominently Gaussian-shaped profile (FWHM ∼ 185 km s−1), while the Hα spectrum appears to be more complex and broader (FWHM ∼ 437 km s−1) and exhibits high-velocity wings. These broad wings in the spectrum might be indicative of outflowing gas. By comparing the moment maps, we see that the [C II] emission line effectively traces the Hibiscus thin gaseous disk, while Hα traces ionized gas that lies beyond the disk plane, including gas that might be in an in- or outflowing state. This difference between various phases of the ISM could conceivably arise because distinct effects of stellar feedback influence them, as suggested by simulations of isolated disk galaxies (Ejdetjärn et al. 2022). This illustrates that the observed velocity dispersion in a given galaxy using Hα data may not solely arise from turbulence within the galactic disks. Instead, a substantial contribution from outflows may be in effect, introducing an additional layer of complexity to the data interpretation.

thumbnail Fig. 3.

Multiwavelength kinematics of “Hibiscus” at z = 4.5. In the top (last) two rows, we display the FIR [C II] 158 μm (nebular Hα) syntactic observation for line spectra, 0, 1, and 2 moment maps in different columns for both face-on and edge-on views.

We note that the spatial extent of the [C II] and Hα emission in Hibiscus differs significantly. The [C II] is four times more extended than the stellar effective radius, similar to observed high-z galaxies (Fujimoto et al. 2019; Carniani et al. 2020; Fudamoto et al. 2022). The Hα distribution is even more far-flung because Hα originates from the T ∼ 104 K photoionized regions outside the disk that are part of an expanding, cooling outflow through which LyC photons percolate. As carbon in these regions is ionized to higher states (e.g., CIII), [C II] emission is limited to denser, more confined regions in which the recombination rates are higher. Interestingly, this shows that Hα halos are intimately linked to the presence and morphology of these outflows, offering intriguing prospects for their detection with JWST.

Finally, it is important to highlight that [C II] kinematics can also be challenging and merits deeper exploration. In particular, observations of the so-called [C II] halos (Gallerani et al. 2018; Fujimoto et al. 2019, 2021; Ginolfi et al. 2020) have been interpreted in the framework of outflow models (Pizzati et al. 2020, 2023), but they have not yet been reproduced by cosmological simulations (Fujimoto et al. 2019; Arata et al. 2020).

4.2. Are high-z dynamically cold disks a transient feature?

To explore the stability of cold disks, we studied the evolutionary path undertaken by individual galaxies in more detail. In Fig. 4 we show the evolution of Vrot/σ as a function of lookback time for Hibiscus and Narcissus. When only [C II] emitting gas is considered, both galaxies exhibit a consistent Vrot/σ around 2 − 4 up until roughly 200 Myr. During this interval, the rotation support rises through the effective accretion of gas and the efficient transfer of angular momentum into the disk. When we estimate the disk orbital time torb = 2πrd/Vrot, it is ∼ 16 Myr for Hibiscus and ∼ 21 Myr for Narcissus. Therefore, these high-z DCDs survive for more than ten orbital times. This characteristic generally holds for massive galaxies in SERRA (see Fig. 3).

thumbnail Fig. 4.

Example of the dynamical evolution of two SERRA galaxies traced by [CII] and Hα. At z = 4.5, Hibiscus (top) has a [CII] dynamically cold disk and a turbulent Hα emitting gas that might feature galactic outflows (see also Fig. 3). At z = 6.8, Narcisuss (bottom) appears as a supercold galaxy in both [C II] and Hα.

Regarding the Vrot/σHα, there is an interesting difference between the two systems. As shown in Fig. 3, the Hα emitting gas is found to be dynamically warm in the last ∼ 200 Myr for Hibiscus, which might be attributable to outflows. However, in the case of Narcissus, the gas traced by the two emission lines follows a similar evolutionary path. Despite a slightly lower σ[CII] than σHα, this galaxy remains dynamically cold according to both tracers. Considering the comparable stellar masses of these galaxies, differences in their star formation histories, feedback effects, or other global properties may be cause the different behavior of the tracers.

5. Conclusions

In this paper, we investigated the possible existence of dynamically cold disks (with significant rotation support) in the early Universe using a sample of 3218 normal star-forming galaxies from the SERRA zoom-in cosmological simulations. We analyzed the kinematic of [C II] and Hα in the redshift range of 4 ≤ z ≤ 9 for LBGs with 8 ≤ log(M⋆/M⊙) ≤ 10.3 and 0 < SFR ≤ 128. Our main conclusions are listed below.

  • Stellar mass and gas velocity dispersion are strongly (weakly) correlated in Hα ([C II]) synthetic observations. The difference mostly arises for M⋆ > 109 M⊙ galaxies where σHα > 2σ[CII].

  • Regardless of galaxy mass and the chosen kinematic tracer, our analysis reveals no significant redshift dependence in the ratio Vrot/σ.

  • Massive (M⋆ ≥ 1010 M⊙) galaxies in SERRA settle into dynamically supercold disks with Vrot/σ > 10 at z > 4. These cold disks are not transient features and last for more than ten galaxy orbital times (∼ 200 Myr).

We have shown that in SERRA galaxies, [C II] effectively traces the thin gaseous disks within the galaxies, while Hα emission can also trace the ionized gas outside the disk. The differences in the kinematics of [C II] and Hα may be attributed to galactic outflows, although further exploration is necessary to substantiate and statistically quantify this point. We showed that the identification of Hα halos could be a signature of these galactic outflows. We predict that more high-z dynamically cold disks will be found with the increasing availability of deep ALMA observations targeting [C II] 158 μm in galaxies with stellar masses exceeding 109 M⊙.

In view of the essential role of multiple tracers in gaining a comprehensive understanding of early galaxy kinematics, we emphasize that the ALMA-JWST/NIRspec synergy will be essential.

1

The FOV for the HDCs had a side of 2.5 kpc.

2

While Hα emission is optically thick, we produced the nonattenuated HDCs and left radiative transfer effects for future work.

3

It is worth noting that this approximation is valid for a thin rotating disk with a low velocity dispersion.

4

At the center of the galaxies, the dynamical mass is dominated by the baryonic component; see Kohandel et al. (2019) for the rotation curves and (Gelli et al. 2020) for the density profiles.

5

The redshift evolution for each mass category was obtained by dividing the category into six redshift bins between 4–9, and the markers indicate the mean of the sample in that redshift bin.

6

We combined the original four mass bins of Fig. 14 in Pillepich et al. 2019 into two composite bins: log(M⋆/M⊙) > 10 and log(M⋆/M⊙) = 9 − 10.

Acknowledgments

MK and AF acknowledge support from the ERC Advanced Grant INTERSTELLAR H2020/740120 (PI: Ferrara). We acknowledge the CINECA award under the ISCRA initiative for the availability of high-performance computing resources and support from the Class B project SERRA HP10BPUZ8F (PI: Pallottini). We gratefully acknowledge the computational resources of the Center for High-Performance Computing (CHPC) at SNS. We acknowledge use of the Python programming language (Van Rossum & de Boer 1991), Astropy (Astropy Collaboration 2013), Cython (Behnel et al. 2011), Matplotlib (Hunter 2007), NumPy (van der Walt et al. 2011), PYNBODY (Pontzen et al. 2013), and SciPy (Virtanen et al. 2020).

References

  1. Andersen, D. R., Bershady, M. A., Sparke, L. S., et al. 2006, ApJS, 166, 505 [NASA ADS] [CrossRef] [Google Scholar]
  2. Arata, S., Yajima, H., Nagamine, K., Abe, M., & Khochfar, S. 2020, MNRAS, 498, 5541 [NASA ADS] [CrossRef] [Google Scholar]
  3. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  4. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bakx, T. J. L. C., Tamura, Y., Hashimoto, T., et al. 2020, MNRAS, 493, 4294 [NASA ADS] [CrossRef] [Google Scholar]
  6. Behnel, S., Bradshaw, R., Citro, C., et al. 2011, Comput. Sci. Eng., 13, 31 [Google Scholar]
  7. Behrens, C., Pallottini, A., Ferrara, A., Gallerani, S., & Vallini, L. 2018, MNRAS, 477, 552 [NASA ADS] [CrossRef] [Google Scholar]
  8. Birkin, J. E., Smail, I., Swinbank, A. M., et al. 2023, MNRAS, submitted [arXiv:2301.05720] [Google Scholar]
  9. Bouwens, R. J., Smit, R., Schouws, S., et al. 2022, ApJ, 931, 160 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bovino, S., Grassi, T., Capelo, P. R., Schleicher, D. R. G., & Banerjee, R. 2016, A&A, 590, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Carniani, S., Ferrara, A., Maiolino, R., et al. 2020, MNRAS, 499, 5136 [NASA ADS] [CrossRef] [Google Scholar]
  12. de Graaff, A., Rix, H. W., Carniani, S., et al. 2024, A&A, 684, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Decataldo, D., Pallottini, A., Ferrara, A., Vallini, L., & Gallerani, S. 2019, MNRAS, 487, 3377 [Google Scholar]
  14. Dekel, A., & Burkert, A. 2014, MNRAS, 438, 1870 [Google Scholar]
  15. Ejdetjärn, T., Agertz, O., Östlin, G., Renaud, F., & Romeo, A. B. 2022, MNRAS, 514, 480 [CrossRef] [Google Scholar]
  16. Epinat, B., Amram, P., Balkowski, C., & Marcelin, M. 2010, MNRAS, 401, 2113 [Google Scholar]
  17. Federrath, C., & Klessen, R. S. 2013, ApJ, 763, 51 [Google Scholar]
  18. Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mex. A&A, 53, 385 [Google Scholar]
  19. Ferreira, L., Adams, N., Conselice, C. J., et al. 2022, ApJ, 938, L2 [NASA ADS] [CrossRef] [Google Scholar]
  20. Förster Schreiber, N. M., Renzini, A., Mancini, C., et al. 2018, ApJS, 238, 21 [Google Scholar]
  21. Fraternali, F., Karim, A., Magnelli, B., et al. 2021, A&A, 647, A194 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Fujimoto, S., Ouchi, M., Ferrara, A., et al. 2019, ApJ, 887, 107 [Google Scholar]
  23. Fujimoto, S., Oguri, M., Brammer, G., et al. 2021, ApJ, 911, 99 [Google Scholar]
  24. Fudamoto, Y., Smit, R., Bowler, R. A. A., et al. 2022, ApJ, 934, 144 [NASA ADS] [CrossRef] [Google Scholar]
  25. Gallerani, S., Pallottini, A., Feruglio, C., et al. 2018, MNRAS, 473, 1909 [Google Scholar]
  26. Gelli, V., Salvadori, S., Pallottini, A., & Ferrara, A. 2020, MNRAS, 498, 4134 [NASA ADS] [CrossRef] [Google Scholar]
  27. Genzel, R., Newman, S., Jones, T., et al. 2011, ApJ, 733, 101 [Google Scholar]
  28. Ginolfi, M., Jones, G. C., Béthermin, M., et al. 2020, A&A, 633, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Girard, M., Fisher, D. B., Bolatto, A. D., et al. 2021, ApJ, 909, 12 [NASA ADS] [CrossRef] [Google Scholar]
  30. Gnerucci, A., Marconi, A., Cresci, G., et al. 2011, A&A, 528, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Grassi, T., Bovino, S., Schleicher, D. R. G., et al. 2014, MNRAS, 439, 2386 [Google Scholar]
  32. Hahn, O., & Abel, T. 2011, MNRAS, 415, 2101 [Google Scholar]
  33. Harikane, Y., Ouchi, M., Inoue, A. K., et al. 2020, ApJ, 896, 93 [Google Scholar]
  34. Hashimoto, T., Inoue, A. K., Mawatari, K., et al. 2019, PASJ, 71, 71 [Google Scholar]
  35. Hayward, C. C., & Hopkins, P. F. 2017, MNRAS, 465, 1682 [Google Scholar]
  36. Herrera-Camus, R., Förster Schreiber, N. M., Price, S. H., et al. 2022, A&A, 665, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Hirashita, H., & Ferrara, A. 2002, MNRAS, 337, 921 [NASA ADS] [CrossRef] [Google Scholar]
  38. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  39. Johnson, H. L., Harrison, C. M., Swinbank, A. M., et al. 2018, MNRAS, 474, 5076 [NASA ADS] [CrossRef] [Google Scholar]
  40. Jones, G. C., Willott, C. J., Carilli, C. L., et al. 2017, ApJ, 845, 175 [NASA ADS] [CrossRef] [Google Scholar]
  41. Jones, G. C., Vergani, D., Romano, M., et al. 2021, MNRAS, 507, 3540 [NASA ADS] [CrossRef] [Google Scholar]
  42. Kartaltepe, J. S., Rose, C., Vanderhoof, B. N., et al. 2023, ApJ, 946, L15 [NASA ADS] [CrossRef] [Google Scholar]
  43. Kennicutt, R. C., Jr 1998, ApJ, 498, 541 [Google Scholar]
  44. Kohandel, M., Pallottini, A., Ferrara, A., et al. 2019, MNRAS, 487, 3007 [NASA ADS] [CrossRef] [Google Scholar]
  45. Kohandel, M., Pallottini, A., Ferrara, A., et al. 2020, MNRAS, 499, 1250 [Google Scholar]
  46. Kretschmer, M., Dekel, A., & Teyssier, R. 2022, MNRAS, 510, 3266 [NASA ADS] [CrossRef] [Google Scholar]
  47. Law, D. R., Steidel, C. C., Erb, D. K., et al. 2009, ApJ, 697, 2057 [NASA ADS] [CrossRef] [Google Scholar]
  48. Le Fèvre, O., Béthermin, M., Faisst, A., et al. 2020, A&A, 643, A1 [Google Scholar]
  49. Lelli, F., Di Teodoro, E. M., Fraternali, F., et al. 2021, Science, 371, 713 [Google Scholar]
  50. Levy, R. C., Bolatto, A. D., Teuben, P., et al. 2018, ApJ, 860, 92 [NASA ADS] [CrossRef] [Google Scholar]
  51. Lupi, A., Pallottini, A., Ferrara, A., et al. 2020, MNRAS, 496, 5160 [Google Scholar]
  52. Mac Low, M.-M. 1999, ApJ, 524, 169 [Google Scholar]
  53. Madau, P., Ferrara, A., & Rees, M. J. 2001, ApJ, 555, 92 [Google Scholar]
  54. Mason, C. A., Treu, T., Fontana, A., et al. 2017, ApJ, 838, 14 [NASA ADS] [CrossRef] [Google Scholar]
  55. Mieda, E., Wright, S. A., Larkin, J. E., et al. 2016, ApJ, 831, 78 [NASA ADS] [CrossRef] [Google Scholar]
  56. Pallottini, A., Ferrara, A., Gallerani, S., Salvadori, S., & D’Odorico, V. 2014a, MNRAS, 440, 2498 [NASA ADS] [CrossRef] [Google Scholar]
  57. Pallottini, A., Gallerani, S., & Ferrara, A. 2014b, MNRAS, 444, L105 [Google Scholar]
  58. Pallottini, A., Ferrara, A., Bovino, S., et al. 2017a, MNRAS, 471, 4128 [NASA ADS] [CrossRef] [Google Scholar]
  59. Pallottini, A., Ferrara, A., Gallerani, S., et al. 2017b, MNRAS, 465, 2540 [CrossRef] [Google Scholar]
  60. Pallottini, A., Ferrara, A., Decataldo, D., et al. 2019, MNRAS, 487, 1689 [Google Scholar]
  61. Pallottini, A., Ferrara, A., Gallerani, S., et al. 2022, MNRAS, 513, 5621 [NASA ADS] [Google Scholar]
  62. Pandya, V., Zhang, H., Huertas-Company, M., et al. 2024, ApJ, 963, 54 [NASA ADS] [CrossRef] [Google Scholar]
  63. Parlanti, E., Carniani, S., Pallottini, A., et al. 2023, A&A, 673, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Parlanti, E., Carniani, S., Übler, H., et al. 2024, A&A, 684, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Pillepich, A., Nelson, D., Springel, V., et al. 2019, MNRAS, 490, 3196 [Google Scholar]
  66. Pizzati, E., Ferrara, A., Pallottini, A., et al. 2020, MNRAS, 495, 160 [Google Scholar]
  67. Pizzati, E., Ferrara, A., Pallottini, A., et al. 2023, MNRAS, 519, 4608 [NASA ADS] [CrossRef] [Google Scholar]
  68. Pontzen, A., Roškar, R., Stinson, G., & Woods, R. 2013, Astrophysics Source Code Library [record ascl:1305.002] [Google Scholar]
  69. Pope, A., McKinney, J., Kamieneski, P., et al. 2023, ApJ, 951, L46 [NASA ADS] [CrossRef] [Google Scholar]
  70. Posses, A. C., Aravena, M., González-López, J., et al. 2023, A&A, 669, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Ravindranath, S., Giavalisco, M., Ferguson, H. C., et al. 2006, ApJ, 652, 963 [NASA ADS] [CrossRef] [Google Scholar]
  72. Rizzo, F., Vegetti, S., Powell, D., et al. 2020, Nature, 584, 201 [Google Scholar]
  73. Rizzo, F., Vegetti, S., Fraternali, F., Stacey, H. R., & Powell, D. 2021, MNRAS, 507, 3952 [NASA ADS] [CrossRef] [Google Scholar]
  74. Rizzo, F., Kohandel, M., Pallottini, A., et al. 2022, A&A, 667, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Robertson, B. E., Tacchella, S., Johnson, B. D., et al. 2023, ApJ, 942, L42 [NASA ADS] [CrossRef] [Google Scholar]
  76. Roman-Oliveira, F., Fraternali, F., & Rizzo, F. 2023, MNRAS, 521, 1045 [NASA ADS] [CrossRef] [Google Scholar]
  77. Romano, M., Cassata, P., Morselli, L., et al. 2021, A&A, 653, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Rosdahl, J., Blaizot, J., Aubert, D., Stranex, T., & Teyssier, R. 2013, MNRAS, 436, 2188 [Google Scholar]
  79. Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
  80. Simons, R. C., Kassin, S. A., Snyder, G. F., et al. 2019, ApJ, 874, 59 [Google Scholar]
  81. Smit, R., Bouwens, R. J., Carniani, S., et al. 2018, Nature, 553, 178 [Google Scholar]
  82. Stott, J. P., Swinbank, A. M., Johnson, H. L., et al. 2016, MNRAS, 457, 1888 [Google Scholar]
  83. Teyssier, R. 2002, A&A, 385, 337 [CrossRef] [EDP Sciences] [Google Scholar]
  84. Teyssier, R., Pontzen, A., Dubois, Y., & Read, J. I. 2013, MNRAS, 429, 3068 [NASA ADS] [CrossRef] [Google Scholar]
  85. Tohill, C. B., Bamford, S., Conselice, C., et al. 2024, ApJ, 962, 164 [NASA ADS] [CrossRef] [Google Scholar]
  86. Tokuoka, T., Inoue, A. K., Hashimoto, T., et al. 2022, ApJ, 933, L19 [CrossRef] [Google Scholar]
  87. Tsukui, T., & Iguchi, S. 2021, Science, 372, 1201 [NASA ADS] [CrossRef] [Google Scholar]
  88. Turner, O. J., Cirasuolo, M., Harrison, C. M., et al. 2017, MNRAS, 471, 1280 [Google Scholar]
  89. Vallini, L., Ferrara, A., Pallottini, A., & Gallerani, S. 2017, MNRAS, 467, 1300 [NASA ADS] [Google Scholar]
  90. Vallini, L., Pallottini, A., Ferrara, A., et al. 2018, MNRAS, 473, 271 [NASA ADS] [CrossRef] [Google Scholar]
  91. van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
  92. van der Wel, A., Chang, Y.-Y., Bell, E. F., et al. 2014, ApJ, 792, L6 [NASA ADS] [CrossRef] [Google Scholar]
  93. Van Rossum, G., & de Boer, J. 1991, CWI Quarterly, 4, 283 [Google Scholar]
  94. Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
  95. Weingartner, J. C., & Draine, B. T. 2001, ApJ, 563, 842 [NASA ADS] [CrossRef] [Google Scholar]
  96. Wisnioski, E., Förster Schreiber, N. M., Fossati, M., et al. 2019, ApJ, 886, 124 [Google Scholar]
  97. Zhang, H., Primack, J. R., Faber, S. M., et al. 2019, MNRAS, 484, 5170 [NASA ADS] [CrossRef] [Google Scholar]
  98. Zolotov, A., Dekel, A., Mandelker, N., et al. 2015, MNRAS, 450, 2327 [Google Scholar]

All Tables

Table 1.

Relevant properties of the simulated sample.

In the text
Table 2.

Dynamical categorization of SERRA galaxies.

In the text

All Figures

thumbnail Fig. 1.

Relation of the velocity dispersion and stellar mass in the SERRA galaxy sample: Blue (red) contours show the 1, 2, and 3-sigma probability density function levels for the M⋆ − σ relation derived from synthetic [C II] (Hα) observations. Individual data points are represented by crosses.
In the text
thumbnail Fig. 2.

Redshift evolution of Vrot/σ in SERRA. The three stellar mass bins are distinguished by the line width; blue (red) markers represent σ from [C II] (Hα) synthetic observations. For comparison, predictions from TNG50 simulations (Pillepich et al. 2019) are shown with filled orange markers for z < 5. The gray triangles denote observational data points with [C II] line kinematics, including high-z DCDs (Rizzo et al. 2021; Lelli et al. 2021; Fraternali et al. 2021; Tsukui & Iguchi 2021; Roman-Oliveira et al. 2023; Pope et al. 2023; Rowland et al., in prep.), ALPINE disk galaxies (Jones et al. 2021), archival 4 < z < 7.7 [C II] data (Parlanti et al. 2023), the first discovered EoR disk galaxies (Smit et al. 2018), and the turbulent HZ4 system at z = 5.5 (Herrera-Camus et al. 2022). The gray squares represent data with nebular Hα and [OIII] kinematics (de Graaff et al. 2024; Parlanti et al. 2024). The filled (empty) markers distinguish spatially (barely) resolved observations.
In the text
thumbnail Fig. 3.

Multiwavelength kinematics of “Hibiscus” at z = 4.5. In the top (last) two rows, we display the FIR [C II] 158 μm (nebular Hα) syntactic observation for line spectra, 0, 1, and 2 moment maps in different columns for both face-on and edge-on views.
In the text
thumbnail Fig. 4.

Example of the dynamical evolution of two SERRA galaxies traced by [CII] and Hα. At z = 4.5, Hibiscus (top) has a [CII] dynamically cold disk and a turbulent Hα emitting gas that might feature galactic outflows (see also Fig. 3). At z = 6.8, Narcisuss (bottom) appears as a supercold galaxy in both [C II] and Hα.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.