| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A17 | |
| Number of page(s) | 8 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202348747 | |
| Published online | 29 March 2024 | |
Detectability of stochastic gravitational wave background from weakly hyperbolic encounters
1
Astronomical Institute of the Czech Academy of Sciences, Boční II 1401/1a, 141 00 Prague, Czech Republic
e-mail: kerachian.morteza@gmail.com
2
Birla Institute of Technology and Science Pilani, Rajasthan 333031, India
3
Inter-University Centre for Astronomy and Astrophysics (IUCAA), Ganeshkhind, Pune, Maharashtra 411007, India
Received:
27
November
2023
Accepted:
31
January
2024
We compute the stochastic gravitational wave (GW) background generated by black hole–black hole (BH–BH) hyperbolic encounters with eccentricities close to one and compare them with the respective sensitivity curves of planned GW detectors. We use the Keplerian potential to model the orbits of the encounters and the quadrupole formula to compute the emitted GWs. We take into account hyperbolic encounters that take place in clusters up to redshift 5 and with BH masses spanning from 5 M⊙ to 55 M⊙. We assume the clusters to be virialized and study several cluster models with different mass and virial velocity, and finally obtain an accumulative result, displaying the background as an average. Using the maxima and minima of our accumulative result for each frequency, we provide analytical expressions for both optimistic and pessimistic scenarios. Our results suggest that the background from these encounters is likely to be detected by the third-generation detectors Cosmic explorer and Einstein telescope, while the tail section at lower frequencies intersects with DECIGO, making it a potential target source for both ground- and space-based future GW detectors.
Key words: black hole physics / gravitational waves / scattering / galaxies: clusters: general
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Up to this point, terrestrial gravitational wave (GW) observatories have detected only binary mergers of stellar compact objects (Abbott et al. 2019, 2021; LIGO Scientific Collaboration et al. 2023). The signal from these sources remains discrete, in the sense that it does not overlap with the signal from another source when detected. This is expected to change in the future (Maggiore et al. 2020; Amaro-Seoane et al. 2017), when GW observatories are expected to receive signals from multiple sources simultaneously. A more extreme case of such overlap is seen when the sources are so numerous that one cannot be discerned from another, creating a stochastic GW background (SGWB).
There are several types of SGWBs depending on their sources (Boileau et al. 2021; Martinovic et al. 2021; Agazie et al. 2023; Afzal et al. 2023; Antoniadis et al. 2024); they can be split into two categories: cosmological sources and astrophysical sources. The latter category contains mainly different types of compact binary coalescences, but also hyperbolic encounters of compact objects. Contrary to the compact binary coalescences for which the signal can last for many cycles, in the case of hyperbolic encounters the signal can be viewed rather as a transient (Morrás et al. 2022). The peak of this transient GW signal lies near the pericenter of the respective hyperbolic trajectory (De Vittori et al. 2012), which should correspond to short bursts of GWs. The exact waveform of these bursts (Cho et al. 2018; Vines et al. 2019; Jakobsen et al. 2021; Saketh et al. 2022; Chowdhuri et al. 2023) is not relevant for the study of an SGWB, because we are interested in the accumulative effect of many events.
It is often argued that bound compact clusters, such as globular clusters (GCs), can be one of the possible dominant channels for hyperbolic encounters in the Universe (Dymnikova et al. 1982; Kocsis et al. 2006). Therefore, encounters in GCs are expected to provide an adequate number of events for an SGWB (Mukherjee et al. 2021). This rate depends on the number of black holes (BHs) in a cluster and on the number of clusters in a galaxy. Therefore, from an astrophysical point of view, detecting a SGWB or failing to do so would put constraints on the numbers mentioned above.
Our work continues the investigation done by Mukherjee et al. (2021), in which an estimate of the detectable event rates was provided. In particular, we investigate BH hyperbolic encounters where eccentricities tend to be almost parabolic; that is, the eccentricity is very close to one. We obtain different energy density profiles of the SGWB generated by these encounters while varying the parameters of the system, such as the masses of the BHs and the virial velocity in the cluster. The comparison of these profiles with the respective sensitivity curves of GW observatories allows us to infer some preferable scenarios for detection.
The remainder of the article is organized as follows: in Sect. 2 we describe how we modeled the orbital dynamics of the hyperbolic encounters and the respective GW radiation. In Sect. 3 we show how we computed the dimensionless GW energy density spectrum for the hyperbolic encounters. In Sect. 4 we present our results and in Sect. 5 we conclude with a discussion of our main findings.
2. Analytical calculations
2.1. Orbital parameters
In this section, we briefly review the orbital parameters for hyperbolic encounters limited within a radius of a cluster, as given by Mukherjee et al. (2021). This motion is planar and each orbit is determined by its initial conditions: the initial distance ri between the bodies, the initial angle θi between ri and the initial velocity of the secondary vi, and the masses of the objects m1 and m2 (for an illustration see Fig. 1). As mentioned above, the initial radius is chosen to be less than the cluster radius, that is ri ≤ Rc, where Rc is the radius of a cluster; vi is estimated from virial theorem; and θi is considered to have an arbitrary value within its physical range1.
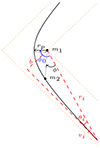 |
Fig. 1. Hyperbolic trajectory of a secondary compact object of mass m2 in the gravitational field of a BH of mass m1. The secondary object is initially located at a distance ri from the primary; the initial angle between the line connecting the bodies and the initial velocity vi is θi. The motion of the secondary can be parametrized by the radial distance r(ϕ) as a function of the azimuthal angle ϕ, where ϕ lies between ri and r(ϕ). The rp is the periapsis, which is the minimum distance between the bodies, and ϕ0 is the periapsis angle, which is the angle between r(ϕ) and rp. As shown here, we define the impact parameter b as the vertical distance between the primary BH and the initial velocity of the secondary; that is, b = ri sin θi. |
As the objects are far from each other, we use the Keplerian potential energy. The Hamiltonian for this system is
where E, pr, and L are the total energy, the radial momentum, and the total angular momentum per unit of reduced mass μ, while M = m1 + m2 is the total mass and 1/μ = 1/m1 + 1/m2 is the reduced mass of the system. Moreover, from Fig. 1 the total angular momentum per μ can be written as L = rivi sin θi. Solving Hamiltonian (1) allows us to find that
where ϕ is the angle between ri and r(ϕ) and p, e, and ϕ0 are given by
with
See Mukherjee et al. (2021) for a detailed derivation of these quantities2.
2.2. Energy radiation in the time domain
As we are dealing with an SGWB, to calculate the gravitation radiation reaction from the hyperbolic encounters, it is reasonable to assume that an estimation of the leading terms of this reaction is sufficient (Roskill et al. 2023). Therefore, we use the quadrupole formula (see, e.g., Maggiore 2007) should be sufficient for the scope of the present work. The quadrupole moment tensor is given by
where the nonzero components of this system are
Then, the power emitted through GW is determined from
By substituting the relations (4), we arrive at
with
The above expression exactly matches the existing literature, except for α, which arises from the different definitions of a and b (see Appendix A; García-Bellido & Nesseris 2018).
We note that the relation between ϕ and t can be derived from 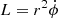 . To get an explicit relation, one can rewrite this in the form
. To get an explicit relation, one can rewrite this in the form
and consequently, we get
2.3. Energy radiation in the frequency domain
To compute the frequency spectrum of the radiated power ΔE, we employ the Fourier transformation (FT) of the energy emission in the time domain; that is,
where P(ω) is the power radiation in the frequency domain given by
and the over-hat represents the FT defined as
Additionally, Eq. (16) implies 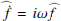 , and consequently
, and consequently 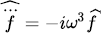 . For simplicity, we use this relation for Eq. (15) and write it in terms of Qij as follows:
. For simplicity, we use this relation for Eq. (15) and write it in terms of Qij as follows:
The radial trajectory given in Eq. (2) is a function of ϕ and the dependence of ϕ in terms of t is given by Eq. (13). However, this parameterization is not suitable if the FT is going to be applied. Therefore, we reparameterize the hyperbolic trajectory in terms of the eccentric anomalyξ as follows:
where ac = a/α, and
is the Keplerian frequency.
In Cartesian coordinates, the trajectory (18) reads
Expressing the trajectory in Cartesian coordinates allows us to rewrite the quadrupole momentum tensor (5)–(8) in terms of ξ. Namely, we have that
By using FT, whose derivation can be found in Appendix B, and the fact that ν = ω/ω0, the power radiation (17) becomes3
where
Equation (26) can be approximated by (García-Bellido & Nesseris 2018)
where
Consequently, the total energy in the frequency domain (14) can be obtained from Eqs. (27) and (25) and is
3. Stochastic gravitational wave background from hyperbolic encounters
To evaluate the SGWB from hyperbolic encounters, we compute the dimensionless GW energy density spectrum as (García-Bellido et al. 2022; Maggiore 2018)
where ξ = {ξ1, …, ξm} is a collection of different encounters and
where fr = f(1 + z) is the GW frequency at the source frame, dEGW/dlnfr is the GW energy emission per logarithmic frequency bin in the source frame, ρc is the energy density of the Universe given by 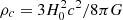 , H0 = 100h100 km s−1 Mpc−1 is the Hubble constant, and N(z; ξ) is the number of GW events density at redshift z, as given by (Zhu et al. 2013):
, H0 = 100h100 km s−1 Mpc−1 is the Hubble constant, and N(z; ξ) is the number of GW events density at redshift z, as given by (Zhu et al. 2013):
in which ℛ(z; ξ) is the event rate density and 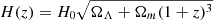 is the Hubble parameter at z. By assuming a standard Λ cold dark matter (ΛCDM) cosmology we have ΩΛ = 0.685, and Ωm = 0.315.
is the Hubble parameter at z. By assuming a standard Λ cold dark matter (ΛCDM) cosmology we have ΩΛ = 0.685, and Ωm = 0.315.
We define the event rate density ℛ(z; ξ) as
where Pclus(z; ξ) is the probability per unit time of the encounters inside each GC, ngc is the number of GCs per Milky Way-equivalent galaxy (MWEG), 𝒩(z) is the number of MWEGs between redshift z and z + dz, V is the comoving volume up to redshift z, and the factor (1 + z) represents the cosmological time dilation. Therefore, the right-hand side of the Eq. (33) provides us with the total event rate density.
By substituting Eqs. (33) and (32) into Eq. (30), we arrive at
In Eq. (34), we take advantage of the fact that
where ν = 2πν0fr = 2πν0f(1 + z) 4, ν0 = 1/ω0, and dEGW(ν; ξ)/dν is given by Eq. (29).
The second integral in Eq. (34) is of particular interest, and we can call it 𝒦(z) for future reference, that is,
We need to integrate the above expression over ξ, which in our case is related to ri and θi, that is, ξ = ξ(ri, θi), to add the contribution from all the radial and angular distributions.
To derive the Pclus(z; ri, θi), let us assume that there is an interaction inside a cluster, and the relative initial angle is θi, as shown in Fig. 1. The probability of such encounters is then
However, this encounter can take place at a given (relative) distance, ri, from the primary body. Therefore, we may want to integrate in a radial direction to add all the contributions in a given volume:
We note that in the above expression, ns is the number density of compact objects inside the cluster. For the number of compact objects, nco, we have 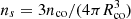 , where Rco is the GC core radius. It is reasonable to express the probability of an encounter per unit of time, that is as a rate of encounters. For this, we impose the relation
, where Rco is the GC core radius. It is reasonable to express the probability of an encounter per unit of time, that is as a rate of encounters. For this, we impose the relation
where tcol is the collision time. Now, if we ignore the relativistic corrections, then tcol ≤ ri/vi, where vi is the initial velocity, which in our case is the virial velocity. We note that the maximum value of tcol is ri/vi, and this therefore expresses the lowest possible rate. This means that we end up with a conservative rate estimate.
By employing our assumption in Eq. (39), we can now obtain the total rate of the entire cluster, as Pindv is the probability per object. By ignoring the small-scale structure, we have
Therefore, by substituting Eqs. (40) into (36), we arrive at
where νi is a function of ri, because νi = 2πν0if(1 + z) with 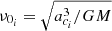 and
and
At this point, we rewrite Eq. (41) in terms of the orbital parameter, that is, eccentricity, instead of the angular coordinate θi. From Eqs. (3) and (4), we have
Substituting θi = Θ(ei, ri, vi) and 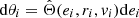 from Eq. (42), into Eq. (41), and we get
from Eq. (42), into Eq. (41), and we get
where
Moreover, 𝒩(z) is determined from
where n(z) is the number of MWEGs per volume at redshift z, and we assume it to be constant at n(z) = 0.01 Mpc−3(Arca Sedda 2020).
Finally, we derive ΩGW(f) by substituting Eqs. (43) and (45) into Eq. (34), and using 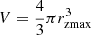 as the comoving volume and rzmax as the comoving distance:
as the comoving volume and rzmax as the comoving distance:
In order to obtain rzmax, we use the equation
from which we can see that redshift zmax = 5 corresponds to a distance of rzmax = 7.84 Gpc.
4. Results
In the previous section, we derive the energy density GW spectrum using Eq. (46) under certain assumptions for a collection of hyperbolic encounters. In this section, we illustrate GW spectra for various parameter options to investigate how certain parameter choices influence these spectra. We also provide an accumulative case representing the reasonable combinations we can take into account to generate an SGWB from hyperbolic encounters.
4.1. Specific cases
In order to observe how changing the parameters in our setup varies the detectability of the SGWB, we fix some parameters and vary others, as follows:
-
We set the number of compact objects nco(z) from Kremer et al. (2020).
-
We fix the periapsis rp to be no smaller than the Schwarzschild radius; that is, rp ≥ rsch, in which we exclude any head-on collision.
-
We evaluate 𝒦(z) from Eq. (43) in a small range }rimin,rimax {=}0.03 pc,0.53 pc{, and a larger range
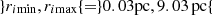 . In both cases, the eccentricity varies from }eimin,eimax {=}eimin,eimin + 4 × 10−9{, where eimin comes from rip = rsch; that is, by using relation (2) for ϕ = ϕ0, we get
. In both cases, the eccentricity varies from }eimin,eimax {=}eimin,eimin + 4 × 10−9{, where eimin comes from rip = rsch; that is, by using relation (2) for ϕ = ϕ0, we getFrom Eqs. (3) and (4), we have p = b2/a,
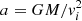 , and b = L/vi; moreover, the total angular momentum can be written as L = rivi sin θi. Therefore, b can be written as b = ri sin θi and
, and b = L/vi; moreover, the total angular momentum can be written as L = rivi sin θi. Therefore, b can be written as b = ri sin θi and 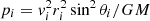 . By substituting Eq. (42), we get
. By substituting Eq. (42), we getTherefore, from Eq. (48) for eimin at each ri, we get
-
We set the primary mass m1 to be no greater than 55 M⊙, and we set the secondary mass m2 to be no greater than 25 M⊙ for the small range of ri, and no greater than 20 M⊙ for the larger range of ri (Kocsis et al. 2006).
-
We assume that the cluster is virialized to start with, and we have
which is the virial velocity for a uniformly distributed mass (Longair 2023). In Eq. (51), ⟨m⟩ is the average mass of a star, and we keep ⟨m⟩=M⊙ to be constant throughout our calculation. However, we vary the total number of stars Ntot, the cluster’s radius Rgc, and m1 and m2 as follows: 1. Case 1: We choose Ntot = 106 and Rgc = 10 pc and evaluate Eq. (46). We observe that in this case for the range of small ri (gray area in the top-left plot of Fig. 2) the SGWB can barely be detected by Cosmic Explorer (CE) for mass ranges 48 M⊙ ≲ m1 ≤ 55 M⊙ and 19 M⊙ ≲ m2 ≤ 25 M⊙. However, for the range of larger ri (orange area in the left top plot of Fig. 2), we observe that the SGWB should be detectable by CE in the mass ranges 37 M⊙ ≲ m1 ≤ 55 M⊙ and 12 M⊙ ≲ m2 ≤ 20 M⊙. 2. Case 2: We set Ntot = 5 × 105 and Rgc = 10 pc. In this case, the respective SGWBs should be detectable by CE for the range of small ri (gray area in the top-right plot of Fig. 2) and for mass ranges 31 M⊙ ≲ m1 ≤ 55 M⊙ and 12 M⊙ ≲ m2 ≤ 25 M⊙, and for the range of larger ri (orange area in the right top plot of Fig. 2) and mass ranges 25 M⊙ < m1 ≤ 55 M⊙ and 7 M⊙ ≲ m2 ≤ 20 M⊙. SGWBs within the range of large ri may only be barely detectable by the Deci-hertz Interferometer Gravitational-wave Observatory (DECIGO). 3. Case 3: We assume Ntot = 106 and Rgc = 15 pc. SGWB could be detected by CE for the mass ranges 40 M⊙ < m1 ≤ 55 M⊙ and 14 M⊙ ≲ m2 ≤ 25 M⊙ for the range of small ri (gray area in the bottom-left plot of Fig. 2), while for the range of larger ri (orange area in the bottom-left plot of Fig. 2) detection is possible in the mass ranges 26 M⊙ < m1 ≤ 55 M⊙ and 9 M⊙ ≲ m2 ≤ 20 M⊙. 4. Case 4: We set Ntot = 5 × 105 and Rgc = 15 pc. We find that the SGWB can be detected by CE for the range of small ri (gray area in the bottom-right plot of Fig. 2) and within the mass ranges 33 M⊙ ≲ m1 ≤ 55 M⊙ and 11 M⊙ ≲ m2 ≤ 25 M⊙. Moreover, we observe that the SGWB can be detected via CE for the range of larger ri (orange area in the right bottom plot of Fig. 2) within the mass ranges 20 M⊙ ≲ m1 ≤ 55 M⊙ and 6 M⊙ ≲ m2 ≤ 20 M⊙, and is likely also detectable with DECIGO, but barely detectable with ET.
 |
Fig. 2. SGWB as detected using weakly hyperbolic encounters. The shaded regions show the SGWB and are produced from Eq. (46), where we set ri in two sets of ranges. The small range varies from {0.03 pc, 0.53 pc}, and the larger range varies from {0.03 pc, 9.03 pc}. In both cases, the eccentricity covers the range of }eimin,eimin + 4 × 10−9{. For the top-left plot, we set Ntot = 106, Rgc = 10 pc (see case 1 in the text for more details.); for the top-right plot, we set Ntot = 5 × 105, Rgc = 10 pc (see case 2 for more details); for the bottom-left plot, we set Ntot = 106, Rgc = 15 pc (see case 3 for more details); for the bottom- right plot, we set Ntot = 5 × 105, Rgc = 15 pc (see case 4 for more details). In all four cases, we integrate up to redshift z = 5. The gray region shows the case for the small ri and the orange region shows the case for the larger ri. Moreover, ET, CE, and DECIGO curves correspond to the sensitivity of the Einstein Telescope (Punturo et al. 2010), the Cosmic Explorer (Evans et al. 2021), and the Deci-hertz Interferometer Gravitational-wave Observatory (Hou et al. 2021) detectors, respectively, for one year of observation (Thrane & Romano 2013). |
4.2. Total contribution to the SGWB from weakly hyperbolic encounters
Here, we present the total contribution to the SGWB from all the previous cases. In particular, nco(z) is the same as was defined in the previous section; we let ri vary in the whole range of }rimin,rimax = {=} 0.03pc,9.03pc{, and we set the same range for the eccentricity as above: }eimin,eimax {=}eimin,eimin + 4 × 10−9{. In Sect. 4.1, we set Ntot and Rgc for each case, thus fixing the virial velocity (51). However, for the total contribution of SGWB, we directly vary the virial velocity in the range 5 km s−1 ≤ vi ≤ 18 km s−1. The resulting Fig. 3 shows the SGWB for the mass ranges 17 M⊙ ≲ m1 ≤ 55 M⊙ and 5 M⊙ ≲ m2 ≤ 25 M⊙.
 |
Fig. 3. Total contribution to the SGWB from weakly hyperbolic encounters (orange area). In this plot, the virial velocity varies within 5 km s−1 ≤ vi ≤ 18 km s−1. The black lines around the orange area show the fitted curves for this SGWB; the bottom line represents the pessimistic scenario, while the top line is the optimistic scenario (see Sect. 4.2 for more details). Moreover, BNS, LIGO-A+, and Voyager curves correspond to the energy density of GW background of the binary neutron star (Abbott et al. 2023), and the sensitivity curves of the Advanced Laser Interferometer Gravitational-wave Observatory (Mishra et al. 2010), and the Voyager (Abbott et al. 2017; Sathyaprakash et al. 2019; see also (LIGO Scientific Collaboration et al. 2021)) detectors respectively for one year of observations. |
In order to provide a reference SGWB for hyperbolic encounters, which could be compared with other SGWB from other GW sources or other GW detectors, we provide a fitted analytical expression for the ΩGW(f) we find. Namely, from Fig. 3, we note that the plot follows a power law with a peak; we aim to fit this plot using the expression below:
We perform two fits, one for the maxima ΩGW(f) of the orange area for each frequency in Fig. 3, which we refer to as the optimistic scenario, and one for the minima ΩGW(f) of the orange area for each frequency, which we refer to as the pessimistic scenario. In the optimistic scenario, we fit the SGWB using imax = 3, while for the pessimistic scenario, we use up to imax = 6. In Table 1, we provide the fitting parameters for both scenarios.
Fitting parameters for the optimistic and pessimistic scenarios for the SGWB from weakly hyperbolic encounters.
5. Discussion
In this work, we studied the SGWB from hyperbolic encounters inside bound compact clusters. Specifically, we investigate weakly hyperbolic encounters with eccentricities close to one, and compute the energy density of the SGWB. By considering some assumptions, given in Sect. 3, we determine the energy density GW spectrum for a collection of hyperbolic encounters.
In Sect. 4, we present our findings and compare them with the sensitivity curves of GW detectors. First, to obtain insight into how certain parameters affect the spectra, we examine different scenarios. We consider two main cases: weakly hyperbolic encounters that occur close to the core of clusters and encounters starting from a radius close to the core out to a radius near the edge of a cluster. As shown in Sect. 4, in both cases, the SGWB from these encounters can be detected mainly by the Cosmic Explorer GW detector. However, the detectability of these spectra depends on the virial velocity and the total mass of the system. By observing the different scenarios, we find the following trends:
-
As we accumulate more encounters, namely by considering more encounters from the core to the edge of the cluster, the chance of detectability increases.
-
The chance of detectability increases by increasing the total mass M of the system.
-
Decreasing the virial velocity increases the chance of detectability.
Having these trends in mind, we provide a total contribution of SGWB from the weakly hyperbolic encounters, where we accumulate all cases and present an analytical expression for the most optimistic and pessimistic scenarios, respectively. We conclude that the SGWB from the weakly hyperbolic encounters appears to be detectable mainly by the Cosmic Explorer and DECIGO detectors, and a marginal detection may be possible with the Einstein Telescope.
This range is discussed in Sect. 4.1.
In Appendix A, we show that this trajectory is a part of a hyperbola with different parametrization, namely with semi-major axis a/α, and semi-minor axis 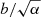 .
.
Acknowledgments
MK, S. Mukherjee, and GLG have been supported by the fellowship Lumina Quaeruntur No. LQ100032102 of the Czech Academy of Sciences. S. Mukherjee is also thankful to the Inspire Faculty Grant DST/INSPIRE/04/2022/001332, DST, Government of India, for support. Moreover, S. Mukherjee and S. Mitra are grateful to DST, Government of India, for support under the Swarnajayanti Fellowship scheme. Finally, we would like to thank Sachiko Kuroyanagi for her advisement and remarks.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017, Class. Quant. Grav., 34, 044001 [NASA ADS] [CrossRef] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019, Phys. Rev. X, 9, 031040 [Google Scholar]
- Abbott, R., Abbott, T. D., Abraham, S., et al. 2021, Phys. Rev. X, 11, 021053 [Google Scholar]
- Abbott, R., Abbott, T. D., Acernese, F., et al. 2023, Phys. Rev. X, 13, 011048 [NASA ADS] [Google Scholar]
- Afzal, A., Agazie, G., Anumarlapudi, A., et al. 2023, ApJ, 951, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Agazie, G., Anumarlapudi, A., Archibald, A. M., et al. 2023, ApJ, 952, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Amaro-Seoane, P., Audley, H., Babak, S., et al. 2017, ArXiv eprints [arXiv:1702.00786] [Google Scholar]
- Antoniadis, J., Arumugam, P., Arumugam, S., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202347433 [Google Scholar]
- Arca Sedda, M. 2020, Commun. Phys., 3, 43 [CrossRef] [Google Scholar]
- Arfken, G. B., Weber, H. J., & Harris, F. E. 2011, in Mathematical Methods for Physicists, 7th edn. (Academic Press) [Google Scholar]
- Boileau, G., Lamberts, A., Christensen, N., Cornish, N. J., & Meyer, R. 2021, ArXiv eprints [arXiv:2105.06793] [Google Scholar]
- Cho, G., Gopakumar, A., Haney, M., & Lee, H. M. 2018, Phys. Rev. D, 98, 024039 [NASA ADS] [CrossRef] [Google Scholar]
- Chowdhuri, A., Singh, R. K., Kangsabanik, K., & Bhattacharyya, A. 2023, ArXiv eprints [arXiv:2306.11787] [Google Scholar]
- De Vittori, L., Jetzer, P., & Klein, A. 2012, Phys. Rev. D, 86, 044017 [NASA ADS] [CrossRef] [Google Scholar]
- Dymnikova, I. G., Popov, A. K., & Zentsova, A. S. 1982, Astrophys. Space Sci., 85, 231 [CrossRef] [Google Scholar]
- Evans, M., Adhikari, R. X., Afle, C., et al. 2021, ArXiv eprints [arXiv:2109.09882] [Google Scholar]
- García-Bellido, J., & Nesseris, S. 2018, Phys. Dark Univ., 21, 61 [CrossRef] [Google Scholar]
- García-Bellido, J., Jaraba, S., & Kuroyanagi, S. 2022, Phys. Dark Univ., 36, 101009 [Google Scholar]
- Gröbner, M., Jetzer, P., Haney, M., Tiwari, S., & Ishibashi, W. 2020, CQG, 37, 067002 [CrossRef] [Google Scholar]
- Hou, S., Li, P., Yu, H., et al. 2021, Phys. Rev. D, 103, 044005 [CrossRef] [Google Scholar]
- Jakobsen, G. U., Mogull, G., Plefka, J., & Steinhoff, J. 2021, Phys. Rev. Lett., 126, 201103 [NASA ADS] [CrossRef] [Google Scholar]
- Kocsis, B., Gáspár, M. E., & Márka, S. 2006, ApJ, 648, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Kremer, K., Ye, C. S., Rui, N. Z., et al. 2020, ApJS, 247, 48 [NASA ADS] [CrossRef] [Google Scholar]
- LIGO Scientific Collaboration, Virgo Collaboration, & KAGRA Collaboration 2021, in GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run, https://dcc.ligo.org/LIGO-P2000318/public [Google Scholar]
- LIGO Scientific Collaboration, Virgo Collaboration, & KAGRA Collaboration 2023, Phys. Rev. X, 13, 041039 [Google Scholar]
- Longair, M. S. 2023, Galaxy Formation (Berlin, Heidelberg: Springer) [CrossRef] [Google Scholar]
- Maggiore, M. 2007, Gravitational Waves. Vol. 1: Theory and Experiments (Oxford University Press) [Google Scholar]
- Maggiore, M. 2018, Gravitational Waves: Volume 2: Astrophysics and Cosmology (Oxford University Press) [Google Scholar]
- Maggiore, M., Van Den Broeck, C., Bartolo, N., et al. 2020, J. Cosmol. Astropart. Phys., 2020, 050 [CrossRef] [Google Scholar]
- Martinovic, K., Meyers, P. M., Sakellariadou, M., & Christensen, N. 2021, Phys. Rev. D, 103, 043023 [NASA ADS] [CrossRef] [Google Scholar]
- Mishra, C. K., Arun, K. G., Iyer, B. R., & Sathyaprakash, B. S. 2010, Phys. Rev. D, 82, 064010 [NASA ADS] [CrossRef] [Google Scholar]
- Morrás, G., García-Bellido, J., & Nesseris, S. 2022, Phys. Dark Univ., 35, 100932 [CrossRef] [Google Scholar]
- Mukherjee, S., Mitra, S., & Chatterjee, S. 2021, MNRAS, 508, 5064 [NASA ADS] [CrossRef] [Google Scholar]
- Punturo, M., Abernathy, M., Acernese, F., et al. 2010, Class. Quant. Grav., 27, 084007 [NASA ADS] [CrossRef] [Google Scholar]
- Roskill, A., Caldarola, M., Kuroyanagi, S., & Nesseris, S. 2023, ArXiv eprints [arXiv:2310.07439] [Google Scholar]
- Saketh, M. V. S., Vines, J., Steinhoff, J., & Buonanno, A. 2022, Phys. Rev. Res., 4, 013127 [NASA ADS] [CrossRef] [Google Scholar]
- Sathyaprakash, B., Bailes, M., Kasliwal, M. M., et al. 2019, BAAS, 51, 276 [NASA ADS] [Google Scholar]
- Thrane, E., & Romano, J. D. 2013, Phys. Rev. D, 88, 124032 [NASA ADS] [CrossRef] [Google Scholar]
- Vines, J., Steinhoff, J., & Buonanno, A. 2019, Phys. Rev. D, 99, 064054 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, X.-J., Howell, E. J., Blair, D. G., & Zhu, Z.-H. 2013, MNRAS, 431, 882 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Hyperbolic motion
For a hyperbolic motion with a given semi-major axis ac and semi-minor axis bc whose focus lies at (h, 0), we have the equation
By setting h = ace, where e is the eccentricity defined as 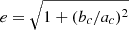 , and using the transformation
, and using the transformation
the hyperbola (A.1) can be written in polar coordinates as
where p is the semilatus rectum given by 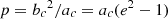 .
.
By setting ac = a/α and 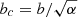 , we arrive at
, we arrive at
Thus, the trajectory given in Sect. 2.1 is actually a part of the hyperbola (A.1), where h = ace, ac = a/α, and 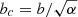 .
.
Appendix B: Derivation of the FT
In section 2.3, we apply the FT to Eqs. (21)-(24) to derive the power radiation in the frequency domain, i.e., Eq. (25). In this section, we present the details of this derivation.
As Eqs. (21)- (24) contain sinhnξ and coshnξ, to derive the FT of these equations we need to determine 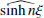 and
and 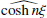 . Following Gröbner et al. (2020), one can get the following FTs:
. Following Gröbner et al. (2020), one can get the following FTs:
where ν = ω/ω0 and
is the modified Bessel function of the second kind. Consequently, for n = 1 and n = 2 Eqs. (B.1) and (B.2) reduce to
where
Now, by applying the transformation (Arfken et al. 2011)
where 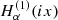 is the Hankel function, we arrive at
is the Hankel function, we arrive at
with
We note that Eqs. (B.10)- (B.13) are similar to the equations derived by García-Bellido & Nesseris (2018) up to a sign in sinhnξ. As the power radiation (25) contains the square of absolute values of these FTs, this sign difference does not affect the result.
All Tables
Fitting parameters for the optimistic and pessimistic scenarios for the SGWB from weakly hyperbolic encounters.
All Figures
 |
Fig. 1. Hyperbolic trajectory of a secondary compact object of mass m2 in the gravitational field of a BH of mass m1. The secondary object is initially located at a distance ri from the primary; the initial angle between the line connecting the bodies and the initial velocity vi is θi. The motion of the secondary can be parametrized by the radial distance r(ϕ) as a function of the azimuthal angle ϕ, where ϕ lies between ri and r(ϕ). The rp is the periapsis, which is the minimum distance between the bodies, and ϕ0 is the periapsis angle, which is the angle between r(ϕ) and rp. As shown here, we define the impact parameter b as the vertical distance between the primary BH and the initial velocity of the secondary; that is, b = ri sin θi. |
| In the text | |
 |
Fig. 2. SGWB as detected using weakly hyperbolic encounters. The shaded regions show the SGWB and are produced from Eq. (46), where we set ri in two sets of ranges. The small range varies from {0.03 pc, 0.53 pc}, and the larger range varies from {0.03 pc, 9.03 pc}. In both cases, the eccentricity covers the range of }eimin,eimin + 4 × 10−9{. For the top-left plot, we set Ntot = 106, Rgc = 10 pc (see case 1 in the text for more details.); for the top-right plot, we set Ntot = 5 × 105, Rgc = 10 pc (see case 2 for more details); for the bottom-left plot, we set Ntot = 106, Rgc = 15 pc (see case 3 for more details); for the bottom- right plot, we set Ntot = 5 × 105, Rgc = 15 pc (see case 4 for more details). In all four cases, we integrate up to redshift z = 5. The gray region shows the case for the small ri and the orange region shows the case for the larger ri. Moreover, ET, CE, and DECIGO curves correspond to the sensitivity of the Einstein Telescope (Punturo et al. 2010), the Cosmic Explorer (Evans et al. 2021), and the Deci-hertz Interferometer Gravitational-wave Observatory (Hou et al. 2021) detectors, respectively, for one year of observation (Thrane & Romano 2013). |
| In the text | |
 |
Fig. 3. Total contribution to the SGWB from weakly hyperbolic encounters (orange area). In this plot, the virial velocity varies within 5 km s−1 ≤ vi ≤ 18 km s−1. The black lines around the orange area show the fitted curves for this SGWB; the bottom line represents the pessimistic scenario, while the top line is the optimistic scenario (see Sect. 4.2 for more details). Moreover, BNS, LIGO-A+, and Voyager curves correspond to the energy density of GW background of the binary neutron star (Abbott et al. 2023), and the sensitivity curves of the Advanced Laser Interferometer Gravitational-wave Observatory (Mishra et al. 2010), and the Voyager (Abbott et al. 2017; Sathyaprakash et al. 2019; see also (LIGO Scientific Collaboration et al. 2021)) detectors respectively for one year of observations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



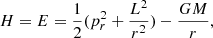
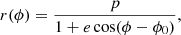
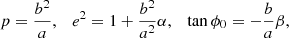
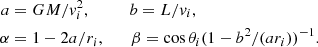
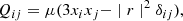
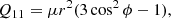
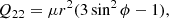
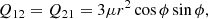
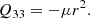
![$$ \begin{aligned} P=&\dfrac{\mathrm{d}E}{\mathrm{d}t}=-\dfrac{G}{45 c^5}(\dddot{Q}_{ij}\dddot{Q}^{ij})=-\dfrac{4L^6G}{15 p^8 \mu ^4 c^5}[1+e \cos (\phi -\phi _0)]^4\nonumber \\&\big \{1+13 e^2+ 48 e\cos (\phi -\phi _0)+11e^2\cos (2\phi -2\phi _0)\big \}. \end{aligned} $$](/articles/aa/full_html/2024/04/aa48747-23/aa48747-23-eq10.gif)
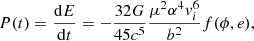
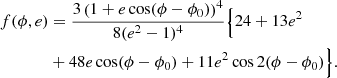
![$$ \begin{aligned} L t= p^2 \int ^{\phi }_{\phi 0} \dfrac{\mathrm{d}\phi }{[1+e\cos (\phi -\phi _0)]^2}, \end{aligned} $$](/articles/aa/full_html/2024/04/aa48747-23/aa48747-23-eq14.gif)
![$$ \begin{aligned} Lt&=- p^2 \Big [\dfrac{2}{(e^2-1)^{3/2}}\tanh ^{-1} \Big (\sqrt{\dfrac{e-1}{e+1}}\tan \big (\dfrac{\phi -\phi _0}{2}\big )\Big )\Big ]\nonumber \\ +&\dfrac{ p^2 e \sin (\phi -\phi _0)}{(e^2-1)(1+e \cos (\phi -\phi _0))}. \end{aligned} $$](/articles/aa/full_html/2024/04/aa48747-23/aa48747-23-eq15.gif)
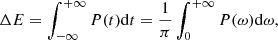
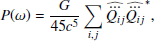
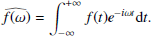
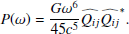

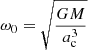
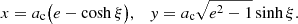
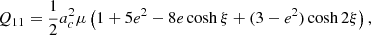
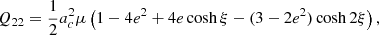
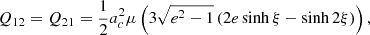
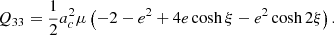
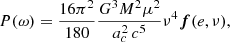
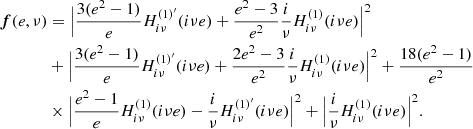
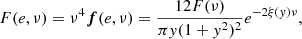
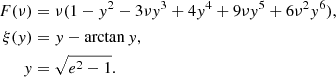
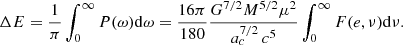
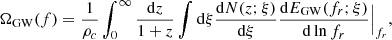
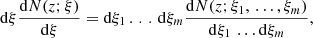
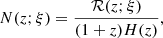
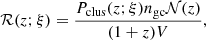
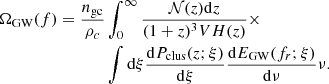
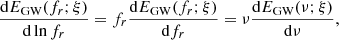
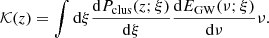
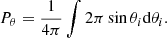
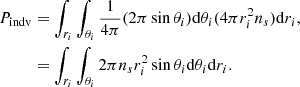
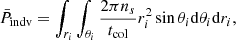
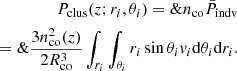
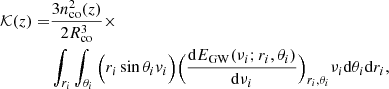
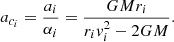
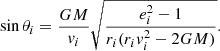
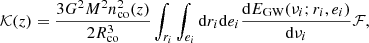
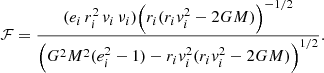
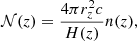
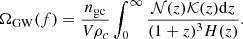
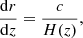
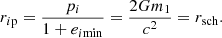
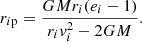
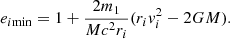
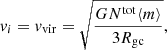
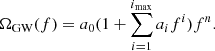
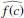
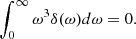
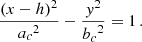

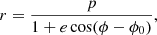
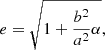
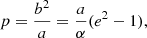
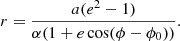
![$$ \begin{aligned} \widehat{\sinh {n\xi }}&= \frac{n}{i \omega } e^{\nu \pi /2} e^{- n \pi i/2}\left[ K_{i \nu +n}(\nu e)+ e^{i \pi n} K_{i \nu -n}(\nu e) \right],\end{aligned} $$](/articles/aa/full_html/2024/04/aa48747-23/aa48747-23-eq83.gif)
![$$ \begin{aligned} \widehat{\cosh {n\xi }}&= \frac{n}{i \omega } e^{\nu \pi /2} e^{- n \pi i/2}\left[ K_{i \nu +n}(\nu e)- e^{i \pi n} K_{i \nu -n}(\nu e) \right], \end{aligned} $$](/articles/aa/full_html/2024/04/aa48747-23/aa48747-23-eq84.gif)
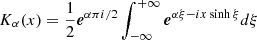
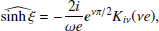
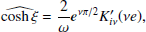
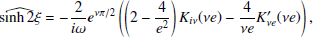
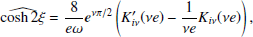
![$$ \begin{aligned} K^{\prime }_\alpha (x)= -\frac{1}{2}\left[ K_{\alpha -1}(x)+K_{\alpha +1}(x)\right]. \end{aligned} $$](/articles/aa/full_html/2024/04/aa48747-23/aa48747-23-eq90.gif)
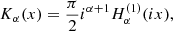
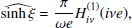
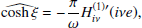
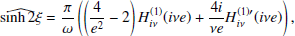
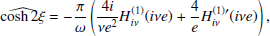
![$$ \begin{aligned} H_\alpha ^{(1)^\prime }(x)=\frac{1}{2}\left[H_{\alpha -1}^{(1)}(x)-H_{\alpha +1}^{(1)}(x) \right]. \end{aligned} $$](/articles/aa/full_html/2024/04/aa48747-23/aa48747-23-eq97.gif)