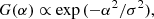| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 10 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202348699 | |
| Published online | 29 March 2024 | |
Revision of the strongest solar energetic particle event of 23 February 1956 (GLE #5) based on the rediscovered original records
1
Institute for Space-Earth Environmental Research, Nagoya University, Nagoya 4648601, Japan
e-mail: hisashi@nagoya-u.jp
2
Institute for Advanced Research, Nagoya University, Nagoya 4648601, Japan
3
Science and Technology Facilities Council, RAL Space, Rutherford Appleton Laboratory, Didcot, UK
4
Nishina Centre, Riken, Wako 3510198, Japan
5
Space Physics and Astronomy Research Unit, University of Oulu, PO Box 8000 90014 Oulu, Finland
e-mail: sergey.koldobskiy@oulu.fi
6
Sodankylä Geophysical Observatory, University of Oulu, PO Box 8000, 90014 Oulu, Finland
7
University of Siedlce, Institute of Mathematics, 08-110 Siedlce, Poland
8
Space Research Centre of Polish Academy of Sciences, 00-716 Warsaw, Poland
Received:
22
November
2023
Accepted:
7
January
2024
Aims. Intense solar eruptions can produce solar energetic particles (SEPs), potentially detectable by ground-based instruments such as neutron monitors (NMs). These events are called ground-level enhancements (GLEs). The strongest GLE with the hardest known SEP spectrum occurred on 23 February 1956 (conventionally numbered GLE #5), providing a benchmark reference for related studies. However, the existing datasets for GLE #5 were compiled from different sources, often secondary; these datasets exhibited significant discrepancies and internal inconsistencies leading to large uncertainties or biases. Here we resolve the inconsistencies and revisit the reconstructions of the energy spectra and angular characteristics of the SEPs for that event, based on our reanalyses on (somehow forgotten) original contemporary records.
Methods. We collected, digitised, and verified the source records for NM measurements during GLE #5 based on contemporaneous publications and unpublished materials in the University of Chicago Archives. Using the revised datasets and full modelling, we critically revised the reconstruction of the energy spectra and angular characteristics of the SEPs and the event-integrated omnidirectional SEP flux (fluence) for GLE #5.
Results. The energy spectrum of the SEPs during the initial and main phases of GLE #5 was revised based on the new dataset, resulting in a slightly softer, but still agreeing within the uncertainties of the recent studies, SEP spectral estimate. The SEP flux was found to be highly anisotropic in the early phase of the event. This provides a revised reference basis for further analyses and modelling of strong and extreme SEP events and their terrestrial impacts.
Key words: Sun: coronal mass ejections (CMEs) / Sun: flares / Sun: particle emission / solar-terrestrial relations
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Solar energetic particles (SEPs) are high-energy ions and electrons accelerated during eruptive processes on the Sun, such as solar flares and coronal mass ejections (e.g. Aschwanden 2012; Desai & Giacalone 2016; Kilpua et al. 2021; Cliver et al. 2022, and references therein). Analyses of SEP data allow us to study different processes in the Sun and heliosphere, namely the acceleration of various populations of energetic particles, their injection into interplanetary space, interactions with magnetic fields in the heliosphere, and related terrestrial effects (e.g. Anastasiadis et al. 2019, and references therein). In this article we consider only ions (mostly protons) as SEPs. Unlike galactic cosmic rays (GCRs), SEPs are not omnipresent near the Earth. However, when accelerated during sporadic solar eruptive processes, their fluxes can be many orders of magnitude greater than those of GCRs in the lower-energy range, up to approximately 1 GeV/n, for several hours or even days. The energy of SEPs is typically several tens of MeV/n, occasionally exceeding 100 MeV/n and rarely reaching the GeV energy range. High-energy SEPs can initiate nucleon-electromagnetic-muon cascades in the atmosphere, whose secondary particles can be detected by ground-based detectors such as neutron monitors (NMs) or ionisation chambers (ICs). This SEP event type is observed as an increase, above the GCR background, in the NM count rate or IC compensation voltage, and is called a ground-level enhancement (GLE; see e.g. Shea & Smart 1982; Poluianov et al. 2015). To be registered by NMs, SEPs must have energy greater than ≈430 MeV/n for NMs located at sea level and ≈300 MeV/n for NMs in high-altitude polar regions (for details, see Mishev & Poluianov 2021; Poluianov & Batalla 2022). Since the first reported detection in February 1942, called GLE #1 (Forbush 1946), 73 such GLEs have been detected by ground-based detectors up to GLE #73 (Mishev et al. 2022; Papaioannou et al. 2022; Klein et al. 2022) at the time of writing, whereas further investigations might be beneficial before the 1970s (Poluianov et al. 2017; Hayakawa et al. 2021). Early GLEs (GLEs #1–4) were mostly registered in the ICs before the regular operations of the NM. From the early 1950s onwards, standard NMs were in continuous operation and provided a homogeneous dataset of cosmic-ray variability, including the registration of GLEs (Simpson 2000; Shea & Smart 2000; Miroshnichenko et al. 2013; Bütikofer 2018; Väisänen et al. 2021). SEP events observed with NMs were collected in the GLE database that originated at the US Air Force Laboratory (Shea et al. 1985; Gentile et al. 1990). Later, the Australian Antarctic Division took over responsibility (Duldig & Watts 2001), and the database is currently under maintenance at the University of Oulu (Usoskin et al. 2020a). The first GLE recorded by the global NM network was GLE #5 (23 February 1956), which was the strongest measured GLE with the hardest known SEP energy spectrum (Vashenyuk et al. 2008; Tuohino et al. 2018; Usoskin et al. 2020b). This GLE immediately led to intensive discussions in the contemporaneous scientific community (e.g. Meyer et al. 1956; Dorman 1957; van Allen & Winckler 1957; Hayakawa et al. 1958). Even today, GLE #5 is of great importance as it is often considered a reference for extreme SEP events that have been recently discovered in cosmogenic isotopes in tree rings and ice cores (Miyake et al. 2012, 2019; Usoskin et al. 2013; Mekhaldi et al. 2015; Brehm et al. 2021; Paleari et al. 2022; Cliver et al. 2022), and for terrestrial and technological impacts of strong and extreme SEP events (Dyer et al. 2003, 2018; Calisto et al. 2013; Miroshnichenko 2018; Miyake et al. 2019; Hands et al. 2022). The physical mechanisms of SEP acceleration during GLE #5 are still a topic of scientific discussion (e.g. McCracken et al. 2023). Accordingly, it is crucial to obtain information that is as accurate and precise as possible for this GLE.
The NM count rate dataset for GLE #5 was collected in the International GLE Database (IGLED1; see Usoskin et al. 2020a) where the verified and best-quality data are presented. However, in 1956, the source data were manually typed and occasionally stored in the form of plots compiled from different sources, some of which were secondary or even modified, leading to notable inhomogeneities and discrepancies with one another. For example, the count rates of the Leeds NM were stored in the IGLED at a 5 min resolution (Belov et al. 2005; Usoskin et al. 2020a), whereas the original measurements of the Leeds NM for GLE #5 were performed with a 15 min integration time (Marsden et al. 1956; Rishbeth et al. 2009). The probable reasons for this discrepancy are as follows. The 5 min Leeds NM data were included in the IGLED from the IZMIRAN database2 (see Fig. 4 in Belov et al. 2005). This dataset appears visually identical to Lev Dorman’s smooth hand-drawn curve interpolated between the original 15 min data points over a log-scale plot, as shown in Fig. V.6 of Dorman (1957, p. 487), which is also stored as images in the IZMIRAN database. This suggests that the 5 min Leeds NM dataset in IGLED is most likely a digitised version of the hand-drawn curves based on Dorman (1957). Similar cases are found for other NM datasets in GLE #5 as well. There were also other discrepancies in the GLE #5 data subsets related to different timings and peak values, partially because the IGLED included data for GLE #5 from the IZMIRAN database and other sources in which some inconsistencies could be present.
For this study we critically revised the existing dataset of NM records for GLE #5 by collecting and digitising the source records of the NM measurements, focusing on primary and contemporary source records to exclude or at least minimise the possibility of data manipulation or alterations performed later. On this basis, we produced a new NM dataset for GLE #5 (publicly available in the IGLED) which is then used for the estimation of the temporal evolution of the energy spectra and pitch-angle distributions of SEPs that caused GLE #5, as well as their full event-integrated fluence. This provides a revised reference basis for further analyses and modelling of strong and extreme SEP events and their terrestrial impacts.
2. Source reports of the contemporaneous neutron monitor measurements
We located source records for contemporaneous NM measurements of GLE #5 to digitise their figures and source tables. These datasets were derived from contemporaneous publications and archival materials in the Simpson Collections at the University of Chicago Archives. We describe the latter as MS (manuscript) Simpson B## (box number) F## (folder number), following the manuscript catalogue of the University of Chicago Archives. For example, MS Simpson B217 F15 stands for Manuscript Simpson, Box 217, Folder 15. Figure 1 shows two examples of Simpson manuscripts from the University of Chicago Archives. The use of the original data presented in this study led to a significant revision of the NM count rate series collected previously in IGLED. The results are summarised in two tables. Table 1 presents the NM stations for which data is available for GLE #5, along with their location characteristics, including geographic coordinates, altitude, and geomagnetic cutoff rigidity for 23 February 1956 (details of its calculation are provided in Sect. 4). Geographic coordinates and altitudes were obtained from individual NM reports and the observatory catalogue of the United States Air Force Cambridge Research Laboratories (Shea 1972). Table 2 lists the references of the data sources and their respective data characteristics. The data profiles of individual stations are discussed below.
 |
Fig. 1. Example images of archival records for the NM measurements during GLE #5. Left panel shows a summary for NM of the USS Arneb at Wellington Harbour (MS Simpson B218 F1). Right panel shows a report for Berkeley NM (MS Simpson B216 F12). Both are reproduced by courtesy of the Hanna Holborn Gray Special Collections Research Center, University of Chicago Library. |
NMs considered in this study.
The Leeds NM dataset was obtained from Marsden et al. (1956, hereafter Ma56). We tabulated the values in the Ma56 Table 1 for the measurements of the two NMs (NM1 and NM2, with 10 cm and 20 cm of the lead moderator, respectively) between 16:30 on 22 February 1956 and 05:00 on 23 February 1956. We also digitised Ma56 Fig. 1 for the average count rate of the two NMs (NM1+NM2)/2 between 03:30 and 13:30 on 23 February 1956. The Ma56 figure and table agree with each other for overlapping periods of time, and confirm that the minimal measurement time resolution was indeed 15 min (Rishbeth et al. 2009), in contrast to the IZMIRAN database that provides datasets in 5 min intervals from Dorman (1957). Therefore, we supplemented the tabulation with our digitisation of Ma56 Fig. 1 as an average for NM1 and NM2 at Leeds for the GLE decay phase. We note that there is a minor difference (≈5%) in the NM1 and NM2 count rates, but their summation makes it closer to the standard IGY design with the moderate lead producer depth of ≈13.5 cm (Stoker et al. 2000).
The GLE #5 measurements at NMs in Chicago, Climax, Sacramento Peak, Huancayo, Mexico, and USS Arneb (located at Wellington Harbour in New Zealand during GLE #5) were collected in the University of Chicago, and were first published as a graphical plot (Fig. 4) in Meyer et al. (1956). In Figs. 2 and 3 of Meyer et al. (1956), the 1 min resolution graphical datasets for Chicago and USS Arneb NMs were shown; they were described in the text as follows (p. 770): “Both the stations at Chicago and on the U.S.S. Arneb were equipped with special alarm systems which change the recording intervals from 15 minutes to one minute intervals as soon as the intensity rises approximately 60% above normal.” However, it was not clear from this text if the data in Meyer et al. (1956) is pressure-corrected or not. The original data tabulated for Fig. 4 of Meyer et al. (1956) were found in the MS Simpson B105 F14 in the University of Chicago Archives as tables with barometrically corrected count rates from 03:00 UT 23 February 1956. Their temporal resolutions were 15 min for Chicago, Climax, Mexico, and USS Arneb NMs and 30 min for Sacramento Peak and Huancayo NMs. However, the note in MS Simpson B105 F14 implies that the Climax NM was interpolated to 15 min data from 20 min data (Meyer et al. 1956). Metadata for the University of Chicago NMs (standard pressure and coordinates of NM locations) were described in Table 2 of Simpson et al. (1953).
Later on, in MS Simpson B218 F1, we found the tabulations of NMs in Chicago, Climax, Sacramento Peak, Huancayo, Mexico, and USS Arneb with their individual time intervals, pressure, and uncorrected and corrected count-rate data that have been collected in the University of Chicago. For Climax NM, we found original 20 min data until 21:00 UT. We also found 1 min resolution tabulated data for USS Arneb, Chicago, and Climax NMs for the time around the GLE peak, which makes an important new finding of this work. The datasets in MS Simpson B218 F1 also allowed us to verify the standard pressure and the barometric correction coefficient that were used back in 1956. We found that the pressure correction for NMs collected in the University of Chicago was not fully correct in comparison with the modern approach; specifically, only the GCR NM counts were corrected for the pressure, while the SEP-related counts were not corrected at all. The existence of uncorrected NM count rates and pressure data allowed us to recalculate the pressure-corrected data using the standard modern approach (Usoskin et al. 2020a).
The Albuquerque NM dataset was published as a figure in Brown (1956). We also located the Albuquerque source table in MS Simpson B217 F15. This record shows a 3 min shift, as discussed in the main text of Brown (1956), and presents count rates with a 15 min resolution in general and a 5 min resolution around the peak. The count rate for 02:03–03:03 UT was obtained from Brown (1956). Notably, the late phase of GLE #5 has not been fully documented for the Albuquerque NM.
The Berkeley NM dataset was known only from Dorman (1957, p. 486), as discussed in Shea et al. (2001). However, we located the source table for the Berkeley NM in the MS Simpson B216 F12. This source table shows the NM measurements with a 15 min resolution. We also found a count rate figure in the MS Simpson B217 F13, which was used to clarify the measurement time intervals.
The Ottawa NM datasets were published with a 5 min resolution and barometric corrections, as shown in Fig. 1 of Rose & Katzman (1956). We located the source table in the MS Simpson B217 F17. Two NMs were in operation in Ottawa during GLE #5: the “old” NM (count rate ≈105 counts min−1) and the “new” NM (count rate ≈300 counts min−1). Unfortunately, the new NM was saturated at 04:00–05:10 UT and failed to measure the GLE peak. Accordingly, we used only the data from the old NM. In addition, we also located a table with barometric measurements and a table for the 1 min resolution observations from 03.30–05:00 UT without pressure corrections (MS Simpson B217 F17). We calculated the pressure-corrected 1 min data for the “old” Ottawa NM. It was unclear what reference pressure was used in 1956 for Ottawa NM, but the best agreement between 5 min and 1 min data was achieved using the value of 1010 mb. Even using this value, 1 min pressure-corrected data still differed insignificantly from 5 min data for overlapping time intervals, which is possible because of a reading error of approximately 5% for 1 min time intervals, as mentioned in the MS Simpson B217 F17. Accordingly, we used the 1 min data for the period of time 03.30–05:00 UT and 5 min data resolution outside this period of time in our study, and applied the correction for the reading error mentioned above.
Two datasets also exist from German NMs, in Göttingen and Weißenau, which were not known to Shea et al. (2001), but were acquired through the IGLED via the IZMIRAN database (Dorman 1957, p. 482). These datasets are shown in Fig. 1 in Meyer (1956) and Fig. 1 of Ehmert & Pfotzer (1956). We digitised these plots to derive 15 and 20 min resolution datasets for the Göttingen and Weißenau NMs, respectively.
During GLE #5 the Stockholm NM in Sweden was in operation. This dataset is shown in Fig. 2 in Sandström & Eckhartt (1956). This diagram was digitised to derive an hourly dataset.
At that time, Japanese scientists operated an NM on Mount Norikura (hereafter Mt. Norikura). This dataset is published in two figures in IRC (1957, p. 225). In addition, we managed to locate their source tables in MS Simpson B218 F2. We derived the Mt. Norikura datasets at 5 min and 15 min resolutions from these source tables. We primarily used 5 min data and added 15 min data when the 5 min dataset was not available.
We omitted the “Mt. Wellington (MTWL)” NM dataset listed in IGLED because it was most likely a result of misinterpretation. The MTWL dataset is not shown in Table 2 of Rishbeth et al. (2009) or in the original database of Louise Gentile (Shea et al. 1985; Gentile et al. 1990), although its name was confirmed only from Belov et al. (2005) onwards. The MTWL NM was certainly located in Tasmania, but it started operations on 10 June 1956 (see Table 1 in McCracken 1959) and could not have detected GLE #5 in February 1956. The Hobart group unequivocally observed GLE #5 not by an NM, but by IC and Geiger-Müller counters (Fenton et al. 1956). The IGLED acquired the MTWL dataset from the IZMIRAN database, which was introduced by confusion. The IZMIRAN dataset seemingly mislabeled Fig. V.33 of Dorman (1957), originally called “Wellington”, as “Mt. Wellington” and accommodated a data file with the name C005MTWL.DAT. The original figure by Dorman indicates that the measurements were actually made by the NM on board the ship USS Arneb in Wellington Harbour in New Zealand and not on Mt. Wellington in Australia, as was erroneously ascribed later (see e.g. Belov et al. 2005). We note that this dataset was not used in the analysis by Usoskin et al. (2020b) because of time series problems.
Additionally, we located a source table for the NM data series from Durham (Lockwood et al. 1956) in the MS Simpson B217 F14. The Durham NM dataset was previously known (Rishbeth et al. 2009), but was not digitally available in IGLED. Durham NM is not a standard International Geophysical Year (IGY) instrument design. However, this NM had a similar to IGY design energy response to the nuclear component of cosmic radiation with a counting rate of ≈200 counts min−1 (Lockwood et al. 1956, p. 247). The source table shows the Durham data at an hourly resolution. The same group operated another IGY NM on Mt Washington; however, this NM did not capture the pre-increase, the onset, or the main phase of GLE #5 and could only confirm the decay phase from 16:30 UT onwards (Lockwood et al. 1956). We did not use this dataset or produce the corresponding IGLED file; quantitative analysis of this record was hardly possible owing to the lack of the documented pre-increase count rate.
Most NM records explicitly mention pressure corrections (see column PC in Table 2). NM records collected in the University of Chicago (except USS Arneb NM) also include uncorrected count rates and pressure measurements, which allows us to recalculate pressure-corrected count rates. Three reports (Göttingen, Weißenau, and Mt. Norikura) did not clarify whether their data were pressure-corrected, as shown in Table 2. Considering the relatively short period of the event registration and its very high magnitude, the use of uncorrected data should not significantly affect the results of the physical interpretation of these NM datasets. Specifically, > 70% of the time-integrated increase I was recorded within the first three hours of the event for all the NMs considered here so that significant changes in the atmospheric pressure are unlikely.
Sources of NM data during GLE #5 and their data specifications.
3. Analyses of the neutron monitor records
We revisited all available NM datasets related to GLE #5. The measurement intervals were not uniform. As shown in Fig. 2, our reanalysis required an overall revision of the NM datasets for GLE #5 with respect to the previously available records collected in the IGLED and IZMIRAN databases. For the peak phase of GLE #5, we now possess 1 min resolution datasets for the Chicago, Climax, Ottawa, and USS Arneb NMs; 5 min resolution for the Mt. Norikura and Albuquerque NMs; 15 min resolution datasets for the Berkeley, Göttingen, Leeds, and Mexico NMs; a 20 min resolution dataset for the Weißenau NM; 30 min resolution datasets for the Huancayo and Sacramento Peak NMs; and hourly resolution datasets for the Stockholm and Durham NMs.
 |
Fig. 2. Comparison of the NM data collected in this study (red bars), the recent version stored in IGLED (before the revision suggested here, denoted as “old IGLED” in the legends and shown as dashed blue lines), and the original version of IGLED compiled in the 1970s–1990s by Louise Gentile (denoted as “LG” in the legends and shown as dotted green lines; Shea et al. 1985; Gentile et al. 1990). |
For further analysis, we set a baseline to estimate the background GCR level for each instrument. A slight difference in the baselines can affect the percentage increase in the GLE level against the GCR background. However, contemporaneous publications occasionally used different baselines without explicit clarification. This is one of the main sources of the differences between the peak values in our study and those in contemporaneous reports. Here we took the baseline following the standard procedures used in IGLED, where it was considered as the mean count rate level over two hours before the hour of GLE onset, when possible. For GLE #5, this implies 01–03 UT of 23 February 1956. However, for a considerable number of records, this was not possible; therefore, we used the time interval closest to that defined by the standard IGLED procedure. This can lead to an additional uncertainty of the order of several percentage points for the increased values for these NM records. The exact intervals used to calculate the baselines are listed in Table 2.
We computed the relative GLE enhancements above the baseline cosmic ray levels and compared them with those in the existing IGLED databases and Louise Gentile’s database (LG). The IZMIRAN dataset is nearly identical to that of IGLED and is not shown in the figure. The revised NM dataset is mostly consistent with LG and differs from the previous version of IGLED for mutually existing NM records, including five more NM records than those used in LG and one more NM (Durham) than those included in the current IGLED version. The temporal resolution was improved to 1 min resolution around the peak phase for the Chicago, Climax, Ottawa, and USS Arneb NMs. The new Huancayo NM dataset has a revised decay phase compared with the LG data because of the more accurately estimated baseline level. The Mt. Norikura NM dataset was also slightly downscaled compared with the LG dataset.
The computed time-integrated increases, which are often used to quantify the strength of GLEs (Asvestari et al. 2017), during GLE #5 are shown in the I column of Table 2. We calculated the I value for a given NM as an integral of GLE signal in Fig. 2, with the time expressed in hours. The de-trending procedure (Usoskin et al. 2020a), which considers possible slow trends in the GCR background, was not applied here. We evaluate the uncertainty of the I determination for the GLE #5 NM data as 10% of I, similarly to Usoskin et al. (2020a). We note that for the Albuquerque and USS Arneb, there were short periods of missing count rates during the GLE decay phase. For the I calculation for these time intervals, we interpolated the GLE increase values, assuming an exponential decay function. The I values calculated using the interpolated values are shown in italics in Table 2.
Occasionally, the original publications did not include all the NM station metadata required for analysis (e.g. the nominal barometric pressure). Therefore, to produce data files in IGLED format, we used all the available station information from the original sources, and if some station information was missing, it was taken from later GLE files from the IGLED database or the World Data Center for Cosmic Rays at Nagoya University3.
The new datasets provided here supersede the previous version of the data files in the IGLED database. Notably, the Chicago, Climax, Ottawa, and USS Arneb data are now available at a 1 min resolution around the peak of GLE #5. Meanwhile, the Huancayo and Mexico datasets are available only at 30 and 20 min resolutions. This result allows us to better constrain the time dependence of the SEP spectra for the low-energy component, whereas it still leaves a large uncertainty in the time dependence of higher-energy SEPs.
4. Assessing the spectra of GLE #5 using the revised data
To analyse GLE #5, we used the magnetosphere as a giant spectrometer, exploiting the fact that NMs at different geographic locations are sensitive to the different energy ranges of the SEP spectra and the direction of particle arrival. Hence, we modelled the response of each station in the global NM network using the updated NM yield function (for details, see Mishev et al. 2020) and performed the corresponding optimisation over the experimental records, similar to that by Cramp et al. (1997) and Vashenyuk et al. (2006).
First, the propagation of charged cosmic ray particles in the magnetosphere was modelled considering the magnetosphere consisting of an internal field (the International Geomagnetic Reference Field (IGRF) geomagnetic model; Alken et al. 2021) and an external field (the Tsyganenko-89 model; Tsyganenko 1989). Combining the internal and external magnetic fields allowed us to compute, with good accuracy, the asymptotic directions and the cutoff rigidities of the NMs used for the analysis (for details, see Kudela & Usoskin 2004; Nevalainen et al. 2013; Larsen et al. 2023, and the discussion therein). The cutoff rigidity at a given location indicates the minimum rigidity (momentum per unit charge) of a charged particle that allows it to reach that location (e.g. Cooke et al. 1991). Figure 3 shows the geographical distribution of the geomagnetic rigidity cutoff at the peak time of GLE #5 calculated using the OTSO model (Oulu–Open-source geomagneToSphere prOpagation tool; Larsen et al. 2023) with a Kp index of 0.333 (Matzka et al. 2021). The tabulated values of the effective cutoff rigidities for the used NMs are shown in Table 1. NMs operated during GLE #5 (denoted by white circles in Fig. 3) cover the entire range of cutoff rigidities from almost no cutoff for polar NM stations to a very high cutoff at Huancayo and Mt. Norikura.
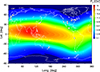 |
Fig. 3. Geographical distribution of the geomagnetic vertical cutoff rigidity for 23 February 1956, prior to the event onset, calculated by the OTSO model (Larsen et al. 2023) using the combination of the IGRF (Alken et al. 2021) and TS89 (Tsyganenko 1989) models for the internal and external part of the magnetosphere, respectively. The locations of the NMs from Table 1 are shown as dots. |
The method employed here follows the approach initially developed by Cramp et al. (1997), with details and applications provided elsewhere (Mishev et al. 2018, 2021a, 2022). Generally, the response of each NM is computed as an integral over the rigidity P of the product of the primary energetic-particle spectrum J(P, t) and NM yield function S(P, h), which encompasses the full complexity of particle propagation in the Earth’s atmosphere and the registration capability of the NM itself (Clem & Dorman 2000). Therefore, the count rate of an NM at a given altitude (atmospheric depth h) and time t can be expressed as
where Pc is the local geomagnetic cutoff rigidity, h is the atmospheric depth (or altitude), Si(P, h) [m2 sr] is the NM yield function for primaries of particle type i (protons and/or α-particles), and Ji(P, t) [GV m2 sr s]−1 is the rigidity spectrum of the primary particles of type i at time t. Accordingly, the NM count rate increase is given as the ratio of the count rates caused by SEPs and GCRs, as computed using Eq. (1). The GCR-related part is modelled using force-field approximation of solar modulation (Gleeson & Axford 1968). We used GCR local interstellar from Vos & Potgieter (2015) with solar modulation potential taken from Usoskin et al. (2017), and heavier GCR species were taken into account according to Koldobskiy et al. (2019). Therefore, knowing the GCR part, the SEP spectrum should be reconstructed by optimising the modelled response to the actual data (see details in Mishev 2023). Optimisation was performed using the method originally developed by Levenberg (1944) and Marquardt (1963) and employs the algorithms proposed by Aleksandrov (1971) and Golub & Van Loan (1980; for further details, see Mishev et al. 2005). This full method was recently verified based on direct space-borne measurements (for details, see Mishev et al. 2021b; Koldobskiy et al. 2019; Koldobskiy & Mishev 2022).
Using the revised NM records and the method described above, we assessed the spectra and angular distributions of SEPs during GLE #5, as shown in Fig. 4. The best spectral fit of the data was achieved using a modified power-law rigidity spectrum:
 |
Fig. 4. Derived rigidity spectra along the axis of symmetry (panel A) and illustration of PAD (given with respect to the axis of symmetry at 1 GV, panel B) during selected periods of GLE #5. The black solid line corresponds to the GCR flux. The times (UT) in the legend refer to the beginnings of the 15 min integration intervals over which the data are taken. |
Here J∥(P) in [m−2 s−1 sr−1 GV−1] is the flux of particles with rigidity P in [GV] along the axis of symmetry of arriving SEPs, J0 is the flux of protons at P = 1 GV, and γ is the power-law exponent with the steepening of δγ (in [GV−1]). Accordingly, the SEP angular distribution, quantified via the pitch angle distribution (PAD), was approximated with a Gaussian shape as
where α is the particle pitch angle and σ is the width of the PAD.
The SEP flux reconstruction for this event is specific because of a relatively small number of NM stations (compared to the analysis of subsequent and modern GLEs; see e.g. Mishev & Usoskin 2020) observing the event, which constraints the use of the network as a giant spectrometer due to large “blind spots” (see e.g. their Fig. 2 in Mishev & Usoskin 2020, and discussion therein), as well as the overlapping asymptotic directions of several NMs (see e.g. their Fig. 2 in Vashenyuk et al. 2008). However, we obtained stable solutions to the equations listed above. They showed a high degree of PAD anisotropy, with the highest values of the SEP flux during the initial phase of the event and isotropisation of the PAD combined with the weakening of the SEP flux during the main phase. The SEP spectra derived using the above-mentioned records differ slightly from previous estimates of the spectra derived using IGLED data, and reveal somewhat softer spectra and a wider PAD, specifically during the initial phase of the event (e.g. Vashenyuk et al. 2008; Tuohino et al. 2018; Mishev 2023).
5. Fluence of solar energetic particles
We also reconstructed the event-integrated SEP fluence using the method of “effective rigidity” (Koldobskiy et al. 2018, 2019; Usoskin et al. 2020a), which considers NMs as threshold detectors. This approach is based on the assumption of the isotropic PAD of SEP fluxes and does not consider temporal variability. Within the effective rigidity approach, individual relative event-integrated NM responses to SEPs IGLE are assumed to be directly proportional to the fluence of SEPs with rigidity above the effective threshold: F(> Reff) = κ ⋅ NGCR ⋅ IGLE, where Reff and κ are the effective rigidity and the scaling factor, respectively, which depend on the cutoff rigidity and altitude of the NM location, being constant for a given NM, and where NGCR is the modelled NM response to GCR particles accounting for the solar modulation conditions during the event. The obtained SEP fluence estimate for GLE #5 is shown in Fig. 5. GLE #5 remains the most powerful SEP event registered directly. The new SEP fluence estimate appears slightly softer but – by lucky coincidence – consistent within the uncertainties with recent estimate based on the previous GLE #5 datasets (Usoskin et al. 2020a). To illustrate this, we fitted the obtained fluence estimates by the power law of rigidity with an exponential cutoff. The obtained best-fit parameters appear to agree within the uncertainties for the analyses based on the new estimates and previous versions of the GLE #5 NM data (shown in Fig. 5). Therefore, the fit parameters obtained in the reconstruction of Usoskin et al. (2020a), and related physical results on the joint fit of low-energy and high-energy GLE fluences (Koldobskiy et al. 2021), as well as reconstructions of historical extreme SEP event fluences using GLE #5 fluence (Usoskin et al. 2020b; Koldobskiy et al. 2022, 2023; Paleari et al. 2022) remain valid.
 |
Fig. 5. SEP fluence during GLE #5 calculated using the effective rigidity method. The results obtained with the data collected in this study are shown as red points, while the reconstruction from Usoskin et al. (2020a) is shown with blue markers. The 68% confidence interval for the best fit with power law of rigidity with exponential cutoff performed in Usoskin et al. (2020a) is shown as grey shade. |
6. Conclusion
In this study we collected, validated, and reanalysed the source records for NM measurements during the GLE #5 event (23 February 1956) using contemporaneous publications as well as unpublished archival reports from the University of Chicago Archives (Table 2). We digitised and encoded the related figures and handwritten or typed tables to derive the count rates of individual NMs during the event. The new dataset notably improved the reliability of individual NM records for GLE #5 (Fig. 2). In particular, some previously used data were found to be based not on the original records, but on the digitisation of handmade smooth curves plotted by Dorman (1957) for individual NMs. The previously considered “Mt. Wellington” NM dataset (Belov et al. 2005; Usoskin et al. 2020a) has been now identified as mislabelled and removed from the database. Furthermore, we added a dataset from Durham NM (Lockwood et al. 1956), which had not been previously included in IGLED. Now we provide 1 min resolution original datasets for the USS Arneb, Chicago, Climax, and Ottawa NMs, while previously, only 5 min data were used in IGLED, which in turn were based not on real counts, but rather on the interpolation of 15 min data. The Ottawa NM 1 min data were previously known in Louise Gentile’s database, whereas this dataset coincided with the Ottawa dataset without pressure corrections in MS Simpson B217 F17. We performed additional checks to find the standard pressure used for this NM in 1956 and computed the SEP variations registered by Ottawa NM with pressure corrections. Together, four rediscovered 1 min precision datasets allow the rise of and the main phase of GLE #5 to be studied in great detail. The revised data are included in the International GLE Database4 (IGLED) to make them fully available to the scientific community.
We used newly available data to reconstruct the physical properties of SEP fluxes during GLE #5. For that purpose, we also computed the geomagnetic cutoff rigidities and corresponding asymptotic directions for individual NM stations observing GLE #5 (Fig. 3 and Table 1). Then we performed a preliminary reconstruction of the temporal evolution of energy spectra and angular characteristics of the SEPs during the initial and main phases of the event. It was found that the SEP fluxes were highly anisotropic, especially during the initial phase of the event. Using the independent effective-energy method, we calculated the event-integrated SEP fluence, which was found to be consistent with recent estimates (Usoskin et al. 2020a,b) based on the previous version of GLE #5 NM data, within the uncertainties.
The revised reference dataset for GLE #5, the most powerful GLE directly registered during the last 85 yr as well as SEP fluxes reconstructed from these newly available data will improve modelling studies of radiation doses and technological hazards related to SEP events, particularly at flight altitudes and in near-Earth space (Dyer et al. 2003, 2018; Sato et al. 2018; Hands et al. 2022). They can also be used to bridge the observational knowledge of strong SEP events and past extreme solar particle events detected as enhancements of cosmogenic isotope concentrations in terrestrial archives such as tree rings and ice cores (Miyake et al. 2019; Cliver et al. 2022; Usoskin 2023).
Available at the World Data Center for Solar-Terrestrial Physics in Moscow: http://www.wdcb.ru/stp/data/cosmic_rays/G_L_E/
Acknowledgments
We thank Hanna Holborn Gray Special Collections Research Center, University of Chicago Library for letting us access and study archival manuscripts in the Simpson Papers. We thank IGLED (The University of Oulu), IZMIRAN, and WDC Cosmic Rays (Nagoya University) for providing data files of NM records around GLE #5. We thank NM observatories of Albuquerque, USS Arneb, Berkeley, Chicago, Climax, Durham, Göttingen, Huancayo, Leeds, Mexico, Mt. Norikura, Ottawa, Sacramento Peak, Stockholm, and Weißenau for operating NM and recording the count rates and pressures during the GLE #5. This work was partly supported by the Academy of Finland (projects 330063 QUASARE, 321882 ESPERA, and 354280 GERACLIS), Horizon Europe program (project ALBATROS), National Science Fund of Bulgaria under contract KP-06-H28/4. H.H.’s research was conducted under the financial support of JSPS Grant-in-Aids JP20K22367, JP20H05643, JP21K13957, and JP22K02956. H.H. was partly funded by JSPS Overseas Challenge Program for Young Researchers, the ISEE director’s leadership fund for FYs 2021–2023, the Young Leader Cultivation (YLC) programme of Nagoya University, Tokai Pathways to Global Excellence (Nagoya University) of the Strategic Professional Development Program for Young Researchers (MEXT), the young researcher units for the advancement of new and undeveloped fields by Institute for Advanced Research of Nagoya University (the Program for Promoting the Enhancement of Research Universities), and the NIHU Multidisciplinary Collaborative Research Projects NINJAL unit “Rediscovery of Citizen Science Culture in the Regions and Today”. We acknowledge the support of the International Space Science Institute (ISSI) in Bern, Switzerland via International Teams No. 510 (SEESUP – Solar Extreme Events: Setting Up a Paradigm), No. 475 (Modeling Space Weather And Total Solar Irradiance Over The Past Century) and No. 585 (REASSESS) and the visiting fellowship programme. H.H. thanks Chiaki Kuroyanagi and Yuta Uchikawa for their help in accessing copies of the book by Dorman (1957) and Margaret A. Shea and Ken G. McCracken for their helpful discussions. I.U. acknowledges the hospitality of ISSI in the framework of the Visiting Scientists Program. We are grateful to Margaret A. Shea and Don Smart for stimulating discussions about Louise Gentile’s original GLE dataset.
References
- Aleksandrov, L. 1971, USSR Comput. Math. Math. Phys., 11, 46 [CrossRef] [Google Scholar]
- Alken, P., Thébault, E., Beggan, C., et al. 2021, EPS, 73, 49 [Google Scholar]
- Anastasiadis, A., Lario, D., Papaioannou, A., Kouloumvakos, A., & Vourlidas, A. 2019, Phil. Trans. R. Soc. A: Math. Phys. Eng. Sci., 377, 20180100 [CrossRef] [Google Scholar]
- Aschwanden, M. 2012, Space Sci. Rev., 171, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Asvestari, E., Willamo, T., Gil, A., et al. 2017, Adv. Space Res., 60, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Belov, A., Eroshenko, E., Mavromichalaki, H., Plainaki, C., & Yanke, V. 2005, Ann. Geophys., 23, 2281 [NASA ADS] [CrossRef] [Google Scholar]
- Brehm, N., Bayliss, A., Christl, M., et al. 2021, Nat. Geosci., 14, 10 [Google Scholar]
- Brown, R. R. 1956, J. Geophys. Res., 61, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Bütikofer, R. 2018, Solar Particle Radiation Storms Forecasting and Analysis, The HESPERIA HORIZON 2020 Project and Beyond (Cham, Switzerland: Springer Nature), 95 [Google Scholar]
- Calisto, M., Usoskin, I., & Rozanov, E. 2013, Environ. Res. Lett., 8, 045010 [NASA ADS] [CrossRef] [Google Scholar]
- Clem, J., & Dorman, L. 2000, Space Sci. Rev., 93, 335 [Google Scholar]
- Cliver, E. W., Schrijver, C. J., Shibata, K., & Usoskin, I. G. 2022, Liv. Rev. Sol. Phys., 19 [Google Scholar]
- Cooke, D., Humble, J., Shea, M., et al. 1991, Il Nuovo Cimento C, 14, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Cramp, J., Duldig, M., Flückiger, E., et al. 1997, J. Geophys. Res., 102, 24237 [NASA ADS] [CrossRef] [Google Scholar]
- Desai, M., & Giacalone, J. 2016, Liv. Rev. Sol. Phys., 13, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Dorman, L. I. 1957, Cosmic Ray Variations (Moscow: State Publishing House) [Google Scholar]
- Duldig, M. L., & Watts, D. J. 2001, Proceedings of the International Cosmic Ray Conference, Int. Cosm. Ray Conf., 8, 3409 [NASA ADS] [Google Scholar]
- Dyer, C. S., Lei, F., Clucas, S. N., Smart, D. F., & Shea, M. A. 2003, IEEE Trans. Nucl. Sci., 50, 2038 [CrossRef] [Google Scholar]
- Dyer, C., Hands, A., Ryden, K., & Lei, F. 2018, IEEE Trans. Nucl. Sci., 65, 432 [CrossRef] [Google Scholar]
- Ehmert, A., & Pfotzer, G. 1956, Z. Naturforsch. A, 11, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Fenton, A. G., McCracken, K. G., Parsons, N. R., & Trost, P. A. 1956, Nature, 177, 1173 [CrossRef] [Google Scholar]
- Forbush, S. 1946, Phys. Rev., 70, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Gentile, C. L., Shea, A. M., & Smart, F. D. 1990, Int. Cosm. Ray Conf., 5, 148 [NASA ADS] [Google Scholar]
- Gleeson, L., & Axford, W. 1968, ApJ, 154, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Golub, G., & Van Loan, C. 1980, SIAM J. Numer. Anal., 17, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Hands, A., Lei, F., Davis, C., Space, et al. 2022, Weather, 20, e2022SW003155 [NASA ADS] [CrossRef] [Google Scholar]
- Hayakawa, S., Ito, K., & Terashima, Y. 1958, Prog. Theor. Phys. Suppl., 6, 1 [CrossRef] [Google Scholar]
- Hayakawa, H., Hattori, K., Pevtsov, A. A., et al. 2021, ApJ, 909, 197 [NASA ADS] [CrossRef] [Google Scholar]
- IRC 1957, Rep. Ionosphere Res. Jpn., 11, 162 [Google Scholar]
- Kilpua, E. K. J., Good, S. W., Dresing, N., et al. 2021, A&A, 656, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klein, K.-L., Musset, S., Vilmer, N., et al. 2022, A&A, 663, A173 [CrossRef] [EDP Sciences] [Google Scholar]
- Koldobskiy, S., & Mishev, A. 2022, Adv. Space Res., 70, 2585 [CrossRef] [Google Scholar]
- Koldobskiy, S. A., Kovaltsov, G. A., & Usoskin, I. G. 2018, Sol. Phys., 293, 110 [Google Scholar]
- Koldobskiy, S. A., Kovaltsov, G. A., Mishev, A. L., & Usoskin, I. G. 2019, Sol. Phys., 294, 94 [Google Scholar]
- Koldobskiy, S., Raukunen, O., Vainio, R., Kovaltsov, G., & Usoskin, I. 2021, A&A, 647, A132 [CrossRef] [EDP Sciences] [Google Scholar]
- Koldobskiy, S., Usoskin, I., & Kovaltsov, G. A. 2022, J. Geophys. Res. Sp. Phys., 127, e2021JA029919 [CrossRef] [Google Scholar]
- Koldobskiy, S., Mekhaldi, F., Kovaltsov, G., & Usoskin, I. 2023, J. Geophys. Res.: Space Phys., e2022JA031186 [Google Scholar]
- Kudela, K., & Usoskin, I. 2004, Czech. J. Phys., 54, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Larsen, N., Mishev, A., & Usoskin, I. 2023, J. Geophys. Res.: Space Phys., 128, e2022JA031061 [NASA ADS] [CrossRef] [Google Scholar]
- Levenberg, K. 1944, Q. Appl. Math., 2, 164 [Google Scholar]
- Lockwood, J. A., Yingst, H. E., Calawa, A. R., & Sarmaniote, G. 1956, Phys. Rev., 103, 247 [CrossRef] [Google Scholar]
- Marquardt, D. 1963, SIAM J. Appl. Math., 11, 431 [CrossRef] [Google Scholar]
- Marsden, P., Berry, J., Fieldhouse, P., & Wilson, J. 1956, J. Atmos. Terr. Phys., 8, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Matzka, J., Bronkalla, O., Tornow, K., Elger, K., & Stolle, C. 2021, Geomagnetic Kp Index. V. 1.0. GFZ Data Services, https://doi.org/10.5880/Kp.0001 [Google Scholar]
- McCracken, K. G. 1959, Phys. Rev., 113, 343 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, K., Shea, M., & Smart, D. 2023, Adv. Space Res., 72, 3414 [NASA ADS] [CrossRef] [Google Scholar]
- Mekhaldi, F., Muscheler, R., Adolphi, F., et al. 2015, Nat. Commun., 6, 8611 [Google Scholar]
- Meyer, B. 1956, Z. Naturforsch. A, 11, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, P., Parker, E. N., & Simpson, J. A. 1956, Phys. Rev., 104, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Miroshnichenko, L. 2018, J. Space Weather Space Clim., 8, A52 [CrossRef] [EDP Sciences] [Google Scholar]
- Miroshnichenko, L., Vashenyuk, E., & Perez-Peraza, J. 2013, Geomagn. Aeron., 53, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Mishev, A. 2023, JASTP, 243, 106021 [NASA ADS] [Google Scholar]
- Mishev, A., & Poluianov, S. 2021, Sol. Phys., 296, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Mishev, A., & Usoskin, I. 2020, J. Space Weather Space Clim., 10, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mishev, A., Mavrodiev, S., & Stamenov, J. 2005, Int. J. Mod. Phys. A, 20, 7016 [NASA ADS] [CrossRef] [Google Scholar]
- Mishev, A., Usoskin, I., Raukunen, O., et al. 2018, Sol. Phys., 293, 136 [Google Scholar]
- Mishev, A. L., Koldobskiy, S. A., Kovaltsov, G. A., Gil, A., & Usoskin, I. G. 2020, J. Geophys. Res.: Space Phys., 125, e2019JA027433 [CrossRef] [Google Scholar]
- Mishev, A., Koldobskiy, S., Kocharov, L., & Usoskin, I. 2021a, Sol. Phys., 296, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Mishev, A., Koldobskiy, S., Usoskin, I., Kocharov, L., & Kovaltsov, G. 2021b, Space Weather, 19, e2020SW002626 [CrossRef] [Google Scholar]
- Mishev, A., Kocharov, L., Koldobskiy, S., et al. 2022, Sol. Phys., 297, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Miyake, F., Nagaya, K., Masuda, K., & Nakamura, T. 2012, Nature, 486, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Miyake, F., Usoskin, I., & Poluianov, S. 2019, Extreme Solar Particle Storms; The Hostile Sun (Bristol, UK: IOP Publishing), 2514 [Google Scholar]
- Nevalainen, J., Usoskin, I., & Mishev, A. 2013, Adv. Space Res., 52, 22 [CrossRef] [Google Scholar]
- Paleari, C. I., Mekhaldi, F., Adolphi, F., et al. 2022, Nat. Commun., 13, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Papaioannou, A., Kouloumvakos, A., Mishev, A., et al. 2022, A&A, 660, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poluianov, S., & Batalla, O. 2022, Adv. Space Res., 70, 2610 [CrossRef] [Google Scholar]
- Poluianov, S., Usoskin, I., Mishev, A., et al. 2015, J. Astron. Space Sci., 32, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Poluianov, S., Usoskin, I., Mishev, A., Shea, M., & Smart, D. 2017, Sol. Phys., 292, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Rishbeth, H., Shea, M. A., & Smart, D. F. 2009, Adv. Space Res., 44, 1096 [NASA ADS] [CrossRef] [Google Scholar]
- Rose, D. C., & Katzman, J. 1956, Can. J. Phys., 34, 884 [NASA ADS] [CrossRef] [Google Scholar]
- Sandström, A., & Eckhartt, D. 1956, Tellus, 8, 279 [CrossRef] [Google Scholar]
- Sato, T., Kataoka, R., Shiota, D., et al. 2018, Space Weather, 16, 924 [CrossRef] [Google Scholar]
- Shea, M. A. 1972, Air Force Surv. Geophys., 243, AFCRL-72-0411, 224 [Google Scholar]
- Shea, M., & Smart, D. 1982, Space Sci. Rev., 32, 251 [NASA ADS] [Google Scholar]
- Shea, M., & Smart, D. 2000, Space Sci. Rev., 93, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Shea, M. A., Smart, D. F., Wada, M., & Inoue, A. 1985, Int. Cosm. Ray Conf., 5, 510 [NASA ADS] [Google Scholar]
- Shea, M. A., Smart, D. F., Pyle, K. R., Duldig, M. L., & Humble, J. E. 2001, Proceedings of the International Cosmic Ray Conference, Int. Cosm. Ray Conf., 8, 3405 [NASA ADS] [Google Scholar]
- Simpson, J. 2000, Space Sci. Rev., 93, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, J. A., Fonger, W., & Treiman, S. B. 1953, Phys. Rev., 90, 934 [CrossRef] [Google Scholar]
- Stoker, P., Dorman, L., & Clem, J. 2000, Space Sci. Rev., 93, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Tsyganenko, N. 1989, Planet. Space Sci., 37, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Tuohino, S., Ibragimov, A., Usoskin, I., & Mishev, A. 2018, Adv. Space Res., 62, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Usoskin, I. G. 2023, Liv. Rev. Sol. Phys., 20, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Usoskin, I. G., Kromer, B., Ludlow, F., et al. 2013, A&A, 552, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Usoskin, I., Gil, A., Kovaltsov, G., Mishev, A., & Mikhailov, V. 2017, J. Geophys. Res., 122, 3875 [NASA ADS] [CrossRef] [Google Scholar]
- Usoskin, I., Koldobskiy, S., Kovaltsov, G., et al. 2020a, A&A, 640, A17 [CrossRef] [EDP Sciences] [Google Scholar]
- Usoskin, I., Koldobskiy, S., Kovaltsov, G., et al. 2020b, J. Geophys. Res.: Space Phys., 125, e2020JA027921 [NASA ADS] [CrossRef] [Google Scholar]
- Väisänen, P., Usoskin, I., & Mursula, K. 2021, J. Geophys. Res.: Space Phys., 126, e2020JA028941 [CrossRef] [Google Scholar]
- van Allen, J. A., & Winckler, J. R. 1957, Phys. Rev., 106, 1072 [CrossRef] [Google Scholar]
- Vashenyuk, E., Balabin, Y., Perez-Peraza, J., Gallegos-Cruz, A., & Miroshnichenko, L. 2006, Adv. Space Res., 38, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Vashenyuk, E., Balabin, Y., & Miroshnichenko, L. 2008, Adv. Space Res., 41, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Vos, E., & Potgieter, M. 2015, ApJ, 815, 119 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Example images of archival records for the NM measurements during GLE #5. Left panel shows a summary for NM of the USS Arneb at Wellington Harbour (MS Simpson B218 F1). Right panel shows a report for Berkeley NM (MS Simpson B216 F12). Both are reproduced by courtesy of the Hanna Holborn Gray Special Collections Research Center, University of Chicago Library. |
| In the text | |
 |
Fig. 2. Comparison of the NM data collected in this study (red bars), the recent version stored in IGLED (before the revision suggested here, denoted as “old IGLED” in the legends and shown as dashed blue lines), and the original version of IGLED compiled in the 1970s–1990s by Louise Gentile (denoted as “LG” in the legends and shown as dotted green lines; Shea et al. 1985; Gentile et al. 1990). |
| In the text | |
 |
Fig. 3. Geographical distribution of the geomagnetic vertical cutoff rigidity for 23 February 1956, prior to the event onset, calculated by the OTSO model (Larsen et al. 2023) using the combination of the IGRF (Alken et al. 2021) and TS89 (Tsyganenko 1989) models for the internal and external part of the magnetosphere, respectively. The locations of the NMs from Table 1 are shown as dots. |
| In the text | |
 |
Fig. 4. Derived rigidity spectra along the axis of symmetry (panel A) and illustration of PAD (given with respect to the axis of symmetry at 1 GV, panel B) during selected periods of GLE #5. The black solid line corresponds to the GCR flux. The times (UT) in the legend refer to the beginnings of the 15 min integration intervals over which the data are taken. |
| In the text | |
 |
Fig. 5. SEP fluence during GLE #5 calculated using the effective rigidity method. The results obtained with the data collected in this study are shown as red points, while the reconstruction from Usoskin et al. (2020a) is shown with blue markers. The 68% confidence interval for the best fit with power law of rigidity with exponential cutoff performed in Usoskin et al. (2020a) is shown as grey shade. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



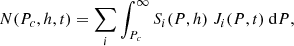
![$$ \begin{aligned} J_\parallel (P) = J_0 P^{-(\gamma +\delta \gamma (P-1 [\mathrm{GV}]))}. \end{aligned} $$](/articles/aa/full_html/2024/04/aa48699-23/aa48699-23-eq2.gif)