| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 15 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202348406 | |
| Published online | 03 April 2024 | |
Radial velocities from Gaia BP/RP spectra★
1
Leiden Observatory, Leiden University,
PO Box 9513,
2300 RA
Leiden,
The Netherlands
e-mail: verberne@strw.leidenuniv.nl
2
Institute for Astronomy, University of Edinburgh,
Royal Observatory, Blackford Hill,
Edinburgh
EH9 3HJ,
UK
3
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge
CB3 0HA,
UK
4
Kavli Institute for Cosmology, University of Cambridge,
Madingley Road,
Cambridge
CB3 0HA,
UK
5
European Southern Observatory,
Karl-Schwarzschild-Strasse 2,
85748
Garching bei Munchen,
Germany
Received:
27
October
2023
Accepted:
15
January
2024
Aims. The Gaia mission has provided us full astrometric solutions for over 1.5B sources. However, only the brightest 34M of them have radial velocity measurements. This paper aims to close that gap by obtaining radial velocity estimates from the low-resolution BP/RP spectra that Gaia now provides. These spectra are currently published for about 220M sources, with this number to increase to the full ~2B Gaia sources with Gαία Data Release 4.
Methods. To obtain the radial velocity measurements, we fitted Gaia BP/RP spectra with models based on a grid of synthetic spectra. From this we obtained the posterior probability on the radial velocity for each object. Our measured velocities show systematic biases that depend mainly on the colours and magnitudes of stars. We corrected for these effects by using external catalogues of radial velocity measurements.
Results. We present a catalogue of about 6.4M sources with our most reliable radial velocity measurements and uncertainties of <300 km s−1 obtained from BP/RP spectra. About 23% of them have no radial velocity measurement from the Gaia RVS. Furthermore, we provide an extended catalogue that contains all 125M sources for which we were able to obtain radial velocity measurements. This catalogue, however, also contains a fraction of measurements for which the reported radial velocities and uncertainties are inaccurate.
Conclusions. Although typical uncertainties in the catalogue are significantly higher compared to those obtained with precision spec-troscopy instruments, the number of potential sources to which this method can be applied is orders of magnitude higher than any previous radial velocity catalogue. Further development of the analysis could therefore prove extremely valuable in our understanding of Galactic dynamics.
Key words: techniques: radial velocities / catalogs / stars: kinematics and dynamics / Galaxy: kinematics and dynamics
The catalogue is available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/684/A29
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The Gaia mission (Gaia Collaboration 2016) has been collecting data since 2014, with its primary scientific data products being the positions, proper motions, and parallaxes of about 1.5B objects. In the recent Gaia Data Release 3 (DR3; Gaia Collaboration 2023), low-resolution spectra of ~220M objects have additionally been published. These spectra were obtained from two low-resolution prism spectrographs: BP observes in the wavelength range 330–680 nm and RP in the 640–1050 nm range; together they are referred to as XP spectra. Their primary purpose is to provide source classification and astrophysical information for the astrometric sources observed, for example stellar metallicity and line-of-sight extinction (Bailer-Jones et al. 2013). In order to measure stellar parameters, such as radial velocities and elemental abundances, Gaia is equipped with the Radial Velocity Spectrometer (RVS; Katz et al. 2023). However, RVS spectra, being limited to GRVS ≤ 16 in Gaia DR4, will not be available for all Gaia sources (Katz et al. 2023). XP spectra, on the other hand, will be published in DR4 for all sources in the astrometric catalogue with a limiting magnitude of G ≈ 20.7 (Gaia Collaboration 2016). The current magnitude limit of XP spectra in Gaia DR3 is G = 17.65 (Gaia Collaboration 2023).
XP spectra have been recognised as a rich source of astro-physical information, with efforts to measure [M/H], [α/M] [Fe/H], log g, Teff, and line-of-sight extinction, among other quantities (e.g. Rix et al. 2022; Zhang et al. 2023; Andrae et al. 2023a,b; Guiglion et al. 2024; Li et al. 2023). This work focuses on obtaining radial velocity measurements, for the first time, from the low-resolution XP spectra. Although the precision of any radial velocity measurement from XP spectra is expected to be lower than that of conventional spectroscopic surveys, the scientific content would still be very significant due to the number of objects (220M currently and ~2B in DR4). This would constitute a factor of ~6.5 increase in the total number of sources with radial velocity measurements compared to the currently largest radial velocity catalogue, Gaia DR3, which contains ~34M measurements. Additionally, the recently launched Euclid space telescope (Laureijs et al. 2011) also includes a low-resolution slitless spectrograph. Although the Euclid instrument operates in the near infrared, the spectral resolution is significantly higher1 compared to Gaia XP spectra, though still considered low-resolution. The method presented in this paper could in principle also be applicable to those data.
This work should be seen as a proof of concept. We focus on demonstrating our ability to obtain radial velocity information from Gaia XP spectra rather than obtaining the most accurate and precise measurements possible for all sub-types of objects appearing in Gaia DR3 XP spectra. We therefore advise readers to carefully consider if our measurements are appropriate for their specific use case.
This paper is structured as follows: Sect. 2 discusses the properties and format of Gaia XP spectra. Section 3 describes the analysis of the XP spectra we carried out to obtain radial velocity measurements. Section 4 provides the post-calibration we applied to our radial velocity measurements using reference radial velocities. Section 5 presents the random forest classifier (RFC) we trained for data quality assurance. Section 6 provides a validation of our calibrated results. Section 7 describes our main and extended catalogues, which we publish together with this paper. In Sect. 8 we discuss the science case of hypervelocity stars (HVSs) for our catalogue. In Sect. 9 we discuss our results and provide prospects for Gaia DR4. In Sect. 10 we give closing remarks.
2 BP/RP spectra
In the following section we discuss a number of important points on the calibration and representation of XP spectra in Gaia DR3. We only considered XP spectra from sources with G < 17.65, which is the main XP catalogue from Gaia consisting of ~219 M sources. The few hundred thousand sources fainter than this limit mainly consist of white dwarfs and quasi-stellar objects (QSOs; Gaia Collaboration 2023).
2.1 Gaia XP calibration
The Gaia mission relies on self-calibration where possible. In the case of spectra, this is only possible to a limited degree. The calibration of multiple measurements, taken possibly years apart using different charge-coupled devices (CCDs) and fields of view, into a single mean spectrum is described by De Angeli et al. (2023) and is done using self-calibration. The calibration onto a physical wavelength and flux scale is described by Montegriffo et al. (2023) and is performed using external measurements.
At wavelengths below 400 nm and above 900 nm, the wavelength calibration is less accurate, because there is an insufficient number of calibrator QSOs with emission lines in that part of the spectrum (see Fig. 19 of Montegriffo et al. 2023). In addition, there is a systematic offset in the RP spectra (Montegriffo et al. 2023), which would lead to a systematic offset in radial velocity if not corrected for. The exact origin of this offset is unknown, but Montegriffo et al. (2023) note that it might be caused by a systematic error in the line-spread-function model.
In terms of flux calibration, the uncertainties are typically underestimated (see Fig. 18 of De Angeli et al. 2023). This underestimation is more pronounced for bright sources but affects the majority of spectra and is wavelength dependent. The underlying cause of this underestimation is unknown.
2.2 Basis function representation
Gaia observes the same sources multiple times over a time span of years, using two different fields-of-view and an array of CCDs (Gaia Collaboration 2016). Small differences in the dispersion, wavelength coverage, instrument degradation, etc. between observations gives the opportunity to extract more spectral information (i.e. higher resolution spectra) from the sources than would be possible given a single observation. Representing this information in flux-wavelength space (henceforth referred to as sampled spectra), would be highly inefficient due to the small nature of the variations compared to the spectral resolution. For this reason, the Gaia consortium instead chose to represent the spectra as a series of coefficients for basis functions that describe the spectra. The BP and RP spectra are represented by 55 such spectral coefficients each, making for a total of 110 coefficients that describe every source. The first few coefficients contain most of the spectral information, since they are optimised for representing ‘typical’ Gaia sources (De Angeli et al. 2023). Alongside the spectral coefficients, Gaia has published their uncertainties and correlation coefficients, allowing us to construct the full covariance matrix for the coefficients of each source.
While providing more information than a sampled spectrum with the same number of samples, the representation in spectral coefficients also introduces challenges. Due to the individual basis functions being continuous functions over the entire wavelength range, the uncertainties on all spectral coefficients are correlated. This means that when converting the basis function representation into sampled flux-wavelength space, all data points are correlated. Random noise in the initial Gaia observations in particular causes random wiggles in the sampled XP spectra that could be mistaken for physical spectral features.
3 Spectral analysis
Now that we have discussed some of the important features of the XP spectra, we now describe the spectral analysis of these data we carried out to obtain radial velocity measurements.
In this study we chose to convert the spectral coefficients to sampled spectra using GaiaXPy2. The conversion is performed through the design matrix as
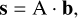 (1)
(1)
with s the mean sampled spectrum, A the design matrix provided by GaiaXPy, and b the spectral coefficients. This gives us two spectra for each source, BP and RP, which we chose to sample on a grid of Δλ = 2 nm. However, we did not use the entire spectra for our analysis: we selected the wavelength range 400500 nm for the BP spectra, while for the RP spectra we selected 640–900 nm. Two example sampled Gaia XP spectra are shown in Fig. 1. The BP range is chosen to include the prominent Balmer lines, but exclude the region below 400 nm, where the wavelength calibration might be problematic, and the region above 500 nm, where for many stars the continuum would dominate the fit. The RP-range is much wider and includes most of the RP spectral range, except the region above 900 nm, where again the wavelength calibration might be problematic (see Sect. 2.1).
Now that we have discussed how we handle the data, we describe in the following how we produced model spectra. We created the model M(Teff, log g, [Fe/H], vr, E(B−V)), where Teff, log g, and [Fe/H] correspond to the effective temperature, surface gravity, and metallicity from the PHOENIX spectral library, respectively (Husser et al. 2013), vr is the radial velocity, and E(B−V) the extinction along the line of sight. For the PHOENIX models, we only considered atmospheres with [α/H] = 0 for computational reasons. We shifted each of these models by a radial velocity with a step size of 30 km s−1. The parameter ranges for radial velocity, Teff, log g, and [Fe/H] are displayed in Table 1. The resulting models were convolved with the resolution of the externally calibrated XP spectra. This was done by interpolating the values from Table 1 in Montegriffo et al. (2023). These interpolated values were then used at each wavelength in the sampled data to spread the flux in wavelength space using a Gaussian with standard deviation 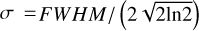 . Lastly, we applied extinction on a source-to-source basis using the 2D extinction map from Schlegel et al. (1998) and the re-calibration from Schlafly & Finkbeiner (2011), assuming all sources to be behind the extinction layer. The extinction law we used is from Fitzpatrick (1999).
. Lastly, we applied extinction on a source-to-source basis using the 2D extinction map from Schlegel et al. (1998) and the re-calibration from Schlafly & Finkbeiner (2011), assuming all sources to be behind the extinction layer. The extinction law we used is from Fitzpatrick (1999).
Having described how we prepared the XP spectra and created model spectra, we now describe how we fitted the spectral models to the XP spectra. Given an XP spectrum from Gaίa, we could determine the likelihood of the data given a model, P(D | M), from
![$P({\bf{D}}\mid {\bf{M}}) = {1 \over {\sqrt {{{(2\pi )}^k}|{\bf{C}}|} }}\exp \left( { - {1 \over 2}{{[{\bf{D}} - {\bf{M}}]}^ \top }{{\bf{C}}^{ - 1}}[{\bf{D}} - {\bf{M}}]} \right)$](/articles/aa/full_html/2024/04/aa48406-23/aa48406-23-eq3.png) (2)
(2)
where D is the data, M the model, k the number of dimensions, and C the covariance matrix of the data (e.g. Hogg et al. 2010). This holds in the case where the uncertainties are Gaussian with correctly estimated variances, which is not strictly true in our case. Because we over-sampled our sampled spectra with respect to the orthogonal bases, our covariance matrix in sampled space does not have full rank. To allow an inversion of the covariance matrix in sampled space, we only considered the diagonal elements and thus discarded correlation information. This caused the uncertainties on the radial velocity measurements to be further underestimated.
We calculated this likelihood for all models, after which we marginalised over the nuisance parameters Teff, log g, and [Fe/H]. We used flat priors on our parameters between the extrema of the parameter grid shown in Table 1. Teff is the exception; for computational reasons, we instead only considered models differing by no more than 500 K from an initial guess for Teff we made based on the BP – RP colour of a source and the extinction. The initial guess for Teff is described in Appendix A. During analysis of the results, we noticed that the performance of this initial guess is poor for E(B−V) ≳ 0.5. For this reason we only report results for sources with E(B−V) < 0.5, for which the method works well.
In order to determine the radial velocity and corresponding uncertainty, we assumed a Gaussian posterior probability on the radial velocity. We fitted a parabola to the log-posterior probability by selecting all radial velocity points with a log-posterior probability of no less than 10 from the maximum log-posterior probability. If fewer than five points in radial velocity space met this requirement, we reduced the threshold by increments of 10 until we had more than five points. If the resulting fit peaked outside our radial velocity range of ±3000 km s−1, we considered the fit to have failed and report no radial velocity.
Now that we have laid the foundation of our method, we can describe the skewness and goodness-of-fit measurements we used to evaluate the reliability of the radial velocity (uncertainty) measurements (see Sect. 5).
By fitting a parabola to the log-posterior probability, we were assuming symmetric uncertainties. To evaluate if this is a reasonable assumption, we determined the skewness for the log-posterior probability distribution using
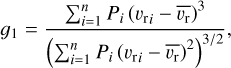 (3)
(3)
where Pi is the posterior probability per radial velocity bin, vri the corresponding radial velocity, and 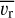 the mean radial velocity given by
the mean radial velocity given by
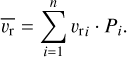 (4)
(4)
This allowed us to identify cases in which the posterior probability distribution is asymmetric and for which the symmetric uncertainties might not be reliable. In addition, we calculated the reduced χ2 of our best fit by approximating the number of degrees of freedom as the number of data points we had (i.e. number of flux vs. wavelength points) minus the number of parameters we fitted (four).
Results of spectral analysis
Here we discuss the results from the spectral analysis presented above. As mentioned, the analysis was applied to all ~219M XP sources with G < 17.65. There are generally three outcomes possible for our spectral analysis. The first outcome is that we obtain a measurement for the radial velocity and corresponding uncertainty of a particular source. It is also possible that a fit failed, because the best-fit radial velocity was outside our parameter range of ±3000 km s−1, or a column in Gaia, such as the BP colour, required by our processing was not measured or was unavailable. The third outcome is that the initial guess for Teff was outside our model range, in which case we did not perform a fit (see Table 1). We summarise the relevant numbers in Table 2.
 |
Fig. 1 Example of two sampled Gaίa XP spectra, in black. The uncertainties in the spectral coefficients are sampled over to indicate the uncertainties in the sampled spectra. The dashed blue and red lines indicate the BP and RP spectral ranges used in the fitting procedure, respectively. On the left we show a hot star, Gaίa DR3 source_id 191594196746880, that displays prominent Balmer features. On the right we show a red source, Gaίa DR3 source_id 31958852451968, that contains broad molecular absorption bands. |
Extrema of the parameter ranges of the grid.
Summary of the raw results of this work.
4 Radial velocity calibration
Because of the calibration issues described in Sect. 2, we expected to see systematic offsets in our measurements of radial velocities that are a function of colour, magnitude, and extinction, in addition to an underestimation of uncertainties. To make matters more complicated, we expected the presence of an ‘outlier’ population, which is a population of objects for which the measured radial velocity spread is well beyond formal errors. In this section we describe how we corrected for these systematics in our radial velocities and their uncertainties obtained from the spectral analysis described in the previous section. We made use of reference radial velocity measurements from dedicated radial velocity surveys. We begin by describing our set of reference radial velocities in Sect. 4.1, followed by the statistical model to describe our XP radial velocities compared to the reference measurements in Sect. 4.2, and finally the fitting procedure of the model to the data in Sect. 4.3.
Summary of the reference radial velocity catalogue used to calibrate and validate our results.
4.1 Reference dataset
The reference radial velocity measurements we used are Gaia RVS DR3 (Katz et al. 2023), Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST) DR8 (low-resolution; Zhao et al. 2012), and Apache Point Observatory Galactic Evolution Experiment (APOGEE) DR17 (Majewski et al. 2017; Abdurro’uf et al. 2022). These catalogues were chosen because of their large size and sky coverage. Importantly, APOGEE and LAMOST contain sources fainter than the Gaia RVS magnitude cut, which is needed to calibrate and validate our results for faint sources. A summary of the relevant statistics from these catalogues is included in Table 3. The Gaia RVS radial velocities are measured with a different instrument and technique and can therefore be considered fully independent of the measurements we provide here. Cross-referencing LAMOST and APOGEE was done using the Gaia DR3 source_id provided for each measurement by both LAMOST and APOGEE. When more than a single measurement was available for either LAMOST or APOGEE, we took the median of all measurements. This provides us with a total number of 23 900 765 sources for which we have both an XP and reference radial velocity measurement. We considered reference radial velocity measurements to be ‘ground truth’ and did not consider uncertainties in them. The reason is that our measurements will have uncertainties much larger than typical uncertainties in any of the reference catalogues. In our calibration we only considered sources that have no neighbours in Gaia within 2 arcseconds. The reason for this is that these sources tend to have blended spectra, due to the size of the spectral extraction window for XP spectra. Our models are not set up to account for blending, which means that radial velocity uncertainty and offset will be different for many of these sources. This further reduces the total number of sources used in calibration to 22 397 143.
4.2 Calibration model
To characterise the systematics in our radial velocity measurements, we adopted a Gaussian mixture model with a likelihood given by
![$\eqalign{ & {\cal L} \propto \prod\limits_{i = 1}^N {\left[ {{{1 - f} \over {\sqrt {2\pi \sigma _i^2} }}\exp \left( { - {{{{\left[ {{v_{{\rm{ref }}}} - {v_{{\rm{rxp }}}} - b} \right]}^2}} \over {2\sigma _i^2}}} \right)} \right.} \cr & + \left. {{f \over {\sqrt {2\pi \sigma _{{\rm{out }}}^2} }}\exp \left( { - {{{{\left[ {{v_{{\rm{rxp }}}} - y} \right]}^2}} \over {2\sigma _{{\rm{out }}}^2}}} \right)} \right], \cr} $](/articles/aa/full_html/2024/04/aa48406-23/aa48406-23-eq7.png) (5)
(5)
with f the outlier fraction, σi the radial velocity uncertainty, 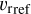 the reference radial velocity measurement, vrxp the XP radial velocity, b the systematic offset between the reference and XP radial velocities, σout the standard deviation of the outlier population, and y the offset of the outlier population. The uncertainties on radial velocity measurements (σi) are described by
the reference radial velocity measurement, vrxp the XP radial velocity, b the systematic offset between the reference and XP radial velocities, σout the standard deviation of the outlier population, and y the offset of the outlier population. The uncertainties on radial velocity measurements (σi) are described by
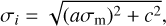 (6)
(6)
with a the underestimation factor on the uncertainties, σm the uncertainty determined from the posterior probability, and c the noise floor parameter.
We used bins in BP – RP colour, apparent G magnitude, and extinction to fit for the free parameters f, a, b, c, σout, and y. We used 20 equally spaced bins in the range 5 ≤ G ≤ 17.65 and 40 bins in the range −0.3 ≤ BP − RP ≤ 5. For extinction, we used bins with a width of ΔE(B−V) = 0.1. Additionally, we used two bins in log g for sources with BP − RP ≥ 1.6875, with a divide at log g = 3.5. We used the log g measurements from Zhang et al. (2023) for this purpose. The split in log g was used because we observed a high degree of systematic offset in the radial velocities we measured between dwarfs and giants at these colours. A description and justification for this split in log g is given in Appendix B. We required at least 64 sources in a particular bin for fitting, with a maximum of 100 000, above which we selected 100 000 sources from the sample at random for computational efficiency. We ran the same calibration procedure using ten equally spaced bins in the range 5 ≤ G ≤ 17.65 and 20 bins in the range −0.3 ≤ BP – RP ≤ 5 (i.e. using bins twice the default size). This ensured that we had calibrations for most sources, even in sparsely populated areas of the colour-magnitude space. If there were still not enough sources in the colour-magnitude bin for a particular source, we did not apply calibration.
4.3 Fitting of the model
To estimate the parameters in our calibration model we used the Markov chain Monte Carlo (MCMC) implementation in emcee (Foreman-Mackey et al. 2013). We used flat priors throughout, except for σout, for which we used a log-uniform prior. Our MCMC approach is as follows: we initialised 64 walkers that we first propagated for 1000 steps to explore the parameter space. To avoid walkers getting stuck in local minima, we rejected walkers that finished with a log-likelihood outside 8.4 of the maximum log-likelihood over all walkers. The value 8.4 ensures that 99% of the walkers would remain if they traced a 6D Gaussian distribution. Another 1000 steps were performed with, again, 64 walkers that were drawn randomly from the last 100 steps of the walkers that remained from the previous run. The last 800 steps of this run were used to compute the medians of the free parameters.
4.4 Results of radial velocity calibration
The number of calibrated radial velocities is 123 835 034 out of a total of 125 145 490. This means that calibration was performed for ~99% of our radial velocity measurements from Sect. 3.
Here we present the radial velocity calibration results for low extinction (E(B–V) < 0.1) sources. Results for higher extinction sources are similar, unless specified. We show the calibrated uncertainties (see Eq. (6)) on the radial velocities measured from the XP spectra in Fig. 2. In the region BP – RP ≥ 1.6875, where we used two bins in log g, we took the source-number average for each bin between the giants and dwarfs. In general, we can see that the lowest uncertainties are obtained from blue and red sources. We observe higher uncertainties for 1 ≲ BP – RP ≲ 2 and the uncertainty generally increases for faint sources. In addition, the figure shows that uncertainties down to ~100 km s–1 are possible for red and blue sources. The reason why uncertainties are relatively high for 1 ≲ BP – RP ≲ 2 is that there are few spectral features in the XP spectra for those sources. Without strong spectral features such as the Balmer lines and molecular absorption bands (see Fig. 1), fitting for a radial velocity becomes less precise.
In Fig. 3 we show the outlier fraction as a function of colour and magnitude. The outlier fraction tends to be low (smaller than 0.1), with a few regions containing notably more outliers. For higher extinction, the outlier fraction increases substantially, which we show in Fig. D.1. In Appendix D we also show the underestimation factor, offset, and noise floor for sources with E(B – V) < 0. 1.
Calibration has been applied to all sources when available. A histogram of the calibrated radial velocity uncertainties along with their cumulative distribution is included in Fig. 4. The median uncertainty on our calibrated radial velocity measurements is about 772 km s−1, but extends all the way down to below 100 km s−1. Sources with a low radial velocity uncertainty tend to be either blue (BP – RP ≲ 0.7) or red (BP – RP ≳ 2).
 |
Fig. 2 Median calibrated uncertainties as a function of colour and apparent magnitude for sources with E(B–V) < 0.1. |
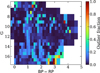 |
Fig. 3 2D histogram of the outlier fraction as a function of colour and apparent magnitude for sources with E(B– V) < 0. 1. |
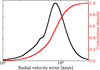 |
Fig. 4 Histogram of the calibrated radial velocity uncertainties (in black) and the cumulative distribution (in red). |
5 Random forest classifier
Although we have a general indication of the reliability of individual measurements from the outlier fraction parameter determined from our calibration model, a quality parameter determined on a source-to-source basis is important to avoid unreliable measurements in the final catalogue. We did this making use of a RFC.
The definition for a bad measurement we used is Δυr/σvr > 3, with Δυr the difference between our calibrated measurement and the reference measurement and σvr the corresponding calibrated uncertainty. For sources for which we had reference radial velocities, we used tenfold cross validation to predict the bad measurement probability. This ensures that the source for which we predicted a bad measurement probability is never part of the training set. For the remaining sources, we trained the RFC on all sources with reference radial velocity measurements. We took care to avoid information leaking from the training parameters to the radial velocities by excluding parameters like the sky coordinates and absorption. We used the scikit-learn RFC with 100 estimators (Pedregosa et al. 2011) and the following parameters for training:
Reduced χ2 of our best-fit model
Teff, log g, and [Fe/H] of the best-fit model for radial velocity
Extinction corrected BP – RP colour of the source
Skewness of the radial velocity posterior (see Eq. (3)).
In addition, we used the following columns provided by the Gaia archive (see the Gaia documentation3 for column descriptions):
phot_g_mean_mag
phot_xp_mean_mag
xp_n_transits
xp_n_blended_transits
xp_n_contaminated_transits
xp_n_measurements
xp_standard_deviation
xp_chi_squared/xp_degrees_of_freedom,
where ‘xp’ indicates that we used the corresponding column of both BP and RP. We found that the extinction corrected colour is the most important out of these, with a feature importance of 0.13. The other columns have a similar importance (between about 0.4 and 0.8), except for the blended and contaminated transits, which have low importance at ≲0.2. This procedure provides us with the likelihood that a particular measurement is unreliable, which we refer to as the bad_measurement parameter.
To verify the effectiveness of the random forest, we looked at the outlier fraction as a function of this bad_measurement parameter. We find good agreement with a one-to-one relation between the two, indication a successful classification.
 |
Fig. 5 Median of the calibrated binned XP radial velocities as a function of the reference radial velocity measurements. These sources have an outlier fraction below 0.2, bad_measurement <0.l, and calibrated uncertainty below 300 km s−1. The solid line is the bisection. |
6 Validation
We have already discussed the results from our spectral analysis and calibration in Sects. 3 and 4.4. In addition, we had access to the quality parameter bad_measurement described in Sect. 5. Using these earlier results, we focus in this section on validating that our measurements indeed measure the radial velocity and evaluate the reliability of our reported uncertainties.
To demonstrate that we are indeed measuring radial velocities from the XP spectra, we included Fig. 5, in which we binned the XP radial velocities based on their reference measurements. The uncertainties on the individual bins were calculated as
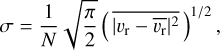 (7)
(7)
where the overline indicates that the mean is taken, υr. is the radial velocity, and N is the number of measurements in the bin. The measurements clearly follow the bisection with the reference radial velocity measurements, demonstrating that we indeed measured stellar radial velocities. To ensure we are not seeing the result of a correlation between radial velocity and position in the colour-magnitude diagram picked up by our calibration model, we also performed this analysis for each colour-magnitude bin separately in Fig. C.1. To further demonstrate our ability to constrain radial velocities, we plot in Fig. 6 the sky projection of the median XP radial velocities compared to Gaia RVS. The quality
cuts we applied to our catalogue are
rv_err < 300 km s−1
CMD_outlier_fraction < 0.2
bad_measurement < 0.1.
In addition, we used the catalogue from Zhang et al. (2023) and selected sources with [Fe/H] ≤ −1 to mainly select halo stars and quality_flags≤ 8. This allowed us to see the dipole caused by the solar motion in both the XP and RVS maps. The dipole disappears at the Galactic plane due to the sample being dominated by non-halo stars in that region.
To evaluate if our radial velocity uncertainties are accurate, we created a histogram of the radial velocity difference of our measurements compared to the reference measurements over the uncertainty (Fig. 7). We determined the standard deviation of this distribution as
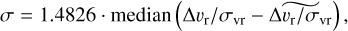 (8)
(8)
with Δvr/σvr the difference between our radial velocity and the reference one over the uncertainty and 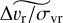 the median of the same quantity. The standard deviation is about 1.03, which means that our reported uncertainties are typically accurate to a few percent. This is in contrast to the uncalibrated measurements, which we also plot in Fig. 7 and which show both a significant offset and a significant uncertainty underestimation.
the median of the same quantity. The standard deviation is about 1.03, which means that our reported uncertainties are typically accurate to a few percent. This is in contrast to the uncalibrated measurements, which we also plot in Fig. 7 and which show both a significant offset and a significant uncertainty underestimation.
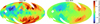 |
Fig. 6 Median XP radial velocity as a function of sky position in Galactic coordinates (left) and the same but using Gaia RVS reference measurements (right). To highlight halo stars, we only show low metallicity stars ([Fe/H] ≤ −1). This increases the radial velocity amplitude as a function of position on the sky. In both maps we can recognise the dipole caused by the solar motion. The other selections of the sources in this figure are described in the main text. The sources are the same in both panels, and we only show colour bins with at least ten measurements. |
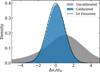 |
Fig. 7 Difference in radial velocity over the uncertainty of both our calibrated and uncalibrated results compared to reference measurements. The solid line is a Gaussian distribution with a standard deviation of 1. The sample used to make this figure has calibrated radial velocity uncertainties of <300 km s−1. |
7 Catalogues
We have published two catalogues along with this paper. The Main Catalogue is the catalogue we recommend for the general user. It includes only relatively precise measurements with low chance of being erroneous. For completion, we also published the Extended Catalogue, which includes all the measurements we obtained. The catalogues are available through an online table4. The columns included are described in Table 4.
7.1 Main Catalogue
To ensure we only published relatively high quality measurements in our Main Catalogue, we applied the following selections:
E(B–V) < 0.5
rv_err < 300 km s−1
CMD_outlier_fraction < 0.1
bad_measurement < 0.1.
The Main Catalogue contains 6 367 355 sources that pass the quality cuts. About 23% of these sources have no previous measurement in Gaia RVS, by far the biggest catalogue in our magnitude range. This means the Main Catalogue contains relatively accurate and precise radial velocity measurements for about 1.5M sources that have no previous measurement available. In Fig. 8 we show the colour-magnitude density of our Main Catalogue.
7.2 Extended Catalogue
For completion, we also provide our entire catalogue, without any quality cuts, which we refer to as our Extended Catalogue. The only exception is that we still only published sources with E(B−V) < 0.5, since we deemed most higher extinction measurements to be unreliable. To assist the user in making use of this catalogue, we provided additional parameters for all sources alongside those provided for the main catalogue, which is a subset of the Extended Catalogue. In the case of a star occupying a point in parameter space with insufficient reference measurements to perform calibration, we still report our XP radial velocity measurement, only without any calibration performed. In those cases we report the CMD_outlier_fraction, offset, underestimation_factor, and noise_floor parameters as NaN values. In Fig. 9 we show the colour-magnitude diagram of the sources appearing in our Extended Catalogue. Since there are many more caveats with this dataset compared to the Main Catalogue, we provide the user with the warning parameter that is supplied as a bitmask. If one of the following conditions was met, the corresponding bit was set to 1.
- 1.
No calibration applied (0001)
- 2.
Neighbour in Gaia within 2 arcsec (0010)
- 3.
CMD_outlier_fraction > 0.2 (0100)
- 4.
bad_measurement > 0.1 (1000).
Description of the fields included in the final published catalogue.
 |
Fig. 8 Colour-magnitude diagram for the sources in our Main Catalogue. |
8 Finding hypervelocity stars
Having presented our Main Catalogue, we now use it to investigate the science case of HVSs.
These stars can have velocities well in excess of 1000 km s−1 (Koposov et al. 2020), making them much faster than stars belonging to other populations. These stars are ejected from the Galactic Centre following a dynamical encounter with our central massive black hole, Sgr A* (Brown 2015). Their identification has proven difficult with only a few dozen promising candidates (Brown et al. 2014) and a single star that can be unambiguously traced back to the centre of our Galaxy (Koposov et al. 2020). Our new catalogue of radial velocities can facilitate blind searches for additional HVSs, helping unravel the dynamics and properties of stars in the centre of our Galaxy as well as providing valuable information about the Galactic potential (e.g. Rossi et al. 2017; Evans et al. 2022).
For the purpose of searching for HVSs it is of interest to determine if we can still obtain reliable radial velocity measurements for extremely high velocity stars. To date, S5-HVS1 is the fastest unbound star known in our Galaxy, with a total velocity in the Galactic frame of 1755 ± 50 km s−1 and a heliocentric radial velocity of 1017 ± 2.7 km s−1 (Koposov et al. 2020). The calibrated radial velocity we measure is 799 ± 273 km s−1, which is consistent with the reference radial velocity measurement of S5-HVS1 within ~0.8σ. The bad_measurement parameter from the RFC is 0.02 for S5-HVS1, indicating a reliable measurement. This establishes that our results are still accurate for extremely high radial velocity sources.
To evaluate the general effectiveness of the selection of high radial velocity star candidates from our Main Catalogue, we produced Fig. 10. In the figure we only selected stars from our Main Catalogue whose 3σ lower limit on vr is at least 300 km s−1 (i.e. vr > 300 + 3 · σvr km s−1) and plot those for which reference radial velocity measurements were available. Although the distribution of our selection still peaks at 0 km s−1, we can see a very significant over-density of high radial velocity sources. Most of the sources in this selection do not have reference radial velocity measurements and, as Fig. 10 shows, the majority of them will not have high radial velocities. However, the selection of HVS candidates for follow-up radial velocity surveys can be viable. Only 3175 sources out of our Main Catalogue of 6.4M sources passed the selection of vr > 300 + 3 · σvr km s−1. The number of candidates could be further reduced by using, for example, astrometric information to constrain the orbits. Follow-up observations to precisely measure their radial velocities will be proposed for the most promising of these HVS candidates.
 |
Fig. 9 Colour-magnitude diagram for the sources in the Extended Catalogue. |
 |
Fig. 10 Density of the reference radial velocity distribution of all sources against those selected by vr > 300 + 3 · σvr km s−1 in our Main Catalogue and for which reference radial velocity measurements are available. |
9 Discussion
Despite the challenges, we have shown that radial velocities can be obtained from Gaia XP measurements to a precision ofbetter than ~300 km s−1 for stars as faint as G = 17.65. Section 9.1 discusses possible improvements to the methods presented in this paper, in Sect. 9.2 we provide prospects for Gaia DR4 and the improvements that we might expect with its release regarding radial velocities from XP spectra, and lastly in Sect. 9.3 we discuss science cases for XP radial velocities in Gaia DR4.
9.1 Improvements to the method
Our current approach is only viable for low to intermediate extinction sources, due to our implementation of an initial guess for Teff. This approximation breaks down for high extinction sources as mentioned in Sect. 3. Practically, this means that our results are not reliable for sources with E(B–V) ≳ 0.5 and we do not report our results for those sources. The issue can be mitigated by for example, using a larger range in Teff during the fitting procedure for high extinction sources, or by fitting every model for all sources.
Additionally, fitting for extinction rather than relying on a 2D extinction map would allow for more accurate measurements, because for individual sources the 2D extinction map is only an estimate of the actual line-of-sight extinction. Including extinction in the fitting procedure is possible, but is also computationally very expensive, which is why we opted to use the 2D map instead.
The analysis could be further improved by choosing the fitting wavelength range on a source-to-source basis: practically, one would choose for each source the wavelength regions that hold the most spectral information. Doing this would improve the precision of the radial velocity measurements. Here, we instead used the same wavelength ranges throughout.
Alternatively to the modelling presented in this work, one could forward-model the spectral coefficients directly. Provided that the design matrix and the model of the instrument are accurate, this should give more precise results.
Improving upon the method is required if the goal is to obtain reliable radial velocity measurements for a revolutionary large set of sources. Even though we started out with XP spectra to about 220M sources, the Main Catalogue only includes around 6.4 M radial velocities (or about 3% of XP sources), with an additional ~ 119 M in the Extended Catalogue. Understanding and correcting for systematic effects remains the most challenging aspect.
9.2 Gaia Data Release 4
In Gaia DR4, XP spectra will be published for about 2B sources, in addition to individual epoch spectra of said sources. Since this is orders of magnitude higher than any current radial velocity catalogue, the potential scientific return on a well-optimised method of radial velocity analysis would be very high.
It is unknown how large the improvement will be in radial velocity accuracy and precision from Gaia DR3 to DR4 using the methods presented here. The reason is that systematics are a very large factor in the radial velocity uncertainty. We might consider the noise floor in Eq. (6) to be the intrinsic systematic uncertainty caused by imperfect calibration of XP spectra in Gaia DR3. If we assume that these systematics are resolved in Gaia DR4, we can provide an outlook for the performance of our method when applied to Gaia DR4. When we ignore the noise floor, the number of sources with radial velocity uncertainties <300 km s−1 in DR3 approximately doubles to ~17M. In addition, there would be about 1M sources with radial velocity uncertainties of < 100 km s−1. The smallest uncertainties that might be achieved are expected to be of the order of 50 km s−1. Although DR4 will mostly include fainter sources than the current limit of G < 17.65, the S/N for a given magnitude will also improve. Gaia DR4 will provide XP spectra to about 9 times as many sources as DR3. A rough approximation of the final number of sources with a particular quality in Gaia DR4 is thus 9 times the number in DR3. This would imply that the XP spectra in Gaia DR4 could provide us with ~153M and ~8M measurements with uncertainties better and 300 and 100 km s−1, respectively. Without systematic uncertainty due to the noise floor, these stars would be mainly red (BP – RP ≲ 2) and blue (BP − RP ≲ 0.7) in colour.
9.3 Science cases in Gaia Data Release 4
Having discussed improvements to both the methods and data with the next data release of Gaia, we now look at prospects for two specific science cases in Gaia DR4: dark companions and HVSs.
Dark companions refer to binary systems in which one of the components emits little to no light in the photometric band used to observe them. These dark companions, such as black holes, can be identified from low-resolution spectra if enough epochs are available over a sufficient time span. The photocentre of Gaia BH1, for instance, has a radial velocity amplitude of about 130 km s−1 (El-Badry et al. 2023; Chakrabarti et al. 2023), far larger than the typical uncertainty in Gaia RVS of only a few km s−1 (Katz et al. 2023). With the release of epoch XP spectra in Gaia DR4, searches for dark companions will become possible in the full Gaia catalogue of ~2B sources. Compared to the astrometric time series, radial velocities have the advantage of being distance independent, thus allowing for a larger search volume. Also, in comparison to Gaia RVS, the XP radial velocities have the advantage of being deeper and therefore covering a larger volume. Gaia RVS will have a limiting magnitude of GRVS ~ 16 in Gaia DR4, compared to the limiting magnitude of mG ~ 10.7 for the XP spectra. We assumed the two photometric bands to be similar5 and approximated the magnitude difference as 4.7. From the magnitude difference, we can calculate the volume ratio as
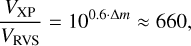 (9)
(9)
with VXP the volume covered by XP spectra, VRVS the volume covered by RVS radial velocities, and Δm the difference in limiting magnitude. The effective volume covered by XP spectra is thus about 660 times as large as that covered by RVS radial velocities. Depending on the final precision and accuracy that can be achieved, dedicated higher-resolution observations might be required to confirm systems with possible dark companions identified from Gaia XP radial velocities.
In addition to finding dark companions, Gaia DR4 XP radial velocities could support the search for HVSs. Because of the high intrinsic velocities of these stars, large uncertainties are less problematic. As demonstrated in Sect. 8, the contamination of a selection of extremely high XP radial velocity sources is substantial in our Main Catalogue. With the improved analysis suggested in Sect. 9.1, in combination with a reduction in systematics that we expect in Gaia DR4, the contamination will decrease. This will allow for more effective follow-up campaigns to identify new HVSs. As mentioned above, the advantage of using Gaia XP spectra is that the effective volume is much larger than that of the Gaia RVS catalogue.
Both for dark companions and HVSs, XP radial velocities will be most effective in identifying them for red (BP – RP ≳ 1) and blue (BP – RP ≲ 0.7) sources, since these sources have the lowest uncertainties in XP radial velocity. This is not expected to change from Gaia DR3 to DR4, since it is inherent to the radial velocity information contained within the XP spectra.
10 Conclusion
As a proof of concept, we have clearly demonstrated that Gaia XP spectra can be used to measure radial velocities. Along with this paper we publish the Main Catalogue, which contains reliable and precise radial velocity measurements for about 6.4 M sources, 23% of which have no previous radial velocity measurements in Gaia. In addition, we publish the Extended Catalogue, which contains all ~115M sources for which we have obtained a radial velocity measurement. This constitutes ~84% of sources with Gaia XP spectra and E(B–V) < 0.5. The extended catalogue, however, contains a significant number of unreliable measurements and should therefore only be used with caution.
In general, sources with BP − RP ≳ 1 and BP − RP ≲ 0.7 tend to give the most precise radial velocity measurements in our catalogue, down to uncertainties of ~ 100 km s−1. In the future, we expect the most precise radial velocity measurements from Gaia XP spectra to have uncertainties of the order of 50 km s−1.
Critically, this work has demonstrated the potential of measuring radial velocities for over 109 sources in Gaia DR4 using XP spectra. This would constitute an orders-of-magnitude increase compared to the largest current catalogue. However, the methods presented here should be further improved to fully exploit the scientific content available to us.
Acknowledgements
The authors thank the anonymous referee for their insightful comments and suggestions on this work. In addition, the authors would like to thank the attendees at the Gaia XPloration workshop for their input and enthusiasm. Special thanks goes to Francesca De Angeli, Anthony Brown, and Vasily Belokurov for their support, helpful insight, and discussions. We would also like to thank Anthony Brown for his feedback on a first draft of this manuscript. EMR acknowledges support from European Research Council (ERC) grant number: 101002511/project acronym: VEGA_P. T.M. acknowledges a European Southern Observatory (ESO) fellowship. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This project was developed in part at the 2023 Gaia XPloration, hosted by the Institute of Astronomy, Cambridge University. This paper made use of the Whole Sky Database (wsdb) created and maintained by Sergey Koposov at the Institute of Astronomy, Cambridge with financial support from the Science & Technology Facilities Council (STFC) and the European Research Council (ERC). This work was performed using the ALICE compute resources provided by Leiden University. This research or product makes use of public auxiliary data provided by ESA/Gaia/DPAC/CU5 and prepared by Carine Babusiaux. Software: NumPy (Harris et al. 2020), SciPy (Virtanen et al. 2020), Matplotlib (Hunter 2007), Astropy (Astropy Collaboration 2013, 2018, 2022), emcee (Foreman-Mackey et al. 2013), Numba (Lam et al. 2015), dustmaps (Green 2018), GaiaXPy, SpectRes (Carnall 2017), extinction (https://extinction.readthedocs.io/en/latest/), healpy (Górski et al. 2005; Zonca et al. 2019), corner (Foreman-Mackey 2016), scikit-learn (Pedregosa et al. 2011).
Appendix A Teff initial guess
For computational efficiency, we made an initial guess for the Teff of each source and only considered models within 500K of this initial guess, as described in Sect. 3.
We made the initial guess for Teff based on the BP – RP colour and 2D extinction along the line of sight. First we corrected the colour of the source for extinction using the extinction law provided by Gaίa6. This is only an approximation, since we do not know the intrinsic colour of a source affected by extinction and use the observed colour instead. By analysing test sources for the entire Teff grid range, we used an empirical exponential fit to the relation between BP – RP and Teff. Only for colours BP – RP ≲ 0 did we find a turn-off from the exponential relation, for which we fitted a linear function. The relation is given by
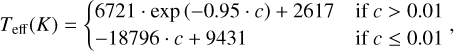 (A.1)
(A.1)
where c denotes the extinction corrected BP − RP colour. If the initial guess for Teff was outside the temperature range of our models (see Table 1), we did not attempt to fit the source and no radial velocity was obtained.
Appendix B log g systematics
For red sources we observed strong systematics in the radial velocity we measured, based on the surface gravity of the stars. We demonstrate this in Fig. B.1, where we used the surface gravity measurements from Zhang et al. (2023) to separate dwarfs from giants. To investigate the origin of this systematic offset we used log g and Teff measurements from APOGEE in comparison to our best-fit values. In Fig. B.2 we show how the radial velocity offset relates to errors in the parameter estimation for dwarfs. We can see that dwarfs tend to get assigned radial velocities that are too high. This also varies as a function of Δlog g and ΔTeff. In particular, if the log g of our best-fit model labels a dwarf as a giant a positive offset is introduced, which can be seen from the colour gradient towards negative Δlog g.
 |
Fig. B.1 Offset between the uncalibrated Gaia XP radial velocities and reference ones as a function of BP − RP colour. We split the dwarfs and the giants using the log g measurements from Zhang et al. (2023). The dashed vertical line shows the limit above which we used two bins in log g for our calibration model. The figure only includes sources with E(B−V) < 0.1 and 12 < G < 13. |
 |
Fig. B.2 Radial velocity offset for dwarfs (log g > 3.5 according to Zhang et al. (2023)) as a function of the difference in the best-fit log g and Teff we obtain versus those from APOGEE. The contour lines give the underlying source density. The stars in the sample have 10 < G < 16, 2 < BP − RP < 2.5, and E(B−V) < 0.1. |
To make this figure and have sufficient sources, we used a much larger range of colour and magnitude than we do for single bins in the calibration. The spread in offsets for individual bins is smaller and therefore less problematic. Fig. B.3 shows the same, but now only for giants. In general we can see that the offset tends to be much lower for giants. It is possible that it is caused by the basis function representation in Gaίa, which undergoes optimisation and might lead to systematic differences in the translation of giant and dwarf spectra. Fortunately, we could effectively mitigate the effects of this bias, whatever its origin. To evaluate our treatment of the observed offset described in Sect. 4.2, we recreated Fig. B.1 for our calibrated sample, which we show in Fig. B.4. The figure clearly demonstrates that the offset between dwarfs and giants for very red sources has been effectively removed. Colour-dependent systematics are still visible in the offset, however, particularly around BP – RP ~ 1.5. This effect is explained in Sect. D and is related to the CMD_outlier_fraction.
Appendix C Further validation
To demonstrate that the calibration we performed does not introduce anapparentradial velocity sensitivity, we includedFig. C.1. This figure gives the median XP radial velocity for bins in reference radial velocity within the Main Catalogue, where each curve is constructed using stars within one colour-magnitude diagram bin. The one-to-one slope demonstrates that within individual colour-magnitude bins we are sensitive to radial velocity. This excludes the possibility that a correlation between colour-magnitude and radial velocity is introducing an apparent radial velocity sensitivity.
 |
Fig. C.1 Median XP radial velocity as a function of bins in reference radial velocity. The dashed red line gives the bisection and the transparent black lines the data for individual bins in the calibration. |
Appendix D Markov chain Monte Carlo examples and results
In Fig. D.1 we show the outlier fraction of the model described in Sect. 4.2 (Eq. 5) as a function of colour and magnitude for the higher E(B−V) bins and not shown in the main text.
In Fig. D.2 we give the underestimation factor, offset, and noise floor for sources with E(B−V) < 0.1. The definition of the offset can be found in equation 5 and the definition of the underestimation factor and noise floor in equation 6.
To provide more insight into what our calibration model does, we show the MCMC results for a number of bins. We show the 11.9575 < G < 12.59 magnitude bin for three different colour bins indicated in Fig. D.3. We note that the method does not work equally well for all bins, which affects the calibration. If we look at the middle and right panels, we see that the overall distribution is skewed. Correcting for the offset in that sample will still result in a median that is significantly higher or lower than 0, because of the skew. This is the residual effect we see in Fig. B.4. Part of this can be explained by log g effects that are still present in this colour region. We chose not to attempt to correct for these effects, because for these intermediate colour sources, there is no clear split in offset between dwarfs and giants. Instead a more elaborate strategy would have to be employed to correct for the remaining systematics.
 |
Fig. D.1 Outlier fractions as a function of colour and magnitude for the remaining E(B−V) bins not shown in the main text. |
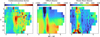 |
Fig. D.2 From left to right: Underestimation factor, offset, and noise floor for sources with E(B−V) < 0.1. |
 |
Fig. D.3 Histograms of the radial velocity difference between the raw XP measurement and the reference values. The three lines show the parameters found by the fit of the predicted distributions of the regular, outlier, and combined populations. The different panels show different bins in BP − RP colour, as indicated above the panels. |
References
- Abdurro’uf, Accetta, K., Aerts, C., et al. 2022, ApJS, 259, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Andrae, R., Fouesneau, M., Sordo, R., et al. 2023a, A&A, 674, A27 [CrossRef] [EDP Sciences] [Google Scholar]
- Andrae, R., Rix, H.-W., & Chandra, V. 2023b, ApJS, 267, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. L., Andrae, R., Arcay, B., et al. 2013, A&A, 559, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, W. R. 2015, ARA&A, 53, 15 [Google Scholar]
- Brown, W. R., Geller, M. J., & Kenyon, S. J. 2014, ApJ, 787, 89 [Google Scholar]
- Carnall, A. C. 2017, arXiv e-prints [arXiv:1705.05165] [Google Scholar]
- Chakrabarti, S., Simon, J. D., Craig, P. A., et al. 2023, AJ, 166, 6 [NASA ADS] [CrossRef] [Google Scholar]
- De Angeli, F., Weiler, M., Montegriffo, P., et al. 2023, A&A, 674, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- El-Badry, K., Rix, H.-W., Quataert, E., et al. 2023, MNRAS, 518, 1057 [Google Scholar]
- Evans, F. A., Marchetti, T., & Rossi, E. M. 2022, MNRAS, 517, 3469 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [Google Scholar]
- Foreman-Mackey, D. 2016, J. Open Source Softw., 1, 24 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Gaia Collaboration (Prusti, T, et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [Google Scholar]
- Green, G. 2018, J. Open Source Softw., 3, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Guiglion, G., Nepal, S., Chiappini, C., et al. 2024, A&A, 682, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hogg, D. W., Bovy, J., & Lang, D. 2010, arXiv e-prints [arXiv:1008.4686] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T. O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katz, D., Sartoretti, P., Guerrier, A., et al. 2023, A&A, 674, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koposov, S. E., Boubert, D., Li, T. S., et al. 2020, MNRAS, 491, 2465 [Google Scholar]
- Lam, S. K., Pitrou, A., & Seibert, S. 2015, in Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC, LLVM '15 (New York: Association for Computing Machinery) [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, arXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Li, J., Wong, K. W. K., Hogg, D. W., Rix, H.-W., & Chandra, V. 2023, ApJS, submitted [arXiv:2309.14294] [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Montegriffo, P., De Angeli, F., Andrae, R., et al. 2023, A&A, 674, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Rix, H.-W., Chandra, V., Andrae, R., et al. 2022, ApJ, 941, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Rossi, E. M., Marchetti, T., Cacciato, M., Kuiack, M., & Sari, R. 2017, MNRAS, 467, 1844 [NASA ADS] [Google Scholar]
- Santana, F. A., Beaton, R. L., Covey, K. R., et al. 2021, AJ, 162, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Yan, H., Li, H., Wang, S., et al. 2022, The Innovation, 3, 100224 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, X., Green, G. M., & Rix, H.-W. 2023, MNRAS, 524, 1855 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, G., Zhao, Y.-H., Chu, Y.-Q., Jing, Y.-P., & Deng, L.-C. 2012, Res. Astron. Astrophys., 12, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Zonca, A., Singer, L., Lenz, D., et al. 2019, J. Open Source Softw., 4, 1298 [Google Scholar]
https://doi.org/10.5281/zenodo.10043238 or at the CDS.
All Tables
Summary of the reference radial velocity catalogue used to calibrate and validate our results.
All Figures
 |
Fig. 1 Example of two sampled Gaίa XP spectra, in black. The uncertainties in the spectral coefficients are sampled over to indicate the uncertainties in the sampled spectra. The dashed blue and red lines indicate the BP and RP spectral ranges used in the fitting procedure, respectively. On the left we show a hot star, Gaίa DR3 source_id 191594196746880, that displays prominent Balmer features. On the right we show a red source, Gaίa DR3 source_id 31958852451968, that contains broad molecular absorption bands. |
| In the text | |
 |
Fig. 2 Median calibrated uncertainties as a function of colour and apparent magnitude for sources with E(B–V) < 0.1. |
| In the text | |
 |
Fig. 3 2D histogram of the outlier fraction as a function of colour and apparent magnitude for sources with E(B– V) < 0. 1. |
| In the text | |
 |
Fig. 4 Histogram of the calibrated radial velocity uncertainties (in black) and the cumulative distribution (in red). |
| In the text | |
 |
Fig. 5 Median of the calibrated binned XP radial velocities as a function of the reference radial velocity measurements. These sources have an outlier fraction below 0.2, bad_measurement <0.l, and calibrated uncertainty below 300 km s−1. The solid line is the bisection. |
| In the text | |
 |
Fig. 6 Median XP radial velocity as a function of sky position in Galactic coordinates (left) and the same but using Gaia RVS reference measurements (right). To highlight halo stars, we only show low metallicity stars ([Fe/H] ≤ −1). This increases the radial velocity amplitude as a function of position on the sky. In both maps we can recognise the dipole caused by the solar motion. The other selections of the sources in this figure are described in the main text. The sources are the same in both panels, and we only show colour bins with at least ten measurements. |
| In the text | |
 |
Fig. 7 Difference in radial velocity over the uncertainty of both our calibrated and uncalibrated results compared to reference measurements. The solid line is a Gaussian distribution with a standard deviation of 1. The sample used to make this figure has calibrated radial velocity uncertainties of <300 km s−1. |
| In the text | |
 |
Fig. 8 Colour-magnitude diagram for the sources in our Main Catalogue. |
| In the text | |
 |
Fig. 9 Colour-magnitude diagram for the sources in the Extended Catalogue. |
| In the text | |
 |
Fig. 10 Density of the reference radial velocity distribution of all sources against those selected by vr > 300 + 3 · σvr km s−1 in our Main Catalogue and for which reference radial velocity measurements are available. |
| In the text | |
 |
Fig. B.1 Offset between the uncalibrated Gaia XP radial velocities and reference ones as a function of BP − RP colour. We split the dwarfs and the giants using the log g measurements from Zhang et al. (2023). The dashed vertical line shows the limit above which we used two bins in log g for our calibration model. The figure only includes sources with E(B−V) < 0.1 and 12 < G < 13. |
| In the text | |
 |
Fig. B.2 Radial velocity offset for dwarfs (log g > 3.5 according to Zhang et al. (2023)) as a function of the difference in the best-fit log g and Teff we obtain versus those from APOGEE. The contour lines give the underlying source density. The stars in the sample have 10 < G < 16, 2 < BP − RP < 2.5, and E(B−V) < 0.1. |
| In the text | |
 |
Fig. B.3 Same as Fig. B.2, but now only for giants. |
| In the text | |
 |
Fig. B.4 Same as Fig. B.1, but after calibration is applied to the bin 11.9575 < G < 12.59. |
| In the text | |
 |
Fig. C.1 Median XP radial velocity as a function of bins in reference radial velocity. The dashed red line gives the bisection and the transparent black lines the data for individual bins in the calibration. |
| In the text | |
 |
Fig. D.1 Outlier fractions as a function of colour and magnitude for the remaining E(B−V) bins not shown in the main text. |
| In the text | |
 |
Fig. D.2 From left to right: Underestimation factor, offset, and noise floor for sources with E(B−V) < 0.1. |
| In the text | |
 |
Fig. D.3 Histograms of the radial velocity difference between the raw XP measurement and the reference values. The three lines show the parameters found by the fit of the predicted distributions of the regular, outlier, and combined populations. The different panels show different bins in BP − RP colour, as indicated above the panels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


