| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 21 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202348332 | |
| Published online | 29 March 2024 | |
A Walk on the Retrograde Side (WRS) project
I. Tidying-up the retrograde halo with high-resolution spectroscopy⋆
1
INAF – Astrophysics and Space Science Observatory of Bologna, Via Gobetti 93/3, 40129 Bologna, Italy
2
Department of Physics and Astronomy, University of Bologna, Via Gobetti 93/2, 40129 Bologna, Italy
e-mail: edoardo.ceccarelli3@unibo.it
3
INAF – Astronomic Observatory of Rome, Via Frascati 33, 00078 Monte Porzio Catone, Italy
4
Department of Physics, University of Roma Tor Vergata, Via della Ricerca Scientifica 1, 00133 Roma, Italy
5
Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
6
School of Physics and Astronomy, University of Birmingham, Birmingham B15 2TT, UK
7
Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
Received:
20
October
2023
Accepted:
26
December
2023
Relics of ancient accretion events experienced by the Milky Way are predominantly located within the stellar halo of our Galaxy. However, debris from different objects display overlapping distributions in dynamical spaces, making it extremely challenging to properly disentangle their contribution to the build-up of the Galaxy. To shed light on this chaotic context, we initiated a program aimed at the homogeneous chemical tagging of the local halo of the Milky Way, focusing on the component in retrograde motion, since this is expected to host a large fraction of stars accreted from past mergers. The A Walk on the Retrograde Side (WRS) project targets retrograde halo stars in the solar neighborhood with accurate 6D phase space information available, measuring the precise chemical abundance of several chemical elements from high-resolution spectroscopy. In this first paper, we present the project and the analysis of high-resolution spectra obtained with UVES at VLT and at LBT for 186 stars. We obtained accurate radial velocity and chemical abundances for several elements for all the target stars. In particular, we focus on the chemical composition of a specific subset of substructures that have been dynamically identified in the literature. Our study reveals that two among the more recently discovered structures in the retrograde halo, namely, Antaeus/L-RL64 and ED-3, have identical chemical patterns and similar integrals of motion, suggesting a common origin. In turn, the abundance patterns of this unified system differ from that of Gaia-Enceladus, confirming that it is an independent structure. Finally, Sequoia exhibits a different chemistry with respect to that of Gaia-Enceladus at [Fe/H] < −1.5 dex, showcasing an excess of stars with lower Mg and Ca in the common metallicity range.
Key words: stars: abundances / Galaxy: abundances / Galaxy: formation / Galaxy: halo
Full Tables 1, 3, 4, 6, and 7 are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/684/A37
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The Λ cold dark matter (ΛCDM) cosmological paradigm predicts that galaxies grow their masses hierarchically through merging events with smaller systems (White & Frenk 1991). The discovery of the ongoing accretion event of the Sagittarius dwarf galaxy (Ibata et al. 1994) has demonstrated for the first time that the Milky Way (MW) is not an exception. As extensively shown by N-body simulations of galaxy formation (Newton et al. 2018), the stellar halo of the surviving galaxy mainly comprises stars that have been accreted from smaller, disrupted satellite galaxies. Nevertheless, it has been established that the stellar halo is not exclusively composed of accreted objects (Carollo et al. 2007; Pillepich et al. 2015; Monachesi et al. 2019; Font et al. 2020; Belokurov & Kravtsov 2022; Khoperskov et al. 2023). Detecting stellar substructures in the Galactic halo yields valuable insights into the formation and evolution of the MW, since the overall configuration of the halo has been deeply affected by the merger history of our Galaxy. Hence, comprehending the characteristics and mechanisms of formation of these substructures plays a pivotal role in reconstructing the evolutionary history of the MW. The search for substructures in the phase space is currently the most common and successful method used to unravel ongoing or recent accretion events (Ibata et al. 1994; Helmi et al. 1999; Bonaca et al. 2012; Helmi 2020; Belokurov et al. 2020). However, phase-mixing has proven some limitations to this approach, making it challenging to identify merging events that took place in the early stages of the MW’s formation. Instead, N-body simulations have shown that debris from the same progenitor maintain a dynamical coherency in the space defined by the integrals of motion (IoM, e.g., energy and angular momentum) in a slowly evolving potential (Johnston et al. 1996; Helmi & de Zeeuw 2000; Gómez et al. 2013). In this context, the advent of the ESA/Gaia mission (Gaia Collaboration 2016) has provided a deeper understanding of the MW overall structure, shedding light on its formation and evolution, thanks to the extremely accurate measurements of the 3D position and velocity for ≈33.8 million of stars brighter than G = 14.0. According to the widely accepted scenario (see Helmi 2020 for a review), a substantial fraction of the MW stellar halo is believed to have formed as a consequence of a merging event with a dwarf galaxy, known as Gaia-Enceladus Sausage (GES, Belokurov et al. 2018; Helmi et al. 2018).
Recent studies revealed that the stellar halo contains an increasing number of other smaller substructures, including streams, clumps, and overdensities that are believed to be the remnants of past accretion events (Koppelman et al. 2019; Massari et al. 2019; Myeong et al. 2019, 2022; Kruijssen et al. 2020; Naidu et al. 2020; Yuan et al. 2020; Horta et al. 2021; Ibata et al. 2021; Malhan et al. 2022; Oria et al. 2022; Ruiz-Lara et al. 2022; Shank et al. 2022; Tenachi et al. 2022; Belokurov et al. 2023; Dodd et al. 2023; Mikkola et al. 2023; Cabrera Garcia et al. 2024). However, the interpretation of these numerous recent discoveries can be extremely challenging. In fact, numerical simulations of a major merger between a MW-like galaxy and a GES-like progenitor have revealed that remnants from the same merging event can result in overdensities at various locations in the space defined by the IoM, which could be mistaken for independent substructures (Koppelman et al. 2020; Amarante et al. 2022; Belokurov et al. 2023; Davies et al. 2023). On the other hand, relics with different origin may significantly overlap in the IoM space (Helmi & de Zeeuw 2000; Naidu et al. 2020; Lövdal et al. 2022; Dodd et al. 2023) and unrelated sources can drastically contaminate samples of candidate members of a given substructure selected kinematically (Buder et al. 2022; Rey et al. 2023).
A possible solution to this dynamical degeneracy can be achieved by adding an entirely independent dimension to the parameter space, that is, the chemical composition of stars (chemical tagging, Freeman & Bland-Hawthorn 2002). Indeed, the chemical abundance patterns of individual stars exhibit characteristics that reflect the star formation and chemical enrichment histories of the site where they were born. Therefore, they can greatly help in understanding the origin of a given substructure, namely, by distinguishing between accreted and in situ formation, and/or to infer the properties of the (now dissolved) progenitor satellite (Gallart et al. 2005; Tolstoy et al. 2009; Nissen & Schuster 2010; Mackereth et al. 2019; Kruijssen et al. 2020; Minelli et al. 2021; Montalbán et al. 2021; Mucciarelli et al. 2021b).
Large spectroscopic surveys, such as APOGEE (Abdurro’uf et al. 2022), GALAH (Buder et al. 2021), and H3 (Conroy et al. 2019), have made it possible to conduct in-depth studies in this field, providing detailed elemental abundances for an enormous number of stars. Many recent works have taken advantage of these large chemical datasets, focusing primarily on the chemical patterns of GES (Aguado et al. 2021; Bonifacio et al. 2021; Feuillet et al. 2021; Hasselquist et al. 2021; Limberg et al. 2022). Still, there are interesting regions of the parameter space where the sampling of chemical abundances is sparse and occasional, as, for example, the highly retrograde halo (RH) that is expected to host a very large fraction of accreted stars (Naidu et al. 2020; Myeong et al. 2022; Horta et al. 2023). Also, the merging and comparison between chemical abundances from different sources has been shown to be somehow problematic due to the lack of homogeneity in the atmospheric parameters and abundances scales of the various surveys (see, e.g., Helmi 2020).
Within this framework, we present a small spectroscopic survey aimed at delivering detailed chemical tagging of RH stars in the solar neighborhood with accurate kinematics, based on the precise measurements of several elements (e.g., Fe, Na, Mg, Al, Ca, Sc, Ti, Mn, Ni, Zn, Y). The A Walk on the Retrograde Side (WRS) project is aimed at obtaining chemical abundances from high-resolution spectroscopy for at least a few hundred stars, using accessible observational facilities. Spectroscopic observations of relatively bright stars (G ≲ 14.0) can be an excellent use of nights with sub-optimal seeing and lunar illumination at large telescopes. This is the niche that is currently being used for WRS observations.
The multi-dimensional dataset we plan to obtain will provide deep insight on the origin of each target star, by looking at similarities in the orbits and abundance patterns among them along with those of known relics of merging events. The approach we propose is complementary to that of large-scale general surveys such as H3 (Naidu et al. 2020, 2022) and APOGEE (Horta et al. 2023). Indeed, the WRS project is highly focused, targeting only RH stars in the solar neighborhood, within D⊙ ≤ 1.0 kpc. Retrograde stars are particularly interesting in this context, as it is more likely that they come from the accretion of ancient satellites, with respect to their prograde counterparts (Carollo et al. 2007). Moreover, the WRS targets are selected among those having very accurate astrometry from the Gaia mission (Gaia Collaboration 2016). In addition to the constraint in distance and to the accurate radial velocity measure obtained within WRS, this ensures the most reliable determination of orbital parameters and IoM for the considered stars. In the end, the stellar spectra obtained for WRS have higher spectral resolution (R ≈ 40 000) than large spectroscopic surveys. This enhanced spectral resolution facilitates the precise determination of chemical abundances and offers finer insights into stellar characteristics.
In this first paper of the series, we describe our sample selection process and present the results of the analysis of a first batch of 186 stars. In particular, we conduct a high-precision and homogeneous abundance analysis on RH stars that are associated with different dynamical substructures, according to Dodd et al. (2023). We compare the results obtained for these substructures with the aim of uncovering their true nature and understanding whether they are all independently accreted components or whether some have originated from the same progenitor.
The paper is structured as follows. In Sect. 2, we describe the selection criteria used to identify RH stars and we present the high-resolution spectroscopic dataset. In Sect. 3, we present the dynamical characteristics of our sample of stars. In Sect. 4, we provide a detailed description of the criteria that were employed to define each individual substructure in the RH. In Sect. 5, we provide a comprehensive account of the detailed procedure employed to conduct the chemical analysis. In Sect. 6, we show the comparison with literature results. In Sect. 7, we showcase an extensive examination of the halo substructures in different chemical planes, focusing in particular on odd-Z elements (Sect. 7.2), α-elements (Sect. 7.3), iron-peak elements (Sect. 7.4), and neutron capture elements (Sect. 7.5). In Sect. 8, we summarize and discuss the main results of our work.
2. Selection of the sample and observations
2.1. Data selection
At the epoch when the WRS project was conceived, we had to face the problem of selecting retrograde stars from catalogues, like the Gaia DR2 (Gaia Collaboration 2018b) and EDR3 (Gaia Collaboration 2021) databases1, where most of the stars were lacking a line of sight velocity (Vlos) measurement in the range of apparent magnitudes of interest (G ≤ 14.0, for the time being). We tackled this issue by realizing that a selection in tangential velocity 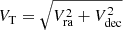 , that is, the linear velocity in the plane of the sky, can be used to effectively select very likely retrograde stars.
, that is, the linear velocity in the plane of the sky, can be used to effectively select very likely retrograde stars.
This technique is illustrated in Fig. 1, where the well-measured Gaia EDR3 stars within 1.0 kpc from the Sun with the complete 6D phase space information available are plotted in a Toomre diagram that is color-coded according to VT2. It is quite clear that in the vicinity of the Sun, high VT values are displayed only by stars on retrograde orbits or on slightly prograde orbits but high 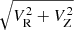 , the latter being equally interesting in our view, as they are typically associated with GES. Hence, we adopted VT > 400 km s−1 as our criterion to select likely retrograde stars. The criterion proved to be very effective as only 16 out of the 186 stars considered here and selected in this way are not retrograde, all of them having Lz < 800 kpc km s−1, while 123 of them have Lz ≤ −500 kpc km s−1. In future observational campaigns, we plan to select retrograde targets directly in VΦ among stars having Vlos measurements in the Gaia DR3 catalogue or catalogues from future Gaia data releases. This will allow us to sample also the mildly retrograde stars at relatively low total velocity (−100 km s−1 ≲ VΦ < 0.0 km s−1 and
, the latter being equally interesting in our view, as they are typically associated with GES. Hence, we adopted VT > 400 km s−1 as our criterion to select likely retrograde stars. The criterion proved to be very effective as only 16 out of the 186 stars considered here and selected in this way are not retrograde, all of them having Lz < 800 kpc km s−1, while 123 of them have Lz ≤ −500 kpc km s−1. In future observational campaigns, we plan to select retrograde targets directly in VΦ among stars having Vlos measurements in the Gaia DR3 catalogue or catalogues from future Gaia data releases. This will allow us to sample also the mildly retrograde stars at relatively low total velocity (−100 km s−1 ≲ VΦ < 0.0 km s−1 and 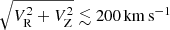 ) that are now excluded by our selection in VT, as well as to target specific substructures.
) that are now excluded by our selection in VT, as well as to target specific substructures.
 |
Fig. 1. Toomre diagram of the ≃2.4 million stars within 1.0 kpc from the Sun, having Vlos values measured in Gaia EDR3 and passing all the quality criteria we adopted for the WRS sample. Stars are color-coded according to their tangential velocity and stars with VT400 km s−1 are highlighted with a black empty square. |
The additional selection criteria we adopted were intended to select well-measured stars in the solar neighborhood. In particular we selected our targets among VT > 400 km s−1 stars having G ≲ 14.0. This suitable magnitude range was selected in order to get high signal to noise ratio (S/N), high-resolution spectra with 8 m class telescopes with relatively short exposures (typically ≤3000 s). Then, we imposed an error on the parallax lower than 10%. This implies small errors in the distance and in the proper motion. We selected stars with a distance from the Sun of D⊙ ≤ 1.0 kpc. We adopted the following criteria in order to ensure that the Gaia astrometry and photometry of the target stars are of the highest quality: RUWE ≤ 1.3 (Gaia Collaboration 2021) and C⋆ < 3σ (Riello et al. 2021). The first criterion is also effective in excluding astrometric binaries (see Andrew et al. 2022, and references therein). Finally, by inspecting the color-magnitude diagram, we excluded by hand a few dwarf stars that may be unresolved binaries, which are located slightly above the main sequence.
The most relevant outcome of the selections above, complemented by uncertainties in the Vlos measured from high-resolution spectra lower than 0.9 km s−1, is that the typical uncertainty on the IoM is just a few percent (see Sect. 3), hence, the noise in the phase space is minimal in our sample. Basic information on our target stars is listed in Table 1.
Main target information: ID, coordinates, apparent magnitudes and parallax from Gaia EDR3, color excess from the EXPLORE tool, and the instrument used to collect the spectrum.
2.2. High-resolution spectroscopy for selected stars
At the present stage, we have collected high-resolution spectra for 98 stars (Program IT-2021B-004 and Program IT-2022B-006, P.I.: M. Bellazzini) with the optical spectrograph PEPSI (Strassmeier et al. 2015) mounted at the Large Binocluar Telescope in Arizona. The observations have been performed with the CD3 grating for the Blue Arm, which cover the spectral range between 4800–5440 Å, and the CD6 grating for the Red Arm with a spectral coverage between 7410–9140 Å, both with a spectral resolution of 40 000. The choice of this set-up for the two arms was dictated by the trade-off between the access to measurable lines, allowing to derive the abundance of scientifically relevant chemical elements, and the efficiency of the spectrograph with the goal of achieving S/N > 30 for a reliable measure of the chemical abundances we are interested in. In order to maximize the number of observed stars, we aimed for short exposures. This translates into a magnitude limit of G < 14.0. CD3 is less efficient than CD6, therefore it drives the exposure times. The short exposures allow us to reach typically S/N ≳ 40 for the CD3 grating and S/N ≳ 60 for CD6. The spectra have been reduced with the dedicated PEPSI pipeline, which contains bias subtraction, flat-fielding, spectral extraction, wavelength calibration and normalization. The observations of close sky region in the same exposure times of the targets have been executed in order to subtract the sky contribution to the stellar spectra.
We also observed 100 stars (Program 0109.B-0522, P.I.: A. Mucciarelli) with the optical spectrograph UVES (Dekker et al. 2000) mounted at the Very Large Telescope of the European Southern Observatory. Observations were performed with UVES in Dichroic mode adopting the standard settings Dic 1 Blue Arm CD2 390 (3600–4800 Å) and Dic 1 Red Arm CD3 564 (4800–6600 Å) and with the 1″ × 12″ slit, thus yielding a resolution of R = 40 000. We are able to obtain, on average, S/N ≳ 20 for the Blue Arm and S/N ≳ 40 for the Red Arm. All the observed spectra have been reduced with the ESO pipeline3. The spectra of 12 targets were collected with both instruments as a reference point for the purpose of calibration and direct comparison.
Detailed information on some representative stellar spectra are listed in Table 2, bracketing the range of exposure times adopted and reporting the achieved S/N in several spectral region of interest. As an example of the quality of the spectroscopic dataset, we plot in Fig. 2 the spectra of four target stars with very similar atmospheric parameters and a difference in [Fe/H] of ≈1.2 dex.
 |
Fig. 2. Comparison between the spectra of two stars observed with PEPSI at LBT, shown on the left. Right column shows the same comparison, but for two stars observed with UVES at VLT. These stars have very similar Teff and log g but they differ in the iron content. Black arrows indicate the position of some atomic lines of interest. |
Magnitude, exposure times, airmass, and S/Ns for some of the observed target spectra with the spectrographs UVES and PEPSI.
3. Orbital parameters
Position, proper motion, and parallax measurements were taken from Gaia EDR3 (Gaia Collaboration 2021). We corrected each star’s parallax for zero-point offsets following the prescriptions described by Lindegren et al. (2021). Also, Vlos was measured from the high-resolution spectra by cross-correlation with template spectra using the fxcor task of IRAF4. For each star, as the template spectrum, we exploited a synthetic spectrum calculated using the correct atmospheric parameters (see Sect. 5.2). The Vlos is measured at the maximum peak of the cross-correlation function. Uncertainties on the line-of-sight velocity were computed following the method described in Tonry & Davis (1979). As shown in the central panel of Fig. 3, they are of the order of 0.1 − 0.9 km s−1, which significantly reduce the uncertainties arising from the Gaia measurements, especially for faint stars. Furthermore, we corrected the measured Vlos for the gravitational redshift effect following the prescription described by Zwitter et al. (2018). Since most of our stars are dwarfs and the precision of our Vlos measures is so high, this correction (albeit small) is non-negligible, ranging from 0.1 − 0.7 km s−1. The distribution of the final Vlos is displayed in the left panel of Fig. 3 and the values are listed in Table 3. The difference between our measurements and those from Gaia DR3 (Gaia Collaboration 2023; Katz et al. 2023), defined as ΔVlos = Vlos, spectrum − Vlos, GaiaDR3, is consistent within 3σ for all except five stars, where σ is calculated as the squared sum of the uncertainties arising from high-resolution spectroscopy and Gaia DR3 (see right panel of Fig. 3). The discrepancy observed in these five stars could hint at a binary nature for these objects. This implies the possibility of their having undergone a distinct and unconventional chemical evolution or either having the spectrum contaminated by the companion star. Consequently, we flag these stars with a distinct marking in Table 3, and they will be omitted from the following chemical analysis. The final Vlos values have been coupled with the parallax and proper motions provided by the EDR3 to draw the complete 6D phase space information for each target.
 |
Fig. 3. Line-of-sight velocity distribution for the entire stellar sample, shown on the left. Central panel shows comparison between the uncertainty on the line-of-sight velocity provided by Gaia (blue filled circles) and the one measured with high-resolution spectroscopy (red filled circles) as a function of observed G magnitude. The blue arrows point out the outliers in the distribution, specifically representing target stars with errors in the Gaia velocity measurement larger than 10 km s−1. Right panel shows the difference between the two measurements of the line-of-sight velocity. The red dashed lines mark the ±3σ threshold. |
Kinematic information for the stars: ID from Gaia EDR3, orbital energy, angular momentum along the z-axis, perpendicular angular momentum, and line-of-sight velocity with uncertainties.
We then transformed the observed kinematic information to the Galactocentric reference frame. To do so, we assume the Sun to be located R0 = 8.122 kpc away from the Galactic Center (GRAVITY Collaboration 2018) and z⊙ = 20.8 pc above the midplane (Bennett & Bovy 2019). We obtain the solar velocity by combining the definition of the local standard of rest by Schönrich et al. (2010) with the proper motion of Sgr A* (Reid & Brunthaler 2004). In this frame, the Sun moves with (U⊙, V⊙, W⊙) = (12.9, 245.6, 7.78) km s−1 (Drimmel & Poggio 2018).
We computed stars orbital parameters with the software AGAMA (Vasiliev 2019) using a McMillan (2017) potential for the MW. We ran 100 Monte Carlo simulations of the orbit for each star assuming Gaussian distributions for the uncertainties in distance, proper motion, and radial velocity. The final values of the dynamical parameters are computed as the median of their derived distributions, with associated uncertainties at the 16th and 84th percentiles. The typical error in E, Lz and L⊥ are ≲0.8%, ≲2.6%, and ≲1.8%, respectively. The distribution of our sample in these dynamical spaces is shown in Sect. 4.
4. Identification of substructures in the RH
Recent studies have revealed that the RH exhibits plenty of substructures that significantly contribute to the total mass budget of the stellar halo (Naidu et al. 2020). In most cases, they have been identified as overdensities in the space of IoM, such as their actions, the total energy (E), the angular momentum along the z-direction (Lz), and the angular momentum perpendicular to Lz (L⊥). We note that L⊥ has been extensively used to identify stars formed in the same progenitor, even if it is not completely conserved in an axisymmetric potential such as the one we assumed for our galaxy (Helmi et al. 1999; Helmi & de Zeeuw 2000; Bonaca et al. 2021).
As a first application of this first bunch of WRS data, we attempted to carry out a chemical characterization of some of the substructures recently listed and discussed by Dodd et al. (2023, D23 hereafter), who built on the findings by Lövdal et al. (2022) and Ruiz-Lara et al. (2022). These authors used a specifically designed clustering algorithm based on the IoM computed using Gaia DR3 data to identify groups of stars sharing similar properties in the phase space.
In the region of the E, Lz, and L⊥ space covered by our sample, the most widely represented among the D23 groups is GES. We sample the most retrograde and high energy slice of GES, based on our selection window. In addition, there are two mid-sized slightly retrograde substructures associated to Sequoia (Myeong et al. 2019) and Thamnos (Koppelman et al. 2019), as well as three newly found, small, high-energy, and extremely retrograde clumps, namely L-RL64, also known as Antaeus (Oria et al. 2022), ED-2, and ED-3, plus other minor groups that do not appear to have significant overlap with our sample (see more details below). Indeed, we find that 179 of our 186 stars are included in the D23 sample. 55 of them are associated with one of the D23 groups. However, there are five groups that have just one member star included in our sample, namely Thamnos, ED-5, ED-6, Group 13, and Group 14. Since no meaningful conclusion can be drawn from an individual star, we do not consider these substructures in the following. Still, we do make the chemical abundances available since they might be of interest for upcoming investigations. Of the remaining 50 stars, 12 are associated to GES, 18 to Sequoia, 11 to Antaeus, 4 to ED-2, and 5 to ED-3.
Starting from these 50 “core members” and with the aim to increase the number of stars associated to a substructure, we performed a clustering analysis with the algorithm DBSCAN (Ester et al. 1996). We used E, Lz, and L⊥ as the input parameters for the clustering algorithm, for the purpose of having a fair comparison with D23. We scaled the space of these parameters with the RobustScaler tool in scikit-learn (Pedregosa et al. 2011). Due to the significant overlap between halo substructures in the IoM spaces, it is difficult for any clustering algorithm to identify each individual overdensity. Furthermore, some of the newly discovered substructures include a low number of stars. For this reasons, the algorithm used in this study was fine-tuned to detect all the small-scale clumps identified by D23. We find the best matching results with D23 by using DBSCAN default hyperparameters and by setting eps = 0.34 and min_samples = 5. Figure 4 shows the position of the final candidate members of each substructure in the IoM space. With our final selection, we were able to relate 119 stars in our parent sample to the known retrograde substructures. In the following sections, we discuss the sample defined for each substructure in detail.
 |
Fig. 4. Distribution of the observed stars in IoM and velocity space (top and bottom panels, respectively). We highlight stars associated with various substructures with different colors (green for GES, brown for Sequoia, blue for Antaeus, magenta for ED-2, orange for ED-3, cyan for Clump-6 and red for Clump-7). |
Before starting the discussion of the various substructures, it is important to note that the identification and classification of completely disrupted relics of ancient merging events is still in its infancy and, as made clear in the following discussion, it is subject to considerable uncertainty. On the one hand, there is no consensus on the best selection criteria to isolate the purest samples of a given substructure and any criterion will imply some degree of contamination from unrelated sources (see, e.g., Buder et al. 2022, for references and discussion). On the other hand, as stated above, there are substructures that may be erroneously considered as an individual entity when they may, in fact, be the sum of independent substructures or the unrecognized part of a larger one (Koppelman et al. 2020; Naidu et al. 2020; Belokurov et al. 2023; Dodd et al. 2023). Here, we aim to get a clearer insight into the nature of some of the retrograde substructures by adding the chemical dimensions, as done by other authors (e.g., Feuillet et al. 2020, 2021; Buder et al. 2022; Horta et al. 2023). Overall, this is not an easy task in the present phase and it is worthwhile to proceed cautiously, taking care of every step along our exploratory path.
4.1. Gaia-Enceladus Sausage
The dominant accreted component in the nearby stellar halo is the remnant of the last major merger event experienced by the MW with an ancient (8–11 Gyr ago) and relatively massive (M⋆ ∼ 108 − 109 M⊙) dwarf galaxy, known as GES (Belokurov et al. 2018; Helmi et al. 2018; Gallart et al. 2019; Mackereth et al. 2019; Massari et al. 2019; Vincenzo et al. 2019; Kruijssen et al. 2020; Hasselquist et al. 2021). One of the defining characteristics of this population is the stars’ highly eccentric orbits and slightly retrograde motion. The metallicity distribution function of GES peaks from [Fe/H] ≃ −1.5 to −1.1 dex, depending on the sample selection and the spectroscopic survey (Naidu et al. 2020; Feuillet et al. 2020; Bonifacio et al. 2021; Bellazzini et al. 2023). Additionally, these stars exhibit lower [α/Fe] values for fixed metallicity when compared to in situ populations, thus suggesting that they originated in an environment characterized by a less efficient star formation (Fernández-Alvar et al. 2018; Helmi et al. 2018; Das et al. 2020; Feuillet et al. 2020; Naidu et al. 2020; Limberg et al. 2022; Myeong et al. 2022; Horta et al. 2023).
Due to the criterion employed to select retrograde stars (see Sect. 2), which significantly cuts the IoM region typically populated by GES stars, we were able to retain only 12 stars in common with D23 belonging to GES. By using the clustering algorithm, all of the original members of this cluster were retained as GES members and an additional 41 stars were added to it, making the total number of stars in this cluster equal to 53 (see the green-colored symbols in Fig. 4 and thereafter).
4.2. Sequoia
The first evidence of the remnant of an accreted dwarf galaxy in the RH was the identification of a clump of stars moving on highly retrograde orbits, with large orbital energy and forming an arc-like structure in the Toomre diagram, now dubbed Sequoia (Myeong et al. 2018, 2019; Koppelman et al. 2018; Matsuno et al. 2019). Sequoia has been proposed to be the remnant of an accreted independent small dwarf galaxy due to its position and smaller extent in the IoM space with respect to GES (Koppelman et al. 2019; Myeong et al. 2019). However, the actual complexity of this substructure is far greater than what was initially perceived. A different scenario has been proposed to explain the Sequoia overdensity, possibly making it tightly related to the GES accretion event. In fact, it has been shown that a GES-like progenitor, depending on its orbital configuration and morphology, is able to display its debris on orbits that reproduce the same arc-like feature associated with Sequoia (Koppelman et al. 2020; Amarante et al. 2022; Belokurov et al. 2023). The chemical composition of Sequoia remains a subject of ongoing debate, as different studies have yielded conflicting results regarding its abundance of α-elements compared to the GES substructure. Several works have reported either an enhancement (Mackereth et al. 2019; Myeong et al. 2019) or a depletion (Monty et al. 2020; Matsuno et al. 2022) of α-elements compared to GES abundances. Moreover, Naidu et al. (2020) found a multiple-peaked metallicity distribution for Sequoia, and claimed that two additional sub-components, namely Arjuna and I’Itoi, occupy the same region in the IoM space (see also, Bellazzini et al. 2023). In addition, Ruiz-Lara et al. (2022) discovered three disconnected clusters in the region of the IoM space previously associated to Sequoia that might be related to different progenitors.
The cross-match provides 18 common members between our targets and the Sequoia sample of stars identified by D23. When using the DBSCAN algorithm, only 8 stars were found to belong to this clump; additionally, 2 stars from the original sample were associated with ED-2 (see Sect. 4.4). This association was primarily based on the alignment of these two stars with the ED-2 clump in the Lz − L⊥ space. However, they were found to move on higher energy orbits with respect to ED-2. Consequently, this distinctive orbital behavior led us to consider the possibility of these stars being affiliated with the Sequoia substructure. In the end, since all the 8 stars are part of the 18 original members, we decided to stick with the original D23 classification for Sequoia. Thus, our final Sequoia sample contains 18 stars (brown-colored symbols in Fig. 4).
4.3. Antaeus/L-RL64
L-RL64 is a newly discovered cluster located in the most retrograde region of the IoM space (Lövdal et al. 2022; Ruiz-Lara et al. 2022). L-RL64 is one of the three clusters associated to the Sequoia merging event and it was initially believed to be its extreme retrograde tail. Subsequently, Oria et al. (2022) independently rediscovered this substructure in the action space, giving it the name Antaeus. The peculiar kinematics of this clump (which we henceforth refer to as Antaeus) combined with the mass estimate derived from its mean metallicity, indicate a different origin for this substructure with respect to Sequoia. Indeed, it is now thought that Antaeus is an independent accretion event, not related to Sequoia (Oria et al. 2022; Ruiz-Lara et al. 2022; Dodd et al. 2023).
The analysis based on D23 data shows that 11 stars in our entire sample are associated with Antaeus. However, the clustering algorithm identifies two separate clumps composed of 15 stars moving on extremely retrograde orbits. Here, we treat them as one single substructure (blue-colored symbols in Fig. 4), since their position in the IoM spaces is totally consistent with the one of Antaeus and 13 out of these 15 stars are labeled by Oria et al. (2022) as members of this group. Thus, with our final selection we define a fair sample of this newly discovered substructure and we will be ableto provide its detailed chemical characterization for the first time.
4.4. ED-2 and ED-3
D23 spotted two new small highly retrograde clusters near Sequoia, namely ED-2 and ED-3, which are extremely tight in the IoM and velocity spaces (see their Fig. 3). We thus have a total of 4 and 5 stars in common with the ED-2 and ED-3 clusters, respectively. The results provided by DBSCAN show that we are able to retain all the 5 stars in the ED-3 clump and also add 1 star to the ED-2 substructure (orange- and magenta-colored symbols in Fig. 4, respectively). Notably, as remarked above, the clustering algorithm spotted 2 additional stars that were previously associated with Sequoia as members of ED-2.
4.5. Thamnos, Clump-6, and Clump-7
Koppelman et al. (2019) revealed the presence of a less prominent substructure with typically lower orbital energy in the retrograde region of the E − Lz space with respect to GES, which they named Thamnos. Given its small extent in the E − Lz plane, they estimate a stellar mass < 5 × 106 M⊙. Thamnos has been suggested to be the remnant of an old merging event with the MW, due to its low mass and peculiar location in the IoM (Kruijssen et al. 2020), but it is still unclear if the stars associated to this group are from a unique remnant or two (Koppelman et al. 2019; Bellazzini et al. 2023).
In our entire sample, only 1 star is linked to Thamnos according to D23. As is in the case with GES, the selection method used does not allow us to include stars with orbital energy as low as Thamnos, which means we are unable to sample this particular substructure. Interestingly, DBSCAN spots two clusters composed of 17 and 6 stars in the low energy regime of our sample at slightly higher orbital energy with respect to Thamnos. These two groups have very similar E and Lz, but they differ in L⊥. It is worth noting that these clumps may be artificial overdensities identified by the algorithm and produced by our selection cut. In the following, we refer to them as Clump-6 and Clump-7 (cyan- and red-colored symbols in Fig. 4).
4.6. Unassociated stars
A significant fraction of our sample, 67 out of 186 stars, does not appear to be associated with any known structure according to D23 and the clustering algorithm. In the rest of the paper, we do not focus on the chemical features of these unassociated stars, as they will be part of future contributions to the WRS project, exploiting their chemistry to determine whether they are accreted.
5. Abundance analysis
5.1. Stellar parameters
Establishing precise atmospheric parameters (i.e., effective temperature, Teff, surface gravity, log g, and microturbulent velocity, vt) is a crucial step to obtaining reliable chemical abundances.
We derived both Teff and log g relying on the EDR3 photometry (see Table 1). In particular, Teff has been calculated with the (BP − RP)0 − Teff relation provided by Mucciarelli et al. (2021a). The color (BP-RP) has been corrected for extinction following the iterative procedure described in Gaia Collaboration (2018a). The color excess E(B − V) adopted for each star is provided by the online tool EXPLORE5. Since the adopted color – Teff relation depends on the star metallicity ([Fe/H]), which is not known a priori, we calculated Teff while assuming a fixed value of [Fe/H] = −1.5 dex for any star. The uncertainty on Teff is due to the errors in photometric data, parallax, color excess, and (BP − RP)0 − Teff relation. Given that the observed targets are bright, very nearby and affected by minimal extinction, the main source of error in the effective temperature arises from the color and Teff relation. Thus, we assumed the dispersion of the (BP − RP)0 − Teff relation, which is 61 K (Mucciarelli et al. 2021a), as the typical internal error on Teff. Surface gravities have been estimated assuming the photometric Teff, a stellar mass derived from a BaSTI isochrone (Pietrinferni et al. 2021) with 12 Gyr, [Fe/H] = −1.5 dex and [α/Fe] = +0.4 dex (according to the typical values for the accreted component of the stellar halo derived in previous studies, Nissen & Schuster 2010, Kruijssen et al. 2020, Montalbán et al. 2021, Horta et al. 2023) and the G-band bolometric corrections described by Andrae et al. (2018). We note that employing an alternative isochrone varying the parameters has a minimal impact on the resulting surface gravity of the star. For instance, when using an isochrone with 10 Gyr age, [Fe/H] = −1.1 dex and [α/Fe] = +0.4 dex, the discrepancy with the first results remains consistently below 0.04 dex. The uncertainties on log g are derived through the propagation of the errors on the effective temperature, photometry, and distance. The obtained values are systematically lower than 0.1 dex. Finally, microturbulent velocities were calculated by requiring no trend between iron abundances and reduced equivalent widths, defined as log10(EW/λ). The uncertainties on vt are estimated as described in Mucciarelli et al. (2013) and they are of the order of 0.2 km s−1.
Subsequently, we improved the estimate of the stellar parameters by using the correct [Fe/H] value derived from the chemical analysis. The final effective temperature value deviates from the initial estimate by a margin persistently lower than 60 K. We excluded from the chemical analysis the three hottest stars of the sample (Teff> 6650 K). This decision stems from the fact that the combination of their atmospheric parameters leads to the formation of extremely weak absorption lines. As a consequence, this renders the measurement of abundances unreliable. In Fig. 5, we show the color-magnitude diagram (CMD) for all the analyzed stars, color-coded based on the metallicity. The final values of the atmospheric parameters are listed in Table 4.
 |
Fig. 5. Gaia EDR3 distance-corrected color-magnitude diagram of the 175 analyzed stars. Targets are color-coded based on the metallicity. |
Stellar parameters for the selected targets: ID from Gaia EDR3, derived effective temperature, surface gravity, microturbulent velocity, and iron abundance ratio.
5.2. Line selection
To obtain the chemical abundances of each star, we made a list of unblended lines to analyze, automatically pre-selected with our own code AUTOKUR and consequently refined with a visual comparison between the observed and the synthetic spectra. The latter were calculated with the code SYNTHE (Kurucz 2005), adopting the stellar parameters of the observed targets (see Sect. 5.1), assuming ATLAS9 (Kurucz 2005) model atmospheres, and using the linelists containing atomic and molecular data from the Kurucz/Castelli6 database. The synthetic spectra have been convolved with a Gaussian profile to reproduce the observed resolution.
To address the fact that the degree of blending for a particular transition is dependent on the metallicity, which is not known a priori in this case, we utilized an iterative approach to establish the list of spectral lines to analyze for each star. The synthetic spectra have been calculated adopting an α-enhanced mixture ([α/Fe] = +0.4 dex) with an initial metallicity of [Fe/H] = −1.5 dex. Following the initial chemical analysis, a revised set of unblended spectral lines has been identified for each star using a synthetic spectrum that was computed using the appropriate chemical composition.
During the visual inspection, we noticed that the spectra of three low-main sequence stars (Teff < 5250 K and log g > 4.60) were highly contaminated by molecular transitions from MgH. Thus, we opted to exclude them from the abundance analysis. In the end, when considering also the exclusion of the 5 binary stars, a total of 11 stars were removed from the initial sample. We chose to exclude them from further consideration in our study. Among these 11 excluded stars, 4 were associated with GES, 1 with ED-2, 1 with Sequoia, 1 with Clump-6 and 4 stars remained unassociated with any specific substructure.
5.3. Chemical analysis
The chemical abundances of Na, Ca, Ti, Fe, Ni, and Zn were derived through a comparison between the observed equivalent widths (EWs) and the theoretical line strengths using the code GALA (Mucciarelli et al. 2013). The EWs were measured with the code DAOSPEC (Stetson & Pancino 2008) via the automatic tool 4DAO (Mucciarelli 2013).
The chemical abundances of elements which show saturated core lines, but with wings that are still sensitive to the abundance or hyperfine/isotopic splitting transitions (Mg, Al, Sc, Mn, and Y) were derived through spectral synthesis with the proprietary code SALVADOR. This program runs a χ2-minimization between the observed line and a grid of synthetic spectra computed on-the-fly by the code SYNTHE, keeping the stellar parameters fixed and varying only the abundance of the matching element.
All the abundances were scaled to the solar composition, taking as reference the values from Grevesse & Sauval (1998). We adopted these solar abundances since the ATLAS9 model atmospheres used in this study are computed based on a chemical mixture consistent with the one outlined in Grevesse & Sauval (1998; see Castelli & Kurucz 2003). For all the elements that were examined, in cases where the spectral lines were not clearly detectable, we determined upper limits by comparing the observed spectra to the synthetic spectra.
To put the chemical abundances measured for the stars in the UVES and PEPSI samples onto the same scale, we made a direct comparison between the final abundances ratios of the 12 stars that have been observed with both instruments. For each element, we determined a median abundance difference (Δabu = [X/Fe]PEPSI − [X/Fe]UVES) and we applied an offset correction by adopting UVES as the reference scale (due to the largest number of available lines) in the cases where:
and where σ is the standard deviation of the abundance differences for a given element and N⋆ is the number of stars with a measured abundance with both instruments for that specific element. For Fe, Ca, Sc, Ni, Zn, and Y, we corrected the abundances for the PEPSI sample by subtracting the offsets listed in Table 5, thus bringing them onto the UVES scale. We focus in the next paragraphs on the methodology we employed specifically to derive chemical abundances for problematic species.
Differences in chemical abundances obtained from the UVES and PEPSI samples, including the calculated offsets, corresponding standard deviations, and the number of stars used for each element.
Sodium. The available two lines of Na in the spectral range of PEPSI are centered at 8183.3 and 8194.8 Å. We highlight that these atomic lines are situated within a spectral region significantly affected by telluric absorption lines. As a precautionary measure to ensure the robustness of our analysis, we visually inspected the possible telluric contamination of the Na lines using appropriate synthetic spectra of the Earth atmosphere calculated with TAPAS (Bertaux et al. 2014). Subsequently, we excluded any Na line exhibiting signs of contamination attributable to telluric features. We applied the correction for departures from LTE conditions from Lind et al. (2011). All the corrections for Na are available through the INSPECT database7. The values listed in Table 6 are corrected for NLTE.
Chemical abundances for the odd-Z, iron-peak and neutron capture elements for the stars associated to known substructures.
Aluminum. Within the UVES spectral range, the presence of Al is characterized by solely two strong lines located at 3944.0 and 3961.5 Å. However, these lines become saturated at [Fe/H] > −1.3 dex. In contrast, the PEPSI sample features only three weak aluminum lines suitable for the chemical analysis: one line at 7836.1 Å and the doublet at 8772–73 Å. Unfortunately, these weak lines are not detected at metallicities lower than ∼ − 1.5 dex. The corrections for non-LTE effects for each line are taken from Lind et al. (2022).
5.4. Abundance uncertainties
When inferring the uncertainties on the abundance ratios, it is essential to consider two primary sources of error: internal errors related to EW measurements and errors arising from the adopted atmospheric parameters. Uncertainties due to EW measurements have been estimated as the dispersion around the mean of the individual line measurements, divided by the root mean square of the number of used lines. For elements whose abundances have been measured using spectral synthesis, we exploited Monte Carlo simulations to estimate the internal error. Specifically, we generated a sample of 500 synthetic spectra with Poissonian noise to reproduce the S/N of the observed spectra and then we repeated the analysis to derive the abundance. The internal error is estimated as the standard deviation of the abundance distribution of the 500 noisy synthetic spectra.
To determine the uncertainties arising from atmospheric parameters, we replicated the chemical analysis by varying only one stellar parameter at a time and keeping the others fixed (see Sect. 5.1 for the details about the derivation of the uncertainties on the atmospheric parameters). Since we refer to chemical abundances with abundance ratios ([X/Fe]), the uncertainties on the iron abundance [Fe/H] have been considered as well.
The intrinsic and systematic components have been summed in quadrature to compute the total uncertainty. Therefore, the final errors have been estimated as:
where σX, Fe is the dispersion around the mean of chemical abundances, NX, Fe is the number of used lines and 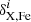 are the abundance differences obtained by varying the parameter i. All the abundance ratios for individual stars are listed in Tables 7 and 6, together with the corresponding uncertainties, as described in Sect. 5.4.
are the abundance differences obtained by varying the parameter i. All the abundance ratios for individual stars are listed in Tables 7 and 6, together with the corresponding uncertainties, as described in Sect. 5.4.
Chemical abundances for the α-elements for the stars associated to known substructures.
6. Comparison with the literature
To put our results in a more general context, in this section we compare chemical abundances of our sample with external datasets, starting with the sample of metal-poor dwarf and subgiant stars associated with the halo population analyzed by Nissen & Schuster (2010; NS10, hereafter). This choice was guided by the extremely high-quality stellar spectra used by NS10 (S/N ranging from 250 to 500) that guarantees accurate measurements of chemical abundances. By using a sample of stars observed with UVES at VLT and FIES at NOT, these authors revealed for the first time the existence of two distinct populations within the nearby MW halo, composed of stars having different kinematics and chemical patterns. NS10 proposed that the Galactic halo population ([Fe/H] ≲ −0.8 dex) following the low-α sequence in the classical [Fe/H] vs. [α/Fe] plane (see the red squares in Fig. 6) is composed of stars accreted from disrupted dwarf galaxies, whereas the high-α population (green triangles in Fig. 6) is made up of stars that have formed in situ, a view that that is generally accepted nowadays (Bonaca et al. 2017; Hayes et al. 2018; Haywood et al. 2018; Helmi et al. 2018; Mackereth et al. 2019; Helmi 2020). To avoid the introduction of systematic errors due to the different chemical analysis and ensure a fair comparison between homogeneous results, we defined our reference targets based on a sub-sample of 41 NS10 stars that have been observed with UVES using the same instrument setup as our targets and covering a range of atmospheric parameters similar to our sample. We re-analyzed the NS10 spectra following the same procedure described in Sect. 5 and using the same linelist. We found a median discrepancy of [Fe/H] = −0.05 dex and σ[Fe/H] = 0.08; given that these values adhere to the criteria described in Eq. (1), we made the decision to adjust the abundances to ensure congruence within the NS10 reference frame. The estimates of [Mg/Fe] display a median difference of 0.01 dex and σ[Mg/Fe] = 0.08.
 |
Fig. 6. Comparison of Mg abundance ratios of the stars from our selection observed with UVES (blue filled circles) and the NS10 reference sub-sample (red filled squares and green filled triangles for low-α and high-α sequences, respectively). The errorbar in the top-right corner indicates the typical uncertainties. |
We show the final comparison in Fig. 6: as expected from the selection we imposed to our targets, which should predominantly include retrograde, accreted objects, stars from our sample (blue symbols) are located in the same region of the α-elements chemical planes as the low-α population from NS10, with abundances that are systematically lower (≈0.2 dex on average) than the high-α population composed of in situ stars. It is also interesting to note that the low-α sequence of NS10 targets basically defines the upper limit of the distribution of our targets, which are mostly at lower [α/Fe] abundances. This might reflect the fact that we are sampling regions of the RH populated also by several different low-mass mergers, for which theoretical models predict low (and different) [α/Fe] levels already at fairly low metallicity (Matsuno et al. 2022). On the other hand, the accreted population of NS10 likely belongs to the most-massive merger, GES.
As a further and independent check of our results, we also made a comparison with chemical abundances from the large and widely used APOGEE DR17 (Abdurro’uf et al. 2022) dataset. We limited the comparison to well-measured APOGEE abundances by selecting only stars having ASPCAPFLAG = 0, STARFLAG = 0, EXTRATARG = 0, SNR > 70, FE_H_ERR < 0.1, and ALPHA_M_ERR < 0.28. The final APOGEE sample (APOGEE control sample hereafter), which we use as a reference throughout the paper, is composed of 192225 stars, with 98.9% of them lying at D⊙ ≤ 2.0 kpc. The left panel of Fig. 7 reveals that, in the [Fe/H] vs. [Mg/Fe] plane, our targets show a good agreement in the common metallicity range of −2.4 ≤ [Fe/H] ≤ −0.8 dex with the low-α population stars from the APOGEE control sample. Interestingly, the stars from our sample that move on more extreme retrograde orbits (Lz < −2500 kpc km s−1) appear to lay on a different pattern with respect to the low-α population at [Fe/H] < −1.5 dex, with lower [Mg/Fe] at fixed metallicity. In the right panel of Fig. 7, we show the [Mg/Mn] vs. [Al/Fe] chemical space, which serves as a diagnostic to distinguish between accreted and in situ populations (Das et al. 2020; Horta et al. 2021). Contrary to the APOGEE control sample, nearly all of our targets are located in the area of the plot where we expect to find accreted stars (Horta et al. 2021), emphasizing the fact that we are observing a poorly explored area of the solar neighborhood. Indeed, only less than 1% of the stars within the APOGEE control sample are located at D⊙ < 1 kpc and move on retrograde orbits. It is worth noting that only 11 stars among our sample are listed in the entire APOGEE DR17 catalogue, with only one of them aligning with the selection criteria expounded above. Moreover, through our program, we have the capability to provide detailed chemical abundance data for elements that are notably absent in APOGEE (e.g., Sc, Zn, and Y) and for elements whose measurements in APOGEE may diverge from theoretical expectations (Na and Ti).
 |
Fig. 7. [Mg/Fe] abundance ratios as a function of [Fe/H] for our sample (color-coded by the angular momentum along the z-direction, Lz) and for the APOGEE control sample (greyscale 2D histogram) shown on the left. The errorbar in the top-right corner displays the typical uncertainties. [Mg/Mn] abundance ratios as a function of [Al/Fe] for the same samples, with the same arrangement shown on the right. Red arrows indicate upper limits. |
The comparisons presented above show that the selection we adopted was very effective in selecting stars that very likely originated in ancient and now-dissolved MW satellites. In addition to the location of our stars in the [Mg/Mn] vs. [Al/Fe] plane, it is worth noting that: (a) our kinematic selection picked up only metal-poor stars ([Fe/H] ≲ −0.8 dex), the majority of which (65%) having [Fe/H] ≤ −1.5 dex, with a significant very metal-poor tail (47 stars with −2.0 ≤ [Fe/H] < −3.0 dex, 26% of the sample), a component that is poorly probed by the APOGEE control sample; and (b) despite the higher resolution, our stars show a larger scatter in [Mg/Fe] with respect to APOGEE, increasing with decreasing metallicity, suggesting again that we are more effective in sampling stars from a variety of disrupted satellites, with different chemical evolutionary paths. In summary, the results of the adopted selection are fully compliant with the main rationale of WRS.
In Fig. 8, we compare the IoM of our targets with those of the NS10 sample and APOGEE. We computed the IoM for the NS10 stars using the 6D phase space information provided by the Gaia EDR3. Instead, for the APOGEE control sample we used the phase space values from Gaia listed in the APOGEE DR17 catalogue. First, Fig. 8 provides a direct view of the efficiency of our selection criterion in picking up halo stars in retrograde motion, as discussed in Sect. 2. However, this criterion does introduce a clear bias, since it prevents us from picking stars with low orbital energy (E ≤ 1.5 × 105 km2 s−2) moving on slightly retrograde orbits (Lz ≥ −0.5 × 103 kpc km s−1). At the same time, it is clear that high-quality APOGEE measures primarily targets disc stars with a quite sparse sampling of the retrograde component of the halo. For what it concerns the NS10 sample, although some high-α stars are interestingly located in the retrograde region (they might be part of the dynamically heated disc, sometimes referred to as the Splash, Belokurov et al. 2020), the bulk of this population moves on disc-like orbits, whereas the low-α moves on high eccentricity orbits, as expected for GES stars.
 |
Fig. 8. Distribution of the targets stars in the IoM space compared with the NS10 stars and the APOGEE sample. The color coding is the same as in Fig. 6. |
7. Chemical abundances of RH substructures
Here, we present the chemical abundances of the substructures in the RH of the MW. Having inspected the [Fe/H] vs. [X/Fe] diagrams for all the elements we measured, we discuss only those that appear to provide the clearest view of the substructures we consider here. In particular, we focus on the abundances of Na, Mg, Al, Ca, Sc, TiI, TiII, Mn, Ni, Zn, and Y. It is of utmost importance to acknowledge that due to impact of the combination of the atmospheric parameters onto the shape of absorption lines, our capacity to measure the chemical abundances for every depicted chemical element across all stars is restricted. Consequently, certain stars may not feature in specific figures.
7.1. Metallicity distribution functions
We go on to examine the metallicity distribution functions (MDFs) of the six substructures that were built exploiting only the IoM. In Fig. 9 we display the results, which suggest that the global MDF of our sample is bimodal, with a primary peak at [Fe/H] ≃ −1.4 dex and a secondary peak at [Fe/H] ≃ −2.4 dex. The high-metallicity end of the RH stars distribution is dominated by GES, with a median metallicity of [Fe/H] = −1.47 dex and σ[Fe/H] = 0.32. Our result is consistent with Bonifacio et al. (2021) and 0.2–0.3 dex more metal-poor than indicated by typical literature values (Vincenzo et al. 2019; Naidu et al. 2020; Feuillet et al. 2021; Buder et al. 2022; Bellazzini et al. 2023). Once again, we wish to emphasize the importance of our adopted selection criterion for GES stars. This criterion is structured in such a way that prevents us from including stars from the solar neighborhood with [Fe/H] > −0.80 dex, while exclusively observing the higher energy populations of GES. As shown in Koppelman et al. (2020), the high-energy debris of a merger event typically consists of the first stars to have been lost by a progenitor, meaning those in its peripheries. As commonly observed in dwarf spheroidal galaxies orbiting the Milky Way (see, e.g., Tolstoy et al. 2023), it is reasonable to expect a negative metallicity gradient that would explain why our targets are slightly more metal-poor than lower-energy GES samples. Stars assigned to Sequoia are, on average, slightly more metal-poor with respect to GES and display a broad MDF, with a median metallicity of [Fe/H] = −1.66 dex and σ[Fe/H] = 0.37, which is consistent with the result by D23. The two most metal-poor stars in Sequoia have a metallicity that overlaps with that of ED-2. However, these 2 stars occupy a place in the IoM space that is significantly different with respect to the ED-2 clump. Moreover, they do not exhibit the distinctive high [Ti/Fe] ratios observed in the stars of ED-2 at a comparable metallicity. As a result, we exclude a possible association of these stars with the ED-2 substructure based on their chemical features. Antaeus displays a coherent MDF with a median metallicity of [Fe/H] = −1.83 dex and σ[Fe/H] = 0.27, which is consistent with the value of [Fe/H] = −1.74 dex provided by Oria et al. (2022). The MDF of ED-3 resembles the one of Antaeus with very small dispersion, having a median metallicity of [Fe/H] = −1.73 dex and σ[Fe/H] = 0.21, thus hinting that the two substructures might be related. ED-2 is the most metal-poor substructure and has an extremely tight MDF with a median metallicity of [Fe/H] = −2.43 dex and σ[Fe/H] = 0.04, which is consistent with the metallicity range reported by Balbinot et al. (2023) for the stars associated to this substructure. In the end, Clump-6 and Clump-7 show rather flat, unpeaked and broad MDFs, with median metallicity of [Fe/H] = −1.89 and −2.02 dex and σ[Fe/H] = 0.48 and 0.29, respectively.
 |
Fig. 9. Metallicity distribution functions for the RH substructures labeled at the top of each panel compared to the MDF of the entire sample of stars. The median metallicity value and the standard deviation of the distribution are also reported. The color coding is the same as in Fig. 4. |
To obtain a clearer view, we explored the space defined by the orbital eccentricity, defined as ecc = (apo − peri)/(apo + peri), where apo and peri are the orbital apocenter and pericenter, respectively; this dynamical parameter can help to efficiently differentiate the various substructures. Each substructure comprises stars that predominantly follow orbits characterized by very similar eccentricity (see Fig. 10). The exceptions are Clump-6 and Clump-7, whose stars are spread across the range of ecc ≃ 0.1 − 0.8.
 |
Fig. 10. Eccentricity distribution functions for the RH substructures labeled at the top of each panel compared to the distribution of the entire sample of stars. The median eccentricity value and the standard deviation of the distribution are also reported. The color coding is the same as in Fig. 4. |
In the left panel of Fig. 11 we plot the behavior of ecc as a function of the metallicity [Fe/H], finding that, in our sample, only stars with [Fe/H] < −1.5 dex are moving on low eccentricity orbits (ecc < 0.4). As made evident in the right-hand panel of Fig. 11, RH substructures are well separated in the ecc − Zmax space as well, where Zmax indicates the maximum absolute height over the Galactic plane reached by a star during its orbit. Once again, the exceptions are Clump-6 and Clump-7. The broad spread in the eccentricity values for the stars in these substructures, coupled with the shape of their MDFs, compels us to attribute the existence of these cluster to a combination of our selection criterion and the choice of hyperparameters in the clustering algorithm. As a result, we do not consider Clump-6 and Clump-7 to be genuine substructures or independent accretion events. Thus, we excluded stars associated to these two clusters from the rest of the analysis.
 |
Fig. 11. Distribution of the RH substructures in the eccentricity vs. [Fe/H] space (left panel) and in the eccentricity vs. Zmax (right panel). The color coding is the same as in Fig. 4. |
Based on the MDF and the eccentricity parameter, three substructures emerge as notably more coherent. GES distinguishes itself as the most metal-rich component, characterized by a peak in the MDF that closely mirrors the primary peak observed in the overall sample. Furthermore, GES comprises stars that exhibit the highest eccentricities in their orbital motion. Then, Antaeus is identified as another well-defined substructure, with its constituent stars primarily having orbits characterized by a relatively high eccentricity (≃0.7). Finally, ED-2 exhibits distinctive features in its MDF and ecc, both being characterized by a remarkably narrow distribution. It is interesting to note that the 2 stars that were incorporated into the ED-2 clump by the clustering algorithm have [Fe/H] ≃ −1.90 dex and also showcase a behavior that is more akin to that of Sequoia in terms of eccentricty (ecc > 0.6) and [TiI/Fe]. These values support our choice to incorporate them as part of Sequoia.
7.2. Odd-Z elements
Odd-Z elements, such as Na and Al, are believed to be mainly synthesized in massive stars exploding as core-collapse supernovae (CC-SNe) at low metallicity and in asymptotic giant branch (AGB) stars at intermediate metallicity (Nomoto et al. 2013). Since they are formed starting from a neutron excess produced in the CNO cycle, their yield depends on the metallicity of the progenitor (Kobayashi et al. 2020).
Recent studies have demonstrated that stars that have formed in situ are enhanced in odd-Z elements abundances with respect to accreted populations and stars in dwarf satellite galaxies of the MW (Tolstoy et al. 2009; Feuillet et al. 2021; Hasselquist et al. 2021; Belokurov & Kravtsov 2022).
We show in Fig. 12 that the stars from our sample display sub-solar values of [Na/Fe], in agreement with the findings by Nissen & Schuster (2010). Moreover, it is evident that Antaeus displays a depletion in Na relative to GES. This distinction is discernible through the positioning of its stars on a distinct sequence, consistently registering values ∼0.2 dex lower. The sequence defined by Antaeus closely resembles the pattern found by Matsuno et al. (2022) for the stars belonging to Sequoia, whereas our stars associated with Sequoia exhibit a behavior that is more akin to that of GES. However, Matsuno et al. (2022) employed a relatively wide retrograde region within the IoM space to identify members of Sequoia (with Lz values ranging from −1600 to −3100 kpc km s−1), making very likely that some Antaeus stars inadvertently contaminate their Sequoia sample, thus potentially contributing to the observed similarities. Figure 12 also shows that the [Al/Fe] trend of our targets is almost flat at [Al/Fe] ∼ −0.3 dex for [Fe/H] < −1.0 dex. The [Al/Fe] abundances observed in the majority of the target stars show a distinctively lower level compared to the typical values observed in the MW disc, thereby indicating a consistency with the position occupied by accreted systems. Interestingly, we find a spread of about 0.5 dex in the values of [Na/Fe] and [Al/Fe] for the associated stars, which might hint at a different fraction of massive stars exploding as hypernovae in the progenitors (Smiljanic et al. 2016).
 |
Fig. 12. Behavior of the odd-Z elements [Na/Fe] and [Al/Fe] abundance ratios as a function of [Fe/H] for GES, Sequoia, Antaeus, ED-2, and ED-3 stars (green, brown, blue, magenta, and orange, respectively). Red arrows indicate the upper limits. The errorbars in the lower-left corner indicate the typical uncertainties. The MW literature data for Na abundances are taken from Edvardsson et al. (1993), Fulbright (2000), Stephens & Boesgaard (2002), Gratton et al. (2003), Reddy et al. (2003, 006), Bensby et al. (2005, 2014), Roederer et al. (2014) and Reggiani et al. (2017). The APOGEE control sample, as defined in Sect. 6, is plotted as a 2D histogram, where black and white colors stand for low and high density regions, respectively. |
7.3. α-elements
With the notable exception of oxygen, the α-elements are mainly synthesized in the core of massive stars and diffused into the interstellar medium through CC-SNe, while a small fraction is also produced in SN Ia (Kobayashi et al. 2020). Thus, the chemical patterns of these elements can be used as a proxy of the different timescales of star formation. A typical indicator of the efficiency of a galaxy’s star formation is the metallicity of the knee in the [α/Fe] vs. [Fe/H] plane, which denotes the beginning of a sizable contribution to the chemical enrichment by SNe Ia (Tinsley 1979; Matteucci & Greggio 1986).
Furthermore, Mg is synthesized through the hydrostatic burning of He, C, and Ne in massive stars (30–35 M⊙) with a negligible contribution by SN Ia (Woosley & Weaver 1995; Arnett 1996). The explosive α-elements (Ca and Ti) are mainly produced in less massive stars (15–25 M⊙), with a considerable fraction formed also in SN Ia (Kobayashi et al. 2020).
As shown in Fig. 13, the interpretation of our findings is rather challenging. The spread of the measured [α/Fe] is significantly larger than our uncertainties. The fact that our sample is systematically more metal-poor than typical disc stars makes the comparison with the APOGEE control sample not trivial (see Mg and Ca in Fig. 13). Indeed, the [Mg/Fe] of our sample seems systematically lower at [Fe/H] > −1.5 dex, when the patterns expected for a dwarf galaxy start to part ways from that expected for the MW (Venn et al. 2004; Tolstoy et al. 2009; Nissen & Schuster 2010; Hayes et al. 2018; Horta et al. 2023). In the most metal-poor regime, the two populations mix, but this is not surprising given that SN Ia still have to start exploding. Conversely, for elements like Ti, where the reliability of APOGEE derived abundances is uncertain, we have opted to juxtapose our findings with established high-resolution spectroscopy literature data. As demonstrated in Fig. 13, our results exhibit a strong concordance with those obtained MW halo. With a knowledge of this general behavior, we can now focus in detail on the α-elements trends of the six substructures and discuss the possible origin of the distinct chemical patterns, described below.
 |
Fig. 13. Same illustration as Fig. 12 for the α-elements [Mg/Fe], [Ca/Fe], [TiI/Fe], and [TiII/Fe] abundance ratios. The MW literature data for TiI and TiII abundances are taken from Edvardsson et al. (1993), Fulbright (2000), Stephens & Boesgaard (2002), Gratton et al. (2003), Reddy et al. (2003, 2006), Barklem et al. (2005), Bensby et al. (2005, 2014), Roederer et al. (2014) and Reggiani et al. (2017). |
Gaia-Enceladus. The Mg abundance ratios of the GES stars overlap the metal-poor tail of the distribution of the low-α MW population, as already observed in previous works (Helmi et al. 2018; Mackereth et al. 2019). The reason for the difference in abundance between GES and high-α stars is commonly believed to be the result of chemical enrichment by SN Ia. In fact, in situ stars have not undergone significant enrichment by SN Ia at [Fe/H] ≃ −1.0 dex, whereas a dwarf galaxy like GES has already experienced such enrichment due to a less efficient star formation history.
Sequoia. The stars associated to Sequoia exhibit flat [α/Fe] patterns across the entire metallicity range. In particular, Sequoia occupies the same region of GES at [Fe/H] > −1.5 dex, especially in the chemical planes of TiI. At lower metallicity, however, the behavior exhibited by the Sequoia substructure more closely resembles that of the smaller retrograde substructures. At the same time, Sequoia seems to display [Mg/Fe] and [Ca/Fe] ratios that are 0.1–0.2 dex lower than GES, in agreement with the results by Matsuno et al. (2022). Based on these findings, we favor the interpretation of Sequoia as an independent merger event with respect to GES. Lower [α/Fe] values cannot be explained by the scenario that considers Sequoia as the outskirt of GES that were first lost during the tidal disruption of the galaxy, as this would mean that the outer regions were polluted by SN Ia ejecta before the inner ones, which is a feature yet not observed in existing dwarf MW satellites.
Antaeus. The abundances of the α-elements suggest that Antaeus follows a distinctive chemical sequence in the all the [α/Fe] planes at lower values at fixed metallicity with respect to the dominant components in the RH (GES and Sequoia). At [Fe/H] ≃ −1.5 dex, the [α/Fe] of Antaeus is consistently 0.1–0.2 dex lower than those observed in GES. We interpret this feature as evidence for the existence of Antaeus as an independent merging event, characterized by a progenitor with lower SFR compared to GES and Sequoia.
ED-3. This substructure is located in a region of the [α/Fe] chemical plane that is consistent with that of Antaeus. Constituted of only five stars, ED-3 overlaps with the Antaeus clump across its entire metallicity range. The two systems display a high degree of proximity in terms of their E and Lz, resulting in significant overlap within this parameter space. Based on this new chemo-dynamical evidence, we conclude that Antaeus/L-RL64 and ED-3 are actually part of the same relic. This evidence is confirmed in all of the chemical planes, as we will show in the next paragraphs.
ED-2. The four stars associated with ED-2 occupy the very metal-poor end of the chemical planes, being all located at −2.6 < [Fe/H] < −2.4 dex. This system exhibits a markedly narrow metallicity distribution and its chemical composition is generally consistent with that of the other RH substructures, with the exception of Ti, where it seems to be enhanced. Its position in the [α/Fe] plane seems to recall the one of I’itoi (Naidu et al. 2022). Given the small sample, any conclusions inferred about the chemical pattern of this system would be premature and require further investigation on a much extended sample of stars.
7.4. Iron-peak elements
The production of iron-peak elements is sourced from a variety of nucleosynthesis formation pathways, with SN Ia, CC-SNe, and hypernovae all making a sizeable contribution to the overall production of these chemical elements (Romano et al. 2010; Leung & Nomoto 2018; Kobayashi et al. 2020; Lach et al. 2020).
Sc is mainly produced in CC-SNe in the burning of C and Ne (Woosley et al. 2002), with a negligible contribution by SN Ia (Kobayashi et al. 2020), while Mn is almost entirely produced by SN Ia, with a relative contribution by CC-SNe and hypernovae even lower than Fe (Kobayashi & Nomoto 2009; Kobayashi et al. 2020). SN Ia are also the predominant channel of formation of Ni, although it can be produced in CC-SNe, as for Fe. Overall, Zn is synthesized in the highest energy hypernovae.
As shown in Fig. 14, all the RH substructures exhibit abundances that are remarkably similar to those observed in accreted populations and low-mass satellite galaxies of the MW (Venn et al. 2004; Nissen & Schuster 1997; Tolstoy et al. 2009). The interpretation of these results is complex, as the small differences between the various substructures can be explained by both the diverse production sites of these elements and the metallicity dependencies of their yields at low metallicities (Weinberg et al. 2022). The chemical patterns of the iron-peak elements for the different substructures seem to reveal that GES and Sequoia display a similar distribution. Moreover, Antaeus and ED-3 exhibit, once again, an overlap in their respective loci within these chemical plane, providing additional support for the hypothesis that they are associated with the same accretion event.
 |
Fig. 14. Same illustration as Fig. 12 for the iron-peak elements [ScII/Fe], [Mn/Fe], [Ni/Fe] and [Zn/Fe] abundance ratios. The MW literature data for Sc and Zn abundances are taken from Stephens & Boesgaard (2002), Gratton et al. (2003), Reddy et al. (2003, 2006), Bensby et al. (2005, 2014), Roederer et al. (2014) and Reggiani et al. (2017). |
7.5. Neutron-capture elements
Of all neutron-capture elements, we focus only on yttrium (Y) in this work. This element is predominantly formed by the slow neutron capture process (s-process, i.e., neutron capture that is slower than the β-decay).
Y is predominantly formed by s-processes in the envelope of low-mass (1–4 M⊙) AGB stars and, to a lesser extent, in massive stars (Busso et al. 1999; Pignatari et al. 2010; Cristallo et al. 2015). At low metallicities, magneto-rotational SNe and mergers of neutron stars contribute significantly to the production of these neutron-capture elements via r-processes, thus explaining the observed scatter (Kasen et al. 2017; Molero et al. 2023).
Despite the huge scatter between abundances of stars born in the same progenitor, the results in Fig. 15 show that the average abundances for the Sequoia substructure is comparable to the one of GES, as previously hinted also by Aguado et al. (2021). Within the common metallicity range, Antaeus and ED-3 exhibit a pronounced degree of overlapping, consistently displaying average abundances that are lower (∼0.1–0.2 dex) than those observed in GES.
 |
Fig. 15. Same illustration as Fig. 12 for the neutron capture element [YII/Fe] abundance ratios. The MW literature data for Y abundances are taken from Edvardsson et al. (1993), Fulbright (2000), Stephens & Boesgaard (2002), Reddy et al. (2003, 2006), Bensby et al. (2005) and Reggiani et al. (2017). |
8. Discussion and conclusions
In this first paper of a series, we introduce the WRS project, describing the methodology employed and highlighting the scientific goals it aims to pursue. To demonstrate the potential of this project, we have narrowed our focus to the subset composed of 90 stars associated by the DBSCAN clustering algorithm with various RH substructures within the IoM space (see Dodd et al. 2023) and we have analyzed their chemical properties. The interpretation of the chemical patterns of unassociated stars will be left to future contributions to the series. We present a concise summary of the principal findings of this paper below.
-
A selection criterion based on tangential velocity only (thus not requiring the Vlos information) is able to select stars that move on retrograde motions with a 91.4% efficiency (by requiring VT > 400 km s−1). All of the stars included in our sample consistently exhibit chemical pattern across all chemical element planes that aligns with the characteristic abundance patterns displayed by accreted systems and dwarf galaxies.
-
In spite of the selection criteria leaving out the bulk of GES stars at higher Lz and lower energy from our sample, GES stands out as the largest and most metal-rich component within the RH. This supports the hypothesis that it represents the remnant of the most massive galaxy that was accreted by the MW.
-
The chemical patterns of GES and Sequoia display similar trends at [Fe/H] > −1.5 dex. However, significant distinctions become evident at lower metallicity, specifically characterized by a discernible difference in the α-elements. In particular (as shown in the top panel of Fig. 16), Sequoia exhibit a pronounced excess of stars with lower [Mg/Fe] and [Ca/Fe] ratios with respect to GES. Consequently, this discrepancy leads us to interpret Sequoia as an independent accretion event distinct from GES.
-
For the first time, we have achieved a comprehensive chemical characterization of Antaeus, encompassing detailed chemical abundances for numerous elements. Our analysis reveals distinct behavior in the chemical space compared to GES within the same metallicity range (see bottom panel of Fig. 16), reinforcing the assertion that it constitutes the remnant of an accretion event independent of GES.
-
Antaeus and ED-3 exhibit analogous positions in the IoM spaces, albeit with some distinctions in L⊥. Additionally, they share similarities in terms of their metallicity distribution function and orbital eccentricity. Furthermore, the chemical patterns observed in Antaeus and ED-3 are consistent across all chemical elements. In the end, we integrated backwards in time (for 2.5 Gyr) the orbits of the stars associated to these two substructures in a McMillan (2017) potential for the MW. As depicted in Fig. 17, stars from the two substructures appear to move on very similar orbits. Collectively, these lines of evidence compel us to interpret them as components of the same merging event. Henceforth, we refer to this merging event as Antaeus.
-
ED-2 is the most metal-poor component, with a remarkably narrow MDF peaked at [Fe/H] = −2.43 dex, in agreement with the findings of Balbinot et al. (2023). The limited number of stars within the ED-2 substructure, coupled with the specific combination of their stellar parameters (Teff > 6000 K and [Fe/H] < −2.4 dex) leading to the manifestation of weak spectral lines, restricts our capacity to attain detailed chemical abundances across all elements. As a consequence, we are unable to definitively assert whether ED-2 constitutes the remnant of a globular cluster or a dwarf galaxy. In this regard, a search for the characteristic anti-correlations commonly associated with globular clusters will serve to dispel this doubt.
 |
Fig. 16. Comparison of the cumulative distribution functions of [Mg/Fe], [Ca/Fe] and [Y/Fe] for Sequoia and GES stars (brown and green lines, respectively) in the common metallicity range (−2.60 < [Fe/H] < −1.20 dex) shown at the top. We report the probability that the two distributions are drawn from the same parent sample according to a Kolmogorov-Smirnov test. Bottom panel is the same as the top, but for Antaeus and GES stars (blue and green lines, respectively) in the common metallicity range (−2.60 < [Fe/H] < −1.45 dex). |
 |
Fig. 17. Orbits of Antaeus (blue lines) and ED-3 (orange lines) stars in the Galactocentric reference frame integrated backwards in time for 2.5 Gyr in a McMillan (2017) potential for the MW. |
In light of the aforementioned complexities in identifying and interpreting MW halo substructures based on orbital information alone, the significance of our results lies in the fact that they are based on a pre-established classification, adding clarity amidst the ongoing confusion surrounding the newly identified substructures. While our study represents a crucial first step towards unraveling their true nature, it is crucial to acknowledge the need for more extensive investigations. Indeed, detailed chemical abundance measurements for a broader range of stars in the Galactic halo remain lacking. Future investigations by WRS will target RH stars that have already been associated to different disrupted progenitors, in order to disentangle ambiguous associations and shed lights on the chemical features of the retrograde substructures. As we continue to expand our knowledge, the pursuit of larger datasets of high-resolution spectroscopy, alongside future large spectroscopic surveys of MW halo stars and dwarf galaxies, such as WEAVE (Dalton et al. 2020) and 4MOST (de Jong et al. 2019), will undoubtedly propel us towards a more comprehensive understanding of the Galactic halo’s diverse substructures. Thus, we will be able to better constrain the evolutionary history of the Milky Way.
That have the information on the Vlos for ≃7.2 × 106 stars with G ≲ 13.0, while the most recent release, DR3 (Gaia Collaboration 2023), includes Vlos for ≃33.8 × 106 stars down to G ≲ 14.0.
The adopted solar motion is from Schönrich et al. (2010), while the distance between the Sun and the Galactic Center and the rotational velocity of the Sun are the same used in McMillan (2017).
See https://data.sdss.org/datamodel/files/APOGEE_ASPCAP/APRED_VERS/ASPCAP_VERS/allStarLite.html for definitions.
Acknowledgments
Based on data acquired using the Large Binocular Telescope (LBT) through the program IT-2021B-006 (P.I. M. Bellazzini) and the strategic program IT-2022B-004 (P.I. M. Bellazzini). The LBT is an international collaboration among institutions in the United States, Italy, and Germany. LBT Corporation partners are The University of Arizona on behalf of the Arizona university system; Istituto Nazionale di Astrofisica, Italy; LBT Beteiligungsgesellschaft, Germany, representing the Max-Planck Society, the Astrophysical Institute Potsdam, and Heidelberg University; The Ohio State University; and The Research Corporation, on behalf of The University of Notre Dame, University of Minnesota, and University of Virginia. Based on observations collected at the ESO-VLT under the program 0109.B-0522 (P.I.A. Mucciarelli). MB, EC, DM and AM acknowledge the support to this study by the PRIN INAF 2023 grant ObFu CHAM – Chemodynamics of the Accreted Halo of the Milky Way (P.I. M. Bellazzini). This research is funded by the project LEGO – Reconstructing the building blocks of the Galaxy by chemical tagging (P.I. A. Mucciarelli), granted by the Italian MUR through contract PRIN 2022LLP8TK_001. DM acknowledges financial support from PRIN-MIUR-22: CHRONOS: adjusting the clock(s) to unveil the CHRONO-chemo-dynamical Structure of the Galaxy” (PI: S. Cassisi) granted by the European Union - Next Generation EU. MB and DM acknowledge the support to activities related to the ESA/Gaia mission by the Italian Space Agency (ASI) through contract 2018-24-HH.0 and its addendum 2018-24-HH.1-2022 to the National Institute for Astrophysics (INAF). This work is a part of a project that has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (CartographY; grant agreement ID 804752). AS acknowledges the support of the Science and Technology Facilities Council. AS acknowledges support from the European Research Council Consolidator Grant funding scheme (project ASTEROCHRONOMETRY, G.A. n. 772293, http://www.asterochronometry.eu). Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation (Grant agreement No. DNRF106). EC and AM are grateful to R. Lallement for her help in deriving the color excess for the target stars. We thank the anonymous referee for constructive comments that helped us to improve the quality of the manuscript. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This work made use of SDSS-IV data. Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the U.S. Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High Performance Computing at the University of Utah. The SDSS website is http://www.sdss4.org. SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, Center for Astrophysics | Harvard & Smithsonian, the Chilean Participation Group, the French Participation Group, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, the Korean Participation Group, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatório Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University.
References
- Abdurro’uf, Accetta, K., Aerts, C., et al. 2022, ApJS, 259, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Aguado, D. S., Belokurov, V., Myeong, G. C., et al. 2021, ApJ, 908, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Amarante, J. A. S., Debattista, V. P., Beraldo e Silva, L., Laporte, C. F. P., & Deg, N. 2022, ApJ, 937, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Andrae, R., Fouesneau, M., Creevey, O., et al. 2018, A&A, 616, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrew, S., Penoyre, Z., Belokurov, V., Evans, N. W., & Oh, S. 2022, MNRAS, 516, 3661 [NASA ADS] [CrossRef] [Google Scholar]
- Arnett, D. 1996, Supernovae and Nucleosynthesis: An Investigation of the History of Matter from the Big Bang to the Present (Princeton: Princeton University Press) [Google Scholar]
- Balbinot, E., Helmi, A., Callingham, T., et al. 2023, A&A, 678, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barklem, P. S., Christlieb, N., Beers, T. C., et al. 2005, A&A, 439, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellazzini, M., Massari, D., De Angeli, F., et al. 2023, A&A, 674, A194 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belokurov, V., & Kravtsov, A. 2022, MNRAS, 514, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., Erkal, D., Evans, N. W., Koposov, S. E., & Deason, A. J. 2018, MNRAS, 478, 611 [Google Scholar]
- Belokurov, V., Sanders, J. L., Fattahi, A., et al. 2020, MNRAS, 494, 3880 [Google Scholar]
- Belokurov, V., Vasiliev, E., Deason, A. J., et al. 2023, MNRAS, 518, 6200 [Google Scholar]
- Bennett, M., & Bovy, J. 2019, MNRAS, 482, 1417 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., Lundström, I., & Ilyin, I. 2005, A&A, 433, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., & Oey, M. S. 2014, A&A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertaux, J. L., Lallement, R., Ferron, S., Boonne, C., & Bodichon, R. 2014, A&A, 564, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonaca, A., Geha, M., & Kallivayalil, N. 2012, ApJ, 760, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Bonaca, A., Conroy, C., Wetzel, A., Hopkins, P. F., & Kereš, D. 2017, ApJ, 845, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Bonaca, A., Naidu, R. P., Conroy, C., et al. 2021, ApJ, 909, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Bonifacio, P., Monaco, L., Salvadori, S., et al. 2021, A&A, 651, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buder, S., Sharma, S., Kos, J., et al. 2021, MNRAS, 506, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Buder, S., Lind, K., Ness, M. K., et al. 2022, MNRAS, 510, 2407 [NASA ADS] [CrossRef] [Google Scholar]
- Busso, M., Gallino, R., & Wasserburg, G. J. 1999, ARA&A, 37, 239 [Google Scholar]
- Cabrera Garcia, J., Beers, T. C., Huang, Y., et al. 2024, MNRAS, 527, 8973 [Google Scholar]
- Carollo, D., Beers, T. C., Lee, Y. S., et al. 2007, Nature, 450, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, eds. N. Piskunov, W. W. Weiss, & D. F. Gray, 210, A20 [Google Scholar]
- Conroy, C., Bonaca, A., Cargile, P., et al. 2019, ApJ, 883, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Straniero, O., Piersanti, L., & Gobrecht, D. 2015, ApJS, 219, 40 [Google Scholar]
- Dalton, G., Trager, S., Abrams, D. C., et al. 2020, SPIE Conf. Ser., 11447, 1144714 [NASA ADS] [Google Scholar]
- Das, P., Hawkins, K., & Jofré, P. 2020, MNRAS, 493, 5195 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, E. Y., Vasiliev, E., Belokurov, V., Evans, N. W., & Dillamore, A. M. 2023, MNRAS, 519, 530 [Google Scholar]
- de Jong, R. S., Agertz, O., Berbel, A. A., et al. 2019, The Messenger, 175, 3 [NASA ADS] [Google Scholar]
- Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, SPIE Conf. Ser., 4008, 534 [Google Scholar]
- Dodd, E., Callingham, T. M., Helmi, A., et al. 2023, A&A, 670, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drimmel, R., & Poggio, E. 2018, Res. Notes Am. Astron. Soc., 2, 210 [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&AS, 102, 603 [NASA ADS] [Google Scholar]
- Ester, M., Kriegel, H. P., Sander, J., & Xu, X. 1996, in Second International Conference on Knowledge Discovery and Data Mining (KDD’96). Proceedings of a conference held August 2-4, 226 [Google Scholar]
- Fernández-Alvar, E., Carigi, L., Schuster, W. J., et al. 2018, ApJ, 852, 50 [CrossRef] [Google Scholar]
- Feuillet, D. K., Feltzing, S., Sahlholdt, C. L., & Casagrande, L. 2020, MNRAS, 497, 109 [Google Scholar]
- Feuillet, D. K., Sahlholdt, C. L., Feltzing, S., & Casagrande, L. 2021, MNRAS, 508, 1489 [NASA ADS] [CrossRef] [Google Scholar]
- Font, A. S., McCarthy, I. G., Poole-Mckenzie, R., et al. 2020, MNRAS, 498, 1765 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K., & Bland-Hawthorn, J. 2002, ARA&A, 40, 487 [Google Scholar]
- Fulbright, J. P. 2000, AJ, 120, 1841 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Babusiaux, C., et al.) 2018a, A&A, 616, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018b, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallart, C., Zoccali, M., & Aparicio, A. 2005, ARA&A, 43, 387 [Google Scholar]
- Gallart, C., Bernard, E. J., Brook, C. B., et al. 2019, Nat. Astron., 3, 932 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, F. A., Helmi, A., Cooper, A. P., et al. 2013, MNRAS, 436, 3602 [CrossRef] [Google Scholar]
- Gratton, R. G., Carretta, E., Desidera, S., et al. 2003, A&A, 406, 131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2018, A&A, 615, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [Google Scholar]
- Hasselquist, S., Hayes, C. R., Lian, J., et al. 2021, ApJ, 923, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, C. R., Majewski, S. R., Shetrone, M., et al. 2018, ApJ, 852, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., et al. 2018, ApJ, 863, 113 [Google Scholar]
- Helmi, A. 2020, ARA&A, 58, 205 [Google Scholar]
- Helmi, A., & de Zeeuw, P. T. 2000, MNRAS, 319, 657 [Google Scholar]
- Helmi, A., White, S. D. M., de Zeeuw, P. T., & Zhao, H. 1999, Nature, 402, 53 [Google Scholar]
- Helmi, A., Babusiaux, C., Koppelman, H. H., et al. 2018, Nature, 563, 85 [Google Scholar]
- Horta, D., Schiavon, R. P., Mackereth, J. T., et al. 2021, MNRAS, 500, 1385 [Google Scholar]
- Horta, D., Schiavon, R. P., Mackereth, J. T., et al. 2023, MNRAS, 520, 5671 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Gilmore, G., & Irwin, M. J. 1994, Nature, 370, 194 [Google Scholar]
- Ibata, R., Malhan, K., Martin, N., et al. 2021, ApJ, 914, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, K. V., Hernquist, L., & Bolte, M. 1996, ApJ, 465, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Kasen, D., Metzger, B., Barnes, J., Quataert, E., & Ramirez-Ruiz, E. 2017, Nature, 551, 80 [Google Scholar]
- Katz, D., Sartoretti, P., Guerrier, A., et al. 2023, A&A, 674, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khoperskov, S., Minchev, I., Libeskind, N., et al. 2023, A&A, 677, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kobayashi, C., & Nomoto, K. 2009, ApJ, 707, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, C., Karakas, A. I., & Lugaro, M. 2020, ApJ, 900, 179 [Google Scholar]
- Koppelman, H., Helmi, A., & Veljanoski, J. 2018, ApJ, 860, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Koppelman, H. H., Helmi, A., Massari, D., Price-Whelan, A. M., & Starkenburg, T. K. 2019, A&A, 631, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koppelman, H. H., Bos, R. O. Y., & Helmi, A. 2020, A&A, 642, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kruijssen, J. M. D., Pfeffer, J. L., Chevance, M., et al. 2020, MNRAS, 498, 2472 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 2005, Mem. Soc. Astron. Ital. Suppl., 8, 14 [Google Scholar]
- Lach, F., Röpke, F. K., Seitenzahl, I. R., et al. 2020, A&A, 644, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leung, S.-C., & Nomoto, K. 2018, ApJ, 861, 143 [Google Scholar]
- Limberg, G., Souza, S. O., Pérez-Villegas, A., et al. 2022, ApJ, 935, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Lind, K., Asplund, M., Barklem, P. S., & Belyaev, A. K. 2011, A&A, 528, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lind, K., Nordlander, T., Wehrhahn, A., et al. 2022, A&A, 665, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Lövdal, S. S., Ruiz-Lara, T., Koppelman, H. H., et al. 2022, A&A, 665, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mackereth, J. T., Schiavon, R. P., Pfeffer, J., et al. 2019, MNRAS, 482, 3426 [Google Scholar]
- Malhan, K., Ibata, R. A., Sharma, S., et al. 2022, ApJ, 926, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Massari, D., Koppelman, H. H., & Helmi, A. 2019, A&A, 630, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsuno, T., Aoki, W., & Suda, T. 2019, ApJ, 874, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuno, T., Koppelman, H. H., Helmi, A., et al. 2022, A&A, 661, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matteucci, F., & Greggio, L. 1986, A&A, 154, 279 [NASA ADS] [Google Scholar]
- McMillan, P. J. 2017, MNRAS, 465, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Mikkola, D., McMillan, P. J., & Hobbs, D. 2023, MNRAS, 519, 1989 [Google Scholar]
- Minelli, A., Mucciarelli, A., Massari, D., et al. 2021, ApJ, 918, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Molero, M., Magrini, L., Matteucci, F., et al. 2023, MNRAS, 523, 2974 [NASA ADS] [CrossRef] [Google Scholar]
- Monachesi, A., Gómez, F. A., Grand, R. J. J., et al. 2019, MNRAS, 485, 2589 [NASA ADS] [CrossRef] [Google Scholar]
- Montalbán, J., Mackereth, J. T., Miglio, A., et al. 2021, Nat. Astron., 5, 640 [Google Scholar]
- Monty, S., Venn, K. A., Lane, J. M. M., Lokhorst, D., & Yong, D. 2020, MNRAS, 497, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Mucciarelli, A. 2013, arXiv e-prints [arXiv:1311.1403] [Google Scholar]
- Mucciarelli, A., Pancino, E., Lovisi, L., Ferraro, F. R., & Lapenna, E. 2013, ApJ, 766, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Mucciarelli, A., Bellazzini, M., & Massari, D. 2021a, A&A, 653, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mucciarelli, A., Massari, D., Minelli, A., et al. 2021b, Nat. Astron., 5, 1247 [NASA ADS] [CrossRef] [Google Scholar]
- Myeong, G. C., Evans, N. W., Belokurov, V., Sanders, J. L., & Koposov, S. E. 2018, ApJ, 856, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Myeong, G. C., Vasiliev, E., Iorio, G., Evans, N. W., & Belokurov, V. 2019, MNRAS, 488, 1235 [Google Scholar]
- Myeong, G. C., Belokurov, V., Aguado, D. S., et al. 2022, ApJ, 938, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Naidu, R. P., Conroy, C., Bonaca, A., et al. 2020, ApJ, 901, 48 [Google Scholar]
- Naidu, R. P., Conroy, C., Bonaca, A., et al. 2022, ApJ, submitted, [arXiv:2204.09057] [Google Scholar]
- Newton, O., Cautun, M., Jenkins, A., Frenk, C. S., & Helly, J. C. 2018, MNRAS, 479, 2853 [CrossRef] [Google Scholar]
- Nissen, P. E., & Schuster, W. J. 1997, A&A, 326, 751 [NASA ADS] [Google Scholar]
- Nissen, P. E., & Schuster, W. J. 2010, A&A, 511, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nomoto, K., Kobayashi, C., & Tominaga, N. 2013, ARA&A, 51, 457 [CrossRef] [Google Scholar]
- Oria, P.-A., Tenachi, W., Ibata, R., et al. 2022, ApJ, 936, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Pietrinferni, A., Hidalgo, S., Cassisi, S., et al. 2021, ApJ, 908, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Pignatari, M., Gallino, R., Heil, M., et al. 2010, ApJ, 710, 1557 [Google Scholar]
- Pillepich, A., Madau, P., & Mayer, L. 2015, ApJ, 799, 184 [Google Scholar]
- Reddy, B. E., Tomkin, J., Lambert, D. L., & Allende Prieto, C. 2003, MNRAS, 340, 304 [Google Scholar]
- Reddy, B. E., Lambert, D. L., & Allende Prieto, C. 2006, MNRAS, 367, 1329 [Google Scholar]
- Reggiani, H., Meléndez, J., Kobayashi, C., Karakas, A., & Placco, V. 2017, A&A, 608, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, M. J., & Brunthaler, A. 2004, ApJ, 616, 872 [Google Scholar]
- Rey, M. P., Agertz, O., Starkenburg, T. K., et al. 2023, MNRAS, 521, 995 [NASA ADS] [CrossRef] [Google Scholar]
- Riello, M., De Angeli, F., Evans, D. W., et al. 2021, A&A, 649, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roederer, I. U., Preston, G. W., Thompson, I. B., et al. 2014, AJ, 147, 136 [Google Scholar]
- Romano, D., Karakas, A. I., Tosi, M., & Matteucci, F. 2010, A&A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruiz-Lara, T., Matsuno, T., Lövdal, S. S., et al. 2022, A&A, 665, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schönrich, R., Binney, J., & Dehnen, W. 2010, MNRAS, 403, 1829 [CrossRef] [Google Scholar]
- Shank, D., Beers, T. C., Placco, V. M., et al. 2022, ApJ, 926, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Smiljanic, R., Romano, D., Bragaglia, A., et al. 2016, A&A, 589, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stephens, A., & Boesgaard, A. M. 2002, AJ, 123, 1647 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B., & Pancino, E. 2008, PASP, 120, 1332 [Google Scholar]
- Strassmeier, K. G., Ilyin, I., Järvinen, A., et al. 2015, Astron. Nachr., 336, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Tenachi, W., Oria, P.-A., Ibata, R., et al. 2022, ApJ, 935, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Tinsley, B. M. 1979, ApJ, 229, 1046 [Google Scholar]
- Tolstoy, E., Hill, V., & Tosi, M. 2009, ARA&A, 47, 371 [Google Scholar]
- Tolstoy, E., Skúladóttir, Á., Battaglia, G., et al. 2023, A&A, 675, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tonry, J., & Davis, M. 1979, AJ, 84, 1511 [Google Scholar]
- Vasiliev, E. 2019, MNRAS, 482, 1525 [Google Scholar]
- Venn, K. A., Irwin, M., Shetrone, M. D., et al. 2004, AJ, 128, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Vincenzo, F., Spitoni, E., Calura, F., et al. 2019, MNRAS, 487, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, D. H., Holtzman, J. A., Johnson, J. A., et al. 2022, ApJS, 260, 32 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., & Frenk, C. S. 1991, ApJ, 379, 52 [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [Google Scholar]
- Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, Z., Myeong, G. C., Beers, T. C., et al. 2020, ApJ, 891, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Zwitter, T., Kos, J., Chiavassa, A., et al. 2018, MNRAS, 481, 645 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Main target information: ID, coordinates, apparent magnitudes and parallax from Gaia EDR3, color excess from the EXPLORE tool, and the instrument used to collect the spectrum.
Magnitude, exposure times, airmass, and S/Ns for some of the observed target spectra with the spectrographs UVES and PEPSI.
Kinematic information for the stars: ID from Gaia EDR3, orbital energy, angular momentum along the z-axis, perpendicular angular momentum, and line-of-sight velocity with uncertainties.
Stellar parameters for the selected targets: ID from Gaia EDR3, derived effective temperature, surface gravity, microturbulent velocity, and iron abundance ratio.
Differences in chemical abundances obtained from the UVES and PEPSI samples, including the calculated offsets, corresponding standard deviations, and the number of stars used for each element.
Chemical abundances for the odd-Z, iron-peak and neutron capture elements for the stars associated to known substructures.
Chemical abundances for the α-elements for the stars associated to known substructures.
All Figures
 |
Fig. 1. Toomre diagram of the ≃2.4 million stars within 1.0 kpc from the Sun, having Vlos values measured in Gaia EDR3 and passing all the quality criteria we adopted for the WRS sample. Stars are color-coded according to their tangential velocity and stars with VT400 km s−1 are highlighted with a black empty square. |
| In the text | |
 |
Fig. 2. Comparison between the spectra of two stars observed with PEPSI at LBT, shown on the left. Right column shows the same comparison, but for two stars observed with UVES at VLT. These stars have very similar Teff and log g but they differ in the iron content. Black arrows indicate the position of some atomic lines of interest. |
| In the text | |
 |
Fig. 3. Line-of-sight velocity distribution for the entire stellar sample, shown on the left. Central panel shows comparison between the uncertainty on the line-of-sight velocity provided by Gaia (blue filled circles) and the one measured with high-resolution spectroscopy (red filled circles) as a function of observed G magnitude. The blue arrows point out the outliers in the distribution, specifically representing target stars with errors in the Gaia velocity measurement larger than 10 km s−1. Right panel shows the difference between the two measurements of the line-of-sight velocity. The red dashed lines mark the ±3σ threshold. |
| In the text | |
 |
Fig. 4. Distribution of the observed stars in IoM and velocity space (top and bottom panels, respectively). We highlight stars associated with various substructures with different colors (green for GES, brown for Sequoia, blue for Antaeus, magenta for ED-2, orange for ED-3, cyan for Clump-6 and red for Clump-7). |
| In the text | |
 |
Fig. 5. Gaia EDR3 distance-corrected color-magnitude diagram of the 175 analyzed stars. Targets are color-coded based on the metallicity. |
| In the text | |
 |
Fig. 6. Comparison of Mg abundance ratios of the stars from our selection observed with UVES (blue filled circles) and the NS10 reference sub-sample (red filled squares and green filled triangles for low-α and high-α sequences, respectively). The errorbar in the top-right corner indicates the typical uncertainties. |
| In the text | |
 |
Fig. 7. [Mg/Fe] abundance ratios as a function of [Fe/H] for our sample (color-coded by the angular momentum along the z-direction, Lz) and for the APOGEE control sample (greyscale 2D histogram) shown on the left. The errorbar in the top-right corner displays the typical uncertainties. [Mg/Mn] abundance ratios as a function of [Al/Fe] for the same samples, with the same arrangement shown on the right. Red arrows indicate upper limits. |
| In the text | |
 |
Fig. 8. Distribution of the targets stars in the IoM space compared with the NS10 stars and the APOGEE sample. The color coding is the same as in Fig. 6. |
| In the text | |
 |
Fig. 9. Metallicity distribution functions for the RH substructures labeled at the top of each panel compared to the MDF of the entire sample of stars. The median metallicity value and the standard deviation of the distribution are also reported. The color coding is the same as in Fig. 4. |
| In the text | |
 |
Fig. 10. Eccentricity distribution functions for the RH substructures labeled at the top of each panel compared to the distribution of the entire sample of stars. The median eccentricity value and the standard deviation of the distribution are also reported. The color coding is the same as in Fig. 4. |
| In the text | |
 |
Fig. 11. Distribution of the RH substructures in the eccentricity vs. [Fe/H] space (left panel) and in the eccentricity vs. Zmax (right panel). The color coding is the same as in Fig. 4. |
| In the text | |
 |
Fig. 12. Behavior of the odd-Z elements [Na/Fe] and [Al/Fe] abundance ratios as a function of [Fe/H] for GES, Sequoia, Antaeus, ED-2, and ED-3 stars (green, brown, blue, magenta, and orange, respectively). Red arrows indicate the upper limits. The errorbars in the lower-left corner indicate the typical uncertainties. The MW literature data for Na abundances are taken from Edvardsson et al. (1993), Fulbright (2000), Stephens & Boesgaard (2002), Gratton et al. (2003), Reddy et al. (2003, 006), Bensby et al. (2005, 2014), Roederer et al. (2014) and Reggiani et al. (2017). The APOGEE control sample, as defined in Sect. 6, is plotted as a 2D histogram, where black and white colors stand for low and high density regions, respectively. |
| In the text | |
 |
Fig. 13. Same illustration as Fig. 12 for the α-elements [Mg/Fe], [Ca/Fe], [TiI/Fe], and [TiII/Fe] abundance ratios. The MW literature data for TiI and TiII abundances are taken from Edvardsson et al. (1993), Fulbright (2000), Stephens & Boesgaard (2002), Gratton et al. (2003), Reddy et al. (2003, 2006), Barklem et al. (2005), Bensby et al. (2005, 2014), Roederer et al. (2014) and Reggiani et al. (2017). |
| In the text | |
 |
Fig. 14. Same illustration as Fig. 12 for the iron-peak elements [ScII/Fe], [Mn/Fe], [Ni/Fe] and [Zn/Fe] abundance ratios. The MW literature data for Sc and Zn abundances are taken from Stephens & Boesgaard (2002), Gratton et al. (2003), Reddy et al. (2003, 2006), Bensby et al. (2005, 2014), Roederer et al. (2014) and Reggiani et al. (2017). |
| In the text | |
 |
Fig. 15. Same illustration as Fig. 12 for the neutron capture element [YII/Fe] abundance ratios. The MW literature data for Y abundances are taken from Edvardsson et al. (1993), Fulbright (2000), Stephens & Boesgaard (2002), Reddy et al. (2003, 2006), Bensby et al. (2005) and Reggiani et al. (2017). |
| In the text | |
 |
Fig. 16. Comparison of the cumulative distribution functions of [Mg/Fe], [Ca/Fe] and [Y/Fe] for Sequoia and GES stars (brown and green lines, respectively) in the common metallicity range (−2.60 < [Fe/H] < −1.20 dex) shown at the top. We report the probability that the two distributions are drawn from the same parent sample according to a Kolmogorov-Smirnov test. Bottom panel is the same as the top, but for Antaeus and GES stars (blue and green lines, respectively) in the common metallicity range (−2.60 < [Fe/H] < −1.45 dex). |
| In the text | |
 |
Fig. 17. Orbits of Antaeus (blue lines) and ED-3 (orange lines) stars in the Galactocentric reference frame integrated backwards in time for 2.5 Gyr in a McMillan (2017) potential for the MW. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



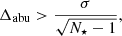
![$$ \begin{aligned}&\sigma _{\rm [Fe/H]} = \sqrt{\frac{\sigma _{Fe}^{2}}{N_{\rm Fe}} + (\delta _{\rm Fe}^{T_{\mathrm{eff} }})^{2} + (\delta _{\rm Fe}^{\mathrm{log} \; g})^{2} + (\delta _{\rm Fe}^{v_{\mathrm{t} }})^{2}} ,\end{aligned} $$](/articles/aa/full_html/2024/04/aa48332-23/aa48332-23-eq5.gif)
![$$ \begin{aligned}&\sigma _{\rm [X/Fe]} = \nonumber \\&\sqrt{\frac{\sigma _{\rm X}^{2}}{N_{\rm X}} + \frac{\sigma _{\rm Fe}^{2}}{N_{\rm Fe}} + (\delta _{\rm X}^{T_{\mathrm{eff} }} - \delta _{\rm Fe}^{T_{\mathrm{eff} }})^{2} + (\delta _{\rm X}^{\mathrm{log} \; g} - \delta _{\rm Fe}^{\mathrm{log} \; g})^{2} +(\delta _{\rm X}^{v_{\mathrm{t} }} - \delta _{\rm Fe}^{v_{\mathrm{t} }})^{2}}, \end{aligned} $$](/articles/aa/full_html/2024/04/aa48332-23/aa48332-23-eq6.gif)