EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 683 (March 2024) A&A, 683 (2024) A73 Full HTML
Open Access
Issue
A&A
Volume 683, March 2024
Article Number A73
Number of page(s) 7
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/202348522
Published online 08 March 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Neutron-capture elements have been extensively studied in the astronomy community for more than three decades, but the chemical evolution of such type of elements in the Milky Way is still a matter of debate (e.g. Sneden et al. 2008; Cowan et al. 2021). Neutron-capture elements are, for instance, essential for tracing the accretion history of the Milky Way (e.g. Helmi 2020; Matsuno et al. 2021) and its satellite Galaxies (e.g. Venn et al. 2012).

In particular, the slow-neutron capture (s-process) dominated elements are mainly organised into two peaks (Burbidge et al. 1957). The first peak is located around the neutron magic number 50, and is responsible for the synthesis of the light-s elements Sr, Y, and Zr. The second peak produces Ba, La, Ce, Pr, and Nd around the neutron magic number 82. There is a third peak as well, which produces Pb. It is common to divide the s-process into a “main” process, a “weak” process, and a “strong” process. The main s-process occurs in asymptotic giant branch (AGB) stars (Busso et al. 1999; Bisterzo et al. 2011) while the weak s-process is known to occur in massive stars and it produces nuclei with mass number below 88 (Pignatari et al. 2010). Finally, the strong s-process is responsible for about 50% of solar 208Pb production by low-metallicity AGB stars (Kaeppeler et al. 1982).

The chemical evolution of neutron-capture elements has been rather well constrained in the Milky Way disc (e.g. Battistini & Bensby 2016; Mishenina et al. 2019). However, not many studies focused on the halo or halo-disc interface. Even with the advent of large-scale spectroscopic surveys (e.g. GALAH; Buder et al. 2019), neutron-capture abundance measurements are available for only a few tens of very metal-poor stars (e.g. Mashonkina et al. 2007; Matsuno et al. 2021), as it requires high-quality and high signal-to-noise spectra in the metal-poor regime ([Fe/H] < −1). Past GCE works have also relied on compilations of abundances from various studies, but these may suffer from systematic biases, owing to the fundamental assumption of local thermodynamical equilibrium (LTE; e.g. Cescutti & Chiappini 2014). High-resolution spectroscopy is indeed a unique technique for determining precise estimates of neutron-capture elemental abundances (e.g. Delgado Mena et al. 2017; Guiglion et al. 2018; Roederer et al. 2022).

Recently Lian et al. (2023) studied the Galactic chemical evolution of Ba and Y using the data from the Gaia-ESO large spectroscopic survey. Most stars in the sample of Lian et al. (2023) cover the metallicity range −1 < [Fe/H] < 0.5 dex, for which Gaia-ESO measured and released high-quality chemical abundances of neutron-capture elements. In this letter, we aim to constrain the chemical evolution of Ba, Y, and Sr in the metal-poor regime (−3 < [Fe/H] < −0.5 dex) in order to further complement the study of Lian et al. (2023). We have also taken one step towards a higher accuracy by computing our abundances in the framework of non-local thermodynamic equilibrium (NLTE).

In Sect. 2, we present the spectroscopic data and spectral analysis. In Sect. 3, we present LTE and NLTE chemical abundance trends of Sr, Y, and Ba, while we confront Galactic chemical evolution models to our observations in Sect. 4. Finally, we present our conclusions in Sect. 5.

2. Data and methodology

We have taken advantage of the high-resolution spectra of Galactic disc and halo stars from Ruchti et al. (2011). These targets were originally observed at intermediate resolution by the RAVE survey (Steinmetz et al. 2006; Matijevič et al. 2017). The sample consists of 323 metal-poor stars, covering the ranges 4050 < Teff < 6500 K, 0.5 < log(g) < 4.5, and −2.8 < [Fe/H] < −0.4 (in NLTE; see Fig. 1). The data have already been used in our previous studies, for instance, in the analysis of NLTE stellar parameters and metallicities (Ruchti et al. 2013), ages (Serenelli et al. 2013), and NLTE Mg abundances (Bergemann et al. 2017a,b). We adopted the 1D-LTE and 1D-NLTE atmospheric parameters from Ruchti et al. (2013).

thumbnail Fig. 1.

Atmospheric parameters and [Fe/H] coverage of the 323 stars of the sample. Left: Kiel diagram (NLTE Teff vs. log(g)), colour-coded with NLTE [Fe/H]. Middle: NLTE [Fe/H] vs. Teff colour-coded with NLTE log(g). Right: NLTE [Fe/H] vs. log(g) colour-coded with NLTE Teff.

In order to derive chemical abundances of Ba II, Y II, and Sr I, we used the spectral fitting code TSFitPy1, based on the LTE version of TurboSpectrum (Plez 2012) as well as its NLTE extension2 (Gerber et al. 2023). TSFitPy allows for radial velocity corrections to be applied to the data and to simultaneously fit the abundance as well as the micro- and macro-turbulence, which are typically needed owing to the lack or realistic convection and turbulent flows in 1D hydrostatic models (see e.g. Dravins 2008; Nordlund et al. 2009; Meunier et al. 2017).

The model atom of Sr used in this work is based on the model described in Bergemann et al. (2012); however, it has been updated with new quantum-mechanical data for inelastic transitions in Sr+H collisions (Gerber et al. 2023). The Ba model comes from Gallagher et al. (2020) and the Y model from Storm & Bergemann (2023). The atomic transition probabilities come from Davidson et al. (1992) for the Ba II lines, García & Campos (1988) for the Sr I lines, and Biémont et al. (2011) for Y (see Heiter et al. 2021 for more details). Ba II lines suffer significantly from hyperfine splitting (HFS) and isotopic shifts and these effects have been included in the calculations, as described in Gallagher et al. (2020). Overall, HFS is negligible for Y II (< 0.5 mÅ) and is not included in the linelist. For Ba II, we adopted the lines at 5853.67, 6141.71, 6496.90 Å that show rather strong features even down to [Fe/H] = −3. For Sr, we used the strong and unblended spectral line of Sr I at 4607.33 Å, while two Y II lines were adopted for the Yttrium measurements (4883.68 and 5087.42 Å). It was already demonstrated in Bergemann et al. (2012) that NLTE provides a robust ionization balance for Sr I and Sr II-based abundances for dwarfs and red giants over the metallicity range relevant to the present work. For Y, the standard validation tests of the NLTE model atom, including validation on metal-poor red giant atmospheres, were presented in Storm & Bergemann (2023). For the atomic and molecular blends, we took advantage of the comprehensive Gaia-ESO survey linelist (Heiter et al. 2021). We adopted the extensively used 1D MARCS model atmospheres from Gustafsson et al. (2008). The solar abundances are taken from Magg et al. (2022).

We carefully checked by eye the quality of the fitted spectral lines to ensure the robustness of the abundance measurements. Examples of Ba II and Y II best-fit profiles are showed in Fig. 2 for two red giants with different metallicities. For a given element, the error budget σ was computed by quadratically summing the line-to-line scatter (σsc) to the propagated errors from the three atmospheric parameters (Teff, log(g), and [Fe/H]) (σatm).

thumbnail Fig. 2.

Examples of Ba II (left) and Y II (right) lines in the spectra of two red giants with [Fe/H]NLTE = −1.65 (top) and [Fe/H]NLTE = −0.77 (bottom). The red shaded area represents the spectral range over which the line is fitted. The orange curve corresponds to the best line-fit. The black vertical corresponds to the central wavelength of the line.

3. Chemical abundance trends of [Sr/Fe], [Y/Fe], and [Ba/Fe]

In Fig. 3, we show the LTE (blue) and NLTE (red) abundances of Sr, Y, and Ba as a function of LTE (top) and NLTE (bottom) metallicity [Fe/H], respectively. Here, LTE [Sr/Fe] shows a slightly increasing behaviour with [Fe/H] and the abundance ratios tend to be strongly sub-solar over the entire metallicity range. NLTE [Sr/Fe] is only slightly sub-solar for [Fe/H] > −1, and solar for [Fe/H] < −1. We note a major difference between both LTE and NLTE of about 0.2 dex in [Sr/Fe]. This is expected, because NLTE effects on the formation of the Sr I line at 4607 Å are positive, as in NLTE the line opacity decreases, leading to weaker lines compared to LTE (Bergemann et al. 2012; Hansen et al. 2013). Overall, the stars-by-star scatter is around 0.17 dex for LTE [Sr/Fe], while the scatter drops to 0.13 for NLTE [Sr/Fe], as a result of NLTE effects shrinking the distribution. This is also the case for the individual abundance uncertainties, as illustrated by the black error bars in the bottom of each panel (computed as mean uncertainties in a 0.5 dex [Fe/H range]). As presented in Fig. 4, it is evident that the metallicity distribution function below [Fe/H] = −1.5 drastically differs between LTE and NLTE: [Fe/H] distribution shrinks in NLTE, compared to LTE. Here, we only probe the halo down to [Fe/H] = −2.7, due to increasing NLTE correction with decreasing [Fe/H].

thumbnail Fig. 3.

Chemical abundances of [Sr/Fe] (left), [Y/Fe] (center), and [Ba/Fe] (right) in LTE as a function of LTE [Fe/H] shown in the top panel. We display both the individual stars and contour-plot. Black error bars correspond to mean uncertainties ⟨σ⟩. Bottom panel is the same as top, but in NLTE. The number of stars is indicated in the top right corner in each panel, with both rows having the same number of stars.

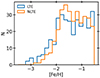thumbnail Fig. 4.

LTE and NLTE metallicity distribution of our stellar sample probing the metal-weak Galactic disc and the halo (see Ruchti et al. 2013). The distribution is not uniform and not statistically complete because of the observational selection function (Ruchti et al. 2011).

In the middle-top panels of Fig. 3, we see that the LTE [Y/Fe] ratio shows a concave shape with [Fe/H], and on average sub-solar (⟨[Y/Fe]⟩= − 0.09), which is consistent with past LTE studies (e.g. Delgado Mena et al. 2017). In contrast, NLTE [Y/Fe] ratios slightly decrease with increasing [Fe/H], from roughly 0.1 at [Fe/H] ≲ −1.2 to ∼ − 0.1 for [Fe/H] ≳ −1.2. We notice that the overall star-to-star [Y/Fe] scatter is equal to 0.17 dex in both LTE and NLTE; this scatter slightly increases with [Fe/H] and ranges from 0.14 to 0.18 in LTE and 0.12 to 0.17 in NLTE. Such an increase is likely due to the presence of [Y/Fe]-rich and poor stars (see below). On average, NLTE [Y/Fe] ratios are higher than LTE [Y/Fe] by ∼0.15 dex at [Fe/H] ≈ −2, while the difference between NLTE and LTE decreases to 0.04 for [Fe/H] ≳ −1. This result is similar, but less pronounced than for [Sr/Fe]. The overall behaviour of NLTE effects in Y with metallicity is consistent with the results of Storm & Bergemann (2023).

In the top-right panel of Fig. 3, we show that the LTE and NLTE [Ba/Fe] abundances follow a similar, albeit not the same, trend. As metallicities above ∼ − 1, NLTE [Ba/Fe] is slightly lower than LTE [Ba/Fe] by about 0.07 dex, consistent with past studies, for instance, our previous work in Gallagher et al. (2020), as we expect the equivalent widths of the Ba II lines to increase due to NLTE effects. NLTE [Ba/Fe] is rather flat for [Fe/H] ≳ −1.25, in agreement with previous studies (e.g. Delgado Mena et al. 2017 in LTE and Korotin et al. 2011 in NLTE). The star-by-star standard deviation of NLTE [Ba/Fe] abundances is 0.16 dex, while it reaches 0.21 dex for LTE [Ba/Fe]. This shows that NLTE abundances have less intrinsic scatter, which has implications for the chemical enrichment of the elements in the Galaxy, as we show in Sect. 4 below.

We notice the presence of stars deficient in [Y/Fe], compared to the main distribution at a given metallicity, as well as some stars with large [Ba/Fe] and [Y/Fe] values. To search for possible correlations between these low- and high-abundance stars, we present in Fig. 5 the NLTE abundances of [Y/Fe] as a function of [Ba/Fe], colour-coded with [Sr/Fe]. Firstly, we found ten stars with [Y/Fe] < −0.3, showing also both solar or sub-solar (< +0.1) [Ba/Fe] and [Sr/Fe]. Secondly, five stars have large [Y/Fe] > 0.2 together with large [Ba/Fe] ([Ba/Fe] > 0.3) and [Sr/Fe] ([Sr/Fe] > 0.15). We investigated on the origin of such enhanced (deficient) stars by checking for potential common membership with the main Milky Way components. We adopted the thin disc, thick disc, and halo kinematics-based membership classification of Ruchti et al. (2011). We find that these enhanced (deficient) stars do not preferentially belong to one particular Galactic component. For instance, among the [Y/Fe]-deficient stars, four stars belong to the thin disc, five stars to the thick disc, and one star to the halo. For the dwarfs and turn-off stars present in this sample, we checked for potential age signatures by adopting the isochrone-based stellar ages from Serenelli et al. (2013). The stars enhanced (deficient) in [Y/Fe] span stellar ages of between 6 and 13 Gyr, with no apparent correlation visible between the stellar ages and enhanced (deficient) n-capture abundances.

thumbnail Fig. 5.

NLTE chemical abundances of [Y/Fe] as a function of [Ba/Fe], color-coded with [Sr/Fe].

4. Confronting chemical evolution model with heavy-to-light s-process element ratios

Here, we investigate the [Ba/Y] ratio, which is a proxy of the heavy-to-light s-process elements (e.g. Lian et al. 2023). We compare our observations to simple one-zone and inhomogeneous (stochastic) Galactic chemical evolution models, with the former being primarily relevant with respect to the understanding of the chemical enrichment of the disc and the latter being qualitatively consistent with the present understanding of the formation of the Galactic halo (see for instance Matteucci 2021 and references therein).

In the left panel of Fig. 6, we present the LTE (blue contours) and NLTE (red contours) distributions of [Ba/Y] ratios for the 187 stars of our sample with available Ba and Y abundances (in both LTE and NLTE). Both LTE and NLTE [Ba/Y] abundances slightly increase with [Fe/H], and present both a similar scatter of 0.17 dex, which is rather constant with [Fe/H]. Overall, we see that [Ba/Y] presents a weak dependence on [Fe/H] over the entire range of [Fe/H]. The main difference is a rigid shift of −0.12 dex between NLTE and LTE [Ba/Y]. The intrinsic scatter of abundance ratios is larger than the individual observational uncertainties of the measurement (ranging from 0.16 to 0.08 in NLTE, see Sect. 2) suggesting that the observational scatter is a signature of chemical enrichment processes. In the right panel of Fig. 6, we show NLTE [Ba/Y] ratio as a function of NLTE [Fe/H]. We also overplotted the Gaia-ESO NLTE [Ba/Y] abundances used in Lian et al. (2023). Even though the abundances between this work and the Gaia-ESO were computed with different spectral analysis pipelines, the data is rather complementary3.

thumbnail Fig. 6.

Chemical abundance ratios [Ba/Y] in both LTE (blue contours) and NLTE (red contours) as a function of [Fe/H] (LTE and NLTE, respectively), for 187 stars (left). Error bars correspond to mean uncertainties in LTE and NLTE. Only NLTE [Ba/Y] (red contours) together with Gaia-ESO sample used by Lian et al. (2023), as well as one-zone chemical evolution models with different yields prescriptions (right).

4.1. One-zone GCE models

As in Lian et al. (2023), we made of the OMEGA+ Galactic chemical evolution (GCE) model (Côté et al. 2017, 2018), which includes gas inflow and outflows. The basic model includes core-collapse supernova (CCSN) yields from Limongi & Chieffi (2018), as well as Type Ia supernovae with yields from different Chandrasekhar- and sub-Chandrasekhar mass explosions as described in Eitner et al. (2023). The GCE model also includes AGB yields from Cristallo et al. (2015). This basic GCE model is displayed in orange in Fig. 6. For comparison, we also display a GCE model that includes recent AGB yields by Karakas (2010), which account for n-capture elements nucleosynthesis for metallicites down to −2 (see Cinquegrana & Karakas 2022 and references there-in for more details). We also show one GCE model with no AGB contribution (in purple) and one with metallicity-independent AGB yields (in green). Finally, we added a GCE model that only includes non-rotating massive stars.

Lian et al. (2023) concluded that the shape of [Ba/Y] in the metal-rich regime ([Fe/H] ≳ −0.6) is driven by the metallicity dependence in the neutron-capture efficiency in AGB stars. The mismatch between the GCE models and observations in this [Fe/H] regime is likely due to an overestimation of the s-process efficiency of low mass AGB stars (Magrini et al. 2021).

In the metallicity range of −2 ≲ [Fe/H] ≲ −0.8, the model without massive star yields shows a strong underproduction of [Ba/Y] and it is not consistent with the data. The large scatter in [Ba/Y] at a given metallicity could be a sign of chemical enrichment from AGBs with masses between 2 and 6 solar masses (their Fig. 5 Lian et al. 2023). We also find that the GCE track computed with non-rotating CCSN yields underpredicts our observations, which supports evidence from the literature that CCSN resulting from the evolution of rapidly rotating massive stars are important sources of s-process elements (e.g. Limongi & Chieffi 2018). In conclusion, such chemical evolution models with different nucleosynthesis prescriptions are not able to reproduce the data, mainly due to the large scatter in [Ba/Y] at a given [Fe/H].

4.2. Stochastic GCE models

Substantial efforts have been made in the GCE model community in trying to reproduce the abundance patterns measured in the Galactic halo stars. Cescutti & Chiappini (2014) and Rizzuti et al. (2021) developed stochastic GCE models. Such models are meant to reproduce the chemical evolution of the Galactic halo, implying a series of nucleosynthesis events, overall on a time scale of 1 Gyr. Their model MRD+s B2 includes r-process contribution from magneto-rotational (MRD) supernovae and s-process nucleosynthesis from two channels: low-mass AGB stars and rotating massive stars (see Cescutti & Chiappini 2014 for more details). In this instance, we adopted the MRD+s B2 model. Here, we explore whether such models can reproduce the scatter we measure in our observations of [Ba/Y]. We notice that contrary to the model of Lian et al. (2023), the models from Cescutti & Chiappini (2014) do not include neutron star mergers.

In the top panel of Fig. 7, we present the LTE and NLTE [Ba/Y] abundance ratios as a function of NLTE [Fe/H] (blue and red contours, respectively). Additionally, we present stochastic GCE (colour-coded with number of stars in the model, i.e. SFR tracer). For [Fe/H] ≲ −2.5, the GCE model shows a large scatter in the [Ba/Y] ratios, ranging from ∼ − 1 to +0.3. Such behaviour is directly attributed to the stochastic sampling of the IMF during the phase of halo formation (Cescutti & Chiappini 2014). The predicted [Ba/Y] trend flattens out for metallicities [Fe/H] ≳ −2.5 and slightly rises up to [Ba/Y] ≈ 0.25 for [Fe/H] ≳ −1. This GCE model matches rather well our LTE [Ba/Y] ratios, however, it overpredicts [Ba/Y] when compared to NLTE [Ba/Y]. This mismatch is simply the consequence of the fact that in this GCE model the yttrium yields were modified to match the LTE observations. Specifically, the r-yields were scaled the LTE pattern of r-process rich stars. This pattern differs by a factor of 3 for Y, whereas it is consistent with the r-process solar residual for the remaining elements (see Cescutti & Chiappini 2014 for more details). Hence, the GCE matches rather well our LTE [Ba/Y] pattern. Such results show that taking into account NLTE effects is key for achieving accurate comparisons between GCEs and observations.

thumbnail Fig. 7.

[Ba/Y] (top) and [Ba/Sr] ratios as a function of [Fe/H]. Blue and red contours show LTE and NLTE abundances, respectively, for 187 stars. We also show stochastic chemical evolution models (MRD+s B2) from Cescutti & Chiappini (2014).

In the bottom panel of Fig. 7, we show similar plots but for the [Ba/Sr] ratios. The GCE model shows a similar trend with [Ba/Y]. Contrary to [Ba/Y], the GCE model matches the NLTE [Ba/Sr] ratios better, while the GCE model underpredicts our LTE [Ba/Sr] ratios. This could be due to the large NLTE effect when measuring the Sr line at 4607 Å. Again, taking properly into account NLTE effects is key when comparing chemical evolution models to observations, especially in the metal-poor regime.

Considering that we provide new NLTE abundances of neutron-capture elements for our stellar sample, it is necessary to confront our data to a stochastic chemical evolution model that is not scaled to reproduce the LTE abundance patterns. It corresponds to the model MRD+s B from Cescutti & Chiappini (2014), which is similar to the model MRD+s B2; however, the r-process contribution to Y production is scaled to the solar residual, as in the case of the other elements, and therefore they are not divided by a factor of 3. We show such a model in Fig. 8, together with the LTE and NLTE abundances of our metal-poor stars. Naturally, the predicted ratio of [Ba/Y] is lower by 0.3 dex compared to the model MRD+s B2. Interestingly, the GCE model based on r-process solar residual is indeed closer to the NLTE observational distributions of [Ba/Y] and [Ba/Sr] in our stellar sample. It is important to remind the reader that our abundances are computed using 1D model atmospheres and we expect the [Ba/Y] ratio to be lower when adopting an updated model atom (Storm et al. 2024), with Y+H collisional processes updated to new quantum-mechanical values. Also, adopting 3D model atmospheres (Storm et al. 2024) can induce larger and more positive 3D NLTE effects for Y II lines. As a result, we do not see evidence for re-scaling the MRD yields for Y to the pattern of the r-process rich stars as used in the model MRD+s B2 of Cescutti & Chiappini (2014); moreover, the r-process solar residuals appear to be more reliable, as expected: they are not affected by the NLTE corrections.

thumbnail Fig. 8.

Same as Fig. 7, but with the MRD+s B model from Cescutti & Chiappini (2014).

5. Conclusions

In this work, we focus on constraining the chemical enrichment of [Ba/Fe], [Sr/Fe], [Y/Fe], and [Ba/Y] ratios of Milky Way stars in the domain of −2.5 ≲ [Fe/H] ≲ −0.5 There is lack of abundance measurements in this [Fe/H] range that makes it challenging to set direct constraints of Galactic chemical evolution.

  1. We used high-resolution (R ∈ [35 000 − 45 000]) and high signal-to-noise observations of RAVE metal-poor stars with previously determined Teff, log(g), and [Fe/H] in both LTE and NLTE (Ruchti et al. 2013).

  2. We measured the 1D LTE and NLTE abundances of [Ba/Fe], [Sr/Fe], and [Y/Fe] with associated uncertainties using the spectral synthesis code TSFitPy, a wrapper for NLTE version of TurboSpectrum. Careful visual checks of the spectral fits were performed in order to ensure the robustness of the determined chemical abundances.

  3. We showed that the bulk of NLTE [Ba/Fe] ratios decreases with increasing [Fe/H], while NLTE [Sr/Fe] is rather constant with [Fe/H], and NLTE [Y/Fe] decreases with [Fe/H]. The combined NLTE effects are of the order of −0.07 dex for [Ba/Fe], +0.18 dex for [Sr/Fe], and +0.10 dex for [Y/Fe] that also includes the NLTE effect on [Fe/H].

  4. Focusing on NLTE abundances, we find that stars enhanced (deficient) in [Ba/Fe] and [Y/Fe] are enhanced (deficient) in [Sr/Fe].

  5. We showed that the NLTE ratios of [Ba/Y] are centred around solar values and the behaviour of the trend is rather flat with NLTE metallicity [Fe/H], implying that [Ba/Y] is not sensitive to [Fe/H]. The star-to-star scatter is substantial and is of the order of 0.2 dex. LTE [Ba/Y] ratios show a similar dispersion as NLTE [Ba/Y], but are shifted by +0.12 dex relative to the solar values even at metallicities close to solar.

  6. Single-zone chemical evolution models are unable to reproduce the [Ba/Y] scatter observed at a given metallicity. Such a scatter can, however, be more captured by stochastic GCE models.

  7. Most importantly, we find a better agreement of the NLTE abundance ratios of light (Sr, Y) and heavy (Ba) element ratios, as compared to the GCE tracks from stochastic chemical evolution models with r-yields scaled with an r-process solar residual. There is no longer any need for modifications to the r-process yields of yttrium following the pattern of r-process rich stars, as done in Cescutti & Chiappini (2014), for instance. Therefore, we conclude that properly taking into account NLTE effects when measuring abundances directly impacts comparisons among galactic chemical evolution models and observations, thereby affecting yield prescriptions and nucleosynthesis channels.

The sample studied here is still rather limited in terms of the number of stars and in the metallicity coverage. Indeed, going to low metallicity, typically down to [Fe/H] of ∼ − 4 or −5, will allow us to probe the early neutron-capture enrichment of the Milky Way in greater detail. In the near future, 4MOST will deliver hundreds of thousands of high-resolution (R ∼ 20 000) optical spectra of the Milky Way disc, halo, and bulge stars (de Jong et al. 2019; Bensby et al. 2019; Christlieb et al. 2019), opening up a new era for NLTE abundances exploration down to very low metallicities. Substantial efforts will have to be made to provide the community with precise and accurate neutron-capture abundances from such facilities.

3

For the present study and the Gaia-ESO survey used the same linelist and model atmosphere grids.

Acknowledgments

We sincerely thank the anonymous referee for the very positive feedback and comments that improved the readability of the paper. G.G. acknowledges support by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – project-IDs: eBer-22-59652 (GU 2240/1-1 “Galactic Archaeology with Convolutional Neural-Networks: Realising the potential of Gaia and 4MOST”). We acknowledge support by the Collaborative Research Centre SFB 881 (projects A5, A10), Heidelberg University, of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) and by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement 949173). M.B. is supported through the Lise Meitner grant from the Max Planck Society. This research was supported by the Munich Institute for Astro-, Particle and BioPhysics (MIAPbP) which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2094 – 390783311. A.S. acknowledges grants PID2019-108709GB-I00 from Ministry of Science and Innovation (MICINN, Spain), Spanish program Unidad de Excelencia María de Maeztu CEX2020-001058-M, 2021-SGR-1526 (Generalitat de Catalunya). A.S. and G.C. acknowledge support from ChETEC-INFRA (EU project no. 101008324). G.C. acknowledges the grant PRIN project n.2022X4TM3H “Cosmic POT” from Ministero dell’Universitá e la Ricerca (MUR).

References

  1. Battistini, C., & Bensby, T. 2016, A&A, 586, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Bensby, T., Bergemann, M., Rybizki, J., et al. 2019, The Messenger, 175, 35 [NASA ADS] [Google Scholar]
  3. Bergemann, M., Hansen, C. J., Bautista, M., & Ruchti, G. 2012, A&A, 546, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bergemann, M., Collet, R., Amarsi, A. M., et al. 2017a, ApJ, 847, 15 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bergemann, M., Collet, R., Schönrich, R., et al. 2017b, ApJ, 847, 16 [Google Scholar]
  6. Biémont, É., Blagoev, K., Engström, L., et al. 2011, MNRAS, 414, 3350 [Google Scholar]
  7. Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., & Käppeler, F. 2011, MNRAS, 418, 284 [Google Scholar]
  8. Buder, S., Lind, K., Ness, M. K., et al. 2019, A&A, 624, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Burbidge, E. M., Burbidge, G. R., Fowler, W. A., & Hoyle, F. 1957, Rev. Mod. Phys., 29, 547 [NASA ADS] [CrossRef] [Google Scholar]
  10. Busso, M., Gallino, R., & Wasserburg, G. J. 1999, ARA&A, 37, 239 [Google Scholar]
  11. Cescutti, G., & Chiappini, C. 2014, A&A, 565, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Christlieb, N., Battistini, C., Bonifacio, P., et al. 2019, The Messenger, 175, 26 [NASA ADS] [Google Scholar]
  13. Cinquegrana, G. C., & Karakas, A. I. 2022, MNRAS, 510, 1557 [Google Scholar]
  14. Côté, B., O’Shea, B. W., Ritter, C., Herwig, F., & Venn, K. A. 2017, ApJ, 835, 128 [Google Scholar]
  15. Côté, B., Silvia, D. W., O’Shea, B. W., Smith, B., & Wise, J. H. 2018, ApJ, 859, 67 [CrossRef] [Google Scholar]
  16. Cowan, J. J., Sneden, C., Lawler, J. E., et al. 2021, Rev. Mod. Phys., 93, 015002 [Google Scholar]
  17. Cristallo, S., Straniero, O., Piersanti, L., & Gobrecht, D. 2015, ApJS, 219, 40 [Google Scholar]
  18. Davidson, M. D., Snoek, L. C., Volten, H., & Doenszelmann, A. 1992, A&A, 255, 457 [NASA ADS] [Google Scholar]
  19. de Jong, R. S., Agertz, O., Berbel, A. A., et al. 2019, The Messenger, 175, 3 [NASA ADS] [Google Scholar]
  20. Delgado Mena, E., Tsantaki, M., Adibekyan, V. Z., et al. 2017, A&A, 606, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Dravins, D. 2008, A&A, 492, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Eitner, P., Bergemann, M., Ruiter, A. J., et al. 2023, A&A, 677, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Gallagher, A. J., Bergemann, M., Collet, R., et al. 2020, A&A, 634, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. García, G., & Campos, J. 1988, J. Quant. Spec. Radiat. Transf., 39, 477 [CrossRef] [Google Scholar]
  25. Gerber, J. M., Magg, E., Plez, B., et al. 2023, A&A, 669, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Guiglion, G., de Laverny, P., Recio-Blanco, A., & Prantzos, N. 2018, A&A, 619, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Hansen, C. J., Bergemann, M., Cescutti, G., et al. 2013, A&A, 551, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Heiter, U., Lind, K., Bergemann, M., et al. 2021, A&A, 645, A106 [EDP Sciences] [Google Scholar]
  30. Helmi, A. 2020, ARA&A, 58, 205 [Google Scholar]
  31. Kaeppeler, F., Beer, H., Wisshak, K., et al. 1982, ApJ, 257, 821 [NASA ADS] [CrossRef] [Google Scholar]
  32. Karakas, A. I. 2010, MNRAS, 403, 1413 [NASA ADS] [CrossRef] [Google Scholar]
  33. Korotin, S., Mishenina, T., Gorbaneva, T., & Soubiran, C. 2011, MNRAS, 415, 2093 [NASA ADS] [CrossRef] [Google Scholar]
  34. Lian, J., Storm, N., Guiglion, G., et al. 2023, MNRAS, 525, 1329 [NASA ADS] [CrossRef] [Google Scholar]
  35. Limongi, M., & Chieffi, A. 2018, ApJS, 237, 13 [NASA ADS] [CrossRef] [Google Scholar]
  36. Magg, E., Bergemann, M., Serenelli, A., et al. 2022, A&A, 661, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Magrini, L., Vescovi, D., Casali, G., et al. 2021, A&A, 646, L2 [EDP Sciences] [Google Scholar]
  38. Mashonkina, L. I., Vinogradova, A. B., Ptitsyn, D. A., Khokhlova, V. S., & Chernetsova, T. A. 2007, Astron. Rep., 51, 903 [NASA ADS] [CrossRef] [Google Scholar]
  39. Matijevič, G., Chiappini, C., Grebel, E. K., et al. 2017, A&A, 603, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Matsuno, T., Hirai, Y., Tarumi, Y., et al. 2021, A&A, 650, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Matteucci, F. 2021, A&ARv, 29, 5 [NASA ADS] [CrossRef] [Google Scholar]
  42. Meunier, N., Lagrange, A. M., Mbemba Kabuiku, L., et al. 2017, A&A, 597, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Mishenina, T., Pignatari, M., Gorbaneva, T., et al. 2019, MNRAS, 484, 3846 [Google Scholar]
  44. Nordlund, Å., Stein, R. F., & Asplund, M. 2009, Liv. Rev. Sol. Phys., 6, 2 [Google Scholar]
  45. Pignatari, M., Gallino, R., Heil, M., et al. 2010, ApJ, 710, 1557 [Google Scholar]
  46. Plez, B. 2012, Astrophysics Source Code Library [record ascl:1205.004] [Google Scholar]
  47. Rizzuti, F., Cescutti, G., Matteucci, F., et al. 2021, MNRAS, 502, 2495 [NASA ADS] [CrossRef] [Google Scholar]
  48. Roederer, I. U., Lawler, J. E., Den Hartog, E. A., et al. 2022, ApJS, 260, 27 [NASA ADS] [CrossRef] [Google Scholar]
  49. Ruchti, G. R., Fulbright, J. P., Wyse, R. F. G., et al. 2011, ApJ, 743, 107 [Google Scholar]
  50. Ruchti, G. R., Bergemann, M., Serenelli, A., Casagrande, L., & Lind, K. 2013, MNRAS, 429, 126 [CrossRef] [Google Scholar]
  51. Serenelli, A. M., Bergemann, M., Ruchti, G., & Casagrande, L. 2013, MNRAS, 429, 3645 [NASA ADS] [CrossRef] [Google Scholar]
  52. Sneden, C., Cowan, J. J., & Gallino, R. 2008, ARA&A, 46, 241 [Google Scholar]
  53. Steinmetz, M., Zwitter, T., Siebert, A., et al. 2006, AJ, 132, 1645 [Google Scholar]
  54. Storm, N., & Bergemann, M. 2023, MNRAS, 525, 3718 [NASA ADS] [CrossRef] [Google Scholar]
  55. Storm, N., Barklem, P. S., Yakovleva, S. A., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202348971 [Google Scholar]
  56. Venn, K. A., Shetrone, M. D., Irwin, M. J., et al. 2012, ApJ, 751, 102 [Google Scholar]

All Figures

thumbnail Fig. 1.

Atmospheric parameters and [Fe/H] coverage of the 323 stars of the sample. Left: Kiel diagram (NLTE Teff vs. log(g)), colour-coded with NLTE [Fe/H]. Middle: NLTE [Fe/H] vs. Teff colour-coded with NLTE log(g). Right: NLTE [Fe/H] vs. log(g) colour-coded with NLTE Teff.
In the text
thumbnail Fig. 2.

Examples of Ba II (left) and Y II (right) lines in the spectra of two red giants with [Fe/H]NLTE = −1.65 (top) and [Fe/H]NLTE = −0.77 (bottom). The red shaded area represents the spectral range over which the line is fitted. The orange curve corresponds to the best line-fit. The black vertical corresponds to the central wavelength of the line.
In the text
thumbnail Fig. 3.

Chemical abundances of [Sr/Fe] (left), [Y/Fe] (center), and [Ba/Fe] (right) in LTE as a function of LTE [Fe/H] shown in the top panel. We display both the individual stars and contour-plot. Black error bars correspond to mean uncertainties ⟨σ⟩. Bottom panel is the same as top, but in NLTE. The number of stars is indicated in the top right corner in each panel, with both rows having the same number of stars.
In the text
thumbnail Fig. 4.

LTE and NLTE metallicity distribution of our stellar sample probing the metal-weak Galactic disc and the halo (see Ruchti et al. 2013). The distribution is not uniform and not statistically complete because of the observational selection function (Ruchti et al. 2011).
In the text
thumbnail Fig. 5.

NLTE chemical abundances of [Y/Fe] as a function of [Ba/Fe], color-coded with [Sr/Fe].
In the text
thumbnail Fig. 6.

Chemical abundance ratios [Ba/Y] in both LTE (blue contours) and NLTE (red contours) as a function of [Fe/H] (LTE and NLTE, respectively), for 187 stars (left). Error bars correspond to mean uncertainties in LTE and NLTE. Only NLTE [Ba/Y] (red contours) together with Gaia-ESO sample used by Lian et al. (2023), as well as one-zone chemical evolution models with different yields prescriptions (right).
In the text
thumbnail Fig. 7.

[Ba/Y] (top) and [Ba/Sr] ratios as a function of [Fe/H]. Blue and red contours show LTE and NLTE abundances, respectively, for 187 stars. We also show stochastic chemical evolution models (MRD+s B2) from Cescutti & Chiappini (2014).
In the text
thumbnail Fig. 8.

Same as Fig. 7, but with the MRD+s B model from Cescutti & Chiappini (2014).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.