| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A247 | |
| Number of page(s) | 12 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202348510 | |
| Published online | 22 March 2024 | |
Cataclysmic variables and the disc instability model in the Gaia DR3 colour–magnitude diagram
Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
e-mail: guillaume.dubus@univ-grenoble-alpes.fr; carine.babusiaux@univ-grenoble-alpes.fr
Received:
6
November
2023
Accepted:
21
January
2024
Context. Cataclysmic variables (CVs) are semi-detached binaries composed of a white dwarf orbiting a lower-mass K or M star.
Aims. We investigate whether CVs are responsible for a new intriguing feature (the “hook”) that appears in the Gaia DR3 colour–magnitude Hertzsprung-Russell diagram (HRD) when selecting sources with low extinction. We also aim to understand the location of CVs in the HRD based on the predictions of the disc instability model (DIM). The DIM forms the foundation of our basic understanding of stable (novae-like) and outbursting CVs (dwarf novae).
Methods. We calculated the expected behaviour of CVs in the Gaia HRD while taking into account the variable light contributed by the accretion disc, the companion, the white dwarf, and the bright spot where the Roche lobe overflow stream from the companion intersects the disc.
Results. We find that the hook feature is most likely composed of CVs. The hook corresponds to the limited region where stable (novae-like) CVs must be located in the HRD according to the DIM. Unstable systems giving rise to dwarf novae outbursts trace counterclockwise loops in the HRD. The overall behaviour is consistent with the location of the various CV subtypes in the HRD.
Conclusions. These results can be used as a basis on which to pinpoint interesting outliers in the HRD, either due to their location or their tracks. These outliers could signal new subtypes, such as cold, stable CVs with truncated discs, or may challenge the disc instability model.
Key words: accretion, accretion disks / stars: dwarf novae / novae, cataclysmic variables / subdwarfs
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Cataclysmic variables (CVs) are semidetached binaries composed of a white dwarf orbiting a lower-mass K or M star (see Hellier 2001 for an introduction, Warner 2003 for a complete monograph, and Webb 2022 for a recent review). The companion star fills its Roche lobe with material lost through the first Lagrangian (L1) point, forming an accretion disc around the white dwarf. CVs have orbital periods Porb ranging from ≈80 min to 10 h, with a gap between Porb = 2 and 3 h in the distribution (period gap). CVs are thought to be born at the high end of this Porb distribution, as the companion first fills its Roche lobe and after a common envelope episode has shrunk the orbit of the initial binary. CVs then evolve to shorter Porb as a result of binary angular momentum losses through stellar wind magnetic braking or gravitational wave emission, with the gap being due to a drop in the braking efficiency. The population of CVs therefore provides insights and constraints for the study of binary stellar evolution, but interesting problems remain.
Accretion in CVs makes for a rich but somewhat daunting phenomenology with a long history. A longstanding question is whether the magnetic field of the white dwarf is strong enough to prevent the formation of an accretion disc (polars or AM Her type) or to partly truncate the disc (intermediate polars or DQ Her type), or is too weak to influence accretion (non-magnetic CV). Another question pertains to the variability on timescales of days to years, with a broad separation between nova-like (NL) CVs, CVs in a (nearly) permanent luminous state, and dwarf novae, and CVs displaying recurrent outbursts with a typical amplitude of 3 to 5 optical magnitudes. NL CVs can be subdivided into various types according to their spectrum (RW Tri, UX UMa, SW Sex) or their light curve (VY Scl, IW And). Dwarf novae (DNe) can also be subdivided according to their outburst morphology (U Gem, Z Cam, SU UMa, WZ Sge, ER UMa). Finally, novae are CVs where the accreted matter piled up on the white dwarf undergoes runaway fusion, leading to an eruption with a typical amplitude of 8 to 15 mag. All of these phenomena are essentially related to how accretion proceeds, making CVs a valuable tool for testing accretion theory.
Cataclysmic variables are typically discovered serendipitously in surveys based on their blue colour, their spectra – with broad emission lines –, or their variability. The advent of synoptic spectral (SDSS, LAMOST, etc.) and variability (OGLE, ATLAS, CRTS, ASAS-SN, ZTF, etc.) surveys has vastly increased the number of identified and candidate CVs. The open CV catalogue currently lists more than 14 000 entries (Jackim et al. 2020). Gaia (Gaia Collaboration 2016) has been particularly impactful as it removes one of the major uncertainties when studying CVs: their distance. This has enabled, for example, renewed estimates of the local density of CVs (Pala et al. 2020; Inight et al. 2021; Canbay et al. 2023), constraints on their secular rate of accretion (Pala et al. 2022), or a test of the disc instability model for DNe and NL CVs (Dubus et al. 2018).
Gaia also provides a treasure trove of information on colour and variability that can be used to distinguish between different classes of objects (Gaia Collaboration 2019; Maíz Apellániz et al. 2023). CVs occupy a clearly distinct region in a GBP − GRP colour versus G magnitude Hertzsprung-Russell diagram (HRD), in between the main sequence and the white dwarf cooling sequence, where their light-curve variability distinguishes them from detached binaries (Eyer et al. 2023). Moreover, the orbital period of a CV is also related to its location in the HRD (Abril et al. 2020; Abrahams et al. 2022). Short-orbital-period CVs, which have faint companions, are located close to the white dwarf cooling sequence, whereas long-orbital-period systems, which harbour more luminous companions, are located close to the main sequence. Different subtypes of CVs also occupy somewhat different locations in the HRD (Ramsay et al. 2018; Isogai et al. 2019; Abril et al. 2020; Abrahams et al. 2022).
Previous Gaia studies dedicated to CVs used compilations of known objects and did not correct for extinction. Here, we investigate a sample of Gaia sources selected for low extinction (Sect. 2). Their average position in the HRD shows a new intriguing feature that we attribute to CVs. To understand this feature, as well as the tracks left by individual CVs in the HRD as a result of their variability, we calculated the expected behaviour of CVs in the HRD taking into account the variable light contributed by the accretion disc. To do this, we model the accretion disc as a thin, radiatively efficient, α disc. Such discs are stable at high mass-accretion rates (NL CVs) but become unstable if their temperature becomes low enough that ionised hydrogen recombines (DNe). The large jump in opacity triggers a thermal-viscous instability and cycles of outbursts. This disc instability model (DIM) forms the basis of our understanding of CV light curves (see Lasota 2001; Hameury 2020, for reviews). We examine the HRD track predicted by the DIM for CVs in Sect. 3. We then discuss the consistency of CV locations in the HRD diagram with the DIM in Sect. 4 before presenting our conclusions.
2. The CV area seen by Gaia
Figure 1 (left panel) shows a zoom onto the Gaia low-extinction HRD (Fig. 5 of Gaia Collaboration 2018) updated with Gaia Collaboration (2021) EDR3 data and the Lallement et al. (2022) extinction map. We selected stars with A0 < 0.1 mag, a relative parallax error of less than 10%, a relative flux error of less than 50% in G and 20% in GBP and GRP, ruwe < 1.41, and a corrected BP and RP flux excess C* of lower than 10 × σC* (Riello et al. 2021)2. This selection leads to more than 26 millions stars, which is six times more than used in Gaia Collaboration (2018). This HRD shows a new prominent feature at MG ∼ 4 and GBP − GRP ∼ 0.2 going from the main sequence to the clump of hot subdwarf B stars (sdBs) that seems to turn at GBP − GRP ∼ 0 and continue down, parallel to the main sequence. We call this feature the “hook”, and we distinguish two areas for the discussion hereafter: the “upper” hook going from main sequence to sdB clump and the “lower” hook going parallel to the main sequence (see Fig. 2).
 |
Fig. 1. Locating CVs in the Gaia low-extinction HRD diagram. Left: Gaia DR3 low-extinction HRD (A0 < 0.1 mag, parallax uncertainty smaller than 10%, ruwe < 1.4, |
 |
Fig. 2. HRD colour-coded according to the mean VarG of all stars with A0 < 0.1, parallax uncertainty smaller than 10%, ruwe < 1.4, and C* < 10 × σC*. The colour scale saturates for VarG values lower than 0 and higher than 1.5. Boxes correspond to areas discussed in the text: the sdB (blue), the upper hook (red), and the lower hook (orange). |
The hook region is in the area of the HRD where we expect to see systems with white dwarfs or sdBs plus main sequence or giant companions. There are 273 sources in the upper hook and 304 sources in the lower hook, of which 9% and 34% (respectively) have been associated to a DR3 variability type in Gaia DR3 (Gaia Collaboration 2023a; Eyer et al. 2023). Besides the wide-ranging short-timescale variability type, which flags systems with variability on a < 0.5 − 1 day timescale, we find that only two variability types populate the hook: CVs and sdBs. These are represented in Fig. 1 (middle left panel), selected with the same criteria as those used to create the main Gaia DR3 HRD (except for the relative flux error criteria, which is removed to allow large relative flux error due to variability in CVs). Both CVs and sdBs are found on the upper hook, while only the CVs follow the full trend going down parallel to the main sequence. The right panel of Fig. 1 shows the heat map scatter plot of the Gaia-identified CVs. There are two clumps: one along the lower hook and another close to the white dwarf sequence, consistent with the overall CV distribution. The heat map scatter plot is clearly bounded at low luminosity by the white dwarf plus companion tracks taken from Knigge et al. (2011, see Appendix A). The measurements are brighter and bluer, which is expected as the accretion disc and bright spot also contribute to the overall light. We note that the shortest period tracks of Knigge et al. (2011) correspond to the peak of Gaia DR3 variables classified as white dwarfs, which are indeed known to be contaminated by white dwarfs with a cooler companion causing large variations in GBP and GRP (Rimoldini et al. 2023).
To further characterise the Gaia-identified CV population, we compare this population in Fig. 1 (middle right panel) with CVs taken from the Ritter & Kolb (2003) catalogue using the same quality criteria (A0 < 0.1 mag, relative parallax error better than 10%, ruwe < 1.4, and C* < 10 × σC*). We show only CVs of DN or NL type, merging SU UMa with DNe and VY Scl with NL CVs for clarity. This figure clearly indicates that CVs located on the hook are NL CVs. The quality criterion on ruwe tends to remove possible astrometric binaries, while the criterion on the flux excess factor tends to remove polluted spectra. Their overall impact is to remove sources whose location in the HRD is contaminated by a nearby unrelated star or by an unknown tertiary companion, making the CV appear redder than it is. Indeed, the yellow stars (middle right panel, Fig. 1) show that these criteria mainly remove the CVs from Ritter & Kolb (2003) that are located redward of the hook.
While the blue part of the upper hook seems to be the continuation of the lower hook and is clearly associated to CVs according to Fig. 1, the origin of the red part of the upper hook is less obvious. In the following, we compare the properties of the upper and lower parts of the hook. The upper hook region of the HRD is known to contain wide binary systems (see e.g. Fig. 12 of Culpan et al. 2022). Figure 3 shows the distribution of the renormalised unit weight error (ruwe) of Gaia astrometry. Following Gaia Collaboration (2023b), we selected stars with ipd_frac_multi_peak < 33 to avoid visual double stars. The upper hook is found to have a larger ruwe than the lower hook area (confirmed by a K-S test with p-value 3e–10). Within the Fig. 3 sample, we have three stars with a Gaia DR3 non-single star (NSS) solution (Gaia Collaboration 2023b), two astrometric and one spectroscopic. These have periods of between 617 and 828 days. Some of the sources in the upper hook are likely to be sdBs in binaries (Culpan et al. 2022). If sources with large ruwe are CVs then they are likely to be triples, as Gaia is more sensitive to longer orbital periods than the typical CV orbital period. For example, TX Col, an NL CV located on the hook but not included in our selection, has a wide component resolved by Gaia at 2.5 arcsec (Igoshev et al. 2020).
 |
Fig. 3. HRD colour-coded according to the ruwe of all stars with A0 < 0.1, parallax uncertainty smaller than 10%, C* < 10 × σC*, ipd_frac_multi_peak < 3. The colour scale saturates for values lower than 0.6 and higher than 1.4. Green squares correspond to orbital solutions provided by Gaia DR3. |
Using a colour–colour diagram does not help to distinguish sdBs from CVs in the hook. Figure 4 reproduces Fig. 5 of Green et al. (2008), who showed that the “pure-spectrum” sdBs (bottom left of Fig. 4) are well separated from the composite-spectrum sdBs. However, there is no clear difference between composite sdBs and CVs in this diagram: upper hook and lower hook stars have similar colours and fall in the composite spectrum sdB area.
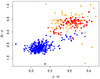 |
Fig. 4. Colour–colour diagram of stars in the areas indicated in Fig. 2, selected with A0 < 0.1, parallax uncertainty smaller than 10%, ruwe < 1.4, C* < 10 × σC*, and a 2MASS Qflag “AAA”. Blue triangles, red squares, and orange circles correspond to stars in the SDB area, the upper-hook area, and the low-hook area, respectively. |
Kinematics can help in this respect. We compared the tangential velocity of the three areas and found that the sdBs and the upper hook share a close distribution (K-S test p-value = 0.01), which contains thick disc and halo kinematics (see also Saffer et al. 2001), while the lower hook has kinematics closer to the thin disc only. Again, this is consistent with the upper hook containing both sdBs and CVs, while the lower hook contains only CVs4.
To look at the variability properties of the hook, we use the VarG index (Barber & Mann 2023):
where σp(G, Nobs) is the fitted Gaia photometric uncertainty obtained from the Riello et al. (2021) tool5 and  is the inverse of the phot_g_mean_flux_over_error parameter. Figure 2 shows that the right part of the upper hook corresponds to an area without specific photometric variation, as opposed to the lower hook, which shows strong photometric variation. This is consistent with the heat map scatter plot of CVs (right panel, Fig. 1). There are also strongly variable systems in the sdB clump, with a fraction of Gaia DR3 variables of 31%, similar to the lower hook area.
is the inverse of the phot_g_mean_flux_over_error parameter. Figure 2 shows that the right part of the upper hook corresponds to an area without specific photometric variation, as opposed to the lower hook, which shows strong photometric variation. This is consistent with the heat map scatter plot of CVs (right panel, Fig. 1). There are also strongly variable systems in the sdB clump, with a fraction of Gaia DR3 variables of 31%, similar to the lower hook area.
Figure 5 shows the variability in the HRD of the six brightest (in absolute magnitude) Gaia DR3 CVs of the upper hook with A0 < 0.1 and a parallax uncertainty of less than 10% (RZ Gru, HQ Mon, V825 Her, YZ Ret, TT Ari, MV Lyr). All are NL systems. MV Lyr is a VY Scl NL that went down to its low state during the Gaia observation time. YZ Ret erupted as a classical nova after the time period covered by DR3, leading to the Gaia Science Alert Gaia 20 elz. The HRD variability of these CVs distinguishes them from sdBs. Indeed, we find that the variables classified as sdB by Gaia and located in the upper-hook area all have horizontal variability in the HRD (see Fig. B.3 for an example), similarly to the sdBs in the main clump and unlike the CVs shown in Fig. 5.
 |
Fig. 5. Variation in the HRD of the intrinsically brightest Gaia DR3 CV of Fig. 1 located in the upper-hook area. |
3. Expectations from CV models
Here, we examine what the disc instability model has to say about the location of CVs in the Gaia HRD. The location of a given CV in the HRD is set by combining the light from its stellar components, the accretion disc, and its bright spot. The companion fills its Roche lobe, and so its mass M2 and radius R2 are essentially set by the system orbital period Porb once the white dwarf mass M1 is fixed (Knigge et al. 2011). However, departures from the main sequence are expected, especially at longer Porb where the companion must be evolved to fill its Roche lobe. In the following, we set M1 = 0.75 M⊙ as in Knigge et al. (2011). We investigated CVs with an Porb of between 80 min and 7 h, resulting in companions with masses ranging from ≈0.07 M⊙ (period minimum) to ≈0.75 M⊙ (Porb = 7 h). We refer to Appendix A for details on the assumptions made to compute the accretion disc, bright spot, star, and white dwarf contributions to the total emission from the system. We do not consider the impact of interstellar extinction on the model magnitudes because we compare to sources selected for A0 < 0.1 mag (Sect. 2).
The accretion parameters can be set once the stellar parameters are known. The contribution of the bright spot, where the material falling from the L1 point shocks the material in the outer disc, depends on the assumed mass transfer rate from the companion Ṁt. The accretion disc contribution, modelled as a multi-colour blackbody, depends on the radial distribution of temperature. We start with expectations from steady disc before considering more complex assumptions.
3.1. Steady disc
For a steady disc, the mass-accretion rate Ṁ is constant throughout the disc and is equal to the mass-transfer (or mass-loss) rate Ṁt from the companion to the accretion disc through the L1 point. The radial distribution of the effective temperature Teff as a function of disc radius R is given by (Shakura & Sunyaev 1973)
where Rin is the radius of the inner edge of the disc. We start by assuming that the accretion disc extends all the way to the white dwarf, and therefore setting Rin equal to the radius of the white dwarf R1. The outer disc radius Rdisc is a function of the mass ratio q = M2/M1 and the orbital separation a. We set Rdisc from the average of the tabulated values of Rdisc/a in Lubow & Shu (1975) and Paczyński (1977).
Figure 6 shows where the systems are located in the HRD with these assumptions. The lines show sequences obtained by varying the disc mass-accretion rate Ṁ from 1012 to 1018 g s−1 for a given Porb. We plot 18 sequences, corresponding to Porb varying from 80 min to 7 h in steps of 20 min. The thin continuous grey lines trace only the accretion disc contribution in the HRD, whereas the dashed lines also include the stellar contributions and those from the bright spot. As expected, the disc is bluer and more luminous as Ṁ increases (Eq. (2)). Discs are also more luminous for long Porb as they grow larger. However, at low Ṁ, the emission is a sum of Rayleigh-Jeans contributions and all tracks converge in the HRD.
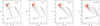 |
Fig. 6. Sequences of colour–magnitude positions assuming a steady accretion disc and, for each panel, a given value of the white dwarf dipole moment (μ30 = μ/1030 G cm3). Each sequence is obtained by varying Ṁ up to 1018 g s−1 for a given Porb. The orbital period increases from the bottom left sequence (Porb = 80 min) to the top right sequence (Porb = 7 h). The thin grey lines trace only the contribution of the disc. The dashed lines add light from the companion star, the white dwarf, and the bright spot. The stars indicate the location of the combined light from the companion and white dwarf for each Porb sequence. The square indicates the position of the most luminous bright spot emission. When μ30 ≠ 0, the inner disc is truncated at the magnetospheric radius Rm. The thick red and blue lines overplotted on the dashed lines highlight the location of hot and cold stable steady discs, respectively. The green rectangles delimit the upper and lower hook regions defined in Fig. 2. |
Comparing the dashed lines with the thin grey lines shows that the contributions from the other sources of light in the system cannot be ignored when positioning systems in the HRD. The stars trace the location of the combined light from the white dwarf and companion star. The contribution from these sources of light was taken into account following the assumptions set out in Appendix A. At low Porb, light from the donor star makes a negligible contribution and the star symbols join the white dwarf sequence. Inversely, the stars join the stellar main sequence in the HRD at high Porb as the white dwarf contribution becomes negligible. At low Ṁ, the contribution from the accretion disc becomes negligible, meaning that the dashed lines connect to the star symbols. At high Ṁ, the accretion disc dominates, but the companion star significantly reddens the colour at long orbital periods. Another source of light is the bright spot emission, which varies with Ṁ and Porb (see Appendix A for details). Its maximum value, shown as a square, is reached for Porb = 80 mn and Ṁ = 1018 g s−1. It has little influence on the HRD sequences plotted here, except at the shortest orbital periods where it slightly reddens the colour at maximum Ṁ compared to disc-only emission.
The vertical thermal equilibrium of a disc annulus with a temperature of ≈6500 K becomes unstable due to the sharp change in opacity associated with hydrogen ionisation. The instability leads to an outburst phase with a high accretion rate followed by quiescence, during which the accretion rate through the disc is low (Lasota 2001). In order to be hot and stable, with hydrogen ionised everywhere, the mass-accretion rate through the disc must be
using the criterion for discs of solar composition derived in Lasota et al. (2008). Similarly, the disc is cold and stable, with hydrogen recombined everywhere, if the mass-accretion rate is below
The thick red lines in Fig. 6 highlight the portion of the dashed lines where the criteria for a hot and stable disc are met. Hot, steady discs (NLs) occupy only a small region of the HRD. Most of the sequences in the HRD are actually unstable and would lead to outburst cycles (dwarf novae). Cold and stable discs are also possible at very low Ṁ, where the contribution of the disc is negligible. These are indistinguishable from the star symbols in this figure.
3.2. Truncated discs
White dwarfs can have a magnetic field that is strong enough to truncate the inner disc (intermediate polars). Figure 6 also shows how the colour–magnitude sequences change when the inner disc is truncated at the magnetospheric radius of
where  is the dipole moment and B is the magnetic field at the white dwarf surface. The magnetospheric radius can also be a good proxy for the radius at which an α disc transitions to magnetic wind-dominated accretion, when the torque exerted by a large-scale magnetic field takes over the transport of angular momentum (Scepi et al. 2019).
is the dipole moment and B is the magnetic field at the white dwarf surface. The magnetospheric radius can also be a good proxy for the radius at which an α disc transitions to magnetic wind-dominated accretion, when the torque exerted by a large-scale magnetic field takes over the transport of angular momentum (Scepi et al. 2019).
The tracks do not all join at low Ṁ when a truncated disc is considered (thin grey lines in Fig. 6). This is because Rin = Rm is now also changing. Increasing μ truncates the inner disc increasingly further out. Stable cold discs are now possible at a higher Ṁ (Eq. (4)). They appear as thick blue lines at high μ in Fig. 6. Additionally, the thick red lines materialising where a hot stable disc is possible cover a larger fraction of the HRD when μ is large: the truncation lowers the overall magnitude but also significantly reddens the colour when the high temperature inner region is removed. The disc can become entirely truncated for large μ and accretion occurs along magnetic field lines (polar CVs).
3.3. Erupting discs
Figure 7 shows examples of colour–magnitude tracks followed by CVs with unstable discs (dwarf novae). Heating and cooling fronts propagate through the disc when it is unstable, cycling the disc from a hot, high-accretion outburst state to a cold, low-accretion quiescent state and back again (see the review by Lasota 2001). The outburst cycles depend on M1, Ṁ, and on the α parameter for turbulent angular momentum transport Shakura & Sunyaev (1973). The value of α must become higher in the hot state (αh) than in the cold state (αc) to reproduce CV outbursts. The outburst cycles also depend on the variations of the inner and outer disc radii during the cycle. The disc is expected to grow during outburst, as increased accretion requires increased angular momentum transported outwards. The radial distribution of the temperature varies strongly during the cycle. It is close to a steady disc at the peak of the outburst and flattish during quiescence. The time evolution of these radial distributions was computed using the disc instability code of Hameury et al. (1998), assuming solar composition. The evolution of the system is then tracked in the HRD using the resulting G and GBP − GRP light curves.
 |
Fig. 7. Colour–magnitude tracks traced in the HDR by representative CVs with unstable accretion discs. Two sets of tracks are plotted, corresponding to Porb = 88 min (bottom set, pinkish colours) and Porb = 6 h (top set, bluish colours). Three tracks are plotted in each set, corresponding to three different mass transfer rates Ṁt. The dots on each track regularly sample the outburst cycle over time. The light curves are shown in Fig. B.1. The green rectangles delimit the upper and lower hook regions defined in Fig. 2. |
We chose two sets of DN binary parameters as representative of the typical light curves produced by the disc instability model. One below the period gap with Porb = 88 min, M1 = 0.6 M⊙, M2 ≈ 0.05 M⊙, αc = 0.04, and αh = 0.2. The other above the period gap with Porb = 6 h, M1 = 1.0 M⊙, M2 ≈ 0.6 M⊙, αc = 0.02, and αh = 0.1. In both cases we assumed that the white dwarf has a dipole moment of μ = 2 × 1030 g cm3, which truncates the inner disc in quiescence. For the short Porb system we computed light curves for Ṁt = 2.5, 10, and 100 × 1015 g s−1. For the long Porb system, we computed light curves for Ṁt = 1.5, 15, and 150 × 1015 g s−1. These values of Ṁt roughly sample the unstable range between a cold stable disc and a hot stable disc. The light curves are shown in Fig. B.1. The parameters were chosen to be close to those used by Hameury et al. (2020) to track the evolution of SS Cyg and VW Hyi in B − V and V using the same DIM code. VW Hyi is identified as a CV by Gaia (but is not in our sample). It stays around GBP − GRP ≈ 0.5 and MG ≈ 10, which is consistent with a quiescent state. SS Cyg is not identified as a variable by Gaia and so we do not have access to its epoch photometry.
The tracks in Fig. 7 take into account all sources of light. Each track forms a hysteresis pattern along which the system evolves anticlockwise, as discussed in Hameury et al. (2020). The location of the outburst peak is in the region of steady discs, as expected given the high Ṁ and Teff radial distribution, which is close to the Teff radial distribution of a steady disc at the outburst peak. The location in quiescence is close to the star symbol representing the combined light from the stellar components, as expected from the reduced contribution of the disc. The decline from the outburst is bluer than in outburst, again as expected given the fact that the disc cools systematically by propagating inwards from the outside, whereas outbursts mostly start inside and propagate outwards.
Each track has 100 dots that uniformly sample the cycle light curve in time. These dots provide a measure of the probability of finding the CV along its HRD track. Low-Ṁt systems spend most of their time in quiescence, and so the dots concentrate on the quiescent portion of the track. High-Ṁt systems close to the stability line are in outburst for a large fraction of their eruption cycle, and so the dots are more spread out along the track in the HRD. Figure B.2 shows the tracks followed by two DNe captured by Gaia DR3, one above and one below the period gap. Their overall behaviour matches well with the expectations from the model (Fig. 7).
4. Discussion
4.1. The hook
We find that the Gaia HRD for stars with low extinction shows an intriguing feature (the “hook”) at MG ∼ 4 and GBP − GRP ∼ 0.2 going from the main sequence to the sdB clump direction (upper hook) and continuing parallel to the main sequence down to MG ≈ 6 (lower hook). We argue that the hook is mostly composed of CVs, with some contamination from sdBs on the upper hook (Fig. 1). Comparison to the Ritter & Kolb (2003) catalogue reveals that these are nova-like (NL) CVs. This is also supported by the location of NL CVs in Fig. 2 of Abril et al. (2020) and in Fig. 3 of Abrahams et al. (2022). The spread in the location of NL CVs is somewhat larger in their HRD than with our selection. This (mostly redward) spread is very likely due to them using different, looser criteria on distance uncertainty, photometric quality, and/or extinction. The yellow stars in the middle right panel of Fig. 1 illustrate the effect of using wider selection criteria.
Nova-like CVs are accreting at a relatively high rate, and so their disc is hot enough for hydrogen to be fully ionised and is therefore stable against the thermal-viscous instability that triggers dwarf nova outbursts. The stability of a stationary disc depends on its size – because the temperature decreases with radius – and on the mass-accretion rate through the disc, as T4 ∝ Ṁ. We find that the stability region is relatively limited in the HRD when the disc size and binary parameters are constrained by the observed distribution of CVs. This stability region overlays well with the hook (Fig. 6); it also appears rather stable against assumptions as to the companion magnitude and colour (compare Figs. 6 to A.1).
The upper hook roughly corresponds to the stable region predicted by the DIM. It is limited in MG because it is rapidly bounded at low luminosity by the disc instability and at high luminosity by the mass-transfer rate from the companion, which becomes unrealistically large (Ṁ > 1018 g s−1). In the colour direction, there is some uncertainty as to how far redward the hook extends because the CVs then have increasingly long Porb, with the companion having an increasingly important contribution to the total light of the system. However, we did not take into account the fact that the companion may become evolved in CVs with Porb ≥ 6 h, which introduces an uncertainty. Blueward, the CVs have shorter orbital periods, evolutionary models predict that the secular mass-transfer rate from their companion drops, and the stability region turns to fainter magnitudes in the HRD diagram. In other words, the lack of CVs left of 4 < MG < 6 and −0.5 < GBP − GRP < 0 implies Ṁ < 1017 g s−1, which is expected for short Porb systems.
The lower hook, which extends parallel to the main sequence, is more difficult to explain. We did not take into account the effects of inclination and limb darkening on the disc contribution. These will make CVs appear fainter and redder: such a systematic trend in the HRD is detectable using CVs (see Howell & Mason 2018). Indeed, all novae-like CVs on the lower hook with MG > 5.3 in Fig. 1 have cos i < 0.5. Inclination effects may therefore partly explain some of the extension at the faintest magnitudes. Another way to extend the stability to fainter systems is if the inner disc is truncated, in the sense that there is no contribution from the accretion flow inward of a certain truncation radius. This truncation radius can be the result of disruption by the white dwarf magnetic field or the result of the disc switching to another type of flow, for instance magnetic wind accretion (Scepi et al. 2019). These effects are all the more important when the mass-accretion rate is low, which is what is expected for low Porb systems. Figure 6 shows that this extends the stability region along the lower hook, with the bluest systems having the shortest orbital periods. Intermediate polars, which have discs truncated by the white dwarf magnetic field, do populate the HRD to fainter magnitudes than the NL CVs in the HRD of Abril et al. (2020) and Abrahams et al. (2022).
These results may be used to identify outliers and intriguing CVs based on their location in the HRD. For example, the NL CV HRD plots in Abril et al. (2020) and Abrahams et al. (2022) show outliers that are very far from the stability region. These outliers may be misclassified; they may be caused by contamination due to unresolved nearby stars; they may harbour odd companions; and they may represent new subclasses. For instance, the NL with MG > 10 plotted in the middle right panel of Fig. 1 could be examples of cold and stable systems. The DIM predicts such systems can exist for low mass-accretion rates if the disc is significantly truncated. The right hand side panel of Fig. 6 shows that such systems must be located in a thin strip (blue lines) close to and connecting to the white dwarf sequence. In fact, all the faint (MG > 8) systems identified as NL CVs in the Ritter & Kolb (2003) catalogue (see the middle right panel, Fig. 1) are also subtyped as polars or intermediate polars, indicating that their disc is truncated.
4.2. Variability in the HRD
Individual CVs will move in the HRD as they fluctuate or undergo outbursts. For accretion discs that remain globally stable, variations in the mass-accretion rate through the disc move the system along well-defined tracks (dashed lines in Fig. 6) on a timescale set by the viscous timescale, of namely ∼0.5 to 1 day. The observed tracks in the HRD of the brightest NL are entirely consistent with this behaviour (Fig. 5). This offers a way to distinguish CVs from sdBs, whose variability is mostly horizontal (in colour) on the HRD. Gaia DR3 only gives access to the light curves for sources classified in Gaia variability classes; that is, we only have access to epoch photometry for the sources identified as CVs, sdBs, and short-timescale variables (the three classes present on the hook). Looking at the 11 stars with short-timescale variations on the hook (Table B.1), only 1 has sdB-like variability (i.e. small MG variability and large GBP − GRP variability). The other 10 have CV-like variability, meaning correlated MG and GBP − GRP variability (Fig. B.3). Of these 10 sources, 5 are already identified as CVs in Simbad (HQ And, 2MASS J09253483+4349179, V1084 Her, V393 Hya, EC 21263–4452) and 5 are currently labelled as hot subdwarf candidates in Simbad. This method can be used to classify other systems as candidate NL CVs once their epoch photometry becomes available in DR4.
Dwarf nova outbursts occur when the disc becomes unstable to the thermal-viscous instability. The CV then traces a complex track in the HRD as the disc temperature evolves as a function of radius and time. To zeroth order, the system at outburst peak is located close to the stability region of the HRD because the disc then has a high Ṁ and a temperature distribution close to stationary. In quiescence, the disc is faint and the system lies on the HRD line formed by adding the contributions from the white dwarf and its stellar companion. The heat map scatter plot of variability clearly shows two corresponding clusters, one associated with the hook in the NL region and one at fainter luminosities (right panel of Fig. 1).
Interpreting these clusters requires knowledge of the probability of catching each CV at a particular location and general knowledge of the CV population. The amount of time the system spends at each location strongly depends on the outburst duty cycle, with the duty cycle increasing as the mass-transfer rate from the companion decreases (Fig. 7). Typically, DNe below the gap, such as WZ Sge systems, have a low Ṁt and a long duty cycle such that a random observation is likely to place them towards the faint end of the HRD. Inversely, DNe above the period gap, such as U Gem systems, are likely to be brighter and located in the upper half of the HRD. Figure 7 also indicates that systems below the period gap can move through a larger region of the HRD than systems above the period gap. This suggests that the brighter cluster in Fig. 1 (right panel) is mostly associated with CVs above the period gap, and that the fainter cluster is mostly associated with systems below the period gap, which is indeed what is observed; see for example Fig. 1 of Abrahams et al. (2022). Finally, we note that DNe run through their outburst loops counterclockwise in Fig. 7. This should be the case for most systems as the temperature always drops from the outside in during decline from outburst, and generally rises from the inside out (outside-in rises to outburst are also possible for high-Ṁ systems, Lasota 2001).
5. Conclusion
We attribute an intriguing feature in the Gaia HRD for low-extinction systems – which we call the “hook” – to CVs. This feature arises as a consequence of the disc instability model: the hook corresponds to the region where stable systems are located in the HRD. Unstable systems, giving rise to DN outbursts, trace loops counterclockwise in the HRD. The general behaviour is consistent with the location of the various CV subtypes in the HRD. These results can be used as a basis to pinpoint interesting outliers in the HRD, either due to their location or their tracks. These outliers may signal new subtypes, such as cold, stable CVs with truncated discs, or may challenge the disc instability model.
ruwe is the astrometric renormalised unit weight error which is ∼1 for astrometrically well-behaved sources (Lindegren et al. 2021). The criteria ruwe > 1.4 is typically used to select problematic astrometric solutions such as astrometric binaries (Gaia Collaboration 2023b).
The total flux measured in BP and RP should be close to the G-band flux so that C = (FBP + FRP)/FG is close to one. C* takes into account the colour dependency of C and is expected to be close to zero, with a scatter σC* that depends on the G magnitude and with large values expected in case of contamination of the BP or RP spectra by other nearby sources (Riello et al. 2021).
We also tested for differences in the kinematics of the NLs and dwarf novae plotted in Fig. 1 using either the Ritter & Kolb (2003) classification or the Gaia CV classification with a rough separation at MG = 7, finding that there are none.
Acknowledgments
The authors acknowledge support from the Centre National d’Études Spatiales (CNES). This research has made use of the Spanish Virtual Observatory (https://svo.cab.inta-csic.es) project funded by MCIN/AEI/10.13039/501100011033/ through grant PID2020-112949GB-I00. This work has made use of data from the European Space Agency (ESA) space mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC). Funding for the DPAC is provided by national institutions, in particular the institutions participating in the Gaia MultiLateral Agreement. This research has made use of the Simbad database, operated at CDS, Strasbourg, France.
References
- Abrahams, E. S., Bloom, J. S., Szkody, P., Rix, H.-W., & Mowlavi, N. 2022, ApJ, 938, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Abril, J., Schmidtobreick, L., Ederoclite, A., & López-Sanjuan, C. 2020, MNRAS, 492, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barber, M. G., & Mann, A. W. 2023, ApJ, 953, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Canbay, R., Bilir, S., Özdönmez, A., & Ak, T. 2023, AJ, 165, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Copperwheat, C. M., Marsh, T. R., Dhillon, V. S., et al. 2010, MNRAS, 402, 1824 [Google Scholar]
- Culpan, R., Geier, S., Reindl, N., et al. 2022, A&A, 662, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubus, G., Otulakowska-Hypka, M., & Lasota, J.-P. 2018, A&A, 617, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [Google Scholar]
- Eyer, L., Audard, M., Holl, B., et al. 2023, A&A, 674, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Babusiaux, C., et al.) 2018, A&A, 616, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Eyer, L., et al.) 2019, A&A, 623, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023a, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Arenou, F., et al.) 2023b, A&A, 674, A34 [CrossRef] [EDP Sciences] [Google Scholar]
- Green, E. M., Fontaine, G., Hyde, E. A., For, B. Q., & Chayer, P. 2008, in Hot Subdwarf Stars and Related Objects, eds. U. Heber, C. S. Jeffery, & R. Napiwotzki, ASP Conf. Ser., 392, 75 [NASA ADS] [Google Scholar]
- Hameury, J. M. 2020, Adv. Space Res., 66, 1004 [Google Scholar]
- Hameury, J.-M., Menou, K., Dubus, G., Lasota, J.-P., & Hure, J.-M. 1998, MNRAS, 298, 1048 [Google Scholar]
- Hameury, J. M., Knigge, C., Lasota, J. P., Hambsch, F. J., & James, R. 2020, A&A, 636, A1 [Google Scholar]
- Hellier, C. 2001, Cataclysmic Variable Stars (London: Springer-Verlarg) [Google Scholar]
- Holberg, J. B., & Bergeron, P. 2006, AJ, 132, 1221 [Google Scholar]
- Howell, S. B., & Mason, E. 2018, AJ, 156, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Igoshev, A. P., Perets, H. B., & Michaely, E. 2020, MNRAS, 494, 1448 [NASA ADS] [CrossRef] [Google Scholar]
- Inight, K., Gänsicke, B. T., Breedt, E., et al. 2021, MNRAS, 504, 2420 [NASA ADS] [CrossRef] [Google Scholar]
- Isogai, K., Kato, T., Imada, A., et al. 2019, PASJ, 71, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Jackim, R., Szkody, P., Hazelton, B., & Benson, N. C. 2020, Res. Notes Am. Astron. Soc., 4, 219 [Google Scholar]
- Knigge, C., Baraffe, I., & Patterson, J. 2011, ApJS, 194, 28 [Google Scholar]
- Lallement, R., Vergely, J. L., Babusiaux, C., & Cox, N. L. J. 2022, A&A, 661, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lasota, J.-P. 2001, New Astron. Rev., 45, 449 [Google Scholar]
- Lasota, J.-P., Dubus, G., & Kruk, K. 2008, A&A, 486, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Lubow, S. H., & Shu, F. H. 1975, ApJ, 198, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J., Holgado, G., Pantaleoni González, M., & Caballero, J. A. 2023, A&A, 677, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nauenberg, M. 1972, ApJ, 175, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1977, ApJ, 216, 822 [CrossRef] [Google Scholar]
- Pala, A. F., Gänsicke, B. T., Breedt, E., et al. 2020, MNRAS, 494, 3799 [Google Scholar]
- Pala, A. F., Gänsicke, B. T., Belloni, D., et al. 2022, MNRAS, 510, 6110 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsay, G., Green, M. J., Marsh, T. R., et al. 2018, A&A, 620, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riello, M., De Angeli, F., Evans, D. W., et al. 2021, A&A, 649, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rimoldini, L., Holl, B., Gavras, P., et al. 2023, A&A, 674, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ritter, H., & Kolb, U. 2003, A&A, 404, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodrigo, C., & Solano, E. 2020, XIV.0 Scientific Meeting (virtual) of the Spanish Astronomical Society, 182 [Google Scholar]
- Rodrigo, C., Solano, E., & Bayo, A. 2012, IVOA Working Draft 15 October 2012 [Google Scholar]
- Saffer, R. A., Green, E. M., & Bowers, T. 2001, in 12th European Workshop on White Dwarfs, eds. J. L. Provencal, H. L. Shipman, J. MacDonald, & S. Goodchild, ASP Conf. Ser., 226, 408 [Google Scholar]
- Scepi, N., Dubus, G., & Lesur, G. 2019, A&A, 626, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Warner, B. 2003, Cataclysmic Variable Stars (Cambridge: Cambridge University Press) [Google Scholar]
- Webb, N. A. 2022, in Handbook of X-ray and Gamma-ray Astrophysics, eds. C. Bambi, & A. Santangelo (Singapore: Springer Nature) [Google Scholar]
Appendix A: Gaia magnitudes from model CV systems
This Appendix describes the assumptions used to compute the G magnitude and GBP − GRP colour of the model CV systems presented in this work. We take into account light from the accretion disc, the companion, the white dwarf, and from the bright spot where matter from the L1 point intersects the accretion disc. We do not take into account light from the boundary layer where material from the accretion disc settles onto the white dwarf. We expect the boundary layer to emit mostly in far-ultraviolet and X-rays, making a negligible contribution to the Gaia magnitudes. We also neglect the possible impact of irradiation of the accretion disc or the stellar companion by the FUV/X-ray light from the white dwarf and its boundary layer, which would depend on further assumptions as to the irradiation geometry, flux, and albedo.
A.1. The accretion disc
The accretion disc magnitudes are computed as described in Section 2.1 of Dubus et al. (2018). The disc has a radial temperature profile, and each ring is assumed to radiate like a blackbody. This disc blackbody emission is converted to Gaia G and GBP − GRP using the filter response from the third Gaia data release as implemented in the SVO Filter Profile Service (Rodrigo et al. 2012; Rodrigo & Solano 2020). This also gives the zeropoints of the three bandpasses : ZG = 3228.75 Jy, ZGBP = 3552.5 Jy, and ZGRP = 2554.95 Jy. The magnitudes also depend on the disc inclination i to the observer. We marginalise over this parameter by assuming that the normal vector of the disc is randomly distributed and averaging over i.
A.2. The stellar components
Given an orbital period Porb and white dwarf mass M1, the companion star mass M2 and radius R2 are derived by assuming it fills its Roche lobe. The Roche lobe radius as a function of q = M2/M1 is approximated by the formula in Eggleton (1983). The mass, radius, and luminosity L2 of the companion are assumed to be related by the usual approximate main sequence relationships:  ,
,  (in Solar units) for M2 < 1 M⊙ and
(in Solar units) for M2 < 1 M⊙ and  for M2 > 1 M⊙. We set the white dwarf effective temperature T1 = 12 500 K, corresponding to GBP − GRP ≈ 0. Its radius R1 is derived from the Nauenberg (1972) mass–radius relationship for white dwarfs. The Gaia magnitudes for both stellar components are then computed from R and L (or T) by assuming blackbody emission.
for M2 > 1 M⊙. We set the white dwarf effective temperature T1 = 12 500 K, corresponding to GBP − GRP ≈ 0. Its radius R1 is derived from the Nauenberg (1972) mass–radius relationship for white dwarfs. The Gaia magnitudes for both stellar components are then computed from R and L (or T) by assuming blackbody emission.
This is rather simplistic, but works reasonably well. Indeed, we show in Fig. A.1 the results obtained using the donor and white dwarf sequences derived specifically for CVs by Knigge et al. (2011). These are valid from the period minimum at 80 min up to Porb = 5.6 h. In this case, we derived the Gaia magnitudes of the companion using the effective temperature GBP − GRP colour relations and luminosity MG relations of Baraffe et al. (2015)6 for the main sequence stars and of Holberg & Bergeron (2006)7 for white dwarfs. Comparing Fig. A.1 with Fig. 6 shows that the same conclusions apply as to the location of the stable zone (red lines in the HRD).
 |
Fig. A.1. Same as Fig. 6, using the companion star and white dwarf properties tabulated in Knigge et al. (2011). Here, Porb sequences are plotted up to 5.6 h (instead of 7 h) for consistency with the tables. |
Here, the accretion-disc magnitudes do not converge to a single line at low Ṁ, because R1 varies with Porb along the sequence. The jump in magnitude around MG ≈ 10 is related to the period gap between Porb = 2 h and 3 h.
A.3. The bright spot
The luminosity of the bright spot is given by the rate at which gravitational energy from the infalling L1 material must be dissipated:
where Rdisc is the disc outer radius and RL1 is the distance to the white dwarf of the L1 Lagrange point. Ṁt is the mass-transfer rate from the companion through the L1 point. We set the effective temperature of the bright spot to TBS = 13 000 K (e.g. Copperwheat et al. 2010). The Gaia magnitudes are calculated from LBS and TBS assuming blackbody emission.
Appendix B: Additional figures
This Appendix contains information to complement the main text. Figure B.1 shows the light curves for the CV tracks plotted on the HRD in Fig. 7. Figure B.2 shows examples of the tracks left on the HRD by two dwarf novae, one above the period gap and one below. Table B.1 and Fig. B.3 present the 11 variables in the upper-hook area that have epoch photometry available within Gaia DR3 thanks to their short-timescale variability detection. One (6627639424019259648) has sdB-like variability while the others have CV-like HRD variability with a clear correlation between MG and GBP − GRP for the not already known CV. Only the variability profile of Gaia DR3 6684803617665459200 is unclear.
 |
Fig. B.1. Light curves for the dwarf novae colour–magnitude tracks plotted in Fig. 7. The recurrence timescale of the outburst cycle sets the time span of each panel. Left panels: Light curves for the system with Porb = 88 min. Right panels: Light curves for the system with Porb = 6 hr. The dots regularly sample in time the outburst cycle. |
 |
Fig. B.2. Two examples of dwarf novae captured by Gaia DR3. The green points indicate the positions in the HRD of each observation while the blue square indicates the mean photometry. Top: VZ Aqr = Gaia DR3 2684755714241156736 with orbital period of 3.8h. Bottom: QW Ser = Gaia DR3 1163811724898541440 with orbital period of 1.79h. |
 |
Fig. B.3. Variation in the HRD of upper hook stars with epoch photometry thanks to their short-timescale variability detection in Gaia DR3. |
Stars in the upper hook with epoch photometry thanks to their short time scale variability detection in Gaia DR3.
All Tables
Stars in the upper hook with epoch photometry thanks to their short time scale variability detection in Gaia DR3.
All Figures
 |
Fig. 1. Locating CVs in the Gaia low-extinction HRD diagram. Left: Gaia DR3 low-extinction HRD (A0 < 0.1 mag, parallax uncertainty smaller than 10%, ruwe < 1.4, |
| In the text | |
 |
Fig. 2. HRD colour-coded according to the mean VarG of all stars with A0 < 0.1, parallax uncertainty smaller than 10%, ruwe < 1.4, and C* < 10 × σC*. The colour scale saturates for VarG values lower than 0 and higher than 1.5. Boxes correspond to areas discussed in the text: the sdB (blue), the upper hook (red), and the lower hook (orange). |
| In the text | |
 |
Fig. 3. HRD colour-coded according to the ruwe of all stars with A0 < 0.1, parallax uncertainty smaller than 10%, C* < 10 × σC*, ipd_frac_multi_peak < 3. The colour scale saturates for values lower than 0.6 and higher than 1.4. Green squares correspond to orbital solutions provided by Gaia DR3. |
| In the text | |
 |
Fig. 4. Colour–colour diagram of stars in the areas indicated in Fig. 2, selected with A0 < 0.1, parallax uncertainty smaller than 10%, ruwe < 1.4, C* < 10 × σC*, and a 2MASS Qflag “AAA”. Blue triangles, red squares, and orange circles correspond to stars in the SDB area, the upper-hook area, and the low-hook area, respectively. |
| In the text | |
 |
Fig. 5. Variation in the HRD of the intrinsically brightest Gaia DR3 CV of Fig. 1 located in the upper-hook area. |
| In the text | |
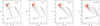 |
Fig. 6. Sequences of colour–magnitude positions assuming a steady accretion disc and, for each panel, a given value of the white dwarf dipole moment (μ30 = μ/1030 G cm3). Each sequence is obtained by varying Ṁ up to 1018 g s−1 for a given Porb. The orbital period increases from the bottom left sequence (Porb = 80 min) to the top right sequence (Porb = 7 h). The thin grey lines trace only the contribution of the disc. The dashed lines add light from the companion star, the white dwarf, and the bright spot. The stars indicate the location of the combined light from the companion and white dwarf for each Porb sequence. The square indicates the position of the most luminous bright spot emission. When μ30 ≠ 0, the inner disc is truncated at the magnetospheric radius Rm. The thick red and blue lines overplotted on the dashed lines highlight the location of hot and cold stable steady discs, respectively. The green rectangles delimit the upper and lower hook regions defined in Fig. 2. |
| In the text | |
 |
Fig. 7. Colour–magnitude tracks traced in the HDR by representative CVs with unstable accretion discs. Two sets of tracks are plotted, corresponding to Porb = 88 min (bottom set, pinkish colours) and Porb = 6 h (top set, bluish colours). Three tracks are plotted in each set, corresponding to three different mass transfer rates Ṁt. The dots on each track regularly sample the outburst cycle over time. The light curves are shown in Fig. B.1. The green rectangles delimit the upper and lower hook regions defined in Fig. 2. |
| In the text | |
 |
Fig. A.1. Same as Fig. 6, using the companion star and white dwarf properties tabulated in Knigge et al. (2011). Here, Porb sequences are plotted up to 5.6 h (instead of 7 h) for consistency with the tables. |
| In the text | |
 |
Fig. B.1. Light curves for the dwarf novae colour–magnitude tracks plotted in Fig. 7. The recurrence timescale of the outburst cycle sets the time span of each panel. Left panels: Light curves for the system with Porb = 88 min. Right panels: Light curves for the system with Porb = 6 hr. The dots regularly sample in time the outburst cycle. |
| In the text | |
 |
Fig. B.2. Two examples of dwarf novae captured by Gaia DR3. The green points indicate the positions in the HRD of each observation while the blue square indicates the mean photometry. Top: VZ Aqr = Gaia DR3 2684755714241156736 with orbital period of 3.8h. Bottom: QW Ser = Gaia DR3 1163811724898541440 with orbital period of 1.79h. |
| In the text | |
 |
Fig. B.3. Variation in the HRD of upper hook stars with epoch photometry thanks to their short-timescale variability detection in Gaia DR3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.






![$$ \begin{aligned} \sigma T_{\rm eff}^4 = \frac{3GM\dot{M}}{8\pi R^3}\left[1-\left(\frac{R}{R_{\rm in}}\right)^{1/2}\right], \end{aligned} $$](/articles/aa/full_html/2024/03/aa48510-23/aa48510-23-eq5.gif)



![$$ \begin{aligned} L_{\rm BS} = \frac{GM\dot{M}_{\rm t}}{2}\left[\frac{1}{R_{\rm disc}}-\frac{1}{R_{\rm L1}}\right], \end{aligned} $$](/articles/aa/full_html/2024/03/aa48510-23/aa48510-23-eq13.gif)